Vertical Gaps in Mathematics

Calculus straddles the border between secondary school and university, and versions of calculus at the two levels often differ. This has long been an issue in the US. ‘Calculus reform’, which began in the 1980s (Douglas Reference Douglas1986), was the result of students’ high failure rates in university calculus courses – whether or not those students had studied high school calculus.

In 2012, the Mathematical Association of America (an association of mostly professional mathematicians at the college level) and the National Council of Teachers of Mathematics (whose membership consists largely of pre-college mathematics teachers) issued a Joint Position Statement on Teaching Calculus that tacitly acknowledged the gap between many high school calculus courses and college-level instruction. It recommended ‘the re-envisioning of the role of calculus in secondary and postsecondary mathematics education’, suggesting that:

1. 1. Students who enroll in a calculus course in secondary school should have demonstrated mastery of algebra, geometry, trigonometry, and coordinate geometry;

2. 2. The calculus course offered in secondary school should have the substance of a mainstream college-level course;

3. 3. The college curriculum should acknowledge the ubiquity of calculus in secondary school, shape the college calculus curriculum so that it is appropriate for those who have experienced introductory calculus in high school, and offer alternatives to calculus. (Mathematical Association of America and National Council of Teachers of Mathematics 2012).

Documentation of the calculus ‘problem’ in the US can be found in Bressoud et al. (Reference Bressoud, Mesa and Rasmussen2015). But the US is hardly an outlier in this regard. The ‘calculus gap’ was a major theme of the working group on calculus at the 13th International Conference on Mathematics Education (see, for example, Bressoud et al. Reference Bressoud, Ghedamsi, Martinez-Luaces and Törner2016) and a recent conference on Calculus in upper secondary and beginning university mathematics in Norway (Monaghan et al. Reference Monaghan, Nardi and Dreyfus2019).

Calculus represents just the beginning of the ‘gap problem’; gaps in expectations widen as students progress through the mathematics curriculum. In K-12, learning mathematics is typically focused on mastering and applying procedures with little ‘distance’ between what the students have been prepared to do and what they are expected to do when assessed. In early college years, expectations for both greater distance and more autonomy in learning represent the first major gap students experience. But there is much more to come. As students advance the nature of the demands on them changes, with the emphasis on applying methods diminishing as the bulk of instruction turns to understanding and proving mathematical results.

Consequently, many students find themselves in a discipline they barely recognize. ‘Transition to proof’ courses are common and often unsuccessful. In simplest terms, students begin to experience the discipline in ways that professionals live the discipline – and it comes as a shock. This was not what they thought it was like to do mathematics!

I suspect this phenomenon is general. My wife became a French major because she loved the language and loved reading it. Little did she know that her PhD in French would involve analysing the literature – had she known, she said, she would have been an English major. Hugh Burkhardt (personal communication, Reference Burkhardt2019) noted that he once chaired a Joint Matriculation Board panel on History A-level.

The Issue of Horizontal as well as Vertical Gaps

The motivation for the ‘Mind the Gap’ conference was that there are significant jumps in expectations – ‘vertical gaps’ – in most if not all academic disciplines as students transition from secondary school to university. As a precursor to what follows, however, it is important to highlight ‘horizontal gaps’, the differences in instruction and perspective between academic disciplines.

The existence of academic or disciplinary ‘silos’ at the university or professional level is broadly acknowledged. According to the American Association of Colleges and Universities (2019, emphasis in original),

Jacobs (Reference Jacobs2014) notes that excessive compartmentalization at the university level keeps undergraduates from making connections that would enable them to have a more holistic and integrated undergraduate educational experience. This lack of horizontal coherence is clearly echoed at the pre-college level. In the US, students in English Language Arts learn different writing genres, e.g. the ‘five paragraph essay’ (see, for example, https://papersowl.com/blog/five-paragraph-essay-outline or https://essaypro.com/blog/5-paragraph-essay/). In mathematics they frequently learn bodies of content, applying learned techniques to exercises close to those they have practised on; ‘problem solving’ is honoured but seldom developed. In science courses they often learn content as reflections of disciplinary epistemology – e.g. the rhetoric is about science as ‘inquiry’, but physics is taught as applications of key principles in important content areas, etc. Like the other fields, history has its own norms – and standards for instruction.Footnote ²

Existing standards foster horizontal incoherence. Forty-one of the 50 states in the US have adopted ‘common core’ standards (Common Core State Standards Initiative 2019). The two subjects taken in almost every grade are English Language Arts (see http://www.corestandards.org/ELA-Literacy/) and Mathematics (see http://www.corestandards.org/Math/. (The ELA standards also contain ‘college and career readiness’ standards for reading and writing, reading standards for literacy in history/social studies, and for literacy in science and technical subjects.) Comparable territory is covered for science by the Next Generation Science Standards (2013), at https://www.nextgenscience.org/.

Of the 93 pages in the Common Core standards for Mathematics, three pages are devoted to descriptions of key mathematical practices (problem solving, reasoning, constructing and critiquing reasoned arguments, etc.), the list of which is then posted periodically as a leitmotif throughout the volume. The vast majority of the volume is devoted to descriptions of the content students are to learn– see, for example, Figure 1.

Figure 1. A sample high school mathematics standard from the Common Core State Standards for Mathematics (p. 69).

The Next Generation Science Standards take a radically different approach to instruction in science, with an emphasis on ‘the three dimensions of science learning’:

Figure 2 presents a sample high school science standard.

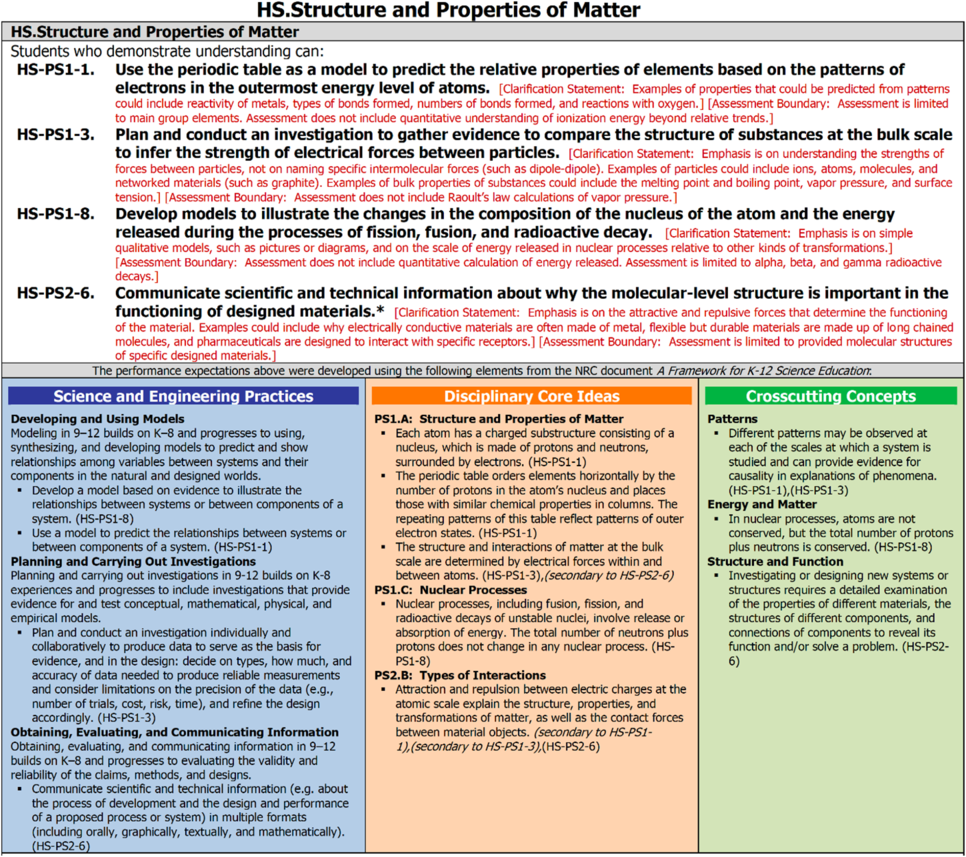
Figure 2. A sample high school science standard (Structure and properties of matter) from the Next Generation Science Standards.

The most closely relevant segment of the Common Core high school standards for English Language Arts, a part of the writing standards for grades 11 and 12, is given in Figure 3.

Figure 3. Sample high school writing standards from the Common Core State Standards for English Language Arts (p. 45).

Consider a typical student’s experience. Mathematics instruction and mathematics writing have their own norms, apart from the other fields. Science focuses on ‘inquiry’ and basic principles. And, although expository writing concerns the marshalling of evidence, writing classrooms in which students take on expository tasks grounded in disciplinary content and expository norms are rare. Instruction is experienced in silos.

This is a major challenge. In 2014, San Francisco Unified School District (SFUSD) had many largely independent instructional departments (mathematics, science, social studies, English language arts, etc.), each of which had its own form of professional development tied to disciplinary standards. SFUSD had more than 1600 pages of professional development manuals! Teachers were living their professional lives and preparing instruction in silos. With that level of fractionalization, it is impossible to conceptualize the coherence of the student’s experience as learner.

In sum, pre-college students typically have little opportunity or experience to view learning as a whole. The gaps they experience between disciplines in secondary school are every bit as challenging as the within-discipline gaps they experience when they enter the university. The challenge they face is twofold, with both horizontal and vertical gaps.

There is a way to address both kinds of gaps.

The Teaching for Robust Understanding (TRU) Framework

We begin with mathematics. The framing question for this discussion is:

This framing question is posed in terms of the learning environment rather than what the teacher does or what content is discussed. This is not to minimize the way the discipline is represented in classroom materials and discourse, or the role of the teacher. However, the most important factors shaping the growth of students’ understandings are the affordances provided by the learning environment for the student’s intellectual and personal development. The Teaching for Robust Understanding (TRU) framework, elaborated below, thus focuses on the environment and the student’s experience of it. In addition, this framing calls for identifying a small number of attributes that matter. Supporting pragmatic improvements requires a small number of foci of improvement. Providing a teacher or a professional learning community with a long list of important items is of little to no value – long lists get lost and are impossible to focus on.

The Teaching for Robust Understanding framework was derived as follows. An extended literature search identified as many aspects of powerful mathematics learning environments as could be found. The hundreds of classroom descriptors identified through the literature review were distilled into a set of five coherent categories, called ‘dimensions of powerful classrooms’. Concurrently, the research team reviewed dozens of videotapes of mathematics classrooms. The team sought consistencies between the emerging dimensions of the TRU Framework and the performance in the videotapes. A classroom scoring rubric was developed, and correlations between classroom performance on the rubric and student outcomes on measures of thinking and problem solving were found (Schoenfeld Reference Schoenfeld2013, Reference Schoenfeld2014, Reference Schoenfeld2017; Schoenfeld et al. Reference Schoenfeld and Floden2018).

A representation of the framework is given in Figure 4. A brief rationale for the importance of the five dimensions of TRU Math is as follows.

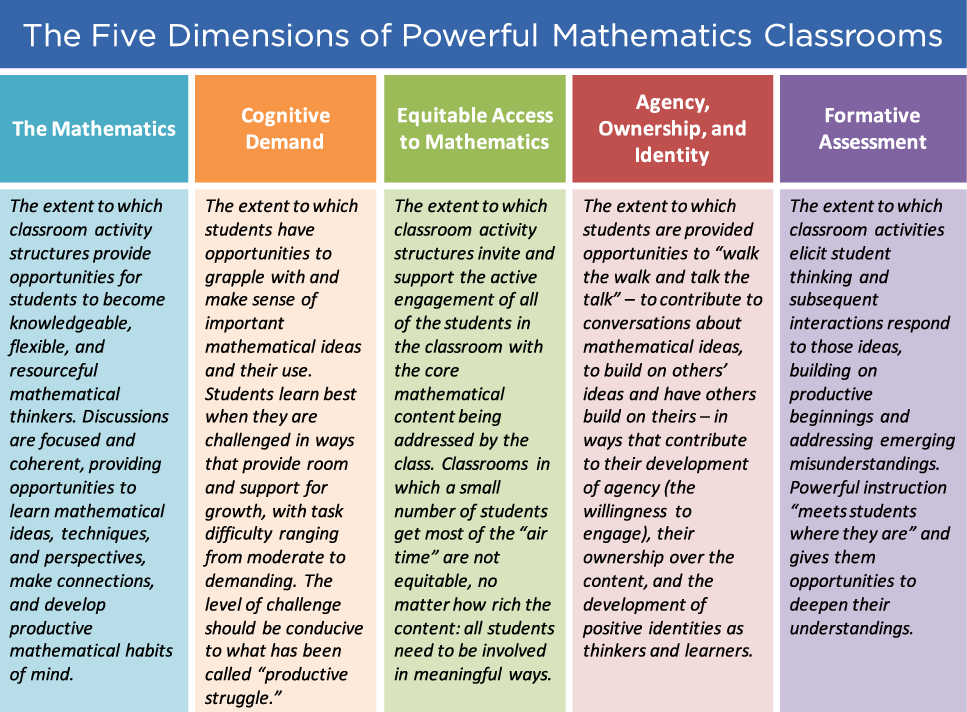
Figure 4. The five dimensions of powerful mathematics classrooms.

Dimension 1, the quality of the mathematics discussed, is clearly critical; what individual students learn is unlikely to be richer than what they experience in the classroom. But whether or not individual students’ understanding rises to that level depends on many other factors, which are captured in the remaining four dimensions.

Cognitive Demand is Dimension 2. Research dating back to Vygotsky’s Zone of Proximal Development (Chaiklin Reference Chaiklin, Kozulin, Ginzis, Ageyev and Miller2003; Vygotsky Reference Vygotsky, Cole, John-Steiner, Scribner and Souberman1978; Wertsch Reference Wertsch, Rogoff and Wertsch1984) indicates that students are more likely to understand and retain material if they are primarily engaged in sense making as opposed to memorizing – that is, if they are engaged in productive struggle, working as a meaningful level of cognitive demand (see, for example, Henningsen and Stein Reference Henningsen and Stein1997; Hess Reference Hess2006; Stein and Smith Reference Stein and Smith1998; Webb Reference Webb2002).

Dimension 3, equitable access, concerns the question of which students instruction is designed for – the most advanced or most promising students, ‘average’ students, or all students? In the TRU framework, it is axiomatic that all students should be fully engaged with the central content and practices of the domain and profit from it.

Dimension 4 is fundamentally about students’ mathematical identities. In the US, there has for decades been a 50% attrition rate from mathematics courses once mathematics becomes optional in the curriculum (National Research Council 1989). Moreover, mathematics is hated and feared by many. Students develop their sense of themselves vis-à-vis mathematics from their classroom experience with mathematics (Lampert Reference Lampert1990; Schoenfeld Reference Schoenfeld1985). Do they see themselves as sense makers, having a sense of agency? Do they see themselves as the passive recipients of mathematical knowledge, whose responsibility is to practice and learn the content demonstrated to them? Or, perhaps, do they see themselves as unfit for mathematics, not gifted while others are? The question is the nature of the affordances that classroom instruction provides to enable students to develop a sense of mathematical agency, the feeling that they can author mathematics and ‘own’ what they have produced, and develop positive mathematics identities (see Aguirre et al. Reference Aguirre, Mayfield-Ingram and Martin2013; Brown-Jeffy and Cooper Reference Brown-Jeffy and Cooper2011; Engle Reference Engle and Dai2011; Gay Reference Gay2018; Institute for Learning 2016; Martin Reference Martin2009).

Dimension 5 concerns formative assessment, the issue of how student thinking is made public so that it can be used to adjust instruction. Much of real learning is in-the-moment and contingent – a student reveals a misconception, a small group comes up with an interesting idea in discussion, etc. The challenge is to bring such thinking out in the open and leverage it for productive discussions; without a meaningful feedback loop the relevant adjustments of cognitive demand are impossible (Bennett et al. Reference Bennett, Andrade and Cizek2019; Black and Wiliam Reference Black and Wiliam1998; Burkhardt and Schoenfeld Reference Burkhardt, Schoenfeld, Bennett, Andrade and Cizek2019).

A few points should be emphasized. First, although there are only five dimensions to the framework, it represents a distillation of the literature on teaching for robust or powerful understanding. Thus, the five dimensions are comprehensive. Moreover, the evidence is that the better a learning environment does along the five dimensions, the more students emerge as knowledgeable and flexible thinkers and problem solvers. Second, the shift of attention from the teacher to the environment is fundamentally important. The key question is not ‘is the teacher doing particular things to support learning?’, it is, ‘are students experiencing instruction so that it is conducive to their growth as mathematical thinkers and learners?’ Third, the framework is not prescriptive; it respects teacher autonomy. There are many ways to be an excellent teacher. The question is, does the learning environment created by the teacher provide each student rich opportunities along the five dimensions of the framework? Crucially important, the framework serves to problematize instruction. Asking ‘how am I doing along each dimension; how can I improve?’ can lead to richer instruction without imposing a particular style or particular norms on teachers.

The TRU project team offers tools for professional development – see https://truframework.org/ for tools and papers. However, those tools are not intended to tell teachers what to do, but to support individual and collective reflection on teaching practices. Discussions of mathematical content focus on the ‘big ideas’ of mathematics and how to emphasize them, independent of grade level (Schoenfeld Reference Schoenfeld2019, Reference Schoenfeld2020); given that dimensions 2 through 5 of the TRU framework focus on the students’ classroom experiences, they are necessarily independent of grade level. Perhaps more important, TRU represents a student-centred way of thinking about instruction, and it provides a language and a framework for focusing on classroom interactions.

K-8 teachers in the US tend to teach one grade only – e.g. a teacher will identify as a ‘seventh grade teacher’. In professional development meetings some years ago, we found that seventh grade teachers were not fully conversant with the ways that their students had been prepared in sixth grade; nor did they know how the content they were teaching in seventh grade would be used by those teaching eighth grade. Gaps exist at every level – although they tend to be most extreme when students make the transitions from elementary to middle school, middle school to secondary school, and of course, secondary school to university.

There is, unfortunately, no research base on the impact of mathematics professional development on gaps at the pre-college level. In fact, there are scant data in general regarding the impact of mathematics teachers’ coaching and professional development (Baldinger Reference Baldinger2018). Thus there does not exist a comparative research base for what follows.

There is reason to believe that the TRU Framework is an effective mechanism for ameliorating gaps. TRU professional development meetings bring together teachers and others to discuss ways to enhance instruction, with the foci suggested in Figure 4. That TRU focuses on ‘big ideas’ is undoubtedly impactful. However, we suspect that the real impact of engagement with TRU is that it provides a common language and perspective for conceptualizing and discussing what matters in instruction. Chicago contains 660 schools and nearly 400,000 students. Two years into professional development with the TRU Framework, the director of mathematics professional development for the Chicago Public Schools noted,

When teachers have common instructional foci and a common language for discussing them, gaps diminish.

Hypothetically, the same can happen vis-à-vis the gap between secondary school and university. As a university faculty member, I can say with confidence that a focus on big ideas and student sense-making (key aspects of TRU) will prepare K-12 students more adequately for mathematics at the university level. The kinds of disciplinary agency and identity developed via TRU are necessary attributes for success at university. Students who enter universities having become more independent, autonomous, and agentive learners will have a much greater likelihood of success.

This is only half the story, for it places the burden of bridging the gap on the shoulders of the K-12 community. Consider the main dimensions of the TRU Framework: focusing on major disciplinary content and practices, supporting sense-making for all students, fostering disciplinary identities, and being responsive to student thinking. It stands to reason that if university mathematics instruction was organized with these goals in mind, students would do better in them – and the gap between K-12 and university could be shortened from both sides. Organizing pedagogical change at the university is, however, a major challenge: faculty are in general more autonomous with regard to instruction and there are fewer opportunities for pedagogical support. Nonetheless, over the past quarter century there has been a marked increase among university mathematicians both in research in mathematics education and in the pedagogy of mathematics at the university level. In Reference Dubinsky, Schoenfeld and Kaput1994, the Conference Board of the Mathematical Sciences published the first volume of Research in Collegiate Mathematics Education (Dubinsky et al. Reference Dubinsky, Schoenfeld and Kaput1994), the first compendium in the US of research articles about University level mathematics education. There were barely enough articles to sustain the publication of an additional volume once every three years. A small informal conference called RUME (Research on Undergraduate Mathematics Education), launched in the early 1990s, became a ‘Special Interest Group’ of the Mathematical Association of America (see http://sigmaa.maa.org/rume/Site/News.html). The group and its annual conferences have grown steadily in size. In 2015 the first issue of the International Journal of Research in Undergraduate Mathematics Education was published. IJRUME, as it is known (https://link.springer.com/journal/40753), publishes four or five issues a year. There is a growing community of university mathematicians and mathematics educators with an interest in the kinds of issues discussed in this paper. However, given the lack of incentives and mechanisms for sustained or collective attention to pedagogical issues, it will take significant efforts, over time, to make progress.

And what of subject areas other than mathematics? A case can be made that both the challenges and productive approaches to dealing with them are much the same as in mathematics. The ‘vertical’ challenges are well known. Moreover, as noted previously, there are horizontal gaps at every grade level. Students face challenges in understanding key intellectual practices in each discipline, and in developing the kinds of independence and agentive behaviour that would enable them to succeed more generally as learners.

This is where the TRU framework has the potential to bridge horizontal gaps, making the learner’s experience more coherent at all grade levels. A first bridge was built in the teacher preparation programmes at the University of California, Berkeley. At Berkeley, as around the US, mathematics and science instruction proceeded along parallel tracks: mathematics focused on ‘problem solving’, while science focused on ‘inquiry’. Although the first dimension of TRU Math focuses on mathematics, dimensions 2 through 5 focus on the student experience of instruction; these clearly apply to science instruction. We replaced the focus on mathematics in the first dimension with a focus on science, using contemporary science education documents such as the Next Generation Science Standards (NGSS 2013) to specify content and process goals for science instruction. These parallels enabled a deeper unification of teacher preparation in the mathematics and science branches of the programme: there were similar sheets for lesson observations in both disciplines, which were identical except for the first dimension, and joint conversations about lesson preparation that emphasized all five dimensions of the framework. Soon afterward the elementary teacher preparation programme at Berkeley joined in, saying that dimensions 2 through 5 of the framework echoed and facilitated the ‘whole child’ approach of the programme. Then English Language Arts joined in as well.

Concurrently, the San Francisco Unified School District, concerned about the incoherence of its instructional and professional development efforts, began to reconceptualize its overall theory of action. Core notions from the TRU framework – access; rich content; agency, authority and identity, and assessment – are at the centre of SFUSD’s theory of action for instructional practice and for curriculum and professional development, for all disciplines – see Figure 5.

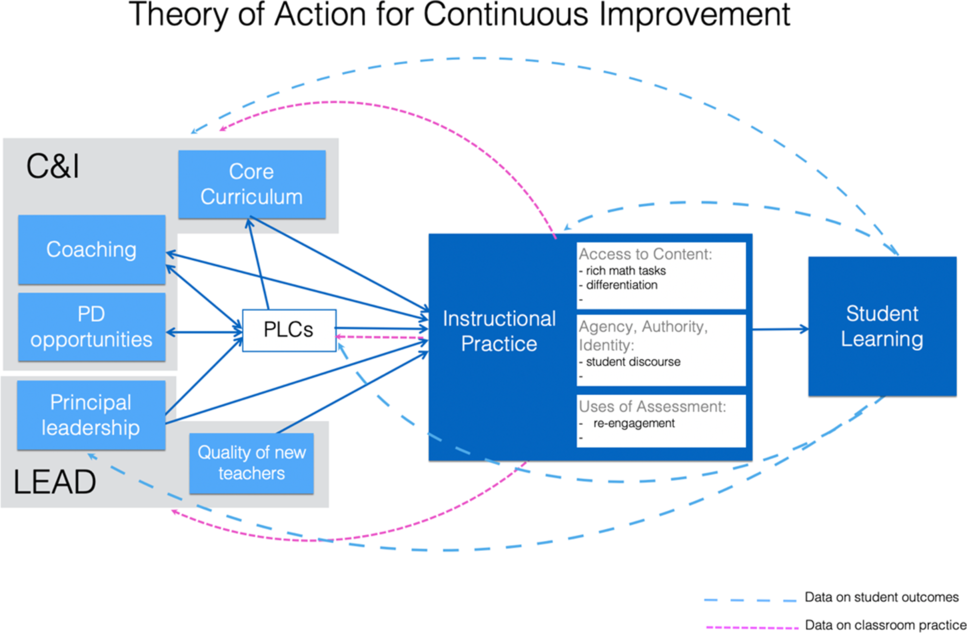
Figure 5. Draft theory of action, San Francisco Unified School District (SFUSD 2015).

In addition, the Chicago Public Schools, an early and successful adopter of the TRU Mathematics framework, is now employing the framework for professional development and instruction in all content areas.

The domain-general version of the TRU Framework is given in Figure 6. Domain-general tools for professional development are available at the TRU Framework website, https://truframework.org/.

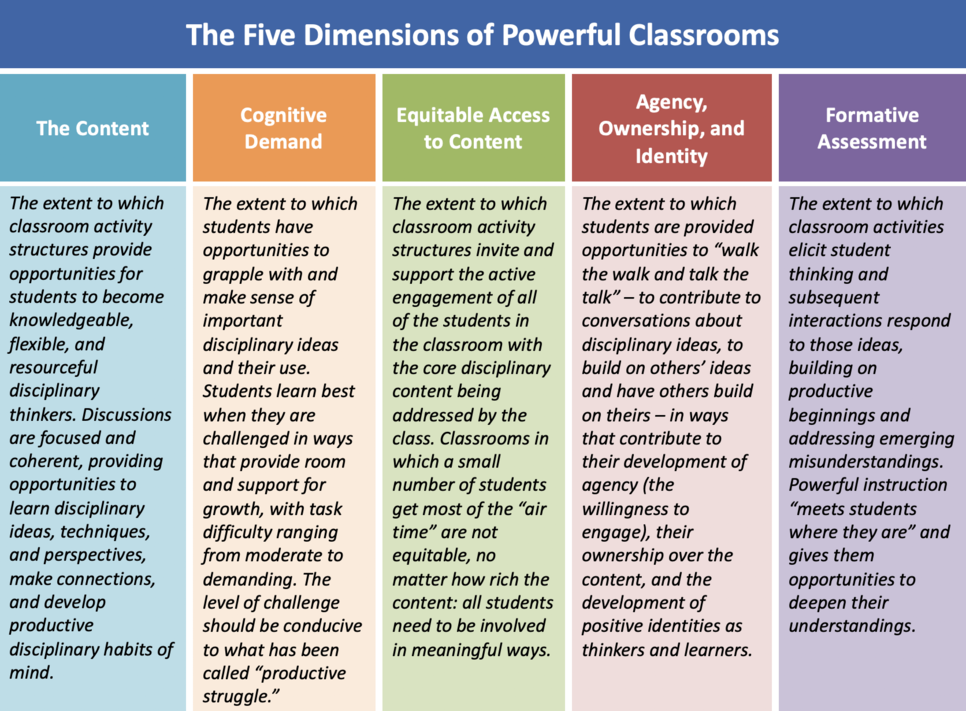
Figure 6. The domain-general version of the TRU framework.

The key point is that the TRU framework provides a perspective for reflection and action, at both the K-12 and collegiate levels. Disciplinary engagement (Dimension 1) can be problematized, with an eye toward having students engage in key sense-making practices and having as much of the content as possible emerge from such sense-making activities. Some of this will be domain-specific, potentially ameliorating vertical gaps; but some of it will also be more general, potentially ameliorating horizontal gaps. A focus on equitable access (Dimension 3) and the kinds of classroom activities that help students build both productive habits of mind as students and positive disciplinary identities (Dimension 4) can have a significant impact on both horizontal and vertical gaps. Finally, curricula, assignments, and classroom activities can be re-examined with an eye toward making student thinking public and maintaining productive struggle (Dimensions 5 and 2), thereby contributing to access and sense-making.

All of this work is in its early stages and discussions of impact on gaps are necessarily conjectural. At present, the efforts that have been undertaken are best conceptualized as a laboratory for exploration rather than a promissory note for improvement with regard to the horizontal and vertical gap problems. But there is at least a plausibility case. Two major school districts that adopted the TRU framework in mathematics found results within mathematics sufficiently promising that they expanded their efforts to all subject areas, seeking to enhance horizontal coherence. Improvements within K-12 look promising with regard to secondary-to-university gaps, but evidence remains to be gathered. Whether these ideas will be taken up at the university level, and to what effect, remains to be seen. Time and data will tell.