Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-29T21:26:32.925Z Has data issue: false hasContentIssue false
  • English
  • Français

ABELIAN $n$ -DIVISION FIELDS OF ELLIPTIC CURVES AND BRAUER GROUPS OF PRODUCT KUMMER & ABELIAN SURFACES

Published online by Cambridge University Press:  29 November 2017

ANTHONY VÁRILLY-ALVARADO  and
BIANCA VIRAY
ANTHONY VÁRILLY-ALVARADO
Affiliation:
Department of Mathematics MS 136, Rice University, Houston, TX 77005, USA; varilly@rice.edu
BIANCA VIRAY
Affiliation:
University of Washington, Department of Mathematics, Box 354350, Seattle, WA 98195, USA; bviray@math.washington.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 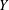$Y$ be a principal homogeneous space of an abelian surface, or a K3 surface, over a finitely generated extension of 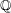$\mathbb{Q}$ . In 2008, Skorobogatov and Zarhin showed that the Brauer group modulo algebraic classes 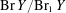$\text{Br}\,Y/\text{Br}_{1}\,Y$ is finite. We study this quotient for the family of surfaces that are geometrically isomorphic to a product of isogenous non-CM elliptic curves, as well as the related family of geometrically Kummer surfaces; both families can be characterized by their geometric Néron–Severi lattices. Over a field of characteristic 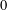$0$ , we prove that the existence of a strong uniform bound on the size of the odd torsion of 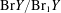$\text{Br}Y/\text{Br}_{1}Y$ is equivalent to the existence of a strong uniform bound on integers $n$ for which there exist non-CM elliptic curves with abelian $n$ -division fields. Using the same methods we show that, for a fixed prime 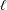$\ell$ , a number field 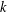$k$ of fixed degree $r$ , and a fixed discriminant of the geometric Néron–Severi lattice, 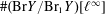$\#(\text{Br}Y/\text{Br}_{1}Y)[\ell ^{\infty }]$ is bounded by a constant that depends only on 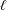$\ell$ , $r$ , and the discriminant.

Information

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e26
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Abramovich, D., ‘A linear lower bound on the gonality of modular curves’, Int. Math. Res. Not. IMRN 20 (1996), 1005–1011.Google Scholar
Abramovich, D. and Várilly-Alvarado, A., ‘Level structures on abelian varieties, Kodaira dimensions, and Lang’s conjecture’, Preprint, 2016, arXiv:1601.02483.Google Scholar
Abramovich, D. and Várilly-Alvarado, A., ‘Level structures on abelian varieties and Vojta’s conjecture’, Compos. Math. 153 (2017), 373–394. With an Appendix by K. Madapusi Pera.CrossRefGoogle Scholar
‘AimPL: Brauer groups and obstruction problems’, available at http://aimpl.org/brauermoduli.Google Scholar
Beauville, A., Complex Algebraic Surfaces, 2nd edn, London Mathematical Society Student Texts, 34 (Cambridge University Press, Cambridge, 1996). Translated from the 1978 French original by R. Barlow, with assistance from N. I. Shepherd-Barron and M. Reid.CrossRefGoogle Scholar
Bilu, Yu., Parent, P. and Rebolledo, M., ‘Rational points on X 0 +(p r )’, Ann. Inst. Fourier (Grenoble) 63(3) (2013), 957–984. (English, with English and French summaries).CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Skorobogatov, A. N., ‘Descente galoisienne sur le groupe de Brauer’, J. Reine Angew. Math. 682 (2013), 141–165. (French, with English and French summaries).CrossRefGoogle Scholar
Contoral-Farfán, V., Tang, Y., Tanimoto, S. and Visse, E., ‘Effective bounds for Brauer groups of Kummer surfaces over number fields’, Preprint, 2016, arXiv:1606.06074.Google Scholar
Deligne, P. and Rapoport, M., ‘Les schémas de modules de courbes elliptiques’, inModular Functions of One Variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, 349 (Springer, Berlin, 1973), 143–316 (French).Google Scholar
Frey, G., ‘Curves with infinitely many points of fixed degree’, Israel J. Math. 85(1–3) (1994), 79–83.CrossRefGoogle Scholar
González-Jiménez, E. and Lozano-Robledo, Á., ‘Elliptic curves with abelian division fields’, Math. Z. 283(3–4) (2016), 835–859.Google Scholar
Gritsenko, V., Hulek, K. and Sankaran, G. K., ‘The Kodaira dimension of the moduli of K3 surfaces’, Invent. Math. 169(3) (2007), 519–567.Google Scholar
Hassett, B., Kresch, A. and Tschinkel, Y., ‘Effective computation of Picard groups and Brauer–Manin obstructions of degree two K3 surfaces over number fields’, Rend. Circ. Mat. Palermo (2) 62(1) (2013), 137–151, doi:10.1007/s12215-013-0116-8.Google Scholar
Huybrechts, D., Lectures on K3 surfaces, Cambridge Studies in Advanced Mathematics, 158 (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Ieronymou, E., Skorobogatov, A. N. and Zarhin, Y. G., ‘On the Brauer group of diagonal quartic surfaces’, J. Lond. Math. Soc. (2) 83(3) (2011), 659–672. With an appendix by Peter Swinnerton-Dyer.Google Scholar
Iwasawa, K., ‘On some types of topological groups’, Ann. of Math. (2) 50 (1949), 507–558.CrossRefGoogle Scholar
Kamienny, S., ‘Torsion points on elliptic curves and q-coefficients of modular forms’, Invent. Math. 109(2) (1992), 221–229.Google Scholar
Kani, E., ‘Elliptic curves on abelian surfaces’, Manuscripta Math. 84(2) (1994), 199–223.CrossRefGoogle Scholar
Manin, Ju. I., ‘The p-torsion of elliptic curves is uniformly bounded’, Izv. Akad. Nauk SSSR Ser. Mat. 33 (1969), 459–465 (Russian).Google Scholar
Masser, D. W. and Wüstholz, G., ‘Estimating isogenies on elliptic curves’, Invent. Math. 100(1) (1990), 1–24, doi:10.1007/BF01231178; MR 1037140.CrossRefGoogle Scholar
Mazur, B., ‘Modular curves and the Eisenstein ideal’, Inst. Hautes Études Sci. Publ. Math. 47 (1977), 33–186, (1978).Google Scholar
Mazur, B., ‘Rational isogenies of prime degree (with an appendix by D. Goldfeld)’, Invent. Math. 44(2) (1978), 129–162.CrossRefGoogle Scholar
McDonald, B. R., ‘Similarity of matrices over Artinian principal ideal rings’, Linear Algebra Appl. 21(2) (1978), 153–162.Google Scholar
McKinnie, K., Sawon, J., Tanimoto, S. and Várilly-Alvarado, A., ‘Brauer groups on K3 surfaces and arithmetic applications’, inBrauer Groups and Obstruction Problems: Moduli Spaces and Arithmetic, Progress in Mathematics, 320 (Birkhäuser, Cham, Switzerland, 2017), 177–218.Google Scholar
Merel, L., ‘Bornes pour la torsion des courbes elliptiques sur les corps de nombres’, Invent. Math. 124(1–3) (1996), 437–449 (French).Google Scholar
Neukirch, J., Class Field Theory, (Springer, Heidelberg, 2013). The Bonn lectures, edited and with a foreword by Alexander Schmidt. Translated from the 1967 German original by F. Lemmermeyer and W. Snyder; Language editor: A. Rosenschon.CrossRefGoogle Scholar
Newton, R., ‘Transcendental Brauer groups of products of CM elliptic curves’, J. Lond. Math. Soc. (2) 93(2) (2016), 397–419, doi:10.1112/jlms/jdv058;MR 3483120.Google Scholar
Nikulin, V. V., ‘On Kummer surfaces’, Izv. Akad. Nauk SSSR Ser. Mat. 39(2) (1975), 278–293. 471 (Russian).Google Scholar
Rouse, J., ‘What are the strongest conjectured uniform versions of Serre’s Open Image Theorem?’, MathOverflow. URL: http://mathoverflow.net/q/203837 (version: 2015-05-02).Google Scholar
Rouse, J. and Zureick-Brown, D., ‘Elliptic curves over ℚ and 2-adic images of Galois’, Res. Number Theory 1 (2015), 1–34.Google Scholar
Serre, J.-P., ‘Propriétés galoisiennes des points d’ordre fini des courbes elliptiques’, Invent. Math. 15(4) (1972), 259–331 (French).CrossRefGoogle Scholar
Serre, J.-P., Abelian l-adic Representations and Elliptic Curves, Research Notes in Mathematics, 7 (A K Peters, Ltd., Wellesley, MA, 1998), with the collaboration of Willem Kuyk and John Labute; revised reprint of the 1968 original.Google Scholar
Skorobogatov, A. N. and Zarhin, Y. G., ‘A finiteness theorem for the Brauer group of abelian varieties and K3 surfaces’, J. Algebraic Geom. 17(3) (2008), 481–502.Google Scholar
Skorobogatov, A. N. and Zarhin, Y. G., ‘The Brauer group of Kummer surfaces and torsion of elliptic curves’, J. Reine Angew. Math. 666 (2012), 115–140.Google Scholar
Tanimoto, S. and Várilly-Alvarado, A., ‘Kodaira dimension of moduli of special cubic fourfolds’, J. Reine Angew. Math. to appear, doi:10.1515/crelle-2016-0053.CrossRefGoogle Scholar
Várilly-Alvarado, A., ‘Arithmetic of K3 surfaces’, inGeometry Over Nonclosed Fields (Springer, New York, 2017), 197–248.Google Scholar