Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-29T09:39:38.222Z Has data issue: false hasContentIssue false
  • English
  • Français

The bandwidth theorem for locally dense graphs

Part of: Graph theory

Published online by Cambridge University Press:  04 November 2020

Katherine Staden  and
Andrew Treglown
Katherine Staden
Affiliation:
Mathematical Institute, University of Oxford, Oxford, OX2 6GG United Kingdom; E-mail: staden@maths.ox.ac.uk
Andrew Treglown
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT United Kingdom; E-mail: a.c.treglown@bham.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The bandwidth theorem of Böttcher, Schacht, and Taraz [Proof of the bandwidth conjecture of Bollobás and Komlós, Mathematische Annalen, 2009] gives a condition on the minimum degree of an n-vertex graph G that ensures G contains every r-chromatic graph H on n vertices of bounded degree and of bandwidth 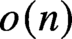$o(n)$, thereby proving a conjecture of Bollobás and Komlós [The Blow-up Lemma, Combinatorics, Probability, and Computing, 1999]. In this paper, we prove a version of the bandwidth theorem for locally dense graphs. Indeed, we prove that every locally dense n-vertex graph G with 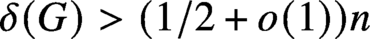$\delta (G)> (1/2+o(1))n$ contains as a subgraph any given (spanning) H with bounded maximum degree and sublinear bandwidth.

Keywords

bandwidthembeddingregularity method

MSC classification

Primary: 05C35: Extremal problems

Information

Type
Discrete Mathematics
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e42
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Allen, P., Böttcher, J., Ehrenmüller, J., and Taraz, A., ‘The bandwidth theorem in sparse graphs’, Advances Combin. (2020):6, 60pp.Google Scholar
Balogh, J. and Lenz, J., ‘Some exact Ramsey-Turán numbers’, Bull. London Math. Soc. 44 (2012), 1251–1258.CrossRefGoogle Scholar
Balogh, J., McDowell, A., Molla, T., and Mycroft, R., ‘Triangle-tilings in graphs without large independent sets’, Combin. Probab. Comput. 27 (2018), 449–474.CrossRefGoogle Scholar
Balogh, J., Molla, T., and Sharifzadeh, M., ‘Triangle factors of graphs without large independent sets and of weighted graphs’, Random Structures Algorithms 49 (2016), 669–693.CrossRefGoogle Scholar
Böttcher, J., Kohayakawa, Y., and Taraz, A., ‘Almost spanning subgraphs of random graphs after adversarial edge removal’, Combin. Probab. Comput. 22 (2013), 639–683.CrossRefGoogle Scholar
Böttcher, J., Montgomery, R., Parczyk, O., and Person, Y., ‘Embedding spanning bounded degree graphs in randomly perturbed graphs’, Mathematika 66 (2020), 422–447.CrossRefGoogle Scholar
Böttcher, J., Preussmann, K., Taraz, A., and Würfl, A., ‘Bandwidth, expansion, treewidth, separators and universality for bounded-degree graphs’, European J. Combin. 31 (2010), 1217–1227.CrossRefGoogle Scholar
Böttcher, J., Schacht, M., and Taraz, A., ‘Spanning $3$ -colourable subgraphs of small bandwidth in dense graphs’, J. Combin. Theory B 98 (2008), 752–777.CrossRefGoogle Scholar
Böttcher, J., Schacht, M., and Taraz, A., ‘Proof of the bandwidth conjecture of Bollobás and Komlós’, Math. Ann. 343 (2009), 175–205.CrossRefGoogle Scholar
Böttcher, J., Taraz, A., and Würfl, A., ‘Spanning embeddings of arrangeable graphs with sublinear bandwidth’, Random Structures Algorithms, 48 (2016), 270–289.CrossRefGoogle Scholar
Chvátal, V., Rödl, V., Szemerédi, E., and Trotter, W.T. Jr., ‘The Ramsey number of a graph with bounded maximum degree’, J. Combin. Theory Ser. B 34 (1983), 239–243.CrossRefGoogle Scholar
Condon, P., Kim, J., Kühn, D., and Osthus, D., ‘A bandwidth theorem for approximate decompositions’, Proc. London Math. Soc. 118 (2019), 1393–1449.CrossRefGoogle Scholar
Dirac, G.A., ‘Some theorems on abstract graphs’, Proc. London Math. Soc. 2 (1952), 69–81.CrossRefGoogle Scholar
Ebsen, O., Maesaka, G.S., Chr. Reiher, Schacht, M., and Schülke, B., ‘Embedding spanning subgraphs in uniformly dense and inseparable graphs’, Random Structures and Algorithms, 57 (2020), 1077–1096.CrossRefGoogle Scholar
Erdős, P., Problem 9, in: Fieldler, M. (ed.), Theory of Graphs and Its Applications (Czech. Acad. Sci. Publ., Prague, 1964), 159.Google Scholar
Erdős, P., Faudree, R.J., Rousseau, C.C., and Schelp, R.H., ‘A local density condition for triangles’, Discrete Math. 127 (1994), 153–161.CrossRefGoogle Scholar
Erdős, P., Hajnal, A., Sós, V.T., and Szemerédi, E., ‘More results on Ramsey–Turán type problems’, Combinatorica 3 (1983), 69–81.CrossRefGoogle Scholar
Erdős, P. and Sós, V.T., ‘Some remarks on Ramsey’s and Turán’s theorem’, in: Combinatorial Theory and Its Applications vol. II (North-Holland, Amsterdam, 1970), 395–404.Google Scholar
Ferber, A., Nenadov, R., Noever, A., Peter, U., and Skoric, N., ‘Robust hamiltonicity of random directed graphs’, J. Combin. Theory Ser. B 126 (2017), 1–23.CrossRefGoogle Scholar
Glock, S. and Joos, F., ‘A rainbow blow-up lemma’, Random Structures Algorithms, to appear.Google Scholar
Hajnal, A. and Szemerédi, E., ‘Proof of a conjecture of Erdős’, in: Combinatorial Theory and Its Applications vol. II 4 (North-Holland, Amsterdam, 1970), 601–623.Google Scholar
Han, J., ‘On perfect matchings and tilings in uniform hypergraphs’, SIAM J. Discrete Math., 32 (2018), 919–932.CrossRefGoogle Scholar
Huang, H., Lee, C., and Sudakov, B., ‘Bandwidth theorem for random graphs’, J. Combin. Theory B 102 (2012), 14–37.CrossRefGoogle Scholar
Knox, F. and Treglown, A., ‘Embedding spanning bipartite graphs of small bandwidth’, Combin. Probab. Comput. 22 (2013), 71–96.CrossRefGoogle Scholar
Kohayakawa, Y., Nagle, B., Rödl, V., and Schacht, M., ‘Weak regularity and linear hypergraphs’, J. Combin. Theory B 100 (2010), 151–160.CrossRefGoogle Scholar
Komlós, J., ‘The blow-up lemma’, Combin. Probab. Comput. 8 (1999), 161–176.CrossRefGoogle Scholar
Komlós, J., Sárkozÿ, G.N., and Szemerédi, E., ‘Blow-up lemma’, Combinatorica 17 (1997), 109–123.CrossRefGoogle Scholar
Komlós, J., Sárközy, G.N., and Szemerédi, E., ‘Proof of the Seymour conjecture for large graphs’, Annals of Combinatorics 2 (1998), 43–60.CrossRefGoogle Scholar
Kühn, D. and Osthus, D., ‘The minimum degree threshold for perfect graph packings’, Combinatorica 29 (2009), 65–107.CrossRefGoogle Scholar
Lee, C., ‘Embedding degenerate graphs of small bandwidth’, submitted, arXiv:1501.05350.Google Scholar
Mubayi, D. and Sós, V.T., ‘Explicit constructions of triple systems for Ramsey–Turán problems’, J. Graph Theory 52 (2006), 211–216.CrossRefGoogle Scholar
Rödl, V., Ruciński, A., and Szemerédi, E., ‘A Dirac-type theorem for 3-uniform hypergraphs’, Combin. Probab. Comput. 15 (2006), 229–251.CrossRefGoogle Scholar
Seymour, P., Problem section, in: McDonough, T.P. and Mavron, V.C. (eds.), Combinatorics: Proceedings of the British Combinatorial Conference 1973 (Cambridge University Press, 1974), 201–202.Google Scholar
Simonovits, M. and T. Sós, V., ‘Ramsey–Turán theory’, Discrete Math. 229 (2001), 293–340.CrossRefGoogle Scholar
Staden, K. and Treglown, A., ‘On degree sequences forcing the square of a Hamilton cycle’, SIAM J. Disc. Math. 31 (2017), 383–437.CrossRefGoogle Scholar
Staden, K. and Treglown, A., ‘On degree sequences forcing the square of a Hamilton cycle’, arXiv version, arXiv:1412.3498.Google Scholar
Szemerédi, E., ‘Regular partitions of graphs’, Problémes Combinatoires et Théorie des Graphes Colloques Internationaux CNRS 260 (1978), 399–401.Google Scholar