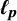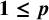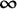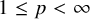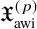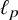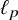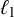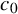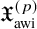1 Introduction
The purpose of this article is to provide an answer to the following problem of Halbeisen and Odell from [Reference Halbeisen and Odell20] and is, in particular, the last step towards the complete separation of a list of asymptotic structures from [Reference Argyros and Motakis9]. Given a Banach space X, let
![]() $\mathscr {F}_0(X)$
denote the family of normalised weakly null sequences in X and
$\mathscr {F}_0(X)$
denote the family of normalised weakly null sequences in X and
![]() $\mathscr {F}_b(X)$
denote the family of normalised block sequences of a fixed basis, if X has one.
$\mathscr {F}_b(X)$
denote the family of normalised block sequences of a fixed basis, if X has one.
Problem 1. Let X be a Banach space that admits a unique asymptotic model with respect to
![]() $\mathscr {F}_0(X)$
, or with respect to
$\mathscr {F}_0(X)$
, or with respect to
![]() $\mathscr {F}_b(X)$
if X has a basis. Does X contain an Asymptotic
$\mathscr {F}_b(X)$
if X has a basis. Does X contain an Asymptotic
![]() $\ell _p$
,
$\ell _p$
,
![]() $1\le p<\infty $
or an Asymptotic
$1\le p<\infty $
or an Asymptotic
![]() $c_0$
subspace?
$c_0$
subspace?
The following definition from [Reference Argyros and Motakis9] provides a more general setting in which we will describe this problem, as well as other previous separation results. A property of a Banach space is called hereditary if it is inherited by all of its closed and infinite dimensional subspaces.
Definition 1.1. Let (P) and (Q) be two hereditary properties of Banach spaces, and assume that (P) implies (Q).
-
(i) If (Q)
 $\not \Rightarrow $
(P), that is, there exists a Banach space satisfying (Q) and failing (P), then we say that (P) is separated from (Q).
$\not \Rightarrow $
(P), that is, there exists a Banach space satisfying (Q) and failing (P), then we say that (P) is separated from (Q). -
(ii) If there exists a Banach space satisfying (Q) and whose every infinite dimensional closed subspace fails (P), then we say that (P) is completely separated from (Q) and write (Q)
 (P).
(P).
We consider properties that are classified into the following three categories: the sequential asymptotic properties, the array asymptotic properties and the global asymptotic properties.
Sequential asymptotic properties are related to the notion of a spreading model from [Reference Brunel and Sucheston15], which describes the asymptotic behaviour of a sequence in a Banach space. We say that a Banach space admits a unique spreading model with respect to some family of normalised sequences
![]() $\mathscr {F}$
, if whenever two sequences from
$\mathscr {F}$
, if whenever two sequences from
![]() $\mathscr {F}$
generate spreading models, then those must be equivalent. If this equivalence happens with some uniform constant, then we say that the space admits a uniformly unique spreading model.
$\mathscr {F}$
generate spreading models, then those must be equivalent. If this equivalence happens with some uniform constant, then we say that the space admits a uniformly unique spreading model.
The category of array asymptotic structures concerns the asymptotic behaviour of arrays of sequences
![]() $(x^i_j)_j$
,
$(x^i_j)_j$
,
![]() $i\in \mathbb {N}$
, in a Banach space. Notions that describe this behaviour are those of asymptotic models from [Reference Halbeisen and Odell20] and joint spreading models from [Reference Argyros, Georgiou and Motakis8]. We define the uniqueness of asymptotic models and the uniform uniqueness of joint spreading models in a similar manner to the uniqueness and uniform uniqueness of spreading models, respectively. Although asymptotic models and joint spreading models are not identical notions, they are strongly related. As Sari pointed out, a Banach space X admits a uniformly unique joint spreading model with respect to
$i\in \mathbb {N}$
, in a Banach space. Notions that describe this behaviour are those of asymptotic models from [Reference Halbeisen and Odell20] and joint spreading models from [Reference Argyros, Georgiou and Motakis8]. We define the uniqueness of asymptotic models and the uniform uniqueness of joint spreading models in a similar manner to the uniqueness and uniform uniqueness of spreading models, respectively. Although asymptotic models and joint spreading models are not identical notions, they are strongly related. As Sari pointed out, a Banach space X admits a uniformly unique joint spreading model with respect to
![]() $\mathscr {F}_b(X)$
or
$\mathscr {F}_b(X)$
or
![]() $\mathscr {F}_0(X)$
if and only if it admits a unique asymptotic model with respect to
$\mathscr {F}_0(X)$
if and only if it admits a unique asymptotic model with respect to
![]() $\mathscr {F}_b(X)$
or
$\mathscr {F}_b(X)$
or
![]() $\mathscr {F}_0(X)$
, respectively (see, e.g. [Reference Argyros, Georgiou, Lagos and Motakis6, Remark 4.21] or [Reference Argyros and Motakis9, Proposition 3.12]). Notably, the property that a Banach space X with a basis admits some
$\mathscr {F}_0(X)$
, respectively (see, e.g. [Reference Argyros, Georgiou, Lagos and Motakis6, Remark 4.21] or [Reference Argyros and Motakis9, Proposition 3.12]). Notably, the property that a Banach space X with a basis admits some
![]() $\ell _p$
as a uniformly unique joint spreading model with respect to
$\ell _p$
as a uniformly unique joint spreading model with respect to
![]() $\mathscr {F}_b(X)$
can be described by the following statement. The case where this happens with respect to
$\mathscr {F}_b(X)$
can be described by the following statement. The case where this happens with respect to
![]() $\mathscr {F}_0(X)$
is given by an easy modification.
$\mathscr {F}_0(X)$
is given by an easy modification.
Proposition 1.2 (Lemma 3.4).
Let
![]() $1\le p\le \infty $
. A Banach space X with a basis admits
$1\le p\le \infty $
. A Banach space X with a basis admits
![]() $\ell _p$
(or
$\ell _p$
(or
![]() $c_0$
for
$c_0$
for
![]() $p=\infty $
) as a uniformly unique joint spreading model with respect to
$p=\infty $
) as a uniformly unique joint spreading model with respect to
![]() $\mathscr {F}_b(X)$
if and only if there exist constants
$\mathscr {F}_b(X)$
if and only if there exist constants
![]() $c,C>0$
, such that for every
$c,C>0$
, such that for every
![]() $\ell \in \mathbb {N}$
, any choice of successive families
$\ell \in \mathbb {N}$
, any choice of successive families
![]() $(F_j)_j$
of normalised blocks in X with
$(F_j)_j$
of normalised blocks in X with
![]() $\#F_j=\ell $
, there is an infinite subset of the naturals
$\#F_j=\ell $
, there is an infinite subset of the naturals
![]() $M=\{m_1<m_2<\ldots \}$
, such that for any choice of
$M=\{m_1<m_2<\ldots \}$
, such that for any choice of
![]() $x_j\in F_j$
,
$x_j\in F_j$
,
![]() $j\in M$
, every
$j\in M$
, every
![]() $G\subset M$
with
$G\subset M$
with
![]() $m_k\le G$
and
$m_k\le G$
and
![]() $\#G\le k$
, for
$\#G\le k$
, for
![]() $k\in \mathbb {N}$
, and any choice of scalars
$k\in \mathbb {N}$
, and any choice of scalars
![]() $a_j$
,
$a_j$
,
![]() $j\in G$
, we have
$j\in G$
, we have
 $$\begin{align*}c\|(a_j)_{j\in G}\|_p \le \| \sum_{j\in G}a_jx_j \| \le C\| (a_j)_{j\in G} \|_p. \end{align*}$$
$$\begin{align*}c\|(a_j)_{j\in G}\|_p \le \| \sum_{j\in G}a_jx_j \| \le C\| (a_j)_{j\in G} \|_p. \end{align*}$$
Even though this property is very close to the weaker one that X admits
![]() $\ell _p$
or
$\ell _p$
or
![]() $c_0$
as a uniformly unique spreading model, it was shown in [Reference Argyros and Motakis9] that these two properties are in fact completely separated for all
$c_0$
as a uniformly unique spreading model, it was shown in [Reference Argyros and Motakis9] that these two properties are in fact completely separated for all
![]() $1\le p\le \infty $
.
$1\le p\le \infty $
.
Finally, global asymptotic properties describe the behaviour of finite block sequences that are chosen sufficiently far apart in a space with a basis. We recall the following definition from [Reference Milman and Tomczak-Jaegermann25].
Definition 1.3. Let X be a Banach space with a basis
![]() $(e_i)_i$
and
$(e_i)_i$
and
![]() $1\le p\le \infty $
. We say that the basis
$1\le p\le \infty $
. We say that the basis
![]() $(e_i)_i$
of X is asymptotic
$(e_i)_i$
of X is asymptotic
![]() $\ell _p$
(asymptotic
$\ell _p$
(asymptotic
![]() $c_0$
when
$c_0$
when
![]() $p=\infty $
) if there exist positive constants
$p=\infty $
) if there exist positive constants
![]() $D_1$
and
$D_1$
and
![]() $D_2$
, such that for all
$D_2$
, such that for all
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $N(n)\in \mathbb {N}$
with the property that whenever
$N(n)\in \mathbb {N}$
with the property that whenever
![]() $N(n)\le x_1< \cdots < x_n$
are vectors in X, then
$N(n)\le x_1< \cdots < x_n$
are vectors in X, then
 $$\begin{align*}\frac{1}{D_1}(\sum_{i=1}^n\|x_i\|^p)^{\frac{1}{p}}\le \|\sum_{i=1}^nx_i\|\le D_2 (\sum_{i=1}^n\|x_i\|^p )^{\frac{1}{p}}, \end{align*}$$
$$\begin{align*}\frac{1}{D_1}(\sum_{i=1}^n\|x_i\|^p)^{\frac{1}{p}}\le \|\sum_{i=1}^nx_i\|\le D_2 (\sum_{i=1}^n\|x_i\|^p )^{\frac{1}{p}}, \end{align*}$$
where for
![]() $p=\infty $
, the above inequality concerns the
$p=\infty $
, the above inequality concerns the
![]() $\|\cdot \|_{\infty }$
. Specifically, we say that
$\|\cdot \|_{\infty }$
. Specifically, we say that
![]() $(e_i)_i$
is D-asymptotic
$(e_i)_i$
is D-asymptotic
![]() $\ell _p$
(D-asymptotic
$\ell _p$
(D-asymptotic
![]() $c_0$
when
$c_0$
when
![]() $p=\infty $
) for
$p=\infty $
) for
![]() $D=D_1D_2$
.
$D=D_1D_2$
.
This definition is given with respect to a fixed basis of the space. The coordinate-free notion of Asymptotic
![]() $\ell _p$
and
$\ell _p$
and
![]() $c_0$
spaces was introduced in [Reference Maurey, Milman and Tomczak-Jaegermann24], generalising the aforementioned one to spaces with or without a basis (note the difference between the terms asymptotic
$c_0$
spaces was introduced in [Reference Maurey, Milman and Tomczak-Jaegermann24], generalising the aforementioned one to spaces with or without a basis (note the difference between the terms asymptotic
![]() $\ell _p$
and Asymptotic
$\ell _p$
and Asymptotic
![]() $\ell _p$
). Moreover, this property is hereditary and any Asymptotic
$\ell _p$
). Moreover, this property is hereditary and any Asymptotic
![]() $\ell _p$
(or
$\ell _p$
(or
![]() $c_0$
) space is asymptotic
$c_0$
) space is asymptotic
![]() $\ell _p$
(respectively,
$\ell _p$
(respectively,
![]() $c_0$
) saturated. Given a Banach space X with a basis, we focus on the following properties, where
$c_0$
) saturated. Given a Banach space X with a basis, we focus on the following properties, where
![]() $1\le p\le \infty $
and whenever
$1\le p\le \infty $
and whenever
![]() $p=\infty $
, then
$p=\infty $
, then
![]() $\ell _p$
should be replaced with
$\ell _p$
should be replaced with
![]() $c_0$
.
$c_0$
.
-
(a)
 $_p$
The space X is Asymptotic
$_p$
The space X is Asymptotic
 $\ell _p$
.
$\ell _p$
. -
(b)
 $_p$
The space X admits
$_p$
The space X admits
 $\ell _p$
as a uniformly unique joint spreading model (or equivalently, a unique asymptotic model, as mentioned above) with respect to
$\ell _p$
as a uniformly unique joint spreading model (or equivalently, a unique asymptotic model, as mentioned above) with respect to
 $\mathscr {F}_b(X)$
.
$\mathscr {F}_b(X)$
. -
(c)
 $_p$
The space X admits
$_p$
The space X admits
 $\ell _p$
as a uniformly unique spreading model with respect to
$\ell _p$
as a uniformly unique spreading model with respect to
 $\mathscr {F}_b(X)$
.
$\mathscr {F}_b(X)$
. -
(d)
 $_p$
The space X admits
$_p$
The space X admits
 $\ell _p$
as a unique spreading model with respect to
$\ell _p$
as a unique spreading model with respect to
 $\mathscr {F}_b(X)$
.
$\mathscr {F}_b(X)$
.
Note that it is fairly straightforward to see that the following implications hold for all
![]() $1\le p\le \infty $
: (a)
$1\le p\le \infty $
: (a)
![]() $_p\Rightarrow $
(b)
$_p\Rightarrow $
(b)
![]() $_p\Rightarrow $
(c)
$_p\Rightarrow $
(c)
![]() $_p\Rightarrow $
(d)
$_p\Rightarrow $
(d)
![]() $_p$
. It is also easy to see that (d)
$_p$
. It is also easy to see that (d)
![]() $_p\not \Rightarrow $
(c)
$_p\not \Rightarrow $
(c)
![]() $_p$
for all
$_p$
for all
![]() $1\le p<\infty $
. In [Reference Baudier, Lancien, Motakis and Schlumprecht14] it was shown that (c)
$1\le p<\infty $
. In [Reference Baudier, Lancien, Motakis and Schlumprecht14] it was shown that (c)
![]() $_p\not \Rightarrow $
(b)
$_p\not \Rightarrow $
(b)
![]() $_p$
for all
$_p$
for all
![]() $1\le p\le \infty $
and that (b)
$1\le p\le \infty $
and that (b)
![]() $_p\not \Rightarrow $
(a)
$_p\not \Rightarrow $
(a)
![]() $_p$
for all
$_p$
for all
![]() $1<p<\infty $
. The latter was also shown in [Reference Argyros, Georgiou and Motakis8], as well as that (b)
$1<p<\infty $
. The latter was also shown in [Reference Argyros, Georgiou and Motakis8], as well as that (b)
![]() $_1\not \Rightarrow $
(a)
$_1\not \Rightarrow $
(a)
![]() $_1$
along with an even stronger result, namely, the existence of a Banach space with a basis satisfying (b)
$_1$
along with an even stronger result, namely, the existence of a Banach space with a basis satisfying (b)
![]() $_1$
and, such that any infinite subsequence of its basis generates a non-Asymptotic
$_1$
and, such that any infinite subsequence of its basis generates a non-Asymptotic
![]() $\ell _1$
subspace. However, it was proved in [Reference Androulakis, Odell, Schlumprecht and Tomczak-Jaegermann12] that (d)
$\ell _1$
subspace. However, it was proved in [Reference Androulakis, Odell, Schlumprecht and Tomczak-Jaegermann12] that (d)
![]() $_{\infty }\Leftrightarrow $
(c)
$_{\infty }\Leftrightarrow $
(c)
![]() $_{\infty }$
and a remarkable result from [Reference Freeman, Odell, Sari and Zheng18] states that (b)
$_{\infty }$
and a remarkable result from [Reference Freeman, Odell, Sari and Zheng18] states that (b)
![]() $_{\infty }\Leftrightarrow $
(a)
$_{\infty }\Leftrightarrow $
(a)
![]() $_{\infty }$
for Banach spaces not containing
$_{\infty }$
for Banach spaces not containing
![]() $\ell _1$
. Towards the complete separation of these properties, it was shown in [Reference Argyros and Motakis9] that (c)
$\ell _1$
. Towards the complete separation of these properties, it was shown in [Reference Argyros and Motakis9] that (c)
![]() (b)
(b)
![]() $_p$
for all
$_p$
for all
![]() $1\le p\le \infty $
and that (d)
$1\le p\le \infty $
and that (d)
![]() (c)
(c)
![]() $_p$
for all
$_p$
for all
![]() $1\le p <\infty $
. Hence, the only remaining open question was whether (b)
$1\le p <\infty $
. Hence, the only remaining open question was whether (b)
![]() (a)
(a)
![]() $_p$
for
$_p$
for
![]() $1\le p<\infty $
. We prove this in the affirmative and, in particular, we show the following.
$1\le p<\infty $
. We prove this in the affirmative and, in particular, we show the following.
Theorem 1.4. For
![]() $1\le p<\infty $
, there exists a reflexive Banach space
$1\le p<\infty $
, there exists a reflexive Banach space
![]() $\mathfrak {X}_{\text {awi}}^{(p)}$
with an unconditional basis that admits
$\mathfrak {X}_{\text {awi}}^{(p)}$
with an unconditional basis that admits
![]() $\ell _p$
as a uniformly unique joint spreading model with respect to
$\ell _p$
as a uniformly unique joint spreading model with respect to
![]() $\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(p)})$
and contains no Asymptotic
$\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(p)})$
and contains no Asymptotic
![]() $\ell _p$
subspaces.
$\ell _p$
subspaces.
To construct these spaces, we use a saturation method with asymptotically weakly incomparable constraints. This method, initialised in [Reference Argyros, Georgiou and Motakis8], employs a tree structure, penetrating every subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(p)}$
, that admits segments with norm strictly less than the
$\mathfrak {X}_{\text {awi}}^{(p)}$
, that admits segments with norm strictly less than the
![]() $\ell _p$
-norm. Thus, we are able to prove that no subspace of
$\ell _p$
-norm. Thus, we are able to prove that no subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(p)}$
is an Asymptotic
$\mathfrak {X}_{\text {awi}}^{(p)}$
is an Asymptotic
![]() $\ell _p$
space. This saturation method is different from the method of saturation with increasing weights from [Reference Argyros and Motakis9], used to define spaces with no subspaces admitting a unique asymptotic model. It does not seem possible to use the method of increasing weights to construct a space with a unique asymptotic model, that is, it is not appropriate for showing (b)
$\ell _p$
space. This saturation method is different from the method of saturation with increasing weights from [Reference Argyros and Motakis9], used to define spaces with no subspaces admitting a unique asymptotic model. It does not seem possible to use the method of increasing weights to construct a space with a unique asymptotic model, that is, it is not appropriate for showing (b)
![]() (a)
(a)
![]() $_p$
. On the other hand, the method of asymptotically weakly incomparable constraints yields spaces with a unique asymptotic model, and thus it cannot be used to show (c)
$_p$
. On the other hand, the method of asymptotically weakly incomparable constraints yields spaces with a unique asymptotic model, and thus it cannot be used to show (c)
![]() (b)
(b)
![]() $_p$
. This method will be discussed in detail in Part 1.
$_p$
. This method will be discussed in detail in Part 1.
In the case of
![]() $1<p<\infty $
, it is possible to obtain a stronger result. Namely, for every countable ordinal
$1<p<\infty $
, it is possible to obtain a stronger result. Namely, for every countable ordinal
![]() $\xi $
, the space separating the two asymptotic properties additionally satisfies the property that every block subspace contains an
$\xi $
, the space separating the two asymptotic properties additionally satisfies the property that every block subspace contains an
![]() $\ell _1$
-tree of order
$\ell _1$
-tree of order
![]() $\omega ^{\xi }$
. This is achieved using the attractors method, which was first introduced in [Reference Argyros, Arvanitakis, Tolias, Castillo and Johnson3] and later also used in [Reference Argyros, Manoussakis and Pelczar-Barwacz10]. The precise statement of this result is the following.
$\omega ^{\xi }$
. This is achieved using the attractors method, which was first introduced in [Reference Argyros, Arvanitakis, Tolias, Castillo and Johnson3] and later also used in [Reference Argyros, Manoussakis and Pelczar-Barwacz10]. The precise statement of this result is the following.
Theorem 1.5 ([Reference Argyros, Georgiou, Manoussakis and Motakis7]).
For every
![]() $1<p<\infty $
and every infinite countable ordinal
$1<p<\infty $
and every infinite countable ordinal
![]() $\xi $
, there exists a hereditarily indecomposable reflexive Banach space
$\xi $
, there exists a hereditarily indecomposable reflexive Banach space
![]() $\mathfrak {X}^{(p)}_{\xi }$
that admits
$\mathfrak {X}^{(p)}_{\xi }$
that admits
![]() $\ell _p$
as a uniformly unique joint spreading model with respect to the family of normalised block sequences and whose every subspace contains an
$\ell _p$
as a uniformly unique joint spreading model with respect to the family of normalised block sequences and whose every subspace contains an
![]() $\ell _1$
-block tree of order
$\ell _1$
-block tree of order
![]() $\omega ^{\xi }$
.
$\omega ^{\xi }$
.
However, in the case of
![]() $\ell _1$
, we are not able to construct a space whose every subspace contains a well-founded tree which is either
$\ell _1$
, we are not able to construct a space whose every subspace contains a well-founded tree which is either
![]() $\ell _p$
for some
$\ell _p$
for some
![]() $1<p<\infty $
or
$1<p<\infty $
or
![]() $c_0$
. This case is more delicate, since as we mentioned, the two properties are in fact equivalent in its dual problem for spaces not containing
$c_0$
. This case is more delicate, since as we mentioned, the two properties are in fact equivalent in its dual problem for spaces not containing
![]() $\ell _1$
.
$\ell _1$
.
The paper is organised as follows: In Section 2, we recall the notions of Schreier families and special convex combinations and prove some of their basic properties, while Section 3 contains the precise definitions of the aforementioned asymptotic structures. In Section 4, we recall certain combinatorial results concerning measures on countably branching well-founded trees from [Reference Argyros, Georgiou and Motakis8], which are a key ingredient in the proof that
![]() $\mathfrak {X}^{(p)}_{\text {awi}}$
admits
$\mathfrak {X}^{(p)}_{\text {awi}}$
admits
![]() $\ell _p$
as a unique asymptotic model for
$\ell _p$
as a unique asymptotic model for
![]() $1\le p <\infty $
. We then split the remainder of the paper into two main parts, each dedicated to the definition and properties of
$1\le p <\infty $
. We then split the remainder of the paper into two main parts, each dedicated to the definition and properties of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
and
$\mathfrak {X}_{\text {awi}}^{(1)}$
and
![]() $\mathfrak {X}_{\text {awi}}^{(p)}$
for
$\mathfrak {X}_{\text {awi}}^{(p)}$
for
![]() $p=2$
, respectively. The construction of
$p=2$
, respectively. The construction of
![]() $\mathfrak {X}_{\text {awi}}^{(p)}$
for
$\mathfrak {X}_{\text {awi}}^{(p)}$
for
![]() $1<p<\infty $
and
$1<p<\infty $
and
![]() $p\neq 2$
follows as an easy modification of our construction and is omitted. Each of these parts contains an introduction in which we describe the main key points of each construction. Finally, we include two appendices containing variants of the basic inequality, which has been used repeatedly in the past in several related constructions (see, e.g. [Reference Argyros, Arvanitakis, Tolias, Castillo and Johnson3], [Reference Argyros and Motakis9], [Reference Argyros, Manoussakis and Pelczar-Barwacz10] and [Reference Deliyanni and Manoussakis16]).
$p\neq 2$
follows as an easy modification of our construction and is omitted. Each of these parts contains an introduction in which we describe the main key points of each construction. Finally, we include two appendices containing variants of the basic inequality, which has been used repeatedly in the past in several related constructions (see, e.g. [Reference Argyros, Arvanitakis, Tolias, Castillo and Johnson3], [Reference Argyros and Motakis9], [Reference Argyros, Manoussakis and Pelczar-Barwacz10] and [Reference Deliyanni and Manoussakis16]).
2 Preliminaries
In this section, we recall some necessary definitions, namely, the Schreier families
![]() $(\mathcal {S}_n)_n$
[Reference Alspach and Argyros2] and the corresponding repeated averages
$(\mathcal {S}_n)_n$
[Reference Alspach and Argyros2] and the corresponding repeated averages
![]() $\{a(n,L):n\in \mathbb {N},\; L\in [\mathbb {N}]^{\infty }\}$
[Reference Argyros, Mercourakis and Tsarpalias11] which we call n-averages, as well as the notion of special convex combinations. For a more thorough discussion of the above, we refer the reader to [Reference Argyros and Tolias13]. We begin with some useful notation.
$\{a(n,L):n\in \mathbb {N},\; L\in [\mathbb {N}]^{\infty }\}$
[Reference Argyros, Mercourakis and Tsarpalias11] which we call n-averages, as well as the notion of special convex combinations. For a more thorough discussion of the above, we refer the reader to [Reference Argyros and Tolias13]. We begin with some useful notation.
Notation. By
![]() $\mathbb {N}=\{1,2,\ldots \}$
, we denote the set of all positive integers. We will use capital letters, such as
$\mathbb {N}=\{1,2,\ldots \}$
, we denote the set of all positive integers. We will use capital letters, such as
![]() $L,M,N,\ldots $
(respectively, lower case letters, such as
$L,M,N,\ldots $
(respectively, lower case letters, such as
![]() $s,t,u,\ldots $
) to denote infinite subsets (respectively, finite subsets) of
$s,t,u,\ldots $
) to denote infinite subsets (respectively, finite subsets) of
![]() $\mathbb {N}$
. For every infinite subset L of
$\mathbb {N}$
. For every infinite subset L of
![]() $\mathbb {N}$
, the notation
$\mathbb {N}$
, the notation
![]() $[L]^{\infty }$
(respectively,
$[L]^{\infty }$
(respectively,
![]() $[L]^{<\infty }$
) stands for the set of all infinite (respectively, finite) subsets of L. For every
$[L]^{<\infty }$
) stands for the set of all infinite (respectively, finite) subsets of L. For every
![]() $s\in [\mathbb {N}]^{<\infty }$
, by
$s\in [\mathbb {N}]^{<\infty }$
, by
![]() $|s|$
, we denote the cardinality of s. For
$|s|$
, we denote the cardinality of s. For
![]() $L\in [\mathbb {N}]^{\infty }$
and
$L\in [\mathbb {N}]^{\infty }$
and
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $[L]^k$
(respectively,
$[L]^k$
(respectively,
![]() $[L]^{\le k}$
) is the set of all
$[L]^{\le k}$
) is the set of all
![]() $s\in [L]^{<\infty }$
with
$s\in [L]^{<\infty }$
with
![]() $|s|=k$
(respectively,
$|s|=k$
(respectively,
![]() $|s|\le k$
). For every
$|s|\le k$
). For every
![]() $s,t\in [\mathbb {N}]^{<\infty }$
, we write
$s,t\in [\mathbb {N}]^{<\infty }$
, we write
![]() $s<t$
if at least one of them is the empty set, or
$s<t$
if at least one of them is the empty set, or
![]() $\max s<\min t$
. Also for
$\max s<\min t$
. Also for
![]() $\emptyset \neq s\in [\mathbb {N}]^{< \infty }$
and
$\emptyset \neq s\in [\mathbb {N}]^{< \infty }$
and
![]() $n\in \mathbb {N}$
, we write
$n\in \mathbb {N}$
, we write
![]() $n<s$
if
$n<s$
if
![]() $n<\min s$
. We shall identify strictly increasing sequences in
$n<\min s$
. We shall identify strictly increasing sequences in
![]() $\mathbb {N}$
with their corresponding range, that is, we view every strictly increasing sequence in
$\mathbb {N}$
with their corresponding range, that is, we view every strictly increasing sequence in
![]() $\mathbb {N}$
as a subset of
$\mathbb {N}$
as a subset of
![]() $\mathbb {N}$
and, conversely, every subset of
$\mathbb {N}$
and, conversely, every subset of
![]() $\mathbb {N}$
as the sequence resulting from the increasing order of its elements. Thus, for an infinite subset
$\mathbb {N}$
as the sequence resulting from the increasing order of its elements. Thus, for an infinite subset
![]() $L=\{l_1<l_2<\ldots \}$
of
$L=\{l_1<l_2<\ldots \}$
of
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $i\in \mathbb {N}$
, we set
$i\in \mathbb {N}$
, we set
![]() $L(i)=l_i$
and, similarly, for a finite subset
$L(i)=l_i$
and, similarly, for a finite subset
![]() $s=\{n_1<\ldots <n_k\}$
of
$s=\{n_1<\ldots <n_k\}$
of
![]() $\mathbb {N}$
and for
$\mathbb {N}$
and for
![]() $1\le i\le k$
, we set
$1\le i\le k$
, we set
![]() $s(i)=n_i$
.
$s(i)=n_i$
.
Finally, throughout the paper, we follow [Reference Lindenstrauss and Tzafriri23] (see also [Reference Albiac and Kalton1]) for standard notation and terminology concerning Banach space theory. For
![]() $x\in c_{00}(\mathbb {N})$
, we denote
$x\in c_{00}(\mathbb {N})$
, we denote
![]() $\text {supp}(x)=\{n\in \mathbb {N}:x(n)\neq 0\}$
, and by
$\text {supp}(x)=\{n\in \mathbb {N}:x(n)\neq 0\}$
, and by
![]() $\operatorname {\mathrm {range}}(x)$
, the minimum interval of
$\operatorname {\mathrm {range}}(x)$
, the minimum interval of
![]() $\mathbb {N}$
containing
$\mathbb {N}$
containing
![]() $\text {supp}(x)$
. Moreover, for
$\text {supp}(x)$
. Moreover, for
![]() $x,y\in c_{00}(\mathbb {N})$
, we write
$x,y\in c_{00}(\mathbb {N})$
, we write
![]() $x<y$
to denote that
$x<y$
to denote that
![]() $\operatorname {\mathrm {maxsupp}}(x)<\operatorname {\mathrm {minsupp}}(y)$
.
$\operatorname {\mathrm {maxsupp}}(x)<\operatorname {\mathrm {minsupp}}(y)$
.
2.1 Schreier families
For a family
![]() $\mathcal {M}$
and a sequence
$\mathcal {M}$
and a sequence
![]() $(E_i)_{i=1}^k$
of finite subsets of
$(E_i)_{i=1}^k$
of finite subsets of
![]() $\mathbb {N}$
, we say that
$\mathbb {N}$
, we say that
![]() $(E_i)_{i=1}^k$
is
$(E_i)_{i=1}^k$
is
![]() $\mathcal {M}$
-admissible if there is
$\mathcal {M}$
-admissible if there is
![]() $\{m_1,\ldots ,m_k\}\in \mathcal {M}$
, such that
$\{m_1,\ldots ,m_k\}\in \mathcal {M}$
, such that
![]() $m_1\le E_1<m_2\le E_2<\cdots <m_k\le E_k$
. Moreover, a sequence
$m_1\le E_1<m_2\le E_2<\cdots <m_k\le E_k$
. Moreover, a sequence
![]() $(x_i)_{i=1}^k$
in
$(x_i)_{i=1}^k$
in
![]() $c_{00}(\mathbb {N})$
is called
$c_{00}(\mathbb {N})$
is called
![]() $\mathcal {M}$
-admissible if
$\mathcal {M}$
-admissible if
![]() $(\text {supp} (x_i))_{i=1}^k$
is
$(\text {supp} (x_i))_{i=1}^k$
is
![]() $\mathcal {M}$
-admissible. In the case where
$\mathcal {M}$
-admissible. In the case where
![]() $\mathcal {M}$
is a spreading family (i.e. whenever
$\mathcal {M}$
is a spreading family (i.e. whenever
![]() $E=\{m_1,\ldots ,m_k\}\in \mathcal {M}$
and
$E=\{m_1,\ldots ,m_k\}\in \mathcal {M}$
and
![]() $F=\{n_1<\ldots <n_k\}$
satisfy
$F=\{n_1<\ldots <n_k\}$
satisfy
![]() $m_i\le n_i$
,
$m_i\le n_i$
,
![]() $i=1,\ldots ,k$
, then
$i=1,\ldots ,k$
, then
![]() $F\in \mathcal {M}$
), a sequence
$F\in \mathcal {M}$
), a sequence
![]() $(E_i)_{i=1}^k$
is
$(E_i)_{i=1}^k$
is
![]() $\mathcal {M}$
-admissible if
$\mathcal {M}$
-admissible if
![]() $\{\min E_i:i=1,\ldots ,k\}\in \mathcal {M}$
, and thus a sequence of vectors
$\{\min E_i:i=1,\ldots ,k\}\in \mathcal {M}$
, and thus a sequence of vectors
![]() $(x_i)_{i=1}^k$
in
$(x_i)_{i=1}^k$
in
![]() $c_{00}(\mathbb {N})$
is
$c_{00}(\mathbb {N})$
is
![]() $\mathcal {M}$
-admissible if
$\mathcal {M}$
-admissible if
![]() $\{\min \text {supp} (x_i):i=1,\ldots ,k\}\in \mathcal {M}$
.
$\{\min \text {supp} (x_i):i=1,\ldots ,k\}\in \mathcal {M}$
.
For
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\mathcal {N}$
families of finite subsets of
$\mathcal {N}$
families of finite subsets of
![]() $\mathbb {N}$
, we define the convolution of
$\mathbb {N}$
, we define the convolution of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
as follows:
$\mathcal {N}$
as follows:
 $$ \begin{align*} \mathcal{M}*\mathcal{N}=\Big\{ & E\subset\mathbb{N}:\text{ there exists an }\mathcal{M}\text{-admissible finite sequence }\\&(E_i)_{i=1}^k\text{ in }\mathcal{N},\text{ such that }E=\cup_{i=1}^kE_i\Big\}\cup\big\{\emptyset\big\}. \end{align*} $$
$$ \begin{align*} \mathcal{M}*\mathcal{N}=\Big\{ & E\subset\mathbb{N}:\text{ there exists an }\mathcal{M}\text{-admissible finite sequence }\\&(E_i)_{i=1}^k\text{ in }\mathcal{N},\text{ such that }E=\cup_{i=1}^kE_i\Big\}\cup\big\{\emptyset\big\}. \end{align*} $$
The Schreier families
![]() $(\mathcal {S}_n)_{n\in \mathbb {N}}$
are defined inductively as follows:
$(\mathcal {S}_n)_{n\in \mathbb {N}}$
are defined inductively as follows:
and if
![]() $\mathcal {S}_n$
, for some
$\mathcal {S}_n$
, for some
![]() $n\in \mathbb {N}$
, has been defined, then
$n\in \mathbb {N}$
, has been defined, then
It follows easily by induction that for every
![]() $n,m\in \mathbb {N}$
,
$n,m\in \mathbb {N}$
,
Furthermore, for each
![]() $n\in \mathbb {N}$
, the family
$n\in \mathbb {N}$
, the family
![]() $\mathcal {S}_n$
is regular. This means that it includes the singletons, it is hereditary, that is, if
$\mathcal {S}_n$
is regular. This means that it includes the singletons, it is hereditary, that is, if
![]() $E\in \mathcal {S}_n$
and
$E\in \mathcal {S}_n$
and
![]() $F\subset E$
, then
$F\subset E$
, then
![]() $F\in \mathcal {S}_n$
, it is spreading and finally it is compact, identified as a subset of
$F\in \mathcal {S}_n$
, it is spreading and finally it is compact, identified as a subset of
![]() $\{0,1\}^{\mathbb {N}}$
.
$\{0,1\}^{\mathbb {N}}$
.
For each
![]() $n\in \mathbb {N}$
, we also define the regular family
$n\in \mathbb {N}$
, we also define the regular family
Then, for
![]() $n,m\in \mathbb {N}$
, we are interested in the family
$n,m\in \mathbb {N}$
, we are interested in the family
![]() $\mathcal {S}_n*\mathcal {A}_m$
, that is, the family of all subsets of
$\mathcal {S}_n*\mathcal {A}_m$
, that is, the family of all subsets of
![]() $\mathbb {N}$
of the form
$\mathbb {N}$
of the form
![]() $E=\cup ^k_{i=1}E_i$
, where
$E=\cup ^k_{i=1}E_i$
, where
![]() $E_1<\ldots <E_k$
,
$E_1<\ldots <E_k$
,
![]() $\#E_i\le m $
for
$\#E_i\le m $
for
![]() $i=1,\ldots ,k$
and
$i=1,\ldots ,k$
and
![]() $\{\min E_i:1\le i \le k\}\in \mathcal {S}_n$
. In fact, any such E is the union of at most m sets in
$\{\min E_i:1\le i \le k\}\in \mathcal {S}_n$
. In fact, any such E is the union of at most m sets in
![]() $\mathcal {S}_n$
, and moreover, if
$\mathcal {S}_n$
, and moreover, if
![]() $m\le E$
, then
$m\le E$
, then
![]() $E\in \mathcal {S}_{n+1}$
, as we show next.
$E\in \mathcal {S}_{n+1}$
, as we show next.
Lemma 2.1. For every
![]() $n,m\in \mathbb {N}$
,
$n,m\in \mathbb {N}$
,
-
(i)
 $\mathcal {S}_n*\mathcal {A}_m\subset \mathcal {A}_m*\mathcal {S}_n$
and
$\mathcal {S}_n*\mathcal {A}_m\subset \mathcal {A}_m*\mathcal {S}_n$
and -
(ii) if
 $E\in \mathcal {S}_n*\mathcal {A}_m$
with
$E\in \mathcal {S}_n*\mathcal {A}_m$
with
 $m\le E$
, then
$m\le E$
, then
 $E\in \mathcal {S}_{n+1}$
.
$E\in \mathcal {S}_{n+1}$
.
Remark 2.2. Let
![]() $k,m\in \mathbb {N}$
and F be a subset of
$k,m\in \mathbb {N}$
and F be a subset of
![]() $\mathbb {N}$
with
$\mathbb {N}$
with
![]() $\#F\le km$
and
$\#F\le km$
and
![]() $k\le F$
. Set
$k\le F$
. Set
![]() $d=\max \{1,\lfloor \#F/m \rfloor \}$
, and define
$d=\max \{1,\lfloor \#F/m \rfloor \}$
, and define
![]() $F_j=\{F(n):n=(j-1)d+1,\ldots ,jd\}$
for each
$F_j=\{F(n):n=(j-1)d+1,\ldots ,jd\}$
for each
![]() $j=1,\ldots ,m-1$
and
$j=1,\ldots ,m-1$
and
![]() $F_m=F\setminus \cup _{j=1}^{m-1}F_j$
. Then, it is immediate to check that
$F_m=F\setminus \cup _{j=1}^{m-1}F_j$
. Then, it is immediate to check that
![]() $F_j\in \mathcal {S}_1$
for every
$F_j\in \mathcal {S}_1$
for every
![]() $i=1,\ldots ,m$
.
$i=1,\ldots ,m$
.
Proof of Lemma 2.1.
Fix
![]() $n,m\in \mathbb {N}$
. We prove (i) by induction on
$n,m\in \mathbb {N}$
. We prove (i) by induction on
![]() $n\in \mathbb {N}$
. For
$n\in \mathbb {N}$
. For
![]() $n=1$
, let
$n=1$
, let
![]() $E\in \mathcal {S}_1*\mathcal {A}_m$
, that is,
$E\in \mathcal {S}_1*\mathcal {A}_m$
, that is,
![]() $E=\cup _{i=1}^kE_i$
with
$E=\cup _{i=1}^kE_i$
with
![]() $k\le E_1<\ldots <E_k$
and
$k\le E_1<\ldots <E_k$
and
![]() $\#E_i\le m$
for every
$\#E_i\le m$
for every
![]() $i=1,\ldots ,k$
. Since
$i=1,\ldots ,k$
. Since
![]() $\#E\le km$
, Remark 2.2 yields a partition
$\#E\le km$
, Remark 2.2 yields a partition
![]() $E=\cup _{j=1}^m F_j$
with
$E=\cup _{j=1}^m F_j$
with
![]() $F_j\in \mathcal {S}_1$
for every
$F_j\in \mathcal {S}_1$
for every
![]() $j=1,\ldots ,m$
, and, hence,
$j=1,\ldots ,m$
, and, hence,
![]() $E\in \mathcal {A}_m*\mathcal {S}_1$
.
$E\in \mathcal {A}_m*\mathcal {S}_1$
.
Suppose that (i) holds for some
![]() $n\in \mathbb {N}$
and let
$n\in \mathbb {N}$
and let
![]() $E\in \mathcal {S}_{n+1}*\mathcal {A}_m$
. Then
$E\in \mathcal {S}_{n+1}*\mathcal {A}_m$
. Then
![]() $E=\cup _{i=1}^kE_i$
for an
$E=\cup _{i=1}^kE_i$
for an
![]() $\mathcal {S}_{n+1}$
-admissible sequence
$\mathcal {S}_{n+1}$
-admissible sequence
![]() $(E_i)_{i=1}^k$
with
$(E_i)_{i=1}^k$
with
![]() $\#E_i\le m$
for every
$\#E_i\le m$
for every
![]() $i=1,\ldots ,m$
. Hence,
$i=1,\ldots ,m$
. Hence,
![]() $\{\min E_i:i=1,\ldots ,k\}=\cup _{j=1}^lF_j$
, where
$\{\min E_i:i=1,\ldots ,k\}=\cup _{j=1}^lF_j$
, where
![]() $F_j\in \mathcal {S}_n$
for every
$F_j\in \mathcal {S}_n$
for every
![]() $j=1,\ldots ,l$
and
$j=1,\ldots ,l$
and
![]() $l\le F_1<\cdots <F_l$
. Define, for each
$l\le F_1<\cdots <F_l$
. Define, for each
![]() $j=1,\ldots ,l$
,
$j=1,\ldots ,l$
,
and note that
![]() $G_j\in \mathcal {S}_{n}*\mathcal {A}_m$
since
$G_j\in \mathcal {S}_{n}*\mathcal {A}_m$
since
![]() $F_j\in \mathcal {S}_n$
. Hence, for every
$F_j\in \mathcal {S}_n$
. Hence, for every
![]() $j=1,\ldots ,l$
, the inductive hypothesis implies that
$j=1,\ldots ,l$
, the inductive hypothesis implies that
![]() $G_j\in \mathcal {A}_m*\mathcal {S}_n$
, that is,
$G_j\in \mathcal {A}_m*\mathcal {S}_n$
, that is,
![]() $G_j=\cup _{i=1}^{m_j}G^j_i$
with
$G_j=\cup _{i=1}^{m_j}G^j_i$
with
![]() $m_j\le m$
and
$m_j\le m$
and
![]() $G^j_i\in \mathcal {S}_n$
for all
$G^j_i\in \mathcal {S}_n$
for all
![]() $i=1,\ldots ,m_j$
. Define
$i=1,\ldots ,m_j$
. Define
Observe that
![]() $H\in \mathcal {S}_1*\mathcal {A}_m$
and apply Remark 2.2 to obtain a partition
$H\in \mathcal {S}_1*\mathcal {A}_m$
and apply Remark 2.2 to obtain a partition
![]() $H=\cup _{q=1}^mH_q$
, where
$H=\cup _{q=1}^mH_q$
, where
![]() $H_q\in \mathcal {S}_1$
for every
$H_q\in \mathcal {S}_1$
for every
![]() $q=1,\ldots ,m$
. Finally, define
$q=1,\ldots ,m$
. Finally, define
for each
![]() $q=1,\ldots ,m$
, and observe that
$q=1,\ldots ,m$
, and observe that
![]() $E=\cup _{q=1}^m\Delta _q$
and that
$E=\cup _{q=1}^m\Delta _q$
and that
![]() $\Delta _q\in \mathcal {S}_1*S_{n}=S_{n+1}$
since
$\Delta _q\in \mathcal {S}_1*S_{n}=S_{n+1}$
since
![]() $H_q\in \mathcal {S}_1$
and
$H_q\in \mathcal {S}_1$
and
![]() $G^j_i\in \mathcal {S}_{n}$
. Thus, we conclude that
$G^j_i\in \mathcal {S}_{n}$
. Thus, we conclude that
![]() $E\in \mathcal {A}_m*\mathcal {S}_{n+1}$
.
$E\in \mathcal {A}_m*\mathcal {S}_{n+1}$
.
Finally, note that (ii) is an immediate consequence of (i).
2.2 Repeated averages
The notion of repeated averages was first defined in [Reference Argyros, Mercourakis and Tsarpalias11]. The notation we use below, however, is somewhat different, and we instead follow the one found in [Reference Argyros and Tolias13], namely,
![]() $\{a(n,L):n\in \mathbb {N},\; L\in [\mathbb {N}]^{\infty }\}$
. The
$\{a(n,L):n\in \mathbb {N},\; L\in [\mathbb {N}]^{\infty }\}$
. The
![]() $n-$
averages
$n-$
averages
![]() $a(n,L)$
are defined as elements of
$a(n,L)$
are defined as elements of
![]() $c_{00}(\mathbb {N})$
in the following manner.
$c_{00}(\mathbb {N})$
in the following manner.
Let
![]() $(e_j)_j$
denote the unit vector basis of
$(e_j)_j$
denote the unit vector basis of
![]() $c_{00}(\mathbb {N})$
and
$c_{00}(\mathbb {N})$
and
![]() $L\in [\mathbb {N}]^{\infty }$
. For
$L\in [\mathbb {N}]^{\infty }$
. For
![]() $n=0$
, we define
$n=0$
, we define
![]() $a(0,L)=e_{l_1}$
, where
$a(0,L)=e_{l_1}$
, where
![]() $l_1=\min L$
. Suppose that
$l_1=\min L$
. Suppose that
![]() $a(n,M)$
has been defined for some
$a(n,M)$
has been defined for some
![]() $n\in \mathbb {N}$
and every
$n\in \mathbb {N}$
and every
![]() $M\in [\mathbb {N}]^{\infty }$
. We define
$M\in [\mathbb {N}]^{\infty }$
. We define
![]() $a(n+1,L)$
in the following way: We set
$a(n+1,L)$
in the following way: We set
![]() $L_1=L$
and
$L_1=L$
and
![]() $L_k=L_{k-1}\setminus \text {supp}( a(n,L_{k-1}))$
for
$L_k=L_{k-1}\setminus \text {supp}( a(n,L_{k-1}))$
for
![]() $k=2,\ldots ,l_1$
and finally define
$k=2,\ldots ,l_1$
and finally define
Remark 2.3. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $L\in [\mathbb {N}]^{\infty }$
. The following properties are easily established by induction.
$L\in [\mathbb {N}]^{\infty }$
. The following properties are easily established by induction.
-
(i)
 $a(n,L)$
is a convex combination of the unit vector basis of
$a(n,L)$
is a convex combination of the unit vector basis of
 $c_{00}(\mathbb {N})$
.
$c_{00}(\mathbb {N})$
. -
(ii)
 $\|a(n,L)\|_{\ell _1}=1$
and
$\|a(n,L)\|_{\ell _1}=1$
and
 $a(n,L)(k)\ge 0$
for all
$a(n,L)(k)\ge 0$
for all
 $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
. -
(iii)
 $\text {supp} (a(n,L))$
is the maximal initial segment of L contained in
$\text {supp} (a(n,L))$
is the maximal initial segment of L contained in
 $\mathcal {S}_n$
.
$\mathcal {S}_n$
. -
(iv)
 $\|a(n,L)\|_{\infty }= l_1^{-n}$
, where
$\|a(n,L)\|_{\infty }= l_1^{-n}$
, where
 $l_1=\min L$
.
$l_1=\min L$
. -
(v) If
 $\text {supp}(a(n,L))=\{i_1<\ldots <i_d\}$
and
$\text {supp}(a(n,L))=\{i_1<\ldots <i_d\}$
and
 $a(n,L)=\sum _{k=1}^da_{i_k}e_{i_k}$
, then we have that
$a(n,L)=\sum _{k=1}^da_{i_k}e_{i_k}$
, then we have that
 $a_{i_1}\ge \ldots \ge a_{i_d}$
.
$a_{i_1}\ge \ldots \ge a_{i_d}$
.
A proof of the following proposition can be found in [Reference Argyros and Tolias13].
Proposition 2.4. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $L\in [\mathbb {N}]^{\infty }$
. For every
$L\in [\mathbb {N}]^{\infty }$
. For every
![]() $F\in \mathcal {S}_{n-1}$
, we have that
$F\in \mathcal {S}_{n-1}$
, we have that
 $$\begin{align*}\sum_{k\in F}a(n,L)(k)<\frac{3}{\min L}. \end{align*}$$
$$\begin{align*}\sum_{k\in F}a(n,L)(k)<\frac{3}{\min L}. \end{align*}$$
2.3 Special convex combinations
Here, we recall the notion of
![]() $(n,\varepsilon )$
-special convex combinations, where
$(n,\varepsilon )$
-special convex combinations, where
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\varepsilon>0$
(see [Reference Argyros and Deliyanni5] and [Reference Argyros and Tolias13]).
$\varepsilon>0$
(see [Reference Argyros and Deliyanni5] and [Reference Argyros and Tolias13]).
Definition 2.5. For
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\varepsilon>0$
, a convex combination
$\varepsilon>0$
, a convex combination
![]() $\sum _{i\in F}c_ie_i$
, of the unit vector basis
$\sum _{i\in F}c_ie_i$
, of the unit vector basis
![]() $(e_i)_i$
of
$(e_i)_i$
of
![]() $c_{00}(\mathbb {N})$
is called an
$c_{00}(\mathbb {N})$
is called an
![]() $(n,\varepsilon )$
-basic special convex combination (or an
$(n,\varepsilon )$
-basic special convex combination (or an
![]() $(n,\varepsilon )$
-basic s.c.c.) if
$(n,\varepsilon )$
-basic s.c.c.) if
-
(i)
 $F\in \mathcal {S}_n$
and
$F\in \mathcal {S}_n$
and -
(ii) for any
 $G\subset F$
with
$G\subset F$
with
 $G\in S_{n-1}$
, we have that
$G\in S_{n-1}$
, we have that
 $\sum _{i\in G}c_i<\varepsilon $
.
$\sum _{i\in G}c_i<\varepsilon $
.
We will also call
![]() $\sum _{i\in F}c_i^{1/2}e_i$
a
$\sum _{i\in F}c_i^{1/2}e_i$
a
![]() $(2,n,\varepsilon )$
-basic special convex combination.
$(2,n,\varepsilon )$
-basic special convex combination.
As follows from Proposition 2.4, every n-average
![]() $a(n,L)$
is an
$a(n,L)$
is an
![]() $(n,3/\min L)$
-basic s.c.c., and this yields the following.
$(n,3/\min L)$
-basic s.c.c., and this yields the following.
Proposition 2.6. Let
![]() $M\in [\mathbb {N}]^{\infty }$
,
$M\in [\mathbb {N}]^{\infty }$
,
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\varepsilon>0$
. Then there is a
$\varepsilon>0$
. Then there is a
![]() $k\in \mathbb {N}$
, such that for any
$k\in \mathbb {N}$
, such that for any
![]() $F\subset M$
, such that F is maximal in
$F\subset M$
, such that F is maximal in
![]() $\mathcal {S}_n$
and
$\mathcal {S}_n$
and
![]() $k\le \min F$
, there exists an
$k\le \min F$
, there exists an
![]() $(n,\varepsilon )$
-basic s.c.c.
$(n,\varepsilon )$
-basic s.c.c.
![]() $x\in c_{00}(\mathbb {N})$
with
$x\in c_{00}(\mathbb {N})$
with
![]() $\text {supp} (x)=F$
.
$\text {supp} (x)=F$
.
Clearly, this also implies the existence of
![]() $(2,n,\varepsilon )$
-basic special convex combinations by taking the square roots of the coefficients of an
$(2,n,\varepsilon )$
-basic special convex combinations by taking the square roots of the coefficients of an
![]() $(n,\varepsilon )$
-b.s.c.c.
$(n,\varepsilon )$
-b.s.c.c.
Definition 2.7. Let
![]() $x_1<\ldots <x_d$
be vectors in
$x_1<\ldots <x_d$
be vectors in
![]() $c_{00}(\mathbb {N})$
, and define
$c_{00}(\mathbb {N})$
, and define
![]() $t_i=\min \text {supp} (x_i)$
,
$t_i=\min \text {supp} (x_i)$
,
![]() $i=1,\ldots ,d$
. We say that the vector
$i=1,\ldots ,d$
. We say that the vector
![]() $\sum _{i=1}^dc_ix_i$
is an
$\sum _{i=1}^dc_ix_i$
is an
![]() $(n,\varepsilon )$
-special convex combination (or an
$(n,\varepsilon )$
-special convex combination (or an
![]() $(n,\varepsilon $
)-s.c.c.) for some
$(n,\varepsilon $
)-s.c.c.) for some
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\varepsilon>0$
if
$\varepsilon>0$
if
![]() $\sum _{i=1}^d c_ie_{t_i}$
is an
$\sum _{i=1}^d c_ie_{t_i}$
is an
![]() $(n,\varepsilon )$
-basic s.c.c. and a
$(n,\varepsilon )$
-basic s.c.c. and a
![]() $(2,n,\varepsilon )$
-special convex combination if
$(2,n,\varepsilon )$
-special convex combination if
![]() $\sum _{i=1}^d c_ie_{t_i}$
is a
$\sum _{i=1}^d c_ie_{t_i}$
is a
![]() $(2,n,\varepsilon )$
-basic s.c.c.
$(2,n,\varepsilon )$
-basic s.c.c.
3 Asymptotic structures
Let us recall the definitions of the asymptotic notions that appear in the results of this paper and were mentioned in the Introduction. Namely, asymptotic models, joint spreading models and the notions of Asymptotic
![]() $\ell _p$
and Asymptotic
$\ell _p$
and Asymptotic
![]() $c_0$
spaces. For a more thorough discussion, including several open problems and known results, we refer the reader to [Reference Argyros and Motakis9, Section 3].
$c_0$
spaces. For a more thorough discussion, including several open problems and known results, we refer the reader to [Reference Argyros and Motakis9, Section 3].
Definition 3.1 [Reference Halbeisen and Odell20].
An infinite array of sequences
![]() $(x^{i}_j)_j$
,
$(x^{i}_j)_j$
,
![]() $i\in \mathbb {N}$
, in a Banach space X, is said to generate a sequence
$i\in \mathbb {N}$
, in a Banach space X, is said to generate a sequence
![]() $(e_i)_i$
, in a seminormed space E, as an asymptotic model if for every
$(e_i)_i$
, in a seminormed space E, as an asymptotic model if for every
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $n\in \mathbb {N}$
, there is a
$n\in \mathbb {N}$
, there is a
![]() $k_0\in \mathbb {N}$
, such that for any natural numbers
$k_0\in \mathbb {N}$
, such that for any natural numbers
![]() $k_0\leq k_1<\cdots <k_n$
and any scalars
$k_0\leq k_1<\cdots <k_n$
and any scalars
![]() $a_1,\ldots ,a_n$
in
$a_1,\ldots ,a_n$
in
![]() $[-1,1]$
, we have
$[-1,1]$
, we have
 $$\begin{align*}\Big|\big\|\sum_{i=1}^na_ix_{k_i}^{i}\big\| - \big\|\sum_{i=1}^na_ie_{i}\big\|\Big| < \varepsilon.\end{align*}$$
$$\begin{align*}\Big|\big\|\sum_{i=1}^na_ix_{k_i}^{i}\big\| - \big\|\sum_{i=1}^na_ie_{i}\big\|\Big| < \varepsilon.\end{align*}$$
A Banach space X is said to admit a unique asymptotic model with respect to a family
![]() $\mathscr {F}$
of normalised sequences in X if whenever two infinite arrays, consisting of sequences from
$\mathscr {F}$
of normalised sequences in X if whenever two infinite arrays, consisting of sequences from
![]() $\mathscr {F}$
, generate asymptotic models, then those must be equivalent. Typical families under consideration are those of normalised weakly null sequences, denoted
$\mathscr {F}$
, generate asymptotic models, then those must be equivalent. Typical families under consideration are those of normalised weakly null sequences, denoted
![]() $\mathscr {F}_0(X)$
, normalised Schauder basis sequences, denoted
$\mathscr {F}_0(X)$
, normalised Schauder basis sequences, denoted
![]() $\mathscr {F}(X)$
, or the family of all normalised block sequences of a fixed basis of X, if it has one, denoted
$\mathscr {F}(X)$
, or the family of all normalised block sequences of a fixed basis of X, if it has one, denoted
![]() $\mathscr {F}_b(X)$
.
$\mathscr {F}_b(X)$
.
Definition 3.2 [Reference Argyros, Georgiou, Lagos and Motakis6].
Let
![]() $M\in [\mathbb {N}]^{\infty }$
and
$M\in [\mathbb {N}]^{\infty }$
and
![]() $k\in \mathbb {N}$
. A plegma (respectively, strict plegma) family in
$k\in \mathbb {N}$
. A plegma (respectively, strict plegma) family in
![]() $[M]^k$
is a finite sequence
$[M]^k$
is a finite sequence
![]() $(s_i)_{i=1}^l$
in
$(s_i)_{i=1}^l$
in
![]() $[M]^k$
satisfying the following.
$[M]^k$
satisfying the following.
-
(i)
 $s_{i_1}(j_1)<s_{i_2}(j_2)$
for every
$s_{i_1}(j_1)<s_{i_2}(j_2)$
for every
 $1\le j_1<j_2\le k$
and
$1\le j_1<j_2\le k$
and
 $1\le i_1,i_2\le l$
.
$1\le i_1,i_2\le l$
. -
(ii)
 $s_{i_1}(j)\le s_{i_2}(j)$
(respectively,
$s_{i_1}(j)\le s_{i_2}(j)$
(respectively,
 $s_{i_1}(j)< s_{i_2}(j)$
) for all
$s_{i_1}(j)< s_{i_2}(j)$
) for all
 $1\le i_1<i_2\le l$
and
$1\le i_1<i_2\le l$
and
 $1\le j\le k$
.
$1\le j\le k$
.
For each
![]() $l\in \mathbb {N}$
, the set of all sequences
$l\in \mathbb {N}$
, the set of all sequences
![]() $(s_i)^l_{i=1}$
which are plegma families in
$(s_i)^l_{i=1}$
which are plegma families in
![]() $[M]^k$
will be denoted by
$[M]^k$
will be denoted by
![]() $Plm_l([M]^k)$
and that of the strict plegma ones by S-
$Plm_l([M]^k)$
and that of the strict plegma ones by S-
![]() $Plm_l([M]^k)$
.
$Plm_l([M]^k)$
.
Definition 3.3 [Reference Argyros, Georgiou, Lagos and Motakis6].
A finite array of sequences
![]() $(x^{i}_j)_j$
,
$(x^{i}_j)_j$
,
![]() $1\leq i\leq l$
, in a Banach space X, is said to generate another array of sequences
$1\leq i\leq l$
, in a Banach space X, is said to generate another array of sequences
![]() $(e_j^{i})_j$
,
$(e_j^{i})_j$
,
![]() $1\leq i\leq l$
, in a seminormed space E, as a joint spreading model if for every
$1\leq i\leq l$
, in a seminormed space E, as a joint spreading model if for every
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $n\in \mathbb {N}$
, there is a
$n\in \mathbb {N}$
, there is a
![]() $k_0\in \mathbb {N}$
, such that for any
$k_0\in \mathbb {N}$
, such that for any
![]() $(s_i)_{i=1}^l\in S$
-
$(s_i)_{i=1}^l\in S$
-
![]() $Plm_{l}([\mathbb {N}]^n)$
with
$Plm_{l}([\mathbb {N}]^n)$
with
![]() $k_0\le s_1(1)$
and for any
$k_0\le s_1(1)$
and for any
![]() $l\times n$
matrix
$l\times n$
matrix
![]() $A=(a_{ij})$
with entries in
$A=(a_{ij})$
with entries in
![]() $[-1,1]$
, we have that
$[-1,1]$
, we have that
 $$\begin{align*}\Big|\big\|\sum_{i=1}^l\sum_{j=1}^na_{ij}x_{s_i(j)}^{i}\big\| - \big\|\sum_{i=1}^l\sum_{j=1}^na_{ij}e_j^{i}\big\|\Big|<\varepsilon.\end{align*}$$
$$\begin{align*}\Big|\big\|\sum_{i=1}^l\sum_{j=1}^na_{ij}x_{s_i(j)}^{i}\big\| - \big\|\sum_{i=1}^l\sum_{j=1}^na_{ij}e_j^{i}\big\|\Big|<\varepsilon.\end{align*}$$
A Banach space X is said to admit a uniformly unique joint spreading model with respect to a family of normalised sequences
![]() $\mathscr {F}$
in X if there exists a constant C, such that whenever two arrays
$\mathscr {F}$
in X if there exists a constant C, such that whenever two arrays
![]() $(x_j^{i})_j$
and
$(x_j^{i})_j$
and
![]() $(y_j^{i})_j$
,
$(y_j^{i})_j$
,
![]() $1\leq i\leq l$
, of sequences from
$1\leq i\leq l$
, of sequences from
![]() $\mathscr {F}$
generate joint spreading models, then those must be C-equivalent. Moreover, a Banach space admits a uniformly unique joint spreading model with respect to a family
$\mathscr {F}$
generate joint spreading models, then those must be C-equivalent. Moreover, a Banach space admits a uniformly unique joint spreading model with respect to a family
![]() $\mathscr {F}$
if and only if it admits a unique asymptotic model with respect to
$\mathscr {F}$
if and only if it admits a unique asymptotic model with respect to
![]() $\mathscr {F}$
(see, e.g. [Reference Argyros, Georgiou, Lagos and Motakis6, Remark 4.21] or [Reference Argyros and Motakis9, Proposition 3.12]). In particular, if a space admits a uniformly unique joint spreading model with respect to some family
$\mathscr {F}$
(see, e.g. [Reference Argyros, Georgiou, Lagos and Motakis6, Remark 4.21] or [Reference Argyros and Motakis9, Proposition 3.12]). In particular, if a space admits a uniformly unique joint spreading model with respect to some family
![]() $\mathscr {F}$
satisfying certain conditions described in [Reference Argyros, Georgiou, Lagos and Motakis6, Proposition 4.9], then this is equivalent to some
$\mathscr {F}$
satisfying certain conditions described in [Reference Argyros, Georgiou, Lagos and Motakis6, Proposition 4.9], then this is equivalent to some
![]() $\ell _p$
. In order to show that a space admits some
$\ell _p$
. In order to show that a space admits some
![]() $\ell _p$
as a uniformly unique joint spreading model, it may be more convenient to prove (ii) of the following lemma, thereby avoiding the use of plegma families.
$\ell _p$
as a uniformly unique joint spreading model, it may be more convenient to prove (ii) of the following lemma, thereby avoiding the use of plegma families.
Lemma 3.4. Let X be a Banach space and
![]() $\mathscr {F}$
be a family of normalised sequences in X. Let also
$\mathscr {F}$
be a family of normalised sequences in X. Let also
![]() $1\le p<\infty $
. The following are equivalent.
$1\le p<\infty $
. The following are equivalent.
-
(i) X admits
 $\ell _p$
as a uniformly unique joint spreading model with respect to the family
$\ell _p$
as a uniformly unique joint spreading model with respect to the family
 $\mathscr {F}$
.
$\mathscr {F}$
. -
(ii) There exist constants
 $c,C>0$
, such that for every array
$c,C>0$
, such that for every array
 $(x^i_j)_j$
,
$(x^i_j)_j$
,
 $1\le i\le l$
, of sequences from
$1\le i\le l$
, of sequences from
 $\mathscr {F}$
, there is
$\mathscr {F}$
, there is
 $M=\{m_1<m_2<\ldots \}$
, an infinite subset of the naturals, such that for any choice of
$M=\{m_1<m_2<\ldots \}$
, an infinite subset of the naturals, such that for any choice of
 $1\le i_j\le l$
,
$1\le i_j\le l$
,
 $j\in M$
, every
$j\in M$
, every
 $F\subset M$
with
$F\subset M$
with
 $m_k\le F$
and
$m_k\le F$
and
 $|F|\le k$
and any choice of scalars
$|F|\le k$
and any choice of scalars
 $a_j$
,
$a_j$
,
 $j\in F$
,
$j\in F$
, $$\begin{align*}c \|(a_j)_{j\in F}\|_p \le \big\| \sum_{j\in F} a_j x^{i_j}_{j} \big\| \le C \|(a_j)_{j\in F}\|_p. \end{align*}$$
$$\begin{align*}c \|(a_j)_{j\in F}\|_p \le \big\| \sum_{j\in F} a_j x^{i_j}_{j} \big\| \le C \|(a_j)_{j\in F}\|_p. \end{align*}$$
Proof. Note that (i) implies that there are constants
![]() $c,C>0$
, such that for every array
$c,C>0$
, such that for every array
![]() $(x^i_j)_j$
,
$(x^i_j)_j$
,
![]() $1\le i\le l$
, of sequences from
$1\le i\le l$
, of sequences from
![]() $\mathscr {F}$
, there is
$\mathscr {F}$
, there is
![]() $N=\{n_1<n_2<\ldots \}$
, an infinite subset of the naturals, such that for any k, any strict plegma family
$N=\{n_1<n_2<\ldots \}$
, an infinite subset of the naturals, such that for any k, any strict plegma family
![]() $(s_i)_{i=1}^l\in S\text {-}Plm_l([N]^k)$
with
$(s_i)_{i=1}^l\in S\text {-}Plm_l([N]^k)$
with
![]() $n_k\le s_1(1)$
and any
$n_k\le s_1(1)$
and any
![]() $l\times k$
matrix
$l\times k$
matrix
![]() $A=(a_{ij})$
of scalars, we have that
$A=(a_{ij})$
of scalars, we have that
 $$\begin{align*}c \|(a_{ij})_{i=1,j=1}^{l,k}\|_p \le \big\| \sum_{i=1}^l\sum_{j=1}^k a_{ij} x^{i}_{s_i(j)} \big\| \le C \|(a_{ij})_{i=1,j=1}^{l,k}\|_p. \end{align*}$$
$$\begin{align*}c \|(a_{ij})_{i=1,j=1}^{l,k}\|_p \le \big\| \sum_{i=1}^l\sum_{j=1}^k a_{ij} x^{i}_{s_i(j)} \big\| \le C \|(a_{ij})_{i=1,j=1}^{l,k}\|_p. \end{align*}$$
Let
![]() $N'=\{ n_{2kl}:k\in \mathbb {N} \}$
and observe that for
$N'=\{ n_{2kl}:k\in \mathbb {N} \}$
and observe that for
![]() $k_1,\ldots ,k_d\in \mathbb {N}$
, there is a strict plegma family
$k_1,\ldots ,k_d\in \mathbb {N}$
, there is a strict plegma family
![]() $(s_i)_{i=1}^l\in S\text {-}Plm_l([N]^d )$
, such that
$(s_i)_{i=1}^l\in S\text {-}Plm_l([N]^d )$
, such that
![]() $n_{2k_jl}\in \{s_i(j):i=1,\ldots ,l\}$
for all
$n_{2k_jl}\in \{s_i(j):i=1,\ldots ,l\}$
for all
![]() $j=1,\ldots , d$
. Hence, we may find
$j=1,\ldots , d$
. Hence, we may find
![]() $M\subset N'$
satisfying (ii) with constants
$M\subset N'$
satisfying (ii) with constants
![]() $c,C$
. Finally, by repeating the sequences in the array, it follows easily that (ii) yields (i).
$c,C$
. Finally, by repeating the sequences in the array, it follows easily that (ii) yields (i).
We recall the main result from [Reference Argyros, Georgiou, Lagos and Motakis6], stating that whenever a Banach space admits a uniformly unique joint spreading model with respect to some family satisfying certain stability conditions, then it satisfies a property concerning its bounded linear operators called the Uniform Approximation on Large Subspaces property (see [Reference Argyros, Georgiou, Lagos and Motakis6, Theorem 5.17] and [Reference Argyros, Georgiou, Lagos and Motakis6, Theorem 5.23]).
Definition 3.5 [Reference Maurey, Milman and Tomczak-Jaegermann24].
A Banach space X is called Asymptotic
![]() $\ell _p$
,
$\ell _p$
,
![]() $1\leq p<\infty $
, (respectively, Asymptotic
$1\leq p<\infty $
, (respectively, Asymptotic
![]() $c_0$
) if there exists a constant C, such that in a two-player n-turn game
$c_0$
) if there exists a constant C, such that in a two-player n-turn game
![]() $G(n,p,C)$
, where in each turn
$G(n,p,C)$
, where in each turn
![]() $k=1,\ldots ,n$
, player (S) picks a finite codimensional subspace
$k=1,\ldots ,n$
, player (S) picks a finite codimensional subspace
![]() $Y_k$
of X, and then player (V) picks a normalised vector
$Y_k$
of X, and then player (V) picks a normalised vector
![]() $x_k\in Y_k$
, player (S) has a winning strategy to force player (V) to pick a sequence
$x_k\in Y_k$
, player (S) has a winning strategy to force player (V) to pick a sequence
![]() $(x_k)_{k=1}^n$
that is C-equivalent to the unit vector basis of
$(x_k)_{k=1}^n$
that is C-equivalent to the unit vector basis of
![]() $\ell ^n_p$
(respectively,
$\ell ^n_p$
(respectively,
![]() $\ell _{\infty }^n)$
.
$\ell _{\infty }^n)$
.
Although this is not the initial formulation, it is equivalent and follows from [Reference Maurey, Milman and Tomczak-Jaegermann24, Subsection 1.5]. The typical example of a nonclassical Asymptotic
![]() $\ell _p$
space is the Tsirelson space from [Reference Figiel and Johnson17]. This is a reflexive Asymptotic
$\ell _p$
space is the Tsirelson space from [Reference Figiel and Johnson17]. This is a reflexive Asymptotic
![]() $\ell _1$
space, and it is the dual of Tsirelson’s original space from [Reference Tsirelson27] which is Asymptotic
$\ell _1$
space, and it is the dual of Tsirelson’s original space from [Reference Tsirelson27] which is Asymptotic
![]() $c_0$
. Finally, whenever a Banach space is Asymptotic
$c_0$
. Finally, whenever a Banach space is Asymptotic
![]() $\ell _p$
or Asymptotic
$\ell _p$
or Asymptotic
![]() $c_0$
, it admits a uniformly unique joint spreading model with respect to
$c_0$
, it admits a uniformly unique joint spreading model with respect to
![]() $\mathscr {F}_0(X)$
(see, e.g. [Reference Argyros, Georgiou, Lagos and Motakis6, Corollary 4.12]).
$\mathscr {F}_0(X)$
(see, e.g. [Reference Argyros, Georgiou, Lagos and Motakis6, Corollary 4.12]).
The above definition is the coordinate-free version of the notion of an asymptotic
![]() $\ell _p$
Banach space with a basis introduced by Milman and Tomczak-Jaegermann in [Reference Milman and Tomczak-Jaegermann25].
$\ell _p$
Banach space with a basis introduced by Milman and Tomczak-Jaegermann in [Reference Milman and Tomczak-Jaegermann25].
Definition 3.6 [Reference Milman and Tomczak-Jaegermann25].
Let X be a Banach space with a Schauder basis
![]() $(e_i)_i$
and
$(e_i)_i$
and
![]() $1\le p< \infty $
. We say that the Schauder basis
$1\le p< \infty $
. We say that the Schauder basis
![]() $(e_i)_i$
of X is asymptotic
$(e_i)_i$
of X is asymptotic
![]() $\ell _p$
if there exist positive constants
$\ell _p$
if there exist positive constants
![]() $D_1$
and
$D_1$
and
![]() $D_2$
, such that for all
$D_2$
, such that for all
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $N(n)\in \mathbb {N}$
with the property that whenever
$N(n)\in \mathbb {N}$
with the property that whenever
![]() $N(n)\le x_1< \cdots < x_n$
are vectors in X, then
$N(n)\le x_1< \cdots < x_n$
are vectors in X, then
 $$\begin{align*}\frac{1}{D_1}(\sum_{i=1}^n\|x_i\|^p)^{\frac{1}{p}}\le \|\sum_{i=1}^nx_i\|\le D_2 (\sum_{i=1}^n\|x_i\|^p)^{\frac{1}{p}}. \end{align*}$$
$$\begin{align*}\frac{1}{D_1}(\sum_{i=1}^n\|x_i\|^p)^{\frac{1}{p}}\le \|\sum_{i=1}^nx_i\|\le D_2 (\sum_{i=1}^n\|x_i\|^p)^{\frac{1}{p}}. \end{align*}$$
Specifically, we say that
![]() $(e_i)_i$
is D-asymptotic
$(e_i)_i$
is D-asymptotic
![]() $\ell _p$
for
$\ell _p$
for
![]() $D=D_1D_2$
. The definition of an asymptotic
$D=D_1D_2$
. The definition of an asymptotic
![]() $c_0$
space is given similarly.
$c_0$
space is given similarly.
It is easy to show that if X has a Schauder basis that is asymptotic
![]() $\ell _p$
, then X is Asymptotic
$\ell _p$
, then X is Asymptotic
![]() $\ell _p$
. Moreover, if X is Asymptotic
$\ell _p$
. Moreover, if X is Asymptotic
![]() $\ell _p$
, then it contains an asymptotic
$\ell _p$
, then it contains an asymptotic
![]() $\ell _p$
sequence. In particular, note that if X has a Schauder basis and Y is an Asymptotic
$\ell _p$
sequence. In particular, note that if X has a Schauder basis and Y is an Asymptotic
![]() $\ell _p$
subspace of X, then Y contains a further subspace that is isomorphic to an asymptotic
$\ell _p$
subspace of X, then Y contains a further subspace that is isomorphic to an asymptotic
![]() $\ell _p$
block subspace.
$\ell _p$
block subspace.
A noteworthy remark is that sequential asymptotic properties, array asymptotic properties and global asymptotic properties of a Banach space X can alternatively be interpreted as properties of special weakly null trees. A collection
![]() $\{x_A:A\in [\mathbb {N}]^{\leq n}\}$
in X is said to be a normalised weakly null tree of height n, if for every
$\{x_A:A\in [\mathbb {N}]^{\leq n}\}$
in X is said to be a normalised weakly null tree of height n, if for every
![]() $A\in [\mathbb {N}]^{\leq n-1}$
,
$A\in [\mathbb {N}]^{\leq n-1}$
,
![]() $(x_{A\cup \{j\}})_{j>\max (A)}$
is a normalised weakly null sequence. Such a tree is said to originate from a sequence
$(x_{A\cup \{j\}})_{j>\max (A)}$
is a normalised weakly null sequence. Such a tree is said to originate from a sequence
![]() $(x_j)_j$
if for all
$(x_j)_j$
if for all
![]() $A = \{a_1,\ldots ,a_i\}$
, we have
$A = \{a_1,\ldots ,a_i\}$
, we have
![]() $x_A = x_{a_i}$
. Similarly, a tree
$x_A = x_{a_i}$
. Similarly, a tree
![]() $\{x_A:A\in [\mathbb {N}]^{\leq n}\}$
is said to originate from an array of sequences
$\{x_A:A\in [\mathbb {N}]^{\leq n}\}$
is said to originate from an array of sequences
![]() $(x^{(i)}_j)_j$
,
$(x^{(i)}_j)_j$
,
![]() $1\leq i\leq n$
if for all
$1\leq i\leq n$
if for all
![]() $A = \{a_1,\ldots ,a_i\}$
, we have
$A = \{a_1,\ldots ,a_i\}$
, we have
![]() $x_A = x^{(i)}_{a_i}$
. Then, X has a uniformly unique
$x_A = x^{(i)}_{a_i}$
. Then, X has a uniformly unique
![]() $\ell _p$
spreading model if and only if there exists
$\ell _p$
spreading model if and only if there exists
![]() $C>0$
, so that every tree
$C>0$
, so that every tree
![]() $\{x_A:A\in [\mathbb {N}]^{\leq n}\}$
originating from a normalised weakly null sequence
$\{x_A:A\in [\mathbb {N}]^{\leq n}\}$
originating from a normalised weakly null sequence
![]() $(x_j)_j$
in X has a maximal branch that is C-equivalent to the unit vector basis of
$(x_j)_j$
in X has a maximal branch that is C-equivalent to the unit vector basis of
![]() $\ell _p^n$
. Similarly, X has a unique
$\ell _p^n$
. Similarly, X has a unique
![]() $\ell _p$
asymptotic model if the same can be said about all trees originating from normalised weakly null arrays in X. Finally, a Banach space X is an Asymptotic
$\ell _p$
asymptotic model if the same can be said about all trees originating from normalised weakly null arrays in X. Finally, a Banach space X is an Asymptotic
![]() $\ell _p$
space (or an Asymptotic
$\ell _p$
space (or an Asymptotic
![]() $c_0$
space if
$c_0$
space if
![]() $p=\infty $
) if there exists
$p=\infty $
) if there exists
![]() $C>0$
, so that every normalised weakly null tree of height n has a maximal branch
$C>0$
, so that every normalised weakly null tree of height n has a maximal branch
![]() $x_{\{a_1\}}, x_{\{a_1,a_2\}},\ldots ,x_{\{a_1,a_2,\ldots ,a_n\}}$
that is C-equivalent to the unit vector basis of
$x_{\{a_1\}}, x_{\{a_1,a_2\}},\ldots ,x_{\{a_1,a_2,\ldots ,a_n\}}$
that is C-equivalent to the unit vector basis of
![]() $\ell _p^n$
. For more details, see [Reference Baudier, Lancien, Motakis and Schlumprecht14, Remark 3.11].
$\ell _p^n$
. For more details, see [Reference Baudier, Lancien, Motakis and Schlumprecht14, Remark 3.11].
4 Measures on countably branching well-founded trees
In this section, we recall certain results from [Reference Argyros, Georgiou and Motakis8] concerning measures on countably branching well-founded trees. These will be used to prove that for all
![]() $1\le p<\infty $
, the space
$1\le p<\infty $
, the space
![]() $\mathfrak {X}^{(p)}_{\text {awi}}$
admits
$\mathfrak {X}^{(p)}_{\text {awi}}$
admits
![]() $\ell _p$
as a unique asymptotic model. In particular, Proposition 4.1 and Lemma 4.6 will be used to prove Lemma 7.2, which is one of the key ingredients in the proof of the main result, Theorem 1.4.
$\ell _p$
as a unique asymptotic model. In particular, Proposition 4.1 and Lemma 4.6 will be used to prove Lemma 7.2, which is one of the key ingredients in the proof of the main result, Theorem 1.4.
Let
![]() $\mathcal {T}=(A,<_{\mathcal {T}})$
, where A is a countably infinite set equipped with a partial order
$\mathcal {T}=(A,<_{\mathcal {T}})$
, where A is a countably infinite set equipped with a partial order
![]() $<_{\mathcal {T}}$
. In the sequel, we use
$<_{\mathcal {T}}$
. In the sequel, we use
![]() $t\in \mathcal {T}$
instead of
$t\in \mathcal {T}$
instead of
![]() $t\in A$
. We assume that
$t\in A$
. We assume that
![]() $<_{\mathcal {T}}$
is such that there is a unique minimal element in
$<_{\mathcal {T}}$
is such that there is a unique minimal element in
![]() $\mathcal {T}$
, and for each
$\mathcal {T}$
, and for each
![]() $t\in \mathcal {T}$
, the set
$t\in \mathcal {T}$
, the set
![]() $S_t=\{s\in \mathcal {T}: s\le _{\mathcal {T}} t \}$
is finite and totally ordered, that is,
$S_t=\{s\in \mathcal {T}: s\le _{\mathcal {T}} t \}$
is finite and totally ordered, that is,
![]() $\mathcal {T}$
is a rooted tree. We also assume that
$\mathcal {T}$
is a rooted tree. We also assume that
![]() $\mathcal {T}$
is well founded, that is, it contains no infinite totally ordered sets, and countably branching, that is, every nonmaximal node has countably infinite immediate successors.
$\mathcal {T}$
is well founded, that is, it contains no infinite totally ordered sets, and countably branching, that is, every nonmaximal node has countably infinite immediate successors.
Observe that
![]() ${\widetilde {\mathcal {T}}}=(\{S_t :{t\in \mathcal {T}}\},<_{\widetilde {\mathcal {T}}})$
, where
${\widetilde {\mathcal {T}}}=(\{S_t :{t\in \mathcal {T}}\},<_{\widetilde {\mathcal {T}}})$
, where
![]() $<_{\widetilde {\mathcal {T}}}$
denotes inclusion, is also a tree, and that
$<_{\widetilde {\mathcal {T}}}$
denotes inclusion, is also a tree, and that
![]() $\mathcal {T}$
is in fact isomorphic to
$\mathcal {T}$
is in fact isomorphic to
![]() ${\widetilde {\mathcal {T}}}$
via the mapping
${\widetilde {\mathcal {T}}}$
via the mapping
![]() $t\mapsto S_t$
. Given
$t\mapsto S_t$
. Given
![]() $t\in \mathcal {T}$
, we will denote
$t\in \mathcal {T}$
, we will denote
![]() $S_t$
by
$S_t$
by
![]() ${\tilde {t}}$
, identifying it as an element of
${\tilde {t}}$
, identifying it as an element of
![]() ${\widetilde {\mathcal {T}}}$
. For each
${\widetilde {\mathcal {T}}}$
. For each
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we denote by
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we denote by
![]() $S({\tilde {t}})$
the set of immediate successors of
$S({\tilde {t}})$
the set of immediate successors of
![]() ${\tilde {t}}$
in
${\tilde {t}}$
in
![]() ${\widetilde {\mathcal {T}}}$
. In particular, if
${\widetilde {\mathcal {T}}}$
. In particular, if
![]() ${\tilde {t}}$
is maximal, then
${\tilde {t}}$
is maximal, then
![]() $S({\tilde {t}})$
is empty. Moreover, for
$S({\tilde {t}})$
is empty. Moreover, for
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we denote
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we denote
![]() $V_{\tilde {t}} = \{\tilde {s}\in {\widetilde {\mathcal {T}}}:{\tilde {t}}\leq _{\widetilde {\mathcal {T}}} \tilde {s}\}$
and view
$V_{\tilde {t}} = \{\tilde {s}\in {\widetilde {\mathcal {T}}}:{\tilde {t}}\leq _{\widetilde {\mathcal {T}}} \tilde {s}\}$
and view
![]() ${\widetilde {\mathcal {T}}}$
as a topological space with the topology generated by the sets
${\widetilde {\mathcal {T}}}$
as a topological space with the topology generated by the sets
![]() $V_{\tilde {t}}$
and
$V_{\tilde {t}}$
and
![]() ${\widetilde {\mathcal {T}}}\setminus V_{\tilde {t}}$
,
${\widetilde {\mathcal {T}}}\setminus V_{\tilde {t}}$
,
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, that is, the pointwise convergence topology. This is a compact metric topology, such that for each
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, that is, the pointwise convergence topology. This is a compact metric topology, such that for each
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the sets of the form
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the sets of the form
![]() $V_{\tilde {t}}\setminus (\cup _{\tilde {s}\in F}V_{\tilde {s}})$
,
$V_{\tilde {t}}\setminus (\cup _{\tilde {s}\in F}V_{\tilde {s}})$
,
![]() $F\subset S({\tilde {t}})$
finite, form a neighbourhood base of clopen sets for
$F\subset S({\tilde {t}})$
finite, form a neighbourhood base of clopen sets for
![]() $\tilde t$
. We denote by
$\tilde t$
. We denote by
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
the cone of all bounded positive measures
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
the cone of all bounded positive measures
![]() $\mu :\mathcal {P}({\widetilde {\mathcal {T}}})\to [0,+\infty )$
. For
$\mu :\mathcal {P}({\widetilde {\mathcal {T}}})\to [0,+\infty )$
. For
![]() $\mu \in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
, we define the support of
$\mu \in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
, we define the support of
![]() $\mu $
to be the set
$\mu $
to be the set
![]() $\mathrm {supp}(\mu ) = \{{\tilde {t}}\in {\widetilde {\mathcal {T}}}:\mu (\{{\tilde {t}}\})>0\}$
. Finally, we say that a subset
$\mathrm {supp}(\mu ) = \{{\tilde {t}}\in {\widetilde {\mathcal {T}}}:\mu (\{{\tilde {t}}\})>0\}$
. Finally, we say that a subset
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
is bounded if
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
is bounded if
![]() $\sup _{\mu \in \mathcal {A}}\mu ({\widetilde {\mathcal {T}}})<\infty $
.
$\sup _{\mu \in \mathcal {A}}\mu ({\widetilde {\mathcal {T}}})<\infty $
.
Proposition 4.1. Let
![]() $(\mu _i)_i$
be a bounded and disjointly supported sequence in
$(\mu _i)_i$
be a bounded and disjointly supported sequence in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
. Then for every
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
. Then for every
![]() $\varepsilon>0$
, there is an
$\varepsilon>0$
, there is an
![]() $L\in [\mathbb {N}]^{\infty }$
and a subset
$L\in [\mathbb {N}]^{\infty }$
and a subset
![]() $G_i$
of
$G_i$
of
![]() $\text {supp}(\mu _{i})$
for each
$\text {supp}(\mu _{i})$
for each
![]() $i\in L$
, satisfying the following.
$i\in L$
, satisfying the following.
-
(i)
 $\mu _{i}({\widetilde {\mathcal {T}}}\setminus G_i)\le \varepsilon $
for every
$\mu _{i}({\widetilde {\mathcal {T}}}\setminus G_i)\le \varepsilon $
for every
 $i\in L$
.
$i\in L$
. -
(ii) The sets
 $G_i$
,
$G_i$
,
 $i\in L$
, are pairwise incomparable.
$i\in L$
, are pairwise incomparable.
For the proof, we refer the reader to [Reference Argyros, Georgiou and Motakis8, Proposition 3.1].
Definition 4.2. Let
![]() $(\mu _i)_i$
be a sequence in
$(\mu _i)_i$
be a sequence in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
and
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
and
![]() $\nu \in \mathcal {M}_+(\mathcal {{\widetilde {\mathcal {T}}}})$
. We say that
$\nu \in \mathcal {M}_+(\mathcal {{\widetilde {\mathcal {T}}}})$
. We say that
![]() $\nu $
is the successor-determined limit of
$\nu $
is the successor-determined limit of
![]() $(\mu _i)_i$
if for all
$(\mu _i)_i$
if for all
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we have
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we have
![]() $\nu (\{{\tilde {t}}\}) = \lim _i\mu _i(S({\tilde {t}}))$
. In this case, we write
$\nu (\{{\tilde {t}}\}) = \lim _i\mu _i(S({\tilde {t}}))$
. In this case, we write
![]() $\nu = \mathrm {succ}\text {-}\!\lim _i\mu _i$
.
$\nu = \mathrm {succ}\text {-}\!\lim _i\mu _i$
.
Recall that a bounded sequence
![]() $(\mu _i)_i$
in
$(\mu _i)_i$
in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
converges in the
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
converges in the
![]() $w^*$
-topology to a
$w^*$
-topology to a
![]() $\mu \in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
if and only if for all clopen sets
$\mu \in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
if and only if for all clopen sets
![]() $V\subset {\widetilde {\mathcal {T}}}$
, we have
$V\subset {\widetilde {\mathcal {T}}}$
, we have
![]() $\lim _i\mu _i(V) = \mu (V)$
if and only if for all
$\lim _i\mu _i(V) = \mu (V)$
if and only if for all
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we have
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, we have
![]() $\lim _i\mu _i(V_{\tilde {t}}) = \mu (V_{\tilde {t}})$
. In this case, we write
$\lim _i\mu _i(V_{\tilde {t}}) = \mu (V_{\tilde {t}})$
. In this case, we write
![]() $\mu = w^*\text {-}\lim _i\mu _i$
.
$\mu = w^*\text {-}\lim _i\mu _i$
.
Lemma 4.3. Let
![]() $(\mu _i)_i$
be a bounded sequence in
$(\mu _i)_i$
be a bounded sequence in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
. There exist a subsequence
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
. There exist a subsequence
![]() $(\mu _{i_n})_n$
of
$(\mu _{i_n})_n$
of
![]() $(\mu _i)_i$
and
$(\mu _i)_i$
and
![]() $\nu \in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
with
$\nu \in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
with
![]() $\nu = \mathrm {succ}\text {-}\!\lim _n\mu _{i_n}$
.
$\nu = \mathrm {succ}\text {-}\!\lim _n\mu _{i_n}$
.
Remark 4.4. It is possible for a bounded sequence
![]() $(\mu _i)_i$
in
$(\mu _i)_i$
in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
to satisfy
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
to satisfy
![]() $w^*\text {-}\lim _i\mu _i\neq \mathrm {succ}\text {-}\!\lim _i\mu _i$
. Take, for example,
$w^*\text {-}\lim _i\mu _i\neq \mathrm {succ}\text {-}\!\lim _i\mu _i$
. Take, for example,
![]() ${\widetilde {\mathcal {T}}} = [\mathbb {N}]^{\leq 2}$
(all subsets of
${\widetilde {\mathcal {T}}} = [\mathbb {N}]^{\leq 2}$
(all subsets of
![]() $\mathbb {N}$
with at most two elements with the partial order of initial segments), and define
$\mathbb {N}$
with at most two elements with the partial order of initial segments), and define
![]() $\mu _i = \delta _{\{i,i+1\}}$
,
$\mu _i = \delta _{\{i,i+1\}}$
,
![]() $i\in \mathbb {N}$
. Then
$i\in \mathbb {N}$
. Then
![]() $w^*\text {-}\lim _i\mu _i = \delta _{\emptyset }$
, whereas
$w^*\text {-}\lim _i\mu _i = \delta _{\emptyset }$
, whereas
![]() $\mathrm {succ}\text {-}\!\lim _i\mu _i = 0$
.
$\mathrm {succ}\text {-}\!\lim _i\mu _i = 0$
.
Although these limits are not necessarily the same, there is an explicit formula relating
![]() $\mathrm {succ}\text {-}\!\lim _i\mu _i$
to
$\mathrm {succ}\text {-}\!\lim _i\mu _i$
to
![]() $w^*\text {-}\lim _i\mu _i$
.
$w^*\text {-}\lim _i\mu _i$
.
Lemma 4.5. Let
![]() $(\mu _i)_i$
be a bounded and disjointly supported sequence in
$(\mu _i)_i$
be a bounded and disjointly supported sequence in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
, such that
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
, such that
![]() $w^*\text {-}\lim _i\mu _i = \mu $
exists, and for all
$w^*\text {-}\lim _i\mu _i = \mu $
exists, and for all
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the limit
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the limit
![]() $\nu (\{{\tilde {t}}\}) = \lim _i\mu _i(S({\tilde {t}})) $
exists as well. Then for every
$\nu (\{{\tilde {t}}\}) = \lim _i\mu _i(S({\tilde {t}})) $
exists as well. Then for every
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
and enumeration
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
and enumeration
![]() $({\tilde {t}}_j)_j$
of
$({\tilde {t}}_j)_j$
of
![]() $S({\tilde {t}})$
, we have
$S({\tilde {t}})$
, we have
In particular,
![]() $\mu (\{{\tilde {t}}\}) = \nu (\{{\tilde {t}}\})$
if and only if the double limit in (4.1) is zero.
$\mu (\{{\tilde {t}}\}) = \nu (\{{\tilde {t}}\})$
if and only if the double limit in (4.1) is zero.
Lemma 4.6. Let
![]() $(\mu _i)_i$
be a bounded and disjointly supported sequence in
$(\mu _i)_i$
be a bounded and disjointly supported sequence in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
, such that
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
, such that
![]() $\mathrm {succ}\text {-}\!\lim _i\mu _i = \nu $
exists. Then there exist an infinite
$\mathrm {succ}\text {-}\!\lim _i\mu _i = \nu $
exists. Then there exist an infinite
![]() $L\subset \mathbb {N}$
and partitions
$L\subset \mathbb {N}$
and partitions
![]() $A_i$
,
$A_i$
,
![]() $B_i$
of
$B_i$
of
![]() $\mathrm {supp}(\mu _i)$
,
$\mathrm {supp}(\mu _i)$
,
![]() $i\in L$
, such that the following are satisfied.
$i\in L$
, such that the following are satisfied.
-
(i) If for all
 $i\in L$
, we define the measure
$i\in L$
, we define the measure
 $\mu _i^1$
by
$\mu _i^1$
by
 $\mu _i^1(C)= \mu _i(C\cap A_i)$
, then
$\mu _i^1(C)= \mu _i(C\cap A_i)$
, then
 $\nu = w^*\text {-}\lim _{i\in L}\mu _i^1 = \mathrm {succ}\text {-}\!\lim _{i\in L}\mu _i^1$
.
$\nu = w^*\text {-}\lim _{i\in L}\mu _i^1 = \mathrm {succ}\text {-}\!\lim _{i\in L}\mu _i^1$
. -
(ii) If for all
 $i\in L$
, we define the measure
$i\in L$
, we define the measure
 $\mu _i^2$
by
$\mu _i^2$
by
 $\mu _i^2(C)= \mu _i(C\cap B_i)$
, then for all
$\mu _i^2(C)= \mu _i(C\cap B_i)$
, then for all
 ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the sequence
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the sequence
 $(\mu _i^2(S({\tilde {t}})))_i$
is eventually zero. In particular,
$(\mu _i^2(S({\tilde {t}})))_i$
is eventually zero. In particular,
 $\mathrm {succ}\text {-}\!\lim _{i\in L}\mu _i^2 = 0$
.
$\mathrm {succ}\text {-}\!\lim _{i\in L}\mu _i^2 = 0$
.
For the proofs, we refer the reader to [Reference Argyros, Georgiou and Motakis8, Lemma 4.10] and [Reference Argyros, Georgiou and Motakis8, Lemma 4.12].
Remark 4.7. Although the results from [Reference Argyros, Georgiou and Motakis8] were formulated for trees
![]() $\mathcal {T}$
defined on infinite subsets of
$\mathcal {T}$
defined on infinite subsets of
![]() $\mathbb {N}$
, this is not a necessary restriction, and they can be naturally extended to the more general setting of countably branching well-founded trees.
$\mathbb {N}$
, this is not a necessary restriction, and they can be naturally extended to the more general setting of countably branching well-founded trees.
PART I The case of
 $\boldsymbol {\ell _1}$
$\boldsymbol {\ell _1}$
5 Definition of the space
 $\mathfrak {X}_{\text {awi}}^{(1)}$
$\mathfrak {X}_{\text {awi}}^{(1)}$
The method of saturation with asymptotically weakly incomparable constraints, that is used in the construction of both spaces presented in this paper, was introduced in [Reference Argyros, Georgiou and Motakis8], where it was shown that (b)
![]() $_1\not \Rightarrow $
(a)
$_1\not \Rightarrow $
(a)
![]() $_1$
. There, it was also used to prove an even stronger result, namely, the existence of a Banach space with a basis admitting
$_1$
. There, it was also used to prove an even stronger result, namely, the existence of a Banach space with a basis admitting
![]() $\ell _1$
as a unique asymptotic model, and in which any infinite subsequence of the basis generates a non-Asymptotic
$\ell _1$
as a unique asymptotic model, and in which any infinite subsequence of the basis generates a non-Asymptotic
![]() $\ell _1$
subspace. This method requires the existence of a well-founded tree defined either on the basis of the space or on a family of functionals of its norming set. In this section, we define the space
$\ell _1$
subspace. This method requires the existence of a well-founded tree defined either on the basis of the space or on a family of functionals of its norming set. In this section, we define the space
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
by introducing its norm via a norming set, which is a subset of the norming set of a Mixed Tsirelson space
$\mathfrak {X}_{\text {awi}}^{(1)}$
by introducing its norm via a norming set, which is a subset of the norming set of a Mixed Tsirelson space
![]() $\mathcal {T}[(m_j,\mathcal {S}_{n_j})_j]$
for an appropriate choice of
$\mathcal {T}[(m_j,\mathcal {S}_{n_j})_j]$
for an appropriate choice of
![]() $(m_j)_j$
and
$(m_j)_j$
and
![]() $(n_j)_j$
described below. The key ingredient in the definition of this norming set is the notion of asymptotically weakly incomparable sequences of functionals, which is also introduced in this section. This notion will allow the space
$(n_j)_j$
described below. The key ingredient in the definition of this norming set is the notion of asymptotically weakly incomparable sequences of functionals, which is also introduced in this section. This notion will allow the space
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
to admit
$\mathfrak {X}_{\text {awi}}^{(1)}$
to admit
![]() $\ell _1$
as a unique asymptotic model, while at the same time, it will force the norm to be small on the branches of a tree, in every subspace of
$\ell _1$
as a unique asymptotic model, while at the same time, it will force the norm to be small on the branches of a tree, in every subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, showing that the space does not contain Asymptotic
$\mathfrak {X}_{\text {awi}}^{(1)}$
, showing that the space does not contain Asymptotic
![]() $\ell _1$
subspaces.
$\ell _1$
subspaces.
5.1 Definition of the space
 $\mathfrak {X}_{\text {awi}}^{(1)}$
$\mathfrak {X}_{\text {awi}}^{(1)}$
Define a pair of strictly increasing sequences of natural numbers
![]() $(m_j)_j$
,
$(m_j)_j$
,
![]() $(n_j)_j$
as follows:
$(n_j)_j$
as follows:
 $$ \begin{align*} m_1 &= 2 & n_1 &= 1 \\ m_{j+1}&=m_j^{m_j} & n_{j+1}&=2^{2m_{j+1}}n_j .\end{align*} $$
$$ \begin{align*} m_1 &= 2 & n_1 &= 1 \\ m_{j+1}&=m_j^{m_j} & n_{j+1}&=2^{2m_{j+1}}n_j .\end{align*} $$
Definition 5.1. Let
![]() $V_{(1)}$
denote the minimal subset of
$V_{(1)}$
denote the minimal subset of
![]() $c_{00}(\mathbb {N})$
that
$c_{00}(\mathbb {N})$
that
-
(i) contains 0 and all
 $\pm e_j^*$
,
$\pm e_j^*$
,
 $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and -
(ii) is closed under the operations
 $(m_j,\mathcal {S}_{n_j})_j$
, that is, if
$(m_j,\mathcal {S}_{n_j})_j$
, that is, if
 $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and
 $f_1<\ldots <f_n$
is an
$f_1<\ldots <f_n$
is an
 $\mathcal {S}_{n_j}$
-admissible sequence (see Section 2.1) in
$\mathcal {S}_{n_j}$
-admissible sequence (see Section 2.1) in
 $V_{(1)}\setminus \{0\}$
, then
$V_{(1)}\setminus \{0\}$
, then
 $m_j^{-1}\sum _{i=1}^nf_i $
is also in
$m_j^{-1}\sum _{i=1}^nf_i $
is also in
 $V_{(1)}$
.
$V_{(1)}$
.
Remark 5.2.
-
(i) If
 $f\in V_{(1)}\setminus \{0\}$
, then either
$f\in V_{(1)}\setminus \{0\}$
, then either
 $f\in \{\pm e^*_j:j\in \mathbb {N}\}$
, or it is of the form
$f\in \{\pm e^*_j:j\in \mathbb {N}\}$
, or it is of the form
 $f=m_j^{-1}\sum _{i=1}^nf_i$
with
$f=m_j^{-1}\sum _{i=1}^nf_i$
with
 $f_1<\ldots <f_n$
an
$f_1<\ldots <f_n$
an
 $\mathcal {S}_{n_j}$
-admissible sequence in
$\mathcal {S}_{n_j}$
-admissible sequence in
 $V_{(1)}$
for some
$V_{(1)}$
for some
 $j\in \mathbb {N}$
.
$j\in \mathbb {N}$
. -
(ii) As usual, we view the elements of
 $V_{(1)}$
as functionals acting on
$V_{(1)}$
as functionals acting on
 $c_{00}(\mathbb {N})$
, inducing a norm
$c_{00}(\mathbb {N})$
, inducing a norm
 $\|\cdot \|_{V_{(1)}}$
. The completion of
$\|\cdot \|_{V_{(1)}}$
. The completion of
 $(c_{00}(\mathbb {N}),\|\cdot \|_{V_{(1)}})$
is the Mixed Tsirelson space
$(c_{00}(\mathbb {N}),\|\cdot \|_{V_{(1)}})$
is the Mixed Tsirelson space
 $\mathcal {T}[(m_j,\mathcal {S}_{n_j})_j]$
introduced for the first time in [Reference Argyros and Deliyanni5]. The first space with a saturated norm defined by a countable family of operations is the Schlumprecht space [Reference Schlumprecht26], which is a fundamental discovery and was used by Gowers and Maurey [Reference Gowers and Maurey19] to define the first hereditarily indecomposable (HI) space.
$\mathcal {T}[(m_j,\mathcal {S}_{n_j})_j]$
introduced for the first time in [Reference Argyros and Deliyanni5]. The first space with a saturated norm defined by a countable family of operations is the Schlumprecht space [Reference Schlumprecht26], which is a fundamental discovery and was used by Gowers and Maurey [Reference Gowers and Maurey19] to define the first hereditarily indecomposable (HI) space.
We now recall the notion of tree analysis which appeared for the first time in [Reference Argyros and Deliyanni4]. This has become a standard tool in proving upper bounds for the estimations of functionals on certain vectors in Mixed Tsirelson spaces. However, it is the first time where the tree analysis has a significant role in the definition of the norming set
![]() $W_{(1)}$
. Additionally, it is also a key ingredient in the proof that
$W_{(1)}$
. Additionally, it is also a key ingredient in the proof that
![]() $\mathfrak {X}^{(1)}_{\text {awi}}$
contains no Asymptotic
$\mathfrak {X}^{(1)}_{\text {awi}}$
contains no Asymptotic
![]() $\ell _1$
subspaces.
$\ell _1$
subspaces.
Let
![]() $\mathcal {A}$
be a rooted tree. For a node
$\mathcal {A}$
be a rooted tree. For a node
![]() $\alpha \in \mathcal {A}$
, we denote by
$\alpha \in \mathcal {A}$
, we denote by
![]() $S(\alpha )$
the set of all immediate successors of
$S(\alpha )$
the set of all immediate successors of
![]() $\alpha $
, by
$\alpha $
, by
![]() $|\alpha |$
the height of
$|\alpha |$
the height of
![]() $\alpha $
, that is,
$\alpha $
, that is,
![]() $|\alpha |=\#\{\beta \in \mathcal {A}:\beta <_{\mathcal {A}}\alpha \}$
, and finally, we denote by
$|\alpha |=\#\{\beta \in \mathcal {A}:\beta <_{\mathcal {A}}\alpha \}$
, and finally, we denote by
![]() $h(\mathcal {A})$
the height of
$h(\mathcal {A})$
the height of
![]() $\mathcal {A}$
, that is, the maximum height over its nodes.
$\mathcal {A}$
, that is, the maximum height over its nodes.
Definition 5.3. Let
![]() $f\in V_{(1)}\setminus \{0\}$
. For a finite tree
$f\in V_{(1)}\setminus \{0\}$
. For a finite tree
![]() $\mathcal {A}$
, a family
$\mathcal {A}$
, a family
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
is called a tree analysis of f if the following are satisfied.
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
is called a tree analysis of f if the following are satisfied.
-
(i)
 $\mathcal {A}$
has a unique root denoted by
$\mathcal {A}$
has a unique root denoted by
 $0$
and
$0$
and
 $f_0=f$
.
$f_0=f$
. -
(ii) Each
 $f_{\alpha }$
is in
$f_{\alpha }$
is in
 $V_{(1)}$
, and if
$V_{(1)}$
, and if
 $\beta <\alpha $
in
$\beta <\alpha $
in
 $\mathcal {A}$
, then
$\mathcal {A}$
, then
 $\text {range}(f_{\alpha })\subset \text {range}(f_{\beta })$
.
$\text {range}(f_{\alpha })\subset \text {range}(f_{\beta })$
. -
(iii) For every maximal node
 $\alpha \in \mathcal {A}$
, we have that
$\alpha \in \mathcal {A}$
, we have that
 $|\alpha |=h(\mathcal {A})$
.
$|\alpha |=h(\mathcal {A})$
. -
(iv) For every nonmaximal node
 $\alpha \in \mathcal {A}$
, either
$\alpha \in \mathcal {A}$
, either
 $f_{\alpha }$
is the result of some
$f_{\alpha }$
is the result of some
 $(m_j,\mathcal {S}_{n_j})$
operation of
$(m_j,\mathcal {S}_{n_j})$
operation of
 $(f_{\beta })_{\beta \in S(\alpha )}$
, i.e.,
$(f_{\beta })_{\beta \in S(\alpha )}$
, i.e.,
 $f_{\alpha }=m_j^{-1}\sum _{\beta \in S(\alpha )} f_{\beta }$
, or
$f_{\alpha }=m_j^{-1}\sum _{\beta \in S(\alpha )} f_{\beta }$
, or
 $f_{\alpha }\in \{\pm e_j^*:j\in \mathbb {N}\}$
and
$f_{\alpha }\in \{\pm e_j^*:j\in \mathbb {N}\}$
and
 $S(\alpha )=\{\beta \}$
with
$S(\alpha )=\{\beta \}$
with
 $f_{\beta }=f_{\alpha }$
.
$f_{\beta }=f_{\alpha }$
. -
(v) For every maximal node
 $\alpha \in \mathcal {A}$
,
$\alpha \in \mathcal {A}$
,
 $f_{\alpha }\in \{\pm e^*_j:j\in \mathbb {N}\}.$
$f_{\alpha }\in \{\pm e^*_j:j\in \mathbb {N}\}.$
Remark 5.4.
-
(i) It follows by minimality that every f in
 $V_{(1)}\setminus \{0\}$
admits a tree analysis, but it may not be unique. For example,
$V_{(1)}\setminus \{0\}$
admits a tree analysis, but it may not be unique. For example,
 $f=(m_{1}m_2)^{-1}e^*_1$
admits two distinct tree analyses.
$f=(m_{1}m_2)^{-1}e^*_1$
admits two distinct tree analyses. -
(ii) The standard definition of a tree analysis does not include 5.3 (iii). This property is included for technical reasons and is used below in the equality of Remark 5.8 (i).
Definition 5.5. Let
![]() $f\in V_{(1)}$
.
$f\in V_{(1)}$
.
-
(i) If
 $f=0$
or
$f=0$
or
 $f\in \{\pm e^*_j:j\in \mathbb {N}\}$
, then we define the weight
$f\in \{\pm e^*_j:j\in \mathbb {N}\}$
, then we define the weight
 $w(f)$
of f as
$w(f)$
of f as
 $w(f)=0$
and
$w(f)=0$
and
 $w(f)=1$
, respectively.
$w(f)=1$
, respectively. -
(ii) If f is the result of an
 $(m_j,S_{n_j})$
-operation for some
$(m_j,S_{n_j})$
-operation for some
 $j\in \mathbb {N}$
, then
$j\in \mathbb {N}$
, then
 $w(f)=m_j$
.
$w(f)=m_j$
.
Remark 5.6. It is not difficult to see that
![]() $w(f)$
, for
$w(f)$
, for
![]() $f\in V_{(1)}$
, is not uniquely determined, that is, f could be the result of more than one distinct
$f\in V_{(1)}$
, is not uniquely determined, that is, f could be the result of more than one distinct
![]() $(m_j,\mathcal {S}_{n_j})$
-operation. However, if we fix a tree analysis
$(m_j,\mathcal {S}_{n_j})$
-operation. However, if we fix a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, then for
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, then for
![]() $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
![]() $f_{\alpha }=(m_{j_{\alpha }})^{-1}\sum _{\beta \in S(\alpha )}f_{\beta }$
, the tree analysis determines the weight
$f_{\alpha }=(m_{j_{\alpha }})^{-1}\sum _{\beta \in S(\alpha )}f_{\beta }$
, the tree analysis determines the weight
![]() $w(f_{\alpha })$
, being equal to
$w(f_{\alpha })$
, being equal to
![]() $m_{j_{\alpha }}$
. Thus, for
$m_{j_{\alpha }}$
. Thus, for
![]() $f\in V_{(1)}$
and a fixed tree analysis
$f\in V_{(1)}$
and a fixed tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, with
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, with
![]() $w(f_{\alpha })$
, we will denote the weight
$w(f_{\alpha })$
, we will denote the weight
![]() $m_{j_{\alpha }}$
determined by
$m_{j_{\alpha }}$
determined by
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, for every
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, for every
![]() $\alpha \in \mathcal {A}$
. In addition, we will denote by
$\alpha \in \mathcal {A}$
. In addition, we will denote by
![]() $\bar {f}_{\alpha }$
the pair
$\bar {f}_{\alpha }$
the pair
![]() $(f_{\alpha },m_{j_{\alpha }})$
.
$(f_{\alpha },m_{j_{\alpha }})$
.
Definition 5.7. Let
![]() $f\in V_{(1)}$
and
$f\in V_{(1)}$
and
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f. Then for
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f. Then for
![]() $\alpha \in \mathcal {A}$
, we define the relative weight
$\alpha \in \mathcal {A}$
, we define the relative weight
![]() $w_f(f_{\alpha })$
of
$w_f(f_{\alpha })$
of
![]() $f_{\alpha }$
as
$f_{\alpha }$
as
 $$\begin{align*}w_f(f_{\alpha}) = \begin{cases} \prod_{\beta<\alpha}w(f_{\beta}) & \text{if }\alpha\neq0\\ 1 &\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}w_f(f_{\alpha}) = \begin{cases} \prod_{\beta<\alpha}w(f_{\beta}) & \text{if }\alpha\neq0\\ 1 &\text{otherwise.} \end{cases} \end{align*}$$
Remark 5.8. Let
![]() $f\in V_{(1)}$
and
$f\in V_{(1)}$
and
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f.
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f.
-
(i) For every
 $k=1,\ldots ,h(\mathcal {A})$
This can be proved by induction and essentially relies on the fact that
$k=1,\ldots ,h(\mathcal {A})$
This can be proved by induction and essentially relies on the fact that $$\begin{align*}f=\sum_{|a|=k}w_f(f_{\alpha})^{-1}f_{\alpha}. \end{align*}$$
$$\begin{align*}f=\sum_{|a|=k}w_f(f_{\alpha})^{-1}f_{\alpha}. \end{align*}$$
 $(f_{\alpha })_{\alpha \in \mathcal {A}}$
satisfies 5.3 (iii).
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
satisfies 5.3 (iii).
-
(ii) If
 $\mathcal {B}$
is a maximal pairwise incomparable subset of
$\mathcal {B}$
is a maximal pairwise incomparable subset of
 $\mathcal {A}$
, then
$\mathcal {A}$
, then $$\begin{align*}f=\sum_{\beta\in\mathcal{B}}w_f(f_{\beta})^{-1}f_{\beta}. \end{align*}$$
$$\begin{align*}f=\sum_{\beta\in\mathcal{B}}w_f(f_{\beta})^{-1}f_{\beta}. \end{align*}$$
-
(iii) For every
 $\alpha \in \mathcal {A}$
, whose immediate predecessor
$\alpha \in \mathcal {A}$
, whose immediate predecessor
 $\beta $
in
$\beta $
in
 $\mathcal {A}$
(if one exists) satisfies
$\mathcal {A}$
(if one exists) satisfies
 $f_{\beta }\notin \{\pm e_j^*:j\in \mathbb {N}\}$
, we have
$f_{\beta }\notin \{\pm e_j^*:j\in \mathbb {N}\}$
, we have
 $w_f(f_{\alpha })\ge 2^{|\alpha |}.$
$w_f(f_{\alpha })\ge 2^{|\alpha |}.$
Fix an injection
![]() $\sigma $
that maps any pair
$\sigma $
that maps any pair
![]() $(f,w(f))$
, for
$(f,w(f))$
, for
![]() $f\in V_{(1)}$
and
$f\in V_{(1)}$
and
![]() $w(f)$
a weight of f, to some
$w(f)$
a weight of f, to some
![]() $m_j$
with
$m_j$
with
![]() $m_j>\max \text {supp} (f)\: w(f)$
whenever
$m_j>\max \text {supp} (f)\: w(f)$
whenever
![]() $f\neq 0$
.
$f\neq 0$
.
Definition 5.9. Define a partial order
![]() $<_{\mathcal {T}}$
on the set of all pairs
$<_{\mathcal {T}}$
on the set of all pairs
![]() $(f,w(f))$
for
$(f,w(f))$
for
![]() $f\in V_{(1)}$
and
$f\in V_{(1)}$
and
![]() $w(f)$
a weight of f, as follows:
$w(f)$
a weight of f, as follows:
![]() $(f,w(f))<_{\mathcal {T}} (g ,w(g))$
either if
$(f,w(f))<_{\mathcal {T}} (g ,w(g))$
either if
![]() $f=0$
or if there exist
$f=0$
or if there exist
![]() $f_1<\ldots <f_n \in V_{(1)}$
and weights
$f_1<\ldots <f_n \in V_{(1)}$
and weights
![]() $w(f_1),\ldots ,w(f_n)$
, such that
$w(f_1),\ldots ,w(f_n)$
, such that
-
(i)
 $(f_i)_{i=1}^n$
is
$(f_i)_{i=1}^n$
is
 $\mathcal {S}_1$
-admissible,
$\mathcal {S}_1$
-admissible, -
(ii)
 $w(f_1)=\sigma (0,0)$
and
$w(f_1)=\sigma (0,0)$
and
 $w(f_i)=\sigma (f_{i-1},w(f_{i-1}))$
for every
$w(f_i)=\sigma (f_{i-1},w(f_{i-1}))$
for every
 $i=2,\ldots ,n$
,
$i=2,\ldots ,n$
, -
(iii) there are
 $1\le i_1<i_2\le n$
, such that
$1\le i_1<i_2\le n$
, such that
 $f=f_{i_1}$
and
$f=f_{i_1}$
and
 $g=f_{i_2}$
.
$g=f_{i_2}$
.
It is easy to see that
![]() $<_{\mathcal {T}}$
induces a tree structure rooted at
$<_{\mathcal {T}}$
induces a tree structure rooted at
![]() $\bar {0}=(0,0)$
. Let us denote this tree by
$\bar {0}=(0,0)$
. Let us denote this tree by
![]() $\mathcal {T}$
, and observe that this is a countably branching well-founded tree, due to 5.9(i). For
$\mathcal {T}$
, and observe that this is a countably branching well-founded tree, due to 5.9(i). For
![]() $t=(f,w(f))\in \mathcal {T}$
, we set
$t=(f,w(f))\in \mathcal {T}$
, we set
![]() $f_t=f$
and
$f_t=f$
and
![]() $w(t)=w(f)$
.
$w(t)=w(f)$
.
It is clear that unlike the case where the tree is defined on the basis of the space, here, incomparable segments need not necessarily have disjoint supports. This forces us to introduce the notion of essentially incomparable nodes, which was first defined in [Reference Argyros, Georgiou and Motakis8]. To this end, we first need to define an additional tree structure that is readily implied by
![]() $\mathcal {T}$
via the projection
$\mathcal {T}$
via the projection
![]() $(f,w(f))\mapsto w(f)$
.
$(f,w(f))\mapsto w(f)$
.
Definition 5.10. Define a partial order
![]() $<_{\mathcal {W}}$
on
$<_{\mathcal {W}}$
on
![]() $\{ m_j:j\in \mathbb {N} \}$
as follows:
$\{ m_j:j\in \mathbb {N} \}$
as follows:
![]() $m_i<_{\mathcal {W}} m_j$
if there exist
$m_i<_{\mathcal {W}} m_j$
if there exist
![]() $t_{1},t_{2}\in \mathcal {T}$
, such that
$t_{1},t_{2}\in \mathcal {T}$
, such that
![]() $t_1<_{\mathcal {T}} t_2$
,
$t_1<_{\mathcal {T}} t_2$
,
![]() $w(t_1)=m_i$
and
$w(t_1)=m_i$
and
![]() $w(t_2)=m_j$
.
$w(t_2)=m_j$
.
As an immediate consequence of the fact that
![]() $\mathcal {T}$
is a countably branching well-founded tree, we have that
$\mathcal {T}$
is a countably branching well-founded tree, we have that
![]() $<_{\mathcal {W}}$
also defines a tree structure. Let us denote this tree by
$<_{\mathcal {W}}$
also defines a tree structure. Let us denote this tree by
![]() $\mathcal {W}$
and note that it is also countably branching and well founded.
$\mathcal {W}$
and note that it is also countably branching and well founded.
Remark 5.11. The above definition implies that if
![]() $t_1,t_2\in \mathcal {T}$
are such that
$t_1,t_2\in \mathcal {T}$
are such that
![]() $w(t_1)<_{\mathcal {W}} w(t_2)$
, then there exist
$w(t_1)<_{\mathcal {W}} w(t_2)$
, then there exist
![]() $t_3,t_4\in \mathcal {T}$
, such that
$t_3,t_4\in \mathcal {T}$
, such that
![]() $t_3<_{\mathcal {T}} t_4$
,
$t_3<_{\mathcal {T}} t_4$
,
![]() $w(t_3)=w(t_1)$
and
$w(t_3)=w(t_1)$
and
![]() $w(t_4)=w(t_2)$
. The tree structure of
$w(t_4)=w(t_2)$
. The tree structure of
![]() $\mathcal {T}$
implies that
$\mathcal {T}$
implies that
![]() $t_3$
is uniquely defined, and we will say that
$t_3$
is uniquely defined, and we will say that
![]() $t_3$
generates
$t_3$
generates
![]() $w(t_2)$
. This is not the case, however, for
$w(t_2)$
. This is not the case, however, for
![]() $t_4$
, and, moreover, it is not necessary that
$t_4$
, and, moreover, it is not necessary that
![]() $t_3<_{\mathcal {T}} t_2$
.
$t_3<_{\mathcal {T}} t_2$
.
Definition 5.12.
-
(i) A subset A of
 $\mathcal {T}\setminus \{\bar {0}\}$
is called essentially incomparable if whenever
$\mathcal {T}\setminus \{\bar {0}\}$
is called essentially incomparable if whenever
 $t_1,t_2\in A$
are such that
$t_1,t_2\in A$
are such that
 $w(t_1)<_{\mathcal {W}} w(t_2)$
, then for the unique
$w(t_1)<_{\mathcal {W}} w(t_2)$
, then for the unique
 $t_3\in \mathcal {T}$
with
$t_3\in \mathcal {T}$
with
 $w(t_3)=w(t_1)$
that generates
$w(t_3)=w(t_1)$
that generates
 $w(t_2)$
, we have that
$w(t_2)$
, we have that
 $f_{t_3}<f_{t_1}$
.
$f_{t_3}<f_{t_1}$
. -
(ii) A subset A of
 $\mathcal {T}$
is called weight incomparable if for any
$\mathcal {T}$
is called weight incomparable if for any
 $t_1\neq t_2$
in A,
$t_1\neq t_2$
in A,
 $w(t_1)\neq w(t_2)$
and the weights
$w(t_1)\neq w(t_2)$
and the weights
 $w(t_1)$
and
$w(t_1)$
and
 $w(t_2)$
are incomparable in
$w(t_2)$
are incomparable in
 $\mathcal {W}$
.
$\mathcal {W}$
. -
(iii) A sequence
 $(A_j)_j$
of subsets of
$(A_j)_j$
of subsets of
 $\mathcal {T}$
is called pairwise weight incomparable if for every
$\mathcal {T}$
is called pairwise weight incomparable if for every
 $j_1\neq j_2$
in
$j_1\neq j_2$
in
 $\mathbb {N}$
,
$\mathbb {N}$
,
 $t_1\in A_{j_1}$
and
$t_1\in A_{j_1}$
and
 $t_2\in A_{j_2}$
,
$t_2\in A_{j_2}$
,
 $w(t_1)\neq w(t_2)$
and the weights
$w(t_1)\neq w(t_2)$
and the weights
 $w(t_1)$
and
$w(t_1)$
and
 $w(t_2)$
are incomparable in
$w(t_2)$
are incomparable in
 $\mathcal {W}$
.
$\mathcal {W}$
.
Remark 5.13.
-
(i) If A is an essentially (respectively, weight) incomparable subset of
 $\mathcal {T}$
, then every
$\mathcal {T}$
, then every
 $B\subset A$
is also essentially (respectively, weight) incomparable.
$B\subset A$
is also essentially (respectively, weight) incomparable. -
(ii) Any subsequence of a pairwise weight incomparable sequence in
 $\mathcal {T}$
is also pairwise weight incomparable.
$\mathcal {T}$
is also pairwise weight incomparable. -
(iii) Any weight incomparable subset of
 $\mathcal {T}$
is essentially incomparable.
$\mathcal {T}$
is essentially incomparable. -
(iv) Let
 $A=\{(f,1):f\in \{\pm e^*_j:j\in \mathbb {N}\} \}$
. Then A is essentialy incomparable, and, additionally, if
$A=\{(f,1):f\in \{\pm e^*_j:j\in \mathbb {N}\} \}$
. Then A is essentialy incomparable, and, additionally, if
 $B\subset \mathcal {T}$
is essentially incomparable, then the same holds for
$B\subset \mathcal {T}$
is essentially incomparable, then the same holds for
 $A\cup B$
.
$A\cup B$
.
We can finally describe the rule used to define the norming set
![]() $W_{(1)}$
of
$W_{(1)}$
of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, namely, asymptotically weakly incomparable constraints.
$\mathfrak {X}_{\text {awi}}^{(1)}$
, namely, asymptotically weakly incomparable constraints.
Definition 5.14. Let J be an initial segment of
![]() $\mathbb {N}$
or
$\mathbb {N}$
or
![]() $ J =\mathbb {N}$
. Then a sequence
$ J =\mathbb {N}$
. Then a sequence
![]() $(f_j)_{j\in J}$
of functionals with successive supports in
$(f_j)_{j\in J}$
of functionals with successive supports in
![]() $V_{(1)}\setminus \{0\}$
is called asymptotically weakly incomparable (AWI) if each
$V_{(1)}\setminus \{0\}$
is called asymptotically weakly incomparable (AWI) if each
![]() $f_j$
admits a tree analysis
$f_j$
admits a tree analysis
![]() $(f_{j,\alpha })_{\alpha \in \mathcal {A}_j}$
,
$(f_{j,\alpha })_{\alpha \in \mathcal {A}_j}$
,
![]() $j\in J$
, such that the following are satisfied.
$j\in J$
, such that the following are satisfied.
-
(i) There is a partition
 $\{\bar {f}_j:j\in J\}= C_1^0\cup C_2^0$
, such that
$\{\bar {f}_j:j\in J\}= C_1^0\cup C_2^0$
, such that
 $C^0_1$
is essentially incomparable and
$C^0_1$
is essentially incomparable and
 $C^0_2$
is weight incomparable.
$C^0_2$
is weight incomparable. -
(ii) For every
 $k,j\in J$
with
$k,j\in J$
with
 $j\ge k+1$
, there exists a partitionsuch that
$j\ge k+1$
, there exists a partitionsuch that $$\begin{align*}\{\bar{f}_{j,\alpha}:\alpha\in \mathcal{A}_j\text{ and }|\alpha|=k\}=C^{k}_{1,j}\cup C^{k}_{2,j}, \end{align*}$$
$$\begin{align*}\{\bar{f}_{j,\alpha}:\alpha\in \mathcal{A}_j\text{ and }|\alpha|=k\}=C^{k}_{1,j}\cup C^{k}_{2,j}, \end{align*}$$
 $\cup _{j=k+1}^{\infty } C^k_{1,j}$
is essentially incomparable and
$\cup _{j=k+1}^{\infty } C^k_{1,j}$
is essentially incomparable and
 $(C^{k}_{2,j})_{j=k+1}^{\infty }$
is pairwise weight incomparable.
$(C^{k}_{2,j})_{j=k+1}^{\infty }$
is pairwise weight incomparable.

Figure 1 The collection of nodes of a fixed level in rectangles across all tree analyses forms an essentially incomparable subset, while circles across a fixed level form a family of pairwise weight incomparable subsets.
Before defining the space
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, we prove that AWI sequences are stable under taking subsequences and under taking restrictions of functionals to subsets. This fact will imply the unconditionality of the basis of
$\mathfrak {X}_{\text {awi}}^{(1)}$
, we prove that AWI sequences are stable under taking subsequences and under taking restrictions of functionals to subsets. This fact will imply the unconditionality of the basis of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
.
$\mathfrak {X}_{\text {awi}}^{(1)}$
.
Remark 5.15. Let
![]() $f\in V_{(1)}$
and
$f\in V_{(1)}$
and
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f. Let
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f. Let
![]() $\Delta $
be a nonempty subset of
$\Delta $
be a nonempty subset of
![]() $\text {supp}(f)$
, and set
$\text {supp}(f)$
, and set
![]() $g=f|_{\Delta }$
. First, note that
$g=f|_{\Delta }$
. First, note that
![]() $g\in V_{(1)}$
. Moreover,
$g\in V_{(1)}$
. Moreover,
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
naturally induces a tree analysis
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
naturally induces a tree analysis
![]() $(g_{\alpha })_{\alpha \in \mathcal {B}}$
for g as follows:
$(g_{\alpha })_{\alpha \in \mathcal {B}}$
for g as follows:
![]() $\mathcal {B}=\{\alpha \in \mathcal {A}:\text {supp}(f_{\alpha })\cap \Delta \neq \emptyset \}$
and
$\mathcal {B}=\{\alpha \in \mathcal {A}:\text {supp}(f_{\alpha })\cap \Delta \neq \emptyset \}$
and
![]() $g_{\alpha }=f_{\alpha }|_{\Delta }$
,
$g_{\alpha }=f_{\alpha }|_{\Delta }$
,
![]() $\alpha \in \mathcal {B}$
. Finally, it is easy to see that
$\alpha \in \mathcal {B}$
. Finally, it is easy to see that
![]() $w(g)=w(f)$
.
$w(g)=w(f)$
.
Proposition 5.16. Let J be an initial segment of
![]() $\mathbb {N}$
or
$\mathbb {N}$
or
![]() $ J =\mathbb {N}$
and
$ J =\mathbb {N}$
and
![]() $(f_j)_{j\in J}$
be an AWI sequence in
$(f_j)_{j\in J}$
be an AWI sequence in
![]() $V_{(1)}$
.
$V_{(1)}$
.
-
(i) Every subsequence of
 $(f_j)_{j\in J}$
is also an AWI sequence in
$(f_j)_{j\in J}$
is also an AWI sequence in
 $V_{(1)}$
.
$V_{(1)}$
. -
(ii) If
 $\Delta _j$
is a nonempty subset of
$\Delta _j$
is a nonempty subset of
 $\text {supp} (f_j)$
and
$\text {supp} (f_j)$
and
 $g_j=f_j|_{\Delta _j}$
,
$g_j=f_j|_{\Delta _j}$
,
 $j\in J$
, then
$j\in J$
, then
 $(g_j)_{j\in J}$
is an AWI sequence in
$(g_j)_{j\in J}$
is an AWI sequence in
 $V_{(1)}$
.
$V_{(1)}$
. -
(iii) If
 $(g_j)_{j\in J}$
is a sequence in
$(g_j)_{j\in J}$
is a sequence in
 $V_{(1)}$
, such that
$V_{(1)}$
, such that
 $|g_j|=|f_j|$
for all
$|g_j|=|f_j|$
for all
 $j\in J$
, then
$j\in J$
, then
 $(g_j)_{j\in J}$
is also AWI.
$(g_j)_{j\in J}$
is also AWI.
Proof. Let for every
![]() $j\in J$
,
$j\in J$
,
![]() $(f_{j,\alpha })_{\alpha \in \mathcal {A}_j}$
be a tree analysis of
$(f_{j,\alpha })_{\alpha \in \mathcal {A}_j}$
be a tree analysis of
![]() $f_j$
with
$f_j$
with
and for every
![]() $k,j\in J$
with
$k,j\in J$
with
![]() $j> k$
$j> k$
witnessing that
![]() $(f_j)_{j\in J}$
is AWI. We will define the desired partitions proving the cases (i)–(iii).
$(f_j)_{j\in J}$
is AWI. We will define the desired partitions proving the cases (i)–(iii).
To prove (i), let N be a subset of J and define
Then
![]() $\{\bar {f}_j:j\in N \} = F^0_1\cup F^0_2$
, where
$\{\bar {f}_j:j\in N \} = F^0_1\cup F^0_2$
, where
![]() $F^0_1$
is essentially incomparable and
$F^0_1$
is essentially incomparable and
![]() $F^0_2$
is weight incomparable. For the remaining part, let
$F^0_2$
is weight incomparable. For the remaining part, let
![]() $k\in N$
, and note that for
$k\in N$
, and note that for
![]() $N_k=\{j\in N:j\ge k\}$
,
$N_k=\{j\in N:j\ge k\}$
,
![]() $\cup _{j\in N_k} C^{k}_{1,j}$
is essentially incomparable and
$\cup _{j\in N_k} C^{k}_{1,j}$
is essentially incomparable and
![]() $(C^{k}_{2,j})_{j\in N_k}$
is pairwise weight incomparable.
$(C^{k}_{2,j})_{j\in N_k}$
is pairwise weight incomparable.
To prove (ii), Remark 5.15 implies that
![]() $g_j\in V_{(1)}$
,
$g_j\in V_{(1)}$
,
![]() $w(g_j)=w(f_j)$
, and we let
$w(g_j)=w(f_j)$
, and we let
![]() $(g_{j,\alpha })_{\alpha \in \mathcal {B}_j}$
be the tree analysis of g induced by
$(g_{j,\alpha })_{\alpha \in \mathcal {B}_j}$
be the tree analysis of g induced by
![]() $(f_{j,\alpha })_{\alpha \in \mathcal {A}_j}$
,
$(f_{j,\alpha })_{\alpha \in \mathcal {A}_j}$
,
![]() $j\in J$
. Define
$j\in J$
. Define
and observe that
![]() $\{\bar {g}_j:j\in J \}=F^0_1\cup F^0_2$
. Moreover, for
$\{\bar {g}_j:j\in J \}=F^0_1\cup F^0_2$
. Moreover, for
![]() $j\in J$
,
$j\in J$
,
![]() $\text {supp} (g_j)\subset \text {supp} (f_j)$
and
$\text {supp} (g_j)\subset \text {supp} (f_j)$
and
![]() $w(g_j)=w(f_j)$
, and, hence, whenever
$w(g_j)=w(f_j)$
, and, hence, whenever
![]() $g_i\neq g_j$
are in
$g_i\neq g_j$
are in
![]() $F^0_1$
with
$F^0_1$
with
![]() $w(g_i)<_{\mathcal {W}} w(g_j)$
, we have
$w(g_i)<_{\mathcal {W}} w(g_j)$
, we have
![]() $w(f_i)<_{\mathcal {W}} w(f_j)$
, implying that the generator
$w(f_i)<_{\mathcal {W}} w(f_j)$
, implying that the generator
![]() $t_3\in \mathcal {T}$
of
$t_3\in \mathcal {T}$
of
![]() $w(f_j)=w(g_j)$
with
$w(f_j)=w(g_j)$
with
![]() $w(t_3)=w(f_i)=w(g_i)$
is such that
$w(t_3)=w(f_i)=w(g_i)$
is such that
![]() $f_{t_3}<f_i$
, and thus
$f_{t_3}<f_i$
, and thus
![]() $f_{t_3}<g_i$
. This yields that
$f_{t_3}<g_i$
. This yields that
![]() $F^0_1$
is essentially incomparable. Clearly,
$F^0_1$
is essentially incomparable. Clearly,
![]() $F^0_2$
is weight incomparable. Next, for
$F^0_2$
is weight incomparable. Next, for
![]() $k,j\in J$
with
$k,j\in J$
with
![]() $j>k$
, define
$j>k$
, define
Note that for each
![]() $k\in J$
,
$k\in J$
,
![]() $(F^{k}_{2,j})_{j=k+1}^{\infty }$
is pairwise weight incomparable, and the proof that
$(F^{k}_{2,j})_{j=k+1}^{\infty }$
is pairwise weight incomparable, and the proof that
![]() $\cup _{j=k+1}^{\infty } F^k_{1,j}$
is essentially incomparable is identical to that for
$\cup _{j=k+1}^{\infty } F^k_{1,j}$
is essentially incomparable is identical to that for
![]() $F^1_0$
. Finally, the proof of (iii) is similar that of (ii).
$F^1_0$
. Finally, the proof of (iii) is similar that of (ii).
Definition 5.17. Let
![]() $W_{(1)}$
be the smallest subset of
$W_{(1)}$
be the smallest subset of
![]() $V_{(1)}$
that is symmetric, contains the singletons and for every
$V_{(1)}$
that is symmetric, contains the singletons and for every
![]() $j\in \mathbb {N}$
and every
$j\in \mathbb {N}$
and every
![]() $\mathcal {S}_{n_j}$
-admissible AWI sequence
$\mathcal {S}_{n_j}$
-admissible AWI sequence
![]() $(f_i)_{i=1}^n$
in
$(f_i)_{i=1}^n$
in
![]() $W_{(1)}$
, we have that
$W_{(1)}$
, we have that
![]() $m_j^{-1}\sum _{i=1}^nf_i$
is in
$m_j^{-1}\sum _{i=1}^nf_i$
is in
![]() $W_{(1)}$
. Moreover, let
$W_{(1)}$
. Moreover, let
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
denote the completion of
$\mathfrak {X}_{\text {awi}}^{(1)}$
denote the completion of
![]() $c_{00}(\mathbb {N})$
with respect to the norm induced by
$c_{00}(\mathbb {N})$
with respect to the norm induced by
![]() $W_{(1)}$
.
$W_{(1)}$
.
Remark 5.18.
-
(i) The norming set
 $W_{(1)}$
can be defined as the increasing union of a sequence
$W_{(1)}$
can be defined as the increasing union of a sequence
 $(W^n_{(1)})_{n=0}^{\infty }$
, where
$(W^n_{(1)})_{n=0}^{\infty }$
, where
 $W^0_{(1)}=\{\pm e^*_k:k\in \mathbb {N}\}\cup \{0\}$
and
$W^0_{(1)}=\{\pm e^*_k:k\in \mathbb {N}\}\cup \{0\}$
and $$ \begin{align*} W^{n+1}_{(1)}=W^n_{(1)}\cup\Big\{\frac{1}{m_j}\sum_{l=1}^df_l:\;&j,d\in\mathbb{N}\text{ and }(f_l)_{l=1}^d \text{ is an } \mathcal{S}_{n_j}\text{-admissible AWI sequence in }W^n_{(1)}\Big\}. \end{align*} $$
$$ \begin{align*} W^{n+1}_{(1)}=W^n_{(1)}\cup\Big\{\frac{1}{m_j}\sum_{l=1}^df_l:\;&j,d\in\mathbb{N}\text{ and }(f_l)_{l=1}^d \text{ is an } \mathcal{S}_{n_j}\text{-admissible AWI sequence in }W^n_{(1)}\Big\}. \end{align*} $$
-
(ii) Note that Remark 5.13 (iv) implies that any sequence of singletons is AWI. Hence, we have that
 $$\begin{align*}W^{1}_{(1)}=W^0_{(1)}\cup\Big\{\frac{1}{m_j}\sum_{k\in E}\epsilon_ke^*_k:\;j\in\mathbb{N}, \; E\in\mathcal{S}_{n_j} \text{ and } \epsilon_k\in\{-1,1\} \text{ for }k\in E \Big\}. \end{align*}$$
$$\begin{align*}W^{1}_{(1)}=W^0_{(1)}\cup\Big\{\frac{1}{m_j}\sum_{k\in E}\epsilon_ke^*_k:\;j\in\mathbb{N}, \; E\in\mathcal{S}_{n_j} \text{ and } \epsilon_k\in\{-1,1\} \text{ for }k\in E \Big\}. \end{align*}$$
-
(iii) Proposition 5.16 yields that the standard unit vector basis of
 $c_{00}(\mathbb {N})$
forms an
$c_{00}(\mathbb {N})$
forms an
 $1$
-unconditional Schauder basis for
$1$
-unconditional Schauder basis for
 $\mathfrak {X}_{\text {awi}}^{(1)}$
.
$\mathfrak {X}_{\text {awi}}^{(1)}$
.
6 Outline of proof
Although unconditionality of the basis of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
is almost immediate, it is not, however, straightforward to show that
$\mathfrak {X}_{\text {awi}}^{(1)}$
is almost immediate, it is not, however, straightforward to show that
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
admits
$\mathfrak {X}_{\text {awi}}^{(1)}$
admits
![]() $\ell _1$
as an asymptotic model. Indeed, this requires Lemma 7.2, which is based on the combinatorial results concerning measures on well-founded trees of Section 4, which first appeared in [Reference Argyros, Georgiou and Motakis8]. This lemma yields that for any choice of successive families
$\ell _1$
as an asymptotic model. Indeed, this requires Lemma 7.2, which is based on the combinatorial results concerning measures on well-founded trees of Section 4, which first appeared in [Reference Argyros, Georgiou and Motakis8]. This lemma yields that for any choice of successive families
![]() $(F_j)_j$
of normalised blocks in
$(F_j)_j$
of normalised blocks in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
and for any
$\mathfrak {X}_{\text {awi}}^{(1)}$
and for any
![]() $\varepsilon>0$
, we may pass to a subsequence
$\varepsilon>0$
, we may pass to a subsequence
![]() $(F_j)_{j\in M}$
and find a family
$(F_j)_{j\in M}$
and find a family
![]() $(G_j)_{j\in M}$
of subsets of
$(G_j)_{j\in M}$
of subsets of
![]() $W_{(1)}$
, such that for any choice of
$W_{(1)}$
, such that for any choice of
![]() $x_j\in F_j$
,
$x_j\in F_j$
,
![]() $j\in M$
, there is a
$j\in M$
, there is a
![]() $g_j\in G_j$
with
$g_j\in G_j$
with
![]() $g_j(x_j)>1-\varepsilon $
so that
$g_j(x_j)>1-\varepsilon $
so that
![]() $(g_j)_{j\in M}$
is AWI. Thus, we are able to prove, employing Lemma 3.4, the aforementioned result.
$(g_j)_{j\in M}$
is AWI. Thus, we are able to prove, employing Lemma 3.4, the aforementioned result.
To prove the nonexistence of Asymptotic
![]() $\ell _1$
subspaces in
$\ell _1$
subspaces in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, we start with the notion of exact pairs. This is a key ingredient in the study of Mixed Tsirelson spaces, used for the first time by Schlumprecht [Reference Schlumprecht26].
$\mathfrak {X}_{\text {awi}}^{(1)}$
, we start with the notion of exact pairs. This is a key ingredient in the study of Mixed Tsirelson spaces, used for the first time by Schlumprecht [Reference Schlumprecht26].
Definition 6.1. We call a pair
![]() $(x,f)$
, where
$(x,f)$
, where
![]() $x\in \mathfrak {X}_{\text {awi}}^{(1)}$
and
$x\in \mathfrak {X}_{\text {awi}}^{(1)}$
and
![]() $f\in W_{(1)}$
, an
$f\in W_{(1)}$
, an
![]() $m_j$
-exact pair if the following hold.
$m_j$
-exact pair if the following hold.
-
(i)
 $\|x\|\le 3$
,
$\|x\|\le 3$
,
 $f(x)=1$
and
$f(x)=1$
and
 $w(f)=m_j$
.
$w(f)=m_j$
. -
(ii) If
 $g\in W_{(1)}$
with
$g\in W_{(1)}$
with
 $w(g)<w(f)$
, then
$w(g)<w(f)$
, then
 $|g(x)|\le 18w(g)^{-1}$
.
$|g(x)|\le 18w(g)^{-1}$
. -
(iii) If
 $g\in W_{(1)}$
with
$g\in W_{(1)}$
with
 $w(g)>w(f)$
, then
$w(g)>w(f)$
, then
 $|g(x)|\le 6(m_{j}^{-1}+m_j w(g)^{-1}) $
.
$|g(x)|\le 6(m_{j}^{-1}+m_j w(g)^{-1}) $
.
If, additionally, for every
![]() $g\in W_{(1)}$
that has a tree analysis
$g\in W_{(1)}$
that has a tree analysis
![]() $(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
![]() $w(g_{\alpha })\neq m_j$
for all
$w(g_{\alpha })\neq m_j$
for all
![]() $\alpha \in \mathcal {A}$
, we have
$\alpha \in \mathcal {A}$
, we have
![]() $|g(x)|\le 18m^{-1}_j$
, then we call
$|g(x)|\le 18m^{-1}_j$
, then we call
![]() $(x,f)$
a strong exact pair.
$(x,f)$
a strong exact pair.
That is, roughly speaking, for an exact pair
![]() $(x,f)$
, the evaluation of a functional g in
$(x,f)$
, the evaluation of a functional g in
![]() $W_{(1)}$
, on x, admits an upper bound depending only on the weight of g. In the case of an
$W_{(1)}$
, on x, admits an upper bound depending only on the weight of g. In the case of an
![]() $m_j$
-strong exact pair
$m_j$
-strong exact pair
![]() $(x,f)$
, any g in
$(x,f)$
, any g in
![]() $W_{(1)}$
with a tree analysis
$W_{(1)}$
with a tree analysis
![]() $(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
![]() $w(g_{\alpha })\neq m_j$
, has negligible evaluation on x. We will consider certain exact pairs which we call standard exact pairs (SEP) (see Definition 8.7) and which we prove to be strong exact pairs. It is the case that such pairs can be found in any block subspace of
$w(g_{\alpha })\neq m_j$
, has negligible evaluation on x. We will consider certain exact pairs which we call standard exact pairs (SEP) (see Definition 8.7) and which we prove to be strong exact pairs. It is the case that such pairs can be found in any block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, and this is used to prove the reflexivity of
$\mathfrak {X}_{\text {awi}}^{(1)}$
, and this is used to prove the reflexivity of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
as well as the following proposition which yields the nonexistence of Asymptotic
$\mathfrak {X}_{\text {awi}}^{(1)}$
as well as the following proposition which yields the nonexistence of Asymptotic
![]() $\ell _1$
subspaces.
$\ell _1$
subspaces.
Proposition 6.2. Given
![]() $0<c<1$
, there is
$0<c<1$
, there is
![]() $n\in \mathbb {N}$
so that in any block subspace Y there is a sequence
$n\in \mathbb {N}$
so that in any block subspace Y there is a sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
of SEPs, where
$(x_1,f_1),\ldots ,(x_n,f_n)$
of SEPs, where
![]() $x_i\in Y$
,
$x_i\in Y$
,
![]() $i=1,\ldots ,n$
, with
$i=1,\ldots ,n$
, with
![]() $\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
, such that
$\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
, such that
![]() $\|x_1+\cdots +x_n\|<c\:n$
.
$\|x_1+\cdots +x_n\|<c\:n$
.
To this end, we first employ the following lemma that highlights the importance of the asymptotically weakly incomparable constraints.
Lemma 6.3. Let
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
be SEPs with
$(x_1,f_1),\ldots ,(x_n,f_n)$
be SEPs with
![]() $\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
. Then, for any
$\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
. Then, for any
![]() $f\in W_{(1)}$
with a tree analysis
$f\in W_{(1)}$
with a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
and
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
and
![]() $k\in \mathbb {N}$
, the number of
$k\in \mathbb {N}$
, the number of
![]() $f_i$
’s,
$f_i$
’s,
![]() $i=1,\ldots ,n$
, such that there exists
$i=1,\ldots ,n$
, such that there exists
![]() $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
![]() $|\alpha |=k$
,
$|\alpha |=k$
,
![]() $w(f_i)=w(f_{\alpha })$
and
$w(f_i)=w(f_{\alpha })$
and
![]() $\text {supp}(x_i)\cap \text {supp}(f_{\alpha })\neq \emptyset $
, is at most
$\text {supp}(x_i)\cap \text {supp}(f_{\alpha })\neq \emptyset $
, is at most
![]() $ek!$
, where e denotes Euler’s number.
$ek!$
, where e denotes Euler’s number.
Then, we consider a sequence of standard exact pairs
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
with
$(x_1,f_1),\ldots ,(x_n,f_n)$
with
![]() $\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
and fix
$\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
and fix
![]() $0<c<1$
. Pick an
$0<c<1$
. Pick an
![]() $m\in \mathbb {N}$
, such that
$m\in \mathbb {N}$
, such that
![]() $3/2^m<c$
. For
$3/2^m<c$
. For
![]() $f\in W_{(1)}$
, with a tree analysis
$f\in W_{(1)}$
, with a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, we consider partitions
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, we consider partitions
![]() $f=g+h$
and
$f=g+h$
and
![]() $g=g_1+g_2$
as follows: First, set
$g=g_1+g_2$
as follows: First, set
and define
![]() $g=f|_G$
and
$g=f|_G$
and
![]() $h=f|_{\mathbb {N}\setminus G}$
(see Figure 2).
$h=f|_{\mathbb {N}\setminus G}$
(see Figure 2).

Figure 2 The tree analysis of f and the induced tree analyses of g and h. The circled nodes
![]() $\alpha $
are such that
$\alpha $
are such that
![]() $w(f_{\alpha })=w(f_k)$
and
$w(f_{\alpha })=w(f_k)$
and
![]() $\text {supp}(x_k)\cap \text {supp}(f_{\alpha })\neq \emptyset $
for some
$\text {supp}(x_k)\cap \text {supp}(f_{\alpha })\neq \emptyset $
for some
![]() $k\in \{1,\ldots ,n\}$
.
$k\in \{1,\ldots ,n\}$
.
To define
![]() $g_1$
, consider the tree analysis
$g_1$
, consider the tree analysis
![]() $(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
of g that is induced by
$(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
of g that is induced by
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, that is,
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, that is,
![]() $g_{\alpha }=f_{\alpha }|_G$
for
$g_{\alpha }=f_{\alpha }|_G$
for
![]() $\alpha \in \mathcal {A}_g$
and
$\alpha \in \mathcal {A}_g$
and
![]() $\mathcal {A}_g=\{\alpha \in \mathcal {A}:\text {supp}(f_{\alpha })\cap G\neq \emptyset \}$
. Then, we define
$\mathcal {A}_g=\{\alpha \in \mathcal {A}:\text {supp}(f_{\alpha })\cap G\neq \emptyset \}$
. Then, we define
for
![]() $k=1,\ldots ,n$
,
$k=1,\ldots ,n$
,
and finally
![]() $g_1 = g|_{G_1}$
(see Figure 3). Observe that Lemma 6.3 implies that
$g_1 = g|_{G_1}$
(see Figure 3). Observe that Lemma 6.3 implies that
 $$ \begin{align} \#\left\{ k\in\{1,\ldots,n\} : g_1(x_k)\neq 0\right\} \le \ell = e \sum_{k=1}^mk!. \end{align} $$
$$ \begin{align} \#\left\{ k\in\{1,\ldots,n\} : g_1(x_k)\neq 0\right\} \le \ell = e \sum_{k=1}^mk!. \end{align} $$
Moreover, the induced tree analysis
![]() $(h_{\alpha })_{\alpha \in \mathcal {A}_h}$
of h is such that
$(h_{\alpha })_{\alpha \in \mathcal {A}_h}$
of h is such that
![]() $w(h_{\alpha })\neq w(f_k)$
for all
$w(h_{\alpha })\neq w(f_k)$
for all
![]() $k=1,\ldots ,n$
, and, therefore, the fact that
$k=1,\ldots ,n$
, and, therefore, the fact that
![]() $(x_k,f_k)$
are strong exact pairs yields
$(x_k,f_k)$
are strong exact pairs yields
Considering a further partition of
![]() $g_2|_{\text {supp}(x_k)}$
, we show that
$g_2|_{\text {supp}(x_k)}$
, we show that
Hence, (6.1), (6.2) and (6.3) imply
 $$\begin{align*}\left|f\left( \frac{1}{n} \sum_{k=1}^n x_k \right)\right| \le \frac{36+\ell}{n}+\frac{3}{2^m}. \end{align*}$$
$$\begin{align*}\left|f\left( \frac{1}{n} \sum_{k=1}^n x_k \right)\right| \le \frac{36+\ell}{n}+\frac{3}{2^m}. \end{align*}$$
Then, our choice of m yields Proposition 6.2 for sufficiently large n and
![]() $w(f_1)$
, where
$w(f_1)$
, where
![]() $w(f_1)$
is chosen appropriately to deal with the case where
$w(f_1)$
is chosen appropriately to deal with the case where
![]() $f\in \{\pm e_j^*:j\in \mathbb {N}\}$
.
$f\in \{\pm e_j^*:j\in \mathbb {N}\}$
.

Figure 3 We consider the m-th level of the induced tree analysis of g. Nodes
![]() $\alpha $
with
$\alpha $
with
![]() $w(f_{\alpha })=w(f_k)$
and
$w(f_{\alpha })=w(f_k)$
and
![]() $|\alpha |\le m$
are used to define
$|\alpha |\le m$
are used to define
![]() $g_1$
, while such nodes of height greater than m define
$g_1$
, while such nodes of height greater than m define
![]() $g_2$
, restricted on each
$g_2$
, restricted on each
![]() $x_k$
for
$x_k$
for
![]() $k=1,\ldots ,n$
.
$k=1,\ldots ,n$
.
Assuming that Y is a C-asymptotic
![]() $\ell _1$
block subspace of
$\ell _1$
block subspace of
![]() $\mathfrak {X}^{(1)}_{\text {awi}}$
, we pick a sequence of standard exact pairs
$\mathfrak {X}^{(1)}_{\text {awi}}$
, we pick a sequence of standard exact pairs
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
in
$(x_1,f_1),\ldots ,(x_n,f_n)$
in
![]() $Y\times W_{(1)}$
, satisfying the conclusion of Proposition 6.2 and derive a contradiction.
$Y\times W_{(1)}$
, satisfying the conclusion of Proposition 6.2 and derive a contradiction.
The remainder of this part of the paper is organised as follows. In Section 7, we prove that
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
admits
$\mathfrak {X}_{\text {awi}}^{(1)}$
admits
![]() $\ell _1$
as a unique asymptotic model. Next, in Section 8, we prove existence and properties of standard exact pairs. The final section of this part contains the results leading up to the proof that
$\ell _1$
as a unique asymptotic model. Next, in Section 8, we prove existence and properties of standard exact pairs. The final section of this part contains the results leading up to the proof that
![]() $\mathfrak {X}^{(1)}_{\text {awi}}$
does not contain Asymptotic
$\mathfrak {X}^{(1)}_{\text {awi}}$
does not contain Asymptotic
![]() $\ell _1$
subspaces.
$\ell _1$
subspaces.
7 Asymptotic models generated by block sequences of
 $\mathfrak {X}_{\text {awi}}^{(1)}$
$\mathfrak {X}_{\text {awi}}^{(1)}$
We show that the space
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
admits a unique asymptotic model, or equivalently, a uniformly unique joint spreading model with respect to
$\mathfrak {X}_{\text {awi}}^{(1)}$
admits a unique asymptotic model, or equivalently, a uniformly unique joint spreading model with respect to
![]() $\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(1)})$
that is equivalent to the unit vector basis of
$\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(1)})$
that is equivalent to the unit vector basis of
![]() $\ell _1$
. The key ingredient in the proof is the following lemma concerning bounded positive measures on the tree of initial segments of
$\ell _1$
. The key ingredient in the proof is the following lemma concerning bounded positive measures on the tree of initial segments of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Remark 7.1. Let us first recall some notation from Section 4. We denote by
![]() ${\widetilde {\mathcal {T}}}$
the tree of initial segments of
${\widetilde {\mathcal {T}}}$
the tree of initial segments of
![]() $\mathcal {T}$
equipped with the partial order induced by inclusion and consider the isomorphism
$\mathcal {T}$
equipped with the partial order induced by inclusion and consider the isomorphism
![]() $t\mapsto {\tilde {t}} =\{s\in \mathcal {T}:s\le _{\mathcal {T}} t\}$
, between
$t\mapsto {\tilde {t}} =\{s\in \mathcal {T}:s\le _{\mathcal {T}} t\}$
, between
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() ${\widetilde {\mathcal {T}}}$
. Similarly, by
${\widetilde {\mathcal {T}}}$
. Similarly, by
![]() ${\widetilde {\mathcal {W}}}$
, we denote the tree of initial segments of
${\widetilde {\mathcal {W}}}$
, we denote the tree of initial segments of
![]() $\mathcal {W}$
and consider the isomorphism
$\mathcal {W}$
and consider the isomorphism
![]() $w\mapsto {\tilde {w}} = \{v\in \mathcal {W}:v\le _{\mathcal {W}} w\}$
between
$w\mapsto {\tilde {w}} = \{v\in \mathcal {W}:v\le _{\mathcal {W}} w\}$
between
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() ${\widetilde {\mathcal {W}}}$
. Finally, for
${\widetilde {\mathcal {W}}}$
. Finally, for
![]() $t\in \mathcal {T}$
, we set
$t\in \mathcal {T}$
, we set
![]() $\tilde {w}(t)=\{{\tilde {w}}\in {\widetilde {\mathcal {W}}}: w\le _{\mathcal {W}} w(t) \}$
.
$\tilde {w}(t)=\{{\tilde {w}}\in {\widetilde {\mathcal {W}}}: w\le _{\mathcal {W}} w(t) \}$
.
Lemma 7.2. Let
![]() $(\mu _i)_i$
be a bounded finitely and disjointly supported sequence in
$(\mu _i)_i$
be a bounded finitely and disjointly supported sequence in
![]() $\mathcal {M}_+({\widetilde {\mathcal {T}}})$
. Assume that the sets
$\mathcal {M}_+({\widetilde {\mathcal {T}}})$
. Assume that the sets
![]() $\cup \{\text {supp} (f_t):{\tilde {t}}\in \text {supp}(\mu _i)\}$
,
$\cup \{\text {supp} (f_t):{\tilde {t}}\in \text {supp}(\mu _i)\}$
,
![]() $i\in \mathbb {N}$
, are disjoint. Then, for every
$i\in \mathbb {N}$
, are disjoint. Then, for every
![]() $\varepsilon>0$
, there exists an infinite subset of the natural numbers L and for each
$\varepsilon>0$
, there exists an infinite subset of the natural numbers L and for each
![]() $i\in L$
subsets
$i\in L$
subsets
![]() $G^1_i$
,
$G^1_i$
,
![]() $G^2_i$
of
$G^2_i$
of
![]() ${\widetilde {\mathcal {T}}}$
, such that
${\widetilde {\mathcal {T}}}$
, such that
-
(i)
 $G^1_i$
,
$G^1_i$
,
 $G^2_i$
are disjoint subsets of
$G^2_i$
are disjoint subsets of
 $\text {supp}(\mu _i)$
for every
$\text {supp}(\mu _i)$
for every
 $i\in L$
,
$i\in L$
, -
(ii)
 $\mu _i({\widetilde {\mathcal {T}}}\setminus G^1_i\cup G^2_i)<\varepsilon $
for every
$\mu _i({\widetilde {\mathcal {T}}}\setminus G^1_i\cup G^2_i)<\varepsilon $
for every
 $i\in L$
,
$i\in L$
, -
(iii)
 $\{t\in \mathcal {T}:{\tilde {t}}\in \cup _{i\in L}G^1_i\}$
is essentially incomparable and
$\{t\in \mathcal {T}:{\tilde {t}}\in \cup _{i\in L}G^1_i\}$
is essentially incomparable and -
(iv) if
 $F_i^2=\{t\in \mathcal {T}:{\tilde {t}}\in G_i^2\}$
,
$F_i^2=\{t\in \mathcal {T}:{\tilde {t}}\in G_i^2\}$
,
 $i\in L$
, then the sequence
$i\in L$
, then the sequence
 $(F_i^2)_{i\in L}$
is pairwise weight incomparable.
$(F_i^2)_{i\in L}$
is pairwise weight incomparable.
Proof. Passing to a subsequence if necessary, we may assume that the (unique) root of
![]() ${\widetilde {\mathcal {T}}}$
is not in the support of any
${\widetilde {\mathcal {T}}}$
is not in the support of any
![]() $\mu _i$
,
$\mu _i$
,
![]() $i\in \mathbb {N}$
,
$i\in \mathbb {N}$
,
![]() $\mathrm {succ}\text {-}\!\lim _i\mu _{i}$
exists and that there exist partitions
$\mathrm {succ}\text {-}\!\lim _i\mu _{i}$
exists and that there exist partitions
![]() $\mathrm {supp}(\mu _i)=A_i\cup B_i$
,
$\mathrm {supp}(\mu _i)=A_i\cup B_i$
,
![]() $i\in \mathbb {N}$
, satisfying the conclusion of Lemma 4.6. Define for each
$i\in \mathbb {N}$
, satisfying the conclusion of Lemma 4.6. Define for each
![]() $i\in \mathbb {N}$
, the measures
$i\in \mathbb {N}$
, the measures
![]() $\mu _i^1$
,
$\mu _i^1$
,
![]() $\mu _i^2\in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
given by
$\mu _i^2\in \mathcal {M}_+({\widetilde {\mathcal {T}}})$
given by
![]() $\mu _i^1(C) = \mu _i(A_i\cap C)$
and
$\mu _i^1(C) = \mu _i(A_i\cap C)$
and
![]() $\mu _i^2(C) = \mu _i(B_i\cap C)$
, and let
$\mu _i^2(C) = \mu _i(B_i\cap C)$
, and let
![]() $\nu = w^*\text {-}\lim _i\mu ^1_i = \mathrm {succ}\text {-}\!\lim _i\mu ^1_i$
. Pick a finite subset F of
$\nu = w^*\text {-}\lim _i\mu ^1_i = \mathrm {succ}\text {-}\!\lim _i\mu ^1_i$
. Pick a finite subset F of
![]() ${\widetilde {\mathcal {T}}}$
, such that
${\widetilde {\mathcal {T}}}$
, such that
![]() $\nu ({\widetilde {\mathcal {T}}}\setminus F) <\varepsilon /2$
. Then,
$\nu ({\widetilde {\mathcal {T}}}\setminus F) <\varepsilon /2$
. Then,
![]() $\nu = w^*\text {-}\lim _i\mu ^1_i$
implies that
$\nu = w^*\text {-}\lim _i\mu ^1_i$
implies that
![]() $\lim _i\mu _i^1({\widetilde {\mathcal {T}}}) = \nu ({\widetilde {\mathcal {T}}})$
, and, thus, since
$\lim _i\mu _i^1({\widetilde {\mathcal {T}}}) = \nu ({\widetilde {\mathcal {T}}})$
, and, thus, since
![]() $\nu = \mathrm {succ}\text {-}\!\lim _i\mu ^1_i$
, we have
$\nu = \mathrm {succ}\text {-}\!\lim _i\mu ^1_i$
, we have
 $$ \begin{align*} \lim_i\Big|\mu^1_i({\widetilde{\mathcal{T}}}) - \mu^1_i(\cup_{\tilde t\in F}S(\tilde t))\Big| = \Big|\nu({\widetilde{\mathcal{T}}}) - \lim_i\sum_{\tilde t\in F}\mu_i^1(S(\tilde t))\Big| = \nu({\widetilde{\mathcal{T}}}\setminus F)<\frac{\varepsilon}{2}. \end{align*} $$
$$ \begin{align*} \lim_i\Big|\mu^1_i({\widetilde{\mathcal{T}}}) - \mu^1_i(\cup_{\tilde t\in F}S(\tilde t))\Big| = \Big|\nu({\widetilde{\mathcal{T}}}) - \lim_i\sum_{\tilde t\in F}\mu_i^1(S(\tilde t))\Big| = \nu({\widetilde{\mathcal{T}}}\setminus F)<\frac{\varepsilon}{2}. \end{align*} $$
Hence, we can find
![]() $i_0\in \mathbb {N}$
, such that for all
$i_0\in \mathbb {N}$
, such that for all
![]() $i\geq i_0$
, we have
$i\geq i_0$
, we have
We set
![]() $\Sigma =\sigma (\{t\in \mathcal {T}:{\tilde {t}}\in F\})$
and
$\Sigma =\sigma (\{t\in \mathcal {T}:{\tilde {t}}\in F\})$
and
Note that
![]() $\Sigma $
and R are finite, since F is finite. Thus, using the fact that the sets
$\Sigma $
and R are finite, since F is finite. Thus, using the fact that the sets
![]() $\cup \{\text {supp} (f_t):{\tilde {t}}\in \text {supp}(\mu _i)\}$
for
$\cup \{\text {supp} (f_t):{\tilde {t}}\in \text {supp}(\mu _i)\}$
for
![]() $i\in \mathbb {N}$
are disjoint, find
$i\in \mathbb {N}$
are disjoint, find
![]() $i_1\in \mathbb {N}$
with
$i_1\in \mathbb {N}$
with
![]() $i_1\geq i_0$
so that
$i_1\geq i_0$
so that
For
![]() $G_i^1 = A_i\cap (\cup _{{\tilde {t}}\in F}S({\tilde {t}}))$
, (7.1) implies that
$G_i^1 = A_i\cap (\cup _{{\tilde {t}}\in F}S({\tilde {t}}))$
, (7.1) implies that
![]() $|\mu _i(A_i) - \mu _i(G_i^1)|<\varepsilon /2$
,
$|\mu _i(A_i) - \mu _i(G_i^1)|<\varepsilon /2$
,
![]() $i\geq i_1$
. We will show that
$i\geq i_1$
. We will show that
![]() $\{t\in \mathcal {T}:{\tilde {t}}\in \cup _{i\geq i_1}G_i^1\}$
is essentially incomparable, that is, that (iii) is satisfied. To this end, first observe that if
$\{t\in \mathcal {T}:{\tilde {t}}\in \cup _{i\geq i_1}G_i^1\}$
is essentially incomparable, that is, that (iii) is satisfied. To this end, first observe that if
![]() ${\tilde {t}}\in \cup _{i\geq i_1}G_i^1$
, then
${\tilde {t}}\in \cup _{i\geq i_1}G_i^1$
, then
![]() $w(t)\in \Sigma $
. Let
$w(t)\in \Sigma $
. Let
![]() ${\tilde {t}}_1,{\tilde {t}}_2\in \cup _{i\geq i_1}G_i^1$
with
${\tilde {t}}_1,{\tilde {t}}_2\in \cup _{i\geq i_1}G_i^1$
with
![]() $w(t_1)<_{\mathcal {W}} w(t_2)$
. It is immediate that if
$w(t_1)<_{\mathcal {W}} w(t_2)$
. It is immediate that if
![]() $t_3\in \mathcal {T}$
is the generator of
$t_3\in \mathcal {T}$
is the generator of
![]() $w(t_2)$
with
$w(t_2)$
with
![]() $w(t_3)=w(t_1)$
, then
$w(t_3)=w(t_1)$
, then
![]() $t_3\in R$
, and, hence, (7.2) implies that
$t_3\in R$
, and, hence, (7.2) implies that
![]() $f_{t_3}<f_{t_1}$
, proving the desired result.
$f_{t_3}<f_{t_1}$
, proving the desired result.
For the remaining part of the proof, recall the root of
![]() ${\widetilde {\mathcal {T}}}$
avoids the supports of all
${\widetilde {\mathcal {T}}}$
avoids the supports of all
![]() $\mu _i^2$
,
$\mu _i^2$
,
![]() $i\ge i_1$
. This implies that every
$i\ge i_1$
. This implies that every
![]() ${\tilde {t}}\in \cup _{i\ge i_1} \text {supp}(\mu _i^2)$
is the successor of some node in
${\tilde {t}}\in \cup _{i\ge i_1} \text {supp}(\mu _i^2)$
is the successor of some node in
![]() ${\widetilde {\mathcal {T}}}$
. Then, since for all
${\widetilde {\mathcal {T}}}$
. Then, since for all
![]() $i\ge i_1$
, the set
$i\ge i_1$
, the set
![]() $B_i = \text {supp}(\mu _i^2)$
is finite (as a subset of the finite support of
$B_i = \text {supp}(\mu _i^2)$
is finite (as a subset of the finite support of
![]() $\mu _i$
), and for each
$\mu _i$
), and for each
![]() ${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the sequence
${\tilde {t}}\in {\widetilde {\mathcal {T}}}$
, the sequence
![]() $(\mu _i^2(S({\tilde {t}})))_{i\ge i_1}$
is eventually zero, we may pass to a subsequence so that for all
$(\mu _i^2(S({\tilde {t}})))_{i\ge i_1}$
is eventually zero, we may pass to a subsequence so that for all
![]() $i_1\le i<j$
, we have
$i_1\le i<j$
, we have
![]() $\{w(t):{\tilde {t}}\in \text {supp}(\mu _i^2)\}\cap \{w(t):{\tilde {t}}\in \text {supp}(\mu _j^2)\} = \emptyset $
. We can, therefore, define the bounded sequence of disjointly supported measures
$\{w(t):{\tilde {t}}\in \text {supp}(\mu _i^2)\}\cap \{w(t):{\tilde {t}}\in \text {supp}(\mu _j^2)\} = \emptyset $
. We can, therefore, define the bounded sequence of disjointly supported measures
![]() $(\nu _i)_{i\ge i_1}$
on
$(\nu _i)_{i\ge i_1}$
on
![]() $\widetilde {\mathcal {W}}$
given by
$\widetilde {\mathcal {W}}$
given by
![]() $\nu _i(\{{\tilde {w}}\}) = \mu _i^2(\{\tilde t\in {\widetilde {\mathcal {T}}}: \tilde {w}(t) = {\tilde {w}}\})$
. Hence, applying Proposition 4.1 and passing to a subsequence, we obtain a subset
$\nu _i(\{{\tilde {w}}\}) = \mu _i^2(\{\tilde t\in {\widetilde {\mathcal {T}}}: \tilde {w}(t) = {\tilde {w}}\})$
. Hence, applying Proposition 4.1 and passing to a subsequence, we obtain a subset
![]() $E_i$
of
$E_i$
of
![]() $\text {supp}(\nu _i)$
, such that
$\text {supp}(\nu _i)$
, such that
![]() $\nu _i({\widetilde {\mathcal {W}}}\setminus E_i)<\varepsilon /2$
and the sets
$\nu _i({\widetilde {\mathcal {W}}}\setminus E_i)<\varepsilon /2$
and the sets
![]() $E_i$
,
$E_i$
,
![]() $i\ge i_1$
, are pairwise incomparable. It is easy to verify that if
$i\ge i_1$
, are pairwise incomparable. It is easy to verify that if
![]() $G^2_i=\{{\tilde {t}}\in B_i:{\tilde {w}}(t)\in E_i \}$
and
$G^2_i=\{{\tilde {t}}\in B_i:{\tilde {w}}(t)\in E_i \}$
and
![]() $F^2_i=\{t\in \mathcal {T}:{\tilde {t}}\in G^2_i\}$
,
$F^2_i=\{t\in \mathcal {T}:{\tilde {t}}\in G^2_i\}$
,
![]() $i\ge i_1$
, then
$i\ge i_1$
, then
![]() $(F^2_i)_{i\ge i_1}$
is pairwise weight incomparable and
$(F^2_i)_{i\ge i_1}$
is pairwise weight incomparable and
![]() $|\mu _i(B_i) - \mu _i(G_i^2)| = \mu ^2_i({\widetilde {\mathcal {T}}}\setminus G^2_i)<\varepsilon /2$
for every
$|\mu _i(B_i) - \mu _i(G_i^2)| = \mu ^2_i({\widetilde {\mathcal {T}}}\setminus G^2_i)<\varepsilon /2$
for every
![]() $i\ge i_1$
.
$i\ge i_1$
.
Lemma 7.3. Let
![]() $x\in \mathfrak {X}_{\text {awi}}^{(1)}$
,
$x\in \mathfrak {X}_{\text {awi}}^{(1)}$
,
![]() $f\in W_{(1)}$
and a tree analysis
$f\in W_{(1)}$
and a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, such that
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, such that
![]() $f_{\alpha }(x)\ge 0$
for every
$f_{\alpha }(x)\ge 0$
for every
![]() $\alpha \in \mathcal {A}$
. Let
$\alpha \in \mathcal {A}$
. Let
![]() $\varepsilon _1,\ldots ,\varepsilon _{h(\mathcal {A})}$
be positive reals and
$\varepsilon _1,\ldots ,\varepsilon _{h(\mathcal {A})}$
be positive reals and
![]() $G_i$
be a subset of
$G_i$
be a subset of
![]() $\{ \alpha \in \mathcal {A}:|\alpha |=i \}$
, such that
$\{ \alpha \in \mathcal {A}:|\alpha |=i \}$
, such that
![]() $\sum _{\alpha \in G_i}w_f(f_{\alpha })^{-1}f_{\alpha }(x)>f(x)-\varepsilon _i$
for every
$\sum _{\alpha \in G_i}w_f(f_{\alpha })^{-1}f_{\alpha }(x)>f(x)-\varepsilon _i$
for every
![]() $1\le i\le h(\mathcal {A})$
, and
$1\le i\le h(\mathcal {A})$
, and
![]() $f(x)>\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
. Then, there exists a
$f(x)>\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
. Then, there exists a
![]() $g\in W_{(1)}$
satisfying the following conditions.
$g\in W_{(1)}$
satisfying the following conditions.
-
(i)
 $\text {supp} (g)\subset \text {supp} (f)$
and
$\text {supp} (g)\subset \text {supp} (f)$
and
 $w(g)=w(f)$
.
$w(g)=w(f)$
. -
(ii)
 $g(x)>f(x)-\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
.
$g(x)>f(x)-\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
. -
(iii) g has a tree analysis
 $(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
, such that for every
$(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
, such that for every
 $\alpha \in \mathcal {A}_g$
, there is a unique
$\alpha \in \mathcal {A}_g$
, there is a unique
 $\beta \in G_{|\alpha |}$
with
$\beta \in G_{|\alpha |}$
with
 $\text {supp} (g_{\alpha })\subset \text {supp} (f_{\beta })$
and
$\text {supp} (g_{\alpha })\subset \text {supp} (f_{\beta })$
and
 $w(g_{\alpha })=w(f_{\beta })$
.
$w(g_{\alpha })=w(f_{\beta })$
.
Proof. Let
![]() $\mathcal {A}_k$
denote the set of all nodes in
$\mathcal {A}_k$
denote the set of all nodes in
![]() $\mathcal {A}$
, such that
$\mathcal {A}$
, such that
![]() $|\alpha |=k$
,
$|\alpha |=k$
,
![]() $1\le k\le h(\mathcal {A})$
. We define g by constructing the tree analysis
$1\le k\le h(\mathcal {A})$
. We define g by constructing the tree analysis
![]() $(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
. First, define by induction
$(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
. First, define by induction
![]() $B_1=\mathcal {A}_1\setminus G_1$
and for
$B_1=\mathcal {A}_1\setminus G_1$
and for
![]() $2\le k \le h(\mathcal {A})$
:
$2\le k \le h(\mathcal {A})$
:
It follows easily that
![]() $\alpha \in B_k$
if and only if there exists
$\alpha \in B_k$
if and only if there exists
![]() $\beta \le \alpha $
, such that
$\beta \le \alpha $
, such that
![]() $\beta \notin G_{|\beta |}$
. Let
$\beta \notin G_{|\beta |}$
. Let
![]() $\mathcal {C}_g= \mathcal {A}_{h(\mathcal {A})}\setminus {B}_{h(\mathcal {A})}$
. Note that
$\mathcal {C}_g= \mathcal {A}_{h(\mathcal {A})}\setminus {B}_{h(\mathcal {A})}$
. Note that
![]() $f_{\alpha }\in \{\pm e_j^*:j\in \mathbb {N}\}$
for every
$f_{\alpha }\in \{\pm e_j^*:j\in \mathbb {N}\}$
for every
![]() $\alpha \in \mathcal {C}_g$
, and let
$\alpha \in \mathcal {C}_g$
, and let
![]() $\Delta _g=\cup \{\text {supp} (f_{\alpha }):\alpha \in \mathcal {C}_g \}$
. Then
$\Delta _g=\cup \{\text {supp} (f_{\alpha }):\alpha \in \mathcal {C}_g \}$
. Then
![]() $g=f|_{\Delta _g}$
and
$g=f|_{\Delta _g}$
and
![]() $(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
is the tree analysis induced by
$(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
is the tree analysis induced by
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
.
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
.
Observe that, by construction, g satisfies (i) and (iii). To see that it also satisfies (ii), we show by induction that for every
![]() $1\le k \le h(\mathcal {A})$
$1\le k \le h(\mathcal {A})$
 $$ \begin{align} \sum_{ \alpha\in\mathcal{A}_k\setminus {B}_k }\frac{f_{\alpha}(x)}{w_f(f_{\alpha})}> f(x) - \sum_{i=1}^k \varepsilon_i. \end{align} $$
$$ \begin{align} \sum_{ \alpha\in\mathcal{A}_k\setminus {B}_k }\frac{f_{\alpha}(x)}{w_f(f_{\alpha})}> f(x) - \sum_{i=1}^k \varepsilon_i. \end{align} $$
This indeed proves (ii), since the left-hand side of (7.3) for
![]() $k=h(\mathcal {A})$
is equal to
$k=h(\mathcal {A})$
is equal to
![]() $g(x)$
. We now prove (7.3) by induction. Assume that the inequality holds for some
$g(x)$
. We now prove (7.3) by induction. Assume that the inequality holds for some
![]() $1\leq k <h(\mathcal {A})$
. Then, for every
$1\leq k <h(\mathcal {A})$
. Then, for every
![]() $\alpha \in \mathcal {A}_{k}\setminus {B}_{k}$
, we have
$\alpha \in \mathcal {A}_{k}\setminus {B}_{k}$
, we have
 $$\begin{align*}f_{\alpha}(x)=\sum_{ \beta\in S(\alpha)\cap G_{k+1} }\frac{f_{\beta}(x)}{w(f_{\alpha})}+\sum_{ \beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w(f_{\alpha})} \end{align*}$$
$$\begin{align*}f_{\alpha}(x)=\sum_{ \beta\in S(\alpha)\cap G_{k+1} }\frac{f_{\beta}(x)}{w(f_{\alpha})}+\sum_{ \beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w(f_{\alpha})} \end{align*}$$
and
 $$\begin{align*}\sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\alpha})w(f_{\alpha})} = \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\beta})}<\varepsilon_{k+1}. \end{align*}$$
$$\begin{align*}\sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\alpha})w(f_{\alpha})} = \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\beta})}<\varepsilon_{k+1}. \end{align*}$$
Hence
 $$ \begin{align*} \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\cap G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\alpha})w(f_{\alpha})}&= \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\frac{f_{\alpha}(x)}{w_{f}(f_{\alpha})}- \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\beta})}\\ &> ( f(x) - \sum_{i=1}^k \varepsilon_i)-\varepsilon_{k+1} \end{align*} $$
$$ \begin{align*} \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\cap G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\alpha})w(f_{\alpha})}&= \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\frac{f_{\alpha}(x)}{w_{f}(f_{\alpha})}- \sum_{\alpha\in\mathcal{A}_k\setminus {B}_k}\sum_{\beta\in S(\alpha)\setminus G_{k+1} }\frac{f_{\beta}(x)}{w_f(f_{\beta})}\\ &> ( f(x) - \sum_{i=1}^k \varepsilon_i)-\varepsilon_{k+1} \end{align*} $$
which, along with the previous inequality, proves the desired result since
Lemma 7.4. Let
![]() $(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
$(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. For every
$\mathfrak {X}_{\text {awi}}^{(1)}$
. For every
![]() $\varepsilon>0$
, there exists an
$\varepsilon>0$
, there exists an
![]() $L\in [\mathbb {N}]^{\infty }$
and a
$L\in [\mathbb {N}]^{\infty }$
and a
![]() $g^i_j\in W_{(1)}$
with
$g^i_j\in W_{(1)}$
with
![]() $g^i_j(x^i_j)>1-\varepsilon $
,
$g^i_j(x^i_j)>1-\varepsilon $
,
![]() $1\le i\le l$
and
$1\le i\le l$
and
![]() $j\in L$
, such that for any choice of
$j\in L$
, such that for any choice of
![]() $1\le i_j\le l$
, the sequence
$1\le i_j\le l$
, the sequence
![]() $(g^{i_j}_j)_{j\in L}$
is AWI.
$(g^{i_j}_j)_{j\in L}$
is AWI.
Proof. Let
![]() $(\varepsilon _k)_{k=0}^{\infty }$
be a sequence of positive reals, such that
$(\varepsilon _k)_{k=0}^{\infty }$
be a sequence of positive reals, such that
![]() $\sum _{k=0}^{\infty }\varepsilon _k<\varepsilon /2$
. For every
$\sum _{k=0}^{\infty }\varepsilon _k<\varepsilon /2$
. For every
![]() $1\le i\le l$
and
$1\le i\le l$
and
![]() $j\in \mathbb {N}$
, pick an
$j\in \mathbb {N}$
, pick an
![]() $f^i_j\in W_{(1)}$
and a tree analysis
$f^i_j\in W_{(1)}$
and a tree analysis
![]() $(f^i_{j,\alpha })_{\alpha \in \mathcal {A}^i_j}$
of
$(f^i_{j,\alpha })_{\alpha \in \mathcal {A}^i_j}$
of
![]() $f^i_j$
, such that
$f^i_j$
, such that
![]() $f^i_j(x^i_j)>1-\varepsilon /2$
and
$f^i_j(x^i_j)>1-\varepsilon /2$
and
![]() $f^i_{j,\alpha }(x^i_j)> 0$
for every
$f^i_{j,\alpha }(x^i_j)> 0$
for every
![]() $\alpha \in \mathcal {A}^i_j$
. For
$\alpha \in \mathcal {A}^i_j$
. For
![]() $1\le i\le l$
and
$1\le i\le l$
and
![]() $j\in \mathbb {N}$
, we set
$j\in \mathbb {N}$
, we set
![]() $t_{j}^i=\bar {f}_j^i$
and
$t_{j}^i=\bar {f}_j^i$
and
![]() $t_{j,\alpha }^i=\bar {f}_{j,\alpha }^i$
,
$t_{j,\alpha }^i=\bar {f}_{j,\alpha }^i$
,
![]() $\alpha \in \mathcal {A}_j^i$
. We will choose, by induction, an
$\alpha \in \mathcal {A}_j^i$
. We will choose, by induction, an
![]() $L\in [\mathbb {N}]^{\infty }$
and, for every
$L\in [\mathbb {N}]^{\infty }$
and, for every
![]() $1\le i\le l$
,
$1\le i\le l$
,
![]() $j\in L$
and
$j\in L$
and
![]() $k\in \mathbb {N}$
, a subset
$k\in \mathbb {N}$
, a subset
![]() $G^{k,i}_j$
of
$G^{k,i}_j$
of
![]() $\{ \alpha \in \mathcal {A}^i_j:|\alpha |=k \}$
satisfying the following conditions. For
$\{ \alpha \in \mathcal {A}^i_j:|\alpha |=k \}$
satisfying the following conditions. For
![]() $k\in \mathbb {N}$
, we set
$k\in \mathbb {N}$
, we set
![]() $L_{>k}=\{j\in L:j>k\}$
.
$L_{>k}=\{j\in L:j>k\}$
.
-
(i) For every
 $j\in L$
, there is a partition
$j\in L$
, there is a partition
 $\{ t^{i}_j:i=1,\ldots ,l\}=C^{0}_{1,j}\cup C^{0}_{2,j}$
, such that
$\{ t^{i}_j:i=1,\ldots ,l\}=C^{0}_{1,j}\cup C^{0}_{2,j}$
, such that
 $\cup _{j\in L}C^{0}_{1,j}$
is essentially incomparable and
$\cup _{j\in L}C^{0}_{1,j}$
is essentially incomparable and
 $(C^{0}_{2,j})_{j\in L}$
is pairwise weight incomparable.
$(C^{0}_{2,j})_{j\in L}$
is pairwise weight incomparable. -
(ii) For every
 $1\le i\le l$
,
$1\le i\le l$
,
 $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
 $j\in L_{>k}$
, there is a partition
$j\in L_{>k}$
, there is a partition
 $G^{k,i}_j=G^{k,i}_{1,j}\cup G^{k,i}_{2,j}$
, such that for any choice of
$G^{k,i}_j=G^{k,i}_{1,j}\cup G^{k,i}_{2,j}$
, such that for any choice of
 $1\le i_j \le l$
,
$1\le i_j \le l$
,
 $\cup _{j\in L_{>k} } \{t^{i_j}_{j,\alpha } : \alpha \in G^{k,i_j}_{1,j} \}$
is essentially incomparable and
$\cup _{j\in L_{>k} } \{t^{i_j}_{j,\alpha } : \alpha \in G^{k,i_j}_{1,j} \}$
is essentially incomparable and
 $(\{ t^{i_j}_{j,\alpha } : \alpha \in G^{k,i_j}_{2,j} \})_{j\in L_{>k}}$
is pairwise weight incomparable.
$(\{ t^{i_j}_{j,\alpha } : \alpha \in G^{k,i_j}_{2,j} \})_{j\in L_{>k}}$
is pairwise weight incomparable. -
(iii) For every
 $i=1,\ldots ,l$
,
$i=1,\ldots ,l$
,
 $j\in L$
and
$j\in L$
and
 $k\in \mathbb {N}$
with
$k\in \mathbb {N}$
with
 $k\le h(\mathcal {A}^i_j)$
$k\le h(\mathcal {A}^i_j)$
 $$\begin{align*}\sum_{\alpha\in G^{k,i}_{j}} w_{f^i_j}(f^i_{j,\alpha})^{-1}f^i_{j,\alpha}(x^i_j)>f^i_j(x^i_j)-\varepsilon_k.\end{align*}$$
$$\begin{align*}\sum_{\alpha\in G^{k,i}_{j}} w_{f^i_j}(f^i_{j,\alpha})^{-1}f^i_{j,\alpha}(x^i_j)>f^i_j(x^i_j)-\varepsilon_k.\end{align*}$$
Observe then that (iii) and an application of the previous lemma yield, for every
![]() $1\le i \le l$
and
$1\le i \le l$
and
![]() $j\in L$
, a functional
$j\in L$
, a functional
![]() $g^i_j\in W_{(1)}$
, such that
$g^i_j\in W_{(1)}$
, such that
 $$\begin{align*}g^i_j(x^i_j)>f^i_j(x^i_j)-\sum_{k=1}^{\infty}\varepsilon_k>1-\varepsilon. \end{align*}$$
$$\begin{align*}g^i_j(x^i_j)>f^i_j(x^i_j)-\sum_{k=1}^{\infty}\varepsilon_k>1-\varepsilon. \end{align*}$$
Fix a choice of
![]() $1\le i_j\le l$
,
$1\le i_j\le l$
,
![]() $j\in L$
. Then, (i) implies that
$j\in L$
. Then, (i) implies that
![]() $\{ t^{i_j}_j:j\in L\}\cap (\cup _{j\in L}C^0_{1,j})$
is essentially incomparable, and that
$\{ t^{i_j}_j:j\in L\}\cap (\cup _{j\in L}C^0_{1,j})$
is essentially incomparable, and that
![]() $\{ t^{i_j}_j:j\in L\}\cap (\cup _{j\in L}C^0_{2,j})$
is weight incomparable. Finally, (ii) and Lemma 7.3 (iii) yield that, for every
$\{ t^{i_j}_j:j\in L\}\cap (\cup _{j\in L}C^0_{2,j})$
is weight incomparable. Finally, (ii) and Lemma 7.3 (iii) yield that, for every
![]() $1\le i\le l$
,
$1\le i\le l$
,
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $j\in L_{>k}$
, there is a partition
$j\in L_{>k}$
, there is a partition
such that
![]() $\cup _{j\in L_{>k}}C^{k,i_j}_{1,j}$
is essentially incomparable and
$\cup _{j\in L_{>k}}C^{k,i_j}_{1,j}$
is essentially incomparable and
![]() $(C^{k,i_j}_{2,j})_{j\in L_{>k}}$
is pairwise weight incomparable. Hence,
$(C^{k,i_j}_{2,j})_{j\in L_{>k}}$
is pairwise weight incomparable. Hence,
![]() $g^i_j$
,
$g^i_j$
,
![]() $1\le i\le l$
and
$1\le i\le l$
and
![]() $j\in L$
satisfy the desired conditions.
$j\in L$
satisfy the desired conditions.
To obtain L, let us first assume that
![]() $\sup _{i,j}h(\mathcal {A}^i_j)=+\infty $
(if
$\sup _{i,j}h(\mathcal {A}^i_j)=+\infty $
(if
![]() $\sup _{i,j}h(\mathcal {A}^i_j)<+\infty $
, then a finite version of the same proof works). Moreover, passing to a subsequence, we may further assume that
$\sup _{i,j}h(\mathcal {A}^i_j)<+\infty $
, then a finite version of the same proof works). Moreover, passing to a subsequence, we may further assume that
![]() $\max _i h(\mathcal {A}_j^i)>k$
whenever
$\max _i h(\mathcal {A}_j^i)>k$
whenever
![]() $j>k$
, for
$j>k$
, for
![]() $j,k\in \mathbb {N}$
. Define, for each
$j,k\in \mathbb {N}$
. Define, for each
![]() $j\in \mathbb {N}$
, the measure
$j\in \mathbb {N}$
, the measure
![]() $\mu ^0_j$
on
$\mu ^0_j$
on
![]() ${\widetilde {\mathcal {T}}}$
given by
${\widetilde {\mathcal {T}}}$
given by
 $$\begin{align*}\mu_j^0=\sum_{i=1}^lf^i_j(x^i_j)\delta_{\tilde{t}_{j}^i }. \end{align*}$$
$$\begin{align*}\mu_j^0=\sum_{i=1}^lf^i_j(x^i_j)\delta_{\tilde{t}_{j}^i }. \end{align*}$$
Applying Lemma 7.2, we obtain an
![]() $L_0\in [\mathbb {N}]^{\infty }$
, such that, for every
$L_0\in [\mathbb {N}]^{\infty }$
, such that, for every
![]() $j\in L_0$
, there exist disjoint subsets
$j\in L_0$
, there exist disjoint subsets
![]() $G^0_{1,j}$
and
$G^0_{1,j}$
and
![]() $G^0_{2,j}$
of
$G^0_{2,j}$
of
![]() $\text {supp} (\mu ^0_j)$
so that the following hold.
$\text {supp} (\mu ^0_j)$
so that the following hold.
-
(
 $\alpha _0$
)
$\alpha _0$
)
 $\mu ^0_j( {\widetilde {\mathcal {T}}} \setminus G^0_{1,j}\cup G^0_{2,j} ) < \varepsilon _0$
for every
$\mu ^0_j( {\widetilde {\mathcal {T}}} \setminus G^0_{1,j}\cup G^0_{2,j} ) < \varepsilon _0$
for every
 $j\in L_0$
.
$j\in L_0$
. -
(
 $\beta _0$
) Define
$\beta _0$
) Define
 $C^0_{1,j}=\{t\in \mathcal {T}:{\tilde {t}}\in G^0_{1,j}\}$
for
$C^0_{1,j}=\{t\in \mathcal {T}:{\tilde {t}}\in G^0_{1,j}\}$
for
 $j\in L_0$
. Then
$j\in L_0$
. Then
 $\cup _{j\in L_0}C^0_{1,j}$
is essentially incomparable.
$\cup _{j\in L_0}C^0_{1,j}$
is essentially incomparable. -
(
 $\gamma _0$
) Define
$\gamma _0$
) Define
 $C^0_{2,j}=\{t\in \mathcal {T}:{\tilde {t}}\in G^0_{2,j}\}$
for
$C^0_{2,j}=\{t\in \mathcal {T}:{\tilde {t}}\in G^0_{2,j}\}$
for
 $j\in L_0$
. Then the sequence
$j\in L_0$
. Then the sequence
 $(C^0_{2,j})_{j\in L_0}$
is pairwise weight incomparable.
$(C^0_{2,j})_{j\in L_0}$
is pairwise weight incomparable.
Note that (
![]() $\alpha _0$
) implies that
$\alpha _0$
) implies that
![]() $\text {supp} (\mu ^0_j)=G^0_{1,j}\cup G^0_{2,j}$
since
$\text {supp} (\mu ^0_j)=G^0_{1,j}\cup G^0_{2,j}$
since
![]() $f^i_j(x^i_j)>1-\varepsilon /2$
, that is,
$f^i_j(x^i_j)>1-\varepsilon /2$
, that is,
![]() $\{{\tilde {t}}^i_j:i=1,\ldots ,l \}=C^0_{1,j}\cup C^0_{2,j}$
. We proceed by induction on
$\{{\tilde {t}}^i_j:i=1,\ldots ,l \}=C^0_{1,j}\cup C^0_{2,j}$
. We proceed by induction on
![]() $\mathbb {N}$
. Suppose we have chosen
$\mathbb {N}$
. Suppose we have chosen
![]() $L_0,\ldots ,L_{k-1}$
and
$L_0,\ldots ,L_{k-1}$
and
![]() $G^0_{1,j_0},G^0_{2,j_0},\ldots ,G^{k-1}_{1,j_{k-1}},G^{k-1}_{2,j_{k-1}}$
for some
$G^0_{1,j_0},G^0_{2,j_0},\ldots ,G^{k-1}_{1,j_{k-1}},G^{k-1}_{2,j_{k-1}}$
for some
![]() $k\in \mathbb {N}$
and every
$k\in \mathbb {N}$
and every
![]() $j_i\in L_i$
, for
$j_i\in L_i$
, for
![]() $i=0,\ldots ,k-1$
. Set
$i=0,\ldots ,k-1$
. Set
![]() $L_k^0=\{j\in L_{k-1}:h(\mathcal {A}^i_j)< k\text { for all }1\le i\le l\}$
. Then, for each
$L_k^0=\{j\in L_{k-1}:h(\mathcal {A}^i_j)< k\text { for all }1\le i\le l\}$
. Then, for each
![]() $j\in L_{k-1}\setminus L^0_{k}$
, define the following measure on
$j\in L_{k-1}\setminus L^0_{k}$
, define the following measure on
![]() ${\widetilde {\mathcal {T}}}$
${\widetilde {\mathcal {T}}}$
 $$\begin{align*}\mu^{k}_j=\sum_{i=1}^l\sum_{\substack { \alpha\in\mathcal{A}^i_j \\ |\alpha|=k } } \frac{f^i_{j,\alpha}(x^i_j)}{w_{f^i_j}(f^i_{j,\alpha})}\delta_{\tilde{t}^i_{j,\alpha}}. \end{align*}$$
$$\begin{align*}\mu^{k}_j=\sum_{i=1}^l\sum_{\substack { \alpha\in\mathcal{A}^i_j \\ |\alpha|=k } } \frac{f^i_{j,\alpha}(x^i_j)}{w_{f^i_j}(f^i_{j,\alpha})}\delta_{\tilde{t}^i_{j,\alpha}}. \end{align*}$$
Again, applying Lemma 7.2 yields an
![]() $L^1_{k}\in [L_{k-1}\setminus L^0_k]^{\infty }$
and disjoint subsets
$L^1_{k}\in [L_{k-1}\setminus L^0_k]^{\infty }$
and disjoint subsets
![]() $G^{k}_{1,j}$
and
$G^{k}_{1,j}$
and
![]() $G^{k}_{2,j}$
of
$G^{k}_{2,j}$
of
![]() $\text {supp} (\mu ^{k}_j)$
,
$\text {supp} (\mu ^{k}_j)$
,
![]() $j\in L^1_k$
, such that
$j\in L^1_k$
, such that
-
(
 $\alpha _{k}$
)
$\alpha _{k}$
)
 $\mu ^k_j( {\widetilde {\mathcal {T}}} \setminus G^k_{1,j}\cup G^k_{2,j} ) < \varepsilon _k$
for every
$\mu ^k_j( {\widetilde {\mathcal {T}}} \setminus G^k_{1,j}\cup G^k_{2,j} ) < \varepsilon _k$
for every
 $j\in L^1_k$
,
$j\in L^1_k$
, -
(
 $\beta _{k}$
)
$\beta _{k}$
)
 $\{t\in \mathcal {T}:{\tilde {t}}\in \cup _{j\in {L^1_k}}G^k_{1,j}\}$
is essentially incomparable and
$\{t\in \mathcal {T}:{\tilde {t}}\in \cup _{j\in {L^1_k}}G^k_{1,j}\}$
is essentially incomparable and -
(
 $\gamma _{k}$
) the sequence
$\gamma _{k}$
) the sequence
 $(\{t:{\tilde {t}}\in G^k_{2,j}\})_{j\in {L^1_k}}$
is pairwise weight incomparable.
$(\{t:{\tilde {t}}\in G^k_{2,j}\})_{j\in {L^1_k}}$
is pairwise weight incomparable.
Then, set
![]() $L_k=L_k^0\cup L_k^1$
and
$L_k=L_k^0\cup L_k^1$
and
![]() $G^k_{i,j}=\{\alpha \in \mathcal {A}_j^i:|\alpha |=k\}$
, for
$G^k_{i,j}=\{\alpha \in \mathcal {A}_j^i:|\alpha |=k\}$
, for
![]() $1\le i\le l$
and
$1\le i\le l$
and
![]() $j\in L_{k}^0$
. Finally, choose L to be a diagonalisation of
$j\in L_{k}^0$
. Finally, choose L to be a diagonalisation of
![]() $(L_k)_{k}$
, that is,
$(L_k)_{k}$
, that is,
![]() $L(k)\in L_k$
for
$L(k)\in L_k$
for
![]() $k\in \mathbb {N}$
. Observe that
$k\in \mathbb {N}$
. Observe that
![]() $(\beta _k)$
and
$(\beta _k)$
and
![]() $(\gamma _k)$
imply (ii), while
$(\gamma _k)$
imply (ii), while
![]() $(\alpha _k)$
implies (iii).
$(\alpha _k)$
implies (iii).
Proposition 7.5. The space
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
admits a unique asymptotic model, with respect to
$\mathfrak {X}_{\text {awi}}^{(1)}$
admits a unique asymptotic model, with respect to
![]() $\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(1)})$
, equivalent to the unit vector basis of
$\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(1)})$
, equivalent to the unit vector basis of
![]() $\ell _1$
.
$\ell _1$
.
Proof. Equivalently, we will show that
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
admits
$\mathfrak {X}_{\text {awi}}^{(1)}$
admits
![]() $\ell _1$
as a uniformly unique joint spreading model with respect to
$\ell _1$
as a uniformly unique joint spreading model with respect to
![]() $\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(1)})$
. To this end, let
$\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(1)})$
. To this end, let
![]() $(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
$(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. Passing to a subsequence, we may assume that
$\mathfrak {X}_{\text {awi}}^{(1)}$
. Passing to a subsequence, we may assume that
![]() $\text {supp} (x^{i_1}_j) < \text {supp} (x^{i_2}_{j+1})$
for every
$\text {supp} (x^{i_1}_j) < \text {supp} (x^{i_2}_{j+1})$
for every
![]() $i_1,i_2=1,\ldots , l$
and
$i_1,i_2=1,\ldots , l$
and
![]() $j\in \mathbb {N}$
. Fix
$j\in \mathbb {N}$
. Fix
![]() $\varepsilon>0$
and apply Lemma 7.4 to obtain an
$\varepsilon>0$
and apply Lemma 7.4 to obtain an
![]() $L\in [\mathbb {N}]^{\infty }$
and a functional
$L\in [\mathbb {N}]^{\infty }$
and a functional
![]() $g^i_j\in W_{(1)}$
, for each
$g^i_j\in W_{(1)}$
, for each
![]() $1\le i\le l$
and
$1\le i\le l$
and
![]() $j\in L$
, such that
$j\in L$
, such that
-
(i)
 $\text {supp} (g^i_j)\subset \text {supp} (x^i_j)$
and
$\text {supp} (g^i_j)\subset \text {supp} (x^i_j)$
and
 $g^i_j(x^i_j)>1-\varepsilon $
, for all
$g^i_j(x^i_j)>1-\varepsilon $
, for all
 $1\le i\le l$
and
$1\le i\le l$
and
 $j\in L$
and
$j\in L$
and -
(ii) the sequence
 $(g^{i_j}_j)_{j\in L}$
is AWI for any choice of
$(g^{i_j}_j)_{j\in L}$
is AWI for any choice of
 $1\le i_j\le l$
,
$1\le i_j\le l$
,
 $j\in L$
.
$j\in L$
.
Fix a choice of
![]() $1\le i_j\le l$
,
$1\le i_j\le l$
,
![]() $j\in L$
, and let
$j\in L$
, and let
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $F\subset L$
with
$F\subset L$
with
![]() $L(k)\le F$
and
$L(k)\le F$
and
![]() $|F|\le k$
. Note that
$|F|\le k$
. Note that
![]() $(g^{i_j}_{j})_{j\in F}$
is an
$(g^{i_j}_{j})_{j\in F}$
is an
![]() $\mathcal {S}_1$
-admissible sequence in
$\mathcal {S}_1$
-admissible sequence in
![]() $W_{(1)}$
and is in fact AWI, as implied by (ii). Hence,
$W_{(1)}$
and is in fact AWI, as implied by (ii). Hence,
![]() $g=1/2\sum _{j\in F} g^{i_j}_{j}$
is in
$g=1/2\sum _{j\in F} g^{i_j}_{j}$
is in
![]() $W_{(1)}$
, and, thus, for any choice of scalars
$W_{(1)}$
, and, thus, for any choice of scalars
![]() $(a_{j})_{j\in F}$
, we calculate
$(a_{j})_{j\in F}$
, we calculate
 $$\begin{align*}\left\| \sum_{j\in F} a_{j} x^{i_j}_{j} \right\| \ge \left\| \sum_{j\in F} |a_{j}| x^{i_j}_{j} \right\| \ge g \left( \sum_{j\in F} |a_{j}| x^{i_j}_{j} \right) \ge \frac{1-\varepsilon}{2} \sum_{j\in F} |a_{j}|. \end{align*}$$
$$\begin{align*}\left\| \sum_{j\in F} a_{j} x^{i_j}_{j} \right\| \ge \left\| \sum_{j\in F} |a_{j}| x^{i_j}_{j} \right\| \ge g \left( \sum_{j\in F} |a_{j}| x^{i_j}_{j} \right) \ge \frac{1-\varepsilon}{2} \sum_{j\in F} |a_{j}|. \end{align*}$$
Then, Lemma 3.4 yields the desired result.
8 Standard exact pairs
We pass to the study of certain basic properties of Mixed Tsirelson spaces which have appeared in several previous papers (see [Reference Argyros and Deliyanni5] and [Reference Argyros and Motakis9]). The goal of this section is to define the standard exact pairs in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
and present their basic properties. In the next section, we will use the existence of sequences of such pairs in any block subspace of
$\mathfrak {X}_{\text {awi}}^{(1)}$
and present their basic properties. In the next section, we will use the existence of sequences of such pairs in any block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
to show that it is not Asymptotic
$\mathfrak {X}_{\text {awi}}^{(1)}$
to show that it is not Asymptotic
![]() $\ell _1$
. The proof of the properties of the standard exact pairs are based on the definition of an auxiliary space and the basic inequality which are given in Appendix A.
$\ell _1$
. The proof of the properties of the standard exact pairs are based on the definition of an auxiliary space and the basic inequality which are given in Appendix A.
8.1 Special convex combinations
We return our attention to special convex combinations, defined in Section 2.3. These types of vectors are used to prove the presence of standard exact pairs in every block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
.
$\mathfrak {X}_{\text {awi}}^{(1)}$
.
Remark 8.1. Let
![]() $(x_k)_k$
be a block sequence in
$(x_k)_k$
be a block sequence in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. Then Proposition 2.4 implies that, for every
$\mathfrak {X}_{\text {awi}}^{(1)}$
. Then Proposition 2.4 implies that, for every
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $n,m\in \mathbb {N}$
and
$n,m\in \mathbb {N}$
and
![]() $M\in [\mathbb {N}]^{\infty }$
, there exist
$M\in [\mathbb {N}]^{\infty }$
, there exist
![]() $F\subset M$
with
$F\subset M$
with
![]() $m\le F$
and scalars
$m\le F$
and scalars
![]() $(a_k)_{k\in F}$
, such that
$(a_k)_{k\in F}$
, such that
![]() $\sum _{k\in F}a_kx_k$
is a
$\sum _{k\in F}a_kx_k$
is a
![]() $(n,\varepsilon )$
-s.c.c.
$(n,\varepsilon )$
-s.c.c.
Lemma 8.2. Let
![]() $(x_k)_k$
be a normalised block sequence in
$(x_k)_k$
be a normalised block sequence in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. For every
$\mathfrak {X}_{\text {awi}}^{(1)}$
. For every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $M\in [\mathbb {N}]^{\infty }$
, such that for every
$M\in [\mathbb {N}]^{\infty }$
, such that for every
![]() $j\in \mathbb {N}$
, every
$j\in \mathbb {N}$
, every
![]() $\mathcal {S}_{n_j}$
-admissible sequence
$\mathcal {S}_{n_j}$
-admissible sequence
![]() $(x_k)_{k\in F}$
with
$(x_k)_{k\in F}$
with
![]() $F\subset M$
and any choice of scalars
$F\subset M$
and any choice of scalars
![]() $(a_k)_{k\in F}$
, we have
$(a_k)_{k\in F}$
, we have
 $$\begin{align*}\Big\|\sum_{k\in F}a_kx_k\Big\|\ge \frac{1-\varepsilon}{m_j}\sum_{k\in F}|a_k|. \end{align*}$$
$$\begin{align*}\Big\|\sum_{k\in F}a_kx_k\Big\|\ge \frac{1-\varepsilon}{m_j}\sum_{k\in F}|a_k|. \end{align*}$$
Proof. Apply Lemma 7.4 to obtain
![]() $M\in [\mathbb {N}]^{\infty }$
and an
$M\in [\mathbb {N}]^{\infty }$
and an
![]() $f_k\in W_{(1)}$
with
$f_k\in W_{(1)}$
with
![]() $f_k(x_k)>1-\varepsilon $
, for each
$f_k(x_k)>1-\varepsilon $
, for each
![]() $k\in M$
, such that
$k\in M$
, such that
![]() $(f_k)_{k\in M}$
is AWI. We may also assume that
$(f_k)_{k\in M}$
is AWI. We may also assume that
![]() $\text {supp} (f_k)\subset \text {supp} (x_k)$
,
$\text {supp} (f_k)\subset \text {supp} (x_k)$
,
![]() $k\in M$
. Pick an
$k\in M$
. Pick an
![]() $F\subset M$
, such that
$F\subset M$
, such that
![]() $(x_k)_{k\in F}$
is
$(x_k)_{k\in F}$
is
![]() $S_{n_j}$
-admissible. Then,
$S_{n_j}$
-admissible. Then,
![]() $(f_k)_{k\in F}$
is
$(f_k)_{k\in F}$
is
![]() $\mathcal {S}_{n_j}$
-admissible and clearly
$\mathcal {S}_{n_j}$
-admissible and clearly
![]() $(f_k)_{k\in F}$
is AWI. Hence,
$(f_k)_{k\in F}$
is AWI. Hence,
![]() $f={m_j}^{-1}\sum _{k\in F}f_k$
is in
$f={m_j}^{-1}\sum _{k\in F}f_k$
is in
![]() $W_{(1)}$
, and we calculate
$W_{(1)}$
, and we calculate
 $$\begin{align*}\|\sum_{k\in F}a_kx_k\| = \|\sum_{k\in F}|a_k|x_k\| \ge f(\sum_{k\in F}|a_k|x_k)\ge \frac{1-\varepsilon}{m_j}\sum_{k \in F}|a_k|. \end{align*}$$
$$\begin{align*}\|\sum_{k\in F}a_kx_k\| = \|\sum_{k\in F}|a_k|x_k\| \ge f(\sum_{k\in F}|a_k|x_k)\ge \frac{1-\varepsilon}{m_j}\sum_{k \in F}|a_k|. \end{align*}$$
Proposition 8.3. Let Y be a block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. Then, for every
$\mathfrak {X}_{\text {awi}}^{(1)}$
. Then, for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\varepsilon>0$
, there exists a
$\varepsilon>0$
, there exists a
![]() $(n,\varepsilon )$
-s.c.c.
$(n,\varepsilon )$
-s.c.c.
![]() $x = \sum _{k=1}^mc_kx_k$
with
$x = \sum _{k=1}^mc_kx_k$
with
![]() $\|x\|> 1/2$
, where
$\|x\|> 1/2$
, where
![]() $x_1,\ldots ,x_m$
are in the unit ball of Y.
$x_1,\ldots ,x_m$
are in the unit ball of Y.
Proof. Towards a contradiction, assume that the conclusion is false. That is, for any
![]() $\mathcal {S}_n$
-admissible sequence
$\mathcal {S}_n$
-admissible sequence
![]() $(x_k)_{k=1}^m$
in the unit ball of Y, such that the vector
$(x_k)_{k=1}^m$
in the unit ball of Y, such that the vector
![]() $x = \sum _{k=1}^mc_kx_k$
is a
$x = \sum _{k=1}^mc_kx_k$
is a
![]() $(n,\varepsilon )$
-s.c.c., we have that
$(n,\varepsilon )$
-s.c.c., we have that
![]() $\|x\| \leq 1/2$
.
$\|x\| \leq 1/2$
.
Start with a normalised block sequence
![]() $(x^{0}_{k})_{k}$
in Y and pass to a subsequence satisfying the conclusion of Lemma 8.2 for
$(x^{0}_{k})_{k}$
in Y and pass to a subsequence satisfying the conclusion of Lemma 8.2 for
![]() $\varepsilon =1/2$
. Using the choice of the sequence
$\varepsilon =1/2$
. Using the choice of the sequence
![]() $(m_{k})_{k}$
, we may find
$(m_{k})_{k}$
, we may find
![]() $j\in \mathbb {N}$
, such that
$j\in \mathbb {N}$
, such that
Set
![]() $d=\lfloor n_j/n\rfloor $
and, using Remark 8.1, define inductively block sequences
$d=\lfloor n_j/n\rfloor $
and, using Remark 8.1, define inductively block sequences
![]() $(x^i_k)_k$
,
$(x^i_k)_k$
,
![]() $i=1,\ldots ,d$
, such that for each
$i=1,\ldots ,d$
, such that for each
![]() $i=1,\ldots ,d$
and
$i=1,\ldots ,d$
and
![]() $k\in \mathbb {N}$
, there is an
$k\in \mathbb {N}$
, there is an
![]() $\mathcal {S}_n$
-admissible sequence
$\mathcal {S}_n$
-admissible sequence
![]() $(x_m^{i-1})_{m\in F_k^i}$
and coefficients
$(x_m^{i-1})_{m\in F_k^i}$
and coefficients
![]() $(c_m^{i})_{m\in F_k^i}$
, such that
$(c_m^{i})_{m\in F_k^i}$
, such that
![]() $\tilde x_k^i = \sum _{m\in F_k^i}c_m^{i}x_m^{i-1}$
is a
$\tilde x_k^i = \sum _{m\in F_k^i}c_m^{i}x_m^{i-1}$
is a
![]() $(n,\varepsilon )$
-s.c.c. and
$(n,\varepsilon )$
-s.c.c. and
![]() $x_k^i = 2\tilde x_k^i$
.
$x_k^i = 2\tilde x_k^i$
.
Using the negation of the desired conclusion, it is straightforward to check by induction that
![]() $\|x_k^i\| \leq 1$
for every
$\|x_k^i\| \leq 1$
for every
![]() $i=1,\ldots ,d$
and
$i=1,\ldots ,d$
and
![]() $k\in \mathbb {N}$
. Moreover, note that each vector
$k\in \mathbb {N}$
. Moreover, note that each vector
![]() $x_k^i$
can be written in the form
$x_k^i$
can be written in the form
 $$ \begin{align*}x_k^i = 2^i\sum_{m\in G_k^i}d_m^ix_m^0\end{align*} $$
$$ \begin{align*}x_k^i = 2^i\sum_{m\in G_k^i}d_m^ix_m^0\end{align*} $$
for some subset
![]() $G_k^i $
of
$G_k^i $
of
![]() $\mathbb {N}$
, such that
$\mathbb {N}$
, such that
![]() $(x_m^0)_{m\in G_k^i}$
is
$(x_m^0)_{m\in G_k^i}$
is
![]() $\mathcal {S}_{ni}$
-admissible and
$\mathcal {S}_{ni}$
-admissible and
![]() $\sum _{m\in G_k^i}d_m^i = 1$
. As the sequence
$\sum _{m\in G_k^i}d_m^i = 1$
. As the sequence
![]() $(x^0_k)_k$
satisfies the conclusion of Lemma 8.2, we deduce that
$(x^0_k)_k$
satisfies the conclusion of Lemma 8.2, we deduce that
 $$ \begin{align*} 1\geq \|x_1^d\| \geq \frac{2^d}{2m_j}> \frac{2^{{n_j}/{n}}}{4m_j}, \end{align*} $$
$$ \begin{align*} 1\geq \|x_1^d\| \geq \frac{2^d}{2m_j}> \frac{2^{{n_j}/{n}}}{4m_j}, \end{align*} $$
since
![]() $n_j-n<dn$
, and this contradicts (8.1).
$n_j-n<dn$
, and this contradicts (8.1).
Proposition 8.4. Let
![]() $x = \sum _{i=1}^mc_ix_i$
be a
$x = \sum _{i=1}^mc_ix_i$
be a
![]() $(n,\varepsilon )$
-s.c.c. in
$(n,\varepsilon )$
-s.c.c. in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
with
$\mathfrak {X}_{\text {awi}}^{(1)}$
with
![]() $\|x_i\| \leq 1$
,
$\|x_i\| \leq 1$
,
![]() $i=1,\ldots ,m$
, and
$i=1,\ldots ,m$
, and
![]() $f\in \mathcal {W}_{(1)}$
with
$f\in \mathcal {W}_{(1)}$
with
![]() $ w(f) = m_j$
, such that
$ w(f) = m_j$
, such that
![]() $n_j<n$
. Then we have
$n_j<n$
. Then we have
Proof. Let
![]() $f = m^{-1}_{j}\sum _{l=1}^df_l$
, where
$f = m^{-1}_{j}\sum _{l=1}^df_l$
, where
![]() $(f_l)_{l=1}^d$
is an
$(f_l)_{l=1}^d$
is an
![]() $\mathcal {S}_{n_j}$
-admissible AWI sequence in
$\mathcal {S}_{n_j}$
-admissible AWI sequence in
![]() $W_{(1)}$
, and define
$W_{(1)}$
, and define
 $$ \begin{align*} A = \big\{i\in\{1,\ldots,m\}: & \text{ there is at most one } 1\leq l\leq d, \\& \text{ such that } \text{range}(x_i)\cap\text{range}(f_l)\neq\emptyset\big\}. \end{align*} $$
$$ \begin{align*} A = \big\{i\in\{1,\ldots,m\}: & \text{ there is at most one } 1\leq l\leq d, \\& \text{ such that } \text{range}(x_i)\cap\text{range}(f_l)\neq\emptyset\big\}. \end{align*} $$
Note that
![]() $|f(x_i)| \leq 1/m_{j}$
, for each
$|f(x_i)| \leq 1/m_{j}$
, for each
![]() $i\in A$
, and, hence
$i\in A$
, and, hence
 $$ \begin{align} \left|f\left(\sum_{i=1}^mc_ix_i\right)\right| \leq \frac{1}{m_{j}}\sum_{i\in A}c_i + \sum_{i\notin A}c_i. \end{align} $$
$$ \begin{align} \left|f\left(\sum_{i=1}^mc_ix_i\right)\right| \leq \frac{1}{m_{j}}\sum_{i\in A}c_i + \sum_{i\notin A}c_i. \end{align} $$
Set
![]() $B = \{1,\ldots ,m\}\setminus A$
. The spreading property of the Schreier families implies that the vectors
$B = \{1,\ldots ,m\}\setminus A$
. The spreading property of the Schreier families implies that the vectors
![]() $(x_i)_{i\in B\setminus \{\min (B)\}}$
are
$(x_i)_{i\in B\setminus \{\min (B)\}}$
are
![]() $\mathcal {S}_{n_{j}}$
-admissible. Moreover, the singleton
$\mathcal {S}_{n_{j}}$
-admissible. Moreover, the singleton
![]() $\{x_{\min B}\}$
is
$\{x_{\min B}\}$
is
![]() $\mathcal {S}_0$
-admissible. Thus,
$\mathcal {S}_0$
-admissible. Thus,
![]() $\sum _{i\in B\setminus \min B}c_i < \varepsilon $
and
$\sum _{i\in B\setminus \min B}c_i < \varepsilon $
and
![]() $c_{\min B}<\varepsilon $
. Applying this to (8.2) immediately yields the desired conclusion.
$c_{\min B}<\varepsilon $
. Applying this to (8.2) immediately yields the desired conclusion.
8.2 Rapidly increasing sequences
These sequences are a standard tool in the study of HI and related constructions. They are the building blocks of standard exact pairs.
Definition 8.5. Let
![]() $C\ge 1$
, I be an interval of
$C\ge 1$
, I be an interval of
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $(j_k)_{k\in I}$
be a strictly increasing sequence of naturals. A block sequence
$(j_k)_{k\in I}$
be a strictly increasing sequence of naturals. A block sequence
![]() $(x_k)_{k\in I}$
in
$(x_k)_{k\in I}$
in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
is called a
$\mathfrak {X}_{\text {awi}}^{(1)}$
is called a
![]() $(C,(j_k)_{k\in I})$
-rapidly increasing sequence (RIS) if
$(C,(j_k)_{k\in I})$
-rapidly increasing sequence (RIS) if
-
(i)
 $\|x_k\|\le C$
for every
$\|x_k\|\le C$
for every
 $k\in I$
,
$k\in I$
, -
(ii)
 $\max \text {supp} (x_{k-1})\le \sqrt {m_{j_k}}$
for every
$\max \text {supp} (x_{k-1})\le \sqrt {m_{j_k}}$
for every
 $k\in I\setminus \{\min I\}$
and
$k\in I\setminus \{\min I\}$
and -
(iii)
 $|f(x_k)|\le C/w(f)$
for every
$|f(x_k)|\le C/w(f)$
for every
 $k\in I$
and
$k\in I$
and
 $f\in W_{(1)}$
with
$f\in W_{(1)}$
with
 $w(f)<m_{j_k}$
.
$w(f)<m_{j_k}$
.
Proposition 8.6. Let Y be a block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
and
$\mathfrak {X}_{\text {awi}}^{(1)}$
and
![]() $C>2$
. Then there exists a strictly increasing sequence
$C>2$
. Then there exists a strictly increasing sequence
![]() $(j_k)_{k\in \mathbb {N}}$
of naturals and a
$(j_k)_{k\in \mathbb {N}}$
of naturals and a
![]() $(C,(j_k)_{k\in \mathbb {N}})$
-RIS
$(C,(j_k)_{k\in \mathbb {N}})$
-RIS
![]() $(x_k)_{k\in \mathbb {N}}$
in Y, such that
$(x_k)_{k\in \mathbb {N}}$
in Y, such that
![]() $1/2< \|x_k\| \le 1$
, for all
$1/2< \|x_k\| \le 1$
, for all
![]() $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
.
Proof. We define the sequences
![]() $(j_k)_k$
and
$(j_k)_k$
and
![]() $(x_k)_k$
inductively as follows. First, choose
$(x_k)_k$
inductively as follows. First, choose
![]() $x_1$
, using Proposition 8.3, to be a
$x_1$
, using Proposition 8.3, to be a
![]() $(n_1,m_{1}^{-2})$
-s.c.c.
$(n_1,m_{1}^{-2})$
-s.c.c.
![]() $x_1$
in Y with
$x_1$
in Y with
![]() $1/2< \|x_1\|\le 1$
, and set
$1/2< \|x_1\|\le 1$
, and set
![]() $j_1=1$
. Suppose that we have chosen
$j_1=1$
. Suppose that we have chosen
![]() $j_1,\ldots ,j_{k-1}$
and
$j_1,\ldots ,j_{k-1}$
and
![]() $x_1,\ldots ,x_{k-1}$
for some
$x_1,\ldots ,x_{k-1}$
for some
![]() $k\in \mathbb {N}$
. Then, choose
$k\in \mathbb {N}$
. Then, choose
![]() $j_k\in \mathbb {N}$
with
$j_k\in \mathbb {N}$
with
![]() $j_k>j_{k-1}$
and
$j_k>j_{k-1}$
and
![]() $\sqrt {m_{j_k}}> \max \text {supp}(x_{k-1})$
, and use Proposition 8.3 to find an
$\sqrt {m_{j_k}}> \max \text {supp}(x_{k-1})$
, and use Proposition 8.3 to find an
![]() $(n_{j_k},m^{-2}_{j_k})$
-s.c.c.
$(n_{j_k},m^{-2}_{j_k})$
-s.c.c.
![]() $x_k$
in Y with
$x_k$
in Y with
![]() $\min \text {supp}(x_k)>\max \text {supp}(x_{k-1})$
and
$\min \text {supp}(x_k)>\max \text {supp}(x_{k-1})$
and
![]() $1/2<\|x_k\| \leq 1$
. Proposition 8.4 then yields that
$1/2<\|x_k\| \leq 1$
. Proposition 8.4 then yields that
![]() $x_k$
satisfies (iii) of Definition 8.5, and, hence, we conclude that the sequences
$x_k$
satisfies (iii) of Definition 8.5, and, hence, we conclude that the sequences
![]() $(j_k)_{k\in \mathbb {N}}$
and
$(j_k)_{k\in \mathbb {N}}$
and
![]() $(x_k)_{k\in \mathbb {N}}$
satisfy the desired conclusion.
$(x_k)_{k\in \mathbb {N}}$
satisfy the desired conclusion.
8.3 Standard exact pairs
We are ready to define standard exact pairs and prove their existence in every block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
.
$\mathfrak {X}_{\text {awi}}^{(1)}$
.
Definition 8.7. Let
![]() $C\ge 1$
and
$C\ge 1$
and
![]() $j_0\in \mathbb {N}$
. We call a pair
$j_0\in \mathbb {N}$
. We call a pair
![]() $(x,f)$
, for
$(x,f)$
, for
![]() $x\in \mathfrak {X}_{\text {awi}}^{(1)}$
and
$x\in \mathfrak {X}_{\text {awi}}^{(1)}$
and
![]() $f\in W_{(1)}$
, a
$f\in W_{(1)}$
, a
![]() $(C,m_{j_0})$
-SEP if there exists a
$(C,m_{j_0})$
-SEP if there exists a
![]() $(C,(j_k)_{k=1}^n)$
-RIS
$(C,(j_k)_{k=1}^n)$
-RIS
![]() $(x_k)_{k=1}^n$
with
$(x_k)_{k=1}^n$
with
![]() $j_0<j_1$
, such that
$j_0<j_1$
, such that
-
(i)
 $x=m_{j_0}\sum _{k=1}^na_kx_k$
and
$x=m_{j_0}\sum _{k=1}^na_kx_k$
and
 $\sum _{k=1}^na_kx_k$
is a
$\sum _{k=1}^na_kx_k$
is a
 $(n_{j_0},m_{j_0}^{-2})$
-s.c.c.,
$(n_{j_0},m_{j_0}^{-2})$
-s.c.c., -
(ii)
 $x_k$
is a
$x_k$
is a
 $(n_{j_k},m_{j_k}^{-2})$
-s.c.c. and
$(n_{j_k},m_{j_k}^{-2})$
-s.c.c. and
 $1/2< \|x_k\|\le 1$
for every
$1/2< \|x_k\|\le 1$
for every
 $k=1,\ldots ,n$
and
$k=1,\ldots ,n$
and -
(iii)
 $f=m_{j_0}^{-1}\sum _{k=1}^nf_k$
, where
$f=m_{j_0}^{-1}\sum _{k=1}^nf_k$
, where
 $(f_k)_{k=1}^n$
is an
$(f_k)_{k=1}^n$
is an
 $S_{n_{j_0}}$
-admissible AWI sequence in
$S_{n_{j_0}}$
-admissible AWI sequence in
 $W_{(1)}$
with
$W_{(1)}$
with
 $f_k(x_k)>1/4$
, for every
$f_k(x_k)>1/4$
, for every
 $k=1,\ldots ,n$
.
$k=1,\ldots ,n$
.
The following proposition is an immediate consequence of the definition of standard exact pairs, the existence of seminormalised rapidly increasing sequences in every block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, as follows from Proposition 8.6 and Lemma 7.4 applied to a sequence.
$\mathfrak {X}_{\text {awi}}^{(1)}$
, as follows from Proposition 8.6 and Lemma 7.4 applied to a sequence.
Proposition 8.8. Let Y be a block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. Then, for every
$\mathfrak {X}_{\text {awi}}^{(1)}$
. Then, for every
![]() $C>2$
and
$C>2$
and
![]() $j_0,m\in \mathbb {N}$
, there exists a
$j_0,m\in \mathbb {N}$
, there exists a
![]() $(C,m_{j_0})$
-SEP
$(C,m_{j_0})$
-SEP
![]() $(x,f)$
with
$(x,f)$
with
![]() $x\in Y$
and
$x\in Y$
and
![]() $m\le \min \text {supp} (x)$
.
$m\le \min \text {supp} (x)$
.
Proof. Applying Proposition 8.6, we obtain a
![]() $(C,(j_k)_{k\in \mathbb {N}})$
-RIS
$(C,(j_k)_{k\in \mathbb {N}})$
-RIS
![]() $(x_k)_{k\in \mathbb {N}}$
in Y, such that
$(x_k)_{k\in \mathbb {N}}$
in Y, such that
![]() $m\le \operatorname {\mathrm {minsupp}}(x_1)$
and
$m\le \operatorname {\mathrm {minsupp}}(x_1)$
and
![]() $1/2< \|x_k\| \le 1$
,
$1/2< \|x_k\| \le 1$
,
![]() $k\in \mathbb {N}$
, with
$k\in \mathbb {N}$
, with
![]() $j_0<j_1$
. Then, applying Lemma 7.4 for
$j_0<j_1$
. Then, applying Lemma 7.4 for
![]() $\varepsilon =1/2$
and passing to a subsequence, we obtain an AWI sequence
$\varepsilon =1/2$
and passing to a subsequence, we obtain an AWI sequence
![]() $(f_k)_{k\in \mathbb {N}}$
in
$(f_k)_{k\in \mathbb {N}}$
in
![]() $W_{(1)}$
so that
$W_{(1)}$
so that
![]() $f_k(x_k)>(1-\varepsilon )/2=1/4$
,
$f_k(x_k)>(1-\varepsilon )/2=1/4$
,
![]() $k\in \mathbb {N}$
. We may assume that
$k\in \mathbb {N}$
. We may assume that
![]() $\text {supp}(f_k)\subset \text {supp}(x_k)$
,
$\text {supp}(f_k)\subset \text {supp}(x_k)$
,
![]() $k\in \mathbb {N}$
. Remark 8.1 then yields the desired SEP.
$k\in \mathbb {N}$
. Remark 8.1 then yields the desired SEP.
Definition 8.9. Let I be an interval of
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $(x_k)_{k\in I}$
be a block sequence in
$(x_k)_{k\in I}$
be a block sequence in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. For every
$\mathfrak {X}_{\text {awi}}^{(1)}$
. For every
![]() $f\in W_{(1)}$
, we define the sets
$f\in W_{(1)}$
, we define the sets
![]() $I_f=\{k\in I:\text {supp} (x_k)\subset \text {range} (f)\}$
,
$I_f=\{k\in I:\text {supp} (x_k)\subset \text {range} (f)\}$
,
![]() $J_f=I_f\cap \{k\in I:\text {supp} (x_k)\cap \text {supp} (f)\neq \emptyset \}$
and
$J_f=I_f\cap \{k\in I:\text {supp} (x_k)\cap \text {supp} (f)\neq \emptyset \}$
and
![]() $I^{\prime }_f=\{k\in I:\text {supp} (x_k)\cap \text {range} (f)\neq \emptyset \}$
.
$I^{\prime }_f=\{k\in I:\text {supp} (x_k)\cap \text {range} (f)\neq \emptyset \}$
.
If
![]() $(x,f)$
is a
$(x,f)$
is a
![]() $(C,m_{j_0})$
-SEP and
$(C,m_{j_0})$
-SEP and
![]() $g\in W_{(1)}$
, then when we write
$g\in W_{(1)}$
, then when we write
![]() $I_g^x$
or
$I_g^x$
or
![]() $J_g^x$
we mean
$J_g^x$
we mean
![]() $I_g$
or
$I_g$
or
![]() $J_g$
, respectively, with respect to the sequence
$J_g$
, respectively, with respect to the sequence
![]() $(x_k)_{k=1}^n$
as in Definition 8.7.
$(x_k)_{k=1}^n$
as in Definition 8.7.
Remark 8.10. Let I be an interval of
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $(x_k)_{k\in I}$
be a block sequence in
$(x_k)_{k\in I}$
be a block sequence in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
. Then, for every
$\mathfrak {X}_{\text {awi}}^{(1)}$
. Then, for every
![]() $f\in W_{(1)}$
, the following hold.
$f\in W_{(1)}$
, the following hold.
-
(i)
 $I_f$
is a finite subset of I and
$I_f$
is a finite subset of I and
 $\# \{k\in I:\text {supp} (x_k)\cap \text {range} (f)\neq \emptyset \} \le \#I_f+2$
.
$\# \{k\in I:\text {supp} (x_k)\cap \text {range} (f)\neq \emptyset \} \le \#I_f+2$
. -
(ii) If
 $f=m_j^{-1}\sum _{l=1}^df_l$
, then
$f=m_j^{-1}\sum _{l=1}^df_l$
, then
 $\cup _{l=1}^dI_{f_l}\subset I_f$
.
$\cup _{l=1}^dI_{f_l}\subset I_f$
. -
(iii) If there exists
 $k\in I$
, such that
$k\in I$
, such that
 $\text {range} (f)\subsetneq \text {range} (x_k)$
, then
$\text {range} (f)\subsetneq \text {range} (x_k)$
, then
 $I_f=\emptyset $
.
$I_f=\emptyset $
.
Proposition 8.11. For every
![]() $(C,m_{j_0})$
-SEP
$(C,m_{j_0})$
-SEP
![]() $(x,f)$
, the following hold.
$(x,f)$
, the following hold.
-
(i) For every
 $g\in W_{(1)}$
$g\in W_{(1)}$
 $$\begin{align*}\big|g(x)\big|\le \begin{cases} \frac{2C}{m_{j_0}},\quad\quad & g=\pm e_i^*\text{ for some }i\in\mathbb{N}\\ 2C[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(g)}],\quad\quad & w(g)\ge m_{j_0} \\ \frac{6C}{w(g)},\quad\quad & w(g)<m_{j_0} \end{cases} \end{align*}$$
$$\begin{align*}\big|g(x)\big|\le \begin{cases} \frac{2C}{m_{j_0}},\quad\quad & g=\pm e_i^*\text{ for some }i\in\mathbb{N}\\ 2C[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(g)}],\quad\quad & w(g)\ge m_{j_0} \\ \frac{6C}{w(g)},\quad\quad & w(g)<m_{j_0} \end{cases} \end{align*}$$
-
(ii) If
 $g\in W_{(1)}$
with a tree analysis
$g\in W_{(1)}$
with a tree analysis
 $(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
 $I^x_{g_{\alpha }}=\emptyset $
for all
$I^x_{g_{\alpha }}=\emptyset $
for all
 $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
 $w(g_{\alpha })= m_{j_0}$
, then
$w(g_{\alpha })= m_{j_0}$
, then $$\begin{align*}|g(x)|\le\frac{6C}{m_{j_0}}.\end{align*}$$
$$\begin{align*}|g(x)|\le\frac{6C}{m_{j_0}}.\end{align*}$$
For the proof, we refer the reader to Appendix A.
Remark 8.12. Proposition 8.11 (ii) remains valid if we replace
![]() $I^x_{g_{\alpha }}$
with
$I^x_{g_{\alpha }}$
with
![]() $J^x_{g_{\alpha }}$
.
$J^x_{g_{\alpha }}$
.
Corollary 8.13. The space
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
is reflexive.
$\mathfrak {X}_{\text {awi}}^{(1)}$
is reflexive.
Proof. The unit vector basis of
![]() $c_{00}(\mathbb {N})$
forms an unconditional Schauder basis for
$c_{00}(\mathbb {N})$
forms an unconditional Schauder basis for
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, and it is also boundedly complete since the space admits a unique
$\mathfrak {X}_{\text {awi}}^{(1)}$
, and it is also boundedly complete since the space admits a unique
![]() $\ell _1$
asymptotic model. Hence, it suffices to show that
$\ell _1$
asymptotic model. Hence, it suffices to show that
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain
$\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain
![]() $\ell _1$
. To this end, suppose that
$\ell _1$
. To this end, suppose that
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
contains
$\mathfrak {X}_{\text {awi}}^{(1)}$
contains
![]() $\ell _1$
and, in particular, from James’s
$\ell _1$
and, in particular, from James’s
![]() $\ell _1$
distortion theorem [Reference James22], there is a normalised block sequence
$\ell _1$
distortion theorem [Reference James22], there is a normalised block sequence
![]() $(x_k)_k$
in
$(x_k)_k$
in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, such that for
$\mathfrak {X}_{\text {awi}}^{(1)}$
, such that for
![]() $0<\varepsilon <1/2$
$0<\varepsilon <1/2$
 $$\begin{align*}\left\| \sum_{k=1}^na_kx_k\right\|\ge (1-\varepsilon)\sum_{k=1}^n|a_k| \end{align*}$$
$$\begin{align*}\left\| \sum_{k=1}^na_kx_k\right\|\ge (1-\varepsilon)\sum_{k=1}^n|a_k| \end{align*}$$
for all
![]() $n\in \mathbb {N}$
and any choice of scalars
$n\in \mathbb {N}$
and any choice of scalars
![]() $a_1,\ldots ,a_n$
. Choose
$a_1,\ldots ,a_n$
. Choose
![]() $j_0\in \mathbb {N}$
, such that
$j_0\in \mathbb {N}$
, such that
![]() $12/m_{j_0}<1-\varepsilon $
. Let also
$12/m_{j_0}<1-\varepsilon $
. Let also
![]() $y_1<\ldots <y_n$
, where each
$y_1<\ldots <y_n$
, where each
![]() $y_i$
is a special convex combination of
$y_i$
is a special convex combination of
![]() $(x_k)_k$
for all
$(x_k)_k$
for all
![]() $i=1,\ldots ,n$
, such that
$i=1,\ldots ,n$
, such that
![]() $x=m_{j_0}\sum _{i=1}^na_ky_k$
is a
$x=m_{j_0}\sum _{i=1}^na_ky_k$
is a
![]() $(3,m_{j_0})$
-SEP (note that
$(3,m_{j_0})$
-SEP (note that
![]() $\|y_i\|\ge 1-\varepsilon>1/2$
for all
$\|y_i\|\ge 1-\varepsilon>1/2$
for all
![]() $i=1,\ldots ,n$
). Then, Proposition 8.11 yields that
$i=1,\ldots ,n$
). Then, Proposition 8.11 yields that
![]() $\|x\|\le 12$
and, since
$\|x\|\le 12$
and, since
![]() $\|x\|=m_{j_0}\|\sum _{i=1}^na_ky_k\|\ge m_{j_0}(1-\varepsilon )$
, we derive a contradiction.
$\|x\|=m_{j_0}\|\sum _{i=1}^na_ky_k\|\ge m_{j_0}(1-\varepsilon )$
, we derive a contradiction.
9 The space
 $\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain asymptotic
$\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain asymptotic
 $\ell _1$
subspaces
$\ell _1$
subspaces
In this last section of the first part of the paper, we show that
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain Asymptotic
$\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain Asymptotic
![]() $\ell _1$
subspaces. It is worth pointing out that unlike the constructions in [Reference Argyros, Georgiou and Motakis8], we are not able to prove the existence of a block tree which is either
$\ell _1$
subspaces. It is worth pointing out that unlike the constructions in [Reference Argyros, Georgiou and Motakis8], we are not able to prove the existence of a block tree which is either
![]() $c_0$
or
$c_0$
or
![]() $\ell _p$
, for some
$\ell _p$
, for some
![]() $1<p<\infty $
, of height greater or equal to
$1<p<\infty $
, of height greater or equal to
![]() $\omega $
, in any subspace of
$\omega $
, in any subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
.
$\mathfrak {X}_{\text {awi}}^{(1)}$
.
Definition 9.1. We say that a sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
, with
$(x_1,f_1),\ldots ,(x_n,f_n)$
, with
![]() $x_i\in \mathfrak {X}_{\text {awi}}^{(1)}$
and
$x_i\in \mathfrak {X}_{\text {awi}}^{(1)}$
and
![]() $f_i\in W_{(1)}$
for
$f_i\in W_{(1)}$
for
![]() $i=1,\ldots ,n$
, is a dependent sequence if each pair
$i=1,\ldots ,n$
, is a dependent sequence if each pair
![]() $(x_i,f_i)$
is a
$(x_i,f_i)$
is a
![]() $(3,m_{j_i})$
-SEP and
$(3,m_{j_i})$
-SEP and
![]() $\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
.
$\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
.
Definition 9.2. Given a dependent sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
, for
$(x_1,f_1),\ldots ,(x_n,f_n)$
, for
![]() $f\in W_{(1)}$
with a tree analysis
$f\in W_{(1)}$
with a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
and each
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
and each
![]() $1\le k\le h(\mathcal {A})$
define
$1\le k\le h(\mathcal {A})$
define
 $$ \begin{align*} D^k_f = \big\{\alpha\in\mathcal{A}:\:&|\alpha|=k \text{ and there exists } 1\le i\le n\text{, such that}\\ & w(f_{\alpha})=w(f_i)\text{ and }\text{supp} (f_{\alpha}) \cap \text{range} (f_i)\neq \emptyset\big\} \end{align*} $$
$$ \begin{align*} D^k_f = \big\{\alpha\in\mathcal{A}:\:&|\alpha|=k \text{ and there exists } 1\le i\le n\text{, such that}\\ & w(f_{\alpha})=w(f_i)\text{ and }\text{supp} (f_{\alpha}) \cap \text{range} (f_i)\neq \emptyset\big\} \end{align*} $$
and
Remark 9.3. Let
![]() $f_1,\ldots ,f_n,f$
be as in the above definition and fix
$f_1,\ldots ,f_n,f$
be as in the above definition and fix
![]() $k\in \mathbb {N}$
. If
$k\in \mathbb {N}$
. If
![]() $f_{\alpha }$
and
$f_{\alpha }$
and
![]() $f_{\beta }$
are such that
$f_{\beta }$
are such that
![]() $\alpha ,\beta \in D^k_f$
and
$\alpha ,\beta \in D^k_f$
and
![]() $w(f_{\alpha })<w(f_{\beta })$
, then
$w(f_{\alpha })<w(f_{\beta })$
, then
![]() $w(f_{\alpha })<_{\mathcal {W}} w(f_{\beta })$
since
$w(f_{\alpha })<_{\mathcal {W}} w(f_{\beta })$
since
![]() $w(f_{\alpha })=w(f_{i_1})$
and
$w(f_{\alpha })=w(f_{i_1})$
and
![]() $w(f_{\beta })=w(f_{i_2})$
for some
$w(f_{\beta })=w(f_{i_2})$
for some
![]() $1\le i_1<i_2\le n$
. This implies that
$1\le i_1<i_2\le n$
. This implies that
![]() $\{\bar {f}_{\alpha },\bar {f}_{\beta } \}$
is not essentially incomparable. Indeed, if it were essentially incomparable, then
$\{\bar {f}_{\alpha },\bar {f}_{\beta } \}$
is not essentially incomparable. Indeed, if it were essentially incomparable, then
![]() $f_{i_1}<f_{\alpha }$
, and this contradicts the fact that
$f_{i_1}<f_{\alpha }$
, and this contradicts the fact that
![]() $\text {supp} (f_{\alpha }) \cap \text {range}(f_{i_1})\neq \emptyset $
in the definition of
$\text {supp} (f_{\alpha }) \cap \text {range}(f_{i_1})\neq \emptyset $
in the definition of
![]() $D^k_f$
.
$D^k_f$
.
Proposition 9.4. Let
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
be a dependent sequence and
$(x_1,f_1),\ldots ,(x_n,f_n)$
be a dependent sequence and
![]() $f\in W_{(1)}$
. Then
$f\in W_{(1)}$
. Then
![]() $\# E^k_f\le e k!$
for every
$\# E^k_f\le e k!$
for every
![]() $k\in \mathbb {N}$
(where e denotes Euler’s number).
$k\in \mathbb {N}$
(where e denotes Euler’s number).
Proof. Denote by
![]() $(a_k)_k$
the sequence satisfying the recurrence relation
$(a_k)_k$
the sequence satisfying the recurrence relation
![]() $a_1=2$
and
$a_1=2$
and
![]() $a_k=ka_{k-1}+1$
,
$a_k=ka_{k-1}+1$
,
![]() $k\ge 2$
. We will show that
$k\ge 2$
. We will show that
![]() $\# E^k_f\le a_k$
for every
$\# E^k_f\le a_k$
for every
![]() $k\in \mathbb {N}$
. Note that this yields the desired result since
$k\in \mathbb {N}$
. Note that this yields the desired result since
![]() $a_k=\sum _{j=0}^kk!/j!\le e k!$
.
$a_k=\sum _{j=0}^kk!/j!\le e k!$
.
Let
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f. We proceed by induction. For
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f. We proceed by induction. For
![]() $k=1$
, the definition of
$k=1$
, the definition of
![]() $W_{(1)}$
, and in particular, that of AWI sequences, yields a partition
$W_{(1)}$
, and in particular, that of AWI sequences, yields a partition
such that
![]() $C^0_1$
is essentially incomparable and
$C^0_1$
is essentially incomparable and
![]() $C^0_2$
is weight incomparable. Then, note that Remark 9.3 implies that
$C^0_2$
is weight incomparable. Then, note that Remark 9.3 implies that
Moreover, since
![]() $C^0_2$
is weight incomparable, we have that
$C^0_2$
is weight incomparable, we have that
and, hence, (9.1) and (9.2) imply that
![]() $\#E^1_f\le 2$
.
$\#E^1_f\le 2$
.
Assume that for some
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
![]() $\#E^k_g\le a_k$
for all functionals g in
$\#E^k_g\le a_k$
for all functionals g in
![]() $W_{(1)}$
, with respect to the dependent sequence
$W_{(1)}$
, with respect to the dependent sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
. We will show that
$(x_1,f_1),\ldots ,(x_n,f_n)$
. We will show that
![]() $\#E^{k+1}_f\le a_{k+1}$
. Let
$\#E^{k+1}_f\le a_{k+1}$
. Let
![]() $\{\alpha \in \mathcal {A}:|\alpha |=1 \}=\{\alpha _1,\ldots ,\alpha _d \}$
, where
$\{\alpha \in \mathcal {A}:|\alpha |=1 \}=\{\alpha _1,\ldots ,\alpha _d \}$
, where
![]() $f_{\alpha _1}<\ldots < f_{\alpha _d}$
and consider the tree analyses
$f_{\alpha _1}<\ldots < f_{\alpha _d}$
and consider the tree analyses
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}_i}$
, where
$(f_{\alpha })_{\alpha \in \mathcal {A}_i}$
, where
![]() $\mathcal {A}_i=\{\alpha \in \mathcal {A}:\alpha _i\le \alpha \}$
for
$\mathcal {A}_i=\{\alpha \in \mathcal {A}:\alpha _i\le \alpha \}$
for
![]() $1\le i \le d$
. The fact that f is in
$1\le i \le d$
. The fact that f is in
![]() $W_{(1)}$
, that is,
$W_{(1)}$
, that is,
![]() $(f_{\alpha _i})_{i=1}^d$
is AWI, implies that there exist partitions
$(f_{\alpha _i})_{i=1}^d$
is AWI, implies that there exist partitions
such that
![]() $\cup _{i=k+1}^d C_{1,i}^{k}$
is essentially incomparable and
$\cup _{i=k+1}^d C_{1,i}^{k}$
is essentially incomparable and
![]() $(C_{2,i}^{k})_{i=k+1}^d$
is pairwise weight incomparable. Here,
$(C_{2,i}^{k})_{i=k+1}^d$
is pairwise weight incomparable. Here,
![]() $|\alpha |$
is the height of
$|\alpha |$
is the height of
![]() $\alpha $
in the tree
$\alpha $
in the tree
![]() $\mathcal {A}_i$
. Then, using Remark 9.3 and arguing as in the previous paragraph, we have
$\mathcal {A}_i$
. Then, using Remark 9.3 and arguing as in the previous paragraph, we have
Moreover, it follows easily that
![]() $D^{k+1}_f\cap C^{k}_{2,i_0}\neq \emptyset $
for at most one
$D^{k+1}_f\cap C^{k}_{2,i_0}\neq \emptyset $
for at most one
![]() $k<i_0\le d$
, and, thus, if such an
$k<i_0\le d$
, and, thus, if such an
![]() $i_0$
exists, we have
$i_0$
exists, we have
If no such
![]() $i_0$
exists, we have
$i_0$
exists, we have
In any case, since the inductive hypothesis yields that
![]() $\# E^{k}_{f_{\alpha _{i_0}}}\le a_k$
, we have
$\# E^{k}_{f_{\alpha _{i_0}}}\le a_k$
, we have
Note that the inductive hypothesis also implies that
and, hence, since
![]() $E^{k+1}_f=\cup _{i=1}^dE^{k}_{f_{\alpha _i}}$
, we conclude that
$E^{k+1}_f=\cup _{i=1}^dE^{k}_{f_{\alpha _i}}$
, we conclude that
 $$\begin{align*}\# E^{k+1}_f \le \sum_{i=1}^{k}\# E^{k}_{f_{\alpha_{i}}} + \# \cup_{i=k+1}^d E^{k}_{f_{\alpha_{i}}}\le ka_k+a_k+1. \end{align*}$$
$$\begin{align*}\# E^{k+1}_f \le \sum_{i=1}^{k}\# E^{k}_{f_{\alpha_{i}}} + \# \cup_{i=k+1}^d E^{k}_{f_{\alpha_{i}}}\le ka_k+a_k+1. \end{align*}$$
This completes the inductive step and the proof.
Lemma 9.5. Let
![]() $(x,f_0)$
be a
$(x,f_0)$
be a
![]() $(3,m_{j_0})$
-SEP. If f is a functional in
$(3,m_{j_0})$
-SEP. If f is a functional in
![]() $W_{(1)}$
with a tree analysis
$W_{(1)}$
with a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
and
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
and
then there exists a partition
![]() $\operatorname {\mathrm {range}}(f)=G\cup D$
, such that
$\operatorname {\mathrm {range}}(f)=G\cup D$
, such that
-
(i)
 $|f|_D(x)|\le 18/m_{j_0}$
and
$|f|_D(x)|\le 18/m_{j_0}$
and -
(ii)
 $|\sum _{\alpha \in \mathcal {B}}f_{\alpha }|_G(x)|\le 3$
.
$|\sum _{\alpha \in \mathcal {B}}f_{\alpha }|_G(x)|\le 3$
.
Proof. Let
![]() $x=m_{j_0}\sum _{k=1}^na_kx_k$
for some
$x=m_{j_0}\sum _{k=1}^na_kx_k$
for some
![]() $(3,(j_k)_{k=1}^n)$
-RIS
$(3,(j_k)_{k=1}^n)$
-RIS
![]() $(x_k)_{k=1}^n$
, and set
$(x_k)_{k=1}^n$
, and set
For every
![]() $\alpha \in \mathcal {B}$
and every
$\alpha \in \mathcal {B}$
and every
![]() $k\in I^x_{f_{\alpha }}$
, Definition 8.5 (iii) implies that
$k\in I^x_{f_{\alpha }}$
, Definition 8.5 (iii) implies that
since
![]() $j_0<j_k$
. Set
$j_0<j_k$
. Set
![]() $G=\cup \{\text {range}(x_k):k\in \cup _{\alpha \in \mathcal {B}}I^x_{f_{\alpha }}\}$
and
$G=\cup \{\text {range}(x_k):k\in \cup _{\alpha \in \mathcal {B}}I^x_{f_{\alpha }}\}$
and
![]() $D=\operatorname {\mathrm {range}}(f)\setminus G$
. Then, (9.4) immediately yields that G satisfies (ii). To see that D satisfies (i), note that if
$D=\operatorname {\mathrm {range}}(f)\setminus G$
. Then, (9.4) immediately yields that G satisfies (ii). To see that D satisfies (i), note that if
![]() $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
![]() $w(f_{\alpha })=m_{j_0}$
and
$w(f_{\alpha })=m_{j_0}$
and
![]() $\text {supp}(f_{\alpha })\cap D=\emptyset $
, there exists
$\text {supp}(f_{\alpha })\cap D=\emptyset $
, there exists
![]() $\beta \in \mathcal {B}$
, such that
$\beta \in \mathcal {B}$
, such that
![]() $\beta \le \alpha $
and
$\beta \le \alpha $
and
![]() $J^x_{f_{\alpha }|D}\subset J^x_{f_{\beta }|D}$
. However, it is easy to see that
$J^x_{f_{\alpha }|D}\subset J^x_{f_{\beta }|D}$
. However, it is easy to see that
![]() $J^x_{f_{\beta }|D}=\emptyset $
, and thus
$J^x_{f_{\beta }|D}=\emptyset $
, and thus
![]() $J^x_{f_{\alpha }|D}=\emptyset $
. Hence, (i) follows from Proposition 8.11 (ii) and Remark 8.12.
$J^x_{f_{\alpha }|D}=\emptyset $
. Hence, (i) follows from Proposition 8.11 (ii) and Remark 8.12.
Proposition 9.6. For every
![]() $0<c<1$
, there exists
$0<c<1$
, there exists
![]() $d\in \mathbb {N}$
, such that for any dependent sequence
$d\in \mathbb {N}$
, such that for any dependent sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
where
$(x_1,f_1),\ldots ,(x_n,f_n)$
where
![]() $d\le n$
, and any
$d\le n$
, and any
![]() $f\in W_{(1)}$
, we have
$f\in W_{(1)}$
, we have
 $$\begin{align*}\left| f(\frac{1}{n}\sum_{i=1}^nx_i ) \right|<c. \end{align*}$$
$$\begin{align*}\left| f(\frac{1}{n}\sum_{i=1}^nx_i ) \right|<c. \end{align*}$$
Proof. First, pick an
![]() $m\in \mathbb {N}$
, such that
$m\in \mathbb {N}$
, such that
![]() $3/ 2^m<c$
, and fix a dependent sequence
$3/ 2^m<c$
, and fix a dependent sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
. Let
$(x_1,f_1),\ldots ,(x_n,f_n)$
. Let
![]() $f\in W_{(1)}$
with
$f\in W_{(1)}$
with
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f, and set
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
be a tree analysis of f, and set
and
![]() $H=\mathbb {N}\setminus G$
. Let
$H=\mathbb {N}\setminus G$
. Let
![]() $g=f|_G$
and
$g=f|_G$
and
![]() $h=f|_{H}$
. Then, consider the tree analysis
$h=f|_{H}$
. Then, consider the tree analysis
![]() $(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
for g, induced by
$(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
for g, induced by
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, and define
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, and define
for
![]() $k=1,\ldots ,n$
and
$k=1,\ldots ,n$
and
Let
![]() $g_1=g|_{G_1}$
and
$g_1=g|_{G_1}$
and
![]() $g_2=g|_{\mathbb {N}\setminus G_1}$
. Recall Remark 5.8 (ii), and observe that for
$g_2=g|_{\mathbb {N}\setminus G_1}$
. Recall Remark 5.8 (ii), and observe that for
![]() $k=1,\ldots ,n$
,
$k=1,\ldots ,n$
,
 $$\begin{align*}g_1(x_k)=\sum_{\alpha\in\mathcal{B}^1_k}\frac{1}{w_g(g_{\alpha})}g_{\alpha}(x_k)\quad\text{ and }\quad g_2(x_k)=\sum_{\alpha\in\mathcal{B}^2_k}\frac{1}{w_g(g_{\alpha})}g_{\alpha}(x_k), \end{align*}$$
$$\begin{align*}g_1(x_k)=\sum_{\alpha\in\mathcal{B}^1_k}\frac{1}{w_g(g_{\alpha})}g_{\alpha}(x_k)\quad\text{ and }\quad g_2(x_k)=\sum_{\alpha\in\mathcal{B}^2_k}\frac{1}{w_g(g_{\alpha})}g_{\alpha}(x_k), \end{align*}$$
where
Consider the tree analysis
![]() $(h_{\alpha })_{\alpha \in \mathcal {A}_h}$
of h, induced by
$(h_{\alpha })_{\alpha \in \mathcal {A}_h}$
of h, induced by
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
. Note that, for every
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
. Note that, for every
![]() $\alpha $
in
$\alpha $
in
![]() $\mathcal {A}_h$
and
$\mathcal {A}_h$
and
![]() $k=1,\ldots ,n$
, such that
$k=1,\ldots ,n$
, such that
![]() $w(h_{\alpha })=w(f_k)$
, we have
$w(h_{\alpha })=w(f_k)$
, we have
![]() $\text {range}(h_{\alpha })\cap \text {range}(x_k)=\emptyset $
, and, hence,
$\text {range}(h_{\alpha })\cap \text {range}(x_k)=\emptyset $
, and, hence,
![]() $k\not \in I_{h_{\alpha }}$
. Proposition 8.11 (ii) then implies that for every
$k\not \in I_{h_{\alpha }}$
. Proposition 8.11 (ii) then implies that for every
![]() $k=1,\ldots ,n$
$k=1,\ldots ,n$
Thus, we obtain
 $$ \begin{align} |h(\frac{1}{n}\sum_{k=1}^nx_k )|\le \frac{18}{n}. \end{align} $$
$$ \begin{align} |h(\frac{1}{n}\sum_{k=1}^nx_k )|\le \frac{18}{n}. \end{align} $$
Next, we apply Lemma 9.5 for
![]() $g_2$
and each
$g_2$
and each
![]() $(x_k,f_k)$
,
$(x_k,f_k)$
,
![]() $k=1,\ldots ,n$
, to obtain partitions
$k=1,\ldots ,n$
, to obtain partitions
![]() $\text {supp}(g_2)\cap \text {supp}(x_k)=G^2_k\cup D^2_k$
, such that
$\text {supp}(g_2)\cap \text {supp}(x_k)=G^2_k\cup D^2_k$
, such that
-
(a)
 $|g|_{D^2_k}(x_k)|\le 18/w(f_k)$
and
$|g|_{D^2_k}(x_k)|\le 18/w(f_k)$
and -
(b)
 $|\sum _{\beta \in \mathcal {B}^2_k}g_{\beta }|_{G^2_k}(x_k)|\le 3$
.
$|\sum _{\beta \in \mathcal {B}^2_k}g_{\beta }|_{G^2_k}(x_k)|\le 3$
.
Then, (b) and Remark 5.8 (iii) yield that
 $$\begin{align*}|g_2|_{G_k^2}(x_k)|=|\sum_{\beta\in\mathcal{B}^2_k}w_g(g_{\beta})^{-1}g_{\beta}|_{G^2_k}(x_k)|\le \sum_{\beta\in\mathcal{B}^2_k}2^{-m}|g_{\beta}|_{G^2_k}(x_k)|\le \frac{3}{2^m}, \end{align*}$$
$$\begin{align*}|g_2|_{G_k^2}(x_k)|=|\sum_{\beta\in\mathcal{B}^2_k}w_g(g_{\beta})^{-1}g_{\beta}|_{G^2_k}(x_k)|\le \sum_{\beta\in\mathcal{B}^2_k}2^{-m}|g_{\beta}|_{G^2_k}(x_k)|\le \frac{3}{2^m}, \end{align*}$$
and, hence, using (a) we obtain
 $$ \begin{align} |g_2(\frac{1}{n}\sum_{k=1}^nx_k)|\le \frac{1}{n}\sum_{k=1}^n\frac{18}{w(f_k)}+\frac{3}{2^m}\le \frac{18}{n}+\frac{3}{2^m}. \end{align} $$
$$ \begin{align} |g_2(\frac{1}{n}\sum_{k=1}^nx_k)|\le \frac{1}{n}\sum_{k=1}^n\frac{18}{w(f_k)}+\frac{3}{2^m}\le \frac{18}{n}+\frac{3}{2^m}. \end{align} $$
Finally, observe that it follows immediately from Proposition 9.4 that
 $$\begin{align*}\{ k\in\{1,\ldots,n\} : g_1(x_k)\neq 0\} \le \ell = e\sum_{k=1}^mk!, \end{align*}$$
$$\begin{align*}\{ k\in\{1,\ldots,n\} : g_1(x_k)\neq 0\} \le \ell = e\sum_{k=1}^mk!, \end{align*}$$
and, thus, by Proposition 8.11 (i),
 $$ \begin{align} |g_1(\frac{1}{n}\sum_{k=1}^nx_k)| \le \frac{\ell}{n}6. \end{align} $$
$$ \begin{align} |g_1(\frac{1}{n}\sum_{k=1}^nx_k)| \le \frac{\ell}{n}6. \end{align} $$
Then for d, such that
Proposition 9.7. The space
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain Asymptotic
$\mathfrak {X}_{\text {awi}}^{(1)}$
does not contain Asymptotic
![]() $\ell _1$
subspaces.
$\ell _1$
subspaces.
Proof. Suppose that
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
contains a
$\mathfrak {X}_{\text {awi}}^{(1)}$
contains a
![]() $C'$
-Asymptotic
$C'$
-Asymptotic
![]() $\ell _1$
subspace Y. By standard arguments, for every
$\ell _1$
subspace Y. By standard arguments, for every
![]() $\varepsilon>0$
, there exists a block subspace of Y which is
$\varepsilon>0$
, there exists a block subspace of Y which is
![]() $C'+\varepsilon $
Asymptotic
$C'+\varepsilon $
Asymptotic
![]() $\ell _1$
. Passing to a further block subspace, we may assume that Y is block and C-asymptotic
$\ell _1$
. Passing to a further block subspace, we may assume that Y is block and C-asymptotic
![]() $\ell _1$
in the sense of [Reference Milman and Tomczak-Jaegermann25], that is, Y admits a Schauder basis
$\ell _1$
in the sense of [Reference Milman and Tomczak-Jaegermann25], that is, Y admits a Schauder basis
![]() $(y_i)_i$
, which is a block subsequence of
$(y_i)_i$
, which is a block subsequence of
![]() $(e_i)_i$
, such that for every
$(e_i)_i$
, such that for every
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $N(n)\in \mathbb {N}$
with the property that whenever
$N(n)\in \mathbb {N}$
with the property that whenever
![]() $N(n)\le x_1\le \ldots \le x_n$
are blocks of
$N(n)\le x_1\le \ldots \le x_n$
are blocks of
![]() $(y_i)_i$
then
$(y_i)_i$
then
 $$ \begin{align} \frac{1}{C}\sum_{k=1}^n\|x_k\| \le \left\|\sum_{k=1}^nx_k\right\|. \end{align} $$
$$ \begin{align} \frac{1}{C}\sum_{k=1}^n\|x_k\| \le \left\|\sum_{k=1}^nx_k\right\|. \end{align} $$
Applying Proposition 9.6 for
![]() $c=1/2C$
, we obtain
$c=1/2C$
, we obtain
![]() $n\in \mathbb {N}$
, such that for any dependent sequence
$n\in \mathbb {N}$
, such that for any dependent sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
, we have
$(x_1,f_1),\ldots ,(x_n,f_n)$
, we have
We apply Proposition 8.8 iteratively to construct a dependent sequence in Y as follows: We find
![]() $x_1\in Y$
with
$x_1\in Y$
with
![]() $N(n)\le \text {supp}(x_1)\cup \text {supp}(f_1)$
,
$N(n)\le \text {supp}(x_1)\cup \text {supp}(f_1)$
,
![]() $w(f_1)=\sigma (\bar {0})$
, and set
$w(f_1)=\sigma (\bar {0})$
, and set
![]() $\bar {f}_1=(f_1,\sigma (\bar {0}))$
, and for
$\bar {f}_1=(f_1,\sigma (\bar {0}))$
, and for
![]() $1<k\le n$
, we find
$1<k\le n$
, we find
![]() $x_k\in Y$
with
$x_k\in Y$
with
![]() $w(f_k)=\sigma (\bar {f}_{k-1})$
, and set
$w(f_k)=\sigma (\bar {f}_{k-1})$
, and set
![]() $\bar {f_k}=(f_k,\sigma (\bar {f}_{k-1}))$
. Note that the sequence
$\bar {f_k}=(f_k,\sigma (\bar {f}_{k-1}))$
. Note that the sequence
![]() $(f_k)_{k=1}^n$
is
$(f_k)_{k=1}^n$
is
![]() $\mathcal {S}_1$
-admissible since
$\mathcal {S}_1$
-admissible since
![]() $n\le N(n)$
. Then, (9.9) implies that
$n\le N(n)$
. Then, (9.9) implies that
since
![]() $\|x_k\|> 1/2$
for each
$\|x_k\|> 1/2$
for each
![]() $k=1,\ldots ,n$
as follows from Definition 8.7, which is a contradiction.
$k=1,\ldots ,n$
as follows from Definition 8.7, which is a contradiction.
Question 9.8. Let
![]() $\xi <\omega _1$
and
$\xi <\omega _1$
and
![]() $1<p\le \infty $
. Does there exist a Banach space X with a Schauder basis admitting a unique
$1<p\le \infty $
. Does there exist a Banach space X with a Schauder basis admitting a unique
![]() $\ell _1$
asymptotic model, such that any block subspace of X contains an
$\ell _1$
asymptotic model, such that any block subspace of X contains an
![]() $\ell _p$
(or
$\ell _p$
(or
![]() $c_0$
if
$c_0$
if
![]() $p=\infty $
) block tree of height greater or equal to
$p=\infty $
) block tree of height greater or equal to
![]() $\omega ^{\xi }$
?
$\omega ^{\xi }$
?
PART II The case of
 $\boldsymbol {\ell _p}$
for
$\boldsymbol {\ell _p}$
for
 $\boldsymbol {1<p<\infty }$
$\boldsymbol {1<p<\infty }$
10 Introduction
In this second part, we treat the case of
![]() $1<p<\infty $
and, in particular, that of
$1<p<\infty $
and, in particular, that of
![]() $p=2$
. The cases where
$p=2$
. The cases where
![]() $p\neq 2$
follow as an easy modification. The definition of
$p\neq 2$
follow as an easy modification. The definition of
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
and the the proofs of its properties are for the most part almost identical to those of
$\mathfrak {X}^{(2)}_{\text {awi}}$
and the the proofs of its properties are for the most part almost identical to those of
![]() $\mathfrak {X}^{(1)}_{\text {awi}}$
. We start with the 2-convexification of a Mixed Tsirelson space and define a countably branching well-founded tree on its norming set. Then, employing the notion of asymptotically weakly incomparable constraints, we define the norming set
$\mathfrak {X}^{(1)}_{\text {awi}}$
. We start with the 2-convexification of a Mixed Tsirelson space and define a countably branching well-founded tree on its norming set. Then, employing the notion of asymptotically weakly incomparable constraints, we define the norming set
![]() $W_{(2)}$
of
$W_{(2)}$
of
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
. To prove that the space admits
$\mathfrak {X}^{(2)}_{\text {awi}}$
. To prove that the space admits
![]() $\ell _2$
as a unique asymptotic model, we use Lemma 3.4 by first applying the combinatorial results of Section 4, in a manner similar to that of Section 7, and prove lower
$\ell _2$
as a unique asymptotic model, we use Lemma 3.4 by first applying the combinatorial results of Section 4, in a manner similar to that of Section 7, and prove lower
![]() $\ell _2$
estimates for arrays of block sequences of
$\ell _2$
estimates for arrays of block sequences of
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
by passing to a subsequence. Then, a result similar to [Reference Deliyanni and Manoussakis16, Proposition 2.9] shows that any block sequence of
$\mathfrak {X}^{(2)}_{\text {awi}}$
by passing to a subsequence. Then, a result similar to [Reference Deliyanni and Manoussakis16, Proposition 2.9] shows that any block sequence of
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
also has an upper
$\mathfrak {X}^{(2)}_{\text {awi}}$
also has an upper
![]() $\ell _2$
estimate. Finally, to prove that
$\ell _2$
estimate. Finally, to prove that
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
does not contain Asymptotic
$\mathfrak {X}^{(2)}_{\text {awi}}$
does not contain Asymptotic
![]() $\ell _2$
subspaces, just like in Part I, we show that any block subspace contains a vector, that is an
$\ell _2$
subspaces, just like in Part I, we show that any block subspace contains a vector, that is an
![]() $\ell _2$
-average of standard exact pairs, with arbitrarily small norm. The existence of standard exact pairs follows again from similar arguments, while the proof that these are strong exact pairs requires a variant of the basic inequality, which we include in Appendix B. In particular, for a block subspace Y and
$\ell _2$
-average of standard exact pairs, with arbitrarily small norm. The existence of standard exact pairs follows again from similar arguments, while the proof that these are strong exact pairs requires a variant of the basic inequality, which we include in Appendix B. In particular, for a block subspace Y and
![]() $0<c<1$
, we show that there is a sequence of standard exact pairs
$0<c<1$
, we show that there is a sequence of standard exact pairs
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
in Y, such that
$(x_1,f_1),\ldots ,(x_n,f_n)$
in Y, such that
![]() $\bar {f}_1\le _{\mathcal {T}}\ldots \le _{\mathcal {T}} \bar {f}_n$
and
$\bar {f}_1\le _{\mathcal {T}}\ldots \le _{\mathcal {T}} \bar {f}_n$
and
![]() $\|x_1+\cdots +x_n\|<c\:\sqrt {n}$
. To prove this, we consider the evaluation of an f in
$\|x_1+\cdots +x_n\|<c\:\sqrt {n}$
. To prove this, we consider the evaluation of an f in
![]() $W_{(2)}$
on such a sequence and partition f into
$W_{(2)}$
on such a sequence and partition f into
![]() $g+h$
and then g into
$g+h$
and then g into
![]() $g_1+g_2$
as in the proof of Proposition 9.6. An upper bound for h follows from the fact that standard exact pairs are strong exact pairs, while that of
$g_1+g_2$
as in the proof of Proposition 9.6. An upper bound for h follows from the fact that standard exact pairs are strong exact pairs, while that of
![]() $g_1$
is, again, an immediate consequence of Lemma 9.4. Finally, for
$g_1$
is, again, an immediate consequence of Lemma 9.4. Finally, for
![]() $g_2$
, unlike the case of Part I, we cannot estimate its action on each
$g_2$
, unlike the case of Part I, we cannot estimate its action on each
![]() $x_k$
,
$x_k$
,
![]() $k=1,\ldots ,n$
using similar arguments. Instead, we need to carefully apply the Cauchy-Schwarz inequality to provide an upper estimate for its action on
$k=1,\ldots ,n$
using similar arguments. Instead, we need to carefully apply the Cauchy-Schwarz inequality to provide an upper estimate for its action on
![]() $x_1+\cdots +x_k$
. We demonstrate this in Lemma 14.2.
$x_1+\cdots +x_k$
. We demonstrate this in Lemma 14.2.
11 The space
 $\mathfrak {X}_{\text {awi}}^{(2)}$
$\mathfrak {X}_{\text {awi}}^{(2)}$
Define a pair of strictly increasing sequences of natural numbers
![]() $(m_j)_j$
,
$(m_j)_j$
,
![]() $(n_j)_j$
as follows:
$(n_j)_j$
as follows:
 $$ \begin{align*} m_1 &= 4 & n_1 &= 1 \\ m_{j+1}&=m_j^{m_j} & n_{j+1}&=2^{2m_{j+1}}n_j .\end{align*} $$
$$ \begin{align*} m_1 &= 4 & n_1 &= 1 \\ m_{j+1}&=m_j^{m_j} & n_{j+1}&=2^{2m_{j+1}}n_j .\end{align*} $$
Definition 11.1. Let
![]() $V_{(2)}$
denote the minimal subset of
$V_{(2)}$
denote the minimal subset of
![]() $c_{00}(\mathbb {N})$
that
$c_{00}(\mathbb {N})$
that
-
(i) contains
 $0$
and all
$0$
and all
 $\pm e_j^*$
,
$\pm e_j^*$
,
 $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and -
(ii) whenever
 $f_1<\ldots <f_n$
is an
$f_1<\ldots <f_n$
is an
 $\mathcal {S}_{n_j}$
-admissible sequence in
$\mathcal {S}_{n_j}$
-admissible sequence in
 $V_{(2)}\setminus \{0\}$
for some
$V_{(2)}\setminus \{0\}$
for some
 $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and
 $\lambda _1,\ldots ,\lambda _n\in \mathbb {Q}$
with
$\lambda _1,\ldots ,\lambda _n\in \mathbb {Q}$
with
 $\sum _{i=1}^n\lambda _i^2\le 1$
, then
$\sum _{i=1}^n\lambda _i^2\le 1$
, then
 $m_j^{-1}\sum _{i=1}^n\lambda _if_i $
is in
$m_j^{-1}\sum _{i=1}^n\lambda _if_i $
is in
 $V_{(2)}$
.
$V_{(2)}$
.
The notion of the weight
![]() $w(f)$
of a functional f in
$w(f)$
of a functional f in
![]() $V_{(2)}$
is identical to that in Section 5. We also define, in a similar manner, the notion of tree analysis of a functional in
$V_{(2)}$
is identical to that in Section 5. We also define, in a similar manner, the notion of tree analysis of a functional in
![]() $V_{(2)}$
, taking into account the
$V_{(2)}$
, taking into account the
![]() $\ell _2$
version of the
$\ell _2$
version of the
![]() $(m_j,\mathcal {S}_{n_j})$
-operations, in the definition of
$(m_j,\mathcal {S}_{n_j})$
-operations, in the definition of
![]() $V_{(2)}$
. Again, it follows from minimality that every f in
$V_{(2)}$
. Again, it follows from minimality that every f in
![]() $V_{(2)}\setminus \{0\}$
admits a tree analysis and finally, for a functional f in
$V_{(2)}\setminus \{0\}$
admits a tree analysis and finally, for a functional f in
![]() $V_{(2)}\setminus \{0\}$
admitting a tree analysis
$V_{(2)}\setminus \{0\}$
admitting a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, we define
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, we define
![]() $w_f(f_{\alpha })$
as in Definition 5.5.
$w_f(f_{\alpha })$
as in Definition 5.5.
Definition 11.2. Let
![]() $f\in V_{(2)}$
with a tree analysis
$f\in V_{(2)}$
with a tree analysis
![]() $(f_{\alpha })_{ \alpha \in \mathcal {A} }$
.
$(f_{\alpha })_{ \alpha \in \mathcal {A} }$
.
-
(i) Let
 $\beta \in \mathcal {A}$
with
$\beta \in \mathcal {A}$
with
 $\beta \neq \emptyset $
. Then, if
$\beta \neq \emptyset $
. Then, if
 $\alpha \in \mathcal {A}$
is the immediate predecessor of
$\alpha \in \mathcal {A}$
is the immediate predecessor of
 $\beta $
, we will denote by
$\beta $
, we will denote by
 $\lambda _{\beta }$
the coefficient of
$\lambda _{\beta }$
the coefficient of
 $f_{\beta }$
in the normal form of
$f_{\beta }$
in the normal form of
 $f_{\alpha }$
, that is,
$f_{\alpha }$
, that is, $$\begin{align*}f_{\alpha} =m_j^{-1} \sum_{\beta\in S(\alpha)}\lambda_{\beta} f_{\beta}, \end{align*}$$
$$\begin{align*}f_{\alpha} =m_j^{-1} \sum_{\beta\in S(\alpha)}\lambda_{\beta} f_{\beta}, \end{align*}$$
where
 $S(\alpha )$
denotes the set of immediate successors of
$S(\alpha )$
denotes the set of immediate successors of
 $\alpha $
and
$\alpha $
and
 $w(f_{\alpha })=m_j$
.
$w(f_{\alpha })=m_j$
. -
(ii) For each
 $\beta \in \mathcal {A}$
, we define
$\beta \in \mathcal {A}$
, we define $$\begin{align*}\lambda_{f,\beta} = \begin{cases} \prod_{\alpha<\beta}\lambda_{\alpha}, &\quad \beta\neq\emptyset \\ 1 .\end{cases} \end{align*}$$
$$\begin{align*}\lambda_{f,\beta} = \begin{cases} \prod_{\alpha<\beta}\lambda_{\alpha}, &\quad \beta\neq\emptyset \\ 1 .\end{cases} \end{align*}$$
Remark 11.3. Let
![]() $f\in V_{(2)}$
with a tree analysis
$f\in V_{(2)}$
with a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
.
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
.
-
(i) For every
 $k=1,\ldots ,h(\mathcal {A})$
$k=1,\ldots ,h(\mathcal {A})$
 $$\begin{align*}f=\sum_{|a|=k}\frac{\lambda_{f,\alpha}}{w_f(f_{\alpha})}f_{\alpha}. \end{align*}$$
$$\begin{align*}f=\sum_{|a|=k}\frac{\lambda_{f,\alpha}}{w_f(f_{\alpha})}f_{\alpha}. \end{align*}$$
-
(ii) If
 $\mathcal {B}$
is a maximal pairwise incomparable subset of
$\mathcal {B}$
is a maximal pairwise incomparable subset of
 $\mathcal {A}$
, then
$\mathcal {A}$
, then $$\begin{align*}f=\sum_{\alpha\in\mathcal{B}}\frac{\lambda_{f,\alpha}}{w_f(f_{\alpha})}f_{\alpha}. \end{align*}$$
$$\begin{align*}f=\sum_{\alpha\in\mathcal{B}}\frac{\lambda_{f,\alpha}}{w_f(f_{\alpha})}f_{\alpha}. \end{align*}$$
-
(iii) For every
 $\alpha \in \mathcal {A}$
, whose immediate predecessor
$\alpha \in \mathcal {A}$
, whose immediate predecessor
 $\beta $
in
$\beta $
in
 $\mathcal {A}$
(if one exists) satisfies
$\mathcal {A}$
(if one exists) satisfies
 $f_{\beta }\notin \{\pm e_j^*:j\in \mathbb {N}\}$
, we have
$f_{\beta }\notin \{\pm e_j^*:j\in \mathbb {N}\}$
, we have
 $w_f(f_{\alpha })\ge 4^{|\alpha |}.$
$w_f(f_{\alpha })\ge 4^{|\alpha |}.$
-
(iv) If
 $\mathcal {B}$
is a pairwise incomparable subset of
$\mathcal {B}$
is a pairwise incomparable subset of
 $\mathcal {A}$
, then
$\mathcal {A}$
, then $$\begin{align*}\sum_{\alpha\in\mathcal{B}}\lambda_{f,\alpha}^2\le1. \end{align*}$$
$$\begin{align*}\sum_{\alpha\in\mathcal{B}}\lambda_{f,\alpha}^2\le1. \end{align*}$$
Next, as in Section 5, we define a tree
![]() $\mathcal {T}$
on the set of all pairs
$\mathcal {T}$
on the set of all pairs
![]() $(f,w(f))$
, for
$(f,w(f))$
, for
![]() $f\in V_{(2)}$
and
$f\in V_{(2)}$
and
![]() $w(f)$
a weight of f and consider the trees
$w(f)$
a weight of f and consider the trees
![]() ${\widetilde {\mathcal {T}}}$
,
${\widetilde {\mathcal {T}}}$
,
![]() $\mathcal {W}$
and
$\mathcal {W}$
and
![]() ${\widetilde {\mathcal {W}}}$
, which are induced by
${\widetilde {\mathcal {W}}}$
, which are induced by
![]() $\mathcal {T}$
and defined identically to those in Section 5. These are countably branching well-founded trees. Finally, let us recall all three incomparability notions of Definition 5.12, as well as the notion of asymptotically weakly incomparable sequences in Definition 5.14.
$\mathcal {T}$
and defined identically to those in Section 5. These are countably branching well-founded trees. Finally, let us recall all three incomparability notions of Definition 5.12, as well as the notion of asymptotically weakly incomparable sequences in Definition 5.14.
Definition 11.4. Let
![]() $W_{(2)}$
be the smallest subset of
$W_{(2)}$
be the smallest subset of
![]() $V_{(2)}$
that is symmetric, contains the singletons and whenever
$V_{(2)}$
that is symmetric, contains the singletons and whenever
![]() $j\in \mathbb {N}$
,
$j\in \mathbb {N}$
,
![]() $f_1<\ldots <f_n$
is an
$f_1<\ldots <f_n$
is an
![]() $\mathcal {S}_{n_j}$
-admissible AWI sequence in
$\mathcal {S}_{n_j}$
-admissible AWI sequence in
![]() $V_{(2)}$
and
$V_{(2)}$
and
![]() $\lambda _1,\ldots ,\lambda _n\in \mathbb {Q}$
with
$\lambda _1,\ldots ,\lambda _n\in \mathbb {Q}$
with
![]() $\sum _{i=1}^n \lambda _i^2\le 1$
, then
$\sum _{i=1}^n \lambda _i^2\le 1$
, then
![]() $m_j^{-1}\sum _{i=1}^n\lambda _if_i\in W_{(2)}$
. Denote by
$m_j^{-1}\sum _{i=1}^n\lambda _if_i\in W_{(2)}$
. Denote by
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
completion of
$\mathfrak {X}_{\text {awi}}^{(2)}$
completion of
![]() $c_{00}(\mathbb {N})$
with respect to the norm induced by
$c_{00}(\mathbb {N})$
with respect to the norm induced by
![]() $W_{(2)}$
.
$W_{(2)}$
.
Remark 11.5.
-
(i) The norming set
 $W_{(2)}$
can be defined as an increasing union of a sequence
$W_{(2)}$
can be defined as an increasing union of a sequence
 $(W^n_{(2)})_{n=0}^{\infty }$
, where
$(W^n_{(2)})_{n=0}^{\infty }$
, where
 $W^0_{(2)}=\{\pm e^*_i:i\in \mathbb {N}\}$
and
$W^0_{(2)}=\{\pm e^*_i:i\in \mathbb {N}\}$
and $$ \begin{align*} W^{n+1}_{(2)}=W^n_{(2)}\cup\Big\{\frac{1}{m_j}\sum_{i=1}^m&\lambda_if_i:j,m\in\mathbb{N},\; (\lambda_i)_{i=1}^m\subset\mathbb{Q}\text{ with }\sum_{i=1}^m\lambda_i^2\le 1\text{ and}\\&(f_i)_{i=1}^m \text{ is an } \mathcal{S}_{n_j}\text{-admissible AWI sequence in }W^n_{(2)}\Big\}. \end{align*} $$
$$ \begin{align*} W^{n+1}_{(2)}=W^n_{(2)}\cup\Big\{\frac{1}{m_j}\sum_{i=1}^m&\lambda_if_i:j,m\in\mathbb{N},\; (\lambda_i)_{i=1}^m\subset\mathbb{Q}\text{ with }\sum_{i=1}^m\lambda_i^2\le 1\text{ and}\\&(f_i)_{i=1}^m \text{ is an } \mathcal{S}_{n_j}\text{-admissible AWI sequence in }W^n_{(2)}\Big\}. \end{align*} $$
-
(ii) Proposition 5.16 yields that the standard unit vector basis of
 $c_{00}(\mathbb {N})$
forms an
$c_{00}(\mathbb {N})$
forms an
 $1$
-unconditional Schauder basis for
$1$
-unconditional Schauder basis for
 $\mathfrak {X}_{\text {awi}}^{(2)}$
.
$\mathfrak {X}_{\text {awi}}^{(2)}$
.
The following lemma is a result similar to [Reference Deliyanni and Manoussakis16, Proposition 2.9], in which we prove upper
![]() $\ell _2$
estimates for block sequences of
$\ell _2$
estimates for block sequences of
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
.
$\mathfrak {X}^{(2)}_{\text {awi}}$
.
Proposition 11.6. For any block sequence
![]() $(x_k)_k$
in
$(x_k)_k$
in
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
, any finite subset F of the naturals and
$\mathfrak {X}_{\text {awi}}^{(2)}$
, any finite subset F of the naturals and
![]() $f\in W_{(2)}$
, we have
$f\in W_{(2)}$
, we have
Proof. Recall from Remark 11.5 that
![]() $W_{(2)}=\cup _{n=0}^{\infty } W^n_{(2)}$
. We will show by induction that for every
$W_{(2)}=\cup _{n=0}^{\infty } W^n_{(2)}$
. We will show by induction that for every
![]() $n\in \mathbb {N}$
, every
$n\in \mathbb {N}$
, every
![]() $f\in W^n_{(2)}$
and any finite subset F of
$f\in W^n_{(2)}$
and any finite subset F of
![]() $\mathbb {N}$
, we have
$\mathbb {N}$
, we have
Clearly, this holds for all
![]() $f\in W^0_{(2)}$
. Hence, let us assume that it also holds for all functionals in
$f\in W^0_{(2)}$
. Hence, let us assume that it also holds for all functionals in
![]() $W^n_{(2)}$
for some
$W^n_{(2)}$
for some
![]() $n\ge 0$
and fix
$n\ge 0$
and fix
![]() $f\in W^{n+1}_{(2)}$
. Then
$f\in W^{n+1}_{(2)}$
. Then
![]() $f=m_j^{-1}\sum _{=1}^m\lambda _if_i$
, where
$f=m_j^{-1}\sum _{=1}^m\lambda _if_i$
, where
![]() $(f_i)_{i=1}^m$
is an
$(f_i)_{i=1}^m$
is an
![]() $S_{n_j}$
-admissible AWI sequence in
$S_{n_j}$
-admissible AWI sequence in
![]() $W^n_{(2)}$
and
$W^n_{(2)}$
and
![]() $\lambda _1,\ldots ,\lambda _m\in \mathbb {Q}$
with
$\lambda _1,\ldots ,\lambda _m\in \mathbb {Q}$
with
![]() $\sum _{i=1}^m\lambda _i^2\le 1$
. Define
$\sum _{i=1}^m\lambda _i^2\le 1$
. Define
![]() $F_1=\{ k\in F :\#I_k\le 1\}$
and
$F_1=\{ k\in F :\#I_k\le 1\}$
and
![]() $F_2=F\setminus F_1$
. We also define
$F_2=F\setminus F_1$
. We also define
Note that if
![]() $k\in F_1$
, then
$k\in F_1$
, then
![]() $k\in K_i$
for at most one
$k\in K_i$
for at most one
![]() $i\in \{1,\ldots ,m\}$
. Thus, using the inductive hypothesis and the Cauchy-Schwarz inequality, we have
$i\in \{1,\ldots ,m\}$
. Thus, using the inductive hypothesis and the Cauchy-Schwarz inequality, we have
 $$ \begin{align} |f(\sum_{k\in F_1}x_k)|&=m_j^{-1}|\sum_{i=1}^m\lambda_if_i(\sum_{k\in K_i}x_k)| \nonumber\\ &\le\frac{2\sqrt{2}}{m_j}\sum_{i=1}^m|\lambda_i|(\sum_{k\in K_i}\|x_k\|^2)^{\frac{1}{2}} \nonumber \\ &\le \sqrt{2} (\sum_{i=1}^m\lambda_i^2)^{\frac{1}{2}}(\sum_{i=1}^m\sum_{k\in K_i}\|x_k\|^2)^{\frac{1}{2}} \nonumber \\ &\le \sqrt{2} (\sum_{k\in F_1}\|x_k\|^2)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} |f(\sum_{k\in F_1}x_k)|&=m_j^{-1}|\sum_{i=1}^m\lambda_if_i(\sum_{k\in K_i}x_k)| \nonumber\\ &\le\frac{2\sqrt{2}}{m_j}\sum_{i=1}^m|\lambda_i|(\sum_{k\in K_i}\|x_k\|^2)^{\frac{1}{2}} \nonumber \\ &\le \sqrt{2} (\sum_{i=1}^m\lambda_i^2)^{\frac{1}{2}}(\sum_{i=1}^m\sum_{k\in K_i}\|x_k\|^2)^{\frac{1}{2}} \nonumber \\ &\le \sqrt{2} (\sum_{k\in F_1}\|x_k\|^2)^{\frac{1}{2}}. \end{align} $$
Moreover, for each
![]() $k\in F_2$
, it is easy to see that
$k\in F_2$
, it is easy to see that
Observe that for each
![]() $i\in \{1,\ldots ,m\}$
there are at most two k’s in
$i\in \{1,\ldots ,m\}$
there are at most two k’s in
![]() $F_2$
, such that
$F_2$
, such that
![]() $\text {supp}(x_k)\cap \text {range}(f_{i})\neq \emptyset $
and, thus, applying the Cauchy-Schwarz inequality and (11.2), we have
$\text {supp}(x_k)\cap \text {range}(f_{i})\neq \emptyset $
and, thus, applying the Cauchy-Schwarz inequality and (11.2), we have
 $$ \begin{align} |f(\sum_{k\in F_2}x_k)|&=m_j^{-1}|\sum_{i=1}^m\lambda_if_i(\sum_{k\in F_2}x_k)|=m_j^{-1}|\sum_{k\in F_2}\sum_{i\in I_k}\lambda_if_i(x_k)| \nonumber\\ &\le\sum_{k\in F_2}(\sum_{i\in I_k}\lambda_i^2)^{\frac{1}{2}}\|x_{k}\|\nonumber\\ &\le(\sum_{k\in F_2}\sum_{i\in I_k}\lambda_i^2)^{\frac{1}{2}}(\sum_{k\in F_2}\|x_k\|^2)^{\frac{1}{2}}\nonumber\\ &\le \sqrt{2}(\sum_{k\in F_2}\|x_k\|^2)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} |f(\sum_{k\in F_2}x_k)|&=m_j^{-1}|\sum_{i=1}^m\lambda_if_i(\sum_{k\in F_2}x_k)|=m_j^{-1}|\sum_{k\in F_2}\sum_{i\in I_k}\lambda_if_i(x_k)| \nonumber\\ &\le\sum_{k\in F_2}(\sum_{i\in I_k}\lambda_i^2)^{\frac{1}{2}}\|x_{k}\|\nonumber\\ &\le(\sum_{k\in F_2}\sum_{i\in I_k}\lambda_i^2)^{\frac{1}{2}}(\sum_{k\in F_2}\|x_k\|^2)^{\frac{1}{2}}\nonumber\\ &\le \sqrt{2}(\sum_{k\in F_2}\|x_k\|^2)^{\frac{1}{2}}. \end{align} $$
12 Asymptotic models generated by block sequences of
 $\mathfrak {X}_{\text {awi}}^{(2)}$
$\mathfrak {X}_{\text {awi}}^{(2)}$
In this section, we prove that
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
admits
$\mathfrak {X}_{\text {awi}}^{(2)}$
admits
![]() $\ell _2$
as a unique asymptotic model. This follows as an easy modification of the results of Section 7, which yield lower
$\ell _2$
as a unique asymptotic model. This follows as an easy modification of the results of Section 7, which yield lower
![]() $\ell _2$
estimates, combined with the upper
$\ell _2$
estimates, combined with the upper
![]() $\ell _2$
estimates of Proposition 11.6. Let us first recall Proposition 7.2, and note that this in fact holds for the trees defined in the previous section. Applying this, we obtain the following variant of Lemma 7.3, using similar arguments.
$\ell _2$
estimates of Proposition 11.6. Let us first recall Proposition 7.2, and note that this in fact holds for the trees defined in the previous section. Applying this, we obtain the following variant of Lemma 7.3, using similar arguments.
Lemma 12.1. Let
![]() $x\in \mathfrak {X}_{\text {awi}}^{(2)}$
,
$x\in \mathfrak {X}_{\text {awi}}^{(2)}$
,
![]() $f\in W_{(2)}$
and a tree analysis
$f\in W_{(2)}$
and a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, such that
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, such that
![]() $f_{\alpha }(x)>0$
for every
$f_{\alpha }(x)>0$
for every
![]() $\alpha \in \mathcal {A}$
. Let
$\alpha \in \mathcal {A}$
. Let
![]() $\varepsilon _1,\ldots ,\varepsilon _{h(\mathcal {A})}$
be positive reals and
$\varepsilon _1,\ldots ,\varepsilon _{h(\mathcal {A})}$
be positive reals and
![]() $G_i$
be a subset of
$G_i$
be a subset of
![]() $\{ \alpha \in \mathcal {A}:|\alpha |=i \}$
, such that
$\{ \alpha \in \mathcal {A}:|\alpha |=i \}$
, such that
 $$\begin{align*}\sum_{\alpha\in G_i}\frac{\lambda_{f,\alpha}}{w_f(f_{\alpha})}f_{\alpha}(x)>f(x)-\varepsilon_i\end{align*}$$
$$\begin{align*}\sum_{\alpha\in G_i}\frac{\lambda_{f,\alpha}}{w_f(f_{\alpha})}f_{\alpha}(x)>f(x)-\varepsilon_i\end{align*}$$
for
![]() $i=1,\ldots , h(\mathcal {A})$
, and
$i=1,\ldots , h(\mathcal {A})$
, and
![]() $f(x)>\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
. Then, there exists a
$f(x)>\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
. Then, there exists a
![]() $g\in W_{(2)}$
, such that
$g\in W_{(2)}$
, such that
-
(i)
 $\text {supp} (g)\subset \text {supp} (f)$
and
$\text {supp} (g)\subset \text {supp} (f)$
and
 $w(g)=w(f)$
.
$w(g)=w(f)$
. -
(ii)
 $g(x)>f(x)-\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
.
$g(x)>f(x)-\sum _{i=1}^{h(\mathcal {A})}\varepsilon _i$
. -
(iii) g has a tree analysis
 $(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
, such that, for every
$(g_{\alpha })_{\alpha \in \mathcal {A}_g}$
, such that, for every
 $\alpha \in \mathcal {A}_g$
with
$\alpha \in \mathcal {A}_g$
with
 $|\alpha |=i$
, there is a unique
$|\alpha |=i$
, there is a unique
 $\beta \in G_i$
, such that
$\beta \in G_i$
, such that
 $\text {supp}( g_{\alpha })\subset \text {supp} (f_{\beta })$
and
$\text {supp}( g_{\alpha })\subset \text {supp} (f_{\beta })$
and
 $w(g_{\alpha })=w(f_{\beta })$
.
$w(g_{\alpha })=w(f_{\beta })$
.
Lemma 12.2. Let
![]() $(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
$(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
. For every
$\mathfrak {X}_{\text {awi}}^{(2)}$
. For every
![]() $\varepsilon>0$
, there exists an
$\varepsilon>0$
, there exists an
![]() $L\in [\mathbb {N}]^{\infty }$
and a
$L\in [\mathbb {N}]^{\infty }$
and a
![]() $g^i_j\in W_{(2)}$
with
$g^i_j\in W_{(2)}$
with
![]() $g^i_j(x^i_j)>1-\varepsilon $
for
$g^i_j(x^i_j)>1-\varepsilon $
for
![]() $ i=1,\ldots , l$
and
$ i=1,\ldots , l$
and
![]() $j\in L$
, such that for any choice of
$j\in L$
, such that for any choice of
![]() $i_j\in \{1,\ldots ,l\}$
, the sequence
$i_j\in \{1,\ldots ,l\}$
, the sequence
![]() $(g^{i_j}_j)_{j\in L}$
is AWI.
$(g^{i_j}_j)_{j\in L}$
is AWI.
Proof. The proof is similar to that of Proposition 7.4 with
![]() $\mu _j^k$
defined as
$\mu _j^k$
defined as
 $$\begin{align*}\mu_j^k= \sum_{i=1}^l\sum_{\substack{\alpha\in\mathcal{A}^i_j\\|\alpha|=k}}\frac{\lambda_{f^i_j,\alpha}f^i_{j,\alpha}(x^i_j)}{w_{f^i_j}(f^i_{j,\alpha})}\delta_{\ {\bar{f}^i_{j,\alpha}}} \end{align*}$$
$$\begin{align*}\mu_j^k= \sum_{i=1}^l\sum_{\substack{\alpha\in\mathcal{A}^i_j\\|\alpha|=k}}\frac{\lambda_{f^i_j,\alpha}f^i_{j,\alpha}(x^i_j)}{w_{f^i_j}(f^i_{j,\alpha})}\delta_{\ {\bar{f}^i_{j,\alpha}}} \end{align*}$$
Proposition 12.3. The space
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
admits a unique asymptotic model, with respect to
$\mathfrak {X}_{\text {awi}}^{(2)}$
admits a unique asymptotic model, with respect to
![]() $\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(2)})$
, equivalent to the unit vector basis of
$\mathscr {F}_b(\mathfrak {X}_{\text {awi}}^{(2)})$
, equivalent to the unit vector basis of
![]() $\ell _2$
.
$\ell _2$
.
Proof. Let
![]() $(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
$(x^1_j)_j,\ldots ,(x^l_j)_j$
be normalised block sequences in
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
. Working as in the proof of Proposition 7.5 applying Lemma 12.2, we have that, passing to a subsequence, for any choice of
$\mathfrak {X}_{\text {awi}}^{(2)}$
. Working as in the proof of Proposition 7.5 applying Lemma 12.2, we have that, passing to a subsequence, for any choice of
![]() $1\le i_j\le l$
for
$1\le i_j\le l$
for
![]() $j\in \mathbb {N}$
, any
$j\in \mathbb {N}$
, any
![]() $F\in \mathcal {S}_1$
and any choice of scalars
$F\in \mathcal {S}_1$
and any choice of scalars
![]() $(a_j)_{j\in F}$
, there is a functional
$(a_j)_{j\in F}$
, there is a functional
![]() $g\in W_{(2)}$
with
$g\in W_{(2)}$
with
 $$\begin{align*}g=\frac{1}{4}\sum_{j\in F}\frac{a_j}{(\sum_{j\in F}a_j^2)^{\frac{1}{2}}} g^{i_j}_{j},\end{align*}$$
$$\begin{align*}g=\frac{1}{4}\sum_{j\in F}\frac{a_j}{(\sum_{j\in F}a_j^2)^{\frac{1}{2}}} g^{i_j}_{j},\end{align*}$$
such that
![]() $g^{i_j}_j(x^{i_j}_j)\ge 1-\varepsilon $
and
$g^{i_j}_j(x^{i_j}_j)\ge 1-\varepsilon $
and
![]() $\text {supp}(g^{i_j}_j)\subset \text {supp}(x^{i_j}_j)$
for
$\text {supp}(g^{i_j}_j)\subset \text {supp}(x^{i_j}_j)$
for
![]() $j\in F$
. Hence, we calculate
$j\in F$
. Hence, we calculate
 $$ \begin{align} \left\| \sum_{j\in F} a_{j} x^{i_j}_{m_j} \right\| \ge g \left( \sum_{j\in F} a_{j} x^{i_j}_{m_j} \right) \ge \frac{1-\varepsilon}{4} (\sum_{j\in F} a_{j}^2 )^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} \left\| \sum_{j\in F} a_{j} x^{i_j}_{m_j} \right\| \ge g \left( \sum_{j\in F} a_{j} x^{i_j}_{m_j} \right) \ge \frac{1-\varepsilon}{4} (\sum_{j\in F} a_{j}^2 )^{\frac{1}{2}}. \end{align} $$
Moreover, Lemma 11.6 implies that
 $$ \begin{align} \left\| \sum_{j\in F} a_{j} x^{i_j}_{j} \right\|\le 2\sqrt{2}(\sum_{j\in F} a_{j}^2)^{\frac{1}{2}} .\end{align} $$
$$ \begin{align} \left\| \sum_{j\in F} a_{j} x^{i_j}_{j} \right\|\le 2\sqrt{2}(\sum_{j\in F} a_{j}^2)^{\frac{1}{2}} .\end{align} $$
Thus, (12.1), (12.2) and Lemma 3.4 yield the desired result.
By the above proposition,
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
cannot contain an isomorphic copy of
$\mathfrak {X}_{\text {awi}}^{(2)}$
cannot contain an isomorphic copy of
![]() $c_0$
or
$c_0$
or
![]() $\ell _1$
. Therefore, by James’s theorem [Reference James21] for spaces with an unconditional basis, we obtain the following.
$\ell _1$
. Therefore, by James’s theorem [Reference James21] for spaces with an unconditional basis, we obtain the following.
Proposition 12.4. The space
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
is reflexive.
$\mathfrak {X}_{\text {awi}}^{(2)}$
is reflexive.
13 Standard exact pairs
The definitions of rapidly increasing sequences and standard exact pairs in
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
are almost identical to these in Part I. We show that standard exact pairs are in fact strong exact pairs. This requires a variant of the basic inequality that we prove in Appendix B.
$\mathfrak {X}^{(2)}_{\text {awi}}$
are almost identical to these in Part I. We show that standard exact pairs are in fact strong exact pairs. This requires a variant of the basic inequality that we prove in Appendix B.
Definition 13.1. Let
![]() $C\ge 1$
,
$C\ge 1$
,
![]() $I\subset \mathbb {N}$
be an interval and
$I\subset \mathbb {N}$
be an interval and
![]() $(j_k)_{k\in I}$
be a strictly increasing sequence of naturals. A block sequence
$(j_k)_{k\in I}$
be a strictly increasing sequence of naturals. A block sequence
![]() $(x_k)_{k\in I}$
in
$(x_k)_{k\in I}$
in
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
is called a
$\mathfrak {X}_{\text {awi}}^{(2)}$
is called a
![]() $(C,(j_k)_{k\in I})$
-rapidly increasing sequence (RIS) if
$(C,(j_k)_{k\in I})$
-rapidly increasing sequence (RIS) if
-
(i)
 $\|x_k\|\le C$
for every
$\|x_k\|\le C$
for every
 $k\in I$
,
$k\in I$
, -
(ii)
 $\max \text {supp} (x_{k-1})\le \sqrt {m_{j_k}}$
for every
$\max \text {supp} (x_{k-1})\le \sqrt {m_{j_k}}$
for every
 $k\in I\setminus \{\min I\}$
and
$k\in I\setminus \{\min I\}$
and -
(iii)
 $|f(x_k)|\le C/w(f)$
for every
$|f(x_k)|\le C/w(f)$
for every
 $k\in I$
and
$k\in I$
and
 $f\in W_{(2)}$
with
$f\in W_{(2)}$
with
 $w(f)<m_{j_k}$
.
$w(f)<m_{j_k}$
.
Definition 13.2. Let
![]() $C\ge 1$
and
$C\ge 1$
and
![]() $j_0\in \mathbb {N}$
. We call a pair
$j_0\in \mathbb {N}$
. We call a pair
![]() $(x,f)$
where
$(x,f)$
where
![]() $x\in \mathfrak {X}_{\text {awi}}^{(2)}$
and
$x\in \mathfrak {X}_{\text {awi}}^{(2)}$
and
![]() $f\in W_{(2)}$
, a
$f\in W_{(2)}$
, a
![]() $(2,C,m_{j_0})$
-standard exact pair if there exists a
$(2,C,m_{j_0})$
-standard exact pair if there exists a
![]() $(C,(j_k)_{k=1}^n)$
-RIS
$(C,(j_k)_{k=1}^n)$
-RIS
![]() $(x_k)_{k=1}^n$
with
$(x_k)_{k=1}^n$
with
![]() $j_0<j_1$
, such that
$j_0<j_1$
, such that
-
(i)
 $x=m_{j_0}\sum _{k=1}^na_kx_k$
and
$x=m_{j_0}\sum _{k=1}^na_kx_k$
and
 $\sum _{k=1}^na_kx_k$
is a
$\sum _{k=1}^na_kx_k$
is a
 $(2,n_{j_0},m_{j_0}^{-4})$
-s.c.c.,
$(2,n_{j_0},m_{j_0}^{-4})$
-s.c.c., -
(ii)
 $x_k$
is a
$x_k$
is a
 $(2,n_{j_k},m_{j_k}^{-4})$
-s.c.c. and
$(2,n_{j_k},m_{j_k}^{-4})$
-s.c.c. and
 $1/2<\|x_k\|\le 1$
for every
$1/2<\|x_k\|\le 1$
for every
 $k=1,\ldots ,n$
,
$k=1,\ldots ,n$
, -
(iii)
 $f=m_{j_0}^{-1}\sum _{k=1}^nf_k$
, where
$f=m_{j_0}^{-1}\sum _{k=1}^nf_k$
, where
 $f_k\in W_{(2)}$
with
$f_k\in W_{(2)}$
with
 $f_k(x_k)>1/4$
for every
$f_k(x_k)>1/4$
for every
 $k=1,\ldots ,n$
$k=1,\ldots ,n$
-
(iv) and
 $48m^2_{j_0}\leq \min \text {supp}(x)$
.
$48m^2_{j_0}\leq \min \text {supp}(x)$
.
The proof of the following proposition, which demonstrates the existence of SEPs in any subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
, is similar to that of Proposition 8.8 and is omitted.
$\mathfrak {X}_{\text {awi}}^{(2)}$
, is similar to that of Proposition 8.8 and is omitted.
Proposition 13.3. Let Y be a block subspace of
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
. Then, for every
$\mathfrak {X}_{\text {awi}}^{(2)}$
. Then, for every
![]() $C>2$
and
$C>2$
and
![]() $j_0,m\in \mathbb {N}$
, there exists a
$j_0,m\in \mathbb {N}$
, there exists a
![]() $(2,C,m_{j_0})$
-SEP
$(2,C,m_{j_0})$
-SEP
![]() $(x,f)$
with
$(x,f)$
with
![]() $x\in Y$
and
$x\in Y$
and
![]() $m\le \min \text {supp} (x)$
.
$m\le \min \text {supp} (x)$
.
Proposition 13.4. For every
![]() $(2,C,m_{j_0})$
-SEP
$(2,C,m_{j_0})$
-SEP
![]() $(x,f)$
, the following hold.
$(x,f)$
, the following hold.
-
(i) For every
 $g\in W_{(2)}$
$g\in W_{(2)}$
 $$\begin{align*}\big|g(x)\big|\le \begin{cases} 4C[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(g)}],\quad\quad & w(g)\ge m_{j_0} \\ \frac{12C}{w(g)},\quad\quad & w(g)<m_{j_0}. \end{cases} \end{align*}$$
$$\begin{align*}\big|g(x)\big|\le \begin{cases} 4C[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(g)}],\quad\quad & w(g)\ge m_{j_0} \\ \frac{12C}{w(g)},\quad\quad & w(g)<m_{j_0}. \end{cases} \end{align*}$$
-
(ii) If
 $g\in W_{(2)}$
with a tree analysis
$g\in W_{(2)}$
with a tree analysis
 $(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
 $I^x_{g_{\alpha }}=\emptyset $
for all
$I^x_{g_{\alpha }}=\emptyset $
for all
 $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
 $w(g_{\alpha })= m_{j_0}$
, then
$w(g_{\alpha })= m_{j_0}$
, then $$\begin{align*}|g(x)|\le\frac{6C}{m_{j_0}}.\end{align*}$$
$$\begin{align*}|g(x)|\le\frac{6C}{m_{j_0}}.\end{align*}$$
Proof. We refer the reader to Appendix B.
14 The space
 $\mathfrak {X}_{\text {awi}}^{(2)}$
does not contain asymptotic
$\mathfrak {X}_{\text {awi}}^{(2)}$
does not contain asymptotic
 $\ell _2$
subspaces
$\ell _2$
subspaces
To prove that
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
contains no asymptotic
$\mathfrak {X}_{\text {awi}}^{(2)}$
contains no asymptotic
![]() $\ell _2$
subspaces, we use almost identical arguments as in the case of
$\ell _2$
subspaces, we use almost identical arguments as in the case of
![]() $\mathfrak {X}^{(1)}_{\text {awi}}$
. In particular, we show that any block subspace contains a vector, that is an
$\mathfrak {X}^{(1)}_{\text {awi}}$
. In particular, we show that any block subspace contains a vector, that is an
![]() $\ell _2$
-average of standard exacts pairs, with arbitrarily small norm. Again, this requires Lemma 9.4. However, in this case, we employ Lemma 14.2 to carefully calculate certain upper bounds, using the Cauchy-Schwarz inequality.
$\ell _2$
-average of standard exacts pairs, with arbitrarily small norm. Again, this requires Lemma 9.4. However, in this case, we employ Lemma 14.2 to carefully calculate certain upper bounds, using the Cauchy-Schwarz inequality.
Definition 14.1. We say that a sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
, where
$(x_1,f_1),\ldots ,(x_n,f_n)$
, where
![]() $x_i\in \mathfrak {X}_{\text {awi}}^{(2)}$
and
$x_i\in \mathfrak {X}_{\text {awi}}^{(2)}$
and
![]() $f_i\in W_{(2)}$
for
$f_i\in W_{(2)}$
for
![]() $i=1,\ldots ,n$
, is a dependent sequence if each
$i=1,\ldots ,n$
, is a dependent sequence if each
![]() $(x_i,f_i)$
is a
$(x_i,f_i)$
is a
![]() $(2,3,m_{j_i})$
-SEP and
$(2,3,m_{j_i})$
-SEP and
![]() $\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
.
$\bar {f}_1<_{\mathcal {T}}\ldots <_{\mathcal {T}} \bar {f}_n$
.
Lemma 14.2. Let
![]() $(x,f)$
be a
$(x,f)$
be a
![]() $(2,3,m_j)$
-SEP, where
$(2,3,m_j)$
-SEP, where
![]() $x=m_j\sum _{k=1}^na_kx_k$
, and let
$x=m_j\sum _{k=1}^na_kx_k$
, and let
![]() $g_1<\cdots <g_m\in W_{(2)}$
with
$g_1<\cdots <g_m\in W_{(2)}$
with
![]() $w(g_i)=m_j$
and
$w(g_i)=m_j$
and
![]() $I_{g_i}^x \neq \emptyset $
for all
$I_{g_i}^x \neq \emptyset $
for all
![]() $i=1,\ldots ,m$
. Then, for any choice of scalars
$i=1,\ldots ,m$
. Then, for any choice of scalars
![]() $\lambda _1,\ldots ,\lambda _m$
, we have
$\lambda _1,\ldots ,\lambda _m$
, we have
 $$\begin{align*}|\sum_{i=1}^m\lambda_ig_i(x)|\le (4\sqrt{2}+1)(\sum_{i=1}^m\lambda_i^2)^{\frac{1}{2}}. \end{align*}$$
$$\begin{align*}|\sum_{i=1}^m\lambda_ig_i(x)|\le (4\sqrt{2}+1)(\sum_{i=1}^m\lambda_i^2)^{\frac{1}{2}}. \end{align*}$$
Proof. For each
![]() $i=1,\ldots ,m$
, let
$i=1,\ldots ,m$
, let
 $$\begin{align*}g_i=\frac{1}{m_j}\sum_{\ell\in L_i} \lambda_{i\ell} g^i_{\ell},\quad \sum_{\ell\in L_i}\lambda_{i\ell}^2\le 1 \end{align*}$$
$$\begin{align*}g_i=\frac{1}{m_j}\sum_{\ell\in L_i} \lambda_{i\ell} g^i_{\ell},\quad \sum_{\ell\in L_i}\lambda_{i\ell}^2\le 1 \end{align*}$$
and define
Then, Lemma 11.6 and the Cauchy-Schwarz inequality imply that
 $$ \begin{align} |\sum_{i=1}^m\lambda_ig_i (m_j\sum_{k\in F_1}a_kx_k )|&=|\sum_{i=1}^m\lambda_im_j^{-1}\sum_{\ell\in L_i}\lambda_{i\ell}g^i_{\ell} (m_j\sum_{k\in I^x_{g_{\ell}^i}}a_kx_k)| \nonumber\\ &\le 2\sqrt{2}|\sum_{i=1}^m\lambda_i\sum_{\ell\in L_i}\lambda_{i\ell}( \sum_{k\in I^x_{g^i_{\ell}}}a_k^2)^{\frac{1}{2}}| \nonumber \\ & \le 2\sqrt{2} |\sum_{i=1}^m\lambda_i(\sum_{\ell\in L_i}\lambda_{i\ell}^2)^{\frac{1}{2}}( \sum_{k\in \cup_{\ell \in L_i}I^x_{g^i_{\ell}}}a_k^2)^{\frac{1}{2}}| \nonumber \\ & \le 2\sqrt{2} (\sum_{i=1}^m\lambda_i^2)^{\frac{1}{2}}( \sum_{k\in K_1}a_k^2)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} |\sum_{i=1}^m\lambda_ig_i (m_j\sum_{k\in F_1}a_kx_k )|&=|\sum_{i=1}^m\lambda_im_j^{-1}\sum_{\ell\in L_i}\lambda_{i\ell}g^i_{\ell} (m_j\sum_{k\in I^x_{g_{\ell}^i}}a_kx_k)| \nonumber\\ &\le 2\sqrt{2}|\sum_{i=1}^m\lambda_i\sum_{\ell\in L_i}\lambda_{i\ell}( \sum_{k\in I^x_{g^i_{\ell}}}a_k^2)^{\frac{1}{2}}| \nonumber \\ & \le 2\sqrt{2} |\sum_{i=1}^m\lambda_i(\sum_{\ell\in L_i}\lambda_{i\ell}^2)^{\frac{1}{2}}( \sum_{k\in \cup_{\ell \in L_i}I^x_{g^i_{\ell}}}a_k^2)^{\frac{1}{2}}| \nonumber \\ & \le 2\sqrt{2} (\sum_{i=1}^m\lambda_i^2)^{\frac{1}{2}}( \sum_{k\in K_1}a_k^2)^{\frac{1}{2}}. \end{align} $$
For each
![]() $k=1,\ldots ,n$
, let
$k=1,\ldots ,n$
, let
Define for each
![]() $i=1,\ldots ,m$
and
$i=1,\ldots ,m$
and
![]() $\ell \in L_i$
$\ell \in L_i$
 $$\begin{align*}\begin{aligned} M^{\ell}_i &= \{k\in K_2:\text{ there is }q\in Q_k\text{ with }\text{supp}(y^k_q)\subset\text{range}(g^i_{\ell})\}\text{ and for }k\in M_i\\ N_{i\ell}^k &= \{q\in Q_k:\text{supp}(y^k_q)\subset\text{range}(g^i_{\ell})\}.\\ \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} M^{\ell}_i &= \{k\in K_2:\text{ there is }q\in Q_k\text{ with }\text{supp}(y^k_q)\subset\text{range}(g^i_{\ell})\}\text{ and for }k\in M_i\\ N_{i\ell}^k &= \{q\in Q_k:\text{supp}(y^k_q)\subset\text{range}(g^i_{\ell})\}.\\ \end{aligned} \end{align*}$$
Also, for
![]() $k\in K_2$
, define
$k\in K_2$
, define
Finally, also define
Note that the sets
![]() $N^k_{i\ell }$
,
$N^k_{i\ell }$
,
![]() $i\in \{1,\ldots ,m\}$
,
$i\in \{1,\ldots ,m\}$
,
![]() $\ell \in L_i$
,
$\ell \in L_i$
,
![]() $k\in M^{\ell }_i$
, are pairwise disjoint with union
$k\in M^{\ell }_i$
, are pairwise disjoint with union
![]() $\cup _{k\in K_2}O_k$
. Applying Lemma 11.6 and the Cauchy-Schwarz inequality once again, we have
$\cup _{k\in K_2}O_k$
. Applying Lemma 11.6 and the Cauchy-Schwarz inequality once again, we have
 $$ \begin{align} |\sum_{i=1}^m\lambda_i g_i |_{F_1}(m_j\sum_{k\in K_2}a_kx_k)| & = |\sum_{i=1}^m\lambda_i \sum_{\ell\in L_i}\lambda_{i\ell} g^i_{\ell}(\sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_kb_{kq}y^k_q)|\nonumber\\ &\leq 2\sqrt 2\sum_{i=1}^m\lambda_i \sum_{\ell\in L_i}\lambda_{i\ell} (\sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2}\nonumber\\ &\leq 2\sqrt 2\sum_{i=1}^m\lambda_i (\sum_{\ell\in L_i}\lambda_{i\ell}^2)^{1/2}(\sum_{\ell\in L_i} \sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2}\nonumber\\ &\leq 2\sqrt 2\sum_{i=1}^m\lambda_i (\sum_{\ell\in L_i} \sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2} \nonumber\\ &\leq 2\sqrt 2(\sum_{i=1}^m\lambda^2_i)^{1/2}(\sum_{i=1}^m\sum_{\ell\in L_i} \sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2} \nonumber\\ & = 2\sqrt 2 (\sum_{i=1}^m\lambda^2_i)^{1/2} (\sum_{k\in K_2}a_k^2\sum_{q \in O_k}b^2_{kq})^{1/2}\nonumber\\ &\leq 2\sqrt 2 (\sum_{i=1}^m\lambda^2_i)^{1/2} (\sum_{k\in K_2}a_k^2)^{1/2}. \end{align} $$
$$ \begin{align} |\sum_{i=1}^m\lambda_i g_i |_{F_1}(m_j\sum_{k\in K_2}a_kx_k)| & = |\sum_{i=1}^m\lambda_i \sum_{\ell\in L_i}\lambda_{i\ell} g^i_{\ell}(\sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_kb_{kq}y^k_q)|\nonumber\\ &\leq 2\sqrt 2\sum_{i=1}^m\lambda_i \sum_{\ell\in L_i}\lambda_{i\ell} (\sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2}\nonumber\\ &\leq 2\sqrt 2\sum_{i=1}^m\lambda_i (\sum_{\ell\in L_i}\lambda_{i\ell}^2)^{1/2}(\sum_{\ell\in L_i} \sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2}\nonumber\\ &\leq 2\sqrt 2\sum_{i=1}^m\lambda_i (\sum_{\ell\in L_i} \sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2} \nonumber\\ &\leq 2\sqrt 2(\sum_{i=1}^m\lambda^2_i)^{1/2}(\sum_{i=1}^m\sum_{\ell\in L_i} \sum_{k\in M^{\ell}_i}\sum_{q\in N_{i\ell}^k}a_k^2b^2_{kq})^{1/2} \nonumber\\ & = 2\sqrt 2 (\sum_{i=1}^m\lambda^2_i)^{1/2} (\sum_{k\in K_2}a_k^2\sum_{q \in O_k}b^2_{kq})^{1/2}\nonumber\\ &\leq 2\sqrt 2 (\sum_{i=1}^m\lambda^2_i)^{1/2} (\sum_{k\in K_2}a_k^2)^{1/2}. \end{align} $$
For each
![]() $i=1,\ldots ,m$
and
$i=1,\ldots ,m$
and
![]() $k\in K_2$
, define
$k\in K_2$
, define
Observe that, since
![]() $(g^i_{\ell })_{\ell \in L_i}$
is
$(g^i_{\ell })_{\ell \in L_i}$
is
![]() $\mathcal {S}_{n_j}$
-admissible,
$\mathcal {S}_{n_j}$
-admissible,
![]() $(y_q^k)_{Q^i_k}$
is
$(y_q^k)_{Q^i_k}$
is
![]() $\mathcal {S}_{n_j+1}$
-admissible for all
$\mathcal {S}_{n_j+1}$
-admissible for all
![]() $i=1,\ldots ,m$
, and Proposition 2.4 thus implies that
$i=1,\ldots ,m$
, and Proposition 2.4 thus implies that
 $$\begin{align*}\sum_{q\in Q^i_k} b_{kq}^2< \frac{3}{\min\text{supp} (x_k)}. \end{align*}$$
$$\begin{align*}\sum_{q\in Q^i_k} b_{kq}^2< \frac{3}{\min\text{supp} (x_k)}. \end{align*}$$
For
![]() $i\in \{1,\ldots ,m\}$
, put
$i\in \{1,\ldots ,m\}$
, put
![]() $K_2^i=\{k\in K_2: \operatorname {\mathrm {range}}(g_i)\cap \operatorname {\mathrm {range}} x_k\neq \emptyset \}$
. The condition
$K_2^i=\{k\in K_2: \operatorname {\mathrm {range}}(g_i)\cap \operatorname {\mathrm {range}} x_k\neq \emptyset \}$
. The condition
![]() $i\in \{1,\ldots ,m\}$
,
$i\in \{1,\ldots ,m\}$
,
![]() $I_{g_i}^x \neq \emptyset $
, for
$I_{g_i}^x \neq \emptyset $
, for
![]() $i\in \{1,\ldots ,m\}$
implies that each
$i\in \{1,\ldots ,m\}$
implies that each
![]() $k\in K_2$
is in at most two sets
$k\in K_2$
is in at most two sets
![]() $K_2^i$
. We then calculate
$K_2^i$
. We then calculate
 $$ \begin{align} |\sum_{i=1}^m\lambda_i g_i |_{F_2}(m_j\sum_{k\in K_2}a_kx_k)| & = |\sum_{i=1}^m\lambda_ig_i(m_j\sum_{k\in K_2\cap I_{g_i}}a_k\sum_{q\in Q_k^i}b_{kq}y^k_q)| \nonumber\\ & \le 2\sqrt{2}m_j\sum_{i=1}^m\lambda_i(\sum_{k\in K_2\cap I_{g_i}}a^2_k\sum_{q\in Q_k^i}b^2_{kq})^{1/2}\nonumber\\ & \leq 2\sqrt{2}m_j(\sum_{i=1}^m\lambda_i^2)^{1/2}(\sum_{i=1}^m\sum_{k\in K_2\cap I_{g_i}}a^2_k\frac{3}{\min\text{supp}(x_k)})^{1/2}\nonumber\\ &\leq 4\sqrt{3}m_j(\sum_{i=1}^m\lambda_i^2)^{1/2}(\sum_{k\in K_2}a_k^2\frac{1}{\min\text{supp}(x_k)})^{1/2}\nonumber\\&\leq (\sum_{i=1}^m\lambda_i^2)^{1/2}\frac{4\sqrt{3}m_j}{\min\text{supp}(x)^{1/2}}\nonumber\\ &\leq (\sum_{i=1}^m\lambda_i^2)^{1/2}\text{ (by Definition 13.2 (iv))} .\end{align} $$
$$ \begin{align} |\sum_{i=1}^m\lambda_i g_i |_{F_2}(m_j\sum_{k\in K_2}a_kx_k)| & = |\sum_{i=1}^m\lambda_ig_i(m_j\sum_{k\in K_2\cap I_{g_i}}a_k\sum_{q\in Q_k^i}b_{kq}y^k_q)| \nonumber\\ & \le 2\sqrt{2}m_j\sum_{i=1}^m\lambda_i(\sum_{k\in K_2\cap I_{g_i}}a^2_k\sum_{q\in Q_k^i}b^2_{kq})^{1/2}\nonumber\\ & \leq 2\sqrt{2}m_j(\sum_{i=1}^m\lambda_i^2)^{1/2}(\sum_{i=1}^m\sum_{k\in K_2\cap I_{g_i}}a^2_k\frac{3}{\min\text{supp}(x_k)})^{1/2}\nonumber\\ &\leq 4\sqrt{3}m_j(\sum_{i=1}^m\lambda_i^2)^{1/2}(\sum_{k\in K_2}a_k^2\frac{1}{\min\text{supp}(x_k)})^{1/2}\nonumber\\&\leq (\sum_{i=1}^m\lambda_i^2)^{1/2}\frac{4\sqrt{3}m_j}{\min\text{supp}(x)^{1/2}}\nonumber\\ &\leq (\sum_{i=1}^m\lambda_i^2)^{1/2}\text{ (by Definition 13.2 (iv))} .\end{align} $$
Proposition 14.3. For every
![]() $0<c<1$
, there exists
$0<c<1$
, there exists
![]() $d\in \mathbb {N}$
, such that whenever
$d\in \mathbb {N}$
, such that whenever
![]() $d\le n$
and
$d\le n$
and
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
is a dependent sequence, then
$(x_1,f_1),\ldots ,(x_n,f_n)$
is a dependent sequence, then
 $$\begin{align*}\|\frac{1}{\sqrt{n}}\sum_{i=1}^nx_i\|<c. \end{align*}$$
$$\begin{align*}\|\frac{1}{\sqrt{n}}\sum_{i=1}^nx_i\|<c. \end{align*}$$
Proof. Pick an
![]() $m\in \mathbb {N}$
, such that
$m\in \mathbb {N}$
, such that
and fix a dependent sequence
![]() $(x_1,f_1),\ldots ,(x_n,f_n)$
. Let
$(x_1,f_1),\ldots ,(x_n,f_n)$
. Let
![]() $f\in W\setminus W_0$
and consider the partitions
$f\in W\setminus W_0$
and consider the partitions
![]() $f=h+g$
and
$f=h+g$
and
![]() $g=g_1+g_2$
as in the proof of Proposition 9.6. Then, the same arguments and Proposition 13.4 yield that
$g=g_1+g_2$
as in the proof of Proposition 9.6. Then, the same arguments and Proposition 13.4 yield that
 $$ \begin{align} |h(\frac{1}{\sqrt{n}}\sum_{k=1}^nx_k )|\le \frac{18}{\sqrt{n}}. \end{align} $$
$$ \begin{align} |h(\frac{1}{\sqrt{n}}\sum_{k=1}^nx_k )|\le \frac{18}{\sqrt{n}}. \end{align} $$
Moreover, Proposition 9.4, again, implies that
 $$\begin{align*}\#\{ k\in\{1,\ldots,n\} : g_1(x_k)\neq 0\} \le \ell = e\sum_{k=1}^mk! \end{align*}$$
$$\begin{align*}\#\{ k\in\{1,\ldots,n\} : g_1(x_k)\neq 0\} \le \ell = e\sum_{k=1}^mk! \end{align*}$$
and, thus, by Propositions 11.6 and 13.4 (i),
 $$ \begin{align} \left|g_1\left(\frac{1}{\sqrt{n}}\sum_{k=1}^nx_k\right)\right| \le 2\sqrt{2} \frac{\sqrt \ell}{\sqrt{n}}24 = 48\sqrt{\frac{2\ell}{n}}. \end{align} $$
$$ \begin{align} \left|g_1\left(\frac{1}{\sqrt{n}}\sum_{k=1}^nx_k\right)\right| \le 2\sqrt{2} \frac{\sqrt \ell}{\sqrt{n}}24 = 48\sqrt{\frac{2\ell}{n}}. \end{align} $$
Finally, we treat
![]() $g_2$
differently from Proposition 9.6. Recall that for
$g_2$
differently from Proposition 9.6. Recall that for
![]() $k=1,\ldots ,n$
,
$k=1,\ldots ,n$
,
Define
so that
![]() $g_2 = g|_{G_2}$
. We further split
$g_2 = g|_{G_2}$
. We further split
![]() $G_2$
as follows
$G_2$
as follows
Proposition 13.4 (ii) implies that for
![]() $k\in \{1,\ldots ,n\}$
,
$k\in \{1,\ldots ,n\}$
,
and, thus,
 $$ \begin{align} |g_2|_{G_2^1}(\frac{1}{\sqrt{n}}\sum_{k\in K_1}x_k)|\le \frac{18}{\sqrt{n}}. \end{align} $$
$$ \begin{align} |g_2|_{G_2^1}(\frac{1}{\sqrt{n}}\sum_{k\in K_1}x_k)|\le \frac{18}{\sqrt{n}}. \end{align} $$
To complete the computation, we need to evaluate the action of
![]() $g_2|_{G_2^2}$
. To that end, for
$g_2|_{G_2^2}$
. To that end, for
![]() $s=m+1,m+2,\ldots $
and
$s=m+1,m+2,\ldots $
and
![]() $k\in \{1,\ldots ,n\}$
, put
$k\in \{1,\ldots ,n\}$
, put
so that for each
![]() $s>m$
, the sets
$s>m$
, the sets
![]() $\mathcal {B}_{k,s}^2$
,
$\mathcal {B}_{k,s}^2$
,
![]() $k\in \{1,\ldots ,n\}$
are pairwise disjoint and the set
$k\in \{1,\ldots ,n\}$
are pairwise disjoint and the set
![]() $\cup _{k=1}^n\mathcal {B}_{k,s}^2$
is pairwise incomparable. We use Lemma 14.2 and the definition of
$\cup _{k=1}^n\mathcal {B}_{k,s}^2$
is pairwise incomparable. We use Lemma 14.2 and the definition of
![]() $G_2^2$
to calculate
$G_2^2$
to calculate
 $$ \begin{align} |g_2|_{G_2^2}(\frac{1}{\sqrt n}\sum_{k=1}^nx_k)| &= |\frac{1}{\sqrt{n}}\sum_{k=1}^n\sum_{\alpha\in\mathcal{B}^2_k}\frac{\lambda_{f_{\alpha}}}{w_{f}(f_{\alpha})}f_{\alpha}|_{G^2_2}(x_{k})|\nonumber\\ &\leq \frac{4\sqrt 2+1}{\sqrt{n}}\sum_{k=1}^n(\sum_{\alpha\in\mathcal{B}^2_k}\frac{\lambda^2_{f_{\alpha}}}{w_{f}(f_{\alpha})^2})^{1/2}\nonumber\\ &\leq (4\sqrt 2+1)(\sum_{k=1}^n\sum_{\alpha\in\mathcal{B}_{k}^2}\frac{\lambda^2_{f_{\alpha}}}{w_{f}(f_{\alpha})^2})^{1/2}\nonumber\\ &\leq(4\sqrt 2+1)(\sum_{s=m+1}^{\infty}\frac{1}{4^{s}}\sum_{\alpha\in\cup_{k=1}^n\mathcal{B}_{k,s}^2}{\lambda^2_{f_{\alpha}}})^{1/2}\nonumber\\ &\leq(4\sqrt{2} + 1)(\sum_{s=m+1}^{\infty}\frac{1}{4^s})^{1/2} = \frac{4\sqrt{2}+1}{2^m\sqrt3} \leq \frac{4}{2^m}. \end{align} $$
$$ \begin{align} |g_2|_{G_2^2}(\frac{1}{\sqrt n}\sum_{k=1}^nx_k)| &= |\frac{1}{\sqrt{n}}\sum_{k=1}^n\sum_{\alpha\in\mathcal{B}^2_k}\frac{\lambda_{f_{\alpha}}}{w_{f}(f_{\alpha})}f_{\alpha}|_{G^2_2}(x_{k})|\nonumber\\ &\leq \frac{4\sqrt 2+1}{\sqrt{n}}\sum_{k=1}^n(\sum_{\alpha\in\mathcal{B}^2_k}\frac{\lambda^2_{f_{\alpha}}}{w_{f}(f_{\alpha})^2})^{1/2}\nonumber\\ &\leq (4\sqrt 2+1)(\sum_{k=1}^n\sum_{\alpha\in\mathcal{B}_{k}^2}\frac{\lambda^2_{f_{\alpha}}}{w_{f}(f_{\alpha})^2})^{1/2}\nonumber\\ &\leq(4\sqrt 2+1)(\sum_{s=m+1}^{\infty}\frac{1}{4^{s}}\sum_{\alpha\in\cup_{k=1}^n\mathcal{B}_{k,s}^2}{\lambda^2_{f_{\alpha}}})^{1/2}\nonumber\\ &\leq(4\sqrt{2} + 1)(\sum_{s=m+1}^{\infty}\frac{1}{4^s})^{1/2} = \frac{4\sqrt{2}+1}{2^m\sqrt3} \leq \frac{4}{2^m}. \end{align} $$
Then, (14.5), (14.6), (14.7) and (14.8) yield that
 $$\begin{align*}|f(x)|\le \frac{36+48\sqrt{2\ell}}{\sqrt n} + \frac{4}{2^m} \leq \frac{36+48\sqrt{2\ell}}{\sqrt n} + \frac{c}{2}, \end{align*}$$
$$\begin{align*}|f(x)|\le \frac{36+48\sqrt{2\ell}}{\sqrt n} + \frac{4}{2^m} \leq \frac{36+48\sqrt{2\ell}}{\sqrt n} + \frac{c}{2}, \end{align*}$$
and, thus, for d, such that
 $$\begin{align*}\frac{36+48\sqrt{2\ell}}{\sqrt d} < \frac{c}{2}, \end{align*}$$
$$\begin{align*}\frac{36+48\sqrt{2\ell}}{\sqrt d} < \frac{c}{2}, \end{align*}$$
we have the desired result.
Proposition 14.4. The space
![]() $\mathfrak {X}_{\text {awi}}^{(2)}$
does not contain Asymptotic
$\mathfrak {X}_{\text {awi}}^{(2)}$
does not contain Asymptotic
![]() $\ell _2$
subspaces.
$\ell _2$
subspaces.
Proof. It is an immediate consequence of Proposition 14.3, using similar arguments as in Proposition 9.7.
Remark 14.5. Unlike the case of
![]() $\ell _1$
, for every
$\ell _1$
, for every
![]() $1<p<\infty $
, it is in fact possible to define a reflexive Banach space with a Schauder basis, admitting a unique
$1<p<\infty $
, it is in fact possible to define a reflexive Banach space with a Schauder basis, admitting a unique
![]() $\ell _p$
asymptotic model with respect to the family of normalised block sequences, whose any block subspace contains an
$\ell _p$
asymptotic model with respect to the family of normalised block sequences, whose any block subspace contains an
![]() $\ell _1$
block tree of height
$\ell _1$
block tree of height
![]() $\omega ^{\xi }$
. Such a space can be defined using the attractors method, which was first introduced in [Reference Argyros, Arvanitakis, Tolias, Castillo and Johnson3] and later used in [Reference Argyros, Manoussakis and Pelczar-Barwacz10].
$\omega ^{\xi }$
. Such a space can be defined using the attractors method, which was first introduced in [Reference Argyros, Arvanitakis, Tolias, Castillo and Johnson3] and later used in [Reference Argyros, Manoussakis and Pelczar-Barwacz10].
15 Appendix A
In this section, we prove the properties of standard exact pairs in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
, given in Proposition 8.11. This requires three steps. First, we need to define an auxiliary space which is also a Mixed Tsirelson space. Then, on the special convex combinations of its basis, we give upper bounds on the evaluations of the functionals in its norming set
$\mathfrak {X}_{\text {awi}}^{(1)}$
, given in Proposition 8.11. This requires three steps. First, we need to define an auxiliary space which is also a Mixed Tsirelson space. Then, on the special convex combinations of its basis, we give upper bounds on the evaluations of the functionals in its norming set
![]() $W_{\text {aux}}^{(1)}$
. Finally, for a standard exact pair
$W_{\text {aux}}^{(1)}$
. Finally, for a standard exact pair
![]() $(x,f)$
, via the basic inequality, we reduce the upper bounds of the evaluations of functionals in
$(x,f)$
, via the basic inequality, we reduce the upper bounds of the evaluations of functionals in
![]() $W_{(1)}$
acting on x, to the corresponding one of a functional g in
$W_{(1)}$
acting on x, to the corresponding one of a functional g in
![]() $W_{\text {aux}}^{(1)}$
on a normalised special convex combination of the basis of the auxiliary space.
$W_{\text {aux}}^{(1)}$
on a normalised special convex combination of the basis of the auxiliary space.
15.1 The auxiliary space
Definition 15.1. Let
![]() $W_{\text {aux}}^{(1)}$
be the minimal subset of
$W_{\text {aux}}^{(1)}$
be the minimal subset of
![]() $c_{00}(\mathbb {N})$
, such that
$c_{00}(\mathbb {N})$
, such that
-
(i)
 $\pm e_i$
is in
$\pm e_i$
is in
 $W_{\text {aux}}^{(1)}$
for all
$W_{\text {aux}}^{(1)}$
for all
 $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and -
(ii) for every
 $j\in \mathbb {N}$
and every
$j\in \mathbb {N}$
and every
 $\mathcal {S}_{n_j+1}$
-admissible sequence of functionals
$\mathcal {S}_{n_j+1}$
-admissible sequence of functionals
 $(f_i)_{i=1}^d$
in
$(f_i)_{i=1}^d$
in
 $W_{\text {aux}}^{(1)}$
, we have that
$W_{\text {aux}}^{(1)}$
, we have that
 $f=m_{j}^{-1}\sum _{i=1}^df_i$
is in
$f=m_{j}^{-1}\sum _{i=1}^df_i$
is in
 $W_{\text {aux}}^{(1)}$
.
$W_{\text {aux}}^{(1)}$
.
The purpose of the following two lemmas is to provide upper bounds for the norms of linear combinations of certain vectors in the auxiliary space.
Lemma 15.2. Let
![]() $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and
![]() $\varepsilon>0$
with
$\varepsilon>0$
with
![]() $\varepsilon \le m_{j}^{-1}$
. For every
$\varepsilon \le m_{j}^{-1}$
. For every
![]() $(n_{j},\varepsilon )$
-basic s.c.c.
$(n_{j},\varepsilon )$
-basic s.c.c.
![]() $x=\sum _{k\in F}c_ke_k$
, the following hold.
$x=\sum _{k\in F}c_ke_k$
, the following hold.
-
(i) For every
 $f\in W_{\text {aux}}^{(1)}$
$f\in W_{\text {aux}}^{(1)}$
 $$\begin{align*}\big|f(x)\big|\le \begin{cases} \varepsilon,\quad\quad & f=\pm e_i^*\text{ for some }i\in\mathbb{N}\\ \frac{1}{w(f)},\quad\quad & w(f)\ge m_{j}\\ \frac{2}{w(f)m_{j}},\quad\quad & w(f)<m_{j}. \end{cases} \end{align*}$$
$$\begin{align*}\big|f(x)\big|\le \begin{cases} \varepsilon,\quad\quad & f=\pm e_i^*\text{ for some }i\in\mathbb{N}\\ \frac{1}{w(f)},\quad\quad & w(f)\ge m_{j}\\ \frac{2}{w(f)m_{j}},\quad\quad & w(f)<m_{j}. \end{cases} \end{align*}$$
-
(ii) If
 $f\in W_{\text {aux}}^{(1)}$
with a tree analysis
$f\in W_{\text {aux}}^{(1)}$
with a tree analysis
 $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
 $w(f_{\alpha })\neq m_{j}$
for all
$w(f_{\alpha })\neq m_{j}$
for all
 $\alpha \in \mathcal {A}$
and
$\alpha \in \mathcal {A}$
and
 $\varepsilon <m_j^{-2}$
, then
$\varepsilon <m_j^{-2}$
, then
 $|f(x)|<2m_j^{-2}$
.
$|f(x)|<2m_j^{-2}$
.
Proof. We may assume that
![]() $\text {supp} (f)\subset F$
and
$\text {supp} (f)\subset F$
and
![]() $f(e_i)\ge 0$
for every
$f(e_i)\ge 0$
for every
![]() $i\in \mathbb {N}$
. If
$i\in \mathbb {N}$
. If
![]() $f=\pm e_i^*$
for some
$f=\pm e_i^*$
for some
![]() $i\in F$
, then
$i\in F$
, then
![]() $|f(x)|=c_i<\varepsilon $
, since x is an
$|f(x)|=c_i<\varepsilon $
, since x is an
![]() $(n_{j},\varepsilon )$
-basic s.c.c. and
$(n_{j},\varepsilon )$
-basic s.c.c. and
![]() $\{i\}\in \mathcal {S}_0$
.
$\{i\}\in \mathcal {S}_0$
.
Suppose that
![]() $m_{j}\le w(f)$
. Then
$m_{j}\le w(f)$
. Then
![]() $\|f\|_{\infty }\le 1/w(f)$
, and, hence
$\|f\|_{\infty }\le 1/w(f)$
, and, hence
In the case where
![]() $w(f)=m_i<m_{j}$
, let
$w(f)=m_i<m_{j}$
, let
![]() $f=m^{-1}_{i}\sum _{l=1}^df_l$
with
$f=m^{-1}_{i}\sum _{l=1}^df_l$
with
![]() $(f_l)_{l=1}^d$
an
$(f_l)_{l=1}^d$
an
![]() $\mathcal {S}_{n_i+1}$
-admissible sequence in
$\mathcal {S}_{n_i+1}$
-admissible sequence in
![]() $W_{\text {aux}}^{(1)}$
. For
$W_{\text {aux}}^{(1)}$
. For
![]() $l=1,\ldots ,d$
, define
$l=1,\ldots ,d$
, define
![]() $D_l=\{k\in F:f_l(e_k)>m^{-1}_{j}\}$
and
$D_l=\{k\in F:f_l(e_k)>m^{-1}_{j}\}$
and
![]() $D=\cup _{l=1}^dD_l$
. Then, [Reference Argyros and Tolias13, Lemma 3.16] implies that
$D=\cup _{l=1}^dD_l$
. Then, [Reference Argyros and Tolias13, Lemma 3.16] implies that
![]() $D_l\in \mathcal {S}_{(\log _2(m_{j})-1)(n_{j-1}+1)}$
for each
$D_l\in \mathcal {S}_{(\log _2(m_{j})-1)(n_{j-1}+1)}$
for each
![]() $l=1,\ldots ,d$
and, hence, since
$l=1,\ldots ,d$
and, hence, since
![]() $(f_l)_{l=1}^d$
is
$(f_l)_{l=1}^d$
is
![]() $S_{n_{j-1}+1}$
-admissible (recall that
$S_{n_{j-1}+1}$
-admissible (recall that
![]() $i<j$
since
$i<j$
since
![]() $m_i<m_j$
) and
$m_i<m_j$
) and
![]() $D_l\subset \text {supp} (f_l)$
,
$D_l\subset \text {supp} (f_l)$
,
![]() $l=1,\ldots ,d$
, we conclude that the sequence
$l=1,\ldots ,d$
, we conclude that the sequence
![]() $(D_l)_{l=1}^d$
is
$(D_l)_{l=1}^d$
is
![]() $S_{n_{j-1}+1}$
-admissible and
$S_{n_{j-1}+1}$
-admissible and
Since x is an
![]() $(n_j,\varepsilon )$
-basic s.c.c. and
$(n_j,\varepsilon )$
-basic s.c.c. and
![]() $\log _2(m_{j})(n_{j-1}+1)<n_j$
, the above implies that
$\log _2(m_{j})(n_{j-1}+1)<n_j$
, the above implies that
![]() $\sum _{k\in D}c_k<\varepsilon $
, and, thus
$\sum _{k\in D}c_k<\varepsilon $
, and, thus
 $$ \begin{align*} f(x)&=\frac{1}{m_i}\sum_{l=1}^df_l(\sum_{k\in F}c_ke_k)=\frac{1}{m_i}(\sum_{l=1}^df_l|_D(\sum_{k\in F}c_ke_k)+\sum_{l=1}^d f_l|_{\mathbb{N}\setminus D}(\sum_{k\in F}c_ke_k))\\ &\le \frac{1}{m_i}(\sum_{k\in D}c_k+\frac{1}{m_{j}})\le \frac{1}{m_i}(\varepsilon+\frac{1}{m_j})\le \frac{2}{m_im_{j}}. \end{align*} $$
$$ \begin{align*} f(x)&=\frac{1}{m_i}\sum_{l=1}^df_l(\sum_{k\in F}c_ke_k)=\frac{1}{m_i}(\sum_{l=1}^df_l|_D(\sum_{k\in F}c_ke_k)+\sum_{l=1}^d f_l|_{\mathbb{N}\setminus D}(\sum_{k\in F}c_ke_k))\\ &\le \frac{1}{m_i}(\sum_{k\in D}c_k+\frac{1}{m_{j}})\le \frac{1}{m_i}(\varepsilon+\frac{1}{m_j})\le \frac{2}{m_im_{j}}. \end{align*} $$
Finally, if there is a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f with
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f with
![]() $w(f_{\alpha })\neq m_j$
for every
$w(f_{\alpha })\neq m_j$
for every
![]() $\alpha \in \mathcal {A}$
, [Reference Argyros and Tolias13, Lemma 3.16] implies that
$\alpha \in \mathcal {A}$
, [Reference Argyros and Tolias13, Lemma 3.16] implies that
![]() $D=\{k\in F:f(e_k)>m_j^{-2}\}\in \mathcal {S}_{(2\log _2(m_j)-1)(n_{j-1}-1)}$
, and since
$D=\{k\in F:f(e_k)>m_j^{-2}\}\in \mathcal {S}_{(2\log _2(m_j)-1)(n_{j-1}-1)}$
, and since
![]() $(2\log _2(m_j)-1)(n_{j-1}-1)<n_j$
, we have that
$(2\log _2(m_j)-1)(n_{j-1}-1)<n_j$
, we have that
![]() $\sum _{k\in D}c_i<\varepsilon $
. Hence, we conclude that
$\sum _{k\in D}c_i<\varepsilon $
. Hence, we conclude that
 $$\begin{align*}f(x)=\sum_{k\in D}c_kf(x_k)+\sum_{k\in F\setminus D}c_kf(x_k)\le \varepsilon + \frac{1}{m^2_j}<\frac{2}{m_j^2}.\\[-36pt] \end{align*}$$
$$\begin{align*}f(x)=\sum_{k\in D}c_kf(x_k)+\sum_{k\in F\setminus D}c_kf(x_k)\le \varepsilon + \frac{1}{m^2_j}<\frac{2}{m_j^2}.\\[-36pt] \end{align*}$$
15.2 The basic inequality
Proposition 15.3 (basic inequality).
Let
![]() $(x_k)_{k\in I}$
be a
$(x_k)_{k\in I}$
be a
![]() $(C,(j_k)_{k\in I})$
-RIS in
$(C,(j_k)_{k\in I})$
-RIS in
![]() $\mathfrak {X}_{\text {awi}}^{(1)}$
with
$\mathfrak {X}_{\text {awi}}^{(1)}$
with
![]() $4\le \min \text {supp} (x_{\min I})$
,
$4\le \min \text {supp} (x_{\min I})$
,
![]() $(a_k)_{k\in I}$
be a sequence of nonzero scalars and
$(a_k)_{k\in I}$
be a sequence of nonzero scalars and
![]() $f\in W_{(1)}$
with
$f\in W_{(1)}$
with
![]() $I_f\neq \emptyset $
. Define
$I_f\neq \emptyset $
. Define
![]() $t_k=\max \text {supp} (x_k)$
,
$t_k=\max \text {supp} (x_k)$
,
![]() $k\in I$
. Then there exist
$k\in I$
. Then there exist
-
(i)
 $g\in W_{\text {aux}}^{(1)}\cup \{0\}$
with
$g\in W_{\text {aux}}^{(1)}\cup \{0\}$
with
 $w(g)=w(f)$
if
$w(g)=w(f)$
if
 $g\neq 0$
and
$g\neq 0$
and
 $\{k:t_k\in \text {supp} (g)\}\subset I_f$
,
$\{k:t_k\in \text {supp} (g)\}\subset I_f$
, -
(ii)
 $h\in \{\text {sign}(a_k) e^*_{t_k}:k\in I_f\}\cup \{0\}$
with
$h\in \{\text {sign}(a_k) e^*_{t_k}:k\in I_f\}\cup \{0\}$
with
 $k_0\in I_f$
and
$k_0\in I_f$
and
 $k_0 < \min \text {supp}(g)$
if
$k_0 < \min \text {supp}(g)$
if
 $h=\text {sign}(a_{k_0})e^*_{t_{k_0}}$
and
$h=\text {sign}(a_{k_0})e^*_{t_{k_0}}$
and -
(iii)
 $j_0\ge \min \{j_k:k\in I_f\}$
,
$j_0\ge \min \{j_k:k\in I_f\}$
,
such that
 $$ \begin{align} |f(\sum_{k\in I_f}a_kx_k)|\le C(1+\frac{1}{\sqrt{m_{j_{0}}}})[h+g(\sum_{k\in I_f}a_ke_{t_k})]. \end{align} $$
$$ \begin{align} |f(\sum_{k\in I_f}a_kx_k)|\le C(1+\frac{1}{\sqrt{m_{j_{0}}}})[h+g(\sum_{k\in I_f}a_ke_{t_k})]. \end{align} $$
Proof. Recall that
![]() $W_{(1)}$
is the increasing union of the sequence
$W_{(1)}$
is the increasing union of the sequence
![]() $(W^n_{(1)})_{n=0}^{\infty }$
defined in Remark 5.18. We prove the statement by induction on
$(W^n_{(1)})_{n=0}^{\infty }$
defined in Remark 5.18. We prove the statement by induction on
![]() $n=0,1,\ldots $
for every
$n=0,1,\ldots $
for every
![]() $f\in W^n_{(1)}$
and every RIS.
$f\in W^n_{(1)}$
and every RIS.
For
![]() $n=0$
and
$n=0$
and
![]() $f\in W^0_{(1)}$
, the fact that
$f\in W^0_{(1)}$
, the fact that
![]() $I_f\neq \emptyset $
implies that
$I_f\neq \emptyset $
implies that
![]() $I_f=\{k_0\}$
, that is,
$I_f=\{k_0\}$
, that is,
![]() $f= e^*_{t_{k_0}}$
or
$f= e^*_{t_{k_0}}$
or
![]() $f=-e^*_{t_{k_0}}$
for some
$f=-e^*_{t_{k_0}}$
for some
![]() $k_0\in I$
. In either case, it is immediate to check that
$k_0\in I$
. In either case, it is immediate to check that
![]() $h=\text {sign}(a_{k_0})e^*_{t_{k_0}}$
,
$h=\text {sign}(a_{k_0})e^*_{t_{k_0}}$
,
![]() $g=0$
and
$g=0$
and
![]() $j_0=j_{k_0}$
are as desired.
$j_0=j_{k_0}$
are as desired.
Fix
![]() $n\in \mathbb {N}$
, and assume that the conclusion holds for every
$n\in \mathbb {N}$
, and assume that the conclusion holds for every
![]() $f\in W^n_{(1)}$
and every RIS. Pick an
$f\in W^n_{(1)}$
and every RIS. Pick an
![]() $f\in W^{n+1}_{(1)}$
with
$f\in W^{n+1}_{(1)}$
with
![]() $f={m_i}^{-1}\sum _{l=1}^df_l$
, where
$f={m_i}^{-1}\sum _{l=1}^df_l$
, where
![]() $(f_l)_{l=1}^d$
is an
$(f_l)_{l=1}^d$
is an
![]() $\mathcal {S}_{n_i}$
-admissible sequence in
$\mathcal {S}_{n_i}$
-admissible sequence in
![]() $W^n_{(1)}$
. We will first treat the two extreme cases, namely, the cases where
$W^n_{(1)}$
. We will first treat the two extreme cases, namely, the cases where
![]() $i\ge \max \{j_k:k\in I_f\}$
and
$i\ge \max \{j_k:k\in I_f\}$
and
![]() $i<\min \{j_k:k\in I_f\}$
.
$i<\min \{j_k:k\in I_f\}$
.
For the first case, set
![]() $k_0=\max I_f$
and
$k_0=\max I_f$
and
![]() $j_0=j_{k_0}$
and choose
$j_0=j_{k_0}$
and choose
![]() $k_1\in I_f$
that maximises the quantity
$k_1\in I_f$
that maximises the quantity
![]() $|a_{k}|$
for
$|a_{k}|$
for
![]() $k\in I_f$
. Then, since
$k\in I_f$
. Then, since
![]() $(x_k)_{k\in I}$
is a RIS, items (i) and (ii) of Definition 8.5 yield that
$(x_k)_{k\in I}$
is a RIS, items (i) and (ii) of Definition 8.5 yield that
 $$ \begin{align*} |f(\sum_{k\in I_f\setminus\{k_0\}}a_kx_k)|&\le \frac{1}{m_i}\max\text{supp} (x_{k_0-1})\|\sum_{k\in I_f\setminus\{k_0\}}a_kx_k\|_{\infty}\\ &\le \frac{ \max\text{supp} (x_{k_0-1}) }{ m_{j_{k_0}} }C|a_{k_1}|\le\frac{C}{\sqrt{m_{j_{k_0}}}}|a_{k_1}|\nonumber ,\end{align*} $$
$$ \begin{align*} |f(\sum_{k\in I_f\setminus\{k_0\}}a_kx_k)|&\le \frac{1}{m_i}\max\text{supp} (x_{k_0-1})\|\sum_{k\in I_f\setminus\{k_0\}}a_kx_k\|_{\infty}\\ &\le \frac{ \max\text{supp} (x_{k_0-1}) }{ m_{j_{k_0}} }C|a_{k_1}|\le\frac{C}{\sqrt{m_{j_{k_0}}}}|a_{k_1}|\nonumber ,\end{align*} $$
and, thus
 $$ \begin{align} |f(\sum_{k\in I_f}a_kx_k )|&\le \frac{C}{\sqrt{m_{j_{k_0}}}}|a_{k_1}| + |f(a_{k_0}x_{k_0})|\\ &\le \frac{C}{\sqrt{m_{j_{k_0}}}}|a_{k_1}|+C|a_{k_1}|=C(1+\frac{1}{\sqrt{m_{j_{k_0}}}} )|a_{k_1}|\nonumber\\ &= C (1+\frac{1}{\sqrt{m_{j_{k_0}}}})\text{sign}(a_{k_1})e^*_{t_{k_1}} (\sum_{k\in I_f}a_ke_{t_k} ).\nonumber \end{align} $$
$$ \begin{align} |f(\sum_{k\in I_f}a_kx_k )|&\le \frac{C}{\sqrt{m_{j_{k_0}}}}|a_{k_1}| + |f(a_{k_0}x_{k_0})|\\ &\le \frac{C}{\sqrt{m_{j_{k_0}}}}|a_{k_1}|+C|a_{k_1}|=C(1+\frac{1}{\sqrt{m_{j_{k_0}}}} )|a_{k_1}|\nonumber\\ &= C (1+\frac{1}{\sqrt{m_{j_{k_0}}}})\text{sign}(a_{k_1})e^*_{t_{k_1}} (\sum_{k\in I_f}a_ke_{t_k} ).\nonumber \end{align} $$
That is,
![]() $h=\text {sign}(a_{k_1})e^*_{t_{k_1}}$
,
$h=\text {sign}(a_{k_1})e^*_{t_{k_1}}$
,
![]() $g=0$
and
$g=0$
and
![]() $j_{k_0}$
yield the conclusion.
$j_{k_0}$
yield the conclusion.
For the second case, the inductive hypothesis implies that, for every
![]() $l=1,\ldots ,d$
with
$l=1,\ldots ,d$
with
![]() $I_{f_l}\neq \emptyset $
, there are
$I_{f_l}\neq \emptyset $
, there are
![]() $g_l$
,
$g_l$
,
![]() $h_l$
and
$h_l$
and
![]() $j_{0,l}$
as in (i)–(iii) of the statement, that satisfy the conclusion for the functional
$j_{0,l}$
as in (i)–(iii) of the statement, that satisfy the conclusion for the functional
![]() $f_l$
. Define
$f_l$
. Define
![]() $J_f=\{k\in I_f: f(x_k)\neq 0\}\setminus \cup _{l=1}^dI_{f_l}$
. Then, for every
$J_f=\{k\in I_f: f(x_k)\neq 0\}\setminus \cup _{l=1}^dI_{f_l}$
. Then, for every
![]() $k\in J_f$
, Definition 8.5 (iii) yields that
$k\in J_f$
, Definition 8.5 (iii) yields that
 $$ \begin{align*} |f(a_{k}x_{k})|\le \frac{C}{m_i}|a_{k}|=\frac{C}{m_i}\text{sign}(a_{k})e^*_{t_{k}} \left(\sum_{k\in I_f}a_{k}e_{t_{k}} \right), \end{align*} $$
$$ \begin{align*} |f(a_{k}x_{k})|\le \frac{C}{m_i}|a_{k}|=\frac{C}{m_i}\text{sign}(a_{k})e^*_{t_{k}} \left(\sum_{k\in I_f}a_{k}e_{t_{k}} \right), \end{align*} $$
and, hence, we calculate
 $$ \begin{align} |f(\sum_{k\in I_f}a_kx_k)|&\le |f(\sum_{k\in \cup_{l=1}^dI_{f_l}}a_kx_k)|+|f(\sum_{k\in J_f}a_kx_k )|\\ &\le\frac{C}{m_i}\sum_{k\in J_f}\text{sign}(a_{k})e^*_{t_{k}}(\sum_{k\in I_f}a_{k}e_{t_{k}})+\frac{C}{m_i}\sum_{l=1}^d[(1+\frac{1}{\sqrt{m_{j_{0,l}}}})(h_l+g_l)](\sum_{k\in I_{f_l}}a_ke_{t_k})\nonumber\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\min I_f}}}})[\frac{1}{m_i}(\sum_{k\in J_f}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^dh_l+g_l)](\sum_{k\in I_f}a_ke_{t_{k}}).\nonumber \end{align} $$
$$ \begin{align} |f(\sum_{k\in I_f}a_kx_k)|&\le |f(\sum_{k\in \cup_{l=1}^dI_{f_l}}a_kx_k)|+|f(\sum_{k\in J_f}a_kx_k )|\\ &\le\frac{C}{m_i}\sum_{k\in J_f}\text{sign}(a_{k})e^*_{t_{k}}(\sum_{k\in I_f}a_{k}e_{t_{k}})+\frac{C}{m_i}\sum_{l=1}^d[(1+\frac{1}{\sqrt{m_{j_{0,l}}}})(h_l+g_l)](\sum_{k\in I_{f_l}}a_ke_{t_k})\nonumber\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\min I_f}}}})[\frac{1}{m_i}(\sum_{k\in J_f}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^dh_l+g_l)](\sum_{k\in I_f}a_ke_{t_{k}}).\nonumber \end{align} $$
Define
 $$\begin{align*}g=\frac{1}{m_i}(\sum_{k\in J_f}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^dh_l+g_l). \end{align*}$$
$$\begin{align*}g=\frac{1}{m_i}(\sum_{k\in J_f}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^dh_l+g_l). \end{align*}$$
Moreover, for each
![]() $l=1,\ldots ,d$
, define
$l=1,\ldots ,d$
, define
and
Let us make the following remarks. First, observe that
![]() $\#K_l\le 2$
. In particular, consider the case where
$\#K_l\le 2$
. In particular, consider the case where
![]() $K_l=\{k_1,k_2\}$
for some
$K_l=\{k_1,k_2\}$
for some
![]() $l=1,\ldots ,d$
. Then,
$l=1,\ldots ,d$
. Then,
![]() $k_1<\min I_{f_l}\le \max I_{f_l}< k_2$
, and since
$k_1<\min I_{f_l}\le \max I_{f_l}< k_2$
, and since
![]() $\text {supp} (h_l)\cup \text {supp} (g_l)$
is a subset of
$\text {supp} (h_l)\cup \text {supp} (g_l)$
is a subset of
![]() $\{t_k:k\in I_{f_l}\}$
, we have
$\{t_k:k\in I_{f_l}\}$
, we have
![]() $t_{k_1}<\text {supp} (h_l)<\text {supp} (g_l)<t_{k_2}$
. Moreover, if
$t_{k_1}<\text {supp} (h_l)<\text {supp} (g_l)<t_{k_2}$
. Moreover, if
![]() $l<d$
and
$l<d$
and
![]() $\text {range} (f_{l+1})\cap \text {supp} (x_{k_2})\neq \emptyset $
, then
$\text {range} (f_{l+1})\cap \text {supp} (x_{k_2})\neq \emptyset $
, then
![]() $k_2\notin K_{l+1}$
and clearly
$k_2\notin K_{l+1}$
and clearly
![]() $k_2<I_{l+1}$
. In the case where
$k_2<I_{l+1}$
. In the case where
![]() $K_l$
is a singleton for some
$K_l$
is a singleton for some
![]() $l=1,\ldots ,d$
, then either
$l=1,\ldots ,d$
, then either
![]() $\text {supp} (h_l)<\text {supp} (g_l)<k$
or
$\text {supp} (h_l)<\text {supp} (g_l)<k$
or
![]() $k<\text {supp} (h_l)<\text {supp} (g_l)$
holds for
$k<\text {supp} (h_l)<\text {supp} (g_l)$
holds for
![]() $K_l=\{k\}$
. Hence, we conclude that
$K_l=\{k\}$
. Hence, we conclude that
![]() $I_1<\cdots <I_d$
. Moreover, let us finally note that
$I_1<\cdots <I_d$
. Moreover, let us finally note that
![]() $\min \text {supp} (f_l)\le I_l$
and
$\min \text {supp} (f_l)\le I_l$
and
![]() $\#I_l\le 4$
for every
$\#I_l\le 4$
for every
![]() $l=1,\ldots ,d$
. For each
$l=1,\ldots ,d$
. For each
![]() $l=1,\ldots ,d$
, let
$l=1,\ldots ,d$
, let
![]() $K_l=\{k_1^l,k^l_2\}$
, where
$K_l=\{k_1^l,k^l_2\}$
, where
![]() $k^l_2$
or
$k^l_2$
or
![]() $k^l_2$
can be ommited if necessary. Then,
$k^l_2$
can be ommited if necessary. Then,
 $$ \begin{align} g=\frac{1}{m_i}\sum_{l=1}^d(\text{sign}(a_{k^l_1})e^*_{t_{k^l_1}}+h_l+g_l+\text{sign}(a_{k^l_2})e^*_{t_{k^l_2}}). \end{align} $$
$$ \begin{align} g=\frac{1}{m_i}\sum_{l=1}^d(\text{sign}(a_{k^l_1})e^*_{t_{k^l_1}}+h_l+g_l+\text{sign}(a_{k^l_2})e^*_{t_{k^l_2}}). \end{align} $$
We will show that the sequence
![]() $(e^*_{t_k})_{k\in J_f} {}^{\frown } (h_l)_{l=1}^d {}^{\frown } (g_l)_{l=1}^d$
is
$(e^*_{t_k})_{k\in J_f} {}^{\frown } (h_l)_{l=1}^d {}^{\frown } (g_l)_{l=1}^d$
is
![]() $\mathcal {S}_{n_i+1}$
-admissible, when the functionals ordered as implied by (15.4), that is, according to the minimum of their supports. This yields that
$\mathcal {S}_{n_i+1}$
-admissible, when the functionals ordered as implied by (15.4), that is, according to the minimum of their supports. This yields that
![]() $g\in W_{\text {aux}}^{(1)}$
, and thus
$g\in W_{\text {aux}}^{(1)}$
, and thus
![]() $h=0$
, g and
$h=0$
, g and
![]() $j_0=j_{\min I_f}$
satisfy the conclusion, as follows from (15.3). More specifically, we will show that
$j_0=j_{\min I_f}$
satisfy the conclusion, as follows from (15.3). More specifically, we will show that
![]() $\cup _{l=1}^dI_l\in \mathcal {S}_{n_i+1}$
. To this end, note that
$\cup _{l=1}^dI_l\in \mathcal {S}_{n_i+1}$
. To this end, note that
![]() $(I_l)_{l=1}^d$
is
$(I_l)_{l=1}^d$
is
![]() $\mathcal {S}_{n_i}$
-admissible, since
$\mathcal {S}_{n_i}$
-admissible, since
![]() $(f_l)_{l=1}^d$
is
$(f_l)_{l=1}^d$
is
![]() $\mathcal {S}_{n_i}$
-admissible,
$\mathcal {S}_{n_i}$
-admissible,
![]() $I_1<\cdots <I_d$
and
$I_1<\cdots <I_d$
and
![]() $\min \text {supp} (f_l)\le I_l$
for every
$\min \text {supp} (f_l)\le I_l$
for every
![]() $l=1,\ldots ,d$
. Thus,
$l=1,\ldots ,d$
. Thus,
![]() $\cup _{l=1}^dI_l\in \mathcal {S}_{n_i}*\mathcal {A}_4$
, since
$\cup _{l=1}^dI_l\in \mathcal {S}_{n_i}*\mathcal {A}_4$
, since
![]() $\#I_l\le 4$
for all
$\#I_l\le 4$
for all
![]() $l=1,\ldots ,d$
. Using item (ii) of Lemma 2.1 and the fact that
$l=1,\ldots ,d$
. Using item (ii) of Lemma 2.1 and the fact that
![]() $4\le \min \text {supp} (x_{\min I})$
, we conclude that
$4\le \min \text {supp} (x_{\min I})$
, we conclude that
![]() $\cup _{l=1}^dI_l\in \mathcal {S}_{n_i+1}$
.
$\cup _{l=1}^dI_l\in \mathcal {S}_{n_i+1}$
.
Finally, in the remaining case where
![]() $\min \{j_k:k\in I_f\}\le i<\max \{j_k:k\in I_f\}$
, define
$\min \{j_k:k\in I_f\}\le i<\max \{j_k:k\in I_f\}$
, define
![]() $I^1_f=\{k\in I_f:j_k\le i\}$
and
$I^1_f=\{k\in I_f:j_k\le i\}$
and
![]() $I^2_f=\{k\in I_f:j_k>i\}$
, and observe that
$I^2_f=\{k\in I_f:j_k>i\}$
, and observe that
![]() $I_f=I_f^1\cup I^2_f$
,
$I_f=I_f^1\cup I^2_f$
,
![]() $\max \{j_k:k\in I^1_f\}\le i$
and
$\max \{j_k:k\in I^1_f\}\le i$
and
![]() $i<\min \{j_k:k\in I^2_f\}$
. Applying the result of the first case for
$i<\min \{j_k:k\in I^2_f\}$
. Applying the result of the first case for
![]() $(x_k)_{k\in I^1_f}$
and that of the second for
$(x_k)_{k\in I^1_f}$
and that of the second for
![]() $(x_k)_{k\in I^2_f}$
, we have
$(x_k)_{k\in I^2_f}$
, we have
 $$ \begin{align} |f(\sum_{k\in I_f}a_kx_k )|&\le |f(\sum_{k\in I^1_f}a_kx_k )|+|f(\sum_{k\in I^2_f}a_kx_k )|\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\max I^1_f}}}} )h (\sum_{k\in I_f}a_ke_{t_{k}} )+|f (\sum_{k\in I^2_f}a_kx_k )|\nonumber\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\max I^1_f}}}})h(\sum_{k\in I_f}a_ke_{t_{k}} )+ C(1+\frac{1}{\sqrt{m_{j_{\min I^2_f}}}})g(\sum_{k\in I_f}a_ke_{t_k})\nonumber\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\max I^1_f}}}})[h+g(\sum_{k\in I_f}a_ke_{t_{k}} )]\nonumber, \end{align} $$
$$ \begin{align} |f(\sum_{k\in I_f}a_kx_k )|&\le |f(\sum_{k\in I^1_f}a_kx_k )|+|f(\sum_{k\in I^2_f}a_kx_k )|\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\max I^1_f}}}} )h (\sum_{k\in I_f}a_ke_{t_{k}} )+|f (\sum_{k\in I^2_f}a_kx_k )|\nonumber\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\max I^1_f}}}})h(\sum_{k\in I_f}a_ke_{t_{k}} )+ C(1+\frac{1}{\sqrt{m_{j_{\min I^2_f}}}})g(\sum_{k\in I_f}a_ke_{t_k})\nonumber\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\max I^1_f}}}})[h+g(\sum_{k\in I_f}a_ke_{t_{k}} )]\nonumber, \end{align} $$
where
![]() $h=\text {sign}(a_{k_1})e^*_{t_{k_1}}$
,
$h=\text {sign}(a_{k_1})e^*_{t_{k_1}}$
,
![]() $k_1\in I^1_f$
maximises the quantity
$k_1\in I^1_f$
maximises the quantity
![]() $|a_k|$
for
$|a_k|$
for
![]() $k\in I^1_f$
and
$k\in I^1_f$
and
![]() $g\in W_{\text {aux}}^{(1)}$
with
$g\in W_{\text {aux}}^{(1)}$
with
![]() $w(g)=w(f)$
.
$w(g)=w(f)$
.
Remark 15.4. Let
![]() $(x_k)_{k\in I}$
and f be as in the statement of Proposition 15.3.
$(x_k)_{k\in I}$
and f be as in the statement of Proposition 15.3.
-
(i) Define
 $E=\text {range} (f)$
, and note that the sequence
$E=\text {range} (f)$
, and note that the sequence
 $(x^{\prime }_k)_{k\in I^{\prime }_f}$
, where
$(x^{\prime }_k)_{k\in I^{\prime }_f}$
, where
 $x^{\prime }_k=x_k|_E$
,
$x^{\prime }_k=x_k|_E$
,
 $k\in I^{\prime }_f$
, is also a
$k\in I^{\prime }_f$
, is also a
 $(C,(j_k)_{k\in I^{\prime }_f})$
-RIS. Then,and
$(C,(j_k)_{k\in I^{\prime }_f})$
-RIS. Then,and $$\begin{align*}f(\sum_{k\in I}a_kx_k )=f(\sum_{k\in I^{\prime}_f}a_kx^{\prime}_k) \end{align*}$$
$$\begin{align*}f(\sum_{k\in I}a_kx_k )=f(\sum_{k\in I^{\prime}_f}a_kx^{\prime}_k) \end{align*}$$
 $\{k\in I^{\prime }_f:\text {supp} (x^{\prime }_k)\subset \text {range} (f)\}=I^{\prime }_f$
. Hence, the basic inequality yields
$\{k\in I^{\prime }_f:\text {supp} (x^{\prime }_k)\subset \text {range} (f)\}=I^{\prime }_f$
. Hence, the basic inequality yields
 $h,g$
and
$h,g$
and
 $j_0$
as in items (i)–(iii), such thatwhere
$j_0$
as in items (i)–(iii), such thatwhere $$\begin{align*}|f(\sum_{k\in I}a_kx_k)|\le C(1+\frac{1}{\sqrt{m_{j_{0}}}})[h+g(\sum_{k\in I^{\prime}_f}a_ke_{z_k} )], \end{align*}$$
$$\begin{align*}|f(\sum_{k\in I}a_kx_k)|\le C(1+\frac{1}{\sqrt{m_{j_{0}}}})[h+g(\sum_{k\in I^{\prime}_f}a_ke_{z_k} )], \end{align*}$$
 $z_k=\max \text {supp} (x^{\prime }_k)$
,
$z_k=\max \text {supp} (x^{\prime }_k)$
,
 $k\in I^{\prime }_f$
.
$k\in I^{\prime }_f$
.
-
(ii) Let
 $j\in \mathbb {N}$
. It follows from the proof of Proposition 15.3 that if f has a tree analysis
$j\in \mathbb {N}$
. It follows from the proof of Proposition 15.3 that if f has a tree analysis
 $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
 $I_{f_{\alpha }}=\emptyset $
for every
$I_{f_{\alpha }}=\emptyset $
for every
 $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
 $w(f_{\alpha })=m_j$
, then the functional
$w(f_{\alpha })=m_j$
, then the functional
 $g\in W_{\text {aux}}^{(1)}\cup \{0\}$
that the basic inequality yields for
$g\in W_{\text {aux}}^{(1)}\cup \{0\}$
that the basic inequality yields for
 $(x_k)_{k\in I}$
and f has a tree analysis
$(x_k)_{k\in I}$
and f has a tree analysis
 $(g_{\beta })_{\beta \in \mathcal {B}}$
with
$(g_{\beta })_{\beta \in \mathcal {B}}$
with
 $w(g_{\beta })\neq m_j$
for every
$w(g_{\beta })\neq m_j$
for every
 $\beta \in \mathcal {B}$
, whenever
$\beta \in \mathcal {B}$
, whenever
 $g\neq 0$
.
$g\neq 0$
.
15.3 Evaluations on standard exact pairs
We prove the following lemma, which yields Proposition 8.11 as an immediate corollary.
Lemma 15.5. For every
![]() $(C,m_{j_0})$
-SEP
$(C,m_{j_0})$
-SEP
![]() $(x,f)$
, the following hold.
$(x,f)$
, the following hold.
-
(i) For every
 $f'\in W_{(1)}$
$f'\in W_{(1)}$
 $$\begin{align*}\big|f'(x)\big|\le \begin{cases} \frac{C}{m_{j_0}}(1+\frac{1}{\sqrt{m_{j_0}}}),\quad\quad & f'=\pm e_i^*\text{ for some }i\in\mathbb{N}\\ C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(f')}],\quad\quad & w(f')\ge m_{j_0} \\ C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{2}{w(f')}],\quad\quad & w(f')<m_{j_0}. \end{cases} \end{align*}$$
$$\begin{align*}\big|f'(x)\big|\le \begin{cases} \frac{C}{m_{j_0}}(1+\frac{1}{\sqrt{m_{j_0}}}),\quad\quad & f'=\pm e_i^*\text{ for some }i\in\mathbb{N}\\ C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(f')}],\quad\quad & w(f')\ge m_{j_0} \\ C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{2}{w(f')}],\quad\quad & w(f')<m_{j_0}. \end{cases} \end{align*}$$
-
(ii) If
 $f'\in W_{(1)}$
with a tree analysis
$f'\in W_{(1)}$
with a tree analysis
 $(f^{\prime }_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(f^{\prime }_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
 $I_{f^{\prime }_{\alpha }}=\emptyset $
for every
$I_{f^{\prime }_{\alpha }}=\emptyset $
for every
 $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
 $w(f^{\prime }_{\alpha })= m_{j_0}$
, then
$w(f^{\prime }_{\alpha })= m_{j_0}$
, then $$\begin{align*}|f'(x)|\le\frac{3C}{m_{j_0}}(1+\frac{1}{\sqrt{m_{j_0}}}).\end{align*}$$
$$\begin{align*}|f'(x)|\le\frac{3C}{m_{j_0}}(1+\frac{1}{\sqrt{m_{j_0}}}).\end{align*}$$
Proof. Let
![]() $(x_k)_{k=1}^n$
be a
$(x_k)_{k=1}^n$
be a
![]() $(C,(j_k)_{k=1}^n)$
-RIS witnessing that
$(C,(j_k)_{k=1}^n)$
-RIS witnessing that
![]() $(x,f)$
is a
$(x,f)$
is a
![]() $(C,m_{j_0})$
-SEP. Applying Proposition 15.3, we obtain h and g as in items (i) and (ii), respectively, that satisfy (15.1) for x and
$(C,m_{j_0})$
-SEP. Applying Proposition 15.3, we obtain h and g as in items (i) and (ii), respectively, that satisfy (15.1) for x and
![]() $f'$
, namely,
$f'$
, namely,
 $$\begin{align*}|f'(x)|\le Cm_{j_0}(1+\frac{1}{\sqrt{m_{j_0}}})[h(\tilde{x})+g(\tilde{x})], \end{align*}$$
$$\begin{align*}|f'(x)|\le Cm_{j_0}(1+\frac{1}{\sqrt{m_{j_0}}})[h(\tilde{x})+g(\tilde{x})], \end{align*}$$
where
![]() $\tilde {x}=\sum _{k\in I}a_ke_{z_k}$
,
$\tilde {x}=\sum _{k\in I}a_ke_{z_k}$
,
![]() $z_k=\max \text {supp} (x_k|_{\text {range} (f')})$
and
$z_k=\max \text {supp} (x_k|_{\text {range} (f')})$
and
![]() $I=\{k=1,\ldots ,n:\text {supp} (x_k)\cap \text {range} (f')\neq \emptyset \}$
. Note that
$I=\{k=1,\ldots ,n:\text {supp} (x_k)\cap \text {range} (f')\neq \emptyset \}$
. Note that
![]() $\tilde {x}$
is a
$\tilde {x}$
is a
![]() $(n_{j_0},m^{-2}_{j_0})$
-b.s.c.c. and, hence, since
$(n_{j_0},m^{-2}_{j_0})$
-b.s.c.c. and, hence, since
![]() $\text {supp} (h)\in \mathcal {S}_0$
, we have
$\text {supp} (h)\in \mathcal {S}_0$
, we have
![]() $h(\tilde {x})<m_{j_0}^{-2}$
.
$h(\tilde {x})<m_{j_0}^{-2}$
.
To prove (i), first observe that if
![]() $g=0$
, which is the case, for example, when
$g=0$
, which is the case, for example, when
![]() $f'=\pm e^*_i$
for some
$f'=\pm e^*_i$
for some
![]() $i\in \mathbb {N}$
, then we already have established a valid upper bound for
$i\in \mathbb {N}$
, then we already have established a valid upper bound for
![]() $|f'(x)|$
. Hence, suppose that
$|f'(x)|$
. Hence, suppose that
![]() $g\neq 0$
. Then, using Lemma 15.2 and the fact that
$g\neq 0$
. Then, using Lemma 15.2 and the fact that
![]() $w(g)=w(f')$
, we obtain the following upper bounds for
$w(g)=w(f')$
, we obtain the following upper bounds for
![]() $g(\tilde {x})$
$g(\tilde {x})$
 $$\begin{align*}g(\tilde{x})\le \begin{cases} \frac{1}{w(f')},\quad\quad & w(f')\ge m_{j_0}\\ \frac{2}{w(f')m_{j_0}},\quad\quad & w(f')<m_{j_0}, \end{cases} \end{align*}$$
$$\begin{align*}g(\tilde{x})\le \begin{cases} \frac{1}{w(f')},\quad\quad & w(f')\ge m_{j_0}\\ \frac{2}{w(f')m_{j_0}},\quad\quad & w(f')<m_{j_0}, \end{cases} \end{align*}$$
which yield the desired upper bounds for
![]() $|f'(x)|$
.
$|f'(x)|$
.
Finally, item (ii) of Remark 15.4 implies that g admits a tree analysis
![]() $(g_{\beta })_{\beta \in \mathcal {B}}$
, such that
$(g_{\beta })_{\beta \in \mathcal {B}}$
, such that
![]() $w(g_{\beta })\neq m_{j_0}$
for every
$w(g_{\beta })\neq m_{j_0}$
for every
![]() $\beta \in \mathcal {B}$
. We derive the desired upper bound using item (ii) of Lemma 15.2, which yields that
$\beta \in \mathcal {B}$
. We derive the desired upper bound using item (ii) of Lemma 15.2, which yields that
![]() $|g(\tilde {x})|\le 2m^{-2}_{j_0}$
.
$|g(\tilde {x})|\le 2m^{-2}_{j_0}$
.
16 Appendix B
We prove another version of the basic inequality that reduces evaluations on standard exact pairs of
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
to evaluations on the basis of an auxiliary space. The results are almost identical to those of Appendix A, and we include them for completeness.
$\mathfrak {X}^{(2)}_{\text {awi}}$
to evaluations on the basis of an auxiliary space. The results are almost identical to those of Appendix A, and we include them for completeness.
16.1 The auxiliary space
Definition 16.1. Let
![]() $W_{\text {aux}}^{(2)}$
be the minimal subset of
$W_{\text {aux}}^{(2)}$
be the minimal subset of
![]() $c_{00}(\mathbb {N})$
, such that
$c_{00}(\mathbb {N})$
, such that
-
(i)
 $\pm e^*_i$
is in
$\pm e^*_i$
is in
 $W_{\text {aux}}^{(2)}$
for all
$W_{\text {aux}}^{(2)}$
for all
 $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and -
(ii) whenever
 $j\in \mathbb {N}$
,
$j\in \mathbb {N}$
,
 $(f_i)_{i=1}^d$
is an
$(f_i)_{i=1}^d$
is an
 $\mathcal {S}_{n_j+1}$
-admissible sequence in
$\mathcal {S}_{n_j+1}$
-admissible sequence in
 $W_{\text {aux}}^{(2)}$
and
$W_{\text {aux}}^{(2)}$
and
 $\lambda _1,\ldots ,\lambda _d\in \mathbb {Q}$
with
$\lambda _1,\ldots ,\lambda _d\in \mathbb {Q}$
with
 $\sum _{i=1}^d\lambda _i^2\le 1$
, then
$\sum _{i=1}^d\lambda _i^2\le 1$
, then
 $f=2m_{j}^{-1}\sum _{i=1}^d\lambda _if_i$
is in
$f=2m_{j}^{-1}\sum _{i=1}^d\lambda _if_i$
is in
 $W_{\text {aux}}^{(2)}$
.
$W_{\text {aux}}^{(2)}$
.
Remark 16.2. For each
![]() $f\in W_{\text {aux}}^{(2)}$
, the weight of f is defined as
$f\in W_{\text {aux}}^{(2)}$
, the weight of f is defined as
![]() $w(f)=0$
if
$w(f)=0$
if
![]() $f=\pm e^*_i$
for some
$f=\pm e^*_i$
for some
![]() $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and
![]() $w(f)=m_j/2$
in the case where
$w(f)=m_j/2$
in the case where
![]() $f=2m_j^{-1}\sum _{i=1}^d\lambda _if_i$
.
$f=2m_j^{-1}\sum _{i=1}^d\lambda _if_i$
.
The following lemma is a slightly modified version of [Reference Argyros and Tolias13, Lemma 3.16]. We use it to prove Lemma 16.4.
Lemma 16.3. Let
![]() $f\in W_{\text {aux}}^{(2)}$
with a tree analysis
$f\in W_{\text {aux}}^{(2)}$
with a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
.
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
.
-
(i) For all
 $j\in \mathbb {N}$
, we have
$j\in \mathbb {N}$
, we have $$\begin{align*}\{k\in\text{supp}(f):w_f(e^*_k)<m_{j}\}\in\mathcal{S}_{(\log_2(m_j)-1)(n_{j-1}+1)}.\end{align*}$$
$$\begin{align*}\{k\in\text{supp}(f):w_f(e^*_k)<m_{j}\}\in\mathcal{S}_{(\log_2(m_j)-1)(n_{j-1}+1)}.\end{align*}$$
-
(ii) If
 $j\in \mathbb {N}$
is such that
$j\in \mathbb {N}$
is such that
 $w(f_{\alpha })\neq m_j$
for each
$w(f_{\alpha })\neq m_j$
for each
 $\alpha \in \mathcal {A}$
, then
$\alpha \in \mathcal {A}$
, then $$\begin{align*}\{k\in\text{supp}(f):w_f(e^*_k)<m_{j}^{2}\}\in\mathcal{S}_{(2\log_2(m_j)-1)(n_{j-1}+1)}.\end{align*}$$
$$\begin{align*}\{k\in\text{supp}(f):w_f(e^*_k)<m_{j}^{2}\}\in\mathcal{S}_{(2\log_2(m_j)-1)(n_{j-1}+1)}.\end{align*}$$
Proof. The proof is similar to [Reference Argyros and Tolias13, Lemma 3.16 ].
Next, we prove a lemma similar to 15.2, for the evaluations of functionals in
![]() $W^{(2)}_{\text {aux}}$
on the
$W^{(2)}_{\text {aux}}$
on the
![]() $\ell _2$
version of basic special convex combinations.
$\ell _2$
version of basic special convex combinations.
Lemma 16.4. Let
![]() $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and
![]() $\varepsilon>0$
with
$\varepsilon>0$
with
![]() $\varepsilon \le m_{j}^{-2}$
. For every
$\varepsilon \le m_{j}^{-2}$
. For every
![]() $(2,n_{j},\varepsilon )$
-basic s.c.c.
$(2,n_{j},\varepsilon )$
-basic s.c.c.
![]() $x=\sum _{k\in F}c_ke_k$
, the following hold.
$x=\sum _{k\in F}c_ke_k$
, the following hold.
-
(i) For every
 $f\in W_{\text {aux}}^{(2)}$
$f\in W_{\text {aux}}^{(2)}$
 $$\begin{align*}\big|f(x)\big|\le \begin{cases} \frac{1}{w(f)},\quad\quad & w(f)\ge m_{j}/2\\ \frac{2}{w(f)m_{j}},\quad\quad & w(f)<m_{j}/2. \end{cases} \end{align*}$$
$$\begin{align*}\big|f(x)\big|\le \begin{cases} \frac{1}{w(f)},\quad\quad & w(f)\ge m_{j}/2\\ \frac{2}{w(f)m_{j}},\quad\quad & w(f)<m_{j}/2. \end{cases} \end{align*}$$
-
(ii) If
 $f\in W^{(2)}_{\text {aux}}$
with a tree analysis
$f\in W^{(2)}_{\text {aux}}$
with a tree analysis
 $(f_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
 $w(f_{\alpha })\neq m_{j}$
for all
$w(f_{\alpha })\neq m_{j}$
for all
 $\alpha \in \mathcal {A}$
and
$\alpha \in \mathcal {A}$
and
 $\varepsilon <m_j^{-4}$
, then
$\varepsilon <m_j^{-4}$
, then
 $|f(x)|<2m_j^{-2}$
.
$|f(x)|<2m_j^{-2}$
.
Proof. Without loss of generality, we may assume that
![]() $\text {supp}(f)\subset F$
and
$\text {supp}(f)\subset F$
and
![]() $f(e_k)\ge 0$
for every
$f(e_k)\ge 0$
for every
![]() $k\in F$
. If
$k\in F$
. If
![]() $m_{j}/2\le w(f)$
, then
$m_{j}/2\le w(f)$
, then
![]() $\|f\|_{2}\le 1/w(f)$
, and, hence
$\|f\|_{2}\le 1/w(f)$
, and, hence
Suppose now that
![]() $m_i<m_{j}$
, and let
$m_i<m_{j}$
, and let
![]() $f=2m^{-1}_{i}\sum _{l=1}^d\lambda _l f_l$
, where
$f=2m^{-1}_{i}\sum _{l=1}^d\lambda _l f_l$
, where
![]() $(f_l)_{l=1}^d$
is an
$(f_l)_{l=1}^d$
is an
![]() $\mathcal {S}_{n_i+1}$
-admissible sequence in
$\mathcal {S}_{n_i+1}$
-admissible sequence in
![]() $W^{(2)}_{\text {aux}}$
. For
$W^{(2)}_{\text {aux}}$
. For
![]() $l=1,\ldots ,d$
, define
$l=1,\ldots ,d$
, define
Then, Lemma 16.3 (i) implies that
![]() $D_l\in \mathcal {S}_{(2\log _2(m_{j})-1)(n_{j-1}+1)}$
for each
$D_l\in \mathcal {S}_{(2\log _2(m_{j})-1)(n_{j-1}+1)}$
for each
![]() $l=1,\ldots ,d$
, and, hence, since
$l=1,\ldots ,d$
, and, hence, since
![]() $(f_l)_{l=1}^d$
is
$(f_l)_{l=1}^d$
is
![]() $S_{n_{j-1}+1}$
-admissible (recall that
$S_{n_{j-1}+1}$
-admissible (recall that
![]() $i<j$
since
$i<j$
since
![]() $m_i<m_j$
) and
$m_i<m_j$
) and
![]() $D_l\subset \text {supp} (f_l)$
,
$D_l\subset \text {supp} (f_l)$
,
![]() $l=1,\ldots ,d$
, we have
$l=1,\ldots ,d$
, we have
Therefore, since x is an
![]() $(2,n_j,\varepsilon )$
-basic s.c.c. and
$(2,n_j,\varepsilon )$
-basic s.c.c. and
![]() $2\log _2(m_{j})(n_{j-1}+1)<n_j$
, we have
$2\log _2(m_{j})(n_{j-1}+1)<n_j$
, we have
![]() $\sum _{k\in D}c^2_k<\varepsilon $
. Moreover, observe that for
$\sum _{k\in D}c^2_k<\varepsilon $
. Moreover, observe that for
![]() $l=1,\ldots ,d $
and
$l=1,\ldots ,d $
and
![]() $k\in F_l$
$k\in F_l$
 $$\begin{align*}f_l(e_k)= \frac{\lambda_{f_l,\alpha_k}}{w_{f_l}(e^*_k)}\le\frac{\lambda_{f_l,\alpha_k}}{m_j}, \end{align*}$$
$$\begin{align*}f_l(e_k)= \frac{\lambda_{f_l,\alpha_k}}{w_{f_l}(e^*_k)}\le\frac{\lambda_{f_l,\alpha_k}}{m_j}, \end{align*}$$
where
![]() $a_k$
is the node in the induced tree analysis of
$a_k$
is the node in the induced tree analysis of
![]() $f_l$
with
$f_l$
with
![]() $f_{l,\alpha _k}=e^*_k$
, and
$f_{l,\alpha _k}=e^*_k$
, and
 $$\begin{align*}\sum_{l=1}^d\lambda_l^2\sum_{k\in F_l}\lambda_{f_l,\alpha_k}^2\le1. \end{align*}$$
$$\begin{align*}\sum_{l=1}^d\lambda_l^2\sum_{k\in F_l}\lambda_{f_l,\alpha_k}^2\le1. \end{align*}$$
We then calculate, using the Cauchy-Schwarz inequality
 $$ \begin{align*} f(x)&=\frac{{2}}{m_i}(\sum_{l=1}^d\lambda_lf_l|_D(\sum_{k\in F}c_ke_k )+\sum_{l=1}^d \lambda_lf_l|_{\mathbb{N}\setminus D}(\sum_{k\in F}c_ke_k))\\ &=\frac{{2}}{m_i}(\sum_{l=1}^d\lambda_l\sum_{k\in D_l}\frac{c_k\lambda_{f_l,\alpha_k}}{w_{f_l}(e^*_k)}+\sum_{l=1}^d\lambda_l\sum_{k\in F_l}\frac{c_k\lambda_{f_l,\alpha_k}}{w_{f_l}(e^*_k)})\\ &\le\frac{{2}}{m_i}(\sum_{l=1}^d\lambda_l\sum_{k\in D_l}c_k\lambda_{f_l,\alpha_k}+\frac{1}{m_j}\sum_{l=1}^d\lambda_l\sum_{k\in F_l}c_k\lambda_{f_l,\alpha_k})\\ &\le \frac{2}{m_i}(\sum_{l=1}^d \lambda_l (\sum_{k\in D_l}c_k^2 )^{\frac{1}{2}} (\sum_{k\in D_l}\lambda_{f_l,\alpha_k}^2 )^{\frac{1}{2}}+\frac{1}{m_{j}}\sum_{l=1}^d\lambda_l(\sum_{k\in F_l}c_k^2)^{\frac{1}{2}}(\sum_{k\in F_l}\lambda_{f_l,\alpha_k}^2)^{\frac{1}{2}}) \\ &\le \frac{{2}}{m_i}((\sum_{l=1}^d\lambda^2_l)^{\frac{1}{2}}(\sum_{k\in D}c_k^2)^{\frac{1}{2}}+\frac{1}{m_j}(\sum_{l=1}^d\sum_{k\in F_l}c_k^2)^{\frac{1}{2}}(\sum_{l=1}^d\lambda^2_l\sum_{k\in F_l}\lambda_{f_l,\alpha_k}^2)^{\frac{1}{2}})\\ &\le \frac{{2}}{m_i}(\sqrt{\varepsilon}+\frac{1}{m_j})\le \frac{4}{m_im_j}. \end{align*} $$
$$ \begin{align*} f(x)&=\frac{{2}}{m_i}(\sum_{l=1}^d\lambda_lf_l|_D(\sum_{k\in F}c_ke_k )+\sum_{l=1}^d \lambda_lf_l|_{\mathbb{N}\setminus D}(\sum_{k\in F}c_ke_k))\\ &=\frac{{2}}{m_i}(\sum_{l=1}^d\lambda_l\sum_{k\in D_l}\frac{c_k\lambda_{f_l,\alpha_k}}{w_{f_l}(e^*_k)}+\sum_{l=1}^d\lambda_l\sum_{k\in F_l}\frac{c_k\lambda_{f_l,\alpha_k}}{w_{f_l}(e^*_k)})\\ &\le\frac{{2}}{m_i}(\sum_{l=1}^d\lambda_l\sum_{k\in D_l}c_k\lambda_{f_l,\alpha_k}+\frac{1}{m_j}\sum_{l=1}^d\lambda_l\sum_{k\in F_l}c_k\lambda_{f_l,\alpha_k})\\ &\le \frac{2}{m_i}(\sum_{l=1}^d \lambda_l (\sum_{k\in D_l}c_k^2 )^{\frac{1}{2}} (\sum_{k\in D_l}\lambda_{f_l,\alpha_k}^2 )^{\frac{1}{2}}+\frac{1}{m_{j}}\sum_{l=1}^d\lambda_l(\sum_{k\in F_l}c_k^2)^{\frac{1}{2}}(\sum_{k\in F_l}\lambda_{f_l,\alpha_k}^2)^{\frac{1}{2}}) \\ &\le \frac{{2}}{m_i}((\sum_{l=1}^d\lambda^2_l)^{\frac{1}{2}}(\sum_{k\in D}c_k^2)^{\frac{1}{2}}+\frac{1}{m_j}(\sum_{l=1}^d\sum_{k\in F_l}c_k^2)^{\frac{1}{2}}(\sum_{l=1}^d\lambda^2_l\sum_{k\in F_l}\lambda_{f_l,\alpha_k}^2)^{\frac{1}{2}})\\ &\le \frac{{2}}{m_i}(\sqrt{\varepsilon}+\frac{1}{m_j})\le \frac{4}{m_im_j}. \end{align*} $$
Finally, if there is a tree analysis
![]() $(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, such that
$(f_{\alpha })_{\alpha \in \mathcal {A}}$
of f, such that
![]() $w(f_{\alpha })\neq m_j$
for every
$w(f_{\alpha })\neq m_j$
for every
![]() $\alpha \in \mathcal {A}$
, Lemma 16.3 (ii) implies that
$\alpha \in \mathcal {A}$
, Lemma 16.3 (ii) implies that
and since
![]() $(2\log _2(m_j)-1)(n_{j-1}-1)<n_j$
, we have that
$(2\log _2(m_j)-1)(n_{j-1}-1)<n_j$
, we have that
![]() $\sum _{k\in D}c^2_k<\varepsilon $
. Hence, using similar arguments as above, we conclude that
$\sum _{k\in D}c^2_k<\varepsilon $
. Hence, using similar arguments as above, we conclude that
 $$\begin{align*}f(x)\le \sqrt{\varepsilon} + \frac{1}{m^2_j}<\frac{2}{m_j^2}. \end{align*}$$
$$\begin{align*}f(x)\le \sqrt{\varepsilon} + \frac{1}{m^2_j}<\frac{2}{m_j^2}. \end{align*}$$
16.2 The basic inequality
Proposition 16.5 (basic inequality).
Let
![]() $(x_k)_{k\in I}$
be a
$(x_k)_{k\in I}$
be a
![]() $(C,(j_k)_{k\in I})$
-RIS in
$(C,(j_k)_{k\in I})$
-RIS in
![]() $\mathfrak {X}^{(2)}_{\text {awi}}$
with
$\mathfrak {X}^{(2)}_{\text {awi}}$
with
![]() $4\le \min \text {supp} (x_{\min I})$
,
$4\le \min \text {supp} (x_{\min I})$
,
![]() $(a_k)_{k\in I}$
be a sequence of nonzero scalars and
$(a_k)_{k\in I}$
be a sequence of nonzero scalars and
![]() $f\in W_{(2)}$
with
$f\in W_{(2)}$
with
![]() $I_f\neq \emptyset $
. Define
$I_f\neq \emptyset $
. Define
![]() $t_k=\max \text {supp} (x_k)$
,
$t_k=\max \text {supp} (x_k)$
,
![]() $k\in I$
. Then there exist
$k\in I$
. Then there exist
-
(i)
 $g\in W_{\text {aux}}^{(2)}\cup \{0\}$
with
$g\in W_{\text {aux}}^{(2)}\cup \{0\}$
with
 $w(g)=w(f)/2$
if
$w(g)=w(f)/2$
if
 $g\neq 0$
and
$g\neq 0$
and
 $\{k:t_k\in \text {supp} (g)\}\subset I_f$
,
$\{k:t_k\in \text {supp} (g)\}\subset I_f$
, -
(ii)
 $h\in \{\text {sign}(a_k) e^*_{t_k}:k\in I_f\}\cup \{0\}$
with
$h\in \{\text {sign}(a_k) e^*_{t_k}:k\in I_f\}\cup \{0\}$
with
 $k_0\in I_f$
and
$k_0\in I_f$
and
 $k_0 < \min \text {supp}(g)$
if
$k_0 < \min \text {supp}(g)$
if
 $h=\text {sign}(a_{k_0})e^*_{t_{k_0}}$
and
$h=\text {sign}(a_{k_0})e^*_{t_{k_0}}$
and -
(iii)
 $j_0\ge \min \{j_k:k\in I_f\},$
$j_0\ge \min \{j_k:k\in I_f\},$
such that
 $$ \begin{align*} |f(\sum_{k\in I_f}a_kx_k)|\le C(1+\frac{1}{\sqrt{m_{j_{0}}}})[h+g(\sum_{k\in I_f}a_ke_{t_k})]. \end{align*} $$
$$ \begin{align*} |f(\sum_{k\in I_f}a_kx_k)|\le C(1+\frac{1}{\sqrt{m_{j_{0}}}})[h+g(\sum_{k\in I_f}a_ke_{t_k})]. \end{align*} $$
Proof. As in Proposition 15.3, we prove the statement by induction on
![]() $n=0,1,\ldots $
for every
$n=0,1,\ldots $
for every
![]() $f\in W^n_{(2)}$
and every RIS. The case of
$f\in W^n_{(2)}$
and every RIS. The case of
![]() $n=0$
follows easily.
$n=0$
follows easily.
Fix
![]() $n\in \mathbb {N}$
, and assume that the conclusion holds for every
$n\in \mathbb {N}$
, and assume that the conclusion holds for every
![]() $f\in W^n_{(2)}$
and every RIS. Pick an
$f\in W^n_{(2)}$
and every RIS. Pick an
![]() $f\in W^{n+1}_{(2)}$
with
$f\in W^{n+1}_{(2)}$
with
![]() $f={m_i}^{-1}\sum _{l=1}^d\lambda _lf_l$
, where
$f={m_i}^{-1}\sum _{l=1}^d\lambda _lf_l$
, where
![]() $(f_l)_{l=1}^d$
is an
$(f_l)_{l=1}^d$
is an
![]() $\mathcal {S}_{n_i}$
-admissible AWI sequence in
$\mathcal {S}_{n_i}$
-admissible AWI sequence in
![]() $W^n_{(2)}$
and
$W^n_{(2)}$
and
![]() $\lambda _1,\ldots ,\lambda _d\in \mathbb {Q}$
with
$\lambda _1,\ldots ,\lambda _d\in \mathbb {Q}$
with
![]() $\sum _{l=1}^d\lambda _l^2\le 1$
. The proof of the case where
$\sum _{l=1}^d\lambda _l^2\le 1$
. The proof of the case where
![]() $i\ge \max \{j_k:k\in I_f\}$
is identical to that of Proposition 15.3.
$i\ge \max \{j_k:k\in I_f\}$
is identical to that of Proposition 15.3.
Suppose then that
![]() $i< \min \{j_k:k\in I_f\}$
. The inductive hypothesis implies that, for every
$i< \min \{j_k:k\in I_f\}$
. The inductive hypothesis implies that, for every
![]() $l=1,\ldots ,d$
with
$l=1,\ldots ,d$
with
![]() $I_{f_l}\neq \emptyset $
, there are
$I_{f_l}\neq \emptyset $
, there are
![]() $g_l$
,
$g_l$
,
![]() $h_l$
and
$h_l$
and
![]() $j_{0,l}$
as in (i)–(iii) of the statement, that satisfy the conclusion for the functional
$j_{0,l}$
as in (i)–(iii) of the statement, that satisfy the conclusion for the functional
![]() $f_l$
. Define
$f_l$
. Define
![]() $J_f=\{k\in I_f: f(x_k)\neq 0\}\setminus \cup _{l=1}^dI_{f_l}$
. For every
$J_f=\{k\in I_f: f(x_k)\neq 0\}\setminus \cup _{l=1}^dI_{f_l}$
. For every
![]() $k\in J_f$
, since
$k\in J_f$
, since
![]() $i<j_k$
, Definition 8.5 (iii) yields that
$i<j_k$
, Definition 8.5 (iii) yields that
 $$ \begin{align*} |f(a_{k}x_{k})|\le (\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\frac{C}{m_i}|a_{k}|=(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\frac{C}{m_i}\text{sign}(a_{k})e^*_{t_{k}}(\sum_{k\in I_f}a_{k}e_{t_{k}}), \end{align*} $$
$$ \begin{align*} |f(a_{k}x_{k})|\le (\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\frac{C}{m_i}|a_{k}|=(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\frac{C}{m_i}\text{sign}(a_{k})e^*_{t_{k}}(\sum_{k\in I_f}a_{k}e_{t_{k}}), \end{align*} $$
where
Hence, we calculate
 $$ \begin{align*} &|f(\sum_{k\in I_f}a_kx_k)|\le|f(\sum_{k\in J_f}a_kx_k)|+ |f(\sum_{k\in \cup_{l=1}^dI_{f_l}}a_kx_k)|\\ &\le\frac{C}{m_i}\sum_{k\in J_f}(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\text{sign}(a_{k})e^*_{t_{k}}(\sum_{k\in I_f}a_{k}e_{t_{k}})+\frac{C}{m_i}\sum_{l=1}^d[(1+\frac{1}{\sqrt{m_{j_{0,l}}}})\lambda_l(h_l+g_l)](\sum_{k\in I_{f_l}}a_ke_{t_k})\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\min I_f}}}})[\frac{1}{m_i}(\sum_{k\in J_f}(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^d\lambda_lh_l+\lambda_lg_l)](\sum_{k\in I_f}a_ke_{t_{k}}). \end{align*} $$
$$ \begin{align*} &|f(\sum_{k\in I_f}a_kx_k)|\le|f(\sum_{k\in J_f}a_kx_k)|+ |f(\sum_{k\in \cup_{l=1}^dI_{f_l}}a_kx_k)|\\ &\le\frac{C}{m_i}\sum_{k\in J_f}(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\text{sign}(a_{k})e^*_{t_{k}}(\sum_{k\in I_f}a_{k}e_{t_{k}})+\frac{C}{m_i}\sum_{l=1}^d[(1+\frac{1}{\sqrt{m_{j_{0,l}}}})\lambda_l(h_l+g_l)](\sum_{k\in I_{f_l}}a_ke_{t_k})\\ &\le C(1+\frac{1}{\sqrt{m_{j_{\min I_f}}}})[\frac{1}{m_i}(\sum_{k\in J_f}(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^d\lambda_lh_l+\lambda_lg_l)](\sum_{k\in I_f}a_ke_{t_{k}}). \end{align*} $$
Define
 $$\begin{align*}g=\frac{2}{m_i}(\sum_{k\in J_f}\frac{1}{2}(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^d\frac{\lambda_l}{2}h_l+\frac{\lambda_l}{2}g_l). \end{align*}$$
$$\begin{align*}g=\frac{2}{m_i}(\sum_{k\in J_f}\frac{1}{2}(\sum_{l\in L_k}\lambda_l^2)^{\frac{1}{2}}\text{sign}(a_{k})e^*_{t_{k}}+\sum_{l=1}^d\frac{\lambda_l}{2}h_l+\frac{\lambda_l}{2}g_l). \end{align*}$$
Then, observe that each
![]() $l=1,\ldots ,d$
, belongs to
$l=1,\ldots ,d$
, belongs to
![]() $L_k$
for at most two
$L_k$
for at most two
![]() $k\in J_f$
, and thus, using the same arguments as in Proposition 15.3, we have that
$k\in J_f$
, and thus, using the same arguments as in Proposition 15.3, we have that
![]() $g\in W_{\text {aux}}^{(2)}$
, and this completes the proof for cases where
$g\in W_{\text {aux}}^{(2)}$
, and this completes the proof for cases where
![]() $i<j_k$
for all
$i<j_k$
for all
![]() $k\in I_f$
.
$k\in I_f$
.
Finally, the proof of the remaining case is the same as in Proposition 15.3.
16.3 Evaluations on standard exact pairs
Finally, we prove the following lemma which shows that standard exact pairs are in fact strong exact pairs.
Lemma 16.6. For every
![]() $(2,C,m_{j_0})$
-SEP
$(2,C,m_{j_0})$
-SEP
![]() $(x,f)$
, the following hold.
$(x,f)$
, the following hold.
-
(i) For every
 $g\in W$
$g\in W$
 $$\begin{align*}\big|g(x)\big|\le \begin{cases} 2C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(g)}],\quad\quad & w(g)\ge m_{j_0} \\ 2C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{2}{w(g)}],\quad\quad & w(g)<m_{j_0}. \end{cases} \end{align*}$$
$$\begin{align*}\big|g(x)\big|\le \begin{cases} 2C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{m_{j_0}}{w(g)}],\quad\quad & w(g)\ge m_{j_0} \\ 2C(1+\frac{1}{\sqrt{m_{j_0}}})[\frac{1}{m_{j_0}}+\frac{2}{w(g)}],\quad\quad & w(g)<m_{j_0}. \end{cases} \end{align*}$$
-
(ii) If
 $g\in W$
with a tree analysis
$g\in W$
with a tree analysis
 $(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
$(g_{\alpha })_{\alpha \in \mathcal {A}}$
, such that
 $I_{g_{\alpha }}=\emptyset $
for every
$I_{g_{\alpha }}=\emptyset $
for every
 $\alpha \in \mathcal {A}$
with
$\alpha \in \mathcal {A}$
with
 $w(g_{\alpha })= m_{j_0}$
, then
$w(g_{\alpha })= m_{j_0}$
, then $$\begin{align*}|g(x)|\le\frac{3C}{m_{j_0}}(1+\frac{1}{\sqrt{m_{j_0}}}).\end{align*}$$
$$\begin{align*}|g(x)|\le\frac{3C}{m_{j_0}}(1+\frac{1}{\sqrt{m_{j_0}}}).\end{align*}$$
Acknowledgments
We would like to thank the anonymous referee for providing many helpful suggestions on how to improve the content of our paper. The fourth author was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) [Discovery Grant RGPIN-2021-03-639].
Conflicts of interests
The authors have no conflict of interest to declare.