1. Introduction
Fix a prime number p, and let
![]() $K/{\mathbf Q}_p$
be a finite extension with residue field k and absolute Galois group
$K/{\mathbf Q}_p$
be a finite extension with residue field k and absolute Galois group
![]() $G_K := \operatorname {\mathrm {Gal}}(\overline {K}/K)$
. In the paper [Reference Caraiani, Emerton, Gee and SavittCEGS20b], inspired by a construction of Kisin [Reference KisinKis09] in the setting of formal deformations, we constructed and began to study the geometry of certain moduli stacks
$G_K := \operatorname {\mathrm {Gal}}(\overline {K}/K)$
. In the paper [Reference Caraiani, Emerton, Gee and SavittCEGS20b], inspired by a construction of Kisin [Reference KisinKis09] in the setting of formal deformations, we constructed and began to study the geometry of certain moduli stacks
![]() ${\mathcal Z}^{\mathrm {dd}}$
. The stacks
${\mathcal Z}^{\mathrm {dd}}$
. The stacks
![]() ${\mathcal Z}^{\mathrm {dd}}$
can be thought of as moduli of two-dimensional tamely potentially Barsotti–Tate representations of
${\mathcal Z}^{\mathrm {dd}}$
can be thought of as moduli of two-dimensional tamely potentially Barsotti–Tate representations of
![]() $G_K$
; they are in fact moduli stacks of étale
$G_K$
; they are in fact moduli stacks of étale
![]() $\varphi $
-modules with descent data, and by construction are equipped with a partial resolution
$\varphi $
-modules with descent data, and by construction are equipped with a partial resolution
where
![]() ${\mathcal C}^{\mathrm {dd},\operatorname {BT}}$
is a moduli stack of rank two Breuil–Kisin modules with tame descent data and height one.
${\mathcal C}^{\mathrm {dd},\operatorname {BT}}$
is a moduli stack of rank two Breuil–Kisin modules with tame descent data and height one.
The purpose of this paper is to make an explicit study of the morphism
![]() $ {\mathcal C}^{\mathrm {dd},\operatorname {BT}} \to {\mathcal Z}^{\mathrm {dd}}$
at the level of irreducible components. To be precise, for each two-dimensional tame inertial type
$ {\mathcal C}^{\mathrm {dd},\operatorname {BT}} \to {\mathcal Z}^{\mathrm {dd}}$
at the level of irreducible components. To be precise, for each two-dimensional tame inertial type
![]() $\tau $
, there are closed substacks
$\tau $
, there are closed substacks
![]() ${\mathcal C}^{\tau ,\operatorname {BT}} \subset {\mathcal C}^{\mathrm {dd},\operatorname {BT}}$
and
${\mathcal C}^{\tau ,\operatorname {BT}} \subset {\mathcal C}^{\mathrm {dd},\operatorname {BT}}$
and
![]() ${\mathcal Z}^{\tau } \subset {\mathcal Z}^{\mathrm {dd}}$
corresponding to representations having inertial type
${\mathcal Z}^{\tau } \subset {\mathcal Z}^{\mathrm {dd}}$
corresponding to representations having inertial type
![]() $\tau $
, and a morphism
$\tau $
, and a morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal Z}^{\tau }$
. These are p-adic formal algebraic stacks; let
${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal Z}^{\tau }$
. These are p-adic formal algebraic stacks; let
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
be the special fibre of
${\mathcal C}^{\tau ,\operatorname {BT},1}$
be the special fibre of
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}$
, and
${\mathcal C}^{\tau ,\operatorname {BT}}$
, and
![]() ${\mathcal Z}^{\tau ,1}$
its scheme-theoretic image in
${\mathcal Z}^{\tau ,1}$
its scheme-theoretic image in
![]() ${\mathcal Z}^{\tau }$
(in the sense of [Reference Emerton and GeeEG21]). These were proved in [Reference Caraiani, Emerton, Gee and SavittCEGS20b] to be equidimensional of dimension
${\mathcal Z}^{\tau }$
(in the sense of [Reference Emerton and GeeEG21]). These were proved in [Reference Caraiani, Emerton, Gee and SavittCEGS20b] to be equidimensional of dimension
![]() $[K:{\mathbf Q}_p]$
. Moreover, the finite type points
$[K:{\mathbf Q}_p]$
. Moreover, the finite type points
![]() $\operatorname {\mathrm {Spec}}({\mathbf F}) \to {\mathcal Z}^{\tau ,1}$
are in bijection with Galois representations
$\operatorname {\mathrm {Spec}}({\mathbf F}) \to {\mathcal Z}^{\tau ,1}$
are in bijection with Galois representations
![]() $G_K \to \operatorname {\mathrm {GL}}_2({\mathbf F})$
admitting a potentially Barsotti–Tate lift of type
$G_K \to \operatorname {\mathrm {GL}}_2({\mathbf F})$
admitting a potentially Barsotti–Tate lift of type
![]() $\tau $
.
$\tau $
.
(In fact,
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is shown in [Reference Caraiani, Emerton, Gee and SavittCEGS20b] to be reduced, from which it follows that
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is shown in [Reference Caraiani, Emerton, Gee and SavittCEGS20b] to be reduced, from which it follows that
![]() ${\mathcal Z}^{\tau ,1}$
is also reduced. The special fibre of
${\mathcal Z}^{\tau ,1}$
is also reduced. The special fibre of
![]() ${\mathcal Z}^{\tau }$
need not be reduced, so it need not equal
${\mathcal Z}^{\tau }$
need not be reduced, so it need not equal
![]() ${\mathcal Z}^{\tau ,1}$
, but it will be proved in the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a] that it is generically reduced, using the results of this paper as input.)
${\mathcal Z}^{\tau ,1}$
, but it will be proved in the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a] that it is generically reduced, using the results of this paper as input.)
Much of the work in our study of the irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
involves an explicit construction of families of extensions of characters. Intuitively, a natural source of ‘families’ of representations
${\mathcal Z}^{\tau ,1}$
involves an explicit construction of families of extensions of characters. Intuitively, a natural source of ‘families’ of representations
![]() $\overline {r}:G_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
is given by the extensions of two fixed characters. Indeed, given two characters
$\overline {r}:G_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
is given by the extensions of two fixed characters. Indeed, given two characters
![]() $\chi _1,\chi _2: G_K \to \overline {{\mathbf F}}^{\times }_p$
, the
$\chi _1,\chi _2: G_K \to \overline {{\mathbf F}}^{\times }_p$
, the
![]() $\overline {{\mathbf F}}_p$
-vector space
$\overline {{\mathbf F}}_p$
-vector space
![]() $\operatorname {\mathrm {Ext}}^1_{G_K}(\chi _2,\chi _1)$
is usually
$\operatorname {\mathrm {Ext}}^1_{G_K}(\chi _2,\chi _1)$
is usually
![]() $[K:{\mathbf Q}_p]$
-dimensional, and a back of the envelope calculation suggests that as a stack, the collection of these representations should have dimension
$[K:{\mathbf Q}_p]$
-dimensional, and a back of the envelope calculation suggests that as a stack, the collection of these representations should have dimension
![]() $[K:{\mathbf Q}_p]-2$
: the difference between an extension and a representation counts for a
$[K:{\mathbf Q}_p]-2$
: the difference between an extension and a representation counts for a
![]() $-1$
, as does the
$-1$
, as does the
![]() ${\mathbf G}_m$
of endomorphisms. Twisting
${\mathbf G}_m$
of endomorphisms. Twisting
![]() $\chi _1,\chi _2$
independently by unramified characters gives a candidate for a
$\chi _1,\chi _2$
independently by unramified characters gives a candidate for a
![]() $[K:{\mathbf Q}_p]$
-dimensional family; if contained in
$[K:{\mathbf Q}_p]$
-dimensional family; if contained in
![]() ${\mathcal Z}^{\tau }$
, then since
${\mathcal Z}^{\tau }$
, then since
![]() ${\mathcal Z}^{\tau }$
is equidimensional of dimension
${\mathcal Z}^{\tau }$
is equidimensional of dimension
![]() $[K:{\mathbf Q}_p]$
, the closure of such a family should be an irreducible component of
$[K:{\mathbf Q}_p]$
, the closure of such a family should be an irreducible component of
![]() ${\mathcal Z}^{\tau }$
.
${\mathcal Z}^{\tau }$
.
Since there are only finitely many possibilities for the restrictions of the
![]() $\chi _i$
to the inertia subgroup
$\chi _i$
to the inertia subgroup
![]() $I_K$
, this gives a finite list of maximal-dimensional families. On the other hand, there are up to unramified twist only finitely many irreducible two-dimensional representations of
$I_K$
, this gives a finite list of maximal-dimensional families. On the other hand, there are up to unramified twist only finitely many irreducible two-dimensional representations of
![]() $G_K$
, which suggests that the irreducible representations should correspond to zero-dimensional substacks. Together, these considerations suggest that the irreducible components of our moduli stack should be given by the closures of the families of extensions considered in the previous paragraph, and in particular, that the irreducible representations should arise as limits of reducible representations. This could not literally be the case for families of Galois representations, rather than families of étale
$G_K$
, which suggests that the irreducible representations should correspond to zero-dimensional substacks. Together, these considerations suggest that the irreducible components of our moduli stack should be given by the closures of the families of extensions considered in the previous paragraph, and in particular, that the irreducible representations should arise as limits of reducible representations. This could not literally be the case for families of Galois representations, rather than families of étale
![]() $\varphi $
-modules, and may seem surprising at first glance, but it is indeed what happens.
$\varphi $
-modules, and may seem surprising at first glance, but it is indeed what happens.
In the body of the paper, we make this analysis rigorous, and we show that the different families that we have constructed exhaust the irreducible components. We can therefore label the irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
as follows. A component is specified by an ordered pair of characters
${\mathcal Z}^{\tau ,1}$
as follows. A component is specified by an ordered pair of characters
![]() $I_K \to \overline {{\mathbf F}}_p^{\times }$
, which via local class field theory corresponds to a pair of characters
$I_K \to \overline {{\mathbf F}}_p^{\times }$
, which via local class field theory corresponds to a pair of characters
![]() $k^{\times }\to \overline {{\mathbf F}}^{\times }_p$
. Such a pair can be thought of as the highest weight of a Serre weight: an irreducible
$k^{\times }\to \overline {{\mathbf F}}^{\times }_p$
. Such a pair can be thought of as the highest weight of a Serre weight: an irreducible
![]() $\overline {{\mathbf F}}_p$
-representation of
$\overline {{\mathbf F}}_p$
-representation of
![]() $\operatorname {\mathrm {GL}}_2(k)$
. To each irreducible component, we have thus associated a Serre weight. (In fact, we need to make a shift in this dictionary, corresponding to half the sum of the positive roots of
$\operatorname {\mathrm {GL}}_2(k)$
. To each irreducible component, we have thus associated a Serre weight. (In fact, we need to make a shift in this dictionary, corresponding to half the sum of the positive roots of
![]() $\operatorname {\mathrm {GL}}_2(k)$
, but we ignore this for the purposes of this introduction.)
$\operatorname {\mathrm {GL}}_2(k)$
, but we ignore this for the purposes of this introduction.)
This might seem artificial, but, in fact, it is completely natural, for the following reason. Following the pioneering work of Serre [Reference SerreSer87] and Buzzard–Diamond–Jarvis [Reference Buzzard, Diamond and JarvisBDJ10] (as extended in [Reference ScheinSch08] and [Reference GeeGee11]), we now know how to associate a set
![]() $W(\overline {r})$
of Serre weights to each continuous representation
$W(\overline {r})$
of Serre weights to each continuous representation
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, with the property that if F is a totally real field and
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, with the property that if F is a totally real field and
![]() $\overline {\rho }:G_F\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
is an irreducible representation coming from a Hilbert modular form, then the possible weights of Hilbert modular forms giving rise to
$\overline {\rho }:G_F\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
is an irreducible representation coming from a Hilbert modular form, then the possible weights of Hilbert modular forms giving rise to
![]() $\overline {\rho }$
are precisely determined by the sets
$\overline {\rho }$
are precisely determined by the sets
![]() $W(\overline {\rho }|_{G_{F_v}})$
for places
$W(\overline {\rho }|_{G_{F_v}})$
for places
![]() $v|p$
of F (see, for example [Reference Barnet-Lamb, Gee and GeraghtyBLGG13, Reference Gee and KisinGK14, Reference Gee, Liu and SavittGLS15]).
$v|p$
of F (see, for example [Reference Barnet-Lamb, Gee and GeraghtyBLGG13, Reference Gee and KisinGK14, Reference Gee, Liu and SavittGLS15]).
Going back to our labelling of irreducible components above, we have associated a Serre weight
![]() $\overline {\sigma }$
to each irreducible component of
$\overline {\sigma }$
to each irreducible component of
![]() ${\mathcal Z}^{\tau ,1}$
. The inertial local Langlands correspondence assigns a finite set of Serre weights
${\mathcal Z}^{\tau ,1}$
. The inertial local Langlands correspondence assigns a finite set of Serre weights
![]() $\operatorname {JH}(\overline {\sigma }(\tau ))$
to
$\operatorname {JH}(\overline {\sigma }(\tau ))$
to
![]() $\tau $
, the Jordan–Hölder factors of the reduction mod p of the representation
$\tau $
, the Jordan–Hölder factors of the reduction mod p of the representation
![]() $\sigma (\tau )$
of
$\sigma (\tau )$
of
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
corresponding to
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
corresponding to
![]() $\tau $
. One of our main theorems is that the components of
$\tau $
. One of our main theorems is that the components of
![]() ${\mathcal Z}^{\tau ,1}$
are labelled precisely by the Serre weights
${\mathcal Z}^{\tau ,1}$
are labelled precisely by the Serre weights
![]() $\overline {\sigma } \in \operatorname {JH}(\overline {\sigma }(\tau ))$
. Furthermore, the component labelled by
$\overline {\sigma } \in \operatorname {JH}(\overline {\sigma }(\tau ))$
. Furthermore, the component labelled by
![]() $\overline {\sigma }$
has a dense set of finite type points
$\overline {\sigma }$
has a dense set of finite type points
![]() $\overline {r}$
with
$\overline {r}$
with
![]() $\overline {\sigma } \in W(\overline {r})$
. In the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a], this will be strengthened to the statement that the representations
$\overline {\sigma } \in W(\overline {r})$
. In the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a], this will be strengthened to the statement that the representations
![]() $\overline {r}$
on the irreducible component labelled by
$\overline {r}$
on the irreducible component labelled by
![]() $\overline {\sigma }$
are precisely the representations with
$\overline {\sigma }$
are precisely the representations with
![]() $\overline {\sigma }\in W(\overline {r})$
.
$\overline {\sigma }\in W(\overline {r})$
.
We also study the irreducible components of the stack
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
. If
${\mathcal C}^{\tau ,\operatorname {BT},1}$
. If
![]() $\tau $
is a nonscalar principal series type, then the set
$\tau $
is a nonscalar principal series type, then the set
![]() $\operatorname {JH}(\overline {\sigma }(\tau ))$
can be identified with a subset of the power set
$\operatorname {JH}(\overline {\sigma }(\tau ))$
can be identified with a subset of the power set
![]() ${\mathcal S}$
of the set of embeddings
${\mathcal S}$
of the set of embeddings
![]() $k\hookrightarrow \overline {{\mathbf F}}_p$
(hence, after fixing one such embedding, with a subset
$k\hookrightarrow \overline {{\mathbf F}}_p$
(hence, after fixing one such embedding, with a subset
![]() ${\mathcal P}_{\tau }$
of
${\mathcal P}_{\tau }$
of
![]() ${\mathbf Z}/f{\mathbf Z}$
). For generic choices of
${\mathbf Z}/f{\mathbf Z}$
). For generic choices of
![]() $\tau $
, this subset is the whole of
$\tau $
, this subset is the whole of
![]() ${\mathcal S}$
. We are able to show, using the theory of Dieudonné modules, that for any nonscalar principal series type
${\mathcal S}$
. We are able to show, using the theory of Dieudonné modules, that for any nonscalar principal series type
![]() $\tau $
, the irreducible components of
$\tau $
, the irreducible components of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
can be identified with
${\mathcal C}^{\tau ,\operatorname {BT},1}$
can be identified with
![]() ${\mathcal S}$
, and those irreducible components not corresponding to elements of
${\mathcal S}$
, and those irreducible components not corresponding to elements of
![]() $\operatorname {JH}(\overline {\sigma }(\tau ))$
have image in
$\operatorname {JH}(\overline {\sigma }(\tau ))$
have image in
![]() ${\mathcal Z}^{\tau }$
of positive codimension. There is an analogous statement for cuspidal types, while for scalar types, both
${\mathcal Z}^{\tau }$
of positive codimension. There is an analogous statement for cuspidal types, while for scalar types, both
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
![]() ${\mathcal Z}^{\tau ,1}$
are irreducible.
${\mathcal Z}^{\tau ,1}$
are irreducible.
To state our main results precisely, we must first introduce a bit more notation. Fix a tame inertial type
![]() $\tau $
and a uniformiser
$\tau $
and a uniformiser
![]() $\pi $
of K. Let L be the unramified quadratic extension of K, and write f for the inertial degree of
$\pi $
of K. Let L be the unramified quadratic extension of K, and write f for the inertial degree of
![]() $K/{\mathbf Q}_p$
. We set
$K/{\mathbf Q}_p$
. We set
![]() $K' = K(\pi ^{1/p^f-1})$
if
$K' = K(\pi ^{1/p^f-1})$
if
![]() $\tau $
is principal series, and set
$\tau $
is principal series, and set
![]() $K' = L(\pi ^{1/(p^{2f}-1)})$
if
$K' = L(\pi ^{1/(p^{2f}-1)})$
if
![]() $\tau $
is cuspidal. Our moduli stacks of p-adic Hodge theoretic objects with descent data will have descent data from
$\tau $
is cuspidal. Our moduli stacks of p-adic Hodge theoretic objects with descent data will have descent data from
![]() $K'$
to K. Let
$K'$
to K. Let
![]() $f'$
be the inertial degree of
$f'$
be the inertial degree of
![]() $K'/{\mathbf Q}_p$
, so that
$K'/{\mathbf Q}_p$
, so that
![]() $f' = f$
if the type
$f' = f$
if the type
![]() $\tau $
is principal series, while
$\tau $
is principal series, while
![]() $f' = 2f$
if the type
$f' = 2f$
if the type
![]() $\tau $
is cuspidal.
$\tau $
is cuspidal.
We say that a subset
![]() $J \subset {\mathbf Z}/f'{\mathbf Z}$
is a profile if:
$J \subset {\mathbf Z}/f'{\mathbf Z}$
is a profile if:
-
○
 $\tau $
is scalar and
$\tau $
is scalar and
 $J = \varnothing $
,
$J = \varnothing $
, -
○
 $\tau $
is a nonscalar principal series type and J is arbitrary or
$\tau $
is a nonscalar principal series type and J is arbitrary or -
○
 $\tau $
is cuspidal and J has the property that
$\tau $
is cuspidal and J has the property that
 $i \in J$
if and only if
$i \in J$
if and only if
 $i+f \not \in J$
.
$i+f \not \in J$
.
If
![]() $\tau $
is nonscalar, then there are exactly
$\tau $
is nonscalar, then there are exactly
![]() $2^f$
profiles.
$2^f$
profiles.
As above, write
![]() $\sigma (\tau )$
for the representation of
$\sigma (\tau )$
for the representation of
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
corresponding to
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
corresponding to
![]() $\tau $
under the inertial local Langlands correspondence of Henniart. The Jordan–Hölder factors of the reduction mod p of
$\tau $
under the inertial local Langlands correspondence of Henniart. The Jordan–Hölder factors of the reduction mod p of
![]() $\sigma (\tau )$
are parameterised by an explicit set of profiles
$\sigma (\tau )$
are parameterised by an explicit set of profiles
![]() ${\mathcal P}_{\tau }$
, and we write
${\mathcal P}_{\tau }$
, and we write
![]() $\overline {\sigma }(\tau )_J$
for the factor corresponding to J.
$\overline {\sigma }(\tau )_J$
for the factor corresponding to J.
To each profile J, we will associate a closed substack
![]() $\overline {\mathcal {C}}(J)$
of
$\overline {\mathcal {C}}(J)$
of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
. The stack
${\mathcal C}^{\tau ,\operatorname {BT},1}$
. The stack
![]() $\overline {{\mathcal Z}}(J)$
is then defined to be the scheme-theoretic image of
$\overline {{\mathcal Z}}(J)$
is then defined to be the scheme-theoretic image of
![]() $\overline {{\mathcal C}}(J)$
under the map
$\overline {{\mathcal C}}(J)$
under the map
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal Z}^{\tau ,1}$
, in the sense of [Reference Emerton and GeeEG21]. Then, the following is our main result, combining Proposition 5.1.3, Theorem 5.1.17, Corollary 5.3.3 and Theorem 5.4.3.
${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal Z}^{\tau ,1}$
, in the sense of [Reference Emerton and GeeEG21]. Then, the following is our main result, combining Proposition 5.1.3, Theorem 5.1.17, Corollary 5.3.3 and Theorem 5.4.3.
Theorem 1.1. The irreducible components of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
![]() ${\mathcal Z}^{\tau ,1}$
are as follows.
${\mathcal Z}^{\tau ,1}$
are as follows.
-
1. The irreducible components of
 ${\mathcal C}^{\tau ,1}$
are precisely the
${\mathcal C}^{\tau ,1}$
are precisely the
 $\overline {{\mathcal C}}(J)$
for profiles J, and if
$\overline {{\mathcal C}}(J)$
for profiles J, and if
 $J\ne J'$
, then
$J\ne J'$
, then
 $\overline {{\mathcal C}}(J)\ne \overline {{\mathcal C}}(J')$
.
$\overline {{\mathcal C}}(J)\ne \overline {{\mathcal C}}(J')$
. -
2. The irreducible components of
 ${\mathcal Z}^{\tau ,1}$
are precisely the
${\mathcal Z}^{\tau ,1}$
are precisely the
 $\overline {{\mathcal Z}}(J)$
for profiles
$\overline {{\mathcal Z}}(J)$
for profiles
 $J\in {\mathcal P}_{\tau }$
, and if
$J\in {\mathcal P}_{\tau }$
, and if
 $J\ne J'$
, then
$J\ne J'$
, then
 $\overline {{\mathcal Z}}(J)\ne \overline {{\mathcal Z}}(J')$
.
$\overline {{\mathcal Z}}(J)\ne \overline {{\mathcal Z}}(J')$
. -
3. For each
 $J \in {\mathcal P}_{\tau }$
, there is a dense open substack
$J \in {\mathcal P}_{\tau }$
, there is a dense open substack
 ${\mathcal U}$
of
${\mathcal U}$
of
 $\overline {{\mathcal C}}(J)$
, such that the map
$\overline {{\mathcal C}}(J)$
, such that the map
 $\overline {{\mathcal C}}(J) \to \overline {{\mathcal Z}}(J)$
restricts to an open immersion on
$\overline {{\mathcal C}}(J) \to \overline {{\mathcal Z}}(J)$
restricts to an open immersion on
 ${\mathcal U}$
.
${\mathcal U}$
. -
4. For each
 $J\in {\mathcal P}_{\tau }$
, there is a dense set of finite type points of
$J\in {\mathcal P}_{\tau }$
, there is a dense set of finite type points of
 $\overline {{\mathcal Z}}(J)$
with the property that the corresponding Galois representations have
$\overline {{\mathcal Z}}(J)$
with the property that the corresponding Galois representations have
 $\overline {\sigma }(\tau )_J$
as a Serre weight, and which furthermore admit a unique Breuil–Kisin model of type
$\overline {\sigma }(\tau )_J$
as a Serre weight, and which furthermore admit a unique Breuil–Kisin model of type
 $\tau $
.
$\tau $
.
Remark 1.2. We emphasise in Theorem 1.1 that the components of
![]() ${\mathcal Z}^{\tau ,1}$
are indexed by profiles
${\mathcal Z}^{\tau ,1}$
are indexed by profiles
![]() $J \in {\mathcal P}_{\tau }$
, not by all profiles. If
$J \in {\mathcal P}_{\tau }$
, not by all profiles. If
![]() $J \not \in {\mathcal P}_{\tau }$
, then the stack
$J \not \in {\mathcal P}_{\tau }$
, then the stack
![]() $\overline {{\mathcal Z}}(J)$
has dimension strictly smaller than
$\overline {{\mathcal Z}}(J)$
has dimension strictly smaller than
![]() $[K:{\mathbf Q}_p]$
, and so is properly contained in some component of
$[K:{\mathbf Q}_p]$
, and so is properly contained in some component of
![]() ${\mathcal Z}^{\tau ,1}$
. We anticipate that the loci
${\mathcal Z}^{\tau ,1}$
. We anticipate that the loci
![]() $\overline {{\mathcal Z}}(J)$
will nevertheless be of interest when
$\overline {{\mathcal Z}}(J)$
will nevertheless be of interest when
![]() $J \not \in {\mathcal P}_{\tau }$
: we expect that they will correspond to ‘phantom’ (partial weight one) Serre weights of relevance to the geometric variant of the weight part of Serre’s conjecture proposed by Diamond–Sasaki [Reference Diamond and SasakiDS17]. This will be the subject of future work.
$J \not \in {\mathcal P}_{\tau }$
: we expect that they will correspond to ‘phantom’ (partial weight one) Serre weights of relevance to the geometric variant of the weight part of Serre’s conjecture proposed by Diamond–Sasaki [Reference Diamond and SasakiDS17]. This will be the subject of future work.
We assume that
![]() $p>2$
in much of the paper; while we expect that our results should also hold if
$p>2$
in much of the paper; while we expect that our results should also hold if
![]() $p=2$
, there are several reasons to exclude this case. We are frequently able to considerably simplify our arguments by assuming that the extension
$p=2$
, there are several reasons to exclude this case. We are frequently able to considerably simplify our arguments by assuming that the extension
![]() $K'/K$
is not just tamely ramified, but in fact of degree prime to p; this is problematic when
$K'/K$
is not just tamely ramified, but in fact of degree prime to p; this is problematic when
![]() $p=2$
, as the consideration of cuspidal types involves a quadratic unramified extension. Furthermore, in the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we will use results on the Breuil–Mézard conjecture which ultimately depend on automorphy lifting theorems that are not available in the case
$p=2$
, as the consideration of cuspidal types involves a quadratic unramified extension. Furthermore, in the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we will use results on the Breuil–Mézard conjecture which ultimately depend on automorphy lifting theorems that are not available in the case
![]() $p=2$
at present (although it is plausible that the methods of [Reference ThorneTho17] could be used to prove them).
$p=2$
at present (although it is plausible that the methods of [Reference ThorneTho17] could be used to prove them).
We conclude this Introduction by discussing the relationship between our results and those of [Reference Emerton and GeeEG23]. Two of us (M.E. and T.G.) have constructed moduli stacks
![]() ${\mathcal X}_{d}$
of rank d étale
${\mathcal X}_{d}$
of rank d étale
![]() $(\varphi ,\Gamma )$
-modules for K, as well as substacks
$(\varphi ,\Gamma )$
-modules for K, as well as substacks
![]() ${\mathcal X}_d^{\lambda ,\tau }$
which may be regarded as stacks of potentially crystalline representations of
${\mathcal X}_d^{\lambda ,\tau }$
which may be regarded as stacks of potentially crystalline representations of
![]() $G_K$
with inertial type
$G_K$
with inertial type
![]() $\tau $
and Hodge type
$\tau $
and Hodge type
![]() $\lambda $
. When
$\lambda $
. When
![]() $d=2$
and
$d=2$
and
![]() $\lambda $
is the trivial Hodge type, these are stacks
$\lambda $
is the trivial Hodge type, these are stacks
![]() ${\mathcal X}_2^{\tau ,\operatorname {BT}}$
of potentially Barsotti–Tate representations of
${\mathcal X}_2^{\tau ,\operatorname {BT}}$
of potentially Barsotti–Tate representations of
![]() $G_K$
of inertial type
$G_K$
of inertial type
![]() $\tau $
, and we anticipate that
$\tau $
, and we anticipate that
![]() ${\mathcal X}_2^{\tau ,\operatorname {BT}}$
is isomorphic to
${\mathcal X}_2^{\tau ,\operatorname {BT}}$
is isomorphic to
![]() ${\mathcal Z}^{\tau ,\operatorname {BT}}$
. (But since we do not need this fact, we have not proved it.)
${\mathcal Z}^{\tau ,\operatorname {BT}}$
. (But since we do not need this fact, we have not proved it.)
One of the main results of the book [Reference Emerton and GeeEG23] is that the irreducible components of the underlying reduced stacks
![]() ${\mathcal X}_{d,\operatorname {red}}$
are in bijection with the irreducible representations of
${\mathcal X}_{d,\operatorname {red}}$
are in bijection with the irreducible representations of
![]() $\operatorname {\mathrm {GL}}_d(k)$
. This bijection is characterised in essentially exactly the same way as our description of the components of
$\operatorname {\mathrm {GL}}_d(k)$
. This bijection is characterised in essentially exactly the same way as our description of the components of
![]() ${\mathcal Z}^{\tau ,1}$
in this paper: a Serre weight has a highest weight, which corresponds to a tuple of inertial characters, which gives rise to a family of successive extensions of one-dimensional representations. Then, the closure of this family is a component of
${\mathcal Z}^{\tau ,1}$
in this paper: a Serre weight has a highest weight, which corresponds to a tuple of inertial characters, which gives rise to a family of successive extensions of one-dimensional representations. Then, the closure of this family is a component of
![]() ${\mathcal X}_{d,\operatorname {red}}$
.
${\mathcal X}_{d,\operatorname {red}}$
.
The crucial difference between our setting and that of [Reference Emerton and GeeEG23] is that we could prove in [Reference Caraiani, Emerton, Gee and SavittCEGS20b] that the stacks
![]() ${\mathcal Z}^{\tau ,1}$
are reduced. The proof makes use of the resolution
${\mathcal Z}^{\tau ,1}$
are reduced. The proof makes use of the resolution
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal Z}^{\tau ,1}$
and the fact that we are able to relate the stack
${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal Z}^{\tau ,1}$
and the fact that we are able to relate the stack
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}$
to a local model at Iwahori level, whose special fibre is known to be reduced. In the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we combine the characterisation of the components of
${\mathcal C}^{\tau ,\operatorname {BT}}$
to a local model at Iwahori level, whose special fibre is known to be reduced. In the sequel [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we combine the characterisation of the components of
![]() ${\mathcal Z}^{\tau ,1}$
from this paper with the reducedness of
${\mathcal Z}^{\tau ,1}$
from this paper with the reducedness of
![]() ${\mathcal Z}^{\tau ,1}$
from [Reference Caraiani, Emerton, Gee and SavittCEGS20b] to prove that the special fibre of
${\mathcal Z}^{\tau ,1}$
from [Reference Caraiani, Emerton, Gee and SavittCEGS20b] to prove that the special fibre of
![]() ${\mathcal Z}^{\tau }$
is generically reduced. This will then allow us to completely characterise all of the finite type points on each component of
${\mathcal Z}^{\tau }$
is generically reduced. This will then allow us to completely characterise all of the finite type points on each component of
![]() ${\mathcal Z}^{\tau ,1}$
(not just a dense set of points), and to prove geometrisations of the Breuil–Mézard conjecture and of the weight part of Serre’s conjecture for the stacks
${\mathcal Z}^{\tau ,1}$
(not just a dense set of points), and to prove geometrisations of the Breuil–Mézard conjecture and of the weight part of Serre’s conjecture for the stacks
![]() ${\mathcal Z}^{\mathrm {dd},1}$
. Furthermore, by means of a comparison of versal rings, these results can be transported to the stacks
${\mathcal Z}^{\mathrm {dd},1}$
. Furthermore, by means of a comparison of versal rings, these results can be transported to the stacks
![]() ${\mathcal X}^{\tau ,\operatorname {BT}}_2$
of [Reference Emerton and GeeEG23] as well.
${\mathcal X}^{\tau ,\operatorname {BT}}_2$
of [Reference Emerton and GeeEG23] as well.
1.3. Notation and conventions
Topological groups
If M is an abelian topological group with a linear topology, then as in [Sta13, Tag 07E7], we say that M is complete if the natural morphism
![]() $M\to \varinjlim _i M/U_i$
is an isomorphism, where
$M\to \varinjlim _i M/U_i$
is an isomorphism, where
![]() $\{U_i\}_{i \in I}$
is some (equivalently any) fundamental system of neighbourhoods of
$\{U_i\}_{i \in I}$
is some (equivalently any) fundamental system of neighbourhoods of
![]() $0$
consisting of subgroups. Note that in some other references, this would be referred to as being complete and separated. In particular, any p-adically complete ring A is by definition p-adically separated.
$0$
consisting of subgroups. Note that in some other references, this would be referred to as being complete and separated. In particular, any p-adically complete ring A is by definition p-adically separated.
Galois theory and local class field theory
If M is a field, we let
![]() $G_M$
denote its absolute Galois group. If M is a global field and v is a place of M, let
$G_M$
denote its absolute Galois group. If M is a global field and v is a place of M, let
![]() $M_v$
denote the completion of M at v. If M is a local field, we write
$M_v$
denote the completion of M at v. If M is a local field, we write
![]() $I_M$
for the inertia subgroup of
$I_M$
for the inertia subgroup of
![]() $G_M$
.
$G_M$
.
Let p be a prime number. Fix a finite extension
![]() $K/{\mathbf Q}_p$
, with ring of integers
$K/{\mathbf Q}_p$
, with ring of integers
![]() ${\mathcal O}_K$
and residue field k. Let e and f be the ramification and inertial degrees of K, respectively, and write
${\mathcal O}_K$
and residue field k. Let e and f be the ramification and inertial degrees of K, respectively, and write
![]() $\# k=p^f$
for the cardinality of k. Let
$\# k=p^f$
for the cardinality of k. Let
![]() $K'/K$
be a finite tamely ramified Galois extension. Let
$K'/K$
be a finite tamely ramified Galois extension. Let
![]() $k'$
be the residue field of
$k'$
be the residue field of
![]() $K'$
, and let
$K'$
, and let
![]() $e',f'$
be the ramification and inertial degrees of
$e',f'$
be the ramification and inertial degrees of
![]() $K'$
, respectively.
$K'$
, respectively.
Our representations of
![]() $G_K$
will have coefficients in
$G_K$
will have coefficients in
![]() $\overline {{\mathbf Q}}_p$
, a fixed algebraic closure of
$\overline {{\mathbf Q}}_p$
, a fixed algebraic closure of
![]() ${\mathbf Q}_p$
whose residue field we denote by
${\mathbf Q}_p$
whose residue field we denote by
![]() $\overline {{\mathbf F}}_p$
. Let E be a finite extension of
$\overline {{\mathbf F}}_p$
. Let E be a finite extension of
![]() ${\mathbf Q}_p$
contained in
${\mathbf Q}_p$
contained in
![]() $\overline {{\mathbf Q}}_p$
and containing the image of every embedding of
$\overline {{\mathbf Q}}_p$
and containing the image of every embedding of
![]() $K'$
into
$K'$
into
![]() $\overline {{\mathbf Q}}_p$
. Let
$\overline {{\mathbf Q}}_p$
. Let
![]() ${\mathcal O}$
be the ring of integers in E, with uniformiser
${\mathcal O}$
be the ring of integers in E, with uniformiser
![]() $\varpi $
and residue field
$\varpi $
and residue field
![]() ${\mathbf F} \subset \overline {{\mathbf F}}_p$
.
${\mathbf F} \subset \overline {{\mathbf F}}_p$
.
Fix an embedding
![]() $\sigma _0:k'\hookrightarrow {\mathbf F}$
, and recursively define
$\sigma _0:k'\hookrightarrow {\mathbf F}$
, and recursively define
![]() $\sigma _i:k'\hookrightarrow {\mathbf F}$
for all
$\sigma _i:k'\hookrightarrow {\mathbf F}$
for all
![]() $i\in {\mathbf Z}$
so that
$i\in {\mathbf Z}$
so that
![]() $\sigma _{i+1}^p=\sigma _i$
; of course, we have
$\sigma _{i+1}^p=\sigma _i$
; of course, we have
![]() $\sigma _{i+f'}=\sigma _i$
for all i. We let
$\sigma _{i+f'}=\sigma _i$
for all i. We let
![]() $e_i\in k'\otimes _{{\mathbf F}_p} {\mathbf F}$
denote the idempotent satisfying
$e_i\in k'\otimes _{{\mathbf F}_p} {\mathbf F}$
denote the idempotent satisfying
![]() $(x\otimes 1)e_i=(1\otimes \sigma _i(x))e_i$
for all
$(x\otimes 1)e_i=(1\otimes \sigma _i(x))e_i$
for all
![]() $x\in k'$
; note that
$x\in k'$
; note that
![]() $\varphi (e_i)=e_{i+1}$
. We also denote by
$\varphi (e_i)=e_{i+1}$
. We also denote by
![]() $e_i$
the natural lift of
$e_i$
the natural lift of
![]() $e_i$
to an idempotent in
$e_i$
to an idempotent in
![]() $W(k')\otimes _{{\mathbf Z}_p}{\mathcal O}$
. If M is an
$W(k')\otimes _{{\mathbf Z}_p}{\mathcal O}$
. If M is an
![]() $W(k')\otimes _{{\mathbf Z}_p}{\mathcal O}$
-module, then we write
$W(k')\otimes _{{\mathbf Z}_p}{\mathcal O}$
-module, then we write
![]() $M_i$
for
$M_i$
for
![]() $e_iM$
.
$e_iM$
.
We write
![]() ${\operatorname {Art}}_K \colon K^{\times }\to W_K^{\mathrm {ab}}$
for the isomorphism of local class field theory, normalised so that uniformisers correspond to geometric Frobenius elements.
${\operatorname {Art}}_K \colon K^{\times }\to W_K^{\mathrm {ab}}$
for the isomorphism of local class field theory, normalised so that uniformisers correspond to geometric Frobenius elements.
Lemma 1.3.1. Let
![]() $\pi $
be any uniformiser of
$\pi $
be any uniformiser of
![]() ${\mathcal O}_K$
. The composite
${\mathcal O}_K$
. The composite
![]() $I_K \to {\mathcal O}_K^{\times } \to k^{\times }$
, where the map
$I_K \to {\mathcal O}_K^{\times } \to k^{\times }$
, where the map
![]() $I_K \to {\mathcal O}_K^{\times }$
is induced by the restriction of
$I_K \to {\mathcal O}_K^{\times }$
is induced by the restriction of
![]() ${\operatorname {Art}}_K^{-1}$
, sends an element
${\operatorname {Art}}_K^{-1}$
, sends an element
![]() $g \in I_K$
to the image in
$g \in I_K$
to the image in
![]() $k^{\times }$
of
$k^{\times }$
of
![]() $g(\pi ^{1/(p^f-1)})/\pi ^{1/(p^f-1)}$
.
$g(\pi ^{1/(p^f-1)})/\pi ^{1/(p^f-1)}$
.
Proof. This follows (for example) from the construction in [Reference YoshidaYos08, Propositions 4.4(iii), 4.7(ii), Corollary 4.9, Definition 4.10].
For each
![]() $\sigma \in \operatorname {\mathrm {Hom}}(k,\overline {{\mathbf F}}_p)$
, we define the fundamental character
$\sigma \in \operatorname {\mathrm {Hom}}(k,\overline {{\mathbf F}}_p)$
, we define the fundamental character
![]() $\omega _{\sigma }$
to
$\omega _{\sigma }$
to
![]() $\sigma $
to be the composite
$\sigma $
to be the composite
where the map
![]() $I_K \to {\mathcal O}_K^{\times }$
is induced by the restriction of
$I_K \to {\mathcal O}_K^{\times }$
is induced by the restriction of
![]() ${\operatorname {Art}}_K^{-1}$
. Let
${\operatorname {Art}}_K^{-1}$
. Let
![]() $\varepsilon $
denote the p-adic cyclotomic character and
$\varepsilon $
denote the p-adic cyclotomic character and
![]() $\overline {\varepsilon }$
the mod p cyclotomic character, so that
$\overline {\varepsilon }$
the mod p cyclotomic character, so that
![]() $\prod _{\sigma \in \operatorname {\mathrm {Hom}}(k,\overline {{\mathbf F}}_p)} \omega _{\sigma }^{e} = \overline {\varepsilon }$
. We will often identify characters of
$\prod _{\sigma \in \operatorname {\mathrm {Hom}}(k,\overline {{\mathbf F}}_p)} \omega _{\sigma }^{e} = \overline {\varepsilon }$
. We will often identify characters of
![]() $I_K$
with characters of
$I_K$
with characters of
![]() $k^{\times }$
via the Artin map.
$k^{\times }$
via the Artin map.
Inertial local Langlands
A two-dimensional tame inertial type is (the isomorphism class of) a tamely ramified representation
![]() $\tau : I_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Z}}_p)$
that extends to a representation of
$\tau : I_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Z}}_p)$
that extends to a representation of
![]() $G_K$
and whose kernel is open. Such a representation is of the form
$G_K$
and whose kernel is open. Such a representation is of the form
![]() $\tau \simeq \eta \oplus \eta '$
, and we say that
$\tau \simeq \eta \oplus \eta '$
, and we say that
![]() $\tau $
is a tame principal series type if
$\tau $
is a tame principal series type if
![]() $\eta ,\eta '$
both extend to characters of
$\eta ,\eta '$
both extend to characters of
![]() $G_K$
. Otherwise,
$G_K$
. Otherwise,
![]() $\eta '=\eta ^q$
, and
$\eta '=\eta ^q$
, and
![]() $\eta $
extends to a character of
$\eta $
extends to a character of
![]() $G_L$
, where
$G_L$
, where
![]() $L/K$
is a quadratic unramified extension. In this case, we say that
$L/K$
is a quadratic unramified extension. In this case, we say that
![]() $\tau $
is a tame cuspidal type.
$\tau $
is a tame cuspidal type.
Henniart’s appendix to [Reference Breuil and MézardBM02] associates a finite dimensional irreducible E-representation
![]() $\sigma (\tau )$
of
$\sigma (\tau )$
of
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
to each inertial type
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
to each inertial type
![]() $\tau $
; we refer to this association as the inertial local Langlands correspondence. Since we are only working with tame inertial types, this correspondence can be made very explicit as follows.
$\tau $
; we refer to this association as the inertial local Langlands correspondence. Since we are only working with tame inertial types, this correspondence can be made very explicit as follows.
If
![]() $\tau \simeq \eta \oplus \eta '$
is a tame principal series type, then we also write
$\tau \simeq \eta \oplus \eta '$
is a tame principal series type, then we also write
![]() $\eta ,\eta ':k^{\times }\to {\mathcal O}^{\times }$
for the multiplicative characters determined by
$\eta ,\eta ':k^{\times }\to {\mathcal O}^{\times }$
for the multiplicative characters determined by
![]() $\eta \circ {\operatorname {Art}}_K|_{{\mathcal O}_{K}^{\times }},\eta '\circ {\operatorname {Art}}_K|_{{\mathcal O}_{K}^{\times }}$
, respectively. If
$\eta \circ {\operatorname {Art}}_K|_{{\mathcal O}_{K}^{\times }},\eta '\circ {\operatorname {Art}}_K|_{{\mathcal O}_{K}^{\times }}$
, respectively. If
![]() $\eta =\eta '$
, then we set
$\eta =\eta '$
, then we set
![]() $\sigma (\tau )=\eta \circ \det $
. Otherwise, we write I for the Iwahori subgroup of
$\sigma (\tau )=\eta \circ \det $
. Otherwise, we write I for the Iwahori subgroup of
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
consisting of matrices which are upper triangular modulo a uniformiser
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
consisting of matrices which are upper triangular modulo a uniformiser
![]() $\varpi _K$
of K, and write
$\varpi _K$
of K, and write
![]() $\chi = \eta '\otimes \eta : I\to {\mathcal O}^{\times }$
for the character
$\chi = \eta '\otimes \eta : I\to {\mathcal O}^{\times }$
for the character
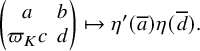 $$\begin{align*}\begin{pmatrix} a&b\\\varpi_K c&d \end{pmatrix}\mapsto \eta'(\overline{a})\eta(\overline{d}). \end{align*}$$
$$\begin{align*}\begin{pmatrix} a&b\\\varpi_K c&d \end{pmatrix}\mapsto \eta'(\overline{a})\eta(\overline{d}). \end{align*}$$
Then,
![]() $\sigma (\tau ) := \operatorname {\mathrm {Ind}}_I^{\operatorname {\mathrm {GL}}_2({\mathcal O}_K)} \chi $
.
$\sigma (\tau ) := \operatorname {\mathrm {Ind}}_I^{\operatorname {\mathrm {GL}}_2({\mathcal O}_K)} \chi $
.
If
![]() $\tau =\eta \oplus \eta ^q$
is a tame cuspidal type, then as above we write
$\tau =\eta \oplus \eta ^q$
is a tame cuspidal type, then as above we write
![]() $L/K$
for a quadratic unramified extension, and l for the residue field of
$L/K$
for a quadratic unramified extension, and l for the residue field of
![]() ${\mathcal O}_L$
. We write
${\mathcal O}_L$
. We write
![]() $\eta :l^{\times }\to {\mathcal O}^{\times }$
for the multiplicative character determined by
$\eta :l^{\times }\to {\mathcal O}^{\times }$
for the multiplicative character determined by
![]() $\eta \circ {\operatorname {Art}}_L|_{{\mathcal O}_{L}^{\times }}$
; then
$\eta \circ {\operatorname {Art}}_L|_{{\mathcal O}_{L}^{\times }}$
; then
![]() $\sigma (\tau )$
is the inflation to
$\sigma (\tau )$
is the inflation to
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
of the cuspidal representation of
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
of the cuspidal representation of
![]() $\operatorname {\mathrm {GL}}_2(k)$
denoted by
$\operatorname {\mathrm {GL}}_2(k)$
denoted by
![]() $\Theta (\eta )$
in [Reference DiamondDia07].
$\Theta (\eta )$
in [Reference DiamondDia07].
p-adic Hodge theory
We normalise Hodge–Tate weights so that all Hodge–Tate weights of the cyclotomic character are equal to
![]() $-1$
. We say that a potentially crystalline representation
$-1$
. We say that a potentially crystalline representation
![]() $\rho :G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Q}}_p)$
has Hodge type
$\rho :G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Q}}_p)$
has Hodge type
![]() $0$
, or is potentially Barsotti–Tate, if for each
$0$
, or is potentially Barsotti–Tate, if for each
![]() $\varsigma :K\hookrightarrow \overline {{\mathbf Q}}_p$
, the Hodge–Tate weights of
$\varsigma :K\hookrightarrow \overline {{\mathbf Q}}_p$
, the Hodge–Tate weights of
![]() $\rho $
with respect to
$\rho $
with respect to
![]() $\varsigma $
are
$\varsigma $
are
![]() $0$
and
$0$
and
![]() $1$
. (Note that this is a more restrictive definition of potentially Barsotti–Tate than is sometimes used; however, we will have no reason to deal with representations with irregular Hodge–Tate weights, and so we exclude them from consideration. Note also that it is more usual in the literature to say that
$1$
. (Note that this is a more restrictive definition of potentially Barsotti–Tate than is sometimes used; however, we will have no reason to deal with representations with irregular Hodge–Tate weights, and so we exclude them from consideration. Note also that it is more usual in the literature to say that
![]() $\rho $
is potentially Barsotti–Tate if it is potentially crystalline, and
$\rho $
is potentially Barsotti–Tate if it is potentially crystalline, and
![]() $\rho ^{\vee }$
has Hodge type
$\rho ^{\vee }$
has Hodge type
![]() $0$
.)
$0$
.)
We say that a potentially crystalline representation
![]() $\rho :G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Q}}_p)$
has inertial type
$\rho :G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Q}}_p)$
has inertial type
![]() $\tau $
if the traces of elements of
$\tau $
if the traces of elements of
![]() $I_K$
acting on
$I_K$
acting on
![]() $\tau $
and on
$\tau $
and on
are equal. (Here,
![]() $V_{\rho }$
is the underlying vector space of
$V_{\rho }$
is the underlying vector space of
![]() $V_{\rho }$
.) A representation
$V_{\rho }$
.) A representation
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
has a potentially Barsotti–Tate lift of type
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
has a potentially Barsotti–Tate lift of type
![]() $\tau $
if and only if
$\tau $
if and only if
![]() $\overline {r}$
admits a lift to a representation
$\overline {r}$
admits a lift to a representation
![]() $r:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Z}}_p)$
of Hodge type
$r:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Z}}_p)$
of Hodge type
![]() $0$
and inertial type
$0$
and inertial type
![]() $\tau $
.
$\tau $
.
Serre weights
By definition, a Serre weight is an irreducible
![]() ${\mathbf F}$
-representation of
${\mathbf F}$
-representation of
![]() $\operatorname {\mathrm {GL}}_2(k)$
. Concretely, such a representation is of the form
$\operatorname {\mathrm {GL}}_2(k)$
. Concretely, such a representation is of the form
where
![]() $0\le s_j,t_j\le p-1$
and not all
$0\le s_j,t_j\le p-1$
and not all
![]() $t_j$
are equal to
$t_j$
are equal to
![]() $p-1$
. We say that a Serre weight is Steinberg if
$p-1$
. We say that a Serre weight is Steinberg if
![]() $s_j=p-1$
for all j, and non-Steinberg otherwise.
$s_j=p-1$
for all j, and non-Steinberg otherwise.
A remark on normalisations
Given a continuous representation
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, there is an associated (nonempty) set of Serre weights
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, there is an associated (nonempty) set of Serre weights
![]() $W(\overline {r})$
, whose precise definition we will recall in Appendix A. There are, in fact, several different definitions of
$W(\overline {r})$
, whose precise definition we will recall in Appendix A. There are, in fact, several different definitions of
![]() $W(\overline {r})$
in the literature; as a result of the papers [Reference Barnet-Lamb, Gee and GeraghtyBLGG13, Reference Gee and KisinGK14, Reference Gee, Liu and SavittGLS15], these definitions are known to be equivalent up to normalisation.
$W(\overline {r})$
in the literature; as a result of the papers [Reference Barnet-Lamb, Gee and GeraghtyBLGG13, Reference Gee and KisinGK14, Reference Gee, Liu and SavittGLS15], these definitions are known to be equivalent up to normalisation.
However, the normalisations of Hodge–Tate weights and of inertial local Langlands used in [Reference Gee and KisinGK14, Reference Gee, Liu and SavittGLS15, Reference Emerton, Gee and SavittEGS15] are not all the same, and so for clarity, we lay out how they differ, and how they compare to the normalisations of this paper.
Our conventions for Hodge–Tate weights and inertial types agree with those of [Reference Gee and KisinGK14, Reference Emerton, Gee and SavittEGS15], but our representation
![]() $\sigma (\tau )$
is the representation
$\sigma (\tau )$
is the representation
![]() $\sigma (\tau ^{\vee })$
of [Reference Gee and KisinGK14, Reference Emerton, Gee and SavittEGS15] (where
$\sigma (\tau ^{\vee })$
of [Reference Gee and KisinGK14, Reference Emerton, Gee and SavittEGS15] (where
![]() $\tau ^{\vee }=\eta ^{-1}\oplus (\eta ')^{-1}$
); to see this, note the dual in the definition of
$\tau ^{\vee }=\eta ^{-1}\oplus (\eta ')^{-1}$
); to see this, note the dual in the definition of
![]() $\sigma (\tau )$
in [Reference Gee and KisinGK14, Theorem 2.1.3] and the discussion in Section 1.9 of [Reference Emerton, Gee and SavittEGS15].Footnote 1
$\sigma (\tau )$
in [Reference Gee and KisinGK14, Theorem 2.1.3] and the discussion in Section 1.9 of [Reference Emerton, Gee and SavittEGS15].Footnote 1
In all cases, one chooses to normalise the set of Serre weights so that the condition of Lemma A.5(1) holds. Consequently, our set of weights
![]() $W(\overline {r})$
is the set of duals of the weights
$W(\overline {r})$
is the set of duals of the weights
![]() $W(\overline {r})$
considered in [Reference Gee and KisinGK14]. In turn, the paper [Reference Gee, Liu and SavittGLS15] has the opposite convention for the signs of Hodge–Tate weights to our convention (and to the convention of [Reference Gee and KisinGK14]), so we find that our set of weights
$W(\overline {r})$
considered in [Reference Gee and KisinGK14]. In turn, the paper [Reference Gee, Liu and SavittGLS15] has the opposite convention for the signs of Hodge–Tate weights to our convention (and to the convention of [Reference Gee and KisinGK14]), so we find that our set of weights
![]() $W(\overline {r})$
is the set of duals of the weights
$W(\overline {r})$
is the set of duals of the weights
![]() $W(\overline {r}^{\vee })$
considered in [Reference Gee, Liu and SavittGLS15].
$W(\overline {r}^{\vee })$
considered in [Reference Gee, Liu and SavittGLS15].
Stacks
We follow the terminology of [Sta13]; in particular, we write ‘algebraic stack’ rather than ‘Artin stack’. More precisely, an algebraic stack is a stack in groupoids in the fppf topology, whose diagonal is representable by algebraic spaces, which admits a smooth surjection from a scheme. See [Sta13, Tag 026N] for a discussion of how this definition relates to others in the literature, and [Sta13, Tag 04XB] for key properties of morphisms representable by algebraic spaces.
For a commutative ring A, an fppf stack over A (or fppf A-stack) is a stack fibred in groupoids over the big fppf site of
![]() $\operatorname {\mathrm {Spec}} A$
.
$\operatorname {\mathrm {Spec}} A$
.
2. Preliminaries
We begin by reviewing the various constructions and results that we will need from [Reference Caraiani, Emerton, Gee and SavittCEGS20b]. Section 2.1 recalls the definition and a few basic algebraic properties of Breuil–Kisin modules with coefficients and descent data, while Section 2.2 does the same for étale
![]() $\varphi $
-modules. In Section 2.3, we define the stacks
$\varphi $
-modules. In Section 2.3, we define the stacks
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
![]() ${\mathcal Z}^{\tau ,1}$
(as well as various other related stacks) and state the main results of [Reference Caraiani, Emerton, Gee and SavittCEGS20b]. Finally, in Section 2.4, we introduce and study stacks of Dieudonné modules that will be used at the end of the paper to determine the irreducible components of
${\mathcal Z}^{\tau ,1}$
(as well as various other related stacks) and state the main results of [Reference Caraiani, Emerton, Gee and SavittCEGS20b]. Finally, in Section 2.4, we introduce and study stacks of Dieudonné modules that will be used at the end of the paper to determine the irreducible components of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
.
${\mathcal C}^{\tau ,\operatorname {BT},1}$
.
2.1. Breuil–Kisin modules with descent data
Recall that we have a finite tamely ramified Galois extension
![]() $K'/K$
. Suppose further that there exists a uniformiser
$K'/K$
. Suppose further that there exists a uniformiser
![]() $\pi '$
of
$\pi '$
of
![]() ${\mathcal O}_{K'}$
, such that
${\mathcal O}_{K'}$
, such that
![]() $\pi :=(\pi ')^{e(K'/K)}$
is an element of K, where
$\pi :=(\pi ')^{e(K'/K)}$
is an element of K, where
![]() $e(K'/K)$
is the ramification index of
$e(K'/K)$
is the ramification index of
![]() $K'/K$
. Recall that
$K'/K$
. Recall that
![]() $k'$
is the residue field of
$k'$
is the residue field of
![]() $K'$
, while
$K'$
, while
![]() $e',f'$
are the ramification and inertial degrees of
$e',f'$
are the ramification and inertial degrees of
![]() $K'$
, respectively. Let
$K'$
, respectively. Let
![]() $E(u)$
be the minimal polynomial of
$E(u)$
be the minimal polynomial of
![]() $\pi '$
over
$\pi '$
over
![]() $W(k')[1/p]$
.
$W(k')[1/p]$
.
Let
![]() $\varphi $
denote the arithmetic Frobenius automorphism of
$\varphi $
denote the arithmetic Frobenius automorphism of
![]() $k'$
, which lifts uniquely to an automorphism of
$k'$
, which lifts uniquely to an automorphism of
![]() $W(k')$
that we also denote by
$W(k')$
that we also denote by
![]() $\varphi $
. Define
$\varphi $
. Define
![]() $\mathfrak {S}:=W(k')[[u]]$
, and extend
$\mathfrak {S}:=W(k')[[u]]$
, and extend
![]() $\varphi $
to
$\varphi $
to
![]() $\mathfrak {S}$
by
$\mathfrak {S}$
by
By our assumptions that
![]() $(\pi ')^{e(K'/K)} \in K$
and that
$(\pi ')^{e(K'/K)} \in K$
and that
![]() $K'/K$
is Galois, for each
$K'/K$
is Galois, for each
![]() $g\in \operatorname {\mathrm {Gal}}(K'/K)$
, we can write
$g\in \operatorname {\mathrm {Gal}}(K'/K)$
, we can write
![]() $g(\pi ')/\pi '=h(g)$
with
$g(\pi ')/\pi '=h(g)$
with
![]() $h(g)\in \mu _{e(K'/K)}(K') \subset W(k')$
, and we let
$h(g)\in \mu _{e(K'/K)}(K') \subset W(k')$
, and we let
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
act on
$\operatorname {\mathrm {Gal}}(K'/K)$
act on
![]() $\mathfrak {S}$
via
$\mathfrak {S}$
via
Let A be a p-adically complete
![]() ${\mathbf Z}_p$
-algebra, set
${\mathbf Z}_p$
-algebra, set
![]() $\mathfrak {S}_A:=(W(k')\otimes _{{\mathbf Z}_p} A)[[u]]$
, and extend the actions of
$\mathfrak {S}_A:=(W(k')\otimes _{{\mathbf Z}_p} A)[[u]]$
, and extend the actions of
![]() $\varphi $
and
$\varphi $
and
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
on
$\operatorname {\mathrm {Gal}}(K'/K)$
on
![]() $\mathfrak {S}$
to actions on
$\mathfrak {S}$
to actions on
![]() $\mathfrak {S}_A$
in the obvious (A-linear) fashion.
$\mathfrak {S}_A$
in the obvious (A-linear) fashion.
Lemma 2.1.1. An
![]() $\mathfrak {S}_A$
-module is projective if and only if it is projective as an
$\mathfrak {S}_A$
-module is projective if and only if it is projective as an
![]() $A[[u]]$
-module.
$A[[u]]$
-module.
Proof. Suppose that
![]() $\mathfrak {M}$
is an
$\mathfrak {M}$
is an
![]() $\mathfrak {S}_A$
-module that is projective as an
$\mathfrak {S}_A$
-module that is projective as an
![]() $A[[u]]$
-module. Certainly
$A[[u]]$
-module. Certainly
![]() $W(k') \otimes _{{\mathbf Z}_p} \mathfrak {M}$
is projective over
$W(k') \otimes _{{\mathbf Z}_p} \mathfrak {M}$
is projective over
![]() $\mathfrak {S}_A$
, and we claim that it has
$\mathfrak {S}_A$
, and we claim that it has
![]() $\mathfrak {M}$
as an
$\mathfrak {M}$
as an
![]() $\mathfrak {S}_A$
-module direct summand. Indeed, this follows by rewriting
$\mathfrak {S}_A$
-module direct summand. Indeed, this follows by rewriting
![]() $\mathfrak {M}$
as
$\mathfrak {M}$
as
![]() $W(k')\otimes _{W(k')} \mathfrak {M}$
and noting that
$W(k')\otimes _{W(k')} \mathfrak {M}$
and noting that
![]() $W(k')$
is a
$W(k')$
is a
![]() $W(k')$
-module direct summand of
$W(k')$
-module direct summand of
![]() $W(k') \otimes _{{\mathbf Z}_p} W(k')$
.
$W(k') \otimes _{{\mathbf Z}_p} W(k')$
.
The actions of
![]() $\varphi $
and
$\varphi $
and
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
on
$\operatorname {\mathrm {Gal}}(K'/K)$
on
![]() $\mathfrak {S}_A$
extend to actions on
$\mathfrak {S}_A$
extend to actions on
![]() $\mathfrak {S}_A[1/u]=(W(k')\otimes _{{\mathbf Z}_p} A)((u))$
in the obvious way. It will sometimes be necessary to consider the subring
$\mathfrak {S}_A[1/u]=(W(k')\otimes _{{\mathbf Z}_p} A)((u))$
in the obvious way. It will sometimes be necessary to consider the subring
![]() $\mathfrak {S}_A^0 :=(W(k)\otimes _{{\mathbf Z}_p} A)[[v]]$
of
$\mathfrak {S}_A^0 :=(W(k)\otimes _{{\mathbf Z}_p} A)[[v]]$
of
![]() $\mathfrak {S}_A$
consisting of power series in
$\mathfrak {S}_A$
consisting of power series in
![]() $v:=u^{e(K'/K)}$
, on which
$v:=u^{e(K'/K)}$
, on which
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
acts trivially.
$\operatorname {\mathrm {Gal}}(K'/K)$
acts trivially.
Definition 2.1.2. Fix a p-adically complete
![]() ${\mathbf Z}_p$
-algebra A. A Breuil–Kisin module with A-coefficients and descent data from
${\mathbf Z}_p$
-algebra A. A Breuil–Kisin module with A-coefficients and descent data from
![]() $K'$
to K (or often simply a Breuil–Kisin module) is a triple
$K'$
to K (or often simply a Breuil–Kisin module) is a triple
![]() $(\mathfrak {M},\varphi _{\mathfrak {M}},\{\hat {g}\}_{g\in \operatorname {\mathrm {Gal}}(K'/K)})$
consisting of a
$(\mathfrak {M},\varphi _{\mathfrak {M}},\{\hat {g}\}_{g\in \operatorname {\mathrm {Gal}}(K'/K)})$
consisting of a
![]() $\mathfrak {S}_A$
-module
$\mathfrak {S}_A$
-module
![]() $\mathfrak {M}$
and a
$\mathfrak {M}$
and a
![]() $\varphi $
-semilinear map
$\varphi $
-semilinear map
![]() $\varphi _{\mathfrak {M}}:\mathfrak {M}\to \mathfrak {M}$
, such that:
$\varphi _{\mathfrak {M}}:\mathfrak {M}\to \mathfrak {M}$
, such that:
-
○ the
 $\mathfrak {S}_A$
-module
$\mathfrak {S}_A$
-module
 $\mathfrak {M}$
is finitely generated and projective, and
$\mathfrak {M}$
is finitely generated and projective, and -
○ the induced map
 $\Phi _{\mathfrak {M}} = 1 \otimes \varphi _{\mathfrak {M}} :\varphi ^{*}\mathfrak {M}\to \mathfrak {M}$
is an isomorphism after inverting
$\Phi _{\mathfrak {M}} = 1 \otimes \varphi _{\mathfrak {M}} :\varphi ^{*}\mathfrak {M}\to \mathfrak {M}$
is an isomorphism after inverting
 $E(u)$
(here, as usual, we write
$E(u)$
(here, as usual, we write
 $\varphi ^{*}\mathfrak {M}:=\mathfrak {S}_A \otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}$
),
$\varphi ^{*}\mathfrak {M}:=\mathfrak {S}_A \otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}$
),
together with additive bijections
![]() $\hat {g}:\mathfrak {M}\to \mathfrak {M}$
, satisfying the further properties that the maps
$\hat {g}:\mathfrak {M}\to \mathfrak {M}$
, satisfying the further properties that the maps
![]() $\hat {g}$
commute with
$\hat {g}$
commute with
![]() $\varphi _{\mathfrak {M}}$
, satisfy
$\varphi _{\mathfrak {M}}$
, satisfy
![]() $\hat {g_1}\circ \hat {g_2}=\widehat {g_1\circ g_2}$
and have
$\hat {g_1}\circ \hat {g_2}=\widehat {g_1\circ g_2}$
and have
![]() $\hat {g}(sm)=g(s)\hat {g}(m)$
for all
$\hat {g}(sm)=g(s)\hat {g}(m)$
for all
![]() $s\in \mathfrak {S}_A$
,
$s\in \mathfrak {S}_A$
,
![]() $m\in \mathfrak {M}$
. We say that
$m\in \mathfrak {M}$
. We say that
![]() $\mathfrak {M}$
has height at most h if the cokernel of
$\mathfrak {M}$
has height at most h if the cokernel of
![]() $\Phi _{\mathfrak {M}}$
is killed by
$\Phi _{\mathfrak {M}}$
is killed by
![]() $E(u)^h$
.
$E(u)^h$
.
The Breuil–Kisin module
![]() $\mathfrak {M}$
is said to be of rank d if the underlying finitely generated projective
$\mathfrak {M}$
is said to be of rank d if the underlying finitely generated projective
![]() $\mathfrak {S}_A$
-module has constant rank d. It is said to be free if the underlying
$\mathfrak {S}_A$
-module has constant rank d. It is said to be free if the underlying
![]() $\mathfrak {S}_A$
-module is free.
$\mathfrak {S}_A$
-module is free.
A morphism of Breuil–Kisin modules with descent data is a morphism of
![]() $\mathfrak {S}_A$
-modules that commutes with
$\mathfrak {S}_A$
-modules that commutes with
![]() $\varphi $
and with the
$\varphi $
and with the
![]() $\hat {g}$
. In the case that
$\hat {g}$
. In the case that
![]() $K'=K$
, the data of the
$K'=K$
, the data of the
![]() $\hat {g}$
is trivial, so it can be forgotten, giving the category of Breuil–Kisin modules with A-coefficients. In this case, it will sometimes be convenient to elide the difference between a Breuil–Kisin module with trivial descent data, and a Breuil–Kisin module without descent data, in order to avoid making separate definitions in the case of Breuil–Kisin modules without descent data.
$\hat {g}$
is trivial, so it can be forgotten, giving the category of Breuil–Kisin modules with A-coefficients. In this case, it will sometimes be convenient to elide the difference between a Breuil–Kisin module with trivial descent data, and a Breuil–Kisin module without descent data, in order to avoid making separate definitions in the case of Breuil–Kisin modules without descent data.
Remark 2.1.3. We refer the reader to [Reference Emerton and GeeEG21, Section 5.1] for a discussion of foundational results concerning finitely generated modules over the power series ring
![]() $A[[u]]$
. In particular (using Lemma 2.1.1), we note the following.
$A[[u]]$
. In particular (using Lemma 2.1.1), we note the following.
-
1. An
 $\mathfrak {S}_A$
-module
$\mathfrak {S}_A$
-module
 $\mathfrak {M}$
is finitely generated and projective if and only if it is u-torsion free and u-adically complete, and
$\mathfrak {M}$
is finitely generated and projective if and only if it is u-torsion free and u-adically complete, and
 $\mathfrak {M}/u\mathfrak {M}$
is a finitely generated projective A-module ([Reference Emerton and GeeEG21, Proposition 5.1.8]).
$\mathfrak {M}/u\mathfrak {M}$
is a finitely generated projective A-module ([Reference Emerton and GeeEG21, Proposition 5.1.8]). -
2. If the
 $\mathfrak {S}_A$
-module
$\mathfrak {S}_A$
-module
 $\mathfrak {M}$
is projective of rank d, then it is Zariski locally free of rank d in the sense that there is a cover of
$\mathfrak {M}$
is projective of rank d, then it is Zariski locally free of rank d in the sense that there is a cover of
 $\operatorname {\mathrm {Spec}} A$
by affine opens
$\operatorname {\mathrm {Spec}} A$
by affine opens
 $\operatorname {\mathrm {Spec}} B_i$
, such that each of the base-changed modules
$\operatorname {\mathrm {Spec}} B_i$
, such that each of the base-changed modules
 $\mathfrak {M}\otimes _{\mathfrak {S}_A}\mathfrak {S}_{B_i}$
is free of rank d ([Reference Emerton and GeeEG21, Proposition 5.1.9]).
$\mathfrak {M}\otimes _{\mathfrak {S}_A}\mathfrak {S}_{B_i}$
is free of rank d ([Reference Emerton and GeeEG21, Proposition 5.1.9]). -
3. If A is coherent (so, in particular, if A is Noetherian), then
 $A[[u]]$
is faithfully flat over A, and so
$A[[u]]$
is faithfully flat over A, and so
 $\mathfrak {S}_A$
is faithfully flat over A, but this need not hold if A is not coherent.
$\mathfrak {S}_A$
is faithfully flat over A, but this need not hold if A is not coherent.
Definition 2.1.4. If Q is any (not necessarily finitely generated) A-module, and
![]() $\mathfrak {M}$
is an
$\mathfrak {M}$
is an
![]() $A[[u]]$
-module, then we let
$A[[u]]$
-module, then we let
![]() $\mathfrak {M}\, \widehat {\otimes }_A Q$
denote the u-adic completion of
$\mathfrak {M}\, \widehat {\otimes }_A Q$
denote the u-adic completion of
![]() $\mathfrak {M}\otimes _A Q$
.
$\mathfrak {M}\otimes _A Q$
.
Lemma 2.1.5. If
![]() $\mathfrak {M}$
is a Breuil–Kisin module and B is an A-algebra, then the base change
$\mathfrak {M}$
is a Breuil–Kisin module and B is an A-algebra, then the base change
![]() $\mathfrak {M} \, \widehat {\otimes }_A B$
is a Breuil–Kisin module.
$\mathfrak {M} \, \widehat {\otimes }_A B$
is a Breuil–Kisin module.
Proof. This is [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma 2.1.4].
We make the following two further remarks concerning base change.
Remark 2.1.6. (1) If A is Noetherian, if Q is finitely generated over A and if
![]() $\mathfrak {N}$
is finitely generated over
$\mathfrak {N}$
is finitely generated over
![]() $A[[u]]$
, then
$A[[u]]$
, then
![]() $\mathfrak {N}\otimes _A Q$
is finitely generated over
$\mathfrak {N}\otimes _A Q$
is finitely generated over
![]() $A[[u]]$
, and hence (by the Artin–Rees lemma) is automatically u-adically complete. Thus, in this case, the natural morphism
$A[[u]]$
, and hence (by the Artin–Rees lemma) is automatically u-adically complete. Thus, in this case, the natural morphism
![]() $\mathfrak {N}\otimes _A Q \to \mathfrak {N}\, \widehat {\otimes }_A Q$
is an isomorphism.
$\mathfrak {N}\otimes _A Q \to \mathfrak {N}\, \widehat {\otimes }_A Q$
is an isomorphism.
(2) Note that
![]() $A[[u]]\, \widehat {\otimes }_A Q = Q[[u]]$
(the
$A[[u]]\, \widehat {\otimes }_A Q = Q[[u]]$
(the
![]() $A[[u]]$
-module consisting of a power series with coefficients in the A-module Q), and so if
$A[[u]]$
-module consisting of a power series with coefficients in the A-module Q), and so if
![]() $\mathfrak {N}$
is Zariski locally free on
$\mathfrak {N}$
is Zariski locally free on
![]() $\operatorname {\mathrm {Spec}} A$
, then
$\operatorname {\mathrm {Spec}} A$
, then
![]() $\mathfrak {N}\, \widehat {\otimes }_A Q$
is Zariski locally isomorphic to a direct sum of copies of
$\mathfrak {N}\, \widehat {\otimes }_A Q$
is Zariski locally isomorphic to a direct sum of copies of
![]() $Q[[u]]$
, and hence is u-torsion free (as well as being u-adically complete). In particular, by Remark 2.1.3(2), this holds if
$Q[[u]]$
, and hence is u-torsion free (as well as being u-adically complete). In particular, by Remark 2.1.3(2), this holds if
![]() $\mathfrak {N}$
is projective.
$\mathfrak {N}$
is projective.
Let A be a
![]() ${\mathbf Z}_p$
-algebra. We define a Dieudonné module of rank d with A-coefficients and descent data from
${\mathbf Z}_p$
-algebra. We define a Dieudonné module of rank d with A-coefficients and descent data from
![]() $K'$
to K to be a finitely generated projective
$K'$
to K to be a finitely generated projective
![]() $W(k')\otimes _{{\mathbf Z}_p}A$
-module D of constant rank d on
$W(k')\otimes _{{\mathbf Z}_p}A$
-module D of constant rank d on
![]() $\operatorname {\mathrm {Spec}} A$
, together with:
$\operatorname {\mathrm {Spec}} A$
, together with:
-
○ A-linear endomorphisms
 $F,V$
satisfying
$F,V$
satisfying
 $FV = VF = p$
, such that F is
$FV = VF = p$
, such that F is
 $\varphi $
-semilinear and V is
$\varphi $
-semilinear and V is
 $\varphi ^{-1}$
-semilinear for the action of
$\varphi ^{-1}$
-semilinear for the action of
 $W(k')$
, and
$W(k')$
, and -
○ a
 $W(k')\otimes _{{\mathbf Z}_p}A$
-semilinear action of
$W(k')\otimes _{{\mathbf Z}_p}A$
-semilinear action of
 $\operatorname {\mathrm {Gal}}(K'/K)$
which commutes with F and V.
$\operatorname {\mathrm {Gal}}(K'/K)$
which commutes with F and V.
Definition 2.1.7. If
![]() $\mathfrak {M}$
is a Breuil–Kisin module of height at most
$\mathfrak {M}$
is a Breuil–Kisin module of height at most
![]() $1$
and rank d with descent data, then there is a corresponding Dieudonné module
$1$
and rank d with descent data, then there is a corresponding Dieudonné module
![]() $D=D(\mathfrak {M})$
of rank d defined as follows. We set
$D=D(\mathfrak {M})$
of rank d defined as follows. We set
![]() $D:=\mathfrak {M}/u\mathfrak {M}$
with the induced action of
$D:=\mathfrak {M}/u\mathfrak {M}$
with the induced action of
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
, and F given by the induced action of
$\operatorname {\mathrm {Gal}}(K'/K)$
, and F given by the induced action of
![]() $\varphi $
. The endomorphism V is determined as follows. Write
$\varphi $
. The endomorphism V is determined as follows. Write
![]() $E(0) = c p$
, so that we have
$E(0) = c p$
, so that we have
![]() $p \equiv c^{-1}E(u) \pmod {u}$
. The condition that the cokernel of
$p \equiv c^{-1}E(u) \pmod {u}$
. The condition that the cokernel of
![]() $\varphi ^{*}\mathfrak {M}\to \mathfrak {M}$
is killed by
$\varphi ^{*}\mathfrak {M}\to \mathfrak {M}$
is killed by
![]() $E(u)$
allows us to factor the multiplication-by-
$E(u)$
allows us to factor the multiplication-by-
![]() $E(u)$
map on
$E(u)$
map on
![]() $\mathfrak {M}$
uniquely as
$\mathfrak {M}$
uniquely as
![]() $\mathfrak {V} \circ \varphi $
, and V is defined to be
$\mathfrak {V} \circ \varphi $
, and V is defined to be
![]() $c^{-1} \mathfrak {V}$
modulo u.
$c^{-1} \mathfrak {V}$
modulo u.
2.2. Étale
 $\varphi $
-modules and Galois representations
$\varphi $
-modules and Galois representations
Definition 2.2.1. Let A be a
![]() ${\mathbf Z}/p^a{\mathbf Z}$
-algebra for some
${\mathbf Z}/p^a{\mathbf Z}$
-algebra for some
![]() $a\ge 1$
. A weak étale
$a\ge 1$
. A weak étale
![]() $\varphi $
-module with A-coefficients and descent data from
$\varphi $
-module with A-coefficients and descent data from
![]() $K'$
to K is a triple
$K'$
to K is a triple
![]() $(M,\varphi _M,\{\hat {g}\})$
consisting of:
$(M,\varphi _M,\{\hat {g}\})$
consisting of:
-
○ a finitely generated
 $\mathfrak {S}_A[1/u]$
-module M;
$\mathfrak {S}_A[1/u]$
-module M; -
○ a
 $\varphi $
-semilinear map
$\varphi $
-semilinear map
 $\varphi _M:M\to M$
with the property that the induced map
$\varphi _M:M\to M$
with the property that the induced map  $$\begin{align*}\Phi_M = 1 \otimes \varphi_M:\varphi^{*}M:=\mathfrak{S}_A[1/u]\otimes_{\varphi,\mathfrak{S}_A[1/u]}M\to M\end{align*}$$
$$\begin{align*}\Phi_M = 1 \otimes \varphi_M:\varphi^{*}M:=\mathfrak{S}_A[1/u]\otimes_{\varphi,\mathfrak{S}_A[1/u]}M\to M\end{align*}$$
is an isomorphism, together with additive bijections
![]() $\hat {g}:M\to M$
for
$\hat {g}:M\to M$
for
![]() $g\in \operatorname {\mathrm {Gal}}(K'/K)$
, satisfying the further properties that the maps
$g\in \operatorname {\mathrm {Gal}}(K'/K)$
, satisfying the further properties that the maps
![]() $\hat {g}$
commute with
$\hat {g}$
commute with
![]() $\varphi _M$
, satisfy
$\varphi _M$
, satisfy
![]() $\hat {g_1}\circ \hat {g_2}=\widehat {g_1\circ g_2}$
and have
$\hat {g_1}\circ \hat {g_2}=\widehat {g_1\circ g_2}$
and have
![]() $\hat {g}(sm)=g(s)\hat {g}(m)$
for all
$\hat {g}(sm)=g(s)\hat {g}(m)$
for all
![]() $s\in \mathfrak {S}_A[1/u]$
,
$s\in \mathfrak {S}_A[1/u]$
,
![]() $m\in M$
. If M as above is projective as an
$m\in M$
. If M as above is projective as an
![]() $\mathfrak {S}_A[1/u]$
-module, then we say simply that M is an étale
$\mathfrak {S}_A[1/u]$
-module, then we say simply that M is an étale
![]() $\varphi $
-module. The étale
$\varphi $
-module. The étale
![]() $\varphi $
-module M is said to be of rank d if the underlying finitely generated projective
$\varphi $
-module M is said to be of rank d if the underlying finitely generated projective
![]() $\mathfrak {S}_A[1/u]$
-module has constant rank d.
$\mathfrak {S}_A[1/u]$
-module has constant rank d.
Remark 2.2.2. We could also consider étale
![]() $\varphi $
-modules for general p-adically complete
$\varphi $
-modules for general p-adically complete
![]() ${\mathbf Z}_p$
-algebras A, but we would need to replace
${\mathbf Z}_p$
-algebras A, but we would need to replace
![]() $\mathfrak {S}_A[1/u]$
by its p-adic completion. As we will not need to consider these modules in this paper, we do not do so here, but we refer the interested reader to [Reference Emerton and GeeEG23].
$\mathfrak {S}_A[1/u]$
by its p-adic completion. As we will not need to consider these modules in this paper, we do not do so here, but we refer the interested reader to [Reference Emerton and GeeEG23].
A morphism of weak étale
![]() $\varphi $
-modules with A-coefficients and descent data from
$\varphi $
-modules with A-coefficients and descent data from
![]() $K'$
to K is a morphism of
$K'$
to K is a morphism of
![]() $\mathfrak {S}_A[1/u]$
-modules that commutes with
$\mathfrak {S}_A[1/u]$
-modules that commutes with
![]() $\varphi $
and with the
$\varphi $
and with the
![]() $\hat {g}$
. Again, in the case
$\hat {g}$
. Again, in the case
![]() $K'=K$
, the descent data are trivial, and we obtain the usual category of étale
$K'=K$
, the descent data are trivial, and we obtain the usual category of étale
![]() $\varphi $
-modules with A-coefficients.
$\varphi $
-modules with A-coefficients.
Note that if A is a
![]() ${\mathbf Z}/p^a{\mathbf Z}$
-algebra, and
${\mathbf Z}/p^a{\mathbf Z}$
-algebra, and
![]() $\mathfrak {M}$
is a Breuil–Kisin module with descent data, then
$\mathfrak {M}$
is a Breuil–Kisin module with descent data, then
![]() $\mathfrak {M}[1/u]$
naturally has the structure of an étale
$\mathfrak {M}[1/u]$
naturally has the structure of an étale
![]() $\varphi $
-module with descent data.
$\varphi $
-module with descent data.
Suppose that A is an
![]() ${\mathcal O}$
-algebra (where
${\mathcal O}$
-algebra (where
![]() ${\mathcal O}$
is as in Section 1.3). In making calculations, it is often convenient to use the idempotents
${\mathcal O}$
is as in Section 1.3). In making calculations, it is often convenient to use the idempotents
![]() $e_i$
(again, as in Section 1.3). In particular, if
$e_i$
(again, as in Section 1.3). In particular, if
![]() $\mathfrak {M}$
is a Breuil–Kisin module, then writing as usual
$\mathfrak {M}$
is a Breuil–Kisin module, then writing as usual
![]() $\mathfrak {M}_i:=e_i\mathfrak {M}$
, we write
$\mathfrak {M}_i:=e_i\mathfrak {M}$
, we write
![]() $\Phi _{\mathfrak {M},i}:\varphi ^{*}(\mathfrak {M}_{i-1})\to \mathfrak {M}_{i}$
for the morphism induced by
$\Phi _{\mathfrak {M},i}:\varphi ^{*}(\mathfrak {M}_{i-1})\to \mathfrak {M}_{i}$
for the morphism induced by
![]() $\Phi _{\mathfrak {M}}$
. Similarly, if M is an étale
$\Phi _{\mathfrak {M}}$
. Similarly, if M is an étale
![]() $\varphi $
-module, then we write
$\varphi $
-module, then we write
![]() $M_i:=e_iM$
, and we write
$M_i:=e_iM$
, and we write
![]() $\Phi _{M,i}:\varphi ^{*}(M_{i-1}) \to M_{i}$
for the morphism induced by
$\Phi _{M,i}:\varphi ^{*}(M_{i-1}) \to M_{i}$
for the morphism induced by
![]() $\Phi _{M}$
.
$\Phi _{M}$
.
To connect étale
![]() $\varphi $
-modules to
$\varphi $
-modules to
![]() $G_{K_{\infty }}$
-representations, we begin by recalling from [Reference KisinKis09] some constructions arising in p-adic Hodge theory and the theory of fields of norms, which go back to [Reference FontaineFon90]. Following Fontaine, we write
$G_{K_{\infty }}$
-representations, we begin by recalling from [Reference KisinKis09] some constructions arising in p-adic Hodge theory and the theory of fields of norms, which go back to [Reference FontaineFon90]. Following Fontaine, we write
![]() $R:=\varprojlim _{x\mapsto x^p}{\mathcal O}_{\bar {K}}/p$
. Fix a compatible system
$R:=\varprojlim _{x\mapsto x^p}{\mathcal O}_{\bar {K}}/p$
. Fix a compatible system
![]() $(\! \sqrt [p^n]{\pi }\,)_{n\ge 0}$
of
$(\! \sqrt [p^n]{\pi }\,)_{n\ge 0}$
of
![]() $p^n$
th roots of
$p^n$
th roots of
![]() $\pi $
in
$\pi $
in
![]() $\bar {K}$
(compatible in the obvious sense that
$\bar {K}$
(compatible in the obvious sense that
![]() $\bigl (\! \sqrt [p^{n+1}]{\pi }\,\bigr )^p = \sqrt [p^n]{\pi }\,$
), and let
$\bigl (\! \sqrt [p^{n+1}]{\pi }\,\bigr )^p = \sqrt [p^n]{\pi }\,$
), and let
![]() $K_{\infty }:=\cup _{n}K(\sqrt [p^n]{\pi })$
, and also
$K_{\infty }:=\cup _{n}K(\sqrt [p^n]{\pi })$
, and also
![]() $K^{\prime }_{\infty }:=\cup _{n}K'(\sqrt [p^n]{\pi })$
. Since
$K^{\prime }_{\infty }:=\cup _{n}K'(\sqrt [p^n]{\pi })$
. Since
![]() $(e(K'/K),p)=1$
, the compatible system
$(e(K'/K),p)=1$
, the compatible system
![]() $(\! \sqrt [p^n]{\pi }\,)_{n\ge 0}$
determines a unique compatible system
$(\! \sqrt [p^n]{\pi }\,)_{n\ge 0}$
determines a unique compatible system
![]() $(\! \sqrt [p^n]{\pi '}\,)_{n\ge 0}$
of
$(\! \sqrt [p^n]{\pi '}\,)_{n\ge 0}$
of
![]() $p^n$
th roots of
$p^n$
th roots of
![]() $\pi '$
, such that
$\pi '$
, such that
![]() $(\! \sqrt [p^n]{\pi '}\,)^{e(K'/K)} =\sqrt [p^n]{\pi }$
. Write
$(\! \sqrt [p^n]{\pi '}\,)^{e(K'/K)} =\sqrt [p^n]{\pi }$
. Write
![]() $\underline {\pi }'=(\sqrt[p^n]{\pi '})_{n\ge 0}\in R$
, and
$\underline {\pi }'=(\sqrt[p^n]{\pi '})_{n\ge 0}\in R$
, and
![]() $[\underline {\pi }']\in W(R)$
for its image under the natural multiplicative map
$[\underline {\pi }']\in W(R)$
for its image under the natural multiplicative map
![]() $R \to W(R)$
. We have a Frobenius-equivariant inclusion
$R \to W(R)$
. We have a Frobenius-equivariant inclusion
![]() $\mathfrak {S}\hookrightarrow W(R)$
by sending
$\mathfrak {S}\hookrightarrow W(R)$
by sending
![]() $u\mapsto [\underline {\pi }']$
. We can naturally identify
$u\mapsto [\underline {\pi }']$
. We can naturally identify
![]() $\operatorname {\mathrm {Gal}}(K^{\prime }_{\infty }/K_{\infty })$
with
$\operatorname {\mathrm {Gal}}(K^{\prime }_{\infty }/K_{\infty })$
with
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
, and doing this, we see that the action of
$\operatorname {\mathrm {Gal}}(K'/K)$
, and doing this, we see that the action of
![]() $g\in G_{K_{\infty }}$
on u is via
$g\in G_{K_{\infty }}$
on u is via
![]() $g(u)=h(g)u$
.
$g(u)=h(g)u$
.
We let
![]() ${\mathcal O}_{{\mathcal E}}$
denote the p-adic completion of
${\mathcal O}_{{\mathcal E}}$
denote the p-adic completion of
![]() $\mathfrak {S}[1/u]$
, and let
$\mathfrak {S}[1/u]$
, and let
![]() ${\mathcal E}$
be the field of fractions of
${\mathcal E}$
be the field of fractions of
![]() ${\mathcal O}_{\mathcal E}$
. The inclusion
${\mathcal O}_{\mathcal E}$
. The inclusion
![]() $\mathfrak {S}\hookrightarrow W(R)$
extends to an inclusion
$\mathfrak {S}\hookrightarrow W(R)$
extends to an inclusion
![]() ${\mathcal E}\hookrightarrow W(\operatorname {Frac}(R))[1/p]$
. Let
${\mathcal E}\hookrightarrow W(\operatorname {Frac}(R))[1/p]$
. Let
![]() ${\mathcal E}^{\text {nr}}$
be the maximal unramified extension of
${\mathcal E}^{\text {nr}}$
be the maximal unramified extension of
![]() ${\mathcal E}$
in
${\mathcal E}$
in
![]() $ W(\operatorname {Frac}(R))[1/p]$
, and let
$ W(\operatorname {Frac}(R))[1/p]$
, and let
![]() ${\mathcal O}_{{\mathcal E}^{\text {nr}}}\subset W(\operatorname {Frac}(R))$
denote its ring of integers. Let
${\mathcal O}_{{\mathcal E}^{\text {nr}}}\subset W(\operatorname {Frac}(R))$
denote its ring of integers. Let
![]() ${\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}$
be the p-adic completion of
${\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}$
be the p-adic completion of
![]() ${\mathcal O}_{{\mathcal E}^{\text {nr}}}$
. Note that
${\mathcal O}_{{\mathcal E}^{\text {nr}}}$
. Note that
![]() ${\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}$
is stable under the action of
${\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}$
is stable under the action of
![]() $G_{K_{\infty }}$
.
$G_{K_{\infty }}$
.
Definition 2.2.3. Suppose that A is a
![]() ${\mathbf Z}/p^a{\mathbf Z}$
-algebra for some
${\mathbf Z}/p^a{\mathbf Z}$
-algebra for some
![]() $a \ge 1$
. If M is a weak étale
$a \ge 1$
. If M is a weak étale
![]() $\varphi $
-module with A-coefficients and descent data, set
$\varphi $
-module with A-coefficients and descent data, set
![]() $T_A(M):=\left ({\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}\otimes _{\mathfrak {S}[1/u]}M \right )^{\varphi =1}$
, an A-module with a
$T_A(M):=\left ({\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}\otimes _{\mathfrak {S}[1/u]}M \right )^{\varphi =1}$
, an A-module with a
![]() $G_{K_{\infty }}$
-action (via the diagonal action on
$G_{K_{\infty }}$
-action (via the diagonal action on
![]() ${\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}$
and M, the latter given by the
${\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}$
and M, the latter given by the
![]() $\hat {g}$
). If
$\hat {g}$
). If
![]() $\mathfrak {M}$
is a Breuil–Kisin module with A-coefficients and descent data, set
$\mathfrak {M}$
is a Breuil–Kisin module with A-coefficients and descent data, set
![]() $T_A(\mathfrak {M}):=T_A(\mathfrak {M}[1/u])$
.
$T_A(\mathfrak {M}):=T_A(\mathfrak {M}[1/u])$
.
Lemma 2.2.4. Suppose that A is a local
![]() ${\mathbf Z}_p$
-algebra and that
${\mathbf Z}_p$
-algebra and that
![]() $|A|<\infty $
. Then,
$|A|<\infty $
. Then,
![]() $T_A$
induces an equivalence of categories from the category of weak étale
$T_A$
induces an equivalence of categories from the category of weak étale
![]() $\varphi $
-modules with A-coefficients and descent data to the category of continuous representations of
$\varphi $
-modules with A-coefficients and descent data to the category of continuous representations of
![]() $G_{K_{\infty }}$
on finite A-modules. If
$G_{K_{\infty }}$
on finite A-modules. If
![]() $A\to A'$
is finite, then there is a natural isomorphism
$A\to A'$
is finite, then there is a natural isomorphism
![]() $T_A(M)\otimes _A A'\buildrel \sim \over \longrightarrow T_{A'}(M\otimes _A A')$
. A weak étale
$T_A(M)\otimes _A A'\buildrel \sim \over \longrightarrow T_{A'}(M\otimes _A A')$
. A weak étale
![]() $\varphi $
-module with A-coefficients and descent data M is free of rank d if and only if
$\varphi $
-module with A-coefficients and descent data M is free of rank d if and only if
![]() $T_A(M)$
is a free A-module of rank d.
$T_A(M)$
is a free A-module of rank d.
Proof. This is due to Fontaine [Reference FontaineFon90, Section 1.2], and can be proved in exactly the same way as [Reference KisinKis09, Lemma 1.2.7].
We will frequently simply write T for
![]() $T_A$
. Note that if we let
$T_A$
. Note that if we let
![]() $M'$
be the étale
$M'$
be the étale
![]() $\varphi $
-module obtained from M by forgetting the descent data, then by definition, we have
$\varphi $
-module obtained from M by forgetting the descent data, then by definition, we have
![]() $T(M')=T(M)|_{G_{K^{\prime }_{\infty }}}$
.
$T(M')=T(M)|_{G_{K^{\prime }_{\infty }}}$
.
Remark 2.2.5. Although étale
![]() $\varphi $
-modules naturally give rise to representations of
$\varphi $
-modules naturally give rise to representations of
![]() $G_{K_{\infty }}$
, those coming from Breuil–Kisin modules of height at most
$G_{K_{\infty }}$
, those coming from Breuil–Kisin modules of height at most
![]() $1$
admit canonical extensions to
$1$
admit canonical extensions to
![]() $G_K$
by [Reference KisinKis09, Proposition 1.1.13].
$G_K$
by [Reference KisinKis09, Proposition 1.1.13].
Lemma 2.2.6. If
![]() $\overline {r},\overline {r}':G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
are continuous representations, both of which arise as the reduction mod p of potentially Barsotti–Tate representations of tame inertial type, and there is an isomorphism
$\overline {r},\overline {r}':G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
are continuous representations, both of which arise as the reduction mod p of potentially Barsotti–Tate representations of tame inertial type, and there is an isomorphism
![]() $\overline {r}|_{G_{K_{\infty }}}\cong \overline {r}'|_{G_{K_{\infty }}} $
, then
$\overline {r}|_{G_{K_{\infty }}}\cong \overline {r}'|_{G_{K_{\infty }}} $
, then
![]() $\overline {r}\cong \overline {r}'$
.
$\overline {r}\cong \overline {r}'$
.
Proof. The extension
![]() $K_{\infty }/K$
is totally wildly ramified. Since the irreducible
$K_{\infty }/K$
is totally wildly ramified. Since the irreducible
![]() $\overline {{\mathbf F}}_p$
-representations of
$\overline {{\mathbf F}}_p$
-representations of
![]() $G_K$
are induced from tamely ramified characters, we see that
$G_K$
are induced from tamely ramified characters, we see that
![]() $\overline {r}|_{G_{K_{\infty }}}$
is irreducible if and only if
$\overline {r}|_{G_{K_{\infty }}}$
is irreducible if and only if
![]() $\overline {r}$
is irreducible, and if
$\overline {r}$
is irreducible, and if
![]() $\overline {r}$
or
$\overline {r}$
or
![]() $\overline {r}'$
is irreducible, then we are done. In the reducible case, we see that
$\overline {r}'$
is irreducible, then we are done. In the reducible case, we see that
![]() $\overline {r}$
and
$\overline {r}$
and
![]() $\overline {r}'$
are extensions of the same characters, and the result then follows from [Reference Gee, Liu and SavittGLS15, Lemma 5.4.2] and Lemma A.5 (2).
$\overline {r}'$
are extensions of the same characters, and the result then follows from [Reference Gee, Liu and SavittGLS15, Lemma 5.4.2] and Lemma A.5 (2).
2.3. Recollections from [Reference Caraiani, Emerton, Gee and SavittCEGS20b]
The main objects of study in this paper are certain algebraic stacks
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}$
and
${\mathcal C}^{\tau ,\operatorname {BT}}$
and
![]() ${\mathcal Z}^{\tau ,1}$
, of rank two Breuil–Kisin modules and étale
${\mathcal Z}^{\tau ,1}$
, of rank two Breuil–Kisin modules and étale
![]() $\varphi $
-modules, respectively, that were introduced and studied in [Reference Caraiani, Emerton, Gee and SavittCEGS20b]. We review their definitions now, and recall the main properties of these stacks that were established in [Reference Caraiani, Emerton, Gee and SavittCEGS20b].
$\varphi $
-modules, respectively, that were introduced and studied in [Reference Caraiani, Emerton, Gee and SavittCEGS20b]. We review their definitions now, and recall the main properties of these stacks that were established in [Reference Caraiani, Emerton, Gee and SavittCEGS20b].
To define
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, we first introduce stacks of Breuil–Kisin modules with descent data; then we impose two conditions on them, corresponding (in the analogy with Galois representations) to fixing an inertial type
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, we first introduce stacks of Breuil–Kisin modules with descent data; then we impose two conditions on them, corresponding (in the analogy with Galois representations) to fixing an inertial type
![]() $\tau $
and requiring all pairs Hodge–Tate weights to be
$\tau $
and requiring all pairs Hodge–Tate weights to be
![]() $\{0,1\}$
.
$\{0,1\}$
.
Take
![]() $K'/K$
to be any Galois extension, such that
$K'/K$
to be any Galois extension, such that
![]() $[K':K]$
is prime to p.
$[K':K]$
is prime to p.
Definition 2.3.1. For each integer
![]() $a\ge 1$
, we let
$a\ge 1$
, we let
![]() ${\mathcal C}_{d,h}^{\mathrm {dd},a}$
be the fppf stack over
${\mathcal C}_{d,h}^{\mathrm {dd},a}$
be the fppf stack over
![]() ${\mathcal O}/\varpi ^a$
, which associates to any
${\mathcal O}/\varpi ^a$
, which associates to any
![]() ${\mathcal O}/\varpi ^a$
-algebra A the groupoid
${\mathcal O}/\varpi ^a$
-algebra A the groupoid
![]() ${\mathcal C}_{d,h}^{\mathrm {dd},a}(A)$
of rank d Breuil–Kisin modules of height at most h with A-coefficients and descent data from
${\mathcal C}_{d,h}^{\mathrm {dd},a}(A)$
of rank d Breuil–Kisin modules of height at most h with A-coefficients and descent data from
![]() $K'$
to K.
$K'$
to K.
By [Sta13, Tag 04WV], we may also regard each of the stacks
![]() ${\mathcal C}_{d,h}^{\mathrm {dd},a}$
as an fppf stack over
${\mathcal C}_{d,h}^{\mathrm {dd},a}$
as an fppf stack over
![]() ${\mathcal O}$
, and we then write
${\mathcal O}$
, and we then write
![]() ${\mathcal C}_{d,h}^{\mathrm {dd}}:=\varinjlim _{a}{\mathcal C}_{d,h}^{\mathrm {dd},a}$
; this is, again, an fppf stack over
${\mathcal C}_{d,h}^{\mathrm {dd}}:=\varinjlim _{a}{\mathcal C}_{d,h}^{\mathrm {dd},a}$
; this is, again, an fppf stack over
![]() ${\mathcal O}$
. We will omit the subscripts
${\mathcal O}$
. We will omit the subscripts
![]() $d,h$
from this notation when doing so will not cause confusion.
$d,h$
from this notation when doing so will not cause confusion.
Definition 2.3.2. Let
![]() $\tau $
be a d-dimensional E-representation of
$\tau $
be a d-dimensional E-representation of
![]() $I(K'/K)$
. We say that an object
$I(K'/K)$
. We say that an object
![]() $\mathfrak {M}$
of
$\mathfrak {M}$
of
![]() ${\mathcal C}^{\mathrm {dd},a}$
has type
${\mathcal C}^{\mathrm {dd},a}$
has type
![]() $\tau $
if Zariski locally on
$\tau $
if Zariski locally on
![]() $\operatorname {\mathrm {Spec}} A$
, there is an
$\operatorname {\mathrm {Spec}} A$
, there is an
![]() $I(K'/K)$
-equivariant isomorphism
$I(K'/K)$
-equivariant isomorphism
![]() $\mathfrak {M}_i/u \mathfrak {M}_i \cong A \otimes _{{\mathcal O}} \tau ^{\circ }$
for each i. (Here, we recall that
$\mathfrak {M}_i/u \mathfrak {M}_i \cong A \otimes _{{\mathcal O}} \tau ^{\circ }$
for each i. (Here, we recall that
![]() $\mathfrak {M}_i := e_i \mathfrak {M}$
, and
$\mathfrak {M}_i := e_i \mathfrak {M}$
, and
![]() $\tau ^{\circ }$
denotes an
$\tau ^{\circ }$
denotes an
![]() ${\mathcal O}$
-lattice in
${\mathcal O}$
-lattice in
![]() $\tau $
.)
$\tau $
.)
Definition 2.3.3. Let
![]() ${\mathcal C}^{\tau }$
be the étale substack of
${\mathcal C}^{\tau }$
be the étale substack of
![]() ${\mathcal C}^{\mathrm {dd}}$
consisting of the objects of type
${\mathcal C}^{\mathrm {dd}}$
consisting of the objects of type
![]() $\tau $
. This is an open and closed substack of
$\tau $
. This is an open and closed substack of
![]() ${\mathcal C}^{\mathrm {dd}}$
(see [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Proposition 3.3.5]).
${\mathcal C}^{\mathrm {dd}}$
(see [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Proposition 3.3.5]).
For the remainder of this section, we fix
![]() $d=2$
and
$d=2$
and
![]() $h=1$
, and write
$h=1$
, and write
![]() $N = K \cdot W(k')[1/p]$
(the maximal subextension of
$N = K \cdot W(k')[1/p]$
(the maximal subextension of
![]() $K'$
which is unramified over K).
$K'$
which is unramified over K).
Suppose that A is an
![]() ${\mathcal O}/\varpi ^a$
-algebra and consider a pair
${\mathcal O}/\varpi ^a$
-algebra and consider a pair
![]() $(\mathfrak {L},\mathfrak {L}^+)$
, where:
$(\mathfrak {L},\mathfrak {L}^+)$
, where:
-
○
 $\mathfrak {L}$
is a rank two projective
$\mathfrak {L}$
is a rank two projective
 ${\mathcal O}_{K'}\otimes _{{\mathbf Z}_p} A$
-module, with a
${\mathcal O}_{K'}\otimes _{{\mathbf Z}_p} A$
-module, with a
 $\operatorname {\mathrm {Gal}}(K'/K)$
-semilinear, A-linear action of
$\operatorname {\mathrm {Gal}}(K'/K)$
-semilinear, A-linear action of
 $\operatorname {\mathrm {Gal}}(K'/K)$
;
$\operatorname {\mathrm {Gal}}(K'/K)$
; -
○
 $\mathfrak {L}^+$
is an
$\mathfrak {L}^+$
is an
 ${\mathcal O}_{K'}\otimes _{{\mathbf Z}_p} A$
-submodule of
${\mathcal O}_{K'}\otimes _{{\mathbf Z}_p} A$
-submodule of
 $\mathfrak {L}$
, which is locally on
$\mathfrak {L}$
, which is locally on
 $\operatorname {\mathrm {Spec}} A$
a direct summand of
$\operatorname {\mathrm {Spec}} A$
a direct summand of
 $\mathfrak {L}$
as an A-module (or equivalently, for which
$\mathfrak {L}$
as an A-module (or equivalently, for which
 $\mathfrak {L}/\mathfrak {L}^+$
is projective as an A-module), and is preserved by
$\mathfrak {L}/\mathfrak {L}^+$
is projective as an A-module), and is preserved by
 $\operatorname {\mathrm {Gal}}(K'/K)$
.
$\operatorname {\mathrm {Gal}}(K'/K)$
.
For each character
![]() $\xi : I(K'/K) \to {\mathcal O}^{\times }$
, let
$\xi : I(K'/K) \to {\mathcal O}^{\times }$
, let
![]() $\mathfrak {L}_{\xi }$
(respectively,
$\mathfrak {L}_{\xi }$
(respectively,
![]() $\mathfrak {L}^+_{\xi }$
) be the
$\mathfrak {L}^+_{\xi }$
) be the
![]() ${\mathcal O}_N\otimes _{{\mathbf Z}_p} A$
-submodule of
${\mathcal O}_N\otimes _{{\mathbf Z}_p} A$
-submodule of
![]() $\mathfrak {L}$
(respectively,
$\mathfrak {L}$
(respectively,
![]() $\mathfrak {L}^+$
) on which
$\mathfrak {L}^+$
) on which
![]() $I(K'/K)$
acts through
$I(K'/K)$
acts through
![]() $\xi $
. We say that the pair
$\xi $
. We say that the pair
![]() $(\mathfrak {L},\mathfrak {L}^+)$
satisfies the strong determinant condition if Zariski locally on
$(\mathfrak {L},\mathfrak {L}^+)$
satisfies the strong determinant condition if Zariski locally on
![]() $\operatorname {\mathrm {Spec}} A$
the following condition holds: for all
$\operatorname {\mathrm {Spec}} A$
the following condition holds: for all
![]() $\alpha \in {\mathcal O}_N$
and all
$\alpha \in {\mathcal O}_N$
and all
![]() $\xi $
, we have
$\xi $
, we have
 $$ \begin{align} \det{\!}_A(\alpha{}|\mathfrak{L}^+_{\xi}) =\prod_{\psi:N\hookrightarrow E}\psi(\alpha{}) \end{align} $$
$$ \begin{align} \det{\!}_A(\alpha{}|\mathfrak{L}^+_{\xi}) =\prod_{\psi:N\hookrightarrow E}\psi(\alpha{}) \end{align} $$
as polynomial functions on
![]() ${\mathcal O}_N$
in the sense of [Reference KottwitzKot92, Section 5.1].
${\mathcal O}_N$
in the sense of [Reference KottwitzKot92, Section 5.1].
Definition 2.3.5. An object
![]() $\mathfrak {M}$
of
$\mathfrak {M}$
of
![]() ${\mathcal C}^{\mathrm {dd},a}$
satisfies the strong determinant condition if the pair
${\mathcal C}^{\mathrm {dd},a}$
satisfies the strong determinant condition if the pair
![]() $(\mathfrak {M}/E(u)\mathfrak {M}, \operatorname {\mathrm {im}} \Phi _{\mathfrak {M}}/E(u)\mathfrak {M})$
satisfies the strong determinant condition, as in the previous paragraph.
$(\mathfrak {M}/E(u)\mathfrak {M}, \operatorname {\mathrm {im}} \Phi _{\mathfrak {M}}/E(u)\mathfrak {M})$
satisfies the strong determinant condition, as in the previous paragraph.
We define
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}$
to be the substack of
${\mathcal C}^{\tau ,\operatorname {BT}}$
to be the substack of
![]() ${\mathcal C}^{\tau }$
of objects satisfying the strong determinant condition. This is a
${\mathcal C}^{\tau }$
of objects satisfying the strong determinant condition. This is a
![]() $\varpi $
-adic formal algebraic stack of finite presentation over
$\varpi $
-adic formal algebraic stack of finite presentation over
![]() ${\mathcal O}$
by [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Proposition 4.2.7], and so its special fibre
${\mathcal O}$
by [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Proposition 4.2.7], and so its special fibre
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is an algebraic stack, locally of finite type over
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is an algebraic stack, locally of finite type over
![]() ${\mathbf F}$
.
${\mathbf F}$
.
The motivation for imposing the strong determinant condition is that the corresponding substack
![]() ${\mathcal C}^{\mathrm {dd},\operatorname {BT}}$
of
${\mathcal C}^{\mathrm {dd},\operatorname {BT}}$
of
![]() ${\mathcal C}^{\mathrm {dd}}$
is precisely the
${\mathcal C}^{\mathrm {dd}}$
is precisely the
![]() ${\mathcal O}$
-flat substack of
${\mathcal O}$
-flat substack of
![]() ${\mathcal C}^{\mathrm {dd}}$
whose
${\mathcal C}^{\mathrm {dd}}$
whose
![]() $\operatorname {\mathrm {Spf}}({\mathcal O}_{E'})$
-points, for any finite extension
$\operatorname {\mathrm {Spf}}({\mathcal O}_{E'})$
-points, for any finite extension
![]() $E'/E$
, correspond to potentially Barsotti–Tate Galois representations
$E'/E$
, correspond to potentially Barsotti–Tate Galois representations
![]() $G_K \to \operatorname {\mathrm {GL}}_2({\mathcal O}_{E'})$
; so
$G_K \to \operatorname {\mathrm {GL}}_2({\mathcal O}_{E'})$
; so
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}$
corresponds to those representations which are furthermore of inertial type
${\mathcal C}^{\tau ,\operatorname {BT}}$
corresponds to those representations which are furthermore of inertial type
![]() $\tau $
. (See [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma 4.2.16], as well as the discussion at [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Remark 4.2.8].)
$\tau $
. (See [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma 4.2.16], as well as the discussion at [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Remark 4.2.8].)
The following result combines [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Corollary 4.5.3, Proposition 5.2.21].
Theorem 2.3.6. We have:
-
1.
 ${\mathcal C}^{\tau ,\operatorname {BT}}$
is analytically normal, and Cohen–Macaulay.
${\mathcal C}^{\tau ,\operatorname {BT}}$
is analytically normal, and Cohen–Macaulay. -
2. The special fibre
 ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is reduced and equidimensional of dimension equal to
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is reduced and equidimensional of dimension equal to
 $[K:{\mathbf Q}_p]$
.
$[K:{\mathbf Q}_p]$
. -
3.
 ${\mathcal C}^{\tau ,\operatorname {BT}}$
is flat over
${\mathcal C}^{\tau ,\operatorname {BT}}$
is flat over
 ${\mathcal O}$
.
${\mathcal O}$
.
We now introduce our stacks of étale
![]() $\varphi $
-modules.
$\varphi $
-modules.
Definition 2.3.7. Let
![]() ${\mathcal R}^{\mathrm {dd},1}$
be the fppf
${\mathcal R}^{\mathrm {dd},1}$
be the fppf
![]() ${\mathbf F}$
-stack, which associates to any
${\mathbf F}$
-stack, which associates to any
![]() ${\mathbf F}$
-algebra A the groupoid
${\mathbf F}$
-algebra A the groupoid
![]() ${\mathcal R}^{\mathrm {dd},1}(A)$
of rank two étale
${\mathcal R}^{\mathrm {dd},1}(A)$
of rank two étale
![]() $\varphi $
-modules with A-coefficients and descent data from
$\varphi $
-modules with A-coefficients and descent data from
![]() $K'$
to K.
$K'$
to K.
Inverting u gives a proper morphism
![]() ${\mathcal C}^{\mathrm {dd},1} \to {\mathcal R}^{\mathrm {dd},1}$
, which then restricts to a proper morphism
${\mathcal C}^{\mathrm {dd},1} \to {\mathcal R}^{\mathrm {dd},1}$
, which then restricts to a proper morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal R}^{\mathrm {dd},1}$
for each
${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal R}^{\mathrm {dd},1}$
for each
![]() $\tau $
.
$\tau $
.
We now briefly remind the reader of some definitions from [Reference Emerton and GeeEG21, Section 3.2]. Let
![]() ${\mathcal X} \to {\mathcal F}$
be a proper morphism of stacks over a locally Noetherian base-scheme S, where
${\mathcal X} \to {\mathcal F}$
be a proper morphism of stacks over a locally Noetherian base-scheme S, where
![]() ${\mathcal X}$
is an algebraic stack which is locally of finite presentation over S, and the diagonal of
${\mathcal X}$
is an algebraic stack which is locally of finite presentation over S, and the diagonal of
![]() ${\mathcal F}$
is representable by algebraic spaces and locally of finite presentation.
${\mathcal F}$
is representable by algebraic spaces and locally of finite presentation.
We refer to [Reference Emerton and GeeEG21, Definition 3.2.8] for the definition of the scheme-theoretic image
![]() ${\mathcal Z}$
of the proper morphism
${\mathcal Z}$
of the proper morphism
![]() ${\mathcal X} \to {\mathcal F}$
. By definition, it is a full subcategory in groupoids of
${\mathcal X} \to {\mathcal F}$
. By definition, it is a full subcategory in groupoids of
![]() ${\mathcal F}$
, and, in fact, by [Reference Emerton and GeeEG21, Lemma 3.2.9], it is a Zariski substack of
${\mathcal F}$
, and, in fact, by [Reference Emerton and GeeEG21, Lemma 3.2.9], it is a Zariski substack of
![]() ${\mathcal F}$
. By [Reference Emerton and GeeEG21, Lemma 3.2.14], the finite type points of
${\mathcal F}$
. By [Reference Emerton and GeeEG21, Lemma 3.2.14], the finite type points of
![]() ${\mathcal Z}$
are precisely the finite type points of
${\mathcal Z}$
are precisely the finite type points of
![]() ${\mathcal F}$
for which the corresponding fibre of
${\mathcal F}$
for which the corresponding fibre of
![]() ${\mathcal X}$
is nonzero.
${\mathcal X}$
is nonzero.
The results of [Reference Emerton and GeeEG21, Section 3.2] give criteria for
![]() ${\mathcal Z}$
to be an algebraic stack, and prove a number of associated results (such as universal properties of the morphism
${\mathcal Z}$
to be an algebraic stack, and prove a number of associated results (such as universal properties of the morphism
![]() ${\mathcal Z}\to {\mathcal F}$
, and a description of versal deformation rings for
${\mathcal Z}\to {\mathcal F}$
, and a description of versal deformation rings for
![]() ${\mathcal Z}$
). This formalism applies, in particular, to the proper morphism
${\mathcal Z}$
). This formalism applies, in particular, to the proper morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal R}^{\mathrm {dd},1}$
, and so we make the following definition.
${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal R}^{\mathrm {dd},1}$
, and so we make the following definition.
Definition 2.3.8. We define
![]() ${\mathcal Z}^{\tau ,1}$
to be the scheme-theoretic image (in the sense of [Reference Emerton and GeeEG21, Definition 3.2.8]) of the morphism
${\mathcal Z}^{\tau ,1}$
to be the scheme-theoretic image (in the sense of [Reference Emerton and GeeEG21, Definition 3.2.8]) of the morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal R}^{\mathrm {dd},1}$
.
${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal R}^{\mathrm {dd},1}$
.
In [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Theorem 5.1.2, Proposition 5.2.20], we established the following properties of this construction.
Proposition 2.3.9.
-
1.
 ${\mathcal Z}^{\tau ,1}$
is an algebraic stack of finite presentation over
${\mathcal Z}^{\tau ,1}$
is an algebraic stack of finite presentation over
 ${\mathbf F}$
, and is a closed substack of
${\mathbf F}$
, and is a closed substack of
 ${\mathcal R}^{\mathrm {dd},1}$
.
${\mathcal R}^{\mathrm {dd},1}$
. -
2. The morphism
 ${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal R}^{\mathrm {dd},1}$
factors through a morphism
${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal R}^{\mathrm {dd},1}$
factors through a morphism
 ${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal Z}^{\mathrm {dd},1}$
which is representable by algebraic spaces, scheme-theoretically dominant and proper.
${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal Z}^{\mathrm {dd},1}$
which is representable by algebraic spaces, scheme-theoretically dominant and proper. -
3. The
 $\overline {{\mathbf F}}_p$
-points of
$\overline {{\mathbf F}}_p$
-points of
 ${\mathcal Z}^{\tau ,1}$
are naturally in bijection with the continuous representations
${\mathcal Z}^{\tau ,1}$
are naturally in bijection with the continuous representations
 $\overline {r} : G_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, which have a potentially Barsotti–Tate lift of type
$\overline {r} : G_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, which have a potentially Barsotti–Tate lift of type
 $\tau $
.
$\tau $
.
Theorem 2.3.10. The algebraic stacks
![]() ${\mathcal Z}^{\tau ,1}$
are equidimensional of dimension equal to
${\mathcal Z}^{\tau ,1}$
are equidimensional of dimension equal to
![]() $[K:{\mathbf Q}_p]$
.
$[K:{\mathbf Q}_p]$
.
2.4. Dieudonné and gauge stacks
In this subsection, we express the passage from Breuil–Kisin modules (with descent data) to Dieudonné modules in stacky terms. The consequent geometric results are most conveniently expressed in the language of effective Cartier on formal algebraic stacks, and so we briefly recall the relevant notions. We also note that the material of this subsection is only used in Section 5.4 below.
To begin with, we choose a tame inertial type
![]() $\tau =\eta \oplus \eta '$
, and we then specialise the choice of
$\tau =\eta \oplus \eta '$
, and we then specialise the choice of
![]() $K'$
in the following way. We fix a uniformiser
$K'$
in the following way. We fix a uniformiser
![]() $\pi $
of K, and if
$\pi $
of K, and if
![]() $\tau $
is a tame principal series type, we take
$\tau $
is a tame principal series type, we take
![]() $K'=K(\pi ^{1/(p^f-1)})$
, while if
$K'=K(\pi ^{1/(p^f-1)})$
, while if
![]() $\tau $
is a tame cuspidal type, we let L be an unramified quadratic extension of K, and set
$\tau $
is a tame cuspidal type, we let L be an unramified quadratic extension of K, and set
![]() $K'=L(\pi ^{1/(p^{2f}-1)})$
. In either case,
$K'=L(\pi ^{1/(p^{2f}-1)})$
. In either case,
![]() $K'/K$
is a Galois extension; in the principal series case, we have
$K'/K$
is a Galois extension; in the principal series case, we have
![]() $e'=(p^f-1)e$
,
$e'=(p^f-1)e$
,
![]() $f'=f$
, and in the cuspidal case, we have
$f'=f$
, and in the cuspidal case, we have
![]() $e'=(p^{2f}-1)e$
,
$e'=(p^{2f}-1)e$
,
![]() $f'=2f$
. Here and below, we refer to this choice of extension as the standard choice (for the fixed type
$f'=2f$
. Here and below, we refer to this choice of extension as the standard choice (for the fixed type
![]() $\tau $
and uniformiser
$\tau $
and uniformiser
![]() $\pi $
).
$\pi $
).
For the rest of this section, we assume that
![]() $\eta \ne \eta '$
. (For our intended application, we will not need to consider Dieudonné modules for scalar types.) Let
$\eta \ne \eta '$
. (For our intended application, we will not need to consider Dieudonné modules for scalar types.) Let
![]() $\mathfrak {M}$
be an object of
$\mathfrak {M}$
be an object of
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}(A)$
, and let
${\mathcal C}^{\tau ,\operatorname {BT}}(A)$
, and let
![]() $D := \mathfrak {M}/u\mathfrak {M}$
be its corresponding Dieudonné module, as in Definition 2.1.7. The group
$D := \mathfrak {M}/u\mathfrak {M}$
be its corresponding Dieudonné module, as in Definition 2.1.7. The group
![]() $I(K'/K)$
is abelian of order prime to p, and so we can write
$I(K'/K)$
is abelian of order prime to p, and so we can write
![]() $D=D_{\eta }\oplus D_{\eta '}$
, where
$D=D_{\eta }\oplus D_{\eta '}$
, where
![]() $D_{\eta }$
is the submodule on which
$D_{\eta }$
is the submodule on which
![]() $I(K'/K)$
acts via
$I(K'/K)$
acts via
![]() $\eta $
. Setting
$\eta $
. Setting
![]() $D_{\eta ,j} := e_j D_{\eta }$
, it follows from the projectivity of
$D_{\eta ,j} := e_j D_{\eta }$
, it follows from the projectivity of
![]() $\mathfrak {M}$
that each
$\mathfrak {M}$
that each
![]() $D_{\eta ,j}$
is an invertible A-module. The maps
$D_{\eta ,j}$
is an invertible A-module. The maps
![]() $F,V$
induce linear maps
$F,V$
induce linear maps
![]() $F:D_{\eta ,j}\to D_{\eta ,j+1}$
and
$F:D_{\eta ,j}\to D_{\eta ,j+1}$
and
![]() $V: D_{\eta ,j+1} \to D_{\eta ,j}$
, such that
$V: D_{\eta ,j+1} \to D_{\eta ,j}$
, such that
![]() $FV = VF = p$
.
$FV = VF = p$
.
Definition 2.4.1. If
![]() $\tau $
is a principal series type, we define a stack
$\tau $
is a principal series type, we define a stack
where the f copies of
![]() $\mathbf G_m$
act as
$\mathbf G_m$
act as
![]() $(u_0,\ldots ,u_{f-1}) \cdot (X_j,Y_j) \mapsto (u_j u_{j+1}^{-1} X_j, u_{j+1} u_j^{-1} Y_j),$
in which we take
$(u_0,\ldots ,u_{f-1}) \cdot (X_j,Y_j) \mapsto (u_j u_{j+1}^{-1} X_j, u_{j+1} u_j^{-1} Y_j),$
in which we take
![]() $u_f := u_0$
.
$u_f := u_0$
.
If, instead,
![]() $\tau $
is a cuspidal type, we define
$\tau $
is a cuspidal type, we define
where the
![]() $f+1$
copies of
$f+1$
copies of
![]() $\mathbf G_m$
act as
$\mathbf G_m$
act as
in which
![]() $\alpha $
and
$\alpha $
and
![]() $u_0,\ldots ,u_f$
are the coordinates of the
$u_0,\ldots ,u_f$
are the coordinates of the
![]() ${\mathbf G}_m$
’s appearing in the definition of
${\mathbf G}_m$
’s appearing in the definition of
![]() ${\mathcal D}_{\eta }$
.
${\mathcal D}_{\eta }$
.
In [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Section 4.6], we explained how the stack
![]() ${\mathcal D}_{\eta }$
classifies the line bundles
${\mathcal D}_{\eta }$
classifies the line bundles
![]() $D_{\eta ,j}$
together with the maps
$D_{\eta ,j}$
together with the maps
![]() $F,V$
, so that in either case (principal series or cuspidal), there is a natural map
$F,V$
, so that in either case (principal series or cuspidal), there is a natural map
![]() ${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal D}_{\eta }$
.
${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal D}_{\eta }$
.
It will be helpful to introduce another stack, the stack
![]() ${\mathcal G}_{\eta }$
of
${\mathcal G}_{\eta }$
of
![]() $\eta $
-gauges. This classifies f-tuples of line bundles
$\eta $
-gauges. This classifies f-tuples of line bundles
![]() ${\mathcal D}_j$
(
${\mathcal D}_j$
(
![]() $j = 0,\ldots ,f-1$
) equipped with sections
$j = 0,\ldots ,f-1$
) equipped with sections
![]() $X_j \in {\mathcal D}_j$
and
$X_j \in {\mathcal D}_j$
and
![]() $Y_j \in {\mathcal D}_j^{-1}$
. Explicitly, it can be written as the quotient stack
$Y_j \in {\mathcal D}_j^{-1}$
. Explicitly, it can be written as the quotient stack
where the f copies of
![]() $\mathbf G_m$
act as follows:
$\mathbf G_m$
act as follows:
There is a morphism of stacks
![]() ${\mathcal D}_{\eta } \to {\mathcal G}_{\eta }$
which we can define explicitly using their descriptions as quotient stacks. Indeed, in the principal series case, we have a morphism
${\mathcal D}_{\eta } \to {\mathcal G}_{\eta }$
which we can define explicitly using their descriptions as quotient stacks. Indeed, in the principal series case, we have a morphism
![]() ${\mathbf G}_m^f \to {\mathbf G}_m^f$
given by
${\mathbf G}_m^f \to {\mathbf G}_m^f$
given by
![]() $(u_j)_{j = 0,\ldots ,f-1} \mapsto (u_j u_{j+1}^{-1})_{j = 0,\ldots ,f-1}$
, which is compatible with the actions of these two groups on
$(u_j)_{j = 0,\ldots ,f-1} \mapsto (u_j u_{j+1}^{-1})_{j = 0,\ldots ,f-1}$
, which is compatible with the actions of these two groups on
![]() $\operatorname {\mathrm {Spec}} W(k)[(X_j,Y_j)_{j=0,\ldots ,f-1}]/(X_j Y_j - p)_{j = 0, \ldots , f-1},$
and we are just considering the map from the quotient by the first
$\operatorname {\mathrm {Spec}} W(k)[(X_j,Y_j)_{j=0,\ldots ,f-1}]/(X_j Y_j - p)_{j = 0, \ldots , f-1},$
and we are just considering the map from the quotient by the first
![]() ${\mathbf G}_m^f$
to the quotient by the second
${\mathbf G}_m^f$
to the quotient by the second
![]() ${\mathbf G}_m^f$
. In the cuspidal case, we have a morphism
${\mathbf G}_m^f$
. In the cuspidal case, we have a morphism
![]() ${\mathbf G}_m^{f+1} \to {\mathbf G}_m^f$
given by
${\mathbf G}_m^{f+1} \to {\mathbf G}_m^f$
given by
![]() $(u_j)_{j = 0,\ldots ,f} \mapsto (u_j u_{j+1}^{-1})_{j = 0,\ldots ,f-1}$
, and the morphism
$(u_j)_{j = 0,\ldots ,f} \mapsto (u_j u_{j+1}^{-1})_{j = 0,\ldots ,f-1}$
, and the morphism
![]() ${\mathcal D}_{\eta } \to {\mathcal G}_{\eta }$
is the obvious one which forgets the factor of
${\mathcal D}_{\eta } \to {\mathcal G}_{\eta }$
is the obvious one which forgets the factor of
![]() ${\mathbf G}_m$
coming from
${\mathbf G}_m$
coming from
![]() $\alpha $
.
$\alpha $
.
Composing our morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal D}_{\eta }$
with the forgetful morphism
${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal D}_{\eta }$
with the forgetful morphism
![]() ${\mathcal D}_{\eta } \to {\mathcal G}_{\eta }$
, we obtain a morphism
${\mathcal D}_{\eta } \to {\mathcal G}_{\eta }$
, we obtain a morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal G}_{\eta }$
.
${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal G}_{\eta }$
.
For our analysis of the irreducible components of the stacks
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
at the end of Section 3, it will be useful to have a more directly geometric interpretation of a morphism
${\mathcal C}^{\tau ,\operatorname {BT},1}$
at the end of Section 3, it will be useful to have a more directly geometric interpretation of a morphism
![]() $S \to {\mathcal G}_{\eta }$
, in the case that the source is a flat
$S \to {\mathcal G}_{\eta }$
, in the case that the source is a flat
![]() $W(k)$
-scheme, or, more generally, a flat p-adic formal algebraic stack over
$W(k)$
-scheme, or, more generally, a flat p-adic formal algebraic stack over
![]() $\operatorname {\mathrm {Spf}} W(k)$
. In order to do this, we will need some basic material on effective Cartier divisors for (formal) algebraic stacks; while it is presumably possible to develop this theory in considerable generality, we only need a very special case, and we limit ourselves to this setting.
$\operatorname {\mathrm {Spf}} W(k)$
. In order to do this, we will need some basic material on effective Cartier divisors for (formal) algebraic stacks; while it is presumably possible to develop this theory in considerable generality, we only need a very special case, and we limit ourselves to this setting.
The property of a closed subscheme being an effective Cartier divisor is not preserved under arbitrary pullback, but it is preserved under flat pullback. More precisely, we have the following result.
Lemma 2.4.2. If X is a scheme, and Z is a closed subscheme of X, then the following are equivalent:
-
1. Z is an effective Cartier divisor on X.
-
2. For any flat morphism of schemes
 $U \to X$
, the pullback
$U \to X$
, the pullback
 $Z\times _{X} U$
is an effective Cartier divisor on U.
$Z\times _{X} U$
is an effective Cartier divisor on U. -
3. For some fpqc covering
 $\{X_i \to X\}$
of X, each of the pullbacks
$\{X_i \to X\}$
of X, each of the pullbacks
 $Z\times _{X} X_i$
is an effective Cartier divisor on
$Z\times _{X} X_i$
is an effective Cartier divisor on
 $X_i$
.
$X_i$
.
Proof. Since Z is an effective Cartier divisor if and only if its ideal sheaf
![]() ${\mathcal I}_Z$
is an invertible sheaf on X, this follows from the fact that the invertibility of a quasi-coherent sheaf is a local property in the fpqc topology.
${\mathcal I}_Z$
is an invertible sheaf on X, this follows from the fact that the invertibility of a quasi-coherent sheaf is a local property in the fpqc topology.
Lemma 2.4.3. If A is a Noetherian adic topological ring, then pullback under the natural morphism
![]() $\operatorname {\mathrm {Spf}} A \to \operatorname {\mathrm {Spec}} A$
induces a bijection between the closed subschemes of
$\operatorname {\mathrm {Spf}} A \to \operatorname {\mathrm {Spec}} A$
induces a bijection between the closed subschemes of
![]() $\operatorname {\mathrm {Spec}} A$
and the closed subspaces of
$\operatorname {\mathrm {Spec}} A$
and the closed subspaces of
![]() $\operatorname {\mathrm {Spf}} A$
.
$\operatorname {\mathrm {Spf}} A$
.
Proof. It follows from [Sta13, Tag 0ANQ] that closed immersions
![]() $Z \to \operatorname {\mathrm {Spf}} A$
are necessarily of the form
$Z \to \operatorname {\mathrm {Spf}} A$
are necessarily of the form
![]() $\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
, and correspond to continuous morphisms
$\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
, and correspond to continuous morphisms
![]() $A \to B$
, for some complete linearly topologised ring B, which are taut (in the sense of [Sta13, Tag 0AMX]), have closed kernel and dense image. Since A is adic, it admits a countable basis of neighbourhoods of the origin, and so it follows from [Sta13, Tag 0APT] (recalling also [Sta13, Tag 0AMV]) that
$A \to B$
, for some complete linearly topologised ring B, which are taut (in the sense of [Sta13, Tag 0AMX]), have closed kernel and dense image. Since A is adic, it admits a countable basis of neighbourhoods of the origin, and so it follows from [Sta13, Tag 0APT] (recalling also [Sta13, Tag 0AMV]) that
![]() $A\to B$
is surjective. Because any ideal of definition I of A is finitely generated, it follows from [Sta13, Tag 0APU] that B is endowed with the I-adic topology. Finally, since A is Noetherian, any ideal in A is I-adically closed. Thus closed immersions
$A\to B$
is surjective. Because any ideal of definition I of A is finitely generated, it follows from [Sta13, Tag 0APU] that B is endowed with the I-adic topology. Finally, since A is Noetherian, any ideal in A is I-adically closed. Thus closed immersions
![]() $\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
are determined by giving the kernel of the corresponding morphism
$\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
are determined by giving the kernel of the corresponding morphism
![]() $A \to B$
, which can be arbitrary. The same is true of closed immersions
$A \to B$
, which can be arbitrary. The same is true of closed immersions
![]() $\operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A$
, and so the lemma follows.
$\operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A$
, and so the lemma follows.
Definition 2.4.4. If A is a Noetherian adic topological ring, then we say that a closed subspace of
![]() $\operatorname {\mathrm {Spf}} A$
is an effective Cartier divisor on
$\operatorname {\mathrm {Spf}} A$
is an effective Cartier divisor on
![]() $\operatorname {\mathrm {Spf}} A$
if the corresponding closed subscheme of
$\operatorname {\mathrm {Spf}} A$
if the corresponding closed subscheme of
![]() $\operatorname {\mathrm {Spec}} A$
is an effective Cartier divisor on
$\operatorname {\mathrm {Spec}} A$
is an effective Cartier divisor on
![]() $\operatorname {\mathrm {Spec}} A$
.
$\operatorname {\mathrm {Spec}} A$
.
Lemma 2.4.5. Let
![]() $\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
be a flat adic morphism of Noetherian affine formal algebraic spaces. If
$\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
be a flat adic morphism of Noetherian affine formal algebraic spaces. If
![]() $Z \hookrightarrow \operatorname {\mathrm {Spf}} A$
is a Cartier divisor, then
$Z \hookrightarrow \operatorname {\mathrm {Spf}} A$
is a Cartier divisor, then
![]() $Z \times _{\operatorname {\mathrm {Spf}} A} \operatorname {\mathrm {Spf}} B \hookrightarrow \operatorname {\mathrm {Spf}} B$
is a Cartier divisor. Conversely, if
$Z \times _{\operatorname {\mathrm {Spf}} A} \operatorname {\mathrm {Spf}} B \hookrightarrow \operatorname {\mathrm {Spf}} B$
is a Cartier divisor. Conversely, if
![]() $\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
is furthermore surjective, and if
$\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
is furthermore surjective, and if
![]() $Z \hookrightarrow \operatorname {\mathrm {Spf}} A$
is a closed subspace for which the base-change
$Z \hookrightarrow \operatorname {\mathrm {Spf}} A$
is a closed subspace for which the base-change
![]() $Z \times _{\operatorname {\mathrm {Spf}} A} \operatorname {\mathrm {Spf}} B \hookrightarrow \operatorname {\mathrm {Spf}} B$
is a Cartier divisor, then Z is a Cartier divisor on
$Z \times _{\operatorname {\mathrm {Spf}} A} \operatorname {\mathrm {Spf}} B \hookrightarrow \operatorname {\mathrm {Spf}} B$
is a Cartier divisor, then Z is a Cartier divisor on
![]() $\operatorname {\mathrm {Spf}} A$
.
$\operatorname {\mathrm {Spf}} A$
.
Proof. The morphism
![]() $\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
corresponds to an adic flat morphism
$\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
corresponds to an adic flat morphism
![]() $A \to B$
([Sta13, Tag 0AN0] and [Reference EmertonEme, Lemma 8.18]) and hence is induced by a flat morphism
$A \to B$
([Sta13, Tag 0AN0] and [Reference EmertonEme, Lemma 8.18]) and hence is induced by a flat morphism
![]() $\operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A$
, which is furthermore faithfully flat if and only if
$\operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A$
, which is furthermore faithfully flat if and only if
![]() $\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
is surjective (again by [Reference EmertonEme, Lemma 8.18]). The present lemma thus follows from Lemma 2.4.2.
$\operatorname {\mathrm {Spf}} B \to \operatorname {\mathrm {Spf}} A$
is surjective (again by [Reference EmertonEme, Lemma 8.18]). The present lemma thus follows from Lemma 2.4.2.
The preceding lemma justifies the following definition.
Definition 2.4.6. We say that a closed substack
![]() ${\mathcal Z}$
of a locally Noetherian formal algebraic stack
${\mathcal Z}$
of a locally Noetherian formal algebraic stack
![]() ${\mathcal X}$
is an effective Cartier divisor on
${\mathcal X}$
is an effective Cartier divisor on
![]() ${\mathcal X}$
if for any morphism
${\mathcal X}$
if for any morphism
![]() $U \to {\mathcal X}$
whose source is a Noetherian affine formal algebraic space, and which is representable by algebraic spaces and flat, the pullback
$U \to {\mathcal X}$
whose source is a Noetherian affine formal algebraic space, and which is representable by algebraic spaces and flat, the pullback
![]() ${\mathcal Z}\times _{{\mathcal X}} U$
is an effective Cartier divisor on U.
${\mathcal Z}\times _{{\mathcal X}} U$
is an effective Cartier divisor on U.
We consider the
![]() $W(k)$
-scheme
$W(k)$
-scheme
![]() $\operatorname {\mathrm {Spec}} W(k)[X,Y]/(XY - p)$
, which we endow with a
$\operatorname {\mathrm {Spec}} W(k)[X,Y]/(XY - p)$
, which we endow with a
![]() ${\mathbf G}_m$
-action via
${\mathbf G}_m$
-action via
![]() $u\cdot (X,Y) := (uX, u^{-1} Y).$
There is an obvious morphism
$u\cdot (X,Y) := (uX, u^{-1} Y).$
There is an obvious morphism
given by
![]() $(X,Y) \to X$
, which is
$(X,Y) \to X$
, which is
![]() ${\mathbf G}_m$
-equivariant (for the action of
${\mathbf G}_m$
-equivariant (for the action of
![]() ${\mathbf G}_m$
on
${\mathbf G}_m$
on
![]() $\mathbf A^1$
given by
$\mathbf A^1$
given by
![]() $u\cdot X:=uX$
), and so induces a morphism
$u\cdot X:=uX$
), and so induces a morphism
Lemma 2.4.8. If
![]() ${\mathcal X}$
is a locally Noetherian p-adic formal algebraic stack which is furthermore flat over
${\mathcal X}$
is a locally Noetherian p-adic formal algebraic stack which is furthermore flat over
![]() $\operatorname {\mathrm {Spf}} W(k)$
, then the groupoid of morphisms
$\operatorname {\mathrm {Spf}} W(k)$
, then the groupoid of morphisms
is in fact a setoid, and is equivalent to the set of effective Cartier divisors on
![]() ${\mathcal X}$
that are contained in the effective Cartier divisor
${\mathcal X}$
that are contained in the effective Cartier divisor
![]() $(\operatorname {\mathrm {Spec}} k) \times _{\operatorname {\mathrm {Spf}} W(k)} {\mathcal X}$
on
$(\operatorname {\mathrm {Spec}} k) \times _{\operatorname {\mathrm {Spf}} W(k)} {\mathcal X}$
on
![]() ${\mathcal X}$
.
${\mathcal X}$
.
Proof. Essentially by definition (and taking into account [Reference EmertonEme, Lemma 8.18]), it suffices to prove this in the case when
![]() ${\mathcal X} = \operatorname {\mathrm {Spf}} B$
, where B is a flat Noetherian adic
${\mathcal X} = \operatorname {\mathrm {Spf}} B$
, where B is a flat Noetherian adic
![]() $W(k)$
-algebra admitting
$W(k)$
-algebra admitting
![]() $(p)$
as an ideal of definition. In this case, the restriction map
$(p)$
as an ideal of definition. In this case, the restriction map
is an equivalence of groupoids. Indeed, the essential surjectivity follows from the (standard and easily verified) fact that if
![]() $\{M_i\}$
is a compatible family of locally free
$\{M_i\}$
is a compatible family of locally free
![]() $B/p^iB$
-modules of rank one, then
$B/p^iB$
-modules of rank one, then
![]() $M := \varprojlim M_i$
is a locally free B-module of rank one, for which each of the natural morphisms
$M := \varprojlim M_i$
is a locally free B-module of rank one, for which each of the natural morphisms
![]() $M/p^iM \to M_i$
is an isomorphism. The full faithfulness follows from the fact that a locally free B-module of rank one is p-adically complete, and so is recovered as the inverse limit of its compatible family of quotients
$M/p^iM \to M_i$
is an isomorphism. The full faithfulness follows from the fact that a locally free B-module of rank one is p-adically complete, and so is recovered as the inverse limit of its compatible family of quotients
![]() $\{M/p^iM\}.$
$\{M/p^iM\}.$
We are therefore reduced to the same statement with
![]() ${\mathcal X} = \operatorname {\mathrm {Spec}} B$
. The composite morphism
${\mathcal X} = \operatorname {\mathrm {Spec}} B$
. The composite morphism
![]() $\operatorname {\mathrm {Spec}} B \to [\mathbf A^1/{\mathbf G}_m]$
induced by (2.4.7) corresponds to giving a pair
$\operatorname {\mathrm {Spec}} B \to [\mathbf A^1/{\mathbf G}_m]$
induced by (2.4.7) corresponds to giving a pair
![]() $({\mathcal D},X)$
, where
$({\mathcal D},X)$
, where
![]() ${\mathcal D}$
is a line bundle on
${\mathcal D}$
is a line bundle on
![]() $\operatorname {\mathrm {Spec}} B$
, and X is a global section of
$\operatorname {\mathrm {Spec}} B$
, and X is a global section of
![]() ${\mathcal D}^{-1}$
. Indeed, giving a morphism
${\mathcal D}^{-1}$
. Indeed, giving a morphism
![]() $\operatorname {\mathrm {Spec}} B \to [\mathbf A^1/{\mathbf G}_m]$
is equivalent to giving a
$\operatorname {\mathrm {Spec}} B \to [\mathbf A^1/{\mathbf G}_m]$
is equivalent to giving a
![]() ${\mathbf G}_m$
-torsor
${\mathbf G}_m$
-torsor
![]() $P \to \operatorname {\mathrm {Spec}} B$
, together with a
$P \to \operatorname {\mathrm {Spec}} B$
, together with a
![]() ${\mathbf G}_m$
-equivariant morphism
${\mathbf G}_m$
-equivariant morphism
![]() $P \to \mathbf A^1$
. Giving a
$P \to \mathbf A^1$
. Giving a
![]() ${\mathbf G}_m$
-torsor P over
${\mathbf G}_m$
-torsor P over
![]() $\operatorname {\mathrm {Spec}} B$
is equivalent to giving an invertible sheaf
$\operatorname {\mathrm {Spec}} B$
is equivalent to giving an invertible sheaf
![]() ${\mathcal D}$
on
${\mathcal D}$
on
![]() $\operatorname {\mathrm {Spec}} B$
(the associated
$\operatorname {\mathrm {Spec}} B$
(the associated
![]() ${\mathbf G}_m$
-torsor is then obtained by deleting the zero section from the line bundle
${\mathbf G}_m$
-torsor is then obtained by deleting the zero section from the line bundle
![]() $D\to X$
corresponding to
$D\to X$
corresponding to
![]() ${\mathcal D}$
), and giving a
${\mathcal D}$
), and giving a
![]() ${\mathbf G}_m$
-equivariant morphism
${\mathbf G}_m$
-equivariant morphism
![]() $P \to \mathbf A^1$
is equivalent to giving a global section of
$P \to \mathbf A^1$
is equivalent to giving a global section of
![]() ${\mathcal D}^{-1}$
.
${\mathcal D}^{-1}$
.
It follows that giving a morphism
![]() $\operatorname {\mathrm {Spec}} B \to [\operatorname {\mathrm {Spec}} W(k)[X,Y]/(XY - p) / {\mathbf G}_m]$
corresponds to giving a line bundle
$\operatorname {\mathrm {Spec}} B \to [\operatorname {\mathrm {Spec}} W(k)[X,Y]/(XY - p) / {\mathbf G}_m]$
corresponds to giving a line bundle
![]() ${\mathcal D}$
and sections
${\mathcal D}$
and sections
![]() $X \in {\mathcal D}^{-1}$
,
$X \in {\mathcal D}^{-1}$
,
![]() $Y \in {\mathcal D}$
satisfying
$Y \in {\mathcal D}$
satisfying
![]() $X Y = p$
. To say that B is flat over
$X Y = p$
. To say that B is flat over
![]() $W(k)$
is just to say that p is a regular element on B, and so we see that X (respectively, Y) is a regular section of
$W(k)$
is just to say that p is a regular element on B, and so we see that X (respectively, Y) is a regular section of
![]() ${\mathcal D}^{-1}$
(respectively,
${\mathcal D}^{-1}$
(respectively,
![]() ${\mathcal D}$
). Again, since p is a regular element on B, we see that Y is uniquely determined by X and the equation
${\mathcal D}$
). Again, since p is a regular element on B, we see that Y is uniquely determined by X and the equation
![]() $X Y = p$
, and so giving a morphism
$X Y = p$
, and so giving a morphism
![]() $\operatorname {\mathrm {Spec}} B\to [\operatorname {\mathrm {Spec}} W(k)[X,Y]/(XY - p) / {\mathbf G}_m]$
is equivalent to giving a line bundle
$\operatorname {\mathrm {Spec}} B\to [\operatorname {\mathrm {Spec}} W(k)[X,Y]/(XY - p) / {\mathbf G}_m]$
is equivalent to giving a line bundle
![]() ${\mathcal D}$
and a regular section X of
${\mathcal D}$
and a regular section X of
![]() ${\mathcal D}^{-1}$
, such that
${\mathcal D}^{-1}$
, such that
![]() $pB \subset X\otimes _B {\mathcal D} \subset {\mathcal D}^{-1}\otimes _B {\mathcal D}\buildrel \sim \over \longrightarrow B$
; this last condition guarantees the existence of the (then uniquely determined) Y.
$pB \subset X\otimes _B {\mathcal D} \subset {\mathcal D}^{-1}\otimes _B {\mathcal D}\buildrel \sim \over \longrightarrow B$
; this last condition guarantees the existence of the (then uniquely determined) Y.
Now, giving a line bundle
![]() ${\mathcal D}$
on
${\mathcal D}$
on
![]() $\operatorname {\mathrm {Spec}} B$
and a regular section
$\operatorname {\mathrm {Spec}} B$
and a regular section
![]() $X\in {\mathcal D}^{-1}$
is the same as giving the zero locus D of X, which is a Cartier divisor on
$X\in {\mathcal D}^{-1}$
is the same as giving the zero locus D of X, which is a Cartier divisor on
![]() $\operatorname {\mathrm {Spec}} B$
. (There is a canonical isomorphism
$\operatorname {\mathrm {Spec}} B$
. (There is a canonical isomorphism
![]() $({\mathcal D},X) \cong \bigl ({\mathcal I}_D,1\bigr )$
, where
$({\mathcal D},X) \cong \bigl ({\mathcal I}_D,1\bigr )$
, where
![]() ${\mathcal I}_D$
denotes the ideal sheaf of D.) The condition that
${\mathcal I}_D$
denotes the ideal sheaf of D.) The condition that
![]() $pB \subset X\otimes _B {\mathcal D}$
is equivalent to the condition that
$pB \subset X\otimes _B {\mathcal D}$
is equivalent to the condition that
![]() $p \in {\mathcal I}_D$
, that is, that D be contained in
$p \in {\mathcal I}_D$
, that is, that D be contained in
![]() $\operatorname {\mathrm {Spec}} B/pB$
, and we are done.
$\operatorname {\mathrm {Spec}} B/pB$
, and we are done.
Lemma 2.4.9. If
![]() ${\mathcal S}$
is a locally Noetherian p-adic formal algebraic stack which is flat over
${\mathcal S}$
is a locally Noetherian p-adic formal algebraic stack which is flat over
![]() $W(k)$
, then giving a morphism
$W(k)$
, then giving a morphism
![]() ${\mathcal S} \to {\mathcal G}_{\eta }$
over
${\mathcal S} \to {\mathcal G}_{\eta }$
over
![]() $W(k)$
is equivalent to giving a collection of effective Cartier divisors
$W(k)$
is equivalent to giving a collection of effective Cartier divisors
![]() ${\mathcal D}_j$
on
${\mathcal D}_j$
on
![]() ${\mathcal S}$
(
${\mathcal S}$
(
![]() $j = 0, \ldots ,f-1$
), with each
$j = 0, \ldots ,f-1$
), with each
![]() ${\mathcal D}_j$
contained in the Cartier divisor
${\mathcal D}_j$
contained in the Cartier divisor
![]() $\overline {{\mathcal S}}$
cut out by the equation
$\overline {{\mathcal S}}$
cut out by the equation
![]() $p = 0$
on
$p = 0$
on
![]() ${\mathcal S}$
(i.e. the special fibre of
${\mathcal S}$
(i.e. the special fibre of
![]() ${\mathcal S}$
).
${\mathcal S}$
).
Proof. This follows immediately from Lemma 2.4.8, by the definition of
![]() ${\mathcal G}_{\eta }$
.
${\mathcal G}_{\eta }$
.
3. Families of extensions of Breuil–Kisin modules
The goal of the next two sections is to construct certain universal families of extensions of rank one Breuil–Kisin modules over
![]() ${\mathbf F}$
with descent data; these families will be used in Section 5 to describe the generic behaviour of the various irreducible components of the special fibres of
${\mathbf F}$
with descent data; these families will be used in Section 5 to describe the generic behaviour of the various irreducible components of the special fibres of
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}$
and
${\mathcal C}^{\tau ,\operatorname {BT}}$
and
![]() ${\mathcal Z}^{\tau }$
.
${\mathcal Z}^{\tau }$
.
In Sections 3.1 and 3.2, we present some generalities on extensions of Breuil–Kisin modules and on families of these extensions, respectively. In Section 3.3, we specialise the discussion of Section 3.2 to the case of extensions of two rank one Breuil–Kisin modules, and thus explain how to construct our desired families of extensions. In Section 4, we recall the fundamental computations related to extensions of rank one Breuil–Kisin modules from [Reference Diamond and SavittDS15], to which the results of Section 3.3 will be applied at the end of Section 4.2 to construct the components
![]() $\overline {{\mathcal C}}(J)$
and
$\overline {{\mathcal C}}(J)$
and
![]() $\overline {{\mathcal Z}}(J)$
of Theorem 1.1.
$\overline {{\mathcal Z}}(J)$
of Theorem 1.1.
We assume throughout this section that
![]() $[K':K]$
is not divisible by p; since we are assuming throughout the paper that
$[K':K]$
is not divisible by p; since we are assuming throughout the paper that
![]() $K'/K$
is tamely ramified, this is equivalent to assuming that
$K'/K$
is tamely ramified, this is equivalent to assuming that
![]() $K'$
does not contain an unramified extension of K of degree p. In our final applications,
$K'$
does not contain an unramified extension of K of degree p. In our final applications,
![]() $K'/K$
will contain unramified extensions of degree at most
$K'/K$
will contain unramified extensions of degree at most
![]() $2$
, and p will be odd, so this assumption will be satisfied. (In fact, we specialise to such a context beginning in Section 5.2.)
$2$
, and p will be odd, so this assumption will be satisfied. (In fact, we specialise to such a context beginning in Section 5.2.)
3.1. Extensions of Breuil–Kisin modules with descent data
When discussing the general theory of extensions of Breuil–Kisin modules, it is convenient to embed the category of Breuil–Kisin modules in a larger category which is abelian, contains enough injectives and projectives, and is closed under passing to arbitrary limits and colimits. The simplest way to obtain such a category is as the category of modules over some ring, and so we briefly recall how a Breuil–Kisin module with A-coefficients and descent data can be interpreted as a module over a certain A-algebra.
Let
![]() $\mathfrak {S}_A[F]$
denote the twisted polynomial ring over
$\mathfrak {S}_A[F]$
denote the twisted polynomial ring over
![]() $\mathfrak {S}_A$
, in which the variable F obeys the following commutation relation with respect to elements
$\mathfrak {S}_A$
, in which the variable F obeys the following commutation relation with respect to elements
![]() $s \in \mathfrak {S}_A$
:
$s \in \mathfrak {S}_A$
:
Let
![]() $\mathfrak {S}_A[F, \operatorname {\mathrm {Gal}}(K'/K)]$
denote the twisted group ring over
$\mathfrak {S}_A[F, \operatorname {\mathrm {Gal}}(K'/K)]$
denote the twisted group ring over
![]() $\mathfrak {S}_A[F]$
, in which the elements
$\mathfrak {S}_A[F]$
, in which the elements
![]() $g \in \operatorname {\mathrm {Gal}}(K'/K)$
commute with F, and obey the following commutation relations with elements
$g \in \operatorname {\mathrm {Gal}}(K'/K)$
commute with F, and obey the following commutation relations with elements
![]() $s \in \mathfrak {S}_A$
:
$s \in \mathfrak {S}_A$
:
One immediately confirms that giving a left
![]() $\mathfrak {S}_A[F, \operatorname {\mathrm {Gal}}(K'/K)]$
-module
$\mathfrak {S}_A[F, \operatorname {\mathrm {Gal}}(K'/K)]$
-module
![]() $\mathfrak {M}$
is equivalent to equipping the underlying
$\mathfrak {M}$
is equivalent to equipping the underlying
![]() $\mathfrak {S}_A$
-module
$\mathfrak {S}_A$
-module
![]() $\mathfrak {M}$
with a
$\mathfrak {M}$
with a
![]() $\varphi $
-linear morphism
$\varphi $
-linear morphism
![]() $\varphi :\mathfrak {M} \to \mathfrak {M}$
and a semi-linear action of
$\varphi :\mathfrak {M} \to \mathfrak {M}$
and a semi-linear action of
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
which commutes with
$\operatorname {\mathrm {Gal}}(K'/K)$
which commutes with
![]() $\varphi $
.
$\varphi $
.
In particular, if we let
![]() $\mathcal {K}(A)$
denote the category of left
$\mathcal {K}(A)$
denote the category of left
![]() $\mathfrak {S}_A[F, \operatorname {\mathrm {Gal}}(K'/K)]$
-modules, then a Breuil–Kisin module with descent data from
$\mathfrak {S}_A[F, \operatorname {\mathrm {Gal}}(K'/K)]$
-modules, then a Breuil–Kisin module with descent data from
![]() $K'$
to K may naturally be regarded as an object of
$K'$
to K may naturally be regarded as an object of
![]() $\mathcal {K}(A)$
. In the following lemma, we record the fact that extensions of Breuil–Kisin modules with descent data may be computed as extensions in the category
$\mathcal {K}(A)$
. In the following lemma, we record the fact that extensions of Breuil–Kisin modules with descent data may be computed as extensions in the category
![]() $\mathcal {K}(A)$
.
$\mathcal {K}(A)$
.
Lemma 3.1.1. If
![]() $0 \to \mathfrak {M}' \to \mathfrak {M} \to \mathfrak {M}" \to 0$
is a short exact sequence in
$0 \to \mathfrak {M}' \to \mathfrak {M} \to \mathfrak {M}" \to 0$
is a short exact sequence in
![]() $\mathcal {K}(A)$
, such that
$\mathcal {K}(A)$
, such that
![]() $\mathfrak {M}'$
(respectively,
$\mathfrak {M}'$
(respectively,
![]() $\mathfrak {M}"$
) is a Breuil–Kisin module with descent data of rank
$\mathfrak {M}"$
) is a Breuil–Kisin module with descent data of rank
![]() $d'$
and height at most
$d'$
and height at most
![]() $h'$
(respectively, of rank
$h'$
(respectively, of rank
![]() $d"$
and height at most
$d"$
and height at most
![]() $h"$
), then
$h"$
), then
![]() $\mathfrak {M}$
is a Breuil–Kisin module with descent data of rank
$\mathfrak {M}$
is a Breuil–Kisin module with descent data of rank
![]() $d'+d"$
and height at most
$d'+d"$
and height at most
![]() $h'+h"$
.
$h'+h"$
.
More generally, if
![]() $E(u)^h\in \operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {M}'})\operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {M}"})$
, then
$E(u)^h\in \operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {M}'})\operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {M}"})$
, then
![]() $\mathfrak {M}$
is a Breuil–Kisin module with descent data of height at most h.
$\mathfrak {M}$
is a Breuil–Kisin module with descent data of height at most h.
Proof. Note that since
![]() $\Phi _{\mathfrak {M}'}[1/E(u)]$
and
$\Phi _{\mathfrak {M}'}[1/E(u)]$
and
![]() $\Phi _{\mathfrak {M}"}[1/E(u)]$
are both isomorphisms by assumption, it follows from the snake lemma that
$\Phi _{\mathfrak {M}"}[1/E(u)]$
are both isomorphisms by assumption, it follows from the snake lemma that
![]() $\Phi _{\mathfrak {M}}[1/E(u)]$
is an isomorphism. Similarly, we have a short exact sequence of
$\Phi _{\mathfrak {M}}[1/E(u)]$
is an isomorphism. Similarly, we have a short exact sequence of
![]() $\mathfrak {S}_A$
-modules
$\mathfrak {S}_A$
-modules
The claims about the height and rank of
![]() $\mathfrak {M}$
follow immediately.
$\mathfrak {M}$
follow immediately.
We now turn to giving an explicit description of the functors
![]() $\operatorname {\mathrm {Ext}}^i(\mathfrak {M}, \text {--} \, )$
for a Breuil–Kisin module with descent data
$\operatorname {\mathrm {Ext}}^i(\mathfrak {M}, \text {--} \, )$
for a Breuil–Kisin module with descent data
![]() $\mathfrak {M}$
.
$\mathfrak {M}$
.
Definition 3.1.2. Let
![]() $\mathfrak {M}$
be a Breuil–Kisin module with A-coefficients and descent data (of some height). If
$\mathfrak {M}$
be a Breuil–Kisin module with A-coefficients and descent data (of some height). If
![]() $\mathfrak {N}$
is any object of
$\mathfrak {N}$
is any object of
![]() $\mathcal {K}(A)$
, then we let
$\mathcal {K}(A)$
, then we let
![]() $C^{\bullet }_{\mathfrak {M}}(\mathfrak {N})$
denote the complex
$C^{\bullet }_{\mathfrak {M}}(\mathfrak {N})$
denote the complex
with differential being given by
Also let
![]() $\Phi _{\mathfrak {M}}^{*}$
denote the map
$\Phi _{\mathfrak {M}}^{*}$
denote the map
![]() $C^0_{\mathfrak {M}}(\mathfrak {N}) \to C^1_{\mathfrak {M}}(\mathfrak {N})$
given by
$C^0_{\mathfrak {M}}(\mathfrak {N}) \to C^1_{\mathfrak {M}}(\mathfrak {N})$
given by
![]() $\alpha \mapsto \alpha \circ \Phi _{\mathfrak {M}}$
. When
$\alpha \mapsto \alpha \circ \Phi _{\mathfrak {M}}$
. When
![]() $\mathfrak {M}$
is clear from the context, we will usually suppress it from the notation and write simply
$\mathfrak {M}$
is clear from the context, we will usually suppress it from the notation and write simply
![]() $C^{\bullet }(\mathfrak {N})$
.
$C^{\bullet }(\mathfrak {N})$
.
Each
![]() $C^i(\mathfrak {N})$
is naturally an
$C^i(\mathfrak {N})$
is naturally an
![]() $\mathfrak {S}_A^0$
-module. The formation of
$\mathfrak {S}_A^0$
-module. The formation of
![]() $C^{\bullet }(\mathfrak {N})$
is evidently functorial in
$C^{\bullet }(\mathfrak {N})$
is evidently functorial in
![]() $\mathfrak {N}$
, and is also exact in
$\mathfrak {N}$
, and is also exact in
![]() $\mathfrak {N}$
, since
$\mathfrak {N}$
, since
![]() $\mathfrak {M}$
, and hence also
$\mathfrak {M}$
, and hence also
![]() $\varphi ^{*}\mathfrak {M}$
, is projective over
$\varphi ^{*}\mathfrak {M}$
, is projective over
![]() $\mathfrak {S}_A$
, and since
$\mathfrak {S}_A$
, and since
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
has prime-to-p order. Thus, the cohomology functors
$\operatorname {\mathrm {Gal}}(K'/K)$
has prime-to-p order. Thus, the cohomology functors
![]() $H^0\bigl (C^{\bullet }(\text {--})\bigr )$
and
$H^0\bigl (C^{\bullet }(\text {--})\bigr )$
and
![]() $H^1\bigl (C^{\bullet }(\text {--})\bigr )$
form a
$H^1\bigl (C^{\bullet }(\text {--})\bigr )$
form a
![]() $\delta $
-functor on
$\delta $
-functor on
![]() $\mathcal {K}(A)$
.
$\mathcal {K}(A)$
.
Lemma 3.1.3. There is a natural isomorphism
Proof. This is immediate.
It follows from this lemma and a standard dimension shifting argument (or, equivalently, the theory of
![]() $\delta $
-functors) that there is an embedding of functors
$\delta $
-functors) that there is an embedding of functors
Lemma 3.1.5. The embedding of functors (3.1.4) is an isomorphism.
Proof. We first describe the embedding (3.1.4) explicitly. Suppose that
is an extension in
![]() $\mathcal {K}(A)$
. Since
$\mathcal {K}(A)$
. Since
![]() $\mathfrak {M}$
is projective over
$\mathfrak {M}$
is projective over
![]() $\mathfrak {S}_A$
, and since
$\mathfrak {S}_A$
, and since
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
is of prime-to-p order, we split this short exact sequence over the twisted group ring
$\operatorname {\mathrm {Gal}}(K'/K)$
is of prime-to-p order, we split this short exact sequence over the twisted group ring
![]() $\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)],$
say via some element
$\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)],$
say via some element
![]() $\sigma \in \operatorname {\mathrm {Hom}}_{\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]}(\mathfrak {M},\mathfrak {E}).$
This splitting is well-defined up to the addition of an element
$\sigma \in \operatorname {\mathrm {Hom}}_{\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]}(\mathfrak {M},\mathfrak {E}).$
This splitting is well-defined up to the addition of an element
![]() $\alpha \in \operatorname {\mathrm {Hom}}_{\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]}(\mathfrak {M},\mathfrak {N}).$
$\alpha \in \operatorname {\mathrm {Hom}}_{\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]}(\mathfrak {M},\mathfrak {N}).$
This splitting is a homomorphism in
![]() $\mathcal {K}(A)$
if and only if the element
$\mathcal {K}(A)$
if and only if the element
vanishes. If we replace
![]() $\sigma $
by
$\sigma $
by
![]() $\sigma +\alpha ,$
then this element is replaced by
$\sigma +\alpha ,$
then this element is replaced by
Thus, the coset of
![]() $\Phi _{\mathfrak {E}}\circ \varphi ^{*}\sigma - \sigma \circ \Phi _{\mathfrak {M}}$
in
$\Phi _{\mathfrak {E}}\circ \varphi ^{*}\sigma - \sigma \circ \Phi _{\mathfrak {M}}$
in
![]() $H^1\bigl (C^{\bullet }(\mathfrak {N})\bigr )$
is well-defined, independent of the choice of
$H^1\bigl (C^{\bullet }(\mathfrak {N})\bigr )$
is well-defined, independent of the choice of
![]() $\sigma ,$
and this coset is the image of the class of the extension
$\sigma ,$
and this coset is the image of the class of the extension
![]() $\mathfrak {E}$
under the embedding
$\mathfrak {E}$
under the embedding
(up to a possible overall sign, which we ignore, since it doesn’t affect the claim of the lemma).
Now, given any element
![]() $\nu \in \operatorname {\mathrm {Hom}}_{\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]}(\varphi ^{*}\mathfrak {M},\mathfrak {N})$
, we may give the
$\nu \in \operatorname {\mathrm {Hom}}_{\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]}(\varphi ^{*}\mathfrak {M},\mathfrak {N})$
, we may give the
![]() $\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]$
-module
$\mathfrak {S}_A[\operatorname {\mathrm {Gal}}(K'/K)]$
-module
![]() $\mathfrak {E} := \mathfrak {N} \oplus \mathfrak {M}$
the structure of a
$\mathfrak {E} := \mathfrak {N} \oplus \mathfrak {M}$
the structure of a
![]() $\mathfrak {S}_A[F,\operatorname {\mathrm {Gal}}(K'/K)]$
-module as follows: we need to define a
$\mathfrak {S}_A[F,\operatorname {\mathrm {Gal}}(K'/K)]$
-module as follows: we need to define a
![]() $\varphi $
-linear morphism
$\varphi $
-linear morphism
![]() $\mathfrak {E}\to \mathfrak {E}$
, or equivalently, a linear morphism
$\mathfrak {E}\to \mathfrak {E}$
, or equivalently, a linear morphism
![]() $\Phi _{\mathfrak {E}}:\varphi ^{*}\mathfrak {E}\to \mathfrak {E}$
. We do this by setting
$\Phi _{\mathfrak {E}}:\varphi ^{*}\mathfrak {E}\to \mathfrak {E}$
. We do this by setting
 $$ \begin{align*}\Phi_{\mathfrak{E}} := \begin{pmatrix} \Phi_{\mathfrak{N}} & \nu \\ 0 & \Phi_{\mathfrak{M}} \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\Phi_{\mathfrak{E}} := \begin{pmatrix} \Phi_{\mathfrak{N}} & \nu \\ 0 & \Phi_{\mathfrak{M}} \end{pmatrix}.\end{align*} $$
Then,
![]() $\mathfrak {E}$
is an extension of
$\mathfrak {E}$
is an extension of
![]() $\mathfrak {M}$
by
$\mathfrak {M}$
by
![]() $\mathfrak {N}$
, and if we let
$\mathfrak {N}$
, and if we let
![]() $\sigma $
denote the obvious embedding of
$\sigma $
denote the obvious embedding of
![]() $\mathfrak {M}$
into
$\mathfrak {M}$
into
![]() $\mathfrak {E}$
, then one computes that
$\mathfrak {E}$
, then one computes that
This shows that (3.1.6) is an isomorphism, as claimed.
Another dimension shifting argument, taking into account the preceding lemma, shows that
![]() $\operatorname {\mathrm {Ext}}^2_{\mathcal {K}(A)}(\mathfrak {M},\text {--} \,)$
embeds into
$\operatorname {\mathrm {Ext}}^2_{\mathcal {K}(A)}(\mathfrak {M},\text {--} \,)$
embeds into
![]() $H^2\bigl ( C^{\bullet }(\text {--}) \bigr ).$
Since the target of this embedding vanishes, we find that the same is true of the source. This yields the following corollary.
$H^2\bigl ( C^{\bullet }(\text {--}) \bigr ).$
Since the target of this embedding vanishes, we find that the same is true of the source. This yields the following corollary.
Corollary 3.1.7. If
![]() $\mathfrak {M}$
is a Breuil–Kisin module with A-coefficients and descent data, then
$\mathfrak {M}$
is a Breuil–Kisin module with A-coefficients and descent data, then
![]() $\operatorname {\mathrm {Ext}}^2_{\mathcal {K}(A)}(\mathfrak {M}, \text {--} \, ) = 0.$
$\operatorname {\mathrm {Ext}}^2_{\mathcal {K}(A)}(\mathfrak {M}, \text {--} \, ) = 0.$
We summarise the above discussion in the following corollary.
Corollary 3.1.8. If
![]() $\mathfrak {M}$
is a Breuil–Kisin module with A-coefficients and descent data, and
$\mathfrak {M}$
is a Breuil–Kisin module with A-coefficients and descent data, and
![]() $\mathfrak {N}$
is an object of
$\mathfrak {N}$
is an object of
![]() $\mathcal {K}(A)$
, then we have a natural short exact sequence
$\mathcal {K}(A)$
, then we have a natural short exact sequence
The following lemma records the behaviour of these complexes with respect to base change.
Lemma 3.1.9. Suppose that
![]() $\mathfrak {M}$
,
$\mathfrak {M}$
,
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data and A-coefficients, that B is an A-algebra and that Q is a B-module. Then, the complexes
$\mathfrak {N}$
are Breuil–Kisin modules with descent data and A-coefficients, that B is an A-algebra and that Q is a B-module. Then, the complexes
![]() $C^{\bullet }_{\mathfrak {M}}(\mathfrak {N} \, \widehat {\otimes }_A Q)$
and
$C^{\bullet }_{\mathfrak {M}}(\mathfrak {N} \, \widehat {\otimes }_A Q)$
and
![]() $C^{\bullet }_{\mathfrak {M} \, \widehat {\otimes }_A B}(\mathfrak {N} \, \widehat {\otimes }_A Q)$
coincide, the former complex formed with respect to
$C^{\bullet }_{\mathfrak {M} \, \widehat {\otimes }_A B}(\mathfrak {N} \, \widehat {\otimes }_A Q)$
coincide, the former complex formed with respect to
![]() $\mathcal {K}(A)$
and the latter with respect to
$\mathcal {K}(A)$
and the latter with respect to
![]() $\mathcal {K}(B)$
.
$\mathcal {K}(B)$
.
Proof. Indeed, there is a natural isomorphism
and similarly with
![]() $\varphi ^{*}\mathfrak {M}$
in place of
$\varphi ^{*}\mathfrak {M}$
in place of
![]() $\mathfrak {M}$
.
$\mathfrak {M}$
.
The following slightly technical lemma is crucial for establishing finiteness properties, and also base-change properties, of Exts of Breuil–Kisin modules.
Lemma 3.1.10. Let A be a
![]() ${\mathcal O}/\varpi ^a$
-algebra for some
${\mathcal O}/\varpi ^a$
-algebra for some
![]() $a\ge 1$
, suppose that
$a\ge 1$
, suppose that
![]() $\mathfrak {M}$
is a Breuil–Kisin module with descent data and A-coefficients, of height at most h, and suppose that
$\mathfrak {M}$
is a Breuil–Kisin module with descent data and A-coefficients, of height at most h, and suppose that
![]() $\mathfrak {N}$
is a u-adically complete, u-torsion free object of
$\mathfrak {N}$
is a u-adically complete, u-torsion free object of
![]() $\mathcal {K}(A)$
.
$\mathcal {K}(A)$
.
Let
![]() $C^{\bullet }$
be the complex defined in Definition 3.1.2
, and write
$C^{\bullet }$
be the complex defined in Definition 3.1.2
, and write
![]() $\delta $
for its differential. Suppose that Q is an A-module with the property that
$\delta $
for its differential. Suppose that Q is an A-module with the property that
![]() $C^i\otimes _A Q$
is v-torsion free for
$C^i\otimes _A Q$
is v-torsion free for
![]() $i=0,1$
and v-adically separated for
$i=0,1$
and v-adically separated for
![]() $i=0$
.
$i=0$
.
Then:
-
1. For any integer
 $M\ge (eah+1)/(p-1)$
,
$M\ge (eah+1)/(p-1)$
,
 $\ker (\delta \otimes \operatorname {id}_Q)\cap v^MC^0\otimes _AQ=0$
.
$\ker (\delta \otimes \operatorname {id}_Q)\cap v^MC^0\otimes _AQ=0$
. -
2. For any integer
 $N \ge (peah+1)/(p-1)$
,
$N \ge (peah+1)/(p-1)$
,
 $\delta \otimes \operatorname {id}_Q$
induces an isomorphism
$\delta \otimes \operatorname {id}_Q$
induces an isomorphism  $$\begin{align*}(\Phi_{\mathfrak{M}}^{*})^{-1}(v^N C^1\otimes_AQ) \stackrel{\sim}{\longrightarrow} v^N (C^1\otimes_AQ).\end{align*}$$
$$\begin{align*}(\Phi_{\mathfrak{M}}^{*})^{-1}(v^N C^1\otimes_AQ) \stackrel{\sim}{\longrightarrow} v^N (C^1\otimes_AQ).\end{align*}$$
Consequently, for N as in (2), the natural morphism of complexes of A-modules
is a quasi-isomorphism.
Since we are assuming that the
![]() $C^i\otimes _AQ$
are v-torsion free, the expression
$C^i\otimes _AQ$
are v-torsion free, the expression
![]() $v^r C^i(\mathfrak {N}) \otimes _A Q$
may be interpreted as denoting either
$v^r C^i(\mathfrak {N}) \otimes _A Q$
may be interpreted as denoting either
![]() $v^r \bigl ( C^i(\mathfrak {N})\otimes _A Q\bigr )$
or
$v^r \bigl ( C^i(\mathfrak {N})\otimes _A Q\bigr )$
or
![]() $\bigl (v^r C^i(\mathfrak {N}) \bigr )\otimes _A Q$
, the two being naturally isomorphic.
$\bigl (v^r C^i(\mathfrak {N}) \bigr )\otimes _A Q$
, the two being naturally isomorphic.
Remark 3.1.11. Before giving the proof of Lemma 3.1.10, we observe that the hypotheses on the
![]() $C^i \otimes _A Q$
are satisfied if either
$C^i \otimes _A Q$
are satisfied if either
![]() $Q=A$
, or else
$Q=A$
, or else
![]() $\mathfrak {N}$
is a projective
$\mathfrak {N}$
is a projective
![]() $\mathfrak {S}_A$
-module and Q is a finitely generated B-module for some finitely generated A-algebra B. (Indeed,
$\mathfrak {S}_A$
-module and Q is a finitely generated B-module for some finitely generated A-algebra B. (Indeed,
![]() $C^1 \otimes _A Q$
is v-adically separated as well in these cases.)
$C^1 \otimes _A Q$
is v-adically separated as well in these cases.)
(1) Since
![]() $\mathfrak {M}$
is projective of finite rank over
$\mathfrak {M}$
is projective of finite rank over
![]() $A[[u]]$
, and since
$A[[u]]$
, and since
![]() $\mathfrak {N}$
is u-adically complete and u-torsion free, each
$\mathfrak {N}$
is u-adically complete and u-torsion free, each
![]() $C^i$
is v-adically separated and v-torsion free. In particular, the hypothesis on Q is always satisfied by
$C^i$
is v-adically separated and v-torsion free. In particular, the hypothesis on Q is always satisfied by
![]() $Q=A$
. (In fact, since
$Q=A$
. (In fact, since
![]() $\mathfrak {N}$
is u-adically complete, it also follows that the
$\mathfrak {N}$
is u-adically complete, it also follows that the
![]() $C^i$
are v-adically complete. Here, we use that
$C^i$
are v-adically complete. Here, we use that
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
has order prime to p to see that
$\operatorname {\mathrm {Gal}}(K'/K)$
has order prime to p to see that
![]() $C^0$
is an
$C^0$
is an
![]() $\mathfrak {S}_A^0$
-module direct summand of
$\mathfrak {S}_A^0$
-module direct summand of
![]() $\operatorname {\mathrm {Hom}}_{\mathfrak {S}_A}(\mathfrak {M},\mathfrak {N})$
, and similarly for
$\operatorname {\mathrm {Hom}}_{\mathfrak {S}_A}(\mathfrak {M},\mathfrak {N})$
, and similarly for
![]() $C^1$
.)
$C^1$
.)
(2) Suppose
![]() $\mathfrak {N}$
is a projective
$\mathfrak {N}$
is a projective
![]() $\mathfrak {S}_A$
-module. Then, the
$\mathfrak {S}_A$
-module. Then, the
![]() $C^i$
are projective
$C^i$
are projective
![]() $\mathfrak {S}_A^0$
-modules, again using that
$\mathfrak {S}_A^0$
-modules, again using that
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
has order prime to p. Since each
$\operatorname {\mathrm {Gal}}(K'/K)$
has order prime to p. Since each
![]() $C^i(\mathfrak {N})/v C^i(\mathfrak {N})$
is A-flat, it follows that
$C^i(\mathfrak {N})/v C^i(\mathfrak {N})$
is A-flat, it follows that
![]() $C^i(\mathfrak {N}) \otimes _A Q$
is v-torsion free. If furthermore B is a finitely generated A-algebra, and Q is a finitely generated B-module, then the
$C^i(\mathfrak {N}) \otimes _A Q$
is v-torsion free. If furthermore B is a finitely generated A-algebra, and Q is a finitely generated B-module, then the
![]() $C^i(\mathfrak {N})\otimes _A Q$
are v-adically separated (being finitely generated modules over the ring
$C^i(\mathfrak {N})\otimes _A Q$
are v-adically separated (being finitely generated modules over the ring
![]() $A[[v]]\otimes _A B$
, which is a finitely generated algebra over the Noetherian ring
$A[[v]]\otimes _A B$
, which is a finitely generated algebra over the Noetherian ring
![]() $A[[v]]$
, and hence is itself Noetherian).
$A[[v]]$
, and hence is itself Noetherian).
Proof of Lemma 3.1.10
Since
![]() $p^a=0$
in A, there exists
$p^a=0$
in A, there exists
![]() $H(u)\in \mathfrak {S}_A$
with
$H(u)\in \mathfrak {S}_A$
with
![]() $u^{e'ah}=E(u)^hH(u)$
in
$u^{e'ah}=E(u)^hH(u)$
in
![]() $\mathfrak {S}_A$
. Thus, the image of
$\mathfrak {S}_A$
. Thus, the image of
![]() $\Phi _{\mathfrak {M}}$
contains
$\Phi _{\mathfrak {M}}$
contains
![]() $u^{e'ah} \mathfrak {M}=v^{eah}\mathfrak {M}$
, and there exists a map
$u^{e'ah} \mathfrak {M}=v^{eah}\mathfrak {M}$
, and there exists a map
![]() $\Upsilon : \mathfrak {M} \to \varphi ^{*} \mathfrak {M}$
, such that
$\Upsilon : \mathfrak {M} \to \varphi ^{*} \mathfrak {M}$
, such that
![]() $\Phi _{\mathfrak {M}} \circ \Upsilon $
is multiplication by
$\Phi _{\mathfrak {M}} \circ \Upsilon $
is multiplication by
![]() $v^{eah}$
.
$v^{eah}$
.
We begin with (1). Suppose that
![]() $f\in \ker (\delta \otimes \operatorname {id}_Q)\cap v^MC^0\otimes _AQ$
. Since
$f\in \ker (\delta \otimes \operatorname {id}_Q)\cap v^MC^0\otimes _AQ$
. Since
![]() $C^0\otimes _AQ$
is v-adically separated, it is enough, applying induction on M, to show that
$C^0\otimes _AQ$
is v-adically separated, it is enough, applying induction on M, to show that
![]() $f\in v^{M+1}C^0\otimes _AQ$
. Since
$f\in v^{M+1}C^0\otimes _AQ$
. Since
![]() $f\in \ker (\delta \otimes \operatorname {id}_Q)$
, we have
$f\in \ker (\delta \otimes \operatorname {id}_Q)$
, we have
![]() $f\circ \Phi _{\mathfrak {M}}=\Phi _{\mathfrak {N}}\circ \varphi ^{*}f$
. Since
$f\circ \Phi _{\mathfrak {M}}=\Phi _{\mathfrak {N}}\circ \varphi ^{*}f$
. Since
![]() $f\in v^MC^0\otimes _AQ$
, we have
$f\in v^MC^0\otimes _AQ$
, we have
![]() $f \circ \Phi _{\mathfrak {M}} = \Phi _{\mathfrak {N}} \circ \varphi ^{*}f \in v^{pM} C^1 \otimes _A Q$
. Precomposing with
$f \circ \Phi _{\mathfrak {M}} = \Phi _{\mathfrak {N}} \circ \varphi ^{*}f \in v^{pM} C^1 \otimes _A Q$
. Precomposing with
![]() $\Upsilon $
gives
$\Upsilon $
gives
![]() $v^{eah} f \in v^{pM} C^0 \otimes _A Q$
. Since
$v^{eah} f \in v^{pM} C^0 \otimes _A Q$
. Since
![]() $C^0 \otimes _A Q$
is v-torsion free, it follows that
$C^0 \otimes _A Q$
is v-torsion free, it follows that
![]() $f\in v^{pM-eah}C^0\otimes _AQ\subseteq u^{M+1}C^0\otimes _AQ$
, as required.
$f\in v^{pM-eah}C^0\otimes _AQ\subseteq u^{M+1}C^0\otimes _AQ$
, as required.
We now move on to (2). Set
![]() $M = N - eah$
. By precomposing with
$M = N - eah$
. By precomposing with
![]() $\Upsilon $
, we see that
$\Upsilon $
, we see that
![]() $\alpha \circ \Phi _{\mathfrak {M}} \in v^N C^1\otimes _A Q$
implies
$\alpha \circ \Phi _{\mathfrak {M}} \in v^N C^1\otimes _A Q$
implies
![]() $\alpha \in v^M C^0\otimes _A Q$
; from this, together with the inequality
$\alpha \in v^M C^0\otimes _A Q$
; from this, together with the inequality
![]() $pM \ge N$
, it is straightforward to check that
$pM \ge N$
, it is straightforward to check that
Note that M satisfies the condition in (1). To complete the proof, we will show that for any M as in (1) and any
![]() $N \ge M + eah$
, the map
$N \ge M + eah$
, the map
![]() $\delta $
induces an isomorphism
$\delta $
induces an isomorphism
By (1),
![]() $\delta \otimes \operatorname {id}_Q$
induces an injection
$\delta \otimes \operatorname {id}_Q$
induces an injection
![]() $(\delta \otimes \operatorname {id}_Q)^{-1}(v^N C^1\otimes _AQ)\cap v^M C^0\otimes _AQ\hookrightarrow v^N C^1\otimes _AQ$
, so it is enough to show that
$(\delta \otimes \operatorname {id}_Q)^{-1}(v^N C^1\otimes _AQ)\cap v^M C^0\otimes _AQ\hookrightarrow v^N C^1\otimes _AQ$
, so it is enough to show that
![]() $(\delta \otimes \operatorname {id}_Q)(v^MC^0\otimes _AQ)\supseteq v^N C^1\otimes _AQ$
. Equivalently, we need to show that
$(\delta \otimes \operatorname {id}_Q)(v^MC^0\otimes _AQ)\supseteq v^N C^1\otimes _AQ$
. Equivalently, we need to show that
is identically zero. Since the formation of cokernels is compatible with tensor products, we see that this morphism is obtained by tensoring the corresponding morphism
with Q over A, so we are reduced to the case
![]() $Q=A$
. (Recall from Remark 3.1.11(1) that the hypotheses of the Lemma are satisfied in this case, and that
$Q=A$
. (Recall from Remark 3.1.11(1) that the hypotheses of the Lemma are satisfied in this case, and that
![]() $C^1$
is v-adically separated.)
$C^1$
is v-adically separated.)
We claim that for any
![]() $g\in v^NC^1$
, we can find an
$g\in v^NC^1$
, we can find an
![]() $f\in v^{N-eah}C^0$
, such that
$f\in v^{N-eah}C^0$
, such that
![]() $\delta (f)-g\in v^{p(N-eah)}C^1$
. Admitting the claim, given any
$\delta (f)-g\in v^{p(N-eah)}C^1$
. Admitting the claim, given any
![]() $g\in v^N C^1$
, we may find
$g\in v^N C^1$
, we may find
![]() $h\in v^MC^0$
with
$h\in v^MC^0$
with
![]() $\delta (h)=g$
by successive approximation in the following way: Set
$\delta (h)=g$
by successive approximation in the following way: Set
![]() $h_0=f$
for f as in the claim; then
$h_0=f$
for f as in the claim; then
![]() $h_0\in v^{N-eah}C^0\subseteq v^MC^0$
, and
$h_0\in v^{N-eah}C^0\subseteq v^MC^0$
, and
![]() $\delta (h_0)-g\in v^{p(N-eah)}C^1\subseteq v^{N+1}C^1$
. Applying the claim again, with N replaced by
$\delta (h_0)-g\in v^{p(N-eah)}C^1\subseteq v^{N+1}C^1$
. Applying the claim again, with N replaced by
![]() $N+1$
, and g replaced by
$N+1$
, and g replaced by
![]() $g-\delta (h_0)$
, we find
$g-\delta (h_0)$
, we find
![]() $f\in v^{N+1-eah}C^0\subseteq v^{M+1}C^0$
with
$f\in v^{N+1-eah}C^0\subseteq v^{M+1}C^0$
with
![]() $\delta (f)-g+\delta (h_0)\in v^{p(N+1-eah)}C^1\subseteq v^{N+1}C^1$
. Setting
$\delta (f)-g+\delta (h_0)\in v^{p(N+1-eah)}C^1\subseteq v^{N+1}C^1$
. Setting
![]() $h_1=h_0+f$
, and proceeding inductively, we obtain a Cauchy sequence converging (in the v-adically complete
$h_1=h_0+f$
, and proceeding inductively, we obtain a Cauchy sequence converging (in the v-adically complete
![]() $A[[v]]$
-module
$A[[v]]$
-module
![]() $C^0$
) to the required element h. It remains to prove the claim. Since
$C^0$
) to the required element h. It remains to prove the claim. Since
![]() $\delta (f)=\Phi _{\mathfrak {N}}\circ \varphi ^{*}f-f\circ \Phi _{\mathfrak {M}} $
, and since if
$\delta (f)=\Phi _{\mathfrak {N}}\circ \varphi ^{*}f-f\circ \Phi _{\mathfrak {M}} $
, and since if
![]() $f\in v^{N-eah}C^0$
, then
$f\in v^{N-eah}C^0$
, then
![]() $\Phi _{\mathfrak {N}}\circ \varphi ^{*}f\in v^{p(N-eah)}C^1$
, it is enough to show that we can find an
$\Phi _{\mathfrak {N}}\circ \varphi ^{*}f\in v^{p(N-eah)}C^1$
, it is enough to show that we can find an
![]() $f\in v^{N-eah}C^0$
with
$f\in v^{N-eah}C^0$
with
![]() $f\circ \Phi _{\mathfrak {M}}=-g$
. Since
$f\circ \Phi _{\mathfrak {M}}=-g$
. Since
![]() $\Phi _{\mathfrak {M}}$
is injective, the map
$\Phi _{\mathfrak {M}}$
is injective, the map
![]() $\Upsilon \circ \Phi _{\mathfrak {M}}$
is also multiplication by
$\Upsilon \circ \Phi _{\mathfrak {M}}$
is also multiplication by
![]() $v^{eah}$
, and so it suffices to take f with
$v^{eah}$
, and so it suffices to take f with
![]() $v^{eah} f = -g \circ \Upsilon \in v^N C^0$
.
$v^{eah} f = -g \circ \Upsilon \in v^N C^0$
.
Corollary 3.1.12. Let A be a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra, and let
${\mathcal O}/\varpi ^a$
-algebra, and let
![]() $\mathfrak {M}$
,
$\mathfrak {M}$
,
![]() $\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients. If B is a finitely generated A-algebra, and Q is a finitely generated B-module, then the natural morphism of complexes of B-modules
$\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients. If B is a finitely generated A-algebra, and Q is a finitely generated B-module, then the natural morphism of complexes of B-modules
is a quasi-isomorphism.
Proof. By Remarks 3.1.11 and 2.1.6(2), we can apply Lemma 3.1.10 to both
![]() $C^i(\mathfrak {N}\, \widehat {\otimes }_AQ)$
and
$C^i(\mathfrak {N}\, \widehat {\otimes }_AQ)$
and
![]() $C^i(\mathfrak {N})\otimes _AQ$
, and we see that it is enough to show that the natural morphism of complexes
$C^i(\mathfrak {N})\otimes _AQ$
, and we see that it is enough to show that the natural morphism of complexes

is a quasi-isomorphism. In fact, it is even an isomorphism.
Proposition 3.1.13. Let A be a
![]() ${\mathcal O}/\varpi ^a$
-algebra for some
${\mathcal O}/\varpi ^a$
-algebra for some
![]() $a\ge 1$
, and let
$a\ge 1$
, and let
![]() $\mathfrak {M}$
,
$\mathfrak {M}$
,
![]() $\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients. Then,
$\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients. Then,
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
and
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
and
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}/u^i\mathfrak {N})$
for
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}/u^i\mathfrak {N})$
for
![]() $i \ge 1$
are finitely presented A-modules.
$i \ge 1$
are finitely presented A-modules.
If, furthermore, A is Noetherian, then
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
and
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
and
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}/u^i\mathfrak {N})$
for
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}/u^i\mathfrak {N})$
for
![]() $i\ge 1$
are also finitely presented (equivalently, finitely generated) A-modules.
$i\ge 1$
are also finitely presented (equivalently, finitely generated) A-modules.
Proof. The statements for
![]() $\mathfrak {N}/u^i\mathfrak {N}$
follow easily from those for
$\mathfrak {N}/u^i\mathfrak {N}$
follow easily from those for
![]() $\mathfrak {N}$
, by considering the short exact sequence
$\mathfrak {N}$
, by considering the short exact sequence
![]() $0 \to u^i\mathfrak {N} \to \mathfrak {N} \to \mathfrak {N}/u^i\mathfrak {N} \to 0$
in
$0 \to u^i\mathfrak {N} \to \mathfrak {N} \to \mathfrak {N}/u^i\mathfrak {N} \to 0$
in
![]() $\mathcal {K}(A)$
and applying Corollary 3.1.7. By Corollary 3.1.8, it is enough to consider the cohomology of the complex
$\mathcal {K}(A)$
and applying Corollary 3.1.7. By Corollary 3.1.8, it is enough to consider the cohomology of the complex
![]() $C^{\bullet }$
. By Lemma 3.1.10 with
$C^{\bullet }$
. By Lemma 3.1.10 with
![]() $Q=A$
, the cohomology of
$Q=A$
, the cohomology of
![]() $C^{\bullet }$
agrees with the cohomology of the induced complex
$C^{\bullet }$
agrees with the cohomology of the induced complex
for an appropriately chosen value of N. It follows that for an appropriately chosen value of N,
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
can be computed as the cokernel of the induced morphism
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
can be computed as the cokernel of the induced morphism
![]() $C^0/v^N C^0 \to C^1/ v^N C^1$
.
$C^0/v^N C^0 \to C^1/ v^N C^1$
.
Under our hypothesis on
![]() $\mathfrak {N}$
,
$\mathfrak {N}$
,
![]() $C^0/v^N C^0$
and
$C^0/v^N C^0$
and
![]() $C^1/v^NC^1$
are finitely generated projective A-modules, and thus finitely presented. It follows that
$C^1/v^NC^1$
are finitely generated projective A-modules, and thus finitely presented. It follows that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is finitely presented.
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is finitely presented.
In the case that A is furthermore assumed to be Noetherian, it is enough to note that since
![]() $v^NC^0\subseteq (\Phi _{\mathfrak {M}}^{*})^{-1}(v^N C^1)$
, the quotient
$v^NC^0\subseteq (\Phi _{\mathfrak {M}}^{*})^{-1}(v^N C^1)$
, the quotient
![]() $C^0/\bigl ((\Phi _{\mathfrak {M}}^{*})^{-1}(v^N C^1) \bigr )$
is a finitely generated A-module.
$C^0/\bigl ((\Phi _{\mathfrak {M}}^{*})^{-1}(v^N C^1) \bigr )$
is a finitely generated A-module.
Proposition 3.1.14. Let A be a
![]() ${\mathcal O}/\varpi ^a$
-algebra for some
${\mathcal O}/\varpi ^a$
-algebra for some
![]() $a\ge 1$
, and let
$a\ge 1$
, and let
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients. Let B be an A-algebra, and let
$\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients. Let B be an A-algebra, and let
![]() $f_B:\mathfrak {M}\, \widehat {\otimes }_AB\to \mathfrak {N}\, \widehat {\otimes }_AB$
be a morphism of Breuil–Kisin modules with B-coefficients.
$f_B:\mathfrak {M}\, \widehat {\otimes }_AB\to \mathfrak {N}\, \widehat {\otimes }_AB$
be a morphism of Breuil–Kisin modules with B-coefficients.
Then, there is a finite type A-subalgebra
![]() $B'$
of B and a morphism of Breuil–Kisin modules
$B'$
of B and a morphism of Breuil–Kisin modules
![]() $f_{B'}:\mathfrak {M}\, \widehat {\otimes }_A B'\to \mathfrak {N}\, \widehat {\otimes }_A B'$
, such that
$f_{B'}:\mathfrak {M}\, \widehat {\otimes }_A B'\to \mathfrak {N}\, \widehat {\otimes }_A B'$
, such that
![]() $f_B$
is the base change of
$f_B$
is the base change of
![]() $f_{B'}$
.
$f_{B'}$
.
Proof. By Lemmas 3.1.3 and 3.1.9 (the latter applied with
![]() $Q=B$
), we can and do think of
$Q=B$
), we can and do think of
![]() $f_B$
as being an element of the kernel of
$f_B$
as being an element of the kernel of
![]() $\delta :C^0(\mathfrak {N}\, \widehat {\otimes }_A B)\to C^1(\mathfrak {N}\, \widehat {\otimes }_A B)$
, the complex
$\delta :C^0(\mathfrak {N}\, \widehat {\otimes }_A B)\to C^1(\mathfrak {N}\, \widehat {\otimes }_A B)$
, the complex
![]() $C^{\bullet }$
here and throughout this proof denoting
$C^{\bullet }$
here and throughout this proof denoting
![]() $C^{\bullet }_{\mathfrak {M}}$
as usual.
$C^{\bullet }_{\mathfrak {M}}$
as usual.
Fix N as in Lemma 3.1.10, and write
![]() $\overline {f}_B$
for the corresponding element of
$\overline {f}_B$
for the corresponding element of
![]() $C^0(\mathfrak {N}\, \widehat {\otimes }_A B)/v^N=(C^0(\mathfrak {N})/v^N)\otimes _A B$
(this equality following easily from the assumption that
$C^0(\mathfrak {N}\, \widehat {\otimes }_A B)/v^N=(C^0(\mathfrak {N})/v^N)\otimes _A B$
(this equality following easily from the assumption that
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are projective
$\mathfrak {N}$
are projective
![]() $\mathfrak {S}_A$
-modules of finite rank). Since
$\mathfrak {S}_A$
-modules of finite rank). Since
![]() $C^0(\mathfrak {N})/v^N$
is a projective A-module of finite rank, it follows that for some finite type A-subalgebra
$C^0(\mathfrak {N})/v^N$
is a projective A-module of finite rank, it follows that for some finite type A-subalgebra
![]() $B'$
of B, there is an element
$B'$
of B, there is an element
![]() $\overline {f}_{B'}\in (C^0(\mathfrak {N})/v^N)\otimes _A B'=C^0(\mathfrak {N}\, \widehat {\otimes }_A B')/v^N$
, such that
$\overline {f}_{B'}\in (C^0(\mathfrak {N})/v^N)\otimes _A B'=C^0(\mathfrak {N}\, \widehat {\otimes }_A B')/v^N$
, such that
![]() $\overline {f}_{B'}\otimes _{B'}B=\overline {f}_B$
. Denote also by
$\overline {f}_{B'}\otimes _{B'}B=\overline {f}_B$
. Denote also by
![]() $\overline {f}_{B'} $
the induced element of
$\overline {f}_{B'} $
the induced element of
By Lemma 3.1.10 (and Lemma 3.1.3), we have a commutative diagram with exact rows
in which the vertical arrows are induced by
![]() $\, \widehat {\otimes }_{B'}B$
. By a diagram chase, we only need to show that
$\, \widehat {\otimes }_{B'}B$
. By a diagram chase, we only need to show that
![]() $\delta (\overline {f}_{B'})=0$
. Since
$\delta (\overline {f}_{B'})=0$
. Since
![]() $\delta (f_B)=0$
, it is enough to show that the right-hand vertical arrow is an injection. This arrow can be rewritten as the tensor product of the injection of A-algebras
$\delta (f_B)=0$
, it is enough to show that the right-hand vertical arrow is an injection. This arrow can be rewritten as the tensor product of the injection of A-algebras
![]() $B'\hookrightarrow B$
with the flat (even projective of finite rank) A-module
$B'\hookrightarrow B$
with the flat (even projective of finite rank) A-module
![]() $C^1(\mathfrak {N})/v^N$
, so the result follows.
$C^1(\mathfrak {N})/v^N$
, so the result follows.
We have the following key base-change result for
![]() $\operatorname {\mathrm {Ext}}^1$
’s of Breuil–Kisin modules with descent data.
$\operatorname {\mathrm {Ext}}^1$
’s of Breuil–Kisin modules with descent data.
Proposition 3.1.15. Suppose that
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a
$\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a
![]() ${\mathcal O}/\varpi ^a$
-algebra A. Then, for any A-algebra B, and for any B-module Q, there are natural isomorphisms
${\mathcal O}/\varpi ^a$
-algebra A. Then, for any A-algebra B, and for any B-module Q, there are natural isomorphisms
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B) \otimes _B Q \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}\, \widehat {\otimes }_A B,\mathfrak {N}\, \widehat {\otimes }_A Q).$
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B) \otimes _B Q \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}\, \widehat {\otimes }_A B,\mathfrak {N}\, \widehat {\otimes }_A Q).$
Proof. We first prove the lemma in the case of an A-module Q. It follows from Lemmas 3.1.5 and 3.1.10 that we may compute
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
as the cokernel of the morphism
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
as the cokernel of the morphism
for some sufficiently large value of N (not depending on
![]() $\mathfrak {N}$
), and hence that we may compute
$\mathfrak {N}$
), and hence that we may compute
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q$
as the cokernel of the morphism
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q$
as the cokernel of the morphism
We may similarly compute
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\, \widehat {\otimes }_A Q)$
as the cokernel of the morphism
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\, \widehat {\otimes }_A Q)$
as the cokernel of the morphism
(Remark 2.1.6 (2) shows that
![]() $\mathfrak {N}\, \widehat {\otimes }_A Q$
satisfies the necessary hypotheses for Lemma 3.1.10 to apply.) Once we note that the natural morphism
$\mathfrak {N}\, \widehat {\otimes }_A Q$
satisfies the necessary hypotheses for Lemma 3.1.10 to apply.) Once we note that the natural morphism
is an isomorphism for
![]() $i = 0$
and
$i = 0$
and
![]() $1$
(because
$1$
(because
![]() $\mathfrak {M}$
is a finitely generated projective
$\mathfrak {M}$
is a finitely generated projective
![]() $\mathfrak {S}_A$
-module), we obtain the desired isomorphism
$\mathfrak {S}_A$
-module), we obtain the desired isomorphism
If B is an A-algebra, and Q is a B-module, then by Lemma 3.1.9, there is a natural isomorphism
combined with the preceding base-change result, this yields one of our claimed isomorphisms, namely
Taking Q to be B itself, we then obtain an isomorphism
This allows us to identify
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q$
, which is naturally isomorphic to
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q$
, which is naturally isomorphic to
![]() $\bigl (\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A B\bigr ) \otimes _B Q$
, with
$\bigl (\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A B\bigr ) \otimes _B Q$
, with
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B)\otimes _B Q$
, yielding the second claimed isomorphism.
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B)\otimes _B Q$
, yielding the second claimed isomorphism.
In contrast to the situation for extensions (cf. Proposition 3.1.15), the formation of homomorphisms between Breuil–Kisin modules is in general not compatible with arbitrary base change, as the following example shows.
Example 3.1.16. Take
![]() $A = ({\mathbf Z}/p{\mathbf Z})[x^{\pm 1}, y^{\pm 1}]$
, and let
$A = ({\mathbf Z}/p{\mathbf Z})[x^{\pm 1}, y^{\pm 1}]$
, and let
![]() $\mathfrak {M}_x$
be the free Breuil–Kisin module of rank one and A-coefficients with
$\mathfrak {M}_x$
be the free Breuil–Kisin module of rank one and A-coefficients with
![]() $\varphi (e) = xe$
for some generator e of
$\varphi (e) = xe$
for some generator e of
![]() $\mathfrak {M}_x$
. Similarly, define
$\mathfrak {M}_x$
. Similarly, define
![]() $\mathfrak {M}_y$
with
$\mathfrak {M}_y$
with
![]() $\varphi (e') = ye'$
for some generator
$\varphi (e') = ye'$
for some generator
![]() $e'$
of
$e'$
of
![]() $\mathfrak {M}_y$
. Then,
$\mathfrak {M}_y$
. Then,
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}_x,\mathfrak {M}_y)=0$
. On the other hand, if
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}_x,\mathfrak {M}_y)=0$
. On the other hand, if
![]() $B=A/(x-y)$
, then
$B=A/(x-y)$
, then
![]() $\mathfrak {M}_x \, \widehat {\otimes }_A B$
and
$\mathfrak {M}_x \, \widehat {\otimes }_A B$
and
![]() $\mathfrak {M}_y \, \widehat {\otimes }_A B$
are isomorphic, so that
$\mathfrak {M}_y \, \widehat {\otimes }_A B$
are isomorphic, so that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)}(\mathfrak {M}_x \, \widehat {\otimes } B, \mathfrak {M}_y \, \widehat {\otimes } B) \not \cong \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}_x,\mathfrak {M}_y) \otimes _A B$
.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)}(\mathfrak {M}_x \, \widehat {\otimes } B, \mathfrak {M}_y \, \widehat {\otimes } B) \not \cong \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}_x,\mathfrak {M}_y) \otimes _A B$
.
However, it is possible to establish such a compatibility in some settings. Corollary 3.1.18, which gives a criterion for the vanishing of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B)$
for any A-algebra B, is a first example of a result in this direction. Lemma 3.1.20 deals with flat base change, and Lemma 3.1.21, which will be important in Section 3.3, proves that formation of homomorphisms is compatible with base change over a dense open subscheme of
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B)$
for any A-algebra B, is a first example of a result in this direction. Lemma 3.1.20 deals with flat base change, and Lemma 3.1.21, which will be important in Section 3.3, proves that formation of homomorphisms is compatible with base change over a dense open subscheme of
![]() $\operatorname {\mathrm {Spec}} A$
.
$\operatorname {\mathrm {Spec}} A$
.
Proposition 3.1.17. Suppose that A is a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra, and that
${\mathcal O}/\varpi ^a$
-algebra, and that
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are objects of
$\mathfrak {N}$
are objects of
![]() $\mathcal {K}(A)$
that are finitely generated over
$\mathcal {K}(A)$
that are finitely generated over
![]() $\mathfrak {S}_A$
(or, equivalently, over
$\mathfrak {S}_A$
(or, equivalently, over
![]() $A[[u]]$
). Suppose also that
$A[[u]]$
). Suppose also that
![]() $\mathfrak {N}$
is a flat
$\mathfrak {N}$
is a flat
![]() $\mathfrak {S}_A$
-module. Consider the following conditions:
$\mathfrak {S}_A$
-module. Consider the following conditions:
-
1.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B) = 0$
for any finite type A-algebra B.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B) = 0$
for any finite type A-algebra B. -
2.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
 $\mathfrak m$
of A.
$\mathfrak m$
of A. -
3.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}, \mathfrak {N}\otimes _A Q) = 0$
for any finitely generated A-module Q.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}, \mathfrak {N}\otimes _A Q) = 0$
for any finitely generated A-module Q.
Then, we have (1)
![]() $\implies $
(2)
$\implies $
(2)
![]() $\iff $
(3). If A is furthermore Jacobson, then all three conditions are equivalent.
$\iff $
(3). If A is furthermore Jacobson, then all three conditions are equivalent.
Proof. If
![]() $\mathfrak m$
is a maximal ideal of A, then
$\mathfrak m$
is a maximal ideal of A, then
![]() $\kappa (\mathfrak m)$
is certainly a finite type A-algebra, and so evidently (1) implies (2). It is even a finitely generated A-module, and so also (2) follows from (3). We next prove that (2) implies (3). To this end, recall that if A is any ring, and M is any A-module, then M injects into the product of its localisations at all maximal ideals. If A is Noetherian, and M is finitely generated, then, by combining this fact with the Artin–Rees Lemma, we see that M embeds into the product of its completions at all maximal ideals. Another way to express this is that, if I runs over all cofinite length ideals in A (i.e. all ideals for which
$\kappa (\mathfrak m)$
is certainly a finite type A-algebra, and so evidently (1) implies (2). It is even a finitely generated A-module, and so also (2) follows from (3). We next prove that (2) implies (3). To this end, recall that if A is any ring, and M is any A-module, then M injects into the product of its localisations at all maximal ideals. If A is Noetherian, and M is finitely generated, then, by combining this fact with the Artin–Rees Lemma, we see that M embeds into the product of its completions at all maximal ideals. Another way to express this is that, if I runs over all cofinite length ideals in A (i.e. all ideals for which
![]() $A/I$
is finite length), then M embeds into the projective limit of the quotients
$A/I$
is finite length), then M embeds into the projective limit of the quotients
![]() $M/IM$
(the point being that this projective limit is the same as the product over all
$M/IM$
(the point being that this projective limit is the same as the product over all
![]() $\mathfrak m$
-adic completions). We are going to apply this observation with A replaced by
$\mathfrak m$
-adic completions). We are going to apply this observation with A replaced by
![]() $\mathfrak {S}_A$
, and with M taken to be
$\mathfrak {S}_A$
, and with M taken to be
![]() $\mathfrak {N}\otimes _A Q$
for some finitely generated A-module Q.
$\mathfrak {N}\otimes _A Q$
for some finitely generated A-module Q.
In
![]() $A[[u]]$
, one sees that u lies in the Jacobson radical (because
$A[[u]]$
, one sees that u lies in the Jacobson radical (because
![]() $1 + fu$
is invertible in
$1 + fu$
is invertible in
![]() $A[[u]]$
for every
$A[[u]]$
for every
![]() $f \in A[[u]]$
), and thus in every maximal ideal, and so the maximal ideals of
$f \in A[[u]]$
), and thus in every maximal ideal, and so the maximal ideals of
![]() $A[[u]]$
are of the form
$A[[u]]$
are of the form
![]() $(\mathfrak m, u)$
, where
$(\mathfrak m, u)$
, where
![]() $\mathfrak m$
runs over the maximal ideals of A. Thus, the ideals of the form
$\mathfrak m$
runs over the maximal ideals of A. Thus, the ideals of the form
![]() $(I,u^n)$
, where I is a cofinite length ideal in A, are cofinal in all cofinite length ideals in
$(I,u^n)$
, where I is a cofinite length ideal in A, are cofinal in all cofinite length ideals in
![]() $A[[u]]$
. Since
$A[[u]]$
. Since
![]() $\mathfrak {S}_A$
is finite over
$\mathfrak {S}_A$
is finite over
![]() $A[[u]]$
, we see that the ideals
$A[[u]]$
, we see that the ideals
![]() $(I,u^n)$
in
$(I,u^n)$
in
![]() $\mathfrak {S}_A$
are also cofinal in all cofinite length ideals in
$\mathfrak {S}_A$
are also cofinal in all cofinite length ideals in
![]() $A[[u]]$
. Since
$A[[u]]$
. Since
![]() $A[[u]]$
, and hence
$A[[u]]$
, and hence
![]() $\mathfrak {S}_A$
, is furthermore Noetherian when A is, we see that if Q is a finitely generated A-module, and
$\mathfrak {S}_A$
, is furthermore Noetherian when A is, we see that if Q is a finitely generated A-module, and
![]() $\mathfrak {N}$
is a finitely generated
$\mathfrak {N}$
is a finitely generated
![]() $\mathfrak {S}_A$
-module, then
$\mathfrak {S}_A$
-module, then
![]() $\mathfrak {N}\otimes _A (Q/IQ)$
is u-adically complete, for any cofinite length ideal I in A, and hence equal to the limit over n of
$\mathfrak {N}\otimes _A (Q/IQ)$
is u-adically complete, for any cofinite length ideal I in A, and hence equal to the limit over n of
![]() $\mathfrak {N} \otimes _A Q/(I,u^n)$
. Putting this together with the observation of the preceding paragraph, we see that the natural morphism
$\mathfrak {N} \otimes _A Q/(I,u^n)$
. Putting this together with the observation of the preceding paragraph, we see that the natural morphism
(where I runs over all cofinite length ideals of A) is an embedding. The induced morphism
is then evidently also an embedding.
Thus, to conclude that
![]() $ \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A Q)$
vanishes, it suffices to show that
$ \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A Q)$
vanishes, it suffices to show that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A (Q/IQ))$
vanishes for each cofinite length ideal I in A. An easy induction (using the flatness of
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A (Q/IQ))$
vanishes for each cofinite length ideal I in A. An easy induction (using the flatness of
![]() $\mathfrak {N}$
) on the length of
$\mathfrak {N}$
) on the length of
![]() $A/I$
reduces this to showing that
$A/I$
reduces this to showing that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M},\mathfrak {N}\otimes _A \kappa (\mathfrak m)\bigr ),$
or, equivalently,
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M},\mathfrak {N}\otimes _A \kappa (\mathfrak m)\bigr ),$
or, equivalently,
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m)\bigr ),$
vanishes for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m)\bigr ),$
vanishes for each maximal ideal
![]() $\mathfrak m$
. Since this is the hypothesis of (2), we see that indeed (2) implies (3).
$\mathfrak m$
. Since this is the hypothesis of (2), we see that indeed (2) implies (3).
It remains to show that (3) implies (1) when A is Jacobson. Applying the result ‘(2) implies (3)’ (with A replaced by B, and taking Q in (3) to be B itself as a B-module) to
![]() $\mathfrak {M}\, \widehat {\otimes }_A B$
and
$\mathfrak {M}\, \widehat {\otimes }_A B$
and
![]() $\mathfrak {N}\, \widehat {\otimes }_A B$
, we see that it suffices to prove the vanishing of
$\mathfrak {N}\, \widehat {\otimes }_A B$
, we see that it suffices to prove the vanishing of
for each maximal ideal
![]() $\mathfrak n$
of B. Since A is Jacobson, the field
$\mathfrak n$
of B. Since A is Jacobson, the field
![]() $\kappa (\mathfrak n)$
is, in fact, a finitely generated A-module, hence
$\kappa (\mathfrak n)$
is, in fact, a finitely generated A-module, hence
![]() $\mathfrak {N}\, \widehat {\otimes }\kappa (\mathfrak n) = \mathfrak {N}\otimes _A \kappa (\mathfrak n)$
, and so the desired vanishing is a special case of (3).
$\mathfrak {N}\, \widehat {\otimes }\kappa (\mathfrak n) = \mathfrak {N}\otimes _A \kappa (\mathfrak n)$
, and so the desired vanishing is a special case of (3).
Corollary 3.1.18. If A is a Noetherian and Jacobson
![]() ${\mathcal O}/\varpi ^a$
-algebra, and if
${\mathcal O}/\varpi ^a$
-algebra, and if
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data and A-coefficients, then the following three conditions are equivalent:
$\mathfrak {N}$
are Breuil–Kisin modules with descent data and A-coefficients, then the following three conditions are equivalent:
-
1.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B) = 0$
for any A-algebra B.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B) = 0$
for any A-algebra B. -
2.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
 $\mathfrak m$
of A.
$\mathfrak m$
of A. -
3.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}, \mathfrak {N}\otimes _A Q) = 0$
for any finitely generated A-module Q.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M}, \mathfrak {N}\otimes _A Q) = 0$
for any finitely generated A-module Q.
Proof. By Proposition 3.1.17, we need only prove that if
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B)$
vanishes for all finitely generated A-algebras B, then it vanishes for all A-algebras B. This is immediate from Proposition 3.1.14.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} (\mathfrak {M}\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B)$
vanishes for all finitely generated A-algebras B, then it vanishes for all A-algebras B. This is immediate from Proposition 3.1.14.
Corollary 3.1.19. Suppose that
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
$\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A, and that furthermore
${\mathcal O}/\varpi ^a$
-algebra A, and that furthermore
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr )$
vanishes for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr )$
vanishes for each maximal ideal
![]() $\mathfrak m$
of A. Then, the A-module
$\mathfrak m$
of A. Then, the A-module
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is projective of finite rank.
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is projective of finite rank.
Proof. By Proposition 3.1.13, in order to prove that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is projective of finite rank over A, it suffices to prove that it is flat over A. For this, it suffices to show that
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is projective of finite rank over A, it suffices to prove that it is flat over A. For this, it suffices to show that
![]() $Q \mapsto \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q$
is exact when applied to finitely generated A-modules Q. Proposition 3.1.15 (together with Remark 2.1.6 (1)) allows us to identify this functor with the functor
$Q \mapsto \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})\otimes _A Q$
is exact when applied to finitely generated A-modules Q. Proposition 3.1.15 (together with Remark 2.1.6 (1)) allows us to identify this functor with the functor
![]() $Q \mapsto \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A Q).$
Note that the functor
$Q \mapsto \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A Q).$
Note that the functor
![]() $Q\mapsto \mathfrak {N}\otimes _A Q$
is an exact functor of Q, since
$Q\mapsto \mathfrak {N}\otimes _A Q$
is an exact functor of Q, since
![]() $\mathfrak {S}_A$
is a flat A-module (as A is Noetherian; see Remark 2.1.3(3)). Thus, taking into account Corollary 3.1.7, we see that it suffices to show that
$\mathfrak {S}_A$
is a flat A-module (as A is Noetherian; see Remark 2.1.3(3)). Thus, taking into account Corollary 3.1.7, we see that it suffices to show that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A Q) = 0$
for each finitely generated A-module Q, under the hypothesis that
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}\otimes _A Q) = 0$
for each finitely generated A-module Q, under the hypothesis that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
![]() $\mathfrak m$
of A. This is the implication (2)
$\mathfrak m$
of A. This is the implication (2)
![]() $\implies $
(3) of Proposition 3.1.17.
$\implies $
(3) of Proposition 3.1.17.
Lemma 3.1.20. Suppose that
![]() $\mathfrak {M}$
is a Breuil–Kisin module with descent data and coefficients in a Noetherian
$\mathfrak {M}$
is a Breuil–Kisin module with descent data and coefficients in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A. Suppose that
${\mathcal O}/\varpi ^a$
-algebra A. Suppose that
![]() $\mathfrak {N}$
is either a Breuil–Kisin module with A-coefficients, or that
$\mathfrak {N}$
is either a Breuil–Kisin module with A-coefficients, or that
![]() $\mathfrak {N}=\mathfrak {N}'/u^N\mathfrak {N}'$
, where
$\mathfrak {N}=\mathfrak {N}'/u^N\mathfrak {N}'$
, where
![]() $\mathfrak {N}'$
is a Breuil–Kisin module with A-coefficients and
$\mathfrak {N}'$
is a Breuil–Kisin module with A-coefficients and
![]() $N\ge 1$
. Then, if B is a finitely generated flat A-algebra, we have a natural isomorphism
$N\ge 1$
. Then, if B is a finitely generated flat A-algebra, we have a natural isomorphism
Proof. By Corollary 3.1.8 and the flatness of B, we have a left exact sequence
and therefore (applying Corollary 3.1.12 to treat the case that
![]() $\mathfrak {N}$
is projective) a left exact sequence
$\mathfrak {N}$
is projective) a left exact sequence
Lemma 3.1.21. Suppose that
![]() $\mathfrak {M}$
is a Breuil–Kisin module with descent data and coefficients in a Noetherian
$\mathfrak {M}$
is a Breuil–Kisin module with descent data and coefficients in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A, which is furthermore a domain. Suppose also that
${\mathcal O}/\varpi ^a$
-algebra A, which is furthermore a domain. Suppose also that
![]() $\mathfrak {N}$
is either a Breuil–Kisin module with A-coefficients, or that
$\mathfrak {N}$
is either a Breuil–Kisin module with A-coefficients, or that
![]() $\mathfrak {N}=\mathfrak {N}'/u^N\mathfrak {N}'$
, where
$\mathfrak {N}=\mathfrak {N}'/u^N\mathfrak {N}'$
, where
![]() $\mathfrak {N}'$
is a Breuil–Kisin module with A-coefficients and
$\mathfrak {N}'$
is a Breuil–Kisin module with A-coefficients and
![]() $N\ge 1$
. Then, there is some nonzero
$N\ge 1$
. Then, there is some nonzero
![]() $f\in A$
with the following property: writing
$f\in A$
with the following property: writing
![]() $\mathfrak {M}_{A_f}=\mathfrak {M}\, \widehat {\otimes }_A A_f$
and
$\mathfrak {M}_{A_f}=\mathfrak {M}\, \widehat {\otimes }_A A_f$
and
![]() $\mathfrak {N}_{A_f}=\mathfrak {N}\, \widehat {\otimes }_A A_f$
, then for any finitely generated
$\mathfrak {N}_{A_f}=\mathfrak {N}\, \widehat {\otimes }_A A_f$
, then for any finitely generated
![]() $A_f$
-algebra B, and any finitely generated B-module Q, there are natural isomorphisms
$A_f$
-algebra B, and any finitely generated B-module Q, there are natural isomorphisms
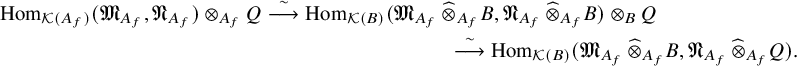 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathcal{K}(A_f)}(\mathfrak{M}_{A_f},\mathfrak{N}_{A_f})\otimes_{A_f}Q \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Hom}}_{\mathcal{K}(B)}&(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B, \mathfrak{N}_{A_f}\, \widehat{\otimes}_{A_f} B)\otimes_B Q\\ &\qquad\quad\buildrel \sim \over \longrightarrow \operatorname{\mathrm{Hom}}_{\mathcal{K}(B)}(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B, \mathfrak{N}_{A_f}\, \widehat{\otimes}_{A_f} Q). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathcal{K}(A_f)}(\mathfrak{M}_{A_f},\mathfrak{N}_{A_f})\otimes_{A_f}Q \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Hom}}_{\mathcal{K}(B)}&(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B, \mathfrak{N}_{A_f}\, \widehat{\otimes}_{A_f} B)\otimes_B Q\\ &\qquad\quad\buildrel \sim \over \longrightarrow \operatorname{\mathrm{Hom}}_{\mathcal{K}(B)}(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B, \mathfrak{N}_{A_f}\, \widehat{\otimes}_{A_f} Q). \end{align*} $$
Proof of Lemma 3.1.21
Note that since A is Noetherian, by Remark 2.1.3(3), we see that
![]() $\mathfrak {N}$
is A-flat. By Corollary 3.1.8, we have an exact sequence
$\mathfrak {N}$
is A-flat. By Corollary 3.1.8, we have an exact sequence
Since by assumption
![]() $\mathfrak {M}$
is a projective
$\mathfrak {M}$
is a projective
![]() $\mathfrak {S}_A$
-module, and
$\mathfrak {S}_A$
-module, and
![]() $\mathfrak {N}$
is a flat A-module, the
$\mathfrak {N}$
is a flat A-module, the
![]() $C^i(\mathfrak {N})$
are also flat A-modules.
$C^i(\mathfrak {N})$
are also flat A-modules.
By Proposition 3.1.13,
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is a finitely generated A-module, so by the generic freeness theorem [Sta13, Tag 051R], there is some nonzero
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is a finitely generated A-module, so by the generic freeness theorem [Sta13, Tag 051R], there is some nonzero
![]() $f\in A$
, such that
$f\in A$
, such that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})_f$
is free over
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})_f$
is free over
![]() $A_f$
.
$A_f$
.
Since localisation is exact, we obtain an exact sequence
and therefore (applying Corollary 3.1.12 to treat the case that
![]() $\mathfrak {N}$
is a Breuil–Kisin module) an exact sequence
$\mathfrak {N}$
is a Breuil–Kisin module) an exact sequence
Since the last three terms are flat over
![]() $A_f$
, this sequence remains exact upon tensoring over
$A_f$
, this sequence remains exact upon tensoring over
![]() $A_f$
with Q. Applying Corollary 3.1.12 again to treat the case that
$A_f$
with Q. Applying Corollary 3.1.12 again to treat the case that
![]() $\mathfrak {N}$
is a Breuil–Kisin module, we see that, in particular, we have a left exact sequence
$\mathfrak {N}$
is a Breuil–Kisin module, we see that, in particular, we have a left exact sequence
and Corollary 3.1.8 together with Lemma 3.1.9 yield one of the desired isomorphisms, namely
If we consider the case when
![]() $Q = B$
, we obtain an isomorphism
$Q = B$
, we obtain an isomorphism
Rewriting the tensor product
![]() $\text {--}\otimes _{A_f} Q $
as
$\text {--}\otimes _{A_f} Q $
as
![]() $\text {--}\otimes _{A_f} B \otimes _B Q,$
we then find that
$\text {--}\otimes _{A_f} B \otimes _B Q,$
we then find that
which gives the second desired isomorphism.
Variants on the preceding result may be proved using other versions of the generic freeness theorem.
Example 3.1.22. Returning to the setting of Example 3.1.16, one can check using Corollary 3.1.18 that the conclusion of Lemma 3.1.21 (for
![]() $\mathfrak {M} = \mathfrak {M}_x$
and
$\mathfrak {M} = \mathfrak {M}_x$
and
![]() $\mathfrak {N} = \mathfrak {M}_y)$
holds with
$\mathfrak {N} = \mathfrak {M}_y)$
holds with
![]() $f = x-y$
. In this case, all of the resulting
$f = x-y$
. In this case, all of the resulting
![]() $\operatorname {\mathrm {Hom}}$
groups vanish (cf. also the proof of Lemma 3.3.7). It then follows from Corollary 3.1.19 that
$\operatorname {\mathrm {Hom}}$
groups vanish (cf. also the proof of Lemma 3.3.7). It then follows from Corollary 3.1.19 that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})_{f}$
is projective over
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})_{f}$
is projective over
![]() $A_f$
, so that the proof of Lemma 3.1.21 even goes through with this choice of f.
$A_f$
, so that the proof of Lemma 3.1.21 even goes through with this choice of f.
As well as considering homomorphisms and extensions of Breuil–Kisin modules, we need to consider the homomorphisms and extensions of their associated étale
![]() $\varphi $
-modules; recall that the passage to associated étale
$\varphi $
-modules; recall that the passage to associated étale
![]() $\varphi $
-modules amounts to inverting u, and so we briefly discuss this process in the general context of the category
$\varphi $
-modules amounts to inverting u, and so we briefly discuss this process in the general context of the category
![]() $\mathcal {K}(A)$
.
$\mathcal {K}(A)$
.
We let
![]() $\mathcal {K}(A)[1/u]$
denote the full subcategory of
$\mathcal {K}(A)[1/u]$
denote the full subcategory of
![]() $\mathcal {K}(A)$
consisting of objects on which multiplication by u is invertible. We may equally well regard it as the category of left
$\mathcal {K}(A)$
consisting of objects on which multiplication by u is invertible. We may equally well regard it as the category of left
![]() $\mathfrak {S}_A[1/u][F,\operatorname {\mathrm {Gal}}(K'/K)]$
-modules (this notation being interpreted in the evident manner). There are natural isomorphisms (of bimodules)
$\mathfrak {S}_A[1/u][F,\operatorname {\mathrm {Gal}}(K'/K)]$
-modules (this notation being interpreted in the evident manner). There are natural isomorphisms (of bimodules)
and
Thus (since
![]() $\mathfrak {S}_A \to \mathfrak {S}_A[1/u]$
is a flat morphism of commutative rings), the morphism of rings
$\mathfrak {S}_A \to \mathfrak {S}_A[1/u]$
is a flat morphism of commutative rings), the morphism of rings
![]() $\mathfrak {S}_A[F,\operatorname {\mathrm {Gal}}(K'/K)] \to \mathfrak {S}_A[1/u][F,\operatorname {\mathrm {Gal}}(K'/K)]$
is both left and right flat.
$\mathfrak {S}_A[F,\operatorname {\mathrm {Gal}}(K'/K)] \to \mathfrak {S}_A[1/u][F,\operatorname {\mathrm {Gal}}(K'/K)]$
is both left and right flat.
If
![]() $\mathfrak {M}$
is an object of
$\mathfrak {M}$
is an object of
![]() $\mathcal {K}(A)$
, then we see from (3.1.23) that
$\mathcal {K}(A)$
, then we see from (3.1.23) that
![]() $\mathfrak {M}[1/u] := \mathfrak {S}_A[1/u]\otimes _{\mathfrak {S}_A} \mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {S}_A[1/u][F,\operatorname {\mathrm {Gal}}(K'/K)] \otimes _{\mathfrak {S}_A[F,\operatorname {\mathrm {Gal}}(K'/K)]} \mathfrak {M}$
is naturally an object of
$\mathfrak {M}[1/u] := \mathfrak {S}_A[1/u]\otimes _{\mathfrak {S}_A} \mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {S}_A[1/u][F,\operatorname {\mathrm {Gal}}(K'/K)] \otimes _{\mathfrak {S}_A[F,\operatorname {\mathrm {Gal}}(K'/K)]} \mathfrak {M}$
is naturally an object of
![]() $\mathcal {K}(A)[1/u]$
. Our preceding remarks about flatness show that
$\mathcal {K}(A)[1/u]$
. Our preceding remarks about flatness show that
![]() $\mathfrak {M} \mapsto \mathfrak {M}[1/u]$
is an exact functor
$\mathfrak {M} \mapsto \mathfrak {M}[1/u]$
is an exact functor
![]() $\mathcal {K}(A)\to \mathcal {K}(A)[1/u]$
.
$\mathcal {K}(A)\to \mathcal {K}(A)[1/u]$
.
Lemma 3.1.25.
-
1. If M and N are objects of
 $\mathcal {K}(A)[1/u]$
, then there is a natural isomorphism
$\mathcal {K}(A)[1/u]$
, then there is a natural isomorphism  $$ \begin{align*}\operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)[1/u]}(M,N) \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)}(M,N).\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)[1/u]}(M,N) \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)}(M,N).\end{align*} $$
-
2. If
 $\mathfrak {M}$
is an object of
$\mathfrak {M}$
is an object of
 $\mathcal {K}(A)$
and N is an object of
$\mathcal {K}(A)$
and N is an object of
 $\mathcal {K}(A)[1/u]$
, then there is a natural isomorphism for all
$\mathcal {K}(A)[1/u]$
, then there is a natural isomorphism for all $$ \begin{align*}\operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)}(\mathfrak{M},N) \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)}(\mathfrak{M}[1/u],N),\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)}(\mathfrak{M},N) \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Ext}}^i_{\mathcal{K}(A)}(\mathfrak{M}[1/u],N),\end{align*} $$
 $i\geq 0$
.
$i\geq 0$
.
Proof. The morphism of (1) can be understood in various ways; for example, by thinking in terms of Yoneda Exts, and recalling that
![]() $\mathcal {K}(A)[1/u]$
is a full subcategory of
$\mathcal {K}(A)[1/u]$
is a full subcategory of
![]() $\mathcal {K}(A).$
If instead we think in terms of projective resolutions, we can begin with a projective resolution
$\mathcal {K}(A).$
If instead we think in terms of projective resolutions, we can begin with a projective resolution
![]() $\mathfrak {P}^{\bullet } \to M$
in
$\mathfrak {P}^{\bullet } \to M$
in
![]() $\mathcal {K}(A)$
, and then consider the induced projective resolution
$\mathcal {K}(A)$
, and then consider the induced projective resolution
![]() $\mathfrak {P}^{\bullet }[1/u]$
of
$\mathfrak {P}^{\bullet }[1/u]$
of
![]() $M[1/u]$
. Noting that
$M[1/u]$
. Noting that
![]() $M[1/u] \buildrel \sim \over \longrightarrow M$
for any object M of
$M[1/u] \buildrel \sim \over \longrightarrow M$
for any object M of
![]() $\mathcal {K}(A)[1/u]$
, we then find (via tensor adjunction) that
$\mathcal {K}(A)[1/u]$
, we then find (via tensor adjunction) that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {P}^{\bullet }, N) \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)[1/u]}(\mathfrak {P}^{\bullet }[1/u], N)$
, which induces the desired isomorphism of
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {P}^{\bullet }, N) \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)[1/u]}(\mathfrak {P}^{\bullet }[1/u], N)$
, which induces the desired isomorphism of
![]() $\operatorname {\mathrm {Ext}}$
’s by passing to cohomology.
$\operatorname {\mathrm {Ext}}$
’s by passing to cohomology.
Taking into account the isomorphism of (1), the claim of (2) is a general fact about tensoring over a flat ring map (as can, again, be seen by considering projective resolutions).
Remark 3.1.26. The preceding lemma is in fact an automatic consequence of the abstract categorical properties of our situation: the functor
![]() $\mathfrak {M} \mapsto \mathfrak {M}[1/u]$
is left adjoint to the inclusion
$\mathfrak {M} \mapsto \mathfrak {M}[1/u]$
is left adjoint to the inclusion
![]() $\mathcal {K}(A)[1/u] \subset \mathcal {K}(A),$
and restricts to (a functor naturally equivalent to) the identity functor on
$\mathcal {K}(A)[1/u] \subset \mathcal {K}(A),$
and restricts to (a functor naturally equivalent to) the identity functor on
![]() $\mathcal {K}(A)[1/u]$
.
$\mathcal {K}(A)[1/u]$
.
The following lemma expresses the Hom between étale
![]() $\varphi $
-modules arising from Breuil–Kisin modules in terms of a certain direct limit.
$\varphi $
-modules arising from Breuil–Kisin modules in terms of a certain direct limit.
Lemma 3.1.27. Suppose that
![]() $\mathfrak {M}$
is a Breuil–Kisin module with descent data in a Noetherian
$\mathfrak {M}$
is a Breuil–Kisin module with descent data in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A, and that
${\mathcal O}/\varpi ^a$
-algebra A, and that
![]() $\mathfrak {N}$
is an object of
$\mathfrak {N}$
is an object of
![]() $\mathcal {K}(A)$
which is finitely generated and u-torsion free as an
$\mathcal {K}(A)$
which is finitely generated and u-torsion free as an
![]() $\mathfrak {S}_A$
-module. Then, there is a natural isomorphism
$\mathfrak {S}_A$
-module. Then, there is a natural isomorphism
where the transition maps are induced by the inclusions
![]() $u^{i+1} \mathfrak {M} \subset u^i \mathfrak {M}$
.
$u^{i+1} \mathfrak {M} \subset u^i \mathfrak {M}$
.
Remark 3.1.28. Note that since
![]() $\mathfrak {N}$
is u-torsion free, the transition maps in the colimit are injections, so the colimit is just an increasing union.
$\mathfrak {N}$
is u-torsion free, the transition maps in the colimit are injections, so the colimit is just an increasing union.
Proof. There are compatible injections
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i\mathfrak {M},\mathfrak {N}) \to \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)[1/u]}(\mathfrak {M}[1/u],\mathfrak {N}[1/u])$
, taking
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i\mathfrak {M},\mathfrak {N}) \to \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)[1/u]}(\mathfrak {M}[1/u],\mathfrak {N}[1/u])$
, taking
![]() $f'\in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i\mathfrak {M},\mathfrak {N})$
to
$f'\in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i\mathfrak {M},\mathfrak {N})$
to
![]() $f\in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u])$
, where
$f\in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u])$
, where
![]() $f(m)=u^{-i}f'(u^im)$
. Conversely, given
$f(m)=u^{-i}f'(u^im)$
. Conversely, given
![]() $f\in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u])$
, there is some i, such that
$f\in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u])$
, there is some i, such that
![]() $f(\mathfrak {M})\subset u^{-i}\mathfrak {N}$
, as required.
$f(\mathfrak {M})\subset u^{-i}\mathfrak {N}$
, as required.
We have the following analogue of Proposition 3.1.17.
Corollary 3.1.29. Suppose that
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data in a Noetherian
$\mathfrak {N}$
are Breuil–Kisin modules with descent data in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A. Consider the following conditions:
${\mathcal O}/\varpi ^a$
-algebra A. Consider the following conditions:
-
1.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)[1/u]} \bigl ((\mathfrak {M}\, \widehat {\otimes }_A B)[1/u], (\mathfrak {N}\, \widehat {\otimes }_A B)[1/u]\bigr ) = 0$
for any finite type A-algebra B.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)[1/u]} \bigl ((\mathfrak {M}\, \widehat {\otimes }_A B)[1/u], (\mathfrak {N}\, \widehat {\otimes }_A B)[1/u]\bigr ) = 0$
for any finite type A-algebra B. -
2.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))[1/u]}\bigl ((\mathfrak {M}\otimes _A \kappa (\mathfrak m))[1/u], (\mathfrak {N}\otimes _A \kappa (\mathfrak m))[1/u] \bigr ) = 0$
for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))[1/u]}\bigl ((\mathfrak {M}\otimes _A \kappa (\mathfrak m))[1/u], (\mathfrak {N}\otimes _A \kappa (\mathfrak m))[1/u] \bigr ) = 0$
for each maximal ideal
 $\mathfrak m$
of A.
$\mathfrak m$
of A. -
3.
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)[1/u]}\bigl (\mathfrak {M}[1/u], (\mathfrak {N}\otimes _A Q)[1/u]\bigr ) = 0$
for any finitely generated A-module Q.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)[1/u]}\bigl (\mathfrak {M}[1/u], (\mathfrak {N}\otimes _A Q)[1/u]\bigr ) = 0$
for any finitely generated A-module Q.
Then, we have (1)
![]() $\implies $
(2)
$\implies $
(2)
![]() $\iff $
(3). If A is furthermore Jacobson, then all three conditions are equivalent.
$\iff $
(3). If A is furthermore Jacobson, then all three conditions are equivalent.
Proof. By Lemma 3.1.27, the three conditions are, respectively, equivalent to the following conditions.
-
(1′)
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} \bigl (u^i(\mathfrak {M}\, \widehat {\otimes }_A B), \mathfrak {N}\, \widehat {\otimes }_A B\bigr ) = 0$
for any finite type A-algebra B and all
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} \bigl (u^i(\mathfrak {M}\, \widehat {\otimes }_A B), \mathfrak {N}\, \widehat {\otimes }_A B\bigr ) = 0$
for any finite type A-algebra B and all
 $i\ge 0$
.
$i\ge 0$
. -
(2′)
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (u^i(\mathfrak {M}\otimes _A \kappa (\mathfrak m)), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl (u^i(\mathfrak {M}\otimes _A \kappa (\mathfrak m)), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
 $\mathfrak m$
of A and all
$\mathfrak m$
of A and all
 $i\ge 0$
.
$i\ge 0$
. -
(3′)
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (u^i\mathfrak {M}, \mathfrak {N}\otimes _A Q\bigr ) = 0$
for any finitely generated A-module Q and all
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (u^i\mathfrak {M}, \mathfrak {N}\otimes _A Q\bigr ) = 0$
for any finitely generated A-module Q and all
 $i\ge 0$
.
$i\ge 0$
.
Since
![]() $\mathfrak {M}$
is projective, the first two conditions are in turn equivalent to
$\mathfrak {M}$
is projective, the first two conditions are in turn equivalent to
-
(1′′)
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} \bigl ((u^i\mathfrak {M})\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B\bigr ) = 0$
for any finite type A-algebra B and all
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(B)} \bigl ((u^i\mathfrak {M})\, \widehat {\otimes }_A B, \mathfrak {N}\, \widehat {\otimes }_A B\bigr ) = 0$
for any finite type A-algebra B and all
 $i\ge 0$
.
$i\ge 0$
. -
(2′′)
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl ((u^i\mathfrak {M})\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa (\mathfrak {m}))}\bigl ((u^i\mathfrak {M})\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr ) = 0$
for each maximal ideal
 $\mathfrak m$
of A and all
$\mathfrak m$
of A and all
 $i\ge 0$
.
$i\ge 0$
.
The result then follows from Proposition 3.1.17.
Definition 3.1.30. If
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are objects of
$\mathfrak {N}$
are objects of
![]() $\mathcal {K}(A)$
, then we define
$\mathcal {K}(A)$
, then we define
The point of this definition is to capture, in the setting of Lemma 2.2.4, the nonsplit extensions of Breuil–Kisin modules whose underlying extension of Galois representations is split.
Suppose now that
![]() $\mathfrak {M}$
is a Breuil–Kisin module. The exact sequence in
$\mathfrak {M}$
is a Breuil–Kisin module. The exact sequence in
![]() $\mathcal {K}(A)$
$\mathcal {K}(A)$
gives an exact sequence of complexes
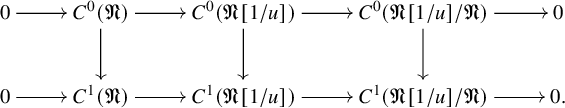
It follows from Corollary 3.1.8, Lemma 3.1.25(2) and the snake lemma that we have an exact sequence
 $$ \begin{align}\begin{aligned}0\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N}[1/u]) \qquad \qquad \\ \to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N}[1/u]/\mathfrak{N}) \to {\text{ker-Ext}}^1_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})\to 0.\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned}0\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N}[1/u]) \qquad \qquad \\ \to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N}[1/u]/\mathfrak{N}) \to {\text{ker-Ext}}^1_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})\to 0.\end{aligned}\end{align} $$
Lemma 3.1.32. If
![]() $\mathfrak {M}$
,
$\mathfrak {M}$
,
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
$\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A, and
${\mathcal O}/\varpi ^a$
-algebra A, and
![]() $\mathfrak {N}$
has height at most h, then
$\mathfrak {N}$
has height at most h, then
![]() $f(\mathfrak {M})$
is killed by
$f(\mathfrak {M})$
is killed by
![]() $u^i$
for any
$u^i$
for any
![]() $f \in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
and any
$f \in \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
and any
![]() $i \ge \lfloor e'ah/(p-1) \rfloor $
.
$i \ge \lfloor e'ah/(p-1) \rfloor $
.
Proof. Suppose that f is an element of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
. Then,
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
. Then,
![]() $f(\mathfrak {M})$
is a finitely generated submodule of
$f(\mathfrak {M})$
is a finitely generated submodule of
![]() $\mathfrak {N}[1/u]/\mathfrak {N}$
, and it is therefore killed by
$\mathfrak {N}[1/u]/\mathfrak {N}$
, and it is therefore killed by
![]() $u^i$
for some
$u^i$
for some
![]() $i\ge 0$
. Choosing i to be the exponent of
$i\ge 0$
. Choosing i to be the exponent of
![]() $f(\mathfrak {M})$
(that is, choosing i to be minimal), it follows that
$f(\mathfrak {M})$
(that is, choosing i to be minimal), it follows that
![]() $(\varphi ^{*}f)(\varphi ^{*}\mathfrak {M})$
has exponent precisely
$(\varphi ^{*}f)(\varphi ^{*}\mathfrak {M})$
has exponent precisely
![]() $ip$
. (From the choice of i, we see that
$ip$
. (From the choice of i, we see that
![]() $u^{i-1} f(\mathfrak {M})$
is nonzero but killed by u, i.e., it is just a
$u^{i-1} f(\mathfrak {M})$
is nonzero but killed by u, i.e., it is just a
![]() $W(k') \otimes A$
-module, and so its pullback by
$W(k') \otimes A$
-module, and so its pullback by
![]() $\varphi :\mathfrak {S}_A\to \mathfrak {S}_A$
has exponent precisely p. Then, by the flatness of
$\varphi :\mathfrak {S}_A\to \mathfrak {S}_A$
has exponent precisely p. Then, by the flatness of
![]() $\varphi :\mathfrak {S}_A\to \mathfrak {S}_A$
, we have
$\varphi :\mathfrak {S}_A\to \mathfrak {S}_A$
, we have
![]() $u^{ip-1}(\varphi ^{*}f)(\varphi ^{*}\mathfrak {M})=u^{p-1}\varphi ^{*}(u^{i-1} f(\mathfrak {M})) \neq 0$
.)
$u^{ip-1}(\varphi ^{*}f)(\varphi ^{*}\mathfrak {M})=u^{p-1}\varphi ^{*}(u^{i-1} f(\mathfrak {M})) \neq 0$
.)
We claim that
![]() $u^{i+e'ah}(\varphi ^{*}f)(\varphi ^{*}\mathfrak {M})=0$
; admitting this, we deduce that
$u^{i+e'ah}(\varphi ^{*}f)(\varphi ^{*}\mathfrak {M})=0$
; admitting this, we deduce that
![]() $i+e'ah\ge ip$
, as required. To see the claim, take
$i+e'ah\ge ip$
, as required. To see the claim, take
![]() $x\in \varphi ^{*}\mathfrak {M}$
, so that
$x\in \varphi ^{*}\mathfrak {M}$
, so that
![]() $\Phi _{\mathfrak {N}}((u^i\varphi ^{*}f)(x))= u^if(\Phi _{\mathfrak {M}}(x))=0$
. It is therefore enough to show that the kernel of
$\Phi _{\mathfrak {N}}((u^i\varphi ^{*}f)(x))= u^if(\Phi _{\mathfrak {M}}(x))=0$
. It is therefore enough to show that the kernel of
is killed by
![]() $u^{e'ah}$
; but this follows immediately from an application of the snake lemma to the commutative diagram
$u^{e'ah}$
; but this follows immediately from an application of the snake lemma to the commutative diagram
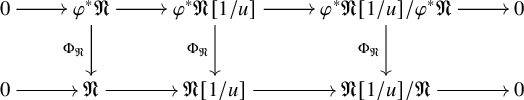
together with the assumption that
![]() $\mathfrak {N}$
has height at most h and an argument as in the first line of the proof of Lemma 3.1.10.
$\mathfrak {N}$
has height at most h and an argument as in the first line of the proof of Lemma 3.1.10.
Lemma 3.1.33. If
![]() $\mathfrak {M}$
,
$\mathfrak {M}$
,
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
$\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A, and
${\mathcal O}/\varpi ^a$
-algebra A, and
![]() $\mathfrak {N}$
has height at most h, then for any
$\mathfrak {N}$
has height at most h, then for any
![]() $i \ge \lfloor e'ah/(p-1) \rfloor $
, we have an exact sequence
$i \ge \lfloor e'ah/(p-1) \rfloor $
, we have an exact sequence
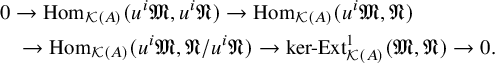 $$\begin{align*}\begin{aligned}0\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(u^i\mathfrak{M},u^i\mathfrak{N})\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(u^i\mathfrak{M},\mathfrak{N}) \qquad \qquad \\ \to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(u^i\mathfrak{M},\mathfrak{N}/u^i\mathfrak{N}) \to {\text{ker-Ext}}^1_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})\to 0.\end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned}0\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(u^i\mathfrak{M},u^i\mathfrak{N})\to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(u^i\mathfrak{M},\mathfrak{N}) \qquad \qquad \\ \to\operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(u^i\mathfrak{M},\mathfrak{N}/u^i\mathfrak{N}) \to {\text{ker-Ext}}^1_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})\to 0.\end{aligned} \end{align*}$$
Proof. Comparing Lemma 3.1.32 with the proof of Lemma 3.1.27, we see that the direct limit in that proof has stabilised at i, and we obtain an isomorphism
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]) \buildrel \sim \over \to \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N})$
sending a map f to
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]) \buildrel \sim \over \to \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N})$
sending a map f to
![]() $f' : u^i m \mapsto u^i f(m)$
. The same formula evidently identifies
$f' : u^i m \mapsto u^i f(m)$
. The same formula evidently identifies
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}( \mathfrak {M},\mathfrak {N})$
with
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}( \mathfrak {M},\mathfrak {N})$
with
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i\mathfrak {M},u^i\mathfrak {N})$
and
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i\mathfrak {M},u^i\mathfrak {N})$
and
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
with
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
with
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N}[1/u]/u^i \mathfrak {N})$
. But any map in the latter group has image contained in
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N}[1/u]/u^i \mathfrak {N})$
. But any map in the latter group has image contained in
![]() $\mathfrak {N}/u^i \mathfrak {N}$
(by Lemma 3.1.32 applied to
$\mathfrak {N}/u^i \mathfrak {N}$
(by Lemma 3.1.32 applied to
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
, together with the identification in the previous sentence), so that
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
, together with the identification in the previous sentence), so that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N}[1/u]/u^i \mathfrak {N}) = \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N}/u^i \mathfrak {N})$
.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N}[1/u]/u^i \mathfrak {N}) = \operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}(u^i \mathfrak {M},\mathfrak {N}/u^i \mathfrak {N})$
.
Proposition 3.1.34. Let
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
be Breuil–Kisin modules with descent data and coefficients in a Noetherian
$\mathfrak {N}$
be Breuil–Kisin modules with descent data and coefficients in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-domain A. Then, there is some nonzero
${\mathcal O}/\varpi ^a$
-domain A. Then, there is some nonzero
![]() $f\in A$
with the following property: if we write
$f\in A$
with the following property: if we write
![]() $\mathfrak {M}_{A_f}=\mathfrak {M}\, \widehat {\otimes }_A A_f$
and
$\mathfrak {M}_{A_f}=\mathfrak {M}\, \widehat {\otimes }_A A_f$
and
![]() $\mathfrak {N}_{A_f}=\mathfrak {N}\, \widehat {\otimes }_A A_f$
, then if B is any finitely generated
$\mathfrak {N}_{A_f}=\mathfrak {N}\, \widehat {\otimes }_A A_f$
, then if B is any finitely generated
![]() $A_f$
-algebra, and if Q is any finitely generated B-module, we have natural isomorphisms
$A_f$
-algebra, and if Q is any finitely generated B-module, we have natural isomorphisms
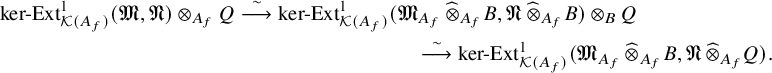 $$ \begin{align*} {\text{ker-Ext}}^1_{\mathcal{K}(A_f)}(\mathfrak{M},\mathfrak{N})\otimes_{A_f}Q \buildrel \sim \over \longrightarrow {\text{ker-Ext}}^1_{\mathcal{K}(A_f)} &(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B,\mathfrak{N}\, \widehat{\otimes}_{A_f} B)\otimes_B Q\\ &\quad \ \buildrel \sim \over \longrightarrow {\text{ker-Ext}}^1_{\mathcal{K}(A_f)}(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B, \mathfrak{N}\, \widehat{\otimes}_{A_f} Q). \end{align*} $$
$$ \begin{align*} {\text{ker-Ext}}^1_{\mathcal{K}(A_f)}(\mathfrak{M},\mathfrak{N})\otimes_{A_f}Q \buildrel \sim \over \longrightarrow {\text{ker-Ext}}^1_{\mathcal{K}(A_f)} &(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B,\mathfrak{N}\, \widehat{\otimes}_{A_f} B)\otimes_B Q\\ &\quad \ \buildrel \sim \over \longrightarrow {\text{ker-Ext}}^1_{\mathcal{K}(A_f)}(\mathfrak{M}_{A_f}\, \widehat{\otimes}_{A_f} B, \mathfrak{N}\, \widehat{\otimes}_{A_f} Q). \end{align*} $$
Proof. In view of Lemma 3.1.33, this follows from Lemma 3.1.21, with
![]() $\mathfrak {M}$
there being our
$\mathfrak {M}$
there being our
![]() $u^i\mathfrak {M}$
, and
$u^i\mathfrak {M}$
, and
![]() $\mathfrak {N}$
being each of
$\mathfrak {N}$
being each of
![]() $\mathfrak {N}$
,
$\mathfrak {N}$
,
![]() $\mathfrak {N}/u^i\mathfrak {N}$
in turn.
$\mathfrak {N}/u^i\mathfrak {N}$
in turn.
The following result will be crucial in our investigation of the decomposition of
![]() ${\mathcal C}^{\mathrm {dd},1}$
and
${\mathcal C}^{\mathrm {dd},1}$
and
![]() ${\mathcal R}^{\mathrm {dd},1}$
into irreducible components.
${\mathcal R}^{\mathrm {dd},1}$
into irreducible components.
Proposition 3.1.35. Suppose that
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
$\mathfrak {N}$
are Breuil–Kisin modules with descent data and coefficients in a Noetherian
![]() ${\mathcal O}/\varpi ^a$
-algebra A which is furthermore a domain, and suppose that
${\mathcal O}/\varpi ^a$
-algebra A which is furthermore a domain, and suppose that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr )$
vanishes for each maximal ideal
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(A)}\bigl (\mathfrak {M}\otimes _A \kappa (\mathfrak m), \mathfrak {N}\otimes _A \kappa (\mathfrak m) \bigr )$
vanishes for each maximal ideal
![]() $\mathfrak m$
of A. Then, there is some nonzero
$\mathfrak m$
of A. Then, there is some nonzero
![]() $f\in A$
with the following property: if we write
$f\in A$
with the following property: if we write
![]() $\mathfrak {M}_{A_f}=\mathfrak {M}\, \widehat {\otimes }_A A_f$
and
$\mathfrak {M}_{A_f}=\mathfrak {M}\, \widehat {\otimes }_A A_f$
and
![]() $\mathfrak {N}_{A_f}=\mathfrak {N}\, \widehat {\otimes }_A A_f$
, then for any finitely generated
$\mathfrak {N}_{A_f}=\mathfrak {N}\, \widehat {\otimes }_A A_f$
, then for any finitely generated
![]() $A_f$
-algebra B, each of
$A_f$
-algebra B, each of
![]() ${\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
,
${\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
,
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
and
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
and
is a finitely generated projective B-module.
Proof. Choose f as in Proposition 3.1.34, let B be a finitely generated
![]() $A_f$
-algebra and let Q be a finitely generated B-module. By Propositions 3.1.15 and 3.1.34, the morphism
$A_f$
-algebra and let Q be a finitely generated B-module. By Propositions 3.1.15 and 3.1.34, the morphism
is naturally identified with the morphism
in particular, it is injective. By Proposition 3.1.15 and Corollary 3.1.19, we see that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f} B)$
is a finitely generated projective B-module; hence, it is also flat. Combining this with the injectivity just proved, we find that
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f} B)$
is a finitely generated projective B-module; hence, it is also flat. Combining this with the injectivity just proved, we find that
for every finitely generated B-module Q, and thus that
is a finitely generated flat, and therefore finitely generated projective, B-module. Thus,
![]() ${\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f}B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
is a direct summand of the finitely generated projective B-module
${\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f}B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
is a direct summand of the finitely generated projective B-module
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
, and so is itself a finitely generated projective B-module.
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{A_f}\, \widehat {\otimes }_{A_f} B,\mathfrak {N}_{A_f}\, \widehat {\otimes }_{A_f}B)$
, and so is itself a finitely generated projective B-module.
3.2. Families of extensions
Let
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients, so that
$\mathfrak {N}$
be Breuil–Kisin modules with descent data and A-coefficients, so that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is an A-module. Suppose that
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is an A-module. Suppose that
![]() $\psi : V \to \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is a homomorphism of A-modules whose source is a projective A-module of finite rank. Then, we may regard
$\psi : V \to \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is a homomorphism of A-modules whose source is a projective A-module of finite rank. Then, we may regard
![]() $\psi $
as an element of
$\psi $
as an element of
and, in this way,
![]() $\psi $
corresponds to an extension
$\psi $
corresponds to an extension
which we refer to as the family of extensions of
![]() $\mathfrak {M}$
by
$\mathfrak {M}$
by
![]() $\mathfrak {N}$
parametrised by V (or by
$\mathfrak {N}$
parametrised by V (or by
![]() $\psi $
, if we want to emphasise our choice of homomorphism). We let
$\psi $
, if we want to emphasise our choice of homomorphism). We let
![]() $\mathfrak {E}_v$
denote the pushforward of
$\mathfrak {E}_v$
denote the pushforward of
![]() $\mathfrak {E}$
under the morphism
$\mathfrak {E}$
under the morphism
![]() $\mathfrak {N}\otimes _A V^{\vee } \to \mathfrak {N}$
given by evaluation on
$\mathfrak {N}\otimes _A V^{\vee } \to \mathfrak {N}$
given by evaluation on
![]() $v\in V$
. In the special case that
$v\in V$
. In the special case that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
itself is a projective A-module of finite rank, we can let V be
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
itself is a projective A-module of finite rank, we can let V be
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
and take
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
and take
![]() $\psi $
to be the identity map; in this case we, refer to (3.2.1) as the universal extension of
$\psi $
to be the identity map; in this case we, refer to (3.2.1) as the universal extension of
![]() $\mathfrak {M}$
by
$\mathfrak {M}$
by
![]() $\mathfrak {N}$
. The reason for this terminology is as follows: if
$\mathfrak {N}$
. The reason for this terminology is as follows: if
![]() $v \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
, then
$v \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
, then
![]() $\mathfrak {E}_v$
is the extension of
$\mathfrak {E}_v$
is the extension of
![]() $\mathfrak {M}$
by
$\mathfrak {M}$
by
![]() $\mathfrak {N}$
corresponding to the element v.
$\mathfrak {N}$
corresponding to the element v.
Let
![]() $B := A[V^{\vee }]$
denote the symmetric algebra over A generated by
$B := A[V^{\vee }]$
denote the symmetric algebra over A generated by
![]() $V^{\vee }$
. The short exact sequence (3.2.1) is a short exact sequence of Breuil–Kisin modules with descent data, and so forming its u-adically completed tensor product with B over A, we obtain a short exact sequence
$V^{\vee }$
. The short exact sequence (3.2.1) is a short exact sequence of Breuil–Kisin modules with descent data, and so forming its u-adically completed tensor product with B over A, we obtain a short exact sequence
of Breuil–Kisin modules with descent data over B (see Lemma 2.1.5). Pushing this short exact sequence forward under the natural map
induced by the inclusion of
![]() $V^{\vee }$
in B and the multiplication map
$V^{\vee }$
in B and the multiplication map
![]() $B\otimes _A B \to B$
, we obtain a short exact sequence
$B\otimes _A B \to B$
, we obtain a short exact sequence
of Breuil–Kisin modules with descent data over B, which we call the family of extensions of
![]() $\mathfrak {M}$
by
$\mathfrak {M}$
by
![]() $\mathfrak {N}$
parametrised by
$\mathfrak {N}$
parametrised by
![]() $\operatorname {\mathrm {Spec}} B$
(which we note is (the total space of) the vector bundle over
$\operatorname {\mathrm {Spec}} B$
(which we note is (the total space of) the vector bundle over
![]() $\operatorname {\mathrm {Spec}} A$
corresponding to the projective A-module V).
$\operatorname {\mathrm {Spec}} A$
corresponding to the projective A-module V).
If
![]() $\alpha _v: B \to A$
is the morphism induced by the evaluation map
$\alpha _v: B \to A$
is the morphism induced by the evaluation map
![]() $V^{\vee } \to A$
given by some element
$V^{\vee } \to A$
given by some element
![]() $v \in V$
, then base changing (3.2.2) by
$v \in V$
, then base changing (3.2.2) by
![]() $\alpha _v$
, we recover the short exact sequence
$\alpha _v$
, we recover the short exact sequence
More generally, suppose that A is a
![]() ${\mathcal O}/\varpi ^a$
-algebra for some
${\mathcal O}/\varpi ^a$
-algebra for some
![]() $a\ge 1$
, and let C be any A-algebra. Suppose that
$a\ge 1$
, and let C be any A-algebra. Suppose that
![]() $\alpha _{\tilde {v}}: B \to C$
is the morphism induced by the evaluation map
$\alpha _{\tilde {v}}: B \to C$
is the morphism induced by the evaluation map
![]() $V^{\vee } \to C$
corresponding to some element
$V^{\vee } \to C$
corresponding to some element
![]() $\tilde {v} \in C\otimes _A V$
. Then, base changing (3.2.2) by
$\tilde {v} \in C\otimes _A V$
. Then, base changing (3.2.2) by
![]() $\alpha _{\tilde {v}}$
yields a short exact sequence
$\alpha _{\tilde {v}}$
yields a short exact sequence
whose associated extension class corresponds to the image of
![]() $\tilde {v}$
under the natural morphism
$\tilde {v}$
under the natural morphism
![]() $C\otimes _A V \to C\otimes _A \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M}, \mathfrak {N}) \cong \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(C)}(\mathfrak {M}\, \widehat {\otimes }_A C, \mathfrak {N}\otimes _A C),$
the first arrow being induced by
$C\otimes _A V \to C\otimes _A \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M}, \mathfrak {N}) \cong \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(C)}(\mathfrak {M}\, \widehat {\otimes }_A C, \mathfrak {N}\otimes _A C),$
the first arrow being induced by
![]() $\psi $
and the second arrow being the isomorphism of Proposition 3.1.15.
$\psi $
and the second arrow being the isomorphism of Proposition 3.1.15.
3.2.3. The functor represented by a universal family
We now suppose that the ring A and the Breuil–Kisin modules
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
have the following properties:
$\mathfrak {N}$
have the following properties:
Assumption 3.2.4. Let A be a Noetherian and Jacobson
![]() ${\mathcal O}/\varpi ^a$
-algebra for some
${\mathcal O}/\varpi ^a$
-algebra for some
![]() $a\ge 1$
, and assume that for each maximal ideal
$a\ge 1$
, and assume that for each maximal ideal
![]() $\mathfrak m$
of A, we have that
$\mathfrak m$
of A, we have that
By Corollary 3.1.19, this assumption implies, in particular, that
![]() $V:= \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is projective of finite rank, and so we may form
$V:= \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(A)}(\mathfrak {M},\mathfrak {N})$
is projective of finite rank, and so we may form
![]() $\operatorname {\mathrm {Spec}} B := \operatorname {\mathrm {Spec}} A[V^{\vee }]$
, which parametrised the universal family of extensions. We are then able to give the following precise description of the functor represented by
$\operatorname {\mathrm {Spec}} B := \operatorname {\mathrm {Spec}} A[V^{\vee }]$
, which parametrised the universal family of extensions. We are then able to give the following precise description of the functor represented by
![]() $\operatorname {\mathrm {Spec}} B$
.
$\operatorname {\mathrm {Spec}} B$
.
Proposition 3.2.5. The scheme
![]() $\operatorname {\mathrm {Spec}} B$
represents the functor which, to any
$\operatorname {\mathrm {Spec}} B$
represents the functor which, to any
![]() ${\mathcal O}/\varpi ^a$
-algebra C, associates the set of isomorphism classes of tuples
${\mathcal O}/\varpi ^a$
-algebra C, associates the set of isomorphism classes of tuples
![]() $(\alpha , \mathfrak {E}, \iota , \pi )$
, where
$(\alpha , \mathfrak {E}, \iota , \pi )$
, where
![]() $\alpha $
is a morphism
$\alpha $
is a morphism
![]() $\alpha : \operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} A$
,
$\alpha : \operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} A$
,
![]() $\mathfrak {E}$
is a Breuil–Kisin module with descent data and coefficients in C and
$\mathfrak {E}$
is a Breuil–Kisin module with descent data and coefficients in C and
![]() $\iota $
and
$\iota $
and
![]() $\pi $
are morphisms
$\pi $
are morphisms
![]() $\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
and
$\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
and
![]() $\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
, respectively, with the property that
$\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
, respectively, with the property that
![]() $0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
is short exact.
$0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
is short exact.
Proof. We have already seen that giving a morphism
![]() $\operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} B$
is equivalent to giving the composite morphism
$\operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} B$
is equivalent to giving the composite morphism
![]() $\alpha :\operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A$
, together with an extension class
$\alpha :\operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A$
, together with an extension class
![]() $[\mathfrak {E}] \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M},\alpha ^{*}\mathfrak {N}).$
Thus to prove the proposition, we just have to show that any automorphism of
$[\mathfrak {E}] \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M},\alpha ^{*}\mathfrak {N}).$
Thus to prove the proposition, we just have to show that any automorphism of
![]() $\mathfrak {E}$
which restricts to the identity on
$\mathfrak {E}$
which restricts to the identity on
![]() $\alpha ^{*}\mathfrak {N}$
and induces the identity on
$\alpha ^{*}\mathfrak {N}$
and induces the identity on
![]() $\alpha ^{*}\mathfrak {M}$
is itself the identity on
$\alpha ^{*}\mathfrak {M}$
is itself the identity on
![]() $\mathfrak {E}$
. This follows from Corollary 3.1.18, together with Assumption 3.2.4.
$\mathfrak {E}$
. This follows from Corollary 3.1.18, together with Assumption 3.2.4.
Fix an integer
![]() $h\ge 0$
so that
$h\ge 0$
so that
![]() $E(u)^h\in \operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {M}})\operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {N}})$
, so that by Lemma 3.1.1, every Breuil–Kisin module parametrised by
$E(u)^h\in \operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {M}})\operatorname {Ann}_{\mathfrak {S}_A}(\operatorname {\mathrm {coker}}\Phi _{\mathfrak {N}})$
, so that by Lemma 3.1.1, every Breuil–Kisin module parametrised by
![]() $\operatorname {\mathrm {Spec}} B$
has height at most h. There is a natural action of
$\operatorname {\mathrm {Spec}} B$
has height at most h. There is a natural action of
![]() ${\mathbf G}_m\times _{{\mathcal O}} {\mathbf G}_m$
on
${\mathbf G}_m\times _{{\mathcal O}} {\mathbf G}_m$
on
![]() $\operatorname {\mathrm {Spec}} B$
, given by rescaling each of
$\operatorname {\mathrm {Spec}} B$
, given by rescaling each of
![]() $\iota $
and
$\iota $
and
![]() $\pi $
. There is also an evident forgetful morphism
$\pi $
. There is also an evident forgetful morphism
![]() $\operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A \times _{{\mathcal O}} {\mathcal C}^{\mathrm {dd},a}$
, given by forgetting
$\operatorname {\mathrm {Spec}} B \to \operatorname {\mathrm {Spec}} A \times _{{\mathcal O}} {\mathcal C}^{\mathrm {dd},a}$
, given by forgetting
![]() $\iota $
and
$\iota $
and
![]() $\pi $
, which is evidently invariant under the
$\pi $
, which is evidently invariant under the
![]() ${\mathbf G}_m\times _{{\mathcal O}} {\mathbf G}_m$
-action. (Here and below,
${\mathbf G}_m\times _{{\mathcal O}} {\mathbf G}_m$
-action. (Here and below,
![]() ${\mathcal C}^{\mathrm {dd},a}$
denotes the moduli stack defined in Section 2.3 for our fixed choice of h and for d equal to the sum of the ranks of
${\mathcal C}^{\mathrm {dd},a}$
denotes the moduli stack defined in Section 2.3 for our fixed choice of h and for d equal to the sum of the ranks of
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
.) We thus obtain a morphism
$\mathfrak {N}$
.) We thus obtain a morphism
Corollary 3.2.7. Suppose that
![]() $\operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M}) = \operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {N}) = C^{\times }$
for any morphism
$\operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M}) = \operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {N}) = C^{\times }$
for any morphism
![]() $\alpha : \operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} A$
. Then the morphism (3.2.6) is an isomorphism, and, consequently, the induced morphism
$\alpha : \operatorname {\mathrm {Spec}} C \to \operatorname {\mathrm {Spec}} A$
. Then the morphism (3.2.6) is an isomorphism, and, consequently, the induced morphism
is a finite type monomorphism.
Proof. By Proposition 3.2.5, a morphism
corresponds to an isomorphism class of tuples
![]() $(\alpha ,\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
$(\alpha ,\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
-
○
 $\alpha $
is a morphism
$\alpha $
is a morphism
 $\alpha :\operatorname {\mathrm {Spec}} C\to \operatorname {\mathrm {Spec}} A$
,
$\alpha :\operatorname {\mathrm {Spec}} C\to \operatorname {\mathrm {Spec}} A$
, -
○
 $\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in C,
$\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in C, -
○
 $\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
and
$\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
and
 $\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
are morphisms with the property that is short exact,
$\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
are morphisms with the property that is short exact, $$ \begin{align*}0 \to \alpha^{*}\mathfrak{N} \buildrel \iota \over \to \mathfrak{E} \buildrel \pi \over \to \alpha^{*} \mathfrak{M} \to 0\end{align*} $$
$$ \begin{align*}0 \to \alpha^{*}\mathfrak{N} \buildrel \iota \over \to \mathfrak{E} \buildrel \pi \over \to \alpha^{*} \mathfrak{M} \to 0\end{align*} $$
-
○
 $\iota ':\alpha ^{*} \mathfrak {N} \to \mathfrak {E}'$
and
$\iota ':\alpha ^{*} \mathfrak {N} \to \mathfrak {E}'$
and
 $\pi ' :\mathfrak {E}' \to \alpha ^{*} \mathfrak {M}$
are morphisms with the property that is short exact.
$\pi ' :\mathfrak {E}' \to \alpha ^{*} \mathfrak {M}$
are morphisms with the property that is short exact. $$ \begin{align*}0 \to \alpha^{*}\mathfrak{N} \buildrel \iota' \over \to \mathfrak{E}' \buildrel \pi' \over \to \alpha^{*} \mathfrak{M} \to 0\end{align*} $$
$$ \begin{align*}0 \to \alpha^{*}\mathfrak{N} \buildrel \iota' \over \to \mathfrak{E}' \buildrel \pi' \over \to \alpha^{*} \mathfrak{M} \to 0\end{align*} $$
Assumption 3.2.4 and Corollary 3.1.18 together show that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {N}, \alpha ^{*}\mathfrak {M})~=~0$
. It follows that the composite
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {N}, \alpha ^{*}\mathfrak {M})~=~0$
. It follows that the composite
![]() $\alpha ^{*}\mathfrak {N}\stackrel {\iota }{\to }\mathfrak {E}\stackrel {\beta }{\to }\mathfrak {E}' $
factors through
$\alpha ^{*}\mathfrak {N}\stackrel {\iota }{\to }\mathfrak {E}\stackrel {\beta }{\to }\mathfrak {E}' $
factors through
![]() $\iota '$
, and the induced endomorphism of
$\iota '$
, and the induced endomorphism of
![]() $\alpha ^{*}\mathfrak {N}$
is injective. Reversing the roles of
$\alpha ^{*}\mathfrak {N}$
is injective. Reversing the roles of
![]() $\mathfrak {E}$
and
$\mathfrak {E}$
and
![]() $\mathfrak {E}'$
, we see that it is in fact an automorphism of
$\mathfrak {E}'$
, we see that it is in fact an automorphism of
![]() $\alpha ^{*}\mathfrak {N}$
, and it follows easily that
$\alpha ^{*}\mathfrak {N}$
, and it follows easily that
![]() $\beta $
also induces an automorphism of
$\beta $
also induces an automorphism of
![]() $\alpha ^{*}\mathfrak {M}$
. Again, Assumption 3.2.4 and Proposition 3.1.18 together show that
$\alpha ^{*}\mathfrak {M}$
. Again, Assumption 3.2.4 and Proposition 3.1.18 together show that
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M}, \alpha ^{*}\mathfrak {N}) = 0$
, from which it follows easily that
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M}, \alpha ^{*}\mathfrak {N}) = 0$
, from which it follows easily that
![]() $\beta $
is determined by the automorphisms of
$\beta $
is determined by the automorphisms of
![]() $\alpha ^{*}\mathfrak {M}$
and
$\alpha ^{*}\mathfrak {M}$
and
![]() $\alpha ^{*}\mathfrak {N}$
that it induces.
$\alpha ^{*}\mathfrak {N}$
that it induces.
Since
![]() $\operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M}) = \operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {N}) = C^{\times }$
by assumption, we see that
$\operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {M}) = \operatorname {\mathrm {Aut}}_{\mathcal {K}(C)}(\alpha ^{*}\mathfrak {N}) = C^{\times }$
by assumption, we see that
![]() $\beta \circ \iota , \iota '$
and
$\beta \circ \iota , \iota '$
and
![]() $\pi ,\pi '\circ \beta $
differ only by the action of
$\pi ,\pi '\circ \beta $
differ only by the action of
![]() ${\mathbf G}_m\times _{{\mathcal O}}{\mathbf G}_m$
, so the first claim of the corollary follows. The claim regarding the monomorphism is immediate from Lemma 3.2.8 below. Finally, note that
${\mathbf G}_m\times _{{\mathcal O}}{\mathbf G}_m$
, so the first claim of the corollary follows. The claim regarding the monomorphism is immediate from Lemma 3.2.8 below. Finally, note that
![]() $[\operatorname {\mathrm {Spec}} B/{\mathbf G}_m\times _{{\mathcal O}} {\mathbf G}_m]$
is of finite type over
$[\operatorname {\mathrm {Spec}} B/{\mathbf G}_m\times _{{\mathcal O}} {\mathbf G}_m]$
is of finite type over
![]() $\operatorname {\mathrm {Spec}} A$
, while
$\operatorname {\mathrm {Spec}} A$
, while
![]() ${\mathcal C}^{\mathrm {dd},a}$
has finite type diagonal. It follows that the morphism
${\mathcal C}^{\mathrm {dd},a}$
has finite type diagonal. It follows that the morphism
![]() $[\operatorname {\mathrm {Spec}} B / {\mathbf G}_m \times _{{\mathcal O}} {\mathbf G}_m ] \rightarrow \operatorname {\mathrm {Spec}} A\times _{{\mathcal O}}{\mathcal C}^{\mathrm {dd},a}$
is of finite type, as required.
$[\operatorname {\mathrm {Spec}} B / {\mathbf G}_m \times _{{\mathcal O}} {\mathbf G}_m ] \rightarrow \operatorname {\mathrm {Spec}} A\times _{{\mathcal O}}{\mathcal C}^{\mathrm {dd},a}$
is of finite type, as required.
Lemma 3.2.8. Let X be a scheme over a base scheme S, let G be a smooth affine group scheme over S and let
![]() $\rho :X\times _S G\to X$
be a (right) action of G on X. Let
$\rho :X\times _S G\to X$
be a (right) action of G on X. Let
![]() $X\to {\mathcal Y}$
be a G-equivariant morphism, whose target is an algebraic stack over S on which G acts trivially. Then, the induced morphism
$X\to {\mathcal Y}$
be a G-equivariant morphism, whose target is an algebraic stack over S on which G acts trivially. Then, the induced morphism
is a monomorphism if and only if the natural morphism
(induced by the morphisms
![]() $\operatorname {pr}_1,\rho :X\times _S G\to X$
) is an isomorphism.
$\operatorname {pr}_1,\rho :X\times _S G\to X$
) is an isomorphism.
Proof. We have a Cartesian diagram as follows.
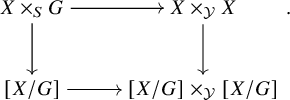
The morphism
![]() $[X/G]\to {\mathcal Y}$
is a monomorphism if and only if the bottom horizontal morphism of this square is an isomorphism; since the right-hand vertical arrow is a smooth surjection, this is the case if and only if the top horizontal morphism is an isomorphism, as required.
$[X/G]\to {\mathcal Y}$
is a monomorphism if and only if the bottom horizontal morphism of this square is an isomorphism; since the right-hand vertical arrow is a smooth surjection, this is the case if and only if the top horizontal morphism is an isomorphism, as required.
3.3. Families of extensions of rank one Breuil–Kisin modules
In this section, we construct universal families of extensions of rank one Breuil–Kisin modules. We will use these rank two families to study our moduli spaces of Breuil–Kisin modules, and the corresponding spaces of étale
![]() $\varphi $
-modules. We show how to compute the dimensions of these universal families; in the subsequent sections, we will combine these results with explicit calculations to determine the irreducible components of our moduli spaces. In particular, we will show that each irreducible component has a dense open substack given by a family of extensions.
$\varphi $
-modules. We show how to compute the dimensions of these universal families; in the subsequent sections, we will combine these results with explicit calculations to determine the irreducible components of our moduli spaces. In particular, we will show that each irreducible component has a dense open substack given by a family of extensions.
3.3.1. Universal unramified twists
Fix a free Breuil–Kisin module with descent data
![]() $\mathfrak {M}$
over
$\mathfrak {M}$
over
![]() ${\mathbf F}$
, and write
${\mathbf F}$
, and write
![]() $\Phi _i$
for
$\Phi _i$
for
![]() $\Phi _{\mathfrak {M},i}:\varphi ^{*}(\mathfrak {M}_{i-1}) \to \mathfrak {M}_{i}$
. (Here we are using the notation of Section 2.1, so that
$\Phi _{\mathfrak {M},i}:\varphi ^{*}(\mathfrak {M}_{i-1}) \to \mathfrak {M}_{i}$
. (Here we are using the notation of Section 2.1, so that
![]() $\mathfrak {M}_i=e_i\mathfrak {M}$
is cut out by the idempotent
$\mathfrak {M}_i=e_i\mathfrak {M}$
is cut out by the idempotent
![]() $e_i$
of Section 1.3.) We will construct the ‘universal unramified twist’ of
$e_i$
of Section 1.3.) We will construct the ‘universal unramified twist’ of
![]() $\mathfrak {M}$
.
$\mathfrak {M}$
.
Definition 3.3.2. If
![]() $\Lambda $
is an
$\Lambda $
is an
![]() ${\mathbf F}$
-algebra, and if
${\mathbf F}$
-algebra, and if
![]() $\lambda \in \Lambda ^{\times }$
, then we define
$\lambda \in \Lambda ^{\times }$
, then we define
![]() $\mathfrak {M}_{\Lambda ,\lambda }$
to be the free Breuil–Kisin module with descent data and
$\mathfrak {M}_{\Lambda ,\lambda }$
to be the free Breuil–Kisin module with descent data and
![]() $\Lambda $
-coefficients whose underlying
$\Lambda $
-coefficients whose underlying
![]() $\mathfrak {S}_{\Lambda }[\operatorname {\mathrm {Gal}}(K'/K)]$
-module is equal to
$\mathfrak {S}_{\Lambda }[\operatorname {\mathrm {Gal}}(K'/K)]$
-module is equal to
![]() $\mathfrak {M}\, \widehat {\otimes }_{\mathbf F}\Lambda $
(so the usual base change of
$\mathfrak {M}\, \widehat {\otimes }_{\mathbf F}\Lambda $
(so the usual base change of
![]() $\mathfrak {M}$
to
$\mathfrak {M}$
to
![]() $\Lambda $
), and for which
$\Lambda $
), and for which
![]() $\Phi _{\mathfrak {M}_{\Lambda ,\lambda }}: \varphi ^{*}\mathfrak {M}_{\Lambda ,\lambda } \to \mathfrak {M}_{\Lambda ,\lambda }$
is defined via the
$\Phi _{\mathfrak {M}_{\Lambda ,\lambda }}: \varphi ^{*}\mathfrak {M}_{\Lambda ,\lambda } \to \mathfrak {M}_{\Lambda ,\lambda }$
is defined via the
![]() $f'$
-tuple
$f'$
-tuple
![]() $(\lambda \Phi _0,\Phi _1,\ldots ,\Phi _{f'-1}).$
We refer to
$(\lambda \Phi _0,\Phi _1,\ldots ,\Phi _{f'-1}).$
We refer to
![]() $\mathfrak {M}_{\Lambda ,\lambda }$
as the unramified twist of
$\mathfrak {M}_{\Lambda ,\lambda }$
as the unramified twist of
![]() $\mathfrak {M}$
by
$\mathfrak {M}$
by
![]() $\lambda $
over
$\lambda $
over
![]() $\Lambda $
.
$\Lambda $
.
If M is a free étale
![]() $\varphi $
-module with descent data, then we define
$\varphi $
-module with descent data, then we define
![]() $M_{\Lambda ,\lambda }$
in the analogous fashion. If we write
$M_{\Lambda ,\lambda }$
in the analogous fashion. If we write
![]() $X=\operatorname {\mathrm {Spec}} \Lambda $
, then we will sometimes write
$X=\operatorname {\mathrm {Spec}} \Lambda $
, then we will sometimes write
![]() $\mathfrak {M}_{X,\lambda }$
(respectively,
$\mathfrak {M}_{X,\lambda }$
(respectively,
![]() $M_{X,\lambda }$
) for
$M_{X,\lambda }$
) for
![]() $\mathfrak {M}_{\Lambda ,\lambda }$
(respectively,
$\mathfrak {M}_{\Lambda ,\lambda }$
(respectively,
![]() $M_{\Lambda ,\lambda }$
).
$M_{\Lambda ,\lambda }$
).
As usual, we write
![]() ${\mathbf G}_m := \operatorname {\mathrm {Spec}} {\mathbf F}[x^{\pm 1}].$
We may then form the rank one Breuil–Kisin module with descent data
${\mathbf G}_m := \operatorname {\mathrm {Spec}} {\mathbf F}[x^{\pm 1}].$
We may then form the rank one Breuil–Kisin module with descent data
![]() $\mathfrak {M}_{{\mathbf G}_m,x},$
which is the universal instance of an unramified twist: given
$\mathfrak {M}_{{\mathbf G}_m,x},$
which is the universal instance of an unramified twist: given
![]() $\lambda \in \Lambda ^{\times }$
, there is a corresponding morphism
$\lambda \in \Lambda ^{\times }$
, there is a corresponding morphism
![]() $\operatorname {\mathrm {Spec}}\Lambda \to {\mathbf G}_m$
determined by the requirement that
$\operatorname {\mathrm {Spec}}\Lambda \to {\mathbf G}_m$
determined by the requirement that
![]() $x \in \Gamma ({\mathbf G}_m, {\mathcal O}_{{\mathbf G}_m}^{\times })$
pulls back to
$x \in \Gamma ({\mathbf G}_m, {\mathcal O}_{{\mathbf G}_m}^{\times })$
pulls back to
![]() $\lambda $
, and
$\lambda $
, and
![]() $\mathfrak {M}_{X,\lambda }$
is obtained by pulling back
$\mathfrak {M}_{X,\lambda }$
is obtained by pulling back
![]() $\mathfrak {M}_{{\mathbf G}_m,x}$
under this morphism (that is, by base changing under the corresponding ring homomorphism
$\mathfrak {M}_{{\mathbf G}_m,x}$
under this morphism (that is, by base changing under the corresponding ring homomorphism
![]() ${\mathbf F}[x^{\pm 1}]\to \Lambda $
).
${\mathbf F}[x^{\pm 1}]\to \Lambda $
).
Lemma 3.3.3. If
![]() $\mathfrak {M}_{\Lambda }$
is a Breuil–Kisin module of rank one with
$\mathfrak {M}_{\Lambda }$
is a Breuil–Kisin module of rank one with
![]() $\Lambda $
-coefficients, then
$\Lambda $
-coefficients, then
![]() $\operatorname {\mathrm {End}}_{\mathcal {K}(\Lambda )}(\mathfrak {M}) = \Lambda .$
Similarly, if
$\operatorname {\mathrm {End}}_{\mathcal {K}(\Lambda )}(\mathfrak {M}) = \Lambda .$
Similarly, if
![]() $M_{\Lambda }$
is a étale
$M_{\Lambda }$
is a étale
![]() $\varphi $
-module of rank one with
$\varphi $
-module of rank one with
![]() $\Lambda $
-coefficients, then
$\Lambda $
-coefficients, then
![]() $\operatorname {\mathrm {End}}_{\mathcal {K}(\Lambda )}(M_{\Lambda }) = \Lambda .$
$\operatorname {\mathrm {End}}_{\mathcal {K}(\Lambda )}(M_{\Lambda }) = \Lambda .$
Proof. We give the proof for
![]() $M_{\Lambda }$
, the argument for
$M_{\Lambda }$
, the argument for
![]() $\mathfrak {M}_{\Lambda }$
being essentially identical. One reduces easily to the case where
$\mathfrak {M}_{\Lambda }$
being essentially identical. One reduces easily to the case where
![]() $M_{\Lambda }$
is free. Since an endomorphism
$M_{\Lambda }$
is free. Since an endomorphism
![]() $\psi $
of
$\psi $
of
![]() $M_{\Lambda }$
is, in particular, an endomorphism of the underlying
$M_{\Lambda }$
is, in particular, an endomorphism of the underlying
![]() $\mathfrak {S}_{\Lambda }[1/u]$
-module, we see that there is some
$\mathfrak {S}_{\Lambda }[1/u]$
-module, we see that there is some
![]() $\lambda \in \mathfrak {S}_{\Lambda }[1/u]$
, such that
$\lambda \in \mathfrak {S}_{\Lambda }[1/u]$
, such that
![]() $\psi $
is given by multiplication by
$\psi $
is given by multiplication by
![]() $\lambda $
. The commutation relation with
$\lambda $
. The commutation relation with
![]() $\Phi _{M_{\Lambda }}$
means that we must have
$\Phi _{M_{\Lambda }}$
means that we must have
![]() $\varphi (\lambda )=\lambda $
, so that certainly (considering the powers of u in
$\varphi (\lambda )=\lambda $
, so that certainly (considering the powers of u in
![]() $\lambda $
of lowest negative and positive degrees)
$\lambda $
of lowest negative and positive degrees)
![]() $\lambda \in W(k')\otimes _{{\mathbf Z}_p}\Lambda $
, and, in fact,
$\lambda \in W(k')\otimes _{{\mathbf Z}_p}\Lambda $
, and, in fact,
![]() $\lambda \in \Lambda $
. Conversely, multiplication by any element of
$\lambda \in \Lambda $
. Conversely, multiplication by any element of
![]() $\Lambda $
is evidently an endomorphism of
$\Lambda $
is evidently an endomorphism of
![]() $M_{\Lambda }$
, as required.
$M_{\Lambda }$
, as required.
Lemma 3.3.4. Let
![]() $\kappa $
be a field of characteristic p, and let
$\kappa $
be a field of characteristic p, and let
![]() $M_{\kappa }, N_{\kappa }$
be étale
$M_{\kappa }, N_{\kappa }$
be étale
![]() $\varphi $
-modules of rank one with
$\varphi $
-modules of rank one with
![]() $\kappa $
-coefficients and descent data. Then, any nonzero element of
$\kappa $
-coefficients and descent data. Then, any nonzero element of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa )}(M_{\kappa }, N_{\kappa })$
is an isomorphism.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(\kappa )}(M_{\kappa }, N_{\kappa })$
is an isomorphism.
Proof. Since
![]() $\kappa ((u))$
is a field, it is enough to show that if one of the induced maps
$\kappa ((u))$
is a field, it is enough to show that if one of the induced maps
![]() $M_{\kappa ,i}\to N_{\kappa ,i}$
is nonzero, then they all are; but this follows from the commutation relation with
$M_{\kappa ,i}\to N_{\kappa ,i}$
is nonzero, then they all are; but this follows from the commutation relation with
![]() $\varphi $
.
$\varphi $
.
Lemma 3.3.5. If
![]() $\lambda ,\lambda ' \in \Lambda ^{\times }$
and
$\lambda ,\lambda ' \in \Lambda ^{\times }$
and
![]() $\mathfrak {M}_{\Lambda ,\lambda } \cong \mathfrak {M}_{\Lambda ,\lambda '}$
(as Breuil–Kisin modules with descent data over
$\mathfrak {M}_{\Lambda ,\lambda } \cong \mathfrak {M}_{\Lambda ,\lambda '}$
(as Breuil–Kisin modules with descent data over
![]() $\Lambda $
), then
$\Lambda $
), then
![]() $\lambda =\lambda '$
. Similarly, if
$\lambda =\lambda '$
. Similarly, if
![]() $M_{\Lambda ,\lambda }\cong M_{\Lambda ,\lambda '}$
, then
$M_{\Lambda ,\lambda }\cong M_{\Lambda ,\lambda '}$
, then
![]() $\lambda =\lambda '$
.
$\lambda =\lambda '$
.
Proof. Again, we give the proof for M, the argument for
![]() $\mathfrak {M}$
being essentially identical. Write
$\mathfrak {M}$
being essentially identical. Write
![]() $M_i={\mathbf F}((u))m_i$
, and write
$M_i={\mathbf F}((u))m_i$
, and write
![]() $\Phi _i(1\otimes m_{i-1})=\theta _{i}m_{i}$
, where
$\Phi _i(1\otimes m_{i-1})=\theta _{i}m_{i}$
, where
![]() $\theta _{i}\ne 0$
. There are
$\theta _{i}\ne 0$
. There are
![]() $\mu _i\in \Lambda [[u]][1/u]$
, such that the given isomorphism
$\mu _i\in \Lambda [[u]][1/u]$
, such that the given isomorphism
![]() $M_{\Lambda ,\lambda }\cong M_{\Lambda ,\lambda '}$
takes
$M_{\Lambda ,\lambda }\cong M_{\Lambda ,\lambda '}$
takes
![]() $m_i$
to
$m_i$
to
![]() $\mu _im_i$
. The commutation relation between the given isomorphism and
$\mu _im_i$
. The commutation relation between the given isomorphism and
![]() $\Phi _{M}$
imposes the condition
$\Phi _{M}$
imposes the condition
where
![]() $\lambda _{i}$
(respectively,
$\lambda _{i}$
(respectively,
![]() $\lambda ^{\prime }_i$
) equals
$\lambda ^{\prime }_i$
) equals
![]() $1$
unless
$1$
unless
![]() $i=0$
, when it equals
$i=0$
, when it equals
![]() $\lambda $
(respectively,
$\lambda $
(respectively,
![]() $\lambda '$
).
$\lambda '$
).
Thus, we have
![]() $\mu _{i}=(\lambda ^{\prime }_i/\lambda _i)\varphi (\mu _{i-1})$
, so that, in particular,
$\mu _{i}=(\lambda ^{\prime }_i/\lambda _i)\varphi (\mu _{i-1})$
, so that, in particular,
![]() $\mu _0=(\lambda '/\lambda )\varphi ^{f'}(\mu _0)$
. Considering the powers of u in
$\mu _0=(\lambda '/\lambda )\varphi ^{f'}(\mu _0)$
. Considering the powers of u in
![]() $\mu _0$
of lowest negative and positive degrees, we conclude that
$\mu _0$
of lowest negative and positive degrees, we conclude that
![]() $\mu _0\in W(k') \otimes \Lambda $
; but then
$\mu _0\in W(k') \otimes \Lambda $
; but then
![]() $\mu _0=\varphi ^{f'}(\mu _0)$
, so that
$\mu _0=\varphi ^{f'}(\mu _0)$
, so that
![]() $\lambda '=\lambda $
, as required.
$\lambda '=\lambda $
, as required.
Remark 3.3.6. If
![]() $\mathfrak {M}$
has height at most h, and we let
$\mathfrak {M}$
has height at most h, and we let
![]() ${\mathcal C}$
(temporarily) denote the moduli stack of rank one Breuil–Kisin modules of height at most h with
${\mathcal C}$
(temporarily) denote the moduli stack of rank one Breuil–Kisin modules of height at most h with
![]() ${\mathbf F}$
-coefficients and descent data, then Lemma 3.3.5 can be interpreted as saying that the morphism
${\mathbf F}$
-coefficients and descent data, then Lemma 3.3.5 can be interpreted as saying that the morphism
![]() ${\mathbf G}_m \to {\mathcal C}$
that classifies
${\mathbf G}_m \to {\mathcal C}$
that classifies
![]() $\mathfrak {M}_{{\mathbf G}_m,x}$
is a monomorphism, that is, the diagonal morphism
$\mathfrak {M}_{{\mathbf G}_m,x}$
is a monomorphism, that is, the diagonal morphism
![]() ${\mathbf G}_m \to {\mathbf G}_m \times _{{\mathcal C}} {\mathbf G}_m$
is an isomorphism. Similarly, the morphism
${\mathbf G}_m \to {\mathbf G}_m \times _{{\mathcal C}} {\mathbf G}_m$
is an isomorphism. Similarly, the morphism
![]() ${\mathbf G}_m\to {\mathcal R}$
(where we temporarily let
${\mathbf G}_m\to {\mathcal R}$
(where we temporarily let
![]() ${\mathcal R}$
denote the moduli stack of rank one étale
${\mathcal R}$
denote the moduli stack of rank one étale
![]() $\varphi $
-modules with
$\varphi $
-modules with
![]() ${\mathbf F}$
-coefficients and descent data) that classifies
${\mathbf F}$
-coefficients and descent data) that classifies
![]() $M_{{\mathbf G}_m,x}$
is a monomorphism.
$M_{{\mathbf G}_m,x}$
is a monomorphism.
Now choose another rank one Breuil–Kisin module with descent data
![]() $\mathfrak {N}$
over
$\mathfrak {N}$
over
![]() ${\mathbf F}$
. Let
${\mathbf F}$
. Let
![]() $(x,y)$
denote the standard coordinates on
$(x,y)$
denote the standard coordinates on
![]() ${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
, and consider the rank one Breuil–Kisin modules with descent data
${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
, and consider the rank one Breuil–Kisin modules with descent data
![]() $\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,x}$
and
$\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,x}$
and
![]() $\mathfrak {N}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,y}$
over
$\mathfrak {N}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,y}$
over
![]() ${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
.
${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
.
Lemma 3.3.7. There is a nonempty irreducible affine open subset
![]() $\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
of
$\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
of
![]() ${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
whose finite type points are exactly the maximal ideals
${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
whose finite type points are exactly the maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() ${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
, such that
${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
, such that
(where we have written
![]() $\bar {x}$
and
$\bar {x}$
and
![]() $\bar {y}$
to denote the images of x and y in
$\bar {y}$
to denote the images of x and y in
![]() $\kappa (\mathfrak m)^{\times }$
).
$\kappa (\mathfrak m)^{\times }$
).
Furthermore, if R is any finite-type
![]() ${A^{\operatorname {dist}}}$
-algebra, and if
${A^{\operatorname {dist}}}$
-algebra, and if
![]() $\mathfrak m$
is any maximal ideal of R, then
$\mathfrak m$
is any maximal ideal of R, then
and also
In particular, Assumption
3.2.4
is satisfied by
![]() $\mathfrak {M}_{{A^{\operatorname {dist}}},x}$
and
$\mathfrak {M}_{{A^{\operatorname {dist}}},x}$
and
![]() $\mathfrak {N}_{{A^{\operatorname {dist}}},y}$
.
$\mathfrak {N}_{{A^{\operatorname {dist}}},y}$
.
Proof. If
![]() $\operatorname {\mathrm {Hom}}\big (\mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}[1/u],\mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}[1/u])=0$
for all maximal ideals
$\operatorname {\mathrm {Hom}}\big (\mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}[1/u],\mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}[1/u])=0$
for all maximal ideals
![]() $\mathfrak {m}$
of
$\mathfrak {m}$
of
![]() ${\mathbf F}[x^{\pm 1},y^{\pm 1}]$
, then we are done:
${\mathbf F}[x^{\pm 1},y^{\pm 1}]$
, then we are done:
![]() $\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} = {\mathbf G}_m\times {\mathbf G}_m$
. Otherwise, we see that for some finite extension
$\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} = {\mathbf G}_m\times {\mathbf G}_m$
. Otherwise, we see that for some finite extension
![]() ${\mathbf F}'/{\mathbf F}$
and some
${\mathbf F}'/{\mathbf F}$
and some
![]() $a,a'\in {\mathbf F}'$
, we have a nonzero morphism
$a,a'\in {\mathbf F}'$
, we have a nonzero morphism
![]() $\mathfrak {M}_{{\mathbf F}',a}[1/u]\to \mathfrak {N}_{{\mathbf F}',a'}[1/u]$
. By Lemma 3.3.4, this morphism must in fact be an isomorphism. Since
$\mathfrak {M}_{{\mathbf F}',a}[1/u]\to \mathfrak {N}_{{\mathbf F}',a'}[1/u]$
. By Lemma 3.3.4, this morphism must in fact be an isomorphism. Since
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are both defined over
$\mathfrak {N}$
are both defined over
![]() ${\mathbf F}$
, we furthermore see that the ratio
${\mathbf F}$
, we furthermore see that the ratio
![]() $a'/a$
lies in
$a'/a$
lies in
![]() ${\mathbf F}$
. We then let
${\mathbf F}$
. We then let
![]() $\operatorname {\mathrm {Spec}}{A^{\operatorname {dist}}}$
be the affine open subset of
$\operatorname {\mathrm {Spec}}{A^{\operatorname {dist}}}$
be the affine open subset of
![]() ${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
, where
${\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m$
, where
![]() $a'x\ne ay$
; the claimed property of
$a'x\ne ay$
; the claimed property of
![]() $\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
then follows easily from Lemma 3.3.5.
$\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
then follows easily from Lemma 3.3.5.
For the remaining statements of the lemma, note that if
![]() $\mathfrak m$
is a maximal ideal in a finite type
$\mathfrak m$
is a maximal ideal in a finite type
![]() $A^{{\operatorname {dist}}}$
-algebra, then its pullback to
$A^{{\operatorname {dist}}}$
-algebra, then its pullback to
![]() $A^{{\operatorname {dist}}}$
is, again, a maximal ideal
$A^{{\operatorname {dist}}}$
is, again, a maximal ideal
![]() $\mathfrak m'$
of
$\mathfrak m'$
of
![]() $A^{{\operatorname {dist}}}$
(since
$A^{{\operatorname {dist}}}$
(since
![]() $A^{{\operatorname {dist}}}$
is Jacobson), and the vanishing of
$A^{{\operatorname {dist}}}$
is Jacobson), and the vanishing of
follows from the corresponding statement for
![]() $\kappa (\mathfrak m')$
, together with Lemma 3.1.20.
$\kappa (\mathfrak m')$
, together with Lemma 3.1.20.
Inverting u induces an embedding
and so certainly the vanishing of the target implies the vanishing of the source.
The statements in which the roles of
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are reversed follow from Lemma 3.3.4.
$\mathfrak {N}$
are reversed follow from Lemma 3.3.4.
Define
![]() $T := \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m)}\big (\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,x},\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m,y})$
; it follows from Proposition 3.1.13 that T is finitely generated over
$T := \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m)}\big (\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,x},\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m,y})$
; it follows from Proposition 3.1.13 that T is finitely generated over
![]() ${\mathbf F}[x^{\pm 1},y^{\pm 1}],$
while Proposition 3.1.15 shows that
${\mathbf F}[x^{\pm 1},y^{\pm 1}],$
while Proposition 3.1.15 shows that
![]() $T_{A^{\operatorname {dist}}} := T\otimes _{{\mathbf F}[x^{\pm 1}, y^{\pm 1}]} {A^{\operatorname {dist}}}$
is naturally isomorphic to
$T_{A^{\operatorname {dist}}} := T\otimes _{{\mathbf F}[x^{\pm 1}, y^{\pm 1}]} {A^{\operatorname {dist}}}$
is naturally isomorphic to
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({A^{\operatorname {dist}}})}\bigl (\mathfrak {M}_{{A^{\operatorname {dist}}},x}, \mathfrak {N}_{{A^{\operatorname {dist}}},y}\bigr )$
. (Here, and elsewhere, we abuse notation by writing x, y for
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({A^{\operatorname {dist}}})}\bigl (\mathfrak {M}_{{A^{\operatorname {dist}}},x}, \mathfrak {N}_{{A^{\operatorname {dist}}},y}\bigr )$
. (Here, and elsewhere, we abuse notation by writing x, y for
![]() $x|_{{A^{\operatorname {dist}}}}$
,
$x|_{{A^{\operatorname {dist}}}}$
,
![]() $y|_{{A^{\operatorname {dist}}}}$
.) Corollary 3.1.19 and Lemma 3.3.7 show that
$y|_{{A^{\operatorname {dist}}}}$
.) Corollary 3.1.19 and Lemma 3.3.7 show that
![]() $T_{A^{\operatorname {dist}}}$
is, in fact, a finitely generated projective
$T_{A^{\operatorname {dist}}}$
is, in fact, a finitely generated projective
![]() ${A^{\operatorname {dist}}}$
-module. If, for any
${A^{\operatorname {dist}}}$
-module. If, for any
![]() ${A^{\operatorname {dist}}}$
-algebra B, we write
${A^{\operatorname {dist}}}$
-algebra B, we write
![]() $T_B := T_{A^{\operatorname {dist}}} \otimes _{A^{\operatorname {dist}}} B \buildrel \sim \over \longrightarrow T\otimes _{{\mathbf F}[x^{\pm 1}, y^{\pm 1}]} B$
, then Proposition 3.1.15, again, shows that
$T_B := T_{A^{\operatorname {dist}}} \otimes _{A^{\operatorname {dist}}} B \buildrel \sim \over \longrightarrow T\otimes _{{\mathbf F}[x^{\pm 1}, y^{\pm 1}]} B$
, then Proposition 3.1.15, again, shows that
![]() $T_B \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}\bigl (\mathfrak {M}_{B,x}, \mathfrak {N}_{B,y}\bigr )$
.
$T_B \buildrel \sim \over \longrightarrow \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}\bigl (\mathfrak {M}_{B,x}, \mathfrak {N}_{B,y}\bigr )$
.
By Propositions 3.1.34 and 3.1.35, together with Lemma 3.3.7, there is a nonempty (so dense) affine open subset
![]() $\operatorname {\mathrm {Spec}}{A^{\operatorname {k-free}}}$
of
$\operatorname {\mathrm {Spec}}{A^{\operatorname {k-free}}}$
of
![]() $\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
with the properties that
$\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
with the properties that
and
 $$ \begin{align*} &T_{A^{\operatorname{k-free}}}/U_{A^{\operatorname{k-free}}} \\ &\qquad\qquad \ \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Ext}}^1_{\mathcal{K}({A^{\operatorname{k-free}}})} (\mathfrak{M}_{{A^{\operatorname{k-free}}},x},\mathfrak{N}_{{A^{\operatorname{k-free}}},y})/{\text{ker-Ext}}^1_{\mathcal{K}({A^{\operatorname{k-free}}})}(\mathfrak{M}_{{A^{\operatorname{k-free}}},x},\mathfrak{N}_{{A^{\operatorname{k-free}}},y}) \end{align*} $$
$$ \begin{align*} &T_{A^{\operatorname{k-free}}}/U_{A^{\operatorname{k-free}}} \\ &\qquad\qquad \ \buildrel \sim \over \longrightarrow \operatorname{\mathrm{Ext}}^1_{\mathcal{K}({A^{\operatorname{k-free}}})} (\mathfrak{M}_{{A^{\operatorname{k-free}}},x},\mathfrak{N}_{{A^{\operatorname{k-free}}},y})/{\text{ker-Ext}}^1_{\mathcal{K}({A^{\operatorname{k-free}}})}(\mathfrak{M}_{{A^{\operatorname{k-free}}},x},\mathfrak{N}_{{A^{\operatorname{k-free}}},y}) \end{align*} $$
are finitely generated and projective over
![]() ${A^{\operatorname {k-free}}}$
, and furthermore so that for all finitely generated
${A^{\operatorname {k-free}}}$
, and furthermore so that for all finitely generated
![]() ${A^{\operatorname {k-free}}}$
-algebras B, the formation of
${A^{\operatorname {k-free}}}$
-algebras B, the formation of
![]() ${\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{B,x},\mathfrak {N}_{B,y})$
and
${\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{B,x},\mathfrak {N}_{B,y})$
and
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{B,x},\mathfrak {N}_{B,y})/{\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{B,x},\mathfrak {N}_{B,y})$
is compatible with base change from
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{B,x},\mathfrak {N}_{B,y})/{\text{ker-Ext}}^1_{\mathcal {K}(B)}(\mathfrak {M}_{B,x},\mathfrak {N}_{B,y})$
is compatible with base change from
![]() $U_{A^{\operatorname {k-free}}}$
and
$U_{A^{\operatorname {k-free}}}$
and
![]() $T_{A^{\operatorname {k-free}}}/U_{A^{\operatorname {k-free}}}$
respectively.
$T_{A^{\operatorname {k-free}}}/U_{A^{\operatorname {k-free}}}$
respectively.
We choose a finite rank projective module V over
![]() ${\mathbf F}[x^{\pm 1},y^{\pm 1}]$
admitting a surjection
${\mathbf F}[x^{\pm 1},y^{\pm 1}]$
admitting a surjection
![]() $V \to T$
. Thus, if we write
$V \to T$
. Thus, if we write
![]() $V_{A^{\operatorname {dist}}} := V\otimes _{{\mathbf F}[x^{\pm 1}, y^{\pm 1}]} {A^{\operatorname {dist}}}$
, then the induced morphism
$V_{A^{\operatorname {dist}}} := V\otimes _{{\mathbf F}[x^{\pm 1}, y^{\pm 1}]} {A^{\operatorname {dist}}}$
, then the induced morphism
![]() $V_{A^{\operatorname {dist}}} \to T_{A^{\operatorname {dist}}}$
is a (split) surjection of
$V_{A^{\operatorname {dist}}} \to T_{A^{\operatorname {dist}}}$
is a (split) surjection of
![]() ${A^{\operatorname {dist}}}$
-modules.
${A^{\operatorname {dist}}}$
-modules.
Following the prescription of Section 3.2, we form the symmetric algebra
![]() ${B^{\operatorname {twist}}} := {\mathbf F}[x^{\pm 1}, y^{\pm 1}][V^{\vee }],$
and construct the family of extensions
${B^{\operatorname {twist}}} := {\mathbf F}[x^{\pm 1}, y^{\pm 1}][V^{\vee }],$
and construct the family of extensions
![]() $\widetilde {\mathfrak {E}}$
over
$\widetilde {\mathfrak {E}}$
over
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
. We may similarly form the symmetric algebras
$\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
. We may similarly form the symmetric algebras
![]() ${B^{\operatorname {dist}}} := {A^{\operatorname {dist}}}[T_{{A^{\operatorname {dist}}}}^{\vee }]$
and
${B^{\operatorname {dist}}} := {A^{\operatorname {dist}}}[T_{{A^{\operatorname {dist}}}}^{\vee }]$
and
![]() ${B^{\operatorname {k-free}}} := {A^{\operatorname {k-free}}}[T_{{A^{\operatorname {k-free}}}}^{\vee }]$
, and construct the families of extensions
${B^{\operatorname {k-free}}} := {A^{\operatorname {k-free}}}[T_{{A^{\operatorname {k-free}}}}^{\vee }]$
, and construct the families of extensions
![]() ${\widetilde {\mathfrak {E}}^{\operatorname {dist}}}$
and
${\widetilde {\mathfrak {E}}^{\operatorname {dist}}}$
and
![]() ${\widetilde {\mathfrak {E}}^{\operatorname {k-free}}}$
over
${\widetilde {\mathfrak {E}}^{\operatorname {k-free}}}$
over
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
and
$\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
and
![]() $\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
, respectively. Since
$\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
, respectively. Since
![]() $T_{A^{\operatorname {k-free}}}/U_{A^{\operatorname {k-free}}}$
is projective, the natural morphism
$T_{A^{\operatorname {k-free}}}/U_{A^{\operatorname {k-free}}}$
is projective, the natural morphism
![]() $T_{{A^{\operatorname {k-free}}}}^{\vee } \to U_{{A^{\operatorname {k-free}}}}^{\vee }$
is surjective, and hence,
$T_{{A^{\operatorname {k-free}}}}^{\vee } \to U_{{A^{\operatorname {k-free}}}}^{\vee }$
is surjective, and hence,
![]() ${C^{\operatorname {k-free}}} := A[U_{{A^{\operatorname {k-free}}}}^{\vee }]$
is a quotient of
${C^{\operatorname {k-free}}} := A[U_{{A^{\operatorname {k-free}}}}^{\vee }]$
is a quotient of
![]() ${B^{\operatorname {k-free}}}$
; geometrically,
${B^{\operatorname {k-free}}}$
; geometrically,
![]() $\operatorname {\mathrm {Spec}} {C^{\operatorname {k-free}}} $
is a subbundle of the vector bundle
$\operatorname {\mathrm {Spec}} {C^{\operatorname {k-free}}} $
is a subbundle of the vector bundle
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
over
$\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
over
![]() $\operatorname {\mathrm {Spec}} {A^{\operatorname {k-free}}}$
.
$\operatorname {\mathrm {Spec}} {A^{\operatorname {k-free}}}$
.
We write
![]() $X := \operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}} \setminus \operatorname {\mathrm {Spec}} {C^{\operatorname {k-free}}}$
; it is an open subscheme of the vector bundle
$X := \operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}} \setminus \operatorname {\mathrm {Spec}} {C^{\operatorname {k-free}}}$
; it is an open subscheme of the vector bundle
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
. The restriction of
$\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
. The restriction of
![]() $\widetilde {\mathfrak {E}}'$
to X is the universal family of extensions over
$\widetilde {\mathfrak {E}}'$
to X is the universal family of extensions over
![]() ${A^{\operatorname {k-free}}}$
which do not split after inverting u.
${A^{\operatorname {k-free}}}$
which do not split after inverting u.
Remark 3.3.8. Since
![]() $\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
and
$\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
and
![]() $\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}}$
are irreducible, each of the vector bundles
$\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}}$
are irreducible, each of the vector bundles
![]() $\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
and
$\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
and
![]() $\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
is also irreducible. In particular,
$\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
is also irreducible. In particular,
![]() $\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
is Zariski dense in
$\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
is Zariski dense in
![]() $\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
, and if X is nonempty, then it is Zariski dense in each of
$\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
, and if X is nonempty, then it is Zariski dense in each of
![]() $\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
and
$\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
and
![]() $\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
. Similarly,
$\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
. Similarly,
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} \times _{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m} \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
is Zariski dense in
$\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} \times _{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m} \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
is Zariski dense in
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
.
$\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
.
The surjection
![]() $V_{A^{\operatorname {dist}}} \to T_{A^{\operatorname {dist}}}$
induces a surjection of vector bundles
$V_{A^{\operatorname {dist}}} \to T_{A^{\operatorname {dist}}}$
induces a surjection of vector bundles
![]() $\pi : \operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}\times _{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m} \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}} \to \operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
over
$\pi : \operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}\times _{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m} \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}} \to \operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
over
![]() $\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
, and there is a natural isomorphism
$\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
, and there is a natural isomorphism
The rank two Breuil–Kisin module with descent data
![]() $\widetilde {\mathfrak {E}}$
is classified by a morphism
$\widetilde {\mathfrak {E}}$
is classified by a morphism
![]() $\xi :\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} \to {\mathcal C}^{\mathrm {dd},1}$
; similarly, the rank two Breuil–Kisin module with descent data
$\xi :\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} \to {\mathcal C}^{\mathrm {dd},1}$
; similarly, the rank two Breuil–Kisin module with descent data
![]() ${\widetilde {\mathfrak {E}}^{\operatorname {dist}}}$
is classified by a morphism
${\widetilde {\mathfrak {E}}^{\operatorname {dist}}}$
is classified by a morphism
![]() $\xi ^{\operatorname {dist}}: \operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}} \to {\mathcal C}^{\mathrm {dd},1}.$
If we write
$\xi ^{\operatorname {dist}}: \operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}} \to {\mathcal C}^{\mathrm {dd},1}.$
If we write
![]() $\xi _{A^{\operatorname {dist}}}$
for the restriction of
$\xi _{A^{\operatorname {dist}}}$
for the restriction of
![]() $\xi $
to the open subset
$\xi $
to the open subset
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} \times _{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m} \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
of
$\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} \times _{{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m} \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
of
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
, then the isomorphism (3.3.9) shows that
$\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
, then the isomorphism (3.3.9) shows that
![]() $\xi ^{\operatorname {dist}}\circ \pi = \xi _{A^{\operatorname {dist}}}$
. We also write
$\xi ^{\operatorname {dist}}\circ \pi = \xi _{A^{\operatorname {dist}}}$
. We also write
![]() $\xi ^{{{\operatorname {k-free}}}}$
for the restriction of
$\xi ^{{{\operatorname {k-free}}}}$
for the restriction of
![]() $\xi ^{{\operatorname {dist}}}$
to
$\xi ^{{\operatorname {dist}}}$
to
![]() $\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
, and
$\operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}$
, and
![]() $\xi _X$
for the restriction of
$\xi _X$
for the restriction of
![]() $\xi ^{{{\operatorname {k-free}}}}$
to X.
$\xi ^{{{\operatorname {k-free}}}}$
to X.
Lemma 3.3.10. The scheme-theoretic images (in the sense of [Reference Emerton and GeeEG21, Definition 3.1.4]) of
![]() $\xi :\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}\to {\mathcal C}^{\mathrm {dd},1}$
,
$\xi :\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}\to {\mathcal C}^{\mathrm {dd},1}$
,
![]() $\xi ^{\operatorname {dist}}:\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}$
and
$\xi ^{\operatorname {dist}}:\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}$
and
![]() $\xi ^{{{\operatorname {k-free}}}}: \operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}\to {\mathcal C}^{\mathrm {dd},1}$
all coincide; in particular, the scheme-theoretic image of
$\xi ^{{{\operatorname {k-free}}}}: \operatorname {\mathrm {Spec}} B^{{{\operatorname {k-free}}}}\to {\mathcal C}^{\mathrm {dd},1}$
all coincide; in particular, the scheme-theoretic image of
![]() $\xi $
is independent of the choice of surjection
$\xi $
is independent of the choice of surjection
![]() $V\to T$
, and the scheme-theoretic image of
$V\to T$
, and the scheme-theoretic image of
![]() $\xi ^{{{\operatorname {k-free}}}}$
is independent of the choice of
$\xi ^{{{\operatorname {k-free}}}}$
is independent of the choice of
![]() ${A^{\operatorname {k-free}}}$
. If X is nonempty, then the scheme-theoretic image of
${A^{\operatorname {k-free}}}$
. If X is nonempty, then the scheme-theoretic image of
![]() $\xi _X: X \to {\mathcal C}^{\mathrm {dd},1}$
also coincides with these other scheme-theoretic images, and is independent of the choice of
$\xi _X: X \to {\mathcal C}^{\mathrm {dd},1}$
also coincides with these other scheme-theoretic images, and is independent of the choice of
![]() ${A^{\operatorname {k-free}}}$
.
${A^{\operatorname {k-free}}}$
.
Proof. This follows from the various observations about Zariski density made in Remark 3.3.8.
Definition 3.3.11. We let
![]() $\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
denote the scheme-theoretic image of
$\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
denote the scheme-theoretic image of
![]() $\xi ^{\operatorname {dist}}:\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}$
, and we let
$\xi ^{\operatorname {dist}}:\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}$
, and we let
![]() $\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
denote the scheme-theoretic image of the composite
$\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
denote the scheme-theoretic image of the composite
![]() $\xi ^{\operatorname {dist}}:\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}\to {\mathcal Z}^{\mathrm {dd},1}$
. Equivalently,
$\xi ^{\operatorname {dist}}:\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}\to {\mathcal Z}^{\mathrm {dd},1}$
. Equivalently,
![]() $\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
is the scheme-theoretic image of the composite
$\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
is the scheme-theoretic image of the composite
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}\to {\mathcal R}^{\mathrm {dd},1}$
(cf. [Reference Emerton and GeeEG21, Proposition 3.2.31]), and the scheme-theoretic image of
$\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}\to {\mathcal C}^{\mathrm {dd},1}\to {\mathcal R}^{\mathrm {dd},1}$
(cf. [Reference Emerton and GeeEG21, Proposition 3.2.31]), and the scheme-theoretic image of
![]() $\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
under the morphism
$\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
under the morphism
![]() ${\mathcal C}^{\mathrm {dd},1} \to {\mathcal Z}^{\mathrm {dd},1}$
. (Note that Lemma 3.3.10 provides various other alternative descriptions of
${\mathcal C}^{\mathrm {dd},1} \to {\mathcal Z}^{\mathrm {dd},1}$
. (Note that Lemma 3.3.10 provides various other alternative descriptions of
![]() $\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
(and therefore also
$\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
(and therefore also
![]() $\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N}$
)) as a scheme-theoretic image.)
$\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N}$
)) as a scheme-theoretic image.)
Remark 3.3.12. Note that
![]() $\overline {{\mathcal C}} (\mathfrak {M},\mathfrak {N})$
and
$\overline {{\mathcal C}} (\mathfrak {M},\mathfrak {N})$
and
![]() $\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
are both reduced (because they are each defined as a scheme-theoretic image of
$\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
are both reduced (because they are each defined as a scheme-theoretic image of
![]() $\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}$
, which is reduced by definition).
$\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}$
, which is reduced by definition).
As well as scheme-theoretic images, as in the preceding lemma and definition we will need to consider images of underlying topological spaces. If
![]() $\mathcal {X}$
is an algebraic stack, we let
$\mathcal {X}$
is an algebraic stack, we let
![]() $|\mathcal {X}|$
be its underlying topological space, as defined in [Sta13, Tag 04Y8].
$|\mathcal {X}|$
be its underlying topological space, as defined in [Sta13, Tag 04Y8].
Lemma 3.3.13. The image of the morphism on underlying topological spaces
![]() $| \operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} | \to | {\mathcal C}^{\mathrm {dd},1}|$
induced by
$| \operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}} | \to | {\mathcal C}^{\mathrm {dd},1}|$
induced by
![]() $\xi $
is a constructible subset of
$\xi $
is a constructible subset of
![]() $| {\mathcal C}^{\mathrm {dd},1}|$
, and is independent of the choice of V.
$| {\mathcal C}^{\mathrm {dd},1}|$
, and is independent of the choice of V.
Proof. The fact that the image of
![]() $|\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}|$
is a constructible subset of
$|\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}|$
is a constructible subset of
![]() $|{\mathcal C}^{\mathrm {dd},1}|$
follows from the fact that
$|{\mathcal C}^{\mathrm {dd},1}|$
follows from the fact that
![]() $\xi $
is a morphism of finite presentation between Noetherian stacks (see [Reference RydhRyd11, App. D]). Suppose now that
$\xi $
is a morphism of finite presentation between Noetherian stacks (see [Reference RydhRyd11, App. D]). Suppose now that
![]() $V'$
is another choice of finite rank projective
$V'$
is another choice of finite rank projective
![]() ${\mathbf F}[x^{\pm 1},y^{\pm 1}]$
-module surjecting onto T. Since it is possible to choose a finite rank projective module surjecting onto the pullback of
${\mathbf F}[x^{\pm 1},y^{\pm 1}]$
-module surjecting onto T. Since it is possible to choose a finite rank projective module surjecting onto the pullback of
![]() $V,V'$
with respect to their maps to T, we see that it suffices to prove the independence claim of the lemma in the case when
$V,V'$
with respect to their maps to T, we see that it suffices to prove the independence claim of the lemma in the case when
![]() $V'$
admits a surjection onto V (compatible with the maps of each of V and
$V'$
admits a surjection onto V (compatible with the maps of each of V and
![]() $V'$
onto T). If we write
$V'$
onto T). If we write
![]() $B' := {\mathbf F}[x^{\pm 1}, y^{\pm 1}][(V')^{\vee }],$
then the natural morphism
$B' := {\mathbf F}[x^{\pm 1}, y^{\pm 1}][(V')^{\vee }],$
then the natural morphism
![]() $\operatorname {\mathrm {Spec}} B' \to \operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
is a surjection, and the morphism
$\operatorname {\mathrm {Spec}} B' \to \operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}$
is a surjection, and the morphism
![]() $\xi ': \operatorname {\mathrm {Spec}} B' \to {\mathcal C}^{\mathrm {dd},1}$
is the composite of this surjection with the morphism
$\xi ': \operatorname {\mathrm {Spec}} B' \to {\mathcal C}^{\mathrm {dd},1}$
is the composite of this surjection with the morphism
![]() $\xi $
. Thus, indeed, the images of
$\xi $
. Thus, indeed, the images of
![]() $|\operatorname {\mathrm {Spec}} B'|$
and of
$|\operatorname {\mathrm {Spec}} B'|$
and of
![]() $|\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}|$
coincide as subsets of
$|\operatorname {\mathrm {Spec}} {B^{\operatorname {twist}}}|$
coincide as subsets of
![]() $|{\mathcal C}^{\mathrm {dd},1}|$
.
$|{\mathcal C}^{\mathrm {dd},1}|$
.
Definition 3.3.14. We write
![]() $|{\mathcal C}(\mathfrak {M},\mathfrak {N})|$
to denote the constructible subset of
$|{\mathcal C}(\mathfrak {M},\mathfrak {N})|$
to denote the constructible subset of
![]() $|{\mathcal C}^{\mathrm {dd},1}|$
described in Lemma 3.3.13.
$|{\mathcal C}^{\mathrm {dd},1}|$
described in Lemma 3.3.13.
Remark 3.3.15. We caution the reader that we don’t define a substack
![]() ${\mathcal C}(\mathfrak {M},\mathfrak {N})$
of
${\mathcal C}(\mathfrak {M},\mathfrak {N})$
of
![]() ${\mathcal C}^{\mathrm {dd},1}$
. Rather, we have defined a closed substack
${\mathcal C}^{\mathrm {dd},1}$
. Rather, we have defined a closed substack
![]() $\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
of
$\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
of
![]() ${\mathcal C}^{\mathrm {dd},1}$
, and a constructible subset
${\mathcal C}^{\mathrm {dd},1}$
, and a constructible subset
![]() $|{\mathcal C}(\mathfrak {M},\mathfrak {N})|$
of
$|{\mathcal C}(\mathfrak {M},\mathfrak {N})|$
of
![]() $|{\mathcal C}^{\mathrm {dd},1}|$
. It follows from the constructions that
$|{\mathcal C}^{\mathrm {dd},1}|$
. It follows from the constructions that
![]() $|\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})|$
is the closure in
$|\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})|$
is the closure in
![]() $|{\mathcal C}^{\mathrm {dd},1}|$
of
$|{\mathcal C}^{\mathrm {dd},1}|$
of
![]() $|{\mathcal C}(\mathfrak {M},\mathfrak {N})|$
.
$|{\mathcal C}(\mathfrak {M},\mathfrak {N})|$
.
As in Section 3.2, there is a natural action of
![]() ${\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m$
on T, and hence on each of
${\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m$
on T, and hence on each of
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
,
$\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
,
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
and X, given by the action of
$\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
and X, given by the action of
![]() ${\mathbf G}_m$
as automorphisms on each of
${\mathbf G}_m$
as automorphisms on each of
![]() $\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,x}$
and
$\mathfrak {M}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,x}$
and
![]() $\mathfrak {N}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,y}$
(which induces a corresponding action on T, hence on
$\mathfrak {N}_{{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m,y}$
(which induces a corresponding action on T, hence on
![]() $T_{A^{\operatorname {dist}}}$
and
$T_{A^{\operatorname {dist}}}$
and
![]() $T_{A^{\operatorname {k-free}}}$
, and hence on
$T_{A^{\operatorname {k-free}}}$
, and hence on
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
and
$\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}$
and
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
). Thus, we may form the corresponding quotient stacks
$\operatorname {\mathrm {Spec}} {B^{\operatorname {k-free}}}$
). Thus, we may form the corresponding quotient stacks
![]() $[\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}} / {\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
and
$[\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}} / {\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
and
![]() $[X / {\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m],$
each of which admits a natural morphism to
$[X / {\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m],$
each of which admits a natural morphism to
![]() ${\mathcal C}^{\mathrm {dd},1}$
.
${\mathcal C}^{\mathrm {dd},1}$
.
Remark 3.3.16. Note that we are making use of two independent copies of
![]() ${\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m$
; one parameterises the different unramified twists of
${\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m$
; one parameterises the different unramified twists of
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
, and the other the automorphisms of (the pullbacks of)
$\mathfrak {N}$
, and the other the automorphisms of (the pullbacks of)
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
.
$\mathfrak {N}$
.
Definition 3.3.17. We say that the pair
![]() $(\mathfrak {M},\mathfrak {N})$
is strict if
$(\mathfrak {M},\mathfrak {N})$
is strict if
![]() $\operatorname {\mathrm {Spec}}{A^{\operatorname {dist}}}={\mathbf G}_m\times _{\mathbf F}{\mathbf G}_m$
.
$\operatorname {\mathrm {Spec}}{A^{\operatorname {dist}}}={\mathbf G}_m\times _{\mathbf F}{\mathbf G}_m$
.
Before stating and proving the main result of this subsection, we prove some lemmas. (The first two of which amount to recollections of standard — and simple — facts.)
Lemma 3.3.18. If
![]() ${\mathcal X}\to {\mathcal Y}$
is a morphism of stacks over S, with
${\mathcal X}\to {\mathcal Y}$
is a morphism of stacks over S, with
![]() ${\mathcal X}$
algebraic and of finite type over S, and
${\mathcal X}$
algebraic and of finite type over S, and
![]() ${\mathcal Y}$
having diagonal which is representable by algebraic spaces and of finite type, then
${\mathcal Y}$
having diagonal which is representable by algebraic spaces and of finite type, then
![]() ${\mathcal X}\times _{{\mathcal Y}}{\mathcal X}$
is an algebraic stack of finite type over S.
${\mathcal X}\times _{{\mathcal Y}}{\mathcal X}$
is an algebraic stack of finite type over S.
Proof. The fact that
![]() ${\mathcal X}\times _{{\mathcal Y}} {\mathcal X}$
is an algebraic stack follows from [Sta13, Tag 04TF]. Since composites of morphisms of finite type are of finite type, in order to show that
${\mathcal X}\times _{{\mathcal Y}} {\mathcal X}$
is an algebraic stack follows from [Sta13, Tag 04TF]. Since composites of morphisms of finite type are of finite type, in order to show that
![]() ${\mathcal X}\times _{{\mathcal Y}} {\mathcal X}$
is of finite type over S, it suffices to show that the natural morphism
${\mathcal X}\times _{{\mathcal Y}} {\mathcal X}$
is of finite type over S, it suffices to show that the natural morphism
![]() ${\mathcal X}\times _{{\mathcal Y}} {\mathcal X} \to {\mathcal X}\times _S {\mathcal X}$
is of finite type. Since this morphism is the base change of the diagonal morphism
${\mathcal X}\times _{{\mathcal Y}} {\mathcal X} \to {\mathcal X}\times _S {\mathcal X}$
is of finite type. Since this morphism is the base change of the diagonal morphism
![]() ${\mathcal Y} \to {\mathcal Y}\times _S {\mathcal Y},$
this follows by assumption.
${\mathcal Y} \to {\mathcal Y}\times _S {\mathcal Y},$
this follows by assumption.
Lemma 3.3.19. The following conditions are equivalent:
(1)
![]() ${\text{ker-Ext}}^1_{\mathcal {K}(\kappa (\mathfrak m))}\bigl ( \mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}, \mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}\bigr )= 0$
for all maximal ideals
${\text{ker-Ext}}^1_{\mathcal {K}(\kappa (\mathfrak m))}\bigl ( \mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}, \mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}\bigr )= 0$
for all maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() ${A^{\operatorname {k-free}}}$
.
${A^{\operatorname {k-free}}}$
.
(2)
![]() $U_{A^{\operatorname {k-free}}} = 0$
.
$U_{A^{\operatorname {k-free}}} = 0$
.
(3)
![]() $\operatorname {\mathrm {Spec}} C^{{{\operatorname {k-free}}}}$
is the trivial vector bundle over
$\operatorname {\mathrm {Spec}} C^{{{\operatorname {k-free}}}}$
is the trivial vector bundle over
![]() $\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}}$
.
$\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}}$
.
Proof. Conditions (2) and (3) are equivalent by definition. Since the formation of
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({A^{\operatorname {k-free}}})}(\mathfrak {M}_{{A^{\operatorname {k-free}}},x},\mathfrak {N}_{{A^{\operatorname {k-free}}},y})$
is compatible with base change, and since
${\text{ker-Ext}}^1_{\mathcal {K}({A^{\operatorname {k-free}}})}(\mathfrak {M}_{{A^{\operatorname {k-free}}},x},\mathfrak {N}_{{A^{\operatorname {k-free}}},y})$
is compatible with base change, and since
![]() ${A^{\operatorname {k-free}}}$
is Jacobson, (1) is equivalent to the assumption that
${A^{\operatorname {k-free}}}$
is Jacobson, (1) is equivalent to the assumption that
that is, that
![]() $U_{A^{\operatorname {k-free}}}=0$
, as required.
$U_{A^{\operatorname {k-free}}}=0$
, as required.
Lemma 3.3.20. If the equivalent conditions of Lemma 3.3.19 hold, then the natural morphism
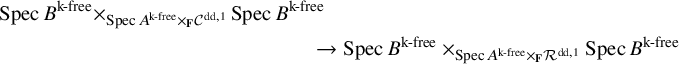 $$ \begin{align*} \operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \times_{\operatorname{\mathrm{Spec}} A^{{{\operatorname{k-free}}}} \times_{\mathbf F} {\mathcal C}^{\mathrm{dd},1}} &\operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \\ &\qquad\qquad\to \operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \times_{\operatorname{\mathrm{Spec}} A^{{{\operatorname{k-free}}}} \times_{\mathbf F} {\mathcal R}^{\mathrm{dd},1}} \operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \times_{\operatorname{\mathrm{Spec}} A^{{{\operatorname{k-free}}}} \times_{\mathbf F} {\mathcal C}^{\mathrm{dd},1}} &\operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \\ &\qquad\qquad\to \operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \times_{\operatorname{\mathrm{Spec}} A^{{{\operatorname{k-free}}}} \times_{\mathbf F} {\mathcal R}^{\mathrm{dd},1}} \operatorname{\mathrm{Spec}} B^{{{\operatorname{k-free}}}} \end{align*} $$
is an isomorphism.
Proof. Since
![]() ${\mathcal C}^{\mathrm {dd},1} \to {\mathcal R}^{\mathrm {dd},1}$
is separated (being proper) and representable, the diagonal morphism
${\mathcal C}^{\mathrm {dd},1} \to {\mathcal R}^{\mathrm {dd},1}$
is separated (being proper) and representable, the diagonal morphism
![]() ${\mathcal C}^{\mathrm {dd},1} \to {\mathcal C}^{\mathrm {dd},1}\times _{{\mathcal R}^{\mathrm {dd},1}} {\mathcal C}^{\mathrm {dd},1}$
is a closed immersion, and hence the morphism in the statement of the lemma is a closed immersion. Thus, in order to show that it is an isomorphism, it suffices to show that it induces a surjection on R-valued points, for any
${\mathcal C}^{\mathrm {dd},1} \to {\mathcal C}^{\mathrm {dd},1}\times _{{\mathcal R}^{\mathrm {dd},1}} {\mathcal C}^{\mathrm {dd},1}$
is a closed immersion, and hence the morphism in the statement of the lemma is a closed immersion. Thus, in order to show that it is an isomorphism, it suffices to show that it induces a surjection on R-valued points, for any
![]() ${\mathbf F}$
-algebra R. Since the source and target are of finite type over
${\mathbf F}$
-algebra R. Since the source and target are of finite type over
![]() ${\mathbf F}$
, by Lemma 3.3.18, we may, in fact, restrict attention to finite type
${\mathbf F}$
, by Lemma 3.3.18, we may, in fact, restrict attention to finite type
![]() ${\mathbf F}$
-algebras.
${\mathbf F}$
-algebras.
A morphism
![]() $\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}} \times _{\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}} \times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
corresponds to an isomorphism class of tuples
$\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}} \times _{\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}} \times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
corresponds to an isomorphism class of tuples
![]() $(\alpha ,\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
$(\alpha ,\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
-
○
 $\alpha $
is a morphism
$\alpha $
is a morphism
 $\alpha :\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} {A^{\operatorname {k-free}}}$
,
$\alpha :\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} {A^{\operatorname {k-free}}}$
, -
○
 $\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in R,
$\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in R, -
○
 $\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
$\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
 $\iota ':\alpha ^{*} \mathfrak {N} \to \mathfrak {E}'$
,
$\iota ':\alpha ^{*} \mathfrak {N} \to \mathfrak {E}'$
,
 $\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
$\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
 $\pi ':\mathfrak {E}' \to \alpha ^{*} \mathfrak {M}$
are morphisms with the properties that
$\pi ':\mathfrak {E}' \to \alpha ^{*} \mathfrak {M}$
are morphisms with the properties that
 $0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
$0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
 $0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to \alpha ^{*} \mathfrak {M} \to 0$
are both short exact.
$0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to \alpha ^{*} \mathfrak {M} \to 0$
are both short exact.
Similarly, a morphism
![]() $\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}} \times _{\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}} \times _{{\mathbf F}} {\mathcal R}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
corresponds to an isomorphism class of tuples
$\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}} \times _{\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}} \times _{{\mathbf F}} {\mathcal R}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
corresponds to an isomorphism class of tuples
![]() $(\alpha ,\mathfrak {E},\mathfrak {E}',\beta ,\iota ,\iota ',\pi ,\pi ')$
, where
$(\alpha ,\mathfrak {E},\mathfrak {E}',\beta ,\iota ,\iota ',\pi ,\pi ')$
, where
-
○
 $\alpha $
is a morphism
$\alpha $
is a morphism
 $\alpha :\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} {A^{\operatorname {k-free}}}$
,
$\alpha :\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} {A^{\operatorname {k-free}}}$
, -
○
 $\mathfrak {E}$
and
$\mathfrak {E}$
and
 $\mathfrak {E}'$
are Breuil–Kisin modules with descent data and coefficients in R, and
$\mathfrak {E}'$
are Breuil–Kisin modules with descent data and coefficients in R, and
 $\beta $
is an isomorphism
$\beta $
is an isomorphism
 $\beta :\mathfrak {E}[1/u]\to \mathfrak {E}'[1/u]$
of etale
$\beta :\mathfrak {E}[1/u]\to \mathfrak {E}'[1/u]$
of etale
 $\varphi $
-modules with descent data and coefficients in R,
$\varphi $
-modules with descent data and coefficients in R, -
○
 $\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
$\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
 $\iota ':\alpha ^{*} \mathfrak {N} \to \mathfrak {E}'$
,
$\iota ':\alpha ^{*} \mathfrak {N} \to \mathfrak {E}'$
,
 $\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
$\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
 $\pi ':\mathfrak {E}' \to \alpha ^{*} \mathfrak {M}$
are morphisms with the properties that
$\pi ':\mathfrak {E}' \to \alpha ^{*} \mathfrak {M}$
are morphisms with the properties that
 $0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
$0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
 $0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to \alpha ^{*} \mathfrak {M} \to 0$
are both short exact.
$0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to \alpha ^{*} \mathfrak {M} \to 0$
are both short exact.
Thus, to prove the claimed surjectivity, we have to show that, given a tuple
![]() $(\alpha ,\mathfrak {E},\mathfrak {E}',\beta ,\iota ,\iota ',\pi ,\pi ')$
associated to a morphism
$(\alpha ,\mathfrak {E},\mathfrak {E}',\beta ,\iota ,\iota ',\pi ,\pi ')$
associated to a morphism
![]() $\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}} \times _{\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}} \times _{{\mathbf F}} {\mathcal R}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
, the isomorphism
$\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}} \times _{\operatorname {\mathrm {Spec}} A^{{{\operatorname {k-free}}}} \times _{{\mathbf F}} {\mathcal R}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}$
, the isomorphism
![]() $\beta $
restricts to an isomorphism
$\beta $
restricts to an isomorphism
![]() $\mathfrak {E} \to \mathfrak {E}'.$
$\mathfrak {E} \to \mathfrak {E}'.$
By Lemma 3.3.19, the natural map
![]() $\operatorname {\mathrm {Ext}}^1(\alpha ^{*}\mathfrak {M},\alpha ^{*}\mathfrak {N})\to \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(R)}(\alpha ^{*}\mathfrak {M}[1/u],\alpha ^{*}\mathfrak {N}[1/u])$
is injective; so the Breuil–Kisin modules
$\operatorname {\mathrm {Ext}}^1(\alpha ^{*}\mathfrak {M},\alpha ^{*}\mathfrak {N})\to \operatorname {\mathrm {Ext}}^1_{\mathcal {K}(R)}(\alpha ^{*}\mathfrak {M}[1/u],\alpha ^{*}\mathfrak {N}[1/u])$
is injective; so the Breuil–Kisin modules
![]() $\mathfrak {E}$
and
$\mathfrak {E}$
and
![]() $\mathfrak {E}'$
are isomorphic. Arguing as in the proof of Corollary 3.2.7, we see that
$\mathfrak {E}'$
are isomorphic. Arguing as in the proof of Corollary 3.2.7, we see that
![]() $\beta $
is equivalent to the data of an R-point of
$\beta $
is equivalent to the data of an R-point of
![]() ${\mathbf G}_m\times _{{\mathcal O}}{\mathbf G}_m$
, corresponding to the automorphisms of
${\mathbf G}_m\times _{{\mathcal O}}{\mathbf G}_m$
, corresponding to the automorphisms of
![]() $\alpha ^{*}\mathfrak {M}[1/u]$
and
$\alpha ^{*}\mathfrak {M}[1/u]$
and
![]() $\alpha ^{*}\mathfrak {N}[1/u]$
that it induces. These restrict to automorphisms of
$\alpha ^{*}\mathfrak {N}[1/u]$
that it induces. These restrict to automorphisms of
![]() $\alpha ^{*}\mathfrak {M}$
and
$\alpha ^{*}\mathfrak {M}$
and
![]() $\alpha ^{*}\mathfrak {N}$
, so that (again, by the proof of Corollary 3.2.7)
$\alpha ^{*}\mathfrak {N}$
, so that (again, by the proof of Corollary 3.2.7)
![]() $\beta $
indeed restricts to an isomorphism
$\beta $
indeed restricts to an isomorphism
![]() $\mathfrak {E}\to \mathfrak {E}'$
, as required.
$\mathfrak {E}\to \mathfrak {E}'$
, as required.
We now present the main result of this subsection.
Proposition 3.3.21.
(1) The morphism
![]() $\xi ^{{\operatorname {dist}}}$
induces a morphism
$\xi ^{{\operatorname {dist}}}$
induces a morphism
which is representable by algebraic spaces, of finite type, and unramified, whose fibres over finite type points are of degree
![]() $\leq 2$
. In the strict case, this induced morphism is, in fact, a monomorphism, while in general, the restriction
$\leq 2$
. In the strict case, this induced morphism is, in fact, a monomorphism, while in general, the restriction
![]() $\xi _X$
of
$\xi _X$
of
![]() $\xi ^{{\operatorname {dist}}}$
induces a finite type monomorphism
$\xi ^{{\operatorname {dist}}}$
induces a finite type monomorphism
(2) If
![]() ${\text{ker-Ext}}^1_{\mathcal {K}(\kappa (\mathfrak m))}\bigl ( \mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}, \mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}\bigr )=0$
for all maximal ideals
${\text{ker-Ext}}^1_{\mathcal {K}(\kappa (\mathfrak m))}\bigl ( \mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}, \mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}\bigr )=0$
for all maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() ${A^{\operatorname {k-free}}}$
, then the composite morphism
${A^{\operatorname {k-free}}}$
, then the composite morphism
is representable by algebraic spaces, of finite type, and unramified, with fibres of degree
![]() $\leq 2.$
In the strict case, this induced morphism is, in fact, a monomorphism, while in general, the composite morphism
$\leq 2.$
In the strict case, this induced morphism is, in fact, a monomorphism, while in general, the composite morphism
is a finite type monomorphism.
Remark 3.3.26. The failure of (3.3.22) to be a monomorphism in general is due, effectively, to the possibility that an extension
![]() $\mathfrak {E}$
of some
$\mathfrak {E}$
of some
![]() $\mathfrak {M}_{R,x}$
by
$\mathfrak {M}_{R,x}$
by
![]() $\mathfrak {N}_{R,y}$
and an extension
$\mathfrak {N}_{R,y}$
and an extension
![]() $\mathfrak {E}'$
of some
$\mathfrak {E}'$
of some
![]() $\mathfrak {M}_{R,x'}$
by
$\mathfrak {M}_{R,x'}$
by
![]() $\mathfrak {N}_{R,y'}$
might be isomorphic as Breuil–Kisin modules while nevertheless
$\mathfrak {N}_{R,y'}$
might be isomorphic as Breuil–Kisin modules while nevertheless
![]() $(x,y)\neq (x',y')$
. As we will see in the proof, whenever this happens, the map
$(x,y)\neq (x',y')$
. As we will see in the proof, whenever this happens, the map
![]() $\mathfrak {N}_{\Lambda ,y} \to \mathfrak {E}\to \mathfrak {E}' \to \mathfrak {M}_{\Lambda ,x'}$
is nonzero, and then
$\mathfrak {N}_{\Lambda ,y} \to \mathfrak {E}\to \mathfrak {E}' \to \mathfrak {M}_{\Lambda ,x'}$
is nonzero, and then
![]() $\mathfrak {E}' \otimes _R \kappa (\mathfrak {m})[1/u]$
is split for some maximal ideal
$\mathfrak {E}' \otimes _R \kappa (\mathfrak {m})[1/u]$
is split for some maximal ideal
![]() $\mathfrak {m}$
of R. This explains why, to obtain a monomorphism, we can restrict either to the strict case or to the substack of extensions that are nonsplit after inverting u.
$\mathfrak {m}$
of R. This explains why, to obtain a monomorphism, we can restrict either to the strict case or to the substack of extensions that are nonsplit after inverting u.
Remark 3.3.27. We have stated this proposition in the strongest form that we are able to prove, but, in fact, its full strength is not required in the subsequent applications. In particular, we don’t need the precise bounds on the degrees of the fibres.
Proof of Proposition 3.3.21
By Corollary 3.2.7 (which we can apply because Assumption 3.2.4 is satisfied, by Lemma 3.3.7), the natural morphism
![]() $[\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}/ {\mathbf G}_m \times _{{\mathbf F}} {\mathbf G}_m ] \to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}\times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}$
is a finite type monomorphism, and hence so is its restriction to the open substack
$[\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}/ {\mathbf G}_m \times _{{\mathbf F}} {\mathbf G}_m ] \to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}\times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}$
is a finite type monomorphism, and hence so is its restriction to the open substack
![]() $[X/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
of its source.
$[X/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
of its source.
Let us momentarily write
![]() ${\mathcal X}$
to denote either
${\mathcal X}$
to denote either
![]() $[\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}/ {\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
or
$[\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}/ {\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
or
![]() $[X/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
. To show that the finite type morphism
$[X/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
. To show that the finite type morphism
![]() ${\mathcal X} \to {\mathcal C}^{\mathrm {dd},1}$
is representable by algebraic spaces, respectively, unramified, respectively, a monomorphism, it suffices to show that the corresponding diagonal morphism
${\mathcal X} \to {\mathcal C}^{\mathrm {dd},1}$
is representable by algebraic spaces, respectively, unramified, respectively, a monomorphism, it suffices to show that the corresponding diagonal morphism
![]() ${\mathcal X} \to {\mathcal X} \times _{{\mathcal C}^{\mathrm {dd},1}} {\mathcal X}$
is a monomorphism, respectively, étale, respectively, an isomorphism.
${\mathcal X} \to {\mathcal X} \times _{{\mathcal C}^{\mathrm {dd},1}} {\mathcal X}$
is a monomorphism, respectively, étale, respectively, an isomorphism.
Now, since
![]() ${\mathcal X} \to \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} \times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}$
is a monomorphism, the diagonal morphism
${\mathcal X} \to \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} \times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}$
is a monomorphism, the diagonal morphism
![]() ${\mathcal X} \to {\mathcal X} \times _{\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}\times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}} {\mathcal X}$
is an isomorphism, and so it is equivalent to show that the morphism of products
${\mathcal X} \to {\mathcal X} \times _{\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}\times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}} {\mathcal X}$
is an isomorphism, and so it is equivalent to show that the morphism of products
is a monomorphism, respectively, étale, respectively, an isomorphism. This is, in turn, equivalent to showing the corresponding properties for the morphisms
or
Now each of these morphisms is a base change of the diagonal
![]() $\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}\to \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} \times _{{\mathbf F}} \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}},$
which is a closed immersion (affine schemes being separated), and so is itself a closed immersion. In particular, it is a monomorphism, and so we have proved the representability by algebraic spaces of each of (3.3.22) and (3.3.23). Since the source and target of each of these monomorphisms is of finite type over
$\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}\to \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} \times _{{\mathbf F}} \operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}},$
which is a closed immersion (affine schemes being separated), and so is itself a closed immersion. In particular, it is a monomorphism, and so we have proved the representability by algebraic spaces of each of (3.3.22) and (3.3.23). Since the source and target of each of these monomorphisms is of finite type over
![]() ${\mathbf F}$
, by Lemma 3.3.18, in order to show that either of these monomorphisms is an isomorphism, it suffices to show that it induces a surjection on R-valued points, for arbitrary finite type
${\mathbf F}$
, by Lemma 3.3.18, in order to show that either of these monomorphisms is an isomorphism, it suffices to show that it induces a surjection on R-valued points, for arbitrary finite type
![]() ${\mathbf F}$
-algebras R. Similarly, to check that the closed immersion (3.3.28) is étale, it suffices to verify that it is formally smooth, and for this, it suffices to verify that it satisfies the infinitesimal lifting property with respect to square zero thickenings of finite type
${\mathbf F}$
-algebras R. Similarly, to check that the closed immersion (3.3.28) is étale, it suffices to verify that it is formally smooth, and for this, it suffices to verify that it satisfies the infinitesimal lifting property with respect to square zero thickenings of finite type
![]() ${\mathbf F}$
-algebras.
${\mathbf F}$
-algebras.
A morphism
![]() $\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}} \times _{{\mathcal C}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}$
corresponds to an isomorphism class of tuples
$\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}} \times _{{\mathcal C}^{\mathrm {dd},1}}\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}$
corresponds to an isomorphism class of tuples
![]() $(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
$(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
-
○
 $\alpha ,\alpha '$
are morphisms
$\alpha ,\alpha '$
are morphisms
 $\alpha ,\alpha ':\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
,
$\alpha ,\alpha ':\operatorname {\mathrm {Spec}} R\to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
, -
○
 $\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in R,
$\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in R, -
○
 $\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
$\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
 $\iota ':(\alpha ')^{*} \mathfrak {N} \to \mathfrak {E}'$
,
$\iota ':(\alpha ')^{*} \mathfrak {N} \to \mathfrak {E}'$
,
 $\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
$\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
 $\pi ':\mathfrak {E}' \to (\alpha ')^{*} \mathfrak {M}$
are morphisms with the properties that
$\pi ':\mathfrak {E}' \to (\alpha ')^{*} \mathfrak {M}$
are morphisms with the properties that
 $0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
$0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
 $0 \to (\alpha ')^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to (\alpha ')^{*} \mathfrak {M} \to 0$
are both short exact.
$0 \to (\alpha ')^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to (\alpha ')^{*} \mathfrak {M} \to 0$
are both short exact.
We begin by proving that (3.3.28) satisfies the infinitesimal lifting criterion (when R is a finite type
![]() ${\mathbf F}$
-algebra). Thus, we assume given a square-zero ideal
${\mathbf F}$
-algebra). Thus, we assume given a square-zero ideal
![]() $I \subset R$
, such that the induced morphism
$I \subset R$
, such that the induced morphism
factors through
![]() $\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}\times _{\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} \times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}} \operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
. In terms of the data
$\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}\times _{\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} \times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}} \operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
. In terms of the data
![]() $(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, we are assuming that
$(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, we are assuming that
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
coincide when restricted to
$\alpha '$
coincide when restricted to
![]() $\operatorname {\mathrm {Spec}} R/I$
, and we must show that
$\operatorname {\mathrm {Spec}} R/I$
, and we must show that
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
themselves coincide.
$\alpha '$
themselves coincide.
To this end, we consider the composite
If we can show the vanishing of this morphism, then by reversing the roles of
![]() $\mathfrak {E}$
and
$\mathfrak {E}$
and
![]() $\mathfrak {E}'$
, we will similarly deduce the vanishing of
$\mathfrak {E}'$
, we will similarly deduce the vanishing of
![]() $\pi \circ \beta ^{-1} \circ \iota '$
, from which we can conclude that
$\pi \circ \beta ^{-1} \circ \iota '$
, from which we can conclude that
![]() $\beta $
induces an isomorphism between
$\beta $
induces an isomorphism between
![]() $\alpha ^{*}\mathfrak {N}$
and
$\alpha ^{*}\mathfrak {N}$
and
![]() $(\alpha ')^{*}\mathfrak {N}$
. Consequently, it also induces an isomorphism between
$(\alpha ')^{*}\mathfrak {N}$
. Consequently, it also induces an isomorphism between
![]() $\alpha ^{*}\mathfrak {M}$
and
$\alpha ^{*}\mathfrak {M}$
and
![]() $(\alpha ')^{*}\mathfrak {M}$
, so it follows from Lemma 3.3.5 that
$(\alpha ')^{*}\mathfrak {M}$
, so it follows from Lemma 3.3.5 that
![]() $\alpha =\alpha '$
, as required.
$\alpha =\alpha '$
, as required.
We show the vanishing of (3.3.30). Suppose to the contrary that it doesn’t vanish, so that we have a nonzero morphism
![]() $\alpha ^{*}\mathfrak {N}\to (\alpha ')^{*}\mathfrak {M}.$
It follows from Proposition 3.1.17 that, for some maximal ideal
$\alpha ^{*}\mathfrak {N}\to (\alpha ')^{*}\mathfrak {M}.$
It follows from Proposition 3.1.17 that, for some maximal ideal
![]() $\mathfrak {m}$
of R, there exists a nonzero morphism
$\mathfrak {m}$
of R, there exists a nonzero morphism
By assumption,
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
coincide modulo I. Since
$\alpha '$
coincide modulo I. Since
![]() $I^2 = 0$
, there is an inclusion
$I^2 = 0$
, there is an inclusion
![]() $I \subset \mathfrak m$
, and so, in particular, we find that
$I \subset \mathfrak m$
, and so, in particular, we find that
Thus, there exists a nonzero morphism
Then, by Lemma 3.3.4, after inverting u, we obtain an isomorphism
contradicting the assumption that
![]() $\alpha $
maps
$\alpha $
maps
![]() $\operatorname {\mathrm {Spec}} R$
into
$\operatorname {\mathrm {Spec}} R$
into
![]() $\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
. This completes the proof that (3.3.28) is formally smooth, and hence that (3.3.22) is unramified.
$\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
. This completes the proof that (3.3.28) is formally smooth, and hence that (3.3.22) is unramified.
We next show that, in the strict case, the closed immersion (3.3.28) is an isomorphism, and thus that (3.3.22) is actually a monomorphism. As noted above, it suffices to show that (3.3.28) induces a surjection on R-valued points for finite type
![]() ${\mathbf F}$
-algebras R, which in terms of the data
${\mathbf F}$
-algebras R, which in terms of the data
![]() $(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, amounts to showing that necessarily
$(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, amounts to showing that necessarily
![]() $\alpha = \alpha '$
. Arguing just as we did above, it suffices to show the vanishing of (3.3.30).
$\alpha = \alpha '$
. Arguing just as we did above, it suffices to show the vanishing of (3.3.30).
Again, we suppose for the sake of contradiction that (3.3.30) does not vanish. It then follows from Proposition 3.1.17 that for some maximal ideal
![]() $\mathfrak {m}$
of R, there exists a nonzero morphism
$\mathfrak {m}$
of R, there exists a nonzero morphism
Then, by Lemma 3.3.4, after inverting u, we obtain an isomorphism
In the strict case, such an isomorphism cannot exist by assumption, and thus (3.3.30) must vanish.
We now turn to proving that (3.3.29) is an isomorphism. Just as in the preceding arguments, it suffices to show that (3.3.30) vanishes, and if not, then we obtain an isomorphism (3.3.31). Since we are considering points of
![]() $X\times X$
, we are given that the induced extension
$X\times X$
, we are given that the induced extension
![]() $\mathfrak {E}'\otimes _R\kappa (\mathfrak m)[1/u]$
is nonsplit, so that the base change of the morphism (3.3.30) from
$\mathfrak {E}'\otimes _R\kappa (\mathfrak m)[1/u]$
is nonsplit, so that the base change of the morphism (3.3.30) from
![]() $R[[u]]$
to
$R[[u]]$
to
![]() $\kappa (\mathfrak m)((u))$
must vanish. Consequently, the composite
$\kappa (\mathfrak m)((u))$
must vanish. Consequently, the composite
![]() $\beta \circ \iota $
induces a nonzero morphism
$\beta \circ \iota $
induces a nonzero morphism
![]() $\alpha ^{*}(\mathfrak {N})\otimes _R\kappa (\mathfrak m)[1/u] \to (\alpha ')^{*}(\mathfrak {N}) \otimes _R\kappa (\mathfrak m)[1/u],$
which, by Lemma 3.3.4, must, in fact, be an isomorphism. Comparing this isomorphism with the isomorphism (3.3.31), we find that
$\alpha ^{*}(\mathfrak {N})\otimes _R\kappa (\mathfrak m)[1/u] \to (\alpha ')^{*}(\mathfrak {N}) \otimes _R\kappa (\mathfrak m)[1/u],$
which, by Lemma 3.3.4, must, in fact, be an isomorphism. Comparing this isomorphism with the isomorphism (3.3.31), we find that
![]() $(\alpha ')^{*}(\mathfrak {N})\otimes _R\kappa (\mathfrak m)[1/u]$
and
$(\alpha ')^{*}(\mathfrak {N})\otimes _R\kappa (\mathfrak m)[1/u]$
and
![]() $(\alpha ')^{*}(\mathfrak {M})\otimes _R\kappa (\mathfrak m)[1/u]$
are isomorphic, contradicting the fact that
$(\alpha ')^{*}(\mathfrak {M})\otimes _R\kappa (\mathfrak m)[1/u]$
are isomorphic, contradicting the fact that
![]() $\alpha '$
maps
$\alpha '$
maps
![]() $\operatorname {\mathrm {Spec}} R$
to
$\operatorname {\mathrm {Spec}} R$
to
![]() $\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
. Thus, in fact, the composite (3.3.30) must vanish, and we have completed the proof that (3.3.23) is a monomorphism.
$\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}}$
. Thus, in fact, the composite (3.3.30) must vanish, and we have completed the proof that (3.3.23) is a monomorphism.
To complete the proof of part (1) of the proposition, we have to show that the fibres of (3.3.22) are of degree at most
![]() $2$
. We have already observed that
$2$
. We have already observed that
![]() $[\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}/ {\mathbf G}_m \times _{{\mathbf F}} {\mathbf G}_m ] \to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}\times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}$
is a monomorphism, so it is enough to check that given a finite extension
$[\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}}/ {\mathbf G}_m \times _{{\mathbf F}} {\mathbf G}_m ] \to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}\times _{{\mathbf F}} {\mathcal C}^{\mathrm {dd},1}$
is a monomorphism, so it is enough to check that given a finite extension
![]() ${\mathbf F}'/{\mathbf F}$
and an isomorphism class of tuples
${\mathbf F}'/{\mathbf F}$
and an isomorphism class of tuples
![]() $(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
$(\alpha ,\alpha ',\beta :\mathfrak {E}\to \mathfrak {E}',\iota ,\iota ',\pi ,\pi ')$
, where
-
○
 $\alpha ,\alpha '$
are distinct morphisms
$\alpha ,\alpha '$
are distinct morphisms
 $\alpha ,\alpha ':\operatorname {\mathrm {Spec}} {\mathbf F}'\to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
,
$\alpha ,\alpha ':\operatorname {\mathrm {Spec}} {\mathbf F}'\to \operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
, -
○
 $\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in
$\beta :\mathfrak {E}\to \mathfrak {E}'$
is an isomorphism of Breuil–Kisin modules with descent data and coefficients in
 ${\mathbf F}'$
,
${\mathbf F}'$
, -
○
 $\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
$\iota :\alpha ^{*} \mathfrak {N} \to \mathfrak {E}$
,
 $\iota ':(\alpha ')^{*} \mathfrak {N} \to \mathfrak {E}'$
,
$\iota ':(\alpha ')^{*} \mathfrak {N} \to \mathfrak {E}'$
,
 $\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
$\pi :\mathfrak {E} \to \alpha ^{*} \mathfrak {M}$
and
 $\pi ':\mathfrak {E}' \to (\alpha ')^{*} \mathfrak {M}$
are morphisms with the properties that
$\pi ':\mathfrak {E}' \to (\alpha ')^{*} \mathfrak {M}$
are morphisms with the properties that
 $0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
$0 \to \alpha ^{*}\mathfrak {N} \buildrel \iota \over \to \mathfrak {E} \buildrel \pi \over \to \alpha ^{*} \mathfrak {M} \to 0$
and
 $0 \to (\alpha ')^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to (\alpha ')^{*} \mathfrak {M} \to 0$
are both short exact,
$0 \to (\alpha ')^{*}\mathfrak {N} \buildrel \iota ' \over \to \mathfrak {E}' \buildrel \pi ' \over \to (\alpha ')^{*} \mathfrak {M} \to 0$
are both short exact,
then
![]() $\alpha '$
is determined by the data of
$\alpha '$
is determined by the data of
![]() $\alpha $
and
$\alpha $
and
![]() $\mathfrak {E}$
. To see this, note that since we are assuming that
$\mathfrak {E}$
. To see this, note that since we are assuming that
![]() $\alpha '\ne \alpha $
, the arguments above show that (3.3.30) does not vanish, so that (since
$\alpha '\ne \alpha $
, the arguments above show that (3.3.30) does not vanish, so that (since
![]() ${\mathbf F}'$
is a field) we have an isomorphism
${\mathbf F}'$
is a field) we have an isomorphism
![]() $\alpha ^{*}\mathfrak {N}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {M}[1/u]$
. Since we are over
$\alpha ^{*}\mathfrak {N}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {M}[1/u]$
. Since we are over
![]() ${A^{\operatorname {dist}}}$
, it follows that
${A^{\operatorname {dist}}}$
, it follows that
![]() $\mathfrak {E}[1/u]\cong \mathfrak {E}'[1/u]$
is split, and that we also have an isomorphism
$\mathfrak {E}[1/u]\cong \mathfrak {E}'[1/u]$
is split, and that we also have an isomorphism
![]() $\alpha ^{*}\mathfrak {M}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {N}[1/u]$
. Thus, if
$\alpha ^{*}\mathfrak {M}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {N}[1/u]$
. Thus, if
![]() $\alpha "$
is another possible choice for
$\alpha "$
is another possible choice for
![]() $\alpha '$
, we have
$\alpha '$
, we have
![]() $(\alpha ")^{*}\mathfrak {M}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {M}[1/u]$
and
$(\alpha ")^{*}\mathfrak {M}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {M}[1/u]$
and
![]() $(\alpha ")^{*}\mathfrak {N}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {N}[1/u]$
, whence
$(\alpha ")^{*}\mathfrak {N}[1/u]\stackrel {\sim }{\longrightarrow }(\alpha ')^{*}\mathfrak {N}[1/u]$
, whence
![]() $\alpha "=\alpha '$
by Lemma 3.3.5, as required.
$\alpha "=\alpha '$
by Lemma 3.3.5, as required.
We turn to proving (2), and thus assume that
for all maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() ${A^{\operatorname {k-free}}}$
.
${A^{\operatorname {k-free}}}$
.
Lemma 3.3.20 shows that
is an isomorphism, from which we deduce that
is a monomorphism. Using this as input, the claims of (2) may be proved in an essentially identical fashion to those of (1).
Corollary 3.3.32. The dimension of
![]() $\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
is equal to the rank of
$\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
is equal to the rank of
![]() $T_{A^{\operatorname {dist}}}$
as a projective
$T_{A^{\operatorname {dist}}}$
as a projective
![]() ${A^{\operatorname {dist}}}$
-module. If
${A^{\operatorname {dist}}}$
-module. If
for all maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $A^{{{\operatorname {k-free}}}}$
, then the dimension of
$A^{{{\operatorname {k-free}}}}$
, then the dimension of
![]() $\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
is also equal to this rank, while if
$\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
is also equal to this rank, while if
for all maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $A^{{{\operatorname {k-free}}}}$
, then the dimension of
$A^{{{\operatorname {k-free}}}}$
, then the dimension of
![]() $\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
is strictly less than this rank.
$\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
is strictly less than this rank.
Proof. The dimension of
![]() $[\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
is equal to the rank of
$[\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m]$
is equal to the rank of
![]() $T_{A^{{\operatorname {dist}}}}$
. (It is the quotient by a two-dimensional group of a vector bundle over a two-dimensional base of rank equal to the rank of
$T_{A^{{\operatorname {dist}}}}$
. (It is the quotient by a two-dimensional group of a vector bundle over a two-dimensional base of rank equal to the rank of
![]() $T_{A^{{\operatorname {dist}}}}$
.) By Lemma 3.3.10,
$T_{A^{{\operatorname {dist}}}}$
.) By Lemma 3.3.10,
![]() $\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
is the scheme-theoretic image of the morphism
$\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
is the scheme-theoretic image of the morphism
![]() $[\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}/{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m] \to {\mathcal C}^{\mathrm {dd},1}$
provided by Proposition 3.3.21(1), which (by that proposition) is representable by algebraic spaces and unramified. Since such a morphism is locally quasi-finite (in fact, in this particular case, we have shown that the fibres of this morphism have degree at most
$[\operatorname {\mathrm {Spec}}{B^{\operatorname {dist}}}/{\mathbf G}_m\times _{{\mathbf F}}{\mathbf G}_m] \to {\mathcal C}^{\mathrm {dd},1}$
provided by Proposition 3.3.21(1), which (by that proposition) is representable by algebraic spaces and unramified. Since such a morphism is locally quasi-finite (in fact, in this particular case, we have shown that the fibres of this morphism have degree at most
![]() $2$
), [Sta13, Tag 0DS6] ensures that
$2$
), [Sta13, Tag 0DS6] ensures that
![]() $\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
has the claimed dimension.
$\overline {{\mathcal C}}(\mathfrak {M},\mathfrak {N})$
has the claimed dimension.
If
![]() ${\text{ker-Ext}}^1_{\mathcal {K}(\kappa (\mathfrak m))}\bigl ( \mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}, \mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}\bigr ) = 0$
for all maximal ideals
${\text{ker-Ext}}^1_{\mathcal {K}(\kappa (\mathfrak m))}\bigl ( \mathfrak {M}_{\kappa (\mathfrak m),\bar {x}}, \mathfrak {N}_{\kappa (\mathfrak m),\bar {y}}\bigr ) = 0$
for all maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $A^{{{\operatorname {k-free}}}}$
, then an identical argument using Proposition 3.3.21(2) implies the claim regarding the dimension of
$A^{{{\operatorname {k-free}}}}$
, then an identical argument using Proposition 3.3.21(2) implies the claim regarding the dimension of
![]() $\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
.
$\overline {{\mathcal Z}}(\mathfrak {M},\mathfrak {N})$
.
Finally, suppose that
for all maximal ideals
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $A^{{{\operatorname {k-free}}}}$
. Then the composite
$A^{{{\operatorname {k-free}}}}$
. Then the composite
![]() $[\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m] \to {\mathcal C}^{\mathrm {dd},1} \to {\mathcal R}^{\mathrm {dd},1}$
has the property that for every point t in the source, the fibre over the image of t has a positive dimensional fibre. [Sta13, Tag 0DS6] then implies the remaining claim of the present lemma.
$[\operatorname {\mathrm {Spec}}{B^{\operatorname {k-free}}}/{\mathbf G}_m\times _{{\mathbf F}} {\mathbf G}_m] \to {\mathcal C}^{\mathrm {dd},1} \to {\mathcal R}^{\mathrm {dd},1}$
has the property that for every point t in the source, the fibre over the image of t has a positive dimensional fibre. [Sta13, Tag 0DS6] then implies the remaining claim of the present lemma.
4. Extensions of rank one Breuil–Kisin modules
4.1. Rank one modules over finite fields, and their extensions
We now wish to apply the results of the previous section to study the geometry of our various moduli stacks. In order to do this, it will be convenient for us to have an explicit description of the rank one Breuil–Kisin modules of height at most
![]() $1$
with descent data over a finite field of characteristic p, and of their possible extensions. Many of the results in this section are proved (for
$1$
with descent data over a finite field of characteristic p, and of their possible extensions. Many of the results in this section are proved (for
![]() $p>2$
) in [Reference Diamond and SavittDS15, Section 1] in the context of Breuil modules, and in those cases, it is possible simply to translate the relevant statements to the Breuil–Kisin module context.
$p>2$
) in [Reference Diamond and SavittDS15, Section 1] in the context of Breuil modules, and in those cases, it is possible simply to translate the relevant statements to the Breuil–Kisin module context.
Assume from now on that
![]() $e(K'/K)$
is divisible by
$e(K'/K)$
is divisible by
![]() $p^{f}-1$
, so that we are in the setting of [Reference Diamond and SavittDS15, Remark 1.7]. (Note that the parallel in [Reference Diamond and SavittDS15] of our field extension
$p^{f}-1$
, so that we are in the setting of [Reference Diamond and SavittDS15, Remark 1.7]. (Note that the parallel in [Reference Diamond and SavittDS15] of our field extension
![]() $K'/K$
, with ramification and inertial indices
$K'/K$
, with ramification and inertial indices
![]() $e',f'$
and
$e',f'$
and
![]() $e,f$
, respectively, is the extension
$e,f$
, respectively, is the extension
![]() $K/L$
with indices
$K/L$
with indices
![]() $e,f$
and
$e,f$
and
![]() $e',f'$
, respectively.)
$e',f'$
, respectively.)
Let
![]() ${\mathbf F}$
be a finite subfield of
${\mathbf F}$
be a finite subfield of
![]() $\overline {{\mathbf F}}_p$
containing the image of some (so all) embedding(s)
$\overline {{\mathbf F}}_p$
containing the image of some (so all) embedding(s)
![]() $k'\hookrightarrow \overline {{\mathbf F}}_p$
. Recall that for each
$k'\hookrightarrow \overline {{\mathbf F}}_p$
. Recall that for each
![]() $g\in \operatorname {\mathrm {Gal}}(K'/K)$
, we write
$g\in \operatorname {\mathrm {Gal}}(K'/K)$
, we write
![]() $g(\pi ')/\pi '=h(g)$
with
$g(\pi ')/\pi '=h(g)$
with
![]() $h(g)\in \mu _{e(K'/K)}(K') \subset W(k')$
. We abuse notation and denote the image of
$h(g)\in \mu _{e(K'/K)}(K') \subset W(k')$
. We abuse notation and denote the image of
![]() $h(g)$
in
$h(g)$
in
![]() $k'$
again by
$k'$
again by
![]() $h(g)$
, so that we obtain a map
$h(g)$
, so that we obtain a map
![]() $h \colon \operatorname {\mathrm {Gal}}(K'/K) \to (k')^{\times }$
. Note that h restricts to a character on the inertia subgroup
$h \colon \operatorname {\mathrm {Gal}}(K'/K) \to (k')^{\times }$
. Note that h restricts to a character on the inertia subgroup
![]() $I(K'/K)$
, and is itself a character when
$I(K'/K)$
, and is itself a character when
![]() $e(K'/K) = p^f-1$
.
$e(K'/K) = p^f-1$
.
Lemma 4.1.1. Every rank one Breuil–Kisin module of height at most
![]() $1$
with descent data and
$1$
with descent data and
![]() ${\mathbf F}$
-coefficients is isomorphic to one of the modules
${\mathbf F}$
-coefficients is isomorphic to one of the modules
![]() $\mathfrak {M}(r,a,c)$
defined by:
$\mathfrak {M}(r,a,c)$
defined by:
-
○
 $\mathfrak {M}(r,a,c)_i={\mathbf F}[[u]]\cdot m_i$
,
$\mathfrak {M}(r,a,c)_i={\mathbf F}[[u]]\cdot m_i$
, -
○
 $\Phi _{\mathfrak {M}(r,a,c),i}(1\otimes m_{i-1})=a_{i} u^{r_{i}} m_{i}$
,
$\Phi _{\mathfrak {M}(r,a,c),i}(1\otimes m_{i-1})=a_{i} u^{r_{i}} m_{i}$
, -
○
 $\hat {g}(\sum _i m_i)=\sum _i h(g)^{c_i} m_i$
for all
$\hat {g}(\sum _i m_i)=\sum _i h(g)^{c_i} m_i$
for all
 $g\in \operatorname {\mathrm {Gal}}(K'/K)$
,
$g\in \operatorname {\mathrm {Gal}}(K'/K)$
,
where
![]() $a_i\in {\mathbf F}^{\times }$
,
$a_i\in {\mathbf F}^{\times }$
,
![]() $r_i\in \{0,\dots ,e'\}$
and
$r_i\in \{0,\dots ,e'\}$
and
![]() $c_i\in {\mathbf Z}/e(K'/K)$
are sequences satisfying
$c_i\in {\mathbf Z}/e(K'/K)$
are sequences satisfying
![]() $pc_{i-1}\equiv c_{i}+r_{i}\pmod {e(K'/K)}$
, the sums in the third bullet point run from
$pc_{i-1}\equiv c_{i}+r_{i}\pmod {e(K'/K)}$
, the sums in the third bullet point run from
![]() $0$
to
$0$
to
![]() $f'-1$
, and the
$f'-1$
, and the
![]() $r_i,c_i,a_i$
are periodic with period dividing f.
$r_i,c_i,a_i$
are periodic with period dividing f.
Furthermore, two such modules
![]() $\mathfrak {M}(r,a,c)$
and
$\mathfrak {M}(r,a,c)$
and
![]() $\mathfrak {M}(s,b,d)$
are isomorphic if and only if
$\mathfrak {M}(s,b,d)$
are isomorphic if and only if
![]() $r_i=s_i$
and
$r_i=s_i$
and
![]() $c_i=d_i$
for all i, and
$c_i=d_i$
for all i, and
![]() $\prod _{i=0}^{f-1}a_i=\prod _{i=0}^{f-1}b_i$
.
$\prod _{i=0}^{f-1}a_i=\prod _{i=0}^{f-1}b_i$
.
Proof. The proof is elementary (see e.g. [Reference SavittSav08, Theorems 2.1, 3.5] for proofs of analogous results).
We will sometimes refer to the element
![]() $m = \sum _i m_i \in \mathfrak {M}(r,a,c)$
as the standard generator of
$m = \sum _i m_i \in \mathfrak {M}(r,a,c)$
as the standard generator of
![]() $\mathfrak {M}(r,a,c)$
.
$\mathfrak {M}(r,a,c)$
.
Remark 4.1.2. When
![]() $p> 2$
, many of the results in this section (such as the above) can be obtained by translating [Reference Diamond and SavittDS15, Lemma 1.3, Corollary 1.8] from the Breuil module context to the Breuil–Kisin module context. We briefly recall the dictionary between these two categories (cf. [Reference KisinKis09, Section 1.1.10]). If A is a finite local
$p> 2$
, many of the results in this section (such as the above) can be obtained by translating [Reference Diamond and SavittDS15, Lemma 1.3, Corollary 1.8] from the Breuil module context to the Breuil–Kisin module context. We briefly recall the dictionary between these two categories (cf. [Reference KisinKis09, Section 1.1.10]). If A is a finite local
![]() ${\mathbf Z}_p$
-algebra, write
${\mathbf Z}_p$
-algebra, write
![]() $S_A = S \otimes _{{\mathbf Z}_p} A$
, where S is Breuil’s ring. We regard
$S_A = S \otimes _{{\mathbf Z}_p} A$
, where S is Breuil’s ring. We regard
![]() $S_A$
as a
$S_A$
as a
![]() $\mathfrak {S}_A$
-algebra via
$\mathfrak {S}_A$
-algebra via
![]() $u\mapsto u$
, and we let
$u\mapsto u$
, and we let
![]() $\varphi :\mathfrak {S}_A\to S_A$
be the composite of this map with
$\varphi :\mathfrak {S}_A\to S_A$
be the composite of this map with
![]() $\varphi $
on
$\varphi $
on
![]() $\mathfrak {S}_A$
. Then, given a Breuil–Kisin module of height at most
$\mathfrak {S}_A$
. Then, given a Breuil–Kisin module of height at most
![]() $1$
with descent data
$1$
with descent data
![]() $\mathfrak {M}$
, we set
$\mathfrak {M}$
, we set
![]() ${\mathcal M}:=S_A\otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}$
. We have a map
${\mathcal M}:=S_A\otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}$
. We have a map
![]() $1\otimes \varphi _{\mathfrak {M}}:S_A\otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}\to S_A \otimes _{\mathfrak {S}_A}\mathfrak {M}$
, and we set
$1\otimes \varphi _{\mathfrak {M}}:S_A\otimes _{\varphi ,\mathfrak {S}_A}\mathfrak {M}\to S_A \otimes _{\mathfrak {S}_A}\mathfrak {M}$
, and we set
and define
![]() $\varphi _1:\operatorname {\mathrm {Fil}}^1{\mathcal M}\to {\mathcal M}$
as the composite
$\varphi _1:\operatorname {\mathrm {Fil}}^1{\mathcal M}\to {\mathcal M}$
as the composite
Finally, we define
![]() $\hat {g}$
on
$\hat {g}$
on
![]() ${\mathcal M}$
via
${\mathcal M}$
via
![]() $\hat {g}(s\otimes m)=g(s)\otimes \hat {g}(m)$
. One checks without difficulty that this makes
$\hat {g}(s\otimes m)=g(s)\otimes \hat {g}(m)$
. One checks without difficulty that this makes
![]() ${\mathcal M}$
a strongly divisible module with descent data (cf. the proofs of [Reference KisinKis09, Proposition 1.1.11, Lemma 1.2.4]).
${\mathcal M}$
a strongly divisible module with descent data (cf. the proofs of [Reference KisinKis09, Proposition 1.1.11, Lemma 1.2.4]).
In the correspondence described above, the Breuil–Kisin module
![]() $\mathfrak {M}((r_i),(a_i),(c_i))$
corresponds to the Breuil module
$\mathfrak {M}((r_i),(a_i),(c_i))$
corresponds to the Breuil module
![]() ${\mathcal M}((e'-r_i),(a_i),(pc_{i-1}))$
of [Reference Diamond and SavittDS15, Lemma 1.3].
${\mathcal M}((e'-r_i),(a_i),(pc_{i-1}))$
of [Reference Diamond and SavittDS15, Lemma 1.3].
Definition 4.1.3. If
![]() $\mathfrak {M} = \mathfrak {M}(r,a,c)$
is a rank one Breuil–Kisin module as described in the preceding lemma, we set
$\mathfrak {M} = \mathfrak {M}(r,a,c)$
is a rank one Breuil–Kisin module as described in the preceding lemma, we set
![]() $\alpha _i(\mathfrak {M}) := (p^{f'-1} r_{i-f'+1} + \cdots + r_{i})/(p^{f'} - 1)$
(equivalently,
$\alpha _i(\mathfrak {M}) := (p^{f'-1} r_{i-f'+1} + \cdots + r_{i})/(p^{f'} - 1)$
(equivalently,
![]() $(p^{f-1} r_{i-f+1} + \cdots + r_{i})/(p^f-1)$
). We may abbreviate
$(p^{f-1} r_{i-f+1} + \cdots + r_{i})/(p^f-1)$
). We may abbreviate
![]() $\alpha _i(\mathfrak {M})$
simply as
$\alpha _i(\mathfrak {M})$
simply as
![]() $\alpha _i$
when
$\alpha _i$
when
![]() $\mathfrak {M}$
is clear from the context.
$\mathfrak {M}$
is clear from the context.
It follows easily from the congruence
![]() $r_i \equiv pc_{i-1} - c_i \pmod {e(K'/K)}$
together with the hypothesis that
$r_i \equiv pc_{i-1} - c_i \pmod {e(K'/K)}$
together with the hypothesis that
![]() $p^f-1 \mid e(K'/K)$
that
$p^f-1 \mid e(K'/K)$
that
![]() $\alpha _i \in {\mathbf Z}$
for all i. Note that the
$\alpha _i \in {\mathbf Z}$
for all i. Note that the
![]() $\alpha _i$
’s are the unique solution to the system of equations
$\alpha _i$
’s are the unique solution to the system of equations
![]() $p \alpha _{i-1} - \alpha _i = r_i$
for all i. Note also that
$p \alpha _{i-1} - \alpha _i = r_i$
for all i. Note also that
![]() $(p^f-1)(c_i-\alpha _i) \equiv 0 \pmod {e(K'/K)}$
, so that
$(p^f-1)(c_i-\alpha _i) \equiv 0 \pmod {e(K'/K)}$
, so that
![]() $h^{c_i-\alpha _i}$
is a character with image in
$h^{c_i-\alpha _i}$
is a character with image in
![]() $k^{\times }$
.
$k^{\times }$
.
Lemma 4.1.4. For any i, we have
![]() $T(\mathfrak {M}(r,a,c))=\left (\sigma _i\circ h^{c_i-\alpha _{i}}\cdot \mathrm {ur}_{\prod _{i=0}^{f-1}a_i}\right )|_{G_{K_{\infty }}}$
, where
$T(\mathfrak {M}(r,a,c))=\left (\sigma _i\circ h^{c_i-\alpha _{i}}\cdot \mathrm {ur}_{\prod _{i=0}^{f-1}a_i}\right )|_{G_{K_{\infty }}}$
, where
![]() $\mathrm {ur}_{\lambda }$
is the unramified character of
$\mathrm {ur}_{\lambda }$
is the unramified character of
![]() $G_K$
sending geometric Frobenius to
$G_K$
sending geometric Frobenius to
![]() $\lambda $
.
$\lambda $
.
Proof. Set
![]() $\mathfrak {N} = \mathfrak {M}(0,(a_i),0)$
, so that
$\mathfrak {N} = \mathfrak {M}(0,(a_i),0)$
, so that
![]() $\mathfrak {N}$
is effectively a Breuil–Kisin module without descent data. Then, for
$\mathfrak {N}$
is effectively a Breuil–Kisin module without descent data. Then, for
![]() $\mathfrak {N}$
, this result follows from the second paragraph of the proof [Reference Gee, Liu and SavittGLS14, Lemma 6.3]. (Note that the functor
$\mathfrak {N}$
, this result follows from the second paragraph of the proof [Reference Gee, Liu and SavittGLS14, Lemma 6.3]. (Note that the functor
![]() $T_{\mathfrak {S}}$
of loc. cit. is dual to our functor T; cf. [Reference FontaineFon90, A 1.2.7]. Note also that the fact that the base field is unramified in loc. cit. does not change the calculation.) If
$T_{\mathfrak {S}}$
of loc. cit. is dual to our functor T; cf. [Reference FontaineFon90, A 1.2.7]. Note also that the fact that the base field is unramified in loc. cit. does not change the calculation.) If
![]() $n = \sum n_i$
is the standard generator of
$n = \sum n_i$
is the standard generator of
![]() $\mathfrak {N}$
as in Lemma 4.1.1, let
$\mathfrak {N}$
as in Lemma 4.1.1, let
![]() $\gamma \in {\mathbf Z}_p^{\mathrm {un}} \otimes _{{\mathbf Z}_p} (k' \otimes _{{\mathbf F}_p} {\mathbf F})$
be an element so that
$\gamma \in {\mathbf Z}_p^{\mathrm {un}} \otimes _{{\mathbf Z}_p} (k' \otimes _{{\mathbf F}_p} {\mathbf F})$
be an element so that
![]() $\gamma n \in ({\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}\otimes _{\mathfrak {S}[1/u]} \mathfrak {N}[1/u])^{\varphi = 1}$
.
$\gamma n \in ({\mathcal O}_{\widehat {{\mathcal E}^{\text {nr}}}}\otimes _{\mathfrak {S}[1/u]} \mathfrak {N}[1/u])^{\varphi = 1}$
.
Now, for
![]() $\mathfrak {M}$
as in the statement of the lemma, it is straightforward to verify that
$\mathfrak {M}$
as in the statement of the lemma, it is straightforward to verify that
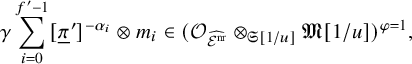 $$ \begin{align*}\gamma \sum_{i=0}^{f'-1} [\underline{\pi}']^{-\alpha_{i}} \otimes m_i \in ({\mathcal O}_{\widehat{{\mathcal E}^{\text{nr}}}}\otimes_{\mathfrak{S}[1/u]} \mathfrak{M}[1/u])^{\varphi=1},\end{align*} $$
$$ \begin{align*}\gamma \sum_{i=0}^{f'-1} [\underline{\pi}']^{-\alpha_{i}} \otimes m_i \in ({\mathcal O}_{\widehat{{\mathcal E}^{\text{nr}}}}\otimes_{\mathfrak{S}[1/u]} \mathfrak{M}[1/u])^{\varphi=1},\end{align*} $$
and the result follows.
One immediately deduces the following.
Corollary 4.1.5. Let
![]() $\mathfrak {M}=\mathfrak {M}(r,a,c)$
and
$\mathfrak {M}=\mathfrak {M}(r,a,c)$
and
![]() $\mathfrak {N}=\mathfrak {M}(s,b,d)$
be rank one Breuil–Kisin modules with descent data as above. We have
$\mathfrak {N}=\mathfrak {M}(s,b,d)$
be rank one Breuil–Kisin modules with descent data as above. We have
![]() $T(\mathfrak {M})=T(\mathfrak {N})$
if and only if
$T(\mathfrak {M})=T(\mathfrak {N})$
if and only if
![]() $c_i - \alpha _i(\mathfrak {M}) \equiv d_i - \alpha _i(\mathfrak {N}) \pmod {e(K'/K)}$
for some i (hence for all i) and
$c_i - \alpha _i(\mathfrak {M}) \equiv d_i - \alpha _i(\mathfrak {N}) \pmod {e(K'/K)}$
for some i (hence for all i) and
![]() $\prod _{i=0}^{f-1}a_i=\prod _{i=0}^{f-1}b_i$
.
$\prod _{i=0}^{f-1}a_i=\prod _{i=0}^{f-1}b_i$
.
Lemma 4.1.6. In the notation of the previous Corollary, there is a nonzero map
![]() $\mathfrak {M}\to \mathfrak {N}$
(equivalently,
$\mathfrak {M}\to \mathfrak {N}$
(equivalently,
![]() $\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})=1$
) if and only if
$\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})=1$
) if and only if
![]() $T(\mathfrak {M})=T(\mathfrak {N})$
and
$T(\mathfrak {M})=T(\mathfrak {N})$
and
![]() $\alpha _i(\mathfrak {M}) \ge \alpha _i(\mathfrak {N})$
for each i.
$\alpha _i(\mathfrak {M}) \ge \alpha _i(\mathfrak {N})$
for each i.
Proof. The proof is essentially the same as that of [Reference Diamond and SavittDS15, Lemma 1.6]. (Indeed, when
![]() $p> 2$
, this lemma can once again be proved by translating directly from [Reference Diamond and SavittDS15] to the Breuil–Kisin module context.)
$p> 2$
, this lemma can once again be proved by translating directly from [Reference Diamond and SavittDS15] to the Breuil–Kisin module context.)
Using the material of Section 3.1, one can compute
![]() $\operatorname {\mathrm {Ext}}^1(\mathfrak {M},\mathfrak {N})$
for any pair of rank one Breuil–Kisin modules
$\operatorname {\mathrm {Ext}}^1(\mathfrak {M},\mathfrak {N})$
for any pair of rank one Breuil–Kisin modules
![]() $\mathfrak {M},\mathfrak {N}$
of height at most
$\mathfrak {M},\mathfrak {N}$
of height at most
![]() $1$
. We begin with the following explicit description of the complex
$1$
. We begin with the following explicit description of the complex
![]() $C^{\bullet }(\mathfrak {N})$
of Section 3.1.
$C^{\bullet }(\mathfrak {N})$
of Section 3.1.
Definition 4.1.7. We write
![]() $\mathscr {C}^0_{u} = \mathscr {C}^0_{u}(\mathfrak {M},\mathfrak {N}) \subset {\mathbf F}((u))^{{\mathbf Z}/f{\mathbf Z}}$
for the space of f-tuples
$\mathscr {C}^0_{u} = \mathscr {C}^0_{u}(\mathfrak {M},\mathfrak {N}) \subset {\mathbf F}((u))^{{\mathbf Z}/f{\mathbf Z}}$
for the space of f-tuples
![]() $(\mu _i)$
, such that each nonzero term of
$(\mu _i)$
, such that each nonzero term of
![]() $\mu _i$
has degree congruent to
$\mu _i$
has degree congruent to
![]() $c_i - d_i \pmod {e(K'/K)}$
, and set
$c_i - d_i \pmod {e(K'/K)}$
, and set
![]() $\mathscr {C}^0 = \mathscr {C}^0_{u} \cap {\mathbf F}[[u]]^{{\mathbf Z}/f{\mathbf Z}}$
.
$\mathscr {C}^0 = \mathscr {C}^0_{u} \cap {\mathbf F}[[u]]^{{\mathbf Z}/f{\mathbf Z}}$
.
We further define
![]() $\mathscr {C}^1_{u} = \mathscr {C}^1_{u}(\mathfrak {M},\mathfrak {N}) \subset {\mathbf F}((u))^{{\mathbf Z}/f{\mathbf Z}}$
to be the space of f-tuples
$\mathscr {C}^1_{u} = \mathscr {C}^1_{u}(\mathfrak {M},\mathfrak {N}) \subset {\mathbf F}((u))^{{\mathbf Z}/f{\mathbf Z}}$
to be the space of f-tuples
![]() $(h_i)$
, such that each nonzero term of
$(h_i)$
, such that each nonzero term of
![]() $h_i$
has degree congruent to
$h_i$
has degree congruent to
![]() $r_i + c_i - d_i \pmod {e(K'/K)}$
, and set
$r_i + c_i - d_i \pmod {e(K'/K)}$
, and set
![]() $\mathscr {C}^1 = \mathscr {C}^1_{u} \cap {\mathbf F}[[u]]^{{\mathbf Z}/f{\mathbf Z}}$
. There is a map
$\mathscr {C}^1 = \mathscr {C}^1_{u} \cap {\mathbf F}[[u]]^{{\mathbf Z}/f{\mathbf Z}}$
. There is a map
![]() $\partial \colon \mathscr {C}^0_{u} \to \mathscr {C}^1_{u}$
defined by
$\partial \colon \mathscr {C}^0_{u} \to \mathscr {C}^1_{u}$
defined by
Evidently, this restricts to a map
![]() $\partial \colon \mathscr {C}^0 \to \mathscr {C}^1$
.
$\partial \colon \mathscr {C}^0 \to \mathscr {C}^1$
.
Lemma 4.1.8. There is an isomorphism of complexes
in which
![]() $(\mu _i) \in \mathscr {C}^0$
is sent to the map
$(\mu _i) \in \mathscr {C}^0$
is sent to the map
![]() $m_i \mapsto \mu _i n_i$
in
$m_i \mapsto \mu _i n_i$
in
![]() $C^0(\mathfrak {N})$
, and
$C^0(\mathfrak {N})$
, and
![]() $(h_i) \in \mathscr {C}^1$
is sent to the map
$(h_i) \in \mathscr {C}^1$
is sent to the map
![]() $(1\otimes m_{i-1}) \mapsto h_i n_i$
in
$(1\otimes m_{i-1}) \mapsto h_i n_i$
in
![]() $C^1(\mathfrak {N})$
.
$C^1(\mathfrak {N})$
.
Proof. Each element of
![]() $\operatorname {\mathrm {Hom}}_{\mathfrak {S}_{{\mathbf F}}}(\mathfrak {M},\mathfrak {N})$
has the form
$\operatorname {\mathrm {Hom}}_{\mathfrak {S}_{{\mathbf F}}}(\mathfrak {M},\mathfrak {N})$
has the form
![]() $m_i \mapsto \mu _i n_i$
for some
$m_i \mapsto \mu _i n_i$
for some
![]() $f'$
-tuple
$f'$
-tuple
![]() $(\mu _i)_{i \in {\mathbf Z}/f'{\mathbf Z}}$
of elements of
$(\mu _i)_{i \in {\mathbf Z}/f'{\mathbf Z}}$
of elements of
![]() ${\mathbf F}[[u]]$
. The condition that this map is
${\mathbf F}[[u]]$
. The condition that this map is
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
-equivariant is easily seen to be equivalent to the conditions that
$\operatorname {\mathrm {Gal}}(K'/K)$
-equivariant is easily seen to be equivalent to the conditions that
![]() $(\mu _i)$
is periodic with period dividing f, and that each nonzero term of
$(\mu _i)$
is periodic with period dividing f, and that each nonzero term of
![]() $\mu _i$
has degree congruent to
$\mu _i$
has degree congruent to
![]() $c_{i}-d_{i} \pmod {e(K'/K)}$
. (For the former, consider the action of a lift to
$c_{i}-d_{i} \pmod {e(K'/K)}$
. (For the former, consider the action of a lift to
![]() $g \in \operatorname {\mathrm {Gal}}(K'/K)$
satisfying
$g \in \operatorname {\mathrm {Gal}}(K'/K)$
satisfying
![]() $h(g)=1$
of a generator of
$h(g)=1$
of a generator of
![]() $\operatorname {\mathrm {Gal}}(k'/k)$
, and for the latter, consider the action of
$\operatorname {\mathrm {Gal}}(k'/k)$
, and for the latter, consider the action of
![]() $I(K'/K)$
; cf. the proof of [Reference Diamond and SavittDS15, Lemma 1.5].) It follows that the map
$I(K'/K)$
; cf. the proof of [Reference Diamond and SavittDS15, Lemma 1.5].) It follows that the map
![]() $\mathscr {C}^0 \to C^0(\mathfrak {N})$
in the statement of the lemma is an isomorphism. An essentially identical argument shows that the given map
$\mathscr {C}^0 \to C^0(\mathfrak {N})$
in the statement of the lemma is an isomorphism. An essentially identical argument shows that the given map
![]() $\mathscr {C}^1 \to C^1(\mathfrak {N})$
is an isomorphism.
$\mathscr {C}^1 \to C^1(\mathfrak {N})$
is an isomorphism.
To conclude, it suffices to observe that if
![]() $\alpha \in C^0(\mathfrak {N})$
is given by
$\alpha \in C^0(\mathfrak {N})$
is given by
![]() $m_i \mapsto \mu _i n_i$
with
$m_i \mapsto \mu _i n_i$
with
![]() $(\mu _i)_i \in \mathscr {C}^0$
, then
$(\mu _i)_i \in \mathscr {C}^0$
, then
![]() $\delta (\alpha ) \in C^1(\mathfrak {N})$
is the map given by
$\delta (\alpha ) \in C^1(\mathfrak {N})$
is the map given by
which follows by a direct calculation.
It follows from Corollary 3.1.8 that
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \cong \operatorname {\mathrm {coker}} \partial $
. If
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \cong \operatorname {\mathrm {coker}} \partial $
. If
![]() $h \in \mathscr {C}^1$
, we write
$h \in \mathscr {C}^1$
, we write
![]() $\mathfrak {P}(h)$
for the element of
$\mathfrak {P}(h)$
for the element of
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
represented by h under this isomorphism.
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
represented by h under this isomorphism.
Remark 4.1.9. Let
![]() $\mathfrak {M}=\mathfrak {M}(r,a,c)$
and
$\mathfrak {M}=\mathfrak {M}(r,a,c)$
and
![]() $\mathfrak {N}=\mathfrak {M}(s,b,d)$
be rank one Breuil–Kisin modules with descent data as in Lemma
4.1.1
. It follows from the proof of Lemma 3.1.5, and, in particular, the description of the map (3.1.6) found there, that the extension
$\mathfrak {N}=\mathfrak {M}(s,b,d)$
be rank one Breuil–Kisin modules with descent data as in Lemma
4.1.1
. It follows from the proof of Lemma 3.1.5, and, in particular, the description of the map (3.1.6) found there, that the extension
![]() $\mathfrak {P}(h)$
is given by the formulas
$\mathfrak {P}(h)$
is given by the formulas
-
○
 $\mathfrak {P}_i={\mathbf F}[[u]]\cdot m_i + {\mathbf F}[[u]]\cdot n_i$
,
$\mathfrak {P}_i={\mathbf F}[[u]]\cdot m_i + {\mathbf F}[[u]]\cdot n_i$
, -
○
 $\Phi _{\mathfrak {P},i}(1\otimes n_{i-1})=b_{i} u^{s_{i}}n_{i}$
,
$\Phi _{\mathfrak {P},i}(1\otimes n_{i-1})=b_{i} u^{s_{i}}n_{i}$
,
 $\Phi _{\mathfrak {P},i}(1\otimes m_{i-1})=a_{i}u^{r_{i}}m_{i}+h_{i} n_{i}$
.
$\Phi _{\mathfrak {P},i}(1\otimes m_{i-1})=a_{i}u^{r_{i}}m_{i}+h_{i} n_{i}$
. -
○
 $\hat {g}(\sum _i m_i)=\sum _i h(g)^{c_i}m_i$
,
$\hat {g}(\sum _i m_i)=\sum _i h(g)^{c_i}m_i$
,
 $\hat {g}(\sum _i n_i)=\sum _i h(g)^{d_i} n_i$
for all
$\hat {g}(\sum _i n_i)=\sum _i h(g)^{d_i} n_i$
for all
 $g\in \operatorname {\mathrm {Gal}}(K'/K)$
.
$g\in \operatorname {\mathrm {Gal}}(K'/K)$
.
From this description, it is easy to see that the extension
![]() $\mathfrak {P}(h)$
has height at most
$\mathfrak {P}(h)$
has height at most
![]() $1$
if and only if each
$1$
if and only if each
![]() $h_i$
is divisible by
$h_i$
is divisible by
![]() $u^{r_i+s_i-e'}$
whenever
$u^{r_i+s_i-e'}$
whenever
![]() $r_i+s_i-e'$
is nonnegative.
$r_i+s_i-e'$
is nonnegative.
Theorem 4.1.10. The dimension of
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
is given by the formula
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
is given by the formula
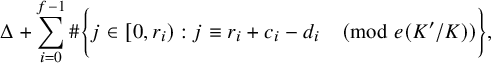 $$\begin{align*}\Delta+\sum_{i=0}^{f-1}\#\biggl\{j\in[0,r_i):j\equiv r_i+c_{i}-d_{i}\quad \pmod{e(K'/K)}\biggr\}, \end{align*}$$
$$\begin{align*}\Delta+\sum_{i=0}^{f-1}\#\biggl\{j\in[0,r_i):j\equiv r_i+c_{i}-d_{i}\quad \pmod{e(K'/K)}\biggr\}, \end{align*}$$
where
![]() $\Delta = \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
is
$\Delta = \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
is
![]() $1$
if there is a nonzero map
$1$
if there is a nonzero map
![]() $\mathfrak {M}\to \mathfrak {N}$
and
$\mathfrak {M}\to \mathfrak {N}$
and
![]() $0$
otherwise, while the subspace consisting of extensions of height at most
$0$
otherwise, while the subspace consisting of extensions of height at most
![]() $1$
has dimension
$1$
has dimension
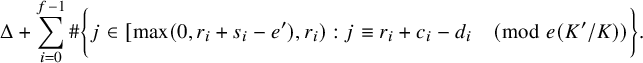 $$\begin{align*}\Delta+\sum_{i=0}^{f-1}\#\biggl\{j\in[\max(0,r_i+s_i-e'),r_i):j\equiv r_i+c_{i}-d_{i}\quad \pmod{e(K'/K)}\biggr\} .\end{align*}$$
$$\begin{align*}\Delta+\sum_{i=0}^{f-1}\#\biggl\{j\in[\max(0,r_i+s_i-e'),r_i):j\equiv r_i+c_{i}-d_{i}\quad \pmod{e(K'/K)}\biggr\} .\end{align*}$$
Proof. When
![]() $p> 2$
, this result (for extensions of height at most
$p> 2$
, this result (for extensions of height at most
![]() $1$
) can be obtained by translating [Reference Diamond and SavittDS15, Theorem 1.11] from Breuil modules to Breuil–Kisin modules. We argue in the same spirit as [Reference Diamond and SavittDS15] using the generalities of Section 3.1.
$1$
) can be obtained by translating [Reference Diamond and SavittDS15, Theorem 1.11] from Breuil modules to Breuil–Kisin modules. We argue in the same spirit as [Reference Diamond and SavittDS15] using the generalities of Section 3.1.
Choose N as in Lemma 3.1.10(2). For brevity, we write
![]() $C^{\bullet }$
in lieu of
$C^{\bullet }$
in lieu of
![]() $C^{\bullet }(\mathfrak {N})$
. We now use the description of
$C^{\bullet }(\mathfrak {N})$
. We now use the description of
![]() $C^{\bullet }$
provided by Lemma 4.1.8. As we have noted,
$C^{\bullet }$
provided by Lemma 4.1.8. As we have noted,
![]() $C^0$
consists of the maps
$C^0$
consists of the maps
![]() $m_i \mapsto \mu _i n_i$
with
$m_i \mapsto \mu _i n_i$
with
![]() $(\mu _i) \in \mathscr {C}^0$
. Since
$(\mu _i) \in \mathscr {C}^0$
. Since
![]() $(\varphi ^{*}_{\mathfrak {M}})^{-1}(v^N C^1)$
contains precisely the maps
$(\varphi ^{*}_{\mathfrak {M}})^{-1}(v^N C^1)$
contains precisely the maps
![]() $m_i \mapsto \mu _i n_i$
in
$m_i \mapsto \mu _i n_i$
in
![]() $C^0$
, such that
$C^0$
, such that
![]() $v^{N} \mid u^{r_i} \mu _i$
, we compute that
$v^{N} \mid u^{r_i} \mu _i$
, we compute that
![]() $\dim _{{\mathbf F}} C^0/\bigl ((\varphi ^{*}_{\mathfrak {M}})^{-1}(v^N C^1)\bigr )$
is the quantity
$\dim _{{\mathbf F}} C^0/\bigl ((\varphi ^{*}_{\mathfrak {M}})^{-1}(v^N C^1)\bigr )$
is the quantity
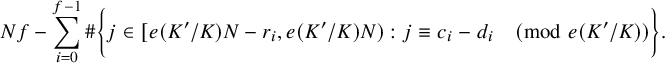 $$ \begin{align*}Nf - \sum_{i=0}^{f-1} \#\biggl\{ j \in [e(K'/K) N-r_i, e(K'/K) N) : j \equiv c_i-d_i\quad \pmod{e(K'/K)}\biggr\}.\end{align*} $$
$$ \begin{align*}Nf - \sum_{i=0}^{f-1} \#\biggl\{ j \in [e(K'/K) N-r_i, e(K'/K) N) : j \equiv c_i-d_i\quad \pmod{e(K'/K)}\biggr\}.\end{align*} $$
We have
![]() $\dim _{{\mathbf F}} C^1/v^NC^1 = Nf$
, so our formula for the dimension of
$\dim _{{\mathbf F}} C^1/v^NC^1 = Nf$
, so our formula for the dimension of
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
now follows from Lemma 3.1.10.
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
now follows from Lemma 3.1.10.
Remark 4.1.11. One can show exactly as in [Reference Diamond and SavittDS15] that each element of
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
can be written uniquely in the form
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
can be written uniquely in the form
![]() $\mathfrak {P}(h)$
for
$\mathfrak {P}(h)$
for
![]() $h \in \mathscr {C}^1$
with
$h \in \mathscr {C}^1$
with
![]() $\deg (h_i) < r_i$
, except that when there exists a nonzero morphism
$\deg (h_i) < r_i$
, except that when there exists a nonzero morphism
![]() $\mathfrak {M}\to \mathfrak {N}$
, the polynomials
$\mathfrak {M}\to \mathfrak {N}$
, the polynomials
![]() $h_i$
for
$h_i$
for
![]() $f \mid i$
may also have a term of degree
$f \mid i$
may also have a term of degree
![]() $\alpha _0(\mathfrak {M})-\alpha _0(\mathfrak {N})+r_0$
in common. Since we will not need this fact, we omit the proof.
$\alpha _0(\mathfrak {M})-\alpha _0(\mathfrak {N})+r_0$
in common. Since we will not need this fact, we omit the proof.
4.2. Extensions of profile J
We now begin the work of showing, for each nonscalar tame type
![]() $\tau $
, that
$\tau $
, that
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
has
${\mathcal C}^{\tau ,\operatorname {BT},1}$
has
![]() $2^f$
irreducible components, indexed by the subsets J of
$2^f$
irreducible components, indexed by the subsets J of
![]() $\{0,1,\dots ,f-1\}$
. We will also describe the irreducible components of
$\{0,1,\dots ,f-1\}$
. We will also describe the irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
. The proof of this hinges on examining the extensions considered in Theorem 4.1.10, and then applying the results of Section 3.3. We will show that most of these families of extensions have positive codimension in
${\mathcal Z}^{\tau ,1}$
. The proof of this hinges on examining the extensions considered in Theorem 4.1.10, and then applying the results of Section 3.3. We will show that most of these families of extensions have positive codimension in
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and are thus negligible from the point of view of determining irreducible components. By a base change argument, we will also be able to show that we can neglect the irreducible Breuil–Kisin modules. The rest of Section 3 is devoted to establishing the necessary bounds on the dimension of the various families of extensions, and to studying the map from
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and are thus negligible from the point of view of determining irreducible components. By a base change argument, we will also be able to show that we can neglect the irreducible Breuil–Kisin modules. The rest of Section 3 is devoted to establishing the necessary bounds on the dimension of the various families of extensions, and to studying the map from
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
to
${\mathcal C}^{\tau ,\operatorname {BT},1}$
to
![]() ${\mathcal R}^{\mathrm {dd},1}$
.
${\mathcal R}^{\mathrm {dd},1}$
.
We now introduce notation that we will use for the remainder of the paper. We fix a tame inertial type
![]() $\tau =\eta \oplus \eta '$
with coefficients in
$\tau =\eta \oplus \eta '$
with coefficients in
![]() $\overline {{\mathbf Q}}_p$
. We allow the case of scalar types (that is, the case
$\overline {{\mathbf Q}}_p$
. We allow the case of scalar types (that is, the case
![]() $\eta =\eta '$
). Assume that the subfield
$\eta =\eta '$
). Assume that the subfield
![]() ${\mathbf F}$
of
${\mathbf F}$
of
![]() $\overline {{\mathbf F}}_p$
is large enough so that the reductions modulo
$\overline {{\mathbf F}}_p$
is large enough so that the reductions modulo
![]() $\mathfrak {m}_{{\mathbf Z}_p}$
of
$\mathfrak {m}_{{\mathbf Z}_p}$
of
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
(which, by abuse of notation, we continue to denote
$\eta '$
(which, by abuse of notation, we continue to denote
![]() $\eta ,\eta '$
) have image in
$\eta ,\eta '$
) have image in
![]() ${\mathbf F}$
. We also fix a uniformiser
${\mathbf F}$
. We also fix a uniformiser
![]() $\pi $
of K.
$\pi $
of K.
Remark 4.2.1. We stress that when we write
![]() $\tau =\eta \oplus \eta '$
, we are implicitly ordering
$\tau =\eta \oplus \eta '$
, we are implicitly ordering
![]() $\eta ,\eta '$
. Much of the notation in this section depends on distinguishing
$\eta ,\eta '$
. Much of the notation in this section depends on distinguishing
![]() $\eta ,\eta '$
, as do some of the constructions later in the paper (in particular, those using the map to the Dieudonné stack of Section 2.4).
$\eta ,\eta '$
, as do some of the constructions later in the paper (in particular, those using the map to the Dieudonné stack of Section 2.4).
As in Section 2.4, we make the following ‘standard choice’ for the extension
![]() $K'/K$
: if
$K'/K$
: if
![]() $\tau $
is a tame principal series type, we take
$\tau $
is a tame principal series type, we take
![]() $K'=K(\pi ^{1/(p^f-1)})$
, while if
$K'=K(\pi ^{1/(p^f-1)})$
, while if
![]() $\tau $
is a tame cuspidal type, we let L be an unramified quadratic extension of K, and set
$\tau $
is a tame cuspidal type, we let L be an unramified quadratic extension of K, and set
![]() $K'=L(\pi ^{1/(p^{2f}-1)})$
. In either case,
$K'=L(\pi ^{1/(p^{2f}-1)})$
. In either case,
![]() $K'/K$
is a Galois extension and
$K'/K$
is a Galois extension and
![]() $\eta , \eta '$
both factor through
$\eta , \eta '$
both factor through
![]() $I(K'/K)$
. In the principal series case, we have
$I(K'/K)$
. In the principal series case, we have
![]() $e'=(p^f-1)e$
,
$e'=(p^f-1)e$
,
![]() $f'=f$
, and in the cuspidal case, we have
$f'=f$
, and in the cuspidal case, we have
![]() $e'=(p^{2f}-1)e$
,
$e'=(p^{2f}-1)e$
,
![]() $f'=2f$
. Either way, we have
$f'=2f$
. Either way, we have
![]() $e(K'/K) = p^{f'}-1$
.
$e(K'/K) = p^{f'}-1$
.
In either case, it follows from Lemma 4.1.1 that a Breuil–Kisin module of rank one with descent data from
![]() $K'$
to K is described by the data of the quantities
$K'$
to K is described by the data of the quantities
![]() $r_i,a_i,c_i$
for
$r_i,a_i,c_i$
for
![]() $0\le i\le f-1$
, and similarly, from Lemma 4.1.8, that extensions between two such Breuil–Kisin modules are described by the
$0\le i\le f-1$
, and similarly, from Lemma 4.1.8, that extensions between two such Breuil–Kisin modules are described by the
![]() $h_i$
for
$h_i$
for
![]() $0\le i\le f-1$
. This common description will enable us to treat the principal series and cuspidal cases largely in parallel.
$0\le i\le f-1$
. This common description will enable us to treat the principal series and cuspidal cases largely in parallel.
The character
![]() $h |_{I_K}$
of Section 4.1 is identified via the Artin map
$h |_{I_K}$
of Section 4.1 is identified via the Artin map
![]() ${\mathcal O}_L^{\times } \to I_L^{\mathrm {ab}} = I_K^{\mathrm {ab}} $
with the reduction map
${\mathcal O}_L^{\times } \to I_L^{\mathrm {ab}} = I_K^{\mathrm {ab}} $
with the reduction map
![]() ${\mathcal O}_L^{\times } \to (k')^{\times }$
. Thus, for each
${\mathcal O}_L^{\times } \to (k')^{\times }$
. Thus, for each
![]() $\sigma \in \operatorname {\mathrm {Hom}}(k',\overline {{\mathbf F}}_p)$
, the map
$\sigma \in \operatorname {\mathrm {Hom}}(k',\overline {{\mathbf F}}_p)$
, the map
![]() $\sigma \circ h|_{I_L}$
is the fundamental character
$\sigma \circ h|_{I_L}$
is the fundamental character
![]() $\omega _{\sigma }$
defined in Section 1.3. Define
$\omega _{\sigma }$
defined in Section 1.3. Define
![]() $k_i,k^{\prime }_i\in {\mathbf Z}/(p^{f'}-1){\mathbf Z}$
for all i by the formulas
$k_i,k^{\prime }_i\in {\mathbf Z}/(p^{f'}-1){\mathbf Z}$
for all i by the formulas
![]() $\eta =\sigma _i\circ h^{k_i}|_{I(K'/K)}$
and
$\eta =\sigma _i\circ h^{k_i}|_{I(K'/K)}$
and
![]() $\eta '=\sigma _i\circ h^{k^{\prime }_i}|_{I(K'/K)}$
. In particular, we have
$\eta '=\sigma _i\circ h^{k^{\prime }_i}|_{I(K'/K)}$
. In particular, we have
![]() $k_i=p^ik_0$
,
$k_i=p^ik_0$
,
![]() $k^{\prime }_i=p^ik^{\prime }_0$
for all i.
$k^{\prime }_i=p^ik^{\prime }_0$
for all i.
Definition 4.2.2. Let
![]() $\mathfrak {M} = \mathfrak {M}(r,a,c)$
and
$\mathfrak {M} = \mathfrak {M}(r,a,c)$
and
![]() $\mathfrak {N}=\mathfrak {M}(s,b,d)$
be Breuil–Kisin modules of rank one with descent data. We say that the pair
$\mathfrak {N}=\mathfrak {M}(s,b,d)$
be Breuil–Kisin modules of rank one with descent data. We say that the pair
![]() $(\mathfrak {M},\mathfrak {N})$
has type
$(\mathfrak {M},\mathfrak {N})$
has type
![]() $\tau $
provided that for all i:
$\tau $
provided that for all i:
-
○ the multisets
 $\{c_i,d_i\}$
and
$\{c_i,d_i\}$
and
 $\{k_i,k^{\prime }_i\}$
are equal, and
$\{k_i,k^{\prime }_i\}$
are equal, and -
○
 $r_i + s_i = e'$
.
$r_i + s_i = e'$
.
Lemma 4.2.3. The following are equivalent.
-
1. The pair
 $(\mathfrak {M},\mathfrak {N})$
has type
$(\mathfrak {M},\mathfrak {N})$
has type
 $\tau $
.
$\tau $
. -
2. Some element of
 $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
of height at most
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
of height at most
 $1$
satisfies the strong determinant condition and is of type
$1$
satisfies the strong determinant condition and is of type
 $\tau $
.
$\tau $
. -
3. Every element of
 $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
has height at most
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
has height at most
 $1$
, satisfies the strong determinant condition and is of type
$1$
, satisfies the strong determinant condition and is of type
 $\tau $
.
$\tau $
.
(Accordingly, we will sometimes refer to the condition that
![]() $r_i+s_i=e'$
for all i as the determinant condition.)
$r_i+s_i=e'$
for all i as the determinant condition.)
Proof. Suppose, first, that the pair
![]() $(\mathfrak {M},\mathfrak {N})$
has type
$(\mathfrak {M},\mathfrak {N})$
has type
![]() $\tau $
. The last sentence of Remark 4.1.9 shows that every element of
$\tau $
. The last sentence of Remark 4.1.9 shows that every element of
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
has height at most
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
has height at most
![]() $1$
. Let
$1$
. Let
![]() $\mathfrak {P}$
be such an element. The condition on the multisets
$\mathfrak {P}$
be such an element. The condition on the multisets
![]() $\{c_i,d_i\}$
guarantees that
$\{c_i,d_i\}$
guarantees that
![]() $\mathfrak {P}$
has type
$\mathfrak {P}$
has type
![]() $\tau $
(an unmixed type in the sense of [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Definition 3.3.2]). By [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Proposition 4.2.12], we see that
$\tau $
(an unmixed type in the sense of [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Definition 3.3.2]). By [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Proposition 4.2.12], we see that
![]() $\dim _{{\mathbf F}} (\operatorname {\mathrm {im}}_{\mathfrak {P},i}/E(u)\mathfrak {P}_i)_{\xi }$
is independent of the character
$\dim _{{\mathbf F}} (\operatorname {\mathrm {im}}_{\mathfrak {P},i}/E(u)\mathfrak {P}_i)_{\xi }$
is independent of the character
![]() $\xi : I(K'/K) \to {\mathbf F}^{\times }$
. From the condition that
$\xi : I(K'/K) \to {\mathbf F}^{\times }$
. From the condition that
![]() $r_i+s_i=e'$
, we know that the sum over all
$r_i+s_i=e'$
, we know that the sum over all
![]() $\xi $
of these dimensions is equal to
$\xi $
of these dimensions is equal to
![]() $e'$
; since they are all equal, each is equal to e, and [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma 4.2.11] tells us that
$e'$
; since they are all equal, each is equal to e, and [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma 4.2.11] tells us that
![]() $\mathfrak {P}$
satisfies the strong determinant condition. This proves that (1) implies (3).
$\mathfrak {P}$
satisfies the strong determinant condition. This proves that (1) implies (3).
Certainly (3) implies (2), so it remains to check that (2) implies (1). Suppose that
![]() $\mathfrak {P} \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
has height at most
$\mathfrak {P} \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
has height at most
![]() $1$
, satisfies the strong determinant condition and has type
$1$
, satisfies the strong determinant condition and has type
![]() $\tau $
. The condition that
$\tau $
. The condition that
![]() $\{c_i,d_i\}=\{k_i,k^{\prime }_i\}$
follows from
$\{c_i,d_i\}=\{k_i,k^{\prime }_i\}$
follows from
![]() $\mathfrak {P}$
having type
$\mathfrak {P}$
having type
![]() $\tau $
, and the condition that
$\tau $
, and the condition that
![]() $r_i+s_i=e'$
follows from the last part of [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma 4.2.11].
$r_i+s_i=e'$
follows from the last part of [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma 4.2.11].
Definition 4.2.4. If
![]() $(\mathfrak {M},\mathfrak {N})$
is a pair of type
$(\mathfrak {M},\mathfrak {N})$
is a pair of type
![]() $\tau $
(respectively,
$\tau $
(respectively,
![]() $\mathfrak {P}$
is an extension of type
$\mathfrak {P}$
is an extension of type
![]() $\tau $
), we define the profile of
$\tau $
), we define the profile of
![]() $(\mathfrak {M},\mathfrak {N})$
(respectively, of
$(\mathfrak {M},\mathfrak {N})$
(respectively, of
![]() $\mathfrak {P}$
) to be the subset
$\mathfrak {P}$
) to be the subset
![]() $J := \{ i \, | \, c_i = k_i\} \subseteq {\mathbf Z}/f'{\mathbf Z}$
, unless
$J := \{ i \, | \, c_i = k_i\} \subseteq {\mathbf Z}/f'{\mathbf Z}$
, unless
![]() $\tau $
is scalar, in which case, we define the profile to be the subset
$\tau $
is scalar, in which case, we define the profile to be the subset
![]() $\varnothing $
. (Equivalently, J is in all cases the complement in
$\varnothing $
. (Equivalently, J is in all cases the complement in
![]() ${\mathbf Z}/f'{\mathbf Z}$
of the set
${\mathbf Z}/f'{\mathbf Z}$
of the set
![]() $\{i \, | \, c_i = k^{\prime }_i\}$
.)
$\{i \, | \, c_i = k^{\prime }_i\}$
.)
Observe that in the cuspidal case, the equality
![]() $c_i = c_{i+f}$
means that
$c_i = c_{i+f}$
means that
![]() $i \in J$
if and only if
$i \in J$
if and only if
![]() $i+f \not \in J$
, so that the set J is determined by its intersection with any f consecutive integers modulo
$i+f \not \in J$
, so that the set J is determined by its intersection with any f consecutive integers modulo
![]() $f' = 2f$
.
$f' = 2f$
.
In the cuspidal case, we will say that a subset
![]() $J \subseteq {\mathbf Z}/f'{\mathbf Z}$
is a profile if it satisfies
$J \subseteq {\mathbf Z}/f'{\mathbf Z}$
is a profile if it satisfies
![]() $i \in J$
if and only if
$i \in J$
if and only if
![]() $i+f\not \in J$
; in the principal series case, we may refer to any subset
$i+f\not \in J$
; in the principal series case, we may refer to any subset
![]() $J \subseteq {\mathbf Z}/f'{\mathbf Z}$
as a profile.
$J \subseteq {\mathbf Z}/f'{\mathbf Z}$
as a profile.
We define the refined profile of the pair
![]() $(\mathfrak {M},\mathfrak {N})$
(respectively, of
$(\mathfrak {M},\mathfrak {N})$
(respectively, of
![]() $\mathfrak {P}$
) to consist of its profile J, together with the f-tuple of invariants
$\mathfrak {P}$
) to consist of its profile J, together with the f-tuple of invariants
![]() $r:= (r_i)_{i = 0}^{f-1}$
. If
$r:= (r_i)_{i = 0}^{f-1}$
. If
![]() $(J,r)$
is a refined profile that arises from some pair (or extension) of type
$(J,r)$
is a refined profile that arises from some pair (or extension) of type
![]() $\tau $
, then we refer to
$\tau $
, then we refer to
![]() $(J,r)$
as a refined profile for
$(J,r)$
as a refined profile for
![]() $\tau $
.
$\tau $
.
We say the pair
![]() $(i-1,i)$
is a transition for J if
$(i-1,i)$
is a transition for J if
![]() $i-1 \in J$
,
$i-1 \in J$
,
![]() $i \not \in J$
or vice versa. (In the first case, we sometimes say that the pair
$i \not \in J$
or vice versa. (In the first case, we sometimes say that the pair
![]() $(i-1,i)$
is a transition out of J, and in the latter case, a transition into J.) Implicit in many of our arguments below is the observation that, in the cuspidal case,
$(i-1,i)$
is a transition out of J, and in the latter case, a transition into J.) Implicit in many of our arguments below is the observation that, in the cuspidal case,
![]() $(i-1,i)$
is a transition if and only if
$(i-1,i)$
is a transition if and only if
![]() $(i+f-1,i+f)$
is a transition.
$(i+f-1,i+f)$
is a transition.
4.2.5. An explicit description of refined profiles
The refined profiles for
![]() $\tau $
admit an explicit description. If
$\tau $
admit an explicit description. If
![]() $\mathfrak {P}$
is of profile J, for some fixed
$\mathfrak {P}$
is of profile J, for some fixed
![]() $J \subseteq {\mathbf Z}/f'{\mathbf Z}$
, then, since
$J \subseteq {\mathbf Z}/f'{\mathbf Z}$
, then, since
![]() $c_i$
,
$c_i$
,
![]() $d_i$
are fixed, we see that the
$d_i$
are fixed, we see that the
![]() $r_i$
and
$r_i$
and
![]() $s_i$
appearing in
$s_i$
appearing in
![]() $\mathfrak {P}$
are determined modulo
$\mathfrak {P}$
are determined modulo
![]() $e(K'/K)=p^{f'}-1$
. Furthermore, we see that
$e(K'/K)=p^{f'}-1$
. Furthermore, we see that
![]() $r_i+s_i\equiv 0\pmod {p^{f'}-1}$
, so that these values are consistent with the determinant condition; conversely, if we make any choice of the
$r_i+s_i\equiv 0\pmod {p^{f'}-1}$
, so that these values are consistent with the determinant condition; conversely, if we make any choice of the
![]() $r_i$
in the given residue class modulo
$r_i$
in the given residue class modulo
![]() $(p^{f'}-1)$
, then the
$(p^{f'}-1)$
, then the
![]() $s_i$
are determined by the determinant condition, and the imposed values are consistent with the descent data. There are, of course, only finitely many choices for the
$s_i$
are determined by the determinant condition, and the imposed values are consistent with the descent data. There are, of course, only finitely many choices for the
![]() $r_i$
, and so there are only finitely many possible refined profiles for
$r_i$
, and so there are only finitely many possible refined profiles for
![]() $\tau $
.
$\tau $
.
To make this precise, recall that we have the congruence
We will write
![]() $[n]$
for the least nonnegative residue class of n modulo
$[n]$
for the least nonnegative residue class of n modulo
![]() $e(K'/K) = p^{f'}-1$
.
$e(K'/K) = p^{f'}-1$
.
If both
![]() $i-1$
and i lie in J, then we have
$i-1$
and i lie in J, then we have
![]() $c_{i-1} = k_{i-1}$
and
$c_{i-1} = k_{i-1}$
and
![]() $c_i = k_i$
. The first of these implies that
$c_i = k_i$
. The first of these implies that
![]() $pc_{i-1} = k_i$
, and therefore
$pc_{i-1} = k_i$
, and therefore
![]() $r_i \equiv 0 \pmod {p^{f'}-1}$
. The same conclusion holds if neither
$r_i \equiv 0 \pmod {p^{f'}-1}$
. The same conclusion holds if neither
![]() $i-1$
and i lie in J. Therefore, if
$i-1$
and i lie in J. Therefore, if
![]() $(i-1,i)$
is not a transition, we may write
$(i-1,i)$
is not a transition, we may write
with
![]() $0 \le y_i \le e$
.
$0 \le y_i \le e$
.
Now suppose instead that
![]() $(i-1,i)$
is a transition (in particular, the type
$(i-1,i)$
is a transition (in particular, the type
![]() $\tau $
is not scalar). This time,
$\tau $
is not scalar). This time,
![]() $pc_{i-1} = d_i$
(instead of
$pc_{i-1} = d_i$
(instead of
![]() $pc_{i-1} = c_i$
), so that
$pc_{i-1} = c_i$
), so that
![]() $r_i \equiv d_i - c_i \pmod {p^{f'}-1}$
. In this case, we write
$r_i \equiv d_i - c_i \pmod {p^{f'}-1}$
. In this case, we write
with
![]() $1 \le y_i \le e$
.
$1 \le y_i \le e$
.
Conversely, for fixed profile J, one checks that each choice of integers
![]() $y_i$
in the ranges described above gives rise to a refined profile for
$y_i$
in the ranges described above gives rise to a refined profile for
![]() $\tau $
.
$\tau $
.
If
![]() $(i-1,i)$
is not a transition and
$(i-1,i)$
is not a transition and
![]() $(h_i) \in \mathscr {C}^1_{u}(\mathfrak {M},\mathfrak {N})$
, then nonzero terms of
$(h_i) \in \mathscr {C}^1_{u}(\mathfrak {M},\mathfrak {N})$
, then nonzero terms of
![]() $h_i$
have degree congruent to
$h_i$
have degree congruent to
![]() $r_i + c_i - d_i \equiv c_i - d_i \pmod {p^{f'}-1}$
. If instead
$r_i + c_i - d_i \equiv c_i - d_i \pmod {p^{f'}-1}$
. If instead
![]() $(i-1,i)$
is a transition and
$(i-1,i)$
is a transition and
![]() $(h_i) \in \mathscr {C}^1_{u}(\mathfrak {M},\mathfrak {N})$
, then nonzero terms of
$(h_i) \in \mathscr {C}^1_{u}(\mathfrak {M},\mathfrak {N})$
, then nonzero terms of
![]() $h_i$
have degree congruent to
$h_i$
have degree congruent to
![]() $r_i + c_i - d_i \equiv 0 \pmod {p^{f'}-1}$
. In either case, comparing with the preceding paragraphs, we see that
$r_i + c_i - d_i \equiv 0 \pmod {p^{f'}-1}$
. In either case, comparing with the preceding paragraphs, we see that
![]() $\#\{ j \in [0,r_i) : j \equiv r_i + c_i - d_i \pmod {e(K'/K)}\}$
is exactly
$\#\{ j \in [0,r_i) : j \equiv r_i + c_i - d_i \pmod {e(K'/K)}\}$
is exactly
![]() $y_i$
.
$y_i$
.
By Theorem 4.1.10, we conclude that for a fixed choice of the
![]() $r_i$
, the dimension of the corresponding
$r_i$
, the dimension of the corresponding
![]() $\operatorname {\mathrm {Ext}}^1$
is
$\operatorname {\mathrm {Ext}}^1$
is
![]() $\Delta + \sum _{i=0}^{f-1} y_i$
(with
$\Delta + \sum _{i=0}^{f-1} y_i$
(with
![]() $\Delta $
, as in the statement of loc. cit.). We say that the refined profile
$\Delta $
, as in the statement of loc. cit.). We say that the refined profile
![]() $\bigl (J, (r_i)_{i =0}^{f-1}\bigr )$
is maximal if the
$\bigl (J, (r_i)_{i =0}^{f-1}\bigr )$
is maximal if the
![]() $r_i$
are chosen to be maximal subject to the above conditions, or equivalently, if the
$r_i$
are chosen to be maximal subject to the above conditions, or equivalently, if the
![]() $y_i$
are all chosen to be e; for each profile J, there is a unique maximal refined profile
$y_i$
are all chosen to be e; for each profile J, there is a unique maximal refined profile
![]() $(J,r)$
.
$(J,r)$
.
4.2.6. The sets
 ${\mathcal P}_{\tau }$
${\mathcal P}_{\tau }$
To each tame type
![]() $\tau $
, we now associate a set
$\tau $
, we now associate a set
![]() ${\mathcal P}_{\tau }$
, which will be a subset of the set of profiles in
${\mathcal P}_{\tau }$
, which will be a subset of the set of profiles in
![]() ${\mathbf Z}/f'{\mathbf Z}$
. (In Appendix A, we will recall, following [Reference DiamondDia07], that the set
${\mathbf Z}/f'{\mathbf Z}$
. (In Appendix A, we will recall, following [Reference DiamondDia07], that the set
![]() ${\mathcal P}_{\tau }$
parameterises the Jordan–Hölder factors of the reduction mod p of
${\mathcal P}_{\tau }$
parameterises the Jordan–Hölder factors of the reduction mod p of
![]() $\sigma (\tau )$
.)
$\sigma (\tau )$
.)
We write
![]() $\eta (\eta ')^{-1} = \prod _{j=0}^{f'-1} (\sigma _j \circ h)^{\gamma _j}$
for uniquely defined integers
$\eta (\eta ')^{-1} = \prod _{j=0}^{f'-1} (\sigma _j \circ h)^{\gamma _j}$
for uniquely defined integers
![]() $0 \le \gamma _j \le p-1$
not all equal to
$0 \le \gamma _j \le p-1$
not all equal to
![]() $p-1$
, so that
$p-1$
, so that
 $$ \begin{align} [k_i - k^{\prime}_i] = \sum_{j=0}^{f'-1} p^{j} \gamma_{i-j} \end{align} $$
$$ \begin{align} [k_i - k^{\prime}_i] = \sum_{j=0}^{f'-1} p^{j} \gamma_{i-j} \end{align} $$
with subscripts taken modulo
![]() $f'$
.
$f'$
.
If
![]() $\tau $
is scalar, then we set
$\tau $
is scalar, then we set
![]() ${\mathcal P}_{\tau }=\{\varnothing \}$
. Otherwise, we let
${\mathcal P}_{\tau }=\{\varnothing \}$
. Otherwise, we let
![]() ${\mathcal P}_{\tau }$
be the collection of profiles
${\mathcal P}_{\tau }$
be the collection of profiles
![]() $J \subseteq {\mathbf Z}/f'{\mathbf Z}$
satisfying the conditions:
$J \subseteq {\mathbf Z}/f'{\mathbf Z}$
satisfying the conditions:
-
○ if
 $i-1\in J$
and
$i-1\in J$
and
 $i\notin J$
, then
$i\notin J$
, then
 $\gamma _{i}\ne p-1$
, and
$\gamma _{i}\ne p-1$
, and -
○ if
 $i-1\notin J$
and
$i-1\notin J$
and
 $i\in J$
, then
$i\in J$
, then
 $\gamma _{i}\ne 0$
.
$\gamma _{i}\ne 0$
.
When
![]() $\tau $
is a cuspidal type, so that
$\tau $
is a cuspidal type, so that
![]() $\eta ' = \eta ^q$
, the integers
$\eta ' = \eta ^q$
, the integers
![]() $\gamma _j$
satisfy
$\gamma _j$
satisfy
![]() $\gamma _{i+f} = p-1-\gamma _i$
for all i; thus the condition that if
$\gamma _{i+f} = p-1-\gamma _i$
for all i; thus the condition that if
![]() $(i-1,i)$
is a transition out of J, then
$(i-1,i)$
is a transition out of J, then
![]() $\gamma _i \neq p-1$
translates exactly into the condition that if
$\gamma _i \neq p-1$
translates exactly into the condition that if
![]() $(i+f-1,i+f)$
is a transition into J, then
$(i+f-1,i+f)$
is a transition into J, then
![]() $\gamma _{i+f} \neq 0$
.
$\gamma _{i+f} \neq 0$
.
4.2.7. Moduli stacks of extensions
We now apply the constructions of stacks and topological spaces of Definitions 3.3.11 and 3.3.14 to the families of extensions considered in Section 4.2.
Definition 4.2.8. If
![]() $(J,r)$
is a refined profile for
$(J,r)$
is a refined profile for
![]() $\tau $
, then we let
$\tau $
, then we let
![]() $\mathfrak {M}(J,r) := \mathfrak {M}(r,1,c)$
and let
$\mathfrak {M}(J,r) := \mathfrak {M}(r,1,c)$
and let
![]() $\mathfrak {N}(J,r) := \mathfrak {M}(s,1,d),$
where c, d and s are determined from J, r and
$\mathfrak {N}(J,r) := \mathfrak {M}(s,1,d),$
where c, d and s are determined from J, r and
![]() $\tau $
according to the discussion of (4.2.5); for instance, we take
$\tau $
according to the discussion of (4.2.5); for instance, we take
![]() $c_i = k_i$
when
$c_i = k_i$
when
![]() $i \in J$
and
$i \in J$
and
![]() $c_i = k^{\prime }_i$
when
$c_i = k^{\prime }_i$
when
![]() $i \not \in J$
. For the unique maximal profile
$i \not \in J$
. For the unique maximal profile
![]() $(J,r)$
refining J, we write simply
$(J,r)$
refining J, we write simply
![]() $\mathfrak {M}(J)$
and
$\mathfrak {M}(J)$
and
![]() $\mathfrak {N}(J)$
.
$\mathfrak {N}(J)$
.
Definition 4.2.9. If
![]() $(J,r)$
is a refined profile for
$(J,r)$
is a refined profile for
![]() $\tau $
, then following Definition 3.3.11, we may construct the reduced closed substack
$\tau $
, then following Definition 3.3.11, we may construct the reduced closed substack
![]() $\overline {{\mathcal C}}\bigl (\mathfrak {M}(J,r),\mathfrak {N}(J,r)\bigr )$
of
$\overline {{\mathcal C}}\bigl (\mathfrak {M}(J,r),\mathfrak {N}(J,r)\bigr )$
of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, as well as the reduced closed substack
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, as well as the reduced closed substack
![]() $\overline {{\mathcal Z}}\bigl (\mathfrak {M}(J,r), \mathfrak {N}(J,r)\bigr )$
of
$\overline {{\mathcal Z}}\bigl (\mathfrak {M}(J,r), \mathfrak {N}(J,r)\bigr )$
of
![]() ${\mathcal Z}^{\tau ,1}.$
We introduce the notation
${\mathcal Z}^{\tau ,1}.$
We introduce the notation
![]() $\overline {{\mathcal C}}(J,r)$
and
$\overline {{\mathcal C}}(J,r)$
and
![]() $\overline {{\mathcal Z}}(J,r)$
for these two stacks, and note that (by definition)
$\overline {{\mathcal Z}}(J,r)$
for these two stacks, and note that (by definition)
![]() $\overline {{\mathcal Z}}(J,r)$
is the scheme-theoretic image of
$\overline {{\mathcal Z}}(J,r)$
is the scheme-theoretic image of
![]() $\overline {{\mathcal C}}(J,r)$
under the morphism
$\overline {{\mathcal C}}(J,r)$
under the morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal Z}^{\tau ,1}$
.
${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal Z}^{\tau ,1}$
.
Remark 4.2.10. As noted in the final sentence of Definition 3.3.11, Lemma 3.3.10 shows that
![]() $\overline {{\mathcal C}}(J,r)$
contains all extensions of refined profile
$\overline {{\mathcal C}}(J,r)$
contains all extensions of refined profile
![]() $(J,r)$
over extensions of
$(J,r)$
over extensions of
![]() ${\mathbf F}$
, and not only those corresponding to a maximal ideal of
${\mathbf F}$
, and not only those corresponding to a maximal ideal of
![]() $A^{{\operatorname {dist}}}$
.
$A^{{\operatorname {dist}}}$
.
Theorem 4.2.11. If
![]() $(J,r)$
is any refined profile for
$(J,r)$
is any refined profile for
![]() $\tau $
, then
$\tau $
, then
![]() $\dim \overline {{\mathcal C}}(J,r) \leq [K:{\mathbf Q}_p],$
with equality if and only if
$\dim \overline {{\mathcal C}}(J,r) \leq [K:{\mathbf Q}_p],$
with equality if and only if
![]() $(J,r)$
is maximal.
$(J,r)$
is maximal.
Proof. This follows from Corollary 3.3.32, Theorem 4.1.10 and Proposition 3.1.15. (See also the discussion following Definition 4.2.4, and note that over
![]() $\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
, we have
$\operatorname {\mathrm {Spec}} {A^{\operatorname {dist}}}$
, we have
![]() $\Delta =0$
by definition.)
$\Delta =0$
by definition.)
Definition 4.2.12. If
![]() $J \subseteq {\mathbf Z}/f'{\mathbf Z}$
is a profile, and if r is chosen so that
$J \subseteq {\mathbf Z}/f'{\mathbf Z}$
is a profile, and if r is chosen so that
![]() $(J,r)$
is a maximal refined profile for
$(J,r)$
is a maximal refined profile for
![]() $\tau $
, then we write
$\tau $
, then we write
![]() $\overline {{\mathcal C}}(J)$
to denote the closed substack
$\overline {{\mathcal C}}(J)$
to denote the closed substack
![]() $\overline {{\mathcal C}}(J,r)$
of
$\overline {{\mathcal C}}(J,r)$
of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and
![]() $\overline {{\mathcal Z}}(J)$
to denote the closed substack
$\overline {{\mathcal Z}}(J)$
to denote the closed substack
![]() $\overline {{\mathcal Z}}(J,r)$
of
$\overline {{\mathcal Z}}(J,r)$
of
![]() ${\mathcal Z}^{\tau ,1}$
. Again, we note that, by definition,
${\mathcal Z}^{\tau ,1}$
. Again, we note that, by definition,
![]() $\overline {{\mathcal Z}}(J)$
is the scheme-theoretic image of
$\overline {{\mathcal Z}}(J)$
is the scheme-theoretic image of
![]() $\overline {{\mathcal C}}(J)$
in
$\overline {{\mathcal C}}(J)$
in
![]() ${\mathcal Z}^{\tau ,1}$
.
${\mathcal Z}^{\tau ,1}$
.
We will see later that the
![]() $\overline {{\mathcal C}}(J)$
are precisely the irreducible components of
$\overline {{\mathcal C}}(J)$
are precisely the irreducible components of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
; in particular, their finite type points can correspond to irreducible Galois representations. While we do not need it in the sequel, we note the following definition and result, describing the underlying topological spaces of the loci of reducible Breuil–Kisin modules of fixed refined profile.
${\mathcal C}^{\tau ,\operatorname {BT},1}$
; in particular, their finite type points can correspond to irreducible Galois representations. While we do not need it in the sequel, we note the following definition and result, describing the underlying topological spaces of the loci of reducible Breuil–Kisin modules of fixed refined profile.
Definition 4.2.13. For each refined type
![]() $(J,r)$
, we write
$(J,r)$
, we write
![]() $|{\mathcal C}(J,r)^{\tau }|$
for the constructible subset
$|{\mathcal C}(J,r)^{\tau }|$
for the constructible subset
![]() $|{\mathcal C}(\mathfrak {M}(J,r),\mathfrak {N}(J,r))|$
of
$|{\mathcal C}(\mathfrak {M}(J,r),\mathfrak {N}(J,r))|$
of
![]() $|{\mathcal C}^{\tau ,\operatorname {BT},1}|$
of Definition 3.3.14 (where
$|{\mathcal C}^{\tau ,\operatorname {BT},1}|$
of Definition 3.3.14 (where
![]() $\mathfrak {M}(J,r)$
,
$\mathfrak {M}(J,r)$
,
![]() $\mathfrak {N}(J,r)$
are the Breuil–Kisin modules of Definition 4.2.8). We write
$\mathfrak {N}(J,r)$
are the Breuil–Kisin modules of Definition 4.2.8). We write
![]() $|{\mathcal Z}(J,r)^{\tau }|$
for the image of
$|{\mathcal Z}(J,r)^{\tau }|$
for the image of
![]() $|{\mathcal C}(J,r)^{\tau }|$
in
$|{\mathcal C}(J,r)^{\tau }|$
in
![]() $|{\mathcal Z}^{\tau ,1}|$
(which is, again, a constructible subset).
$|{\mathcal Z}^{\tau ,1}|$
(which is, again, a constructible subset).
Lemma 4.2.14. The
![]() $\overline {{\mathbf F}}_p$
-points of
$\overline {{\mathbf F}}_p$
-points of
![]() $|{\mathcal C}(J,r)^{\tau }|$
are precisely the reducible Breuil–Kisin modules with
$|{\mathcal C}(J,r)^{\tau }|$
are precisely the reducible Breuil–Kisin modules with
![]() $\overline {{\mathbf F}}_p$
-coefficients of type
$\overline {{\mathbf F}}_p$
-coefficients of type
![]() $\tau $
and refined profile
$\tau $
and refined profile
![]() $(J,r)$
.
$(J,r)$
.
Proof. This is immediate from the definition.
5. Components of Breuil–Kisin and Galois moduli stacks
Now that we have constructed the morphisms
![]() $\overline {{\mathcal C}}(J) \to \overline {{\mathcal Z}}(J)$
for each J, we can begin our study of the components of the stacks
$\overline {{\mathcal C}}(J) \to \overline {{\mathcal Z}}(J)$
for each J, we can begin our study of the components of the stacks
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
![]() ${\mathcal Z}^{\tau ,1}$
. The first step in Section 5.1 is to determine precisely for which J the scheme-theoretic image
${\mathcal Z}^{\tau ,1}$
. The first step in Section 5.1 is to determine precisely for which J the scheme-theoretic image
![]() $\overline {{\mathcal Z}}(J)$
has dimension smaller than
$\overline {{\mathcal Z}}(J)$
has dimension smaller than
![]() $[K:{\mathbf Q}_p]$
, and hence is not a component of
$[K:{\mathbf Q}_p]$
, and hence is not a component of
![]() ${\mathcal Z}^{\tau ,1}$
. In Section 5.2, we study the irreducible locus in
${\mathcal Z}^{\tau ,1}$
. In Section 5.2, we study the irreducible locus in
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
and prove that it lies in a closed substack of positive codimension. We are then ready to establish our main results in Sections 5.3 and 5.4.
${\mathcal C}^{\tau ,\operatorname {BT},1}$
and prove that it lies in a closed substack of positive codimension. We are then ready to establish our main results in Sections 5.3 and 5.4.
5.1.
 ${\text{ker-Ext}}^1$
and vertical components
${\text{ker-Ext}}^1$
and vertical components
In this section, we will establish some basic facts about
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, and use these results to study the images of our irreducible components in
${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, and use these results to study the images of our irreducible components in
![]() ${\mathcal Z}^{\tau ,1}$
. Let
${\mathcal Z}^{\tau ,1}$
. Let
![]() $\mathfrak {M} = \mathfrak {M}(r,a,c)$
and
$\mathfrak {M} = \mathfrak {M}(r,a,c)$
and
![]() $\mathfrak {N} = \mathfrak {M}(s,b,c)$
be Breuil–Kisin modules as in Section 4.1.
$\mathfrak {N} = \mathfrak {M}(s,b,c)$
be Breuil–Kisin modules as in Section 4.1.
Recall from (3.1.31) that the dimension of
![]() ${\text{ker-Ext}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
is bounded above by the dimension of
${\text{ker-Ext}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
is bounded above by the dimension of
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
; more precisely, by Lemma 2.2.4, we find in this setting that
$\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
; more precisely, by Lemma 2.2.4, we find in this setting that
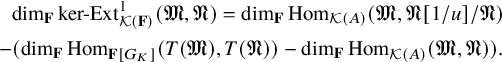 $$ \begin{align}\begin{aligned} \dim_{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal{K}({\mathbf F})}(\mathfrak{M},\mathfrak{N}) = \dim_{{\mathbf F}} \operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N}[1/u]/\mathfrak{N}) \\- (\dim_{{\mathbf F}} \operatorname{\mathrm{Hom}}_{{\mathbf F}[G_K]}(T(\mathfrak{M}),T(\mathfrak{N})) - \dim_{{\mathbf F}} \operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})). \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \dim_{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal{K}({\mathbf F})}(\mathfrak{M},\mathfrak{N}) = \dim_{{\mathbf F}} \operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N}[1/u]/\mathfrak{N}) \\- (\dim_{{\mathbf F}} \operatorname{\mathrm{Hom}}_{{\mathbf F}[G_K]}(T(\mathfrak{M}),T(\mathfrak{N})) - \dim_{{\mathbf F}} \operatorname{\mathrm{Hom}}_{\mathcal{K}(A)}(\mathfrak{M},\mathfrak{N})). \end{aligned} \end{align} $$
A map
![]() $f : \mathfrak {M} \to \mathfrak {N}[1/u]/\mathfrak {N}$
has the form
$f : \mathfrak {M} \to \mathfrak {N}[1/u]/\mathfrak {N}$
has the form
![]() $f(m_i) = \mu _i n_i$
for some
$f(m_i) = \mu _i n_i$
for some
![]() $f'$
-tuple of elements
$f'$
-tuple of elements
![]() $\mu _i \in {\mathbf F}((u))/{\mathbf F}[[u]]$
. By the same argument as in the first paragraph of the proof of Lemma 4.1.8, such a map belongs to
$\mu _i \in {\mathbf F}((u))/{\mathbf F}[[u]]$
. By the same argument as in the first paragraph of the proof of Lemma 4.1.8, such a map belongs to
![]() $C^0(\mathfrak {N}[1/u]/\mathfrak {N})$
(i.e. it is
$C^0(\mathfrak {N}[1/u]/\mathfrak {N})$
(i.e. it is
![]() $\operatorname {\mathrm {Gal}}(K'/K)$
-equivariant) if and only if the
$\operatorname {\mathrm {Gal}}(K'/K)$
-equivariant) if and only if the
![]() $\mu _i$
are periodic with period dividing f, and each nonzero term of
$\mu _i$
are periodic with period dividing f, and each nonzero term of
![]() $\mu _i$
has degree congruent to
$\mu _i$
has degree congruent to
![]() $c_i-d_i\ \pmod {e(K'/K)}$
. One computes that
$c_i-d_i\ \pmod {e(K'/K)}$
. One computes that
![]() $\delta (f)(1\otimes m_{i-1}) = (u^{s_i} \varphi (\mu _{i-1}) - u^{r_i} \mu _i)n_i$
, and so
$\delta (f)(1\otimes m_{i-1}) = (u^{s_i} \varphi (\mu _{i-1}) - u^{r_i} \mu _i)n_i$
, and so
![]() $f \in C^0(\mathfrak {N}[1/u]/\mathfrak {N})$
lies in
$f \in C^0(\mathfrak {N}[1/u]/\mathfrak {N})$
lies in
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
precisely when
$\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
precisely when
for all i.
Remark 5.1.3. Let
![]() $f \in \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
be given as above. Choose any lifting
$f \in \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
be given as above. Choose any lifting
![]() $\tilde {\mu }_i$
of
$\tilde {\mu }_i$
of
![]() $\mu _i$
to
$\mu _i$
to
![]() ${\mathbf F}((u))$
. Then (with notation as in Definition 4.1.7), the tuple
${\mathbf F}((u))$
. Then (with notation as in Definition 4.1.7), the tuple
![]() $(\tilde {\mu }_i)$
is an element of
$(\tilde {\mu }_i)$
is an element of
![]() $\mathscr {C}^0_{u}$
, and we define
$\mathscr {C}^0_{u}$
, and we define
![]() $h_i = \partial (\tilde {\mu }_i)$
. Then,
$h_i = \partial (\tilde {\mu }_i)$
. Then,
![]() $h_i$
lies in
$h_i$
lies in
![]() ${\mathbf F}[[u]]$
for all i, so that
${\mathbf F}[[u]]$
for all i, so that
![]() $(h_i) \in \mathscr {C}^1$
, and a comparison with the construction of (3.1.31) and the proof of Lemma 4.1.8 shows that f maps to the extension class in
$(h_i) \in \mathscr {C}^1$
, and a comparison with the construction of (3.1.31) and the proof of Lemma 4.1.8 shows that f maps to the extension class in
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
represented by
${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
represented by
![]() $\mathfrak {P}(h)$
.
$\mathfrak {P}(h)$
.
Recall that Lemma 3.1.32 implies that nonzero terms appearing in
![]() $\mu _i$
have degree at least
$\mu _i$
have degree at least
![]() $-\lfloor e'/(p-1) \rfloor $
. From this, we obtain the following trivial bound on
$-\lfloor e'/(p-1) \rfloor $
. From this, we obtain the following trivial bound on
![]() ${\text{ker-Ext}}$
.
${\text{ker-Ext}}$
.
Lemma 5.1.4. We have
![]() $\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \le \lceil e/(p-1) \rceil f$
.
$\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \le \lceil e/(p-1) \rceil f$
.
Proof. The degrees of nonzero terms of
![]() $\mu _i$
all lie in a single congruence class modulo
$\mu _i$
all lie in a single congruence class modulo
![]() $e(K'/K)$
, and are bounded below by
$e(K'/K)$
, and are bounded below by
![]() $-e'/(p-1)$
. Therefore, there are at most
$-e'/(p-1)$
. Therefore, there are at most
![]() $\lceil e/(p-1) \rceil $
nonzero terms, and since the
$\lceil e/(p-1) \rceil $
nonzero terms, and since the
![]() $\mu _i$
are periodic with period dividing f, the lemma follows.
$\mu _i$
are periodic with period dividing f, the lemma follows.
Remark 5.1.5. It follows directly from Corollary 5.1.4 that if
![]() $p> 3$
and
$p> 3$
and
![]() $e\neq 1$
, then we have
$e\neq 1$
, then we have
![]() $\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \le [K:{\mathbf Q}_p]/2$
, for then
$\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \le [K:{\mathbf Q}_p]/2$
, for then
![]() $\lceil e/(p-1) \rceil \le e/2$
. Moreover, these inequalities are strict if
$\lceil e/(p-1) \rceil \le e/2$
. Moreover, these inequalities are strict if
![]() $e> 2$
.
$e> 2$
.
We will require a more precise computation of
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
in the setting of Section 4.2, where the pair
${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
in the setting of Section 4.2, where the pair
![]() $(\mathfrak {M},\mathfrak {N})$
has maximal refined profile
$(\mathfrak {M},\mathfrak {N})$
has maximal refined profile
![]() $(J,r)$
. We now return to that setting and its notation.
$(J,r)$
. We now return to that setting and its notation.
Let
![]() $\tau $
be a tame type. We will find the following notation to be helpful. We let
$\tau $
be a tame type. We will find the following notation to be helpful. We let
![]() $\gamma _i^{*} = \gamma _i$
if
$\gamma _i^{*} = \gamma _i$
if
![]() $i-1 \not \in J$
, and
$i-1 \not \in J$
, and
![]() $\gamma _i^{*} = p-1-\gamma _i$
if
$\gamma _i^{*} = p-1-\gamma _i$
if
![]() $i-1 \in J$
. (Here, the integers
$i-1 \in J$
. (Here, the integers
![]() $\gamma _i$
are as in Section 4.2.6. In the case of scalar types, this means that we have
$\gamma _i$
are as in Section 4.2.6. In the case of scalar types, this means that we have
![]() $\gamma ^{*}_i = 0$
for all i.) Since
$\gamma ^{*}_i = 0$
for all i.) Since
![]() $p[k_{i-1}-k^{\prime }_{i-1}] - [k_i - k^{\prime }_i] = (p^{f'}-1)\gamma _i$
, an elementary but useful calculation shows that
$p[k_{i-1}-k^{\prime }_{i-1}] - [k_i - k^{\prime }_i] = (p^{f'}-1)\gamma _i$
, an elementary but useful calculation shows that
when
![]() $(i-1,i)$
is a transition, and that in this case,
$(i-1,i)$
is a transition, and that in this case,
![]() $\gamma _i^{*} =0$
if and only if
$\gamma _i^{*} =0$
if and only if
![]() $[d_{i-1}-c_{i-1}] < p^{f'-1}$
. Similarly, if
$[d_{i-1}-c_{i-1}] < p^{f'-1}$
. Similarly, if
![]() $\tau $
is not a scalar type and
$\tau $
is not a scalar type and
![]() $(i-1,i)$
is not a transition, then
$(i-1,i)$
is not a transition, then
The main computational result of this section is the following.
Proposition 5.1.8. Let
![]() $(J,r)$
be any maximal refined profile for
$(J,r)$
be any maximal refined profile for
![]() $\tau $
, and suppose that the pair
$\tau $
, and suppose that the pair
![]() $(\mathfrak {M},\mathfrak {N})$
has refined profile
$(\mathfrak {M},\mathfrak {N})$
has refined profile
![]() $(J,r)$
. Then,
$(J,r)$
. Then,
![]() $\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
is equal to
$\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
is equal to
except that when
![]() $e=1$
,
$e=1$
,
![]() $\prod _i a_i = \prod _i b_i$
, and the quantity displayed above is f, then the dimension of
$\prod _i a_i = \prod _i b_i$
, and the quantity displayed above is f, then the dimension of
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
is equal to
${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
is equal to
![]() $f-1$
.
$f-1$
.
Proof. The argument has two parts. First, we show that
![]() $\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
is precisely the displayed quantity in the statement of the proposition; then we check that
$\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N})$
is precisely the displayed quantity in the statement of the proposition; then we check that
![]() $\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]} (T(\mathfrak {M}),T(\mathfrak {N})) - \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
is equal to
$\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]} (T(\mathfrak {M}),T(\mathfrak {N})) - \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
is equal to
![]() $1$
in the exceptional case of the statement, and
$1$
in the exceptional case of the statement, and
![]() $0$
otherwise. The result then follows from (5.1.1).
$0$
otherwise. The result then follows from (5.1.1).
Let
![]() $f : m_i \mapsto \mu _i n_i$
be an element of
$f : m_i \mapsto \mu _i n_i$
be an element of
![]() $C^0(\mathfrak {N}[1/u]/\mathfrak {N})$
. Since
$C^0(\mathfrak {N}[1/u]/\mathfrak {N})$
. Since
![]() $u^{e'}$
kills
$u^{e'}$
kills
![]() $\mu _i$
, and all nonzero terms of
$\mu _i$
, and all nonzero terms of
![]() $\mu _i$
have degree congruent to
$\mu _i$
have degree congruent to
![]() $c_i-d_i \pmod {p^{f'}-1}$
, certainly all nonzero terms of
$c_i-d_i \pmod {p^{f'}-1}$
, certainly all nonzero terms of
![]() $\mu _i$
have degree at least
$\mu _i$
have degree at least
![]() $-e' + [c_i-d_i]$
. On the other hand, since the profile
$-e' + [c_i-d_i]$
. On the other hand, since the profile
![]() $(J,r)$
is maximal, we have
$(J,r)$
is maximal, we have
![]() $r_i = e' - [c_i-d_i]$
when
$r_i = e' - [c_i-d_i]$
when
![]() $(i-1,i)$
is a transition and
$(i-1,i)$
is a transition and
![]() $r_i = e'$
otherwise. In either case,
$r_i = e'$
otherwise. In either case,
![]() $u^{r_i}$
kills
$u^{r_i}$
kills
![]() $\mu _i$
, so that (5.1.2) becomes simply the condition that
$\mu _i$
, so that (5.1.2) becomes simply the condition that
![]() $u^{s_i}$
kills
$u^{s_i}$
kills
![]() $\varphi (\mu _{i-1})$
.
$\varphi (\mu _{i-1})$
.
If
![]() $(i-1,i)$
is not a transition, then
$(i-1,i)$
is not a transition, then
![]() $s_i=0$
, and we conclude that
$s_i=0$
, and we conclude that
![]() $\mu _{i-1}=0$
. Suppose instead that
$\mu _{i-1}=0$
. Suppose instead that
![]() $(i-1,i)$
is a transition, so that
$(i-1,i)$
is a transition, so that
![]() $s_i = [c_i-d_i]$
. Then, all nonzero terms of
$s_i = [c_i-d_i]$
. Then, all nonzero terms of
![]() $\mu _{i-1}$
have degree at least
$\mu _{i-1}$
have degree at least
![]() $-s_i/p> -p^{f'-1} > -e(K'/K)$
. Since those terms must have degree congruent to
$-s_i/p> -p^{f'-1} > -e(K'/K)$
. Since those terms must have degree congruent to
![]() $c_{i-1}-d_{i-1} \pmod {p^{f'}-1}$
, it follows that
$c_{i-1}-d_{i-1} \pmod {p^{f'}-1}$
, it follows that
![]() $\mu _{i-1}$
has at most one nonzero term (of degree
$\mu _{i-1}$
has at most one nonzero term (of degree
![]() $-[d_{i-1}-c_{i-1}]$
), and this only if
$-[d_{i-1}-c_{i-1}]$
), and this only if
![]() $[d_{i-1}-c_{i-1}] < p^{f'-1}$
, or equivalently,
$[d_{i-1}-c_{i-1}] < p^{f'-1}$
, or equivalently,
![]() $\gamma _i^{*} = 0$
(as noted above). Conversely, if
$\gamma _i^{*} = 0$
(as noted above). Conversely, if
![]() $\gamma _i^{*}=0$
, then
$\gamma _i^{*}=0$
, then
vanishes in
![]() ${\mathbf F}((u))/{\mathbf F}[[u]]$
. We conclude that
${\mathbf F}((u))/{\mathbf F}[[u]]$
. We conclude that
![]() $\mu _{i-1}$
may have a single nonzero term if and only if
$\mu _{i-1}$
may have a single nonzero term if and only if
![]() $(i-1,i)$
is a transition and
$(i-1,i)$
is a transition and
![]() $\gamma _i^{*}=0$
, and this completes the first part of the argument.
$\gamma _i^{*}=0$
, and this completes the first part of the argument.
Turn now to the second part. Looking at Corollary 4.1.5 and Lemma 4.1.6, to compare
![]() $\operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]}(T(\mathfrak {M}),T(\mathfrak {N}))$
and
$\operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]}(T(\mathfrak {M}),T(\mathfrak {N}))$
and
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, we need to compute the quantities
$\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, we need to compute the quantities
![]() $\alpha _i(\mathfrak {M})-\alpha _i(\mathfrak {N})$
. By definition, this quantity is equal to
$\alpha _i(\mathfrak {M})-\alpha _i(\mathfrak {N})$
. By definition, this quantity is equal to
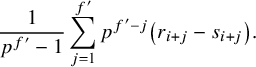 $$ \begin{align}\frac{1}{p^{f'}-1} \sum_{j=1}^{f'} p^{f'-j} \left( r_{i+j} - s_{i+j} \right).\end{align} $$
$$ \begin{align}\frac{1}{p^{f'}-1} \sum_{j=1}^{f'} p^{f'-j} \left( r_{i+j} - s_{i+j} \right).\end{align} $$
Suppose first that
![]() $\tau $
is nonscalar. When
$\tau $
is nonscalar. When
![]() $(i+j-1,i+j)$
is a transition, we have
$(i+j-1,i+j)$
is a transition, we have
![]() $r_{i+j}-s_{i+j} = (e-1)(p^{f'}-1) + [d_{i+j}-c_{i+j}] - [c_{i+j}-d_{i+j}]$
, and otherwise, we have
$r_{i+j}-s_{i+j} = (e-1)(p^{f'}-1) + [d_{i+j}-c_{i+j}] - [c_{i+j}-d_{i+j}]$
, and otherwise, we have
![]() $r_{i+j}-s_{i+j} = e( p^{f'}-1)= (e-1)(p^{f'}-1) + [d_{i+j}-c_{i+j}] + [c_{i+j}-d_{i+j}]$
. Substituting these expressions into (5.1.9), adding and subtracting
$r_{i+j}-s_{i+j} = e( p^{f'}-1)= (e-1)(p^{f'}-1) + [d_{i+j}-c_{i+j}] + [c_{i+j}-d_{i+j}]$
. Substituting these expressions into (5.1.9), adding and subtracting
![]() $\frac {1}{p^{f'}-1} p^{f'} [d_i-c_i]$
, and regrouping gives
$\frac {1}{p^{f'}-1} p^{f'} [d_i-c_i]$
, and regrouping gives
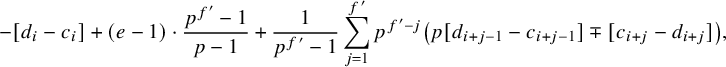 $$\begin{align*}-[d_i-c_i] + (e-1) \cdot \frac{p^{f'}-1}{p-1} + \frac{1}{p^{f'}-1}\sum_{j=1}^{f'} p^{f'-j} \left( p[d_{i+j-1} - c_{i+j-1}] \mp [c_{i+j} - d_{i+j}] \right),\end{align*}$$
$$\begin{align*}-[d_i-c_i] + (e-1) \cdot \frac{p^{f'}-1}{p-1} + \frac{1}{p^{f'}-1}\sum_{j=1}^{f'} p^{f'-j} \left( p[d_{i+j-1} - c_{i+j-1}] \mp [c_{i+j} - d_{i+j}] \right),\end{align*}$$
where the sign is
![]() $-$
if
$-$
if
![]() $(i+j-1,i+j)$
is a transition and
$(i+j-1,i+j)$
is a transition and
![]() $+$
if not. Applying the formulas (5.1.6) and (5.1.7), we conclude that
$+$
if not. Applying the formulas (5.1.6) and (5.1.7), we conclude that
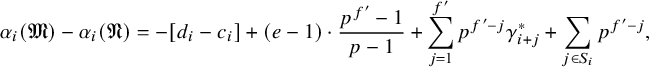 $$ \begin{align} \alpha_i(\mathfrak{M})-\alpha_i(\mathfrak{N}) = -[d_i-c_i] + (e-1) \cdot \frac{p^{f'}-1}{p-1} + \sum_{j=1}^{f'} p^{f'-j} \gamma^{*}_{i+j} + \sum_{j \in S_i} p^{f'-j}, \end{align} $$
$$ \begin{align} \alpha_i(\mathfrak{M})-\alpha_i(\mathfrak{N}) = -[d_i-c_i] + (e-1) \cdot \frac{p^{f'}-1}{p-1} + \sum_{j=1}^{f'} p^{f'-j} \gamma^{*}_{i+j} + \sum_{j \in S_i} p^{f'-j}, \end{align} $$
where the set
![]() $S_i$
consists of
$S_i$
consists of
![]() $1 \le j \le f$
, such that
$1 \le j \le f$
, such that
![]() $(i+j-1,i+j)$
is not a transition. Finally, a moment’s inspection shows that the same formula still holds if
$(i+j-1,i+j)$
is not a transition. Finally, a moment’s inspection shows that the same formula still holds if
![]() $\tau $
is scalar (recalling that
$\tau $
is scalar (recalling that
![]() $J = \varnothing $
in that case).
$J = \varnothing $
in that case).
Suppose that we are in the exceptional case of the proposition, so that
![]() $e=1$
,
$e=1$
,
![]() $\gamma _i^{*}=0$
for all i, and every pair
$\gamma _i^{*}=0$
for all i, and every pair
![]() $(i-1,i)$
is a transition. The formula (5.1.10) gives
$(i-1,i)$
is a transition. The formula (5.1.10) gives
![]() $\alpha _i(\mathfrak {M})-\alpha _i(\mathfrak {N}) = -[d_i-c_i]$
. Since also
$\alpha _i(\mathfrak {M})-\alpha _i(\mathfrak {N}) = -[d_i-c_i]$
. Since also
![]() $\prod _i a_i = \prod _i b_i$
, the conditions of Corollary 4.1.5 are satisfied, so that
$\prod _i a_i = \prod _i b_i$
, the conditions of Corollary 4.1.5 are satisfied, so that
![]() $T(\mathfrak {M})=T(\mathfrak {N})$
; but on the other hand,
$T(\mathfrak {M})=T(\mathfrak {N})$
; but on the other hand,
![]() $\alpha _i(\mathfrak {M}) < \alpha _i(\mathfrak {N})$
, so that by Lemma 4.1.6, there are no nonzero maps
$\alpha _i(\mathfrak {M}) < \alpha _i(\mathfrak {N})$
, so that by Lemma 4.1.6, there are no nonzero maps
![]() $\mathfrak {M}\to \mathfrak {N}$
, and
$\mathfrak {M}\to \mathfrak {N}$
, and
![]() $\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]} (T(\mathfrak {M}),T(\mathfrak {N})) - \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N}) = 1.$
$\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]} (T(\mathfrak {M}),T(\mathfrak {N})) - \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N}) = 1.$
If instead we are not in the exceptional case of the proposition, then either
![]() $\prod _i a_i \neq \prod _i b_i$
, or else (5.1.10) gives
$\prod _i a_i \neq \prod _i b_i$
, or else (5.1.10) gives
![]() $\alpha _i(\mathfrak {M}) - \alpha _i(\mathfrak {N})> -[d_i-c_i]$
for all i. Suppose that
$\alpha _i(\mathfrak {M}) - \alpha _i(\mathfrak {N})> -[d_i-c_i]$
for all i. Suppose that
![]() $T(\mathfrak {M}) \cong T(\mathfrak {N})$
. It follows from Corollary 4.1.5 that
$T(\mathfrak {M}) \cong T(\mathfrak {N})$
. It follows from Corollary 4.1.5 that
![]() $\alpha _i(\mathfrak {M}) - \alpha _i(\mathfrak {N}) \equiv -[d_i-c_i] \pmod {e(K'/K)}$
. Combined with the previous inequality, we deduce that
$\alpha _i(\mathfrak {M}) - \alpha _i(\mathfrak {N}) \equiv -[d_i-c_i] \pmod {e(K'/K)}$
. Combined with the previous inequality, we deduce that
![]() $\alpha _i(\mathfrak {M}) - \alpha _i(\mathfrak {N})> 0$
, and Lemma 4.1.6 guarantees the existence of a nonzero map
$\alpha _i(\mathfrak {M}) - \alpha _i(\mathfrak {N})> 0$
, and Lemma 4.1.6 guarantees the existence of a nonzero map
![]() $\mathfrak {M} \to \mathfrak {N}$
. We deduce that, in any event,
$\mathfrak {M} \to \mathfrak {N}$
. We deduce that, in any event,
![]() $\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]} (T(\mathfrak {M}),T(\mathfrak {N})) = \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
, completing the proof.
$\dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{{\mathbf F}[G_K]} (T(\mathfrak {M}),T(\mathfrak {N})) = \dim _{{\mathbf F}} \operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N})$
, completing the proof.
Corollary 5.1.11. Let
![]() $(J,r)$
be any maximal refined profile for
$(J,r)$
be any maximal refined profile for
![]() $\tau $
, and suppose that the pair
$\tau $
, and suppose that the pair
![]() $(\mathfrak {M},\mathfrak {N})$
has refined profile
$(\mathfrak {M},\mathfrak {N})$
has refined profile
![]() $(J,r)$
. If
$(J,r)$
. If
![]() $J \in {\mathcal P}_{\tau }$
, then
$J \in {\mathcal P}_{\tau }$
, then
![]() $\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N}) = 0$
. Indeed, this is an if and only if except possibly when
$\dim _{{\mathbf F}} {\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})} (\mathfrak {M},\mathfrak {N}) = 0$
. Indeed, this is an if and only if except possibly when
![]() $K={\mathbf Q}_p$
, the type
$K={\mathbf Q}_p$
, the type
![]() $\tau $
is cuspidal, and
$\tau $
is cuspidal, and
![]() $T(\mathfrak {M}(J,r)) \cong T(\mathfrak {N}(J,r))$
.
$T(\mathfrak {M}(J,r)) \cong T(\mathfrak {N}(J,r))$
.
Proof. The first statement is immediate from Proposition 5.1.8, comparing the definition of
![]() $\gamma _i^{*}$
with the defining condition on elements of
$\gamma _i^{*}$
with the defining condition on elements of
![]() ${\mathcal P}_{\tau }$
; in fact, this gives an if and only if unless we are in the exceptional case in Proposition 5.1.8 and
${\mathcal P}_{\tau }$
; in fact, this gives an if and only if unless we are in the exceptional case in Proposition 5.1.8 and
![]() $f-1=0$
. In that case,
$f-1=0$
. In that case,
![]() $e=f=1$
, so
$e=f=1$
, so
![]() $K={\mathbf Q}_p$
. In the principal series case for
$K={\mathbf Q}_p$
. In the principal series case for
![]() $K={\mathbf Q}_p$
, there can be no transitions, so the type is cuspidal. Then,
$K={\mathbf Q}_p$
, there can be no transitions, so the type is cuspidal. Then,
![]() $\gamma _i^{*}=0$
for
$\gamma _i^{*}=0$
for
![]() $i=0,1$
and an elementary analysis of (5.1.6) shows that there exists
$i=0,1$
and an elementary analysis of (5.1.6) shows that there exists
![]() $x \in {\mathbf Z}/(p-1){\mathbf Z}$
, such that
$x \in {\mathbf Z}/(p-1){\mathbf Z}$
, such that
![]() $c_i = 1 +x(p+1)$
,
$c_i = 1 +x(p+1)$
,
![]() $d_i = p+x(p+1)$
for
$d_i = p+x(p+1)$
for
![]() $i=0,1$
. Then,
$i=0,1$
. Then,
![]() $r_i = p-1$
and
$r_i = p-1$
and
![]() $s_i = p(p-1)$
, and Lemma 4.1.4 gives
$s_i = p(p-1)$
, and Lemma 4.1.4 gives
![]() $T(\mathfrak {M}(J,r)) \cong T(\mathfrak {N}(J,r))$
.
$T(\mathfrak {M}(J,r)) \cong T(\mathfrak {N}(J,r))$
.
Recall, that
![]() $\overline {{\mathcal Z}}(J)$
is by definition the scheme-theoretic image of
$\overline {{\mathcal Z}}(J)$
is by definition the scheme-theoretic image of
![]() $\overline {{\mathcal C}}(J)$
in
$\overline {{\mathcal C}}(J)$
in
![]() ${\mathcal Z}^{\tau ,1}$
. In the remainder of this section, we show that the
${\mathcal Z}^{\tau ,1}$
. In the remainder of this section, we show that the
![]() $\overline {{\mathcal Z}}(J)$
with
$\overline {{\mathcal Z}}(J)$
with
![]() $J\in {\mathcal P}_{\tau }$
are pairwise distinct irreducible components of
$J\in {\mathcal P}_{\tau }$
are pairwise distinct irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
. In Section 5.3 below, we will show that they, in fact, exhaust the irreducible components of
${\mathcal Z}^{\tau ,1}$
. In Section 5.3 below, we will show that they, in fact, exhaust the irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
.
${\mathcal Z}^{\tau ,1}$
.
Theorem 5.1.12.
![]() $\overline {{\mathcal Z}}(J)$
has dimension at most
$\overline {{\mathcal Z}}(J)$
has dimension at most
![]() $[K:{\mathbf Q}_p]$
, with equality occurring if and only if
$[K:{\mathbf Q}_p]$
, with equality occurring if and only if
![]() $J\in {\mathcal P}_{\tau }$
. Consequently, the
$J\in {\mathcal P}_{\tau }$
. Consequently, the
![]() $\overline {{\mathcal Z}}(J)$
with
$\overline {{\mathcal Z}}(J)$
with
![]() $J\in {\mathcal P}_{\tau }$
are irreducible components of
$J\in {\mathcal P}_{\tau }$
are irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
.
${\mathcal Z}^{\tau ,1}$
.
Proof. The first part is immediate from Corollary 3.3.32, Proposition 3.1.15, Corollary 5.1.11 and Theorem 4.2.11 (noting that the exceptional case of Corollary 5.1.11 occurs away from
![]() $\textrm {max-Spec}\, A^{{\operatorname {dist}}}$
). Since
$\textrm {max-Spec}\, A^{{\operatorname {dist}}}$
). Since
![]() ${\mathcal Z}^{\tau ,1}$
is equidimensional of dimension
${\mathcal Z}^{\tau ,1}$
is equidimensional of dimension
![]() $[K:{\mathbf Q}_p]$
by Theorem 2.3.10, and the
$[K:{\mathbf Q}_p]$
by Theorem 2.3.10, and the
![]() $\overline {{\mathcal Z}}(J)$
are closed and irreducible by construction, the second part follows from the first together with [Sta13, Tag 0DS2].
$\overline {{\mathcal Z}}(J)$
are closed and irreducible by construction, the second part follows from the first together with [Sta13, Tag 0DS2].
We also note the following result.
Proposition 5.1.13. If
![]() $J\in {\mathcal P}_{\tau }$
, then there is a dense open substack
$J\in {\mathcal P}_{\tau }$
, then there is a dense open substack
![]() ${\mathcal U}$
of
${\mathcal U}$
of
![]() $\overline {{\mathcal C}}(J)$
, such that the canonical morphism
$\overline {{\mathcal C}}(J)$
, such that the canonical morphism
![]() $\overline {{\mathcal C}}(J) \to \overline {{\mathcal Z}}(J)$
restricts to an open immersion on
$\overline {{\mathcal C}}(J) \to \overline {{\mathcal Z}}(J)$
restricts to an open immersion on
![]() ${\mathcal U}$
.
${\mathcal U}$
.
For later use, we note the following computation. Recall that we write
![]() $\mathfrak {N}(J) = \mathfrak {N}(J,r)$
for the maximal profile
$\mathfrak {N}(J) = \mathfrak {N}(J,r)$
for the maximal profile
![]() $(J,r)$
refining J, and that
$(J,r)$
refining J, and that
![]() $\tau =\eta \oplus \eta '$
.
$\tau =\eta \oplus \eta '$
.
Proposition 5.1.14. For each profile J, we have
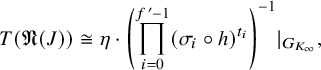 $$\begin{align*}T(\mathfrak{N}(J)) \cong \eta \cdot \left(\prod_{i=0}^{f'-1} (\sigma_i \circ h)^{t_i}\right)^{-1} |_{G_{K_{\infty}}}, \end{align*}$$
$$\begin{align*}T(\mathfrak{N}(J)) \cong \eta \cdot \left(\prod_{i=0}^{f'-1} (\sigma_i \circ h)^{t_i}\right)^{-1} |_{G_{K_{\infty}}}, \end{align*}$$
where
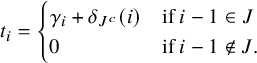 $$\begin{align*}t_i = \begin{cases} \gamma_i + \delta_{J^c}(i) & \text{if } i-1 \in J \\ 0 & \text{if } i-1\not\in J. \end{cases}\end{align*}$$
$$\begin{align*}t_i = \begin{cases} \gamma_i + \delta_{J^c}(i) & \text{if } i-1 \in J \\ 0 & \text{if } i-1\not\in J. \end{cases}\end{align*}$$
Here,
![]() $\delta _{J^c}$
is the characteristic function of the complement of J in
$\delta _{J^c}$
is the characteristic function of the complement of J in
![]() ${\mathbf Z}/f'{\mathbf Z}$
, and we are abusing notation by writing
${\mathbf Z}/f'{\mathbf Z}$
, and we are abusing notation by writing
![]() $\eta $
for the function
$\eta $
for the function
![]() $\sigma _i \circ h^{k_i}$
, which agrees with
$\sigma _i \circ h^{k_i}$
, which agrees with
![]() $\eta $
on
$\eta $
on
![]() $I_K$
.
$I_K$
.
In particular, the map
![]() $J \mapsto T(\mathfrak {N}(J))$
is injective on
$J \mapsto T(\mathfrak {N}(J))$
is injective on
![]() ${\mathcal P}_{\tau }$
.
${\mathcal P}_{\tau }$
.
Remark 5.1.15. In the cuspidal case, it is not a priori clear that the formula in Proposition 5.1.14 gives a character of
![]() $G_{K_{\infty }}$
(rather than a character only when restricted to
$G_{K_{\infty }}$
(rather than a character only when restricted to
![]() $G_{L_{\infty }}$
), but this is an elementary (if somewhat painful) calculation using the definition of the
$G_{L_{\infty }}$
), but this is an elementary (if somewhat painful) calculation using the definition of the
![]() $\gamma _i$
’s and the relation
$\gamma _i$
’s and the relation
![]() $\gamma _i + \gamma _{i+f} = p-1$
.
$\gamma _i + \gamma _{i+f} = p-1$
.
Proof. We begin by explaining how the final statement follows from the rest of the proposition. First, observe that if
![]() $J \in {\mathcal P}_{\tau }$
then
$J \in {\mathcal P}_{\tau }$
then
![]() $0 \le t_i \le p-1$
for all i. Indeed, the only possibility for a contradiction would be if
$0 \le t_i \le p-1$
for all i. Indeed, the only possibility for a contradiction would be if
![]() $\gamma _i = p-1$
and
$\gamma _i = p-1$
and
![]() $i \not \in J$
, but then the definition of
$i \not \in J$
, but then the definition of
![]() ${\mathcal P}_{\tau }$
requires that we cannot have
${\mathcal P}_{\tau }$
requires that we cannot have
![]() $i-1 \in J$
. Next, note that we never have
$i-1 \in J$
. Next, note that we never have
![]() $t_i = p-1$
for all i. Indeed, this would require
$t_i = p-1$
for all i. Indeed, this would require
![]() $J = {\mathbf Z}/f'{\mathbf Z}$
and
$J = {\mathbf Z}/f'{\mathbf Z}$
and
![]() $\gamma _i=p-1$
for all i, but by definition, the
$\gamma _i=p-1$
for all i, but by definition, the
![]() $\gamma _i$
are not all equal to
$\gamma _i$
are not all equal to
![]() $p-1$
.
$p-1$
.
The observations in the previous paragraph imply that (for
![]() $J \in {\mathcal P}_{\tau }$
) the character
$J \in {\mathcal P}_{\tau }$
) the character
![]() $T(\mathfrak {N}(J))$
uniquely determines the integers
$T(\mathfrak {N}(J))$
uniquely determines the integers
![]() $t_i$
, and so it remains to show that the integers
$t_i$
, and so it remains to show that the integers
![]() $t_i$
determine the set J. If
$t_i$
determine the set J. If
![]() $t_i = 0$
for all i, then either
$t_i = 0$
for all i, then either
![]() $J = \varnothing $
or
$J = \varnothing $
or
![]() $J = {\mathbf Z}/f'{\mathbf Z}$
. (For otherwise, there is a transition out of J, and
$J = {\mathbf Z}/f'{\mathbf Z}$
. (For otherwise, there is a transition out of J, and
![]() $\delta _{J^c}(i) \neq 0$
for some
$\delta _{J^c}(i) \neq 0$
for some
![]() $i-1 \in J$
.) But if
$i-1 \in J$
.) But if
![]() $J = {\mathbf Z}/f'{\mathbf Z}$
, then
$J = {\mathbf Z}/f'{\mathbf Z}$
, then
![]() $\gamma _i = 0$
for all i and
$\gamma _i = 0$
for all i and
![]() $\tau $
is scalar; but for scalar types, we have
$\tau $
is scalar; but for scalar types, we have
![]() ${\mathbf Z}/f'{\mathbf Z} \not \in {\mathcal P}_{\tau }$
, a contradiction. Thus,
${\mathbf Z}/f'{\mathbf Z} \not \in {\mathcal P}_{\tau }$
, a contradiction. Thus,
![]() $t_i =0$
for all i implies
$t_i =0$
for all i implies
![]() $J = \varnothing $
.
$J = \varnothing $
.
For the rest of this part of the argument, we may therefore suppose
![]() $t_i \neq 0$
for some i, which forces
$t_i \neq 0$
for some i, which forces
![]() $i-1 \in J$
. The entire set J will then be determined by recursion if we can show that knowledge of
$i-1 \in J$
. The entire set J will then be determined by recursion if we can show that knowledge of
![]() $t_i$
along with whether or not
$t_i$
along with whether or not
![]() $i \in J$
determines whether or not
$i \in J$
determines whether or not
![]() $i-1 \in J$
. Given the defining formula for
$i-1 \in J$
. Given the defining formula for
![]() $t_i$
, the only possible ambiguity is if
$t_i$
, the only possible ambiguity is if
![]() $t_i = 0$
and
$t_i = 0$
and
![]() $\gamma _i + \delta _{J^c}(i) = 0$
, so that
$\gamma _i + \delta _{J^c}(i) = 0$
, so that
![]() $\gamma _i = 0$
and
$\gamma _i = 0$
and
![]() $i \in J$
. But the definition of
$i \in J$
. But the definition of
![]() ${\mathcal P}_{\tau }$
requires
${\mathcal P}_{\tau }$
requires
![]() $i-1 \in J$
in this case. This completes the proof.
$i-1 \in J$
in this case. This completes the proof.
We now turn to proving the formula for
![]() $T(\mathfrak {N}(J))$
. We will use Lemma 4.1.4 applied at
$T(\mathfrak {N}(J))$
. We will use Lemma 4.1.4 applied at
![]() $i=0$
, for which we have to compute
$i=0$
, for which we have to compute
![]() $\alpha _0 - d_0$
writing
$\alpha _0 - d_0$
writing
![]() $\alpha _0 = \alpha _0(\mathfrak {N})$
. Recall that we have already computed
$\alpha _0 = \alpha _0(\mathfrak {N})$
. Recall that we have already computed
![]() $\alpha _0(\mathfrak {M}(J)) - \alpha _0(\mathfrak {N}(J))$
in the proof of Proposition 5.1.8. Since
$\alpha _0(\mathfrak {M}(J)) - \alpha _0(\mathfrak {N}(J))$
in the proof of Proposition 5.1.8. Since
![]() $\alpha _0(\mathfrak {M}(J)) + \alpha _0(\mathfrak {N}(J)) = e(p^{f'}-1)/(p-1)$
, taking the difference between these formulas gives
$\alpha _0(\mathfrak {M}(J)) + \alpha _0(\mathfrak {N}(J)) = e(p^{f'}-1)/(p-1)$
, taking the difference between these formulas gives
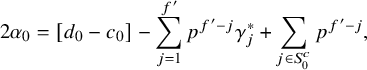 $$\begin{align*}2 \alpha_0 = [d_0 - c_0] - \sum_{j=1}^{f'} p^{f'-j} \gamma_j^{*} + \sum_{j \in S_0^c} p^{f'-j}, \end{align*}$$
$$\begin{align*}2 \alpha_0 = [d_0 - c_0] - \sum_{j=1}^{f'} p^{f'-j} \gamma_j^{*} + \sum_{j \in S_0^c} p^{f'-j}, \end{align*}$$
where
![]() $S_0^c$
consists of those
$S_0^c$
consists of those
![]() $1\le j \le f$
, such that
$1\le j \le f$
, such that
![]() $(j-1,j)$
is a transition. Subtract
$(j-1,j)$
is a transition. Subtract
![]() $2[d_0]$
from both sides, and add the expression
$2[d_0]$
from both sides, and add the expression
![]() $-[k_0-k^{\prime }_0] + \sum _{j=1}^{f'} p^{f'-j} \gamma _j$
(which vanishes by definition) to the right-hand side. Note that
$-[k_0-k^{\prime }_0] + \sum _{j=1}^{f'} p^{f'-j} \gamma _j$
(which vanishes by definition) to the right-hand side. Note that
![]() $[d_0 - c_0] - [k_0-k^{\prime }_0] - 2[d_0]$
is equal to
$[d_0 - c_0] - [k_0-k^{\prime }_0] - 2[d_0]$
is equal to
![]() $-2[k_0]$
if
$-2[k_0]$
if
![]() $0 \not \in J$
, and to
$0 \not \in J$
, and to
![]() $e(K'/K)-2[k_0-k_0']-2[k_0']$
if
$e(K'/K)-2[k_0-k_0']-2[k_0']$
if
![]() $0 \in J$
. Since
$0 \in J$
. Since
![]() $\gamma _j - \gamma _j^{*} = 2\gamma _j - (p-1)$
if
$\gamma _j - \gamma _j^{*} = 2\gamma _j - (p-1)$
if
![]() $j-1 \in J$
and is
$j-1 \in J$
and is
![]() $0$
otherwise, the preceding expression rearranges to give (after dividing by
$0$
otherwise, the preceding expression rearranges to give (after dividing by
![]() $2$
)
$2$
)
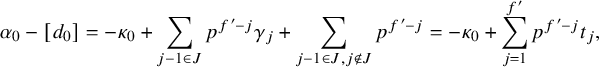 $$\begin{align*}\alpha_0 - [d_0] = -\kappa_0 + \sum_{j-1\in J} p^{f'-j} \gamma_j + \sum_{j-1\in J, j\not\in J} p^{f'-j} = -\kappa_0 + \sum_{j=1}^{f'} p^{f'-j} t_j,\end{align*}$$
$$\begin{align*}\alpha_0 - [d_0] = -\kappa_0 + \sum_{j-1\in J} p^{f'-j} \gamma_j + \sum_{j-1\in J, j\not\in J} p^{f'-j} = -\kappa_0 + \sum_{j=1}^{f'} p^{f'-j} t_j,\end{align*}$$
where
![]() $\kappa _0 = [k_0]$
if
$\kappa _0 = [k_0]$
if
![]() $0 \not \in J$
and
$0 \not \in J$
and
![]() $\kappa _0 = [k_0 - k^{\prime }_0] +[k^{\prime }_0]$
if
$\kappa _0 = [k_0 - k^{\prime }_0] +[k^{\prime }_0]$
if
![]() $0 \in J$
. Since in either case,
$0 \in J$
. Since in either case,
![]() $\kappa _0 \equiv k_0 \pmod {e(K'/K)}$
, the result now follows from Lemma 4.1.4.
$\kappa _0 \equiv k_0 \pmod {e(K'/K)}$
, the result now follows from Lemma 4.1.4.
Definition 5.1.16. Let
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2({\mathbf F}')$
be representation. Then we say that a Breuil–Kisin module
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2({\mathbf F}')$
be representation. Then we say that a Breuil–Kisin module
![]() $\mathfrak {M}$
with
$\mathfrak {M}$
with
![]() ${\mathbf F}'$
-coefficients is a Breuil–Kisin model of
${\mathbf F}'$
-coefficients is a Breuil–Kisin model of
![]() $\overline {r}$
of type
$\overline {r}$
of type
![]() $\tau $
if
$\tau $
if
![]() $\mathfrak {M}$
is an
$\mathfrak {M}$
is an
![]() ${\mathbf F}'$
-point of
${\mathbf F}'$
-point of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and
![]() $T_{{\mathbf F}'}(\mathfrak {M})\cong \overline {r}|_{G_{K_{\infty }}}$
.
$T_{{\mathbf F}'}(\mathfrak {M})\cong \overline {r}|_{G_{K_{\infty }}}$
.
Recall that for each continuous representation
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, there is an associated (nonempty) set of Serre weights
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, there is an associated (nonempty) set of Serre weights
![]() $W(\overline {r})$
whose precise definition is recalled in Appendix A.
$W(\overline {r})$
whose precise definition is recalled in Appendix A.
Theorem 5.1.17. The
![]() $\overline {{\mathcal Z}}(J)$
, with
$\overline {{\mathcal Z}}(J)$
, with
![]() $J\in {\mathcal P}_{\tau }$
, are pairwise distinct closed substacks of
$J\in {\mathcal P}_{\tau }$
, are pairwise distinct closed substacks of
![]() ${\mathcal Z}^{\tau ,1}$
. For each
${\mathcal Z}^{\tau ,1}$
. For each
![]() $J\in {\mathcal P}_{\tau }$
, there is a dense set of finite type points of
$J\in {\mathcal P}_{\tau }$
, there is a dense set of finite type points of
![]() $\overline {{\mathcal Z}}(J)$
with the property that the corresponding Galois representations have
$\overline {{\mathcal Z}}(J)$
with the property that the corresponding Galois representations have
![]() $\overline {\sigma }(\tau )_J$
as a Serre weight, and which furthermore admit a unique Breuil–Kisin model of type
$\overline {\sigma }(\tau )_J$
as a Serre weight, and which furthermore admit a unique Breuil–Kisin model of type
![]() $\tau $
.
$\tau $
.
Proof. Recall from Definition 3.3.11 that
![]() $\overline {{\mathcal Z}}(J)$
is defined to be the scheme-theoretic image of a morphism
$\overline {{\mathcal Z}}(J)$
is defined to be the scheme-theoretic image of a morphism
![]() $\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}} \to {\mathcal Z}^{\mathrm {dd},1}.$
As in the proof of Lemma 3.3.13, since the source and target of this morphism are of finite presentation over
$\operatorname {\mathrm {Spec}} {B^{\operatorname {dist}}} \to {\mathcal Z}^{\mathrm {dd},1}.$
As in the proof of Lemma 3.3.13, since the source and target of this morphism are of finite presentation over
![]() ${\mathbf F}$
, its image is a dense constructible subset of its scheme-theoretic image, and so contains a dense open subset, which we may interpret as a dense open substack
${\mathbf F}$
, its image is a dense constructible subset of its scheme-theoretic image, and so contains a dense open subset, which we may interpret as a dense open substack
![]() ${\mathcal U}$
of
${\mathcal U}$
of
![]() $\overline {{\mathcal Z}}(J).$
From the definition of
$\overline {{\mathcal Z}}(J).$
From the definition of
![]() ${B^{\operatorname {dist}}},$
the finite type points of
${B^{\operatorname {dist}}},$
the finite type points of
![]() ${\mathcal U}$
correspond to reducible Galois representations admitting a model of type
${\mathcal U}$
correspond to reducible Galois representations admitting a model of type
![]() $\tau $
and refined profile
$\tau $
and refined profile
![]() $(J,r)$
, for which
$(J,r)$
, for which
![]() $(J,r)$
is maximal.
$(J,r)$
is maximal.
That the
![]() $\overline {{\mathcal Z}}(J)$
are pairwise distinct is immediate from the above and Proposition 5.1.14. Combining this observation with Theorem 4.2.11, we see that by deleting the intersections of
$\overline {{\mathcal Z}}(J)$
are pairwise distinct is immediate from the above and Proposition 5.1.14. Combining this observation with Theorem 4.2.11, we see that by deleting the intersections of
![]() $\overline {{\mathcal Z}}(J)$
with the
$\overline {{\mathcal Z}}(J)$
with the
![]() $\overline {{\mathcal Z}}(J',r')$
for all refined profiles
$\overline {{\mathcal Z}}(J',r')$
for all refined profiles
![]() $(J',r')\ne (J,r)$
, we obtain a dense open substack
$(J',r')\ne (J,r)$
, we obtain a dense open substack
![]() ${\mathcal U}'$
whose finite type points have the property that every Breuil–Kisin model of type
${\mathcal U}'$
whose finite type points have the property that every Breuil–Kisin model of type
![]() $\tau $
of the corresponding Galois representation has profile
$\tau $
of the corresponding Galois representation has profile
![]() $(J,r)$
. The unicity of such a Breuil–Kisin model then follows from Corollary 5.1.11.
$(J,r)$
. The unicity of such a Breuil–Kisin model then follows from Corollary 5.1.11.
It remains to show that every such Galois representation
![]() $\overline {r}$
has
$\overline {r}$
has
![]() $\overline {\sigma }(\tau )_J$
as a Serre weight. Suppose first that
$\overline {\sigma }(\tau )_J$
as a Serre weight. Suppose first that
![]() $\tau $
is a principal series type. We claim that (writing
$\tau $
is a principal series type. We claim that (writing
![]() $\overline {\sigma }(\tau )_J = \overline {\sigma }_{\vec {t},\vec {s}} \otimes (\eta ' \circ \det )$
as in Appendix A), we have
$\overline {\sigma }(\tau )_J = \overline {\sigma }_{\vec {t},\vec {s}} \otimes (\eta ' \circ \det )$
as in Appendix A), we have
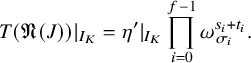 $$\begin{align*}T(\mathfrak{N}(J))|_{I_K}=\eta'|_{I_K} \prod_{i=0}^{f-1}\omega_{\sigma_i}^{s_i+t_i}.\end{align*}$$
$$\begin{align*}T(\mathfrak{N}(J))|_{I_K}=\eta'|_{I_K} \prod_{i=0}^{f-1}\omega_{\sigma_i}^{s_i+t_i}.\end{align*}$$
To see this, note that by Proposition 5.1.14, it is enough to show that
![]() $\eta |_{I_K}=\eta '|_{I_K} \prod _{i=0}^{f-1}\omega _{\sigma _i}^{s_i+2t_i}$
, which follows by comparing the central characters of
$\eta |_{I_K}=\eta '|_{I_K} \prod _{i=0}^{f-1}\omega _{\sigma _i}^{s_i+2t_i}$
, which follows by comparing the central characters of
![]() $\overline {\sigma }(\tau )_J$
and
$\overline {\sigma }(\tau )_J$
and
![]() $\overline {\sigma }(\tau )$
(or from a direct computation with the quantities
$\overline {\sigma }(\tau )$
(or from a direct computation with the quantities
![]() $s_i,t_i$
).
$s_i,t_i$
).
Since
![]() $\det \overline {r}|_{I_K}=\eta \eta '\overline {\varepsilon }^{-1}$
, we have
$\det \overline {r}|_{I_K}=\eta \eta '\overline {\varepsilon }^{-1}$
, we have
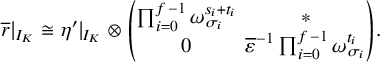 $$\begin{align*}\overline{r}|_{I_K}\cong \eta'|_{I_K} \otimes \begin{pmatrix} \prod_{i=0}^{f-1}\omega_{\sigma_i}^{s_i+t_i} &*\\ 0 & \overline{\varepsilon}^{-1}\prod_{i=0}^{f-1}\omega_{\sigma_i}^{t_i} \end{pmatrix}.\end{align*}$$
$$\begin{align*}\overline{r}|_{I_K}\cong \eta'|_{I_K} \otimes \begin{pmatrix} \prod_{i=0}^{f-1}\omega_{\sigma_i}^{s_i+t_i} &*\\ 0 & \overline{\varepsilon}^{-1}\prod_{i=0}^{f-1}\omega_{\sigma_i}^{t_i} \end{pmatrix}.\end{align*}$$
The result then follows from Lemma A.6, using Lemma A.5(2) and the fact that the fibre of the morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal R}^{\mathrm {dd},1}$
above
${\mathcal C}^{\tau ,\operatorname {BT},1} \to {\mathcal R}^{\mathrm {dd},1}$
above
![]() $\overline {r}$
is nonempty to see that
$\overline {r}$
is nonempty to see that
![]() $\overline {r}$
is not très ramifiée.
$\overline {r}$
is not très ramifiée.
The argument in the cuspidal case proceeds analogously, noting that if the character
![]() $\theta $
(as in Appendix A) corresponds to
$\theta $
(as in Appendix A) corresponds to
![]() $\widetilde {\theta }$
under local class field theory, then
$\widetilde {\theta }$
under local class field theory, then
![]() $\widetilde {\theta } |_{I_K} = \eta ' \prod _{i=0}^{f'-1} \omega _{\sigma ^{\prime }_i}^{t_i}$
, and that from central characters, we have
$\widetilde {\theta } |_{I_K} = \eta ' \prod _{i=0}^{f'-1} \omega _{\sigma ^{\prime }_i}^{t_i}$
, and that from central characters, we have
![]() $\eta \eta ' = (\widetilde {\theta } |_{I_K})^2 \prod _{i=0}^{f-1} \omega _{\sigma _i}^{s_i}$
.
$\eta \eta ' = (\widetilde {\theta } |_{I_K})^2 \prod _{i=0}^{f-1} \omega _{\sigma _i}^{s_i}$
.
Remark 5.1.18. With more work, we could use the results of [Reference Gee, Liu and SavittGLS15] and our results on dimensions of families of extensions to strengthen Theorem 5.1.17, showing that there is a dense set of finite type points of
![]() $\overline {{\mathcal Z}}(J)$
with the property that the corresponding Galois representations have
$\overline {{\mathcal Z}}(J)$
with the property that the corresponding Galois representations have
![]() $\overline {\sigma }(\tau )_J$
as their unique non-Steinberg Serre weight. In fact, we will prove this as part of our work on the geometric Breuil–Mézard conjecture in [Reference Caraiani, Emerton, Gee and SavittCEGS20a] (which uses Theorem 5.1.17 as an input).
$\overline {\sigma }(\tau )_J$
as their unique non-Steinberg Serre weight. In fact, we will prove this as part of our work on the geometric Breuil–Mézard conjecture in [Reference Caraiani, Emerton, Gee and SavittCEGS20a] (which uses Theorem 5.1.17 as an input).
5.2. Irreducible Galois representations
We now show that the points of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
which are irreducible (that is, cannot be written as an extension of rank one Breuil–Kisin modules) lie in a closed substack of positive codimension. This, in essence, amounts to bounding the dimensions of the Kisin varieties (for Breuil–Kisin modules of height at most
${\mathcal C}^{\tau ,\operatorname {BT},1}$
which are irreducible (that is, cannot be written as an extension of rank one Breuil–Kisin modules) lie in a closed substack of positive codimension. This, in essence, amounts to bounding the dimensions of the Kisin varieties (for Breuil–Kisin modules of height at most
![]() $1$
with descent data of type
$1$
with descent data of type
![]() $\tau $
) corresponding to irreducible representations. We begin with the following useful observation.
$\tau $
) corresponding to irreducible representations. We begin with the following useful observation.
Lemma 5.2.1. The rank two Breuil–Kisin modules with descent data and
![]() $\overline {{\mathbf F}}_p$
-coefficients which are irreducible (that is, which cannot be written as an extension of rank one Breuil–Kisin modules with descent data) are precisely those whose corresponding étale
$\overline {{\mathbf F}}_p$
-coefficients which are irreducible (that is, which cannot be written as an extension of rank one Breuil–Kisin modules with descent data) are precisely those whose corresponding étale
![]() $\varphi $
-modules are irreducible, or equivalently, whose corresponding
$\varphi $
-modules are irreducible, or equivalently, whose corresponding
![]() $G_K$
-representations are irreducible.
$G_K$
-representations are irreducible.
Proof. Let
![]() $\mathfrak {M}$
be a Breuil–Kisin module with descent data corresponding to a finite type point of
$\mathfrak {M}$
be a Breuil–Kisin module with descent data corresponding to a finite type point of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}_{\mathrm {dd}}$
, let
${\mathcal C}^{\tau ,\operatorname {BT},1}_{\mathrm {dd}}$
, let
![]() $M=\mathfrak {M}[1/u]$
and let
$M=\mathfrak {M}[1/u]$
and let
![]() $\overline {\rho }$
be the
$\overline {\rho }$
be the
![]() $G_K$
-representation corresponding to M. As noted in the proof of Lemma 2.2.6,
$G_K$
-representation corresponding to M. As noted in the proof of Lemma 2.2.6,
![]() $\overline {\rho }$
is reducible if and only if
$\overline {\rho }$
is reducible if and only if
![]() $\overline {\rho }|_{G_{K_{\infty }}}$
is reducible, and by Lemma 2.2.4, this is equivalent to M being reducible. That this is, in turn, equivalent to
$\overline {\rho }|_{G_{K_{\infty }}}$
is reducible, and by Lemma 2.2.4, this is equivalent to M being reducible. That this is, in turn, equivalent to
![]() $\mathfrak {M}$
being reducible may be proved in the same way as [Reference Gee, Liu and SavittGLS14, Lemma 5.5].
$\mathfrak {M}$
being reducible may be proved in the same way as [Reference Gee, Liu and SavittGLS14, Lemma 5.5].
Recall that
![]() $L/K$
denotes the unramified quadratic extension; then the irreducible representations
$L/K$
denotes the unramified quadratic extension; then the irreducible representations
![]() $\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
are all induced from characters of
$\overline {\rho }:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
are all induced from characters of
![]() $G_L$
. Bearing in mind Lemma 5.2.1, this means that we can study irreducible Breuil–Kisin modules via a consideration of base change of Breuil–Kisin modules from K to L, and our previous study of reducible Breuil–Kisin modules. Since this will require us to consider Breuil–Kisin modules (and moduli stacks thereof) over both K and L, we will have to introduce additional notation in order to indicate over which of the two fields we might be working. We do this simply by adding a subscript ‘K’ or ‘L’ to our current notation. We will also omit other decorations which are being held fixed throughout the present discussion. Thus, we write
$G_L$
. Bearing in mind Lemma 5.2.1, this means that we can study irreducible Breuil–Kisin modules via a consideration of base change of Breuil–Kisin modules from K to L, and our previous study of reducible Breuil–Kisin modules. Since this will require us to consider Breuil–Kisin modules (and moduli stacks thereof) over both K and L, we will have to introduce additional notation in order to indicate over which of the two fields we might be working. We do this simply by adding a subscript ‘K’ or ‘L’ to our current notation. We will also omit other decorations which are being held fixed throughout the present discussion. Thus, we write
![]() ${\mathcal C}_{K}^{\tau }$
to denote the moduli stack that was previously denoted
${\mathcal C}_{K}^{\tau }$
to denote the moduli stack that was previously denoted
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and
![]() ${\mathcal C}_{L}^{\tau _{|L}}$
to denote the corresponding moduli stack for Breuil–Kisin modules over L, with the type taken to be the restriction
${\mathcal C}_{L}^{\tau _{|L}}$
to denote the corresponding moduli stack for Breuil–Kisin modules over L, with the type taken to be the restriction
![]() $\tau _{|L}$
of
$\tau _{|L}$
of
![]() $\tau $
from K to L. (Note that whether
$\tau $
from K to L. (Note that whether
![]() $\tau $
is principal series or cuspidal, the restriction
$\tau $
is principal series or cuspidal, the restriction
![]() $\tau _{| L}$
is principal series.)
$\tau _{| L}$
is principal series.)
As usual, we fix a uniformiser
![]() $\pi $
of K, which we also take to be our fixed uniformiser of L. Also, throughout this section, we take
$\pi $
of K, which we also take to be our fixed uniformiser of L. Also, throughout this section, we take
![]() $K' = L(\pi ^{1/(p^{2f}-1)})$
, so that
$K' = L(\pi ^{1/(p^{2f}-1)})$
, so that
![]() $K'/L$
is the standard choice of extension for
$K'/L$
is the standard choice of extension for
![]() $\tau $
and
$\tau $
and
![]() $\pi $
regarded as a type and uniformiser for L.
$\pi $
regarded as a type and uniformiser for L.
Write
![]() $\phi : W(k')[[u]] \to W(k')[[u]]$
for the automorphism fixing u and acting on
$\phi : W(k')[[u]] \to W(k')[[u]]$
for the automorphism fixing u and acting on
![]() $W(k')$
via the automorphism induced by the nontrivial automorphism of
$W(k')$
via the automorphism induced by the nontrivial automorphism of
![]() $k'/k$
. If
$k'/k$
. If
![]() $\mathfrak {P}$
is a Breuil–Kisin module with descent data from
$\mathfrak {P}$
is a Breuil–Kisin module with descent data from
![]() $K'$
to L, then we let
$K'$
to L, then we let
![]() $\mathfrak {P}^{(f)}$
be the Breuil–Kisin module given by the pullback of
$\mathfrak {P}^{(f)}$
be the Breuil–Kisin module given by the pullback of
![]() $\mathfrak {P}$
along
$\mathfrak {P}$
along
![]() $\phi $
, and such that the descent data on
$\phi $
, and such that the descent data on
![]() $\mathfrak {P}^{(f)}$
is given by
$\mathfrak {P}^{(f)}$
is given by
![]() $\hat {g}(s \otimes m) = \hat {g}(s) \otimes \hat {g}^{p^f}(m)$
for
$\hat {g}(s \otimes m) = \hat {g}(s) \otimes \hat {g}^{p^f}(m)$
for
![]() $s\in W(k')[[u]]$
and
$s\in W(k')[[u]]$
and
![]() $m \in \mathfrak {P}$
. In particular, we have
$m \in \mathfrak {P}$
. In particular, we have
![]() $\mathfrak {M}(r,a,c)^{(f)} = \mathfrak {M}(r',a',c')$
, where
$\mathfrak {M}(r,a,c)^{(f)} = \mathfrak {M}(r',a',c')$
, where
![]() $r^{\prime }_i = r_{i+f}$
,
$r^{\prime }_i = r_{i+f}$
,
![]() $a^{\prime }_i=a_{i+f}$
, and
$a^{\prime }_i=a_{i+f}$
, and
![]() $c^{\prime }_i=c_{i+f}$
.
$c^{\prime }_i=c_{i+f}$
.
We let
![]() $\sigma $
denote the nontrivial automorphism of L over K, and write
$\sigma $
denote the nontrivial automorphism of L over K, and write
![]() $G := \operatorname {\mathrm {Gal}}(L/K)= \langle \sigma \rangle $
, a cyclic group of order two. There is an action
$G := \operatorname {\mathrm {Gal}}(L/K)= \langle \sigma \rangle $
, a cyclic group of order two. There is an action
![]() $\alpha $
of G on
$\alpha $
of G on
![]() ${\mathcal C}_{L}$
defined via
${\mathcal C}_{L}$
defined via
![]() $\alpha _{\sigma }: \mathfrak {P} \mapsto \mathfrak {P}^{(f)}$
. More precisely, this induces an action of
$\alpha _{\sigma }: \mathfrak {P} \mapsto \mathfrak {P}^{(f)}$
. More precisely, this induces an action of
![]() $G:= \langle \sigma \rangle $
on
$G:= \langle \sigma \rangle $
on
![]() ${\mathcal C}_{L}^{\tau _{|L}}$
in the strictFootnote 2 sense that
${\mathcal C}_{L}^{\tau _{|L}}$
in the strictFootnote 2 sense that
We now define the fixed point stack for this action.
Definition 5.2.2. We let the fixed point stack
![]() $({\mathcal C}_{L}^{\tau _{|L}})^G$
denote the stack whose A-valued points consist of an A-valued point
$({\mathcal C}_{L}^{\tau _{|L}})^G$
denote the stack whose A-valued points consist of an A-valued point
![]() $\mathfrak {M}$
of
$\mathfrak {M}$
of
![]() ${\mathcal C}_L^{\tau _{|L}}$
, together with an isomorphism
${\mathcal C}_L^{\tau _{|L}}$
, together with an isomorphism
![]() $\imath : \mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {M}^{(f)}$
which satisfies the cocycle condition that the composite
$\imath : \mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {M}^{(f)}$
which satisfies the cocycle condition that the composite
is equal to the identity morphism
![]() $\operatorname {id}_{\mathfrak {M}}$
.
$\operatorname {id}_{\mathfrak {M}}$
.
We now give another description of
![]() $({\mathcal C}_L^{\tau _{|L}})^G$
, in terms of various fibre products, which is technically useful. This alternate description involves two steps. In the first step, we define fixed points of the automorphism
$({\mathcal C}_L^{\tau _{|L}})^G$
, in terms of various fibre products, which is technically useful. This alternate description involves two steps. In the first step, we define fixed points of the automorphism
![]() $\alpha _{\sigma }$
, without imposing the additional condition that the fixed point data be compatible with the relation
$\alpha _{\sigma }$
, without imposing the additional condition that the fixed point data be compatible with the relation
![]() $\sigma ^2~=~1$
in G. Namely, we define
$\sigma ^2~=~1$
in G. Namely, we define
where the first morphism
![]() ${\mathcal C}_{L}^{\tau _{|L}}\to {\mathcal C}_{L}^{\tau _{|L}} \times {\mathcal C}_{L}^{\tau _{|L}}$
is the diagonal, and the second is
${\mathcal C}_{L}^{\tau _{|L}}\to {\mathcal C}_{L}^{\tau _{|L}} \times {\mathcal C}_{L}^{\tau _{|L}}$
is the diagonal, and the second is
![]() $\operatorname {id}\times \alpha _{\sigma }$
. Working through the definitions, one finds that an A-valued point of
$\operatorname {id}\times \alpha _{\sigma }$
. Working through the definitions, one finds that an A-valued point of
![]() $({\mathcal C}_L^{\tau _{|L}})^{\alpha _{\sigma }}$
consists of a pair
$({\mathcal C}_L^{\tau _{|L}})^{\alpha _{\sigma }}$
consists of a pair
![]() $(\mathfrak {M},\mathfrak {M}')$
of objects of
$(\mathfrak {M},\mathfrak {M}')$
of objects of
![]() ${\mathcal C}_L^{\tau _{|L}}$
over A, equipped with isomorphisms
${\mathcal C}_L^{\tau _{|L}}$
over A, equipped with isomorphisms
![]() $\alpha : \mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {M}'$
and
$\alpha : \mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {M}'$
and
![]() $\beta : \mathfrak {M} \buildrel \sim \over \longrightarrow (\mathfrak {M}')^{(f)}$
. The morphism
$\beta : \mathfrak {M} \buildrel \sim \over \longrightarrow (\mathfrak {M}')^{(f)}$
. The morphism
where
![]() $\imath := (\alpha ^{-1})^{(f)} \circ \beta : \mathfrak {M} \to \mathfrak {M}^{(f)}$
, induces an isomorphism between
$\imath := (\alpha ^{-1})^{(f)} \circ \beta : \mathfrak {M} \to \mathfrak {M}^{(f)}$
, induces an isomorphism between
![]() $({\mathcal C}_L^{\tau _{|L}})^{\alpha _{\sigma }}$
and the stack classifying points
$({\mathcal C}_L^{\tau _{|L}})^{\alpha _{\sigma }}$
and the stack classifying points
![]() $\mathfrak {M}$
of
$\mathfrak {M}$
of
![]() ${\mathcal C}_L^{\tau _{|L}}$
equipped with an isomorphism
${\mathcal C}_L^{\tau _{|L}}$
equipped with an isomorphism
![]() $\imath : \mathfrak {M} \to \mathfrak {M}^{(f)}$
. (However, no cocycle condition has been imposed on
$\imath : \mathfrak {M} \to \mathfrak {M}^{(f)}$
. (However, no cocycle condition has been imposed on
![]() $\imath $
.)
$\imath $
.)
Let
![]() $I_{{\mathcal C}_L^{\tau _{|L}}}$
denote the inertia stack of
$I_{{\mathcal C}_L^{\tau _{|L}}}$
denote the inertia stack of
![]() ${\mathcal C}_L^{\tau _{|L}}.$
We define a morphism
${\mathcal C}_L^{\tau _{|L}}.$
We define a morphism
via
where, as in Definition 5.2.2, we regard the composite
![]() $\imath ^{(f)}\circ \imath $
as an automorphism of
$\imath ^{(f)}\circ \imath $
as an automorphism of
![]() $\mathfrak {M}$
via the identity
$\mathfrak {M}$
via the identity
![]() $(\mathfrak {M}^{(f)})^{(f)} = \mathfrak {M}.$
Of course, we also have the identity section
$(\mathfrak {M}^{(f)})^{(f)} = \mathfrak {M}.$
Of course, we also have the identity section
![]() $e: {\mathcal C}_L^{\tau _{|L}} \to I_{{\mathcal C}_L^{\tau _{|L}}}$
. We now define
$e: {\mathcal C}_L^{\tau _{|L}} \to I_{{\mathcal C}_L^{\tau _{|L}}}$
. We now define
If we use the description of
![]() $({\mathcal C}_L^{\tau |_{L}})^{\alpha _{\sigma }}$
as classifying pairs
$({\mathcal C}_L^{\tau |_{L}})^{\alpha _{\sigma }}$
as classifying pairs
![]() $(\mathfrak {M},\imath ),$
then (just unwinding definitions) this fibre product classifies tuples
$(\mathfrak {M},\imath ),$
then (just unwinding definitions) this fibre product classifies tuples
![]() $(\mathfrak {M},\imath ,\mathfrak {M}',\alpha )$
, where
$(\mathfrak {M},\imath ,\mathfrak {M}',\alpha )$
, where
![]() $\alpha $
is an isomorphism
$\alpha $
is an isomorphism
![]() $\mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {M}'$
which furthermore identifies
$\mathfrak {M} \buildrel \sim \over \longrightarrow \mathfrak {M}'$
which furthermore identifies
![]() $\imath ^{(f)}\circ \imath $
with
$\imath ^{(f)}\circ \imath $
with
![]() $\operatorname {id}_{\mathfrak {M}'}$
. Forgetting
$\operatorname {id}_{\mathfrak {M}'}$
. Forgetting
![]() $\mathfrak {M}'$
and
$\mathfrak {M}'$
and
![]() $\alpha $
then induces an isomorphism between
$\alpha $
then induces an isomorphism between
![]() $({\mathcal C}_L^{\tau |_L})^G$
, as defined via the above fibre product, and the stack defined in Definition 5.2.2.
$({\mathcal C}_L^{\tau |_L})^G$
, as defined via the above fibre product, and the stack defined in Definition 5.2.2.
To compare this fixed point stack to
![]() ${\mathcal C}^{\tau }_K$
, we make the following observations. Given a Breuil–Kisin module with descent data from
${\mathcal C}^{\tau }_K$
, we make the following observations. Given a Breuil–Kisin module with descent data from
![]() $K'$
to K, we obtain a Breuil–Kisin module with descent data from
$K'$
to K, we obtain a Breuil–Kisin module with descent data from
![]() $K'$
to L via the obvious forgetful map. Conversely, given a Breuil–Kisin module
$K'$
to L via the obvious forgetful map. Conversely, given a Breuil–Kisin module
![]() $\mathfrak {P}$
with descent data from
$\mathfrak {P}$
with descent data from
![]() $K'$
to L, the additional data required to enrich this to a Breuil–Kisin module with descent data from
$K'$
to L, the additional data required to enrich this to a Breuil–Kisin module with descent data from
![]() $K'$
to K can be described as follows: let
$K'$
to K can be described as follows: let
![]() $\theta \in \operatorname {\mathrm {Gal}}(K'/K)$
denote the unique element which fixes
$\theta \in \operatorname {\mathrm {Gal}}(K'/K)$
denote the unique element which fixes
![]() $\pi ^{1/(p^{2f}-1)}$
and acts nontrivially on L. Then, to enrich the descent data on
$\pi ^{1/(p^{2f}-1)}$
and acts nontrivially on L. Then, to enrich the descent data on
![]() $\mathfrak {P}$
to descent data from
$\mathfrak {P}$
to descent data from
![]() $K'$
to K, it is necessary and sufficient to give an additive map
$K'$
to K, it is necessary and sufficient to give an additive map
![]() $\hat \theta : \mathfrak {P} \to \mathfrak {P}$
satisfying
$\hat \theta : \mathfrak {P} \to \mathfrak {P}$
satisfying
![]() $\hat \theta (sm) = \theta (s)\hat \theta (m)$
for all
$\hat \theta (sm) = \theta (s)\hat \theta (m)$
for all
![]() $s \in \mathfrak {S}_{{\mathbf F}}$
and
$s \in \mathfrak {S}_{{\mathbf F}}$
and
![]() $m \in \mathfrak {P}$
, and such that
$m \in \mathfrak {P}$
, and such that
![]() $\hat \theta \hat g \hat \theta = \hat g^{p^f}$
for all
$\hat \theta \hat g \hat \theta = \hat g^{p^f}$
for all
![]() $g \in \operatorname {\mathrm {Gal}}(K'/L)$
.
$g \in \operatorname {\mathrm {Gal}}(K'/L)$
.
In turn, the data of the additive map
![]() $\hat \theta :\mathfrak {P}\to \mathfrak {P}$
is equivalent to giving the data of the map
$\hat \theta :\mathfrak {P}\to \mathfrak {P}$
is equivalent to giving the data of the map
![]() $\theta (\hat \theta ):\mathfrak {P}\to \mathfrak {P}^{(f)}$
obtained by composing
$\theta (\hat \theta ):\mathfrak {P}\to \mathfrak {P}^{(f)}$
obtained by composing
![]() $\hat \theta $
with the Frobenius on
$\hat \theta $
with the Frobenius on
![]() $L/K$
. The defining properties of
$L/K$
. The defining properties of
![]() $\hat \theta $
are equivalent to asking that this map is an isomorphism of Breuil–Kisin modules with descent data satisfying the cocycle condition of Definition 5.2.2; accordingly, we have a natural morphism
$\hat \theta $
are equivalent to asking that this map is an isomorphism of Breuil–Kisin modules with descent data satisfying the cocycle condition of Definition 5.2.2; accordingly, we have a natural morphism
![]() ${\mathcal C}_K^{\tau } \to ({\mathcal C}_L^{\tau _{|L}})^G$
, and a restriction morphism
${\mathcal C}_K^{\tau } \to ({\mathcal C}_L^{\tau _{|L}})^G$
, and a restriction morphism
The following simple lemma summarises the basic facts about base change in the situation we are considering.
Lemma 5.2.4. There is an isomorphism
![]() ${\mathcal C}_K^{\tau } \buildrel \sim \over \longrightarrow ({\mathcal C}_L^{\tau _{|L}})^G$
.
${\mathcal C}_K^{\tau } \buildrel \sim \over \longrightarrow ({\mathcal C}_L^{\tau _{|L}})^G$
.
Proof. This follows immediately from the preceding discussion.
Remark 5.2.5. In the proof of Theorem 5.2.9, we will make use of the following analogue of Lemma 5.2.4 for étale
![]() $\varphi $
-modules. Write
$\varphi $
-modules. Write
![]() ${\mathcal R}_K$
,
${\mathcal R}_K$
,
![]() ${\mathcal R}_L$
for the moduli stacks of Definition 2.3.7, that is, for the moduli stacks of rank two étale
${\mathcal R}_L$
for the moduli stacks of Definition 2.3.7, that is, for the moduli stacks of rank two étale
![]() $\varphi $
-modules with descent data, respectively, to K or to L. Then, we have an action of G on
$\varphi $
-modules with descent data, respectively, to K or to L. Then, we have an action of G on
![]() ${\mathcal R}_L$
defined via
${\mathcal R}_L$
defined via
![]() $M\mapsto M^{(f)}$
, with
$M\mapsto M^{(f)}$
, with
![]() $M^{(f)}$
defined analogously to
$M^{(f)}$
defined analogously to
![]() $\mathfrak {P}^{(f)}$
, and we define the fixed point stack
$\mathfrak {P}^{(f)}$
, and we define the fixed point stack
![]() $({\mathcal R}_L)^G$
exactly as in Definition 5.2.2: namely, an A-valued point of
$({\mathcal R}_L)^G$
exactly as in Definition 5.2.2: namely, an A-valued point of
![]() $({\mathcal R}_L)^G$
consists of an A-valued point M of
$({\mathcal R}_L)^G$
consists of an A-valued point M of
![]() ${\mathcal R}_L$
, together with an isomorphism
${\mathcal R}_L$
, together with an isomorphism
![]() $\iota :M\stackrel {\sim }{\longrightarrow } M^{(f)}$
satisfying the cocycle condition. The preceding discussion goes through in this setting, and shows that there is an isomorphism
$\iota :M\stackrel {\sim }{\longrightarrow } M^{(f)}$
satisfying the cocycle condition. The preceding discussion goes through in this setting, and shows that there is an isomorphism
![]() ${\mathcal R}_K\stackrel {\sim }{\longrightarrow } ({\mathcal R}_L)^G$
.
${\mathcal R}_K\stackrel {\sim }{\longrightarrow } ({\mathcal R}_L)^G$
.
We also note that the morphisms
![]() ${\mathcal C}_K^{\tau } \to {\mathcal C}_L^{\tau _{|L}}$
and
${\mathcal C}_K^{\tau } \to {\mathcal C}_L^{\tau _{|L}}$
and
![]() ${\mathcal C}_K^{\tau } \to {\mathcal R}_K$
induce a monomorphism
${\mathcal C}_K^{\tau } \to {\mathcal R}_K$
induce a monomorphism
One way to see this is to rewrite this morphism (using the previous discussion) as a morphism
and note that the descent data via G on an object classified by the source of this morphism are determined by the induced descent data on its image in
![]() $({\mathcal R}_L)^G$
.
$({\mathcal R}_L)^G$
.
We now use the Lemma 5.2.4 to study the locus of finite type points of
![]() ${\mathcal C}_K^{\tau }$
which correspond to irreducible Breuil–Kisin modules. Any irreducible Breuil–Kisin module over K becomes reducible when restricted to L, and so may be described as an extension
${\mathcal C}_K^{\tau }$
which correspond to irreducible Breuil–Kisin modules. Any irreducible Breuil–Kisin module over K becomes reducible when restricted to L, and so may be described as an extension
where
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
are Breuil–Kisin modules of rank one with descent data from
$\mathfrak {N}$
are Breuil–Kisin modules of rank one with descent data from
![]() $K'$
to L, and
$K'$
to L, and
![]() $\mathfrak {P}$
is additionally equipped with an isomorphism
$\mathfrak {P}$
is additionally equipped with an isomorphism
![]() $\mathfrak {P} \cong \mathfrak {P}^{(f)}$
, satisfying the cocycle condition of Definition 5.2.2.
$\mathfrak {P} \cong \mathfrak {P}^{(f)}$
, satisfying the cocycle condition of Definition 5.2.2.
Note that the characters
![]() $T(\mathfrak {M})$
,
$T(\mathfrak {M})$
,
![]() $T(\mathfrak {N})$
of
$T(\mathfrak {N})$
of
![]() $G_{L_{\infty }}$
are distinct and cannot be extended to characters of
$G_{L_{\infty }}$
are distinct and cannot be extended to characters of
![]() $G_K$
. Indeed, this condition is plainly necessary for an extension
$G_K$
. Indeed, this condition is plainly necessary for an extension
![]() $\mathfrak {P}$
to arise as the base change of an irreducible Breuil–Kisin module (see the proof of Lemma 2.2.6). Conversely, if
$\mathfrak {P}$
to arise as the base change of an irreducible Breuil–Kisin module (see the proof of Lemma 2.2.6). Conversely, if
![]() $T(\mathfrak {M})$
,
$T(\mathfrak {M})$
,
![]() $T(\mathfrak {N})$
of
$T(\mathfrak {N})$
of
![]() $G_{L_{\infty }}$
are distinct and cannot be extended to characters of
$G_{L_{\infty }}$
are distinct and cannot be extended to characters of
![]() $G_K$
, then for any
$G_K$
, then for any
![]() $\mathfrak {P} \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
whose descent data can be enriched to give descent data from
$\mathfrak {P} \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
whose descent data can be enriched to give descent data from
![]() $K'$
to K, this enrichment is necessarily irreducible. In particular, the existence of such a
$K'$
to K, this enrichment is necessarily irreducible. In particular, the existence of such a
![]() $\mathfrak {P}$
implies that the descent data on
$\mathfrak {P}$
implies that the descent data on
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
cannot be enriched to give descent data from
$\mathfrak {N}$
cannot be enriched to give descent data from
![]() $K'$
to K.
$K'$
to K.
We additionally have the following observation.
Lemma 5.2.7. If
![]() $\mathfrak {M},\mathfrak {N}$
are such that there is an extension
$\mathfrak {M},\mathfrak {N}$
are such that there is an extension
whose descent data can be enriched to give an irreducible Breuil–Kisin module over K, then there exists a nonzero map
![]() $\mathfrak {N} \to \mathfrak {M}^{(f)}$
.
$\mathfrak {N} \to \mathfrak {M}^{(f)}$
.
Proof. The composition
![]() $\mathfrak {N} \to \mathfrak {P} \xrightarrow {\hat \theta } \mathfrak {P} \to \mathfrak {M}$
, in which the first and last arrows are the natural inclusions and projections, must be nonzero (or else
$\mathfrak {N} \to \mathfrak {P} \xrightarrow {\hat \theta } \mathfrak {P} \to \mathfrak {M}$
, in which the first and last arrows are the natural inclusions and projections, must be nonzero (or else
![]() $\hat \theta $
would give descent data on
$\hat \theta $
would give descent data on
![]() $\mathfrak {N}$
from
$\mathfrak {N}$
from
![]() $K'$
to K). It is not itself a map of Breuil–Kisin modules, because
$K'$
to K). It is not itself a map of Breuil–Kisin modules, because
![]() $\hat \theta $
is semilinear, but is a map of Breuil–Kisin modules when viewed as a map
$\hat \theta $
is semilinear, but is a map of Breuil–Kisin modules when viewed as a map
![]() $\mathfrak {N} \to \mathfrak {M}^{(f)}$
.
$\mathfrak {N} \to \mathfrak {M}^{(f)}$
.
We now consider (for our fixed
![]() $\mathfrak {M}$
,
$\mathfrak {M}$
,
![]() $\mathfrak {N}$
, and working over L rather than over K) the scheme
$\mathfrak {N}$
, and working over L rather than over K) the scheme
![]() $\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
as in Section 3.3. Following Lemma 5.2.7, we assume that there exists a nonzero map
$\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
as in Section 3.3. Following Lemma 5.2.7, we assume that there exists a nonzero map
![]() $\mathfrak {N} \to \mathfrak {M}^{(f)}$
. The observations made above show that we are in the strict case, and thus that
$\mathfrak {N} \to \mathfrak {M}^{(f)}$
. The observations made above show that we are in the strict case, and thus that
![]() $\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} = {\mathbf G}_m\times {\mathbf G}_m$
and that furthermore we may (and do) set
$\operatorname {\mathrm {Spec}} A^{{\operatorname {dist}}} = {\mathbf G}_m\times {\mathbf G}_m$
and that furthermore we may (and do) set
![]() $V = T$
. We consider the fibre product with the restriction morphism (5.2.3)
$V = T$
. We consider the fibre product with the restriction morphism (5.2.3)
Let
![]() ${\mathbf G}_m \hookrightarrow {\mathbf G}_m\times {\mathbf G}_m$
be the diagonal closed immersion, and let
${\mathbf G}_m \hookrightarrow {\mathbf G}_m\times {\mathbf G}_m$
be the diagonal closed immersion, and let
![]() $(\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}})_{|{\mathbf G}_m}$
denote the pullback of
$(\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}})_{|{\mathbf G}_m}$
denote the pullback of
![]() $\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
along this closed immersion. By Lemma 5.2.7, the projection
$\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
along this closed immersion. By Lemma 5.2.7, the projection
![]() $Y(\mathfrak {M},\mathfrak {N}) \to \operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
factors through
$Y(\mathfrak {M},\mathfrak {N}) \to \operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}}$
factors through
![]() $(\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}})_{|{\mathbf G}_m},$
and combining this with Lemma 5.2.4, we see that
$(\operatorname {\mathrm {Spec}} B^{{\operatorname {dist}}})_{|{\mathbf G}_m},$
and combining this with Lemma 5.2.4, we see that
![]() $Y(\mathfrak {M},\mathfrak {N})$
may also be described as the fibre product
$Y(\mathfrak {M},\mathfrak {N})$
may also be described as the fibre product
Recalling the warning of Remark 3.3.16, Proposition 3.3.21 now shows that there is a monomorphism
and thus, by Lemma 3.2.8, that there is an isomorphism
(An inspection of the proof of Proposition 3.3.21 shows that, in fact, this result is more-or-less proved directly, as the key step in proving the proposition.) An elementary manipulation with fibre products then shows that there is an isomorphism
and thus, by another application of Lemma 3.2.8, we find that there is a monomorphism
We define
![]() ${\mathcal C}_{\operatorname {irred}}$
to be the union over all such pairs
${\mathcal C}_{\operatorname {irred}}$
to be the union over all such pairs
![]() $(\mathfrak {M},\mathfrak {N})$
of the scheme-theoretic images of the various projections
$(\mathfrak {M},\mathfrak {N})$
of the scheme-theoretic images of the various projections
![]() $Y(\mathfrak {M},\mathfrak {N}) \to ({\mathcal C}_L^{\tau _{|L}})^G$
. Note that this image depends on
$Y(\mathfrak {M},\mathfrak {N}) \to ({\mathcal C}_L^{\tau _{|L}})^G$
. Note that this image depends on
![]() $(\mathfrak {M},\mathfrak {N})$
up to simultaneous unramified twists of
$(\mathfrak {M},\mathfrak {N})$
up to simultaneous unramified twists of
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
, and there are only finitely many such pairs
$\mathfrak {N}$
, and there are only finitely many such pairs
![]() $(\mathfrak {M},\mathfrak {N})$
up to such unramified twist. By definition,
$(\mathfrak {M},\mathfrak {N})$
up to such unramified twist. By definition,
![]() ${\mathcal C}_{\operatorname {irred}}$
is a closed substack of
${\mathcal C}_{\operatorname {irred}}$
is a closed substack of
![]() ${\mathcal C}^{\tau }_K$
which contains every finite type point of
${\mathcal C}^{\tau }_K$
which contains every finite type point of
![]() ${\mathcal C}^{\tau }_K$
corresponding to an irreducible Breuil–Kisin module.
${\mathcal C}^{\tau }_K$
corresponding to an irreducible Breuil–Kisin module.
The following is the main result of this section.
Theorem 5.2.9. The closed substack
![]() ${\mathcal C}_{\operatorname {irred}}$
of
${\mathcal C}_{\operatorname {irred}}$
of
![]() ${\mathcal C}_K^{\tau }={\mathcal C}^{\tau ,\operatorname {BT},1}$
, which contains every finite type point of
${\mathcal C}_K^{\tau }={\mathcal C}^{\tau ,\operatorname {BT},1}$
, which contains every finite type point of
![]() ${\mathcal C}^{\tau }_K$
corresponding to an irreducible Breuil–Kisin module, has dimension strictly less than
${\mathcal C}^{\tau }_K$
corresponding to an irreducible Breuil–Kisin module, has dimension strictly less than
![]() $[K:{\mathbf Q}_p]$
.
$[K:{\mathbf Q}_p]$
.
Proof. As noted above, there are only finitely many pairs
![]() $(\mathfrak {M},\mathfrak {N})$
up to unramified twist, so it is enough to show that for each of them, the scheme-theoretic image of the monomorphism (5.2.8) has dimension less than
$(\mathfrak {M},\mathfrak {N})$
up to unramified twist, so it is enough to show that for each of them, the scheme-theoretic image of the monomorphism (5.2.8) has dimension less than
![]() $[K:{\mathbf Q}_p]$
.
$[K:{\mathbf Q}_p]$
.
By [Sta13, Tag 0DS6], to prove the present theorem, it then suffices to show that
![]() $\dim Y(\mathfrak {M},\mathfrak {N}) \leq [K:{\mathbf Q}_p] + 1$
(since
$\dim Y(\mathfrak {M},\mathfrak {N}) \leq [K:{\mathbf Q}_p] + 1$
(since
![]() $\dim {\mathbf G}_m\times {\mathbf G}_m = 2$
). To establish this, it suffices to show, for each point
$\dim {\mathbf G}_m\times {\mathbf G}_m = 2$
). To establish this, it suffices to show, for each point
![]() $x \in {\mathbf G}_m({\mathbf F}'),$
where
$x \in {\mathbf G}_m({\mathbf F}'),$
where
![]() ${\mathbf F}'$
is a finite extension of
${\mathbf F}'$
is a finite extension of
![]() ${\mathbf F}$
, that the dimension of the fibre
${\mathbf F}$
, that the dimension of the fibre
![]() $Y(\mathfrak {M},\mathfrak {N})_x$
is bounded by
$Y(\mathfrak {M},\mathfrak {N})_x$
is bounded by
![]() $[K:{\mathbf Q}_p]$
. After relabelling, as we may, the field
$[K:{\mathbf Q}_p]$
. After relabelling, as we may, the field
![]() ${\mathbf F}'$
as
${\mathbf F}'$
as
![]() ${\mathbf F}$
and the Breuil–Kisin modules
${\mathbf F}$
and the Breuil–Kisin modules
![]() $\mathfrak {M}_x$
and
$\mathfrak {M}_x$
and
![]() $\mathfrak {N}_x$
as
$\mathfrak {N}_x$
as
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
, we may suppose that, in fact,
$\mathfrak {N}$
, we may suppose that, in fact,
![]() ${\mathbf F}'={\mathbf F}$
and
${\mathbf F}'={\mathbf F}$
and
![]() $x=1$
.
$x=1$
.
Manipulating the fibre product appearing in the definition of
![]() $Y(\mathfrak {M},\mathfrak {N})$
, we find that
$Y(\mathfrak {M},\mathfrak {N})$
, we find that
where the fibre product is taken with respect to the morphism
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \to {\mathcal C}_L^{\tau }$
that associates the corresponding rank two extension to an extension of rank one Breuil–Kisin modules, and the restriction morphism (5.2.3).
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}) \to {\mathcal C}_L^{\tau }$
that associates the corresponding rank two extension to an extension of rank one Breuil–Kisin modules, and the restriction morphism (5.2.3).
In order to bound the dimension of
![]() $Y(\mathfrak {M},\mathfrak {N})_1$
, it will be easier to first embed it into another, larger, fibre product, which we now introduce. Namely, the monomorphism (5.2.6) induces a monomorphism
$Y(\mathfrak {M},\mathfrak {N})_1$
, it will be easier to first embed it into another, larger, fibre product, which we now introduce. Namely, the monomorphism (5.2.6) induces a monomorphism
Any finite type point of this fibre product lies over a fixed isomorphism class of finite type points of
![]() ${\mathcal R}_K$
(corresponding to some fixed irreducible Galois representation); we let P be a choice of such a point. The restriction of P then lies in a fixed isomorphism class of finite type points of
${\mathcal R}_K$
(corresponding to some fixed irreducible Galois representation); we let P be a choice of such a point. The restriction of P then lies in a fixed isomorphism class of finite type points of
![]() ${\mathcal R}_L$
(namely, the isomorphism class of the direct sum
${\mathcal R}_L$
(namely, the isomorphism class of the direct sum
![]() $\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] \cong \mathfrak {M}[1/u] \oplus \mathfrak {M}^{(f)}[1/u]$
). Thus, the projection
$\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] \cong \mathfrak {M}[1/u] \oplus \mathfrak {M}^{(f)}[1/u]$
). Thus, the projection
![]() $Y'(\mathfrak {M},\mathfrak {N})_1 \to {\mathcal R}_K$
factors through the residual gerbe of P, while the morphism
$Y'(\mathfrak {M},\mathfrak {N})_1 \to {\mathcal R}_K$
factors through the residual gerbe of P, while the morphism
![]() $Y'(\mathfrak {M},\mathfrak {N})_1 \to {\mathcal R}_L$
factors through the residual gerbe of
$Y'(\mathfrak {M},\mathfrak {N})_1 \to {\mathcal R}_L$
factors through the residual gerbe of
![]() $\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] \cong \mathfrak {M}[1/u] \oplus \mathfrak {M}^{(f)}[1/u]$
. Since P corresponds via Lemma 2.2.4 to an irreducible Galois representation, we find that
$\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] \cong \mathfrak {M}[1/u] \oplus \mathfrak {M}^{(f)}[1/u]$
. Since P corresponds via Lemma 2.2.4 to an irreducible Galois representation, we find that
![]() $\operatorname {\mathrm {Aut}}(P) = {\mathbf G}_m$
. Since
$\operatorname {\mathrm {Aut}}(P) = {\mathbf G}_m$
. Since
![]() $\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] $
corresponds via Lemma 2.2.4 to the direct sum of two nonisomorphic Galois characters, we find that
$\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] $
corresponds via Lemma 2.2.4 to the direct sum of two nonisomorphic Galois characters, we find that
![]() $\operatorname {\mathrm {Aut}}(\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] ) = {\mathbf G}_m \times {\mathbf G}_m$
.
$\operatorname {\mathrm {Aut}}(\mathfrak {M}[1/u]\oplus \mathfrak {N}[1/u] ) = {\mathbf G}_m \times {\mathbf G}_m$
.
Thus, we obtain monomorphisms
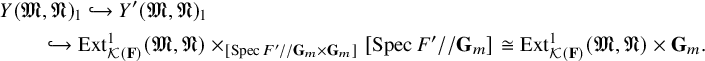 $$ \begin{align} &Y(\mathfrak{M},\mathfrak{N})_1 \hookrightarrow Y'(\mathfrak{M},\mathfrak{N})_1\notag\\ &\qquad \hookrightarrow \operatorname{\mathrm{Ext}}^1_{\mathcal{K}({\mathbf F})}(\mathfrak{M},\mathfrak{N}) \times_{[\operatorname{\mathrm{Spec}} F'//{\mathbf G}_m\times {\mathbf G}_m]} [\operatorname{\mathrm{Spec}} F'//{\mathbf G}_m] \cong \operatorname{\mathrm{Ext}}^1_{\mathcal{K}({\mathbf F})}(\mathfrak{M},\mathfrak{N}) \times {\mathbf G}_m. \end{align} $$
$$ \begin{align} &Y(\mathfrak{M},\mathfrak{N})_1 \hookrightarrow Y'(\mathfrak{M},\mathfrak{N})_1\notag\\ &\qquad \hookrightarrow \operatorname{\mathrm{Ext}}^1_{\mathcal{K}({\mathbf F})}(\mathfrak{M},\mathfrak{N}) \times_{[\operatorname{\mathrm{Spec}} F'//{\mathbf G}_m\times {\mathbf G}_m]} [\operatorname{\mathrm{Spec}} F'//{\mathbf G}_m] \cong \operatorname{\mathrm{Ext}}^1_{\mathcal{K}({\mathbf F})}(\mathfrak{M},\mathfrak{N}) \times {\mathbf G}_m. \end{align} $$
In Proposition 5.2.12, we obtain a description of the image of
![]() $Y(\mathfrak {M},\mathfrak {N})_1$
under this monomorphism which allows us to bound its dimension by
$Y(\mathfrak {M},\mathfrak {N})_1$
under this monomorphism which allows us to bound its dimension by
![]() $[K:{\mathbf Q}_p]$
, as required.
$[K:{\mathbf Q}_p]$
, as required.
We now prove the bound on the dimension of
![]() $Y(\mathfrak {M},\mathfrak {N})_1$
that we used in the proof of Theorem 5.2.9. Before establishing this bound, we make some further remarks. To begin with, we remind the reader that we are working with Breuil–Kisin modules, étale
$Y(\mathfrak {M},\mathfrak {N})_1$
that we used in the proof of Theorem 5.2.9. Before establishing this bound, we make some further remarks. To begin with, we remind the reader that we are working with Breuil–Kisin modules, étale
![]() $\varphi $
-modules, etc., over L rather than K, so that, for example, the structure parameters of
$\varphi $
-modules, etc., over L rather than K, so that, for example, the structure parameters of
![]() $\mathfrak {M}, \mathfrak {N}$
are periodic modulo
$\mathfrak {M}, \mathfrak {N}$
are periodic modulo
![]() $f' = 2f$
(not modulo f), and the pair
$f' = 2f$
(not modulo f), and the pair
![]() $(\mathfrak {M},\mathfrak {N})$
has type
$(\mathfrak {M},\mathfrak {N})$
has type
![]() $\tau |_L$
. We will readily apply various pieces of notation that were introduced above in the context of the field K, adapted in the obvious manner to the context of the field L. (This applies, in particular, to the notation
$\tau |_L$
. We will readily apply various pieces of notation that were introduced above in the context of the field K, adapted in the obvious manner to the context of the field L. (This applies, in particular, to the notation
![]() $\mathscr {C}^1_{u}$
,
$\mathscr {C}^1_{u}$
,
![]() $\mathscr {C}^0_{u}$
, etc. introduced in Definition 4.1.7.)
$\mathscr {C}^0_{u}$
, etc. introduced in Definition 4.1.7.)
We write
![]() $m, n$
for the standard generators of
$m, n$
for the standard generators of
![]() $\mathfrak {M}$
and
$\mathfrak {M}$
and
![]() $\mathfrak {N}$
. The existence of the nonzero map
$\mathfrak {N}$
. The existence of the nonzero map
![]() $\mathfrak {N} \to \mathfrak {M}^{(f)}$
implies that
$\mathfrak {N} \to \mathfrak {M}^{(f)}$
implies that
![]() $\alpha _i(\mathfrak {N}) \ge \alpha _{i+f}(\mathfrak {M})$
for all i, and also that
$\alpha _i(\mathfrak {N}) \ge \alpha _{i+f}(\mathfrak {M})$
for all i, and also that
![]() $\prod _i a_i = \prod _i b_i$
. Thanks to the latter, we will lose no generality by assuming that
$\prod _i a_i = \prod _i b_i$
. Thanks to the latter, we will lose no generality by assuming that
![]() $a_i = b_i =1 $
for all i. Let
$a_i = b_i =1 $
for all i. Let
![]() $\tilde m$
be the standard generator for
$\tilde m$
be the standard generator for
![]() $\mathfrak {M}^{(f)}$
. The map
$\mathfrak {M}^{(f)}$
. The map
![]() $\mathfrak {N} \to \mathfrak {M}^{(f)}$
will (up to a scalar) have the form
$\mathfrak {N} \to \mathfrak {M}^{(f)}$
will (up to a scalar) have the form
![]() $n_i \mapsto u^{x_i} \tilde m_{i}$
for integers
$n_i \mapsto u^{x_i} \tilde m_{i}$
for integers
![]() $x_i$
satisfying
$x_i$
satisfying
![]() $px_{i-1}-x_i = s_i - r_{i+f}$
for all i; thus,
$px_{i-1}-x_i = s_i - r_{i+f}$
for all i; thus,
![]() $x_i = \alpha _{i}(\mathfrak {N}) - \alpha _{i+f}(\mathfrak {M})$
for all i. Since the characters
$x_i = \alpha _{i}(\mathfrak {N}) - \alpha _{i+f}(\mathfrak {M})$
for all i. Since the characters
![]() $T(\mathfrak {M})$
and
$T(\mathfrak {M})$
and
![]() $T(\mathfrak {N})$
are conjugate, we must have
$T(\mathfrak {N})$
are conjugate, we must have
![]() $x_i \equiv d_i - c_{i+f} \pmod {p^{f'}-1}$
for all i (cf. Lemma 4.1.4). Moreover, the strong determinant condition
$x_i \equiv d_i - c_{i+f} \pmod {p^{f'}-1}$
for all i (cf. Lemma 4.1.4). Moreover, the strong determinant condition
![]() $s_i + r_i = e'$
for all i implies that
$s_i + r_i = e'$
for all i implies that
![]() $x_i = x_{i+f}$
.
$x_i = x_{i+f}$
.
We stress that we make no claims about the optimality of the following result; we merely prove ‘just what we need’ for our applications. Indeed, the estimates of [Reference HellmannHel09, Theorem 1.1] and [Reference CarusoCar17, Theorem 1] suggest that improvement should be possible by the methods of those papers.
Proposition 5.2.12. We have
![]() $\dim Y(\mathfrak {M},\mathfrak {N})_1 \le [K:{\mathbf Q}_p]$
.
$\dim Y(\mathfrak {M},\mathfrak {N})_1 \le [K:{\mathbf Q}_p]$
.
Remark 5.2.13. Since the image of
![]() $Y(\mathfrak {M},\mathfrak {N})_1$
in
$Y(\mathfrak {M},\mathfrak {N})_1$
in
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
lies in
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
lies in
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
with fibres that can be seen to have dimension at most one, many cases of Proposition 5.2.12 will already follow from Remark 5.1.5 (applied with L in place of K).
${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
with fibres that can be seen to have dimension at most one, many cases of Proposition 5.2.12 will already follow from Remark 5.1.5 (applied with L in place of K).
Proof of Proposition 5.2.12
Let
![]() $\mathfrak {P} = \mathfrak {P}(h)$
be an element of
$\mathfrak {P} = \mathfrak {P}(h)$
be an element of
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
whose descent data can be enriched to give descent data from
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
whose descent data can be enriched to give descent data from
![]() $K'$
to K, and let
$K'$
to K, and let
![]() $\widetilde {\mathfrak {P}}$
be such an enrichment. By Lemma 5.2.7 (and the discussion preceding that lemma), the étale
$\widetilde {\mathfrak {P}}$
be such an enrichment. By Lemma 5.2.7 (and the discussion preceding that lemma), the étale
![]() $\varphi $
-module
$\varphi $
-module
![]() $\mathfrak {P}[\frac 1u]$
is isomorphic to
$\mathfrak {P}[\frac 1u]$
is isomorphic to
![]() $\mathfrak {M}[\frac 1u] \oplus \mathfrak {M}^{(f)}[\frac 1u]$
. All extensions of the
$\mathfrak {M}[\frac 1u] \oplus \mathfrak {M}^{(f)}[\frac 1u]$
. All extensions of the
![]() $G_{L_{\infty }}$
-representation
$G_{L_{\infty }}$
-representation
![]() $T(\mathfrak {M}[\frac 1u] \oplus \mathfrak {M}^{(f)}[\frac 1u])$
to a representation of
$T(\mathfrak {M}[\frac 1u] \oplus \mathfrak {M}^{(f)}[\frac 1u])$
to a representation of
![]() $G_{K_{\infty }}$
are isomorphic (and given by the induction of
$G_{K_{\infty }}$
are isomorphic (and given by the induction of
![]() $T(\mathfrak {M}[\frac 1u])$
to
$T(\mathfrak {M}[\frac 1u])$
to
![]() $G_{K_{\infty }}$
), so the same is true of the étale
$G_{K_{\infty }}$
), so the same is true of the étale
![]() $\varphi $
-modules with descent data from
$\varphi $
-modules with descent data from
![]() $K'$
to K that enrich the descent data on
$K'$
to K that enrich the descent data on
![]() $\mathfrak {M}[\frac 1u] \oplus \mathfrak {M}^{(f)}[\frac 1u]$
. One such enrichment, which we denote P, has
$\mathfrak {M}[\frac 1u] \oplus \mathfrak {M}^{(f)}[\frac 1u]$
. One such enrichment, which we denote P, has
![]() $\hat \theta $
that interchanges m and
$\hat \theta $
that interchanges m and
![]() $\tilde m$
. Thus,
$\tilde m$
. Thus,
![]() $\widetilde {\mathfrak {P}}[\frac 1u]$
is isomorphic to P.
$\widetilde {\mathfrak {P}}[\frac 1u]$
is isomorphic to P.
As in the proof of Lemma 5.2.7, the hypothesis that
![]() $T(\mathfrak {M}) \not \cong T(\mathfrak {N})$
implies that any nonzero map (equivalently, isomorphism) of étale
$T(\mathfrak {M}) \not \cong T(\mathfrak {N})$
implies that any nonzero map (equivalently, isomorphism) of étale
![]() $\varphi $
-modules with descent data
$\varphi $
-modules with descent data
![]() $\lambda : \widetilde {\mathfrak {P}}[\frac 1u] \to P$
takes the submodule
$\lambda : \widetilde {\mathfrak {P}}[\frac 1u] \to P$
takes the submodule
![]() $\mathfrak {N}[\frac 1u]$
to
$\mathfrak {N}[\frac 1u]$
to
![]() $\mathfrak {M}^{(f)}[\frac 1u]$
. We may scale the map
$\mathfrak {M}^{(f)}[\frac 1u]$
. We may scale the map
![]() $\lambda $
so that it restricts to the map
$\lambda $
so that it restricts to the map
![]() $n_i \to u^{x_i} \tilde m_i$
on
$n_i \to u^{x_i} \tilde m_i$
on
![]() $\mathfrak {N}$
. Then, there is an element
$\mathfrak {N}$
. Then, there is an element
![]() $\xi \in {\mathbf F}^{\times }$
so that
$\xi \in {\mathbf F}^{\times }$
so that
![]() $\lambda $
induces multiplication by
$\lambda $
induces multiplication by
![]() $\xi $
on the common quotients
$\xi $
on the common quotients
![]() $\mathfrak {M}[\frac 1u]$
. That is, the map
$\mathfrak {M}[\frac 1u]$
. That is, the map
![]() $\lambda $
may be assumed to have the form
$\lambda $
may be assumed to have the form
 $$ \begin{align} \begin{pmatrix} n_{i} \\ m_{i} \end{pmatrix} \mapsto \begin{pmatrix} u^{x_i} & 0 \\ \nu_i & \xi \end{pmatrix} \begin{pmatrix} \tilde m_{i} \\ m_{i} \end{pmatrix} \end{align} $$
$$ \begin{align} \begin{pmatrix} n_{i} \\ m_{i} \end{pmatrix} \mapsto \begin{pmatrix} u^{x_i} & 0 \\ \nu_i & \xi \end{pmatrix} \begin{pmatrix} \tilde m_{i} \\ m_{i} \end{pmatrix} \end{align} $$
for some
![]() $(\nu _i) \in {\mathbf F}((u))^{f'}$
. The condition that the map
$(\nu _i) \in {\mathbf F}((u))^{f'}$
. The condition that the map
![]() $\lambda $
commutes with the descent data from
$\lambda $
commutes with the descent data from
![]() $K'$
to L is seen to be equivalent to the condition that nonzero terms in
$K'$
to L is seen to be equivalent to the condition that nonzero terms in
![]() $\nu _i$
have degree congruent to
$\nu _i$
have degree congruent to
![]() $c_i -d_i + x_i \pmod {p^{f'}-1}$
; or equivalently, if we define
$c_i -d_i + x_i \pmod {p^{f'}-1}$
; or equivalently, if we define
![]() $\mu _i := \nu _i u^{-x_i}$
for all i, that the tuple
$\mu _i := \nu _i u^{-x_i}$
for all i, that the tuple
![]() $\mu = (\mu _i)$
is an element of the set
$\mu = (\mu _i)$
is an element of the set
![]() $\mathscr {C}^0_{u} = \mathscr {C}^0_{u}(\mathfrak {M},\mathfrak {N})$
of Definition 4.1.7.
$\mathscr {C}^0_{u} = \mathscr {C}^0_{u}(\mathfrak {M},\mathfrak {N})$
of Definition 4.1.7.
The condition that
![]() $\lambda $
commutes with
$\lambda $
commutes with
![]() $\varphi $
can be checked to give
$\varphi $
can be checked to give
 $$ \begin{align*} \varphi \begin{pmatrix} n_{i-1} \\ m_{i-1} \end{pmatrix} = \begin{pmatrix} u^{s_i} & 0 \\ \varphi(\nu_{i-1}) u^{r_{i+f}-x_i} - \nu_i u^{r_i-x_i} & u^{r_i} \end{pmatrix}\begin{pmatrix} n_{i} \\ m_{i} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \varphi \begin{pmatrix} n_{i-1} \\ m_{i-1} \end{pmatrix} = \begin{pmatrix} u^{s_i} & 0 \\ \varphi(\nu_{i-1}) u^{r_{i+f}-x_i} - \nu_i u^{r_i-x_i} & u^{r_i} \end{pmatrix}\begin{pmatrix} n_{i} \\ m_{i} \end{pmatrix}. \end{align*} $$
The extension
![]() $\mathfrak {P}$
is of the form
$\mathfrak {P}$
is of the form
![]() $\mathfrak {P}(h)$
, for some
$\mathfrak {P}(h)$
, for some
![]() $h \in \mathscr {C}^1$
, as in Definition 4.1.7. The lower-left entry of the first matrix on the right-hand side of the above equation must then be
$h \in \mathscr {C}^1$
, as in Definition 4.1.7. The lower-left entry of the first matrix on the right-hand side of the above equation must then be
![]() $h_i$
. Since
$h_i$
. Since
![]() $r_{i+f}-x_i = s_i - px_{i-1}$
, the resulting condition can be rewritten as
$r_{i+f}-x_i = s_i - px_{i-1}$
, the resulting condition can be rewritten as
or equivalently, that
![]() $h = \partial (\mu )$
. Comparing with Remark 5.1.3, we recover the fact that the extension class of
$h = \partial (\mu )$
. Comparing with Remark 5.1.3, we recover the fact that the extension class of
![]() $\mathfrak {P}$
is an element of
$\mathfrak {P}$
is an element of
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, and the tuple
${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, and the tuple
![]() $\mu $
determines an element of the space
$\mu $
determines an element of the space
![]() $\mathscr {H}$
defined as follows.
$\mathscr {H}$
defined as follows.
Definition 5.2.15. The map
![]() $\partial \colon \mathscr {C}^0_{u} \to \mathscr {C}^1_{u}$
induces a map
$\partial \colon \mathscr {C}^0_{u} \to \mathscr {C}^1_{u}$
induces a map
![]() $\mathscr {C}^0_{u}/\mathscr {C}^0 \to \mathscr {C}^1_{u}/\partial (\mathscr {C}^0)$
, which we also denote
$\mathscr {C}^0_{u}/\mathscr {C}^0 \to \mathscr {C}^1_{u}/\partial (\mathscr {C}^0)$
, which we also denote
![]() $\partial $
. We let
$\partial $
. We let
![]() $\mathscr {H} \subset \mathscr {C}^0_{u}/\mathscr {C}^0$
denote the subspace consisting of elements
$\mathscr {H} \subset \mathscr {C}^0_{u}/\mathscr {C}^0$
denote the subspace consisting of elements
![]() $\mu $
, such that
$\mu $
, such that
![]() $\partial (\mu ) \in \mathscr {C}^1/\partial (\mathscr {C}^0)$
.
$\partial (\mu ) \in \mathscr {C}^1/\partial (\mathscr {C}^0)$
.
By the discussion following Lemma 4.1.8, an element
![]() $\mu \in \mathscr {H}$
determines an extension
$\mu \in \mathscr {H}$
determines an extension
![]() $\mathfrak {P}(\partial (\mu ))$
. Indeed, Remark 5.1.3 and the proof of (3.1.31) taken together show that there is a natural isomorphism, in the style of Lemma 4.1.8, between the morphism
$\mathfrak {P}(\partial (\mu ))$
. Indeed, Remark 5.1.3 and the proof of (3.1.31) taken together show that there is a natural isomorphism, in the style of Lemma 4.1.8, between the morphism
![]() $\partial : \mathscr {H} \to \mathscr {C}^1/\partial (\mathscr {C}^0)$
and the connection map
$\partial : \mathscr {H} \to \mathscr {C}^1/\partial (\mathscr {C}^0)$
and the connection map
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N}) \to \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, with
$\operatorname {\mathrm {Hom}}_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N}[1/u]/\mathfrak {N}) \to \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
, with
![]() $\operatorname {\mathrm {im}}\partial $
corresponding to
$\operatorname {\mathrm {im}}\partial $
corresponding to
![]() ${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
.
${\text{ker-Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
.
Conversely, let h be an element of
![]() $\partial (\mathscr {C}^0_{u}) \cap \mathscr {C}^1$
, and set
$\partial (\mathscr {C}^0_{u}) \cap \mathscr {C}^1$
, and set
![]() $\nu _i = u^{x_i} \mu _i$
. The condition that there is a Breuil–Kisin module
$\nu _i = u^{x_i} \mu _i$
. The condition that there is a Breuil–Kisin module
![]() $\widetilde {\mathfrak {P}}$
with descent data from
$\widetilde {\mathfrak {P}}$
with descent data from
![]() $K'$
to K and
$K'$
to K and
![]() $\xi \in {\mathbf F}^{\times }$
, such that
$\xi \in {\mathbf F}^{\times }$
, such that
![]() $\lambda : \widetilde {\mathfrak {P}}[\frac 1u] \to P$
defined as above is an isomorphism is precisely the condition that the map
$\lambda : \widetilde {\mathfrak {P}}[\frac 1u] \to P$
defined as above is an isomorphism is precisely the condition that the map
![]() $\hat \theta $
on P pulls back via
$\hat \theta $
on P pulls back via
![]() $\lambda $
to a map that preserves
$\lambda $
to a map that preserves
![]() $\mathfrak {P}$
. One computes that this pullback is
$\mathfrak {P}$
. One computes that this pullback is
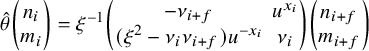 $$ \begin{align*} \hat\theta \begin{pmatrix} n_{i} \\ m_{i} \end{pmatrix} = \xi^{-1} \begin{pmatrix} -\nu_{i+f} & u^{x_i} \\ (\xi^2-\nu_i \nu_{i+f}) u^{-x_i} & \nu_i \end{pmatrix} \begin{pmatrix} n_{i+f} \\ m_{i+f} \end{pmatrix} \end{align*} $$
$$ \begin{align*} \hat\theta \begin{pmatrix} n_{i} \\ m_{i} \end{pmatrix} = \xi^{-1} \begin{pmatrix} -\nu_{i+f} & u^{x_i} \\ (\xi^2-\nu_i \nu_{i+f}) u^{-x_i} & \nu_i \end{pmatrix} \begin{pmatrix} n_{i+f} \\ m_{i+f} \end{pmatrix} \end{align*} $$
recalling that
![]() $x_i =x_{i+f}$
.
$x_i =x_{i+f}$
.
We deduce that
![]() $\hat \theta $
preserves
$\hat \theta $
preserves
![]() $\mathfrak {P}$
precisely when the
$\mathfrak {P}$
precisely when the
![]() $\nu _i$
are integral and
$\nu _i$
are integral and
![]() $\nu _i \nu _{i+f} \equiv \xi ^2 \pmod {u^{x_i}}$
for all i. For i with
$\nu _i \nu _{i+f} \equiv \xi ^2 \pmod {u^{x_i}}$
for all i. For i with
![]() $x_i=0$
, the latter condition is automatic given the former, which is equivalent to the condition that
$x_i=0$
, the latter condition is automatic given the former, which is equivalent to the condition that
![]() $\mu _i$
and
$\mu _i$
and
![]() $\mu _{i+f}$
are both integral. If instead
$\mu _{i+f}$
are both integral. If instead
![]() $x_i> 0$
, then we have the nontrivial condition
$x_i> 0$
, then we have the nontrivial condition
![]() $\nu _{i+f} \equiv \xi ^2 \nu _{i}^{-1} \pmod {u^{x_i}}$
; in other words, that
$\nu _{i+f} \equiv \xi ^2 \nu _{i}^{-1} \pmod {u^{x_i}}$
; in other words, that
![]() $\mu _i, \mu _{i+f}$
have u-adic valuation exactly
$\mu _i, \mu _{i+f}$
have u-adic valuation exactly
![]() $-x_i$
, and their principal parts determine one another via the equation
$-x_i$
, and their principal parts determine one another via the equation
![]() $\mu _{i+f} \equiv \xi ^2 (u^{2x_i} \mu _i )^{-1} \pmod {1}$
.
$\mu _{i+f} \equiv \xi ^2 (u^{2x_i} \mu _i )^{-1} \pmod {1}$
.
Let
![]() $\mathbf {G}_{m,\xi }$
be the multiplicative group with parameter
$\mathbf {G}_{m,\xi }$
be the multiplicative group with parameter
![]() $\xi $
. We now (using the notation of Definition 5.2.15) define
$\xi $
. We now (using the notation of Definition 5.2.15) define
![]() $\mathscr {H}' \subset \mathscr {C}^0_{u}/\mathscr {C}^0 \times \mathbf {G}_{m,\xi }$
to be the subvariety consisting of the pairs
$\mathscr {H}' \subset \mathscr {C}^0_{u}/\mathscr {C}^0 \times \mathbf {G}_{m,\xi }$
to be the subvariety consisting of the pairs
![]() $(\mu ,\xi )$
with exactly the preceding properties; that is, we regard
$(\mu ,\xi )$
with exactly the preceding properties; that is, we regard
![]() $\mathscr {C}^0_{u}/\mathscr {C}^0$
as an Ind-affine space in the obvious way, and define
$\mathscr {C}^0_{u}/\mathscr {C}^0$
as an Ind-affine space in the obvious way, and define
![]() $\mathscr {H}'$
to be the pairs
$\mathscr {H}'$
to be the pairs
![]() $(\mu ,\xi )$
satisfying
$(\mu ,\xi )$
satisfying
-
○ if
 $x_i=0$
, then
$x_i=0$
, then
 $\operatorname {\mathrm {val}}_i \mu = \operatorname {\mathrm {val}}_{i+f} \mu =\infty $
, and
$\operatorname {\mathrm {val}}_i \mu = \operatorname {\mathrm {val}}_{i+f} \mu =\infty $
, and -
○ if
 $x_i>0$
, then
$x_i>0$
, then
 $\operatorname {\mathrm {val}}_i \mu = \operatorname {\mathrm {val}}_{i+f} \mu = -x_i$
and
$\operatorname {\mathrm {val}}_i \mu = \operatorname {\mathrm {val}}_{i+f} \mu = -x_i$
and
 $\mu _{i+f} \equiv \xi ^2 (u^{2x_i} \mu _i)^{-1}\ \pmod {u^0}$
,
$\mu _{i+f} \equiv \xi ^2 (u^{2x_i} \mu _i)^{-1}\ \pmod {u^0}$
,
where we write
![]() $\operatorname {\mathrm {val}}_i \mu $
for the u-adic valuation of
$\operatorname {\mathrm {val}}_i \mu $
for the u-adic valuation of
![]() $\mu _i$
, putting
$\mu _i$
, putting
![]() $\operatorname {\mathrm {val}}_i \mu = \infty $
when
$\operatorname {\mathrm {val}}_i \mu = \infty $
when
![]() $\mu _i$
is integral.
$\mu _i$
is integral.
Putting all this together with (5.2.10), we find that the map
sending
![]() $(\mu ,\xi )$
to the pair
$(\mu ,\xi )$
to the pair
![]() $(\mathfrak {P},\widetilde {\mathfrak {P}})$
is a well-defined surjection, where
$(\mathfrak {P},\widetilde {\mathfrak {P}})$
is a well-defined surjection, where
![]() $\mathfrak {P} = \mathfrak {P}(\partial (\mu ))$
,
$\mathfrak {P} = \mathfrak {P}(\partial (\mu ))$
,
![]() $\widetilde {\mathfrak {P}}$
is the enrichment of
$\widetilde {\mathfrak {P}}$
is the enrichment of
![]() $\mathfrak {P}$
to a Breuil–Kisin module with descent data from
$\mathfrak {P}$
to a Breuil–Kisin module with descent data from
![]() $K'$
to K in which
$K'$
to K in which
![]() $\hat \theta $
is pulled back to
$\hat \theta $
is pulled back to
![]() $\mathfrak {P}$
from P via the map
$\mathfrak {P}$
from P via the map
![]() $\lambda $
as in (5.2.14). (Note that
$\lambda $
as in (5.2.14). (Note that
![]() $Y(\mathfrak {M},\mathfrak {N})_1$
is reduced and of finite type, for example, by (5.2.11), so the surjectivity can be checked on
$Y(\mathfrak {M},\mathfrak {N})_1$
is reduced and of finite type, for example, by (5.2.11), so the surjectivity can be checked on
![]() $\overline {{\mathbf F}}_p$
-points.) In particular,
$\overline {{\mathbf F}}_p$
-points.) In particular,
![]() $\dim Y(\mathfrak {M},\mathfrak {N})_1 \le \dim \mathscr {H}'.$
$\dim Y(\mathfrak {M},\mathfrak {N})_1 \le \dim \mathscr {H}'.$
Note that
![]() $\mathscr {H}'$
will be empty, if for some i, we have
$\mathscr {H}'$
will be empty, if for some i, we have
![]() $x_i> 0$
but
$x_i> 0$
but
![]() $x_i + c_i-d_i \not \equiv 0 \pmod {p^{f'}-1}$
(so that
$x_i + c_i-d_i \not \equiv 0 \pmod {p^{f'}-1}$
(so that
![]() $\nu _i$
cannot be a u-adic unit). Otherwise, the dimension of
$\nu _i$
cannot be a u-adic unit). Otherwise, the dimension of
![]() $\mathscr {H}'$
is easily computed to be
$\mathscr {H}'$
is easily computed to be
![]() $D = 1+\sum _{i=0}^{f-1} \lceil x_i/(p^{f'}-1) \rceil $
(indeed, if d is the number of nonzero
$D = 1+\sum _{i=0}^{f-1} \lceil x_i/(p^{f'}-1) \rceil $
(indeed, if d is the number of nonzero
![]() $x_i$
’s, then
$x_i$
’s, then
![]() $\mathscr {H}' \cong {\mathbf G}_m^{d+1} \times {\mathbf G}_a^{D-d-1}$
), and since
$\mathscr {H}' \cong {\mathbf G}_m^{d+1} \times {\mathbf G}_a^{D-d-1}$
), and since
![]() $x_i \le e'/(p-1)$
, we find that
$x_i \le e'/(p-1)$
, we find that
![]() $\mathscr {H}'$
has dimension at most
$\mathscr {H}'$
has dimension at most
![]() $1 + \lceil e/(p-1) \rceil f$
. This establishes the bound
$1 + \lceil e/(p-1) \rceil f$
. This establishes the bound
![]() $\dim Y(\mathfrak {M},\mathfrak {N})_1 \le 1 + \lceil e/(p-1) \rceil f$
.
$\dim Y(\mathfrak {M},\mathfrak {N})_1 \le 1 + \lceil e/(p-1) \rceil f$
.
Since
![]() $p> 2$
, this bound already establishes the theorem when
$p> 2$
, this bound already establishes the theorem when
![]() $e> 1$
. If instead,
$e> 1$
. If instead,
![]() $e=1$
, the above bound gives
$e=1$
, the above bound gives
![]() $\dim Y(\mathfrak {M},\mathfrak {N}) \le [K:{\mathbf Q}_p] + 1$
. Suppose for the sake of contradiction that equality holds. This is only possible if
$\dim Y(\mathfrak {M},\mathfrak {N}) \le [K:{\mathbf Q}_p] + 1$
. Suppose for the sake of contradiction that equality holds. This is only possible if
![]() $\mathscr {H}' \cong {\mathbf G}_m^{f+1}$
,
$\mathscr {H}' \cong {\mathbf G}_m^{f+1}$
,
![]() $\mathscr {H}' \subset \mathscr {H} \times \mathbf {G}_{m,\xi }$
and
$\mathscr {H}' \subset \mathscr {H} \times \mathbf {G}_{m,\xi }$
and
![]() $x_i = [d_i - c_i]> 0$
for all i. Define
$x_i = [d_i - c_i]> 0$
for all i. Define
![]() $\mu ^{(i)} \in \mathscr {C}^0_{u}$
to be the element, such that
$\mu ^{(i)} \in \mathscr {C}^0_{u}$
to be the element, such that
![]() $\mu _{i} = u^{-[d_{i}-c_{i}]}$
, and
$\mu _{i} = u^{-[d_{i}-c_{i}]}$
, and
![]() $\mu _j = 0$
for
$\mu _j = 0$
for
![]() $j \neq i$
. Let
$j \neq i$
. Let
![]() ${\mathbf F}"/{\mathbf F}$
be any finite extension, such that
${\mathbf F}"/{\mathbf F}$
be any finite extension, such that
![]() $\#{\mathbf F}"> 3$
. For each nonzero
$\#{\mathbf F}"> 3$
. For each nonzero
![]() $z \in {\mathbf F}"$
, define
$z \in {\mathbf F}"$
, define
![]() $\mu _z = \sum _{j \neq i,i+f} \mu ^{(i)} + z \mu ^{(i)} + z^{-1} \mu ^{(i+f)}$
, so that
$\mu _z = \sum _{j \neq i,i+f} \mu ^{(i)} + z \mu ^{(i)} + z^{-1} \mu ^{(i+f)}$
, so that
![]() $(\mu _z, 1)$
is an element of
$(\mu _z, 1)$
is an element of
![]() $\mathscr {H}'({\mathbf F}")$
. Since
$\mathscr {H}'({\mathbf F}")$
. Since
![]() $\mathscr {H}' \subset \mathscr {H} \times \mathbf {G}_{m,\xi }$
and
$\mathscr {H}' \subset \mathscr {H} \times \mathbf {G}_{m,\xi }$
and
![]() $\mathscr {H}$
is linear, the differences between the
$\mathscr {H}$
is linear, the differences between the
![]() $\mu _z$
for varying z lie in
$\mu _z$
for varying z lie in
![]() $\mathscr {H}({\mathbf F}")$
, and (e.g. by considering
$\mathscr {H}({\mathbf F}")$
, and (e.g. by considering
![]() $\mu _1 - \mu _{-1}$
and
$\mu _1 - \mu _{-1}$
and
![]() $\mu _1 - \mu _{z}$
for any
$\mu _1 - \mu _{z}$
for any
![]() $z \in {\mathbf F}"$
with
$z \in {\mathbf F}"$
with
![]() $z\neq z^{-1}$
) we deduce that each
$z\neq z^{-1}$
) we deduce that each
![]() $\mu ^{(i)}$
lies in
$\mu ^{(i)}$
lies in
![]() $\mathscr {H}$
. In particular, each
$\mathscr {H}$
. In particular, each
![]() $\partial (\mu ^{(i)})$
lies in
$\partial (\mu ^{(i)})$
lies in
![]() $\mathscr {C}^1$
.
$\mathscr {C}^1$
.
If
![]() $(i-1,i)$
were not a transition, then (since
$(i-1,i)$
were not a transition, then (since
![]() $e=1$
), we would have either
$e=1$
), we would have either
![]() $r_i =0 $
or
$r_i =0 $
or
![]() $s_i = 0$
. The former would contradict
$s_i = 0$
. The former would contradict
![]() $\partial (\mu ^{(i)}) \in \mathscr {C}^1$
(since the ith component of
$\partial (\mu ^{(i)}) \in \mathscr {C}^1$
(since the ith component of
![]() $\partial (\mu ^{(i)})$
would be
$\partial (\mu ^{(i)})$
would be
![]() $u^{-[d_i-c_i]}$
, of negative degree), and, similarly, the latter would contradict
$u^{-[d_i-c_i]}$
, of negative degree), and, similarly, the latter would contradict
![]() $\partial (\mu ^{(i-1)}) \in \mathscr {C}^1$
. Thus,
$\partial (\mu ^{(i-1)}) \in \mathscr {C}^1$
. Thus,
![]() $(i-1,i)$
is a transition for all i. In fact, the same observations show more precisely that
$(i-1,i)$
is a transition for all i. In fact, the same observations show more precisely that
![]() $r_i \ge x_i = [d_i-c_i]$
and
$r_i \ge x_i = [d_i-c_i]$
and
![]() $s_i \ge p x_{i-1} = p [d_{i-1}-c_{i-1}]$
. Summing these inequalities and subtracting
$s_i \ge p x_{i-1} = p [d_{i-1}-c_{i-1}]$
. Summing these inequalities and subtracting
![]() $e'$
, we obtain
$e'$
, we obtain
![]() $0 \ge p [d_{i-1}-c_{i-1}] - [c_i-d_i]$
, and comparing with (5.1.6) shows that we must also have
$0 \ge p [d_{i-1}-c_{i-1}] - [c_i-d_i]$
, and comparing with (5.1.6) shows that we must also have
![]() $\gamma _i^{*}=0$
for all i. Since
$\gamma _i^{*}=0$
for all i. Since
![]() $e=1$
and
$e=1$
and
![]() $(i-1,i)$
is a transition for all i, the refined profile of the pair
$(i-1,i)$
is a transition for all i, the refined profile of the pair
![]() $(\mathfrak {M},\mathfrak {N})$
is automatically maximal; but then we are in the exceptional case of Proposition 5.1.8, which (recalling the proof of that proposition) implies that
$(\mathfrak {M},\mathfrak {N})$
is automatically maximal; but then we are in the exceptional case of Proposition 5.1.8, which (recalling the proof of that proposition) implies that
![]() $T(\mathfrak {M}) \cong T(\mathfrak {N})$
. This is the desired contradiction.
$T(\mathfrak {M}) \cong T(\mathfrak {N})$
. This is the desired contradiction.
5.3. Irreducible components
We can now use our results on families of extensions of characters to classify the irreducible components of the stacks
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
${\mathcal C}^{\tau ,\operatorname {BT},1}$
and
![]() ${\mathcal Z}^{\tau ,1}$
. In the article [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we will combine these results with results coming from Taylor–Wiles patching (in particular, the results of [Reference Gee and KisinGK14, Reference Emerton and GeeEG14]) to describe the closed points of each irreducible component of
${\mathcal Z}^{\tau ,1}$
. In the article [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we will combine these results with results coming from Taylor–Wiles patching (in particular, the results of [Reference Gee and KisinGK14, Reference Emerton and GeeEG14]) to describe the closed points of each irreducible component of
![]() ${\mathcal Z}^{\tau ,1}$
in terms of the weight part of Serre’s conjecture.
${\mathcal Z}^{\tau ,1}$
in terms of the weight part of Serre’s conjecture.
Corollary 5.3.1. Each irreducible component of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is of the form
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is of the form
![]() $\overline {{\mathcal C}}(J)$
for some J; conversely, each
$\overline {{\mathcal C}}(J)$
for some J; conversely, each
![]() $\overline {{\mathcal C}}(J)$
is an irreducible component of
$\overline {{\mathcal C}}(J)$
is an irreducible component of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
.
${\mathcal C}^{\tau ,\operatorname {BT},1}$
.
Remark 5.3.2. Note that at this point, we have not established that different sets J give distinct irreducible components
![]() $\overline {{\mathcal C}}(J)$
; we will prove this in Section 5.4 below by a consideration of Dieudonné modules.
$\overline {{\mathcal C}}(J)$
; we will prove this in Section 5.4 below by a consideration of Dieudonné modules.
Proof of Corollary 5.3.1
By Theorem 2.3.6(2),
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is equidimensional of dimension
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is equidimensional of dimension
![]() $[K:{\mathbf Q}_p]$
. By construction, the
$[K:{\mathbf Q}_p]$
. By construction, the
![]() $\overline {{\mathcal C}}(J)$
are irreducible substacks of
$\overline {{\mathcal C}}(J)$
are irreducible substacks of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and by Theorem 4.2.11, they also have dimension
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, and by Theorem 4.2.11, they also have dimension
![]() $[K:{\mathbf Q}_p]$
, so they are, in fact, irreducible components by [Sta13, Tag 0DS2].
$[K:{\mathbf Q}_p]$
, so they are, in fact, irreducible components by [Sta13, Tag 0DS2].
By Theorems 5.2.9 and 4.2.11, we see that there is a closed substack
![]() ${\mathcal C}_{\mathrm {small}}$
of
${\mathcal C}_{\mathrm {small}}$
of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
of dimension strictly less than
${\mathcal C}^{\tau ,\operatorname {BT},1}$
of dimension strictly less than
![]() $[K:{\mathbf Q}_p]$
, with the property that every finite type point of
$[K:{\mathbf Q}_p]$
, with the property that every finite type point of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is a point of at least one of the
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is a point of at least one of the
![]() $\overline {{\mathcal C}}(J)$
or of
$\overline {{\mathcal C}}(J)$
or of
![]() ${\mathcal C}_{\mathrm {small}}$
(or both). Indeed, every extension of refined profile
${\mathcal C}_{\mathrm {small}}$
(or both). Indeed, every extension of refined profile
![]() $(J,r)$
lies on
$(J,r)$
lies on
![]() $\overline {{\mathcal C}}(J,r)$
, by Remark 4.2.10, so we can take
$\overline {{\mathcal C}}(J,r)$
, by Remark 4.2.10, so we can take
![]() ${\mathcal C}_{\mathrm {small}}$
to be the union of the stack
${\mathcal C}_{\mathrm {small}}$
to be the union of the stack
![]() ${\mathcal C}_{\mathrm {irred}}$
of Theorem 5.2.9 and the stacks
${\mathcal C}_{\mathrm {irred}}$
of Theorem 5.2.9 and the stacks
![]() $\overline {{\mathcal C}}(J,r)$
for nonmaximal profiles
$\overline {{\mathcal C}}(J,r)$
for nonmaximal profiles
![]() $(J,r)$
. Since
$(J,r)$
. Since
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is equidimensional of dimension
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is equidimensional of dimension
![]() $[K:{\mathbf Q}_p]$
, it follows that the
$[K:{\mathbf Q}_p]$
, it follows that the
![]() $\overline {{\mathcal C}}(J)$
exhaust the irreducible components of
$\overline {{\mathcal C}}(J)$
exhaust the irreducible components of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, as required.
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, as required.
We now deduce a classification of the irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
. In the paper [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we will give a considerable refinement of this, giving a precise description of the finite type points of the irreducible components in terms of the weight part of Serre’s conjecture.
${\mathcal Z}^{\tau ,1}$
. In the paper [Reference Caraiani, Emerton, Gee and SavittCEGS20a], we will give a considerable refinement of this, giving a precise description of the finite type points of the irreducible components in terms of the weight part of Serre’s conjecture.
Corollary 5.3.3. The irreducible components of
![]() ${\mathcal Z}^{\tau ,1}$
are precisely the
${\mathcal Z}^{\tau ,1}$
are precisely the
![]() $\overline {{\mathcal Z}}(J)$
for
$\overline {{\mathcal Z}}(J)$
for
![]() $J\in {\mathcal P}_{\tau }$
, and if
$J\in {\mathcal P}_{\tau }$
, and if
![]() $J\ne J'$
, then
$J\ne J'$
, then
![]() $\overline {{\mathcal Z}}(J)\ne \overline {{\mathcal Z}}(J')$
.
$\overline {{\mathcal Z}}(J)\ne \overline {{\mathcal Z}}(J')$
.
Proof. By Theorem 5.1.12, if
![]() $J\in {\mathcal P}_{\tau }$
, then
$J\in {\mathcal P}_{\tau }$
, then
![]() $\overline {{\mathcal Z}}(J)$
is an irreducible component of
$\overline {{\mathcal Z}}(J)$
is an irreducible component of
![]() ${\mathcal Z}^{\tau ,1}$
. Furthermore, these
${\mathcal Z}^{\tau ,1}$
. Furthermore, these
![]() $\overline {{\mathcal Z}}(J)$
are pairwise distinct by Theorem 5.1.17.
$\overline {{\mathcal Z}}(J)$
are pairwise distinct by Theorem 5.1.17.
Since the morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal Z}^{\tau ,1}$
is scheme-theoretically dominant, it follows from Corollary 5.3.1 that each irreducible component of
${\mathcal C}^{\tau ,\operatorname {BT},1}\to {\mathcal Z}^{\tau ,1}$
is scheme-theoretically dominant, it follows from Corollary 5.3.1 that each irreducible component of
![]() ${\mathcal Z}^{\tau ,1}$
is dominated by some
${\mathcal Z}^{\tau ,1}$
is dominated by some
![]() $\overline {{\mathcal C}}(J)$
. Applying Theorem 5.1.12, again, we see that if
$\overline {{\mathcal C}}(J)$
. Applying Theorem 5.1.12, again, we see that if
![]() $J\notin {\mathcal P}_{\tau }$
, then
$J\notin {\mathcal P}_{\tau }$
, then
![]() $\overline {{\mathcal C}}(J)$
does not dominate an irreducible component, as required.
$\overline {{\mathcal C}}(J)$
does not dominate an irreducible component, as required.
5.4. Dieudonné modules and the morphism to the gauge stack
We now study the images of the irreducible components
![]() $\overline {{\mathcal C}}(J)$
in the gauge stack
$\overline {{\mathcal C}}(J)$
in the gauge stack
![]() ${\mathcal G}_{\eta }$
; this amounts to computing the Dieudonné modules and Galois representations associated to the extensions of Breuil–Kisin modules that we considered in Section 3. Suppose throughout this subsection that
${\mathcal G}_{\eta }$
; this amounts to computing the Dieudonné modules and Galois representations associated to the extensions of Breuil–Kisin modules that we considered in Section 3. Suppose throughout this subsection that
![]() $\tau $
is a nonscalar type, and that
$\tau $
is a nonscalar type, and that
![]() $(J,r)$
is a maximal refined profile. Recall that in the cuspidal case, this entails that
$(J,r)$
is a maximal refined profile. Recall that in the cuspidal case, this entails that
![]() $i \in J$
if and only if
$i \in J$
if and only if
![]() $i + f \not \in J$
.
$i + f \not \in J$
.
Lemma 5.4.1. Let
![]() $\mathfrak {P} \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
be an extension of type
$\mathfrak {P} \in \operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
be an extension of type
![]() $\tau $
and refined profile
$\tau $
and refined profile
![]() $(J,r)$
. Then for
$(J,r)$
. Then for
![]() $i \in {\mathbf Z}/f'{\mathbf Z}$
, we have
$i \in {\mathbf Z}/f'{\mathbf Z}$
, we have
![]() $F=0$
on
$F=0$
on
![]() $D(\mathfrak {P})_{\eta ,i-1}$
if
$D(\mathfrak {P})_{\eta ,i-1}$
if
![]() $i\in J$
, while
$i\in J$
, while
![]() $V=0$
on
$V=0$
on
![]() $D(\mathfrak {P})_{\eta ,i}$
if
$D(\mathfrak {P})_{\eta ,i}$
if
![]() $i\notin J$
.
$i\notin J$
.
Proof. Recall that
![]() $D(\mathfrak {P}) = \mathfrak {P}/u\mathfrak {P}$
. Let
$D(\mathfrak {P}) = \mathfrak {P}/u\mathfrak {P}$
. Let
![]() $w_i$
be the image of
$w_i$
be the image of
![]() $m_i$
in
$m_i$
in
![]() $D(\mathfrak {P})$
if
$D(\mathfrak {P})$
if
![]() $i \in J$
, and let
$i \in J$
, and let
![]() $w_i$
be the image of
$w_i$
be the image of
![]() $n_i$
in
$n_i$
in
![]() $D(\mathfrak {P})$
if
$D(\mathfrak {P})$
if
![]() $i \not \in J$
. It follows easily from the definitions that
$i \not \in J$
. It follows easily from the definitions that
![]() $D(\mathfrak {P})_{\eta ,i}$
is generated over
$D(\mathfrak {P})_{\eta ,i}$
is generated over
![]() ${\mathbf F}$
by
${\mathbf F}$
by
![]() $w_i$
.
$w_i$
.
Recall that the actions of
![]() $F,V$
on
$F,V$
on
![]() $D(\mathfrak {P})$
are as specified in Definition 2.1.7. In particular, F is induced by
$D(\mathfrak {P})$
are as specified in Definition 2.1.7. In particular, F is induced by
![]() $\varphi $
, while V is
$\varphi $
, while V is
![]() $c^{-1} \mathfrak {V}$
mod u, where
$c^{-1} \mathfrak {V}$
mod u, where
![]() $\mathfrak {V}$
is the unique map on
$\mathfrak {V}$
is the unique map on
![]() $\mathfrak {P}$
satisfying
$\mathfrak {P}$
satisfying
![]() $\mathfrak {V} \circ \varphi = E(u)$
, and
$\mathfrak {V} \circ \varphi = E(u)$
, and
![]() $c = E(0)$
. For the Breuil–Kisin module
$c = E(0)$
. For the Breuil–Kisin module
![]() $\mathfrak {P}$
, we have
$\mathfrak {P}$
, we have
and so one checks (using that
![]() $E(u) = u^{e'}$
in
$E(u) = u^{e'}$
in
![]() ${\mathbf F}$
) that
${\mathbf F}$
) that
From Definition 4.2.4 and the discussion immediately following it, we recall that if
![]() $(i-1,i)$
is not a transition, then
$(i-1,i)$
is not a transition, then
![]() $r_i = e'$
,
$r_i = e'$
,
![]() $s_i=0$
, and
$s_i=0$
, and
![]() $h_i$
is divisible by u (the latter because nonzero terms of
$h_i$
is divisible by u (the latter because nonzero terms of
![]() $h_i$
have degrees congruent to
$h_i$
have degrees congruent to
![]() $r_i+c_i-d_i \pmod {p^{f'}-1}$
, and
$r_i+c_i-d_i \pmod {p^{f'}-1}$
, and
![]() $c_i \not \equiv d_i$
since
$c_i \not \equiv d_i$
since
![]() $\tau $
is nonscalar). On the other hand, if
$\tau $
is nonscalar). On the other hand, if
![]() $(i-1,i)$
is a transition, then
$(i-1,i)$
is a transition, then
![]() $r_i , s_i>0$
, and nonzero terms of
$r_i , s_i>0$
, and nonzero terms of
![]() $h_i$
have degrees divisible by
$h_i$
have degrees divisible by
![]() $p^{f'}-1$
; in that case, we write
$p^{f'}-1$
; in that case, we write
![]() $h_i^0$
for the constant coefficient of
$h_i^0$
for the constant coefficient of
![]() $h_i$
, and we remark that
$h_i$
, and we remark that
![]() $h_i^0$
does not vanish identically on
$h_i^0$
does not vanish identically on
![]() $\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
.
$\operatorname {\mathrm {Ext}}^1_{\mathcal {K}({\mathbf F})}(\mathfrak {M},\mathfrak {N})$
.
Suppose, for instance, that
![]() $i-1 \in J$
and
$i-1 \in J$
and
![]() $i \in J$
. Then,
$i \in J$
. Then,
![]() $w_{i-1}$
and
$w_{i-1}$
and
![]() $w_i$
are the images in
$w_i$
are the images in
![]() $D(\mathfrak {P})$
of
$D(\mathfrak {P})$
of
![]() $m_{i-1}$
and
$m_{i-1}$
and
![]() $m_{i}$
. From the above formulas, we see that
$m_{i}$
. From the above formulas, we see that
![]() $u^{r_i} = u^{e'}$
and
$u^{r_i} = u^{e'}$
and
![]() $h_i$
are both divisible by u, while on the other hand,
$h_i$
are both divisible by u, while on the other hand,
![]() $u^{s_i} = 1$
. We deduce that
$u^{s_i} = 1$
. We deduce that
![]() $F(w_{i-1}) = 0$
and
$F(w_{i-1}) = 0$
and
![]() $V(w_i) = c^{-1} a_i^{-1} w_{i-1}$
. Computing along similar lines, it is easy to check the following four cases.
$V(w_i) = c^{-1} a_i^{-1} w_{i-1}$
. Computing along similar lines, it is easy to check the following four cases.
-
1.
 $i-1\in J,i\in J$
. Then,
$i-1\in J,i\in J$
. Then,
 $F(w_{i-1}) = 0$
and
$F(w_{i-1}) = 0$
and
 $V(w_i) = c^{-1} a_i^{-1} w_{i-1}$
.
$V(w_i) = c^{-1} a_i^{-1} w_{i-1}$
. -
2.
 $i-1\notin J,i\notin J$
. Then,
$i-1\notin J,i\notin J$
. Then,
 $F(w_{i-1})=b_{i}w_{i}$
,
$F(w_{i-1})=b_{i}w_{i}$
,
 $V(w_{i})=0$
.
$V(w_{i})=0$
. -
3.
 $i-1\in J$
,
$i-1\in J$
,
 $i\notin J$
. Then,
$i\notin J$
. Then,
 $F(w_{i-1})=h_{i}^0w_{i}$
,
$F(w_{i-1})=h_{i}^0w_{i}$
,
 $V(w_{i})=0$
.
$V(w_{i})=0$
. -
4.
 $i-1\notin J$
,
$i-1\notin J$
,
 $i\in J$
. Then,
$i\in J$
. Then,
 $F(w_{i-1})=0$
,
$F(w_{i-1})=0$
,
 $V(w_{i})=-c^{-1} a_{i}^{-1}b_{i}^{-1}h_{i}^0w_{i-1}$
.
$V(w_{i})=-c^{-1} a_{i}^{-1}b_{i}^{-1}h_{i}^0w_{i-1}$
.
In particular, if
![]() $i\in J$
, then
$i\in J$
, then
![]() $F(w_i)=0$
, while if
$F(w_i)=0$
, while if
![]() $i\notin J$
, then
$i\notin J$
, then
![]() $V(w_{i+1})=0$
.
$V(w_{i+1})=0$
.
Since
![]() ${\mathcal C}^{\tau ,\operatorname {BT}}$
is flat over
${\mathcal C}^{\tau ,\operatorname {BT}}$
is flat over
![]() ${\mathcal O}$
by Theorem 2.3.6, it follows from Lemma 2.4.9 that the natural morphism
${\mathcal O}$
by Theorem 2.3.6, it follows from Lemma 2.4.9 that the natural morphism
![]() ${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal G}_{\eta }$
is determined by an f-tuple of effective Cartier divisors
${\mathcal C}^{\tau ,\operatorname {BT}} \to {\mathcal G}_{\eta }$
is determined by an f-tuple of effective Cartier divisors
![]() $\{{\mathcal D}_j\}_{0 \le j < f}$
lying in the special fibre
$\{{\mathcal D}_j\}_{0 \le j < f}$
lying in the special fibre
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
. Concretely,
${\mathcal C}^{\tau ,\operatorname {BT},1}$
. Concretely,
![]() ${\mathcal D}_j$
is the zero locus of
${\mathcal D}_j$
is the zero locus of
![]() $X_j$
, which is the zero locus of
$X_j$
, which is the zero locus of
![]() $F:D_{\eta ,j}\to D_{\eta ,j+1}$
. The zero locus of
$F:D_{\eta ,j}\to D_{\eta ,j+1}$
. The zero locus of
![]() $Y_j$
(which is the zero locus of
$Y_j$
(which is the zero locus of
![]() $V:D_{\eta ,j+1}\to D_{\eta ,j}$
) is another Cartier divisor
$V:D_{\eta ,j+1}\to D_{\eta ,j}$
) is another Cartier divisor
![]() ${\mathcal D}_j'$
. Since
${\mathcal D}_j'$
. Since
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
is reduced, we conclude that each of
${\mathcal C}^{\tau ,\operatorname {BT},1}$
is reduced, we conclude that each of
![]() ${\mathcal D}_j$
and
${\mathcal D}_j$
and
![]() ${\mathcal D}_j'$
is simply a union of irreducible components of
${\mathcal D}_j'$
is simply a union of irreducible components of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
, each component appearing precisely once in precisely one of either
${\mathcal C}^{\tau ,\operatorname {BT},1}$
, each component appearing precisely once in precisely one of either
![]() ${\mathcal D}_j$
or
${\mathcal D}_j$
or
![]() ${\mathcal D}_j'$
.
${\mathcal D}_j'$
.
Proposition 5.4.2.
![]() ${\mathcal D}_j$
is equal to the union of the irreducible components
${\mathcal D}_j$
is equal to the union of the irreducible components
![]() $\overline {{\mathcal C}}(J)$
of
$\overline {{\mathcal C}}(J)$
of
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
for those J that contain
${\mathcal C}^{\tau ,\operatorname {BT},1}$
for those J that contain
![]() $j+1$
.
$j+1$
.
Proof. Lemma 5.4.1 shows that if
![]() $j+1\in J$
, then
$j+1\in J$
, then
![]() $X_j=0$
, while if
$X_j=0$
, while if
![]() $j+1\notin J$
, then
$j+1\notin J$
, then
![]() $Y_j=0$
. In the latter case, by an inspection of case (3) of the proof of Lemma 5.4.1, we have
$Y_j=0$
. In the latter case, by an inspection of case (3) of the proof of Lemma 5.4.1, we have
![]() $X_j=0$
if and only if
$X_j=0$
if and only if
![]() $j\in J$
and
$j\in J$
and
![]() $h_{j+1}^0=0$
. Since
$h_{j+1}^0=0$
. Since
![]() $h_{j+1}^0$
does not vanish identically on an irreducible component, we see that the irreducible components on which
$h_{j+1}^0$
does not vanish identically on an irreducible component, we see that the irreducible components on which
![]() $X_j$
vanishes identically are precisely those for which
$X_j$
vanishes identically are precisely those for which
![]() $j+1\in J$
, as claimed.
$j+1\in J$
, as claimed.
Theorem 5.4.3. The algebraic stack
![]() ${\mathcal C}^{\tau ,\operatorname {BT},1}$
has precisely
${\mathcal C}^{\tau ,\operatorname {BT},1}$
has precisely
![]() $2^f$
irreducible components, namely, the irreducible substacks
$2^f$
irreducible components, namely, the irreducible substacks
![]() $\overline {{\mathcal C}}(J)$
.
$\overline {{\mathcal C}}(J)$
.
A Serre weights and tame types
We begin by recalling some results from [Reference DiamondDia07] on the Jordan–Hölder factors of the reductions modulo p of lattices in principal series and cuspidal representations of
![]() $\operatorname {\mathrm {GL}}_2(k)$
, following [Reference Emerton, Gee and SavittEGS15, Section 3] (but with slightly different normalisations than those of loc. cit.).
$\operatorname {\mathrm {GL}}_2(k)$
, following [Reference Emerton, Gee and SavittEGS15, Section 3] (but with slightly different normalisations than those of loc. cit.).
Let
![]() $\tau $
be a tame inertial type. Recall from Section 1.3 that we associate a representation
$\tau $
be a tame inertial type. Recall from Section 1.3 that we associate a representation
![]() $\sigma (\tau )$
of
$\sigma (\tau )$
of
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
to
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
to
![]() $\tau $
as follows: if
$\tau $
as follows: if
![]() $\tau \simeq \eta \oplus \eta '$
is a tame principal series type, then we set
$\tau \simeq \eta \oplus \eta '$
is a tame principal series type, then we set
![]() $\sigma (\tau ) := \operatorname {\mathrm {Ind}}_I^{\operatorname {\mathrm {GL}}_2({\mathcal O}_K)} \eta '\otimes \eta $
, while if
$\sigma (\tau ) := \operatorname {\mathrm {Ind}}_I^{\operatorname {\mathrm {GL}}_2({\mathcal O}_K)} \eta '\otimes \eta $
, while if
![]() $\tau =\eta \oplus \eta ^q$
is a tame cuspidal type, then
$\tau =\eta \oplus \eta ^q$
is a tame cuspidal type, then
![]() $\sigma (\tau )$
is the inflation to
$\sigma (\tau )$
is the inflation to
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
of the cuspidal representation of
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
of the cuspidal representation of
![]() $\operatorname {\mathrm {GL}}_2(k)$
denoted by
$\operatorname {\mathrm {GL}}_2(k)$
denoted by
![]() $\Theta (\eta )$
in [Reference DiamondDia07]. (Here, we have identified
$\Theta (\eta )$
in [Reference DiamondDia07]. (Here, we have identified
![]() $\eta ,\eta '$
with their composites with
$\eta ,\eta '$
with their composites with
![]() ${\operatorname {Art}}_K$
.)
${\operatorname {Art}}_K$
.)
Write
![]() $\overline {\sigma }(\tau )$
for the semisimplification of the reduction modulo p of (a
$\overline {\sigma }(\tau )$
for the semisimplification of the reduction modulo p of (a
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
-stable
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
-stable
![]() ${\mathcal O}$
-lattice in)
${\mathcal O}$
-lattice in)
![]() $\sigma (\tau )$
. The action of
$\sigma (\tau )$
. The action of
![]() $\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
on
$\operatorname {\mathrm {GL}}_2({\mathcal O}_K)$
on
![]() $\overline {\sigma }(\tau )$
factors through
$\overline {\sigma }(\tau )$
factors through
![]() $\operatorname {\mathrm {GL}}_2(k)$
, so the Jordan–Hölder factors
$\operatorname {\mathrm {GL}}_2(k)$
, so the Jordan–Hölder factors
![]() $\operatorname {JH}(\overline {\sigma }(\tau ))$
of
$\operatorname {JH}(\overline {\sigma }(\tau ))$
of
![]() $\overline {\sigma }(\tau )$
are Serre weights. By the results of [Reference DiamondDia07], these Jordan–Hölder factors of
$\overline {\sigma }(\tau )$
are Serre weights. By the results of [Reference DiamondDia07], these Jordan–Hölder factors of
![]() $\overline {\sigma }(\tau )$
are pairwise nonisomorphic, and are parametrised by a certain set
$\overline {\sigma }(\tau )$
are pairwise nonisomorphic, and are parametrised by a certain set
![]() ${\mathcal P}_{\tau }$
that we now recall.
${\mathcal P}_{\tau }$
that we now recall.
Suppose first that
![]() $\tau =\eta \oplus \eta '$
is a tame principal series type. Set
$\tau =\eta \oplus \eta '$
is a tame principal series type. Set
![]() $f'=f$
in this case. We define
$f'=f$
in this case. We define
![]() $0 \le \gamma _i \le p-1$
(for
$0 \le \gamma _i \le p-1$
(for
![]() $i \in {\mathbf Z}/f{\mathbf Z}$
) to be the unique integers not all equal to
$i \in {\mathbf Z}/f{\mathbf Z}$
) to be the unique integers not all equal to
![]() $p-1$
, such that
$p-1$
, such that
![]() $\eta (\eta ')^{-1} = \prod _{i=0}^{f-1} \omega _{\sigma _i}^{\gamma _i}$
. If, instead,
$\eta (\eta ')^{-1} = \prod _{i=0}^{f-1} \omega _{\sigma _i}^{\gamma _i}$
. If, instead,
![]() $\tau = \eta \oplus \eta '$
is a cuspidal type, set
$\tau = \eta \oplus \eta '$
is a cuspidal type, set
![]() $f'=2f$
. We define
$f'=2f$
. We define
![]() $0 \le \gamma _i \le p-1$
(for
$0 \le \gamma _i \le p-1$
(for
![]() $i \in {\mathbf Z}/f'{\mathbf Z}$
) to be the unique integers, such that
$i \in {\mathbf Z}/f'{\mathbf Z}$
) to be the unique integers, such that
![]() $\eta (\eta ')^{-1} = \prod _{i=0}^{f'-1} \omega _{\sigma ^{\prime }_i}^{\gamma _i}$
. Here, the
$\eta (\eta ')^{-1} = \prod _{i=0}^{f'-1} \omega _{\sigma ^{\prime }_i}^{\gamma _i}$
. Here, the
![]() $\sigma ^{\prime }_i$
are the embeddings
$\sigma ^{\prime }_i$
are the embeddings
![]() $l \to {\mathbf F}$
, where l is the quadratic extension of k,
$l \to {\mathbf F}$
, where l is the quadratic extension of k,
![]() $\sigma ^{\prime }_0$
is a fixed choice of embedding extending
$\sigma ^{\prime }_0$
is a fixed choice of embedding extending
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $(\sigma ^{\prime }_{i+1})^p = \sigma ^{\prime }_i$
for all i.
$(\sigma ^{\prime }_{i+1})^p = \sigma ^{\prime }_i$
for all i.
If
![]() $\tau $
is scalar, then we set
$\tau $
is scalar, then we set
![]() ${\mathcal P}_{\tau }=\{\varnothing \}$
. Otherwise, we have
${\mathcal P}_{\tau }=\{\varnothing \}$
. Otherwise, we have
![]() $\eta \ne \eta '$
, and we let
$\eta \ne \eta '$
, and we let
![]() ${\mathcal P}_{\tau }$
be the collection of subsets
${\mathcal P}_{\tau }$
be the collection of subsets
![]() $J \subset {\mathbf Z}/f'{\mathbf Z}$
satisfying the conditions:
$J \subset {\mathbf Z}/f'{\mathbf Z}$
satisfying the conditions:
-
○ if
 $i-1\in J$
and
$i-1\in J$
and
 $i\notin J$
, then
$i\notin J$
, then
 $\gamma _{i}\ne p-1$
, and
$\gamma _{i}\ne p-1$
, and -
○ if
 $i-1\notin J$
and
$i-1\notin J$
and
 $i\in J$
, then
$i\in J$
, then
 $\gamma _{i}\ne 0$
$\gamma _{i}\ne 0$
and, in the cuspidal case, satisfying the further condition that
![]() $i \in J$
if and only if
$i \in J$
if and only if
![]() $i+f \not \in J$
.
$i+f \not \in J$
.
The Jordan–Hölder factors of
![]() $\overline {\sigma }(\tau )$
are by definition Serre weights, and are parametrised by
$\overline {\sigma }(\tau )$
are by definition Serre weights, and are parametrised by
![]() ${\mathcal P}_{\tau }$
as follows (see [Reference Emerton, Gee and SavittEGS15, Sections 3.2, 3.3]). For any
${\mathcal P}_{\tau }$
as follows (see [Reference Emerton, Gee and SavittEGS15, Sections 3.2, 3.3]). For any
![]() $J\subseteq {\mathbf Z}/f'{\mathbf Z}$
, we let
$J\subseteq {\mathbf Z}/f'{\mathbf Z}$
, we let
![]() $\delta _J$
denote the characteristic function of J, and if
$\delta _J$
denote the characteristic function of J, and if
![]() $J \in {\mathcal P}_{\tau }$
, we define
$J \in {\mathcal P}_{\tau }$
, we define
![]() $s_{J,i}$
by
$s_{J,i}$
by
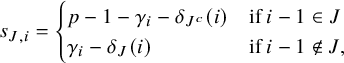 $$\begin{align*}s_{J,i}=\begin{cases} p-1-\gamma_{i}-\delta_{J^c}(i)&\text{if }i-1 \in J \\ \gamma_{i}-\delta_J(i)&\text{if }i-1\notin J, \end{cases}\end{align*}$$
$$\begin{align*}s_{J,i}=\begin{cases} p-1-\gamma_{i}-\delta_{J^c}(i)&\text{if }i-1 \in J \\ \gamma_{i}-\delta_J(i)&\text{if }i-1\notin J, \end{cases}\end{align*}$$
and we set
![]() $t_{J,i}=\gamma _{i}+\delta _{J^c}(i)$
if
$t_{J,i}=\gamma _{i}+\delta _{J^c}(i)$
if
![]() $i-1\in J$
and
$i-1\in J$
and
![]() $0$
otherwise. Write
$0$
otherwise. Write
![]() $\vec {s}$
for the tuple
$\vec {s}$
for the tuple
![]() $(s_{J,i})$
, suppressing the J from the notation for readability, and, similarly, write
$(s_{J,i})$
, suppressing the J from the notation for readability, and, similarly, write
![]() $\vec {t}$
for the tuple
$\vec {t}$
for the tuple
![]() $(t_{J,i})$
. Recall that the Serre weight
$(t_{J,i})$
. Recall that the Serre weight
![]() $\overline {\sigma }_{\vec {t},\vec {s}}$
is defined in (1.3.2).
$\overline {\sigma }_{\vec {t},\vec {s}}$
is defined in (1.3.2).
In the principal series case, we let
![]() $\overline {\sigma }(\tau )_J :=\overline {\sigma }_{\vec {t},\vec {s}}\otimes \eta '\circ \det $
for each
$\overline {\sigma }(\tau )_J :=\overline {\sigma }_{\vec {t},\vec {s}}\otimes \eta '\circ \det $
for each
![]() $J \in {\mathcal P}_{\tau }$
; the
$J \in {\mathcal P}_{\tau }$
; the
![]() $\overline {\sigma }(\tau )_J$
are precisely the Jordan–Hölder factors of
$\overline {\sigma }(\tau )_J$
are precisely the Jordan–Hölder factors of
![]() $\overline {\sigma }(\tau )$
.
$\overline {\sigma }(\tau )$
.
In the cuspidal case, one checks that
![]() $s_{J,i} = s_{J,i+f}$
for all i, and also that the character
$s_{J,i} = s_{J,i+f}$
for all i, and also that the character
![]() $\eta ' \cdot \prod _{i=0}^{f'-1} (\sigma ^{\prime }_i)^{t_{J,i}} : l^{\times } \to {\mathbf F}^{\times }$
factors as
$\eta ' \cdot \prod _{i=0}^{f'-1} (\sigma ^{\prime }_i)^{t_{J,i}} : l^{\times } \to {\mathbf F}^{\times }$
factors as
![]() $\theta \circ N_{l/k}$
, where
$\theta \circ N_{l/k}$
, where
![]() $N_{l/k}$
is the norm map. We let
$N_{l/k}$
is the norm map. We let
![]() $\overline {\sigma }(\tau )_J :=\overline {\sigma }_{0,\vec {s}}\otimes \theta \circ \det $
for each
$\overline {\sigma }(\tau )_J :=\overline {\sigma }_{0,\vec {s}}\otimes \theta \circ \det $
for each
![]() $J \in {\mathcal P}_{\tau }$
; the
$J \in {\mathcal P}_{\tau }$
; the
![]() $\overline {\sigma }(\tau )_J$
are precisely the Jordan–Hölder factors of
$\overline {\sigma }(\tau )_J$
are precisely the Jordan–Hölder factors of
![]() $\overline {\sigma }(\tau )$
.
$\overline {\sigma }(\tau )$
.
Remark A.1. The parameterisations above are easily deduced from those given in [Reference Emerton, Gee and SavittEGS15, Sections 3.2, 3.3] for the Jordan–Hölder factors of the representations
![]() $\operatorname {\mathrm {Ind}}_I^{\operatorname {\mathrm {GL}}_2({\mathcal O}_K)} \eta '\otimes \eta $
and
$\operatorname {\mathrm {Ind}}_I^{\operatorname {\mathrm {GL}}_2({\mathcal O}_K)} \eta '\otimes \eta $
and
![]() $\Theta (\eta )$
. (Note that there is a minor mistake in [Reference Emerton, Gee and SavittEGS15, Section 3.1]: since the conventions of [Reference Emerton, Gee and SavittEGS15] regarding the inertial Langlands correspondence agree with those of [Reference Gee and KisinGK14], the explicit identification of
$\Theta (\eta )$
. (Note that there is a minor mistake in [Reference Emerton, Gee and SavittEGS15, Section 3.1]: since the conventions of [Reference Emerton, Gee and SavittEGS15] regarding the inertial Langlands correspondence agree with those of [Reference Gee and KisinGK14], the explicit identification of
![]() $\sigma (\tau )$
with a principal series or cuspidal type in [Reference Emerton, Gee and SavittEGS15, Section 3.1] is missing a dual. The explicit parameterisation we are using here is, of course, independent of this issue.
$\sigma (\tau )$
with a principal series or cuspidal type in [Reference Emerton, Gee and SavittEGS15, Section 3.1] is missing a dual. The explicit parameterisation we are using here is, of course, independent of this issue.
This mistake has the unfortunate effect that various explicit formulae in [Reference Emerton, Gee and SavittEGS15, Section 7] need to be modified in a more or less obvious fashion; note that since
![]() $\sigma (\tau )$
is self dual up to twist, all formulae can be fixed by making twists and/or exchanging
$\sigma (\tau )$
is self dual up to twist, all formulae can be fixed by making twists and/or exchanging
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
. In particular, the definition of the strongly divisible module before [Reference Emerton, Gee and SavittEGS15, Remark 7.3.2] is incorrect as written, and can be fixed by either reversing the roles of
$\eta '$
. In particular, the definition of the strongly divisible module before [Reference Emerton, Gee and SavittEGS15, Remark 7.3.2] is incorrect as written, and can be fixed by either reversing the roles of
![]() $\eta ,\eta '$
or changing the definition of the quantity
$\eta ,\eta '$
or changing the definition of the quantity
![]() $c^{(j)}$
defined there.)
$c^{(j)}$
defined there.)
Remark A.2. In the cuspidal case, write
![]() $\eta $
in the form
$\eta $
in the form
![]() $(\sigma ^{\prime }_0)^{(q+1)b+1+c}$
, where
$(\sigma ^{\prime }_0)^{(q+1)b+1+c}$
, where
![]() $0\le b\le q-2$
,
$0\le b\le q-2$
,
![]() $0\le c\le q-1$
. Set
$0\le c\le q-1$
. Set
![]() $t^{\prime }_{J,i} = t_{J,i+f}$
for integers
$t^{\prime }_{J,i} = t_{J,i+f}$
for integers
![]() $1\le i \le f$
. Then one can check that
$1\le i \le f$
. Then one can check that
![]() $\overline {\sigma }(\tau )_J = \overline {\sigma }_{\vec {t}',\vec {s}} \otimes (\sigma _0^{(q+1)b + \delta _J(0)} \circ \det ).$
$\overline {\sigma }(\tau )_J = \overline {\sigma }_{\vec {t}',\vec {s}} \otimes (\sigma _0^{(q+1)b + \delta _J(0)} \circ \det ).$
We now recall some facts about the set of Serre weights
![]() $W(\overline {r})$
associated to a representation
$W(\overline {r})$
associated to a representation
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
.
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
.
Definition A.3. We say that a crystalline representation
![]() $r : G_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Q}}_p)$
has type
$r : G_K \to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf Q}}_p)$
has type
![]() $\overline {\sigma }_{\vec {t},\vec {s}}$
provided that for each embedding
$\overline {\sigma }_{\vec {t},\vec {s}}$
provided that for each embedding
![]() $\sigma _j : k \hookrightarrow {\mathbf F}$
, there is an embedding
$\sigma _j : k \hookrightarrow {\mathbf F}$
, there is an embedding
![]() $\widetilde {\sigma }_j : K \hookrightarrow \overline {{\mathbf Q}}_p$
lifting
$\widetilde {\sigma }_j : K \hookrightarrow \overline {{\mathbf Q}}_p$
lifting
![]() $\sigma _j$
, such that the
$\sigma _j$
, such that the
![]() $\widetilde {\sigma }_j$
-labelled Hodge–Tate weights of r are
$\widetilde {\sigma }_j$
-labelled Hodge–Tate weights of r are
![]() $\{-s_j-t_j,1-t_j\}$
, and the remaining
$\{-s_j-t_j,1-t_j\}$
, and the remaining
![]() $(e-1)f$
pairs of Hodge–Tate weights of r are all
$(e-1)f$
pairs of Hodge–Tate weights of r are all
![]() $\{0,1\}$
. (In particular, the representations of type
$\{0,1\}$
. (In particular, the representations of type
![]() $\overline {\sigma }_{\vec {0},\vec {0}}$
(the trivial weight) are the same as those of Hodge type
$\overline {\sigma }_{\vec {0},\vec {0}}$
(the trivial weight) are the same as those of Hodge type
![]() $0$
.)
$0$
.)
Definition A.4. Given a representation
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, we define
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
, we define
![]() $W(\overline {r})$
to be the set of Serre weights
$W(\overline {r})$
to be the set of Serre weights
![]() $\overline {\sigma }$
, such that
$\overline {\sigma }$
, such that
![]() $\overline {r}$
has a crystalline lift of type
$\overline {r}$
has a crystalline lift of type
![]() $\overline {\sigma }$
.
$\overline {\sigma }$
.
There are several definitions of the set
![]() $W(\overline {r})$
in the literature, which by the papers [Reference Barnet-Lamb, Gee and GeraghtyBLGG13, Reference Gee and KisinGK14, Reference Gee, Liu and SavittGLS15] are known to be equivalent (up to normalisation). While the preceding definition is perhaps the most compact, it is the description of
$W(\overline {r})$
in the literature, which by the papers [Reference Barnet-Lamb, Gee and GeraghtyBLGG13, Reference Gee and KisinGK14, Reference Gee, Liu and SavittGLS15] are known to be equivalent (up to normalisation). While the preceding definition is perhaps the most compact, it is the description of
![]() $W(\overline {r})$
via the Breuil–Mézard conjecture that appears to be the most amenable to generalisation. (See [Reference Gee, Herzig and SavittGHS18] for much more discussion.)
$W(\overline {r})$
via the Breuil–Mézard conjecture that appears to be the most amenable to generalisation. (See [Reference Gee, Herzig and SavittGHS18] for much more discussion.)
Recall that
![]() $\overline {r}$
is très ramifiée if it is a twist of an extension of the trivial character by the mod p cyclotomic character, and if furthermore the splitting field of its projective image is not of the form
$\overline {r}$
is très ramifiée if it is a twist of an extension of the trivial character by the mod p cyclotomic character, and if furthermore the splitting field of its projective image is not of the form
![]() $K(\alpha _1^{1/p},\dots ,\alpha _s^{1/p})$
for some
$K(\alpha _1^{1/p},\dots ,\alpha _s^{1/p})$
for some
![]() $\alpha _1,\dots ,\alpha _s\in {\mathcal O}_K^{\times }$
.
$\alpha _1,\dots ,\alpha _s\in {\mathcal O}_K^{\times }$
.
Lemma A.5.
-
1. If
 $\tau $
is a tame type, then
$\tau $
is a tame type, then
 $\overline {r}$
has a potentially Barsotti–Tate lift of type
$\overline {r}$
has a potentially Barsotti–Tate lift of type
 $\tau $
if and only if
$\tau $
if and only if
 $W(\overline {r})\cap \operatorname {JH}(\overline {\sigma }(\tau ))\ne \emptyset$
.
$W(\overline {r})\cap \operatorname {JH}(\overline {\sigma }(\tau ))\ne \emptyset$
. -
2. The following conditions are equivalent:
-
(a)
 $\overline {r}$
admits a potentially Barsotti–Tate lift of some tame type.
$\overline {r}$
admits a potentially Barsotti–Tate lift of some tame type. -
(b)
 $W(\overline {r})$
contains a non-Steinberg Serre weight.
$W(\overline {r})$
contains a non-Steinberg Serre weight. -
(c)
 $\overline {r}$
is not très ramifiée.
$\overline {r}$
is not très ramifiée.
-
Proof. This is [Reference Caraiani, Emerton, Gee and SavittCEGS20b, Lemma A.4].
Lemma A.6. Suppose that
![]() $\overline {\sigma }_{\vec {t},\vec {s}}$
is a non-Steinberg Serre weight. Suppose that
$\overline {\sigma }_{\vec {t},\vec {s}}$
is a non-Steinberg Serre weight. Suppose that
![]() $\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
is a reducible representation satisfying
$\overline {r}:G_K\to \operatorname {\mathrm {GL}}_2(\overline {{\mathbf F}}_p)$
is a reducible representation satisfying
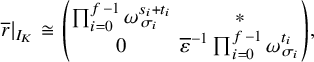 $$\begin{align*}\overline{r}|_{I_K}\cong \begin{pmatrix} \prod_{i=0}^{f-1}\omega_{\sigma_i}^{s_i+t_i} &*\\ 0 & \overline{\varepsilon}^{-1}\prod_{i=0}^{f-1}\omega_{\sigma_i}^{t_i} \end{pmatrix} ,\end{align*}$$
$$\begin{align*}\overline{r}|_{I_K}\cong \begin{pmatrix} \prod_{i=0}^{f-1}\omega_{\sigma_i}^{s_i+t_i} &*\\ 0 & \overline{\varepsilon}^{-1}\prod_{i=0}^{f-1}\omega_{\sigma_i}^{t_i} \end{pmatrix} ,\end{align*}$$
and that
![]() $\overline {r}$
is not très ramifiée. Then,
$\overline {r}$
is not très ramifiée. Then,
![]() $\overline {\sigma }_{\vec {t},\vec {s}}\in W(\overline {r})$
.
$\overline {\sigma }_{\vec {t},\vec {s}}\in W(\overline {r})$
.
Proof. Write
![]() $\overline {r}$
as an extension of characters
$\overline {r}$
as an extension of characters
![]() $\overline {\chi }$
by
$\overline {\chi }$
by
![]() $\overline {\chi }'$
. It is straightforward from the classification of crystalline characters as in [Reference Gee, Herzig and SavittGHS18, Lemma 5.1.6] that there exist crystalline lifts
$\overline {\chi }'$
. It is straightforward from the classification of crystalline characters as in [Reference Gee, Herzig and SavittGHS18, Lemma 5.1.6] that there exist crystalline lifts
![]() $\chi ,\chi '$
of
$\chi ,\chi '$
of
![]() $\overline {\chi },\overline {\chi }'$
so that
$\overline {\chi },\overline {\chi }'$
so that
![]() $\chi ,\chi '$
have Hodge–Tate weights
$\chi ,\chi '$
have Hodge–Tate weights
![]() $1-t_j$
and
$1-t_j$
and
![]() $-s_j-t_j$
, respectively, at one embedding lifting each
$-s_j-t_j$
, respectively, at one embedding lifting each
![]() $\sigma _j$
and Hodge–Tate weights
$\sigma _j$
and Hodge–Tate weights
![]() $1$
and
$1$
and
![]() $0$
, respectively, at the others. In the case that
$0$
, respectively, at the others. In the case that
![]() $\overline {r}$
is not the twist of an extension of
$\overline {r}$
is not the twist of an extension of
![]() $\overline {\varepsilon }^{-1}$
by
$\overline {\varepsilon }^{-1}$
by
![]() $1$
, the result follows because the corresponding
$1$
, the result follows because the corresponding
![]() $H^1_f(G_K,\chi '\otimes \chi ^{-1})$
agrees with the full
$H^1_f(G_K,\chi '\otimes \chi ^{-1})$
agrees with the full
![]() $H^1(G_K,\chi '\otimes \chi ^{-1})$
(as a consequence of the usual dimension formulas for
$H^1(G_K,\chi '\otimes \chi ^{-1})$
(as a consequence of the usual dimension formulas for
![]() $H^1_f$
, [Reference NekovářNek93, Proposition 1.24]).
$H^1_f$
, [Reference NekovářNek93, Proposition 1.24]).
If
![]() $\overline {r}$
is a twist of an extension of
$\overline {r}$
is a twist of an extension of
![]() $\overline {\varepsilon }^{-1}$
by
$\overline {\varepsilon }^{-1}$
by
![]() $1$
, the assumption that
$1$
, the assumption that
![]() $\overline {\sigma }_{\vec {t},\vec {s}}$
is non-Steinberg implies
$\overline {\sigma }_{\vec {t},\vec {s}}$
is non-Steinberg implies
![]() $s_j = 0$
for all j. The hypothesis that
$s_j = 0$
for all j. The hypothesis that
![]() $\overline {r}$
is not très ramifiée guarantees that
$\overline {r}$
is not très ramifiée guarantees that
![]() $\overline {r}\otimes \prod _{i=0}^{f-1}\omega _{\sigma _i}^{-t_i} $
is finite flat, so has a Barsotti–Tate lift, and we deduce that
$\overline {r}\otimes \prod _{i=0}^{f-1}\omega _{\sigma _i}^{-t_i} $
is finite flat, so has a Barsotti–Tate lift, and we deduce that
![]() $\overline {\sigma }_{\vec {t},\vec {0}} \in W(\overline {r})$
.
$\overline {\sigma }_{\vec {t},\vec {0}} \in W(\overline {r})$
.
Acknowledgements
We would like to thank Kalyani Kansal for helpful comments. The first author was supported in part by National Science Foundation (NSF) grant DMS-1501064, by a Royal Society University Research Fellowship, and by European Research Council (ERC) Starting Grant 804176. The second author was supported in part by the NSF grants DMS-1303450, DMS-1601871, DMS-1902307, DMS-1952705 and DMS-2201242. The third author was supported in part by a Leverhulme Prize, Engineering and Physical Sciences Research Council (EPSRC) grant EP/L025485/1, Marie Curie Career Integration Grant 303605, ERC Starting Grant 306326 and a Royal Society Wolfson Research Merit Award. The fourth author was supported in part by NSF CAREER grant DMS-1564367 and NSF grants DMS-1702161 and DMS-1952566.
Competing interest
The authors have no competing interest to declare.


