1 Introduction
Suppose R is a commutative ring, and
![]() $n,r$
are integers satisfying
$n,r$
are integers satisfying
![]() $0 \le r \le n$
. An R-module P is stably free of type
$0 \le r \le n$
. An R-module P is stably free of type
![]() $(n,r)$
if there exists an isomorphism of R-modules:
$(n,r)$
if there exists an isomorphism of R-modules:
The most important nontrivial instance is that of
![]() $r=n-1$
, since any isomorphism (1) entails an isomorphism
$r=n-1$
, since any isomorphism (1) entails an isomorphism
so that
![]() $P \oplus R^{n-r-1}$
is stably free of type
$P \oplus R^{n-r-1}$
is stably free of type
![]() $(n,n-1)$
. In a sense that is made precise in [Reference Raynaud22, Théorème 6.5], a general stably free module of type
$(n,n-1)$
. In a sense that is made precise in [Reference Raynaud22, Théorème 6.5], a general stably free module of type
![]() $(n,n-1)$
does not admit a free summand of large rank, and is a fortiori not free.
$(n,n-1)$
does not admit a free summand of large rank, and is a fortiori not free.
We set up some notation. Let k be a commutative base ring. The letter k may be omitted from the notation where no confusion can arise. Fix a pair of integers
![]() $(n,r)$
where
$(n,r)$
where
![]() $0 \le r \le n$
. As set out in [Reference Raynaud22], there is a commutative k-algebra
$0 \le r \le n$
. As set out in [Reference Raynaud22], there is a commutative k-algebra
![]() $A_{n,n-r}$
and a stably free module
$A_{n,n-r}$
and a stably free module
![]() $P_{n,n-r}$
of type
$P_{n,n-r}$
of type
![]() $(n,r)$
over
$(n,r)$
over
![]() $A_{n,n-r}$
that is universal: for any commutative k-algebra R and any stably free R-module P of type
$A_{n,n-r}$
that is universal: for any commutative k-algebra R and any stably free R-module P of type
![]() $(n,r)$
, there is a ring homomorphism
$(n,r)$
, there is a ring homomorphism
![]() $A_{n,n-r} \to R$
such that
$A_{n,n-r} \to R$
such that
![]() $P \cong R \otimes _{A_{n,n-r}} P_{n,n-r}$
as R-modules.
$P \cong R \otimes _{A_{n,n-r}} P_{n,n-r}$
as R-modules.
There exists a sequence of positive integers called James numbers and written
![]() $b_2, b_3, \dots $
, which were defined by James [Reference James16], and calculated by [Reference Atiyah and Todd9] and [Reference Adams and Walker1]. Explicitly, they are described by their p-adic valuations,
$b_2, b_3, \dots $
, which were defined by James [Reference James16], and calculated by [Reference Atiyah and Todd9] and [Reference Adams and Walker1]. Explicitly, they are described by their p-adic valuations,
![]() $v_p$
, for all primes p:
$v_p$
, for all primes p:
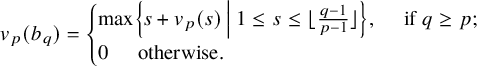 $$\begin{align*}v_p(b_q) = \begin{cases} \max\left\{s + v_p(s) \:\Big|\: 1 \le s \le \lfloor \frac{ q-1 }{p-1} \rfloor \right\}, \quad \text{ if }q \ge p; \\ 0 \quad\ \, \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}v_p(b_q) = \begin{cases} \max\left\{s + v_p(s) \:\Big|\: 1 \le s \le \lfloor \frac{ q-1 }{p-1} \rfloor \right\}, \quad \text{ if }q \ge p; \\ 0 \quad\ \, \text{otherwise.} \end{cases} \end{align*}$$
The first few James numbers may easily be listed:
The following is the module-theoretic content of [Reference Raynaud22, Théorème 6.5].
Theorem (Raynaud)
If k is a field of characteristic
![]() $0$
, then the universal stably free module
$0$
, then the universal stably free module
![]() $P_{n,n-1}$
of type
$P_{n,n-1}$
of type
![]() $(n,n-1)$
does not admit a free summand of rank
$(n,n-1)$
does not admit a free summand of rank
![]() $q-1$
, except possibly if
$q-1$
, except possibly if
![]() $b_q \mid n$
.
$b_q \mid n$
.
This result does not make any assertion about the situation when
![]() $b_q \mid n$
. It is well known that if n is even (viz. divisible by
$b_q \mid n$
. It is well known that if n is even (viz. divisible by
![]() $b_2$
), then
$b_2$
), then
![]() $P_{n,n-1}$
admits a free summand of rank
$P_{n,n-1}$
admits a free summand of rank
![]() $1$
, as is shown in Example 4.2 below. The cases of larger q are more obscure.
$1$
, as is shown in Example 4.2 below. The cases of larger q are more obscure.
In this paper, we prove the following. This is the module-theoretic content of Theorem 8.1.
Theorem. Suppose R is a commutative ring containing
![]() $\mathbb {Q}$
. Let n be a natural number. If P is a stably free module of type
$\mathbb {Q}$
. Let n be a natural number. If P is a stably free module of type
![]() $(24n, 24n-1)$
, then P admits a free summand of rank
$(24n, 24n-1)$
, then P admits a free summand of rank
![]() $2$
. If R contains a subfield of
$2$
. If R contains a subfield of
![]() $\mathbb {R}$
that has a unique quadratic extension (up to isomorphism), then P admits a free summand of rank
$\mathbb {R}$
that has a unique quadratic extension (up to isomorphism), then P admits a free summand of rank
![]() $3$
.
$3$
.
The result also applies with a k-scheme X playing the part of the k-algebra R. In this case, the stably free module becomes a stably trivial vector bundle.
Remark 1.1. The condition on R in the second part of the theorem above is satisfied if R contains a characteristic-
![]() $0$
quadratically closed field F. To see why, we argue as follows. The field F contains a quadratically closed subfield E consisting of algebraic numbers, and E may be embedded in
$0$
quadratically closed field F. To see why, we argue as follows. The field F contains a quadratically closed subfield E consisting of algebraic numbers, and E may be embedded in
![]() $\mathbb {C}$
. Let i denote a square root of
$\mathbb {C}$
. Let i denote a square root of
![]() $-1\in \mathbb {C}$
, and let
$-1\in \mathbb {C}$
, and let
![]() $z \mapsto \bar z$
denote ordinary complex conjugation. The subfield of E fixed by conjugation is
$z \mapsto \bar z$
denote ordinary complex conjugation. The subfield of E fixed by conjugation is
![]() $E'=E\cap \mathbb {R}$
. We claim that
$E'=E\cap \mathbb {R}$
. We claim that
![]() $E'$
meets the conditions of the theorem.
$E'$
meets the conditions of the theorem.
By construction,
![]() $E' \subseteq \mathbb {R}$
. When viewed as a vector space over
$E' \subseteq \mathbb {R}$
. When viewed as a vector space over
![]() $E'$
, the field E decomposes as a direct sum of eigenspaces for complex conjugation, so that we see
$E'$
, the field E decomposes as a direct sum of eigenspaces for complex conjugation, so that we see
![]() $E=E' \oplus i E'$
, which implies that
$E=E' \oplus i E'$
, which implies that
![]() $E=E'(i)$
. Since E is quadratically closed, we deduce that it is the unique quadratic extension of
$E=E'(i)$
. Since E is quadratically closed, we deduce that it is the unique quadratic extension of
![]() $E'$
, up to isomorphism.
$E'$
, up to isomorphism.
Geometry
The methods of [Reference Raynaud22] are geometric and homotopy-theoretic, and so too are the methods of this paper. We specialize to the case where the base ring k is a field of characteristic
![]() $0$
.
$0$
.
If
![]() $a \le b$
are natural numbers, we embed the group scheme
$a \le b$
are natural numbers, we embed the group scheme
![]() $\operatorname {GL}(a)$
into
$\operatorname {GL}(a)$
into
![]() $\operatorname {GL}(b)$
by
$\operatorname {GL}(b)$
by
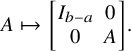 $$\begin{align*}A \mapsto \begin{bmatrix} I_{b-a} & 0 \\ 0 & A \end{bmatrix}.\end{align*}$$
$$\begin{align*}A \mapsto \begin{bmatrix} I_{b-a} & 0 \\ 0 & A \end{bmatrix}.\end{align*}$$
We let
denote the Stiefel variety. There is a canonical projection
![]() $\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
.
$\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
.
The ring
![]() $A_{n,n-r}$
that we referred to previously is the coordinate ring of
$A_{n,n-r}$
that we referred to previously is the coordinate ring of
![]() $V_r(\mathbb {A}^n)$
, and
$V_r(\mathbb {A}^n)$
, and
![]() $P_{n,n-r}$
is a module over it. As a special case of [Reference Raynaud22, Proposition 2.4], the map
$P_{n,n-r}$
is a module over it. As a special case of [Reference Raynaud22, Proposition 2.4], the map
![]() $\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
has a section if and only if
$\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
has a section if and only if
![]() $P_{n,n-1}$
has a free summand of rank
$P_{n,n-1}$
has a free summand of rank
![]() $r-1$
. Therefore, the question of whether all stably free modules of type
$r-1$
. Therefore, the question of whether all stably free modules of type
![]() $(n,n-1)$
(over k-algebras) admit free summands of rank
$(n,n-1)$
(over k-algebras) admit free summands of rank
![]() $r-1$
is equivalent to the following:
$r-1$
is equivalent to the following:
Question 1.2. Does the morphism of k-schemes
![]() $\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
admit a section?
$\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
admit a section?
James answered the topological analogue of this question in [Reference James16]: if
![]() $W_r(\mathbb {C}^n)$
denotes the complex Stiefel manifold of orthonormal r-frames in
$W_r(\mathbb {C}^n)$
denotes the complex Stiefel manifold of orthonormal r-frames in
![]() $\mathbb {C}^n$
, then projection onto the first frame
$\mathbb {C}^n$
, then projection onto the first frame
![]() $\rho _{\mathbb {C}}: W_r(\mathbb {C}^n) \to S^{2n-1}$
has a continuous section if and only if n is divisible by the integer
$\rho _{\mathbb {C}}: W_r(\mathbb {C}^n) \to S^{2n-1}$
has a continuous section if and only if n is divisible by the integer
![]() $b_r$
.
$b_r$
.
Using Steenrod operations in étale cohomology, Raynaud showed that, over a characteristic
![]() $0$
field k, the map
$0$
field k, the map
![]() $\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
does not have a section if n is not divisible by
$\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
does not have a section if n is not divisible by
![]() $b_r$
(this is the geometric content of [Reference Raynaud22, Théorème 6.5] above).
$b_r$
(this is the geometric content of [Reference Raynaud22, Théorème 6.5] above).
Method
The method of proof in this paper is to convert the algebro-geometric problem of Question 1.2 to a problem in
![]() $\mathbb {A}^1$
-homotopy theory. This mimics how an analogous question about vector bundles on topological spaces has been fully solved by the methods of homotopy theory and the calculation of certain periodicities, by [Reference James16], [Reference Toda26], [Reference Atiyah and Todd9] and [Reference Adams and Walker1]. The structure of the topological argument is to reduce the problem to determining whether a certain class in
$\mathbb {A}^1$
-homotopy theory. This mimics how an analogous question about vector bundles on topological spaces has been fully solved by the methods of homotopy theory and the calculation of certain periodicities, by [Reference James16], [Reference Toda26], [Reference Atiyah and Todd9] and [Reference Adams and Walker1]. The structure of the topological argument is to reduce the problem to determining whether a certain class in
![]() $\pi _{2n-2}(W_{r-1}(\mathbb {C}^{n-1}))$
vanishes, which then may be calculated using techniques developed by Adams.
$\pi _{2n-2}(W_{r-1}(\mathbb {C}^{n-1}))$
vanishes, which then may be calculated using techniques developed by Adams.
The analogous obstruction in
![]() $\mathbb {A}^1$
-homotopy theory is defined in Notation 7.1. In Proposition 7.2, we show that the existence of a section is equivalent to the vanishing of the obstruction. One direction of this is trivial. To construct the section knowing that the obstruction vanishes, however, we use the Lindel–Popescu Theorem ([Reference Lindel18]) about homotopy invariance of algebraic vector bundles, an observation of [Reference Raynaud22, Proposition 2.4], and the result of [Reference Asok, Hoyois and Wendt7, Theorem 2.4.2] which relates abstract morphisms in the
$\mathbb {A}^1$
-homotopy theory is defined in Notation 7.1. In Proposition 7.2, we show that the existence of a section is equivalent to the vanishing of the obstruction. One direction of this is trivial. To construct the section knowing that the obstruction vanishes, however, we use the Lindel–Popescu Theorem ([Reference Lindel18]) about homotopy invariance of algebraic vector bundles, an observation of [Reference Raynaud22, Proposition 2.4], and the result of [Reference Asok, Hoyois and Wendt7, Theorem 2.4.2] which relates abstract morphisms in the
![]() $\mathbb {A}^1$
-homotopy category to naive homotopy classes of morphisms of schemes.
$\mathbb {A}^1$
-homotopy category to naive homotopy classes of morphisms of schemes.
Having converted the problem to one in
![]() $\mathbb {A}^1$
-homotopy theory, we now solve it in Propositions 7.4 and 7.7 by using realization methods: comparing the global sections of
$\mathbb {A}^1$
-homotopy theory, we now solve it in Propositions 7.4 and 7.7 by using realization methods: comparing the global sections of
![]() $\mathbb {A}^1$
-homotopy sheaves of spaces with the homotopy groups of their real- or complex-realizations. For the Stiefel varieties at issue, we can prove that the comparison maps in question are isomorphisms. In this way, we show that the answer to the algebraic question is ‘the same’ as the answer for complex vector bundles.
$\mathbb {A}^1$
-homotopy sheaves of spaces with the homotopy groups of their real- or complex-realizations. For the Stiefel varieties at issue, we can prove that the comparison maps in question are isomorphisms. In this way, we show that the answer to the algebraic question is ‘the same’ as the answer for complex vector bundles.
The major inputs are the calculations of the stable homotopy sheaves of spheres by [Reference Röndigs, Spitzweck and Østvær23] and [Reference Röndigs, Spitzweck and Østvær24] and the Freudenthal suspension theorem of [Reference Asok, Bachmann and Hopkins2], by which we can understand unstable
![]() $\mathbb {A}^1$
-homotopy sheaves of spheres, from which we can calculate the unstable
$\mathbb {A}^1$
-homotopy sheaves of spheres, from which we can calculate the unstable
![]() $\mathbb {A}^1$
-homotopy sheaves of Stiefel varieties.
$\mathbb {A}^1$
-homotopy sheaves of Stiefel varieties.
Finally, to establish the stronger form of our main theorem when k is quadratically closed, or is a subfield of
![]() $\mathbb {R}$
admitting only one quadratic extension, we use an argument from [Reference James16], now applied to the
$\mathbb {R}$
admitting only one quadratic extension, we use an argument from [Reference James16], now applied to the
![]() $\mathbb {A}^1$
-homotopy sheaves.
$\mathbb {A}^1$
-homotopy sheaves.
Positive and mixed characteristic
The morphism
![]() $\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
may be defined over
$\rho : V_r(\mathbb {A}^n) \to V_1(\mathbb {A}^n)$
may be defined over
![]() $\mathbb {Z}$
, and over
$\mathbb {Z}$
, and over
![]() $\mathbb {Z}$
the spaces
$\mathbb {Z}$
the spaces
![]() $V_r(\mathbb {A}^n)$
still represent stably free modules. In Proposition 7.4, we prove that when
$V_r(\mathbb {A}^n)$
still represent stably free modules. In Proposition 7.4, we prove that when
![]() $r=3$
and
$r=3$
and
![]() $n=24m$
, the base-change morphism
$n=24m$
, the base-change morphism
![]() $\rho $
over
$\rho $
over
![]() $\mathbb {Q}$
has a section. In particular, this means that
$\mathbb {Q}$
has a section. In particular, this means that
![]() $\rho $
has a section over
$\rho $
has a section over
![]() $\mathbb {Z}[\frac {1}{N}]$
, where N is some positive integer: only finitely many primes need to be inverted in order to construct the section. We remark that a priori the integer N may depend on n.
$\mathbb {Z}[\frac {1}{N}]$
, where N is some positive integer: only finitely many primes need to be inverted in order to construct the section. We remark that a priori the integer N may depend on n.
In particular, we can declare that for any given
![]() $n=24m$
, there exists some integer N so that if R is a ring in which N is invertible and P is a stably free R-module of type
$n=24m$
, there exists some integer N so that if R is a ring in which N is invertible and P is a stably free R-module of type
![]() $(n,n-1)$
, then P has a free summand of rank
$(n,n-1)$
, then P has a free summand of rank
![]() $2$
. We do not know the smallest possible positive integer N, although
$2$
. We do not know the smallest possible positive integer N, although
![]() $N=6$
is a plausible conjecture.
$N=6$
is a plausible conjecture.
One might also wonder whether the methods used to prove Proposition 7.4 can be made to work over a prime field
![]() $\mathbb {F}_p$
of characteristic p. There are two difficulties: most seriously, the main results [Reference Röndigs, Spitzweck and Østvær23] and [Reference Röndigs, Spitzweck and Østvær24] do not fully determine the homotopy groups in question: the p-torsion is not determined, since the exponential characteristic of the ground field must be inverted throughout.
$\mathbb {F}_p$
of characteristic p. There are two difficulties: most seriously, the main results [Reference Röndigs, Spitzweck and Østvær23] and [Reference Röndigs, Spitzweck and Østvær24] do not fully determine the homotopy groups in question: the p-torsion is not determined, since the exponential characteristic of the ground field must be inverted throughout.
Secondly, the complex realization functor must be replaced by
![]() $\ell $
-étale realization (see, for example, [Reference Isaksen15]), which takes values in
$\ell $
-étale realization (see, for example, [Reference Isaksen15]), which takes values in
![]() $\ell $
-complete spaces or pro-spaces where
$\ell $
-complete spaces or pro-spaces where
![]() $\ell \neq p$
. We expect our obstructions to lie in groups isomorphic to
$\ell \neq p$
. We expect our obstructions to lie in groups isomorphic to
![]() $\mathbb {Z}/(24)$
contingent on a strengthening of [Reference Röndigs, Spitzweck and Østvær23] and [Reference Röndigs, Spitzweck and Østvær24] that holds without inverting the exponential characteristic. Therefore, we will have to use realization for the primes
$\mathbb {Z}/(24)$
contingent on a strengthening of [Reference Röndigs, Spitzweck and Østvær23] and [Reference Röndigs, Spitzweck and Østvær24] that holds without inverting the exponential characteristic. Therefore, we will have to use realization for the primes
![]() $2, 3$
, which implies that the constraint
$2, 3$
, which implies that the constraint
![]() $p \neq 2,3$
is probably unavoidable.
$p \neq 2,3$
is probably unavoidable.
2 Homotopy-theory conventions and notation
For the rest of the paper, we work over a field k of characteristic
![]() $0$
. Other restrictions may be imposed on k from time to time. Unless otherwise stated, all schemes appearing are k-schemes. The category of motivic spaces over k is
$0$
. Other restrictions may be imposed on k from time to time. Unless otherwise stated, all schemes appearing are k-schemes. The category of motivic spaces over k is
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
, the category of simplicial presheaves of sets on
$\mathbf {sPre}(\mathbf {Sm}_k)$
, the category of simplicial presheaves of sets on
![]() $\mathbf {Sm}_k$
, which is itself the category of smooth finite type separated k-schemes. We use the homotopy theory of [Reference Morel and Voevodsky20]. The notation
$\mathbf {Sm}_k$
, which is itself the category of smooth finite type separated k-schemes. We use the homotopy theory of [Reference Morel and Voevodsky20]. The notation
![]() $\mathbf {H}(k)$
is used for the homotopy category. A pointed object consists of an object X and a morphism
$\mathbf {H}(k)$
is used for the homotopy category. A pointed object consists of an object X and a morphism
![]() $\operatorname {Spec} k \to X$
. There is a homotopy theory of pointed objects, and the associated homotopy category is denoted
$\operatorname {Spec} k \to X$
. There is a homotopy theory of pointed objects, and the associated homotopy category is denoted
![]() $\mathbf {H}(k)_\bullet $
. The notation
$\mathbf {H}(k)_\bullet $
. The notation
![]() $X_+$
is used to denote the addition of a disjoint basepoint to X.
$X_+$
is used to denote the addition of a disjoint basepoint to X.
2.1 Homotopy sheaves
The paper makes extensive use of the
![]() $\mathbb {A}^1$
-homotopy theory of spheres. If
$\mathbb {A}^1$
-homotopy theory of spheres. If
![]() $p,q$
are nonnegative integers, then we define
$p,q$
are nonnegative integers, then we define
where
![]() $S^p$
is the ordinary simplicial sphere.
$S^p$
is the ordinary simplicial sphere.
If X is a pointed object of
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
, then we write
$\mathbf {sPre}(\mathbf {Sm}_k)$
, then we write
for the Nisnevich sheaf associated to the functor
When
![]() $p \ge 1$
, then
$p \ge 1$
, then
![]() $\boldsymbol {\pi }_{p+q\alpha }(X)$
is a sheaf of groups, and of abelian groups if
$\boldsymbol {\pi }_{p+q\alpha }(X)$
is a sheaf of groups, and of abelian groups if
![]() $p \ge 2$
.
$p \ge 2$
.
The symbols
![]() ${{\mathbf K}}^{\mathsf {MW}}_n$
and
${{\mathbf K}}^{\mathsf {MW}}_n$
and
![]() ${{\mathbf K}}^{\mathsf {M}}_n$
will be used for the unramified sheaves constructed in [Reference Morel19, Section 3.2]. We make use of the contraction
${{\mathbf K}}^{\mathsf {M}}_n$
will be used for the unramified sheaves constructed in [Reference Morel19, Section 3.2]. We make use of the contraction
![]() $\mathbf {A} \mapsto \mathbf {A}_{-1}$
, for which we refer to [Reference Morel19, p. 33] and [Reference Morel19, Theorem 6.13], which implies that
$\mathbf {A} \mapsto \mathbf {A}_{-1}$
, for which we refer to [Reference Morel19, p. 33] and [Reference Morel19, Theorem 6.13], which implies that
2.2 Naive homotopy
If X is a k-scheme, we write
![]() $j_0, j_1: X \to X \times \mathbb {A}^1_k$
for the closed inclusions at
$j_0, j_1: X \to X \times \mathbb {A}^1_k$
for the closed inclusions at
![]() $0$
,
$0$
,
![]() $1$
, respectively.
$1$
, respectively.
Two morphisms
![]() $f_0, f_1: X \to Y$
are said to be naively homotopic if there is a morphism
$f_0, f_1: X \to Y$
are said to be naively homotopic if there is a morphism
![]() ${H : X \times \mathbb {A}^1_k \to Y}$
such that
${H : X \times \mathbb {A}^1_k \to Y}$
such that
![]() $H \circ j_0 = f_0$
and
$H \circ j_0 = f_0$
and
![]() $H \circ j_1 = f_1$
.
$H \circ j_1 = f_1$
.
2.3 Pointed homotopy
If X, Y are objects of
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
, then we will write
$\mathbf {sPre}(\mathbf {Sm}_k)$
, then we will write
![]() $\{X,Y\}$
for the set of morphisms
$\{X,Y\}$
for the set of morphisms
![]() $X \to Y$
in the homotopy category
$X \to Y$
in the homotopy category
![]() $\mathbf {H}(k)$
. If X and Y are pointed objects of
$\mathbf {H}(k)$
. If X and Y are pointed objects of
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
, then the notation
$\mathbf {sPre}(\mathbf {Sm}_k)$
, then the notation
![]() $[X,Y]$
will be used to denote the set of morphisms
$[X,Y]$
will be used to denote the set of morphisms
![]() $X\to Y$
in
$X\to Y$
in
![]() $\mathbf {H}(k)_\bullet $
. There is a natural bijection
$\mathbf {H}(k)_\bullet $
. There is a natural bijection
Proposition 2.1. Suppose
![]() $X,Y$
are two pointed objects of
$X,Y$
are two pointed objects of
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
, and Y is
$\mathbf {sPre}(\mathbf {Sm}_k)$
, and Y is
![]() $\mathbb {A}^1$
-simply-connected. The natural map
$\mathbb {A}^1$
-simply-connected. The natural map
is a bijection.
Proof. We work in the
![]() $\mathbb {A}^1$
-injective model category. There is nothing to be lost in assuming X is cofibrant and Y is fibrant.
$\mathbb {A}^1$
-injective model category. There is nothing to be lost in assuming X is cofibrant and Y is fibrant.
There is a cofibre sequence of pointed objects
We write ![]() for the mapping object of
for the mapping object of
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
and
$\mathbf {sPre}(\mathbf {Sm}_k)$
and ![]() for its pointed analogue. Apply
for its pointed analogue. Apply ![]() to (2) to obtain an
to (2) to obtain an
![]() $\mathbb {A}^1$
-homotopy fibre sequence:
$\mathbb {A}^1$
-homotopy fibre sequence:
Since Y is assumed simply-connected, the result may be deduced by taking global sections of
![]() $\pi _0$
applied to this fibre sequence.
$\pi _0$
applied to this fibre sequence.
3 Stiefel varieties
3.1 Some notation
We frequently adopt the functor-of-points approach to k-schemes. That is, a k-scheme Y represents a contravariant functor on the category
![]() $\mathbf {Sch}_k$
of k-schemes
$\mathbf {Sch}_k$
of k-schemes
In fact, we may restrict the source of the functor to the category of affine k-schemes, or equivalently to k-algebras:
The assignment
![]() $Y \mapsto h_Y$
yields a full embedding of
$Y \mapsto h_Y$
yields a full embedding of
![]() $\mathbf {Sch}_k$
in the category of functors
$\mathbf {Sch}_k$
in the category of functors
![]() $k\text {-}\mathbf {Alg} \to \mathbf {Set}$
, [Reference Eisenbud and Harris12, Proposition VI-2]. As a consequence, we will abuse notation and write ‘Y’ when ‘
$k\text {-}\mathbf {Alg} \to \mathbf {Set}$
, [Reference Eisenbud and Harris12, Proposition VI-2]. As a consequence, we will abuse notation and write ‘Y’ when ‘
![]() $h_Y$
’ is technically correct. Furthermore, we will specify k-schemes Y by describing their functors of points
$h_Y$
’ is technically correct. Furthermore, we will specify k-schemes Y by describing their functors of points
![]() $R \mapsto Y(R)$
, and we will define morphisms of k-schemes
$R \mapsto Y(R)$
, and we will define morphisms of k-schemes
![]() $Y \to Y'$
by giving the associated natural transformation of functors.
$Y \to Y'$
by giving the associated natural transformation of functors.
3.2 Definitions
If
![]() $r \le n$
are two natural numbers, then we define
$r \le n$
are two natural numbers, then we define
![]() $V_r(\mathbb {A}^n)$
to be the affine k-scheme representing the functor
$V_r(\mathbb {A}^n)$
to be the affine k-scheme representing the functor
This is a closed subscheme of
![]() $\operatorname {Mat}_{r \times n}^2$
, and is therefore affine. We consider
$\operatorname {Mat}_{r \times n}^2$
, and is therefore affine. We consider
![]() $V_r(\mathbb {A}^n)$
as a pointed object of
$V_r(\mathbb {A}^n)$
as a pointed object of
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
with basepoint given by the k-rational point
$\mathbf {sPre}(\mathbf {Sm}_k)$
with basepoint given by the k-rational point
Remark 3.1. The spaces
![]() $V_r(\mathbb {A}^n)$
are a kind of Stiefel variety. The obvious projection furnishes an
$V_r(\mathbb {A}^n)$
are a kind of Stiefel variety. The obvious projection furnishes an
![]() $\mathbb {A}^1$
-equivalence from
$\mathbb {A}^1$
-equivalence from
![]() $V_r(\mathbb {A}^n)$
to the k-scheme
$V_r(\mathbb {A}^n)$
to the k-scheme
![]() $V^{\prime }_r(\mathbb {A}^n)$
representing the functor
$V^{\prime }_r(\mathbb {A}^n)$
representing the functor
which might be considered the true Stiefel variety. There is a morphism
![]() $p:V_r(\mathbb {A}^n) \to V^{\prime }_r(\mathbb {A}^n)$
given by forgetting the choice of B. One may cover
$p:V_r(\mathbb {A}^n) \to V^{\prime }_r(\mathbb {A}^n)$
given by forgetting the choice of B. One may cover
![]() $V^{\prime }_r(\mathbb {A}^n)$
by Zariski-open subschemes U so that the morphism
$V^{\prime }_r(\mathbb {A}^n)$
by Zariski-open subschemes U so that the morphism
![]() $p|_{p^{-1}(U)} : p^{-1}(U) \to U$
is isomorphic to the projections
$p|_{p^{-1}(U)} : p^{-1}(U) \to U$
is isomorphic to the projections
![]() $U \times \mathbb {A}^{(n-r)r} \to U$
, that is, p is a Zariski-locally trivial, smooth morphism with affine-space fibres, and therefore by a standard argument, p is an
$U \times \mathbb {A}^{(n-r)r} \to U$
, that is, p is a Zariski-locally trivial, smooth morphism with affine-space fibres, and therefore by a standard argument, p is an
![]() $\mathbb {A}^1$
-equivalence (see, for example, [Reference Asok and Doran3, Lemma 2.4]).
$\mathbb {A}^1$
-equivalence (see, for example, [Reference Asok and Doran3, Lemma 2.4]).
By forgetting the bottom
![]() $r-r'$
rows, we obtain a pointed morphism
$r-r'$
rows, we obtain a pointed morphism
![]() $\rho _{r,r'} : V_r(\mathbb {A}^n) \to V_{r'}(\mathbb {A}^n)$
. This will be written
$\rho _{r,r'} : V_r(\mathbb {A}^n) \to V_{r'}(\mathbb {A}^n)$
. This will be written
![]() $\rho $
when there is no risk of ambiguity.
$\rho $
when there is no risk of ambiguity.
Two cases of
![]() $V_r(\mathbb {A}^n)$
have notation of their own:
$V_r(\mathbb {A}^n)$
have notation of their own:
We remark that
![]() $Q_{2n-1}$
is
$Q_{2n-1}$
is
![]() $\mathbb {A}^1$
-homotopy equivalent to
$\mathbb {A}^1$
-homotopy equivalent to
![]() $\mathbb {A}^n\setminus \{0\}\simeq S^{n-1+n\alpha }$
.
$\mathbb {A}^n\setminus \{0\}\simeq S^{n-1+n\alpha }$
.
If we embed
![]() $\operatorname {GL}(n-r)$
in
$\operatorname {GL}(n-r)$
in
![]() $\operatorname {GL}(n)$
in the lower-right position
$\operatorname {GL}(n)$
in the lower-right position
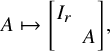 $$\begin{align*}A \mapsto \begin{bmatrix} I_r & \\ & A \end{bmatrix}, \end{align*}$$
$$\begin{align*}A \mapsto \begin{bmatrix} I_r & \\ & A \end{bmatrix}, \end{align*}$$
then we arrive at a quotient presentation
![]() $V_r(\mathbb {A}^n) = \operatorname {GL}(n)/\operatorname {GL}(n-r)$
.
$V_r(\mathbb {A}^n) = \operatorname {GL}(n)/\operatorname {GL}(n-r)$
.
If
![]() $\mathbb {F}$
is
$\mathbb {F}$
is
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {C}$
, we denote the Stiefel manifold of orthonormal r-frames in
$\mathbb {C}$
, we denote the Stiefel manifold of orthonormal r-frames in
![]() $\mathbb {F}^n$
by
$\mathbb {F}^n$
by
![]() $W_r(\mathbb {F}^n)$
.
$W_r(\mathbb {F}^n)$
.
3.3 Fibre sequences
Using results from [Reference Morel19, Chapter 6] and [Reference Morel19, Proposition 8.11], we have a diagram of pointed spaces
in which any three consecutive terms form an
![]() $\mathbb {A}^1$
-homotopy fibre sequence.
$\mathbb {A}^1$
-homotopy fibre sequence.
From here, standard homotopy theory (e.g., [Reference Hovey14, Proposition 6.3.6]) implies that the induced sequence of quotients
is an
![]() $\mathbb {A}^1$
-homotopy fibre sequence whenever
$\mathbb {A}^1$
-homotopy fibre sequence whenever
![]() $n,r,s$
are integers satisfying
$n,r,s$
are integers satisfying
![]() $0 \le s <r \le n$
.
$0 \le s <r \le n$
.
Proposition 3.2. The space
![]() $V_r(\mathbb {A}^n)$
is
$V_r(\mathbb {A}^n)$
is
![]() $\mathbb {A}^1$
-
$\mathbb {A}^1$
-
![]() $(n-r-1)$
-connected.
$(n-r-1)$
-connected.
Proof. In the case where
![]() $r=1$
, we use the
$r=1$
, we use the
![]() $\mathbb {A}^1$
-equivalence
$\mathbb {A}^1$
-equivalence
![]() $V_1(\mathbb {A}^n) \simeq S^{n-1+n\alpha }$
. The sphere is
$V_1(\mathbb {A}^n) \simeq S^{n-1+n\alpha }$
. The sphere is
![]() $n-2$
-connected by results of Morel ([Reference Morel19, Theorem 6.38]).
$n-2$
-connected by results of Morel ([Reference Morel19, Theorem 6.38]).
The general result now follows by induction on r, using the
![]() $s=1$
case of (5).
$s=1$
case of (5).
Corollary 3.3. Suppose
![]() $n, r$
are natural numbers satisfying
$n, r$
are natural numbers satisfying
![]() $r \le n-2$
. Then for any pointed object X of
$r \le n-2$
. Then for any pointed object X of
![]() $\mathbf {sPre}(\mathbf {Sm}_k)$
, the natural map
$\mathbf {sPre}(\mathbf {Sm}_k)$
, the natural map
is a bijection.
3.4 Interpretation as spaces of stably free modules
The k-scheme
![]() $V_r(\mathbb {A}^n)$
represents a space of matrices as laid out in (3). Given a pair of matrices
$V_r(\mathbb {A}^n)$
represents a space of matrices as laid out in (3). Given a pair of matrices
![]() $(A,B)$
satisfying
$(A,B)$
satisfying
![]() $AB^T = I_r$
, we may form the split short exact sequence of R-modules:
$AB^T = I_r$
, we may form the split short exact sequence of R-modules:
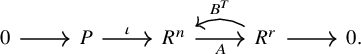
Therefore,
![]() $(A,B)$
determine an R-module
$(A,B)$
determine an R-module
![]() $P = \ker (A)$
, up to isomorphism over
$P = \ker (A)$
, up to isomorphism over
![]() $R^n$
, along with an isomorphism
$R^n$
, along with an isomorphism
![]() $P \oplus R^r \to R^n$
, given by
$P \oplus R^r \to R^n$
, given by
![]() $\iota + B^T$
. Conversely, given an R-module P and an isomorphism
$\iota + B^T$
. Conversely, given an R-module P and an isomorphism
![]() $f: P \oplus R^r \to R^n$
, we may produce a morphism
$f: P \oplus R^r \to R^n$
, we may produce a morphism
![]() $B^T = f|_{R^r}$
and
$B^T = f|_{R^r}$
and
![]() $A = \operatorname {proj}_2 \circ f^{-1}$
. This allows us to say that
$A = \operatorname {proj}_2 \circ f^{-1}$
. This allows us to say that
![]() $V_r(\mathbb {A}^n)$
represents the functor that assigns to a ring R the set of equivalence classes of pairs
$V_r(\mathbb {A}^n)$
represents the functor that assigns to a ring R the set of equivalence classes of pairs
![]() $(P, f)$
where P is an R-module and
$(P, f)$
where P is an R-module and
![]() $f: P \oplus R^r \to R^n$
is an isomorphism: two pairs
$f: P \oplus R^r \to R^n$
is an isomorphism: two pairs
![]() $(P, f)$
and
$(P, f)$
and
![]() $(P', f')$
being equivalent when there exists an isomorphism
$(P', f')$
being equivalent when there exists an isomorphism
![]() $h : P \to P'$
for which the diagram
$h : P \to P'$
for which the diagram

is commutative. In this language, the morphism
![]() $\rho : V_r(\mathbb {A}^n) \to V_{r'}(\mathbb {A}^n)$
takes a pair
$\rho : V_r(\mathbb {A}^n) \to V_{r'}(\mathbb {A}^n)$
takes a pair
![]() $(P,f)$
to
$(P,f)$
to
![]() $(P\oplus R^{r-r'}, f)$
.
$(P\oplus R^{r-r'}, f)$
.
The preceding discussion concerns the functor represented by the k-scheme
![]() $V_r(\mathbb {A}^n)$
on the category of commutative k-algebras, viz., on affine k-schemes. On the category of all k-schemes,
$V_r(\mathbb {A}^n)$
on the category of commutative k-algebras, viz., on affine k-schemes. On the category of all k-schemes,
![]() $V_r(\mathbb {A}^n)$
represents the functor
$V_r(\mathbb {A}^n)$
represents the functor
since
![]() $V_r(\mathbb {A}^n)$
is itself affine and therefore
$V_r(\mathbb {A}^n)$
is itself affine and therefore
![]() $V_r(\mathbb {A}^n)(X) = V_r(\mathbb {A}^n)(\operatorname {Spec} \Gamma (X, \mathcal {O}_X))$
by reference to [Reference Hartshorne13, II, Exercise 2.4], for instance.
$V_r(\mathbb {A}^n)(X) = V_r(\mathbb {A}^n)(\operatorname {Spec} \Gamma (X, \mathcal {O}_X))$
by reference to [Reference Hartshorne13, II, Exercise 2.4], for instance.
The matrices A and B of global sections of
![]() $\mathcal {O}_X$
allow us to set up a split short exact sequence
$\mathcal {O}_X$
allow us to set up a split short exact sequence

as in the affine case,. Therefore, the k-scheme
![]() $V_r(\mathbb {A}^n)$
represents the functor that assigns to a k-scheme X the set of equivalence classes of pairs
$V_r(\mathbb {A}^n)$
represents the functor that assigns to a k-scheme X the set of equivalence classes of pairs
![]() $(\mathcal {P}, f)$
, where
$(\mathcal {P}, f)$
, where
![]() $\mathcal {P}$
is a locally free
$\mathcal {P}$
is a locally free
![]() $\mathcal {O}_X$
-module and
$\mathcal {O}_X$
-module and
![]() $f: \mathcal {P} \oplus \mathcal {O}_X^r \to \mathcal {O}_X^n$
is an isomorphism. Two pairs
$f: \mathcal {P} \oplus \mathcal {O}_X^r \to \mathcal {O}_X^n$
is an isomorphism. Two pairs
![]() $(\mathcal {P}, f)$
and
$(\mathcal {P}, f)$
and
![]() $(\mathcal {P}', f')$
are equivalent when a commutative diagram analogous to (7) exists. Note that the sheaves
$(\mathcal {P}', f')$
are equivalent when a commutative diagram analogous to (7) exists. Note that the sheaves
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $\mathcal {O}_X$
-modules appearing here are necessarily coherent.
$\mathcal {O}_X$
-modules appearing here are necessarily coherent.
On
![]() $V_{r}(\mathbb {A}^{n})$
itself, there exists a tautological
$V_{r}(\mathbb {A}^{n})$
itself, there exists a tautological
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\mathcal {P}_{\mathrm {taut}}$
and a tautological isomorphism
$\mathcal {P}_{\mathrm {taut}}$
and a tautological isomorphism
![]() $f_{\mathrm {taut}} : \mathcal {P}_{\mathrm {taut}} \oplus \mathcal {O}_{V_{r}(\mathbb {A}^{n})}^r \to \mathcal {O}^n_{V_{r}(\mathbb {A}^{n})}$
. Since
$f_{\mathrm {taut}} : \mathcal {P}_{\mathrm {taut}} \oplus \mathcal {O}_{V_{r}(\mathbb {A}^{n})}^r \to \mathcal {O}^n_{V_{r}(\mathbb {A}^{n})}$
. Since
![]() $V_{r}(\mathbb {A}^{n})$
is an affine variety, we may alternatively view the above as a tautological module
$V_{r}(\mathbb {A}^{n})$
is an affine variety, we may alternatively view the above as a tautological module
![]() $P_{\mathrm {taut}}$
and a tautological isomorphism in the category of modules over the coordinate ring of
$P_{\mathrm {taut}}$
and a tautological isomorphism in the category of modules over the coordinate ring of
![]() $V_r(\mathbb {A}^n)$
.
$V_r(\mathbb {A}^n)$
.
4 Homotopy sections
Definition 4.1. Consider the morphism
![]() $\rho =\rho _{r,1}: V_r(\mathbb {A}^n) \to Q_{2n-1}$
. A homotopy section of
$\rho =\rho _{r,1}: V_r(\mathbb {A}^n) \to Q_{2n-1}$
. A homotopy section of
![]() $\rho $
is a morphism
$\rho $
is a morphism
![]() $\psi : Q_{2n-1} \to V_r(\mathbb {A}^n)$
in
$\psi : Q_{2n-1} \to V_r(\mathbb {A}^n)$
in
![]() $\mathbf {H}(k)$
with the property that
$\mathbf {H}(k)$
with the property that
![]() $\rho \circ \psi = \mathrm {id}_{Q_{2n-1}}$
in
$\rho \circ \psi = \mathrm {id}_{Q_{2n-1}}$
in
![]() $\mathbf {H}(k)$
. Similarly, a pointed homotopy section of
$\mathbf {H}(k)$
. Similarly, a pointed homotopy section of
![]() $\rho $
is a morphism
$\rho $
is a morphism
![]() $\phi : Q_{2n-1} \to V_r(\mathbb {A}^n)$
in
$\phi : Q_{2n-1} \to V_r(\mathbb {A}^n)$
in
![]() $\mathbf {H}(k)_\bullet $
with the property that
$\mathbf {H}(k)_\bullet $
with the property that
![]() $\rho \circ \phi = \mathrm {id}_{Q_{2n-1}}$
in
$\rho \circ \phi = \mathrm {id}_{Q_{2n-1}}$
in
![]() $\mathbf {H}(k)_\bullet $
.
$\mathbf {H}(k)_\bullet $
.
Example 4.2. When n is even, there is a well-known section of
![]() $\rho _{2,1}$
in the category of k-schemes given by
$\rho _{2,1}$
in the category of k-schemes given by
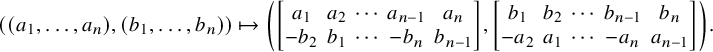 $$\begin{align*}((a_1, \dots, a_n),(b_1, \dots, b_n)) \mapsto \left( \begin{bmatrix} a_1 & a_2 & \cdots & a_{n-1} & a_n \\ -b_2 & b_1 & \cdots & -b_n & b_{n-1} \end{bmatrix}, \begin{bmatrix} b_1 & b_2 & \cdots & b_{n-1} & b_n \\ -a_2 & a_1 & \cdots & -a_n & a_{n-1} \end{bmatrix} \right). \end{align*}$$
$$\begin{align*}((a_1, \dots, a_n),(b_1, \dots, b_n)) \mapsto \left( \begin{bmatrix} a_1 & a_2 & \cdots & a_{n-1} & a_n \\ -b_2 & b_1 & \cdots & -b_n & b_{n-1} \end{bmatrix}, \begin{bmatrix} b_1 & b_2 & \cdots & b_{n-1} & b_n \\ -a_2 & a_1 & \cdots & -a_n & a_{n-1} \end{bmatrix} \right). \end{align*}$$
This section gives rise to a pointed homotopy section of
![]() $\rho _{2,1}$
.
$\rho _{2,1}$
.
Proposition 4.3. Let R be a regular ring of essentially finite type over k. Suppose
![]() $f_0 , f_1 : \operatorname {Spec} R \to V_r(\mathbb {A}^n)$
are naively homotopic. Write
$f_0 , f_1 : \operatorname {Spec} R \to V_r(\mathbb {A}^n)$
are naively homotopic. Write
![]() $P_0$
and
$P_0$
and
![]() $P_1$
for the represented stably free modules. Then
$P_1$
for the represented stably free modules. Then
![]() $P_0 \cong P_1$
as R-modules.
$P_0 \cong P_1$
as R-modules.
Proof. Let
![]() $H : \operatorname {Spec} R[t] \to V_r(\mathbb {A}^n)$
be the naive homotopy. By pulling the tautological
$H : \operatorname {Spec} R[t] \to V_r(\mathbb {A}^n)$
be the naive homotopy. By pulling the tautological
![]() $\mathcal {P}_{\mathrm {taut}}$
back to
$\mathcal {P}_{\mathrm {taut}}$
back to
![]() $\operatorname {Spec} R[t]$
along H, we obtain a stably free
$\operatorname {Spec} R[t]$
along H, we obtain a stably free
![]() $R[t]$
-module
$R[t]$
-module
![]() $P_H$
. The stably free modules
$P_H$
. The stably free modules
![]() $P_i$
are then obtained as
$P_i$
are then obtained as
![]() $P_i \cong R \otimes _{R[t]} P_H$
using the two evaluation homomorphisms
$P_i \cong R \otimes _{R[t]} P_H$
using the two evaluation homomorphisms
![]() $e_0: t \mapsto 0$
and
$e_0: t \mapsto 0$
and
![]() $e_1: t \mapsto 1$
.
$e_1: t \mapsto 1$
.
Since R is regular, the Lindel–Popescu theorem, specifically the main result of [Reference Lindel18], implies that
![]() $P_0 \cong P_1$
.
$P_0 \cong P_1$
.
Proposition 4.4. Suppose
![]() $r,n$
are positive integers such that
$r,n$
are positive integers such that
![]() $\rho : V_{r}(\mathbb {A}^{n}) \to Q_{2n-1}$
has a homotopy section. Suppose X is a k-scheme and
$\rho : V_{r}(\mathbb {A}^{n}) \to Q_{2n-1}$
has a homotopy section. Suppose X is a k-scheme and
![]() $\mathcal {P}$
is a sheaf of
$\mathcal {P}$
is a sheaf of
![]() $\mathcal {O}_X$
-modules on X with the property that
$\mathcal {O}_X$
-modules on X with the property that
![]() $\mathcal {P} \oplus \mathcal {O}_X \cong \mathcal {O}_X^n$
. There exists a sheaf
$\mathcal {P} \oplus \mathcal {O}_X \cong \mathcal {O}_X^n$
. There exists a sheaf
![]() $\mathcal {Q}$
of
$\mathcal {Q}$
of
![]() $\mathcal {O}_X$
-modules and an isomorphism
$\mathcal {O}_X$
-modules and an isomorphism
![]() $ \mathcal {Q} \oplus \mathcal {O}_X^{r-1} \cong \mathcal {P}$
.
$ \mathcal {Q} \oplus \mathcal {O}_X^{r-1} \cong \mathcal {P}$
.
Proof. Fix an isomorphism
![]() $f: \mathcal {P} \oplus \mathcal {O}_X \to \mathcal {O}_X^{n}$
. The pair
$f: \mathcal {P} \oplus \mathcal {O}_X \to \mathcal {O}_X^{n}$
. The pair
![]() $(\mathcal {P}, f)$
determines a morphism
$(\mathcal {P}, f)$
determines a morphism
![]() $h: X \to Q_{2n-1}$
, and
$h: X \to Q_{2n-1}$
, and
![]() $f: \mathcal {P} \oplus \mathcal {O}_X \to \mathcal {O}_X^{n}$
is pulled back from the tautological isomorphism over
$f: \mathcal {P} \oplus \mathcal {O}_X \to \mathcal {O}_X^{n}$
is pulled back from the tautological isomorphism over
![]() $Q_{2n-1}$
. Therefore, it suffices to produce
$Q_{2n-1}$
. Therefore, it suffices to produce
![]() $\mathcal {Q}_{\mathrm {taut}}$
over
$\mathcal {Q}_{\mathrm {taut}}$
over
![]() $Q_{2n-1}$
so that
$Q_{2n-1}$
so that
![]() $\mathcal {Q}_{\mathrm {taut}} \oplus \mathcal {O}_{Q_{2n-1}}^{r-1} \cong \mathcal {P}_{\mathrm {taut}}$
. That is, we may suppose that
$\mathcal {Q}_{\mathrm {taut}} \oplus \mathcal {O}_{Q_{2n-1}}^{r-1} \cong \mathcal {P}_{\mathrm {taut}}$
. That is, we may suppose that
![]() $X = Q_{2n-1}$
and
$X = Q_{2n-1}$
and
![]() $\mathcal {P}=\mathcal {P}_{\mathrm {taut}}$
.
$\mathcal {P}=\mathcal {P}_{\mathrm {taut}}$
.
By hypothesis, there exists a morphism
![]() $\psi :Q_{2n-1} \to V_{r}(\mathbb {A}^{n})$
in
$\psi :Q_{2n-1} \to V_{r}(\mathbb {A}^{n})$
in
![]() $\mathbf {H}(k)$
with the property that
$\mathbf {H}(k)$
with the property that
![]() $\rho \circ \psi = \mathrm {id}_{Q_{2n-1}}$
. Using [Reference Asok, Hoyois and Wendt7, Theorem 2.4.2], we may suppose that
$\rho \circ \psi = \mathrm {id}_{Q_{2n-1}}$
. Using [Reference Asok, Hoyois and Wendt7, Theorem 2.4.2], we may suppose that
![]() $\psi $
is a morphism in the category of k-schemes and that there exists a naive
$\psi $
is a morphism in the category of k-schemes and that there exists a naive
![]() $\mathbb {A}^1$
-homotopy
$\mathbb {A}^1$
-homotopy
for which
![]() $H_0 = \rho \circ \psi $
and
$H_0 = \rho \circ \psi $
and
![]() $H_1 = \mathrm {id}_{Q_{2n-1} }$
.
$H_1 = \mathrm {id}_{Q_{2n-1} }$
.
The morphism
![]() $\psi : Q_{2n-1} \to V_{r}(\mathbb {A}^{n})$
classifies a pair
$\psi : Q_{2n-1} \to V_{r}(\mathbb {A}^{n})$
classifies a pair
![]() $(\mathcal {Q}, g)$
where
$(\mathcal {Q}, g)$
where
![]() $g : \mathcal {Q} \oplus \mathcal {O}_{Q_{2n-1}}^r \cong \mathcal {O}^{n}_{Q_{2n-1}}$
. The composite
$g : \mathcal {Q} \oplus \mathcal {O}_{Q_{2n-1}}^r \cong \mathcal {O}^{n}_{Q_{2n-1}}$
. The composite
![]() $\rho \circ \psi $
classifies the pair
$\rho \circ \psi $
classifies the pair
![]() $(\mathcal {Q} \oplus \mathcal {O}_{Q_{2n-1}}^{r-1}, g)$
. The existence of the naive
$(\mathcal {Q} \oplus \mathcal {O}_{Q_{2n-1}}^{r-1}, g)$
. The existence of the naive
![]() $\mathbb {A}^1$
homotopy implies that
$\mathbb {A}^1$
homotopy implies that
![]() $\mathcal {Q} \oplus \mathcal {O}_{Q_{2n-1}}^{r-1}$
is isomorphic to
$\mathcal {Q} \oplus \mathcal {O}_{Q_{2n-1}}^{r-1}$
is isomorphic to
![]() $\mathcal {P}$
, using Proposition 4.3.
$\mathcal {P}$
, using Proposition 4.3.
Remark 4.5. The topological analogues of the maps considered above, that is,
![]() $\rho _{\mathbb {C}}: W_r(\mathbb {C}^n) \to W_1(\mathbb {C}^n)$
and
$\rho _{\mathbb {C}}: W_r(\mathbb {C}^n) \to W_1(\mathbb {C}^n)$
and
![]() $\rho _{\mathbb {R}}: W_r(\mathbb {R}^n) \to W_1(\mathbb {R}^n)$
, are Serre fibrations. This means that homotopy sections of these continuous functions may be deformed to give strict sections, by a lifting argument. The luxury of deforming a homotopy section to a strict section is unavailable to us in the
$\rho _{\mathbb {R}}: W_r(\mathbb {R}^n) \to W_1(\mathbb {R}^n)$
, are Serre fibrations. This means that homotopy sections of these continuous functions may be deformed to give strict sections, by a lifting argument. The luxury of deforming a homotopy section to a strict section is unavailable to us in the
![]() $\mathbb {A}^1$
-homotopy theory.
$\mathbb {A}^1$
-homotopy theory.
In spite of the previous remark, the proposition below can be proved.
Proposition 4.6. Let
![]() $n,r$
be positive integers satisfying
$n,r$
be positive integers satisfying
![]() $r \le n-2$
. The following are equivalent
$r \le n-2$
. The following are equivalent
-
1. The morphism
 $\rho : V_r(\mathbb {A}^n) \to Q_{2n-1}$
has a section in the category of k-schemes;
$\rho : V_r(\mathbb {A}^n) \to Q_{2n-1}$
has a section in the category of k-schemes; -
2. The morphism
 $\rho : V_r(\mathbb {A}^n) \to Q_{2n-1}$
has a homotopy section;
$\rho : V_r(\mathbb {A}^n) \to Q_{2n-1}$
has a homotopy section; -
3. The morphism
 $\rho : V_r(\mathbb {A}^n) \to Q_{2n-1}$
has a pointed homotopy section.
$\rho : V_r(\mathbb {A}^n) \to Q_{2n-1}$
has a pointed homotopy section.
Proof. The implications 1
![]() $\Rightarrow $
2 and 3
$\Rightarrow $
2 and 3
![]() $\Rightarrow $
2 are obvious.
$\Rightarrow $
2 are obvious.
(2
![]() $\Rightarrow $
1). If a homotopy section of
$\Rightarrow $
1). If a homotopy section of
![]() $\rho $
exists, then Proposition 4.4 asserts that the universal projective module
$\rho $
exists, then Proposition 4.4 asserts that the universal projective module
![]() $P_{n,n-r}$
has a free summand of rank
$P_{n,n-r}$
has a free summand of rank
![]() $r-1$
. It follows from [Reference Raynaud22, Proposition 2.4] that a section of
$r-1$
. It follows from [Reference Raynaud22, Proposition 2.4] that a section of
![]() $\rho $
exists in the category of k-schemes.
$\rho $
exists in the category of k-schemes.
(2
![]() $\Rightarrow $
3). One may restate Condition 3 as saying that the class of the identity map is in the image of
$\Rightarrow $
3). One may restate Condition 3 as saying that the class of the identity map is in the image of
Since
![]() $1 \le r \le n-2$
, both
$1 \le r \le n-2$
, both
![]() $V_r(\mathbb {A}^n)$
and
$V_r(\mathbb {A}^n)$
and
![]() $Q_{2n-1}$
are
$Q_{2n-1}$
are
![]() $\mathbb {A}^1$
-simply connected by Proposition 3.2, so that Corollary 3.3 implies that the vertical arrows in the commuting square below are bijections
$\mathbb {A}^1$
-simply connected by Proposition 3.2, so that Corollary 3.3 implies that the vertical arrows in the commuting square below are bijections
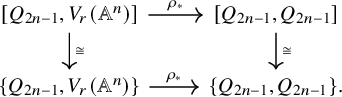
Condition 2 asserts that the class of the identity map is in the image of the lower arrow, so that Condition 3 follows.
5 Realization
We refer the reader to [Reference Dugger and Isaksen11] for the foundational theory of topological realizations.
We give an overview to fix notation. There are functors
-
○ Suppose
 $i: k \hookrightarrow \mathbb {C}$
is an embedding of k in
$i: k \hookrightarrow \mathbb {C}$
is an embedding of k in
 $\mathbb {C}$
. There exists complex realization, a functor
$\mathbb {C}$
. There exists complex realization, a functor
 $\mathfrak {C} \colon \mathbf {H}(k)_\bullet \to \mathbf {H}_\bullet $
, which is the composite of
$\mathfrak {C} \colon \mathbf {H}(k)_\bullet \to \mathbf {H}_\bullet $
, which is the composite of
 $i^*$
and the complex realization of [Reference Dugger and Isaksen11].
$i^*$
and the complex realization of [Reference Dugger and Isaksen11]. -
○ Suppose
 $i: k \hookrightarrow \mathbb {R}$
is an embedding of k in
$i: k \hookrightarrow \mathbb {R}$
is an embedding of k in
 $\mathbb {R}$
. There exists real realization, a functor
$\mathbb {R}$
. There exists real realization, a functor
 $\mathfrak {R} : \mathbf {H}(k)_\bullet \to \mathbf {H}_\bullet $
, which is the composite of
$\mathfrak {R} : \mathbf {H}(k)_\bullet \to \mathbf {H}_\bullet $
, which is the composite of
 $i^*$
and the real realization of [Reference Dugger and Isaksen11].
$i^*$
and the real realization of [Reference Dugger and Isaksen11].
These realization functors have the following properties:
-
○ They are compatible with the
 $\mathbf {H}_\bullet $
-module structure on source and target (i.e.,
$\mathbf {H}_\bullet $
-module structure on source and target (i.e.,
 $\mathfrak {C}(K \wedge X) \simeq K \wedge \mathfrak {C}(X)$
for a pointed simplicial set K, and similarly for the real realization).
$\mathfrak {C}(K \wedge X) \simeq K \wedge \mathfrak {C}(X)$
for a pointed simplicial set K, and similarly for the real realization). -
○ Their values on the quotient schemes
 $V_r(\mathbb {A}^n) =\operatorname {GL}(n)/\operatorname {GL}(n-r)$
are known. Specifically,
$V_r(\mathbb {A}^n) =\operatorname {GL}(n)/\operatorname {GL}(n-r)$
are known. Specifically,  $$\begin{align*}\mathfrak{C}(V_r(\mathbb{A}^n))\simeq W_r(\mathbb{C}^n), \quad \mathfrak{R}(V_r(\mathbb{A}^n))\simeq W_r(\mathbb{R}^n). \end{align*}$$
$$\begin{align*}\mathfrak{C}(V_r(\mathbb{A}^n))\simeq W_r(\mathbb{C}^n), \quad \mathfrak{R}(V_r(\mathbb{A}^n))\simeq W_r(\mathbb{R}^n). \end{align*}$$
-
○ They take the groups
 $\operatorname {GL}(n)$
to groups.
$\operatorname {GL}(n)$
to groups. -
○ Their values on the spheres
 $S^{p+q\alpha }$
are known. Specifically, Similarly, their values on the motivic Hopf maps of [Reference Dugger and Isaksen10] are known:
$S^{p+q\alpha }$
are known. Specifically, Similarly, their values on the motivic Hopf maps of [Reference Dugger and Isaksen10] are known: $$\begin{align*}\mathfrak{C}(S^{p+q\alpha})\simeq S^{p+q}, \quad \mathfrak{R}(S^{p+q\alpha})\simeq S^p. \end{align*}$$
$$\begin{align*}\mathfrak{C}(S^{p+q\alpha})\simeq S^{p+q}, \quad \mathfrak{R}(S^{p+q\alpha})\simeq S^p. \end{align*}$$
 $$ \begin{gather*} \mathfrak{C}(\eta) =\eta_{\mathrm{top}}, \quad \mathfrak{C}(\nu) =\nu_{\mathrm{top}}; \\ \mathfrak{R}(\eta) = 2, \quad \mathfrak{R}(\nu) = \eta_{\mathrm{top}}.\end{gather*} $$
$$ \begin{gather*} \mathfrak{C}(\eta) =\eta_{\mathrm{top}}, \quad \mathfrak{C}(\nu) =\nu_{\mathrm{top}}; \\ \mathfrak{R}(\eta) = 2, \quad \mathfrak{R}(\nu) = \eta_{\mathrm{top}}.\end{gather*} $$
-
○ There are equivalences
 $$\begin{align*}\mathfrak{C}(B\operatorname{GL}(n)) \simeq B \operatorname{GL}(n;\mathbb{C}), \quad \mathfrak{R}(B\operatorname{GL}(n)) \simeq B \operatorname{GL}(n;\mathbb{R}).\end{align*}$$
$$\begin{align*}\mathfrak{C}(B\operatorname{GL}(n)) \simeq B \operatorname{GL}(n;\mathbb{C}), \quad \mathfrak{R}(B\operatorname{GL}(n)) \simeq B \operatorname{GL}(n;\mathbb{R}).\end{align*}$$
Assume
![]() $p \ge 1$
is an integer. There are homomorphisms of groups, natural in X:
$p \ge 1$
is an integer. There are homomorphisms of groups, natural in X:
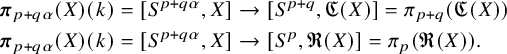 $$ \begin{align} \begin{aligned} \boldsymbol{\pi}_{p+q\alpha}(X)(k) = [S^{p+q\alpha}, X] & \to [S^{p+q}, \mathfrak{C}(X)] = \pi_{p+q}(\mathfrak{C}(X))\\ \boldsymbol{\pi}_{p+q\alpha}(X)(k) = [S^{p+q\alpha}, X] & \to [S^{p}, \mathfrak{R}(X)] = \pi_{p}(\mathfrak{R}(X)). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \boldsymbol{\pi}_{p+q\alpha}(X)(k) = [S^{p+q\alpha}, X] & \to [S^{p+q}, \mathfrak{C}(X)] = \pi_{p+q}(\mathfrak{C}(X))\\ \boldsymbol{\pi}_{p+q\alpha}(X)(k) = [S^{p+q\alpha}, X] & \to [S^{p}, \mathfrak{R}(X)] = \pi_{p}(\mathfrak{R}(X)). \end{aligned} \end{align} $$
5.1 Exactness of realization
The realization functors we consider do not preserve homotopy fibre sequences in general. Nonetheless, when applied to the sequences of (5), they produce homotopy fibre sequences. As a consequence, we can use realization to produce commutative diagrams of homotopy groups. We give the formal statement in the case of complex realization only. The other case is similar.
Proposition 5.1. Complex realization
![]() $\mathfrak C$
produces a commutative diagram of long exact sequences of homotopy groups:
$\mathfrak C$
produces a commutative diagram of long exact sequences of homotopy groups:
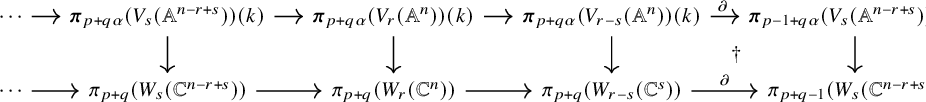
Proof. The lower sequence is exact because there is a homotopy fibre sequence
In (9), commutativity of the squares other than the one marked with a dagger
![]() $\dagger $
follows from the naturality of the homomorphism in (8). The square marked with the dagger is not a priori induced by a map of schemes. Nonetheless, it can be factored
$\dagger $
follows from the naturality of the homomorphism in (8). The square marked with the dagger is not a priori induced by a map of schemes. Nonetheless, it can be factored

The identification
![]() $\boldsymbol {\pi }_{p+q\alpha }(B\operatorname {GL}(n-r+s))(k)= \boldsymbol {\pi }_{p-1+q\alpha }(\operatorname {GL}(n-r+s))(k)$
is made as follows: there is a canonical map
$\boldsymbol {\pi }_{p+q\alpha }(B\operatorname {GL}(n-r+s))(k)= \boldsymbol {\pi }_{p-1+q\alpha }(\operatorname {GL}(n-r+s))(k)$
is made as follows: there is a canonical map
so that any morphism
![]() $S^{p+q\alpha } \to G$
yields a morphism
$S^{p+q\alpha } \to G$
yields a morphism
![]() $S^{p+1+q\alpha } \to S^1 \wedge G \to BG$
by composition. When
$S^{p+1+q\alpha } \to S^1 \wedge G \to BG$
by composition. When
![]() $G= \operatorname {GL}(n-r+s)$
, the adjoint to
$G= \operatorname {GL}(n-r+s)$
, the adjoint to
![]() $S^1 \wedge G \to BG$
is an
$S^1 \wedge G \to BG$
is an
![]() $\mathbb {A}^1$
-weak equivalence by [Reference Morel19, Theorem 6.46], so that indeed we obtain the asserted identification.
$\mathbb {A}^1$
-weak equivalence by [Reference Morel19, Theorem 6.46], so that indeed we obtain the asserted identification.
Complex realization of (10) yields a similar map
![]() $S^1 \wedge G(\mathbb {C}) \to BG(\mathbb {C})$
, so that the square marked with an asterisk
$S^1 \wedge G(\mathbb {C}) \to BG(\mathbb {C})$
, so that the square marked with an asterisk
![]() $\ast $
also commutes.
$\ast $
also commutes.
6 Constant homotopy sheaves
Fix a subfield
![]() $i: k \hookrightarrow \mathbb {C}$
. Throughout this section, n denotes a natural number.
$i: k \hookrightarrow \mathbb {C}$
. Throughout this section, n denotes a natural number.
Definition 6.1. Suppose X is a pointed motivic space over k, and
![]() $\boldsymbol {\pi }_{p + q\alpha }(X)$
is a strictly
$\boldsymbol {\pi }_{p + q\alpha }(X)$
is a strictly
![]() $\mathbb {A}^1$
-invariant homotopy sheaf. We will say that
$\mathbb {A}^1$
-invariant homotopy sheaf. We will say that
![]() $\boldsymbol {\pi }_{p+q\alpha }(X)$
has the constant (resp. surjective, injective) realization property if the map
$\boldsymbol {\pi }_{p+q\alpha }(X)$
has the constant (resp. surjective, injective) realization property if the map
is an isomorphism (resp. surjective, injective).
Remark 6.2. If instead we fix a subfield
![]() $i : k \hookrightarrow \mathbb {R}$
, we may define the constant (resp. surjective, injective) real realization property by using
$i : k \hookrightarrow \mathbb {R}$
, we may define the constant (resp. surjective, injective) real realization property by using
![]() $\mathfrak R$
instead of
$\mathfrak R$
instead of
![]() $\mathfrak C$
.
$\mathfrak C$
.
Example 6.3. Let
![]() $n \ge 4$
. The homotopy sheaves
$n \ge 4$
. The homotopy sheaves
![]() $\boldsymbol {\pi }_{n}(Q_{2n-1})$
may be partly calculated from the main theorem of [Reference Röndigs, Spitzweck and Østvær23] and [Reference Asok, Bachmann and Hopkins2, Theorem 6.3.6]. There is an exact sequence
$\boldsymbol {\pi }_{n}(Q_{2n-1})$
may be partly calculated from the main theorem of [Reference Röndigs, Spitzweck and Østvær23] and [Reference Asok, Bachmann and Hopkins2, Theorem 6.3.6]. There is an exact sequence
which becomes short exact after
![]() $n-4$
-fold contraction. Furthermore,
$n-4$
-fold contraction. Furthermore,
![]() $\boldsymbol {\pi }^s_{1-3\alpha }(\mathbf {kq})$
is identified with a sheaf
$\boldsymbol {\pi }^s_{1-3\alpha }(\mathbf {kq})$
is identified with a sheaf
![]() $\mathbf {GW}^3_4$
as defined in [Reference Schlichting and Tripathi25] or [Reference Asok and Fasel5] (see [Reference Asok, Fasel and Williams6, Diagram 3.9]).
$\mathbf {GW}^3_4$
as defined in [Reference Schlichting and Tripathi25] or [Reference Asok and Fasel5] (see [Reference Asok, Fasel and Williams6, Diagram 3.9]).
Therefore, once we contract (11)
![]() $n+1$
-times, we obtain a short exact sequence
$n+1$
-times, we obtain a short exact sequence
using the identities
![]() $(\mathbf {GW}^i_j)_{-1} = \mathbf {GW}^{i-1}_{j-1}$
and
$(\mathbf {GW}^i_j)_{-1} = \mathbf {GW}^{i-1}_{j-1}$
and
![]() $\mathbf {GW}^i_j = \mathbf {GW}^{i+4}_j$
. By [Reference Walter27, Theorem 10.1], the sheaf
$\mathbf {GW}^i_j = \mathbf {GW}^{i+4}_j$
. By [Reference Walter27, Theorem 10.1], the sheaf
![]() $\mathbf {GW}^3_0$
is constant on fields, with value
$\mathbf {GW}^3_0$
is constant on fields, with value
![]() $\eta \eta _{\mathrm {top}}\mathbb {Z}/(2)$
– see, for instance, [Reference Röndigs, Spitzweck and Østvær23, p. 58].
$\eta \eta _{\mathrm {top}}\mathbb {Z}/(2)$
– see, for instance, [Reference Röndigs, Spitzweck and Østvær23, p. 58].
The complex realization of
![]() $\eta \eta _{\mathrm {top}}$
is
$\eta \eta _{\mathrm {top}}$
is
![]() $\eta _{\mathrm {top}}^2$
, which generates
$\eta _{\mathrm {top}}^2$
, which generates
![]() $\pi _{2n+1}(S^{2n-1})$
, so that
$\pi _{2n+1}(S^{2n-1})$
, so that
![]() $\boldsymbol {\pi }_{n+(n+1)\alpha }(Q_{2n-1})$
has the surjective realization property.
$\boldsymbol {\pi }_{n+(n+1)\alpha }(Q_{2n-1})$
has the surjective realization property.
Remark 6.4. If we assume further that k is quadratically and cubically closed, so that
![]() ${{\mathbf K}}^{\mathsf {M}}_1(k)/(24) \cong 0$
, then
${{\mathbf K}}^{\mathsf {M}}_1(k)/(24) \cong 0$
, then
![]() $\boldsymbol {\pi }_{n+(n+1)\alpha }(Q_{2n-1})$
has the constant realization property.
$\boldsymbol {\pi }_{n+(n+1)\alpha }(Q_{2n-1})$
has the constant realization property.
Example 6.5. We may contract (12) one more time. Then we obtain
so that
![]() $ \boldsymbol {\pi }_{n+(n+2)\alpha }(Q_{2n-1})$
is constant with value
$ \boldsymbol {\pi }_{n+(n+2)\alpha }(Q_{2n-1})$
is constant with value
![]() $\mathbb {Z}/(24)$
. It has the constant realization property, being generated by the class of
$\mathbb {Z}/(24)$
. It has the constant realization property, being generated by the class of
![]() $\nu $
, which realizes to give
$\nu $
, which realizes to give
![]() $\nu _{\mathrm {top}}$
, which also generates
$\nu _{\mathrm {top}}$
, which also generates
![]() $\pi _{2n+2}(S^{2n-1})$
.
$\pi _{2n+2}(S^{2n-1})$
.
Example 6.6. In this example, the symbol
![]() $\rho$
is used in the same sense as in [Reference Röndigs, Spitzweck and Østvær24]. Let
$\rho$
is used in the same sense as in [Reference Röndigs, Spitzweck and Østvær24]. Let
![]() $n \ge 5$
. The homotopy sheaves
$n \ge 5$
. The homotopy sheaves
![]() $\boldsymbol {\pi }_{n+1}(Q_{2n-1})$
may be partly calculated from the main theorem of [Reference Röndigs, Spitzweck and Østvær24] and [Reference Asok, Bachmann and Hopkins2, Theorem 6.3.6]. There is an exact sequence
$\boldsymbol {\pi }_{n+1}(Q_{2n-1})$
may be partly calculated from the main theorem of [Reference Röndigs, Spitzweck and Østvær24] and [Reference Asok, Bachmann and Hopkins2, Theorem 6.3.6]. There is an exact sequence
and after
![]() $n+2$
contractions, this yields an isomorphism
$n+2$
contractions, this yields an isomorphism
If
![]() $k \hookrightarrow \mathbb {R}$
is a field with a real embedding, then the class of
$k \hookrightarrow \mathbb {R}$
is a field with a real embedding, then the class of
![]() $\{-1,-1\}$
in
$\{-1,-1\}$
in
![]() ${{\mathbf K}}^{\mathsf {M}}_2(k)/(2) \cong \mathrm {H}_{\text {\'et}}^2(k; \mathbb {Z}/(2))$
corresponds to
${{\mathbf K}}^{\mathsf {M}}_2(k)/(2) \cong \mathrm {H}_{\text {\'et}}^2(k; \mathbb {Z}/(2))$
corresponds to
![]() $\rho ^2\nu ^2 \in \boldsymbol {\pi }_{n+1+(n+2)\alpha }(Q_{2n-1})(k)$
. Similarly, after
$\rho ^2\nu ^2 \in \boldsymbol {\pi }_{n+1+(n+2)\alpha }(Q_{2n-1})(k)$
. Similarly, after
![]() $n+3$
or
$n+3$
or
![]() $n+4$
contractions, the classes of
$n+4$
contractions, the classes of
![]() $\{-1\} \in {{\mathbf K}}^{\mathsf {M}}_1(k)/(2)$
and
$\{-1\} \in {{\mathbf K}}^{\mathsf {M}}_1(k)/(2)$
and
![]() $1 \in \mathbb {Z}/(2)$
correspond to
$1 \in \mathbb {Z}/(2)$
correspond to
![]() $\rho \nu ^2$
and
$\rho \nu ^2$
and
![]() $\nu ^2$
.
$\nu ^2$
.
Since the real realization of
![]() $\rho $
is the identity, and the real realization of
$\rho $
is the identity, and the real realization of
![]() $\nu $
is
$\nu $
is
![]() $\eta _{\mathrm {top}}$
, we deduce that
$\eta _{\mathrm {top}}$
, we deduce that
![]() $\boldsymbol {\pi }_{n+1+(n+d)\alpha }(Q_{2n-1})$
has the constant real realization property when
$\boldsymbol {\pi }_{n+1+(n+d)\alpha }(Q_{2n-1})$
has the constant real realization property when
![]() $d \in \{2,3,4\}$
and
$d \in \{2,3,4\}$
and
![]() ${{\mathbf K}}^{\mathsf {M}}_{4-d}(k)/(2) \cong \mathbb {Z}/(2)$
.
${{\mathbf K}}^{\mathsf {M}}_{4-d}(k)/(2) \cong \mathbb {Z}/(2)$
.
7 The existence of homotopy sections
Consider the homotopy long exact sequence of
A portion of this sequence appears below:
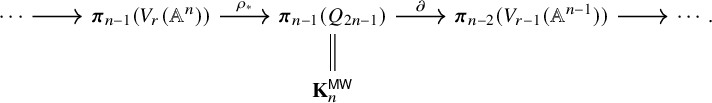
Notation 7.1. Following [Reference James16], we denote the image of the identity map under
by
![]() $\beta _r^n$
and call this element the obstruction.
$\beta _r^n$
and call this element the obstruction.
The following proposition justifies this terminology.
Proposition 7.2. Let n and r be integers with
![]() $2 \le r \le n-2$
. The following are equivalent:
$2 \le r \le n-2$
. The following are equivalent:
-
1. The morphism
 $\rho _{1,r}: V_r(\mathbb {A}^n) \to Q_{2n-1}$
admits a section in the category of k-schemes;
$\rho _{1,r}: V_r(\mathbb {A}^n) \to Q_{2n-1}$
admits a section in the category of k-schemes; -
2. The morphism
 $\rho _{1,r}: V_r(\mathbb {A}^n) \to Q_{2n-1}$
admits a pointed homotopy section;
$\rho _{1,r}: V_r(\mathbb {A}^n) \to Q_{2n-1}$
admits a pointed homotopy section; -
3. The map
is surjective; $$\begin{align*}{\rho_{1,r}}_* : \boldsymbol{\pi}_{n-1}(V_{r}(\mathbb{A}^{n})) \to \boldsymbol{\pi}_{n-1}(Q_{2n-1}) = {{\mathbf K}}^{\mathsf{MW}}_n \end{align*}$$
$$\begin{align*}{\rho_{1,r}}_* : \boldsymbol{\pi}_{n-1}(V_{r}(\mathbb{A}^{n})) \to \boldsymbol{\pi}_{n-1}(Q_{2n-1}) = {{\mathbf K}}^{\mathsf{MW}}_n \end{align*}$$
-
4. In the homotopy long exact sequence (14), the boundary map
 $\partial : \boldsymbol {\pi }_{n-1}(Q_{2n-1}) \to \boldsymbol {\pi }_{n-2}(V_{r-1}(\mathbb {A}^{n-1}))$
vanishes;
$\partial : \boldsymbol {\pi }_{n-1}(Q_{2n-1}) \to \boldsymbol {\pi }_{n-2}(V_{r-1}(\mathbb {A}^{n-1}))$
vanishes; -
5. The obstruction
 $\beta _r^n$
vanishes.
$\beta _r^n$
vanishes.
Proof. The equivalence of 1 and 2 is given by Proposition 4.6, and the other forward implications are trivial. It remains to show 5
![]() $\Rightarrow $
2.
$\Rightarrow $
2.
Suppose the obstruction vanishes. Using [Reference Asok, Wickelgren and Williams8, Lemma 5.1.3], we may identify
![]() $\partial $
with a specific element of
$\partial $
with a specific element of
![]() $\boldsymbol {\pi }_{n-2+n\alpha }(V_{r-1}(\mathbb {A}^{n-1}))(k)$
, which is tautologically
$\boldsymbol {\pi }_{n-2+n\alpha }(V_{r-1}(\mathbb {A}^{n-1}))(k)$
, which is tautologically
![]() $\partial _{-n}(k)(\mathrm {id}) = \beta _r^n = 0$
. That is,
$\partial _{-n}(k)(\mathrm {id}) = \beta _r^n = 0$
. That is,
![]() $\partial =0$
as a morphism of sheaves.
$\partial =0$
as a morphism of sheaves.
To construct a pointed homotopy section, we argue as follows. There is an
![]() $\mathbb {A}^1$
-homotopy fibre sequence
$\mathbb {A}^1$
-homotopy fibre sequence
and the map
![]() $\partial $
may be obtained by applying
$\partial $
may be obtained by applying
![]() $\boldsymbol {\pi }_{n-2+n\alpha }$
to f. Letting j denote the adjoint of the identity map in
$\boldsymbol {\pi }_{n-2+n\alpha }$
to f. Letting j denote the adjoint of the identity map in
![]() $\mathbf H(k)_\bullet $
, we obtain a homotopy commutative diagram
$\mathbf H(k)_\bullet $
, we obtain a homotopy commutative diagram
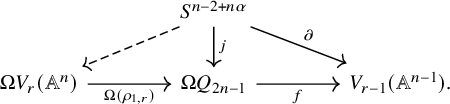
Since
![]() $\partial $
is null, the dashed arrow may be constructed, and by adjunction, a pointed homotopy section of
$\partial $
is null, the dashed arrow may be constructed, and by adjunction, a pointed homotopy section of
![]() $\rho _{r,1}$
exists.
$\rho _{r,1}$
exists.
Proposition 7.3. Let n and r be integers with
![]() $2 \le r \le n-2$
. Let
$2 \le r \le n-2$
. Let
![]() $i : k \hookrightarrow \mathbb {C}$
be a fixed embedding. Suppose that
$i : k \hookrightarrow \mathbb {C}$
be a fixed embedding. Suppose that
![]() $\boldsymbol {\pi }_{n-2+n\alpha }(V_{r-1}(\mathbb {A}^{n-1}))$
has the injective realization property and that
$\boldsymbol {\pi }_{n-2+n\alpha }(V_{r-1}(\mathbb {A}^{n-1}))$
has the injective realization property and that
![]() $\rho (\mathbb {C}): W_{r}(\mathbb {C}^{n}) \to S^{2n-1}$
has a section. Then
$\rho (\mathbb {C}): W_{r}(\mathbb {C}^{n}) \to S^{2n-1}$
has a section. Then
![]() $\rho : V_{r}(\mathbb {A}^{n}) \to Q_{2n-1}$
has a section.
$\rho : V_{r}(\mathbb {A}^{n}) \to Q_{2n-1}$
has a section.
Proof. Entirely analogously to Proposition 7.2, one deduces that
![]() $\rho (\mathbb {C}): W_r(\mathbb {C}^n) \to S^{2n-1}$
has a section if and only if the boundary homomorphism
$\rho (\mathbb {C}): W_r(\mathbb {C}^n) \to S^{2n-1}$
has a section if and only if the boundary homomorphism
![]() $ \partial (\mathbb {C}): \pi _{2n-1}(S^{2n-1}) \to \pi _{2n-2}(W_{r-1}(\mathbb {C}^{n-1}))$
is
$ \partial (\mathbb {C}): \pi _{2n-1}(S^{2n-1}) \to \pi _{2n-2}(W_{r-1}(\mathbb {C}^{n-1}))$
is
![]() $0$
(i.e., if it takes the class of the identity in
$0$
(i.e., if it takes the class of the identity in
![]() $\pi _{2n-1}(S^{2n-1}) = \mathbb {Z}$
to
$\pi _{2n-1}(S^{2n-1}) = \mathbb {Z}$
to
![]() $0$
).
$0$
).
There is, therefore, a commutative diagram
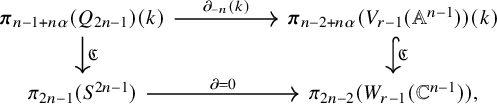
from which it follows that
![]() $\partial _{-n}(k)=0$
, and therefore that
$\partial _{-n}(k)=0$
, and therefore that
![]() $\rho $
has a section, by Proposition 7.2.
$\rho $
has a section, by Proposition 7.2.
7.1 The case
 $r=3$
$r=3$
Proposition 7.4. Let
![]() $n \ge 3$
be an integer. Let
$n \ge 3$
be an integer. Let
![]() $k=\mathbb {Q}$
. Then
$k=\mathbb {Q}$
. Then
![]() $\rho : V_{3}(\mathbb {A}^{n}) \to Q_{2n-1}$
has a section if and only if
$\rho : V_{3}(\mathbb {A}^{n}) \to Q_{2n-1}$
has a section if and only if
![]() $n \equiv 0 \pmod {24}$
.
$n \equiv 0 \pmod {24}$
.
Proof. Unless n is a positive multiple of
![]() $b_3=24$
, then the method of [Reference Raynaud22, Théorème 6.5] prevents
$b_3=24$
, then the method of [Reference Raynaud22, Théorème 6.5] prevents
![]() $\rho _{3,1}$
from having a section. Therefore, we assume n is a positive multiple of
$\rho _{3,1}$
from having a section. Therefore, we assume n is a positive multiple of
![]() $24$
. In this case, [Reference James16] asserts that a section of
$24$
. In this case, [Reference James16] asserts that a section of
![]() $W_3(\mathbb {C}^n) \to S^{2n-1}$
exists. Therefore, we need only prove that
$W_3(\mathbb {C}^n) \to S^{2n-1}$
exists. Therefore, we need only prove that
![]() $\pi _{n-2+n\alpha }(V_2(\mathbb {A}^{n-1}))$
has the injective realization property. In fact, it has the constant realization property.
$\pi _{n-2+n\alpha }(V_2(\mathbb {A}^{n-1}))$
has the injective realization property. In fact, it has the constant realization property.
We consider the long exact sequence of homotopy sheaves
The first sheaf appearing has the surjective realization property (Example 6.3), and the next sheaf has the constant (a fortiori, injective) realization property (Example 6.5). The last two sheaves are both isomorphic to the Witt sheaf by results of [Reference Morel19], and the map between them is the isomorphism
![]() $\times \eta $
, by [Reference Asok and Fasel4, Lemma 3.5].
$\times \eta $
, by [Reference Asok and Fasel4, Lemma 3.5].
It follows from an easy diagram chase that
![]() $\boldsymbol {\pi }_{n-2+n\alpha }(V_2(\mathbb {A}^{n-1})) $
has the constant realization property. We conclude by Proposition 7.3.
$\boldsymbol {\pi }_{n-2+n\alpha }(V_2(\mathbb {A}^{n-1})) $
has the constant realization property. We conclude by Proposition 7.3.
7.2 The case
 $r=4$
$r=4$
First, we need a technical lemma concerning the obstruction.
Lemma 7.5. Let n and r be integers with
![]() $2 \le r \le n$
, and suppose that
$2 \le r \le n$
, and suppose that
![]() $\psi : Q_{2n-1} \to V_{r-1}(\mathbb {A}^n)$
is a pointed homotopy section. Then the obstruction
$\psi : Q_{2n-1} \to V_{r-1}(\mathbb {A}^n)$
is a pointed homotopy section. Then the obstruction
![]() $\beta _r^n$
is the image of
$\beta _r^n$
is the image of
![]() $\psi $
under the composition
$\psi $
under the composition
Proof. There is a map of
![]() $\mathbb {A}^1$
-homotopy fibre sequences
$\mathbb {A}^1$
-homotopy fibre sequences
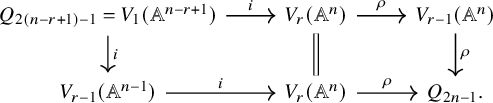
In particular, the diagram
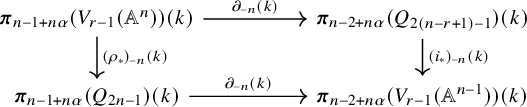
commutes. Then
as desired.
Remark 7.6. In Proposition 7.7 below, the case of quadratically closed k is redundant because of the argument of Remark 1.1. We include this case here because the proof is short, and we expect the same proof to apply when k is a quadratically closed field of characteristic greater than
![]() $3$
.
$3$
.
Proposition 7.7. Let
![]() $n \geq 4$
be an integer and k be a subfield of
$n \geq 4$
be an integer and k be a subfield of
![]() $\mathbb {C}$
satisfying one of the following:
$\mathbb {C}$
satisfying one of the following:
-
1. k is quadratically closed.
-
2. k is a subfield of
 $\mathbb {R}$
and admits a unique quadratic extension (up to isomorphism).
$\mathbb {R}$
and admits a unique quadratic extension (up to isomorphism).
Then the map
![]() $\rho _{4,1}: V_4(\mathbb {A}^n) \to Q_{2n-1}$
has a section if and only if
$\rho _{4,1}: V_4(\mathbb {A}^n) \to Q_{2n-1}$
has a section if and only if
![]() $n \equiv 0 \pmod {24}$
.
$n \equiv 0 \pmod {24}$
.
Proof. As in the
![]() $r=3$
case, the method of [Reference Raynaud22, Théorème 6.5] allows us to assume that n is a positive multiple of
$r=3$
case, the method of [Reference Raynaud22, Théorème 6.5] allows us to assume that n is a positive multiple of
![]() $b_4=24$
. Let
$b_4=24$
. Let
![]() $\psi : V_1(\mathbb {A}^n) \to V_3(\mathbb {A}^n)$
be a pointed homotopy section (which exists by Proposition 7.4), and consider the sequence
$\psi : V_1(\mathbb {A}^n) \to V_3(\mathbb {A}^n)$
be a pointed homotopy section (which exists by Proposition 7.4), and consider the sequence
We claim that
![]() $(\partial _{-n}(k))(\psi ) = 0$
. With the help of Proposition 7.2 and Lemma 7.5, the result follows from this claim. Note that the middle group in (15) is in the stable range (Example 6.6) and coincides with the corresponding stable homotopy group of the motivic sphere spectrum
$(\partial _{-n}(k))(\psi ) = 0$
. With the help of Proposition 7.2 and Lemma 7.5, the result follows from this claim. Note that the middle group in (15) is in the stable range (Example 6.6) and coincides with the corresponding stable homotopy group of the motivic sphere spectrum ![]() (compare (13)).
(compare (13)).
If k is quadratically closed, we have
![]() ${{\mathbf K}}_1^M(k)/(2) = 0$
by assumption, so there is nothing left to be done.
${{\mathbf K}}_1^M(k)/(2) = 0$
by assumption, so there is nothing left to be done.
For the second case, real realization induces the commuting diagram
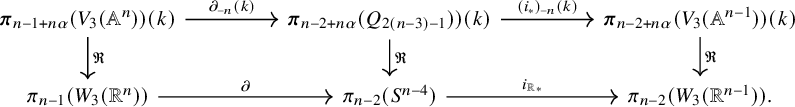
Under the left vertical map, the class of the section
![]() $\psi : Q_{2n-1} \to V_3(\mathbb {A}^n)$
is taken to the class of a section
$\psi : Q_{2n-1} \to V_3(\mathbb {A}^n)$
is taken to the class of a section
![]() $S^{n-1} \to W_3(\mathbb {R}^n)$
. It follows from [Reference James16, p. 2.1] that the element
$S^{n-1} \to W_3(\mathbb {R}^n)$
. It follows from [Reference James16, p. 2.1] that the element
is the obstruction to the existence of a section of
![]() $\rho _{\mathbb {R}}: W_4(\mathbb {R}^n) \to S^{n-1}$
. This obstruction vanishes by [Reference James17, Proposition 1.1]. Moreover, the source and target of the middle realization map in (16) are in the stable range, so by the assumption and Example 6.6, the middle realization map is an isomorphism. Consequently, to prove the claim, it suffices to show that
$\rho _{\mathbb {R}}: W_4(\mathbb {R}^n) \to S^{n-1}$
. This obstruction vanishes by [Reference James17, Proposition 1.1]. Moreover, the source and target of the middle realization map in (16) are in the stable range, so by the assumption and Example 6.6, the middle realization map is an isomorphism. Consequently, to prove the claim, it suffices to show that
![]() ${i_{\mathbb {R}}}_*: \pi _{n-2}(S^{n-4}) \to \pi _{n-2}(W_3(\mathbb {R}^{n-1}))$
is injective.
${i_{\mathbb {R}}}_*: \pi _{n-2}(S^{n-4}) \to \pi _{n-2}(W_3(\mathbb {R}^{n-1}))$
is injective.
A portion of the long exact sequence in homotopy groups associated with the homotopy fibre sequence
is
The isomorphisms
![]() $\pi _{n-2}(W_3(\mathbb {R}^{n-1})) \cong \mathbb {Z}/2 \oplus \mathbb {Z}/2$
and
$\pi _{n-2}(W_3(\mathbb {R}^{n-1})) \cong \mathbb {Z}/2 \oplus \mathbb {Z}/2$
and
![]() $\pi _{n-2}(W_2(\mathbb {R}^{n-1})) \cong \mathbb {Z}/(2)$
can be read from the tables of [Reference Paechter21], from which we conclude that
$\pi _{n-2}(W_2(\mathbb {R}^{n-1})) \cong \mathbb {Z}/(2)$
can be read from the tables of [Reference Paechter21], from which we conclude that
![]() ${i_{\mathbb {R}}}_*$
is injective.
${i_{\mathbb {R}}}_*$
is injective.
8 The main result
Proposition 4.4 and Propositions 7.4 and 7.7 have the following immediate consequence, which is the main result of this paper.
Theorem 8.1. Suppose X is a scheme over a subfield k of
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\mathcal {P}$
is a sheaf of
$\mathcal {P}$
is a sheaf of
![]() $\mathcal {O}_X$
-modules with the property
$\mathcal {O}_X$
-modules with the property
![]() $\mathcal {P} \oplus \mathcal {O}_X \cong \mathcal {O}_X^{24n}$
for some positive integer n. Then there exists a sheaf of
$\mathcal {P} \oplus \mathcal {O}_X \cong \mathcal {O}_X^{24n}$
for some positive integer n. Then there exists a sheaf of
![]() $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
![]() $\mathcal {Q}$
such that
$\mathcal {Q}$
such that
Suppose further that k is quadratically closed or is a subfield of
![]() $\mathbb {R}$
that admits a unique quadratic extension (up to isomorphism). Then there is a sheaf of
$\mathbb {R}$
that admits a unique quadratic extension (up to isomorphism). Then there is a sheaf of
![]() $\mathcal {O}_X$
-modules
$\mathcal {O}_X$
-modules
![]() $\mathcal {Q}'$
and an isomorphism
$\mathcal {Q}'$
and an isomorphism
Competing interest
The authors have no competing interests to declare.
Funding statement
We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), RGPIN-2021-02603.
















