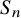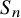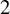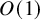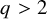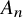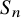1 Introduction
The hypercontractive inequality is a fundamental result in analysis that allows one to compare various norms of low-degree functions over a given domain. A celebrated example is the Boolean hypercube
![]() ${\left \{ 0,1 \right \}}^{n}$
equipped with the uniform measure, in which case the inequality states that for any function
${\left \{ 0,1 \right \}}^{n}$
equipped with the uniform measure, in which case the inequality states that for any function
![]() $f\colon {\left \{ 0,1 \right \}}^{n}\to \mathbb {R}$
of degree at most d, one has that
$f\colon {\left \{ 0,1 \right \}}^{n}\to \mathbb {R}$
of degree at most d, one has that
![]() $\left \|f\right \|_q\leqslant \sqrt {q-1}^d\left \|f\right \|_2$
for any
$\left \|f\right \|_q\leqslant \sqrt {q-1}^d\left \|f\right \|_2$
for any
![]() $q\geqslant 2$
. (Here and throughout the paper, we use expectation norms,
$q\geqslant 2$
. (Here and throughout the paper, we use expectation norms,
![]() $\left \|f\right \|_q = {\mathop {\mathbb {E}}_{x}\left [ {\left |f(x)\right |{}^q} \right ]}^{1/q}$
, where the input distribution is clear from context – uniform in this case). While the inequality may appear technical and mysterious at first sight, it has proven itself as remarkably useful and lies at the heart of numerous important results (e.g., [Reference Kahn, Kalai and Linial15, Reference Friedgut11, Reference Bourgain2, Reference Mossel, O’Donnell and Oleszkiewicz23]).
$\left \|f\right \|_q = {\mathop {\mathbb {E}}_{x}\left [ {\left |f(x)\right |{}^q} \right ]}^{1/q}$
, where the input distribution is clear from context – uniform in this case). While the inequality may appear technical and mysterious at first sight, it has proven itself as remarkably useful and lies at the heart of numerous important results (e.g., [Reference Kahn, Kalai and Linial15, Reference Friedgut11, Reference Bourgain2, Reference Mossel, O’Donnell and Oleszkiewicz23]).
While the hypercontractive inequality holds for general product spaces, in some important cases it is very weak quantitatively. Such cases include the p-biased cube for
![]() $p=o(1)$
, the multi-cube
$p=o(1)$
, the multi-cube
![]() $[m]^n$
for
$[m]^n$
for
![]() $m = \omega (1)$
and the bilinear graph (closely related to the Grassmann graph). This quantitative deficiency causes various analytical and combinatorial problems on these domains to be considerably more challenging, and indeed much less is known there (and what is known is considerably more difficult to prove; see, for example, [Reference Friedgut and Bourgain12]).
$m = \omega (1)$
and the bilinear graph (closely related to the Grassmann graph). This quantitative deficiency causes various analytical and combinatorial problems on these domains to be considerably more challenging, and indeed much less is known there (and what is known is considerably more difficult to prove; see, for example, [Reference Friedgut and Bourgain12]).
1.1 Global hypercontractivity
Recently, initially motivated by the study of PCPs (probabilistically checkable proofs) and later by sharp-threshold results, variants of the hypercontractive inequality have been established in such domains [Reference Khot, Minzer and Safra20, Reference Keevash, Lifshitz, Long and Minzer17, Reference Keevash, Lifshitz, Long and Minzer18]. In these variants, one states an inequality that holds for all functions but is only meaningful for a special (important) class of functions, called global functions. Informally, a function f on a given product domain
![]() $\Omega = \Omega _1\times \dots \times \Omega _n$
is called global if its
$\Omega = \Omega _1\times \dots \times \Omega _n$
is called global if its
![]() $2$
-norm, as well as the
$2$
-norm, as well as the
![]() $2$
-norms of its restrictions, are all small.Footnote
1
This makes these variants applicable in cases that were previously out of reach, leading to new results, but at the same time harder to apply since one has to make sure it is applied to a global function to get a meaningful bound (see [Reference Keevash, Lifshitz, Long and Minzer17, Reference Lifshitz and Minzer22, Reference Keevash, Lifshitz, Long and Minzer18] for example applications). It is worth noting that these variants are in fact generalizations of the standard hypercontractive inequality since one can easily show that in domains such as the Boolean hypercube, all low-degree functions are global.
$2$
-norms of its restrictions, are all small.Footnote
1
This makes these variants applicable in cases that were previously out of reach, leading to new results, but at the same time harder to apply since one has to make sure it is applied to a global function to get a meaningful bound (see [Reference Keevash, Lifshitz, Long and Minzer17, Reference Lifshitz and Minzer22, Reference Keevash, Lifshitz, Long and Minzer18] for example applications). It is worth noting that these variants are in fact generalizations of the standard hypercontractive inequality since one can easily show that in domains such as the Boolean hypercube, all low-degree functions are global.
By now, there are various proofs of the aforementioned results: (1) a proof by reduction to the Boolean hypercube, (2) a direct proof by expanding
![]() $\left \|f\right \|_q^q$
(for even q’s) and (3) an inductive proof on n.Footnote
2
All of these proofs use the product structure of the domain very strongly, and therefore, it is unclear how to adapt them beyond the realm of product spaces.
$\left \|f\right \|_q^q$
(for even q’s) and (3) an inductive proof on n.Footnote
2
All of these proofs use the product structure of the domain very strongly, and therefore, it is unclear how to adapt them beyond the realm of product spaces.
1.2 Hypercontractivity on non-product spaces
Significant challenges arise when trying to analyze non-product spaces. The simplest examples of such spaces are the slice (all points in a Boolean hypercube with a fixed Hamming weight), the multi-slice (all points in a multi-cube with a fixed ‘histogram’) and the symmetric group. The classical hypercontractive inequality is equivalent to another inequality, the log-Sobolev inequality. Sharp log-Sobolev inequalities were proven for the symmetric group and the slice by Lee and Yau [Reference Lee and Yau21], and for the multi-slice by Salez [Reference Salez26] (improving on earlier work of Filmus, O’Donnell and Wu [Reference Filmus, O’Donnell and Wu10]).
While such log-Sobolev inequalities are useful for balanced slices and multi-slices, their usefulness for domains such as the symmetric group is limited due to the similarity between
![]() $S_n$
and domains where hypercontractivity is known to be weak, such as
$S_n$
and domains where hypercontractivity is known to be weak, such as
![]() $[n]^n$
(identifying a permutation
$[n]^n$
(identifying a permutation
![]() $\pi $
with the list
$\pi $
with the list
![]() $\pi (1),\dots ,\pi (n)$
) and the
$\pi (1),\dots ,\pi (n)$
) and the
![]() $\tfrac 1n$
-biased cube (identifying a permutation with the corresponding permutation matrix). For this reason, Diaconis and Shahshahani [Reference Diaconis and Shahshahani4] resorted to representation-theoretic techniques in their analysis of the convergence of Markov chains on
$\tfrac 1n$
-biased cube (identifying a permutation with the corresponding permutation matrix). For this reason, Diaconis and Shahshahani [Reference Diaconis and Shahshahani4] resorted to representation-theoretic techniques in their analysis of the convergence of Markov chains on
![]() $S_n$
. We rectify this issue in a different way by extending global hypercontractivity to
$S_n$
. We rectify this issue in a different way by extending global hypercontractivity to
![]() $S_n$
.
$S_n$
.
1.3 Main results
The main goal of this paper is to study the symmetric group
![]() $S_n$
, which is probably the most fundamental non-product domain. Throughout this paper, we will consider
$S_n$
, which is probably the most fundamental non-product domain. Throughout this paper, we will consider
![]() $S_n$
as a probability space equipped with the uniform measure and use expectation norms as well as the corresponding expectation inner product, according to the uniform measure. We will think of
$S_n$
as a probability space equipped with the uniform measure and use expectation norms as well as the corresponding expectation inner product, according to the uniform measure. We will think of
![]() $S_n$
as a subset of
$S_n$
as a subset of
![]() $[n]^n$
and thereby for
$[n]^n$
and thereby for
![]() $\pi \in S_n$
refer to
$\pi \in S_n$
refer to
![]() $\pi (1)$
as ‘the first coordinate of the input’.
$\pi (1)$
as ‘the first coordinate of the input’.
To state our main results, we begin with defining the notion of globalness on
![]() $S_n$
. Given
$S_n$
. Given
![]() $f\colon S_n\to \mathbb {R}$
and a subset
$f\colon S_n\to \mathbb {R}$
and a subset
![]() $T \subseteq [n]\times [n]$
of the form
$T \subseteq [n]\times [n]$
of the form
![]() ${\left \{ (i_1,j_1),\ldots ,(i_t,j_t) \right \}}$
, where all of the i’s are distinct and all of the j’s are distinct (we call such subsets consistent), we denote by
${\left \{ (i_1,j_1),\ldots ,(i_t,j_t) \right \}}$
, where all of the i’s are distinct and all of the j’s are distinct (we call such subsets consistent), we denote by
![]() $S_{n}^T$
the set of permutations
$S_{n}^T$
the set of permutations
![]() $\pi \in S_n$
respecting T (i.e., such that
$\pi \in S_n$
respecting T (i.e., such that
![]() $\pi (i_\ell ) = j_\ell $
for all
$\pi (i_\ell ) = j_\ell $
for all
![]() $\ell =1,\ldots ,t$
), sometimes known as a double coset.Footnote
3
We denote by
$\ell =1,\ldots ,t$
), sometimes known as a double coset.Footnote
3
We denote by
![]() $f_{\rightarrow T}\colon S_n^T\to \mathbb {R}$
the restriction of f to
$f_{\rightarrow T}\colon S_n^T\to \mathbb {R}$
the restriction of f to
![]() $S_n^T$
, and equip
$S_n^T$
, and equip
![]() $S_n^T$
with the uniform measure.
$S_n^T$
with the uniform measure.
Definition 1.1. A function
![]() $f\colon S_n\to \mathbb {R}$
is called
$f\colon S_n\to \mathbb {R}$
is called
![]() $\varepsilon $
-global with constant C if for any consistent T, it holds that
$\varepsilon $
-global with constant C if for any consistent T, it holds that
![]() $\|f_{\rightarrow T}\|_2\leqslant C^{|T|}\varepsilon $
.
$\|f_{\rightarrow T}\|_2\leqslant C^{|T|}\varepsilon $
.
Our basic hypercontractive inequality is concerned with a certain self-adjoint Markov operator
![]() $\mathrm {T}^{(\rho )}$
and its effect on low-degree functions. Here, the degree of a function f is the minimal d such that f can be expressed as a linear combination of indicators of sets
$\mathrm {T}^{(\rho )}$
and its effect on low-degree functions. Here, the degree of a function f is the minimal d such that f can be expressed as a linear combination of indicators of sets
![]() $S_n^T$
for
$S_n^T$
for
![]() $|T| \leqslant d$
.Footnote
4
$|T| \leqslant d$
.Footnote
4
We defer the precise definition of
![]() $\mathrm {T}^{(\rho )}$
to Section 1.5; for now, we encourage the reader to think of it as averaging after a long random walk on the transposition graph (in which two permutations are connected by an edge if they differ by a transposition), say of length
$\mathrm {T}^{(\rho )}$
to Section 1.5; for now, we encourage the reader to think of it as averaging after a long random walk on the transposition graph (in which two permutations are connected by an edge if they differ by a transposition), say of length
![]() $\Theta (n)$
.
$\Theta (n)$
.
Theorem 1.2. There is a collection of self-adjoint operators
![]() $\mathrm {T}^{(\rho )}\colon L^2(S_n)\to L^2(S_n)$
for which the following holds.
$\mathrm {T}^{(\rho )}\colon L^2(S_n)\to L^2(S_n)$
for which the following holds.
For any even
![]() $q\in \mathbb {N}$
and
$q\in \mathbb {N}$
and
![]() $C>0$
, there is
$C>0$
, there is
![]() $\rho _0>0$
such that for all
$\rho _0>0$
such that for all
![]() $\rho \leqslant \rho _0$
, the operator
$\rho \leqslant \rho _0$
, the operator
![]() $\mathrm {T}^{(\rho )}$
satisfies the following:
$\mathrm {T}^{(\rho )}$
satisfies the following:
-
1. If
 $f\colon S_n\to \mathbb {R}$
is
$f\colon S_n\to \mathbb {R}$
is
 $\varepsilon $
-global with constant C, then
$\varepsilon $
-global with constant C, then
 $\left \|\mathrm {T}^{(\rho )} f\right \|_q\leqslant \varepsilon ^{\frac {q-2}{q}}\left \|f\right \|_2^{2/q}$
.
$\left \|\mathrm {T}^{(\rho )} f\right \|_q\leqslant \varepsilon ^{\frac {q-2}{q}}\left \|f\right \|_2^{2/q}$
. -
2. There is an absolute constant K, such for all
 $d\in \mathbb {N}$
satisfying
$d\in \mathbb {N}$
satisfying
 $d\leqslant \sqrt {\log n}/K$
, if f is a degree d function, then
$d\leqslant \sqrt {\log n}/K$
, if f is a degree d function, then
 $\left \|T^{(\rho )} f\right \|_2 \geqslant \rho ^{-K\cdot d} \cdot \left \|f\right \|_2$
.
$\left \|T^{(\rho )} f\right \|_2 \geqslant \rho ^{-K\cdot d} \cdot \left \|f\right \|_2$
.
As is often the case, once one has a hypercontractive inequality involving a noise operator whose eigenvalues are well understood, one can state a hypercontractive inequality for low-degree functions. For us, however, it will be important to relax the notion of globalness appropriately, and we therefore consider the notion of bounded globalness.
Definition 1.3. A function
![]() $f\colon S_n\to \mathbb {R}$
is called
$f\colon S_n\to \mathbb {R}$
is called
![]() $(d,\varepsilon )$
-global if for any consistent T of size at most d, it holds that
$(d,\varepsilon )$
-global if for any consistent T of size at most d, it holds that
![]() $\|f_{\rightarrow T}\|_2\leqslant \varepsilon $
.
$\|f_{\rightarrow T}\|_2\leqslant \varepsilon $
.
A natural example of
![]() $(d,\varepsilon )$
-global functions is the low-degree part of f, denoted by
$(d,\varepsilon )$
-global functions is the low-degree part of f, denoted by
![]() $f^{\leqslant d}$
, which is the degree d function which is closest to f in
$f^{\leqslant d}$
, which is the degree d function which is closest to f in
![]() $L_2$
-norm.
$L_2$
-norm.
With Definition 1.3 in hand, we can now state our hypercontractive inequality for low-degree functions.
Theorem 1.4. There exists
![]() $K>0$
such that the following holds. Let
$K>0$
such that the following holds. Let
![]() $q\in \mathbb {N}$
be even and
$q\in \mathbb {N}$
be even and
![]() $n\geqslant q^{K\cdot d^{2}}$
. If f is a
$n\geqslant q^{K\cdot d^{2}}$
. If f is a
![]() $\left (2d,\varepsilon \right )$
-global function of degree d, then
$\left (2d,\varepsilon \right )$
-global function of degree d, then
![]() $\|f\|_{q}\leqslant q^{O\left (d^{3}\right )}\varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
$\|f\|_{q}\leqslant q^{O\left (d^{3}\right )}\varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
Remark 1.5. The focus of the current paper is the case that n is very large compared to the degree d, and therefore, the technical conditions imposed on n in Theorems 1.2 and 1.4 will hold for us. It would be interesting to relax or even remove these conditions altogether, and we leave further investigation to future work.
1.4 Applications
We present some applications of Theorem 1.2 and Theorem 1.4, as outlined below.
1.4.1 The level-d inequality
Our first application is concerned with the weight a global function has on its low degrees, which is an analog of the classical level-d inequality on the Boolean hypercube (e.g., [Reference O’Donnell24, Corollary 9.25]).
Theorem 1.6. There exists an absolute constant
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() ${d,n\in \mathbb {N}}$
and
${d,n\in \mathbb {N}}$
and
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $n\geqslant 2^{C\cdot d^3} \log (1/\varepsilon )^{C\cdot d}$
. If
$n\geqslant 2^{C\cdot d^3} \log (1/\varepsilon )^{C\cdot d}$
. If
![]() $f\colon S_n\to \mathbb {Z}$
is
$f\colon S_n\to \mathbb {Z}$
is
![]() $(2d,\varepsilon )$
-global, then
$(2d,\varepsilon )$
-global, then
![]() $\left \|f^{\leqslant d}\right \|_2^2\leqslant 2^{C \cdot d^4}\varepsilon ^4 \log ^{C\cdot d}(1/\varepsilon )$
.
$\left \|f^{\leqslant d}\right \|_2^2\leqslant 2^{C \cdot d^4}\varepsilon ^4 \log ^{C\cdot d}(1/\varepsilon )$
.
Theorem 1.6 should be compared to the level-d inequality on the hypercube, which asserts that for any function
![]() $f\colon {\left \{ 0,1 \right \}}^{n}\to {\left \{ 0,1 \right \}}^{}$
with
$f\colon {\left \{ 0,1 \right \}}^{n}\to {\left \{ 0,1 \right \}}^{}$
with
![]() $\mathop {\mathbb {E}}[f] = \delta < 1/2$
we have that
$\mathop {\mathbb {E}}[f] = \delta < 1/2$
we have that
![]() $\left \|f^{\leqslant d}\right \|_2^2\leqslant \delta ^2\left (\frac {10\log (1/\delta )}{d}\right )^{d}$
, for all
$\left \|f^{\leqslant d}\right \|_2^2\leqslant \delta ^2\left (\frac {10\log (1/\delta )}{d}\right )^{d}$
, for all
![]() $d\leqslant \log (1/\delta )$
. (Quantitatively, the parameter
$d\leqslant \log (1/\delta )$
. (Quantitatively, the parameter
![]() $\delta $
should be compared to
$\delta $
should be compared to
![]() $\varepsilon ^2$
in Theorem 1.6 due to normalisation).
$\varepsilon ^2$
in Theorem 1.6 due to normalisation).
Note that it may be the case that
![]() $\varepsilon $
in Theorem 1.6 is much larger than
$\varepsilon $
in Theorem 1.6 is much larger than
![]() $\left \|f\right \|_2^{1/2}$
, and then Theorem 1.6 becomes trivial.Footnote
5
Fortunately, we can prove a stronger version of Theorem 1.6 for functions f whose
$\left \|f\right \|_2^{1/2}$
, and then Theorem 1.6 becomes trivial.Footnote
5
Fortunately, we can prove a stronger version of Theorem 1.6 for functions f whose
![]() $2$
-norm is not exponentially small, which actually follows relatively easily from Theorem 1.6.
$2$
-norm is not exponentially small, which actually follows relatively easily from Theorem 1.6.
Theorem 1.7. There exists an absolute constant
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() $d,n\in \mathbb {N}$
,
$d,n\in \mathbb {N}$
,
![]() $\varepsilon>0$
be parameters and let
$\varepsilon>0$
be parameters and let
![]() $f\colon S_n\to \mathbb {Z}$
be a
$f\colon S_n\to \mathbb {Z}$
be a
![]() $(2d,\varepsilon )$
-global function. If
$(2d,\varepsilon )$
-global function. If
![]() $n\geqslant 2^{C\cdot d^3} \log (1/\left \|f\right \|_2)^{C \cdot d}$
, then
$n\geqslant 2^{C\cdot d^3} \log (1/\left \|f\right \|_2)^{C \cdot d}$
, then
On the proof of the level-d inequality.
In contrast to the case of the hypercube, Theorem 1.6 does not immediately follow from Theorem 1.2 or Theorem 1.4 and requires more work, as we explain below. Recall that one proof of the level-d inequality on the hypercube proceeds, using hypercontractivity, as follows:
choosing suitable q and rearranging. Our hypercontractive inequality does not allow us to make the final transition and instead only tells us that
![]() $\left \|f^{\leqslant d}\right \|_q \leqslant O_{d,q}(\varepsilon ^{(q-2)/q}) \left \|f^{\leqslant d}\right \|_2^{2/q}$
(using the fact that
$\left \|f^{\leqslant d}\right \|_q \leqslant O_{d,q}(\varepsilon ^{(q-2)/q}) \left \|f^{\leqslant d}\right \|_2^{2/q}$
(using the fact that
![]() $f^{\leqslant d}$
is
$f^{\leqslant d}$
is
![]() $(2d,\varepsilon )$
-global, a property inherited from f). Executing this plan only implies, at best, the quantitatively weaker statement that
$(2d,\varepsilon )$
-global, a property inherited from f). Executing this plan only implies, at best, the quantitatively weaker statement that
![]() $\left \|f^{\leqslant d}\right \|_2^2\leqslant \varepsilon ^{3/2} \log ^{O_d(1)}(1/\varepsilon )$
. Here, the difference between
$\left \|f^{\leqslant d}\right \|_2^2\leqslant \varepsilon ^{3/2} \log ^{O_d(1)}(1/\varepsilon )$
. Here, the difference between
![]() $\varepsilon ^{3/2}$
and
$\varepsilon ^{3/2}$
and
![]() $\varepsilon ^2$
is often crucial because such results are often only useful for very small
$\varepsilon ^2$
is often crucial because such results are often only useful for very small
![]() $\varepsilon $
anyway.
$\varepsilon $
anyway.
In reality,
![]() $f^{\leqslant d}$
is a lot more global than f: for example, the level d inequality implies that
$f^{\leqslant d}$
is a lot more global than f: for example, the level d inequality implies that
![]() $f^{\leqslant d}$
itself has
$f^{\leqslant d}$
itself has
![]() $2$
-norm proportional to
$2$
-norm proportional to
![]() $\varepsilon ^2$
rather than
$\varepsilon ^2$
rather than
![]() $ \varepsilon $
. In order to show this, we use an inductive approach.
$ \varepsilon $
. In order to show this, we use an inductive approach.
Consider the restriction of
![]() $f^{\leqslant d}$
which maximizes the
$f^{\leqslant d}$
which maximizes the
![]() $2$
-norm. If it is the function
$2$
-norm. If it is the function
![]() $f^{\leqslant d}$
itself, then
$f^{\leqslant d}$
itself, then
![]() $f^{\leqslant d}$
is
$f^{\leqslant d}$
is
![]() $(2d, O_d(\left \|f^{\leqslant d}\right \|_2))$
-global, which enables us to carry out the hypercube argument. Otherwise, we show that there is a ‘derivative’Footnote
6
g of
$(2d, O_d(\left \|f^{\leqslant d}\right \|_2))$
-global, which enables us to carry out the hypercube argument. Otherwise, we show that there is a ‘derivative’Footnote
6
g of
![]() $f^{\leqslant d}$
which achieves roughly the same
$f^{\leqslant d}$
which achieves roughly the same
![]() $2$
-norm as that restriction of
$2$
-norm as that restriction of
![]() $f^{\leqslant d}$
and has the further property that all of its derivatives have smaller
$f^{\leqslant d}$
and has the further property that all of its derivatives have smaller
![]() $2$
-norms, which implies that g is
$2$
-norms, which implies that g is
![]() $(2d, O_d(\left \|g\right \|_2))$
-global. Applying the induction hypothesis (using that g has degree lower than f), we get that
$(2d, O_d(\left \|g\right \|_2))$
-global. Applying the induction hypothesis (using that g has degree lower than f), we get that
![]() $\left \|g\right \|_2 = \tilde {O}_d(\varepsilon ^2)$
, which implies that
$\left \|g\right \|_2 = \tilde {O}_d(\varepsilon ^2)$
, which implies that
![]() $f^{\leqslant d}$
is
$f^{\leqslant d}$
is
![]() $(2d, \tilde {O}_d(\varepsilon ^2))$
-global. This suffices for the hypercube argument to go through.
$(2d, \tilde {O}_d(\varepsilon ^2))$
-global. This suffices for the hypercube argument to go through.
Since g is a derivative, it is integer-valued rather than Boolean. Accordingly, we strengthen the induction hypothesis, proving a statement for all integer-valued functions.
1.4.2 Global product-free sets are small
We say that a family of permutations
![]() $F\subseteq S_n$
is product-free if there are no
$F\subseteq S_n$
is product-free if there are no
![]() $\pi _1,\pi _2,\pi _3\in S_n$
such that
$\pi _1,\pi _2,\pi _3\in S_n$
such that
![]() $\pi _3 = \pi _2\circ \pi _1$
. What is the size of the largest product-free family F?
$\pi _3 = \pi _2\circ \pi _1$
. What is the size of the largest product-free family F?
With the formulation above, one can of course take F to be the set of odd permutations, which has size
![]() $\left |S_n\right |/2$
. What happens if we forbid such permutations (i.e., only consider families of even permutations)?
$\left |S_n\right |/2$
. What happens if we forbid such permutations (i.e., only consider families of even permutations)?
Questions of this sort generalise the well-studied problem of finding arithmetic sequences in dense sets. More relevant to us is the work of Gowers [Reference Gowers14], which studies this problem for a wide range of groups (referred therein as ‘quasi-random groups’) and the work of Eberhard [Reference Eberhard6] which specialized this question to
![]() $A_n$
and improves on Gowers’ result. More specifically, Gowers shows that a product-free set
$A_n$
and improves on Gowers’ result. More specifically, Gowers shows that a product-free set
![]() $F\subseteq A_n$
has size at most
$F\subseteq A_n$
has size at most
![]() $O\left (\frac {1}{n^{1/3}}\left |A_n\right |\right )$
, and Eberhard improves this bound to
$O\left (\frac {1}{n^{1/3}}\left |A_n\right |\right )$
, and Eberhard improves this bound to
![]() $\left |F\right | = O\left (\frac {\log ^{7/2}n}{\sqrt {n}} \left |A_n\right |\right )$
. Eberhard’s result is tight up to the polylogarithmic factor, as evidenced by the family
$\left |F\right | = O\left (\frac {\log ^{7/2}n}{\sqrt {n}} \left |A_n\right |\right )$
. Eberhard’s result is tight up to the polylogarithmic factor, as evidenced by the family
In this section, we consider the problem of determining the maximal size of a global, product-free set in
![]() $A_n$
. In particular, we show the following:
$A_n$
. In particular, we show the following:
Theorem 1.8. There exists
![]() $N\in \mathbb {N}$
such that the following holds for all
$N\in \mathbb {N}$
such that the following holds for all
![]() $n\geqslant N$
. For every
$n\geqslant N$
. For every
![]() $C>0$
, there is
$C>0$
, there is
![]() $K>0$
such that if
$K>0$
such that if
![]() $F\subseteq A_n$
is product-free and is
$F\subseteq A_n$
is product-free and is
![]() $(6,C\cdot \sqrt {\delta })$
-global, where
$(6,C\cdot \sqrt {\delta })$
-global, where
![]() $\delta = \left |F\right |/\left |A_n\right |$
, then
$\delta = \left |F\right |/\left |A_n\right |$
, then
![]() $\delta \leqslant \frac {\log ^K n}{n}$
.
$\delta \leqslant \frac {\log ^K n}{n}$
.
Remark 1.9. A few remarks are in order.
-
1. We note that the above result achieves a stronger bound than the family in (1). There is no contradiction here, of course, since that family is very much not global: restricting to
 $\pi (1) = 2$
increases the measure of F significantly.
$\pi (1) = 2$
increases the measure of F significantly. -
2. The junta method, which can be used to study many problems in extremal combinatorics, often considers the question for global families as a key component. The rough idea is to show that one can approximate a family F by a union of families
 $\tilde {F}$
that satisfy an appropriate pseudo-randomness condition, such that if F is product-free, then so are the families
$\tilde {F}$
that satisfy an appropriate pseudo-randomness condition, such that if F is product-free, then so are the families
 $\tilde {F}$
. Furthermore, inside any not-too-small pseudo-random family
$\tilde {F}$
. Furthermore, inside any not-too-small pseudo-random family
 $\tilde {F}$
, one may find a global family
$\tilde {F}$
, one may find a global family
 $\tilde {F}'$
by making any small restriction that increases the size of the family considerably. Thus, in this way one may hope to reduce the general question to the question on global families (see [Reference Keevash, Lifshitz, Long and Minzer18], for example).
$\tilde {F}'$
by making any small restriction that increases the size of the family considerably. Thus, in this way one may hope to reduce the general question to the question on global families (see [Reference Keevash, Lifshitz, Long and Minzer18], for example).While at the moment we do not know how to employ the junta method in the case of product-free sets in
 $A_n$
, one may still hope that it is possible, providing some motivation for Theorem 1.8.
$A_n$
, one may still hope that it is possible, providing some motivation for Theorem 1.8. -
3. Our result is, in fact, more general and can be used to study the
 $3$
-set version of this problem; see Corollary 7.9.
$3$
-set version of this problem; see Corollary 7.9. -
4. We suspect that much stronger quantitative bounds should hold for global families; we elaborate on this suspicion in Section 7.2.4.
1.4.3 Isoperimetric inequalities
Using our hypercontractive inequalities, we are able to prove several isoperimetric inequalities for global sets. Let
![]() $S\subseteq S_n$
be a set and consider the transposition random walk
$S\subseteq S_n$
be a set and consider the transposition random walk
![]() $\mathrm {T}$
that from a permutation
$\mathrm {T}$
that from a permutation
![]() $\pi \in S_n$
moves to
$\pi \in S_n$
moves to
![]() $\pi \circ \tau $
, where
$\pi \circ \tau $
, where
![]() $\tau $
is a randomly chosen transposition. We show that if S is ‘not too sensitive along any transposition’,Footnote
7
then the probability to exit S in a random step according to
$\tau $
is a randomly chosen transposition. We show that if S is ‘not too sensitive along any transposition’,Footnote
7
then the probability to exit S in a random step according to
![]() $\mathrm {T}$
must be significant, similarly to the classical KKL Theorem on the hypercube [Reference Kahn, Kalai and Linial15]. The formal statement of this result is given in Theorem 7.13.
$\mathrm {T}$
must be significant, similarly to the classical KKL Theorem on the hypercube [Reference Kahn, Kalai and Linial15]. The formal statement of this result is given in Theorem 7.13.
We are also able to analyse longer random walks according to
![]() $\mathrm {T}$
, of order n, and show that one has small-set expansion for global sets. See Theorem 7.12 for a formal statement.
$\mathrm {T}$
, of order n, and show that one has small-set expansion for global sets. See Theorem 7.12 for a formal statement.
1.4.4 Deducing the results for other non-product domains
Our results for
![]() $S_n$
imply analogous results for the multi-slice. The deduction is done in a black-box fashion, by a natural correspondence between functions over
$S_n$
imply analogous results for the multi-slice. The deduction is done in a black-box fashion, by a natural correspondence between functions over
![]() $S_n$
and functions over the multi-slice that preserves degrees, globalness and
$S_n$
and functions over the multi-slice that preserves degrees, globalness and
![]() $L_p$
norms.
$L_p$
norms.
This allows us to deduce analogs of our results for
![]() $S_n$
essentially for free (see Section 7.4) as well as a stability result for the classical Kruskal–Katona Theorem (see Theorem 7.20).
$S_n$
essentially for free (see Section 7.4) as well as a stability result for the classical Kruskal–Katona Theorem (see Theorem 7.20).
1.4.5 Other applications
Our hypercontractive inequality has also been used in the study of Probabilistically Checkable Proofs [Reference Braverman, Khot and Minzer3]. More specifically, the inequality has been applied to study a new hardness conjecture, referred to as ‘Rich
![]() $2$
-to-
$2$
-to-
![]() $1$
Games Conjecture’ in [Reference Braverman, Khot and Minzer3], and show that if true, it implies Khot’s Unique-Games Conjecture [Reference Khot19].
$1$
Games Conjecture’ in [Reference Braverman, Khot and Minzer3], and show that if true, it implies Khot’s Unique-Games Conjecture [Reference Khot19].
1.5 Our techniques
In this section, we outline the techniques used in the proofs of Theorem 1.2 and Theorem 1.4.
1.5.1 The coupling approach: Proof overview
Obtaining hypercontractive operators via coupling
Consider two finite probability spaces X and Y and suppose that
![]() $\mathcal {C} = (\mathbf {x},\mathbf {y})$
is a coupling between them (we encourage the reader to think of X as
$\mathcal {C} = (\mathbf {x},\mathbf {y})$
is a coupling between them (we encourage the reader to think of X as
![]() $S_n$
, and of Y as a product space in which we already know hypercontractivity to hold). Using the coupling
$S_n$
, and of Y as a product space in which we already know hypercontractivity to hold). Using the coupling
![]() $\mathcal {C}$
, we may define the averaging operators
$\mathcal {C}$
, we may define the averaging operators
![]() $\mathrm {T}_{X\to Y}\colon L^{2}\left (X\right )\to L^{2}\left (Y\right )$
and
$\mathrm {T}_{X\to Y}\colon L^{2}\left (X\right )\to L^{2}\left (Y\right )$
and
![]() $\mathrm {T}_{Y\to X}\colon L^{2}\left (Y\right )\to L^{2}\left (X\right )$
as
$\mathrm {T}_{Y\to X}\colon L^{2}\left (Y\right )\to L^{2}\left (X\right )$
as
Jensen’s inequality implies that each one of the operators
![]() $\mathrm {T}_{X\to Y}$
and
$\mathrm {T}_{X\to Y}$
and
![]() $\mathrm {T}_{Y\to X}$
is a contraction with respect to the
$\mathrm {T}_{Y\to X}$
is a contraction with respect to the
![]() $L^p$
-norm, for any
$L^p$
-norm, for any
![]() $p\geqslant 1$
. The benefit of considering these operators is that given an operator
$p\geqslant 1$
. The benefit of considering these operators is that given an operator
![]() $\mathrm {T}_Y$
with desirable properties (say, it is hypercontractive; for example, it satisfies
$\mathrm {T}_Y$
with desirable properties (say, it is hypercontractive; for example, it satisfies
![]() $\|\mathrm {T}_{Y}f\|_{4}\leqslant \|f\|_{2}$
), we may consider the lifted operator on X given by
$\|\mathrm {T}_{Y}f\|_{4}\leqslant \|f\|_{2}$
), we may consider the lifted operator on X given by
![]() $\mathrm {T}_X \stackrel {\mathit {def}}{=} \mathrm {T}_{Y\to X}\mathrm {T}_{Y}\mathrm {T}_{X\to Y}$
and hope that it too satisfies some desirable properties. Indeed, it is easy to see that if
$\mathrm {T}_X \stackrel {\mathit {def}}{=} \mathrm {T}_{Y\to X}\mathrm {T}_{Y}\mathrm {T}_{X\to Y}$
and hope that it too satisfies some desirable properties. Indeed, it is easy to see that if
![]() $\mathrm {T}_Y$
is hypercontractive, then
$\mathrm {T}_Y$
is hypercontractive, then
![]() $\mathrm {T}_X$
is also hypercontractive:
$\mathrm {T}_X$
is also hypercontractive:
We show that the same connection continues to hold for global hypercontractive inequalities (that is, hypercontractive inequalities for global functions) such as the one given in [Reference Keevash, Lifshitz, Long and Minzer17, Reference Keevash, Lifshitz, Long and Minzer18] (and more concretely, Theorem 2.5 below); the proof in this case is slightly more involved.
This approach allows us to prove Theorem 1.2. In order to deduce Theorem 1.4, we show that the effect of
![]() $\mathrm {T}_X$
on low-degree functions is similar to the effect of standard noise operators: it decreases the
$\mathrm {T}_X$
on low-degree functions is similar to the effect of standard noise operators: it decreases the
![]() $2$
-norm by at most a constant factor. This allows us to derive Theorem 1.4.
$2$
-norm by at most a constant factor. This allows us to derive Theorem 1.4.
1.5.2 Instantiating the coupling approach for the symmetric group
The coupled space
Let
![]() $L = [n]^2$
and let m be large, depending polynomially on n (
$L = [n]^2$
and let m be large, depending polynomially on n (
![]() $m=n^2$
will do). We will couple
$m=n^2$
will do). We will couple
![]() $S_n$
and
$S_n$
and
![]() $L^m$
, where the idea is to think of each element of L as local information about the coupled permutation
$L^m$
, where the idea is to think of each element of L as local information about the coupled permutation
![]() $\pi $
. That is, the element
$\pi $
. That is, the element
![]() $(i,j)\in L$
encodes the fact that
$(i,j)\in L$
encodes the fact that
![]() $\pi $
maps i to j.
$\pi $
maps i to j.
Our coupling
We say that a set
![]() $T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \} \subseteq L$
of pairs is consistentif there exists a permutation
$T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \} \subseteq L$
of pairs is consistentif there exists a permutation
![]() $\pi $
with
$\pi $
with
![]() $\pi \left (i_{k}\right )=j_{k}$
for each
$\pi \left (i_{k}\right )=j_{k}$
for each
![]() $k\in \left [t\right ]$
, and any such permutation
$k\in \left [t\right ]$
, and any such permutation
![]() $\pi $
is said to be consistent with T.
$\pi $
is said to be consistent with T.
Our coupling between
![]() $S_n$
and
$S_n$
and
![]() $L^m$
is the following:
$L^m$
is the following:
-
1. Choose an element
 $\mathbf {x}\sim L^m$
uniformly at random.
$\mathbf {x}\sim L^m$
uniformly at random. -
2. Greedily construct from
 $\mathbf {x}$
a set T of consistent pairs. That is, starting from
$\mathbf {x}$
a set T of consistent pairs. That is, starting from
 $k=1$
to m, we consider the k-th coordinate of
$k=1$
to m, we consider the k-th coordinate of
 $\mathbf {x}$
, denoted by
$\mathbf {x}$
, denoted by
 $(i_k,j_k)$
, and check whether adding it to T would keep it consistent. If so, we add
$(i_k,j_k)$
, and check whether adding it to T would keep it consistent. If so, we add
 $(i_k,j_k)$
to T; otherwise, we do not.
$(i_k,j_k)$
to T; otherwise, we do not. -
3. Choose a permutation
 $\boldsymbol {\pi }$
consistent with T uniformly at random.
$\boldsymbol {\pi }$
consistent with T uniformly at random.
The resulting operator
Finally, we can specify our hypercontractive operator on
![]() $S_{n}$
. Let
$S_{n}$
. Let
![]() $X=S_{n}$
,
$X=S_{n}$
,
![]() $Y=L^{m}$
and
$Y=L^{m}$
and
![]() $T_{X\to Y},T_{Y\to X}$
be the operators corresponding to the coupling that we have just constructed. Let
$T_{X\to Y},T_{Y\to X}$
be the operators corresponding to the coupling that we have just constructed. Let
![]() $\mathrm {T}_{Y}=\mathrm {T}_{\rho }$
be the noise operator on the product space
$\mathrm {T}_{Y}=\mathrm {T}_{\rho }$
be the noise operator on the product space
![]() $L^{m}$
, which can be defined in two equivalent ways:
$L^{m}$
, which can be defined in two equivalent ways:
-
1. Every element
 $(i_k,j_k)$
is retained with probability
$(i_k,j_k)$
is retained with probability
 $\rho $
and resampled (according to the uniform distribution over L) otherwise.
$\rho $
and resampled (according to the uniform distribution over L) otherwise. -
2. The d’th Fourier level is multiplied by
 $\rho ^d$
.Footnote
8
$\rho ^d$
.Footnote
8
Then
![]() $\mathrm {T}^{\left (\rho \right )}=\mathrm {T}_{Y\to X}\mathrm {T}_{Y}\mathrm {T}_{X\to Y}$
is our desired operator on
$\mathrm {T}^{\left (\rho \right )}=\mathrm {T}_{Y\to X}\mathrm {T}_{Y}\mathrm {T}_{X\to Y}$
is our desired operator on
![]() $S_{n}$
.
$S_{n}$
.
We next explain how to analyse the operator
![]() $\mathrm {T}_Y$
.
$\mathrm {T}_Y$
.
Showing that
 $\mathrm {T}_Y$
satisfies global hypercontractivity
$\mathrm {T}_Y$
satisfies global hypercontractivity
Recall the simplistic argument (2), showing that hypercontractivity of
![]() $\mathrm {T}_X$
implies the hypercontractivity of
$\mathrm {T}_X$
implies the hypercontractivity of
![]() $\mathrm {T}_Y$
. We intend to show, in a similar way, that global hypercontractivity is also carried over by the coupling. Towards this end, we must show that the notion of globalness is preserved: namely, if f is global, then
$\mathrm {T}_Y$
. We intend to show, in a similar way, that global hypercontractivity is also carried over by the coupling. Towards this end, we must show that the notion of globalness is preserved: namely, if f is global, then
![]() $g = \mathrm {T}_{S_n\to L^m} f$
is also global (the definition of globalness for functions on
$g = \mathrm {T}_{S_n\to L^m} f$
is also global (the definition of globalness for functions on
![]() $L^m$
is completely analogous to Definition 1.1).
$L^m$
is completely analogous to Definition 1.1).
Here we encounter a mismatch between the notion of globalness assumed by Theorem 1.4 – namely, f is assumed to be
![]() $(2d,\varepsilon )$
-global, and the notion of globalness required by the global hypercontractive result of [Reference Keevash, Lifshitz, Long and Minzer17], which applies to
$(2d,\varepsilon )$
-global, and the notion of globalness required by the global hypercontractive result of [Reference Keevash, Lifshitz, Long and Minzer17], which applies to
![]() $\delta $
-global functions. We bridge this gap using the equivalence of
$\delta $
-global functions. We bridge this gap using the equivalence of
![]() $(2d,\varepsilon )$
-globalness and
$(2d,\varepsilon )$
-globalness and
![]() $\delta $
-globalness for degree d functions, where
$\delta $
-globalness for degree d functions, where
![]() $\delta ,\varepsilon $
differ by constant factors.
$\delta ,\varepsilon $
differ by constant factors.
1.5.3 The direct approach: proof overview
Our second approach to establish hypercontractive inequalities goes via a rather different route. One of the proofs of hypercontractivity in product domains proceeds by finding a convenient, orthonormal basis for the space of real-valued functions over
![]() $\Omega $
(which in product spaces is easy as the basis tensorizes). This way, proving hypercontractivity amounts to studying moments of these basis functions, which is often not very hard to do due to the simple nature of the basis.
$\Omega $
(which in product spaces is easy as the basis tensorizes). This way, proving hypercontractivity amounts to studying moments of these basis functions, which is often not very hard to do due to the simple nature of the basis.
When dealing with non-product spaces such as
![]() $S_n$
, we do not know how to produce such a convenient orthonormal basis. Nevertheless, our direct approach presented in Section 6 relies on a representation of a function
$S_n$
, we do not know how to produce such a convenient orthonormal basis. Nevertheless, our direct approach presented in Section 6 relies on a representation of a function
![]() $f\colon S_n\to \mathbb {R}$
in a canonical form that is almost as good as in product spaces. To construct this representation, we start with obvious spanning sets such as
$f\colon S_n\to \mathbb {R}$
in a canonical form that is almost as good as in product spaces. To construct this representation, we start with obvious spanning sets such as
 $$\begin{align*}\left\{ \left. \prod\limits_{\ell=1}^d 1_{\pi(i_{\ell}) = j_{\ell}} \;\right\vert \left|{\left\{ i_1,\ldots,i_d \right\}}\right| = \left|{\left\{ j_1,\ldots,j_d \right\}}\right| = d \right\}. \end{align*}$$
$$\begin{align*}\left\{ \left. \prod\limits_{\ell=1}^d 1_{\pi(i_{\ell}) = j_{\ell}} \;\right\vert \left|{\left\{ i_1,\ldots,i_d \right\}}\right| = \left|{\left\{ j_1,\ldots,j_d \right\}}\right| = d \right\}. \end{align*}$$
This set contains many redundancies (and thus is not a basis), and we show how to use these to enforce a system of linear constraints on the coefficients of the representation that turn out to be very useful in proving hypercontractive inequalities.
1.6 Organisation of the paper
In Section 2, we present some basic preliminaries. Sections 3, 4 and 5 are devoted for presenting our approach to hypercontractivity via coupling and algebraic arguments, and in Section 6, we present our direct approach. In Sections 7 and 8, we present several consequences of our hypercontractive inequalities: the level-d inequality in Section 8 and the other applications in Section 7.
2 Preliminaries
We think of the product operation in
![]() $S_n$
as function composition, and so
$S_n$
as function composition, and so
![]() $(\tau \sigma )(i) = (\tau \circ \sigma )(i) = \tau (\sigma (i))$
.
$(\tau \sigma )(i) = (\tau \circ \sigma )(i) = \tau (\sigma (i))$
.
Throughout the paper, we consider the space of real-valued functions on
![]() $S_n$
equipped with the expectation inner product, denoted by
$S_n$
equipped with the expectation inner product, denoted by
![]() $L^{2}\left (S_{n}\right )$
. Namely, for any
$L^{2}\left (S_{n}\right )$
. Namely, for any
![]() $f,g\colon S_n\to \mathbb {R}$
, we define
$f,g\colon S_n\to \mathbb {R}$
, we define
![]() $\langle {f},{g}\rangle = \mathop {\mathbb {E}}_{\sigma \in S_n}[f(\sigma )g(\sigma )]$
. A basic property of this space is that it is an
$\langle {f},{g}\rangle = \mathop {\mathbb {E}}_{\sigma \in S_n}[f(\sigma )g(\sigma )]$
. A basic property of this space is that it is an
![]() $S_{n}$
-bimodule, as can be seen by defining the left operation on a function f and a permutation
$S_{n}$
-bimodule, as can be seen by defining the left operation on a function f and a permutation
![]() $\tau $
as
$\tau $
as ![]() and the right operation
and the right operation
![]() $f^{\tau }(\sigma ) = f(\sigma \circ \tau )$
.
$f^{\tau }(\sigma ) = f(\sigma \circ \tau )$
.
2.1 The level decomposition
We will define the concept of degree d function in several equivalent ways. The most standard definition is the one which we already mentioned in the introduction.
Definition 2.1. Let
![]() $T = \{(i_1,j_1),\ldots ,(i_t,j_t)\} \subseteq L$
be a set of t consistent pairs and recall that
$T = \{(i_1,j_1),\ldots ,(i_t,j_t)\} \subseteq L$
be a set of t consistent pairs and recall that
![]() $S_n^T$
is the set of all permutations such that
$S_n^T$
is the set of all permutations such that
![]() $\pi (i_k) = j_k$
for all
$\pi (i_k) = j_k$
for all
![]() $k \in [t]$
.
$k \in [t]$
.
The space
![]() $V_d$
consists of all linear combinations of functions of the form
$V_d$
consists of all linear combinations of functions of the form
![]() $1_T = 1_{S_n^T}$
for
$1_T = 1_{S_n^T}$
for
![]() $|T| \leqslant d$
. We say that a real-valued function on
$|T| \leqslant d$
. We say that a real-valued function on
![]() $S_n$
has degree (at most) d if it belongs to
$S_n$
has degree (at most) d if it belongs to
![]() $V_d$
.
$V_d$
.
By construction,
![]() $V_{d-1} \subseteq V_d$
for all
$V_{d-1} \subseteq V_d$
for all
![]() $d \geqslant 1$
. We define the space of functions of pure degree d as
$d \geqslant 1$
. We define the space of functions of pure degree d as
It is easy to see that
![]() $V_n = V_{n-1}$
, and so we can decompose the space of all real-valued functions on
$V_n = V_{n-1}$
, and so we can decompose the space of all real-valued functions on
![]() $S_n$
as follows:
$S_n$
as follows:
We comment that the representation theory of
![]() $S_n$
refines this decomposition into a finer one, indexed by partitions
$S_n$
refines this decomposition into a finer one, indexed by partitions
![]() $\lambda $
of n; the space
$\lambda $
of n; the space
![]() $V_{=d}$
corresponds to partitions in which the largest part is exactly
$V_{=d}$
corresponds to partitions in which the largest part is exactly
![]() $n-d$
.
$n-d$
.
We may write any function
![]() $f\colon S_n\to \mathbb {R}$
in terms of our decomposition uniquely as
$f\colon S_n\to \mathbb {R}$
in terms of our decomposition uniquely as
![]() $\sum \limits _{i=0}^{n-1}{f^{=i}}$
, where
$\sum \limits _{i=0}^{n-1}{f^{=i}}$
, where
![]() $f^{=i}\in V_{=i}$
. It will also be convenient for us to have a notation for the projection of f onto
$f^{=i}\in V_{=i}$
. It will also be convenient for us to have a notation for the projection of f onto
![]() $V_{d}$
, which is nothing but
$V_{d}$
, which is nothing but
![]() $f^{\leqslant d} = f^{=0} + f^{=1}+\dots +f^{=d}$
.
$f^{\leqslant d} = f^{=0} + f^{=1}+\dots +f^{=d}$
.
We will need an alternative description of
![]() $V_{=d}$
in terms of juntas.
$V_{=d}$
in terms of juntas.
Definition 2.2. Let
![]() $A,B \subseteq [n]$
. For every
$A,B \subseteq [n]$
. For every
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
, let
$b \in B$
, let
![]() $e_{ab} = 1_{\pi (a)=b}$
. We say that a function
$e_{ab} = 1_{\pi (a)=b}$
. We say that a function
![]() $f\colon S_n \to \mathbb {R}$
is an
$f\colon S_n \to \mathbb {R}$
is an
![]() $(A,B)$
-junta if f can be written as a function of the
$(A,B)$
-junta if f can be written as a function of the
![]() $e_{ab}$
. We denote the space of
$e_{ab}$
. We denote the space of
![]() $(A,B)$
-juntas by
$(A,B)$
-juntas by
![]() $V_{A,B}$
.
$V_{A,B}$
.
A function is a d-junta if it is an
![]() $(A,B)$
-junta for some
$(A,B)$
-junta for some
![]() $|A|=|B|=d$
.
$|A|=|B|=d$
.
Lemma 2.3. The space
![]() $V_{A,B}$
is spanned by the functions
$V_{A,B}$
is spanned by the functions
![]() $1_T$
for
$1_T$
for
![]() $T \subseteq A \times B$
. Consequently,
$T \subseteq A \times B$
. Consequently,
![]() $V_d$
is the span of the d-juntas.
$V_d$
is the span of the d-juntas.
Proof. If
![]() $A = \{i_1,\ldots ,i_d\}$
and
$A = \{i_1,\ldots ,i_d\}$
and
![]() $B = \{j_1,\ldots ,j_d\}$
, then an
$B = \{j_1,\ldots ,j_d\}$
, then an
![]() $(A,B)$
-junta f can be written as a function of
$(A,B)$
-junta f can be written as a function of
![]() $e_{i_sj_t}$
, and in particular as a polynomial in these functions. Since
$e_{i_sj_t}$
, and in particular as a polynomial in these functions. Since
![]() $e_{i_sj_{t_1}} e_{i_sj_{t_2}} = e_{i_{s_1}j_t} e_{i_{s_2}j_t} = 0$
, if
$e_{i_sj_{t_1}} e_{i_sj_{t_2}} = e_{i_{s_1}j_t} e_{i_{s_2}j_t} = 0$
, if
![]() $t_1 \neq t_2$
and
$t_1 \neq t_2$
and
![]() $s_1 \neq s_2$
, it follows that f can be written as a linear combination of functions
$s_1 \neq s_2$
, it follows that f can be written as a linear combination of functions
![]() $1_T$
for
$1_T$
for
![]() $T \subseteq A \times B$
.
$T \subseteq A \times B$
.
Conversely, if
![]() $T = \{(a_1,b_1),\ldots ,(a_d,b_d)\}$
, then
$T = \{(a_1,b_1),\ldots ,(a_d,b_d)\}$
, then
![]() $1_T = e_{a_1b_1} \cdots e_{a_db_d}$
.
$1_T = e_{a_1b_1} \cdots e_{a_db_d}$
.
To see the truth of the second part of the lemma, notice that if
![]() $|A|=|B|=d$
and
$|A|=|B|=d$
and
![]() $T \subseteq A \times B$
, then
$T \subseteq A \times B$
, then
![]() $|T| \leqslant d$
, and conversely, if
$|T| \leqslant d$
, and conversely, if
![]() $|T| \leqslant d$
, then
$|T| \leqslant d$
, then
![]() $T \subseteq A \times B$
for some
$T \subseteq A \times B$
for some
![]() $A,B$
such that
$A,B$
such that
![]() $|A|=|B|=d$
.
$|A|=|B|=d$
.
We will also need an alternative description of
![]() $V_{A,B}$
.
$V_{A,B}$
.
Lemma 2.4. For each
![]() $A,B$
, the space
$A,B$
, the space
![]() $V_{A,B}$
consists of all functions
$V_{A,B}$
consists of all functions
![]() $f\colon S_n \to \mathbb {R}$
such that
$f\colon S_n \to \mathbb {R}$
such that ![]() for all
for all
![]() $\sigma $
fixing A pointwise and
$\sigma $
fixing A pointwise and
![]() $\tau $
fixing B pointwise.
$\tau $
fixing B pointwise.
Proof. Let
![]() $U_{A,B}$
consist of all functions f satisfying the stated condition (i.e.,
$U_{A,B}$
consist of all functions f satisfying the stated condition (i.e.,
![]() $f(\pi ) = f(\tau \pi \sigma )$
whenever
$f(\pi ) = f(\tau \pi \sigma )$
whenever
![]() $\sigma $
fixes A pointwise and
$\sigma $
fixes A pointwise and
![]() $\tau $
fixes B pointwise).
$\tau $
fixes B pointwise).
Let
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
. If
$b \in B$
. If
![]() $\sigma $
fixes a and
$\sigma $
fixes a and
![]() $\tau $
fixes b, then
$\tau $
fixes b, then
![]() $\pi (a) = b$
iff
$\pi (a) = b$
iff
![]() $\tau \pi \sigma (a) = b$
, showing that
$\tau \pi \sigma (a) = b$
, showing that
![]() $e_{ab} \in U_{A,B}$
. It follows that
$e_{ab} \in U_{A,B}$
. It follows that
![]() $V_{A,B} \subseteq U_{A,B}$
.
$V_{A,B} \subseteq U_{A,B}$
.
In the other direction, let
![]() $f \in U_{A,B}$
. Suppose for definiteness that
$f \in U_{A,B}$
. Suppose for definiteness that
![]() $A = [a]$
and
$A = [a]$
and
![]() $B = [b]$
. Let
$B = [b]$
. Let
![]() $\pi $
be a permutation such that
$\pi $
be a permutation such that
![]() $\pi (1) = 1, \ldots , \pi (t) = t$
, and
$\pi (1) = 1, \ldots , \pi (t) = t$
, and
![]() $\pi (i)> b$
for
$\pi (i)> b$
for
![]() $i=t+1,\ldots ,a$
. Applying a permutation fixing B pointwise on the left, we turn
$i=t+1,\ldots ,a$
. Applying a permutation fixing B pointwise on the left, we turn
![]() $\pi $
into a permutation
$\pi $
into a permutation
![]() $\pi '$
such that
$\pi '$
such that
![]() $\pi '(1),\ldots ,\pi '(a) = 1,\ldots ,t,b+1,\ldots ,b+(a-t)$
. Applying a permutation fixing A pointwise on the right, we turn
$\pi '(1),\ldots ,\pi '(a) = 1,\ldots ,t,b+1,\ldots ,b+(a-t)$
. Applying a permutation fixing A pointwise on the right, we turn
![]() $\pi '$
into the permutation
$\pi '$
into the permutation
![]() $1,\ldots ,t,b+1,\ldots ,b+(a-t),\ldots ,n,t+1,\ldots ,a$
. This shows that if
$1,\ldots ,t,b+1,\ldots ,b+(a-t),\ldots ,n,t+1,\ldots ,a$
. This shows that if
![]() $\pi _1,\pi _2$
are two permutations satisfying
$\pi _1,\pi _2$
are two permutations satisfying
![]() $e_{ab}(\pi _1) = e_{ab}(\pi _2)$
for all
$e_{ab}(\pi _1) = e_{ab}(\pi _2)$
for all
![]() $a \in A,b \in B$
, then we can find permutations
$a \in A,b \in B$
, then we can find permutations
![]() $\sigma _1,\sigma _2$
fixing A pointwise and permutations
$\sigma _1,\sigma _2$
fixing A pointwise and permutations
![]() $\tau _1,\tau _2$
fixing B pointwise such that
$\tau _1,\tau _2$
fixing B pointwise such that
![]() $\tau _1 \pi _1 \sigma _1 = \tau _2 \pi _2 \sigma _2$
, and so
$\tau _1 \pi _1 \sigma _1 = \tau _2 \pi _2 \sigma _2$
, and so
![]() $f(\pi _1) = f(\pi _2)$
. This shows that
$f(\pi _1) = f(\pi _2)$
. This shows that
![]() $f \in V_{A,B}$
.
$f \in V_{A,B}$
.
2.2 Hypercontractivity in product spaces
We will make use of the following hypercontractive inequality, essentially due to [Reference Keevash, Lifshitz, Long and Minzer18]. For that, we first remark that we consider the natural analog definitions of globalness for product spaces. Namely, for a finite product space
![]() $(\Omega ,\mu ) = (\Omega _1\times \dots \times \Omega _m,\mu _1\times \dots \times \mu _m)$
, we say that
$(\Omega ,\mu ) = (\Omega _1\times \dots \times \Omega _m,\mu _1\times \dots \times \mu _m)$
, we say that
![]() $f\colon \Omega \to \mathbb {R}$
is
$f\colon \Omega \to \mathbb {R}$
is
![]() $\varepsilon $
-global with a constant C, if for any
$\varepsilon $
-global with a constant C, if for any
![]() $T\subseteq [m]$
and
$T\subseteq [m]$
and
![]() $x\in \prod _{i\in T}\Omega _i$
, it holds that
$x\in \prod _{i\in T}\Omega _i$
, it holds that
![]() $\|f_{T\rightarrow x}\|_{2,\mu _x}\leqslant C^{|T|}\varepsilon $
, where
$\|f_{T\rightarrow x}\|_{2,\mu _x}\leqslant C^{|T|}\varepsilon $
, where
![]() $\mu _x$
is the distribution
$\mu _x$
is the distribution
![]() $\mu $
conditioned on coordinates of T being equal to x. Similarly, we say that f is
$\mu $
conditioned on coordinates of T being equal to x. Similarly, we say that f is
![]() $(d,\varepsilon )$
-global if for any
$(d,\varepsilon )$
-global if for any
![]() $|T|\leqslant d$
and
$|T|\leqslant d$
and
![]() $x\in \prod _{i\in T}\Omega _i$
, it holds that
$x\in \prod _{i\in T}\Omega _i$
, it holds that
![]() $\|f_{T\rightarrow x}\|_{2,\mu _x}\leqslant \varepsilon $
.
$\|f_{T\rightarrow x}\|_{2,\mu _x}\leqslant \varepsilon $
.
Theorem 2.5. Let
![]() $q\in \mathbb {N}$
be even, and suppose f is
$q\in \mathbb {N}$
be even, and suppose f is
![]() $\varepsilon $
-global with constant C, and let
$\varepsilon $
-global with constant C, and let
![]() $\rho \leqslant \frac {1}{(10qC)^2}$
. Then
$\rho \leqslant \frac {1}{(10qC)^2}$
. Then
![]() $\|\mathrm {T}_{\rho }f\|_{q}\leqslant \varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
$\|\mathrm {T}_{\rho }f\|_{q}\leqslant \varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
A variant of Theorem 2.5 appears in [Reference Keevash, Lifshitz, Long and Minzer17, Lemma 7.9]. This version differs from Theorem 2.5 in two regards: it is for
![]() $C = 1$
, and it works only when
$C = 1$
, and it works only when
![]() $|\Omega _i| = 2$
. The version for general C follows by first applying
$|\Omega _i| = 2$
. The version for general C follows by first applying
![]() $T_{1/C}$
. The proof of [Reference Keevash, Lifshitz, Long and Minzer18, Lemma 5.15] shows how to reduce the setting of general
$T_{1/C}$
. The proof of [Reference Keevash, Lifshitz, Long and Minzer18, Lemma 5.15] shows how to reduce the setting of general
![]() $\Omega $
to the setting of [Reference Keevash, Lifshitz, Long and Minzer17].
$\Omega $
to the setting of [Reference Keevash, Lifshitz, Long and Minzer17].
3 Hypercontractivity: The coupling approach
3.1 Hypercontractivity from full globalness
In this section, we prove the following hypercontractive results for our operator
![]() $\mathrm {T}^{\left (\rho \right )}$
assuming f is global. We begin by proving two simple propositions.
$\mathrm {T}^{\left (\rho \right )}$
assuming f is global. We begin by proving two simple propositions.
Proposition 3.1. Suppose
![]() $f\colon S_n\to \mathbb {R}$
is
$f\colon S_n\to \mathbb {R}$
is
![]() $\varepsilon $
-global with constant C and let
$\varepsilon $
-global with constant C and let
![]() $g=\mathrm {T}_{S_{n}\to L^{m}}f$
. Then g is
$g=\mathrm {T}_{S_{n}\to L^{m}}f$
. Then g is
![]() $\varepsilon $
-global with constant C.
$\varepsilon $
-global with constant C.
Proof. Let S be a set of size t and let
![]() $x=\big ((i_{k},j_{k})\big )_{k\in S}\in L^{S}$
. Let
$x=\big ((i_{k},j_{k})\big )_{k\in S}\in L^{S}$
. Let
![]() $y\sim L^{\left [m\right ]\setminus S}$
be chosen uniformly and let
$y\sim L^{\left [m\right ]\setminus S}$
be chosen uniformly and let
![]() $\sigma $
be the random permutation that our coupling process outputs given
$\sigma $
be the random permutation that our coupling process outputs given
![]() $\left (x,y\right )$
. We have
$\left (x,y\right )$
. We have
by Cauchy–Schwarz. Next, we consider the values of
![]() $\sigma \left (i_{k}\right )$
for
$\sigma \left (i_{k}\right )$
for
![]() $k\in S$
, condition on them and denote
$k\in S$
, condition on them and denote
![]() $T=\left \{ \left (i_{k},\sigma (i_k)\right )\right \} $
. The conditional distribution of
$T=\left \{ \left (i_{k},\sigma (i_k)\right )\right \} $
. The conditional distribution of
![]() $\sigma $
given T is uniform by the symmetry of elements in
$\sigma $
given T is uniform by the symmetry of elements in
![]() $\left [n\right ]\setminus \left \{ i_{k}|\,k\in S\right \}$
, so for any permutation
$\left [n\right ]\setminus \left \{ i_{k}|\,k\in S\right \}$
, so for any permutation
![]() $\pi $
on
$\pi $
on
![]() $\left [n\right ]\setminus \left \{ i_{k}|\,k\in S\right \}$
, we have that
$\left [n\right ]\setminus \left \{ i_{k}|\,k\in S\right \}$
, we have that
![]() $\sigma \pi $
has the same probability as
$\sigma \pi $
has the same probability as
![]() $\sigma $
. Also, the collection
$\sigma $
. Also, the collection
![]() $\{\sigma \pi \}$
consists of all permutations satisfying T, so
$\{\sigma \pi \}$
consists of all permutations satisfying T, so
Fact 3.2. Suppose that we are given two probability spaces
![]() $\left (X,\mu _{X}\right ),\left (Y,\mu _{Y}\right )$
. Suppose further that for each
$\left (X,\mu _{X}\right ),\left (Y,\mu _{Y}\right )$
. Suppose further that for each
![]() $x\in X$
, we have a distribution
$x\in X$
, we have a distribution
![]() $N\left (x\right )$
on Y, such that if we choose
$N\left (x\right )$
on Y, such that if we choose
![]() $x\sim \mu _{X}$
and
$x\sim \mu _{X}$
and
![]() $y\sim N\left (x\right )$
, then the marginal distribution of y is
$y\sim N\left (x\right )$
, then the marginal distribution of y is
![]() $\mu _{Y}$
. Define an operator
$\mu _{Y}$
. Define an operator
![]() $\mathrm {T}_{Y\to X}\colon L^{2}\left (Y\right )\to L^{2}\left (X\right )$
by setting
$\mathrm {T}_{Y\to X}\colon L^{2}\left (Y\right )\to L^{2}\left (X\right )$
by setting
Then
![]() $\|\mathrm {T}_{Y\to X}f\|_{q}\leqslant \|f\|_{q}$
for each
$\|\mathrm {T}_{Y\to X}f\|_{q}\leqslant \|f\|_{q}$
for each
![]() $q\geqslant 1$
.
$q\geqslant 1$
.
We can now prove one variant of our hypercontractive inequality for global functions over the symmetric group.
Theorem 3.3. Let
![]() $q\in \mathbb {N}$
be even,
$q\in \mathbb {N}$
be even,
![]() $C,\varepsilon>0$
, and
$C,\varepsilon>0$
, and
![]() $\rho \leqslant \frac {1}{(10qC)^2}$
. If
$\rho \leqslant \frac {1}{(10qC)^2}$
. If
![]() $f\colon S_{n}\to \mathbb {R}$
is
$f\colon S_{n}\to \mathbb {R}$
is
![]() $\varepsilon $
-global with constant C, then
$\varepsilon $
-global with constant C, then
![]() $\left \|\mathrm {T}^{\left (\rho \right )}f\right \|_{q}\leqslant \varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
$\left \|\mathrm {T}^{\left (\rho \right )}f\right \|_{q}\leqslant \varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
Proof. Let
![]() $f\colon S_n\to \mathbb {R}$
be
$f\colon S_n\to \mathbb {R}$
be
![]() $\varepsilon $
-global with constant C. By Proposition 3.1, the function
$\varepsilon $
-global with constant C. By Proposition 3.1, the function
![]() $g=\mathrm {T}_{S_{n}\to L^{m}}f$
is also
$g=\mathrm {T}_{S_{n}\to L^{m}}f$
is also
![]() $\varepsilon $
-constant with constant C, and by Fact 3.2, we have
$\varepsilon $
-constant with constant C, and by Fact 3.2, we have
Now by Theorem 2.5 we may upper-bound the last norm by
![]() $\varepsilon ^{q-2}\|g\|_{2}^{2}$
, and using Fact 3.2 again, we may bound
$\varepsilon ^{q-2}\|g\|_{2}^{2}$
, and using Fact 3.2 again, we may bound
![]() $\left \|g\right \|_2^2\leqslant \left \|f\right \|_2^2$
.
$\left \|g\right \|_2^2\leqslant \left \|f\right \|_2^2$
.
Remark 3.4. Once the statement has been proven for even q’s, a qualitatively similar statement can be automatically deduced for all q’s, as follows. Fix q and take the smallest
![]() $q\leqslant q'\leqslant q+2$
that is an even integer. Then for
$q\leqslant q'\leqslant q+2$
that is an even integer. Then for
![]() $\rho \leqslant \frac {1}{(10(q+2)C)^2}\leqslant \frac {1}{(10q'C)^2}$
, we may bound
$\rho \leqslant \frac {1}{(10(q+2)C)^2}\leqslant \frac {1}{(10q'C)^2}$
, we may bound
where in the last inequality we used
![]() $q'\leqslant q+2$
and
$q'\leqslant q+2$
and
![]() $\left \|f\right \|_2\leqslant \varepsilon $
.
$\left \|f\right \|_2\leqslant \varepsilon $
.
3.2 Hypercontractivity for low-degree functions
Next, we use Theorem 3.3 to prove our hypercontractive inequality for low-degree functions that assumes considerably weaker globalness properties of f – namely, Theorem 1.4. The proof of the above theorem makes use of the following key lemmas. The first of which asserts that just like in the cube, bounded globalness of a low-degree function implies (full) globalness.
Lemma 3.5. Suppose
![]() $n\geqslant Cd\log d$
for a sufficiently large constant C. Let
$n\geqslant Cd\log d$
for a sufficiently large constant C. Let
![]() $f\colon S_n\to \mathbb {R}$
be a
$f\colon S_n\to \mathbb {R}$
be a
![]() $\left (2d,\varepsilon \right )$
-global function of degree d. Then, f is
$\left (2d,\varepsilon \right )$
-global function of degree d. Then, f is
![]() $\varepsilon $
-global with constant
$\varepsilon $
-global with constant
![]() $4^8$
.
$4^8$
.
Thus, to deduce Theorem 1.4 from Theorem 3.3, it suffices to show that f may be approximated by linear combinations of
![]() $\mathrm {T}^{(\rho ^i)} f$
for
$\mathrm {T}^{(\rho ^i)} f$
for
![]() $i=1,2,\ldots $
in
$i=1,2,\ldots $
in
![]() $L^q$
, and this is the content of our second lemma. First, let us introduce some convenient notations. For a polynomial
$L^q$
, and this is the content of our second lemma. First, let us introduce some convenient notations. For a polynomial
![]() $P(z)=a_{0}+a_{1}z+\cdots +a_{k}z^k$
, we denote the spectral norm of P by
$P(z)=a_{0}+a_{1}z+\cdots +a_{k}z^k$
, we denote the spectral norm of P by
![]() $\|P\|=\sum _{i=0}^{k}\left |a_{i}\right |$
. We remark that it is easily seen that
$\|P\|=\sum _{i=0}^{k}\left |a_{i}\right |$
. We remark that it is easily seen that
![]() $\|P_{1}P_{2}\|\leqslant \|P_{1}\|\|P_{2}\|$
for any two polynomials
$\|P_{1}P_{2}\|\leqslant \|P_{1}\|\|P_{2}\|$
for any two polynomials
![]() $P_1,P_2$
.
$P_1,P_2$
.
Lemma 3.6. Let
![]() $n\geqslant C^{d^{3}}q^{-Cd}$
for a sufficiently large constant C and let
$n\geqslant C^{d^{3}}q^{-Cd}$
for a sufficiently large constant C and let
![]() $\rho =1/(400 C^3q^2)$
. Then there exists a polynomial P satisfying
$\rho =1/(400 C^3q^2)$
. Then there exists a polynomial P satisfying
![]() $P\left (0\right )=0$
and
$P\left (0\right )=0$
and
![]() $\|P\|\leqslant q^{O\left (d^{3}\right )}$
, such that
$\|P\|\leqslant q^{O\left (d^{3}\right )}$
, such that
for every function f of degree at most d.
We defer the proofs of Lemmas 3.5 and 3.6 to Sections 4 and 5, respectively. In the remainder of this section, we derive Theorem 1.4 from them, restated below.
Theorem 1.4 (Restated).
There exists
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() $q\in \mathbb {N}$
be even,
$q\in \mathbb {N}$
be even,
![]() $n\geqslant q^{C\cdot d^{2}}$
. If f is a
$n\geqslant q^{C\cdot d^{2}}$
. If f is a
![]() $\left (2d,\varepsilon \right )$
-global function of degree d, then
$\left (2d,\varepsilon \right )$
-global function of degree d, then
![]() $\|f\|_{q}\leqslant q^{O\left (d^{3}\right )}\varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
$\|f\|_{q}\leqslant q^{O\left (d^{3}\right )}\varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
.
Proof. Choose
![]() $\rho = 1/(400 C^3 q^2)$
and let P be as in Lemma 3.6. Then
$\rho = 1/(400 C^3 q^2)$
and let P be as in Lemma 3.6. Then
As for the first term, we have
 $$\begin{align*}\left\|\sum_{i=1}^{l}a_{i}\left(\mathrm{T}^{\left(\rho\right)}\right)^{i}f\right\|_{q} \leqslant \sum_{i=1}^{l}\left|a_{i}\right|\left\|\left(\mathrm{T}^{\left(\rho\right)}\right)^{i}f\right\|_{q} \leqslant \left\|P\right\|\left\|\mathrm{T}^{\left(\rho\right)}f\right\|_{q} \leqslant q^{O\left(d^{3}\right)} \left\|\mathrm{T}^{\left(\rho\right)}f\right\|_{q}. \end{align*}$$
$$\begin{align*}\left\|\sum_{i=1}^{l}a_{i}\left(\mathrm{T}^{\left(\rho\right)}\right)^{i}f\right\|_{q} \leqslant \sum_{i=1}^{l}\left|a_{i}\right|\left\|\left(\mathrm{T}^{\left(\rho\right)}\right)^{i}f\right\|_{q} \leqslant \left\|P\right\|\left\|\mathrm{T}^{\left(\rho\right)}f\right\|_{q} \leqslant q^{O\left(d^{3}\right)} \left\|\mathrm{T}^{\left(\rho\right)}f\right\|_{q}. \end{align*}$$
To estimate
![]() $\left \|\mathrm {T}^{\left (\rho \right )}f\right \|_{q}$
, note first that by Lemma 3.5, f is
$\left \|\mathrm {T}^{\left (\rho \right )}f\right \|_{q}$
, note first that by Lemma 3.5, f is
![]() $\varepsilon $
-global for constant
$\varepsilon $
-global for constant
![]() $4^8$
; thus, given that C is large enough, we may apply Theorem 3.3 to deduce that
$4^8$
; thus, given that C is large enough, we may apply Theorem 3.3 to deduce that
![]() $\left \|\mathrm {T}^{\left (\rho \right )}f\right \|_{q}\leqslant \varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
. As
$\left \|\mathrm {T}^{\left (\rho \right )}f\right \|_{q}\leqslant \varepsilon ^{\frac {q-2}{q}}\|f\|_{2}^{\frac {2}{q}}$
. As
![]() $\|f\|_{2}\leqslant \varepsilon $
, we conclude that
$\|f\|_{2}\leqslant \varepsilon $
, we conclude that
4 Proof of Lemma 3.5
We begin by proving Lemma 3.5. A proof of the corresponding statement in product spaces proceeds by showing that a function is
![]() $(d,\varepsilon )$
-global if and only if the
$(d,\varepsilon )$
-global if and only if the
![]() $2$
-norms of derivatives of f of order d are small. Since then derivatives of order higher than d of f are automatically
$2$
-norms of derivatives of f of order d are small. Since then derivatives of order higher than d of f are automatically
![]() $0$
(by degree considerations), they are automatically small. Thus, if f is a
$0$
(by degree considerations), they are automatically small. Thus, if f is a
![]() $(d,\varepsilon )$
-global function of degree d, then all derivatives of f have small
$(d,\varepsilon )$
-global function of degree d, then all derivatives of f have small
![]() $2$
-norm, and by the reverse relation it follows that f is
$2$
-norm, and by the reverse relation it follows that f is
![]() $\varepsilon $
-global for some constant C.
$\varepsilon $
-global for some constant C.
Our proof follows a similar high-level idea. The main challenge in the proof is to find an appropriate analog of discrete derivatives from product spaces that both reduces the degree of the function f and can be related to restrictions of f. Towards this end, we make the following key definition.
Definition 4.1. Let
![]() $i_{1}\ne i_{2}\in \left [n\right ]$
and
$i_{1}\ne i_{2}\in \left [n\right ]$
and
![]() $j_{1}\ne j_{2}\in \left [n\right ]$
.
$j_{1}\ne j_{2}\in \left [n\right ]$
.
-
1. The Laplacian of f along
 $(i_1,i_2)$
is defined as
$(i_1,i_2)$
is defined as
 $\mathrm {L}_{\left (i_{1},i_{2}\right )}\left [f\right ]=f-f^{\left (i_{1}\,i_{2}\right )}$
, where we denote by
$\mathrm {L}_{\left (i_{1},i_{2}\right )}\left [f\right ]=f-f^{\left (i_{1}\,i_{2}\right )}$
, where we denote by
 $\left (i_{1}\,i_{2}\right )$
the transposition of
$\left (i_{1}\,i_{2}\right )$
the transposition of
 $i_1$
and
$i_1$
and
 $i_2$
.
$i_2$
. -
2. The derivative of f along
 $(i_1,i_2)\rightarrow (j_1,j_2)$
is
$(i_1,i_2)\rightarrow (j_1,j_2)$
is
 $(\mathrm {L}_{\left (i_{1},i_{2}\right )}f)_{(i_1,i_2)\rightarrow (j_1,j_2)}$
. More explicity, it is a function defined on
$(\mathrm {L}_{\left (i_{1},i_{2}\right )}f)_{(i_1,i_2)\rightarrow (j_1,j_2)}$
. More explicity, it is a function defined on
 $S_n^{{(i_1,j_1),(i_2,j_2)}}$
(that is isomorphic to
$S_n^{{(i_1,j_1),(i_2,j_2)}}$
(that is isomorphic to
 $S_{n-2}$
) whose value on
$S_{n-2}$
) whose value on
 $\pi $
is
$\pi $
is  $$\begin{align*}f(\pi) - f(\pi\circ (i_1,i_2)). \end{align*}$$
$$\begin{align*}f(\pi) - f(\pi\circ (i_1,i_2)). \end{align*}$$
-
3. For distinct
 $i_1,\ldots ,i_t$
and distinct
$i_1,\ldots ,i_t$
and distinct
 $j_1,\ldots ,j_t$
, let S be the sequence
$j_1,\ldots ,j_t$
, let S be the sequence
 $\left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )$
and define the Laplacian of f along S as
$\left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )$
and define the Laplacian of f along S as
 $L_{S}\left [f\right ]=L_{i_{1},j_{1}}\circ \cdots \circ L_{i_{t},j_{t}}\circ f$
.
$L_{S}\left [f\right ]=L_{i_{1},j_{1}}\circ \cdots \circ L_{i_{t},j_{t}}\circ f$
.For
 $(k_1,\ell _1),\ldots ,(k_t,\ell _t)$
, the derivative of f along
$(k_1,\ell _1),\ldots ,(k_t,\ell _t)$
, the derivative of f along
 $S\rightarrow (k_1,\ell _1),\ldots ,(k_t,\ell _t)$
is
$S\rightarrow (k_1,\ell _1),\ldots ,(k_t,\ell _t)$
is  $$\begin{align*}\mathrm{D}_{S\to \left(k_{1},\ell_{1}\right),\ldots,\left(k_{t},\ell_{t}\right) } f= \left(L_{S}\left[f\right]\right)_{S\rightarrow \left(i_{1},k_{1}\right),\left(j_{1},\ell_{1}\right),\ldots,\left(i_{t},k_{t}\right),\left(j_{t},\ell_{t}\right). } \end{align*}$$
$$\begin{align*}\mathrm{D}_{S\to \left(k_{1},\ell_{1}\right),\ldots,\left(k_{t},\ell_{t}\right) } f= \left(L_{S}\left[f\right]\right)_{S\rightarrow \left(i_{1},k_{1}\right),\left(j_{1},\ell_{1}\right),\ldots,\left(i_{t},k_{t}\right),\left(j_{t},\ell_{t}\right). } \end{align*}$$
We call
 $\mathrm {D}$
a derivative of order t. We also include the case where
$\mathrm {D}$
a derivative of order t. We also include the case where
 $t=0$
and call the identity operator a
$t=0$
and call the identity operator a
 $0$
-derivative.
$0$
-derivative.
The following two claims show that the definition of derivatives above is good, in the sense that
![]() $2$
-norms of derivatives relate to globalness, and derivatives indeed reduce the degree of f.
$2$
-norms of derivatives relate to globalness, and derivatives indeed reduce the degree of f.
Claim 4.2. Let
![]() $t\in \mathbb {N}$
, and
$t\in \mathbb {N}$
, and
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $f\colon S_{n}\to \mathbb {R}$
.
$f\colon S_{n}\to \mathbb {R}$
.
-
1. If f is
 $(2t,\varepsilon )$
-global, then for each derivative
$(2t,\varepsilon )$
-global, then for each derivative
 $\mathrm {D}$
of order t, we have that
$\mathrm {D}$
of order t, we have that
 $\left \|\mathrm {D} f\right \|_2\leqslant 2^{t} \varepsilon $
.
$\left \|\mathrm {D} f\right \|_2\leqslant 2^{t} \varepsilon $
. -
2. If
 $t\leqslant n/2$
, and for all
$t\leqslant n/2$
, and for all
 $\ell \leqslant t$
and every derivative
$\ell \leqslant t$
and every derivative
 $\mathrm {D}$
of order
$\mathrm {D}$
of order
 $\ell $
, we have that
$\ell $
, we have that
 $\left \|\mathrm {D} f\right \|_2\leqslant \varepsilon $
, then f is
$\left \|\mathrm {D} f\right \|_2\leqslant \varepsilon $
, then f is
 $(t,2^t \varepsilon )$
-global.
$(t,2^t \varepsilon )$
-global.
Proof. To prove the first item, observe that
![]() $\mathrm {D}f$
is a signed sum of
$\mathrm {D}f$
is a signed sum of
![]() $2^t$
functions of the form
$2^t$
functions of the form
![]() $f^\sigma _{\to T}$
, where
$f^\sigma _{\to T}$
, where
![]() $|T| = 2t$
. Globalness of f implies that
$|T| = 2t$
. Globalness of f implies that
![]() $\left \|f^\sigma _{\to T}\right \|_2 \leqslant \varepsilon $
, and so
$\left \|f^\sigma _{\to T}\right \|_2 \leqslant \varepsilon $
, and so
![]() $\left \|\mathrm {D} f\right \|_2 \leqslant 2^t \varepsilon $
by the triangle inequality.
$\left \|\mathrm {D} f\right \|_2 \leqslant 2^t \varepsilon $
by the triangle inequality.
The rest of the proof is devoted to establishing the second item, also by induction on t.
Base case
![]() $\boldsymbol{t=0,1}$
.
$\boldsymbol{t=0,1}$
.
The case
![]() $t=0$
is trivial, and we prove the case
$t=0$
is trivial, and we prove the case
![]() $t=1$
. Let
$t=1$
. Let
![]() $i_{1},i_{2}\in \left [n\right ]$
be distinct and let
$i_{1},i_{2}\in \left [n\right ]$
be distinct and let
![]() $j_{1},j_{2}\in \left [n\right ]$
be distinct. Since
$j_{1},j_{2}\in \left [n\right ]$
be distinct. Since
![]() $\|\mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}f\|_2\leqslant \varepsilon $
, we get from the triangle inequality that
$\|\mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}f\|_2\leqslant \varepsilon $
, we get from the triangle inequality that
Multiplying (3) by
![]() $\|f_{i_{1}\to j{}_{1},i_{2}\to j_{2}}\|_{2}+\|f_{i_{2}\to j_{1},i_{1}\to j_{2}}\|_{2}$
, we get that
$\|f_{i_{1}\to j{}_{1},i_{2}\to j_{2}}\|_{2}+\|f_{i_{2}\to j_{1},i_{1}\to j_{2}}\|_{2}$
, we get that
Taking average over
![]() $j_{2}$
and using the triangle inequality on the left-hand side, we get that
$j_{2}$
and using the triangle inequality on the left-hand side, we get that
By Cauchy–Schwarz,
![]() $\mathbb {E}_{j_{2}}\left [\|f_{i_{1}\to j{}_{1},i_{2}\to j_{2}}\|_{2}\right ]\leqslant \mathbb {E}_{j_{2}}\left [\|f_{i_{1}\to j{}_{1},i_{2}\to j_{2}}\|_{2}^2\right ]^{1/2} =\|f_{i_{1}\to j{}_{1}}\|_{2}$
, and similarly for the other term, so we conclude
$\mathbb {E}_{j_{2}}\left [\|f_{i_{1}\to j{}_{1},i_{2}\to j_{2}}\|_{2}\right ]\leqslant \mathbb {E}_{j_{2}}\left [\|f_{i_{1}\to j{}_{1},i_{2}\to j_{2}}\|_{2}^2\right ]^{1/2} =\|f_{i_{1}\to j{}_{1}}\|_{2}$
, and similarly for the other term, so we conclude
and dividing both sides of the inequality by
![]() $\|f_{i_{1}\to j_{1}}\|_{2}+\|f_{i_{2}\to j_{1}}\|_{2}$
, we get
$\|f_{i_{1}\to j_{1}}\|_{2}+\|f_{i_{2}\to j_{1}}\|_{2}$
, we get
Since
![]() $\mathbb {E}_{i_{2}\sim \left [n\right ]}\|f_{i_{2}\to j_{1}}\|_{2}^{2}=\|f\|_{2}^{2}\leqslant \varepsilon $
, we get that there is
$\mathbb {E}_{i_{2}\sim \left [n\right ]}\|f_{i_{2}\to j_{1}}\|_{2}^{2}=\|f\|_{2}^{2}\leqslant \varepsilon $
, we get that there is
![]() $i_2$
such that
$i_2$
such that
![]() $\|f_{i_{2}\to j_{1}}\|_{2}\leqslant \varepsilon $
, and the above inequality implies that
$\|f_{i_{2}\to j_{1}}\|_{2}\leqslant \varepsilon $
, and the above inequality implies that
![]() $\|f_{i_{1}\to j_{1}}\|_{2}\leqslant 2\varepsilon $
for all
$\|f_{i_{1}\to j_{1}}\|_{2}\leqslant 2\varepsilon $
for all
![]() $i_1$
. This completes the proof for the case
$i_1$
. This completes the proof for the case
![]() $t=1$
.
$t=1$
.
The inductive step.
Let
![]() $t>1$
. We prove that f is
$t>1$
. We prove that f is
![]() $\left (t,2^{t}\varepsilon \right )$
-global, or equivalently that
$\left (t,2^{t}\varepsilon \right )$
-global, or equivalently that
![]() $f_{\to T}$
is
$f_{\to T}$
is
![]() $\left (1,2^{t}\varepsilon \right )$
-global for all consistent sets T of size
$\left (1,2^{t}\varepsilon \right )$
-global for all consistent sets T of size
![]() $t-1$
. Indeed, fix a consistent T of size
$t-1$
. Indeed, fix a consistent T of size
![]() $t-1$
.
$t-1$
.
By the induction hypothesis,
![]() $\|f_{\to T}\|_{2}\leqslant 2^{t-1}\varepsilon $
, and the claim would follow from the
$\|f_{\to T}\|_{2}\leqslant 2^{t-1}\varepsilon $
, and the claim would follow from the
![]() $t=1$
case once we show that
$t=1$
case once we show that
![]() $\|\mathrm {D}f_{\rightarrow T}\|_{2}\leqslant 2^{t-1}\varepsilon $
for all order
$\|\mathrm {D}f_{\rightarrow T}\|_{2}\leqslant 2^{t-1}\varepsilon $
for all order
![]() $1$
derivatives
$1$
derivatives
![]() $\mathrm {D}=\mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}$
, where
$\mathrm {D}=\mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}$
, where
![]() $i_{1},i_{2}$
do not appear as the first coordinate of an element in T, and
$i_{1},i_{2}$
do not appear as the first coordinate of an element in T, and
![]() $j_{1},j_{2}$
do not appear as a second coordinate of an element of T (we are using the fact here that the case
$j_{1},j_{2}$
do not appear as a second coordinate of an element of T (we are using the fact here that the case
![]() $t=1$
applies, as
$t=1$
applies, as
![]() $S_{n}^{T}$
is isomorphic to
$S_{n}^{T}$
is isomorphic to
![]() $S_{n-\left |T\right |}$
as
$S_{n-\left |T\right |}$
as
![]() $S_{n-\left |T\right |}$
-bimodules). Fix such
$S_{n-\left |T\right |}$
-bimodules). Fix such
![]() $\mathrm {D}$
and let
$\mathrm {D}$
and let
![]() $g=\mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}f$
. By hypothesis, for any order
$g=\mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}f$
. By hypothesis, for any order
![]() $t-1$
derivative
$t-1$
derivative
![]() $\tilde {\mathrm {D}}$
, we have that
$\tilde {\mathrm {D}}$
, we have that
![]() $\|\tilde {\mathrm {D}}g\|_{2}\leqslant \varepsilon $
, hence by the induction hypothesis
$\|\tilde {\mathrm {D}}g\|_{2}\leqslant \varepsilon $
, hence by the induction hypothesis
![]() $\|g{}_{\rightarrow T}\|_{2}\leqslant 2^{t-1}\varepsilon $
. Since restrictions and derivatives commute, we have
$\|g{}_{\rightarrow T}\|_{2}\leqslant 2^{t-1}\varepsilon $
. Since restrictions and derivatives commute, we have
![]() $g{}_{\rightarrow T} = \mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}f_{\rightarrow T}$
, and we conclude that
$g{}_{\rightarrow T} = \mathrm {D}_{\left (i_{1},i_{2}\right )\to \left (j_{1},j_{2}\right )}f_{\rightarrow T}$
, and we conclude that
![]() $f_{\rightarrow T}$
is
$f_{\rightarrow T}$
is
![]() $\left (1,2^{t}\varepsilon \right )$
-global, as desired.
$\left (1,2^{t}\varepsilon \right )$
-global, as desired.
Claim 4.3. If f is of degree d, and
![]() $\mathrm {D}$
is a t-derivative, then
$\mathrm {D}$
is a t-derivative, then
![]() $\mathrm {D}f$
is of degree
$\mathrm {D}f$
is of degree
![]() $\leqslant d-t$
.
$\leqslant d-t$
.
Proof. It is sufficient to consider the case
![]() $t=1$
of the proposition, as we may apply it repeatedly. By linearity of the derivative
$t=1$
of the proposition, as we may apply it repeatedly. By linearity of the derivative
![]() $\mathrm {D}$
, it is enough to show it in the case where
$\mathrm {D}$
, it is enough to show it in the case where
![]() $f=e_{i_{1} j_{1}}\cdots e_{i_{t} j_{t}}$
. Now note that the Laplacian
$f=e_{i_{1} j_{1}}\cdots e_{i_{t} j_{t}}$
. Now note that the Laplacian
![]() $L_{(k_{1}k_{2})}$
annihilates f unless either
$L_{(k_{1}k_{2})}$
annihilates f unless either
![]() $k_{1}$
is equal to some
$k_{1}$
is equal to some
![]() $i_{\ell }$
, or
$i_{\ell }$
, or
![]() $k_{2}$
is equal to some
$k_{2}$
is equal to some
![]() $i_{\ell }$
, or both, and we only have to consider these cases. Each derivative corresponding to the Laplacian
$i_{\ell }$
, or both, and we only have to consider these cases. Each derivative corresponding to the Laplacian
![]() $L_{(k_1,k_2)}$
restricts both the image of
$L_{(k_1,k_2)}$
restricts both the image of
![]() $k_{1}$
and the image of
$k_{1}$
and the image of
![]() $k_{2}$
, so after applying this restriction on
$k_{2}$
, so after applying this restriction on
![]() $L_{(k_1,k_2)} f$
, we either get the
$L_{(k_1,k_2)} f$
, we either get the
![]() $0$
function, a function of degree
$0$
function, a function of degree
![]() $d-1$
or a function of degree
$d-1$
or a function of degree
![]() $d-2$
.
$d-2$
.
We are now ready to prove Lemma 3.5. To prove that f is global, we handle restrictions of size
![]() $t\leqslant n/2$
and restrictions of size
$t\leqslant n/2$
and restrictions of size
![]() $t>n/2$
separately in the following two claims.
$t>n/2$
separately in the following two claims.
Claim 4.4. Suppose
![]() $f\colon S_n\to \mathbb {R}$
is a
$f\colon S_n\to \mathbb {R}$
is a
![]() $\left (2d,\varepsilon \right )$
-global function of degree d. Then f is
$\left (2d,\varepsilon \right )$
-global function of degree d. Then f is
![]() $\left (t,4^{t}\varepsilon \right )$
-global for each
$\left (t,4^{t}\varepsilon \right )$
-global for each
![]() $t\leqslant \frac {n}{2}$
.
$t\leqslant \frac {n}{2}$
.
Proof. By the second item in Claim 4.2, it is enough to show that for each t-derivative
![]() $\mathrm {D}$
, we have
$\mathrm {D}$
, we have
![]() $\|\mathrm {D}f\|_{2}\leqslant 2^{t}\varepsilon $
. For
$\|\mathrm {D}f\|_{2}\leqslant 2^{t}\varepsilon $
. For
![]() $t\leqslant d$
, this follows from the first item in Claim 4.2, and for
$t\leqslant d$
, this follows from the first item in Claim 4.2, and for
![]() $t>d$
, it follows from Proposition 4.3 as we have that
$t>d$
, it follows from Proposition 4.3 as we have that
![]() $\mathrm {D} f = 0$
for all derivatives of order t.
$\mathrm {D} f = 0$
for all derivatives of order t.
For
![]() $t\geqslant \frac {n}{2}$
, we use the obvious fact f is always
$t\geqslant \frac {n}{2}$
, we use the obvious fact f is always
![]() $\left (t,\|f\|_{\infty }\right )$
-global and upper-bound the infinity norm of f using the following claim.
$\left (t,\|f\|_{\infty }\right )$
-global and upper-bound the infinity norm of f using the following claim.
Claim 4.5. Let f be a
![]() $\left (2d,\varepsilon \right )$
-global function of degree d. Then
$\left (2d,\varepsilon \right )$
-global function of degree d. Then
![]() $\|f\|_{\infty }\leqslant \sqrt {\left (6d\right )!}4^{3n}\varepsilon $
.
$\|f\|_{\infty }\leqslant \sqrt {\left (6d\right )!}4^{3n}\varepsilon $
.
Proof. We prove the claim by induction on n. The case
![]() $n=1$
is obvious, so let
$n=1$
is obvious, so let
![]() $n>1$
.
$n>1$
.
If
![]() $3d\leqslant \frac {n}{2}$
, then by Claim 4.4 we have that f is
$3d\leqslant \frac {n}{2}$
, then by Claim 4.4 we have that f is
![]() $\left (3d,4^{3d}\varepsilon \right )$
-global, and hence for each set S of size d, the function
$\left (3d,4^{3d}\varepsilon \right )$
-global, and hence for each set S of size d, the function
![]() $f_{\rightarrow S}$
is
$f_{\rightarrow S}$
is
![]() $\left (2d,4^{3d}\varepsilon \right )$
-global. Therefore, the induction hypothesis implies that
$\left (2d,4^{3d}\varepsilon \right )$
-global. Therefore, the induction hypothesis implies that
Suppose now that
![]() $n\leqslant 6d$
. Then
$n\leqslant 6d$
. Then
![]() $\|f\|_{\infty }^{2}\leqslant \left (6d\right )!\|f\|_{2}^{2}$
since the probability of each atom in
$\|f\|_{\infty }^{2}\leqslant \left (6d\right )!\|f\|_{2}^{2}$
since the probability of each atom in
![]() $S_{6d}$
is
$S_{6d}$
is
![]() $\frac {1}{\left (6d\right )!}$
. Hence,
$\frac {1}{\left (6d\right )!}$
. Hence,
![]() $\|f\|_{\infty }\leqslant \sqrt {\left (6d\right )!}\varepsilon $
.
$\|f\|_{\infty }\leqslant \sqrt {\left (6d\right )!}\varepsilon $
.
Note that
![]() $(6d)!\leqslant 4^n$
given C is sufficiently large, so for
$(6d)!\leqslant 4^n$
given C is sufficiently large, so for
![]() $t>n/2$
, Claim 4.5 implies that f is
$t>n/2$
, Claim 4.5 implies that f is
![]() $(t, 4^{4n}\varepsilon ) = (t, 4^{8t}\varepsilon )$
-global.
$(t, 4^{4n}\varepsilon ) = (t, 4^{8t}\varepsilon )$
-global.
5 Proof of Lemma 3.6
Proof overview.
Our argument first constructs, in Section 5.4, a very strong approximating polynomial in the
![]() $L_2$
-norm. As we show in Section 5.5, the approximation will in fact be strong enough to imply, in a black-box way, that it is also an approximating polynomial in
$L_2$
-norm. As we show in Section 5.5, the approximation will in fact be strong enough to imply, in a black-box way, that it is also an approximating polynomial in
![]() $L_q$
.
$L_q$
.
To construct an
![]() $L_2$
approximating polynomial, we use spectral considerations. Lemma 5.4 shows that
$L_2$
approximating polynomial, we use spectral considerations. Lemma 5.4 shows that
![]() $\mathrm {T}^{(\rho )}$
preserves the space of degree d functions. Denote by
$\mathrm {T}^{(\rho )}$
preserves the space of degree d functions. Denote by
![]() $\lambda _1,\ldots ,\lambda _{\ell }$
the eigenvalues of
$\lambda _1,\ldots ,\lambda _{\ell }$
the eigenvalues of
![]() $\mathrm {T}^{(\rho )}$
on the space of degree d functions. Note that if P is a polynomial such that
$\mathrm {T}^{(\rho )}$
on the space of degree d functions. Note that if P is a polynomial such that
![]() $P(\lambda _i) = 1$
for all i, then
$P(\lambda _i) = 1$
for all i, then
![]() $P(\mathrm {T}^{\rho }) f = f$
for all f of degree d. However, as
$P(\mathrm {T}^{\rho }) f = f$
for all f of degree d. However, as
![]() $\ell $
may be very large, there may not be a polynomial P with small
$\ell $
may be very large, there may not be a polynomial P with small
![]() $\left \|P\right \|$
satisfying
$\left \|P\right \|$
satisfying
![]() $P(\lambda _i) = 1$
for all i, and to circumvent this issue, we must argue that, at least effectively,
$P(\lambda _i) = 1$
for all i, and to circumvent this issue, we must argue that, at least effectively,
![]() $\ell $
is small. Indeed, while we do not show that
$\ell $
is small. Indeed, while we do not show that
![]() $\ell $
is small, we do show (in Section 5.3) that there are d distinct values,
$\ell $
is small, we do show (in Section 5.3) that there are d distinct values,
![]() $\lambda _1(\rho ),\ldots ,\lambda _d(\rho )$
, such that each
$\lambda _1(\rho ),\ldots ,\lambda _d(\rho )$
, such that each
![]() $\lambda _i$
is very close to one of the
$\lambda _i$
is very close to one of the
![]() $\lambda _j(\rho )$
’s. This, by interpolation, implies that we may find a low-degree polynomial P such that
$\lambda _j(\rho )$
’s. This, by interpolation, implies that we may find a low-degree polynomial P such that
![]() $P(\lambda _i)$
is very close to
$P(\lambda _i)$
is very close to
![]() $1$
for all
$1$
for all
![]() $i=1,\ldots ,\ell $
. Finally, to argue that
$i=1,\ldots ,\ell $
. Finally, to argue that
![]() $\left \|P\right \|$
is small, we show that each
$\left \|P\right \|$
is small, we show that each
![]() $\lambda _i(\rho )$
is bounded away from
$\lambda _i(\rho )$
is bounded away from
![]() $0$
.
$0$
.
It remains then to establish the claimed properties of the eigenvalues
![]() $\lambda _1,\ldots ,\lambda _{\ell }$
, and we do so in several steps. We first identify, in Section 5.1, the eigenspaces of
$\lambda _1,\ldots ,\lambda _{\ell }$
, and we do so in several steps. We first identify, in Section 5.1, the eigenspaces of
![]() $\mathrm {T}^{(\rho )}$
among the space of low-degree functions, and we show that each one of them contains a junta. Intuitively, for juntas, it is much easier to understand the action of the
$\mathrm {T}^{(\rho )}$
among the space of low-degree functions, and we show that each one of them contains a junta. Intuitively, for juntas, it is much easier to understand the action of the
![]() $\mathrm {T}^{(\rho )}$
since when looking on very few coordinates,
$\mathrm {T}^{(\rho )}$
since when looking on very few coordinates,
![]() $S_n$
looks like a product space. Indeed, using this logic, we are able to show in Section 5.2 that all eigenvalues of
$S_n$
looks like a product space. Indeed, using this logic, we are able to show in Section 5.2 that all eigenvalues of
![]() $\mathrm {T}^{(\rho )}$
on low-degree functions are bounded away from
$\mathrm {T}^{(\rho )}$
on low-degree functions are bounded away from
![]() $0$
. To argue that the eigenvalues are concentrated on a few values, which we do in Section 5.3, we use the fact that taking symmetry into account, the number of linearly independent juntas is small.
$0$
. To argue that the eigenvalues are concentrated on a few values, which we do in Section 5.3, we use the fact that taking symmetry into account, the number of linearly independent juntas is small.
Our proof uses several notations appearing in Section 2.1, including the actions of
![]() $S_n$
on functions from the left
$S_n$
on functions from the left ![]() and from the right
and from the right
![]() $f^\sigma $
, the level decomposition
$f^\sigma $
, the level decomposition
![]() $V_d$
, the spaces
$V_d$
, the spaces
![]() $V_{A,B}$
and the concept of d-junta.
$V_{A,B}$
and the concept of d-junta.
5.1 Identifying the eigenspaces of
 $\mathrm {T}^{(\rho )}$
$\mathrm {T}^{(\rho )}$
5.1.1
 $\mathrm {T}^{\left (\rho \right )}$
commutes with the action of
$\mathrm {T}^{\left (\rho \right )}$
commutes with the action of
 $S_{n}$
as a bimodule
$S_{n}$
as a bimodule
Lemma 5.1. The operator
![]() $\mathrm {T}^{\left (\rho \right )}$
commutes with the action of
$\mathrm {T}^{\left (\rho \right )}$
commutes with the action of
![]() $S_{n}$
as a bimodule.
$S_{n}$
as a bimodule.
The proof relies on the following claims.
Claim 5.2. If
![]() $\mathrm {T},\mathrm {S}$
are operators that commute with the action of
$\mathrm {T},\mathrm {S}$
are operators that commute with the action of
![]() $S_{n}$
as a bimodule, then so is
$S_{n}$
as a bimodule, then so is
![]() $\mathrm {T\circ S}$
.
$\mathrm {T\circ S}$
.
Proof. We have ![]() .
.
Let X and Y be
![]() $S_n$
-bimodules and consider
$S_n$
-bimodules and consider
![]() $X\times Y$
as an
$X\times Y$
as an
![]() $S_n$
-bimodule with the operation
$S_n$
-bimodule with the operation ![]() . We say that a probability distribution
. We say that a probability distribution
![]() $\mu $
on
$\mu $
on
![]() $X\times Y$
is invariant under the action of
$X\times Y$
is invariant under the action of
![]() $S_n$
on both sides if
$S_n$
on both sides if ![]() for all
for all
![]() $x\in X$
,
$x\in X$
,
![]() $y\in Y$
and
$y\in Y$
and
![]() $\sigma _1,\sigma _2\in S_n$
.
$\sigma _1,\sigma _2\in S_n$
.
Claim 5.3. Let
![]() $X,Y$
be
$X,Y$
be
![]() $S_{n}$
-bimodules that are coupled by the probability measure
$S_{n}$
-bimodules that are coupled by the probability measure
![]() $\mu $
and suppose that
$\mu $
and suppose that
![]() $\mu $
is invariant under the action of
$\mu $
is invariant under the action of
![]() $S_{n}$
from both sides. Then the operators
$S_{n}$
from both sides. Then the operators
![]() $\mathrm {T}_{X\to Y},\mathrm {T}_{Y\to X}$
commute with the action of
$\mathrm {T}_{X\to Y},\mathrm {T}_{Y\to X}$
commute with the action of
![]() $S_{n}$
from both sides.
$S_{n}$
from both sides.
Proof. We prove the claim for
![]() $\mathrm {T}_{X\to Y}$
(the argument for
$\mathrm {T}_{X\to Y}$
(the argument for
![]() $\mathrm {T}_{Y\to X}$
is identical). Let
$\mathrm {T}_{Y\to X}$
is identical). Let
![]() $\mu _{X},\mu _{Y}$
be the marginal distributions of
$\mu _{X},\mu _{Y}$
be the marginal distributions of
![]() $\mu $
on X and on Y, and for each
$\mu $
on X and on Y, and for each
![]() $x\in X$
, denote by
$x\in X$
, denote by
![]() $1_{x}$
the indicator function of x. Then the set
$1_{x}$
the indicator function of x. Then the set
![]() $\left \{ 1_{x}\right \} _{x\in X}$
is a basis for
$\left \{ 1_{x}\right \} _{x\in X}$
is a basis for
![]() $L^{2}\left (X\right )$
, and so it is enough to show that for all x and
$L^{2}\left (X\right )$
, and so it is enough to show that for all x and
![]() $\sigma _1,\sigma _2\in S_n$
, it holds that
$\sigma _1,\sigma _2\in S_n$
, it holds that ![]() . Note that as these are two functions over Y, it is enough to show that
. Note that as these are two functions over Y, it is enough to show that
for all y, since
![]() $\left \{1_y\right \}_{y\in Y}$
forms a basis for
$\left \{1_y\right \}_{y\in Y}$
forms a basis for
![]() $L^2(Y)$
.
$L^2(Y)$
.
Fix x and y. Since
![]() $\mu $
is invariant under the action of
$\mu $
is invariant under the action of
![]() $S_n$
on both sides, it follows that
$S_n$
on both sides, it follows that
![]() $\mu _{Y}$
is invariant under the action of
$\mu _{Y}$
is invariant under the action of
![]() $S_{n}$
, so we have
$S_{n}$
, so we have
where in the penultimate transition, we used the fact that ![]() . However, we also have that the last fact holds for
. However, we also have that the last fact holds for
![]() $1_x$
, and so
$1_x$
, and so

The claim now follows from the fact that
![]() $\mu $
is invariant under the action of
$\mu $
is invariant under the action of
![]() $S_{n}$
from both sides.
$S_{n}$
from both sides.
We are now ready to move on to the proof of Lemma 5.1.
Proof of Lemma 5.1.
We let
![]() $S_{n}$
act on L from the right by setting
$S_{n}$
act on L from the right by setting
![]() $\left (i,j\right )\pi =\left (\pi \left (i\right ),j\right )$
and from the left by setting
$\left (i,j\right )\pi =\left (\pi \left (i\right ),j\right )$
and from the left by setting
![]() $\pi \left (i,j\right )=\left (i,\pi \left (j\right )\right )$
. For a function f on
$\pi \left (i,j\right )=\left (i,\pi \left (j\right )\right )$
. For a function f on
![]() $L^{m}$
, we write
$L^{m}$
, we write ![]() for the function
for the function
By Claim 5.3, the operators
![]() $\mathrm {T}_{\rho },\mathrm {T}_{S_{n}\to L^{m}},\mathrm {T}_{L^{m}\to S_{n}}$
commute with the action of
$\mathrm {T}_{\rho },\mathrm {T}_{S_{n}\to L^{m}},\mathrm {T}_{L^{m}\to S_{n}}$
commute with the action of
![]() $S_{n}$
as a bimodule, and therefore so is
$S_{n}$
as a bimodule, and therefore so is
![]() $\mathrm {T}^{\left (\rho \right )}$
by Claim 5.2.
$\mathrm {T}^{\left (\rho \right )}$
by Claim 5.2.
5.1.2 Showing that the spaces
 $V_{A,B}$
and
$V_{A,B}$
and
 $V_{d}$
are invariant under
$V_{d}$
are invariant under
 $\mathrm {T}^{\left (\rho \right )}$
$\mathrm {T}^{\left (\rho \right )}$
First we show that
![]() $V_{A,B}$
is an invariant subspace of
$V_{A,B}$
is an invariant subspace of
![]() $\mathrm {T}^{\left (\rho \right )}$
.
$\mathrm {T}^{\left (\rho \right )}$
.
Lemma 5.4. Let
![]() $\mathrm {T}$
be an endomorphism of
$\mathrm {T}$
be an endomorphism of
![]() $L^{2}\left (S_{n}\right )$
as an
$L^{2}\left (S_{n}\right )$
as an
![]() $S_{n}$
-bimodule. Then
$S_{n}$
-bimodule. Then
![]() $\mathrm {T}V_{A,B}\subseteq V_{A,B}$
. Moreover,
$\mathrm {T}V_{A,B}\subseteq V_{A,B}$
. Moreover,
![]() $TV_{d}\subseteq V_{d}$
.
$TV_{d}\subseteq V_{d}$
.
Proof. Let
![]() $f\in V_{A,B}$
. We need to show that
$f\in V_{A,B}$
. We need to show that
![]() $\mathrm {T}f\in V_{A,B}$
. Let
$\mathrm {T}f\in V_{A,B}$
. Let
![]() $\sigma _{1}\in S_{\left [n\right ]\setminus A},\sigma _{2}\in S_{\left [n\right ]\setminus B}$
. Then
$\sigma _{1}\in S_{\left [n\right ]\setminus A},\sigma _{2}\in S_{\left [n\right ]\setminus B}$
. Then
where the first equality used the fact that
![]() $\mathrm {T}$
commutes with the action of
$\mathrm {T}$
commutes with the action of
![]() $S_{n}$
from both sides, and the second inequality follows from Lemma 2.4. The ‘moreover’ part follows from Lemma 2.3.
$S_{n}$
from both sides, and the second inequality follows from Lemma 2.4. The ‘moreover’ part follows from Lemma 2.3.
Lemma 5.5. Let
![]() $\lambda $
be an eigenvalue of
$\lambda $
be an eigenvalue of
![]() $\mathrm {T}^{\left (\rho \right )}$
as an operator from
$\mathrm {T}^{\left (\rho \right )}$
as an operator from
![]() $V_{d}$
to itself. Let
$V_{d}$
to itself. Let
![]() $V_{d,\lambda }$
be the eigenspace corresponding to
$V_{d,\lambda }$
be the eigenspace corresponding to
![]() $\lambda $
. Then
$\lambda $
. Then
![]() $V_{d,\lambda }$
contains a d-junta.
$V_{d,\lambda }$
contains a d-junta.
Proof. Since each space
![]() $V_{A,B}$
is
$V_{A,B}$
is
![]() $\mathrm {T}^{\left (\rho \right )}$
invariant, we may decompose each
$\mathrm {T}^{\left (\rho \right )}$
invariant, we may decompose each
![]() $V_{A,B}$
into eigenspaces
$V_{A,B}$
into eigenspaces
![]() $V_{A,B}^{\left (\lambda \right )}$
. Let
$V_{A,B}^{\left (\lambda \right )}$
. Let
Then for each
![]() $\lambda $
,
$\lambda $
,
![]() $V_{d}^{(\lambda )}$
is an eigenspace of
$V_{d}^{(\lambda )}$
is an eigenspace of
![]() $\mathrm {T}^{\left (\rho \right )}$
with eigenvalue
$\mathrm {T}^{\left (\rho \right )}$
with eigenvalue
![]() $\lambda $
, and
$\lambda $
, and
By uniqueness, it follows that
![]() $V_{d,\lambda } = V_{d}^{(\lambda )}$
for all
$V_{d,\lambda } = V_{d}^{(\lambda )}$
for all
![]() $\lambda $
. Fix
$\lambda $
. Fix
![]() $\lambda $
; then we get that there are
$\lambda $
; then we get that there are
![]() $|A|,|B|\leqslant d$
such that
$|A|,|B|\leqslant d$
such that
![]() $V_{A,B}^{\lambda }\subseteq V_{d,\lambda }$
, and since any function in
$V_{A,B}^{\lambda }\subseteq V_{d,\lambda }$
, and since any function in
![]() $V_{A,B}$
is a d-junta by definition, the proof is concluded.
$V_{A,B}$
is a d-junta by definition, the proof is concluded.
We comment that the representation theory of
![]() $S_n$
supplies us with explicit formulas for
$S_n$
supplies us with explicit formulas for
![]() $2d$
-juntas in
$2d$
-juntas in
![]() $V_{d,\lambda }$
(arising in the construction of Specht modules), which can be turned into d-juntas by symmetrization. Since we will not need such explicit formulas here, we skip this description.
$V_{d,\lambda }$
(arising in the construction of Specht modules), which can be turned into d-juntas by symmetrization. Since we will not need such explicit formulas here, we skip this description.
5.2 Finding a basis for
 $V_{A,B}$
$V_{A,B}$
We now move on to the study of the spaces
![]() $V_{A,B}$
. These spaces have small dimension and are therefore easy to analyse. We first construct a set
$V_{A,B}$
. These spaces have small dimension and are therefore easy to analyse. We first construct a set
![]() $\left \{ v_{T}\right \} $
of functions in
$\left \{ v_{T}\right \} $
of functions in
![]() $V_{A,B}$
that form a nearly-orthonormal basis.
$V_{A,B}$
that form a nearly-orthonormal basis.
Definition 5.6. Let
![]() $T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{k},j_{k}\right )\right \} \subseteq \left [d\right ]^{2}$
be consistent. Let
$T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{k},j_{k}\right )\right \} \subseteq \left [d\right ]^{2}$
be consistent. Let
![]() $1_{T}$
be the indicator function of permutations
$1_{T}$
be the indicator function of permutations
![]() $\pi $
in
$\pi $
in
![]() $S_{n}$
that satisfy the restrictions given by T (i.e.,
$S_{n}$
that satisfy the restrictions given by T (i.e.,
![]() $\pi \left (i_{1}\right )=j_{1},\ldots ,\pi \left (i_{i_{k}}\right )=j_{k}$
). We define
$\pi \left (i_{1}\right )=j_{1},\ldots ,\pi \left (i_{i_{k}}\right )=j_{k}$
). We define
![]() $v_{T}=\frac {1_{T}}{\|1_{T}\|_{2}}$
.
$v_{T}=\frac {1_{T}}{\|1_{T}\|_{2}}$
.
Since the spaces
![]() $V_{A,B}$
are isomorphic (as
$V_{A,B}$
are isomorphic (as
![]() $S_{n-d}$
bimodules) for all sets
$S_{n-d}$
bimodules) for all sets
![]() $A,B$
of size d, we shall focus on the case where
$A,B$
of size d, we shall focus on the case where
![]() $A = B =[d]$
.
$A = B =[d]$
.
Lemma 5.7. Let
![]() $d\leqslant \frac {n}{2}$
and let
$d\leqslant \frac {n}{2}$
and let
![]() $T\ne S$
be sets of size d. Then
$T\ne S$
be sets of size d. Then
![]() $\left \langle v_{T},v_{S}\right \rangle \leqslant O\left (\frac {1}{n}\right )$
.
$\left \langle v_{T},v_{S}\right \rangle \leqslant O\left (\frac {1}{n}\right )$
.
Proof. If
![]() $T\cup S$
is not consistent, then
$T\cup S$
is not consistent, then
![]() $1_{T}1_{S}=0$
and so
$1_{T}1_{S}=0$
and so
![]() $\left \langle v_{T},v_{S}\right \rangle =0$
. Otherwise,
$\left \langle v_{T},v_{S}\right \rangle =0$
. Otherwise,
 $$\begin{align*}\left\langle v_{T},v_{S}\right\rangle =\frac{\mathbb{E}\left|1_{T\cup S}\right|}{\|1_{T}\|_{2}\|1_{S}\|_{2}}=\frac{\left(n-\left|T\cup S\right|\right)!}{\sqrt{\left(n-\left|T\right|\right)!\left(n-\left|S\right|\right)!}}\leqslant \frac{(n-d-1)!}{(n-d)!} = O\left(\frac{1}{n}\right).\\[-46pt] \end{align*}$$
$$\begin{align*}\left\langle v_{T},v_{S}\right\rangle =\frac{\mathbb{E}\left|1_{T\cup S}\right|}{\|1_{T}\|_{2}\|1_{S}\|_{2}}=\frac{\left(n-\left|T\cup S\right|\right)!}{\sqrt{\left(n-\left|T\right|\right)!\left(n-\left|S\right|\right)!}}\leqslant \frac{(n-d-1)!}{(n-d)!} = O\left(\frac{1}{n}\right).\\[-46pt] \end{align*}$$
Proposition 5.8. There exists an absolute constant
![]() $c>0$
such that for all consistent
$c>0$
such that for all consistent
![]() $T\subseteq L$
, we have
$T\subseteq L$
, we have
Proof. Let
![]() $x\sim L^{m},y\sim N_{\rho }\left (x\right )$
and let
$x\sim L^{m},y\sim N_{\rho }\left (x\right )$
and let
![]() $\sigma _{x},\sigma _{y}\in S_{n}$
be corresponding permutations chosen according to the coupling. We have
$\sigma _{x},\sigma _{y}\in S_{n}$
be corresponding permutations chosen according to the coupling. We have
as
![]() $\left \|1_T\right \|_2^2=\frac {\left (n-\left |T\right |\right )!}{n!}$
. We now interpret
$\left \|1_T\right \|_2^2=\frac {\left (n-\left |T\right |\right )!}{n!}$
. We now interpret
![]() $\left \langle \mathrm {T}^{\left (\rho \right )}1_{T},1_{T}\right \rangle $
as the probability that both
$\left \langle \mathrm {T}^{\left (\rho \right )}1_{T},1_{T}\right \rangle $
as the probability that both
![]() $\sigma _{x}$
and
$\sigma _{x}$
and
![]() $\sigma _{y}$
satisfy the restrictions given by T. For each sequence S over
$\sigma _{y}$
satisfy the restrictions given by T. For each sequence S over
![]() $[2n]$
of size
$[2n]$
of size
![]() $\left |T\right |$
, consider the event
$\left |T\right |$
, consider the event
![]() $A_{S}$
that
$A_{S}$
that
![]() $x_{S}=y_{S}=T$
, while all the coordinates of the vectors
$x_{S}=y_{S}=T$
, while all the coordinates of the vectors
![]() $x_{\left [2n\right ]\setminus S},y_{\left [2n\right ]\setminus S}$
do not contradict T nor belong to T. Then
$x_{\left [2n\right ]\setminus S},y_{\left [2n\right ]\setminus S}$
do not contradict T nor belong to T. Then
 $$\begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{T}\right\rangle \geqslant\sum_{S\text{ a }|T|\text{-sequence of }\left[2n\right]}\Pr\left[A_{S}\right]. \end{align*}$$
$$\begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{T}\right\rangle \geqslant\sum_{S\text{ a }|T|\text{-sequence of }\left[2n\right]}\Pr\left[A_{S}\right]. \end{align*}$$
Now the probability that
![]() $x_{S}=T$
is
$x_{S}=T$
is
![]() $\left (\frac {1}{n}\right )^{2\left |T\right |}$
. Conditioned on
$\left (\frac {1}{n}\right )^{2\left |T\right |}$
. Conditioned on
![]() $x_{S}=T$
, the probability that
$x_{S}=T$
, the probability that
![]() $y_{S}=T$
is at least
$y_{S}=T$
is at least
![]() $\rho ^{\left |T\right |}$
. When we condition on
$\rho ^{\left |T\right |}$
. When we condition on
![]() $x_{S}=y_{S}=T$
, we obtain that the probability that
$x_{S}=y_{S}=T$
, we obtain that the probability that
![]() $x_{\left [n\right ]\setminus S}$
and
$x_{\left [n\right ]\setminus S}$
and
![]() $y_{\left [n\right ]\setminus S}$
do not involve any coordinate contradicting T or in T is at least
$y_{\left [n\right ]\setminus S}$
do not involve any coordinate contradicting T or in T is at least
![]() $\left (1-\frac {2\left |T\right |}{n}\right )^{2n}=2^{-\Theta \left (|T|\right )}$
. Hence,
$\left (1-\frac {2\left |T\right |}{n}\right )^{2n}=2^{-\Theta \left (|T|\right )}$
. Hence,
![]() $\Pr \left [A_{S}\right ]\geqslant \left (\frac {1}{n}\right )^{2\left |T\right |}\Omega \left (\rho \right )^{\left |T\right |}$
. So wrapping everything up, we obtain that
$\Pr \left [A_{S}\right ]\geqslant \left (\frac {1}{n}\right )^{2\left |T\right |}\Omega \left (\rho \right )^{\left |T\right |}$
. So wrapping everything up, we obtain that
Lemma 5.9. Let
![]() $\rho \in \left (0,1\right )$
. Then for all sets
$\rho \in \left (0,1\right )$
. Then for all sets
![]() $T\ne S$
of size at most
$T\ne S$
of size at most
![]() $n/2$
, we have
$n/2$
, we have
![]() $\left \langle \mathrm {T}^{\left (\rho \right )}v_{T},v_{S}\right \rangle =O\left (\frac {1}{\sqrt {n}}\right )$
.
$\left \langle \mathrm {T}^{\left (\rho \right )}v_{T},v_{S}\right \rangle =O\left (\frac {1}{\sqrt {n}}\right )$
.
Proof. Suppose without loss of generality that
![]() $\|1_{T}\|_{2}^{2}\leqslant \|1_{S}\|_{2}^{2}$
, so
$\|1_{T}\|_{2}^{2}\leqslant \|1_{S}\|_{2}^{2}$
, so
![]() $\left |T\right |\geqslant \left |S\right |$
. Choose
$\left |T\right |\geqslant \left |S\right |$
. Choose
![]() $x\sim L^{m},y\sim N_{\rho }\left (x\right )$
and let
$x\sim L^{m},y\sim N_{\rho }\left (x\right )$
and let
![]() $\sigma _{x},\sigma _{y}$
by the corresponding random permutations given by the coupling. We have
$\sigma _{x},\sigma _{y}$
by the corresponding random permutations given by the coupling. We have
 $$\begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle ={\frac{\Pr\left[1_{T}\left(\sigma_{x}\right)=1,1_{S}\left(\sigma_{y}\right)=1\right]}{\sqrt{\mathbb{E}1_{T}\mathbb{E}1_{S}}}}. \end{align*}$$
$$\begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle ={\frac{\Pr\left[1_{T}\left(\sigma_{x}\right)=1,1_{S}\left(\sigma_{y}\right)=1\right]}{\sqrt{\mathbb{E}1_{T}\mathbb{E}1_{S}}}}. \end{align*}$$
As the probability in the numerator is at most
![]() $\mathbb {E}\left [1_{T}\right ]$
, we have
$\mathbb {E}\left [1_{T}\right ]$
, we have
 $$\begin{align*}\left\langle T^{\left(\rho\right)}v_{T},v_{S}\right\rangle \leqslant\sqrt{\frac{\mathbb{E}\left[1_{T}\right]}{\mathbb{E}\left[1_{S}\right]}}=\sqrt{\frac{\left(n-\left|T\right|\right)!}{\left(n-\left|S\right|\right)!}}, \end{align*}$$
$$\begin{align*}\left\langle T^{\left(\rho\right)}v_{T},v_{S}\right\rangle \leqslant\sqrt{\frac{\mathbb{E}\left[1_{T}\right]}{\mathbb{E}\left[1_{S}\right]}}=\sqrt{\frac{\left(n-\left|T\right|\right)!}{\left(n-\left|S\right|\right)!}}, \end{align*}$$
and the proposition follows in the case that
![]() $\left |S\right |<\left |T\right |$
.
$\left |S\right |<\left |T\right |$
.
It remains to prove the proposition provided that
![]() $\left |S\right |=\left |T\right |$
. Let
$\left |S\right |=\left |T\right |$
. Let
![]() $\left (i,j\right )\in S\setminus T$
. Note that
$\left (i,j\right )\in S\setminus T$
. Note that
Let us condition further on
![]() $\sigma _{x}\left (i\right )$
. Conditioned on
$\sigma _{x}\left (i\right )$
. Conditioned on
![]() $\sigma _{x}\left (i\right )=j$
, we have that
$\sigma _{x}\left (i\right )=j$
, we have that
![]() $\sigma _{x}$
is a random permutation sending i to j, and so
$\sigma _{x}$
is a random permutation sending i to j, and so
![]() $\Pr \left [1_{T}\left (\sigma _{X}\right )=1\right ]$
is either 0 (if
$\Pr \left [1_{T}\left (\sigma _{X}\right )=1\right ]$
is either 0 (if
![]() $\left (i,j\right )$
contradicts T) or
$\left (i,j\right )$
contradicts T) or
![]() $\frac {\left (n-1-\left |T\right |\right )!}{\left (n-1\right )!}=O\left (\|1_{T}\|_{2}^{2}\right )$
(if
$\frac {\left (n-1-\left |T\right |\right )!}{\left (n-1\right )!}=O\left (\|1_{T}\|_{2}^{2}\right )$
(if
![]() $\left (i,j\right )$
is consistent with T).
$\left (i,j\right )$
is consistent with T).
Conditioned on
![]() $\sigma _{x}\left (i\right )\ne j$
(and on
$\sigma _{x}\left (i\right )\ne j$
(and on
![]() $\sigma _{y}\left (i\right )=j$
), we again obtain that
$\sigma _{y}\left (i\right )=j$
), we again obtain that
![]() $\sigma _{x}$
is a random permutation that does not send i to j, in which case,
$\sigma _{x}$
is a random permutation that does not send i to j, in which case,
if
![]() $\left (i,j\right )$
contradicts T, and
$\left (i,j\right )$
contradicts T, and
if
![]() $\left (i,j\right )$
is consistent with T. This completes the proof of the lemma.
$\left (i,j\right )$
is consistent with T. This completes the proof of the lemma.
Proposition 5.10. Let C be a sufficiently large constant. If
![]() $n\geqslant \left (\frac {\rho }{C}\right )^{-d}C^{d^{2}}$
and f is a d-junta, then
$n\geqslant \left (\frac {\rho }{C}\right )^{-d}C^{d^{2}}$
and f is a d-junta, then
Proof. Since
![]() $\left \{ v_{T}\right \} _{T\subseteq \left [d\right ]^{2}}$
span the space
$\left \{ v_{T}\right \} _{T\subseteq \left [d\right ]^{2}}$
span the space
![]() $V_{\left [d\right ],\left [d\right ]}$
of
$V_{\left [d\right ],\left [d\right ]}$
of
![]() $\left (\left [d\right ],\left [d\right ]\right )$
-juntas by Lemma 2.3, we may write
$\left (\left [d\right ],\left [d\right ]\right )$
-juntas by Lemma 2.3, we may write
![]() $f=\sum a_{T}v_{T}$
. Now
$f=\sum a_{T}v_{T}$
. Now
 $$ \begin{align*} \left\langle \mathrm{T}^{\left(\rho\right)}f,f\right\rangle & =\sum_{T}a_{T}^{2}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{T}\right\rangle +\sum_{T\ne S}a_{T}a_{S}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle. \end{align*} $$
$$ \begin{align*} \left\langle \mathrm{T}^{\left(\rho\right)}f,f\right\rangle & =\sum_{T}a_{T}^{2}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{T}\right\rangle +\sum_{T\ne S}a_{T}a_{S}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle. \end{align*} $$
By Lemma 5.9, we have
 $$ \begin{align*} \left|\sum_{T\ne S}a_{T}a_{S}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle \right| \leqslant O\left(\sum_{T\ne S}\frac{\left|a_{T}a_{S}\right|}{\sqrt{n}}\right) \leqslant O\left(\frac{1}{\sqrt{n}}\right)\left(\sum_{T}\left|a_{T}\right|\right)^{2} \leqslant\frac{2^{O\left(d^{2}\right)}}{\sqrt{n}}\left(\sum_{T}\left|a_{T}\right|{}^{2}\right), \end{align*} $$
$$ \begin{align*} \left|\sum_{T\ne S}a_{T}a_{S}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle \right| \leqslant O\left(\sum_{T\ne S}\frac{\left|a_{T}a_{S}\right|}{\sqrt{n}}\right) \leqslant O\left(\frac{1}{\sqrt{n}}\right)\left(\sum_{T}\left|a_{T}\right|\right)^{2} \leqslant\frac{2^{O\left(d^{2}\right)}}{\sqrt{n}}\left(\sum_{T}\left|a_{T}\right|{}^{2}\right), \end{align*} $$
where the last inequality is by Cauchy–Schwarz. However, by Proposition 5.8, we have
 $$\begin{align*}\sum_{T}a_{T}^{2}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{T}\right\rangle \geqslant\rho^{O\left(d\right)}\left(\sum_{T}a_{T}^{2}\right). \end{align*}$$
$$\begin{align*}\sum_{T}a_{T}^{2}\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{T}\right\rangle \geqslant\rho^{O\left(d\right)}\left(\sum_{T}a_{T}^{2}\right). \end{align*}$$
Using a similar calculation, one sees that
 $$\begin{align*}\|f\|_{2}^{2}=\left(1\pm\frac{2^{O\left(d^{2}\right)}}{n}\right)\sum_{T}a_{T}^{2}, \end{align*}$$
$$\begin{align*}\|f\|_{2}^{2}=\left(1\pm\frac{2^{O\left(d^{2}\right)}}{n}\right)\sum_{T}a_{T}^{2}, \end{align*}$$
so we get that
 $$\begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}f,f\right\rangle \geqslant\left(\rho^{O(d)} - \frac{2^{O\left(d^{2}\right)}}{\sqrt{n}}\right)\sum_{T}a_{T}^{2} \geqslant\left(\rho^{O(d)} - \frac{2^{O\left(d^{2}\right)}}{\sqrt{n}}\right)\left\|f\right\|_2^2 \geqslant \rho^{O(d)}\left\|f\right\|_2^2.\\[-47pt] \end{align*}$$
$$\begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}f,f\right\rangle \geqslant\left(\rho^{O(d)} - \frac{2^{O\left(d^{2}\right)}}{\sqrt{n}}\right)\sum_{T}a_{T}^{2} \geqslant\left(\rho^{O(d)} - \frac{2^{O\left(d^{2}\right)}}{\sqrt{n}}\right)\left\|f\right\|_2^2 \geqslant \rho^{O(d)}\left\|f\right\|_2^2.\\[-47pt] \end{align*}$$
Corollary 5.11. Let C be a sufficiently large absolute constant. If
![]() $n\geqslant \left (\frac {\rho }{C}\right )^{-d}C^{d^{2}}$
, then all the eigenvalues of
$n\geqslant \left (\frac {\rho }{C}\right )^{-d}C^{d^{2}}$
, then all the eigenvalues of
![]() $\mathrm {T}^{\left (\rho \right )}$
as an operator from
$\mathrm {T}^{\left (\rho \right )}$
as an operator from
![]() $V_{d}$
to itself are at least
$V_{d}$
to itself are at least
![]() $\rho ^{O\left (d\right )}$
.
$\rho ^{O\left (d\right )}$
.
Proof. By Lemma 5.5, each eigenspace
![]() $V_{d,\lambda }$
contains a d-junta. Let
$V_{d,\lambda }$
contains a d-junta. Let
![]() $f\in V_{d,\lambda }$
be a nonzero d-junta. Then by Proposition 5.10,
$f\in V_{d,\lambda }$
be a nonzero d-junta. Then by Proposition 5.10,
 $$\begin{align*}\lambda=\frac{\left\langle \mathrm{T}^{\left(\rho\right)}f,f\right\rangle }{\|f\|_{2}^{2}}\geqslant\rho^{O\left(d\right)}.\\[-45pt] \end{align*}$$
$$\begin{align*}\lambda=\frac{\left\langle \mathrm{T}^{\left(\rho\right)}f,f\right\rangle }{\|f\|_{2}^{2}}\geqslant\rho^{O\left(d\right)}.\\[-45pt] \end{align*}$$
5.3 Showing that the eigenvalues of
 $\mathrm {T}^{\left (\rho \right )}$
on
$\mathrm {T}^{\left (\rho \right )}$
on
 $V_{d}$
are concentrated on at most d values
$V_{d}$
are concentrated on at most d values
Let
![]() $\lambda _{i}\left (\rho \right )=\left \langle \mathrm {T}^{\left (\rho \right )}v_{T},v_{T}\right \rangle $
, where T is a set of size i. Then symmetry implies that
$\lambda _{i}\left (\rho \right )=\left \langle \mathrm {T}^{\left (\rho \right )}v_{T},v_{T}\right \rangle $
, where T is a set of size i. Then symmetry implies that
![]() $\lambda _{i}\left (\rho \right )$
does not depend on the choice of T.
$\lambda _{i}\left (\rho \right )$
does not depend on the choice of T.
Lemma 5.12. Suppose that
![]() $n\geqslant \left (\frac {\rho }{C}\right )^{O\left (d\right )}C^{d^{2}}$
. Then each eigenvalue of
$n\geqslant \left (\frac {\rho }{C}\right )^{O\left (d\right )}C^{d^{2}}$
. Then each eigenvalue of
![]() $\mathrm {T}^{\left (\rho \right )}$
as an operator on
$\mathrm {T}^{\left (\rho \right )}$
as an operator on
![]() $V_{d}$
is equal to
$V_{d}$
is equal to
![]() $\lambda _{i}(\rho )\left (1\pm n^{-\frac {1}{3}}\right )$
for some
$\lambda _{i}(\rho )\left (1\pm n^{-\frac {1}{3}}\right )$
for some
![]() $i\leqslant d$
.
$i\leqslant d$
.
Proof. Let
![]() $\lambda $
be an eigenvalue of
$\lambda $
be an eigenvalue of
![]() $\mathrm {T}^{\left (\rho \right )}$
and let f be a corresponding eigenfunction in
$\mathrm {T}^{\left (\rho \right )}$
and let f be a corresponding eigenfunction in
![]() $V_{\left [d\right ],\left [d\right ]}$
. Write
$V_{\left [d\right ],\left [d\right ]}$
. Write
where the sum is over all
![]() $S=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \} \subseteq \left [d\right ]$
. Then
$S=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \} \subseteq \left [d\right ]$
. Then
![]() $0=\mathrm {T}^{\left (\rho \right )}f-\lambda f$
, but, however, for each set S, we have
$0=\mathrm {T}^{\left (\rho \right )}f-\lambda f$
, but, however, for each set S, we have
 $$ \begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}f-\lambda f,v_{S}\right\rangle & =a_{S}\left(\left\langle \mathrm{T}^{\left(\rho\right)}v_{S},v_{S}\right\rangle -\lambda\right) \pm\sum_{\left|S\right|\ne\left|T\right|}\left|a_{T}\right|\left(\left|\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle \right|+\left|\lambda\right|\left|\left\langle v_{T},v_{S}\right\rangle\right|\right)\\ & =a_{S}\left(\lambda_{\left|S\right|}\left(\rho\right)-\lambda\right)\pm O\left(\frac{\sum_{T\ne S}\left|a_{T}\right|}{\sqrt{n}}\right). \end{align*} $$
$$ \begin{align*}\left\langle \mathrm{T}^{\left(\rho\right)}f-\lambda f,v_{S}\right\rangle & =a_{S}\left(\left\langle \mathrm{T}^{\left(\rho\right)}v_{S},v_{S}\right\rangle -\lambda\right) \pm\sum_{\left|S\right|\ne\left|T\right|}\left|a_{T}\right|\left(\left|\left\langle \mathrm{T}^{\left(\rho\right)}v_{T},v_{S}\right\rangle \right|+\left|\lambda\right|\left|\left\langle v_{T},v_{S}\right\rangle\right|\right)\\ & =a_{S}\left(\lambda_{\left|S\right|}\left(\rho\right)-\lambda\right)\pm O\left(\frac{\sum_{T\ne S}\left|a_{T}\right|}{\sqrt{n}}\right). \end{align*} $$
Thus, for all S, we have that
 $$\begin{align*}\left|a_S\right|\left|\lambda_{\left|S\right|}\left(\rho\right)-\lambda\right|\leqslant O\left(\frac{\sum_{T\ne S}\left|a_{T}\right|}{\sqrt{n}}\right). \end{align*}$$
$$\begin{align*}\left|a_S\right|\left|\lambda_{\left|S\right|}\left(\rho\right)-\lambda\right|\leqslant O\left(\frac{\sum_{T\ne S}\left|a_{T}\right|}{\sqrt{n}}\right). \end{align*}$$
However, choosing S that maximizes
![]() $\left |a_{S}\right |$
, we find that
$\left |a_{S}\right |$
, we find that
![]() $\left |a_{S}\right |\geqslant \frac {\sum _{T\ne S}\left |a_{T}\right |}{2^{d^{2}}}$
, and plugging that into the previous inequality yields that
$\left |a_{S}\right |\geqslant \frac {\sum _{T\ne S}\left |a_{T}\right |}{2^{d^{2}}}$
, and plugging that into the previous inequality yields that
![]() $\left |\lambda _{\left |S\right |}\left (\rho \right )-\lambda \right |\leqslant \frac {O\left (2^{d^{2}}\right )}{\sqrt {n}}\leqslant n^{-0.4}\rho ^{-d}\leqslant n^{-1/3}\lambda _{\left |S\right |}\left (\rho \right )$
, provided that C is sufficiently large.
$\left |\lambda _{\left |S\right |}\left (\rho \right )-\lambda \right |\leqslant \frac {O\left (2^{d^{2}}\right )}{\sqrt {n}}\leqslant n^{-0.4}\rho ^{-d}\leqslant n^{-1/3}\lambda _{\left |S\right |}\left (\rho \right )$
, provided that C is sufficiently large.
5.4 An
 $L^2$
variant of Lemma 3.6
$L^2$
variant of Lemma 3.6
Lemma 5.13. Let
![]() $n\geqslant \rho ^{-Cd^{3}}$
for a sufficiently large constant C. There exists a polynomial
$n\geqslant \rho ^{-Cd^{3}}$
for a sufficiently large constant C. There exists a polynomial
![]() $P(z)=\sum _{i=1}^{k}a_{i}z^{i}$
, such that
$P(z)=\sum _{i=1}^{k}a_{i}z^{i}$
, such that
![]() $\|P\|\leqslant \rho ^{-O\left (d^{3}\right )}$
and
$\|P\|\leqslant \rho ^{-O\left (d^{3}\right )}$
and
![]() $\|P\left (\mathrm {T}^{\left (\rho \right )}\right )f-f\|_{2}\leqslant n^{-2d}\|f\|_{2}$
.
$\|P\left (\mathrm {T}^{\left (\rho \right )}\right )f-f\|_{2}\leqslant n^{-2d}\|f\|_{2}$
.
Proof. Choose
![]() $P(z) = 1-\prod _{i=1}^{d}\left (\lambda _{i}^{-1}z-1\right )^{9d}$
, where
$P(z) = 1-\prod _{i=1}^{d}\left (\lambda _{i}^{-1}z-1\right )^{9d}$
, where
![]() $\lambda _i = \lambda _i(\rho )$
. Orthogonally decompose
$\lambda _i = \lambda _i(\rho )$
. Orthogonally decompose
![]() $\mathrm {T}^{\left (\rho \right )}$
to write
$\mathrm {T}^{\left (\rho \right )}$
to write
![]() $f=\sum _{\lambda }f^{=\lambda }$
for nonzero orthogonal functions
$f=\sum _{\lambda }f^{=\lambda }$
for nonzero orthogonal functions
![]() $f^{=\lambda }\in V_{d}$
satisfying
$f^{=\lambda }\in V_{d}$
satisfying
![]() $\mathrm {T}^{\left (\rho \right )}f^{=\lambda }=\lambda f^{=\lambda }$
, and let
$\mathrm {T}^{\left (\rho \right )}f^{=\lambda }=\lambda f^{=\lambda }$
, and let
![]() $g=P\left (\mathrm {T}^{\left (\rho \right )}\right )f-f$
. Then
$g=P\left (\mathrm {T}^{\left (\rho \right )}\right )f-f$
. Then
![]() $g=\sum _{\lambda }\left (P\left (\lambda \right )-1\right )f^{=\lambda }$
. Therefore,
$g=\sum _{\lambda }\left (P\left (\lambda \right )-1\right )f^{=\lambda }$
. Therefore,
Suppose the maximum is attained at
![]() $\lambda _{\star }$
. By Lemma 5.12, there is
$\lambda _{\star }$
. By Lemma 5.12, there is
![]() $i\leqslant d$
such that
$i\leqslant d$
such that
![]() $\lambda _{\star }=\lambda _{i}(1\pm n^{-\frac {1}{3}})$
, and so
$\lambda _{\star }=\lambda _{i}(1\pm n^{-\frac {1}{3}})$
, and so
 $$\begin{align*}\left|\left(\lambda_i^{-1} \lambda_{\star} - 1\right)^{9d}\right| \leqslant n^{-3d}. \end{align*}$$
$$\begin{align*}\left|\left(\lambda_i^{-1} \lambda_{\star} - 1\right)^{9d}\right| \leqslant n^{-3d}. \end{align*}$$
For any
![]() $j\neq i$
, we have by Proposition 5.10 that
$j\neq i$
, we have by Proposition 5.10 that
![]() $\lambda _{j}\geqslant \rho ^{O(d)}$
, and so
$\lambda _{j}\geqslant \rho ^{O(d)}$
, and so
 $$\begin{align*}\left|\left(\lambda_i^{-1} \lambda_{\star} - 1\right)^{9d}\right| \leqslant \rho^{-O(d^2)}. \end{align*}$$
$$\begin{align*}\left|\left(\lambda_i^{-1} \lambda_{\star} - 1\right)^{9d}\right| \leqslant \rho^{-O(d^2)}. \end{align*}$$
Combining the two inequalities, we get that
where the last inequality follows from the lower bound on n. To finish up the proof then, we must upper-bound
![]() $\left \|P\right \|$
, and this is relatively straightforward:
$\left \|P\right \|$
, and this is relatively straightforward:
 $$\begin{align*}\left\|P\right\|\leqslant 1 + \left\|\prod_{i=1}^{d}\left(\lambda_{i}^{-1}z-1\right)^{9d}\right\| \leqslant 1 + \prod_{i=1}^{d}\left\|\lambda_{i}^{-1}z-1\right\|^{9d} = 1 + \prod_{i=1}^{d}(1+\lambda^{-1})^{9d} \leqslant 1 + \prod_{i=1}^{d}(1+\rho^{-O(d)})^{9d}, \end{align*}$$
$$\begin{align*}\left\|P\right\|\leqslant 1 + \left\|\prod_{i=1}^{d}\left(\lambda_{i}^{-1}z-1\right)^{9d}\right\| \leqslant 1 + \prod_{i=1}^{d}\left\|\lambda_{i}^{-1}z-1\right\|^{9d} = 1 + \prod_{i=1}^{d}(1+\lambda^{-1})^{9d} \leqslant 1 + \prod_{i=1}^{d}(1+\rho^{-O(d)})^{9d}, \end{align*}$$
which is at most
![]() $\rho ^{-O(d^3)}$
. In the second inequality, we used the fact that
$\rho ^{-O(d^3)}$
. In the second inequality, we used the fact that
![]() $\left \|P_1 P_2\right \|\leqslant \left \|P_1\right \|\left \|P_2\right \|$
.
$\left \|P_1 P_2\right \|\leqslant \left \|P_1\right \|\left \|P_2\right \|$
.
5.5 Deducing the
 $L^q$
approximation
$L^q$
approximation
To deduce the
![]() $L^q$
approximation of the polynomial P from Lemma 5.13, we use the following basic type of hypercontractive inequality (this bound is often times too weak quantitatively, but it is good enough for us since we have a very strong
$L^q$
approximation of the polynomial P from Lemma 5.13, we use the following basic type of hypercontractive inequality (this bound is often times too weak quantitatively, but it is good enough for us since we have a very strong
![]() $L_2$
approximation).
$L_2$
approximation).
Lemma 5.14. Let C be sufficiently large and let
![]() $n\geqslant C^{d^{2}}q^{2d}$
. Let
$n\geqslant C^{d^{2}}q^{2d}$
. Let
![]() $f\colon S_{n}\to \mathbb {R}$
be a function of degree d. Then
$f\colon S_{n}\to \mathbb {R}$
be a function of degree d. Then
![]() $\|f\|_{q}\leqslant q^{O(d)}n^{d}\|f\|_{2}$
.
$\|f\|_{q}\leqslant q^{O(d)}n^{d}\|f\|_{2}$
.
Proof. Let
![]() $\rho =\frac {1}{(10\cdot 4^8\cdot q)^{2}}$
. Decomposing f into the
$\rho =\frac {1}{(10\cdot 4^8\cdot q)^{2}}$
. Decomposing f into the
![]() $\sum \limits _{\lambda } f_{=\lambda }$
where
$\sum \limits _{\lambda } f_{=\lambda }$
where
![]() $T^{(\rho )} f_{=\lambda } = \lambda f_{=\lambda }$
, we may find g of degree d, such that
$T^{(\rho )} f_{=\lambda } = \lambda f_{=\lambda }$
, we may find g of degree d, such that
![]() $f=\mathrm {T}^{\left (\rho \right )}g$
– namely,
$f=\mathrm {T}^{\left (\rho \right )}g$
– namely,
![]() $g = \sum \limits _{\lambda }\lambda ^{-1} f_{=\lambda }$
. By Parseval and Corollary 5.11, we get that
$g = \sum \limits _{\lambda }\lambda ^{-1} f_{=\lambda }$
. By Parseval and Corollary 5.11, we get that
![]() $\|g\|_{2}\leqslant \rho ^{-O(d)}\|f\|_{2}$
. Thus, we have that
$\|g\|_{2}\leqslant \rho ^{-O(d)}\|f\|_{2}$
. Thus, we have that
![]() $\left \|f\right \|_q = \left \|T^{(\rho )} g\right \|_q$
, and to upper-bound this norm, we intend to use Theorem 3.3, and for that, we show that g is global with fairly weak parameters.
$\left \|f\right \|_q = \left \|T^{(\rho )} g\right \|_q$
, and to upper-bound this norm, we intend to use Theorem 3.3, and for that, we show that g is global with fairly weak parameters.
Let
![]() $T\subseteq L$
be consistent of size at most
$T\subseteq L$
be consistent of size at most
![]() $2d$
. Then
$2d$
. Then
 $$\begin{align*}\|g_{\rightarrow T}\|_{2}^2 = \frac{\mathop{\mathbb{E}}_{x} g(x) 1_T(x)}{\mathop{\mathbb{E}}_x[1_T(x)]} \leqslant \sqrt{ \frac{\mathop{\mathbb{E}}_{x} g(x)^2}{\mathop{\mathbb{E}}_x[1_T(x)]}} \leqslant n^{\frac{\left|T\right|}{2}}\|g\|_{2}^{2} \leqslant n^{\frac{\left|T\right|}{2}}\rho^{-O(d)} \|f\|_{2}^{2}, \end{align*}$$
$$\begin{align*}\|g_{\rightarrow T}\|_{2}^2 = \frac{\mathop{\mathbb{E}}_{x} g(x) 1_T(x)}{\mathop{\mathbb{E}}_x[1_T(x)]} \leqslant \sqrt{ \frac{\mathop{\mathbb{E}}_{x} g(x)^2}{\mathop{\mathbb{E}}_x[1_T(x)]}} \leqslant n^{\frac{\left|T\right|}{2}}\|g\|_{2}^{2} \leqslant n^{\frac{\left|T\right|}{2}}\rho^{-O(d)} \|f\|_{2}^{2}, \end{align*}$$
and so g is
![]() $(2d,\varepsilon )$
global for
$(2d,\varepsilon )$
global for
![]() $\varepsilon =n^{d/2}\rho ^{-O(d)}\|f\|_{2}$
. Lemma 3.5 now implies that g is
$\varepsilon =n^{d/2}\rho ^{-O(d)}\|f\|_{2}$
. Lemma 3.5 now implies that g is
![]() $\varepsilon $
-global with constant
$\varepsilon $
-global with constant
![]() $4^8$
. By the choice of
$4^8$
. By the choice of
![]() $\rho $
, we may now use Theorem 3.3 to deduce that
$\rho $
, we may now use Theorem 3.3 to deduce that
Finally, we combine Lemma 5.13 and Lemma 5.14 to deduce the
![]() $L^q$
approximating polynomial.
$L^q$
approximating polynomial.
Proof of Lemma 3.6.
Let f be a function of degree d. By Lemma 5.13, there exists a P with
![]() $\|P\|\leqslant \rho ^{-O\left (d^{3}\right )}$
and
$\|P\|\leqslant \rho ^{-O\left (d^{3}\right )}$
and
![]() $P\left (0\right )=0$
such that the function
$P\left (0\right )=0$
such that the function
![]() $g=P\left (\mathrm {T}^{\left (\rho \right )}\right )f-f$
satisfies
$g=P\left (\mathrm {T}^{\left (\rho \right )}\right )f-f$
satisfies
![]() $\|g\|_{2}\leqslant n^{-2d}\|f\|_{2.}$
By Lemma 5.14,
$\|g\|_{2}\leqslant n^{-2d}\|f\|_{2.}$
By Lemma 5.14,
![]() $\|g\|_{q}\leqslant q^{4d}n^{-d}\|f\|_{2}\leqslant \frac {1}{\sqrt {n}}\|f\|_{2}$
, provided that C is sufficiently large, completing the proof.
$\|g\|_{q}\leqslant q^{4d}n^{-d}\|f\|_{2}\leqslant \frac {1}{\sqrt {n}}\|f\|_{2}$
, provided that C is sufficiently large, completing the proof.
6 Hypercontractivity: The direct approach
In this section, we give an alternative proof of a variant of Theorem 1.4. This approach starts by identifying a trivial spanning set of the space
![]() $V_t$
of degree t functions from Definition 2.1.
$V_t$
of degree t functions from Definition 2.1.
Notations. For technical reasons, it will be convenient for us to work with ordered sets. We denote by
![]() $[n]_t$
the collection of ordered sets of size t, which are simply t-tuples of distinct elements from
$[n]_t$
the collection of ordered sets of size t, which are simply t-tuples of distinct elements from
![]() $[n]$
, but we also allow set operations (such as
$[n]$
, but we also allow set operations (such as
![]() $\setminus $
) on them. We also denote
$\setminus $
) on them. We also denote
![]() $n_t = \left |[n]_t\right | = n(n-1)\cdots (n-t+1)$
. For ordered sets
$n_t = \left |[n]_t\right | = n(n-1)\cdots (n-t+1)$
. For ordered sets
![]() $I = {\left \{ i_1,\ldots ,i_t \right \}}$
,
$I = {\left \{ i_1,\ldots ,i_t \right \}}$
,
![]() $J = {\left \{ j_1,\ldots ,j_t \right \}}$
, we denote by
$J = {\left \{ j_1,\ldots ,j_t \right \}}$
, we denote by
![]() $1_{I\rightarrow J}(\pi )$
the indicator of
$1_{I\rightarrow J}(\pi )$
the indicator of
![]() $\pi (i_k) = j_k$
for all
$\pi (i_k) = j_k$
for all
![]() $k=1,\ldots ,t$
; for convenience, we also denote this by
$k=1,\ldots ,t$
; for convenience, we also denote this by
![]() $\pi (I) = J$
.
$\pi (I) = J$
.
With the above notations, the following set clearly spans
![]() $V_t$
, by definition:
$V_t$
, by definition:
We remark that this set is not a basis, since these functions are linearly dependent. For example, for
![]() $t=1$
we, have
$t=1$
we, have
![]() $\sum _{i=1}^{n} 1_{\pi (1) = i} - 1 = 0$
. This implies that a function
$\sum _{i=1}^{n} 1_{\pi (1) = i} - 1 = 0$
. This implies that a function
![]() $f\in V_{1}$
has several different representations as a linear combination of functions from the spanning set (4). The key to our approach is to show that there is a way to canonically choose such a linear combination, which is both unique and works well with computations of high moments.
$f\in V_{1}$
has several different representations as a linear combination of functions from the spanning set (4). The key to our approach is to show that there is a way to canonically choose such a linear combination, which is both unique and works well with computations of high moments.
Definition 6.1. Let
![]() $f\in V_{=t}$
and suppose that
$f\in V_{=t}$
and suppose that
![]() $f = \sum \limits _{I,J\in [n]_t} {a}({I},{J}) 1_{I\rightarrow J}$
. We say that this representation is normalised if
$f = \sum \limits _{I,J\in [n]_t} {a}({I},{J}) 1_{I\rightarrow J}$
. We say that this representation is normalised if
-
1. For any
 $1\leqslant r\leqslant t$
,
$1\leqslant r\leqslant t$
,
 $J = {\left \{ j_1,\ldots ,j_t \right \}}$
and
$J = {\left \{ j_1,\ldots ,j_t \right \}}$
and
 $I = {\left \{ i_1,\ldots ,i_{r-1}, i_{r+1},\ldots , i_t \right \}}$
we have that
$I = {\left \{ i_1,\ldots ,i_{r-1}, i_{r+1},\ldots , i_t \right \}}$
we have that  $$\begin{align*}\sum\limits_{i_r\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) = 0. \end{align*}$$
$$\begin{align*}\sum\limits_{i_r\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) = 0. \end{align*}$$
-
2. Analogously, for any
 $1\leqslant r\leqslant t$
,
$1\leqslant r\leqslant t$
,
 $I = {\left \{ i_1,\ldots ,i_t \right \}}$
and
$I = {\left \{ i_1,\ldots ,i_t \right \}}$
and
 $J = {\left \{ j_1,\ldots ,j_{r-1}, j_{r+1},\ldots , j_t \right \}}$
, we have that
$J = {\left \{ j_1,\ldots ,j_{r-1}, j_{r+1},\ldots , j_t \right \}}$
, we have that  $$\begin{align*}\sum\limits_{j_r\not\in J} {a}({I},{{\left\{ j_1,\ldots, j_t \right\}}}) = 0. \end{align*}$$
$$\begin{align*}\sum\limits_{j_r\not\in J} {a}({I},{{\left\{ j_1,\ldots, j_t \right\}}}) = 0. \end{align*}$$
-
3. Symmetry: for all ordered sets
 $I,J$
of size t and
$I,J$
of size t and
 $\pi \in S_t$
, we have
$\pi \in S_t$
, we have
 ${a}({I},{J}) = {a}({\pi (I)},{\pi (J)})$
.
${a}({I},{J}) = {a}({\pi (I)},{\pi (J)})$
.
More loosely, we say that a representation according to the spanning set (4) is normalised if averaging the coefficients according to a single coordinate results in
![]() $0$
. We also refer to the equalities in Definition 4 as ‘normalising relations’. In this section, we show that a normalised representation always exists and then show how it is useful in establishing hypercontractive statements similar to Theorem 1.4.
$0$
. We also refer to the equalities in Definition 4 as ‘normalising relations’. In this section, we show that a normalised representation always exists and then show how it is useful in establishing hypercontractive statements similar to Theorem 1.4.
Normalised representations first appear in the context of the slice by Dunkl [Reference Dunkl5], who called normalised representations harmonic functions. See also the monograph of Bannai and Ito [Reference Bannai and Ito1, III.3] and the papers [Reference Filmus8, Reference Filmus and Mossel9]. Ryan O’Donnell (personal communication) has proposed calling them zero-flux representations.
6.1 Finding a normalised representation
Lemma 6.2. Let
![]() $0\leqslant t\leqslant t$
and let
$0\leqslant t\leqslant t$
and let
![]() $f\in V_{t}$
. Then we may write
$f\in V_{t}$
. Then we may write
![]() $f = h + g$
, where
$f = h + g$
, where
![]() $h\in V_{t-1}$
and g is given by a set of coefficients satisfying the normalising relations
$h\in V_{t-1}$
and g is given by a set of coefficients satisfying the normalising relations
![]() $g = \sum \limits _{I,J\in [n]_t}{a}({I},{J})1_{I\rightarrow J}(\pi )$
.
$g = \sum \limits _{I,J\in [n]_t}{a}({I},{J})1_{I\rightarrow J}(\pi )$
.
Proof. The proof is by induction on t.
Fix
![]() $t\geqslant 1$
and
$t\geqslant 1$
and
![]() $f\in V_{t}$
. Then we may write
$f\in V_{t}$
. Then we may write
![]() $f(\pi ) = \sum \limits _{I,J\in [n]_t} {a}({I},{J}) 1_{I\rightarrow J}(\pi )$
, where the coefficients satisfy the symmetry property from Definition 6.1.
$f(\pi ) = \sum \limits _{I,J\in [n]_t} {a}({I},{J}) 1_{I\rightarrow J}(\pi )$
, where the coefficients satisfy the symmetry property from Definition 6.1.
Throughout the proof, we will change the coefficients in a sequential process and always maintain the form
![]() $f = h + \sum \limits _{\left |I\right | = \left |J\right |=t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
for
$f = h + \sum \limits _{\left |I\right | = \left |J\right |=t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
for
![]() $h\in V_{t-1}$
.
$h\in V_{t-1}$
.
Take
![]() $r\in [t]$
, and for each
$r\in [t]$
, and for each
![]() $I = {\left \{ i_1,\ldots ,i_t \right \}}$
,
$I = {\left \{ i_1,\ldots ,i_t \right \}}$
,
![]() $J = {\left \{ j_1,\ldots ,j_t \right \}}$
, define the coefficients
$J = {\left \{ j_1,\ldots ,j_t \right \}}$
, define the coefficients
 $$ \begin{align} {b}({I},{J}) = {a}({I},{J}) - \frac{1}{n-t+1}\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}} {a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}). \end{align} $$
$$ \begin{align} {b}({I},{J}) = {a}({I},{J}) - \frac{1}{n-t+1}\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}} {a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}). \end{align} $$
In Claim 6.3 below, we prove that after making this change of coefficients, we may write
![]() $f = h + \sum \limits _{\left |I\right | = \left |J\right |=t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
and that the coefficients
$f = h + \sum \limits _{\left |I\right | = \left |J\right |=t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
and that the coefficients
![]() ${b}({I},{J})$
satisfy all normalising relations that the
${b}({I},{J})$
satisfy all normalising relations that the
![]() ${a}({I},{J})$
do, as well as the normalising relations from the first collection in Definition 6.1 for r. We repeat this process for all
${a}({I},{J})$
do, as well as the normalising relations from the first collection in Definition 6.1 for r. We repeat this process for all
![]() $r\in [t]$
.
$r\in [t]$
.
After this process is done, we have
![]() $f = h + \sum \limits _{I,J\in [n]_t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
, where the coefficients
$f = h + \sum \limits _{I,J\in [n]_t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
, where the coefficients
![]() ${a}({I},{J})$
satisfy the first collection of normalising relations from Definition 6.1. We can now perform the analogous process on the J part, and by symmetry obtain that after this process, the second collection of normalising relations in Definition 6.1 hold. One only has to check that this does not destroy the first collection of normalising relations, which we also prove in Claim 6.3.
${a}({I},{J})$
satisfy the first collection of normalising relations from Definition 6.1. We can now perform the analogous process on the J part, and by symmetry obtain that after this process, the second collection of normalising relations in Definition 6.1 hold. One only has to check that this does not destroy the first collection of normalising relations, which we also prove in Claim 6.3.
Finally, we symmetrize f to ensure that it satisfies the symmetry condition. To do so, we replace
![]() $b(I,J)$
with the average of
$b(I,J)$
with the average of
![]() $b(\pi (I),\pi (J))$
over all
$b(\pi (I),\pi (J))$
over all
![]() $\pi \in S_t$
, which does not change the function since
$\pi \in S_t$
, which does not change the function since
![]() $1_{I\to J} = 1_{\pi (I)\to \pi (J)}$
.
$1_{I\to J} = 1_{\pi (I)\to \pi (J)}$
.
Claim 6.3. The change of coefficients (5) has the following properties:
-
1. The coefficients
 ${b}({I},{J})$
satisfy the normalising relation in the first item for r in Definition 6.1.
${b}({I},{J})$
satisfy the normalising relation in the first item for r in Definition 6.1. -
2. If the coefficients
 ${a}({I},{J})$
satisfy the normalising relation in the first item in Definition 6.1 for
${a}({I},{J})$
satisfy the normalising relation in the first item in Definition 6.1 for
 $r' \neq r$
, then so do
$r' \neq r$
, then so do
 ${b}({I},{J})$
.
${b}({I},{J})$
. -
3. If the coefficients
 ${a}({I},{J})$
satisfy the normalising relation in the second item in Definition 6.1 for
${a}({I},{J})$
satisfy the normalising relation in the second item in Definition 6.1 for
 $r'$
, then so do
$r'$
, then so do
 ${b}({I},{J})$
.
${b}({I},{J})$
. -
4. We may write
 $f = h + \sum \limits _{\left |I\right | = \left |J\right |=t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
, where
$f = h + \sum \limits _{\left |I\right | = \left |J\right |=t} {b}({I},{J}) 1_{I\rightarrow J}(\pi )$
, where
 $h\in V_{t-1}$
.
$h\in V_{t-1}$
.
Proof. We prove each one of the items separately.
Proof of the first item.
Fix
![]() $I = {\left \{ i_1,\ldots ,i_{r-1},i_{r+1}\ldots ,i_t \right \}}$
,
$I = {\left \{ i_1,\ldots ,i_{r-1},i_{r+1}\ldots ,i_t \right \}}$
,
![]() $J = {\left \{ j_1,\ldots ,j_t \right \}}$
and calculate:
$J = {\left \{ j_1,\ldots ,j_t \right \}}$
and calculate:
 $$ \begin{align} \sum\limits_{i_r\not\in I} {b}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) &= \sum\limits_{i_r\not\in I} \Bigg({a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) - \frac{1}{n-t+1}\sum\limits_{i\not\in I}{a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}) \Bigg)\notag\\ &= \sum\limits_{i_r\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) -\frac{1}{n-t+1} \sum\limits_{\substack{i_r\not\in I\\i\not\in I}} {a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}). \end{align} $$
$$ \begin{align} \sum\limits_{i_r\not\in I} {b}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) &= \sum\limits_{i_r\not\in I} \Bigg({a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) - \frac{1}{n-t+1}\sum\limits_{i\not\in I}{a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}) \Bigg)\notag\\ &= \sum\limits_{i_r\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) -\frac{1}{n-t+1} \sum\limits_{\substack{i_r\not\in I\\i\not\in I}} {a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}). \end{align} $$
As in the second double sum, for each
![]() $i_r$
the coefficient
$i_r$
the coefficient
![]() ${a}({{\left \{ i_1,\ldots ,i_{r-1}, i_r, i_{r+1},\ldots ,i_t \right \}}},{J})$
is counted
${a}({{\left \{ i_1,\ldots ,i_{r-1}, i_r, i_{r+1},\ldots ,i_t \right \}}},{J})$
is counted
![]() $n-\left |I\right | = n-t+1$
times, we get that the above expression is equal to
$n-\left |I\right | = n-t+1$
times, we get that the above expression is equal to
![]() $0$
.
$0$
.
Proof of the second item.
Fix
![]() $r' \neq r$
and suppose
$r' \neq r$
and suppose
![]() ${a}({\cdot },{\cdot })$
satisfy the first set of normalising relations for
${a}({\cdot },{\cdot })$
satisfy the first set of normalising relations for
![]() $r'$
. Without loss of generality, assume
$r'$
. Without loss of generality, assume
![]() $r'<r$
. Let
$r'<r$
. Let
![]() $I = {\left \{ i_1,\ldots ,i_{r'-1},i_{r'+1},\ldots ,i_t \right \}}$
,
$I = {\left \{ i_1,\ldots ,i_{r'-1},i_{r'+1},\ldots ,i_t \right \}}$
,
![]() $J = {\left \{ j_1,\ldots ,j_t \right \}}$
. Below, we let
$J = {\left \{ j_1,\ldots ,j_t \right \}}$
. Below, we let
![]() $i, i_{r'}$
be summation indices and we denote
$i, i_{r'}$
be summation indices and we denote
![]() $I' = {\left \{ i_1,\ldots ,i_{r'-1},i_{r'},i_{r'+1},\ldots ,i_{r-1},i,i_r,\ldots ,,i_t \right \}}$
. Calculating as in (6):
$I' = {\left \{ i_1,\ldots ,i_{r'-1},i_{r'},i_{r'+1},\ldots ,i_{r-1},i,i_r,\ldots ,,i_t \right \}}$
. Calculating as in (6):
 $$ \begin{align} \sum\limits_{i_{r'}\not\in I} {b}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) &= \sum\limits_{i_{r'}\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) - \frac{1}{n-t+1}\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}}{a}({I'},{J})\notag\\ &= \sum\limits_{i_{r'}\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) -\frac{1}{n-t+1} \sum\limits_{i_{r'}\not\in I} \sum\limits_{i\not\in I\setminus{\left\{ i_{r} \right\}}}{a}({I'},{J}). \end{align} $$
$$ \begin{align} \sum\limits_{i_{r'}\not\in I} {b}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) &= \sum\limits_{i_{r'}\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) - \frac{1}{n-t+1}\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}}{a}({I'},{J})\notag\\ &= \sum\limits_{i_{r'}\not\in I} {a}({{\left\{ i_1,\ldots,i_t \right\}}},{J}) -\frac{1}{n-t+1} \sum\limits_{i_{r'}\not\in I} \sum\limits_{i\not\in I\setminus{\left\{ i_{r} \right\}}}{a}({I'},{J}). \end{align} $$
The first sum is
![]() $0$
by the assumption of the second item. For the second sum, we interchange the order of summation to see that it is equal to
$0$
by the assumption of the second item. For the second sum, we interchange the order of summation to see that it is equal to
![]() $\sum \limits _{i\not \in I\setminus {\left \{ i_r \right \}}} \sum \limits _{i_{r'}\not \in I} {a}({I'},{J})$
, and note that for each i, the inner sum is
$\sum \limits _{i\not \in I\setminus {\left \{ i_r \right \}}} \sum \limits _{i_{r'}\not \in I} {a}({I'},{J})$
, and note that for each i, the inner sum is
![]() $0$
again by the assumption of the second item.
$0$
again by the assumption of the second item.
Proof of the third item.
Fix
![]() $r'$
and suppose
$r'$
and suppose
![]() ${a}({\cdot },{\cdot })$
satisfy the second set of normalising relations for
${a}({\cdot },{\cdot })$
satisfy the second set of normalising relations for
![]() $r'$
. Fix
$r'$
. Fix
![]() $I = \{i_1,\ldots ,i_t\}$
,
$I = \{i_1,\ldots ,i_t\}$
,
![]() $J = \{j_1,\ldots ,j_{r'-1},j_{r'+1},\ldots ,j_t\}$
,
$J = \{j_1,\ldots ,j_{r'-1},j_{r'+1},\ldots ,j_t\}$
,
![]() $I' = \{i_1,\ldots ,i_{r-1},i,i_{r+1},\ldots ,i_t\}$
,
$I' = \{i_1,\ldots ,i_{r-1},i,i_{r+1},\ldots ,i_t\}$
,
![]() $J' = \{j_1,\ldots ,j_t\}$
and calculate
$J' = \{j_1,\ldots ,j_t\}$
and calculate
 $$ \begin{align} \sum_{j_r \notin J} b(I,J') &= \sum_{j_r \notin J} \left(a(I,J') - \frac{1}{n-t+1} \sum_{i \notin I \setminus \{i_r\}} a(I',J') \right) \notag \\ &= \sum_{j_r \notin J} a(I,J') - \frac{1}{n-t+1} \sum_{i \notin I \setminus \{i_r\}} \sum_{j_r \notin J} a(I',J'). \end{align} $$
$$ \begin{align} \sum_{j_r \notin J} b(I,J') &= \sum_{j_r \notin J} \left(a(I,J') - \frac{1}{n-t+1} \sum_{i \notin I \setminus \{i_r\}} a(I',J') \right) \notag \\ &= \sum_{j_r \notin J} a(I,J') - \frac{1}{n-t+1} \sum_{i \notin I \setminus \{i_r\}} \sum_{j_r \notin J} a(I',J'). \end{align} $$
Once again, both sums vanish due to the assumption.
Proof of the fourth item.
For
![]() $I = {\left \{ i_1,\ldots ,i_t \right \}}$
,
$I = {\left \{ i_1,\ldots ,i_t \right \}}$
,
![]() $J = {\left \{ j_1,\ldots ,j_t \right \}}$
, denote
$J = {\left \{ j_1,\ldots ,j_t \right \}}$
, denote
 $$\begin{align*}{c}({I},{J}) = \frac{1}{n-t+1}\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}}{a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}), \end{align*}$$
$$\begin{align*}{c}({I},{J}) = \frac{1}{n-t+1}\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}}{a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}), \end{align*}$$
so that
![]() ${a}({I},{J}) = {b}({I},{J}) + {c}({I},{J})$
. Plugging this into the representation of f, we see that it is enough to prove that
${a}({I},{J}) = {b}({I},{J}) + {c}({I},{J})$
. Plugging this into the representation of f, we see that it is enough to prove that
![]() $h(\pi ) = \sum \limits _{I,J} {c}({I},{J}) 1_{I\rightarrow J}(\pi )$
is in
$h(\pi ) = \sum \limits _{I,J} {c}({I},{J}) 1_{I\rightarrow J}(\pi )$
is in
![]() $V_{t-1}$
. Writing
$V_{t-1}$
. Writing
![]() $I' = I\setminus {\left \{ i_r \right \}}$
,
$I' = I\setminus {\left \{ i_r \right \}}$
,
![]() $J' = J\setminus {\left \{ j_r \right \}}$
and expanding, we see that
$J' = J\setminus {\left \{ j_r \right \}}$
and expanding, we see that
 $$ \begin{align*} h(\pi) &= \frac{1}{n-t+1}\sum\limits_{I,J}1_{I\rightarrow J}(\pi)\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}}{a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J})\\ &= \frac{1}{n-t+1}\sum\limits_{I',J'} \sum\limits_{i\not\in I', j_r\not\in J'} {a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}) \sum\limits_{i_r\not\in I'} 1_{I\rightarrow J}(\pi). \end{align*} $$
$$ \begin{align*} h(\pi) &= \frac{1}{n-t+1}\sum\limits_{I,J}1_{I\rightarrow J}(\pi)\sum\limits_{i\not\in I\setminus{\left\{ i_r \right\}}}{a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J})\\ &= \frac{1}{n-t+1}\sum\limits_{I',J'} \sum\limits_{i\not\in I', j_r\not\in J'} {a}({{\left\{ i_1,\ldots,i_{r-1}, i, i_{r+1},\ldots,i_t \right\}}},{J}) \sum\limits_{i_r\not\in I'} 1_{I\rightarrow J}(\pi). \end{align*} $$
Noting that
![]() $\sum \limits _{i_r\not \in I'} 1_{I\rightarrow J}(\pi ) = 1_{I'\rightarrow J'}(\pi )$
is in the spanning set (4) for
$\sum \limits _{i_r\not \in I'} 1_{I\rightarrow J}(\pi ) = 1_{I'\rightarrow J'}(\pi )$
is in the spanning set (4) for
![]() $t-1$
, the proof is concluded.
$t-1$
, the proof is concluded.
Applying Lemma 6.2 iteratively, we may write each
![]() $f\colon S_n\to \mathbb {R}$
of degree at most t as
$f\colon S_n\to \mathbb {R}$
of degree at most t as
![]() $f = f_0+\ldots +f_d$
, where for each
$f = f_0+\ldots +f_d$
, where for each
![]() $k=0,1,\ldots ,d$
, the function
$k=0,1,\ldots ,d$
, the function
![]() $f_k$
is in
$f_k$
is in
![]() $V_k$
and is given by a list of coefficients satisfying the normalising relations.
$V_k$
and is given by a list of coefficients satisfying the normalising relations.
6.2 Usefulness of normalised representations
In this section, we establish a claim that demonstrates the usefulness of the normalising relations. Informally, this claim often serves as a replacement for the orthogonality property that is so useful in product spaces. Formally, it allows us to turn long sums into short sums and is very helpful in various computations arising in computations in norms of functions on
![]() $S_n$
that are given in a normalised representation.
$S_n$
that are given in a normalised representation.
Claim 6.4. Let
![]() $r\in {\left \{ 1,\ldots ,d \right \}}$
,
$r\in {\left \{ 1,\ldots ,d \right \}}$
,
![]() $0\leqslant t<r$
. Let J be of size r, I be of size at least r, and
$0\leqslant t<r$
. Let J be of size r, I be of size at least r, and
![]() $R\subseteq I$
of size
$R\subseteq I$
of size
![]() $r-t$
. Then
$r-t$
. Then
 $$\begin{align*}\sum\limits_{T \in ([n]\setminus I)_t}{{a}({R\circ T},{J})} =(-1)^t~\sum\limits_{T\in (I\setminus R)_t}{a}({R\circ T},{J}). \end{align*}$$
$$\begin{align*}\sum\limits_{T \in ([n]\setminus I)_t}{{a}({R\circ T},{J})} =(-1)^t~\sum\limits_{T\in (I\setminus R)_t}{a}({R\circ T},{J}). \end{align*}$$
Here,
![]() $R\circ T$
denotes the element in
$R\circ T$
denotes the element in
![]() $[n]_r$
resulting from appending T at the end of R.
$[n]_r$
resulting from appending T at the end of R.
Proof. By symmetry, it suffices to prove the statement for R that are prefixes of I. We prove the claim by induction on t. The case
![]() $t=0$
is trivial, so assume the claim holds for
$t=0$
is trivial, so assume the claim holds for
![]() $t-1$
, where
$t-1$
, where
![]() $t\geqslant 1$
, and prove for t. The left-hand side is equal to
$t\geqslant 1$
, and prove for t. The left-hand side is equal to
 $$\begin{align*}\sum\limits_{\substack{i_1,\ldots,i_t\not\in I\\ \text{distinct}}}{{a}({R\circ (i_1,\ldots,i_t)},{J})}. \end{align*}$$
$$\begin{align*}\sum\limits_{\substack{i_1,\ldots,i_t\not\in I\\ \text{distinct}}}{{a}({R\circ (i_1,\ldots,i_t)},{J})}. \end{align*}$$
For fixed
![]() $i_1,\ldots ,i_{t-1}\not \in I$
, by the normalising relations, we have that
$i_1,\ldots ,i_{t-1}\not \in I$
, by the normalising relations, we have that
 $$\begin{align*}\sum\limits_{i_t\not\in I\cup{\left\{ i_1,\ldots,i_{t-1} \right\}}}{{a}({R\circ (i_1,\ldots,i_{t-1})\circ (i_t)},{J})} = -\sum\limits_{i_t\in I\setminus R}{{a}({R\circ (i_1,i_2,\ldots,i_{t-1})\circ (i_t)},{J})}. \end{align*}$$
$$\begin{align*}\sum\limits_{i_t\not\in I\cup{\left\{ i_1,\ldots,i_{t-1} \right\}}}{{a}({R\circ (i_1,\ldots,i_{t-1})\circ (i_t)},{J})} = -\sum\limits_{i_t\in I\setminus R}{{a}({R\circ (i_1,i_2,\ldots,i_{t-1})\circ (i_t)},{J})}. \end{align*}$$
Hence,
 $$\begin{align*}\sum\limits_{\substack{i_1,\ldots,i_t\not\in I\\ \text{distinct}}}{ {a}({R\circ (i_1,\ldots,i_t)},{J})} =-\sum\limits_{i_t\in I\setminus R}{ \sum\limits_{\substack{~~~i_1,\ldots,i_{t-1}\not\in I\cup {\left\{ i_t \right\}}\\ \text{distinct}}}{{a}({R\circ (i_1,i_2,\ldots,i_{t-1})\circ i_t},{J})}}. \end{align*}$$
$$\begin{align*}\sum\limits_{\substack{i_1,\ldots,i_t\not\in I\\ \text{distinct}}}{ {a}({R\circ (i_1,\ldots,i_t)},{J})} =-\sum\limits_{i_t\in I\setminus R}{ \sum\limits_{\substack{~~~i_1,\ldots,i_{t-1}\not\in I\cup {\left\{ i_t \right\}}\\ \text{distinct}}}{{a}({R\circ (i_1,i_2,\ldots,i_{t-1})\circ i_t},{J})}}. \end{align*}$$
For fixed
![]() $i_t\in I\setminus R$
, using the induction hypothesis, the inner sum is equal to
$i_t\in I\setminus R$
, using the induction hypothesis, the inner sum is equal to
 $$\begin{align*}(-1)^{t-1} \sum\limits_{T\in (I\setminus (R\cup{\left\{ i_t \right\}}))_{t-1}}{a}({R\circ T\circ (i_t)},{J}). \end{align*}$$
$$\begin{align*}(-1)^{t-1} \sum\limits_{T\in (I\setminus (R\cup{\left\{ i_t \right\}}))_{t-1}}{a}({R\circ T\circ (i_t)},{J}). \end{align*}$$
Plugging that in,
 $$ \begin{align*} \sum\limits_{\substack{i_1,\ldots,i_t\not\in I\\ \text{distinct}}}{ {a}({R\circ (i_1,\ldots,i_t)},{J})} &=(-1)^{t-1}~\sum\limits_{i_t\in I\setminus R}{-\sum\limits_{T\in (I\setminus (R\cup{\left\{ i_t \right\}}))_{t-1}}{a}({R\circ T\circ (i_t)},{J})}\\ &=(-1)^t \sum\limits_{T'\in (I\setminus R)_t}{a}({R\circ T'},{J}).\\[-47pt] \end{align*} $$
$$ \begin{align*} \sum\limits_{\substack{i_1,\ldots,i_t\not\in I\\ \text{distinct}}}{ {a}({R\circ (i_1,\ldots,i_t)},{J})} &=(-1)^{t-1}~\sum\limits_{i_t\in I\setminus R}{-\sum\limits_{T\in (I\setminus (R\cup{\left\{ i_t \right\}}))_{t-1}}{a}({R\circ T\circ (i_t)},{J})}\\ &=(-1)^t \sum\limits_{T'\in (I\setminus R)_t}{a}({R\circ T'},{J}).\\[-47pt] \end{align*} $$
6.3 Analytic influences and the hypercontractive statement
Key to the hypercontractive statement proved in this section is an analytic notion of influence. Given a fixed representation of f as
![]() $\sum \limits _{k=0}^{n}\sum \limits _{I,J\in [n]_k}{{a}({I},{J}) 1_{I\rightarrow J}}$
where for each k the coefficients
$\sum \limits _{k=0}^{n}\sum \limits _{I,J\in [n]_k}{{a}({I},{J}) 1_{I\rightarrow J}}$
where for each k the coefficients
![]() ${a}({I},{J})$
satisfy the normalising relations, we define the analytic notion of influences as follows.
${a}({I},{J})$
satisfy the normalising relations, we define the analytic notion of influences as follows.
Definition 6.5. For
![]() $S,T\subseteq [n]$
of the same size s, define
$S,T\subseteq [n]$
of the same size s, define
 $$\begin{align*}I_{S,T}[f] = \sum\limits_{r\geqslant 0} \sum\limits_{\substack{I\in ([n]\setminus S)_r\\J\in ([n]\setminus T)_r}} { (r+s)!^2 \frac{1}{n^{r+s}} {a}({S\circ I},{T\circ J})^2}. \end{align*}$$
$$\begin{align*}I_{S,T}[f] = \sum\limits_{r\geqslant 0} \sum\limits_{\substack{I\in ([n]\setminus S)_r\\J\in ([n]\setminus T)_r}} { (r+s)!^2 \frac{1}{n^{r+s}} {a}({S\circ I},{T\circ J})^2}. \end{align*}$$
Definition 6.6. A function f is called
![]() $\varepsilon $
-analytically-global if for all
$\varepsilon $
-analytically-global if for all
![]() $S,T$
,
$S,T$
,
![]() $I_{S,T}[f]\leqslant \varepsilon $
.
$I_{S,T}[f]\leqslant \varepsilon $
.
Remark 6.7. With some work, it can be shown that for
![]() $d\ll n$
, a degree d function being
$d\ll n$
, a degree d function being
![]() $\varepsilon $
-analytically global is equivalent to f being
$\varepsilon $
-analytically global is equivalent to f being
![]() $(2d,\delta )$
-global in the sense of Definition 1.3, where
$(2d,\delta )$
-global in the sense of Definition 1.3, where
![]() $\delta = O_d(\varepsilon )$
. Thus, at least qualitatively, the hypercontractive statement below is in fact equivalent to Theorem 1.4.
$\delta = O_d(\varepsilon )$
. Thus, at least qualitatively, the hypercontractive statement below is in fact equivalent to Theorem 1.4.
We can now state our variant of the hypercontractive inequality that uses analytic influences.
Theorem 6.8. There exists an absolute constant
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $d,n\in \mathbb {N}$
for which
$d,n\in \mathbb {N}$
for which
![]() $n\geqslant 2^{C\cdot d\log d}$
, the following holds. If
$n\geqslant 2^{C\cdot d\log d}$
, the following holds. If
![]() $f\in V_{d}$
is given by a list of coefficients satisfying the normalising relations, say
$f\in V_{d}$
is given by a list of coefficients satisfying the normalising relations, say
![]() $f = \sum \limits _{I,J\in [n]_d} {a}({I},{J}) 1_{I\rightarrow J}$
, then
$f = \sum \limits _{I,J\in [n]_d} {a}({I},{J}) 1_{I\rightarrow J}$
, then
 $$\begin{align*}{\mathop{\mathbb{E}}_{\pi}\left[ {f(\pi)^4} \right]}\leqslant \sum\limits_{\left|S\right|=\left|T\right|}\left(\frac{4}{n}\right)^{\left|S\right|} I_{S,T}[f]^2. \end{align*}$$
$$\begin{align*}{\mathop{\mathbb{E}}_{\pi}\left[ {f(\pi)^4} \right]}\leqslant \sum\limits_{\left|S\right|=\left|T\right|}\left(\frac{4}{n}\right)^{\left|S\right|} I_{S,T}[f]^2. \end{align*}$$
p-biased hypercontractivity.
The last ingredient we use in our proof is a hypercontractive inequality on the p-biased cube from [Reference Keevash, Lifshitz, Long and Minzer17]. Let
![]() $g\colon {\left \{ 0,1 \right \}}^{m}\to \mathbb {R}$
be a degree d function, where we think of
$g\colon {\left \{ 0,1 \right \}}^{m}\to \mathbb {R}$
be a degree d function, where we think of
![]() ${\left \{ 0,1 \right \}}^{m}$
as equipped with the p-biased product measure. Then we may write g in the basis of characters (i.e., as a linear combination of
${\left \{ 0,1 \right \}}^{m}$
as equipped with the p-biased product measure. Then we may write g in the basis of characters (i.e., as a linear combination of
![]() ${\left \{ \chi _S \right \}}_{S\subseteq [m]}$
, where
${\left \{ \chi _S \right \}}_{S\subseteq [m]}$
, where
![]() $\chi _S(x) = \prod \limits _{i\in S}\frac {x_i - p}{\sqrt {p(1-p)}}$
). This is the p-biased Fourier transform of f:
$\chi _S(x) = \prod \limits _{i\in S}\frac {x_i - p}{\sqrt {p(1-p)}}$
). This is the p-biased Fourier transform of f:
Next, we define the generalised influences of sets (which are very close in spirit to the analytic notion of influences considered herein). For
![]() $T\subseteq [n]$
, we denote
$T\subseteq [n]$
, we denote
The following result is an easy consequence of [Reference Keevash, Lifshitz, Long and Minzer17, Theorem 3.4] (the deduction of it from this result is done in the same way as the proof of [Reference Keevash, Lifshitz, Long and Minzer17, Lemma 3.6]).
Theorem 6.9. Suppose
![]() $g\colon {\left \{ 0,1 \right \}}^{m}\to \mathbb {R}$
. Then
$g\colon {\left \{ 0,1 \right \}}^{m}\to \mathbb {R}$
. Then
![]() $\left \|g\right \|_4^4\leqslant \sum \limits _{T\subseteq [n]}(3p)^{\left |T\right |} I_T[g]^2$
.
$\left \|g\right \|_4^4\leqslant \sum \limits _{T\subseteq [n]}(3p)^{\left |T\right |} I_T[g]^2$
.
6.4 Proof of Theorem 6.8
Write f according to its normalised representation as
![]() $f(\pi ) = \sum \limits _{I,J\in [n]_d} {a}({I},{J}) 1_{I\rightarrow J}$
. We intend to define a function
$f(\pi ) = \sum \limits _{I,J\in [n]_d} {a}({I},{J}) 1_{I\rightarrow J}$
. We intend to define a function
![]() $g\colon {\left \{ 0,1 \right \}}^{n\times n} \to \mathbb {R}$
that will behave similarly to f, as follows. We think of
$g\colon {\left \{ 0,1 \right \}}^{n\times n} \to \mathbb {R}$
that will behave similarly to f, as follows. We think of
![]() ${\left \{ 0,1 \right \}}^{n\times n}$
as equipped with the p-biased measure for
${\left \{ 0,1 \right \}}^{n\times n}$
as equipped with the p-biased measure for
![]() $p=1/n$
and think of an input
$p=1/n$
and think of an input
![]() $x\in {\left \{ 0,1 \right \}}^{n\times n}$
as a matrix. The rationale is that the bit
$x\in {\left \{ 0,1 \right \}}^{n\times n}$
as a matrix. The rationale is that the bit
![]() $x_{i,j}$
being
$x_{i,j}$
being
![]() $1$
will encode the fact that
$1$
will encode the fact that
![]() $\pi (i) = j$
, but we will never actually think about it this way. Thus, we define g as
$\pi (i) = j$
, but we will never actually think about it this way. Thus, we define g as
 $$\begin{align*}g(x) = \sum\limits_{I,J\in[n]_d} {a}({I},{J}) \prod\limits_{\ell=1}^{d}\left(x_{I_\ell,J_\ell} - \frac{1}{n}\right). \end{align*}$$
$$\begin{align*}g(x) = \sum\limits_{I,J\in[n]_d} {a}({I},{J}) \prod\limits_{\ell=1}^{d}\left(x_{I_\ell,J_\ell} - \frac{1}{n}\right). \end{align*}$$
For
![]() $I,J$
, we denote by
$I,J$
, we denote by
![]() $S_{I,J}\subseteq [n\times n]$
the set of coordinates
$S_{I,J}\subseteq [n\times n]$
the set of coordinates
![]() $\left \{ \left. (I_{\ell },J_{\ell }) \;\right \vert \ell =1,\ldots ,d \right \}$
and note that with this notation,
$\left \{ \left. (I_{\ell },J_{\ell }) \;\right \vert \ell =1,\ldots ,d \right \}$
and note that with this notation,
 $$\begin{align*}g(x) = \sum\limits_{I,J\in[n]_d} \sqrt{p(1-p)}^{d} {a}({I},{J}) \chi_{S_{I,J}}(x). \end{align*}$$
$$\begin{align*}g(x) = \sum\limits_{I,J\in[n]_d} \sqrt{p(1-p)}^{d} {a}({I},{J}) \chi_{S_{I,J}}(x). \end{align*}$$
To complete the proof, we first show (Claim 6.10) that
![]() $\left \|f\right \|_4^4\leqslant (1+o(1))\left \|g\right \|_4^4$
and then prove the desired upper bound on the
$\left \|f\right \|_4^4\leqslant (1+o(1))\left \|g\right \|_4^4$
and then prove the desired upper bound on the
![]() $4$
-norm of g using Theorem 6.9.
$4$
-norm of g using Theorem 6.9.
Claim 6.10.
![]() $\left \|f\right \|_4^4\leqslant (1+o(1))\left \|g\right \|_4^4$
$\left \|f\right \|_4^4\leqslant (1+o(1))\left \|g\right \|_4^4$
Proof. Deferred to Section 6.4.1.
We now upper-bound
![]() $\left \|g\right \|_4^4$
. Using Theorem 6.9,
$\left \|g\right \|_4^4$
. Using Theorem 6.9,
and the next claim bounds the generalised influences of g by the analytic influences of f.
For two sets
![]() $I=\{i_1,\ldots ,i_t\}$
,
$I=\{i_1,\ldots ,i_t\}$
,
![]() $J=\{j_1,\ldots ,j_t\}$
of the same size, let
$J=\{j_1,\ldots ,j_t\}$
of the same size, let
![]() $S(I,J) = \{(i_1,j_1),\ldots ,(i_t,j_t)\} \subseteq [n]\times [n]$
.
$S(I,J) = \{(i_1,j_1),\ldots ,(i_t,j_t)\} \subseteq [n]\times [n]$
.
Claim 6.11. Let
![]() $T = S(I',J')$
be such that
$T = S(I',J')$
be such that
![]() $I_T[g]\neq 0$
. Then
$I_T[g]\neq 0$
. Then
![]() $I_T[g]\leqslant I_{I',J'}[f]$
.
$I_T[g]\leqslant I_{I',J'}[f]$
.
Proof. Take T in this sum for which
![]() $I_T[g]\neq 0$
and denote
$I_T[g]\neq 0$
and denote
![]() $t=\left |T\right |$
. Then
$t=\left |T\right |$
. Then
![]() $T = {\left \{ (i_1,j_1),\ldots ,(i_t,j_t) \right \}} = S(I',J')$
for
$T = {\left \{ (i_1,j_1),\ldots ,(i_t,j_t) \right \}} = S(I',J')$
for
![]() $I' = {\left \{ i_1,\ldots ,i_t \right \}}$
,
$I' = {\left \{ i_1,\ldots ,i_t \right \}}$
,
![]() $J'={\left \{ j_1,\ldots ,j_t \right \}}$
that are consistent. For
$J'={\left \{ j_1,\ldots ,j_t \right \}}$
that are consistent. For
![]() $Q\subseteq [n]\times [n]$
of size d such that
$Q\subseteq [n]\times [n]$
of size d such that
![]() $T\subseteq Q$
, let
$T\subseteq Q$
, let
![]() $S_{Q,T} = \left \{ \left. (I,J) \;\right \vert T\subseteq S(I,J) = Q \right \}$
and note that by the symmetry normalising relation,
$S_{Q,T} = \left \{ \left. (I,J) \;\right \vert T\subseteq S(I,J) = Q \right \}$
and note that by the symmetry normalising relation,
![]() ${a}({I},{J})$
is constant on
${a}({I},{J})$
is constant on
![]() $(I,J)\in S_{Q,T}$
. We thus get
$(I,J)\in S_{Q,T}$
. We thus get
 $$\begin{align*}I_T[g] =\sum\limits_{Q}{\left(\sum\limits_{(I,J)\in S_{Q,T}}\sqrt{p(1-p)}^d{a}({I},{J})\right)^2} \leqslant d! p^d\sum\limits_{Q}{\sum\limits_{(I,J)\in S_{Q,T}}{a}({I},{J})^2}, \end{align*}$$
$$\begin{align*}I_T[g] =\sum\limits_{Q}{\left(\sum\limits_{(I,J)\in S_{Q,T}}\sqrt{p(1-p)}^d{a}({I},{J})\right)^2} \leqslant d! p^d\sum\limits_{Q}{\sum\limits_{(I,J)\in S_{Q,T}}{a}({I},{J})^2}, \end{align*}$$
where we used the fact that the size of
![]() $S_{Q,T}$
is
$S_{Q,T}$
is
![]() $d!$
. Rewriting the sum by first choosing the locations of T in
$d!$
. Rewriting the sum by first choosing the locations of T in
![]() $(I,J)$
, we get that the last sum is at most
$(I,J)$
, we get that the last sum is at most
 $$\begin{align*}d_t \sum\limits_{\substack{I\in ([n]\setminus I')_{d-t}\\J\in ([n]\setminus J')_{d-t}}} {a}({I'\circ I},{J'\circ J})^2. \end{align*}$$
$$\begin{align*}d_t \sum\limits_{\substack{I\in ([n]\setminus I')_{d-t}\\J\in ([n]\setminus J')_{d-t}}} {a}({I'\circ I},{J'\circ J})^2. \end{align*}$$
Combining all, we get that
 $I_T[g]\leqslant \sum \limits _{\substack {I\in ([n]\setminus I')_{d-t}\\J\in ([n]\setminus J')_{d-t}}} d!^2\frac {1}{n^d} {a}({I'\circ I},{J'\circ J})^2 = I_{I',J'}[g]$
.
$I_T[g]\leqslant \sum \limits _{\substack {I\in ([n]\setminus I')_{d-t}\\J\in ([n]\setminus J')_{d-t}}} d!^2\frac {1}{n^d} {a}({I'\circ I},{J'\circ J})^2 = I_{I',J'}[g]$
.
Plugging in Claim 6.11 into (9) and using Claim 6.10 finishes the proof of Theorem 6.8.
6.4.1 Proof of Claim 6.10
Let
![]() $I_r$
and
$I_r$
and
![]() $J_r$
be d-tuples of distinct indices from
$J_r$
be d-tuples of distinct indices from
![]() $[n]$
. Then
$[n]$
. Then
 $$\begin{align*}{\mathop{\mathbb{E}}_{\pi}\left[ {f(\pi)^4} \right]} =\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4}}{{a}({I_1},{J_1})\cdots{a}({I_4},{J_4}) {\mathop{\mathbb{E}}_{\pi}\left[ {1_{\pi(I_1) = J_1}\cdots 1_{\pi(I_4) = J_4}} \right]}}. \end{align*}$$
$$\begin{align*}{\mathop{\mathbb{E}}_{\pi}\left[ {f(\pi)^4} \right]} =\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4}}{{a}({I_1},{J_1})\cdots{a}({I_4},{J_4}) {\mathop{\mathbb{E}}_{\pi}\left[ {1_{\pi(I_1) = J_1}\cdots 1_{\pi(I_4) = J_4}} \right]}}. \end{align*}$$
Consider the collection of constraints on
![]() $\pi $
in the product of the indicators. To be nonzero, the constraints should be consistent, so we only consider such tuples. Let M be the number of different elements that appear in
$\pi $
in the product of the indicators. To be nonzero, the constraints should be consistent, so we only consider such tuples. Let M be the number of different elements that appear in
![]() $I_1,\ldots ,I_4$
(which is at least d and at most
$I_1,\ldots ,I_4$
(which is at least d and at most
![]() $4d$
). We partition the outer sum according to M and upper-bound the contribution from each M separately. Fix M; then the contribution from it is
$4d$
). We partition the outer sum according to M and upper-bound the contribution from each M separately. Fix M; then the contribution from it is
 $$\begin{align*}\frac{1}{n_M}\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\ \text{type }M}}{a}({I_1},{J_1})\cdots{a}({I_4},{J_4}). \end{align*}$$
$$\begin{align*}\frac{1}{n_M}\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\ \text{type }M}}{a}({I_1},{J_1})\cdots{a}({I_4},{J_4}). \end{align*}$$
We would like to further partition this sum according to the pattern in which the M different elements of
![]() $I_1,\ldots ,I_4$
are divided between them (and by consistency, this determines the way the M different elements of
$I_1,\ldots ,I_4$
are divided between them (and by consistency, this determines the way the M different elements of
![]() $J_1,\ldots ,J_4$
are divided between them). There are at most
$J_1,\ldots ,J_4$
are divided between them). There are at most
![]() $(2^4-1)^M\leqslant 2^{16d}$
different such configurations; thus, we fix one such configuration and upper-bound it (at the end multiplying the bound by
$(2^4-1)^M\leqslant 2^{16d}$
different such configurations; thus, we fix one such configuration and upper-bound it (at the end multiplying the bound by
![]() $2^{16d}$
). Thus, we have distinct
$2^{16d}$
). Thus, we have distinct
![]() $i_1,\ldots ,i_M$
ranging over
$i_1,\ldots ,i_M$
ranging over
![]() $[n]$
, and the coordinate of each
$[n]$
, and the coordinate of each
![]() $I_r$
is composed of the
$I_r$
is composed of the
![]() $i_1,\ldots ,i_M$
(and similarly
$i_1,\ldots ,i_M$
(and similarly
![]() $j_1,\ldots ,j_M$
and the
$j_1,\ldots ,j_M$
and the
![]() $J_r$
’s), and our sum is
$J_r$
’s), and our sum is
 $$ \begin{align} \frac{1}{n_M}\sum\limits_{\substack{i_1,\ldots,i_M \text{ distinct}\\ j_1,\ldots,j_M\text{ distinct}}}{a}({I_1},{J_1})\cdots{a}({I_4},{J_4}). \end{align} $$
$$ \begin{align} \frac{1}{n_M}\sum\limits_{\substack{i_1,\ldots,i_M \text{ distinct}\\ j_1,\ldots,j_M\text{ distinct}}}{a}({I_1},{J_1})\cdots{a}({I_4},{J_4}). \end{align} $$
We partition the
![]() $i_t$
’s into the number of times they occur: let
$i_t$
’s into the number of times they occur: let
![]() $A_1,\ldots ,A_4$
be the sets of
$A_1,\ldots ,A_4$
be the sets of
![]() $i_t$
that appear in
$i_t$
that appear in
![]() $1,2,3$
or
$1,2,3$
or
![]() $4$
of the
$4$
of the
![]() $I_r$
’s. We note that
$I_r$
’s. We note that
![]() $i_t$
and
$i_t$
and
![]() $j_t$
appear in the same
$j_t$
appear in the same
![]() $I_r$
’s and always together (otherwise the constraints would be contradictory), and in particular,
$I_r$
’s and always together (otherwise the constraints would be contradictory), and in particular,
![]() $i_t\in A_j$
iff
$i_t\in A_j$
iff
![]() $j_t\in A_j$
. Also,
$j_t\in A_j$
. Also,
![]() $M = \left |A_1\right | + \left |A_2\right |+\left |A_3\right |+\left |A_4\right |$
.
$M = \left |A_1\right | + \left |A_2\right |+\left |A_3\right |+\left |A_4\right |$
.
We consider contributions from configurations where
![]() $A_1=\emptyset $
and
$A_1=\emptyset $
and
![]() $A_1\neq \emptyset $
separately, and to control the latter group, we show that the above sum may be upper-bounded by
$A_1\neq \emptyset $
separately, and to control the latter group, we show that the above sum may be upper-bounded by
![]() $M^{2M}$
sums in which
$M^{2M}$
sums in which
![]() $A_1 = \emptyset $
. To do that, we show how to reduce the size of
$A_1 = \emptyset $
. To do that, we show how to reduce the size of
![]() $A_1$
by allowing more sums and then apply it iteratively.
$A_1$
by allowing more sums and then apply it iteratively.
Without loss of generality, assume
![]() $i_1\in A_1$
; then it is in exactly one of the
$i_1\in A_1$
; then it is in exactly one of the
![]() $I_r$
’s – without loss of generality, the last coordinate of
$I_r$
’s – without loss of generality, the last coordinate of
![]() $I_4$
. We rewrite the sum as
$I_4$
. We rewrite the sum as
 $$ \begin{align} \frac{1}{n_M}\sum\limits_{\substack{i_1,\ldots,i_M}}{a}({I_1},{J_1}){a}({I_2},{J_2}){a}({I_3},{J_3}) \sum\limits_{\substack{i_1\in [n]\setminus{\left\{ i_2,\ldots,i_M \right\}}\\ j_1\in [n]\setminus{\left\{ j_2,\ldots,j_M \right\}}}}{{a}({I_4},{J_4})}. \end{align} $$
$$ \begin{align} \frac{1}{n_M}\sum\limits_{\substack{i_1,\ldots,i_M}}{a}({I_1},{J_1}){a}({I_2},{J_2}){a}({I_3},{J_3}) \sum\limits_{\substack{i_1\in [n]\setminus{\left\{ i_2,\ldots,i_M \right\}}\\ j_1\in [n]\setminus{\left\{ j_2,\ldots,j_M \right\}}}}{{a}({I_4},{J_4})}. \end{align} $$
Consider the innermost sum. Applying Claim 6.4 twice, we have
 $$\begin{align*}\sum\limits_{\substack{i_1\in [n]\setminus{\left\{ i_2,\ldots,i_M \right\}}\\ j_1\in [n]\setminus{\left\{ j_2,\ldots,j_M \right\}}}}{{a}({I_4},{J_4})} =\sum\limits_{\substack{i_1\in {\left\{ i_2,\ldots,i_M \right\}}\setminus I_4\\ j_1\in {\left\{ j_2,\ldots,j_M \right\}}\setminus J_4}}{{a}({I_4},{J_4})}. \end{align*}$$
$$\begin{align*}\sum\limits_{\substack{i_1\in [n]\setminus{\left\{ i_2,\ldots,i_M \right\}}\\ j_1\in [n]\setminus{\left\{ j_2,\ldots,j_M \right\}}}}{{a}({I_4},{J_4})} =\sum\limits_{\substack{i_1\in {\left\{ i_2,\ldots,i_M \right\}}\setminus I_4\\ j_1\in {\left\{ j_2,\ldots,j_M \right\}}\setminus J_4}}{{a}({I_4},{J_4})}. \end{align*}$$
Plugging that into (11), we are able to write the sum therein using
![]() $(M-r)^2$
sums (one for each choice of
$(M-r)^2$
sums (one for each choice of
![]() $i_1\in {\left \{ i_2,\ldots ,i_M \right \}}\setminus I_4$
and
$i_1\in {\left \{ i_2,\ldots ,i_M \right \}}\setminus I_4$
and
![]() $j_1\in {\left \{ j_2,\ldots ,j_M \right \}}\setminus J_4$
) on
$j_1\in {\left \{ j_2,\ldots ,j_M \right \}}\setminus J_4$
) on
![]() $i_2,\ldots ,i_M,j_2,\ldots ,j_M$
, and thus, we have reduced the size of
$i_2,\ldots ,i_M,j_2,\ldots ,j_M$
, and thus, we have reduced the size of
![]() $A_1$
by at least
$A_1$
by at least
![]() $1$
and have decreased M by at least
$1$
and have decreased M by at least
![]() $1$
. The last bit implies that the original normalising factor is smaller by a factor of at least
$1$
. The last bit implies that the original normalising factor is smaller by a factor of at least
![]() $1/n$
than the new one. Iteratively applying this procedure, we end up with
$1/n$
than the new one. Iteratively applying this procedure, we end up with
![]() $A_1=\emptyset $
, and we assume that henceforth. Thus, letting
$A_1=\emptyset $
, and we assume that henceforth. Thus, letting
![]() $\mathcal {H}$
be the set of consistent
$\mathcal {H}$
be the set of consistent
![]() $(I_1,\ldots ,I_4,J_1,\ldots ,J_4)$
in which each element in
$(I_1,\ldots ,I_4,J_1,\ldots ,J_4)$
in which each element in
![]() $I_1\cup \dots \cup I_4$
appears in at least two of the
$I_1\cup \dots \cup I_4$
appears in at least two of the
![]() $I_i$
’s, we get that
$I_i$
’s, we get that
 $$ \begin{align} {\mathop{\mathbb{E}}_{\pi}\left[ {f(\pi)^4} \right]} &\leqslant \left(1+\frac{d^{O(d)}}{n}\right) \sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\ \text{from }\mathcal{H}}} {\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right| {\mathop{\mathbb{E}}_{\pi}\left[ {1_{\pi(I_1) = J_1}\cdots 1_{\pi(I_4) = J_4}} \right]}}\notag\\ &\leqslant (1+o(1)) \sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\ \text{from }\mathcal{H}}} {\frac{1}{n^{\left|I_1\cup\dots\cup I_4\right|}}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right|}, \end{align} $$
$$ \begin{align} {\mathop{\mathbb{E}}_{\pi}\left[ {f(\pi)^4} \right]} &\leqslant \left(1+\frac{d^{O(d)}}{n}\right) \sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\ \text{from }\mathcal{H}}} {\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right| {\mathop{\mathbb{E}}_{\pi}\left[ {1_{\pi(I_1) = J_1}\cdots 1_{\pi(I_4) = J_4}} \right]}}\notag\\ &\leqslant (1+o(1)) \sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\ \text{from }\mathcal{H}}} {\frac{1}{n^{\left|I_1\cup\dots\cup I_4\right|}}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right|}, \end{align} $$
where in the last inequality we used
Next, we lower-bound
![]() $\left \|g\right \|_4^4$
. Expanding as before,
$\left \|g\right \|_4^4$
. Expanding as before,
 $$\begin{align*}{\mathop{\mathbb{E}}_{x}\left[ {g(\pi)^4} \right]} =\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4}}{ \sqrt{p(1-p)}^{4d}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right| {\mathop{\mathbb{E}}_{x}\left[ {\chi_{S(I_1,J_1)}(x)\cdots\chi_{S(I_4,J_4)}(x)} \right]}}. \end{align*}$$
$$\begin{align*}{\mathop{\mathbb{E}}_{x}\left[ {g(\pi)^4} \right]} =\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4}}{ \sqrt{p(1-p)}^{4d}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right| {\mathop{\mathbb{E}}_{x}\left[ {\chi_{S(I_1,J_1)}(x)\cdots\chi_{S(I_4,J_4)}(x)} \right]}}. \end{align*}$$
A direct computation shows that the expectation of a normalised p-biased bit (i.e.,
![]() $\frac {x_{i,j} - p}{\sqrt {p(1-p)}}$
) is
$\frac {x_{i,j} - p}{\sqrt {p(1-p)}}$
) is
![]() $0$
, the expectation of its square is
$0$
, the expectation of its square is
![]() $1$
, the expectation of its third power is
$1$
, the expectation of its third power is
![]() $\frac {1+o(1)}{\sqrt {p(1-p)}}$
, and the expectation of its fourth power is
$\frac {1+o(1)}{\sqrt {p(1-p)}}$
, and the expectation of its fourth power is
![]() $\frac {1+o(1)}{p(1-p)}$
. This tells us that all summands in the above formula are nonnegative, and therefore, we can omit all those that correspond to
$\frac {1+o(1)}{p(1-p)}$
. This tells us that all summands in the above formula are nonnegative, and therefore, we can omit all those that correspond to
![]() $(I_1,\ldots ,I_4)$
and
$(I_1,\ldots ,I_4)$
and
![]() $(J_1,\ldots ,J_4)$
not from
$(J_1,\ldots ,J_4)$
not from
![]() $\mathcal {H}$
and only decrease the quantity. For
$\mathcal {H}$
and only decrease the quantity. For
![]() $j=2,3,4$
, denote by
$j=2,3,4$
, denote by
![]() $h_j$
the number of elements that appear in j of the
$h_j$
the number of elements that appear in j of the
![]() $I_1,\ldots ,I_4$
. Then we get that the inner term is at least
$I_1,\ldots ,I_4$
. Then we get that the inner term is at least
Note that
![]() $2h_2+3h_3+4h_4 = 4d$
; we get that
$2h_2+3h_3+4h_4 = 4d$
; we get that
![]() $4d-h_3-2h_4 = 2(h_2+h_3+h_4) = 2\left |I_1\cup \dots \cup I_4\right |$
. Combining everything, we get that
$4d-h_3-2h_4 = 2(h_2+h_3+h_4) = 2\left |I_1\cup \dots \cup I_4\right |$
. Combining everything, we get that
 $$ \begin{align} {\mathop{\mathbb{E}}_{x}\left[ {g(\pi)^4} \right]} &\geqslant(1-o(1))\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\\text{from }\mathcal{H}}}{ (p(1-p))^{\left|I_1\cup\dots\cup I_4\right|}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right|}\notag\\ &\geqslant (1-o(1))\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\\text{from }\mathcal{H}}}{ \frac{1}{n^{\left|I_1\cup\dots\cup I_4\right|}}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right|}. \end{align} $$
$$ \begin{align} {\mathop{\mathbb{E}}_{x}\left[ {g(\pi)^4} \right]} &\geqslant(1-o(1))\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\\text{from }\mathcal{H}}}{ (p(1-p))^{\left|I_1\cup\dots\cup I_4\right|}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right|}\notag\\ &\geqslant (1-o(1))\sum\limits_{\substack{I_1,\ldots,I_4\\ J_1,\ldots,J_4\\\text{from }\mathcal{H}}}{ \frac{1}{n^{\left|I_1\cup\dots\cup I_4\right|}}\left|{a}({I_1},{J_1})\right|\cdots\left|{a}({I_4},{J_4})\right|}. \end{align} $$
Combining (12) and (13) shows that
![]() $\left \|f\right \|_4^4\leqslant (1+o(1))\left \|g\right \|_4^4$
.
$\left \|f\right \|_4^4\leqslant (1+o(1))\left \|g\right \|_4^4$
.
6.5 Deducing hypercontractivity for low-degree functions
With Theorem 6.8 in hand, one may deduce the following inequality as an easy corollary.
Corollary 6.12. There exists an absolute constant
![]() $C>0$
such that for all
$C>0$
such that for all
![]() $d,n\in \mathbb {N}$
for which
$d,n\in \mathbb {N}$
for which
![]() $n\geqslant 2^{C\cdot d\log d}$
, the following holds. If
$n\geqslant 2^{C\cdot d\log d}$
, the following holds. If
![]() $f\in V_{d}(S_n)$
is
$f\in V_{d}(S_n)$
is
![]() $\varepsilon $
-analytically-global, then
$\varepsilon $
-analytically-global, then
![]() $\left \|f\right \|_4^4\leqslant 2^{C \cdot d\log d} \varepsilon ^2$
.
$\left \|f\right \|_4^4\leqslant 2^{C \cdot d\log d} \varepsilon ^2$
.
Proof. Since the proof is straightforward, we only outline its steps. Writing
![]() $f = f_{0}+\dots +f_{d}$
for
$f = f_{0}+\dots +f_{d}$
for
![]() $f_{k}\in V_{k}$
given by normalising relations, one bounds
$f_{k}\in V_{k}$
given by normalising relations, one bounds
![]() $\left \|f\right \|_4^4\leqslant (d+1)^3 \sum \limits _{k=0}^{d} \left \|f_{k}\right \|_4^4$
and uses Theorem 6.8 on each
$\left \|f\right \|_4^4\leqslant (d+1)^3 \sum \limits _{k=0}^{d} \left \|f_{k}\right \|_4^4$
and uses Theorem 6.8 on each
![]() $f_{k}$
. Finally,
$f_{k}$
. Finally,
![]() $I_{I',J'}[f_{k}]\leqslant I_{I',J'}[f]\leqslant \varepsilon $
.
$I_{I',J'}[f_{k}]\leqslant I_{I',J'}[f]\leqslant \varepsilon $
.
7 Applications
7.1 Global functions are concentrated on the high degrees
The first application of our hypercontractive is the following level-d inequality.
Theorem 1.6 (Restated).
There exists an absolute constant
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() $d,n\in \mathbb {N}$
and
$d,n\in \mathbb {N}$
and
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $n\geqslant 2^{C d^3} \log (1/\varepsilon )^{C d}$
. If
$n\geqslant 2^{C d^3} \log (1/\varepsilon )^{C d}$
. If
![]() $f\colon S_n\to \{0,1\}$
is
$f\colon S_n\to \{0,1\}$
is
![]() $(2d,\varepsilon )$
-global, then
$(2d,\varepsilon )$
-global, then
![]() $\|f^{\leqslant d}\|_2^2 \leqslant 2^{C \cdot d^4}\varepsilon ^4 \log ^{C\cdot d}(1/\varepsilon )$
.
$\|f^{\leqslant d}\|_2^2 \leqslant 2^{C \cdot d^4}\varepsilon ^4 \log ^{C\cdot d}(1/\varepsilon )$
.
Proof. Deferred to Section 8.
This result is analogous to the level d inequality on the Boolean hypercube [Reference O’Donnell24, Corollary 9.25], but it is quantitatively weaker because our dependence on d is poorer; for instance, it remains meaningful only for
![]() $d\leqslant \log (1/\varepsilon )^{1/4}$
, while the original statement on the Boolean hypercube remains effective up to
$d\leqslant \log (1/\varepsilon )^{1/4}$
, while the original statement on the Boolean hypercube remains effective up to
![]() $d\sim \log (1/\varepsilon )$
. Still, we show in Section 7.2 that this statement suffices to recover results regarding the size of the largest product-free sets in
$d\sim \log (1/\varepsilon )$
. Still, we show in Section 7.2 that this statement suffices to recover results regarding the size of the largest product-free sets in
![]() $S_n$
.
$S_n$
.
It would be interesting to prove a quantitatively better version of Theorem 1.6 in terms of d. In particular, is it the case that for
![]() $d = c\log (1/\varepsilon )$
, it holds that
$d = c\log (1/\varepsilon )$
, it holds that
![]() $\|f^{=d}\|^2 = \varepsilon ^{2+\Omega (1)}$
for sufficiently small (but constant)
$\|f^{=d}\|^2 = \varepsilon ^{2+\Omega (1)}$
for sufficiently small (but constant)
![]() $c>0$
?
$c>0$
?
We remark that once Theorem 1.6 has been established (or more precisely, the slightly stronger statement in Proposition 8.11), one can strengthen it at the expense of assuming that n is larger – namely, establish Theorem 1.7 from the introduction. We defer its proof to Section 8.8.
7.2 Global product-free sets are small
In this section, we prove a strengthening of Theorem 1.8. Conceptually, the proof is very simple. Starting from Gowers’ approach, we convert this problem into one about independent sets in a Cayley graph associated with F and use a Hoffman-type bound to solve that problem.
Fix a global product-free set
![]() $F\subseteq A_n$
and construct the (directed) graph
$F\subseteq A_n$
and construct the (directed) graph
![]() $G_F$
as follows. Its vertex set is
$G_F$
as follows. Its vertex set is
![]() $S_n$
, and
$S_n$
, and
![]() $(\pi ,\sigma )$
is an edge if
$(\pi ,\sigma )$
is an edge if
![]() $\pi ^{-1}\sigma \in F$
. Note that
$\pi ^{-1}\sigma \in F$
. Note that
![]() $G_F$
is a Cayley graph, and that if F is product-free, then F is an independent set in
$G_F$
is a Cayley graph, and that if F is product-free, then F is an independent set in
![]() $G_F$
. Our plan is thus to (1) study the eigenvalues of
$G_F$
. Our plan is thus to (1) study the eigenvalues of
![]() $G_F$
and prove good upper bounds on them and then (2) bound the size of F using a Hoffman-type bound.
$G_F$
and prove good upper bounds on them and then (2) bound the size of F using a Hoffman-type bound.
Let
![]() $T_F$
be the adjacency operator of
$T_F$
be the adjacency operator of
![]() $G_F$
(i.e., the random walk that from a vertex
$G_F$
(i.e., the random walk that from a vertex
![]() $\pi $
transitions to a random neighbour
$\pi $
transitions to a random neighbour
![]() $\sigma $
in
$\sigma $
in
![]() $G_F$
). We may consider the action of
$G_F$
). We may consider the action of
![]() $T_F$
on functions
$T_F$
on functions
![]() $f\colon S_n\to \mathbb {R}$
as
$f\colon S_n\to \mathbb {R}$
as
We will next study the eigenspaces and eigenvalues of
![]() $T_F$
, and for that we need some basic facts regarding the representation theory of
$T_F$
, and for that we need some basic facts regarding the representation theory of
![]() $S_n$
. We will then study the fraction of edges between any two global functions
$S_n$
. We will then study the fraction of edges between any two global functions
![]() $\mathcal {A},\mathcal {B}$
, and Theorem 1.8 will just be the special case that
$\mathcal {A},\mathcal {B}$
, and Theorem 1.8 will just be the special case that
![]() $\mathcal {A} = \mathcal {B} = F$
.
$\mathcal {A} = \mathcal {B} = F$
.
Throughout this section, we set
![]() $\delta = \frac {\left |F\right |}{\left |S_n\right |}$
.
$\delta = \frac {\left |F\right |}{\left |S_n\right |}$
.
7.2.1 Basic facts about representation theory of
 $S_n$
$S_n$
We will need some basic facts about the representation theory of
![]() $S_n$
, and our exposition will follow standard textbooks (e.g., [Reference Fulton and Harris13]).
$S_n$
, and our exposition will follow standard textbooks (e.g., [Reference Fulton and Harris13]).
A partition of
![]() $[n]$
, denoted by
$[n]$
, denoted by
![]() $\lambda \vdash n$
, is a sequence of integers
$\lambda \vdash n$
, is a sequence of integers
![]() $\lambda = (\lambda _1,\ldots ,\lambda _k)$
where
$\lambda = (\lambda _1,\ldots ,\lambda _k)$
where
![]() $\lambda _1\geqslant \lambda _2\geqslant \dots \geqslant \lambda _k\geqslant 1$
sum up to n. It is well known that partitions index equivalence classes of representations of
$\lambda _1\geqslant \lambda _2\geqslant \dots \geqslant \lambda _k\geqslant 1$
sum up to n. It is well known that partitions index equivalence classes of representations of
![]() $S_n$
; thus, we may associate with each partition
$S_n$
; thus, we may associate with each partition
![]() $\lambda $
a character
$\lambda $
a character
![]() $\chi _{\lambda }\colon S_n \to \mathbb {C}$
, which in the case of the symmetric group is real-valued. The dimension of
$\chi _{\lambda }\colon S_n \to \mathbb {C}$
, which in the case of the symmetric group is real-valued. The dimension of
![]() $\lambda $
is
$\lambda $
is
![]() $\textsf {dim}(\lambda ) = \chi _\lambda (e)$
, where e is the identity permutation.
$\textsf {dim}(\lambda ) = \chi _\lambda (e)$
, where e is the identity permutation.
Given a partition
![]() $\lambda $
, a
$\lambda $
, a
![]() $\lambda $
-tabloid is a partition of
$\lambda $
-tabloid is a partition of
![]() $[n]$
into sets
$[n]$
into sets
![]() $A_1,\ldots ,A_k$
such that
$A_1,\ldots ,A_k$
such that
![]() $\left |A_i\right | = \lambda _i$
. Thus, for
$\left |A_i\right | = \lambda _i$
. Thus, for
![]() $\lambda $
-tabloids
$\lambda $
-tabloids
![]() $A = (A_1,\ldots ,A_k)$
and
$A = (A_1,\ldots ,A_k)$
and
![]() $B = (B_1,\ldots ,B_k)$
, we define
$B = (B_1,\ldots ,B_k)$
, we define
![]() $T_{A,B} = \left \{ \left. \pi \in S_n \;\right \vert \pi (A_i) = B_i ~\forall i=1,\ldots ,k \right \}$
and refer to any such
$T_{A,B} = \left \{ \left. \pi \in S_n \;\right \vert \pi (A_i) = B_i ~\forall i=1,\ldots ,k \right \}$
and refer to any such
![]() $T_{A,B}$
as a
$T_{A,B}$
as a
![]() $\lambda $
-coset.
$\lambda $
-coset.
With these notations, we may define the space
![]() $V_{\lambda }(S_n)$
, which is the linear span of the indicator functions of all
$V_{\lambda }(S_n)$
, which is the linear span of the indicator functions of all
![]() $\lambda $
-cosets. We note that
$\lambda $
-cosets. We note that
![]() $V_{\lambda }(S_n)$
is clearly a left
$V_{\lambda }(S_n)$
is clearly a left
![]() $S_n$
-module, where the action of
$S_n$
-module, where the action of
![]() $S_n$
is given as
$S_n$
is given as ![]() defined by
defined by ![]() .
.
Next, we need to define an ordering on partitions that will let us further refine the spaces
![]() $V_{\lambda }$
.
$V_{\lambda }$
.
Definition 7.1. Let
![]() $\lambda = (\lambda _1,\ldots ,\lambda _k)$
,
$\lambda = (\lambda _1,\ldots ,\lambda _k)$
,
![]() $\mu = (\mu _1,\ldots ,\mu _{s})$
be partitions of
$\mu = (\mu _1,\ldots ,\mu _{s})$
be partitions of
![]() $[n]$
. We say that
$[n]$
. We say that
![]() $\lambda $
dominates
$\lambda $
dominates
![]() $\mu $
and denote
$\mu $
and denote
![]() $\lambda \trianglerighteq \mu $
, if for all
$\lambda \trianglerighteq \mu $
, if for all
![]() $j=1,\ldots ,k$
, it holds that
$j=1,\ldots ,k$
, it holds that
![]() $\sum \limits _{i=1}^{j} \lambda _i\geqslant \sum \limits _{i=1}^{j} \mu _i$
.
$\sum \limits _{i=1}^{j} \lambda _i\geqslant \sum \limits _{i=1}^{j} \mu _i$
.
With this definition, one may easily show that
![]() $V_{\mu }\subseteq V_{\lambda }$
whenever
$V_{\mu }\subseteq V_{\lambda }$
whenever
![]() $\mu \trianglerighteq \lambda $
, and furthermore that
$\mu \trianglerighteq \lambda $
, and furthermore that
![]() $V_{\mu } = V_{\lambda }$
if and only if
$V_{\mu } = V_{\lambda }$
if and only if
![]() $\mu = \lambda $
. It thus makes sense to define the spaces
$\mu = \lambda $
. It thus makes sense to define the spaces
 $$\begin{align*}V_{=\lambda} = V_{\lambda}\cap\bigcap_{\mu\vartriangleright \lambda} V_{\mu}^{\perp}. \end{align*}$$
$$\begin{align*}V_{=\lambda} = V_{\lambda}\cap\bigcap_{\mu\vartriangleright \lambda} V_{\mu}^{\perp}. \end{align*}$$
The spaces
![]() $V_{=\lambda }$
are orthogonal, and their direct sum is
$V_{=\lambda }$
are orthogonal, and their direct sum is
![]() ${\left \{ f\colon S_n\to \mathbb {R} \right \}}$
, so we may write any function
${\left \{ f\colon S_n\to \mathbb {R} \right \}}$
, so we may write any function
![]() $f\colon S_n\to \mathbb {R}$
as
$f\colon S_n\to \mathbb {R}$
as
![]() $f = \sum \limits _{\lambda \vdash n}{ f^{=\lambda }}$
in a unique way.
$f = \sum \limits _{\lambda \vdash n}{ f^{=\lambda }}$
in a unique way.
Definition 7.2. Let
![]() $\lambda = (\lambda _1,\ldots ,\lambda _k)$
be a partition of n. The transpose partition,
$\lambda = (\lambda _1,\ldots ,\lambda _k)$
be a partition of n. The transpose partition,
![]() $\lambda ^t$
, is
$\lambda ^t$
, is
![]() $(\mu _1,\ldots ,\mu _{k'})$
, where
$(\mu _1,\ldots ,\mu _{k'})$
, where
![]() $k' = \lambda _1$
and
$k' = \lambda _1$
and
![]() $\mu _j = \left |\left \{ \left. i \;\right \vert \lambda _i\geqslant j \right \}\right |$
.
$\mu _j = \left |\left \{ \left. i \;\right \vert \lambda _i\geqslant j \right \}\right |$
.
Alternatively, if we think of a partition as represented by top-left justified rows, then the transpose of a partition is obtained by reflecting the diagram across the main diagonal. For example,
![]() $(3,1)^t = (2,1,1)$
:
$(3,1)^t = (2,1,1)$
:

There are two partitions that are very easy to understand:
![]() $\lambda = (n)$
and its transpose,
$\lambda = (n)$
and its transpose,
![]() $\lambda = (1^t)$
. For
$\lambda = (1^t)$
. For
![]() $\lambda = (n)$
, the space
$\lambda = (n)$
, the space
![]() $V_{=\lambda }$
consists of constant functions, and one has
$V_{=\lambda }$
consists of constant functions, and one has
![]() $\chi _{\lambda } = 1$
. Thus,
$\chi _{\lambda } = 1$
. Thus,
![]() $f^{=(n)}$
is just the average of f (i.e.,
$f^{=(n)}$
is just the average of f (i.e.,
![]() $\mu (f) \stackrel {\mathit {def}}{=} {\mathop {\mathbb {E}}_{\pi }\left [ {f(\pi )} \right ]}$
). For
$\mu (f) \stackrel {\mathit {def}}{=} {\mathop {\mathbb {E}}_{\pi }\left [ {f(\pi )} \right ]}$
). For
![]() $\lambda = (1^n)$
, the space
$\lambda = (1^n)$
, the space
![]() $V_{=\lambda }$
consists of multiples of the sign function of permutations,
$V_{=\lambda }$
consists of multiples of the sign function of permutations,
![]() ${\sf sign}\colon S_n\to {\left \{ -1,1 \right \}}$
and
${\sf sign}\colon S_n\to {\left \{ -1,1 \right \}}$
and
![]() $\chi _{\lambda } = \mathsf {sign}$
. One therefore has
$\chi _{\lambda } = \mathsf {sign}$
. One therefore has
![]() $f^{=\lambda } = \langle {f},{\mathsf {sign}}\rangle \mathsf {sign}$
.
$f^{=\lambda } = \langle {f},{\mathsf {sign}}\rangle \mathsf {sign}$
.
For general partitions
![]() $\lambda $
, it is well known that the dimensions of
$\lambda $
, it is well known that the dimensions of
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda ^t$
are equal, and one has that
$\lambda ^t$
are equal, and one has that
![]() $\chi _{\lambda ^{t}} = \mathsf {sign}\cdot \chi _{\lambda }$
. We will need the following statement that generalises this correspondence to
$\chi _{\lambda ^{t}} = \mathsf {sign}\cdot \chi _{\lambda }$
. We will need the following statement that generalises this correspondence to
![]() $f^{=\lambda }$
and
$f^{=\lambda }$
and
![]() $f^{=\lambda ^t}$
.
$f^{=\lambda ^t}$
.
Lemma 7.3. Let
![]() $f\colon S_n\to \mathbb {R}$
and let
$f\colon S_n\to \mathbb {R}$
and let
![]() $\lambda \vdash n$
. Then
$\lambda \vdash n$
. Then
![]() $(f\cdot \mathsf {sign})^{=\lambda } = f^{=\lambda ^t}\mathsf {sign}$
.
$(f\cdot \mathsf {sign})^{=\lambda } = f^{=\lambda ^t}\mathsf {sign}$
.
Proof. The statement follows directly from the inversion formula for
![]() $f^{=\lambda }$
, which states that
$f^{=\lambda }$
, which states that
![]() $f^{=\lambda }(\pi ) = \mathsf {dim}(\lambda ){\mathop {\mathbb {E}}_{\sigma \in S_n}\left [ {f(\sigma )\chi _{\lambda }(\pi \sigma ^{-1})} \right ]}$
. By change of variables, we see that
$f^{=\lambda }(\pi ) = \mathsf {dim}(\lambda ){\mathop {\mathbb {E}}_{\sigma \in S_n}\left [ {f(\sigma )\chi _{\lambda }(\pi \sigma ^{-1})} \right ]}$
. By change of variables, we see that
 $$\begin{align*}&(f\cdot \mathsf{sign})^{=\lambda}(\pi) \\&\quad=\mathsf{dim}(\lambda){\mathop{\mathbb{E}}_{\sigma\in S_n}\left[ {f(\sigma^{-1}\pi)\mathsf{sign}(\sigma^{-1}\pi)\chi_{\lambda}(\sigma)} \right]} =\mathsf{sign}(\pi)\mathsf{dim}(\lambda){\mathop{\mathbb{E}}_{\sigma\in S_n}\left[ {f(\sigma^{-1}\pi)\mathsf{sign}(\sigma)\chi_{\lambda}(\sigma)} \right]}, \end{align*}$$
$$\begin{align*}&(f\cdot \mathsf{sign})^{=\lambda}(\pi) \\&\quad=\mathsf{dim}(\lambda){\mathop{\mathbb{E}}_{\sigma\in S_n}\left[ {f(\sigma^{-1}\pi)\mathsf{sign}(\sigma^{-1}\pi)\chi_{\lambda}(\sigma)} \right]} =\mathsf{sign}(\pi)\mathsf{dim}(\lambda){\mathop{\mathbb{E}}_{\sigma\in S_n}\left[ {f(\sigma^{-1}\pi)\mathsf{sign}(\sigma)\chi_{\lambda}(\sigma)} \right]}, \end{align*}$$
where we used the fact that
![]() $\mathsf {sign}$
is multiplicative and
$\mathsf {sign}$
is multiplicative and
![]() $\mathsf {sign}(\sigma ^{-1}) = \mathsf {sign}(\sigma )$
. Now, as
$\mathsf {sign}(\sigma ^{-1}) = \mathsf {sign}(\sigma )$
. Now, as
![]() $\mathsf {sign}(\sigma )\chi _{\lambda }(\sigma ) = \chi _{\lambda ^t}(\sigma )$
, we get by changing variables again that
$\mathsf {sign}(\sigma )\chi _{\lambda }(\sigma ) = \chi _{\lambda ^t}(\sigma )$
, we get by changing variables again that
which is equal to
![]() $\mathsf {sign}(\pi ) f^{=\lambda ^t}(\pi )$
by the inversion formula.
$\mathsf {sign}(\pi ) f^{=\lambda ^t}(\pi )$
by the inversion formula.
Lastly, we remark that if
![]() $\lambda $
is a partition such that
$\lambda $
is a partition such that
![]() $\lambda = n-k$
, then
$\lambda = n-k$
, then
![]() $V_{=\lambda }\subseteq V_k$
. It follows by Parseval that
$V_{=\lambda }\subseteq V_k$
. It follows by Parseval that
 $$ \begin{align} \sum\limits_{\substack{\lambda\vdash n\\\lambda_1 = n-k}}\left\|f^{=\lambda}\right\|_2^2\leqslant \left\|f^{\leqslant k}\right\|_2^2. \end{align} $$
$$ \begin{align} \sum\limits_{\substack{\lambda\vdash n\\\lambda_1 = n-k}}\left\|f^{=\lambda}\right\|_2^2\leqslant \left\|f^{\leqslant k}\right\|_2^2. \end{align} $$
7.2.2 The eigenvalues of
 $T_F^{*}T_F$
$T_F^{*}T_F$
Claim 7.4. For all
![]() $\lambda \vdash n$
, we have that
$\lambda \vdash n$
, we have that
![]() $T_F V_{=\lambda }\subseteq V_{=\lambda }$
; the same holds for
$T_F V_{=\lambda }\subseteq V_{=\lambda }$
; the same holds for
![]() $T_F^{*}$
.
$T_F^{*}$
.
Proof. First, we show that
![]() $T_F V_{\lambda }\subseteq V_{\lambda }$
, and for that, it is enough to show that
$T_F V_{\lambda }\subseteq V_{\lambda }$
, and for that, it is enough to show that
![]() $T_F 1_{T_{A,B}}\in V_{\lambda }$
for all
$T_F 1_{T_{A,B}}\in V_{\lambda }$
for all
![]() $\lambda $
-tabloids
$\lambda $
-tabloids
![]() $A = (A_1,\ldots ,A_k)$
and
$A = (A_1,\ldots ,A_k)$
and
![]() $B = (B_1,\ldots ,B_k)$
. Fix
$B = (B_1,\ldots ,B_k)$
. Fix
![]() $a\in F$
and note that
$a\in F$
and note that
![]() $1_{T_{A,B}}(\sigma a) = 1_{T_{a(A),B}}(\sigma )$
, where
$1_{T_{A,B}}(\sigma a) = 1_{T_{a(A),B}}(\sigma )$
, where
![]() $a(A) = (a(A_1),\ldots ,a(A_k))$
, so
$a(A) = (a(A_1),\ldots ,a(A_k))$
, so
![]() $1_{T_{A,B}}(\sigma a)$
, as a function of
$1_{T_{A,B}}(\sigma a)$
, as a function of
![]() $\sigma $
, is also an indicator of a
$\sigma $
, is also an indicator of a
![]() $\lambda $
-coset. Since
$\lambda $
-coset. Since
![]() $T_F 1_{T_{A,B}}$
is a linear combination of such functions, it follows that
$T_F 1_{T_{A,B}}$
is a linear combination of such functions, it follows that
![]() $T_F 1_{T_{A,B}}\in V_{\lambda }$
. A similar argument shows that the same holds for the adjoint operator of
$T_F 1_{T_{A,B}}\in V_{\lambda }$
. A similar argument shows that the same holds for the adjoint operator of
![]() $T_F^{*} = T_{F^{-1}}$
, where
$T_F^{*} = T_{F^{-1}}$
, where
![]() $F^{-1} = \left \{ \left. a^{-1} \;\right \vert a\in F \right \}$
.
$F^{-1} = \left \{ \left. a^{-1} \;\right \vert a\in F \right \}$
.
Thus, for
![]() $f\in V_{=\lambda }$
, we automatically have that
$f\in V_{=\lambda }$
, we automatically have that
![]() $f\in V_{\lambda }$
, and we next show orthogonality to
$f\in V_{\lambda }$
, and we next show orthogonality to
![]() $V_{\mu }$
for all
$V_{\mu }$
for all
![]() $\mu \triangleright \lambda $
. Indeed, let
$\mu \triangleright \lambda $
. Indeed, let
![]() $\mu $
be such partition and let
$\mu $
be such partition and let
![]() $g\in V_{\mu }$
; then by the above,
$g\in V_{\mu }$
; then by the above,
![]() $T_F^{*} g\in V_{\mu }$
and so
$T_F^{*} g\in V_{\mu }$
and so
![]() $\langle {T_F f},{g}\rangle = \langle {f},{T_F^{*} g}\rangle = 0$
, and the proof is complete. The argument for
$\langle {T_F f},{g}\rangle = \langle {f},{T_F^{*} g}\rangle = 0$
, and the proof is complete. The argument for
![]() $T_F^{*}$
is analogous.
$T_F^{*}$
is analogous.
Thus, we may find a basis of each
![]() $V_{=\lambda }$
consisting of eigenvectors of
$V_{=\lambda }$
consisting of eigenvectors of
![]() $T_F^{*} T_F$
. The following claim shows that the multiplicity of each corresponding eigenvalue is at least
$T_F^{*} T_F$
. The following claim shows that the multiplicity of each corresponding eigenvalue is at least
![]() $\mathsf {dim}(\lambda )$
.
$\mathsf {dim}(\lambda )$
.
Claim 7.5. Let
![]() $f\in V_{=\lambda }(S_n)$
be nonzero. Then
$f\in V_{=\lambda }(S_n)$
be nonzero. Then
![]() ${\sf dim}({\sf Span}({\left \{ {}^{\pi } f \right \}}_{\pi \in S_n}))\geqslant \mathsf {dim}(\lambda )$
.
${\sf dim}({\sf Span}({\left \{ {}^{\pi } f \right \}}_{\pi \in S_n}))\geqslant \mathsf {dim}(\lambda )$
.
Proof. Let
![]() $\rho _{\lambda }\colon S_n \to V_{=\lambda }$
be a representation and denote by W the span of
$\rho _{\lambda }\colon S_n \to V_{=\lambda }$
be a representation and denote by W the span of ![]() . Note that W is a subspace of
. Note that W is a subspace of
![]() $V_{=\lambda }$
, and it holds that
$V_{=\lambda }$
, and it holds that
![]() $(\rho |_{W},W)$
is a sub-representation of
$(\rho |_{W},W)$
is a sub-representation of
![]() $\rho $
. Since each irreducible representation
$\rho $
. Since each irreducible representation
![]() $V\subseteq V_{=\lambda }$
of
$V\subseteq V_{=\lambda }$
of
![]() $S_n$
has dimension
$S_n$
has dimension
![]() $\mathsf {dim}(\lambda )$
, it follows that
$\mathsf {dim}(\lambda )$
, it follows that
![]() $\mathsf {dim}(W)\geqslant \mathsf {dim}(\lambda )$
, and we are done.
$\mathsf {dim}(W)\geqslant \mathsf {dim}(\lambda )$
, and we are done.
We can thus use the trace method to bound the magnitude of each eigenvalue.
Lemma 7.6. Let
![]() $f\in V_{=\lambda }$
be an eigenvector of
$f\in V_{=\lambda }$
be an eigenvector of
![]() $T_F^{*} T_F$
with eigenvalue
$T_F^{*} T_F$
with eigenvalue
![]() $\alpha _{\lambda }$
. Then
$\alpha _{\lambda }$
. Then
Proof. By Claim 7.5, we may find a collection of
![]() $\mathsf {dim}(\lambda )$
permutations and call it
$\mathsf {dim}(\lambda )$
permutations and call it
![]() $\Pi $
, such that
$\Pi $
, such that ![]() is linearly independent. Since f is an eigenvector of
is linearly independent. Since f is an eigenvector of
![]() $T_F^{*} T_F$
, it follows that each one of
$T_F^{*} T_F$
, it follows that each one of ![]() is an eigenvector with eigenvalue
is an eigenvector with eigenvalue
![]() $\alpha _{\lambda }$
. It follows that
$\alpha _{\lambda }$
. It follows that
![]() $\mathsf {Tr}(T_{F}^{*}T_F) \geqslant \left |\Pi \right | \alpha _{\lambda } = \mathsf {dim}(\lambda )\alpha _{\lambda }$
.
$\mathsf {Tr}(T_{F}^{*}T_F) \geqslant \left |\Pi \right | \alpha _{\lambda } = \mathsf {dim}(\lambda )\alpha _{\lambda }$
.
However, interpreting
![]() $\mathsf {Tr}(T_{F}^{*} T_F)$
probabilistically as the probability to return to the starting vertex in
$\mathsf {Tr}(T_{F}^{*} T_F)$
probabilistically as the probability to return to the starting vertex in
![]() $2$
-steps,
$2$
-steps,
 $$\begin{align*}\mathsf{Tr}(T_{F}^{*} T_F) =\sum\limits_{\pi} {\Pr_{a_1\in F^{-1},a_2\in F}\left[ {\pi = \pi a_1 a_2} \right]} =n!{\Pr_{a_1\in F^{-1},a_2\in F}\left[ {a_2 = a_{1}^{-1}} \right]} = n! \frac{1}{\left|F\right|} =\frac{1}{\delta}. \end{align*}$$
$$\begin{align*}\mathsf{Tr}(T_{F}^{*} T_F) =\sum\limits_{\pi} {\Pr_{a_1\in F^{-1},a_2\in F}\left[ {\pi = \pi a_1 a_2} \right]} =n!{\Pr_{a_1\in F^{-1},a_2\in F}\left[ {a_2 = a_{1}^{-1}} \right]} = n! \frac{1}{\left|F\right|} =\frac{1}{\delta}. \end{align*}$$
Combining the two bounds on
![]() $\mathsf {Tr}(T_{F}^{*} T_F)$
completes the proof.
$\mathsf {Tr}(T_{F}^{*} T_F)$
completes the proof.
To use this lemma effectively, we have the following bound on
![]() $\mathsf {dim}(\lambda )$
that follows from the hook length formula.
$\mathsf {dim}(\lambda )$
that follows from the hook length formula.
Lemma 7.7 (Claim 1, Theorem 19 in [Reference Ellis, Friedgut and Pilpel7]).
Let
![]() $\lambda \vdash n$
be given as
$\lambda \vdash n$
be given as
![]() $\lambda = (\lambda _1,\ldots ,\lambda _k)$
and denote
$\lambda = (\lambda _1,\ldots ,\lambda _k)$
and denote
![]() $d = \min (n-\lambda _1,k)$
.
$d = \min (n-\lambda _1,k)$
.
-
1. If
 $d = 0$
, then
$d = 0$
, then
 $\mathsf {dim}(\lambda ) = 1$
.
$\mathsf {dim}(\lambda ) = 1$
. -
2. If
 $d>0$
, then
$d>0$
, then
 $\mathsf {dim}(\lambda )\geqslant \left (\frac {n}{d\cdot e}\right )^d$
.
$\mathsf {dim}(\lambda )\geqslant \left (\frac {n}{d\cdot e}\right )^d$
. -
3. If
 $d> n/10$
, then
$d> n/10$
, then
 $\mathsf {dim}(\lambda )\geqslant 1.05^n$
.
$\mathsf {dim}(\lambda )\geqslant 1.05^n$
.
7.2.3 Applying Hoffman’s bound
With the information we have gathered regarding the representation theory of
![]() $S_n$
and the eigenvalues of
$S_n$
and the eigenvalues of
![]() $T_F$
, we can use the spectral method to prove lower bounds on
$T_F$
, we can use the spectral method to prove lower bounds on
![]() $\langle {T_F g},{h}\rangle $
for Boolean functions
$\langle {T_F g},{h}\rangle $
for Boolean functions
![]() $g,h$
that are global, as in the following lemma.
$g,h$
that are global, as in the following lemma.
Lemma 7.8. There exists
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\varepsilon>0$
be such that
$\varepsilon>0$
be such that
![]() $n\geqslant \log (1/\varepsilon )^C$
and suppose that
$n\geqslant \log (1/\varepsilon )^C$
and suppose that
![]() $g,h\colon A_n\to {\left \{ 0,1 \right \}}^{}$
are
$g,h\colon A_n\to {\left \{ 0,1 \right \}}^{}$
are
![]() $(6,\varepsilon )$
-global. Then
$(6,\varepsilon )$
-global. Then
 $$\begin{align*}\langle{T_F g},{h}\rangle \geqslant \frac{\mathop{\mathbb{E}}[g]\mathop{\mathbb{E}}[h]}{2} - C\frac{\varepsilon^4 \log^{C}(1/\varepsilon)}{\sqrt{n\delta}} - \frac{C}{\sqrt{n^4\delta}}\sqrt{\mathop{\mathbb{E}}[g]\mathop{\mathbb{E}}[h]}. \end{align*}$$
$$\begin{align*}\langle{T_F g},{h}\rangle \geqslant \frac{\mathop{\mathbb{E}}[g]\mathop{\mathbb{E}}[h]}{2} - C\frac{\varepsilon^4 \log^{C}(1/\varepsilon)}{\sqrt{n\delta}} - \frac{C}{\sqrt{n^4\delta}}\sqrt{\mathop{\mathbb{E}}[g]\mathop{\mathbb{E}}[h]}. \end{align*}$$
Proof. Extend
![]() $g,h$
to
$g,h$
to
![]() $S_n$
by defining them to be
$S_n$
by defining them to be
![]() $0$
outside
$0$
outside
![]() $A_n$
.
$A_n$
.
Recall that
![]() $T_F$
preserves each
$T_F$
preserves each
![]() $V_{=\lambda }$
. Decomposing
$V_{=\lambda }$
. Decomposing
![]() $g = \sum _{\lambda \vdash n} g^{=\lambda }$
where
$g = \sum _{\lambda \vdash n} g^{=\lambda }$
where
![]() $g^{=\lambda }\in V_{=\lambda }$
and h similarly, we have by Plancherel that
$g^{=\lambda }\in V_{=\lambda }$
and h similarly, we have by Plancherel that
![]() $\langle {T_F g},{h}\rangle =\sum \limits _{\lambda ,\theta } \langle {T_F g^{=\lambda }},{h^{=\lambda }}\rangle $
. For the trivial partition
$\langle {T_F g},{h}\rangle =\sum \limits _{\lambda ,\theta } \langle {T_F g^{=\lambda }},{h^{=\lambda }}\rangle $
. For the trivial partition
![]() $\lambda = (n)$
, we have that
$\lambda = (n)$
, we have that
![]() $g^{=\lambda } \equiv \mu (g)=\mathop {\mathbb {E}}[g]/2$
,
$g^{=\lambda } \equiv \mu (g)=\mathop {\mathbb {E}}[g]/2$
,
![]() $h^{=\lambda } \equiv \mu (h)=\mathop {\mathbb {E}}[h]/2$
. For
$h^{=\lambda } \equiv \mu (h)=\mathop {\mathbb {E}}[h]/2$
. For
![]() $\lambda = (1^n)$
, since
$\lambda = (1^n)$
, since
![]() $F\subseteq A_n$
, it follows that
$F\subseteq A_n$
, it follows that
![]() $T_F \mathsf {sign} = \mathsf {sign}$
, and so
$T_F \mathsf {sign} = \mathsf {sign}$
, and so
![]() $T_F g^{=\lambda } = \mu (f) \mathsf {sign}$
,
$T_F g^{=\lambda } = \mu (f) \mathsf {sign}$
,
![]() $h^{=\lambda } = \mu (g) \mathsf {sign}$
. Thus, denoting
$h^{=\lambda } = \mu (g) \mathsf {sign}$
. Thus, denoting
![]() $\lambda = (\lambda _1,\ldots ,\lambda _k)$
, we have that
$\lambda = (\lambda _1,\ldots ,\lambda _k)$
, we have that
 $$ \begin{align} \langle{T_F g},{h}\rangle\geqslant 2\mu(g)\mu(h) - \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3\text{ or }k\geqslant n-3}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2 - \sum\limits_{\substack{\lambda\neq (n),(1^n)\\ \lambda_1\leqslant n-4\text{ and }k\leqslant n-4}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2. \end{align} $$
$$ \begin{align} \langle{T_F g},{h}\rangle\geqslant 2\mu(g)\mu(h) - \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3\text{ or }k\geqslant n-3}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2 - \sum\limits_{\substack{\lambda\neq (n),(1^n)\\ \lambda_1\leqslant n-4\text{ and }k\leqslant n-4}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2. \end{align} $$
We upper-bound the second and third terms on the right-hand side, from which the lemma follows. We begin with the second term and handle separately
![]() $\lambda $
’s such that
$\lambda $
’s such that
![]() $\lambda _1\geqslant n-3$
and
$\lambda _1\geqslant n-3$
and
![]() $\lambda $
’s such that
$\lambda $
’s such that
![]() $k\geqslant n-3$
.
$k\geqslant n-3$
.
![]() $\lambda $
’s such that
$\lambda $
’s such that
![]() $\lambda \neq (n), (1^n)$
and
$\lambda \neq (n), (1^n)$
and
![]() $\lambda _1\geqslant n-3$
.
$\lambda _1\geqslant n-3$
.
We first upper-bound
![]() $\left \|T_F g^{=\lambda }\right \|_{2}$
. As
$\left \|T_F g^{=\lambda }\right \|_{2}$
. As
![]() $T_{F}^{*} T_F$
preserves each space
$T_{F}^{*} T_F$
preserves each space
![]() $V_{=\lambda }$
and is symmetric, we may write this space as a sum of eigenspaces of
$V_{=\lambda }$
and is symmetric, we may write this space as a sum of eigenspaces of
![]() $T_{F}^{*} T_F$
, say
$T_{F}^{*} T_F$
, say
![]() $\bigoplus _{\theta } V_{=\lambda }^{\theta }$
. Writing
$\bigoplus _{\theta } V_{=\lambda }^{\theta }$
. Writing
![]() $g^{=\lambda } = \sum _{\theta } g^{=\lambda ,\theta }$
where
$g^{=\lambda } = \sum _{\theta } g^{=\lambda ,\theta }$
where
![]() $g^{=\lambda ,\theta }\in V_{=\lambda }^{\theta }$
, we have that
$g^{=\lambda ,\theta }\in V_{=\lambda }^{\theta }$
, we have that
By Lemma 7.6, we have
![]() $\theta \leqslant \frac {1}{\mathsf {dim}(\lambda )\delta }$
, which by Fact 7.7 is at most
$\theta \leqslant \frac {1}{\mathsf {dim}(\lambda )\delta }$
, which by Fact 7.7 is at most
![]() $O\left (\frac {1}{n\delta }\right )$
. We thus get that
$O\left (\frac {1}{n\delta }\right )$
. We thus get that
 $$\begin{align*}\left\|T_F g^{=\lambda}\right\|_{2}^2 \leqslant O\left(\frac{1}{n\delta}\right)\sum\limits_{\theta}{\left\|g^{=\lambda,\theta}\right\|_2^2} \leqslant O\left(\frac{1}{n\delta}\right)\left\|g^{=\lambda}\right\|_2^2. \end{align*}$$
$$\begin{align*}\left\|T_F g^{=\lambda}\right\|_{2}^2 \leqslant O\left(\frac{1}{n\delta}\right)\sum\limits_{\theta}{\left\|g^{=\lambda,\theta}\right\|_2^2} \leqslant O\left(\frac{1}{n\delta}\right)\left\|g^{=\lambda}\right\|_2^2. \end{align*}$$
Plugging this into the second sum in (15), we get that the contribution from
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda _1\geqslant n-3$
is at most
$\lambda _1\geqslant n-3$
is at most
 $$\begin{align*}O\left(\frac{1}{\sqrt{n\delta}}\right) \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3}} \left\|g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2 \leqslant O\left(\frac{1}{\sqrt{n\delta}}\right) \left\|g^{\leqslant 3}\right\|_2\left\|h^{\leqslant 3}\right\|_2, \end{align*}$$
$$\begin{align*}O\left(\frac{1}{\sqrt{n\delta}}\right) \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3}} \left\|g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2 \leqslant O\left(\frac{1}{\sqrt{n\delta}}\right) \left\|g^{\leqslant 3}\right\|_2\left\|h^{\leqslant 3}\right\|_2, \end{align*}$$
where we used Cauchy-Schwarz and (14). By Theorem 1.6,
![]() $\left \|g^{\leqslant 3}\right \|_2^2,\left \|h^{\leqslant 3}\right \|_2^2\leqslant C\cdot \varepsilon ^4 \log ^{C}(1/\varepsilon )$
for some absolute constant C. We thus get that
$\left \|g^{\leqslant 3}\right \|_2^2,\left \|h^{\leqslant 3}\right \|_2^2\leqslant C\cdot \varepsilon ^4 \log ^{C}(1/\varepsilon )$
for some absolute constant C. We thus get that
 $$\begin{align*}\sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2\leqslant \frac{1}{\sqrt{n\delta}}C'\cdot \varepsilon^4 \log^{C}(1/\varepsilon). \end{align*}$$
$$\begin{align*}\sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_2\leqslant \frac{1}{\sqrt{n\delta}}C'\cdot \varepsilon^4 \log^{C}(1/\varepsilon). \end{align*}$$
![]() $\lambda $
’s such that
$\lambda $
’s such that
![]() $k\geqslant n-3$
.
$k\geqslant n-3$
.
The treatment here is pretty much identical to the previous case, except that we look at the functions
![]() $\tilde {g} = g\cdot \mathsf {sign}$
and
$\tilde {g} = g\cdot \mathsf {sign}$
and
![]() $\tilde {h} = h\cdot \mathsf {sign}$
. That is, first note that the globalness of
$\tilde {h} = h\cdot \mathsf {sign}$
. That is, first note that the globalness of
![]() $g,h$
implies that
$g,h$
implies that
![]() $\tilde {g},\tilde {h}$
are also global with the same parameters, and since
$\tilde {g},\tilde {h}$
are also global with the same parameters, and since
![]() $g,h$
are Boolean,
$g,h$
are Boolean,
![]() $\tilde {g},\tilde {h}$
are integer valued. Moreover, by Lemma 7.3, we have that
$\tilde {g},\tilde {h}$
are integer valued. Moreover, by Lemma 7.3, we have that
 $$\begin{align*}\sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ k\geqslant n-3}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_{2} = \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ k\geqslant n-3}} \left\|T_F \tilde{g}^{=\lambda^t}\right\|_{2}\left\|\tilde{h}^{=\lambda^t}\right\|_{2} = \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3}} \left\|T_F \tilde{g}^{\lambda}\right\|_{2}\left\|\tilde{h}^{\lambda}\right\|_{2}, \end{align*}$$
$$\begin{align*}\sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ k\geqslant n-3}} \left\|T_F g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_{2} = \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ k\geqslant n-3}} \left\|T_F \tilde{g}^{=\lambda^t}\right\|_{2}\left\|\tilde{h}^{=\lambda^t}\right\|_{2} = \sum\limits_{\substack{\lambda\vdash n\\\lambda\neq (n),(1^n)\\ \lambda_1\geqslant n-3}} \left\|T_F \tilde{g}^{\lambda}\right\|_{2}\left\|\tilde{h}^{\lambda}\right\|_{2}, \end{align*}$$
and from here, the argument is identical.
Bounding the third term in (15).
Repeating the eigenspace argument from above, for all
![]() $\lambda \vdash n$
such that
$\lambda \vdash n$
such that
![]() $\lambda _1\leqslant n-4$
and
$\lambda _1\leqslant n-4$
and
![]() $k\leqslant n-4$
, we have
$k\leqslant n-4$
, we have
 $$\begin{align*}\left\|T_F g^{=\lambda}\right\|_{2}\leqslant O\left(\frac{1}{\sqrt{n^4\delta}}\right) \left\|g^{=\lambda}\right\|_{2}. \end{align*}$$
$$\begin{align*}\left\|T_F g^{=\lambda}\right\|_{2}\leqslant O\left(\frac{1}{\sqrt{n^4\delta}}\right) \left\|g^{=\lambda}\right\|_{2}. \end{align*}$$
Thus, the third sum in (15) is at most
 $$\begin{align*}O\left(\frac{1}{\sqrt{n^4\delta}}\right)\sum\limits_{\lambda\vdash n}\left\|g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_{2} \leqslant O\left(\frac{1}{\sqrt{n^4\delta}}\right)\left\|g\right\|_2\left\|h\right\|_2, \end{align*}$$
$$\begin{align*}O\left(\frac{1}{\sqrt{n^4\delta}}\right)\sum\limits_{\lambda\vdash n}\left\|g^{=\lambda}\right\|_{2}\left\|h^{=\lambda}\right\|_{2} \leqslant O\left(\frac{1}{\sqrt{n^4\delta}}\right)\left\|g\right\|_2\left\|h\right\|_2, \end{align*}$$
where we used Cauchy–Schwarz and Parseval.
We can now prove the strengthening of Theorem 1.8, stated below.
Corollary 7.9. There exists
![]() $K\in \mathbb {N}$
such that the following holds for all
$K\in \mathbb {N}$
such that the following holds for all
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $n\geqslant \log ^K(1/\varepsilon )$
. If
$n\geqslant \log ^K(1/\varepsilon )$
. If
![]() $\mathcal {A},\mathcal {B}\subseteq A_n$
are
$\mathcal {A},\mathcal {B}\subseteq A_n$
are
![]() $(6,\varepsilon )$
-global, and
$(6,\varepsilon )$
-global, and
![]() $\mu (\mathcal {A})\mu (\mathcal {B})\geqslant K\max (n^{-4}\delta ^{-1}, (n\delta )^{-1/2}\varepsilon ^{4}\log ^{K}(1/\varepsilon ))$
, then
$\mu (\mathcal {A})\mu (\mathcal {B})\geqslant K\max (n^{-4}\delta ^{-1}, (n\delta )^{-1/2}\varepsilon ^{4}\log ^{K}(1/\varepsilon ))$
, then
Proof. Taking
![]() $g = 1_{\mathcal {A}}$
,
$g = 1_{\mathcal {A}}$
,
![]() $h = 1_{\mathcal {B}}$
, by Lemma 7.8, we have
$h = 1_{\mathcal {B}}$
, by Lemma 7.8, we have
 $$\begin{align*}\langle{T_F g},{h}\rangle \geqslant \frac{1}{2} \mu(\mathcal{A})\mu(\mathcal{B}) - C'\frac{\varepsilon^4\log^{C'}(1/\varepsilon)}{\sqrt{n\delta}} - \frac{C'}{n^2\sqrt{\delta}}\sqrt{\mu(\mathcal{A})\mu(\mathcal{B})}, \end{align*}$$
$$\begin{align*}\langle{T_F g},{h}\rangle \geqslant \frac{1}{2} \mu(\mathcal{A})\mu(\mathcal{B}) - C'\frac{\varepsilon^4\log^{C'}(1/\varepsilon)}{\sqrt{n\delta}} - \frac{C'}{n^2\sqrt{\delta}}\sqrt{\mu(\mathcal{A})\mu(\mathcal{B})}, \end{align*}$$
where
![]() $C'$
is an absolute constants. Now the conditions on the parameters implies that the first term dominates the other two.
$C'$
is an absolute constants. Now the conditions on the parameters implies that the first term dominates the other two.
We note that Theorem 1.8 immediately follows since there one has
![]() $g = h = 1_F$
and
$g = h = 1_F$
and
![]() $\langle {T_F g},{h}\rangle = 0$
, so one gets that the condition on the parameters fail, and therefore, the lower bound on
$\langle {T_F g},{h}\rangle = 0$
, so one gets that the condition on the parameters fail, and therefore, the lower bound on
![]() $\mu (\mathcal {A})\mu (\mathcal {B})$
(which in this case is just
$\mu (\mathcal {A})\mu (\mathcal {B})$
(which in this case is just
![]() $\delta ^2$
) fails; plugging in
$\delta ^2$
) fails; plugging in
![]() $\varepsilon = C\cdot \sqrt {\delta }$
and rearranging finishes the proof.
$\varepsilon = C\cdot \sqrt {\delta }$
and rearranging finishes the proof.
7.2.4 Improving on Theorem 1.8?
We remark that it is within reason to expect that global, product-free families in
![]() $A_n$
must in fact be much smaller. To be more precise, one may expect that for all
$A_n$
must in fact be much smaller. To be more precise, one may expect that for all
![]() $t\in \mathbb {N}$
, there is
$t\in \mathbb {N}$
, there is
![]() $j\in \mathbb {N}$
such that for
$j\in \mathbb {N}$
such that for
![]() $n\geqslant n_0(t)$
, if F is
$n\geqslant n_0(t)$
, if F is
![]() $(j,O(\sqrt {\delta }))$
-global (where
$(j,O(\sqrt {\delta }))$
-global (where
![]() $\delta = \left |F\right |/\left |S_n\right |$
), then
$\delta = \left |F\right |/\left |S_n\right |$
), then
![]() $\delta \leqslant O_t(n^{-t})$
. The bottleneck in our approach comes from the use of the trace method (which does not use the globalness of F at all) and the bounds it gives on the eigenvalues of
$\delta \leqslant O_t(n^{-t})$
. The bottleneck in our approach comes from the use of the trace method (which does not use the globalness of F at all) and the bounds it gives on the eigenvalues of
![]() $T_F^{*} T_F$
corresponding to low-degree functions: they become meaningless as soon as
$T_F^{*} T_F$
corresponding to low-degree functions: they become meaningless as soon as
![]() $\delta \geqslant 1/n$
.
$\delta \geqslant 1/n$
.
Inspecting the above proof, our approach only requires a super-logarithmic upper bound on the eigenvalues to go through. More precisely, we need that the first few nontrivial eigenvalues of
![]() $T_F^{*} T_F$
are at most
$T_F^{*} T_F$
are at most
![]() $(\log n)^{-K(t)}$
, for sufficiently large
$(\log n)^{-K(t)}$
, for sufficiently large
![]() $K(t)$
. We feel that something like that should follow in greater generality from the fact that the set of generators in the Cayley graph (namely, F) is global. To support that, note that if we were dealing with Abelian groups, then the eigenvalue
$K(t)$
. We feel that something like that should follow in greater generality from the fact that the set of generators in the Cayley graph (namely, F) is global. To support that, note that if we were dealing with Abelian groups, then the eigenvalue
![]() $\alpha $
of
$\alpha $
of
![]() $T_F$
corresponding to a character
$T_F$
corresponding to a character
![]() $\chi $
could be computed as
$\chi $
could be computed as
![]() $\lambda = \frac {1}{\left |F\right |}\sum \limits _{a\in F}{\chi (a)}$
, which by rewriting is nothing but a (normalised) Fourier coefficient of F (i.e.,
$\lambda = \frac {1}{\left |F\right |}\sum \limits _{a\in F}{\chi (a)}$
, which by rewriting is nothing but a (normalised) Fourier coefficient of F (i.e.,
![]() $\frac {1}{\delta } \widehat {1_F}(\chi )$
), which we expect to be small by the globalness of F.
$\frac {1}{\delta } \widehat {1_F}(\chi )$
), which we expect to be small by the globalness of F.
7.3 Isoperimetric inequalities in the transpositions Cayley graph
In this section, we consider
![]() $\mathrm {T}$
, which is the adjacency operator of the transpositions graph. That is, it is the transition matrix of the (left) Cayley graph
$\mathrm {T}$
, which is the adjacency operator of the transpositions graph. That is, it is the transition matrix of the (left) Cayley graph
![]() $(S_n,A)$
, where A is the set of transpositions (and the multiplication happens from the left). We show that for a global set S, starting a walk from a vertex in S and performing
$(S_n,A)$
, where A is the set of transpositions (and the multiplication happens from the left). We show that for a global set S, starting a walk from a vertex in S and performing
![]() $\approx c n$
steps according to
$\approx c n$
steps according to
![]() $\mathrm {T}$
escapes S with probability close to
$\mathrm {T}$
escapes S with probability close to
![]() $1$
.
$1$
.
Poisson process random walk.
To be more precise, we consider the following random walk: from a permutation
![]() $\pi \in S$
, choose a number
$\pi \in S$
, choose a number
![]() $k\sim \mathsf {Poisson}(t)$
, take
$k\sim \mathsf {Poisson}(t)$
, take
![]() $\tau $
which is a product of k random transpositions, and go to
$\tau $
which is a product of k random transpositions, and go to
![]() $\sigma = \tau \circ \pi $
. We show that starting with a random
$\sigma = \tau \circ \pi $
. We show that starting with a random
![]() $\pi \in S$
, the probability that we escape S (i.e., that
$\pi \in S$
, the probability that we escape S (i.e., that
![]() $S\sigma \not \in S$
) is close to
$S\sigma \not \in S$
) is close to
![]() $1$
.
$1$
.
To prove this result, we first note that the distribution of an outgoing neighbour from
![]() $\pi $
is exactly
$\pi $
is exactly
![]() $e^{-t(I-\mathrm {T})} 1_{\pi }$
, where
$e^{-t(I-\mathrm {T})} 1_{\pi }$
, where
![]() $1_{\pi }$
is the indicator vector of
$1_{\pi }$
is the indicator vector of
![]() $\pi $
. Therefore, the distribution of
$\pi $
. Therefore, the distribution of
![]() $\sigma $
where
$\sigma $
where
![]() $\pi \in S$
is random is
$\pi \in S$
is random is
![]() $e^{-t(I-\mathrm {T})} \frac {1_S}{\left |S\right |}$
, where
$e^{-t(I-\mathrm {T})} \frac {1_S}{\left |S\right |}$
, where
![]() $1_S$
is the indicator vector of S. Thus, the probability that
$1_S$
is the indicator vector of S. Thus, the probability that
![]() $\sigma $
is in S (i.e., of the complementary event) is
$\sigma $
is in S (i.e., of the complementary event) is
where
![]() $\mu (S)$
is the measure of S. We upper-bound this quantity using spectral considerations. We will only need our hypercontractive inequality and basic knowledge of the eigenvalues of
$\mu (S)$
is the measure of S. We upper-bound this quantity using spectral considerations. We will only need our hypercontractive inequality and basic knowledge of the eigenvalues of
![]() $\mathrm {T}$
, which can be found, for example, in [Reference Filmus, O’Donnell and Wu10, Corollary 21]. This is the content of the first three items in the lemma below (we also prove a fourth item, which will be useful for us later on).
$\mathrm {T}$
, which can be found, for example, in [Reference Filmus, O’Donnell and Wu10, Corollary 21]. This is the content of the first three items in the lemma below (we also prove a fourth item, which will be useful for us later on).
Lemma 7.10. Let
![]() $\lambda \in \mathbb {R}$
be an eigenvalue of
$\lambda \in \mathbb {R}$
be an eigenvalue of
![]() $\mathrm {T}$
and
$\mathrm {T}$
and
![]() $f\in V_{d}(S_n)$
be a corresponding eigenvector.
$f\in V_{d}(S_n)$
be a corresponding eigenvector.
-
1.
 $\mathrm {T} V_{=d}(S_n) \subseteq V_{=d}(S_n)$
.
$\mathrm {T} V_{=d}(S_n) \subseteq V_{=d}(S_n)$
. -
2.
 $1-\frac {2d}{n-1}\leqslant \lambda \leqslant 1-\frac {d}{n-1}$
.
$1-\frac {2d}{n-1}\leqslant \lambda \leqslant 1-\frac {d}{n-1}$
. -
3. If
 $d\leqslant n/2$
, then we have the stronger bound
$d\leqslant n/2$
, then we have the stronger bound
 $1-\frac {2d}{n-1}\leqslant \lambda \leqslant 1-\left (1-\frac {d-1}{n}\right )\frac {2d}{n-1}$
.
$1-\frac {2d}{n-1}\leqslant \lambda \leqslant 1-\left (1-\frac {d-1}{n}\right )\frac {2d}{n-1}$
. -
4. If
 $\mathrm {L}$
is a Laplacian of order
$\mathrm {L}$
is a Laplacian of order
 $1$
, then
$1$
, then
 $\mathrm {L}$
and
$\mathrm {L}$
and
 $\mathrm {T}$
commute. Thus,
$\mathrm {T}$
commute. Thus,
 $\mathrm {T}$
commutes with all Laplacians.
$\mathrm {T}$
commutes with all Laplacians.
Proof. For the first item, we first note that
![]() $\mathrm {T}$
commutes with the right action of
$\mathrm {T}$
commutes with the right action of
![]() $S_n$
on functions:
$S_n$
on functions:
Also,
![]() $\mathrm {T}$
is self adjoint, so
$\mathrm {T}$
is self adjoint, so
![]() $\mathrm {T}^{*}$
also commutes with the action of
$\mathrm {T}^{*}$
also commutes with the action of
![]() $S_n$
. The first item now follows as in the proof of Claim 7.4.
$S_n$
. The first item now follows as in the proof of Claim 7.4.
The second and third items are exactly [Reference Filmus, O’Donnell and Wu10, Corollary 21]. For the last item, for any function f and an order
![]() $1$
Laplacian
$1$
Laplacian
![]() $\mathrm {L} = \mathrm {L}_{(i,j)}$
,
$\mathrm {L} = \mathrm {L}_{(i,j)}$
,
where in the third transition we used the fact that
![]() $\mathrm {T}$
commutes with the right action of
$\mathrm {T}$
commutes with the right action of
![]() $S_n$
.
$S_n$
.
We remark that the first item above implies that we may find a basis of the space of real-valued functions consisting of eigenvectors of
![]() $\mathrm {T}$
, where each function is from
$\mathrm {T}$
, where each function is from
![]() $V_{=d}(S_n)$
for some d. Lastly, we need the following (straightforward) fact.
$V_{=d}(S_n)$
for some d. Lastly, we need the following (straightforward) fact.
Fact 7.11. If
![]() $f\in V_{d}(S_n)$
is an eigenvector of
$f\in V_{d}(S_n)$
is an eigenvector of
![]() $\mathrm {T}$
with eigenvalue
$\mathrm {T}$
with eigenvalue
![]() $\lambda $
, then f is an eigenvector of
$\lambda $
, then f is an eigenvector of
![]() $e^{-t(I-\mathrm {T})}$
with eigenvalue
$e^{-t(I-\mathrm {T})}$
with eigenvalue
![]() $e^{-t(1-\lambda )}$
.
$e^{-t(1-\lambda )}$
.
Theorem 7.12. There exists
![]() $C>0$
such that the following holds for all
$C>0$
such that the following holds for all
![]() $d\in \mathbb {N}$
,
$d\in \mathbb {N}$
,
![]() $t,\varepsilon>0$
and
$t,\varepsilon>0$
and
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $n\geqslant 2^{C\cdot d^3} \log ^{C\cdot d}(1/\varepsilon )$
. If
$n\geqslant 2^{C\cdot d^3} \log ^{C\cdot d}(1/\varepsilon )$
. If
![]() $S\subseteq S_n$
is a set of vertices such that
$S\subseteq S_n$
is a set of vertices such that
![]() $1_S$
is
$1_S$
is
![]() $(2d,\varepsilon )$
-global, then
$(2d,\varepsilon )$
-global, then
 $$\begin{align*}{\Pr_{\substack{\pi\in S \\ \sigma\sim e^{-t(I-T)} \pi}}\left[ {\sigma\not\in S} \right]}\geqslant 1-\left(2^{C\cdot d^4}\varepsilon\log^{C\cdot d}(1/\varepsilon) + e^{-\frac{(d+1)t}{n-1}}\right). \end{align*}$$
$$\begin{align*}{\Pr_{\substack{\pi\in S \\ \sigma\sim e^{-t(I-T)} \pi}}\left[ {\sigma\not\in S} \right]}\geqslant 1-\left(2^{C\cdot d^4}\varepsilon\log^{C\cdot d}(1/\varepsilon) + e^{-\frac{(d+1)t}{n-1}}\right). \end{align*}$$
Proof. Consider the complementary event that
![]() $\sigma \in S$
and note that the desired probability can be written analytically as
$\sigma \in S$
and note that the desired probability can be written analytically as
![]() $\frac {1}{\mu (S)} \langle {1_S},{ e^{-t(I-\mathrm {T})} 1_S}\rangle $
, where
$\frac {1}{\mu (S)} \langle {1_S},{ e^{-t(I-\mathrm {T})} 1_S}\rangle $
, where
![]() $\mu (S)$
is the measure of S. Now, writing
$\mu (S)$
is the measure of S. Now, writing
![]() $f = 1_S$
and expanding
$f = 1_S$
and expanding
![]() $f = f_{=0} + f_{=1}+\cdots $
, we consider each one of
$f = f_{=0} + f_{=1}+\cdots $
, we consider each one of
![]() $e^{-t(I-\mathrm {T})} f^{=j}$
separately. We claim that
$e^{-t(I-\mathrm {T})} f^{=j}$
separately. We claim that
Indeed, note that we may write
![]() $f^{=j} = \sum \limits _{}{a_r f_{j,r}}$
, where
$f^{=j} = \sum \limits _{}{a_r f_{j,r}}$
, where
![]() $f_{j,r}\in V_{=j}(S_n)$
are orthogonal and eigenvectors of
$f_{j,r}\in V_{=j}(S_n)$
are orthogonal and eigenvectors of
![]() $\mathrm {T}$
with eigenvalue
$\mathrm {T}$
with eigenvalue
![]() $\lambda _{j,r}$
, and so by Fact 7.11,
$\lambda _{j,r}$
, and so by Fact 7.11,
![]() $e^{-t(I-\mathrm {T})} f^{=j} =\sum \limits _{r} e^{-t(1-\lambda _{j,r})} f_{j,r}$
. By Parseval, we deduce that
$e^{-t(I-\mathrm {T})} f^{=j} =\sum \limits _{r} e^{-t(1-\lambda _{j,r})} f_{j,r}$
. By Parseval, we deduce that
 $$\begin{align*}\left\|e^{-t(I-\mathrm{T})} f^{=j}\right\|_2^2 \leqslant \sum\limits_{r} e^{-t(1-\lambda_{j,r})} \left\|f_{j,r}\right\|_2^2 \leqslant \max_{r}e^{-t(1-\lambda_{j,r})}\sum\limits_{r} \left\|f_{j,r}\right\|_2^2 =\max_{r}e^{-t(1-\lambda_{j,r})}\left\|f^{=j}\right\|_2^2. \end{align*}$$
$$\begin{align*}\left\|e^{-t(I-\mathrm{T})} f^{=j}\right\|_2^2 \leqslant \sum\limits_{r} e^{-t(1-\lambda_{j,r})} \left\|f_{j,r}\right\|_2^2 \leqslant \max_{r}e^{-t(1-\lambda_{j,r})}\sum\limits_{r} \left\|f_{j,r}\right\|_2^2 =\max_{r}e^{-t(1-\lambda_{j,r})}\left\|f^{=j}\right\|_2^2. \end{align*}$$
Inequality (16) now follows from the second item in Lemma 7.10.
We now expand out the expression we have for the probability of the complementary event using Plancherel:
 $$ \begin{align}\frac{1}{\mu(S)} \langle{1_S},{ e^{-t(I-\mathrm{T})} 1_S}\rangle =\frac{1}{\mu(S)}\sum\limits_{j} \langle{f^{=j}},{e^{-t(I-\mathrm{T})} f^{=j}}\rangle &\leqslant \frac{1}{\mu(S)}\sum\limits_{j} \left\|f^{=j}\right\|_2\left\|e^{-t(I-\mathrm{T})} f^{=j}\right\|_2 \nonumber\\[7pt] &\leqslant\frac{1}{\mu(S)}\sum\limits_{j} e^{-\frac{jt}{n-1}}\left\|f^{=j}\right\|_2^2, \end{align} $$
$$ \begin{align}\frac{1}{\mu(S)} \langle{1_S},{ e^{-t(I-\mathrm{T})} 1_S}\rangle =\frac{1}{\mu(S)}\sum\limits_{j} \langle{f^{=j}},{e^{-t(I-\mathrm{T})} f^{=j}}\rangle &\leqslant \frac{1}{\mu(S)}\sum\limits_{j} \left\|f^{=j}\right\|_2\left\|e^{-t(I-\mathrm{T})} f^{=j}\right\|_2 \nonumber\\[7pt] &\leqslant\frac{1}{\mu(S)}\sum\limits_{j} e^{-\frac{jt}{n-1}}\left\|f^{=j}\right\|_2^2, \end{align} $$
where in the last two transitions we used Cauchy–Schwarz and inequality (16). Lastly, we bound
![]() $\left \|f^{=j}\right \|_2^2$
. For
$\left \|f^{=j}\right \|_2^2$
. For
![]() $j> d$
, we have that
$j> d$
, we have that
![]() $\sum \limits _{j> d}\left \|f^{=j}\right \|_2^2\leqslant \mu (S)$
by Parseval, and for
$\sum \limits _{j> d}\left \|f^{=j}\right \|_2^2\leqslant \mu (S)$
by Parseval, and for
![]() $j\leqslant d$
, we use hypercontractivity.
$j\leqslant d$
, we use hypercontractivity.
First, bound
![]() $\left \|f^{=j}\right \|_2\leqslant \left \|f^{\leqslant j}\right \|_2$
and note that the function
$\left \|f^{=j}\right \|_2\leqslant \left \|f^{\leqslant j}\right \|_2$
and note that the function
![]() $f^{\leqslant j}$
is
$f^{\leqslant j}$
is
![]() $(2j, 2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon ))$
-global by Claim A.1. Thus, using Hölder’s inequality and Theorem 1.4, we get that
$(2j, 2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon ))$
-global by Claim A.1. Thus, using Hölder’s inequality and Theorem 1.4, we get that
Rearranging gives
![]() $\left \|f^{\leqslant j}\right \|_2^2 \leqslant 2^{O(j^4)} \mu (S) \varepsilon \log ^{O(j)}(1/\varepsilon )$
.
$\left \|f^{\leqslant j}\right \|_2^2 \leqslant 2^{O(j^4)} \mu (S) \varepsilon \log ^{O(j)}(1/\varepsilon )$
.
Plugging our estimates into (17), we get
 $$ \begin{align*} \frac{1}{\mu(S)} \langle{1_S},{ e^{-t(I-\mathrm{T})} 1_S}\rangle \leqslant \sum\limits_{j=0}^{d} 2^{O(j^4)}e^{-\frac{jt}{n-1}} \varepsilon\log^{O(j)}(1/\varepsilon) +e^{-\frac{(d+1)t}{n-1}} \leqslant 2^{O(d^4)}\varepsilon\log^{O(d)}(1/\varepsilon) + e^{-\frac{(d+1)t}{n-1}}.\\[-30pt] \end{align*} $$
$$ \begin{align*} \frac{1}{\mu(S)} \langle{1_S},{ e^{-t(I-\mathrm{T})} 1_S}\rangle \leqslant \sum\limits_{j=0}^{d} 2^{O(j^4)}e^{-\frac{jt}{n-1}} \varepsilon\log^{O(j)}(1/\varepsilon) +e^{-\frac{(d+1)t}{n-1}} \leqslant 2^{O(d^4)}\varepsilon\log^{O(d)}(1/\varepsilon) + e^{-\frac{(d+1)t}{n-1}}.\\[-30pt] \end{align*} $$
Using exactly the same technique, one can prove a lower bound on the probability of escaping a global set in a single step, as stated below. This result is similar in spirit to a variant of the KKL Theorem over the Boolean hypercube [Reference Kahn, Kalai and Linial15], and therefore, we modify the formulation slightly. Given a function
![]() $f\colon S_n\to \mathbb {R}$
, we define the influence of coordinate
$f\colon S_n\to \mathbb {R}$
, we define the influence of coordinate
![]() $i\in [n]$
to be
$i\in [n]$
to be
and define the total influence of f to be
![]() $I[f] = I_1[f]+\dots +I_n[f]$
.
$I[f] = I_1[f]+\dots +I_n[f]$
.
Theorem 7.13. There exists
![]() $C>0$
such that the following holds for all
$C>0$
such that the following holds for all
![]() $d\in \mathbb {N}$
and
$d\in \mathbb {N}$
and
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $n\geqslant 2^{C\cdot d^3}$
. Suppose
$n\geqslant 2^{C\cdot d^3}$
. Suppose
![]() $S\subseteq S_n$
is such that for all derivative operators
$S\subseteq S_n$
is such that for all derivative operators
![]() $\mathrm {D}\neq I$
of order at most d, it holds that
$\mathrm {D}\neq I$
of order at most d, it holds that
![]() $\left \|\mathrm {D}1_S\right \|_2\leqslant 2^{-C\cdot d^4}$
. Then
$\left \|\mathrm {D}1_S\right \|_2\leqslant 2^{-C\cdot d^4}$
. Then
Proof. Deferred to Appendix A.
7.4 Deducing results for the multi-cube
Our hypercontractive inequalities also imply similar hypercontractive inequalities on different non-product domains. One example from [Reference Braverman, Khot and Minzer3] is the domain of
![]() $2$
-to-
$2$
-to-
![]() $1$
maps (i.e.,
$1$
maps (i.e.,
![]() $\left \{ \left. \pi \colon [2n]\to [n] \;\right \vert \left |\pi ^{-1}(i)\right | = 2~\forall i\in [n] \right \}$
). A more general domain, which we consider below, is the multi-slice.
$\left \{ \left. \pi \colon [2n]\to [n] \;\right \vert \left |\pi ^{-1}(i)\right | = 2~\forall i\in [n] \right \}$
). A more general domain, which we consider below, is the multi-slice.
Definition 7.14. Let
![]() $m,n\in \mathbb {N}$
such that
$m,n\in \mathbb {N}$
such that
![]() $n \geqslant m$
and let
$n \geqslant m$
and let
![]() $k_1,\ldots ,k_m\in \mathbb {N}$
sum up to n. The multi-slice
$k_1,\ldots ,k_m\in \mathbb {N}$
sum up to n. The multi-slice
![]() $\mathcal {U}_{k_1,\ldots ,k_m}$
of dimension n consists of all vectors
$\mathcal {U}_{k_1,\ldots ,k_m}$
of dimension n consists of all vectors
![]() $x\in [m]^n$
that, for all
$x\in [m]^n$
that, for all
![]() $j\in [m]$
, have exactly
$j\in [m]$
, have exactly
![]() $k_j$
of their coordinates equal to j.
$k_j$
of their coordinates equal to j.
We consider the multi-slice as a probability space with the uniform measure.
In exactly the same way one defines the degree decomposition over
![]() $S_n$
, one may consider the degree decomposition over the mutli-slice. A function
$S_n$
, one may consider the degree decomposition over the mutli-slice. A function
![]() $f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
is said to be a d-junta if there are
$f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
is said to be a d-junta if there are
![]() $A\subseteq [n]$
of size at most d and
$A\subseteq [n]$
of size at most d and
![]() $g\colon [m]^d\to \mathbb {R}$
such that
$g\colon [m]^d\to \mathbb {R}$
such that
![]() $f(x) = g(x_A)$
. We then define the space
$f(x) = g(x_A)$
. We then define the space
![]() $V_d(\mathcal {U}_{k_1,\ldots ,k_m})$
spanned by d-juntas. Also, one may analogously define globalness of functions over the multi-slice. A d-restriction consists of a set
$V_d(\mathcal {U}_{k_1,\ldots ,k_m})$
spanned by d-juntas. Also, one may analogously define globalness of functions over the multi-slice. A d-restriction consists of a set
![]() $A\subseteq [n]$
of size d and
$A\subseteq [n]$
of size d and
![]() $\alpha \in [m]^A$
, and the corresponding restriction is the function
$\alpha \in [m]^A$
, and the corresponding restriction is the function
![]() $f_{A\rightarrow \alpha }(z) = f(x_A = \alpha , x_{\bar {A}} = z)$
(whose domain is a different multi-slice).
$f_{A\rightarrow \alpha }(z) = f(x_A = \alpha , x_{\bar {A}} = z)$
(whose domain is a different multi-slice).
Definition 7.15. We say
![]() $f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
is
$f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
is
![]() $(d,\varepsilon )$
-global if for any d-restriction
$(d,\varepsilon )$
-global if for any d-restriction
![]() $(A,\alpha )$
, it holds that
$(A,\alpha )$
, it holds that
![]() $\left \|f_{A\rightarrow \alpha }\right \|_2\leqslant \varepsilon $
.
$\left \|f_{A\rightarrow \alpha }\right \|_2\leqslant \varepsilon $
.
7.4.1 Hypercontractivity
Our hypercontractive inequality for the multi-slice reads as follows.
Theorem 7.16. There exists an absolute constant
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() $d,q,n\in \mathbb {N}$
be such that
$d,q,n\in \mathbb {N}$
be such that
![]() $n\geqslant q^{C\cdot d^2}$
and let
$n\geqslant q^{C\cdot d^2}$
and let
![]() $f\in V_d(\mathcal {U}_{k_1,\ldots ,k_m})$
. If f is
$f\in V_d(\mathcal {U}_{k_1,\ldots ,k_m})$
. If f is
![]() $(2d,\varepsilon )$
-global, then
$(2d,\varepsilon )$
-global, then
Proof. We construct a simple deterministic coupling
![]() $\mathcal {C}$
between
$\mathcal {C}$
between
![]() $S_n$
and
$S_n$
and
![]() $\mathcal {U}_{k_1,\ldots ,k_m}$
.
$\mathcal {U}_{k_1,\ldots ,k_m}$
.
Fix a partition of
![]() $[n]$
into sets
$[n]$
into sets
![]() $K_1,\ldots ,K_m$
such that
$K_1,\ldots ,K_m$
such that
![]() $\left |K_j\right | = k_j$
for all j. Given a permutation
$\left |K_j\right | = k_j$
for all j. Given a permutation
![]() $\pi $
, we define
$\pi $
, we define
![]() $\mathcal {C}(\pi ) = x$
as follows: for all
$\mathcal {C}(\pi ) = x$
as follows: for all
![]() $i\in [n]$
,
$i\in [n]$
,
![]() $j\in [m]$
, we set
$j\in [m]$
, we set
![]() $x_i = j$
if
$x_i = j$
if
![]() $\pi (i)\in K_j$
. Define the mapping
$\pi (i)\in K_j$
. Define the mapping
![]() $M\colon L_2(\mathcal {U}_{k_1,\ldots ,k_m})\to L_2(S_n)$
that maps a function
$M\colon L_2(\mathcal {U}_{k_1,\ldots ,k_m})\to L_2(S_n)$
that maps a function
![]() $h\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
to
$h\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
to
![]() $M h\colon S_n\to \mathbb {R}$
defined by
$M h\colon S_n\to \mathbb {R}$
defined by
![]() $(M h)(\pi ) = h(\mathcal {C}(\pi ))$
.
$(M h)(\pi ) = h(\mathcal {C}(\pi ))$
.
Let
![]() $g = Mf$
. We claim that g has degree at most d and is global. To see that
$g = Mf$
. We claim that g has degree at most d and is global. To see that
![]() $g\in V_d(S_n)$
, it is enough to show that the mapping
$g\in V_d(S_n)$
, it is enough to show that the mapping
![]() $f\rightarrow g$
is linear (which is clear) and maps a d-junta into a d-junta, which is also straightforward. To see that g is global, let
$f\rightarrow g$
is linear (which is clear) and maps a d-junta into a d-junta, which is also straightforward. To see that g is global, let
![]() $T = {\left \{ (i_1,r_1),\ldots ,(i_\ell ,r_\ell ) \right \}}$
be consistent and define the r-restriction
$T = {\left \{ (i_1,r_1),\ldots ,(i_\ell ,r_\ell ) \right \}}$
be consistent and define the r-restriction
![]() $(A,\alpha )$
as
$(A,\alpha )$
as
![]() $A = {\left \{ i_1,\ldots ,i_{\ell } \right \}}$
, and
$A = {\left \{ i_1,\ldots ,i_{\ell } \right \}}$
, and
![]() $\alpha _{i_s} = j$
if
$\alpha _{i_s} = j$
if
![]() $r_s\in K_j$
. Note that the distribution of
$r_s\in K_j$
. Note that the distribution of
![]() $x\in \mathcal {U}_{k_1,\ldots ,k_m}$
conditioned on
$x\in \mathcal {U}_{k_1,\ldots ,k_m}$
conditioned on
![]() $x_A$
is exactly the same as of
$x_A$
is exactly the same as of
![]() $\mathcal {C}(\pi )$
conditioned on
$\mathcal {C}(\pi )$
conditioned on
![]() $\pi $
respecting T, so if
$\pi $
respecting T, so if
![]() $r\leqslant 2d$
, we get that
$r\leqslant 2d$
, we get that
and g is
![]() $(2d,\varepsilon )$
-global. The result thus follows from Theorem 1.4 and the fact that M preserves
$(2d,\varepsilon )$
-global. The result thus follows from Theorem 1.4 and the fact that M preserves
![]() $L_p$
norms for all
$L_p$
norms for all
![]() $p\geqslant 1$
.
$p\geqslant 1$
.
The coupling in the proof of Theorem 7.16 also implies in the same way a level-d inequality over
![]() $\mathcal {U}_{k_1,\ldots ,k_m}$
from the corresponding result in
$\mathcal {U}_{k_1,\ldots ,k_m}$
from the corresponding result in
![]() $S_n$
, Theorem 1.6, as well as isoperimetric inequalities, as we describe next.
$S_n$
, Theorem 1.6, as well as isoperimetric inequalities, as we describe next.
7.4.2 Level-d inequality
As on
![]() $S_n$
, for
$S_n$
, for
![]() $f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
, we let
$f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
, we let
![]() $f^{\leqslant d}$
be the projection of f onto
$f^{\leqslant d}$
be the projection of f onto
![]() $V_d(\mathcal {U}_{k_1,\ldots ,k_m})$
. Our level-d inequality for the multi-slice thus reads as follows:
$V_d(\mathcal {U}_{k_1,\ldots ,k_m})$
. Our level-d inequality for the multi-slice thus reads as follows:
Corollary 7.17. There exists an absolute constant
![]() $C>0$
such that the following holds. Let
$C>0$
such that the following holds. Let
![]() $d,n\in \mathbb {N}$
and
$d,n\in \mathbb {N}$
and
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $n\geqslant 2^{C d^3} \log (1/\varepsilon )^{C d}$
. If
$n\geqslant 2^{C d^3} \log (1/\varepsilon )^{C d}$
. If
![]() $f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \{0,1\}$
is
$f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \{0,1\}$
is
![]() $(2d,\varepsilon )$
-global, then
$(2d,\varepsilon )$
-global, then
![]() $\left \|f^{\leqslant d}\right \|_2^2\leqslant 2^{C \cdot d^4}\varepsilon ^4 \log ^{C\cdot d}(1/\varepsilon )$
.
$\left \|f^{\leqslant d}\right \|_2^2\leqslant 2^{C \cdot d^4}\varepsilon ^4 \log ^{C\cdot d}(1/\varepsilon )$
.
Proof. The proof relies on an additional easy property of the mapping M from the proof of Theorem 7.16. As in
![]() $S_n$
, we define the space of pure degree d functions over
$S_n$
, we define the space of pure degree d functions over
![]() $\mathcal {U}_{k_1,\ldots ,k_m}$
as
$\mathcal {U}_{k_1,\ldots ,k_m}$
as
![]() $V_{=d}(\mathcal {U}_{k_1,\ldots ,k_m}) = V_{d}(\mathcal {U}_{k_1,\ldots ,k_m})\cap V_{d-1}(\mathcal {U}_{k_1,\ldots ,k_m})^{\bot }$
and let
$V_{=d}(\mathcal {U}_{k_1,\ldots ,k_m}) = V_{d}(\mathcal {U}_{k_1,\ldots ,k_m})\cap V_{d-1}(\mathcal {U}_{k_1,\ldots ,k_m})^{\bot }$
and let
![]() $f^{=d}$
be the projection of f onto
$f^{=d}$
be the projection of f onto
![]() $V_{=d}(\mathcal {U}_{k_1,\ldots ,k_m})$
. We thus have
$V_{=d}(\mathcal {U}_{k_1,\ldots ,k_m})$
. We thus have
![]() $f^{\leqslant d} = f^{=0}+f^{=1}+\dots +f^{=d}$
, and so
$f^{\leqslant d} = f^{=0}+f^{=1}+\dots +f^{=d}$
, and so
![]() $f^{=d} = f^{\leqslant d} - f^{\leqslant d-1}$
.
$f^{=d} = f^{\leqslant d} - f^{\leqslant d-1}$
.
Write
![]() $h_i = M f^{=i}$
and note that
$h_i = M f^{=i}$
and note that
![]() $h_i$
is of degree at most i. Also, we note that as restrictions of size
$h_i$
is of degree at most i. Also, we note that as restrictions of size
![]() $r<i$
over
$r<i$
over
![]() $S_n$
are mapped to restrictions of size r over
$S_n$
are mapped to restrictions of size r over
![]() $\mathcal {U}_{k_1,\ldots ,k_m}$
, it follows that
$\mathcal {U}_{k_1,\ldots ,k_m}$
, it follows that
![]() $h_i$
is perpendicular to degree
$h_i$
is perpendicular to degree
![]() $i-1$
functions, and so
$i-1$
functions, and so
![]() $h_i\in V_{=i}(S_n)$
. By linearity of M,
$h_i\in V_{=i}(S_n)$
. By linearity of M,
![]() $M f = h_0+h_1+\dots + h_n$
, and by uniqueness of the pure degree decomposition, it follows that
$M f = h_0+h_1+\dots + h_n$
, and by uniqueness of the pure degree decomposition, it follows that
![]() $h_i = (M f)^{=i}$
. We therefore have that
$h_i = (M f)^{=i}$
. We therefore have that
where the last inequality is by Theorem 1.6.
7.4.3 Isoperimetric inequalities
One can also deduce the obvious analogs of Theorems 7.12, 7.13 for the multi-slice. Since we use it for our final application, we include here the statement of the analog of Theorem 7.13.
For
![]() $f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
, consider the Laplacians
$f\colon \mathcal {U}_{k_1,\ldots ,k_m}\to \mathbb {R}$
, consider the Laplacians
![]() $\mathrm {L}_{i,j}$
that map a function f to a function
$\mathrm {L}_{i,j}$
that map a function f to a function
![]() $L_{i,j} f$
defined as
$L_{i,j} f$
defined as
![]() $\mathrm {L}_{i,j} f(x) = f(x) - f(x^{(i,j)})$
and define
$\mathrm {L}_{i,j} f(x) = f(x) - f(x^{(i,j)})$
and define
![]() $I_i[f] = {\mathop {\mathbb {E}}_{j\neq i}\left [ {\left \|L_{i,j} f\right \|_2^2} \right ]}$
and
$I_i[f] = {\mathop {\mathbb {E}}_{j\neq i}\left [ {\left \|L_{i,j} f\right \|_2^2} \right ]}$
and
![]() $I[f] = \sum \limits _{i=1}^{n} I_i[f]$
. Similarly to Definition 4.1, we define a derivative of f as a restriction of the corresponding Laplacian (i.e., for
$I[f] = \sum \limits _{i=1}^{n} I_i[f]$
. Similarly to Definition 4.1, we define a derivative of f as a restriction of the corresponding Laplacian (i.e., for
![]() $i,j\in [n]$
,
$i,j\in [n]$
,
![]() $a,b\in [m]$
, we define
$a,b\in [m]$
, we define
![]() $\mathrm {D}_{(i,j)\rightarrow (a,b)} f = (\mathrm {L}_{i,j} f(x))_{(i,j)\rightarrow (a,b)}$
).
$\mathrm {D}_{(i,j)\rightarrow (a,b)} f = (\mathrm {L}_{i,j} f(x))_{(i,j)\rightarrow (a,b)}$
).
Theorem 7.18. There exists
![]() $C>0$
such that the following holds for all
$C>0$
such that the following holds for all
![]() $d\in \mathbb {N}$
and
$d\in \mathbb {N}$
and
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $n\geqslant 2^{C\cdot d^3}$
. Suppose
$n\geqslant 2^{C\cdot d^3}$
. Suppose
![]() $S\subseteq \mathcal {U}_{k_1,\ldots ,k_m}$
such that for all derivative operators
$S\subseteq \mathcal {U}_{k_1,\ldots ,k_m}$
such that for all derivative operators
![]() $\mathrm {D}\neq I$
of order at most d, it holds that
$\mathrm {D}\neq I$
of order at most d, it holds that
![]() $\left \|\mathrm {D}1_S\right \|_2\leqslant 2^{-C\cdot d^4}$
. Then
$\left \|\mathrm {D}1_S\right \|_2\leqslant 2^{-C\cdot d^4}$
. Then
![]() $I[1_S]\geqslant \frac {1}{4} d\cdot {\sf var}(1_S)$
.
$I[1_S]\geqslant \frac {1}{4} d\cdot {\sf var}(1_S)$
.
We omit the straightforward derivation from Theorem 7.13.
7.5 Stability result for the Kruskal–Katona theorem on the slice
Our final application is the following sharp threshold result for the slice, which can be also seen as a stability version of the Kruskal–Katona theorem (see [Reference O’Donnell and Wimmer25, Reference Keevash16] for other, incomparable stability versions). For a family of subsets
![]() $\mathcal {F} \subseteq {[n]\choose k}$
, we denote
$\mathcal {F} \subseteq {[n]\choose k}$
, we denote
![]() $\mu (\mathcal {F}) = \left |\mathcal {F}\right |/{n\choose k}$
and define the upper shadow of
$\mu (\mathcal {F}) = \left |\mathcal {F}\right |/{n\choose k}$
and define the upper shadow of
![]() $\mathcal {F}$
as
$\mathcal {F}$
as
 $$\begin{align*}\mathcal{F}\uparrow = \left\{ \left. X\in{n\choose k+1} \;\right\vert \exists A\subseteq X, A\in \mathcal{F} \right\}. \end{align*}$$
$$\begin{align*}\mathcal{F}\uparrow = \left\{ \left. X\in{n\choose k+1} \;\right\vert \exists A\subseteq X, A\in \mathcal{F} \right\}. \end{align*}$$
The Kruskal–Katona theorem is a basic result in combinatorics that gives a lower bound on the measure of the upper shadow of a family
![]() $\mathcal {F}$
in terms of the measure of the family itself. Below, we state a convenient, simplified version of it due to Lovász, which uses the generalised binomial coefficients.
$\mathcal {F}$
in terms of the measure of the family itself. Below, we state a convenient, simplified version of it due to Lovász, which uses the generalised binomial coefficients.
Theorem 7.19. Let
![]() $\mathcal {F}\subseteq {[n]\choose k}$
and suppose that
$\mathcal {F}\subseteq {[n]\choose k}$
and suppose that
![]() $\left |\mathcal {F}\right | = {n-a\choose n-k}$
. Then
$\left |\mathcal {F}\right | = {n-a\choose n-k}$
. Then
![]() $\left |\mathcal {F}\uparrow \right |\geqslant {n-a\choose n-k-1}$
.
$\left |\mathcal {F}\uparrow \right |\geqslant {n-a\choose n-k-1}$
.
In general, Theorem 7.19 is tight, as can be shown by considering ‘subcubes’ (i.e., families of the form
![]() $\mathcal {H}_A = \left \{ \left. X\in {[n]\choose k} \;\right \vert X\supseteq A \right \}$
for some
$\mathcal {H}_A = \left \{ \left. X\in {[n]\choose k} \;\right \vert X\supseteq A \right \}$
for some
![]() $A\subseteq [n]$
); these correspond to
$A\subseteq [n]$
); these correspond to
![]() $a = |A|$
. This raises the question of whether a stronger version of Theorem 7.19 holds for families that are ‘far from having a structure such as
$a = |A|$
. This raises the question of whether a stronger version of Theorem 7.19 holds for families that are ‘far from having a structure such as
![]() $\mathcal {H}_A$
’. Alternatively, this question can be viewed as a stability version of Theorem 7.19: must a family for which Theorem 7.19 is almost tight be of a similar structure to
$\mathcal {H}_A$
’. Alternatively, this question can be viewed as a stability version of Theorem 7.19: must a family for which Theorem 7.19 is almost tight be of a similar structure to
![]() $\mathcal {H}_A$
?
$\mathcal {H}_A$
?
Below, we mainly consider the case that
![]() $k=o(n)$
and show an improved version of Theorem 7.19 for families that are ‘far from
$k=o(n)$
and show an improved version of Theorem 7.19 for families that are ‘far from
![]() $\mathcal {H}_A$
’. To formalize this, we consider the notion of restrictions: for
$\mathcal {H}_A$
’. To formalize this, we consider the notion of restrictions: for
![]() $A\subseteq I\subseteq [n]$
, we define
$A\subseteq I\subseteq [n]$
, we define
and also define its measure
![]() $\mu (\mathcal {F}_{I\rightarrow A})$
appropriately. We say a family
$\mu (\mathcal {F}_{I\rightarrow A})$
appropriately. We say a family
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $(d,\varepsilon )$
-global if for any
$(d,\varepsilon )$
-global if for any
![]() $\left |I\right |\leqslant d$
and
$\left |I\right |\leqslant d$
and
![]() $A\subseteq I$
, it holds that
$A\subseteq I$
, it holds that
![]() $\mu (\mathcal {F}_{I\rightarrow A})\leqslant \varepsilon $
.
$\mu (\mathcal {F}_{I\rightarrow A})\leqslant \varepsilon $
.
Theorem 7.20. There exists
![]() $C>0$
, such that the following holds for all
$C>0$
, such that the following holds for all
![]() $d,n\in \mathbb {N}$
such that
$d,n\in \mathbb {N}$
such that
![]() $n\geqslant 2^{C\cdot d^4}$
. Let
$n\geqslant 2^{C\cdot d^4}$
. Let
![]() $\mathcal {F}\subseteq {[n]\choose k}$
and suppose that
$\mathcal {F}\subseteq {[n]\choose k}$
and suppose that
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $(d,2^{-C\cdot d^4})$
-global. Then
$(d,2^{-C\cdot d^4})$
-global. Then
![]() $\mu (\mathcal {F}\uparrow )\geqslant \left (1+\frac {d}{64k}\right ) \mu (\mathcal {F})$
.
$\mu (\mathcal {F}\uparrow )\geqslant \left (1+\frac {d}{64k}\right ) \mu (\mathcal {F})$
.
Proof. Let
![]() $f = 1_{\mathcal {F}}$
,
$f = 1_{\mathcal {F}}$
,
![]() $g = 1_{\mathcal {F}\uparrow }$
and consider the operator
$g = 1_{\mathcal {F}\uparrow }$
and consider the operator
![]() $M\colon {[n]\choose k} \to {[n]\choose k+1}$
that from a set
$M\colon {[n]\choose k} \to {[n]\choose k+1}$
that from a set
![]() $A\subseteq [n]$
of size k moves to a random set of size
$A\subseteq [n]$
of size k moves to a random set of size
![]() $k+1$
containing it. We also consider M as an operator
$k+1$
containing it. We also consider M as an operator
![]() $M\colon L_2\left ({[n]\choose k}\right )\rightarrow L_2\left ({[n]\choose k+1}\right )$
defined as
$M\colon L_2\left ({[n]\choose k}\right )\rightarrow L_2\left ({[n]\choose k+1}\right )$
defined as
![]() $M f(B)={\mathop {\mathbb {E}}_{A\subseteq B}\left [ {f(A)} \right ]}$
(this operator is sometimes known as the raising or up operator). Note that for all
$M f(B)={\mathop {\mathbb {E}}_{A\subseteq B}\left [ {f(A)} \right ]}$
(this operator is sometimes known as the raising or up operator). Note that for all
![]() $B\in {[n]\choose k+1}$
, it holds that
$B\in {[n]\choose k+1}$
, it holds that
![]() $g(B) M f(B) = M f(B)$
and that the average of
$g(B) M f(B) = M f(B)$
and that the average of
![]() $M f$
is the same as the average of f (i.e.,
$M f$
is the same as the average of f (i.e.,
![]() $\mu (\mathcal {F})$
). Thus,
$\mu (\mathcal {F})$
). Thus,
Using the fact that the
![]() $2$
-norm of g squared is the measure of
$2$
-norm of g squared is the measure of
![]() $\mathcal {F}\uparrow $
and rearranging, we get that
$\mathcal {F}\uparrow $
and rearranging, we get that
 $$ \begin{align} \mu(\mathcal{F}\uparrow)\geqslant\frac{\mu(\mathcal{F})^2}{\langle{f},{M^{*} M f}\rangle} = \frac{\mu(\mathcal{F})^2}{{\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim MM^{*} x}}\left[ {x\in \mathcal{F},y\in \mathcal{F}} \right]}}. \end{align} $$
$$ \begin{align} \mu(\mathcal{F}\uparrow)\geqslant\frac{\mu(\mathcal{F})^2}{\langle{f},{M^{*} M f}\rangle} = \frac{\mu(\mathcal{F})^2}{{\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim MM^{*} x}}\left[ {x\in \mathcal{F},y\in \mathcal{F}} \right]}}. \end{align} $$
We next lower-bound
![]() ${\Pr _{\substack {x\in _R{[n]\choose k}\\ y\sim MM^{*} x}}\left [ {x\in \mathcal {F},y\not \in \mathcal {F}} \right ]}$
, which will give us an upper bound on the denominator. Towards this end, we relate this probability to the total influence of
${\Pr _{\substack {x\in _R{[n]\choose k}\\ y\sim MM^{*} x}}\left [ {x\in \mathcal {F},y\not \in \mathcal {F}} \right ]}$
, which will give us an upper bound on the denominator. Towards this end, we relate this probability to the total influence of
![]() $1_{\mathcal {F}}$
as defined in Section 7.4.3. Note that the distribution of y conditioned on x is this: with probability
$1_{\mathcal {F}}$
as defined in Section 7.4.3. Note that the distribution of y conditioned on x is this: with probability
![]() $1/(k+1)$
, we have
$1/(k+1)$
, we have
![]() $y=x$
, and otherwise
$y=x$
, and otherwise
![]() $y = x^{(i,j)}$
, where
$y = x^{(i,j)}$
, where
![]() $i,j$
are random coordinates such that
$i,j$
are random coordinates such that
![]() $x_i \neq x_j$
. Consider
$x_i \neq x_j$
. Consider
![]() $z\sim \mathrm {T} x$
, where
$z\sim \mathrm {T} x$
, where
![]() $\mathrm {T}$
is the operator of applying a random transposition; the probability that it interchanges two coordinates
$\mathrm {T}$
is the operator of applying a random transposition; the probability that it interchanges two coordinates
![]() $i,j$
such that
$i,j$
such that
![]() $x_i\neq x_j$
is
$x_i\neq x_j$
is
![]() $k(n-k)/\binom {n}{2}$
, and so we get
$k(n-k)/\binom {n}{2}$
, and so we get
 $$ \begin{align*}&{\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim MM^{*} x}}\left[ {x\in \mathcal{F},y\not\in \mathcal{F}} \right]} =\frac{k}{k+1}\frac{n(n-1)}{2k(n-k)}{\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim \mathrm{T} x}}\left[ {x\in \mathcal{F},y\not\in \mathcal{F}} \right]} \\ &\quad=\frac{k}{k+1}\frac{n(n-1)}{2k(n-k)} \frac{1}{2} {\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim \mathrm{T} x}}\left[ {1_{\mathcal{F}}(x) \neq 1_{\mathcal{F}}(y)} \right]} =\frac{k}{k+1}\frac{n(n-1)}{2k(n-k)}\frac{1}{2n} I[1_{\mathcal{F}}] \geqslant \frac{1}{8k}I[1_{\mathcal{F}}], \end{align*} $$
$$ \begin{align*}&{\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim MM^{*} x}}\left[ {x\in \mathcal{F},y\not\in \mathcal{F}} \right]} =\frac{k}{k+1}\frac{n(n-1)}{2k(n-k)}{\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim \mathrm{T} x}}\left[ {x\in \mathcal{F},y\not\in \mathcal{F}} \right]} \\ &\quad=\frac{k}{k+1}\frac{n(n-1)}{2k(n-k)} \frac{1}{2} {\Pr_{\substack{x\in_R{[n]\choose k}\\ y\sim \mathrm{T} x}}\left[ {1_{\mathcal{F}}(x) \neq 1_{\mathcal{F}}(y)} \right]} =\frac{k}{k+1}\frac{n(n-1)}{2k(n-k)}\frac{1}{2n} I[1_{\mathcal{F}}] \geqslant \frac{1}{8k}I[1_{\mathcal{F}}], \end{align*} $$
which is at least
![]() $\frac {d}{64k}\mu (f)$
by Theorem 7.18 (and the fact that
$\frac {d}{64k}\mu (f)$
by Theorem 7.18 (and the fact that
![]() $\mathsf {var}(f) = \mu (f)(1-\mu (f))\geqslant \mu (f)/2$
). It follows that the denominator in (18) is at most
$\mathsf {var}(f) = \mu (f)(1-\mu (f))\geqslant \mu (f)/2$
). It follows that the denominator in (18) is at most
![]() $\mu (f)\left (1-\frac {d}{64k}\right )$
, and plugging this into (18), we get that
$\mu (f)\left (1-\frac {d}{64k}\right )$
, and plugging this into (18), we get that
 $$\begin{align*}\mu(\mathcal{F}\uparrow) \geqslant \left(1+\frac{d}{64k}\right) \mu(\mathcal{F}).\\[-42pt] \end{align*}$$
$$\begin{align*}\mu(\mathcal{F}\uparrow) \geqslant \left(1+\frac{d}{64k}\right) \mu(\mathcal{F}).\\[-42pt] \end{align*}$$
Let us compare this to Theorem 7.19. Suppose that
![]() $|\mathcal {F}| = \binom {n-a}{n-k}$
. Then Theorem 7.19 states that
$|\mathcal {F}| = \binom {n-a}{n-k}$
. Then Theorem 7.19 states that
 $$\begin{align*}\frac{\mu(\mathcal{F} \uparrow)}{\mu(\mathcal{F})} \geqslant \frac{\binom{n-a}{n-k-1}}{\binom{n}{k+1}} \frac{\binom{n}{k}}{\binom{n-a}{n-k}} = \frac{k+1}{k+1-a} \approx 1 + \frac{a}{k}. \end{align*}$$
$$\begin{align*}\frac{\mu(\mathcal{F} \uparrow)}{\mu(\mathcal{F})} \geqslant \frac{\binom{n-a}{n-k-1}}{\binom{n}{k+1}} \frac{\binom{n}{k}}{\binom{n-a}{n-k}} = \frac{k+1}{k+1-a} \approx 1 + \frac{a}{k}. \end{align*}$$
Theorem 7.20 states that if
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $(d,2^{-C \cdot d^4})$
-global, then we can improve
$(d,2^{-C \cdot d^4})$
-global, then we can improve
![]() $a/k$
to
$a/k$
to
![]() $d/k$
. Stated differently, if the ratio above is only
$d/k$
. Stated differently, if the ratio above is only
![]() $1 + a/k$
, then
$1 + a/k$
, then
![]() $\mathcal {F}$
must be ‘somewhat close to
$\mathcal {F}$
must be ‘somewhat close to
![]() $\mathcal {H}_A$
’ for some A of size
$\mathcal {H}_A$
’ for some A of size
![]() $O(a)$
.
$O(a)$
.
We can also compare Theorem 7.20 to Bourgain’s sharp threshold theorem [Reference Friedgut and Bourgain12, Appendix], which states that if f is a monotone Boolean function satisfying
![]() $p I^p[f] \leqslant Cs \mu _p(f)$
, then
$p I^p[f] \leqslant Cs \mu _p(f)$
, then
![]() $\mu _p(f_{S \to 1}) \geqslant e^{-O(s^2)}$
for some S of size s. Recall that Russo’s lemma shows that
$\mu _p(f_{S \to 1}) \geqslant e^{-O(s^2)}$
for some S of size s. Recall that Russo’s lemma shows that
![]() $I^p[f]$
is the derivative of
$I^p[f]$
is the derivative of
![]() $\mu _p(f)$
. It thus corresponds to
$\mu _p(f)$
. It thus corresponds to
![]() $[\mu (\mathcal {F} \uparrow ) - \mu (\mathcal {F})]/(\tfrac {k+1}{n} - \tfrac {k}{n})$
. Multiplying by
$[\mu (\mathcal {F} \uparrow ) - \mu (\mathcal {F})]/(\tfrac {k+1}{n} - \tfrac {k}{n})$
. Multiplying by
![]() $p = k/n$
, the assumption of Bourgain’s theorem translates to
$p = k/n$
, the assumption of Bourgain’s theorem translates to
![]() $k(\mu (\mathcal {F} \uparrow ) - \mu (\mathcal {F})) \leqslant C s \mu (\mathcal {F})$
– that is,
$k(\mu (\mathcal {F} \uparrow ) - \mu (\mathcal {F})) \leqslant C s \mu (\mathcal {F})$
– that is,
![]() $\mu (\mathcal {F} \uparrow ) \leqslant (1 + \tfrac {Cs}{k}) \mu (\mathcal {F})$
. The conclusion is that there is a restriction of size s whose measure is
$\mu (\mathcal {F} \uparrow ) \leqslant (1 + \tfrac {Cs}{k}) \mu (\mathcal {F})$
. The conclusion is that there is a restriction of size s whose measure is
![]() $2^{-O(s^2)}$
. This almost matches the contrapositive of Theorem 7.20, up to the power of d in the exponent. (In contrast, Theorem 7.19 corresponds to the isoperimetric inequality
$2^{-O(s^2)}$
. This almost matches the contrapositive of Theorem 7.20, up to the power of d in the exponent. (In contrast, Theorem 7.19 corresponds to the isoperimetric inequality
![]() $pI^p[f] \leqslant \mu _p(f) \log _p \mu _p(f)$
.)
$pI^p[f] \leqslant \mu _p(f) \log _p \mu _p(f)$
.)
8 Proof of the level-d inequality
The goal of this section is to prove Theorem 1.6.
8.1 Proof overview
Proof overview in an idealized setting.
We first describe the proof idea in an idealized setting in which derivative operators, and truncations, interact well. By that, we mean that if
![]() $\mathrm {D}$
is an order
$\mathrm {D}$
is an order
![]() $\ell $
derivative, and f is a function, then
$\ell $
derivative, and f is a function, then
![]() $\mathrm {D} (f^{\leqslant d}) = (\mathrm {D} f)^{\leqslant d-\ell }$
. We remark that this property holds in product spaces but may fail in non-product domains such as
$\mathrm {D} (f^{\leqslant d}) = (\mathrm {D} f)^{\leqslant d-\ell }$
. We remark that this property holds in product spaces but may fail in non-product domains such as
![]() $S_n$
.
$S_n$
.
Adapting the proof of the level-d inequality from the hypercube (using Theorem 1.4 instead of standard hypercontractivity), one may easily establish a weaker version of Theorem 1.6, wherein
![]() $\varepsilon ^2$
is replaced by
$\varepsilon ^2$
is replaced by
![]() $\varepsilon ^{3/2}$
, as follows. Take
$\varepsilon ^{3/2}$
, as follows. Take
![]() $q =\log (1/\varepsilon )$
; then
$q =\log (1/\varepsilon )$
; then
Since f is integer-valued, we have that
![]() $\left \|f\right \|_{1+1/(q-1)}$
is at most
$\left \|f\right \|_{1+1/(q-1)}$
is at most
![]() $\left \|f\right \|_2^{2(q-1)/q}\leqslant \varepsilon ^{2(q-1)/q}$
. Using the assumption of our idealized setting and Parseval, we get that for every derivative
$\left \|f\right \|_2^{2(q-1)/q}\leqslant \varepsilon ^{2(q-1)/q}$
. Using the assumption of our idealized setting and Parseval, we get that for every derivative
![]() $\mathrm {D}$
of order
$\mathrm {D}$
of order
![]() $\ell $
, we have that
$\ell $
, we have that
![]() $\left \|\mathrm {D} (f^{\leqslant d})\right \|_2 = \left \|(\mathrm {D} f)^{\leqslant d-\ell }\right \|_2\leqslant \left \|\mathrm {D} f\right \|_2$
. Thus, using the globalness of f and both items of Claim 4.2, we get that
$\left \|\mathrm {D} (f^{\leqslant d})\right \|_2 = \left \|(\mathrm {D} f)^{\leqslant d-\ell }\right \|_2\leqslant \left \|\mathrm {D} f\right \|_2$
. Thus, using the globalness of f and both items of Claim 4.2, we get that
![]() $f^{\leqslant d}$
is
$f^{\leqslant d}$
is
![]() $(d,2^{O(d)}\varepsilon )$
-global, and so by Theorem 1.4, we get that
$(d,2^{O(d)}\varepsilon )$
-global, and so by Theorem 1.4, we get that
![]() $\left \|f^{\leqslant d}\right \|_q\leqslant (2q)^{O(d^3)}\varepsilon $
. All in all, we get that
$\left \|f^{\leqslant d}\right \|_q\leqslant (2q)^{O(d^3)}\varepsilon $
. All in all, we get that
![]() $\left \|f^{\leqslant d}\right \|_2^2\leqslant (2q)^{O(d^3)}\varepsilon ^{3}$
, which falls short of Theorem 1.6 by a factor of
$\left \|f^{\leqslant d}\right \|_2^2\leqslant (2q)^{O(d^3)}\varepsilon ^{3}$
, which falls short of Theorem 1.6 by a factor of
![]() $\varepsilon $
.
$\varepsilon $
.
The quantitative deficiency in this argument stems from the fact that
![]() $f^{\leqslant d}$
is in fact much more global than what the simplistic argument above establishes, and it shows that we prove things by induction on d. This induction is also the reason we have strengthened Theorem 1.6 from the introduction to Proposition 8.11 below.
$f^{\leqslant d}$
is in fact much more global than what the simplistic argument above establishes, and it shows that we prove things by induction on d. This induction is also the reason we have strengthened Theorem 1.6 from the introduction to Proposition 8.11 below.
Returning to the real setting.
To lift the assumption of the ideal setting, we return to discuss restrictions (as opposed to derivatives). Again, we would have been in good shape if restrictions were to commute with degree truncations, but this again fails, just like derivatives. Instead, we use the following observation (Claim 8.4). Suppose
![]() $k\geqslant d+\ell +2$
, let g be a function of pure degree k, and let S be a restriction of size at most
$k\geqslant d+\ell +2$
, let g be a function of pure degree k, and let S be a restriction of size at most
![]() $\ell $
. Then the restricted function
$\ell $
. Then the restricted function
![]() $g_S$
is perpendicular to degree
$g_S$
is perpendicular to degree
![]() $k-\ell -1> d$
functions, and so
$k-\ell -1> d$
functions, and so
![]() $(g_S)^{\leqslant d} = ((g^{\leqslant k})_S)^{\leqslant d}$
.
$(g_S)^{\leqslant d} = ((g^{\leqslant k})_S)^{\leqslant d}$
.
Note that for
![]() $k=d$
, this statement exactly corresponds to truncations and restrictions commuting, but the conditions of the statement always require that
$k=d$
, this statement exactly corresponds to truncations and restrictions commuting, but the conditions of the statement always require that
![]() $k>d$
at the very least. In fact, in our setting we will have
$k>d$
at the very least. In fact, in our setting we will have
![]() $\ell = 2d$
, so we would need to use the statement with
$\ell = 2d$
, so we would need to use the statement with
![]() $k = 3d+2$
. Thus, to use this statement effectively, we cannot apply it on our original function f and instead have to find an appropriate choice of g such that
$k = 3d+2$
. Thus, to use this statement effectively, we cannot apply it on our original function f and instead have to find an appropriate choice of g such that
![]() $g^{\leqslant k}, g^{\leqslant d}\approx f^{\leqslant d}$
, and moreover, that they remain close under restrictions (so, in particular, we preserve our globalness). Indeed, we are able to design such g by applying appropriate sparse linear combinations of powers of the natural transposition operator of
$g^{\leqslant k}, g^{\leqslant d}\approx f^{\leqslant d}$
, and moreover, that they remain close under restrictions (so, in particular, we preserve our globalness). Indeed, we are able to design such g by applying appropriate sparse linear combinations of powers of the natural transposition operator of
![]() $S_n$
on f.
$S_n$
on f.
8.2 Constructing the auxiliary function g
In this section, we construct the function g.
Lemma 8.1. There is an absolute constant
![]() $C>0$
, such that the following holds. Suppose
$C>0$
, such that the following holds. Suppose
![]() $n\geqslant 2^{C\cdot d^{3}}$
and let
$n\geqslant 2^{C\cdot d^{3}}$
and let
![]() $\mathrm {T}$
be the adjacency operator of the transpositions graph (see Section 7.3). There exists a polynomial P with
$\mathrm {T}$
be the adjacency operator of the transpositions graph (see Section 7.3). There exists a polynomial P with
![]() $\left \|P\right \|\leqslant 2^{C\cdot d^4}$
such that
$\left \|P\right \|\leqslant 2^{C\cdot d^4}$
such that
 $$\begin{align*}\left\|P(\mathrm{T}) (f^{\leqslant 4d})-f^{\leqslant d}\right\|_{2}\leqslant\left(\frac{1}{n}\right)^{19d}\left\|f^{\leqslant 4d}\right\|_{2}. \end{align*}$$
$$\begin{align*}\left\|P(\mathrm{T}) (f^{\leqslant 4d})-f^{\leqslant d}\right\|_{2}\leqslant\left(\frac{1}{n}\right)^{19d}\left\|f^{\leqslant 4d}\right\|_{2}. \end{align*}$$
Proof. Let
 $$\begin{align*}Q(z) = \sum_{i=1}^{d}\prod_{j\in\left[4d\right]\setminus\left\{ i\right\} }\left(\frac{z^{n}-e^{-2j}}{e^{-2i}-e^{-2j}}\right)^{20d} \end{align*}$$
$$\begin{align*}Q(z) = \sum_{i=1}^{d}\prod_{j\in\left[4d\right]\setminus\left\{ i\right\} }\left(\frac{z^{n}-e^{-2j}}{e^{-2i}-e^{-2j}}\right)^{20d} \end{align*}$$
and define
![]() $P(z) = 1 - (1-Q(z))^{20d}$
. We first prove the upper bound on
$P(z) = 1 - (1-Q(z))^{20d}$
. We first prove the upper bound on
![]() $\left \|P\right \|$
; note that
$\left \|P\right \|$
; note that
 $$\begin{align*}\left\|Q\right\| \leqslant\sum_{i=1}^{d}\prod_{j\in\left[4d\right]\setminus\left\{ i\right\} }\left\|\frac{z^{n}-e^{-2j}}{e^{-2i}-e^{-2j}}\right\|^{20d} =\sum_{i=1}^{d}\prod_{j\in\left[4d\right]\setminus\left\{ i\right\} }\left(\frac{1+e^{-2j}}{e^{-2i}-e^{-2j}}\right)^{20d}=2^{O\left(d^{3}\right)}, \end{align*}$$
$$\begin{align*}\left\|Q\right\| \leqslant\sum_{i=1}^{d}\prod_{j\in\left[4d\right]\setminus\left\{ i\right\} }\left\|\frac{z^{n}-e^{-2j}}{e^{-2i}-e^{-2j}}\right\|^{20d} =\sum_{i=1}^{d}\prod_{j\in\left[4d\right]\setminus\left\{ i\right\} }\left(\frac{1+e^{-2j}}{e^{-2i}-e^{-2j}}\right)^{20d}=2^{O\left(d^{3}\right)}, \end{align*}$$
so
![]() $\left \|P\right \|\leqslant (1+2^{O(d^3)})^{20d} = 2^{O(d^4)}$
.
$\left \|P\right \|\leqslant (1+2^{O(d^3)})^{20d} = 2^{O(d^4)}$
.
Next, we show that for
![]() $g = P(\mathrm {T}) f$
, it holds that
$g = P(\mathrm {T}) f$
, it holds that
![]() $\left \|g^{\leqslant 4d}-f^{\leqslant d}\right \|_{2}\leqslant \left (\frac {1}{n}\right )^{10d}\left \|f^{\leqslant 4d}\right \|_{2}$
, and we do so by eigenvalue considerations. Let
$\left \|g^{\leqslant 4d}-f^{\leqslant d}\right \|_{2}\leqslant \left (\frac {1}{n}\right )^{10d}\left \|f^{\leqslant 4d}\right \|_{2}$
, and we do so by eigenvalue considerations. Let
![]() $d<\ell \leqslant 4d$
and let
$d<\ell \leqslant 4d$
and let
![]() $\lambda $
be an eigenvalue of
$\lambda $
be an eigenvalue of
![]() $\mathrm {T}$
corresponding to a function of pure degree
$\mathrm {T}$
corresponding to a function of pure degree
![]() $\ell $
. Since
$\ell $
. Since
![]() $\ell \leqslant n/2$
, Lemma 7.10 implies that
$\ell \leqslant n/2$
, Lemma 7.10 implies that
![]() $\lambda = 1-\frac {2\ell }{n} + O\left (\frac {\ell ^2}{n^2}\right )$
, and so
$\lambda = 1-\frac {2\ell }{n} + O\left (\frac {\ell ^2}{n^2}\right )$
, and so
![]() $\lambda ^{n}=e^{-2\ell }\pm O\left (\frac {d^{2}}{n}\right )$
. Thus, as each one of the products in
$\lambda ^{n}=e^{-2\ell }\pm O\left (\frac {d^{2}}{n}\right )$
. Thus, as each one of the products in
![]() $Q(\lambda )$
contains a term for
$Q(\lambda )$
contains a term for
![]() $\ell $
, we get that
$\ell $
, we get that
 $$\begin{align*}\left|Q(\lambda)\right|\leqslant d\cdot\left(\frac{2^{O(d^2)}}{n}\right)^{20d} \leqslant \frac{2^{O(d^3)}}{n^{20d}}, \end{align*}$$
$$\begin{align*}\left|Q(\lambda)\right|\leqslant d\cdot\left(\frac{2^{O(d^2)}}{n}\right)^{20d} \leqslant \frac{2^{O(d^3)}}{n^{20d}}, \end{align*}$$
so
![]() $\left |P(\lambda )\right | = 1-(1-\frac {2^{O(d^3)}}{n^{20d}})^d \leqslant \frac {1}{n^{19d}}$
. Next, let
$\left |P(\lambda )\right | = 1-(1-\frac {2^{O(d^3)}}{n^{20d}})^d \leqslant \frac {1}{n^{19d}}$
. Next, let
![]() $\ell \leqslant d$
and let
$\ell \leqslant d$
and let
![]() $\lambda $
be an eigenvalue of
$\lambda $
be an eigenvalue of
![]() $\mathrm {T}$
corresponding to a function of pure degree
$\mathrm {T}$
corresponding to a function of pure degree
![]() $\ell $
. As before,
$\ell $
. As before,
![]() $\lambda ^n = e^{-2\ell }\pm O\left (\frac {d^{2}}{n}\right )$
, but now in
$\lambda ^n = e^{-2\ell }\pm O\left (\frac {d^{2}}{n}\right )$
, but now in
![]() $Q(\lambda )$
there is one product that omits the term for
$Q(\lambda )$
there is one product that omits the term for
![]() $\ell $
. A direct computation gives that
$\ell $
. A direct computation gives that
 $$\begin{align*}Q(\lambda) = \prod\limits_{j\in [4d]\setminus\{\ell\}} \left(\frac{\lambda^n-e^{-2j}}{e^{-2\ell}-e^{-2j}}\right)^{20d} + \frac{2^{O(d^3)}}{n^{20d}} =\prod\limits_{j\in [4d]\setminus\{\ell\}}\left(1-O\left(\frac{2^{O(d)}}{n}\right)\right)+ \frac{2^{O(d^3)}}{n^{20d}}, \end{align*}$$
$$\begin{align*}Q(\lambda) = \prod\limits_{j\in [4d]\setminus\{\ell\}} \left(\frac{\lambda^n-e^{-2j}}{e^{-2\ell}-e^{-2j}}\right)^{20d} + \frac{2^{O(d^3)}}{n^{20d}} =\prod\limits_{j\in [4d]\setminus\{\ell\}}\left(1-O\left(\frac{2^{O(d)}}{n}\right)\right)+ \frac{2^{O(d^3)}}{n^{20d}}, \end{align*}$$
so
![]() $Q(\lambda ) = 1- O\left (\frac {2^{O(d)}}{n}\right )$
. Thus,
$Q(\lambda ) = 1- O\left (\frac {2^{O(d)}}{n}\right )$
. Thus,
 $$\begin{align*}\left|P(\lambda)-1\right| = O\left(\frac{2^{O(d^2)}}{n^{20d}}\right) \leqslant \frac{1}{n^{19d}}. \end{align*}$$
$$\begin{align*}\left|P(\lambda)-1\right| = O\left(\frac{2^{O(d^2)}}{n^{20d}}\right) \leqslant \frac{1}{n^{19d}}. \end{align*}$$
It follows that
![]() $g^{\leqslant 4d} - f^{\leqslant d} = \sum \limits _{\ell = 0}^{4d} c_{\ell } f^{=\ell }$
for
$g^{\leqslant 4d} - f^{\leqslant d} = \sum \limits _{\ell = 0}^{4d} c_{\ell } f^{=\ell }$
for
![]() $\left |c_{\ell }\right | \leqslant \frac {1}{n^{19d}}$
, and the result follows from Parseval.
$\left |c_{\ell }\right | \leqslant \frac {1}{n^{19d}}$
, and the result follows from Parseval.
8.3 Properties of Cayley operators and restrictions
In this section, we study random walks along Cayley graphs on
![]() $S_n$
. The specific transition operator we will later be concerned with is the transposition operator from Lemma 7.10 and its powers, but we will present things in greater generality.
$S_n$
. The specific transition operator we will later be concerned with is the transposition operator from Lemma 7.10 and its powers, but we will present things in greater generality.
8.3.1 Random walks
Definition 8.2. A Markov chain
![]() $\mathrm {M}$
on
$\mathrm {M}$
on
![]() $S_n$
is called a Cayley random walk if for any
$S_n$
is called a Cayley random walk if for any
![]() $\sigma ,\tau ,\pi \in S_n$
, the transition probability from
$\sigma ,\tau ,\pi \in S_n$
, the transition probability from
![]() $\sigma $
to
$\sigma $
to
![]() $\tau $
is the same as the transition probability from
$\tau $
is the same as the transition probability from
![]() $\sigma \pi $
to
$\sigma \pi $
to
![]() $\tau \pi $
.
$\tau \pi $
.
In other words, a Markov chain
![]() $\mathrm {M}$
is called Cayley if the transition probability from
$\mathrm {M}$
is called Cayley if the transition probability from
![]() $\sigma $
to
$\sigma $
to
![]() $\tau $
is only a function of
$\tau $
is only a function of
![]() $\sigma \tau ^{-1}$
. We will be interested in the interaction between random walks and restrictions, and towards this end we first establish the following claim, asserting that a Cayley random walk either never transitions between two restrictions T and
$\sigma \tau ^{-1}$
. We will be interested in the interaction between random walks and restrictions, and towards this end we first establish the following claim, asserting that a Cayley random walk either never transitions between two restrictions T and
![]() $T'$
or can always transition between the two.
$T'$
or can always transition between the two.
Claim 8.3. Suppose
![]() $\mathrm {M}$
is a Cayley random walk on
$\mathrm {M}$
is a Cayley random walk on
![]() $S_n$
, let
$S_n$
, let
![]() $i_1,\ldots ,i_t\in [n]$
be distinct and let
$i_1,\ldots ,i_t\in [n]$
be distinct and let
![]() $T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
,
$T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
,
![]() $T'=\left \{ \left (i_{1},j_{1}'\right ),\ldots ,\left (i_{t},j_{t}'\right )\right \}$
be consistent sets. Then one of the following two must hold:
$T'=\left \{ \left (i_{1},j_{1}'\right ),\ldots ,\left (i_{t},j_{t}'\right )\right \}$
be consistent sets. Then one of the following two must hold:
-
1.
 $\Pr _{\substack {u\in S_{n}^{T'}\\ v\sim \mathrm {M}v}}\big [v\in S_{n}^{T}\big ] = 0$
.
$\Pr _{\substack {u\in S_{n}^{T'}\\ v\sim \mathrm {M}v}}\big [v\in S_{n}^{T}\big ] = 0$
. -
2. For all
 $\pi \in S_{n}^{T}$
, it holds that
$\pi \in S_{n}^{T}$
, it holds that
 $\Pr _{\substack {u\in S_{n}^{T'}\\ v\sim \mathrm {M}v}}\big [v = \pi \big ]> 0$
.
$\Pr _{\substack {u\in S_{n}^{T'}\\ v\sim \mathrm {M}v}}\big [v = \pi \big ]> 0$
.
Proof. If the first item holds, then we are done, so let us assume otherwise. Then there are
![]() $u\in S_{n}^{T'}$
,
$u\in S_{n}^{T'}$
,
![]() $v\in S_{n}^{T}$
such that
$v\in S_{n}^{T}$
such that
![]() $\mathrm {M}$
has positive probability of transitioning from u to v. Denoting
$\mathrm {M}$
has positive probability of transitioning from u to v. Denoting
![]() $\tau = u v^{-1}$
, we note that
$\tau = u v^{-1}$
, we note that
![]() $\tau (j_{\ell }) = j_{\ell }'$
for all
$\tau (j_{\ell }) = j_{\ell }'$
for all
![]() $\ell =1,\ldots , t$
. Fix
$\ell =1,\ldots , t$
. Fix
![]() $\pi \in S_n^{T}$
. Since
$\pi \in S_n^{T}$
. Since
![]() $\mathrm {M}$
is a Cayley operator, the transition probability from
$\mathrm {M}$
is a Cayley operator, the transition probability from
![]() $\tau \pi $
to
$\tau \pi $
to
![]() $\pi $
is positive, and since
$\pi $
is positive, and since
![]() $\tau \pi $
is in
$\tau \pi $
is in
![]() $S_{n}^{T'}$
, the proof is concluded.
$S_{n}^{T'}$
, the proof is concluded.
If
![]() $\mathrm {M}$
satisfies the second item of the above claim with T and
$\mathrm {M}$
satisfies the second item of the above claim with T and
![]() $T'$
, we say that
$T'$
, we say that
![]() $\mathrm {M}$
is compatible with
$\mathrm {M}$
is compatible with
![]() $(T,T')$
.
$(T,T')$
.
8.3.2 Degree decomposition on restrictions
Let
![]() $T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
be consistent. A function
$T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
be consistent. A function
![]() $f\in L^2(S_n^{T})$
is called a d-junta if there is
$f\in L^2(S_n^{T})$
is called a d-junta if there is
![]() $S\subseteq [n]\setminus \{i_1,\ldots ,i_t\}$
of size d such that
$S\subseteq [n]\setminus \{i_1,\ldots ,i_t\}$
of size d such that
![]() $f(\pi )$
only depends on
$f(\pi )$
only depends on
![]() $\pi (i)$
for
$\pi (i)$
for
![]() $i \in S$
(we say that
$i \in S$
(we say that
![]() $f(\pi )$
only depends on
$f(\pi )$
only depends on
![]() $\pi (S)$
). With this definition in hand, we may define the space of degree d functions on
$\pi (S)$
). With this definition in hand, we may define the space of degree d functions on
![]() $S_n^{T}$
, denoted by
$S_n^{T}$
, denoted by
![]() $V_d(S_n^T)$
, as the span of all d-juntas and subsequently define projections onto this subspaces. That is, for each
$V_d(S_n^T)$
, as the span of all d-juntas and subsequently define projections onto this subspaces. That is, for each
![]() $f\in L^2(S_n^{T})$
, we denote by
$f\in L^2(S_n^{T})$
, we denote by
![]() $f^{\leqslant d}$
the projection of f onto
$f^{\leqslant d}$
the projection of f onto
![]() $V_d(S_n^T)$
. Finally, we define the pure degree d part of f as
$V_d(S_n^T)$
. Finally, we define the pure degree d part of f as
![]() $f^{=d} = f^{\leqslant d} - f^{\leqslant d-1}$
.
$f^{=d} = f^{\leqslant d} - f^{\leqslant d-1}$
.
We have the following basic property of pure degree d functions.
Claim 8.4. Suppose that
![]() $f\colon S_n\to \mathbb {R}$
is of pure degree d. Let T be a set of size
$f\colon S_n\to \mathbb {R}$
is of pure degree d. Let T be a set of size
![]() $\ell <d$
. Then
$\ell <d$
. Then
![]() $f_{T}$
is orthogonal to all functions in
$f_{T}$
is orthogonal to all functions in
![]() $V_{d-1-\ell }$
.
$V_{d-1-\ell }$
.
Proof. Clearly, it is enough to show that
![]() $f_T$
is orthogonal to all
$f_T$
is orthogonal to all
![]() $(d-1-\ell )$
-juntas. Fix
$(d-1-\ell )$
-juntas. Fix
![]() $g\colon S_{n}^{T}\to \mathbb {R}$
to be a
$g\colon S_{n}^{T}\to \mathbb {R}$
to be a
![]() $(d-1-\ell )$
-junta and let h be its extension to
$(d-1-\ell )$
-junta and let h be its extension to
![]() $S_n$
by setting it to be
$S_n$
by setting it to be
![]() $0$
outside
$0$
outside
![]() $S_n^T$
. Then h is a
$S_n^T$
. Then h is a
![]() $\left (d-1\right )$
-junta, and so
$\left (d-1\right )$
-junta, and so
8.3.3 Extension to functions
Any random walk
![]() $\mathrm {M}$
on
$\mathrm {M}$
on
![]() $S_n$
extends to an operator on functions on
$S_n$
extends to an operator on functions on
![]() $S_n$
, which maps
$S_n$
, which maps
![]() $f\colon S_n \to \mathbb {R}$
to the function
$f\colon S_n \to \mathbb {R}$
to the function
![]() $\mathrm {M}f\colon S_n \to \mathbb {R}$
given by
$\mathrm {M}f\colon S_n \to \mathbb {R}$
given by
8.4 Strengthening Proposition 3.1
Our main goal in this section is to prove the following statement that both strengthens and generalises Proposition 3.1.
Proposition 8.5. Let
![]() $f\colon S_{n}\to \mathbb {R}$
. Let
$f\colon S_{n}\to \mathbb {R}$
. Let
![]() $\mathrm {M}$
be a Cayley random walk on
$\mathrm {M}$
be a Cayley random walk on
![]() $S_{n}$
, let
$S_{n}$
, let
![]() $g=\mathrm {M}f$
and let
$g=\mathrm {M}f$
and let
![]() $T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \} $
be a consistent set. Then for all d,
$T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \} $
be a consistent set. Then for all d,
 $$\begin{align*}\|\left(g_{T}\right)^{\leqslant d}\|_{2}\leqslant \max_{\substack{T'=\left\{ \left(i_{1},j_{1}'\right),\ldots,\left(i_{t},j_{t}'\right)\right\}\\ \mathrm{M}\text{ compatible with }(T,T')}}\|\left(f_{T'}\right)^{\leqslant d}\|_{2}. \end{align*}$$
$$\begin{align*}\|\left(g_{T}\right)^{\leqslant d}\|_{2}\leqslant \max_{\substack{T'=\left\{ \left(i_{1},j_{1}'\right),\ldots,\left(i_{t},j_{t}'\right)\right\}\\ \mathrm{M}\text{ compatible with }(T,T')}}\|\left(f_{T'}\right)^{\leqslant d}\|_{2}. \end{align*}$$
Let
![]() $\mathrm {M}$
be a Cayley random walk and let
$\mathrm {M}$
be a Cayley random walk and let
![]() $T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
and
$T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
and
![]() $T'=\left \{ \left (i_{1},j_{1}'\right ),\ldots ,\left (i_{t},j_{t}'\right )\right \}$
be consistent so that
$T'=\left \{ \left (i_{1},j_{1}'\right ),\ldots ,\left (i_{t},j_{t}'\right )\right \}$
be consistent so that
![]() $\mathrm {M}$
is compatible with
$\mathrm {M}$
is compatible with
![]() $(T,T')$
. Put
$(T,T')$
. Put
![]() $I = \{(i_1,i_1),\ldots ,(i_t,i_t)\}$
. Define the operator
$I = \{(i_1,i_1),\ldots ,(i_t,i_t)\}$
. Define the operator
![]() $\mathrm {M}_{S_n^T\rightarrow S_n^{T'}}\colon L^2(S_n^T)\to L^2(S_n^{T'})$
in the following way: given a function
$\mathrm {M}_{S_n^T\rightarrow S_n^{T'}}\colon L^2(S_n^T)\to L^2(S_n^{T'})$
in the following way: given a function
![]() $f\in L^2(S_n^T)$
, we define
$f\in L^2(S_n^T)$
, we define
 $$\begin{align*}\mathrm{M}_{S_n^{T'}\rightarrow S_n^{T}} f(\pi) = \mathop{\mathbb{E}}_{\substack{u\in_R S_n^{T}\\ v\sim \mathrm{M} u}}\big[f(u)\;\big|\;v = \pi\big]. \end{align*}$$
$$\begin{align*}\mathrm{M}_{S_n^{T'}\rightarrow S_n^{T}} f(\pi) = \mathop{\mathbb{E}}_{\substack{u\in_R S_n^{T}\\ v\sim \mathrm{M} u}}\big[f(u)\;\big|\;v = \pi\big]. \end{align*}$$
Drawing inspiration from the proof of Proposition 3.1, we study the operator
![]() $\mathrm {M}_{S_{n}^{T}\to S_{n}^{T'}}$
. Since we are also dealing with degree truncations, we have to study its interaction with this operator. Indeed, a key step in the proof is to show that the two operators commute in the following sense: for all
$\mathrm {M}_{S_{n}^{T}\to S_{n}^{T'}}$
. Since we are also dealing with degree truncations, we have to study its interaction with this operator. Indeed, a key step in the proof is to show that the two operators commute in the following sense: for all
![]() $d\in \mathbb {N}$
and
$d\in \mathbb {N}$
and
![]() $f\in L^{2}(S_n^T)$
, it holds that
$f\in L^{2}(S_n^T)$
, it holds that
Towards this end, we view
![]() $L^2(S_n^{T})$
(and similarly
$L^2(S_n^{T})$
(and similarly
![]() $L^2(S_n^{T'})$
) as a right
$L^2(S_n^{T'})$
) as a right
![]() $S_n^I$
-module using the following operation: a function-permutation pair
$S_n^I$
-module using the following operation: a function-permutation pair
![]() $(f,\pi )\in L^2(S_n^{T})\times S_n^I$
is mapped to a function
$(f,\pi )\in L^2(S_n^{T})\times S_n^I$
is mapped to a function
![]() $f^{\pi } \in L^2(S_n^{T})$
defined as
$f^{\pi } \in L^2(S_n^{T})$
defined as
Claim 8.6. With the setup above,
![]() $\mathrm {M}_{S_{n}^{T}\to S_{n}^{T'}}\colon L^{2}\left (S_{n}^{T}\right )\to L^{2}\left (S_{n}^{T'}\right )$
is a homomorphism of
$\mathrm {M}_{S_{n}^{T}\to S_{n}^{T'}}\colon L^{2}\left (S_{n}^{T}\right )\to L^{2}\left (S_{n}^{T'}\right )$
is a homomorphism of
![]() $S_{n}^{I}$
-modules.
$S_{n}^{I}$
-modules.
Proof. The proof is essentially the same as the proof of Lemma 5.1 and is therefore omitted.
Therefore, it is sufficient to prove that any homomorphism commutes with taking pure degree d part, which is the content of the following claim.
Claim 8.7. Let
![]() $T,T'$
be consistent as above and let
$T,T'$
be consistent as above and let
![]() $\mathrm {A}\colon L^{2}(S_{n}^{T})\to L^{2}(S_{n}^{T'})$
be a homomorphism of right
$\mathrm {A}\colon L^{2}(S_{n}^{T})\to L^{2}(S_{n}^{T'})$
be a homomorphism of right
![]() $S_{n}^{I}$
-modules. Then for all
$S_{n}^{I}$
-modules. Then for all
![]() $f\in L^2(S_n^T)$
, we have that
$f\in L^2(S_n^T)$
, we have that
Proof. We first claim that
![]() $\mathrm {A}$
preserves degrees (i.e.,
$\mathrm {A}$
preserves degrees (i.e.,
![]() $\mathrm {A} V_{d}(S_n^{T})\subseteq V_{d}(S_n^{T'})$
). To show this, it is enough to note that if
$\mathrm {A} V_{d}(S_n^{T})\subseteq V_{d}(S_n^{T'})$
). To show this, it is enough to note that if
![]() $f\in L^2(S_n^T)$
is a d-junta, then
$f\in L^2(S_n^T)$
is a d-junta, then
![]() $\mathrm {A} f$
is a d-junta. Let f be a d-junta and suppose that
$\mathrm {A} f$
is a d-junta. Let f be a d-junta and suppose that
![]() $S\subseteq [n]$
is a set of size at most d such that
$S\subseteq [n]$
is a set of size at most d such that
![]() $f(\sigma )$
only depends on
$f(\sigma )$
only depends on
![]() $\sigma (S)$
. Then for any
$\sigma (S)$
. Then for any
![]() $\pi $
that has S as fixed points, we have that
$\pi $
that has S as fixed points, we have that
![]() $f(\sigma ) = f(\sigma \pi ^{-1}) = f^{\pi }(\sigma )$
, so
$f(\sigma ) = f(\sigma \pi ^{-1}) = f^{\pi }(\sigma )$
, so
![]() $f = f^{\pi }$
. Applying
$f = f^{\pi }$
. Applying
![]() $\mathrm {A}$
and using the previous claim, we get that
$\mathrm {A}$
and using the previous claim, we get that
![]() $\mathrm {A} f = \mathrm {A} f^{\pi } = (\mathrm {A} f)^{\pi }$
. This implies that
$\mathrm {A} f = \mathrm {A} f^{\pi } = (\mathrm {A} f)^{\pi }$
. This implies that
![]() $\mathrm {A}f$
is invariant under any permutation that keeps S as fixed points, so it is an S-junta.
$\mathrm {A}f$
is invariant under any permutation that keeps S as fixed points, so it is an S-junta.
Let
![]() $V_{=d}(S_n^{T})$
be the space of functions of pure degree d (i.e.,
$V_{=d}(S_n^{T})$
be the space of functions of pure degree d (i.e.,
![]() $V_{d}(S_n^{T})\cap V_{d-1}(S_n^{T})^{\perp }$
). We claim that
$V_{d}(S_n^{T})\cap V_{d-1}(S_n^{T})^{\perp }$
). We claim that
![]() $\mathrm {A}$
also preserves pure degrees (i.e.,
$\mathrm {A}$
also preserves pure degrees (i.e.,
![]() $\mathrm {A} V_{=d}(S_n^{T})\subseteq V_{=d}(S_n^{T'})$
). By the previous paragraph, it is enough to show that if
$\mathrm {A} V_{=d}(S_n^{T})\subseteq V_{=d}(S_n^{T'})$
). By the previous paragraph, it is enough to show that if
![]() $f\in V_{=d}(S_n^{T})$
, then
$f\in V_{=d}(S_n^{T})$
, then
![]() $\mathrm {A}f$
is orthogonal to
$\mathrm {A}f$
is orthogonal to
![]() $V_{d-1}(S_n^{T'})$
. Letting
$V_{d-1}(S_n^{T'})$
. Letting
![]() $\mathrm {A}^{*}$
be the adjoint operator of
$\mathrm {A}^{*}$
be the adjoint operator of
![]() $\mathrm {A}$
, it is easily seen that
$\mathrm {A}$
, it is easily seen that
![]() $\mathrm {A}^{*}\colon L^{2}(S_{n}^{T'})\to L^{2}(S_{n}^{T})$
is also a homomorphism between right
$\mathrm {A}^{*}\colon L^{2}(S_{n}^{T'})\to L^{2}(S_{n}^{T})$
is also a homomorphism between right
![]() $S_n^{I}$
-modules, and by the previous paragraph, it follows that
$S_n^{I}$
-modules, and by the previous paragraph, it follows that
![]() $\mathrm {A}^{*}$
preserves degrees. Thus, for any
$\mathrm {A}^{*}$
preserves degrees. Thus, for any
![]() $g\in V_{d-1}(S_n^{T'})$
, we have that
$g\in V_{d-1}(S_n^{T'})$
, we have that
![]() $\mathrm {A}^{*} g\in V_{d-1}(S_n^{T})$
, and so
$\mathrm {A}^{*} g\in V_{d-1}(S_n^{T})$
, and so
We can now prove the statement of the claim. Fix
![]() $f\in L^2(S_n^T)$
and d. Then by the above paragraph,
$f\in L^2(S_n^T)$
and d. Then by the above paragraph,
![]() $\mathrm {A}\left (f^{=d}\right )\in V_{=d}(S_n^{T'})$
, and by linearity of
$\mathrm {A}\left (f^{=d}\right )\in V_{=d}(S_n^{T'})$
, and by linearity of
![]() $\mathrm {A}$
, we have
$\mathrm {A}$
, we have
![]() $\sum \limits _{d}\mathrm {A}\left (f^{=d}\right ) = \mathrm {A} f$
. The claim follows from the uniqueness of the degree decomposition.
$\sum \limits _{d}\mathrm {A}\left (f^{=d}\right ) = \mathrm {A} f$
. The claim follows from the uniqueness of the degree decomposition.
We define a transition operator on restrictions as follows. From a restriction
![]() $T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
, we sample
$T=\left \{ \left (i_{1},j_{1}\right ),\ldots ,\left (i_{t},j_{t}\right )\right \}$
, we sample
![]() $T'\sim N(T)$
as follows. Take
$T'\sim N(T)$
as follows. Take
![]() $\pi \in S_{n}^T$
uniformly, sample
$\pi \in S_{n}^T$
uniformly, sample
![]() $\sigma \sim \mathrm {M}\pi $
and then let
$\sigma \sim \mathrm {M}\pi $
and then let
![]() $T'$
be
$T'$
be
![]() $\{(i_1,\sigma (i_1)),\ldots ,(i_t,\sigma (i_t))\}$
. The following claim is immediate:
$\{(i_1,\sigma (i_1)),\ldots ,(i_t,\sigma (i_t))\}$
. The following claim is immediate:
Claim 8.8.
![]() $(\mathrm {M} f)_T = \mathop {\mathbb {E}}_{T'\sim N(T)}\big [\mathrm {M}_{S_{n}^{T'}\to S_{n}^{T}} f_{T'}\big ]$
.
$(\mathrm {M} f)_T = \mathop {\mathbb {E}}_{T'\sim N(T)}\big [\mathrm {M}_{S_{n}^{T'}\to S_{n}^{T}} f_{T'}\big ]$
.
We are now ready to prove Proposition 8.5.
Proof of Proposition 8.5.
By Claim 8.8, we have
![]() $g_{T}=\mathbb {E}_{T'\sim T}\mathrm {M}_{S_{n}^{T'}\to S_{n}^{T}}f_{T'}$
. Using Claim 8.7 and the linearity of the operator
$g_{T}=\mathbb {E}_{T'\sim T}\mathrm {M}_{S_{n}^{T'}\to S_{n}^{T}}f_{T'}$
. Using Claim 8.7 and the linearity of the operator
![]() $f\mapsto f^{= d}$
, we get
$f\mapsto f^{= d}$
, we get
Summing this up using linearity again, we conclude that
Taking norms and using the triangle inequality gives us that
The proof is now concluded by appealing to Fact 3.2.
8.5 A weak level-d inequality
The last ingredient we will need in the proof of Theorem 1.6 is a weak version of the level-d inequality, which does not take the globalness of f into consideration.
Lemma 8.9. Let C be sufficiently large, let
![]() $n\geqslant \log \left (1/\varepsilon \right )^{d}C^{d^{2}}$
and let
$n\geqslant \log \left (1/\varepsilon \right )^{d}C^{d^{2}}$
and let
![]() $f\colon S_{n}\to \left \{ 0,1\right \} $
satisfy
$f\colon S_{n}\to \left \{ 0,1\right \} $
satisfy
![]() $\|f\|_{2}\leqslant \varepsilon $
. Then
$\|f\|_{2}\leqslant \varepsilon $
. Then
Proof. Set
![]() $q=\log (1/\varepsilon )$
, and without loss of generality, assume q is an even integer (otherwise, we may change q by a constant factor to ensure that). Using Hölder’s inequality, Lemma 5.14 and the fact that
$q=\log (1/\varepsilon )$
, and without loss of generality, assume q is an even integer (otherwise, we may change q by a constant factor to ensure that). Using Hölder’s inequality, Lemma 5.14 and the fact that
![]() $\|f\|_{q/(q-1)}=O\left (\varepsilon ^{2}\right )$
, we obtain
$\|f\|_{q/(q-1)}=O\left (\varepsilon ^{2}\right )$
, we obtain
and the lemma follows by rearranging.
8.6 Interchanging truncations and derivatives with small errors
Lemma 8.10. There is
![]() $C>0$
, such that the following holds for
$C>0$
, such that the following holds for
![]() $n\geqslant 2^{C\cdot d^3}$
. For all derivatives
$n\geqslant 2^{C\cdot d^3}$
. For all derivatives
![]() $\mathrm {D}$
of order
$\mathrm {D}$
of order
![]() $t\leqslant d$
, we have
$t\leqslant d$
, we have
 $$\begin{align*}\left\|D\left(f^{\leqslant d}\right)\right\|_{2} \leqslant 2^{O\left(d\right)^{4}}\max_{t-\text{derivative }\mathrm{D}'}\left\|\left(\mathrm{D}'f\right)^{\leqslant d-t}\right\|_{2} +\left(\frac{1}{n}\right)^{10 d}\left\|f^{\leqslant 4d}\right\|_2. \end{align*}$$
$$\begin{align*}\left\|D\left(f^{\leqslant d}\right)\right\|_{2} \leqslant 2^{O\left(d\right)^{4}}\max_{t-\text{derivative }\mathrm{D}'}\left\|\left(\mathrm{D}'f\right)^{\leqslant d-t}\right\|_{2} +\left(\frac{1}{n}\right)^{10 d}\left\|f^{\leqslant 4d}\right\|_2. \end{align*}$$
Proof. Let
![]() $\mathrm {T}_{d}=P\left ({\mathrm {T}}\right )$
be as in Lemma 8.1 and write
$\mathrm {T}_{d}=P\left ({\mathrm {T}}\right )$
be as in Lemma 8.1 and write
![]() $f^{\leqslant d} = \mathrm {T}_d (f^{\leqslant 4d}) + g$
, where
$f^{\leqslant d} = \mathrm {T}_d (f^{\leqslant 4d}) + g$
, where
![]() $\left \|g\right \|_2\leqslant n^{-19d} \left \|f^{\leqslant 4d}\right \|_2$
. Let S be a consistent restriction of t coordinates and let
$\left \|g\right \|_2\leqslant n^{-19d} \left \|f^{\leqslant 4d}\right \|_2$
. Let S be a consistent restriction of t coordinates and let
![]() $\mathrm {D}$
be a derivative along S. Then there is
$\mathrm {D}$
be a derivative along S. Then there is
![]() $R\subseteq L$
of size t such that
$R\subseteq L$
of size t such that
![]() $\mathrm {D}f=\left (\mathrm {L}f\right )_{S\rightarrow R}$
. By Claim 4.3, the degree of
$\mathrm {D}f=\left (\mathrm {L}f\right )_{S\rightarrow R}$
. By Claim 4.3, the degree of
![]() $\mathrm {D}(f^{\leqslant d})$
is at most
$\mathrm {D}(f^{\leqslant d})$
is at most
![]() $d-t$
; thus,
$d-t$
; thus,
We want to compare the right-hand side with
![]() $\left (\mathrm {D}\left (\mathrm {T}_{d} f\right )\right )^{\leqslant d-t}$
, but first we show that in it, one may truncate all degrees higher than
$\left (\mathrm {D}\left (\mathrm {T}_{d} f\right )\right )^{\leqslant d-t}$
, but first we show that in it, one may truncate all degrees higher than
![]() $4d$
in f. Note that by Claim 8.7, for each
$4d$
in f. Note that by Claim 8.7, for each
![]() $k> 4d$
, the function
$k> 4d$
, the function
![]() $\mathrm {T}_{d} f^{=k}$
has pure degree k, so
$\mathrm {T}_{d} f^{=k}$
has pure degree k, so
![]() $\mathrm {D}(\mathrm {T}_{d} f^{=k})$
is perpendicular to degree
$\mathrm {D}(\mathrm {T}_{d} f^{=k})$
is perpendicular to degree
![]() $k-t-1$
functions. Since
$k-t-1$
functions. Since
![]() $k-2t-1 \geqslant d-t$
, we have that its level
$k-2t-1 \geqslant d-t$
, we have that its level
![]() $d-t$
projection is
$d-t$
projection is
![]() $0$
, so
$0$
, so
![]() $\left (\mathrm {D}\left (\mathrm {T}_{d} f\right )\right )^{\leqslant d-t} = \left (\mathrm {D}\left (\mathrm {T}_{d} f^{\leqslant 4d}\right )\right )^{\leqslant d-t}$
. It follows that
$\left (\mathrm {D}\left (\mathrm {T}_{d} f\right )\right )^{\leqslant d-t} = \left (\mathrm {D}\left (\mathrm {T}_{d} f^{\leqslant 4d}\right )\right )^{\leqslant d-t}$
. It follows that
 $$ \begin{align}\left\|\mathrm{D} (f^{\leqslant d}) - \left(\mathrm{D}\left(\mathrm{T}_{d} f\right)\right)^{\leqslant d-t}\right\|_2=\left\|\left(\mathrm{D}\left(f^{\leqslant d} - \mathrm{T}_{d} (f^{\leqslant 4d})\right)\right)^{\leqslant d-t}\right\|_2\leqslant \left\|\mathrm{D} g\right\|_2&\leqslant n^{2t}\left\|g\right\|_2 \nonumber\\&\leqslant n^{2t-19d}\left\|f^{\leqslant 4d}\right\|_2. \end{align} $$
$$ \begin{align}\left\|\mathrm{D} (f^{\leqslant d}) - \left(\mathrm{D}\left(\mathrm{T}_{d} f\right)\right)^{\leqslant d-t}\right\|_2=\left\|\left(\mathrm{D}\left(f^{\leqslant d} - \mathrm{T}_{d} (f^{\leqslant 4d})\right)\right)^{\leqslant d-t}\right\|_2\leqslant \left\|\mathrm{D} g\right\|_2&\leqslant n^{2t}\left\|g\right\|_2 \nonumber\\&\leqslant n^{2t-19d}\left\|f^{\leqslant 4d}\right\|_2. \end{align} $$
Our task now is to bound
![]() $\left \|\left (\mathrm {D}\left (\mathrm {T}_{d} f\right )\right )^{\leqslant d-t}\right \|_2$
. Since
$\left \|\left (\mathrm {D}\left (\mathrm {T}_{d} f\right )\right )^{\leqslant d-t}\right \|_2$
. Since
![]() $\mathrm {T}$
commutes with Laplacians, it follows that
$\mathrm {T}$
commutes with Laplacians, it follows that
![]() $\mathrm {T}_d$
also commutes with Laplacians, and so
$\mathrm {T}_d$
also commutes with Laplacians, and so
By Proposition 8.5, for all i and
![]() $h\colon S_n\to \mathbb {R}$
, we have
$h\colon S_n\to \mathbb {R}$
, we have
and so
Applying this for
![]() $h = Lf$
gives that
$h = Lf$
gives that
where the last transition is by the definition of derivatives. Combining (20), (21), (22) and using the triangle inequality finishes the proof.
8.7 Proof of the level-d inequality
We end this section by deriving the following proposition, which by Claim 4.2 implies Theorem 1.6.
Proposition 8.11. There exists an absolute constant
![]() $C>0$
such that the following holds for all
$C>0$
such that the following holds for all
![]() $d\in \mathbb {N}$
,
$d\in \mathbb {N}$
,
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $n\geqslant 2^{C\cdot d^3} \log (1/\varepsilon )^{C\cdot d}$
. Let
$n\geqslant 2^{C\cdot d^3} \log (1/\varepsilon )^{C\cdot d}$
. Let
![]() $f\colon S_n\to \mathbb {Z}$
be a function, such that for all
$f\colon S_n\to \mathbb {Z}$
be a function, such that for all
![]() $t\leqslant d$
and all t-derivatives
$t\leqslant d$
and all t-derivatives
![]() $\mathrm {D}$
, we have
$\mathrm {D}$
, we have
![]() $\|\mathrm {D}f\|_{2}\leqslant \varepsilon $
. Then
$\|\mathrm {D}f\|_{2}\leqslant \varepsilon $
. Then
Proof. The proof is by induction on d. If
![]() $d=0$
, then
$d=0$
, then
 $$\begin{align*}\left\|f^{\leqslant d}\right\|_{2} = \left|{\mathop{\mathbb{E}}_{}\left[ {f(\pi)} \right]}\right| \leqslant {\mathop{\mathbb{E}}_{}\left[ {\left|f(\pi)\right|{}^2} \right]} =\left\|f\right\|_2^2 \leqslant \varepsilon^2, \end{align*}$$
$$\begin{align*}\left\|f^{\leqslant d}\right\|_{2} = \left|{\mathop{\mathbb{E}}_{}\left[ {f(\pi)} \right]}\right| \leqslant {\mathop{\mathbb{E}}_{}\left[ {\left|f(\pi)\right|{}^2} \right]} =\left\|f\right\|_2^2 \leqslant \varepsilon^2, \end{align*}$$
where in the second transition we used the fact that f is integer-valued.
We now prove the inductive step. Fix
![]() $d\geqslant 1$
. Let
$d\geqslant 1$
. Let
![]() $1\leqslant t\leqslant d$
and let
$1\leqslant t\leqslant d$
and let
![]() $\mathrm {D}$
be a t-derivative. By Lemma 8.10, there is an absolute constant
$\mathrm {D}$
be a t-derivative. By Lemma 8.10, there is an absolute constant
![]() $C_1>0$
such that
$C_1>0$
such that
Fix
![]() $\mathrm {D}'$
. The function
$\mathrm {D}'$
. The function
![]() $\mathrm {D}'f$
takes integer values and is defined on a domain that is isomorphic to
$\mathrm {D}'f$
takes integer values and is defined on a domain that is isomorphic to
![]() $S_{n-t}$
, so by the induction hypothesis we have
$S_{n-t}$
, so by the induction hypothesis we have
 $$\begin{align*}\left\|\left(\mathrm{D}'f\right)^{\leqslant d-t}\right\|_{2}\leqslant e^{C\left(d-t\right)^{4}}\varepsilon^{2}\log\left(\frac{1}{\varepsilon}\right)^{C\left(d-t\right)}. \end{align*}$$
$$\begin{align*}\left\|\left(\mathrm{D}'f\right)^{\leqslant d-t}\right\|_{2}\leqslant e^{C\left(d-t\right)^{4}}\varepsilon^{2}\log\left(\frac{1}{\varepsilon}\right)^{C\left(d-t\right)}. \end{align*}$$
As for
![]() $\|f^{\leqslant 4d}\|_{2}^{2}$
, applying Lemma 8.9, we see it is at most
$\|f^{\leqslant 4d}\|_{2}^{2}$
, applying Lemma 8.9, we see it is at most
![]() $n^{8d}\varepsilon ^4 \log ^{Cd}(1/\varepsilon )$
. Plugging these two estimates into (23), we get that
$n^{8d}\varepsilon ^4 \log ^{Cd}(1/\varepsilon )$
. Plugging these two estimates into (23), we get that
provided that C is sufficiently large.
If
 $$\begin{align*}\left\|f^{\leqslant d}\right\|_{2}^{2}\leqslant e^{2Cd^{4}}\varepsilon^{4}\log\left(\frac{1}{\varepsilon}\right)^{2Cd}, \end{align*}$$
$$\begin{align*}\left\|f^{\leqslant d}\right\|_{2}^{2}\leqslant e^{2Cd^{4}}\varepsilon^{4}\log\left(\frac{1}{\varepsilon}\right)^{2Cd}, \end{align*}$$
we are done, so assume otherwise. We get that
![]() $\left \|\mathrm {D}'\left (f^{\leqslant d}\right )\right \|_{2} \leqslant \|f^{\leqslant d}\|_{2}$
for all derivatives of order at most d, and from Claim 4.3,
$\left \|\mathrm {D}'\left (f^{\leqslant d}\right )\right \|_{2} \leqslant \|f^{\leqslant d}\|_{2}$
for all derivatives of order at most d, and from Claim 4.3,
![]() $\left \|\mathrm {D}'\left (f^{\leqslant d}\right )\right \|_{2} = 0$
for higher-order derivatives, and so by Claim 4.2, the function
$\left \|\mathrm {D}'\left (f^{\leqslant d}\right )\right \|_{2} = 0$
for higher-order derivatives, and so by Claim 4.2, the function
![]() $f^{\leqslant d}$
is
$f^{\leqslant d}$
is
![]() $(2d,4^{d}\|f^{\leqslant d}\|_{2})$
-global, and by Lemma 3.5, we get that
$(2d,4^{d}\|f^{\leqslant d}\|_{2})$
-global, and by Lemma 3.5, we get that
![]() $f^{\leqslant d}$
is
$f^{\leqslant d}$
is
![]() $4^{d}\|f^{\leqslant d}\|_{2}$
-global with constant
$4^{d}\|f^{\leqslant d}\|_{2}$
-global with constant
![]() $4^8$
. In this case, we apply the standard argument as presented in the overview, as outlined below.
$4^8$
. In this case, we apply the standard argument as presented in the overview, as outlined below.
Set
![]() $q=\log \left (1/\varepsilon \right )$
, and without loss of generality, assume q is an even integer (otherwise, we may change q by a constant factor to ensure that). Set
$q=\log \left (1/\varepsilon \right )$
, and without loss of generality, assume q is an even integer (otherwise, we may change q by a constant factor to ensure that). Set
![]() $\rho =\frac {1}{(10 q 4^8)^2}$
. From Lemmas 5.1, 5.4 we have that
$\rho =\frac {1}{(10 q 4^8)^2}$
. From Lemmas 5.1, 5.4 we have that
![]() $\mathrm {T}^{(\rho )}$
preserves degrees, and so by Corollary 5.11, we get
$\mathrm {T}^{(\rho )}$
preserves degrees, and so by Corollary 5.11, we get
where we also used Hölder’s inequality. By Theorem 3.3, we have
![]() $\left \|\mathrm {T}^{(\rho )} f^{\leqslant d}\right \|_{q}\leqslant 4^{d}\left \|f^{\leqslant d}\right \|_{2}$
, and by a direction computation,
$\left \|\mathrm {T}^{(\rho )} f^{\leqslant d}\right \|_{q}\leqslant 4^{d}\left \|f^{\leqslant d}\right \|_{2}$
, and by a direction computation,
![]() $\left \|f\right \|_{q/(q-1)}\leqslant \varepsilon ^{2(q-1)/q}$
. Plugging these two estimates into the inequality above and rearranging yields that
$\left \|f\right \|_{q/(q-1)}\leqslant \varepsilon ^{2(q-1)/q}$
. Plugging these two estimates into the inequality above and rearranging yields that
for large enough C.
8.8 Deducing the strong level-d inequality: proof of Theorem 1.7
Let
![]() $\delta = 2^{C_1\cdot d^4} \varepsilon ^2\log ^{C_1\cdot d}(1/\varepsilon )$
for sufficiently large absolute constant
$\delta = 2^{C_1\cdot d^4} \varepsilon ^2\log ^{C_1\cdot d}(1/\varepsilon )$
for sufficiently large absolute constant
![]() $C_1$
. By Claim A.1, we get that
$C_1$
. By Claim A.1, we get that
![]() $f^{\leqslant d}$
is
$f^{\leqslant d}$
is
![]() $\delta $
-global with constant
$\delta $
-global with constant
![]() $4^8$
. Set
$4^8$
. Set
![]() $q = \log (1/\left \|f\right \|_2)$
, and let
$q = \log (1/\left \|f\right \|_2)$
, and let
![]() $\rho = 1/(10\cdot 4^8\cdot q)^2$
be from Theorem 3.3. From Lemmas 5.1, 5.4 we have that
$\rho = 1/(10\cdot 4^8\cdot q)^2$
be from Theorem 3.3. From Lemmas 5.1, 5.4 we have that
![]() $\mathrm {T}^{(\rho )}$
preserves degrees, and so by Corollary 5.11 we get
$\mathrm {T}^{(\rho )}$
preserves degrees, and so by Corollary 5.11 we get
Using
![]() $\left \|f\right \|_{q/(q-1)} \leqslant \left \|f\right \|_2^{2(q-1)/q} = \left \|f\right \|_2^2 \left \|f\right \|_2^{-2/q}\leqslant O(\left \|f\right \|_2^2)$
and Theorem 3.3 to bound
$\left \|f\right \|_{q/(q-1)} \leqslant \left \|f\right \|_2^{2(q-1)/q} = \left \|f\right \|_2^2 \left \|f\right \|_2^{-2/q}\leqslant O(\left \|f\right \|_2^2)$
and Theorem 3.3 to bound
![]() $\left \|\mathrm {T}^{(\rho )} f^{\leqslant d}\right \|_q\leqslant \delta $
, it follows that
$\left \|\mathrm {T}^{(\rho )} f^{\leqslant d}\right \|_q\leqslant \delta $
, it follows that
where we used
![]() $\left \|f\right \|_2^2\leqslant \varepsilon $
.
$\left \|f\right \|_2^2\leqslant \varepsilon $
.
A Missing proofs
A.1 Globalness of f implies globalness of
 $f^{\leqslant d}$
$f^{\leqslant d}$
Claim A.1. There exists an absolute constant
![]() $C>0$
such that the following holds for all
$C>0$
such that the following holds for all
![]() $n,d\in \mathbb {N}$
and
$n,d\in \mathbb {N}$
and
![]() $\varepsilon>0$
satisfying
$\varepsilon>0$
satisfying
![]() $n\geqslant 2^{C\cdot d^3} \log (1/\varepsilon )^{C\cdot d}$
. Suppose
$n\geqslant 2^{C\cdot d^3} \log (1/\varepsilon )^{C\cdot d}$
. Suppose
![]() $f\colon S_n\to \mathbb {Z}$
is
$f\colon S_n\to \mathbb {Z}$
is
![]() $(2d,\varepsilon )$
-global. Then for all
$(2d,\varepsilon )$
-global. Then for all
![]() $j\leqslant d$
, the function
$j\leqslant d$
, the function
![]() $f^{\leqslant j}$
is
$f^{\leqslant j}$
is
-
1.
 $(2j,2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon ))$
-global.
$(2j,2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon ))$
-global. -
2.
 $2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon )$
-global with constant
$2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon )$
-global with constant
 $4^8$
.
$4^8$
.
Proof. If
![]() $j=0$
, then the claim is clear as
$j=0$
, then the claim is clear as
![]() $f^{\leqslant j}$
is just the constant
$f^{\leqslant j}$
is just the constant
![]() ${\mathop {\mathbb {E}}_{}\left [ {f(\pi )} \right ]}$
, and its absolute value is at most
${\mathop {\mathbb {E}}_{}\left [ {f(\pi )} \right ]}$
, and its absolute value is at most
![]() $\left \|f\right \|_2^2\leqslant \varepsilon ^2$
.
$\left \|f\right \|_2^2\leqslant \varepsilon ^2$
.
Suppose
![]() $j\geqslant 1$
and let
$j\geqslant 1$
and let
![]() $\mathrm {D}$
be a derivative of order
$\mathrm {D}$
be a derivative of order
![]() $1\leqslant r\leqslant j$
. Then by Claim 4.2, we have
$1\leqslant r\leqslant j$
. Then by Claim 4.2, we have
![]() $\left \|\mathrm {D} f\right \|_2\leqslant 2^{2j}\varepsilon $
. Therefore, applying Proposition 8.11 on
$\left \|\mathrm {D} f\right \|_2\leqslant 2^{2j}\varepsilon $
. Therefore, applying Proposition 8.11 on
![]() $\mathrm {D} f$
, we get that
$\mathrm {D} f$
, we get that
Using Lemma 8.10, we get that
 $$\begin{align*}\left\|\mathrm{D}(f^{\leqslant j})\right\|_2 \leqslant 2^{O\left(j\right)^{4}}\max_{1-\text{derivative }\mathrm{D}'}\left\|\left(\mathrm{D}'f\right)^{\leqslant j-1}\right\|_{2} +\left(\frac{1}{n}\right)^{10j}\left\|f^{\leqslant 4j}\right\|_2 \leqslant 2^{O(j^4)} \varepsilon^2 \log^{O(j)}(1/\varepsilon), \end{align*}$$
$$\begin{align*}\left\|\mathrm{D}(f^{\leqslant j})\right\|_2 \leqslant 2^{O\left(j\right)^{4}}\max_{1-\text{derivative }\mathrm{D}'}\left\|\left(\mathrm{D}'f\right)^{\leqslant j-1}\right\|_{2} +\left(\frac{1}{n}\right)^{10j}\left\|f^{\leqslant 4j}\right\|_2 \leqslant 2^{O(j^4)} \varepsilon^2 \log^{O(j)}(1/\varepsilon), \end{align*}$$
where in the last inequality we our earlier estimate and Lemma 8.9. For derivatives of order higher than j, we have that
![]() $\mathrm {D}(f^{\leqslant j}) = 0$
from Claim 4.3. Thus, Claim 4.2 implies that
$\mathrm {D}(f^{\leqslant j}) = 0$
from Claim 4.3. Thus, Claim 4.2 implies that
![]() $f^{\leqslant j}$
is
$f^{\leqslant j}$
is
![]() $(2j,2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon ))$
-global. The second item immediately follows from Lemma 3.5.
$(2j,2^{O(j^4)}\varepsilon ^2 \log ^{O(j)}(1/\varepsilon ))$
-global. The second item immediately follows from Lemma 3.5.
A.2 Proof of Theorem 7.13
Our proof will make use of the following simple fact.
Fact A.2. Let
![]() $g\colon S_n\to \mathbb {R}$
.
$g\colon S_n\to \mathbb {R}$
.
-
1. We have the Poincaré inequality:
 $\mathsf {var}(g)\leqslant \frac {1}{n}\sum \limits _{\mathrm {L}_1} \left \|\mathrm {L}_1 g\right \|_2^2$
, where the sum is over all
$\mathsf {var}(g)\leqslant \frac {1}{n}\sum \limits _{\mathrm {L}_1} \left \|\mathrm {L}_1 g\right \|_2^2$
, where the sum is over all
 $1$
-Laplacians.
$1$
-Laplacians. -
2. We have
 $I[g] = \frac {2}{n-1}\sum \limits _{\mathrm {L}_1} \left \|\mathrm {L}_1 g\right \|_2^2$
, where again the sum is over all
$I[g] = \frac {2}{n-1}\sum \limits _{\mathrm {L}_1} \left \|\mathrm {L}_1 g\right \|_2^2$
, where again the sum is over all
 $1$
-Laplacians.
$1$
-Laplacians.
Proof. The second item is straightforward by the definitions, and we focus on the first one. Let
![]() $\tilde {\mathrm {L}} g = {\mathop {\mathbb {E}}_{\mathrm {L}_1}\left [ {\mathrm {L}_1 g} \right ]} = (I-\mathrm {T}) g$
. If
$\tilde {\mathrm {L}} g = {\mathop {\mathbb {E}}_{\mathrm {L}_1}\left [ {\mathrm {L}_1 g} \right ]} = (I-\mathrm {T}) g$
. If
![]() $\alpha _{d,r}$
is an eigenvalue of
$\alpha _{d,r}$
is an eigenvalue of
![]() $\mathrm {T}$
corresponding to a function from
$\mathrm {T}$
corresponding to a function from
![]() $V_{=d}(S_n)$
, then by the second item in Lemma 7.10, we have
$V_{=d}(S_n)$
, then by the second item in Lemma 7.10, we have
![]() $\alpha _{d,r}\leqslant 1-\frac {d}{n-1}$
.
$\alpha _{d,r}\leqslant 1-\frac {d}{n-1}$
.
Note that we may find an orthonormal basis of
![]() $V_{=d}(S_n)$
consisting of eigenvectors of
$V_{=d}(S_n)$
consisting of eigenvectors of
![]() $\mathrm {T}$
, and therefore, we may first write
$\mathrm {T}$
, and therefore, we may first write
![]() $g = \sum \limits _{d} g^{=d}$
, where
$g = \sum \limits _{d} g^{=d}$
, where
![]() $g^{=d}\in V_{=d}(S_n)$
, and then further decompose each
$g^{=d}\in V_{=d}(S_n)$
, and then further decompose each
![]() $g_d$
to
$g_d$
to
![]() $g_d = \sum \limits _{r=0}^{r_d} g_{d,r}$
, where
$g_d = \sum \limits _{r=0}^{r_d} g_{d,r}$
, where
![]() $g_{d,r}\in V_{=d}(S_n)$
are all orthogonal and eigenvectors of
$g_{d,r}\in V_{=d}(S_n)$
are all orthogonal and eigenvectors of
![]() $\mathrm {T}$
. We thus get
$\mathrm {T}$
. We thus get
 $$ \begin{align} \langle{g},{\tilde{\mathrm{L}} g}\rangle =\sum\limits_{d}\sum\limits_{r=0}^{r_d} (1-\alpha_{d,r}) \left\|g^{d,r}\right\|_2^2 \geqslant \sum\limits_{d}\sum\limits_{r=0}^{r_d}\frac{d}{n-1} \left\|g^{d,r}\right\|_2^2 = \sum\limits_{d}\frac{d}{n-1}\left\|g^{=d}\right\|_2^2 \geqslant \frac{1}{n-1}\mathsf{var}(g). \end{align} $$
$$ \begin{align} \langle{g},{\tilde{\mathrm{L}} g}\rangle =\sum\limits_{d}\sum\limits_{r=0}^{r_d} (1-\alpha_{d,r}) \left\|g^{d,r}\right\|_2^2 \geqslant \sum\limits_{d}\sum\limits_{r=0}^{r_d}\frac{d}{n-1} \left\|g^{d,r}\right\|_2^2 = \sum\limits_{d}\frac{d}{n-1}\left\|g^{=d}\right\|_2^2 \geqslant \frac{1}{n-1}\mathsf{var}(g). \end{align} $$
However,
 $$\begin{align*}\langle{g},{\tilde{L} g}\rangle ={\mathop{\mathbb{E}}_{\pi}\left[ {{\mathop{\mathbb{E}}_{\tau\text{ a transposition}}\left[ {g(\pi)(g(\pi) - g(\pi\circ \tau))} \right]}} \right]} =\frac{1}{2} {\mathop{\mathbb{E}}_{\tau\text{ a transposition}}\left[ {{\mathop{\mathbb{E}}_{\pi}\left[ {(g(\pi) - g(\pi\circ \tau))^2} \right]}} \right]}, \end{align*}$$
$$\begin{align*}\langle{g},{\tilde{L} g}\rangle ={\mathop{\mathbb{E}}_{\pi}\left[ {{\mathop{\mathbb{E}}_{\tau\text{ a transposition}}\left[ {g(\pi)(g(\pi) - g(\pi\circ \tau))} \right]}} \right]} =\frac{1}{2} {\mathop{\mathbb{E}}_{\tau\text{ a transposition}}\left[ {{\mathop{\mathbb{E}}_{\pi}\left[ {(g(\pi) - g(\pi\circ \tau))^2} \right]}} \right]}, \end{align*}$$
which is the same as
![]() $\frac {1}{2{n\choose 2}}\sum \limits _{\mathrm {L}_1}{\left \|\mathrm {L}_1g\right \|_2^2}$
. Combining this with the previous lower bound gives the first item.
$\frac {1}{2{n\choose 2}}\sum \limits _{\mathrm {L}_1}{\left \|\mathrm {L}_1g\right \|_2^2}$
. Combining this with the previous lower bound gives the first item.
Proof of Theorem 7.13.
Let
![]() $f = 1_S$
. Then
$f = 1_S$
. Then
![]() $I[f] = \frac {n-1}{2}{\Pr _{\substack {\pi \in S_n\\ \sigma \sim \mathrm {T}\pi }}\left [ {f(\pi )\neq f(\sigma )} \right ]}$
, and arithmetizing that we have that it is equal to
$I[f] = \frac {n-1}{2}{\Pr _{\substack {\pi \in S_n\\ \sigma \sim \mathrm {T}\pi }}\left [ {f(\pi )\neq f(\sigma )} \right ]}$
, and arithmetizing that we have that it is equal to
![]() $\frac {n-1}{2}\langle {f},{(I-\mathrm {T}) f}\rangle $
. Thus, writing
$\frac {n-1}{2}\langle {f},{(I-\mathrm {T}) f}\rangle $
. Thus, writing
![]() $f = f^{=0}+f^{=1}+\dots $
, where
$f = f^{=0}+f^{=1}+\dots $
, where
![]() $f^{=j}\in V_{=j}(S_n)$
, we have, as in inequality (A.1), that
$f^{=j}\in V_{=j}(S_n)$
, we have, as in inequality (A.1), that
 $$ \begin{align} \frac{n-1}{2}\langle{f},{(I-\mathrm{T}) f}\rangle \geqslant \frac{n-1}{2}\sum\limits_{j=0}^{n} \frac{j}{n-1} \left\|f^{=j}\right\|_2^2 \geqslant \frac{d}{2}\left\|f^{>d}\right\|_2^2. \end{align} $$
$$ \begin{align} \frac{n-1}{2}\langle{f},{(I-\mathrm{T}) f}\rangle \geqslant \frac{n-1}{2}\sum\limits_{j=0}^{n} \frac{j}{n-1} \left\|f^{=j}\right\|_2^2 \geqslant \frac{d}{2}\left\|f^{>d}\right\|_2^2. \end{align} $$
To finish the proof, we show that
![]() $\left \|f^{>d}\right \|_2^2\geqslant \Omega (\mathsf {var}(f))$
. To do that, we upper-bound the weight of f on degrees
$\left \|f^{>d}\right \|_2^2\geqslant \Omega (\mathsf {var}(f))$
. To do that, we upper-bound the weight of f on degrees
![]() $1$
to d.
$1$
to d.
Let
![]() $g = f^{\leqslant d}$
. We intend to bound
$g = f^{\leqslant d}$
. We intend to bound
![]() $\mathsf {var}(g)$
using the Poincaré inequality – namely, the first item in Fact A.2. Fix an order
$\mathsf {var}(g)$
using the Poincaré inequality – namely, the first item in Fact A.2. Fix an order
![]() $1$
Laplacian
$1$
Laplacian
![]() $\mathrm {L}_1$
. We have
$\mathrm {L}_1$
. We have
As f is Boolean,
![]() $\mathrm {L}_1 f$
is
$\mathrm {L}_1 f$
is
![]() ${\left \{ -1,0,1 \right \}}$
-valued and so
${\left \{ -1,0,1 \right \}}$
-valued and so
![]() $\left \|\mathrm {L}_1 f\right \|_{4/3} = \left \|\mathrm {L}_1 f\right \|_{2}^{3/2}$
, and next we bound
$\left \|\mathrm {L}_1 f\right \|_{4/3} = \left \|\mathrm {L}_1 f\right \|_{2}^{3/2}$
, and next we bound
![]() $\left \|\mathrm {L}_1 g\right \|_4$
. Note that
$\left \|\mathrm {L}_1 g\right \|_4$
. Note that
 $$ \begin{align} \left\|\mathrm{L}_1 g\right\|_4^4 = {\mathop{\mathbb{E}}_{\substack{\mathrm{D}_1\\\text{order }1\text{ derivative}\\ \text{consistent with }\mathrm{L}_1}}\left[ { } \right]} {\left\|\mathrm{D}_1 g\right\|_4^4}, \end{align} $$
$$ \begin{align} \left\|\mathrm{L}_1 g\right\|_4^4 = {\mathop{\mathbb{E}}_{\substack{\mathrm{D}_1\\\text{order }1\text{ derivative}\\ \text{consistent with }\mathrm{L}_1}}\left[ { } \right]} {\left\|\mathrm{D}_1 g\right\|_4^4}, \end{align} $$
and we analyse
![]() $\left \|\mathrm {D}_1 g\right \|_4^4$
for all derivatives
$\left \|\mathrm {D}_1 g\right \|_4^4$
for all derivatives
![]() $\mathrm {D}_1$
. For that, we use hypercontractivity, and we first have to show that
$\mathrm {D}_1$
. For that, we use hypercontractivity, and we first have to show that
![]() $\mathrm {D}_1 g$
is global.
$\mathrm {D}_1 g$
is global.
Fix a
![]() $1$
-derivative
$1$
-derivative
![]() $\mathrm {D}_1$
and set
$\mathrm {D}_1$
and set
![]() $h = \mathrm {D}_1 g$
. By Lemma 8.10 (with
$h = \mathrm {D}_1 g$
. By Lemma 8.10 (with
![]() $\tilde {f} = f-{\mathop {\mathbb {E}}_{}\left [ {f} \right ]}$
instead of f), we get that for all
$\tilde {f} = f-{\mathop {\mathbb {E}}_{}\left [ {f} \right ]}$
instead of f), we get that for all
![]() $r\leqslant d-1$
and order r derivatives
$r\leqslant d-1$
and order r derivatives
![]() $\mathrm {D}$
, we have
$\mathrm {D}$
, we have
 $$ \begin{align*}\left\|\mathrm{D} h\right\|_{2} = \left\|\mathrm{D}\mathrm{D}_1\left(\tilde{f}^{\leqslant d}\right)\right\|_{2} &\leqslant 2^{O\left(d^{4}\right)} \max_{\substack{\mathrm{D}'\text{ an }r-\text{derivative}\\\mathrm{D}_1'\text{ a }1-\text{derivative}}} \left\|\left(\mathrm{D}'\mathrm{D}_1'\tilde{f} \right)^{\leqslant d-r-1}\right\|_{2}+n^{-10d}\left\|\tilde{f}^{\leqslant 4d}\right\|_{2}\\ &\leqslant 2^{-C\cdot d^4/2} + n^{-10d}\sqrt{\mathsf{var}(f)} \stackrel{\mathit{def}}{=} \delta, \end{align*} $$
$$ \begin{align*}\left\|\mathrm{D} h\right\|_{2} = \left\|\mathrm{D}\mathrm{D}_1\left(\tilde{f}^{\leqslant d}\right)\right\|_{2} &\leqslant 2^{O\left(d^{4}\right)} \max_{\substack{\mathrm{D}'\text{ an }r-\text{derivative}\\\mathrm{D}_1'\text{ a }1-\text{derivative}}} \left\|\left(\mathrm{D}'\mathrm{D}_1'\tilde{f} \right)^{\leqslant d-r-1}\right\|_{2}+n^{-10d}\left\|\tilde{f}^{\leqslant 4d}\right\|_{2}\\ &\leqslant 2^{-C\cdot d^4/2} + n^{-10d}\sqrt{\mathsf{var}(f)} \stackrel{\mathit{def}}{=} \delta, \end{align*} $$
where we used
![]() $\mathrm {D}'\mathrm {D}_1'\tilde {f} = \mathrm {D}'\mathrm {D}_1'f$
, which by assumption, has
$\mathrm {D}'\mathrm {D}_1'\tilde {f} = \mathrm {D}'\mathrm {D}_1'f$
, which by assumption, has
![]() $2$
-norm at most
$2$
-norm at most
![]() $2^{-C\cdot d^4}$
, and
$2^{-C\cdot d^4}$
, and
![]() $\left \|\tilde {f}^{\leqslant 4d}\right \|_{2}\leqslant \left \|\tilde {f}\right \|_2 = \sqrt {\mathsf {var}(f)}$
. For
$\left \|\tilde {f}^{\leqslant 4d}\right \|_{2}\leqslant \left \|\tilde {f}\right \|_2 = \sqrt {\mathsf {var}(f)}$
. For
![]() $r\geqslant d$
, we have by Claim 4.3 that
$r\geqslant d$
, we have by Claim 4.3 that
![]() $\left \|\mathrm {D} h\right \|_{2}=0$
. Thus, all derivatives of h have small
$\left \|\mathrm {D} h\right \|_{2}=0$
. Thus, all derivatives of h have small
![]() $2$
-norm, and by Claim 4.2, we get that h is
$2$
-norm, and by Claim 4.2, we get that h is
![]() $(2d,2^{d}\delta )$
-global. Thus, from Theorem 1.4, we have that
$(2d,2^{d}\delta )$
-global. Thus, from Theorem 1.4, we have that
Plugging inequality (A.5) into (A.4) yields that
 $$\begin{align*}\left\|\mathrm{L}_1 g\right\|_4^4 \leqslant 2^{O(d^3)}\delta^{2} {\mathop{\mathbb{E}}_{\substack{\mathrm{D}_1\\\text{order }1\text{ derivative}\\ \text{consistent with }\mathrm{L}_1}}\left[ { } \right]} {\left\|\mathrm{D}_1 g\right\|_2^2} =2^{O(d^3)}\delta^{2}\left\|\mathrm{L}_1 g\right\|_2^2 \leqslant 2^{O(d^3)}\delta^{2}\left\|\mathrm{L}_1 f\right\|_2^2. \end{align*}$$
$$\begin{align*}\left\|\mathrm{L}_1 g\right\|_4^4 \leqslant 2^{O(d^3)}\delta^{2} {\mathop{\mathbb{E}}_{\substack{\mathrm{D}_1\\\text{order }1\text{ derivative}\\ \text{consistent with }\mathrm{L}_1}}\left[ { } \right]} {\left\|\mathrm{D}_1 g\right\|_2^2} =2^{O(d^3)}\delta^{2}\left\|\mathrm{L}_1 g\right\|_2^2 \leqslant 2^{O(d^3)}\delta^{2}\left\|\mathrm{L}_1 f\right\|_2^2. \end{align*}$$
Plugging this, and the bound we have on the
![]() $4/3$
-norm
$4/3$
-norm
![]() $\mathrm {L}_1 f$
, into (A.3), we get that
$\mathrm {L}_1 f$
, into (A.3), we get that
Summing this inequality over all
![]() $1$
-Laplacians and using Fact A.2, we get that
$1$
-Laplacians and using Fact A.2, we get that
 $$\begin{align*}\mathsf{var}(g) \leqslant \frac{1}{n}\sum\limits_{\mathrm{L}_1}\left\|\mathrm{L}_1 g\right\|_2^2 \leqslant 2^{O(d^3)}\delta^{1/2}\frac{2}{n-1}\sum\limits_{\mathrm{L}_1}\left\|\mathrm{L}_1 f\right\|_2^2 = 2^{C\cdot d^3}\delta^{1/2}I[f] \end{align*}$$
$$\begin{align*}\mathsf{var}(g) \leqslant \frac{1}{n}\sum\limits_{\mathrm{L}_1}\left\|\mathrm{L}_1 g\right\|_2^2 \leqslant 2^{O(d^3)}\delta^{1/2}\frac{2}{n-1}\sum\limits_{\mathrm{L}_1}\left\|\mathrm{L}_1 f\right\|_2^2 = 2^{C\cdot d^3}\delta^{1/2}I[f] \end{align*}$$
for some absolute constant C, and we consider two cases.
The case that
![]() $\boldsymbol{I[f]\leqslant 2^{-C\cdot d^3}\delta ^{-1/2}\mathsf {var}(f)/2}$
.
$\boldsymbol{I[f]\leqslant 2^{-C\cdot d^3}\delta ^{-1/2}\mathsf {var}(f)/2}$
.
In this case, we get that
![]() $\mathsf {var}(g)\leqslant \mathsf {var}(f)/2$
, and so
$\mathsf {var}(g)\leqslant \mathsf {var}(f)/2$
, and so
![]() $\left \|f^{>d}\right \| = \mathsf {var}(f) - \mathsf {var}(g)\geqslant \mathsf {var}(f)/2$
. Plugging this into (A.2) finishes the proof.
$\left \|f^{>d}\right \| = \mathsf {var}(f) - \mathsf {var}(g)\geqslant \mathsf {var}(f)/2$
. Plugging this into (A.2) finishes the proof.
The case that
![]() $\boldsymbol{I[f]\geqslant 2^{-C\cdot d^3}\delta ^{-1/2}\mathsf {var}(f)/2}$
.
$\boldsymbol{I[f]\geqslant 2^{-C\cdot d^3}\delta ^{-1/2}\mathsf {var}(f)/2}$
.
By definition of
![]() $\delta $
, we get that either
$\delta $
, we get that either
![]() $I[f]\geqslant 2^{C\cdot d^4/4} \mathsf {var}(f)$
, in which case we are done, or
$I[f]\geqslant 2^{C\cdot d^4/4} \mathsf {var}(f)$
, in which case we are done, or
![]() $I[f]\geqslant 2^{-O(d^3)} n^{5d}\mathsf {var}(f)^{3/4}$
, in which case we are done by the lower bound on n.
$I[f]\geqslant 2^{-O(d^3)} n^{5d}\mathsf {var}(f)^{3/4}$
, in which case we are done by the lower bound on n.
Competing interest
The authors have no competing interest to declare.
Financial support
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 802020-ERC-HARMONIC.
Dor Minzer was funded by NSF CCF award 2227876 and NSF CAREER award 2239160.