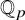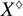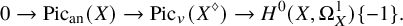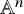1 Introduction
Let p be a prime, and let K be a perfectoid field extension of
![]() $\mathbb {Q}_p$
; for example, we could take
$\mathbb {Q}_p$
; for example, we could take
![]() $K=\mathbb {C}_p$
. Let X be a smooth rigid space over K, considered as an adic space. Then there is a hierarchy of topologies on X
$K=\mathbb {C}_p$
. Let X be a smooth rigid space over K, considered as an adic space. Then there is a hierarchy of topologies on X
where
![]() $X_{\mathrm {pro\acute {e}t}}$
is the pro-étale site defined by Scholze in [Reference Scholze36, Definition 3.9].
$X_{\mathrm {pro\acute {e}t}}$
is the pro-étale site defined by Scholze in [Reference Scholze36, Definition 3.9].
It is a natural question whether the notions of vector bundles agree in these various topologies: To make this precise, let us denote by
![]() $\mathrm {VB}_{\tau }(X)$
the category of finite locally free modules over the structure sheaf where
$\mathrm {VB}_{\tau }(X)$
the category of finite locally free modules over the structure sheaf where
![]() $\tau $
is any of the above topologies. Here, for the pro-étale topology, we use the completed structure sheaf [Reference Scholze36, Definition 4.1].
$\tau $
is any of the above topologies. Here, for the pro-étale topology, we use the completed structure sheaf [Reference Scholze36, Definition 4.1].
By a rigid version of étale descent (see [Reference Fresnel and van der Put18, Proposition 8.2.3]), the natural functor
![]() is an equivalence of categories. One may similarly ask:
is an equivalence of categories. One may similarly ask:
Question 1.1. How far is the following functor from being an equivalence of categories:
It is easy to see that an equivalence would be too much to ask for: As has been observed in the literature [Reference Chojecki, Hansen and Johansson9, before §1.2], descent of analytic vector bundles along pro-étale covers is in general not effective, giving rise to ‘new’ vector bundles in the pro-étale topology. It is known that pro-étale vector bundles arise naturally, for example, in the context of p-adic modular forms, as well as in the p-adic Simpson correspondence [Reference Liu and Zhu30, §2][Reference Würthen41, §3][Reference Mann and Werner32, §7]. However, a systematic description of these additional vector bundles has not yet been given.
1.1 The Hodge–Tate logarithm
The main goal of this article is to answer Question 1.1 for line bundles. Here we can make the question more precise by passing to the Picard group of isomorphism classes and ask for the cokernel of the natural homomorphism
![]() $\operatorname {Pic}_{\mathrm {an}}(X)=\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(X)\to \operatorname {Pic}_{\mathrm {pro\acute {e}t}}(X).$
$\operatorname {Pic}_{\mathrm {an}}(X)=\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(X)\to \operatorname {Pic}_{\mathrm {pro\acute {e}t}}(X).$
Our main result is that this admits a p-adic Hodge-theoretical description in terms of differentials on X that we regard as a ‘Hodge–Tate sequence for
![]() $\mathbb {G}_m$
’.
$\mathbb {G}_m$
’.
Theorem 1.2. Let K be a perfectoid field over
![]() $\mathbb {Q}_p$
. Let X be a smooth rigid space over K.
$\mathbb {Q}_p$
. Let X be a smooth rigid space over K.
-
1. The p-adic logarithm defines a natural left-exact sequence, functorial in X,
(1.2) $$ \begin{align} 0\to \operatorname{Pic}_{\mathrm{an}}(X)\to \operatorname{Pic}_{\mathrm{pro\acute{e}t}}(X)\xrightarrow{ \mathrm{HT}\log} H^0(X,\Omega^1_X)\{-1\}. \end{align} $$
$$ \begin{align} 0\to \operatorname{Pic}_{\mathrm{an}}(X)\to \operatorname{Pic}_{\mathrm{pro\acute{e}t}}(X)\xrightarrow{ \mathrm{HT}\log} H^0(X,\Omega^1_X)\{-1\}. \end{align} $$
-
2. If K is algebraically closed, the sequence is right-exact in either of the following cases:
-
(a) X is proper, or
-
(b) X is of pure dimension 1 and paracompact.
-
-
3. If X is affinoid, the sequence becomes right-exact after inverting p.
Remark 1.3. The
![]() $\{-1\}$
in Theorem 1.2 is a Breuil–Kisin–Fargues twist (see Definition 2.24) that can be identified with a Tate twist
$\{-1\}$
in Theorem 1.2 is a Breuil–Kisin–Fargues twist (see Definition 2.24) that can be identified with a Tate twist
![]() $(-1)$
if K contains all p-power roots of unity. One can always choose a distinguished element for K to fix an isomorphism
$(-1)$
if K contains all p-power roots of unity. One can always choose a distinguished element for K to fix an isomorphism
![]() $\Omega ^1_X\{-1\}\cong \Omega ^1_X$
.
$\Omega ^1_X\{-1\}\cong \Omega ^1_X$
.
We note that if K is not perfectoid, already
![]() $\operatorname {Pic}_{\mathrm {pro\acute {e}t}}(\operatorname {Spa}(K))$
is in general very large.
$\operatorname {Pic}_{\mathrm {pro\acute {e}t}}(\operatorname {Spa}(K))$
is in general very large.
Theorem 1.2 can equivalently be formulated in a slightly different technical setting: Recently, Scholze constructed the category of diamonds [Reference Scholze35, §11], into which seminormal rigid spaces over K embed fully faithfully by way of a diamondification functor
![]() $X\mapsto X^{\diamondsuit }$
[Reference Scholze and Weinstein39, Proposition 10.2.3]. While étale cohomology of diamonds has been studied in great detail [Reference Scholze35], vector bundles on diamonds are much less well-understood.
$X\mapsto X^{\diamondsuit }$
[Reference Scholze and Weinstein39, Proposition 10.2.3]. While étale cohomology of diamonds has been studied in great detail [Reference Scholze35], vector bundles on diamonds are much less well-understood.
The category of (locally spatial) diamonds can be equipped with three well-behaved topologies: The étale, quasi-pro-étale and v-topology. If X is a smooth rigid space, then for the étale topology, there is an equivalence of sites
![]() $X_{{\mathrm {\acute {e}t}}}=X^{\diamondsuit }_{{\mathrm {\acute {e}t}}}$
[Reference Scholze and Weinstein39, Theorem 10.4.2] that identifies the structure sheaves. It is therefore harmless in this context to identify X with its associated diamond, and we can thus extend the hierarchy of topologies in equation (1.1) to
$X_{{\mathrm {\acute {e}t}}}=X^{\diamondsuit }_{{\mathrm {\acute {e}t}}}$
[Reference Scholze and Weinstein39, Theorem 10.4.2] that identifies the structure sheaves. It is therefore harmless in this context to identify X with its associated diamond, and we can thus extend the hierarchy of topologies in equation (1.1) to
For affinoid perfectoid spaces, the notions of vector bundles agree for all of these topologies by a result of Kedlaya–Liu [Reference Kedlaya and Liu27, Theorem 3.5.8]. Since the last three of these sites are locally perfectoid, it follows that
![]() $\mathrm {VB}_{\mathrm {pro\acute {e}t}}(X)= \mathrm {VB}_{\mathrm {qpro\acute {e}t}}(X)= \mathrm {VB}_{v}(X)$
, so also in this more refined setting, there are essentially two different classes of vector bundles. In particular,
$\mathrm {VB}_{\mathrm {pro\acute {e}t}}(X)= \mathrm {VB}_{\mathrm {qpro\acute {e}t}}(X)= \mathrm {VB}_{v}(X)$
, so also in this more refined setting, there are essentially two different classes of vector bundles. In particular,
and we can equivalently regard Theorem 1.2 as describing v-line bundles on X. This is the technical setting which we shall adopt throughout this article.
As our first application of Theorem 1.2, we deduce several useful criteria for telling whether a v-line bundle is analytic, that is, descends to a line bundle in the analytic topology.
Corollary 1.4. Let L be a v-line bundle on X. Let
![]() $V\subseteq X$
be any Zariski-dense analytic open subspace. Then L is analytic if and only if
$V\subseteq X$
be any Zariski-dense analytic open subspace. Then L is analytic if and only if
![]() $L|_V$
is analytic.
$L|_V$
is analytic.
Corollary 1.5. Assume that X is connected, and let L be a v-line bundle on X. If we have
![]() $H^0(X,L)\neq 0$
, then L is analytic.
$H^0(X,L)\neq 0$
, then L is analytic.
For example, these give a new proof that the sheaf of overconvergent modular forms defined by Chojecki–Hansen–Johansson [Reference Chojecki, Hansen and Johansson9] is analytic (see Example 3.10).
In order to shed some light on how the additional v-topological line bundles arise, let us consider the case of proper X: We introduce a diamantine universal pro-finite-étale cover
![]() $\widetilde X\to X$
constructed by taking the limit over all connected finite étale covers in the category of diamonds. This is a pro-étale torsor under the étale fundamental group
$\widetilde X\to X$
constructed by taking the limit over all connected finite étale covers in the category of diamonds. This is a pro-étale torsor under the étale fundamental group
![]() $\pi _1(X)$
, and the Cartan–Leray sequence thus induces a left-exact sequence
$\pi _1(X)$
, and the Cartan–Leray sequence thus induces a left-exact sequence
This interprets continuous characters of
![]() $\pi _1(X)$
as descent data for the trivial line bundle along
$\pi _1(X)$
as descent data for the trivial line bundle along
![]() $\widetilde X\to X$
. Using Scholze’s p-adic Hodge theory, one can show that the images of these under
$\widetilde X\to X$
. Using Scholze’s p-adic Hodge theory, one can show that the images of these under
![]() $\operatorname {HTlog}$
generate
$\operatorname {HTlog}$
generate
![]() $H^0(X, \Omega ^1_X)\{-1\}$
. This is our strategy to prove Theorem 1.2.2a.
$H^0(X, \Omega ^1_X)\{-1\}$
. This is our strategy to prove Theorem 1.2.2a.
1.2 The p-adic Simpson correspondence for line bundles
The proper case of Theorem 1.2 is very closely related to the still mostly conjectural p-adic Simpson correspondence [Reference Faltings17][Reference Deninger and Werner15]: Namely, the theorem shows that we may interpret v-topological line bundles on X as Higgs bundles of rank
![]() $1$
on X, up to a choice of splitting.
$1$
on X, up to a choice of splitting.
On the other hand, equation (1.3) shows that characters of
![]() $\pi _1(X)$
give rise to v-line bundles: This is closely related to the observation by Liu–Zhu [Reference Liu and Zhu30, Remark 2.6] that pro-étale vector bundles are essentially the same as Faltings’ generalised representations. As our main application of Theorem 1.2, we use this to construct the p-adic Simpson correspondence for line bundles.
$\pi _1(X)$
give rise to v-line bundles: This is closely related to the observation by Liu–Zhu [Reference Liu and Zhu30, Remark 2.6] that pro-étale vector bundles are essentially the same as Faltings’ generalised representations. As our main application of Theorem 1.2, we use this to construct the p-adic Simpson correspondence for line bundles.
Theorem 1.6. Let X be a connected smooth proper rigid space over a complete algebraically closed extension K of
![]() $\mathbb {Q}_p$
. Fix
$\mathbb {Q}_p$
. Fix
![]() $x\in X(K)$
. Then there is an equivalence of tensor categories
$x\in X(K)$
. Then there is an equivalence of tensor categories

depending on choices of a Hodge–Tate splitting and of an exponential function.
The construction is entirely global and avoids any localisation steps to affinoid opens. Apart from Theorem 1.2, our main innovation for the proof is the introduction of the diamantine universal cover
![]() $\widetilde X\to X$
, which is a good replacement for the topological universal cover in complex geometry and its role in the complex Simpson correspondence [Reference Simpson40].
$\widetilde X\to X$
, which is a good replacement for the topological universal cover in complex geometry and its role in the complex Simpson correspondence [Reference Simpson40].
We believe that this new approach to the p-adic Simpson correspondence, via the Leray sequence of the projection
![]() $X_{v}\to X_{{\mathrm {\acute {e}t}}}$
for the sheaf
$X_{v}\to X_{{\mathrm {\acute {e}t}}}$
for the sheaf
![]() $\mathbb {G}_m$
, provides new insights also for the general case: In particular, we expect the perspective provided by the universal cover
$\mathbb {G}_m$
, provides new insights also for the general case: In particular, we expect the perspective provided by the universal cover
![]() $\widetilde X\to X$
to help answer Faltings’ open question asking for the correct subcategory of Higgs bundles on X for the formulation of the p-adic Simpson correspondence, which so far has not yet been identified in general. We will explore this further in future work: In [Reference Heuer23] we use this perspective to explain how the right-hand side of the above correspondence can be interpreted more conceptually in terms of moduli spaces. As a further application, we use Theorem 1.6 in [Reference Heuer, Mann and Werner24] to construct the p-adic Simpson correspondence for abeloid varieties.
$\widetilde X\to X$
to help answer Faltings’ open question asking for the correct subcategory of Higgs bundles on X for the formulation of the p-adic Simpson correspondence, which so far has not yet been identified in general. We will explore this further in future work: In [Reference Heuer23] we use this perspective to explain how the right-hand side of the above correspondence can be interpreted more conceptually in terms of moduli spaces. As a further application, we use Theorem 1.6 in [Reference Heuer, Mann and Werner24] to construct the p-adic Simpson correspondence for abeloid varieties.
1.3 Affine space and affinoid spaces
In order to investigate what answers to Question 1.1 we can expect beyond the proper case, we also determine the v-Picard group of the rigid affine space
![]() $\mathbb {A}^n$
over K.
$\mathbb {A}^n$
over K.
Theorem 1.7. For any
![]() $n\in \mathbb {N}$
, the Hodge–Tate logarithm defines an isomorphism
$n\in \mathbb {N}$
, the Hodge–Tate logarithm defines an isomorphism
To the best of our knowledge, this is the first case in which the nonexistence of a p-adic Simpson correspondence outside the proper case can be seen explicitly: In contrast to Theorem 1.2.2,
![]() $\operatorname {Pic}_v(\mathbb {A}^n)$
only sees the closed differentials rather than all of
$\operatorname {Pic}_v(\mathbb {A}^n)$
only sees the closed differentials rather than all of
![]() $\Omega ^1\{-1\}$
. It follows that right-exactness in Theorem 1.2 fails already for a closed disc of radius
$\Omega ^1\{-1\}$
. It follows that right-exactness in Theorem 1.2 fails already for a closed disc of radius
![]() $\geq 2$
.
$\geq 2$
.
On the other hand, Theorem 1.7 ties in nicely with recent results of Colmez–Nizioł [Reference Colmez and Nizioł11] and Le Bras [Reference Le Bras28] describing the pro-étale cohomology of
![]() $\mathbb {A}^n$
.
$\mathbb {A}^n$
.
Notation
Throughout, let K be a perfectoid field extension of
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\mathcal {O}_K$
be the ring of integers,
$\mathcal {O}_K$
be the ring of integers,
![]() $\mathfrak {m}$
its maximal ideal, k the residue field. Let C be the completion of an algebraic closure of K.
$\mathfrak {m}$
its maximal ideal, k the residue field. Let C be the completion of an algebraic closure of K.
We use almost mathematics with respect to
![]() $(\mathcal {O}_K,\mathfrak m)$
and write
$(\mathcal {O}_K,\mathfrak m)$
and write
![]() $\stackrel {a}{=}$
if a natural map becomes an isomorphism after passing to the almost category.
$\stackrel {a}{=}$
if a natural map becomes an isomorphism after passing to the almost category.
By a rigid space over K we shall by definition mean an adic space in the sense of Huber [Reference Huber25] that is locally of topologically finite type over
![]() $\operatorname {Spa}(K,\mathcal {O}_K)$
.
$\operatorname {Spa}(K,\mathcal {O}_K)$
.
Let
![]() $\operatorname {Perf}_K$
be the category of perfectoid spaces over K. Throughout, we shall consider diamonds over
$\operatorname {Perf}_K$
be the category of perfectoid spaces over K. Throughout, we shall consider diamonds over
![]() $\operatorname {Spa}(K,\mathcal {O}_K)$
in the sense of [Reference Scholze35], which in this relative setting we may consider as v-sheaves on
$\operatorname {Spa}(K,\mathcal {O}_K)$
in the sense of [Reference Scholze35], which in this relative setting we may consider as v-sheaves on
![]() $\operatorname {Perf}_K$
. We recall the diamondification functor [Reference Scholze and Weinstein39, §10.1]
$\operatorname {Perf}_K$
. We recall the diamondification functor [Reference Scholze and Weinstein39, §10.1]
which is fully faithful on seminormal rigid spaces by [Reference Kedlaya and Liu27, Theorem 8.2.3]. For any analytic adic space X, we write
![]() $X^{\diamondsuit }$
for the associated diamond when we would like to emphasize the category we work in. We often drop this from the notation and identify seminormal rigid spaces and perfectoid spaces with their associated diamonds when this is clear from the context.
$X^{\diamondsuit }$
for the associated diamond when we would like to emphasize the category we work in. We often drop this from the notation and identify seminormal rigid spaces and perfectoid spaces with their associated diamonds when this is clear from the context.
For a smooth rigid space X, we denote by
![]() $X_{\mathrm {pro\acute {e}t}}$
the pro-étale site in the sense of [Reference Scholze36, Definition 3.9], which is now sometimes referred to as the ‘flattened pro-étale site’.
$X_{\mathrm {pro\acute {e}t}}$
the pro-étale site in the sense of [Reference Scholze36, Definition 3.9], which is now sometimes referred to as the ‘flattened pro-étale site’.
Let us fix notation for some rigid groups we will use:
![]() $\mathbb {G}_a$
denotes the rigid analytic affine line
$\mathbb {G}_a$
denotes the rigid analytic affine line
![]() $\mathbb {A}^1$
with its additive structure,
$\mathbb {A}^1$
with its additive structure,
![]() $\mathbb {G}_a^+$
denotes the subgroup defined by the closed ball of radius 1 around the origin.
$\mathbb {G}_a^+$
denotes the subgroup defined by the closed ball of radius 1 around the origin.
![]() $\mathbb {G}_m$
denotes the rigid analytic affine line punctured at the origin with its multiplicative group structure. We denote by
$\mathbb {G}_m$
denotes the rigid analytic affine line punctured at the origin with its multiplicative group structure. We denote by
![]() $\mathcal {O},\mathcal {O}^+,\mathcal {O}^{\times }$
the sheaves that these groups represent on the étale, pro-étale, quasi-pro-étale or v-site. We will indicate the topology by an index, for example,
$\mathcal {O},\mathcal {O}^+,\mathcal {O}^{\times }$
the sheaves that these groups represent on the étale, pro-étale, quasi-pro-étale or v-site. We will indicate the topology by an index, for example,
![]() $\mathcal {O}_{\tau }$
for
$\mathcal {O}_{\tau }$
for
![]() $\tau ={\mathrm {\acute {e}t}},\mathrm {qpro\acute {e}t},v$
, …unless this is clear from the context.
$\tau ={\mathrm {\acute {e}t}},\mathrm {qpro\acute {e}t},v$
, …unless this is clear from the context.
2 Vector bundles on diamonds
In this section, we prove Theorem 1.2.1 using the Leray spectral sequence of
![]() $\nu :X_v\to X_{{\mathrm {\acute {e}t}}}$
for the sheaf
$\nu :X_v\to X_{{\mathrm {\acute {e}t}}}$
for the sheaf
![]() $\mathcal {O}^{\times }$
. To avoid any ambiguity, we begin with a definition of v-vector bundles.
$\mathcal {O}^{\times }$
. To avoid any ambiguity, we begin with a definition of v-vector bundles.
2.1 Definition and basic properties
For
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $\operatorname {GL}_n^{\diamondsuit }$
be the diamond associated to
$\operatorname {GL}_n^{\diamondsuit }$
be the diamond associated to
![]() $\operatorname {GL}_n$
considered as a rigid space over K.
$\operatorname {GL}_n$
considered as a rigid space over K.
Definition 2.1. Let Y be a diamond over
![]() $\operatorname {Spd}(K)$
. A v-vector bundle of rank
$\operatorname {Spd}(K)$
. A v-vector bundle of rank
![]() $n\in \mathbb {N}$
on Y is a
$n\in \mathbb {N}$
on Y is a
![]() $\operatorname {GL}_n^{\diamondsuit }$
-torsor for the v-topology, that is, a v-sheaf
$\operatorname {GL}_n^{\diamondsuit }$
-torsor for the v-topology, that is, a v-sheaf
![]() $V\to Y$
with a
$V\to Y$
with a
![]() $\operatorname {GL}_n^{\diamondsuit }$
-action
$\operatorname {GL}_n^{\diamondsuit }$
-action
![]() $\operatorname {GL}_n^{\diamondsuit }\times V\to V$
over Y for which there is a v-cover
$\operatorname {GL}_n^{\diamondsuit }\times V\to V$
over Y for which there is a v-cover
![]() $Y'\to Y$
with a
$Y'\to Y$
with a
![]() $\operatorname {GL}_n^{\diamondsuit }$
-equivariant Cartesian diagram
$\operatorname {GL}_n^{\diamondsuit }$
-equivariant Cartesian diagram

As usual, one sees that this geometric definition is equivalent to the sheaf-theoretic one where a v-vector bundle is defined as a locally free
![]() $\mathcal {O}_v$
-modules of rank n on
$\mathcal {O}_v$
-modules of rank n on
![]() $Y_v$
.
$Y_v$
.
In the case of perfectoid spaces, the above v-topological notion of vector bundles is equivalent to the usual notion of vector bundles in the analytic topology:
Theorem 2.2 (Kedlaya–Liu [Reference Kedlaya and Liu27, Theorem 3.5.8]).
Let X be a perfectoid space over K. Then any v-vector bundle on X is already trivial locally in the analytic topology on X.
As a consequence, vector bundles are in general trivial in the quasi-pro-étale topology.
Corollary 2.3. Let Y be a diamond, and let V be a v-vector bundle on Y. Then there is a presentation
![]() $Y=X/R$
for some perfectoid space X and some pro-étale equivalence relation
$Y=X/R$
for some perfectoid space X and some pro-étale equivalence relation
![]() $R\subseteq X\times X$
such that the pullback of V to X is trivial. In particular, any v-vector bundle on Y is already trivial in the quasi-pro-étale topology.
$R\subseteq X\times X$
such that the pullback of V to X is trivial. In particular, any v-vector bundle on Y is already trivial in the quasi-pro-étale topology.
Proof. Let
![]() $Y=X/R$
be any presentation, then by Theorem 2.2, there is an analytic cover
$Y=X/R$
be any presentation, then by Theorem 2.2, there is an analytic cover
![]() $X'\to X$
such that the pullback of V to X becomes trivial over
$X'\to X$
such that the pullback of V to X becomes trivial over
![]() $X'$
. Let
$X'$
. Let
![]() $R'\subseteq X'\times X'$
be the base change of
$R'\subseteq X'\times X'$
be the base change of
![]() $R\to X\times X$
, then by [Reference Scholze35, Proposition 11.3.3-4], this is again a pro-étale equivalence relation, and we have
$R\to X\times X$
, then by [Reference Scholze35, Proposition 11.3.3-4], this is again a pro-étale equivalence relation, and we have
![]() $X'/R'=X/R$
.
$X'/R'=X/R$
.
Corollary 2.4. Let Y be a diamond. Then any v-vector bundle on Y is a diamond.
Proof. Let V be a v-vector bundle on Y. By Corollary 2.3, there is a quasi-pro-étale cover
![]() $Y'\to Y$
trivialising V. We thus have a quasi-pro-étale surjective morphism of v-sheaves
$Y'\to Y$
trivialising V. We thus have a quasi-pro-étale surjective morphism of v-sheaves
![]() $\operatorname {GL}_n^{\diamondsuit } \times Y'\to V$
from a diamond, so by [Reference Scholze35, Proposition 11.6] V is itself a diamond.
$\operatorname {GL}_n^{\diamondsuit } \times Y'\to V$
from a diamond, so by [Reference Scholze35, Proposition 11.6] V is itself a diamond.
In particular, for any v-cover
![]() $X\to Y$
by a perfectoid X, we can describe v-vector bundles on Y in terms of analytic vector bundles on X equipped with descent data. More generally.
$X\to Y$
by a perfectoid X, we can describe v-vector bundles on Y in terms of analytic vector bundles on X equipped with descent data. More generally.
Definition 2.5. Let
![]() $q:X\to Y$
be a v-cover of diamonds. Write
$q:X\to Y$
be a v-cover of diamonds. Write
![]() $\pi _1,\pi _2:X\times _Y X\rightrightarrows X$
for the projection maps. Let
$\pi _1,\pi _2:X\times _Y X\rightrightarrows X$
for the projection maps. Let
![]() $ V$
be a v-vector bundle on X. Then a descent datum on V with respect to q is an isomorphism of v-vector bundles on
$ V$
be a v-vector bundle on X. Then a descent datum on V with respect to q is an isomorphism of v-vector bundles on
![]() $X\times _Y X$
$X\times _Y X$
such that the cocycle condition holds. For a v-vector bundle
![]() $V_0$
on
$V_0$
on
![]() $Y=X/R$
, the pullback along
$Y=X/R$
, the pullback along
![]() $q:X\to Y$
carries a canonical descent datum induced by
$q:X\to Y$
carries a canonical descent datum induced by
![]() $q\circ \pi _{1}=q\circ \pi _2$
. A descent datum
$q\circ \pi _{1}=q\circ \pi _2$
. A descent datum
![]() $\varphi $
is called effective if it is isomorphic to a descent datum of this form.
$\varphi $
is called effective if it is isomorphic to a descent datum of this form.
Lemma 2.6. Let
![]() $q:X\to Y$
be a v-cover of diamonds. Then any descent datum on a v-vector bundle on X is effective: The v-vector bundle on Y attached to
$q:X\to Y$
be a v-cover of diamonds. Then any descent datum on a v-vector bundle on X is effective: The v-vector bundle on Y attached to
![]() is
is
In particular, v-vector bundles of rank n on Y up to isomorphism are classified by the set
In the special case that the diamond Y is the quotient of a perfectoid space X by the action of a profinite group, the descent data defining vector bundles can be described as
![]() $1$
-cocycles in continuous group cohomology, as we shall now discuss.
$1$
-cocycles in continuous group cohomology, as we shall now discuss.
2.2 The Cartan–Leray spectral sequence
Definition 2.7. Let
![]() $f:X\to Y$
be a morphism of diamonds over
$f:X\to Y$
be a morphism of diamonds over
![]() $\operatorname {Spd}(K)$
. Let G be a locally profinite group, regarded as a diamond via [Reference Scholze35, Example 11.12]. We say that f is Galois with group G if f is a quasi-pro-étale G-torsor (cf [Reference Scholze35, Definition 10.12]): Explicitly, this means that f is a quasi-pro-étale cover and there is a G-action on X that leaves f invariant such that the action and projection maps induce an isomorphism
$\operatorname {Spd}(K)$
. Let G be a locally profinite group, regarded as a diamond via [Reference Scholze35, Example 11.12]. We say that f is Galois with group G if f is a quasi-pro-étale G-torsor (cf [Reference Scholze35, Definition 10.12]): Explicitly, this means that f is a quasi-pro-étale cover and there is a G-action on X that leaves f invariant such that the action and projection maps induce an isomorphism
Let
![]() $f:X\to Y$
be Galois with group G, and let
$f:X\to Y$
be Galois with group G, and let
![]() $\mathcal F$
be a sheaf of topological abelian groups on
$\mathcal F$
be a sheaf of topological abelian groups on
![]() $Y_v$
. Generalising from the case of finite G known from étale cohomology, one might hope that there is in this situation a Cartan–Leray spectral sequence relating the continuous group cohomology of
$Y_v$
. Generalising from the case of finite G known from étale cohomology, one might hope that there is in this situation a Cartan–Leray spectral sequence relating the continuous group cohomology of
![]() $H^j_v(X,\mathcal F)$
with
$H^j_v(X,\mathcal F)$
with
![]() $H^j_v(Y,\mathcal F)$
. However, apart from special cases (e.g., if
$H^j_v(Y,\mathcal F)$
. However, apart from special cases (e.g., if
![]() $\mathcal F$
is a sheaf of discrete abelian groups pulled back from
$\mathcal F$
is a sheaf of discrete abelian groups pulled back from
![]() $Y_{{\mathrm {\acute {e}t}}}$
(see [Reference Chojecki, Hansen and Johansson9, Remark 2.25])), it is not clear how to make this precise: Topological abelian groups do not form an abelian category, and it is in general not clear what topology
$Y_{{\mathrm {\acute {e}t}}}$
(see [Reference Chojecki, Hansen and Johansson9, Remark 2.25])), it is not clear how to make this precise: Topological abelian groups do not form an abelian category, and it is in general not clear what topology
![]() $H^j_v(X,\mathcal F)$
should be endowed with. These issues can be fixed using the formalism of condensed abelian groups of Clausen–Scholze [Reference Scholze38].
$H^j_v(X,\mathcal F)$
should be endowed with. These issues can be fixed using the formalism of condensed abelian groups of Clausen–Scholze [Reference Scholze38].
For our purposes, however, the following ad hoc version in low degrees will be sufficient.
Proposition 2.8. Let
![]() $q:X\to Y$
be a morphism of diamonds over K that is Galois for the action of a locally profinite group G on X. Let
$q:X\to Y$
be a morphism of diamonds over K that is Galois for the action of a locally profinite group G on X. Let
![]() $\tau =v$
or
$\tau =v$
or
![]() $\mathrm {qpro\acute {e}t}$
, and let
$\mathrm {qpro\acute {e}t}$
, and let
![]() $\mathcal F$
be a sheaf of not necessarily abelian topological groups on
$\mathcal F$
be a sheaf of not necessarily abelian topological groups on
![]() $Y_{\tau }$
with the property that for
$Y_{\tau }$
with the property that for
![]() $i=1,2$
we have
$i=1,2$
we have
For example, for
![]() $\mathcal F=\mathcal {O}, \mathcal O^{\times }, \operatorname {GL}_n(\mathcal {O}),\dots $
, this condition holds for any
$\mathcal F=\mathcal {O}, \mathcal O^{\times }, \operatorname {GL}_n(\mathcal {O}),\dots $
, this condition holds for any
![]() $i\geq 0$
. Then:
$i\geq 0$
. Then:
-
1. There is a left-exact sequence of pointed sets (of abelian groups if
 $\mathcal F$
is abelian):
$\mathcal F$
is abelian):  $$\begin{align*}0\to H^1_{{\operatorname{cts}}}(G,\mathcal F(X))\to H^1_{\tau}(Y,\mathcal F)\to H^1_{\tau}(X,\mathcal F)^G.\end{align*}$$
$$\begin{align*}0\to H^1_{{\operatorname{cts}}}(G,\mathcal F(X))\to H^1_{\tau}(Y,\mathcal F)\to H^1_{\tau}(X,\mathcal F)^G.\end{align*}$$
-
2. Assume that
 $\mathcal F$
is abelian, that equation (2.1) also holds for
$\mathcal F$
is abelian, that equation (2.1) also holds for
 $i=3$
and that the specialisation map is injective. Then this extends to a ‘Cartan–Leray
$i=3$
and that the specialisation map is injective. Then this extends to a ‘Cartan–Leray $$\begin{align*}H^1_{\tau}(X\times G,\mathcal F)\to \operatorname{Map}(G,H^1_{\tau}(X,\mathcal F))\end{align*}$$
$$\begin{align*}H^1_{\tau}(X\times G,\mathcal F)\to \operatorname{Map}(G,H^1_{\tau}(X,\mathcal F))\end{align*}$$
 $5$
-term exact sequence’
$5$
-term exact sequence’  $$\begin{align*}0\to H^1_{{\operatorname{cts}}}(G,\mathcal F(X))\to H^1_{\tau}(Y,\mathcal F)\to H^1_{\tau}(X,\mathcal F)^G\to H^2_{{\operatorname{cts}}}(G,\mathcal F(X))\to H^2_{\tau}(Y,\mathcal F). \end{align*}$$
$$\begin{align*}0\to H^1_{{\operatorname{cts}}}(G,\mathcal F(X))\to H^1_{\tau}(Y,\mathcal F)\to H^1_{\tau}(X,\mathcal F)^G\to H^2_{{\operatorname{cts}}}(G,\mathcal F(X))\to H^2_{\tau}(Y,\mathcal F). \end{align*}$$
-
3. If moreover
 $H^j_{\tau }(X,\mathcal F)$
carries a topology for all
$H^j_{\tau }(X,\mathcal F)$
carries a topology for all
 $j\geq 1$
such that for all
$j\geq 1$
such that for all
 $i\geq 0$
we have (2.2)then we obtain the full Cartan–Leray spectral sequence
$i\geq 0$
we have (2.2)then we obtain the full Cartan–Leray spectral sequence $$ \begin{align} H^j_{\tau}(X\times G^i,\mathcal F)= \operatorname{Map}_{{\operatorname{cts}}}(G^i,H^j_{\tau}(X,\mathcal F)), \end{align} $$
$$ \begin{align} H^j_{\tau}(X\times G^i,\mathcal F)= \operatorname{Map}_{{\operatorname{cts}}}(G^i,H^j_{\tau}(X,\mathcal F)), \end{align} $$
 $$\begin{align*}E^{ij}_2=H^i_{{\operatorname{cts}}}(G,H^j_{\tau}(X,\mathcal F))\Rightarrow H^{i+j}_{\tau}(Y,\mathcal F).\end{align*}$$
$$\begin{align*}E^{ij}_2=H^i_{{\operatorname{cts}}}(G,H^j_{\tau}(X,\mathcal F))\Rightarrow H^{i+j}_{\tau}(Y,\mathcal F).\end{align*}$$
The last part is implicit in [Reference Scholze36, §5] where it is used in the following form.
Corollary 2.9. If
![]() $\mathcal F$
satisfies equation (2.1) and is
$\mathcal F$
satisfies equation (2.1) and is
![]() $\tau $
-acyclic on
$\tau $
-acyclic on
![]() $X\times G^i$
for all
$X\times G^i$
for all
![]() $i\geq 0$
, then we have
$i\geq 0$
, then we have
Proof of Proposition 2.8.
These all follow from the Čech-to-sheaf spectral sequence of the
![]() $\tau $
-cover
$\tau $
-cover
![]() $X\to Y$
. The associated Čech-complex is of the form
$X\to Y$
. The associated Čech-complex is of the form
which by equation (2.1) for
![]() $i=0,1,2$
and
$i=0,1,2$
and
![]() $j=0$
in part 1, respectively by equation (2.2) in part 3, is equal to
$j=0$
in part 1, respectively by equation (2.2) in part 3, is equal to
By a standard computation, this is precisely the complex of continuous cochains, which by definition computes
![]() $H^i_{{\operatorname {cts}}}(G,H^j_{\tau }(X,\mathcal F))$
. This shows part 1 and part 3.
$H^i_{{\operatorname {cts}}}(G,H^j_{\tau }(X,\mathcal F))$
. This shows part 1 and part 3.
For part 2, the first and fourth term of the mentioned
![]() $5$
-term exact sequence are given by the Čech-cohomology
$5$
-term exact sequence are given by the Čech-cohomology
![]() $\check {H}^i((X\to Y),\mathcal F)$
for
$\check {H}^i((X\to Y),\mathcal F)$
for
![]() $i=1,2$
. By the assumption on equation (2.1), this is computed by the complex (2.3) and thus agrees with
$i=1,2$
. By the assumption on equation (2.1), this is computed by the complex (2.3) and thus agrees with
![]() $H^i_{{\operatorname {cts}}}(G,\mathcal F(X))$
.
$H^i_{{\operatorname {cts}}}(G,\mathcal F(X))$
.
It remains to compute the third term of the sequence, which is the kernel of the map
This is precisely
![]() $ H^1_{\tau }(X,\mathcal F)^G$
if the displayed injectivity condition holds.
$ H^1_{\tau }(X,\mathcal F)^G$
if the displayed injectivity condition holds.
It remains to check that equation (2.1) holds in the given examples: It suffices to show this for
![]() $i=1$
and for X in the basis of affinoid perfectoid spaces in
$i=1$
and for X in the basis of affinoid perfectoid spaces in
![]() $Y_{\tau }$
. But here we have
$Y_{\tau }$
. But here we have
where
![]() $\hat {\otimes }$
is the completed tensor product in Banach K-algebras. Since
$\hat {\otimes }$
is the completed tensor product in Banach K-algebras. Since
![]() $\mathcal {O}(X)$
is uniform, these can be computed by considering the respective p-adically complete integral subspaces
$\mathcal {O}(X)$
is uniform, these can be computed by considering the respective p-adically complete integral subspaces
![]() $\mathcal {O}^+(X)$
and
$\mathcal {O}^+(X)$
and
![]() $\mathcal {O}^+(G)$
, forming the tensor product over
$\mathcal {O}^+(G)$
, forming the tensor product over
![]() $\mathcal {O}_K$
, completing p-adically, and inverting p.
$\mathcal {O}_K$
, completing p-adically, and inverting p.
The case of
![]() $M_n(\mathcal {O})$
follows by forming products, the case of
$M_n(\mathcal {O})$
follows by forming products, the case of
![]() $\operatorname {GL}_n(\mathcal {O})$
by taking units.
$\operatorname {GL}_n(\mathcal {O})$
by taking units.
As an immediate application, this tells us that continuous
![]() $1$
-cocycles are precisely the descent data for
$1$
-cocycles are precisely the descent data for
![]() $X\to Y$
on the trivial vector bundle
$X\to Y$
on the trivial vector bundle
![]() $\mathcal {O}^n$
on X.
$\mathcal {O}^n$
on X.
Corollary 2.10. Let
![]() $X\to Y$
be Galois with group G, then there is a left-exact sequence
$X\to Y$
be Galois with group G, then there is a left-exact sequence
More functorially, this is given by sending any continuous
![]() $1$
-cocycle
$1$
-cocycle
![]() $c:G\to \operatorname {GL}_n(\mathcal {O}(X))$
to the v-vector bundle V on Y defined on
$c:G\to \operatorname {GL}_n(\mathcal {O}(X))$
to the v-vector bundle V on Y defined on
![]() $Y'\in Y_v$
by
$Y'\in Y_v$
by
2.3 The sheaf of principal units
In this section, let X be either a smooth rigid space over K or a perfectoid space over K. We consider the (big) site
![]() $X_{\tau }$
for
$X_{\tau }$
for
![]() $\tau $
one of the following topologies: the étale or pro-étale topology from [Reference Huber25, §2.1] and [Reference Scholze36, Definition 3.9] if X is rigid, or the étale, pro-étale or v-topology from [Reference Scholze35, Definition 8.1] if X is perfectoid. In particular,
$\tau $
one of the following topologies: the étale or pro-étale topology from [Reference Huber25, §2.1] and [Reference Scholze36, Definition 3.9] if X is rigid, or the étale, pro-étale or v-topology from [Reference Scholze35, Definition 8.1] if X is perfectoid. In particular,
![]() $\operatorname {Perf}_{K,\tau }={\operatorname {Spa}(K)}_{\tau }$
.
$\operatorname {Perf}_{K,\tau }={\operatorname {Spa}(K)}_{\tau }$
.
Definition 2.11. We denote by
![]() $U_{\tau }:=1+\mathfrak {m}\mathcal {O}_{\tau }^+\subseteq \mathcal {O}_{\tau }^{\times }$
the subsheaf of
$U_{\tau }:=1+\mathfrak {m}\mathcal {O}_{\tau }^+\subseteq \mathcal {O}_{\tau }^{\times }$
the subsheaf of
![]() $\mathcal {O}_{\tau }^{\times }$
of principal units. This is represented in diamonds over K by the open disc of radius
$\mathcal {O}_{\tau }^{\times }$
of principal units. This is represented in diamonds over K by the open disc of radius
![]() $1$
centred at
$1$
centred at
![]() $1\in \mathbb {G}_m$
. It contains the sheaf of p-power roots of unity
$1\in \mathbb {G}_m$
. It contains the sheaf of p-power roots of unity
![]() $\mu _{p^{\infty }}\subseteq U_{\tau }$
but not all roots of unity
$\mu _{p^{\infty }}\subseteq U_{\tau }$
but not all roots of unity
![]() $\mu \subseteq \mathcal {O}_{\tau }^{\times }$
.
$\mu \subseteq \mathcal {O}_{\tau }^{\times }$
.
The following sheaf will be very useful to compute Picard groups of diamonds: Roughly, it plays the same role in determining the cohomology of
![]() $\mathcal {O}^{\times }_{\tau }$
as the sheaf
$\mathcal {O}^{\times }_{\tau }$
as the sheaf
![]() $\mathcal {O}_{\tau }^+/p$
has for
$\mathcal {O}_{\tau }^+/p$
has for
![]() $\mathcal {O}^+_{\tau }$
.
$\mathcal {O}^+_{\tau }$
.
Definition 2.12. We denote by
![]() $\overline {\mathcal {O}}_{\tau }^{\times }$
the abelian sheaf on
$\overline {\mathcal {O}}_{\tau }^{\times }$
the abelian sheaf on
![]() $X_{\tau }$
defined as the quotient
$X_{\tau }$
defined as the quotient
We will often simply denote the sheaf
![]() $\overline {\mathcal {O}}_v^{\times }$
on
$\overline {\mathcal {O}}_v^{\times }$
on
![]() $\operatorname {Perf}_{K,v}$
by
$\operatorname {Perf}_{K,v}$
by
![]() $\overline {\mathcal {O}}^{\times }$
.
$\overline {\mathcal {O}}^{\times }$
.
Definition 2.13. Let G be a topological abelian group, written multiplicatively. Following [Reference Robertson34, §3], we call an element
![]() $x\in G$
a topological torsion element if
$x\in G$
a topological torsion element if
In all situations that we will encounter, this will be equivalent to the condition that there is
![]() $N\in \mathbb {N}$
for which
$N\in \mathbb {N}$
for which
![]() $x^{Np^n}\to 1$
for
$x^{Np^n}\to 1$
for
![]() $n\to \infty $
. For example, the topological torsion subgroup of
$n\to \infty $
. For example, the topological torsion subgroup of
![]() $K^{\times }$
is
$K^{\times }$
is
![]() $(1+\mathfrak {m}_K)\mu (K)$
, where
$(1+\mathfrak {m}_K)\mu (K)$
, where
![]() $\mu (K)\subseteq K^{\times }$
is the subgroup of all roots of unity.
$\mu (K)\subseteq K^{\times }$
is the subgroup of all roots of unity.
Definition 2.14. We denote by
![]() $\mathcal {O}^{\times ,\mathrm {tt}}\subseteq \mathcal {O}^{\times }$
the topologically torsion subsheaf. Explicitly, this is the subsheaf generated by
$\mathcal {O}^{\times ,\mathrm {tt}}\subseteq \mathcal {O}^{\times }$
the topologically torsion subsheaf. Explicitly, this is the subsheaf generated by
![]() $U=1+\mathfrak {m}\mathcal {O}^+$
and the subsheaf
$U=1+\mathfrak {m}\mathcal {O}^+$
and the subsheaf
![]() $\mu $
of roots of unity.
$\mu $
of roots of unity.
Definition 2.15. For multiplicative sheaves like
![]() $\overline {\mathcal {O}}^{\times }$
, we write
$\overline {\mathcal {O}}^{\times }$
, we write
![]() $\overline {\mathcal {O}}^{\times }[\tfrac {1}{p}]$
for the sheaf
$\overline {\mathcal {O}}^{\times }[\tfrac {1}{p}]$
for the sheaf
![]() $\varinjlim _{x\mapsto x^p}\overline {\mathcal {O}}^{\times }$
obtained by inverting p on the sheaf of abelian groups. We caution that this involves a sheafification, so we do not in general have
$\varinjlim _{x\mapsto x^p}\overline {\mathcal {O}}^{\times }$
obtained by inverting p on the sheaf of abelian groups. We caution that this involves a sheafification, so we do not in general have
![]() $\mathcal {O}^{\times }[\tfrac {1}{p}](X)=\mathcal {O}^{\times }(X)[\tfrac {1}{p}]$
(e.g., not for
$\mathcal {O}^{\times }[\tfrac {1}{p}](X)=\mathcal {O}^{\times }(X)[\tfrac {1}{p}]$
(e.g., not for
![]() $X=\mathbb {G}_m$
). However, this holds on quasi-compact objects, like affinoids in any of the sites we consider.
$X=\mathbb {G}_m$
). However, this holds on quasi-compact objects, like affinoids in any of the sites we consider.
Lemma 2.16.
-
1. We have
 $\overline {\mathcal {O}}_{\tau }^{\times }[\tfrac {1}{p}]=\overline {\mathcal {O}}_{\tau }^{\times }$
, that is, the sheaf
$\overline {\mathcal {O}}_{\tau }^{\times }[\tfrac {1}{p}]=\overline {\mathcal {O}}_{\tau }^{\times }$
, that is, the sheaf
 $\overline {\mathcal {O}}_{\tau }^{\times }$
is uniquely p-divisible.
$\overline {\mathcal {O}}_{\tau }^{\times }$
is uniquely p-divisible. -
2. We have
 $(\mathcal {O}^{\times }_{\tau }/\mathcal {O}_{\tau }^{\times ,\mathrm {tt}})\otimes _{\mathbb {Z}}\mathbb {Q}=\mathcal {O}^{\times }_{\tau }/\mathcal {O}_{\tau }^{\times ,\mathrm {tt}}$
, that is, the sheaf
$(\mathcal {O}^{\times }_{\tau }/\mathcal {O}_{\tau }^{\times ,\mathrm {tt}})\otimes _{\mathbb {Z}}\mathbb {Q}=\mathcal {O}^{\times }_{\tau }/\mathcal {O}_{\tau }^{\times ,\mathrm {tt}}$
, that is, the sheaf
 $\mathcal {O}^{\times }_{\tau }/\mathcal {O}_{\tau }^{\times ,\mathrm {tt}}$
is uniquely divisible.
$\mathcal {O}^{\times }_{\tau }/\mathcal {O}_{\tau }^{\times ,\mathrm {tt}}$
is uniquely divisible.
Proof. This follows from the commutative diagram of exact sequences in the étale topology

The second part follows from the same argument for the exact sequence
Our interest in
![]() $\overline {\mathcal {O}}^{\times }$
stems from the following key approximation lemma, which says that, in contrast to
$\overline {\mathcal {O}}^{\times }$
stems from the following key approximation lemma, which says that, in contrast to
![]() $\mathcal {O}^{\times }_{\mathrm {pro\acute {e}t}}$
, the sheaf
$\mathcal {O}^{\times }_{\mathrm {pro\acute {e}t}}$
, the sheaf
![]() $\overline {\mathcal {O}}^{\times }_{\mathrm {pro\acute {e}t}}$
arises via pullback from the étale site.
$\overline {\mathcal {O}}^{\times }_{\mathrm {pro\acute {e}t}}$
arises via pullback from the étale site.
Lemma 2.17. Let X be a smooth rigid space over K. Let
![]() $X_{\infty }$
be an affinoid perfectoid object in
$X_{\infty }$
be an affinoid perfectoid object in
![]() $X_{\mathrm {pro\acute {e}t}}$
that can be represented as
$X_{\mathrm {pro\acute {e}t}}$
that can be represented as
![]() $X_{\infty }=\varprojlim _{i\in I} X_i$
for some affinoids
$X_{\infty }=\varprojlim _{i\in I} X_i$
for some affinoids
![]() $X_i$
. Then
$X_i$
. Then
In particular, for the morphism of sites
![]() $u:X_{\mathrm {pro\acute {e}t}}\to X_{{\mathrm {\acute {e}t}}}$
, we have
$u:X_{\mathrm {pro\acute {e}t}}\to X_{{\mathrm {\acute {e}t}}}$
, we have
Similarly, we have
![]() $\mathcal {O}^{\times }_{\mathrm {pro\acute {e}t}}/\mathcal {O}^{\times ,\mathrm {tt}}_{\mathrm {pro\acute {e}t}}=u^{\ast }(\mathcal {O}^{\times }_{{\mathrm {\acute {e}t}}}/\mathcal {O}^{\times ,\mathrm {tt}}_{{\mathrm {\acute {e}t}}})$
.
$\mathcal {O}^{\times }_{\mathrm {pro\acute {e}t}}/\mathcal {O}^{\times ,\mathrm {tt}}_{\mathrm {pro\acute {e}t}}=u^{\ast }(\mathcal {O}^{\times }_{{\mathrm {\acute {e}t}}}/\mathcal {O}^{\times ,\mathrm {tt}}_{{\mathrm {\acute {e}t}}})$
.
For the proof, we crucially use that we work in the ‘flattened pro-étale site’ of [Reference Scholze36], rather than finer variants. We also need the p-adic logarithm sequence, which we now recall.
2.4 The p-adic exponential and its higher direct image
In complex geometry, a useful tool to study line bundles is the exponential exact sequence
Over
![]() $\mathbb {Q}_p$
, we have the following analogue of this sequence.
$\mathbb {Q}_p$
, we have the following analogue of this sequence.
Lemma 2.18. Let
![]() $p'=p$
if
$p'=p$
if
![]() $p>2$
and
$p>2$
and
![]() $p'=4$
if
$p'=4$
if
![]() $p=2$
. The p-adic exponential and logarithm map define homomorphisms of rigid group varieties
$p=2$
. The p-adic exponential and logarithm map define homomorphisms of rigid group varieties
such that
![]() $\log (1+p'\mathbb {G}_a^+)\subseteq p'\mathbb {G}_a^+$
and
$\log (1+p'\mathbb {G}_a^+)\subseteq p'\mathbb {G}_a^+$
and
![]() $\exp \circ \log ={\operatorname {id}}$
on
$\exp \circ \log ={\operatorname {id}}$
on
![]() $1+p'\mathbb {G}_a^+$
and
$1+p'\mathbb {G}_a^+$
and
![]() $\log \circ \exp ={\operatorname {id}}$
on
$\log \circ \exp ={\operatorname {id}}$
on
![]() $p'\mathbb {G}_a^+$
.
$p'\mathbb {G}_a^+$
.
In particular, the logarithm defines a short exact sequence of sheaves
whereas the exponential defines a short exact sequence
Proof. The first sequence is well-known; see, for example, [Reference de Jong12, §7]. We sketch the argument:
Clearly
![]() $\log (x)=\sum (-1)^{n}(x-1)^n/n$
and
$\log (x)=\sum (-1)^{n}(x-1)^n/n$
and
![]() $\exp (x)=\sum x^n/n!$
define rigid analytic maps over
$\exp (x)=\sum x^n/n!$
define rigid analytic maps over
![]() $\mathbb {Q}_p$
as described. By classical non-Archimedean analysis, these have the desired properties on
$\mathbb {Q}_p$
as described. By classical non-Archimedean analysis, these have the desired properties on
![]() $\mathbb {C}_p$
-points. It follows that they also hold on the level of rigid groups.
$\mathbb {C}_p$
-points. It follows that they also hold on the level of rigid groups.
To get the first exact sequence, one observes that the kernel of
![]() $\log $
has to be
$\log $
has to be
![]() $\mu _{p^{\infty }}$
since, for any
$\mu _{p^{\infty }}$
since, for any
![]() $x\in U$
, some power
$x\in U$
, some power
![]() $x^{p^n}$
lies in
$x^{p^n}$
lies in
![]() $1+p'\mathcal {O}^+$
where
$1+p'\mathcal {O}^+$
where
![]() $\log $
is injective. The logarithm is surjective in the étale topology since, for any
$\log $
is injective. The logarithm is surjective in the étale topology since, for any
![]() $x\in \mathcal {O}$
with
$x\in \mathcal {O}$
with
![]() $p^{n}x\in p'\mathcal {O}^+$
, any
$p^{n}x\in p'\mathcal {O}^+$
, any
![]() $p^{n}$
-th root y of the unit
$p^{n}$
-th root y of the unit
![]() $\exp (p^{n}x)$
, which exists étale-locally, will satisfy
$\exp (p^{n}x)$
, which exists étale-locally, will satisfy
![]() $\log (y)=\tfrac {1}{p^{n}}\log (\exp (p^{n}x))=x$
.
$\log (y)=\tfrac {1}{p^{n}}\log (\exp (p^{n}x))=x$
.
For the exponential sequence, consider the short exact sequence (we omit
![]() $\tau $
)
$\tau $
)
After inverting p, this becomes the exact sequence (2.5): This is because
![]() $(1+\mathfrak {m}\mathcal {O}^+)/(1+p'\mathcal {O}^+)$
is
$(1+\mathfrak {m}\mathcal {O}^+)/(1+p'\mathcal {O}^+)$
is
![]() $p^{\infty }$
-torsion, and thus
$p^{\infty }$
-torsion, and thus
![]() $\mathcal {O}^{\times }/(1+p'\mathcal {O}^+)[\tfrac {1}{p}]=\overline {\mathcal {O}}^{\times }[\tfrac {1}{p}]=\overline {\mathcal {O}}^{\times }$
by Lemma 2.16.1.
$\mathcal {O}^{\times }/(1+p'\mathcal {O}^+)[\tfrac {1}{p}]=\overline {\mathcal {O}}^{\times }[\tfrac {1}{p}]=\overline {\mathcal {O}}^{\times }$
by Lemma 2.16.1.
As an immediate consequence, we get an explicit description of
![]() $\overline {\mathcal {O}}^{\times }$
on a basis of
$\overline {\mathcal {O}}^{\times }$
on a basis of
![]() $X_{\tau }$
.
$X_{\tau }$
.
Lemma 2.19. Let Y be a quasi-compact object of
![]() $X_{\tau }$
such that
$X_{\tau }$
such that
![]() $H^1_{\tau }(Y,\mathcal {O})=0$
. Then
$H^1_{\tau }(Y,\mathcal {O})=0$
. Then
Proof. We evaluate equation (2.5) at Y and commute
![]() $[\tfrac {1}{p}]$
with
$[\tfrac {1}{p}]$
with
![]() $H^0(Y,-)$
like in Definition 2.15.
$H^0(Y,-)$
like in Definition 2.15.
We now use this to prove the key lemma from the last subsection.
Proof of Lemma 2.17.
It suffices to prove this locally on an analytic cover of
![]() $X_{\infty }$
, so we may assume that the map
$X_{\infty }$
, so we may assume that the map
has dense image. We claim that in this case the map
has dense image, too. To see this, let
![]() $f\in \mathcal {O}^{\times }(X_{\infty })$
, and let
$f\in \mathcal {O}^{\times }(X_{\infty })$
, and let
![]() $\phi (f_i)\to f$
with
$\phi (f_i)\to f$
with
![]() $f_i\in \mathcal {O}(X_i)$
be any converging sequence in the image, and similarly
$f_i\in \mathcal {O}(X_i)$
be any converging sequence in the image, and similarly
![]() $\phi (f^{\prime }_i)\to f^{-1}$
, then we have
$\phi (f^{\prime }_i)\to f^{-1}$
, then we have
![]() $\phi (f_if^{\prime }_i)\to 1$
. In particular, for i large enough, we have
$\phi (f_if^{\prime }_i)\to 1$
. In particular, for i large enough, we have
![]() $\phi (f_if^{\prime }_i)\in 1+\mathfrak {m}\mathcal {O}^+(X_{\infty })=U(X_{\infty })$
.
$\phi (f_if^{\prime }_i)\in 1+\mathfrak {m}\mathcal {O}^+(X_{\infty })=U(X_{\infty })$
.
Claim 2.20. For
![]() $i\gg 0$
, we have
$i\gg 0$
, we have
Proof. The inclusion ‘
![]() $\supseteq $
’ is clear. To see the other, recall that
$\supseteq $
’ is clear. To see the other, recall that
![]() $f\in \mathcal {O}(X_i)$
is in
$f\in \mathcal {O}(X_i)$
is in
![]() $\mathcal {O}^+(X_i)$
if and only if
$\mathcal {O}^+(X_i)$
if and only if
![]() $|f(x)|\leq 1$
for all
$|f(x)|\leq 1$
for all
![]() $x\in X_i$
. Since
$x\in X_i$
. Since
![]() $X_{\infty }\to X_i$
is surjective on the underlying topological spaces for
$X_{\infty }\to X_i$
is surjective on the underlying topological spaces for
![]() $i\gg 0$
, this can be checked after pullback to
$i\gg 0$
, this can be checked after pullback to
![]() $X_{\infty }$
.
$X_{\infty }$
.
This implies that
for
![]() $i\gg 0$
, and thus
$i\gg 0$
, and thus
![]() $f_i\in \mathcal {O}^{\times }(X_i)$
, as desired.
$f_i\in \mathcal {O}^{\times }(X_i)$
, as desired.
We conclude from combining equation (2.6) and Claim 2.20 that the induced map
is an isomorphism. Since the
![]() $X_i$
are affinoid and
$X_i$
are affinoid and
![]() $X_{\infty }$
is affinoid perfectoid, it follows from Lemma 2.19 applied to the étale site on the left and the pro-étale site on the right that also
$X_{\infty }$
is affinoid perfectoid, it follows from Lemma 2.19 applied to the étale site on the left and the pro-étale site on the right that also
is an isomorphism. This proves the first part. The second follows from [Reference Scholze36, Lemma 3.16].
The case of
![]() $\mathcal {O}^{\times }/\mathcal {O}^{\times ,\mathrm {tt}}$
follows since, by Lemma 2.16, we have
$\mathcal {O}^{\times }/\mathcal {O}^{\times ,\mathrm {tt}}$
follows since, by Lemma 2.16, we have
![]() $\mathcal {O}^{\times }/\mathcal {O}^{\times ,\mathrm {tt}}=\overline {\mathcal {O}}^{\times }\otimes _{\mathbb {Z}}\mathbb {Q}$
.
$\mathcal {O}^{\times }/\mathcal {O}^{\times ,\mathrm {tt}}=\overline {\mathcal {O}}^{\times }\otimes _{\mathbb {Z}}\mathbb {Q}$
.
We now use this to prove the main result of this section.
Proposition 2.21. Let X be a smooth rigid space over K. Then for the morphism of sites
![]() $\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
, the short exact sequences (2.4) and (2.5) induce natural isomorphisms
$\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
, the short exact sequences (2.4) and (2.5) induce natural isomorphisms

For the proof, we use Lemma 2.17 as a stepping stone to get to the v-topology.
Lemma 2.22. In the setting of Proposition 2.21, we have
-
1.
 $\displaystyle \nu _{\ast }\overline {\mathcal {O}}^{\times }_{v}=\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}$
,
$\displaystyle \nu _{\ast }\overline {\mathcal {O}}^{\times }_{v}=\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}$
, -
2.
 $R^1\nu _{\ast }\overline {\mathcal {O}}^{\times }_{v}=0$
.
$R^1\nu _{\ast }\overline {\mathcal {O}}^{\times }_{v}=0$
.
Proof. We can split up
![]() $\nu $
into the two morphisms of sites
$\nu $
into the two morphisms of sites
As
![]() $\mathcal {O}_v$
and
$\mathcal {O}_v$
and
![]() $\mathcal {O}_{\mathrm {pro\acute {e}t}}$
are both acyclic on affinoid perfectoids, we know that
$\mathcal {O}_{\mathrm {pro\acute {e}t}}$
are both acyclic on affinoid perfectoids, we know that
Commuting
![]() $w_{\ast }$
and
$w_{\ast }$
and
![]() $[\tfrac {1}{p}]$
like in Definition 2.15, we also have
$[\tfrac {1}{p}]$
like in Definition 2.15, we also have
By the long exact sequence of
![]() $w_{\ast }$
for equation (2.5), this together implies that
$w_{\ast }$
for equation (2.5), this together implies that
Similarly, since any v-topological line bundle on an affinoid perfectoid space is trivial in the analytic topology by Theorem 2.2 and affinoid perfectoids form a basis of
![]() $X_{\mathrm {pro\acute {e}t}}$
, we have
$X_{\mathrm {pro\acute {e}t}}$
, we have
It follows from
![]() $R^2w_{\ast }\mathcal {O}=0$
that
$R^2w_{\ast }\mathcal {O}=0$
that
We now combine these to get to
![]() $\nu $
: By the Leray spectral sequence, the above implies
$\nu $
: By the Leray spectral sequence, the above implies
We have thus reduced to considering
![]() $u:X_{\mathrm {pro\acute {e}t}}\to X_{{\mathrm {\acute {e}t}}}$
. Here we have
$u:X_{\mathrm {pro\acute {e}t}}\to X_{{\mathrm {\acute {e}t}}}$
. Here we have
![]() $\overline {\mathcal {O}}^{\times }_{\mathrm {pro\acute {e}t}}=u^{\ast }\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}$
by Lemma 2.17, which by [Reference Scholze36, Corollary 3.17. (i)] implies
$\overline {\mathcal {O}}^{\times }_{\mathrm {pro\acute {e}t}}=u^{\ast }\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}$
by Lemma 2.17, which by [Reference Scholze36, Corollary 3.17. (i)] implies
![]() $\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}=u_{\ast }\overline {\mathcal {O}}^{\times }_{\mathrm {pro\acute {e}t}}$
as well as
$\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}=u_{\ast }\overline {\mathcal {O}}^{\times }_{\mathrm {pro\acute {e}t}}$
as well as
Putting everything together, this proves the lemma.
Lemma 2.23. Let Y be any diamond, then for
![]() $\nu :Y_v\to Y_{{\mathrm {\acute {e}t}}}$
we have
$\nu :Y_v\to Y_{{\mathrm {\acute {e}t}}}$
we have
![]() $R\nu _{\ast }\mu _{p^{\infty }}=\mu _{p^{\infty }}$
.
$R\nu _{\ast }\mu _{p^{\infty }}=\mu _{p^{\infty }}$
.
Proof. Since
![]() $\mu _{p^{\infty }}$
is an étale sheaf, this follows from [Reference Scholze35, Propositions 14.7, 14.8].
$\mu _{p^{\infty }}$
is an étale sheaf, this follows from [Reference Scholze35, Propositions 14.7, 14.8].
We now have everything in place to prove Proposition 2.21.
Proof of Proposition 2.21.
The first part follows from Lemma 2.23 and the sequence (2.4).
For the second isomorphism, consider the long exact sequence of the exponential (2.5)
By Lemma 2.22.1, we have
![]() $\nu _{\ast }\overline {\mathcal {O}}^{\times }=\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}$
. As we have a map
$\nu _{\ast }\overline {\mathcal {O}}^{\times }=\overline {\mathcal {O}}^{\times }_{{\mathrm {\acute {e}t}}}$
. As we have a map
![]() $\mathcal {O}_{{\mathrm {\acute {e}t}}}^{\times }[\tfrac {1}{p}]\to \nu _{\ast }(\mathcal {O}^{\times }[\tfrac {1}{p}])$
(in fact an isomorphism by Remark 2.26 below, but we do not need this here), this shows that the boundary map vanishes. Thus,
$\mathcal {O}_{{\mathrm {\acute {e}t}}}^{\times }[\tfrac {1}{p}]\to \nu _{\ast }(\mathcal {O}^{\times }[\tfrac {1}{p}])$
(in fact an isomorphism by Remark 2.26 below, but we do not need this here), this shows that the boundary map vanishes. Thus,
![]() $\exp $
in the sequence is injective. The last term vanishes by Lemma 2.22.2; hence,
$\exp $
in the sequence is injective. The last term vanishes by Lemma 2.22.2; hence,
![]() $\exp $
is an isomorphism. Finally, the colimit of the Kummer sequence
$\exp $
is an isomorphism. Finally, the colimit of the Kummer sequence
combines with Lemma 2.23 to show that we have
![]() $R^i\nu _{\ast }\mathcal {O}^{\times }=R^i\nu _{\ast }\mathcal {O}^{\times }[\tfrac {1}{p}]$
for any
$R^i\nu _{\ast }\mathcal {O}^{\times }=R^i\nu _{\ast }\mathcal {O}^{\times }[\tfrac {1}{p}]$
for any
![]() $i\geq 1$
.
$i\geq 1$
.
With these preparations, we can now deduce the first part of Theorem 1.2, using a variant of a result of Scholze describing
![]() $R^1\nu _{\ast }\mathcal {O}$
.
$R^1\nu _{\ast }\mathcal {O}$
.
Definition 2.24. Let
![]() $\theta :W(\mathcal {O}_{K^{\flat }})\to \mathcal {O}_K$
be Fontaine’s map. For any
$\theta :W(\mathcal {O}_{K^{\flat }})\to \mathcal {O}_K$
be Fontaine’s map. For any
![]() $i\in \mathbb {Z}$
, we denote by
$i\in \mathbb {Z}$
, we denote by
![]() $\mathcal {O}_K\{i\}:=(\ker \theta )^i/(\ker \theta )^{i+1}$
the i-th Breuil–Kisin–Fargues twist. This is noncanonically isomorphic to
$\mathcal {O}_K\{i\}:=(\ker \theta )^i/(\ker \theta )^{i+1}$
the i-th Breuil–Kisin–Fargues twist. This is noncanonically isomorphic to
![]() $\mathcal {O}_K$
as an
$\mathcal {O}_K$
as an
![]() $\mathcal {O}_K$
-module. For any
$\mathcal {O}_K$
-module. For any
![]() $\mathcal {O}_K$
-module M or a sheaf of such, we set
$\mathcal {O}_K$
-module M or a sheaf of such, we set
As explained in [Reference Bhatt, Morrow and Scholze3, Example 4.24], if K contains all p-power roots of unity, then there is a canonical isomorphism
where the right-hand side denotes the Tate twist
![]() $K(i)=K\otimes _{\mathbb {Z}}\mathbb {Z}_p(i)$
. In this sense, Breuil–Kisin–Fargues twists are a generalisation of Tate twists to general perfectoid base fields.
$K(i)=K\otimes _{\mathbb {Z}}\mathbb {Z}_p(i)$
. In this sense, Breuil–Kisin–Fargues twists are a generalisation of Tate twists to general perfectoid base fields.
Finally, we set
Proposition 2.25 [Reference Scholze37, Proposition 3.23].
Let K be a perfectoid field extension of
![]() $\mathbb {Q}_p$
, and let X be a smooth rigid space over K. Let
$\mathbb {Q}_p$
, and let X be a smooth rigid space over K. Let
![]() $\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
be the natural morphism of sites. Then there are canonical isomorphisms on
$\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
be the natural morphism of sites. Then there are canonical isomorphisms on
![]() $X_{{\mathrm {\acute {e}t}}}$
for all
$X_{{\mathrm {\acute {e}t}}}$
for all
![]() $i\geq 0$
:
$i\geq 0$
:
Remark 2.26. Already for
![]() $i=0$
, this is the nontrivial result that
$i=0$
, this is the nontrivial result that
![]() $\nu _{\ast }\mathcal {O}=\mathcal {O}$
, proved more generally by Kedlaya–Liu for seminormal rigid spaces [Reference Kedlaya and Liu27, Theorem 8.2.3].
$\nu _{\ast }\mathcal {O}=\mathcal {O}$
, proved more generally by Kedlaya–Liu for seminormal rigid spaces [Reference Kedlaya and Liu27, Theorem 8.2.3].
The notation
![]() $ \widetilde {\Omega }^i_X$
is motivated by [Reference Bhatt, Morrow and Scholze3, §8], where a much finer integral result about
$ \widetilde {\Omega }^i_X$
is motivated by [Reference Bhatt, Morrow and Scholze3, §8], where a much finer integral result about
![]() $\mathcal {O}^+$
is proved for X that admits a smooth formal model.
$\mathcal {O}^+$
is proved for X that admits a smooth formal model.
Proof. For algebraically closed K, this is shown in [Reference Scholze37, Proposition 3.23] for
![]() $X_{\mathrm {pro\acute {e}t}}\to X_{{\mathrm {\acute {e}t}}}$
. But for
$X_{\mathrm {pro\acute {e}t}}\to X_{{\mathrm {\acute {e}t}}}$
. But for
![]() $w:X_{v}\to X_{\mathrm {pro\acute {e}t}}$
, we have
$w:X_{v}\to X_{\mathrm {pro\acute {e}t}}$
, we have
![]() $Rw_{\ast }\mathcal {O}=\mathcal {O}_{\mathrm {pro\acute {e}t}}$
, so the case of
$Rw_{\ast }\mathcal {O}=\mathcal {O}_{\mathrm {pro\acute {e}t}}$
, so the case of
![]() $\nu $
follows.
$\nu $
follows.
The case of general perfectoid K follows from this by Galois descent by an argument similar to that of [Reference Scholze36, Proposition 6.16.(ii)]. Since we do not know a reference for this in the literature in the desired generality, we sketch a proof here: Recall that C is the completion of an algebraic closure of K. It suffices to prove that, for any smooth affinoid rigid space
![]() $X=\operatorname {Spa}(A)$
over K that is standard-étale over a torus
$X=\operatorname {Spa}(A)$
over K that is standard-étale over a torus
![]() $\mathbb T^d$
, we have a natural isomorphism
$\mathbb T^d$
, we have a natural isomorphism
To see this, let
![]() $X_C=\operatorname {Spa}(A_C)$
and let
$X_C=\operatorname {Spa}(A_C)$
and let
![]() $\widetilde X=\operatorname {Spa}(\widetilde A)$
be the pullback along the toric tower
$\widetilde X=\operatorname {Spa}(\widetilde A)$
be the pullback along the toric tower
![]() $\widetilde {\mathbb T}^d\to \mathbb T^d$
. Let
$\widetilde {\mathbb T}^d\to \mathbb T^d$
. Let
![]() $\widetilde X_C=\operatorname {Spa}(\widetilde A_C)$
, then we have a Cartesian square of pro-étale covers in
$\widetilde X_C=\operatorname {Spa}(\widetilde A_C)$
, then we have a Cartesian square of pro-étale covers in
![]() $X_{\mathrm {pro\acute {e}t}}$
$X_{\mathrm {pro\acute {e}t}}$

in which the horizontal maps are Galois with group
![]() $G:=\operatorname {Gal}(C|K)$
and the map on the right is Galois with group
$G:=\operatorname {Gal}(C|K)$
and the map on the right is Galois with group
![]() $\mathbb {Z}_p^d(1)$
. Since
$\mathbb {Z}_p^d(1)$
. Since
![]() $\widetilde X$
and
$\widetilde X$
and
![]() $\widetilde X_C$
are each affinoid perfectoid,
$\widetilde X_C$
are each affinoid perfectoid,
![]() $\mathcal {O}$
is acyclic on them. The Cartan–Leray sequence of Corollary 2.9 for the right map therefore shows
$\mathcal {O}$
is acyclic on them. The Cartan–Leray sequence of Corollary 2.9 for the right map therefore shows
by the first part. More generally, for any
![]() $n\geq 0$
, the same Cartan–Leray sequence for
$n\geq 0$
, the same Cartan–Leray sequence for
![]() $\widetilde X_C\times G^n\to X_C\times G^n$
combines with [Reference Scholze36, Lemma 5.5] to show that, for
$\widetilde X_C\times G^n\to X_C\times G^n$
combines with [Reference Scholze36, Lemma 5.5] to show that, for
![]() $n\geq 0$
, we have
$n\geq 0$
, we have
We thus get the full Cartan–Leray spectral sequence from Proposition 2.8.3:
The étale map
![]() $X\to \mathbb T^d$
induces an isomorphism
$X\to \mathbb T^d$
induces an isomorphism
![]() $\Omega ^j_{X}\cong \mathcal {O}_X^k$
, where
$\Omega ^j_{X}\cong \mathcal {O}_X^k$
, where
![]() $k={d\choose j}$
. Consequently,
$k={d\choose j}$
. Consequently,
as topological G-modules. We claim that
![]() $H^i_{{\operatorname {cts}}}(G,A_C)=0$
for
$H^i_{{\operatorname {cts}}}(G,A_C)=0$
for
![]() $i\geq 1$
. Indeed, observe that the map
$i\geq 1$
. Indeed, observe that the map
![]() $A_C\to \widetilde A_C$
is split in topological G-modules: This is because by [Reference Scholze36, Lemma 4.5], we can pullback the canonical module-splitting of
$A_C\to \widetilde A_C$
is split in topological G-modules: This is because by [Reference Scholze36, Lemma 4.5], we can pullback the canonical module-splitting of
![]() $\widetilde {\mathbb T}^d\to \mathbb T^d$
. We thus have an injection
$\widetilde {\mathbb T}^d\to \mathbb T^d$
. We thus have an injection
by Corollary 2.9, this time applied to the top map using that
![]() $\widetilde X$
is affinoid perfectoid.
$\widetilde X$
is affinoid perfectoid.
All in all, this shows that the above spectral sequence collapses and induces isomorphisms
Definition 2.27. We denote by
![]() $\operatorname {HT}$
the induced map in the Leray sequence
$\operatorname {HT}$
the induced map in the Leray sequence
Combining Propositions 2.21 and 2.25, we see:
Corollary 2.28. The logarithm induces a canonical and functorial isomorphism
This shows the first part of Theorem 1.2: In fact, it implies the following stronger form which also bounds the cokernel on the right in terms of the Brauer group of X.
Theorem 2.29. Let X be a smooth rigid space over K. Then the
![]() $5$
-term exact sequence of the Leray spectral sequence of
$5$
-term exact sequence of the Leray spectral sequence of
![]() $\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
for the sheaf
$\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
for the sheaf
![]() $\mathcal {O}^{\times }$
is of the form
$\mathcal {O}^{\times }$
is of the form
This is functorial in
![]() $X\to \operatorname {Spa}(K)$
, in particular compatible with any base change in K.
$X\to \operatorname {Spa}(K)$
, in particular compatible with any base change in K.
Proof. We consider the 5-term exact sequence of the Leray sequence for
![]() $\nu :X_v\to X_{{\mathrm {\acute {e}t}}}$
. By Remark 2.26, we have
$\nu :X_v\to X_{{\mathrm {\acute {e}t}}}$
. By Remark 2.26, we have
![]() $\nu _{\ast }\mathcal {O}^{\times }=\mathcal {O}^{\times }_{{\mathrm {\acute {e}t}}}$
, so its first term is
$\nu _{\ast }\mathcal {O}^{\times }=\mathcal {O}^{\times }_{{\mathrm {\acute {e}t}}}$
, so its first term is
![]() $\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(X)$
. This is equal to
$\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(X)$
. This is equal to
![]() $\operatorname {Pic}_{\mathrm {an}}(X)$
by [Reference Fresnel and van der Put18, Proposition 8.2.3]. By Corollary 2.28, the third term is as described.
$\operatorname {Pic}_{\mathrm {an}}(X)$
by [Reference Fresnel and van der Put18, Proposition 8.2.3]. By Corollary 2.28, the third term is as described.
Remark 2.30. In [Reference Heuer21, Theorem 2.18], it is shown that Lemma 2.22 generalises, and we in fact have
![]() $R\nu _{\ast }\overline {\mathcal {O}}^{\times }=\overline {\mathcal {O}}^{\times }$
. It follows that, for any
$R\nu _{\ast }\overline {\mathcal {O}}^{\times }=\overline {\mathcal {O}}^{\times }$
. It follows that, for any
![]() $i\geq 1$
, the exponential induces isomorphisms
$i\geq 1$
, the exponential induces isomorphisms
![]() $R^i\nu _{\ast }\mathcal {O}^{\times }=R^i\nu _{\ast }\mathcal {O}=\Omega ^i_X\{-i\}$
. This gives a ‘multiplicative Hodge–Tate spectral sequence’ relating, for example, the étale to the v-topological Brauer group in terms of Hodge cohomology.
$R^i\nu _{\ast }\mathcal {O}^{\times }=R^i\nu _{\ast }\mathcal {O}=\Omega ^i_X\{-i\}$
. This gives a ‘multiplicative Hodge–Tate spectral sequence’ relating, for example, the étale to the v-topological Brauer group in terms of Hodge cohomology.
3 Analyticity criteria
As a first application, we now deduce from Theorem 1.2.1 some criteria for deciding whether a given v-line bundle is analytic. We think that these will be useful in practice (for instance, see Example 3.10). We start with a direct consequence of exactness of the
![]() $\operatorname {HTlog}$
-sequence.
$\operatorname {HTlog}$
-sequence.
Corollary 3.1. Let X be a smooth rigid space and L a v-line bundle on X. Let
![]() $V\subseteq X$
be any Zariski-dense open subspace. Then L is analytic if
$V\subseteq X$
be any Zariski-dense open subspace. Then L is analytic if
![]() $L|_{V}$
is. More generally, let
$L|_{V}$
is. More generally, let
![]() $f:Y\to X$
be a smooth morphism with Zariski-dense image. Then L is analytic if and only if
$f:Y\to X$
be a smooth morphism with Zariski-dense image. Then L is analytic if and only if
![]() $f^{\ast }L$
is.
$f^{\ast }L$
is.
Proof. By Theorem 1.2.1, L is analytic if and only if
![]() $\operatorname {HTlog}(L)=0$
. As we can check this locally, we may assume that X and Y are affinoid. Then since f is smooth with Zariski-dense image, the map
$\operatorname {HTlog}(L)=0$
. As we can check this locally, we may assume that X and Y are affinoid. Then since f is smooth with Zariski-dense image, the map
![]() $H^0(X,\Omega ^1)\hookrightarrow H^0(Y,\Omega ^1)$
is injective. Now use that
$H^0(X,\Omega ^1)\hookrightarrow H^0(Y,\Omega ^1)$
is injective. Now use that
![]() $\operatorname {HTlog}$
is functorial.
$\operatorname {HTlog}$
is functorial.
Second, we can use this to give a characterisation in terms of nontrivial sections.
Proposition 3.2. Let X be a smooth connected rigid space and L a v-line bundle on X. If
![]() $H^0(V,L)\neq 0$
for some open
$H^0(V,L)\neq 0$
for some open
![]() $V\subseteq X$
, then L is analytic.
$V\subseteq X$
, then L is analytic.
Proof. The statement is local on X, so we can assume that X is affinoid and étale over a torus. In particular, there is a toric pro-étale affinoid perfectoid Galois cover
with Galois group G. By Corollary 3.1, it suffices to prove that L becomes trivial on some nonempty open subspace
![]() $V\subseteq X_n$
for some n.
$V\subseteq X_n$
for some n.
Since L is trivial analytic-locally on
![]() $X_{\infty }$
by Theorem 2.2, we can after passing to some affinoid open
$X_{\infty }$
by Theorem 2.2, we can after passing to some affinoid open
![]() $V_n\subseteq X_n$
assume that it is trivial on
$V_n\subseteq X_n$
assume that it is trivial on
![]() $X_{\infty }$
. In this case, we know by Corollary 2.10 that L is associated to a
$X_{\infty }$
. In this case, we know by Corollary 2.10 that L is associated to a
![]() $1$
-cocycle
$1$
-cocycle
![]() $c:G\to \mathcal {O}^{\times }(X_{\infty })$
, that is, we have
$c:G\to \mathcal {O}^{\times }(X_{\infty })$
, that is, we have
Assume now that we have a nontrivial element
![]() $f\in H^0(X,L)$
. We claim that this is invertible on the pullback of some open
$f\in H^0(X,L)$
. We claim that this is invertible on the pullback of some open
![]() $V\subseteq X_n$
for some n. To see this, we use:
$V\subseteq X_n$
for some n. To see this, we use:
Claim 3.3. There is
![]() $x\in X_{\infty }(C,\mathcal {O}_C)$
with
$x\in X_{\infty }(C,\mathcal {O}_C)$
with
![]() $f(x)\neq 0$
.
$f(x)\neq 0$
.
Proof. Write
![]() $X_i=\operatorname {Spa}(A_i,A_i^+)$
for
$X_i=\operatorname {Spa}(A_i,A_i^+)$
for
![]() $i\in \mathbb {N}$
, then by [Reference Scholze36, Lemma 4.5] we have
$i\in \mathbb {N}$
, then by [Reference Scholze36, Lemma 4.5] we have
![]() $X_{\infty }=\operatorname {Spa}(A,A^+)$
, where
$X_{\infty }=\operatorname {Spa}(A,A^+)$
, where
![]() $A=(\varinjlim A_i^+)^{\wedge }[\tfrac {1}{p}]$
. We have compatible maps for each
$A=(\varinjlim A_i^+)^{\wedge }[\tfrac {1}{p}]$
. We have compatible maps for each
![]() $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and
![]() $k\in \mathbb {N}$
$k\in \mathbb {N}$
which are injective by the maximum modulus principle since
![]() $A_i$
is smooth, so
$A_i$
is smooth, so
![]() $A_{I,C}$
is reduced, and C is algebraically closed. In the colimit over i, we obtain an injection
$A_{I,C}$
is reduced, and C is algebraically closed. In the colimit over i, we obtain an injection
Taking the inverse limit over k and inverting p, we get an injection
This gives the desired statement.
We deduce from the claim that there is
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $|f(x)|\geq |\varpi ^k|$
. Consequently, the rational open
$|f(x)|\geq |\varpi ^k|$
. Consequently, the rational open
![]() $V_{\infty }$
of
$V_{\infty }$
of
![]() $X_{\infty }$
defined by
$X_{\infty }$
defined by
![]() $|f|\geq |\varpi ^k|$
is nonempty. We can therefore find a nonempty rational open V in some
$|f|\geq |\varpi ^k|$
is nonempty. We can therefore find a nonempty rational open V in some
![]() $X_n$
whose pullback to
$X_n$
whose pullback to
![]() $X_{\infty }$
is contained in
$X_{\infty }$
is contained in
![]() $U_{\infty }$
. We replace
$U_{\infty }$
. We replace
![]() $V_{\infty }$
by this pullback, then in particular, f is invertible on
$V_{\infty }$
by this pullback, then in particular, f is invertible on
![]() $V_{\infty }$
.
$V_{\infty }$
.
But if
![]() $f\in \mathcal {O}^{\times }(V_{\infty })$
, then multiplication by f defines an isomorphism
$f\in \mathcal {O}^{\times }(V_{\infty })$
, then multiplication by f defines an isomorphism
![]() . In particular, L is trivial on V, in particular analytic, and thus it is analytic on X.
. In particular, L is trivial on V, in particular analytic, and thus it is analytic on X.
Combining Corollary 3.1 and Proposition 3.2, we deduce a stronger version.
Corollary 3.4. Let X be a smooth connected rigid space. Then a v-line bundle L on X is analytic if and only if
![]() $\nu _{\ast }L\neq 0$
, where
$\nu _{\ast }L\neq 0$
, where
![]() $\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
is the natural morphism of sites.
$\nu :X_{v}\to X_{{\mathrm {\acute {e}t}}}$
is the natural morphism of sites.
Corollary 3.5. Let X be a smooth connected rigid space. Let V be an analytic vector bundle and L a v-line bundle on X. If there is a nontrivial map
![]() $L\to V$
, then L is analytic.
$L\to V$
, then L is analytic.
Proof. The statement is local on X, so we can assume that
![]() $V=\mathcal {O}^n$
is trivial. Thus,
$V=\mathcal {O}^n$
is trivial. Thus,
![]() $f:L\to \mathcal {O}^n$
consists of functions
$f:L\to \mathcal {O}^n$
consists of functions
![]() $f_i:L\to \mathcal {O}$
for
$f_i:L\to \mathcal {O}$
for
![]() $i=1,\dots ,n$
and f is nontrivial if one of the
$i=1,\dots ,n$
and f is nontrivial if one of the
![]() $f_i$
is. We are thus reduced to
$f_i$
is. We are thus reduced to
![]() $V=\mathcal {O}$
. But then
$V=\mathcal {O}$
. But then
![]() $f\neq 0$
if and only if its dual
$f\neq 0$
if and only if its dual
![]() $f^{\vee }:\mathcal {O}\to L^{\vee }$
is nontrivial. By Proposition 3.2, this implies that
$f^{\vee }:\mathcal {O}\to L^{\vee }$
is nontrivial. By Proposition 3.2, this implies that
![]() $L^{\vee }$
is analytic, and thus so is L.
$L^{\vee }$
is analytic, and thus so is L.
Third, the property of ‘being analytic’ on products can be checked on fibres.
Corollary 3.6. Let X and Y be a smooth rigid spaces, and let L be a v-line bundle on
![]() $X\times Y$
. Assume that there are Zariski-dense sets of points
$X\times Y$
. Assume that there are Zariski-dense sets of points
![]() $S\subseteq X(K)$
and
$S\subseteq X(K)$
and
![]() $T\subseteq Y(K)$
such that
$T\subseteq Y(K)$
such that
![]() $L_x$
on Y for
$L_x$
on Y for
![]() $x\in S$
and
$x\in S$
and
![]() $L_y$
on X for
$L_y$
on X for
![]() $y\in T$
are all analytic. Then L is analytic.
$y\in T$
are all analytic. Then L is analytic.
Proof. We can without loss of generality assume that X and Y are affinoid. As they are smooth,
![]() $\Omega ^1_X$
and
$\Omega ^1_X$
and
![]() $\Omega ^1_Y$
are vector bundles, and after localising further we may assume that they are free, with bases
$\Omega ^1_Y$
are vector bundles, and after localising further we may assume that they are free, with bases
![]() $v_1,\dots v_n$
and
$v_1,\dots v_n$
and
![]() $w_1,\dots w_m$
, respectively. We then have
$w_1,\dots w_m$
, respectively. We then have
this follows from the corresponding algebraic statement for finitely generated K-algebras.
The corollary now follows from Theorem 1.2.1: According to the above decomposition,
 $$\begin{align*}\operatorname{HTlog}(L)=\sum_{i=1}^n f_i\otimes v_i +\sum_{j=1}^m g_j\otimes w_j. \end{align*}$$
$$\begin{align*}\operatorname{HTlog}(L)=\sum_{i=1}^n f_i\otimes v_i +\sum_{j=1}^m g_j\otimes w_j. \end{align*}$$
Then
![]() $\operatorname {HTlog}(L_x)=\sum g_j(x)w_j\in \widetilde {\Omega }^1(Y)$
. If this vanishes for all
$\operatorname {HTlog}(L_x)=\sum g_j(x)w_j\in \widetilde {\Omega }^1(Y)$
. If this vanishes for all
![]() $x\in S$
, then all
$x\in S$
, then all
![]() $g_j$
vanish on
$g_j$
vanish on
![]() $S\times Y$
and thus also on its Zariski-closure
$S\times Y$
and thus also on its Zariski-closure
![]() $X\times Y$
. Thus,
$X\times Y$
. Thus,
![]() $g_j=0$
, similarly for
$g_j=0$
, similarly for
![]() $y\in T$
.
$y\in T$
.
Fourth, we note that if we add good reduction assumptions, then any v-line bundle trivialised by a Galois cover of good reduction is already trivial in the Zariski topology.
Definition 3.7. Let
![]() $\mathfrak X$
be a formal scheme of topologically finite type over
$\mathfrak X$
be a formal scheme of topologically finite type over
![]() $\mathcal {O}_K$
. Let G be a profinite group. We say that a morphism
$\mathcal {O}_K$
. Let G be a profinite group. We say that a morphism
![]() $\mathfrak X_{\infty }\to \mathfrak X$
is a pro-étale G-torsor with group G if there is a cofiltered inverse system
$\mathfrak X_{\infty }\to \mathfrak X$
is a pro-étale G-torsor with group G if there is a cofiltered inverse system
![]() $(\mathfrak X_i)_{i\in I}$
of finite étale Galois torsors
$(\mathfrak X_i)_{i\in I}$
of finite étale Galois torsors
![]() $\mathfrak X_i\to \mathfrak X$
of group
$\mathfrak X_i\to \mathfrak X$
of group
![]() $G_i$
such that
$G_i$
such that
![]() $\mathfrak X_{\infty }=\varprojlim \mathfrak X_i$
and
$\mathfrak X_{\infty }=\varprojlim \mathfrak X_i$
and
![]() $G=\varprojlim G_i$
. Then
$G=\varprojlim G_i$
. Then
![]() $\mathfrak X$
automatically has a G-action.
$\mathfrak X$
automatically has a G-action.
Proposition 3.8. Let
![]() $\mathfrak X$
be a formal scheme of topologically finite type over
$\mathfrak X$
be a formal scheme of topologically finite type over
![]() $\mathcal {O}_K$
, and let
$\mathcal {O}_K$
, and let
![]() ${\mathfrak X_{\infty }\to \mathfrak X}$
be a pro-étale G-torsor. Then for any
${\mathfrak X_{\infty }\to \mathfrak X}$
be a pro-étale G-torsor. Then for any
![]() $1$
-cocycle
$1$
-cocycle
![]() $c:G\to \mathcal O(\mathfrak X_{\infty })^{\times }$
, the associated v-line bundle on the generic fibre
$c:G\to \mathcal O(\mathfrak X_{\infty })^{\times }$
, the associated v-line bundle on the generic fibre
![]() $\mathcal X$
is the analytification of a Zariski-line bundle on
$\mathcal X$
is the analytification of a Zariski-line bundle on
![]() $\mathfrak X$
.
$\mathfrak X$
.
Proof. With notation as in Definition 3.7, the statement is local on
![]() $\mathfrak X_0:=\mathfrak X$
, so we can reduce to the case that
$\mathfrak X_0:=\mathfrak X$
, so we can reduce to the case that
![]() $\mathfrak X$
is affine and thus so are the
$\mathfrak X$
is affine and thus so are the
![]() $\mathfrak X_i=\operatorname {Spf}(A_i)$
as well as
$\mathfrak X_i=\operatorname {Spf}(A_i)$
as well as
![]() $\mathfrak X_{\infty }=\operatorname {Spf}(A_{\infty })$
.
$\mathfrak X_{\infty }=\operatorname {Spf}(A_{\infty })$
.
Let
![]() $\mathcal X_i$
be the rigid generic fibre of
$\mathcal X_i$
be the rigid generic fibre of
![]() $\mathfrak X_i$
, and let
$\mathfrak X_i$
, and let
![]() $\mathcal X_{\infty }=\varprojlim \mathcal X_i$
as a diamond. Since
$\mathcal X_{\infty }=\varprojlim \mathcal X_i$
as a diamond. Since
![]() $\mathfrak X_i$
is affine, we then have a natural G-equivariant morphism of
$\mathfrak X_i$
is affine, we then have a natural G-equivariant morphism of
![]() $\mathcal {O}_K$
-algebras
$\mathcal {O}_K$
-algebras
Using Corollary 2.10, we thus indeed get a v-line bundle L on
![]() $\mathcal X$
associated to c. Furthermore, by Corollary 2.10, this L is given on any
$\mathcal X$
associated to c. Furthermore, by Corollary 2.10, this L is given on any
![]() $Y\to \mathcal X$
in
$Y\to \mathcal X$
in
![]() $\mathcal X_v$
by
$\mathcal X_v$
by
It thus suffices to prove that Zariski-locally on
![]() $\mathfrak X_0$
there is
$\mathfrak X_0$
there is
![]() $f\in \mathcal {O}(\mathfrak X_{\infty })^{\times }$
such that
$f\in \mathcal {O}(\mathfrak X_{\infty })^{\times }$
such that
![]() $g^{\ast }f=c(g)f$
, since then
$g^{\ast }f=c(g)f$
, since then
![]() $L|_Y=f\mathcal {O}|_Y$
, which shows that L is trivial on Y.
$L|_Y=f\mathcal {O}|_Y$
, which shows that L is trivial on Y.
Consider now for each
![]() $n\in \mathbb {N}$
the reduction of the cocycle c mod
$n\in \mathbb {N}$
the reduction of the cocycle c mod
![]() $p^n$
$p^n$
As this factors over a finite quotient of G [Reference Neukirch, Schmidt and Wingberg33, (1.2.5) Proposition], we can like before associate to this an étale line bundle
![]() $L_n$
on
$L_n$
on
![]() $\mathfrak X_{0}/p^n$
. By étale descent, this is associated to a finite locally free
$\mathfrak X_{0}/p^n$
. By étale descent, this is associated to a finite locally free
![]() $A_0/p^n$
-module
$A_0/p^n$
-module
![]() $M_n$
of rank
$M_n$
of rank
![]() $1$
. Then also
$1$
. Then also
![]() $M=\varprojlim M_n$
is finite locally free with
$M=\varprojlim M_n$
is finite locally free with
![]() $M/p^n=M_n$
by [Reference de Jong13, Tag 0D4B]. Passing from
$M/p^n=M_n$
by [Reference de Jong13, Tag 0D4B]. Passing from
![]() $\mathfrak X_0$
to any Zariski-cover where M is free, any generator of M induces a compatible system of
$\mathfrak X_0$
to any Zariski-cover where M is free, any generator of M induces a compatible system of
![]() $f_n\in (A_{\infty }/p^n)^{\times }$
such that
$f_n\in (A_{\infty }/p^n)^{\times }$
such that
![]() $g^{\ast }f_n=c(g)f_n$
. Then
$g^{\ast }f_n=c(g)f_n$
. Then
![]() $f=(f_n)_n\in \varprojlim _n (A_{\infty }/p^n)^{\times }=\mathcal {O}(\mathfrak X_{\infty })^{\times }$
has the desired properties.
$f=(f_n)_n\in \varprojlim _n (A_{\infty }/p^n)^{\times }=\mathcal {O}(\mathfrak X_{\infty })^{\times }$
has the desired properties.
Finally, we note, due to the functoriality in Theorem 2.29, the morphism
![]() $\operatorname {HTlog}$
is Galois-equivariant if X has a model
$\operatorname {HTlog}$
is Galois-equivariant if X has a model
![]() $X_0\to \operatorname {Spa}(K_0)$
over a subfield
$X_0\to \operatorname {Spa}(K_0)$
over a subfield
![]() $K_0\subseteq K$
. In particular:
$K_0\subseteq K$
. In particular:
Corollary 3.9. Suppose that X is the base change to K of a smooth rigid space
![]() $X_0$
defined over a finite extension E of
$X_0$
defined over a finite extension E of
![]() $\mathbb {Q}_p$
. Then any v-line bundle on
$\mathbb {Q}_p$
. Then any v-line bundle on
![]() $X_0$
becomes analytic on X.
$X_0$
becomes analytic on X.
Proof. It suffices to consider the case that
![]() $K=\mathbb {C}_p$
. Let
$K=\mathbb {C}_p$
. Let
![]() $L_0$
be a v-line bundle on
$L_0$
be a v-line bundle on
![]() $X_0$
, and let L be its base change to X. Then the class of L in
$X_0$
, and let L be its base change to X. Then the class of L in
![]() $\operatorname {Pic}(X)$
is
$\operatorname {Pic}(X)$
is
![]() $G_{E}$
-invariant. By equivariance of
$G_{E}$
-invariant. By equivariance of
![]() $\operatorname {HTlog}$
, this implies that
$\operatorname {HTlog}$
, this implies that
![]() $\operatorname {HTlog}(L)\in H^0(X,\Omega _X^1)(-1)=H^0(X_0,\Omega _{X_0}^1)\otimes _{E}\mathbb {C}_p(-1)$
is Galois-equivariant. But
$\operatorname {HTlog}(L)\in H^0(X,\Omega _X^1)(-1)=H^0(X_0,\Omega _{X_0}^1)\otimes _{E}\mathbb {C}_p(-1)$
is Galois-equivariant. But
![]() $\mathbb {C}_p(-1)^{G_{E}}=0$
, so
$\mathbb {C}_p(-1)^{G_{E}}=0$
, so
![]() $\operatorname {HTlog}(L)=0$
, which means that L is analytic.
$\operatorname {HTlog}(L)=0$
, which means that L is analytic.
Example 3.10. In order to illustrate how the above criteria can be used in practice, we now sketch various new proofs that the sheaf
![]() $\omega ^{\kappa }$
of overconvergent p-adic modular forms defined by Chojecki–Hansen–Johansson [Reference Chojecki, Hansen and Johansson9, Definition 2.18] is an analytic line bundle, at least when we work over a perfectoid base field K, like, for example,
$\omega ^{\kappa }$
of overconvergent p-adic modular forms defined by Chojecki–Hansen–Johansson [Reference Chojecki, Hansen and Johansson9, Definition 2.18] is an analytic line bundle, at least when we work over a perfectoid base field K, like, for example,
![]() $\mathbb {C}_p$
. The sheaf
$\mathbb {C}_p$
. The sheaf
![]() $\omega ^{\kappa }$
is defined on an overconvergent neighbourhood
$\omega ^{\kappa }$
is defined on an overconvergent neighbourhood
![]() $\mathcal X(\epsilon )$
of the ordinary locus of the modular curve: By definition, it is given by a v-descent datum for a certain pro-étale map
$\mathcal X(\epsilon )$
of the ordinary locus of the modular curve: By definition, it is given by a v-descent datum for a certain pro-étale map
![]() $\mathcal X_{\Gamma (p^{\infty })}(\epsilon )_a\to \mathcal X(\epsilon )$
. It is therefore clear from the definition that it is a v-line bundle. We can now employ any of the above criteria to see that
$\mathcal X_{\Gamma (p^{\infty })}(\epsilon )_a\to \mathcal X(\epsilon )$
. It is therefore clear from the definition that it is a v-line bundle. We can now employ any of the above criteria to see that
![]() $\omega ^{\kappa }$
is already analytic (see [Reference Birkbeck, Heuer and Williams5, §3.4] for more details):
$\omega ^{\kappa }$
is already analytic (see [Reference Birkbeck, Heuer and Williams5, §3.4] for more details):
-
1. By Corollary 3.1, it suffices to prove that
 $\omega ^{\kappa }$
is analytic on the ordinary locus
$\omega ^{\kappa }$
is analytic on the ordinary locus
 $\mathcal X(0)\subseteq \mathcal X(\epsilon )$
, which is a Zariski-dense open subspace. But here the statement is essentially classical and originally due to Katz [Reference Katz26, §4]: One reduces the definition to the Igusa tower, where one has a pro-étale formal model, and then invokes Proposition 3.8.
$\mathcal X(0)\subseteq \mathcal X(\epsilon )$
, which is a Zariski-dense open subspace. But here the statement is essentially classical and originally due to Katz [Reference Katz26, §4]: One reduces the definition to the Igusa tower, where one has a pro-étale formal model, and then invokes Proposition 3.8. -
2. By Proposition 3.2, it suffices to show that
 $\omega ^{\kappa }$
has a nontrivial section. Such a section is given by the Eisenstein series (one first has to check that this matches the definition).
$\omega ^{\kappa }$
has a nontrivial section. Such a section is given by the Eisenstein series (one first has to check that this matches the definition). -
3. The bundle
 $\omega ^{\kappa }$
can be defined for rigid analytic families of weights
$\omega ^{\kappa }$
can be defined for rigid analytic families of weights
 $\kappa $
and naturally extends to a v-bundle
$\kappa $
and naturally extends to a v-bundle
 $\omega $
on
$\omega $
on
 $\mathcal X(\epsilon )\times \mathcal W$
, where
$\mathcal X(\epsilon )\times \mathcal W$
, where
 $\mathcal W$
parametrises p-adic weights. We can now use Corollary 3.6 and check analyticity on fibres: It is easy to see that
$\mathcal W$
parametrises p-adic weights. We can now use Corollary 3.6 and check analyticity on fibres: It is easy to see that
 $\omega $
becomes trivial over each point of
$\omega $
becomes trivial over each point of
 $\mathcal X(\epsilon )$
. It thus suffices to prove that
$\mathcal X(\epsilon )$
. It thus suffices to prove that
 $\omega ^{\kappa }$
is analytic for a Zariski-dense subset of weights in
$\omega ^{\kappa }$
is analytic for a Zariski-dense subset of weights in
 $\mathcal W$
. Such a set is given by the classical weights.
$\mathcal W$
. Such a set is given by the classical weights. -
4. The family
 $\mathcal X(\epsilon )\times \mathcal W$
can already be defined over a finite extension of
$\mathcal X(\epsilon )\times \mathcal W$
can already be defined over a finite extension of
 $\mathbb {Q}_p$
, and the definition of the v-bundle
$\mathbb {Q}_p$
, and the definition of the v-bundle
 $\omega ^{\kappa }$
already makes sense on the model. Then Corollary 3.9 says that its base change to any perfectoid field is analytic.
$\omega ^{\kappa }$
already makes sense on the model. Then Corollary 3.9 says that its base change to any perfectoid field is analytic.
4 The image of the Hodge–Tate logarithm
Now that we have constructed the left-exact sequence
we would like to determine the image of
![]() $\operatorname {HTlog}$
in order to give a complete answer to Question 1.1 for line bundles. Towards this goal, we consider in this section the one-dimensional, the affinoid and the proper case, thus completing the proof of Theorem 1.2.
$\operatorname {HTlog}$
in order to give a complete answer to Question 1.1 for line bundles. Towards this goal, we consider in this section the one-dimensional, the affinoid and the proper case, thus completing the proof of Theorem 1.2.
4.1 The case of curves
We start with part 2b of Theorem 1.2: This says that, for a smooth paracompact rigid space of pure dimension
![]() $1$
over an algebraically closed field, the above sequence is in fact also right-exact. We note that paracompactness is quite a weak condition: For example, by the main theorem of [Reference Liu and van der Put29], any separated one-dimensional rigid space is paracompact.
$1$
over an algebraically closed field, the above sequence is in fact also right-exact. We note that paracompactness is quite a weak condition: For example, by the main theorem of [Reference Liu and van der Put29], any separated one-dimensional rigid space is paracompact.
The reason why this condition appears is the following lemma.
Lemma 4.1 [Reference de Jong and van der Put14, Corollary 2.5.10].
Let X be a paracompact rigid space of dimension d. Then
![]() $H^i_{\mathrm {an}}(X,F)=0$
for any abelian sheaf F on
$H^i_{\mathrm {an}}(X,F)=0$
for any abelian sheaf F on
![]() $X_{\mathrm {an}}$
and any
$X_{\mathrm {an}}$
and any
![]() $i>d$
.
$i>d$
.
This is used to prove the following lemma on the Brauer group of curves, which by the 5-term exact sequence of Theorem 2.29 completes the proof of Theorem 1.2.2b.
Lemma 4.2. Let K be algebraically closed. Let X be a paracompact rigid space of dimension
![]() $1$
over K. Then
$1$
over K. Then
![]() $H^2_{{\mathrm {\acute {e}t}}}(X,\mathcal {O}^{\times })=0$
.
$H^2_{{\mathrm {\acute {e}t}}}(X,\mathcal {O}^{\times })=0$
.
Proof. This is proved by Berkovich for good k-analytic spaces [Reference Berkovich2, Lemma 6.1.2], which via the comparison to rigid spaces [Reference Huber25, §8.3, Theorem 8.3.5] proves the result for taut rigid spaces. More generally, one can also argue purely in the rigid analytic category.
Let
![]() $r\colon X_{{\mathrm {\acute {e}t}}}\to X_{\mathrm {an}}$
be the natural morphism of sites. Then we have
$r\colon X_{{\mathrm {\acute {e}t}}}\to X_{\mathrm {an}}$
be the natural morphism of sites. Then we have
by [Reference Fresnel and van der Put18, Lemma 8.3.1, Proposition 8.2.3 and Corollary 8.3.2]. Thus, the natural map
is an isomorphism. But the left-hand side vanishes by Lemma 4.1 as X is paracompact.
The case of curves has a few interesting consequences for the general case, which we will later use to compute
![]() $\operatorname {Pic}_v(\mathbb {A}^n)$
. These are based on functoriality of
$\operatorname {Pic}_v(\mathbb {A}^n)$
. These are based on functoriality of
![]() $\operatorname {HTlog}$
.
$\operatorname {HTlog}$
.
Remark 4.3. A general strategy to describe the image of
![]() $\operatorname {HTlog}$
is as follows: If
$\operatorname {HTlog}$
is as follows: If
![]() $f:X\to Y$
is a morphism of smooth rigid spaces, then by functoriality we obtain a commutative diagram
$f:X\to Y$
is a morphism of smooth rigid spaces, then by functoriality we obtain a commutative diagram

In particular, we have
![]() $f^{\ast }(\operatorname {im}\mathrm {HT}\log_Y )\subseteq \operatorname {im} \mathrm {HT}\log_X $
. For example, one could use this to reduce the case of projective X in Theorem 1.2.2 to that of abelian varieties via the Albanese variety
$f^{\ast }(\operatorname {im}\mathrm {HT}\log_Y )\subseteq \operatorname {im} \mathrm {HT}\log_X $
. For example, one could use this to reduce the case of projective X in Theorem 1.2.2 to that of abelian varieties via the Albanese variety
![]() $X\to A$
. But this no longer works in general for proper X; see [Reference Hansen and Li20, Example 5.6].
$X\to A$
. But this no longer works in general for proper X; see [Reference Hansen and Li20, Example 5.6].
Corollary 4.4. Let X be any smooth rigid space. Then for any
![]() $f\in \mathcal {O}(X)$
, the differential
$f\in \mathcal {O}(X)$
, the differential
![]() $df\in H^0(X,\Omega ^1)$
is in the image of
$df\in H^0(X,\Omega ^1)$
is in the image of
![]() $\operatorname {HTlog}\{1\}:\operatorname {Pic}_v(X)\{1\}\to H^0(X,\Omega ^1_X)$
.
$\operatorname {HTlog}\{1\}:\operatorname {Pic}_v(X)\{1\}\to H^0(X,\Omega ^1_X)$
.
Proof. Associated to f we have a map
![]() $f:X\to \mathbb {A}^1$
that sends the parameter T on
$f:X\to \mathbb {A}^1$
that sends the parameter T on
![]() $\mathbb {A}^1$
to f. Since
$\mathbb {A}^1$
to f. Since
![]() $\mathbb {A}^1$
is a paracompact curve, Theorem 1.2.2b shows that
$\mathbb {A}^1$
is a paracompact curve, Theorem 1.2.2b shows that
![]() $\operatorname {Pic}_v(\mathbb {A}^1)=H^0(\mathbb {A}^1,\widetilde {\Omega }^1)$
. The desired statement now follows from Remark 4.3 since
$\operatorname {Pic}_v(\mathbb {A}^1)=H^0(\mathbb {A}^1,\widetilde {\Omega }^1)$
. The desired statement now follows from Remark 4.3 since
![]() $f^{\ast }$
sends
$f^{\ast }$
sends
![]() $dT\mapsto df$
.
$dT\mapsto df$
.
4.2 The cokernel in the affinoid case
Next, we prove part 3 of Theorem 1.2, which is also an easy consequence of Proposition 2.21: We need to see that, for X an affinoid smooth rigid space, we get a short exact sequence
Proof of Theorem 1.2.3.
The morphism of Leray 5-term exact sequences associated to the exponential (2.5) gives a commutative diagram of connecting homomorphisms

where the map on the left is an isomorphism by Proposition 2.21. It therefore suffices to see that the top morphism is zero, as then so is the bottom one. But since X is affinoid,
where the first equality holds by [Reference Fresnel and van der Put18, Proposition 8.2.3(2)].
The remaining part of Theorem 1.2 is the proper case 2a, which is arguably the most interesting one. For this we need a further ingredient: the universal cover of X.
4.3 The diamantine universal cover
In this subsection, we more generally let X be any connected rigid space over any non-Archimedean field K. As before, we denote by C the completed algebraic closure of K. Fix a geometric point
![]() $x\in X(C)$
. Since X is a locally Noetherian adic space, we have the étale fundamental group
$x\in X(C)$
. Since X is a locally Noetherian adic space, we have the étale fundamental group
![]() $\pi _{1}(X,x)$
, a profinite group that governs the finite étale covers of X: More precisely, let
$\pi _{1}(X,x)$
, a profinite group that governs the finite étale covers of X: More precisely, let
![]() $X_{\mathrm {prof\acute {e}t}}=\mathrm {Pro}(X_{\mathrm {f\acute {e}t}})$
be the category of pro-finite-étale covers of X. Let
$X_{\mathrm {prof\acute {e}t}}=\mathrm {Pro}(X_{\mathrm {f\acute {e}t}})$
be the category of pro-finite-étale covers of X. Let
![]() $\pi _{1}(X,x)\mathrm {-pfSets}$
be the category of profinite sets with a continuous
$\pi _{1}(X,x)\mathrm {-pfSets}$
be the category of profinite sets with a continuous
![]() $\pi _{1}(X,x)$
-action. Then:
$\pi _{1}(X,x)$
-action. Then:
Proposition 4.5 [Reference Scholze36, Proposition 3.5].
There is an equivalence of categories
 $$ \begin{align*} F:X_{\mathrm{prof\acute{e}t}}&\:\to\: \pi_{1}(X,x)\text{-}\mathrm{pfSets}\\ (Y_i)_{i\in I} &\:\mapsto\: F(X):=\varprojlim_{i\in I}\operatorname{Hom}_X(x,Y_i). \end{align*} $$
$$ \begin{align*} F:X_{\mathrm{prof\acute{e}t}}&\:\to\: \pi_{1}(X,x)\text{-}\mathrm{pfSets}\\ (Y_i)_{i\in I} &\:\mapsto\: F(X):=\varprojlim_{i\in I}\operatorname{Hom}_X(x,Y_i). \end{align*} $$
In particular, we have a universal object in
![]() $X_{\mathrm {prof\acute {e}t}}$
, which corresponds to
$X_{\mathrm {prof\acute {e}t}}$
, which corresponds to
![]() $\pi _{1}(X,x)$
endowed with the translation action on itself. Since cofiltered inverse limits exists in the category of diamonds [Reference Scholze35, Lemma 11.22], we can associate a diamond to this object.
$\pi _{1}(X,x)$
endowed with the translation action on itself. Since cofiltered inverse limits exists in the category of diamonds [Reference Scholze35, Lemma 11.22], we can associate a diamond to this object.
Definition 4.6. The universal pro-finite-étale cover
![]() $\widetilde X\to X$
is defined as the diamond
$\widetilde X\to X$
is defined as the diamond
where the index category consists of all connected finite étale covers
![]() $(X',x')\to (X,x)$
with
$(X',x')\to (X,x)$
with
![]() $x'\in X'(C)$
a choice of lift of the base point
$x'\in X'(C)$
a choice of lift of the base point
![]() $x\in X(C)$
. This is a spatial diamond, and the canonical projection
$x\in X(C)$
. This is a spatial diamond, and the canonical projection
is a pro-finite-étale
![]() $\pi _{1}(X,x)$
-torsor in a canonical way. Here the additional datum of the lift
$\pi _{1}(X,x)$
-torsor in a canonical way. Here the additional datum of the lift
![]() $x'$
in the index category is necessary to make this action canonical and to make the association
$x'$
in the index category is necessary to make this action canonical and to make the association
![]() $X\mapsto \widetilde X$
functorial in a canonical way. It gives a distinguished point
$X\mapsto \widetilde X$
functorial in a canonical way. It gives a distinguished point
![]() $\widetilde x\in \widetilde X(C)$
.
$\widetilde x\in \widetilde X(C)$
.
Example 4.7.
-
1. For
 $X=\operatorname {Spa}(K)$
, we have
$X=\operatorname {Spa}(K)$
, we have
 $\widetilde X=\operatorname {Spa}(C)$
. In particular, for any X we have
$\widetilde X=\operatorname {Spa}(C)$
. In particular, for any X we have
 $\widetilde X=\widetilde {X_C}$
, that is, the universal cover is the universal cover of the base change to C.
$\widetilde X=\widetilde {X_C}$
, that is, the universal cover is the universal cover of the base change to C. -
2. If X is an abelian variety, or more generally an abeloid variety, and
 $K=C$
then is the limit over multiplication by n on X, where n ranges through
$K=C$
then is the limit over multiplication by n on X, where n ranges through $$\begin{align*}\widetilde X=\textstyle\varprojlim_{[n]}X \end{align*}$$
$$\begin{align*}\widetilde X=\textstyle\varprojlim_{[n]}X \end{align*}$$
 $\mathbb {N}$
. This is represented by a perfectoid space [Reference Blakestad, Gvirtz, Heuer, Shchedrina, Shimizu, Wear and Yao6, Corollary 5.9] with the interesting feature that it is ‘p-adic locally constant in X’, that is, many different X have isomorphic
$\mathbb {N}$
. This is represented by a perfectoid space [Reference Blakestad, Gvirtz, Heuer, Shchedrina, Shimizu, Wear and Yao6, Corollary 5.9] with the interesting feature that it is ‘p-adic locally constant in X’, that is, many different X have isomorphic
 $\widetilde X$
[Reference Heuer22].
$\widetilde X$
[Reference Heuer22].
-
3. If X is a connected smooth proper curve of genus
 $\geq 1$
, then
$\geq 1$
, then
 $\widetilde X$
is also represented by a perfectoid space [Reference Blakestad, Gvirtz, Heuer, Shchedrina, Shimizu, Wear and Yao6, Corollary 5.7] and has first been considered by Hansen.
$\widetilde X$
is also represented by a perfectoid space [Reference Blakestad, Gvirtz, Heuer, Shchedrina, Shimizu, Wear and Yao6, Corollary 5.7] and has first been considered by Hansen. -
4. In the other extreme, if X is a space over
 $K=C$
without any nonsplit finite étale covers, for example,
$K=C$
without any nonsplit finite étale covers, for example,
 $X=\mathbb {P}^n$
or X a K3 surface, then we simply have
$X=\mathbb {P}^n$
or X a K3 surface, then we simply have
 $\widetilde X=X$
. In particular,
$\widetilde X=X$
. In particular,
 $\widetilde X$
is not always perfectoid. We do not know if X is always represented by an adic space.
$\widetilde X$
is not always perfectoid. We do not know if X is always represented by an adic space.
We call
![]() $\widetilde X$
the universal pro-finite-étale cover due to the following universal property.
$\widetilde X$
the universal pro-finite-étale cover due to the following universal property.
Lemma 4.8. Let
![]() $Y\to X$
be any pro-finite-étale cover, that is, an element of
$Y\to X$
be any pro-finite-étale cover, that is, an element of
![]() $X_{\mathrm {prof\acute {e}t}}$
, and fix a lift
$X_{\mathrm {prof\acute {e}t}}$
, and fix a lift
![]() $y\in Y(C)$
of x. Then there is a unique morphism
$y\in Y(C)$
of x. Then there is a unique morphism
![]() $(\widetilde X,\widetilde x)\to (Y,y)$
over X.
$(\widetilde X,\widetilde x)\to (Y,y)$
over X.
Proof. By the limit property, it suffices to see this for finite étale
![]() $Y\to X$
. Passing to the connected component of y, we see
$Y\to X$
. Passing to the connected component of y, we see
![]() $(Y,y)$
appears in the index of the limit defining
$(Y,y)$
appears in the index of the limit defining
![]() $\widetilde X$
.
$\widetilde X$
.
Let us from now on assume that X is proper. Then, more interestingly,
![]() $\widetilde X\to X$
is also a topological universal cover in the following sense.
$\widetilde X\to X$
is also a topological universal cover in the following sense.
Proposition 4.9. Let X be a connected seminormal proper rigid space over K. Then for any
![]() $n\in \mathbb {N}$
and F any of the v-sheaves
$n\in \mathbb {N}$
and F any of the v-sheaves
![]() $\mathbb {Z}/n, \mathbb {Z}_p, \widehat {\mathbb {Z}}, \mathcal {O}^{+a}/p^n, \mathcal {O}^{+a}, \mathcal {O}, U, \mathcal {O}^{\times ,\mathrm {tt}}$
, we have
$\mathbb {Z}/n, \mathbb {Z}_p, \widehat {\mathbb {Z}}, \mathcal {O}^{+a}/p^n, \mathcal {O}^{+a}, \mathcal {O}, U, \mathcal {O}^{\times ,\mathrm {tt}}$
, we have
 $$ \begin{align*} H^0(\widetilde X,F)&= H^0(\operatorname{Spa}(C),F),\\ H^1_{v}(\widetilde X,F)&= 0. \end{align*} $$
$$ \begin{align*} H^0(\widetilde X,F)&= H^0(\operatorname{Spa}(C),F),\\ H^1_{v}(\widetilde X,F)&= 0. \end{align*} $$
Remark 4.10. This implies that
![]() $\widetilde X\to X$
is the ‘universal cover for
$\widetilde X\to X$
is the ‘universal cover for
![]() ${\widehat {\mathbb {Z}}}$
-coefficients’, that is, it has a universal lifting property for morphisms from diamonds Y with
${\widehat {\mathbb {Z}}}$
-coefficients’, that is, it has a universal lifting property for morphisms from diamonds Y with
![]() $H^1_v(Y,\widehat {\mathbb {Z}})=0$
into X [Reference Heuer22, Corollary 3.10]. If X is either a curve of genus
$H^1_v(Y,\widehat {\mathbb {Z}})=0$
into X [Reference Heuer22, Corollary 3.10]. If X is either a curve of genus
![]() $g\geq 1$
or an abeloid variety, we in fact have
$g\geq 1$
or an abeloid variety, we in fact have
![]() $H^i_{v}(\widetilde X,-)=0$
for all
$H^i_{v}(\widetilde X,-)=0$
for all
![]() $i\geq 1$
for all of these coefficients [Reference Heuer21, Proposition 4.2]. But for a general smooth proper rigid space X, this is no longer true as the example of
$i\geq 1$
for all of these coefficients [Reference Heuer21, Proposition 4.2]. But for a general smooth proper rigid space X, this is no longer true as the example of
![]() $\mathbb {P}^1$
shows.
$\mathbb {P}^1$
shows.
Proof. We start with
![]() $\mathbb {Z}/n$
-coefficients: By [Reference Scholze35, Proposition 14.9], we have for any
$\mathbb {Z}/n$
-coefficients: By [Reference Scholze35, Proposition 14.9], we have for any
![]() $i\geq 0$
:
$i\geq 0$
:
For
![]() $i=0$
, since each
$i=0$
, since each
![]() $X'$
is connected, this implies
$X'$
is connected, this implies
![]() $H^0(\widetilde X,\mathbb {Z}/n)=\mathbb {Z}/n$
. In the limit over
$H^0(\widetilde X,\mathbb {Z}/n)=\mathbb {Z}/n$
. In the limit over
![]() $n\in \mathbb {N}$
, we get
$n\in \mathbb {N}$
, we get
![]() $H^0(\widetilde X,\widehat {\mathbb {Z}})=\widehat {\mathbb {Z}}$
and similarly for
$H^0(\widetilde X,\widehat {\mathbb {Z}})=\widehat {\mathbb {Z}}$
and similarly for
![]() $\mathbb {Z}_p$
.
$\mathbb {Z}_p$
.
For
![]() $i=1$
, the group
$i=1$
, the group
![]() $H^1_{{\mathrm {\acute {e}t}}}(X',\mathbb {Z}/n)=H^1_{v}(X',\mathbb {Z}/n)$
parametrises the finite étale
$H^1_{{\mathrm {\acute {e}t}}}(X',\mathbb {Z}/n)=H^1_{v}(X',\mathbb {Z}/n)$
parametrises the finite étale
![]() $\mathbb {Z}/n$
-torsors on
$\mathbb {Z}/n$
-torsors on
![]() $X'$
. Since any
$X'$
. Since any
![]() $\mathbb {Z}/n$
-torsor is trivialised by a connected finite étale cover of X, each cohomology class gets killed in the inverse system defining
$\mathbb {Z}/n$
-torsor is trivialised by a connected finite étale cover of X, each cohomology class gets killed in the inverse system defining
![]() $\widetilde X$
. It follows that
$\widetilde X$
. It follows that
Since the v-site is replete, we have
![]() $\mathrm {R}\!\varprojlim \mathbb {Z}/n=\widehat {\mathbb {Z}}$
as sheaves on
$\mathrm {R}\!\varprojlim \mathbb {Z}/n=\widehat {\mathbb {Z}}$
as sheaves on
![]() $X_v$
by [Reference Bhatt and Scholze4, Proposition 3.1.10], so the Grothendieck spectral sequence for
$X_v$
by [Reference Bhatt and Scholze4, Proposition 3.1.10], so the Grothendieck spectral sequence for
![]() $\mathrm {R}\Gamma (\widetilde X,-)\circ \mathrm {R}\!\varprojlim $
yields an exact sequence
$\mathrm {R}\Gamma (\widetilde X,-)\circ \mathrm {R}\!\varprojlim $
yields an exact sequence
The first term vanishes by the first part. The last also vanishes, so
![]() $H^1_{v}(\widetilde X,\widehat {\mathbb {Z}})=0$
as desired.
$H^1_{v}(\widetilde X,\widehat {\mathbb {Z}})=0$
as desired.
The case of
![]() $\mathbb {Z}_p$
-cofficients follows as
$\mathbb {Z}_p$
-cofficients follows as
![]() $\mathbb {Z}_p$
is a direct factor of
$\mathbb {Z}_p$
is a direct factor of
![]() $\widehat {\mathbb {Z}}$
.
$\widehat {\mathbb {Z}}$
.
To see the remaining cases, we can by Example 4.7 assume without loss of generality that
![]() $K=C$
. We then have the primitive comparison theorem [Reference Scholze37, Theorem 3.17], according to which we have for any
$K=C$
. We then have the primitive comparison theorem [Reference Scholze37, Theorem 3.17], according to which we have for any
![]() $i\geq 0$
and
$i\geq 0$
and
![]() $m\geq 0$
and any finite étale cover
$m\geq 0$
and any finite étale cover
![]() $X'\to X$
$X'\to X$
where we use that X is seminormal to identify
![]() $\mathcal {O}^+_{X_{{\mathrm {\acute {e}t}}}}$
and
$\mathcal {O}^+_{X_{{\mathrm {\acute {e}t}}}}$
and
![]() $\mathcal {O}^+_{X^{\diamondsuit }_{{\mathrm {\acute {e}t}}}}$
. For
$\mathcal {O}^+_{X^{\diamondsuit }_{{\mathrm {\acute {e}t}}}}$
. For
![]() $i=0$
, we deduce in the limit that
$i=0$
, we deduce in the limit that
![]() $ H^0(\widetilde X,\mathcal {O}^+)\stackrel {a}{=} \mathcal {O}_K$
. For
$ H^0(\widetilde X,\mathcal {O}^+)\stackrel {a}{=} \mathcal {O}_K$
. For
![]() $i=1$
, we conclude from equation (4.2) applied to
$i=1$
, we conclude from equation (4.2) applied to
![]() $n=p^m$
that
$n=p^m$
that
It then follows from the same
![]() $\mathrm {R}\!\varprojlim $
-argument as above that
$\mathrm {R}\!\varprojlim $
-argument as above that
The case of U follows from the long exact sequence of the logarithm (2.4). The case of
![]() $\mathcal {O}^{\times ,\mathrm {tt}}$
similarly follows from a logarithm sequence modified to include all roots of unity
$\mathcal {O}^{\times ,\mathrm {tt}}$
similarly follows from a logarithm sequence modified to include all roots of unity
![]() $\mu $
:
$\mu $
:
Assume now that
![]() $K=C$
. Our guiding analogy will be that
$K=C$
. Our guiding analogy will be that
![]() $\widetilde X\to X$
behaves like the topological universal cover in complex geometry. We are going to make this precise in the next section, but as a first instance, we recover the statement (cmp. [Reference Scholze36, Theorem 1.2]):
$\widetilde X\to X$
behaves like the topological universal cover in complex geometry. We are going to make this precise in the next section, but as a first instance, we recover the statement (cmp. [Reference Scholze36, Theorem 1.2]):
Corollary 4.11. Let T be the maximal torsionfree abelian pro-p-quotient of
![]() $\pi _1(X,x)$
. Then T is a finite free
$\pi _1(X,x)$
. Then T is a finite free
![]() $\mathbb {Z}_p$
-module, and there is a natural isomorphism
$\mathbb {Z}_p$
-module, and there is a natural isomorphism
Proof. By Proposition 4.9 and Proposition 2.8.1 (Cartan–Leray) for
![]() $\widetilde X\to X$
with
$\widetilde X\to X$
with
![]() $\mathcal F=\mathbb {Z}_p$
, we have
$\mathcal F=\mathbb {Z}_p$
, we have
![]() $\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X,x),\mathbb {Z}_p)=H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Z}_p)$
. The equality follows by applying
$\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X,x),\mathbb {Z}_p)=H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Z}_p)$
. The equality follows by applying
![]() $\operatorname {Hom}(-,\mathbb {Z}_p)$
. It follows that T is finite free as
$\operatorname {Hom}(-,\mathbb {Z}_p)$
. It follows that T is finite free as
![]() $H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Z}_p)$
is finitely generated [Reference Scholze36, Theorem 1.1].
$H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Z}_p)$
is finitely generated [Reference Scholze36, Theorem 1.1].
The relevance of the universal cover
![]() $\widetilde X$
to Theorem 1.2.2a is now the following.
$\widetilde X$
to Theorem 1.2.2a is now the following.
Corollary 4.12. For any
![]() $n\geq 1$
, there is a short exact sequence of pointed sets
$n\geq 1$
, there is a short exact sequence of pointed sets
Proof. This follows from Corollary 2.10 (Cartan–Leray) applied to the pro-finite-étale
![]() $\pi _1(X,x)$
-torsor
$\pi _1(X,x)$
-torsor
![]() $\widetilde X\to X$
and
$\widetilde X\to X$
and
![]() $\mathcal F=\mathcal {O}^{\times }$
and the fact that
$\mathcal F=\mathcal {O}^{\times }$
and the fact that
![]() $\mathcal {O}(\widetilde X)=K$
by Proposition 4.9.
$\mathcal {O}(\widetilde X)=K$
by Proposition 4.9.
We can thus see characters of
![]() $\pi _1(X,x)$
as descent data on the trivial line bundle on
$\pi _1(X,x)$
as descent data on the trivial line bundle on
![]() $\widetilde X$
. This is part of a much more general picture that we study in the next section. For now, the crucial point is that it gives us ‘enough’ v-line bundles in
$\widetilde X$
. This is part of a much more general picture that we study in the next section. For now, the crucial point is that it gives us ‘enough’ v-line bundles in
![]() $\operatorname {Pic}_v(X)$
to generate
$\operatorname {Pic}_v(X)$
to generate
![]() $H^0(X,\widetilde {\Omega }^1_X)$
.
$H^0(X,\widetilde {\Omega }^1_X)$
.
4.4 The proper case
We now have everything in place to finish the remaining case of Theorem 1.2.
Proof of Theorem 1.2.2a.
By passing to connected components, we may without loss of generality assume that X is connected. Fix a base point
![]() $x\in X(K)$
.
$x\in X(K)$
.
Recall from the proof of Theorem 1.2.1 that the term
![]() $H^0(X,\Omega ^1_X)\{-1\}$
arises from the Leray spectral sequence as
$H^0(X,\Omega ^1_X)\{-1\}$
arises from the Leray spectral sequence as
![]() $H^0(X,R^1\nu _{\ast }\mathcal {O}^{\times })$
. We now compare this to the Leray spectral sequence for
$H^0(X,R^1\nu _{\ast }\mathcal {O}^{\times })$
. We now compare this to the Leray spectral sequence for
![]() $\mathcal {O}$
, which we recall gives the Hodge–Tate spectral sequence. By [Reference Bhatt, Morrow and Scholze3, Theorem 13.3.(ii)], the latter degenerates at the
$\mathcal {O}$
, which we recall gives the Hodge–Tate spectral sequence. By [Reference Bhatt, Morrow and Scholze3, Theorem 13.3.(ii)], the latter degenerates at the
![]() $E_2$
-page since X is proper. Consequently,
$E_2$
-page since X is proper. Consequently,
is surjective.
We now compare this to the Cartan–Leray sequences of Proposition 2.8.1 for
![]() $\widetilde X\to X$
. By Proposition 4.9, we have
$\widetilde X\to X$
. By Proposition 4.9, we have
![]() $H^1_v(\widetilde X,\mathcal {O})=0$
. Hence, the Cartan–Leray sequence of
$H^1_v(\widetilde X,\mathcal {O})=0$
. Hence, the Cartan–Leray sequence of
![]() $\mathcal {O}$
is of the form
$\mathcal {O}$
is of the form
Similarly, by Corollary 4.12, there is a contribution of
![]() $ \operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X,x),K^{\times })$
to
$ \operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X,x),K^{\times })$
to
![]() $\operatorname {Pic}_v(X)$
. Passing from
$\operatorname {Pic}_v(X)$
. Passing from
![]() $\mathcal {O}^{\times }$
to
$\mathcal {O}^{\times }$
to
![]() $U=1+\mathfrak {m}\mathcal {O}^+\subseteq \mathcal {O}^{\times }$
, we compare these Cartan–Leray sequences via the logarithm
$U=1+\mathfrak {m}\mathcal {O}^+\subseteq \mathcal {O}^{\times }$
, we compare these Cartan–Leray sequences via the logarithm
![]() $\log :U\to \mathcal {O}$
and get by construction of
$\log :U\to \mathcal {O}$
and get by construction of
![]() $\operatorname {HTlog}$
a commutative diagram
$\operatorname {HTlog}$
a commutative diagram

To prove that
![]() $\operatorname {HTlog}$
is surjective, it thus remains to see that the left vertical map is surjective. To see this, we note that any continuous homomorphism
$\operatorname {HTlog}$
is surjective, it thus remains to see that the left vertical map is surjective. To see this, we note that any continuous homomorphism
![]() $\varphi :\pi _1(X,x)\to K$
factors through the maximal torsionfree abelian pro-p-quotient, which is a finite free
$\varphi :\pi _1(X,x)\to K$
factors through the maximal torsionfree abelian pro-p-quotient, which is a finite free
![]() $\mathbb {Z}_p$
-module by Corollary 4.11. We can thus lift it to a continuous homomorphism
$\mathbb {Z}_p$
-module by Corollary 4.11. We can thus lift it to a continuous homomorphism
since
![]() $\log :1+\mathfrak {m}\to K$
is surjective, K being algebraically closed.
$\log :1+\mathfrak {m}\to K$
is surjective, K being algebraically closed.
5 Application to the p-adic Simpson correspondence
Let K be an algebraically closed complete extension of
![]() $\mathbb {Q}_p$
. Then the proper case of Theorem 1.2.2 is very closely related to the p-adic Simpson correspondence from the pro-étale/v-topological perspective of [Reference Liu and Zhu30, §2][Reference Würthen41, §3][Reference Mann and Werner32, §7]: In this section, we show that Theorem 1.2 can be used to construct the p-adic Simpson correspondence in rank 1.
$\mathbb {Q}_p$
. Then the proper case of Theorem 1.2.2 is very closely related to the p-adic Simpson correspondence from the pro-étale/v-topological perspective of [Reference Liu and Zhu30, §2][Reference Würthen41, §3][Reference Mann and Werner32, §7]: In this section, we show that Theorem 1.2 can be used to construct the p-adic Simpson correspondence in rank 1.
5.1 Overview
In order to provide some context, let us briefly describe a few known results about the p-adic Simpson correspondence. We refer to [Reference Würthen41, §1] for a much more detailed overview.
Let X be a connected proper smooth rigid space over K. Fix a base point
![]() $x\in X(K)$
. Inspired by the complex Corlette–Simpson correspondence [Reference Simpson40], the p-adic Simpson correspondence pioneered independently by Deninger–Werner [Reference Deninger and Werner15] and Faltings [Reference Faltings17] is a conjectural equivalence between the category
$x\in X(K)$
. Inspired by the complex Corlette–Simpson correspondence [Reference Simpson40], the p-adic Simpson correspondence pioneered independently by Deninger–Werner [Reference Deninger and Werner15] and Faltings [Reference Faltings17] is a conjectural equivalence between the category
![]() $\mathrm {Rep}_{K}(\pi _1(X,x))$
of continuous representations
$\mathrm {Rep}_{K}(\pi _1(X,x))$
of continuous representations
on finite dimensional K-vector spaces W, and a certain subcategory of the Higgs bundles on X, yet to be identified. Here by a Higgs bundle we shall mean a pair
![]() $(E,\theta )$
of an analytic vector bundle E on X together with a
$(E,\theta )$
of an analytic vector bundle E on X together with a
![]() $1$
-form
$1$
-form
![]() $\theta \in H^0(X,\operatorname {End}(E)\otimes \widetilde {\Omega }_X^1)$
satisfying
$\theta \in H^0(X,\operatorname {End}(E)\otimes \widetilde {\Omega }_X^1)$
satisfying
![]() $\theta \wedge \theta =0$
. Such
$\theta \wedge \theta =0$
. Such
![]() $\theta $
are called Higgs fields. We recall that
$\theta $
are called Higgs fields. We recall that
![]() $\widetilde {\Omega }_X^1:=\Omega ^1_X(-1)$
, where the
$\widetilde {\Omega }_X^1:=\Omega ^1_X(-1)$
, where the
![]() $(-1)$
is a Tate twist; it is natural to include it in this context since it appears in the p-adic Hodge–Tate sequence.
$(-1)$
is a Tate twist; it is natural to include it in this context since it appears in the p-adic Hodge–Tate sequence.
In the case that
![]() $K=\mathbb {C}_p$
and X is algebraic and defined over a finite extension of
$K=\mathbb {C}_p$
and X is algebraic and defined over a finite extension of
![]() $\mathbb {Q}_p$
, Deninger–Werner have identified a category
$\mathbb {Q}_p$
, Deninger–Werner have identified a category
![]() $\mathcal B^s(X_{\mathbb {C}_p})$
of algebraic vector bundles V with ‘numerically flat reduction’ for which they can construct a functor [Reference Deninger and Werner16, §9-§10]
$\mathcal B^s(X_{\mathbb {C}_p})$
of algebraic vector bundles V with ‘numerically flat reduction’ for which they can construct a functor [Reference Deninger and Werner16, §9-§10]
generalising their earlier work in the case of curves [Reference Deninger and Werner15, Theorem 1.1]. This gives the desired functor in the case of vanishing Higgs field, that is,
![]() $\theta =0$
.
$\theta =0$
.
Würthen has recently extended this to the setting of proper connected seminormal rigid analytic varieties over
![]() $\mathbb {C}_p$
, for which he constructs a fully faithful functor on analytic vector bundles E [Reference Würthen41, Theorem 1.1]. Moreover, he shows that the condition of numerically flat reduction implies that E is trivialised by a pro-finite-étale cover of X [Reference Würthen41, Proposition 4.13]. Passing from the analytic to the v-topology, Mann–Werner [Reference Mann and Werner32, Theorem 0.1] extend this to v-vector bundles and show that the condition of numerically flat reduction can be checked on proper covers. They then set up an equivalence of categories of such v-vector bundles to those
$\mathbb {C}_p$
, for which he constructs a fully faithful functor on analytic vector bundles E [Reference Würthen41, Theorem 1.1]. Moreover, he shows that the condition of numerically flat reduction implies that E is trivialised by a pro-finite-étale cover of X [Reference Würthen41, Proposition 4.13]. Passing from the analytic to the v-topology, Mann–Werner [Reference Mann and Werner32, Theorem 0.1] extend this to v-vector bundles and show that the condition of numerically flat reduction can be checked on proper covers. They then set up an equivalence of categories of such v-vector bundles to those
![]() $\mathbb {C}_p$
-local systems on X that arise from
$\mathbb {C}_p$
-local systems on X that arise from
![]() $\mathcal {O}_{\mathbb {C}_p}$
-local systems by inverting p.
$\mathcal {O}_{\mathbb {C}_p}$
-local systems by inverting p.
In an independent line of research, for algebraic X that have an integral model with toroidal singularities over a complete discrete valuation ring, Faltings constructed an equivalence of categories from ‘small’ Higgs bundles to a category of ‘small generalised representations’ [Reference Faltings17, Theorem 5]. Here generalised representations form a category into which representations of
![]() $\pi _1(X,x)$
embed fully faithfully. He then proved that the smallness assumption can be removed for curves [Reference Faltings17, Theorem 6]. This construction was further developed by Abbes–Gros and Tsuji [Reference Abbes, Gros and Tsuji1]. However, towards a p-adic Simpson correspondence, it is currently not known which Higgs bundles correspond to actual representations of
$\pi _1(X,x)$
embed fully faithfully. He then proved that the smallness assumption can be removed for curves [Reference Faltings17, Theorem 6]. This construction was further developed by Abbes–Gros and Tsuji [Reference Abbes, Gros and Tsuji1]. However, towards a p-adic Simpson correspondence, it is currently not known which Higgs bundles correspond to actual representations of
![]() $\pi _1(X,x)$
.
$\pi _1(X,x)$
.
Reinterpreting these objects in the setting of Scholze’s p-adic Hodge theory, Liu–Zhu were able to define a functor from
![]() $\mathbb {Q}_p$
-local systems on any smooth rigid space defined over a finite extension of
$\mathbb {Q}_p$
-local systems on any smooth rigid space defined over a finite extension of
![]() $\mathbb {Q}_p$
to nilpotent Higgs bundles [Reference Liu and Zhu30, Theorem 2.1, Remark 2.6]. But it is not clear how this can be extended to a functor on all of
$\mathbb {Q}_p$
to nilpotent Higgs bundles [Reference Liu and Zhu30, Theorem 2.1, Remark 2.6]. But it is not clear how this can be extended to a functor on all of
![]() $\mathrm {Rep}_{K}(\pi _1(X,x))$
.
$\mathrm {Rep}_{K}(\pi _1(X,x))$
.
Despite these many recent advances, a construction of a more general functor either from Higgs bundles beyond the case of
![]() $\theta =0$
or from all K-linear representations beyond small or
$\theta =0$
or from all K-linear representations beyond small or
![]() $\mathbb {Q}_p$
-representations has not been found yet.
$\mathbb {Q}_p$
-representations has not been found yet.
5.2 Pro-finite-étale vector bundles via the universal cover
The aim of this section is to construct the p-adic Simpson correspondence of rank
![]() $1$
in full generality, that is, for smooth proper rigid spaces defined over any algebraically closed non-Archimedean extension K of
$1$
in full generality, that is, for smooth proper rigid spaces defined over any algebraically closed non-Archimedean extension K of
![]() $\mathbb {Q}_p$
. Here we note that in rank
$\mathbb {Q}_p$
. Here we note that in rank
![]() $1$
, a Higgs bundle is simply a pair
$1$
, a Higgs bundle is simply a pair
![]() $(L, \theta )$
of an analytic line bundle L on X and a global differential
$(L, \theta )$
of an analytic line bundle L on X and a global differential
![]() $\theta \in H^0(X,\widetilde {\Omega }^1)$
, which is automatically a Higgs field. The basic idea is that by Theorem 1.2.2a, Higgs bundles of rank
$\theta \in H^0(X,\widetilde {\Omega }^1)$
, which is automatically a Higgs field. The basic idea is that by Theorem 1.2.2a, Higgs bundles of rank
![]() $1$
are essentially the v-line bundles, at least after certain choices. Under this correspondence, the condition of vanishing Chern classes in the complex case is replaced by the following.
$1$
are essentially the v-line bundles, at least after certain choices. Under this correspondence, the condition of vanishing Chern classes in the complex case is replaced by the following.
Definition 5.1. We say that a v-vector bundle on X is pro-finite-étale if it is trivialised by a pro-finite-étale cover of X. Equivalently, it is trivialised by the universal cover
![]() $\widetilde X\to X$
from Definition 4.6. We denote by
$\widetilde X\to X$
from Definition 4.6. We denote by
![]() $\operatorname {Pic}_{\mathrm {prof\acute {e}t}}(X)\subseteq \operatorname {Pic}_v(X)$
the subgroup of pro-finite-étale line bundles and by
$\operatorname {Pic}_{\mathrm {prof\acute {e}t}}(X)\subseteq \operatorname {Pic}_v(X)$
the subgroup of pro-finite-étale line bundles and by
![]() $\operatorname {Pic}_{\mathrm {prof\acute {e}t},\mathrm {an}}(X)$
its intersection with
$\operatorname {Pic}_{\mathrm {prof\acute {e}t},\mathrm {an}}(X)$
its intersection with
![]() $\operatorname {Pic}_{\mathrm {an}}(X)$
.
$\operatorname {Pic}_{\mathrm {an}}(X)$
.
We call a Higgs bundle
![]() $(E,\theta )$
pro-finite-étale if E is pro-finite-étale.
$(E,\theta )$
pro-finite-étale if E is pro-finite-étale.
The first step in the complex Simpson correspondence is to associate to any finite-dimensional complex representation of the fundamental group of a compact Kähler manifold a holomorphic vector bundle that becomes trivial on the topological universal cover. Using the p-adic universal cover
![]() $q:\widetilde X\to X$
of Definition 4.6, we get an analogous construction:
$q:\widetilde X\to X$
of Definition 4.6, we get an analogous construction:
Theorem 5.2. Let X be a connected seminormal proper rigid space over K. Fix
![]() $x\in X(K)$
. Then the universal cover
$x\in X(K)$
. Then the universal cover
![]() $\widetilde X\to X$
induces an exact equivalence of tensor categories
$\widetilde X\to X$
induces an exact equivalence of tensor categories

where the v-vector bundle
![]() $V_{\rho }$
on X associated to
$V_{\rho }$
on X associated to
![]() $\rho $
is defined on
$\rho $
is defined on
![]() $Y\in X_v$
by
$Y\in X_v$
by
Proof. By Lemma 4.8, the right-hand side are precisely the v-vector bundles trivialised by the v-cover
![]() $\widetilde X\to X$
. By Lemma 2.6, these correspond to descent data on trivial vector bundles on
$\widetilde X\to X$
. By Lemma 2.6, these correspond to descent data on trivial vector bundles on
![]() $\widetilde X$
. By Proposition 4.9, trivial vector bundles on
$\widetilde X$
. By Proposition 4.9, trivial vector bundles on
![]() $\widetilde X$
are equivalent to finite-dimensional K-vector spaces via the functor
$\widetilde X$
are equivalent to finite-dimensional K-vector spaces via the functor
![]() $W\mapsto W\otimes _K\mathcal {O}_{\widetilde X}$
. The desired equivalence now follows from Corollary 2.10 which implies that descent data on
$W\mapsto W\otimes _K\mathcal {O}_{\widetilde X}$
. The desired equivalence now follows from Corollary 2.10 which implies that descent data on
![]() $W\otimes _K\mathcal {O}_{\widetilde X}$
are equivalent to continuous representations
$W\otimes _K\mathcal {O}_{\widetilde X}$
are equivalent to continuous representations
![]() $\rho :\pi _1(X,x)\to \operatorname {GL}(W)$
by sending
$\rho :\pi _1(X,x)\to \operatorname {GL}(W)$
by sending
![]() $\rho $
to
$\rho $
to
![]() $V_{\rho }$
.
$V_{\rho }$
.
To see that
![]() $V\mapsto V(\widetilde X)$
defines a quasi-inverse, observe that via
$V\mapsto V(\widetilde X)$
defines a quasi-inverse, observe that via
![]() $\widetilde X\times _X\widetilde X=\pi _1(X,x)\times \widetilde X$
,
$\widetilde X\times _X\widetilde X=\pi _1(X,x)\times \widetilde X$
,
Via the evaluation at
![]() $0$
, this is in natural bijection with W, as we wanted to see.
$0$
, this is in natural bijection with W, as we wanted to see.
It is clear that both functors are exact and preserve tensors: Indeed, whether a sequence on X is exact can be checked on
![]() $\widetilde X$
, where it is exact if and only if it is on global sections.
$\widetilde X$
, where it is exact if and only if it is on global sections.
Remark 5.3. Restricting to pro-finite-étale analytic vector bundles on the right-hand side recovers the fully faithful functor of Würthen [Reference Würthen41, Theorems 3.10 and 3.14]. In this sense, Theorem 5.2 explains how this functor can be extended to an equivalence of categories.
Remark 5.4. The same argument for
![]() $\operatorname {GL}_n(\mathcal {O})$
replaced by
$\operatorname {GL}_n(\mathcal {O})$
replaced by
![]() $\operatorname {GL}_n(\mathcal {O}^+)$
shows that v-locally free
$\operatorname {GL}_n(\mathcal {O}^+)$
shows that v-locally free
![]() $\mathcal {O}^+$
-modules can be interpreted as the ‘generalised representations’ of rank n in the sense of [Reference Faltings17, §2]; This has also been observed by Liu–Zhu [Reference Liu and Zhu30, Remark 2.6].
$\mathcal {O}^+$
-modules can be interpreted as the ‘generalised representations’ of rank n in the sense of [Reference Faltings17, §2]; This has also been observed by Liu–Zhu [Reference Liu and Zhu30, Remark 2.6].
We now apply this to formulate a p-adic Simpson correspondence in rank one. For this it is desirable to characterise pro-finite-étale line bundles on X in a more explicit way.
Definition 5.5. A v-line bundle L on X is topologically torsion if L is in the image of
where
![]() $\mathcal {O}^{\times ,\mathrm {tt}}\subseteq \mathcal {O}^{\times }$
is the topological torsion subsheaf of Definition 2.14. We denote the image of this map by
$\mathcal {O}^{\times ,\mathrm {tt}}\subseteq \mathcal {O}^{\times }$
is the topological torsion subsheaf of Definition 2.14. We denote the image of this map by
![]() $\operatorname {Pic}_v^{\mathrm {tt}}(X)$
and by
$\operatorname {Pic}_v^{\mathrm {tt}}(X)$
and by
![]() $\operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
the intersection of
$\operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
the intersection of
![]() $\operatorname {Pic}_v^{\mathrm {tt}}(X)$
with
$\operatorname {Pic}_v^{\mathrm {tt}}(X)$
with
![]() $\operatorname {Pic}_{\mathrm {an}}(X)$
.
$\operatorname {Pic}_{\mathrm {an}}(X)$
.
Example 5.6. We will show in [Reference Heuer23, §3] that
![]() $\operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
is precisely the topological torsion subgroup of
$\operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
is precisely the topological torsion subgroup of
![]() $\operatorname {Pic}_{\mathrm {an}}(X)$
endowed with its natural topology as K-points of the rigid analytic Picard variety. If X is projective with torsionfree Néron–Severi group and
$\operatorname {Pic}_{\mathrm {an}}(X)$
endowed with its natural topology as K-points of the rigid analytic Picard variety. If X is projective with torsionfree Néron–Severi group and
![]() $K=\mathbb {C}_p$
, this happens to equal
$K=\mathbb {C}_p$
, this happens to equal
![]() $\operatorname {Pic}_{\mathrm {an}}^0(X)$
, but this is no longer true for any nontrivial extension of K.
$\operatorname {Pic}_{\mathrm {an}}^0(X)$
, but this is no longer true for any nontrivial extension of K.
For example, if X is an abelian variety with good reduction
![]() $\overline {X}$
over k, let
$\overline {X}$
over k, let
![]() $X^{\vee }$
be the dual abelian variety with its reduction
$X^{\vee }$
be the dual abelian variety with its reduction
![]() $\overline {X}^{\vee }$
. Then
$\overline {X}^{\vee }$
. Then
![]() $\operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
is precisely the preimage of the torsion subgroup of
$\operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
is precisely the preimage of the torsion subgroup of
![]() $\overline {X}^{\vee }(k)$
under the specialisation map
$\overline {X}^{\vee }(k)$
under the specialisation map
![]() $\operatorname {Pic}^0(X)=X^{\vee }(K)\to \overline {X}^{\vee }(k)$
.
$\operatorname {Pic}^0(X)=X^{\vee }(K)\to \overline {X}^{\vee }(k)$
.
5.3 The p-adic Simpson correspondence for line bundles
We can now give our second main application of Theorem 1.2.
Theorem 5.7 (p-adic Simpson correspondence of rank one).
Let X be a connected smooth proper rigid space over K. Fix a base point
![]() $x\in X(K)$
.
$x\in X(K)$
.
-
1. There is a short exact sequence, functorial in X,
 $$\begin{align*}0\to \operatorname{Pic}_{\mathrm{prof\acute{e}t},\mathrm{an}}(X)\to \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1(X,x),K^{\times})\to H^0(X,\widetilde{\Omega}_X^1)\to 0. \end{align*}$$
$$\begin{align*}0\to \operatorname{Pic}_{\mathrm{prof\acute{e}t},\mathrm{an}}(X)\to \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1(X,x),K^{\times})\to H^0(X,\widetilde{\Omega}_X^1)\to 0. \end{align*}$$
-
2. Any choice of a splitting of
 $\log \colon 1+\mathfrak {m}\to K$
as well as a splitting of the Hodge–Tate sequence define an equivalence of tensor categories
$\log \colon 1+\mathfrak {m}\to K$
as well as a splitting of the Hodge–Tate sequence define an equivalence of tensor categories 
-
3. We have
 $\operatorname {Pic}_{\mathrm {prof\acute {e}t},\mathrm {an}}(X)= \operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
, so the right-hand side can equivalently be described as the topological torsion Higgs bundles.
$\operatorname {Pic}_{\mathrm {prof\acute {e}t},\mathrm {an}}(X)= \operatorname {Pic}_{\mathrm {an}}^{\mathrm {tt}}(X)$
, so the right-hand side can equivalently be described as the topological torsion Higgs bundles.
In particular, this singles out pro-finite-étale Higgs line bundles as the desired subcategory for the Simpson correspondence in rank
![]() $1$
. Before we discuss the proof, we make some remarks on how this relates to the works discussed in the last subsection.
$1$
. Before we discuss the proof, we make some remarks on how this relates to the works discussed in the last subsection.
Remark 5.8. The choices made in Theorem 5.7.2 are essentially the same as the ones made by Faltings in his construction of a p-adic Simpson correspondence for small generalised representations: The only difference is that, in the generality we work in, one needs to choose a splitting of the Hodge–Tate sequence. There is a canonical such splitting if X is defined over a discretely valued non-Archimedean extension of
![]() $\mathbb {Q}_p$
[Reference Scholze36, Corollary 1.8], which is part of the assumption of Faltings’ setup. In our setup, since X is quasi-compact, a choice of splitting is induced by a choice of lifting of X to
$\mathbb {Q}_p$
[Reference Scholze36, Corollary 1.8], which is part of the assumption of Faltings’ setup. In our setup, since X is quasi-compact, a choice of splitting is induced by a choice of lifting of X to
![]() $B_{\mathrm {dR}}^+(K)/\xi ^2$
, which also appears in Faltings’ work. This lift is arguably a ‘better’ choice than that of a splitting of the map
$B_{\mathrm {dR}}^+(K)/\xi ^2$
, which also appears in Faltings’ work. This lift is arguably a ‘better’ choice than that of a splitting of the map
![]() $\operatorname {HT}$
, as the equivalence then becomes functorial in rigid spaces with a choice of lift.
$\operatorname {HT}$
, as the equivalence then becomes functorial in rigid spaces with a choice of lift.
Remark 5.9. We note that the ‘topological torsion’ condition is strictly weaker than the ‘smallness’ condition imposed by Faltings in [Reference Faltings17, §2].
Remark 5.10. For an analytic line bundle L on X, the condition
![]() $L\in \operatorname {Pic}_{\mathrm {prof\acute {e}t},\mathrm {an}}(X)$
means precisely that L is in the category
$L\in \operatorname {Pic}_{\mathrm {prof\acute {e}t},\mathrm {an}}(X)$
means precisely that L is in the category
![]() $\mathcal B^{\mathrm {p\acute {e}t}}(\mathcal {O}_X)$
of ‘trivialisable’ analytic vector bundles in the sense of [Reference Würthen41, Theorem 3.10]. But we explicitly also include the case of general
$\mathcal B^{\mathrm {p\acute {e}t}}(\mathcal {O}_X)$
of ‘trivialisable’ analytic vector bundles in the sense of [Reference Würthen41, Theorem 3.10]. But we explicitly also include the case of general
![]() $\theta $
.
$\theta $
.
Remark 5.11. If X is algebraic, L is analytic and
![]() $K=\mathbb {C}_p$
, then one can show that the condition from part 3 is equivalent to L having numerically flat reduction in the sense of Deninger–Werner, using [Reference Würthen41, Proposition 4.13]. In this light, Theorem 5.7 confirms at least in rank
$K=\mathbb {C}_p$
, then one can show that the condition from part 3 is equivalent to L having numerically flat reduction in the sense of Deninger–Werner, using [Reference Würthen41, Proposition 4.13]. In this light, Theorem 5.7 confirms at least in rank
![]() $1$
that this is the correct replacement for the complex condition of being ‘semistable with vanishing Chern classes’, also beyond the case of vanishing Higgs fields.
$1$
that this is the correct replacement for the complex condition of being ‘semistable with vanishing Chern classes’, also beyond the case of vanishing Higgs fields.
Remark 5.12. More generally, Theorem 5.2 suggests that pro-finite-étale Higgs bundles are a promising step towards the correct subcategory for the p-adic Simpson correspondence. In particular, this would mean that the functor constructed in [Reference Mann and Werner32] is already the correct functor from Higgs bundles to local systems. We will pursue this further in future work.
Proof of Theorem 5.7.
The first part follows from Theorem 1.2.2a and Corollary 4.12: We only need to see that the composition
is surjective. But this follows from diagram (4.3) in the proof of Theorem 1.2.2a.
To deduce the second part, we first note that the choices made induce a splitting s of
In particular, they define a splitting of the sequence in part 1. This gives a bijection between isomorphism classes. In order to upgrade this to an equivalence of categories, we use the equivalence of Theorem 5.2: This shows that it suffices to construct a tensor equivalence

To define this, we first observe that to any Higgs bundle
![]() $(E,\theta )$
, the splitting s associates a character
$(E,\theta )$
, the splitting s associates a character
![]() $s(\theta ):\pi _1(X,x)\to K^{\times }$
to which Theorem 5.2 attaches a v-line bundle
$s(\theta ):\pi _1(X,x)\to K^{\times }$
to which Theorem 5.2 attaches a v-line bundle
![]() $L_{\theta }$
. We now define the functor by sending
$L_{\theta }$
. We now define the functor by sending
This is indeed functorial as any morphism of Higgs line bundles
![]() $(E_1,\theta _1)\to (E_2,\theta _2)$
is trivial unless
$(E_1,\theta _1)\to (E_2,\theta _2)$
is trivial unless
![]() $\theta _1=\theta _2$
, in which case it is simply the datum of a morphism
$\theta _1=\theta _2$
, in which case it is simply the datum of a morphism
![]() $E_1\to E_2$
.
$E_1\to E_2$
.
A quasi-inverse can be defined as follows: Let E be any pro-finite-étale v-line bundle on X, and let
![]() $\theta (E)\in H^0(X,\widetilde {\Omega }^1_X)$
be the image of the isomorphism class of E under
$\theta (E)\in H^0(X,\widetilde {\Omega }^1_X)$
be the image of the isomorphism class of E under
![]() $\operatorname {HTlog}$
. Then we define a functor by
$\operatorname {HTlog}$
. Then we define a functor by
where the line bundle is analytic by left-exactness of the sequence in Theorem 1.2.
This is also functorial, for trivial reasons: For any two pro-finite-étale line bundles
![]() $L,L'$
, the line bundle of endomorphisms
$L,L'$
, the line bundle of endomorphisms
![]() $L'\otimes L^{-1}$
pulls back to the trivial bundle along
$L'\otimes L^{-1}$
pulls back to the trivial bundle along
![]() $\widetilde X\to X$
because
$\widetilde X\to X$
because
![]() $L'$
and L do. Since
$L'$
and L do. Since
![]() $\mathcal {O}(\widetilde X)=K$
, it follows that
$\mathcal {O}(\widetilde X)=K$
, it follows that
 $$\begin{align*}H^0(X,L'\otimes L^{-1})=H^0(\widetilde X,L'\otimes L^{-1})^{\pi_1(X,x)}\cong \begin{cases} K&\text{if } L'\cong L,\\ 0 & \text{otherwise.} \end{cases} \\[-15pt]\end{align*}$$
$$\begin{align*}H^0(X,L'\otimes L^{-1})=H^0(\widetilde X,L'\otimes L^{-1})^{\pi_1(X,x)}\cong \begin{cases} K&\text{if } L'\cong L,\\ 0 & \text{otherwise.} \end{cases} \\[-15pt]\end{align*}$$
We have thus constructed the desired equivalence of categories. That this is a tensor equivalence follows from the linearity of the section s, which implies that
It remains to prove part 3. This is achieved by the following lemma.
Lemma 5.13. Inside
![]() $\operatorname {Pic}_v(X)$
, we have
$\operatorname {Pic}_v(X)$
, we have
![]() $\operatorname {Pic}_v^{\mathrm {tt}}(X)=\operatorname {Pic}_{\mathrm {prof\acute {e}t}}(X)$
.
$\operatorname {Pic}_v^{\mathrm {tt}}(X)=\operatorname {Pic}_{\mathrm {prof\acute {e}t}}(X)$
.
Proof. For the inclusion
![]() $\supseteq $
, we use that any continuous homomorphism
$\supseteq $
, we use that any continuous homomorphism
![]() $\pi _1(X,x)\to K^{\times }$
factors through
$\pi _1(X,x)\to K^{\times }$
factors through
![]() $\mathcal {O}^{\times ,\mathrm {tt}}(K)$
. Comparing Cartan–Leray sequences, we get a commutative diagram
$\mathcal {O}^{\times ,\mathrm {tt}}(K)$
. Comparing Cartan–Leray sequences, we get a commutative diagram

By Corollary 4.12, the image of the bottom-left map is precisely
![]() $\operatorname {Pic}_{\mathrm {prof\acute {e}t}}(X)$
. The diagram shows that this is included in the image of the map in the middle, which is precisely
$\operatorname {Pic}_{\mathrm {prof\acute {e}t}}(X)$
. The diagram shows that this is included in the image of the map in the middle, which is precisely
![]() $\operatorname {Pic}_v^{\mathrm {tt}}(X)$
.
$\operatorname {Pic}_v^{\mathrm {tt}}(X)$
.
By the same diagram, the inclusion
![]() $\subseteq $
holds as
$\subseteq $
holds as
![]() $H^1_v(\widetilde X,\mathcal {O}^{\times ,\mathrm {tt}})=1$
by Proposition 4.9.
$H^1_v(\widetilde X,\mathcal {O}^{\times ,\mathrm {tt}})=1$
by Proposition 4.9.
6 The v-Picard group of affine space
 $\mathbb {A}^n$
$\mathbb {A}^n$
By the Theorem of Quillen–Suslin, every vector bundle on
![]() $\operatorname {Spec}(K[X_1,\dots ,X_n])$
is trivial. Similarly, every analytic vector bundle on the rigid affine space
$\operatorname {Spec}(K[X_1,\dots ,X_n])$
is trivial. Similarly, every analytic vector bundle on the rigid affine space
![]() $\mathbb {A}^n$
is trivial [Reference Gruson19, §V.3 Proposition 2.(ii)]. This is no longer true in the v-topology. In this final section, we prove:
$\mathbb {A}^n$
is trivial [Reference Gruson19, §V.3 Proposition 2.(ii)]. This is no longer true in the v-topology. In this final section, we prove:
Theorem 6.1. For any
![]() $n\in \mathbb {N}$
, the Hodge–Tate logarithm induces an isomorphism
$n\in \mathbb {N}$
, the Hodge–Tate logarithm induces an isomorphism
More generally, for
![]() $k\geq 0$
and
$k\geq 0$
and
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
![]() $\operatorname {Pic}_v(\mathbb {G}_m^k\times \mathbb {A}^n)=H^0(\mathbb {G}_m^k\times \mathbb {A}^n,\widetilde {\Omega }^1)^{d=0}$
.
$\operatorname {Pic}_v(\mathbb {G}_m^k\times \mathbb {A}^n)=H^0(\mathbb {G}_m^k\times \mathbb {A}^n,\widetilde {\Omega }^1)^{d=0}$
.
Remark 6.2. We are interested in the case of
![]() $\mathbb {G}_m\times \mathbb {A}$
since its de Rham complex is no longer exact on global sections. This shows that we should really think of line bundles as living in
$\mathbb {G}_m\times \mathbb {A}$
since its de Rham complex is no longer exact on global sections. This shows that we should really think of line bundles as living in
![]() $(\widetilde {\Omega }^1)^{d=0}$
rather than
$(\widetilde {\Omega }^1)^{d=0}$
rather than
![]() $d(\mathcal {O})$
.
$d(\mathcal {O})$
.
Definition 6.3. We denote by
![]() $B^n=\operatorname {Spa}(K\langle T_1,\dots ,T_n\rangle )\subseteq \mathbb {A}^n$
the closed unit ball. For any
$B^n=\operatorname {Spa}(K\langle T_1,\dots ,T_n\rangle )\subseteq \mathbb {A}^n$
the closed unit ball. For any
![]() $s\in |K|$
, denote by
$s\in |K|$
, denote by
![]() $B_s^n\subseteq \mathbb {A}^n$
the closed ball defined by
$B_s^n\subseteq \mathbb {A}^n$
the closed ball defined by
![]() $|T_i|\leq s$
for all
$|T_i|\leq s$
for all
![]() $i=1,\dots ,n$
.
$i=1,\dots ,n$
.
We often use that
![]() $B_s^n\cong B^n$
by rescaling. In particular,
$B_s^n\cong B^n$
by rescaling. In particular,
![]() $\operatorname {Pic}_{\mathrm {an}}(B_s^n)=1$
by [Reference Lütkebohmert31, Satz 1].
$\operatorname {Pic}_{\mathrm {an}}(B_s^n)=1$
by [Reference Lütkebohmert31, Satz 1].
Corollary 6.4. In contrast to Theorem 1.2.2, the map
![]() $\operatorname {HTlog}:\operatorname {Pic}_v(B^n)\to H^0(B^n,\widetilde {\Omega }^1)$
is no longer surjective for
$\operatorname {HTlog}:\operatorname {Pic}_v(B^n)\to H^0(B^n,\widetilde {\Omega }^1)$
is no longer surjective for
![]() $n\geq 2$
.
$n\geq 2$
.
Proof. If it was, it would be an isomorphism. Covering
![]() $\mathbb {A}^n$
by the
$\mathbb {A}^n$
by the
![]() $B^n_s$
, this shows
$B^n_s$
, this shows
where the first isomorphism uses
![]() $\operatorname {Pic}_{\mathrm {an}}(\mathbb {A}^n)=1$
. This is a contradiction to Theorem 6.1.
$\operatorname {Pic}_{\mathrm {an}}(\mathbb {A}^n)=1$
. This is a contradiction to Theorem 6.1.
Remark 6.5. This is interesting in the context of the p-adic Simpson correspondence since it gives a concrete example in which we cannot have an equivalence between v-line bundles and Higgs bundles like in the proper case: Faltings ‘local p-adic Simpson correspondence’ shows that one can always obtain an equivalence between small v-bundles and small Higgs bundles, where ‘small’ is a technical term that roughly means ‘p-adically close to
![]() $0$
’. Since any such correspondence should be compatible with localisation, in particular with
$0$
’. Since any such correspondence should be compatible with localisation, in particular with
![]() $\operatorname {HTlog}$
, the Corollary shows that, for
$\operatorname {HTlog}$
, the Corollary shows that, for
![]() $B^n$
, the equivalence does not extend beyond the small case.
$B^n$
, the equivalence does not extend beyond the small case.
We will give two different proofs of the first part of Theorem 6.1: The first relies on a comparison to Le Bras’s result about
![]() $\mathrm {R}\Gamma _{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,\mathbb {Q}_p)$
using the Poincaré lemma in
$\mathrm {R}\Gamma _{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,\mathbb {Q}_p)$
using the Poincaré lemma in
![]() $X_{\mathrm {pro\acute {e}t}}$
. We note that, in general, this restricts the setup to K being the completion of an algebraic closure of a discretely valued field. The second proof is self-contained and uses rigid analytic computations. It is slightly more general as it does not require the Poincaré lemma.
$X_{\mathrm {pro\acute {e}t}}$
. We note that, in general, this restricts the setup to K being the completion of an algebraic closure of a discretely valued field. The second proof is self-contained and uses rigid analytic computations. It is slightly more general as it does not require the Poincaré lemma.
6.1 Preparations
Lemma 6.6. Let
![]() $n\geq 1$
. Let Y be any diamond over
$n\geq 1$
. Let Y be any diamond over
![]() $\operatorname {Spa}(K)$
. Then
$\operatorname {Spa}(K)$
. Then
Proof. For the first identity, we can by induction assume
![]() $n=1$
. Since
$n=1$
. Since
![]() $\overline {\mathcal {O}}^{\times }$
is a v-sheaf, it suffices to prove the statement for
$\overline {\mathcal {O}}^{\times }$
is a v-sheaf, it suffices to prove the statement for
![]() $Y=\operatorname {Spa}(R,R^+)$
an affinoid perfectoid space. Then
$Y=\operatorname {Spa}(R,R^+)$
an affinoid perfectoid space. Then
![]() $\mathcal {O}(Y\times B)=R\langle T\rangle $
and we need to prove that, for any
$\mathcal {O}(Y\times B)=R\langle T\rangle $
and we need to prove that, for any
![]() $f\in R\langle T\rangle ^{\times }$
of the form
$f\in R\langle T\rangle ^{\times }$
of the form
![]() $f=1+a_1T+a_2T^2+\dots $
, we have
$f=1+a_1T+a_2T^2+\dots $
, we have
![]() $a_i\in \mathfrak {m} R^+=R^{\circ \circ }$
for all
$a_i\in \mathfrak {m} R^+=R^{\circ \circ }$
for all
![]() $i\geq 1$
. We can check this on points of Y, which reduces us to the case of
$i\geq 1$
. We can check this on points of Y, which reduces us to the case of
![]() $(R,R^+)=(C,C^+)$
a field. Since
$(R,R^+)=(C,C^+)$
a field. Since
![]() $\mathfrak {m} C^+=\mathfrak {m}\mathcal {O}_C$
, we can reduce to
$\mathfrak {m} C^+=\mathfrak {m}\mathcal {O}_C$
, we can reduce to
![]() $C^+=\mathcal {O}_C$
, where the statement is classical; see [Reference Bosch, Güntzer and Remmert7, §5.3.1 Proposition 1].
$C^+=\mathcal {O}_C$
, where the statement is classical; see [Reference Bosch, Güntzer and Remmert7, §5.3.1 Proposition 1].
For the second part, Lemma 2.22.2 reduces to showing
![]() $H^1_{{\mathrm {\acute {e}t}}}(B^n,\overline {\mathcal {O}}^{\times })=1$
. This follows from the exponential sequence (2.5) as
$H^1_{{\mathrm {\acute {e}t}}}(B^n,\overline {\mathcal {O}}^{\times })=1$
. This follows from the exponential sequence (2.5) as
![]() $\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B^n)=1$
and
$\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B^n)=1$
and
![]() $H^2_{{\mathrm {\acute {e}t}}}(B^n,\mathcal {O})=0$
.
$H^2_{{\mathrm {\acute {e}t}}}(B^n,\mathcal {O})=0$
.
Lemma 6.7. For any
![]() $n\geq 1$
, we have
$n\geq 1$
, we have
![]() $H^1_v(\mathbb {A}^n,U)= H^1_v(\mathbb {A}^n,\mathcal {O}^{\times })$
.
$H^1_v(\mathbb {A}^n,U)= H^1_v(\mathbb {A}^n,\mathcal {O}^{\times })$
.
Proof. It suffices to prove that the second and fourth map in the long exact sequence
are trivial. This follows from Lemma 6.6 by the Čech-to-sheaf sequence of
![]() $\mathbb {A}^n=\cup _{s\in \mathbb {N}} B_s^n$
.
$\mathbb {A}^n=\cup _{s\in \mathbb {N}} B_s^n$
.
6.2 Proof via comparison to pro-étale cohomology
In this section, let us assume that
![]() $K=\mathbb {C}_p$
. Then Theorem 6.1 is closely related to a result of Colmez–Nizioł [Reference Colmez and Nizioł11], and independently of Le Bras [Reference Le Bras28], who both show:
$K=\mathbb {C}_p$
. Then Theorem 6.1 is closely related to a result of Colmez–Nizioł [Reference Colmez and Nizioł11], and independently of Le Bras [Reference Le Bras28], who both show:
Theorem 6.8 [Reference Colmez and Nizioł11, Theorem 1], [Reference Le Bras28, Théorème 3.2].
Over
![]() $\mathbb {C}_p$
, we have for all
$\mathbb {C}_p$
, we have for all
![]() $i\geq 1$
:
$i\geq 1$
:
In this subsection, we explain how Le Bras’s proof of this result can be used to prove Theorem 6.1 over
![]() $\mathbb {C}_p$
. For this, we first note that
$\mathbb {C}_p$
. For this, we first note that
![]() $H^i_{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,\mathbb {Z}/p^n) =H^i_{{\mathrm {\acute {e}t}}}(\mathbb {A}^n, \mathbb {Z}/p^n)=0$
for
$H^i_{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,\mathbb {Z}/p^n) =H^i_{{\mathrm {\acute {e}t}}}(\mathbb {A}^n, \mathbb {Z}/p^n)=0$
for
![]() $i\geq 1$
, and thus
$i\geq 1$
, and thus
which shows
Proposition 6.9. The long exact sequence of the logarithm (2.4) induces a sequence
which is short exact and isomorphic to the
![]() $(-1)$
-twist of the sequence
$(-1)$
-twist of the sequence
Proof. Let
![]() $X=\mathbb {A}_{\mathbb {Q}_p}^n$
be the rigid affine space over
$X=\mathbb {A}_{\mathbb {Q}_p}^n$
be the rigid affine space over
![]() $\mathbb {Q}_p$
so that
$\mathbb {Q}_p$
so that
![]() $\mathbb {A}^n=\mathbb {A}^n_{\mathbb {C}_p}=X_{\mathbb {C}_p}$
. Choose an isomorphism
$\mathbb {A}^n=\mathbb {A}^n_{\mathbb {C}_p}=X_{\mathbb {C}_p}$
. Choose an isomorphism
![]() $\mathbb {Z}_p\cong \mathbb {Z}_p(1)$
, that is, a compatible system of
$\mathbb {Z}_p\cong \mathbb {Z}_p(1)$
, that is, a compatible system of
![]() $p^n$
-th roots of unity
$p^n$
-th roots of unity
![]() $\epsilon \in \mathbb {C}_p^{\flat }=\varprojlim _{x\mapsto x^p}\mathbb {C}_p$
.
$\epsilon \in \mathbb {C}_p^{\flat }=\varprojlim _{x\mapsto x^p}\mathbb {C}_p$
.
In order to prove Theorem 6.8, Le Bras considers Colmez’s fundamental exact sequence [Reference Colmez10, Proposition 8.25.3] in its incarnation in terms of period sheaves on
![]() $X_{\mathrm {pro\acute {e}t}}$
:
$X_{\mathrm {pro\acute {e}t}}$
:
where
![]() $t=\log ([\varepsilon ])$
(see [Reference Le Bras28, §8] for the definition of these sheaves). For
$t=\log ([\varepsilon ])$
(see [Reference Le Bras28, §8] for the definition of these sheaves). For
![]() $i>0$
, he shows
$i>0$
, he shows
![]() $H^{i}_{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,\mathbb {B}[\tfrac {1}{t}]^{\varphi =1})=0$
and
$H^{i}_{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,\mathbb {B}[\tfrac {1}{t}]^{\varphi =1})=0$
and
![]() $H_{\mathrm {pro\acute {e}t}}^i(\mathbb {A}^n,{{\mathbb B}_{\mathrm {dR}}})=0$
. This gives an isomorphism for
$H_{\mathrm {pro\acute {e}t}}^i(\mathbb {A}^n,{{\mathbb B}_{\mathrm {dR}}})=0$
. This gives an isomorphism for
![]() $i>1$
:
$i>1$
:
As pointed out to us by Le Bras, this isomorphism is related to our setting in §2 by way of the following commutative diagram of sheaves on
![]() $X_{\mathrm {pro\acute {e}t}}$
with short exact rows:
$X_{\mathrm {pro\acute {e}t}}$
with short exact rows:

Using equation (6.2), the
![]() $5$
-lemma and Lemma 6.7, the top two lines induce an isomorphism
$5$
-lemma and Lemma 6.7, the top two lines induce an isomorphism
From the bottom two rows, we thus get a morphism of long exact sequences

The map on the top left is injective: This follows from Theorem 1.2.1 using
![]() $\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(\mathbb {A}^n)=1$
. Consequently, using that the bottom map is an isomorphism,
$\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(\mathbb {A}^n)=1$
. Consequently, using that the bottom map is an isomorphism,
![]() $\operatorname {Pic}_v(\mathbb {A}^n)$
gets identified with the kernel of the middle vertical map. Using
$\operatorname {Pic}_v(\mathbb {A}^n)$
gets identified with the kernel of the middle vertical map. Using
![]() $H^1_{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,{\mathbb B_{\mathrm {dR}}})=0$
and the diagram
$H^1_{\mathrm {pro\acute {e}t}}(\mathbb {A}^n,{\mathbb B_{\mathrm {dR}}})=0$
and the diagram

this can in turn be identified with the kernel of the boundary map
This can now be understood via Scholze’s Poincaré lemma [Reference Scholze36, Corollary 6.13] and its corollaries [Reference Le Bras28, Remarque 3.18][Reference Bosco8, Corollary 3.2.4]: For
![]() $\nu :\mathbb {A}^n_{\mathrm {pro\acute {e}t}}\to \mathbb {A}^n_{{\mathrm {\acute {e}t}}}$
, we have
$\nu :\mathbb {A}^n_{\mathrm {pro\acute {e}t}}\to \mathbb {A}^n_{{\mathrm {\acute {e}t}}}$
, we have
Here following [Reference Le Bras28, before Proposition 3.16], for any vector bundle F on
![]() $X_{{\mathrm {\acute {e}t}}}$
, the sheaf
$X_{{\mathrm {\acute {e}t}}}$
, the sheaf
![]() $F\hat {\otimes }_{\mathbb {Q}_p}B_{\mathrm {dR}}^+$
is defined, via the equivalence
$F\hat {\otimes }_{\mathbb {Q}_p}B_{\mathrm {dR}}^+$
is defined, via the equivalence
![]() $X_{\mathbb {C}_p,{\mathrm {\acute {e}t}}}=\varprojlim _{L|\mathbb {Q}_p} X_{L,{\mathrm {\acute {e}t}}}$
, where
$X_{\mathbb {C}_p,{\mathrm {\acute {e}t}}}=\varprojlim _{L|\mathbb {Q}_p} X_{L,{\mathrm {\acute {e}t}}}$
, where
![]() $L|\mathbb {Q}_p$
ranges over all finite extensions, as the compatible system of sheaves
$L|\mathbb {Q}_p$
ranges over all finite extensions, as the compatible system of sheaves
![]() $F_{X_L}\hat {\otimes }_{L}B_{\mathrm {dR}}^+$
.
$F_{X_L}\hat {\otimes }_{L}B_{\mathrm {dR}}^+$
.
It follows from this that we get a distinguished triangle in
![]() $D(\mathbb {A}^n_{{\mathrm {\acute {e}t}}})$
, written vertically
$D(\mathbb {A}^n_{{\mathrm {\acute {e}t}}})$
, written vertically

where the right-hand side is in fact a short exact sequence of complexes. Chasing the diagram, this shows that the kernel of equation (6.4) gets identified with that of the
![]() $(-1)$
-twist of
$(-1)$
-twist of
Remark 6.10. Bosco [Reference Bosco8] has generalised Le Bras’s method to show that, more generally, for any smooth Stein space X defined over a discretely valued field extension
![]() $L|\mathbb {Q}_p$
, there is over the completion K of the algebraic closure of L an exact sequence
$L|\mathbb {Q}_p$
, there is over the completion K of the algebraic closure of L an exact sequence
Elaborating on the above proof, one might therefore be able to show in this generality that the sequence from Theorem 1.2.1 is a short exact sequence
6.3 The intermediate space
 $\widetilde B\times \mathbb {A}$
$\widetilde B\times \mathbb {A}$
While being conceptually satisfying, the approach of the last section only works for K a completed algebraic closure of a discretely valued field. In the rest of this section, we shall give an alternative proof of Theorem 6.1 that avoids the input of the Poincaré lemma and works over general algebraically closed complete K. It uses more classical methods and arguably gives a more concrete reason why
![]() $\mathbb {A}^n$
has a ‘minimal amount’ of v-line bundles (‘minimal’ as we know
$\mathbb {A}^n$
has a ‘minimal amount’ of v-line bundles (‘minimal’ as we know
![]() $\operatorname {Pic}_v(\mathbb {A}^n)$
must include
$\operatorname {Pic}_v(\mathbb {A}^n)$
must include
![]() $H^0(\mathbb {A}^n,\widetilde {\Omega }^1)^{d=0}$
by Corollary 4.4).
$H^0(\mathbb {A}^n,\widetilde {\Omega }^1)^{d=0}$
by Corollary 4.4).
The basic idea behind the proof is that for any rigid space X, the space
![]() $X\times \mathbb {A}$
has no more invertible global sections than X and therefore has few descent data for line bundles from pro-étale covers. We would like to apply this to
$X\times \mathbb {A}$
has no more invertible global sections than X and therefore has few descent data for line bundles from pro-étale covers. We would like to apply this to
![]() $X=B:=B^1$
, which has an explicit perfectoid
$X=B:=B^1$
, which has an explicit perfectoid
![]() $\mathbb {Z}_p$
-Galois cover
$\mathbb {Z}_p$
-Galois cover
![]() $\widetilde B$
that is easy to work with. Since
$\widetilde B$
that is easy to work with. Since
![]() $\mathcal {O}^{\times }(B\times \mathbb {A})=\mathcal {O}^{\times }(B)$
, the Cartan–Leray exact sequence Corollary 2.10 for the Galois cover
$\mathcal {O}^{\times }(B\times \mathbb {A})=\mathcal {O}^{\times }(B)$
, the Cartan–Leray exact sequence Corollary 2.10 for the Galois cover
![]() $\widetilde B\times \mathbb {A}\to B\times \mathbb {A}$
is then of the form
$\widetilde B\times \mathbb {A}\to B\times \mathbb {A}$
is then of the form
Using Theorem 1.2.2b, we would like to see that the map
![]() $\operatorname {HTlog}$
identifies this with
$\operatorname {HTlog}$
identifies this with
where if
![]() $T_1$
is the coordinate on B and
$T_1$
is the coordinate on B and
![]() $T_2$
that on
$T_2$
that on
![]() $\mathbb {A}$
, the last map sends
$\mathbb {A}$
, the last map sends
![]() $fdT_1+gdT_2\mapsto gdT_2$
. However, this fails to be exact because the de Rham complex of B is not exact on global sections. As usual, this can be fixed by replacing B by the ‘overconvergent unit ball’. Covering
$fdT_1+gdT_2\mapsto gdT_2$
. However, this fails to be exact because the de Rham complex of B is not exact on global sections. As usual, this can be fixed by replacing B by the ‘overconvergent unit ball’. Covering
![]() $\mathbb {A}$
by overconvergent unit balls of increasing radii, we get the desired result.
$\mathbb {A}$
by overconvergent unit balls of increasing radii, we get the desired result.
To simplify notation, let us fix a trivialisation
![]() $\mathbb {Z}_p(1)\cong \mathbb {Z}_p$
We start by constructing the explicit perfectoid Galois cover
$\mathbb {Z}_p(1)\cong \mathbb {Z}_p$
We start by constructing the explicit perfectoid Galois cover
![]() $\widetilde B\to B$
. For this we use the pro-étale perfectoid
$\widetilde B\to B$
. For this we use the pro-étale perfectoid
![]() $\mathbb {Z}_p$
-torsor
$\mathbb {Z}_p$
-torsor
Lemma 6.11. Embed
![]() $B\hookrightarrow \mathbb {G}_m$
via
$B\hookrightarrow \mathbb {G}_m$
via
![]() $T\mapsto 1+pT$
. Then the pullback
$T\mapsto 1+pT$
. Then the pullback
![]() $\widetilde B:=B\times _{\mathbb {G}_m}\widetilde {\mathbb {G}}_m$
of B along
$\widetilde B:=B\times _{\mathbb {G}_m}\widetilde {\mathbb {G}}_m$
of B along
![]() $\widetilde {\mathbb {G}}_m\to \mathbb {G}_m$
is isomorphic over K to the perfectoid unit disc
$\widetilde {\mathbb {G}}_m\to \mathbb {G}_m$
is isomorphic over K to the perfectoid unit disc
![]() $\operatorname {Spa} K\langle X^{1/p^{\infty }}\rangle $
.
$\operatorname {Spa} K\langle X^{1/p^{\infty }}\rangle $
.
Here T and X are different formal variables, and the map is not given by sending
![]() $T\mapsto X$
.
$T\mapsto X$
.
Proof. We have
![]() $\widetilde B=\operatorname {Spa}(R,R^{\circ })$
, where
$\widetilde B=\operatorname {Spa}(R,R^{\circ })$
, where
![]() $R:=K\langle Y^{\pm 1/p^{\infty }}\rangle \langle \tfrac {Y-1}{p}\rangle $
; thus,
$R:=K\langle Y^{\pm 1/p^{\infty }}\rangle \langle \tfrac {Y-1}{p}\rangle $
; thus,
![]() $\widetilde B$
is affinoid perfectoid. Let
$\widetilde B$
is affinoid perfectoid. Let
![]() $p^{\flat }\in K^{\flat }$
be such that
$p^{\flat }\in K^{\flat }$
be such that
![]() $|p^{\flat }|=|p|$
. Write
$|p^{\flat }|=|p|$
. Write
![]() $Y'$
for the parameter of
$Y'$
for the parameter of
![]() $\mathbb {G}_{m,K^{\flat }}$
. Then
$\mathbb {G}_{m,K^{\flat }}$
. Then
This shows
![]() $\widetilde B^{\flat }=\operatorname {Spa}(R^{\flat },R^{\flat \circ })$
, where
$\widetilde B^{\flat }=\operatorname {Spa}(R^{\flat },R^{\flat \circ })$
, where
![]() $R^{\flat }=K^{\flat }\langle Y^{\prime \pm 1/p^{\infty }}\rangle \langle \tfrac {Y'-1}{p^{\flat }}\rangle $
. But
$R^{\flat }=K^{\flat }\langle Y^{\prime \pm 1/p^{\infty }}\rangle \langle \tfrac {Y'-1}{p^{\flat }}\rangle $
. But
![]() $R^{\flat }$
is isomorphic to
$R^{\flat }$
is isomorphic to
![]() $K^{\flat }\langle X^{ 1/p^{\infty }}\rangle $
via the map that sends
$K^{\flat }\langle X^{ 1/p^{\infty }}\rangle $
via the map that sends
![]() $X^{1/p^n}\mapsto (\tfrac {Y'-1}{p^{\flat }})^{1/p^n}$
.
$X^{1/p^n}\mapsto (\tfrac {Y'-1}{p^{\flat }})^{1/p^n}$
.
Lemma 6.12. For any affinoid perfectoid space X over K, there is a natural isomorphism
In particular, for any profinite set S, we have
![]() $H^1_v(S\times X\times B,\mathcal {O})=\operatorname {Map}_{{\operatorname {cts}}}(S,H^1_v(X\times B,\mathcal {O}))$
.
$H^1_v(S\times X\times B,\mathcal {O})=\operatorname {Map}_{{\operatorname {cts}}}(S,H^1_v(X\times B,\mathcal {O}))$
.
Proof. By Corollary 2.9, the
![]() $\mathbb {Z}_p$
-Galois cover
$\mathbb {Z}_p$
-Galois cover
![]() $X\times \widetilde B\to X\times B$
induces isomorphisms
$X\times \widetilde B\to X\times B$
induces isomorphisms
where the last isomorphism is from [Reference Scholze36, Lemma 5.5]. Then we use that for
![]() $X=\operatorname {Spa}(K)$
we already know that
$X=\operatorname {Spa}(K)$
we already know that
![]() $H^1_{{\operatorname {cts}}}(\mathbb {Z}_p,\mathcal {O}(\widetilde B))=H^1_v(B,\mathcal {O})=H^0(B,\widetilde {\Omega }^1)$
.
$H^1_{{\operatorname {cts}}}(\mathbb {Z}_p,\mathcal {O}(\widetilde B))=H^1_v(B,\mathcal {O})=H^0(B,\widetilde {\Omega }^1)$
.
Lemma 6.13. For any profinite set S, the logarithm defines an injection
In particular, the specialisation
![]() $H^1_v(\widetilde B\times B\times {S},U)\to \operatorname {Map}(S,H^1_v(\widetilde B\times B,U))$
is injective.
$H^1_v(\widetilde B\times B\times {S},U)\to \operatorname {Map}(S,H^1_v(\widetilde B\times B,U))$
is injective.
Proof. Choose a profinite presentation
![]() $S=\varprojlim _{i\in I} S_i$
. We need to show that the map
$S=\varprojlim _{i\in I} S_i$
. We need to show that the map
vanishes. For this, we use that by Lemma 6.11 there is an isomorphism of diamonds
where
![]() $B^{(n)}$
is B in the variable
$B^{(n)}$
is B in the variable
![]() $X^{1/p^n}$
. By [Reference Scholze35, Proposition 14.9], we have
$X^{1/p^n}$
. By [Reference Scholze35, Proposition 14.9], we have
The result now follows as by Lemma 6.6, we have
![]() $H^1_{{\mathrm {\acute {e}t}}}(B^2\times S_i,U)\hookrightarrow \operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B^2\times S_i)=1$
.
$H^1_{{\mathrm {\acute {e}t}}}(B^2\times S_i,U)\hookrightarrow \operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B^2\times S_i)=1$
.
Lemma 6.14. Let Y be either of B or
![]() $\widetilde B$
. Then
$\widetilde B$
. Then
Proof. Arguing like in Lemma 6.7, for the first equality it suffices to prove that
![]() $\overline {\mathcal {O}}^{\times }(Y\times \mathbb {A})=K^{\times }/(1+\mathfrak {m})$
and
$\overline {\mathcal {O}}^{\times }(Y\times \mathbb {A})=K^{\times }/(1+\mathfrak {m})$
and
![]() $H^1_v(Y\times \mathbb {A},\overline {\mathcal {O}}^{\times })=1$
. For
$H^1_v(Y\times \mathbb {A},\overline {\mathcal {O}}^{\times })=1$
. For
![]() $B\times \mathbb {A}$
, this can be seen exactly like in Lemma 6.7. To deduce the case of
$B\times \mathbb {A}$
, this can be seen exactly like in Lemma 6.7. To deduce the case of
![]() $\widetilde B\times \mathbb {A}$
, write
$\widetilde B\times \mathbb {A}$
, write
![]() $\widetilde B\sim \varprojlim _n B^{(n)}$
as a tilde-limit, where
$\widetilde B\sim \varprojlim _n B^{(n)}$
as a tilde-limit, where
![]() $ B^{(n)}$
is the unit disc in the parameter
$ B^{(n)}$
is the unit disc in the parameter
![]() $X^{1/p^n}$
, then by Lemma 2.22,
$X^{1/p^n}$
, then by Lemma 2.22,
The second equality follows from the Čech-to-sheaf sequence by the following lemma.
Lemma 6.15. Let Y be any affinoid rigid or perfectoid space. Then for the cover
![]() $\mathfrak U=(Y\times B_s)_{s\in \mathbb {N}}$
of
$\mathfrak U=(Y\times B_s)_{s\in \mathbb {N}}$
of
![]() $Y\times \mathbb {A}$
, we have
$Y\times \mathbb {A}$
, we have
![]() $\check {H}^i(\mathfrak U,U)= \check {H}^i(\mathfrak U,\mathcal {O}^{\times })=1$
for
$\check {H}^i(\mathfrak U,U)= \check {H}^i(\mathfrak U,\mathcal {O}^{\times })=1$
for
![]() $i\geq 1$
.
$i\geq 1$
.
Proof. The vanishing for
![]() $i\geq 2$
follows from
$i\geq 2$
follows from
![]() $\mathfrak U$
being an increasing cover indexed over
$\mathfrak U$
being an increasing cover indexed over
![]() $\mathbb {N}$
. For
$\mathbb {N}$
. For
![]() $i = 1$
, it suffices by Lemma 6.6 to see that, for
$i = 1$
, it suffices by Lemma 6.6 to see that, for
![]() $R=\mathcal {O}(Y)$
, the following map is surjective:
$R=\mathcal {O}(Y)$
, the following map is surjective:
This can be seen like in [Reference Fresnel and van der Put18, Lemma 6.3.1]: Let
![]() $g=(g_s)_{s\in \mathbb {N}}$
be an element on the right. After rescaling by an element of
$g=(g_s)_{s\in \mathbb {N}}$
be an element on the right. After rescaling by an element of
![]() $(1+\mathfrak {m} R^{\circ })_{s\in \mathbb {N}}$
, we can assume that
$(1+\mathfrak {m} R^{\circ })_{s\in \mathbb {N}}$
, we can assume that
![]() $g_s = 1+p^{s}T(\dots )$
. Then for any
$g_s = 1+p^{s}T(\dots )$
. Then for any
![]() $r\in \mathbb {N}$
, the product
$r\in \mathbb {N}$
, the product
![]() $f_r:=\prod _{s\geq r} g_s$
converges and defines a preimage
$f_r:=\prod _{s\geq r} g_s$
converges and defines a preimage
![]() $(f_r)_{r\in \mathbb {N}}$
.
$(f_r)_{r\in \mathbb {N}}$
.
6.4 The overconvergent Picard group of the cylinder
 $B\times \mathbb {A}$
$B\times \mathbb {A}$
In the rigid setting, the de Rham complex of the closed unit disc B is not exact on global sections, the issue being convergence of primitive functions at the boundary. It is well-known that this can be resolved by considering overconvergent functions. For
![]() $B\times \mathbb {A}$
, this means:
$B\times \mathbb {A}$
, this means:
Lemma 6.16. Recall that
![]() $B_s$
is the disc of radius
$B_s$
is the disc of radius
![]() $s\in |K|$
. The de Rham complex of
$s\in |K|$
. The de Rham complex of
![]() $B_s\times \mathbb {A}$
$B_s\times \mathbb {A}$
becomes exact after applying
![]() $\varinjlim _{s>1}$
.
$\varinjlim _{s>1}$
.
The key calculation is now that of the ‘overconvergent Picard group’ of
![]() $B\times \mathbb {A}$
.
$B\times \mathbb {A}$
.
Proposition 6.17. The Hodge–Tate logarithm from Theorem 1.2.1 defines an isomorphism
Proof. By Lemma 6.15, we have
![]() $\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B_s\times \mathbb {A})=\varprojlim _{r\in \mathbb {N}}\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B_s\times B_r)=1$
. It therefore follows from Theorem 1.2.1 that the Hodge–Tate logarithm is an injective map
$\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B_s\times \mathbb {A})=\varprojlim _{r\in \mathbb {N}}\operatorname {Pic}_{{\mathrm {\acute {e}t}}}(B_s\times B_r)=1$
. It therefore follows from Theorem 1.2.1 that the Hodge–Tate logarithm is an injective map
We already know that the image contains all closed differentials: By Lemma 6.16,
which we know is in the image by Corollary 4.4.
To prove the converse, we start by considering the Cartan–Leray sequences for U and
![]() $\mathcal {O}$
associated to
$\mathcal {O}$
associated to
![]() $\widetilde B\times B\to B\times B$
. Lemmas 6.12 and 6.13 guarantee that the conditions of Proposition 2.8.2 are satisfied, so the logarithm induces a morphism of short exact sequences
$\widetilde B\times B\to B\times B$
. Lemmas 6.12 and 6.13 guarantee that the conditions of Proposition 2.8.2 are satisfied, so the logarithm induces a morphism of short exact sequences

The right vertical map is injective by Lemma 6.13. The bottom row can be identified with
by Lemma 6.12. This expresses that any differential decomposes as
![]() $g(T_1,T_2)dT_1+f(T_1,T_2)dT_2$
, where
$g(T_1,T_2)dT_1+f(T_1,T_2)dT_2$
, where
![]() $T_1$
is the differential on the first factor of
$T_1$
is the differential on the first factor of
![]() $B\times B$
and
$B\times B$
and
![]() $T_2$
is that on the second.
$T_2$
is that on the second.
We now replace B by
![]() $B_s$
, then by Lemma 6.14 we get for
$B_s$
, then by Lemma 6.14 we get for
![]() $s\to \infty $
a commutative diagram
$s\to \infty $
a commutative diagram

here the top-left entry is as described by the Cartan–Leray sequence of
![]() $\widetilde B\times \mathbb {A}\to B\times \mathbb {A}$
.
$\widetilde B\times \mathbb {A}\to B\times \mathbb {A}$
.
We now have a closer look at the left vertical map: Here
![]() $\mathcal {O}^{\times }(\widetilde B\times \mathbb {A})=\mathcal {O}^{\times }(\widetilde B)$
, for which
$\mathcal {O}^{\times }(\widetilde B\times \mathbb {A})=\mathcal {O}^{\times }(\widetilde B)$
, for which
is an isomorphism by Theorem 1.2.2b. We conclude that the image of the leftmost vertical map in diagram (6.6) consists precisely of the submodule
![]() $H^0(B,\Omega ^1)$
.
$H^0(B,\Omega ^1)$
.
Next, we replace the first factor B by
![]() $B_s$
which in the colimit
$B_s$
which in the colimit
![]() $s\to 1$
results in a diagram
$s\to 1$
results in a diagram

with exact rows. We claim that the bottom sequence restricts to an exact sequence
Left-exactness is clear. For any differential
![]() $\omega _2=f(T_1,T_2)dT_2$
in
$\omega _2=f(T_1,T_2)dT_2$
in
![]() $\mathcal {O}(B_s)\hat {\otimes } H^0(\mathbb {A},\Omega ^1)$
, we can find
$\mathcal {O}(B_s)\hat {\otimes } H^0(\mathbb {A},\Omega ^1)$
, we can find
![]() $h(T_1,T_2)\in \mathcal {O}(B_s\times \mathbb {A})$
such that
$h(T_1,T_2)\in \mathcal {O}(B_s\times \mathbb {A})$
such that
![]() $\partial h/\partial T_2=-\partial f/\partial T_1$
. For any such function,
$\partial h/\partial T_2=-\partial f/\partial T_1$
. For any such function,
![]() $\omega :=hdT_1+fdT_2$
is a closed differential on
$\omega :=hdT_1+fdT_2$
is a closed differential on
![]() $B_s\times \mathbb {A}$
which the last map sends to
$B_s\times \mathbb {A}$
which the last map sends to
![]() $\omega _2$
.
$\omega _2$
.
By Lemma 6.16, we can even find
![]() $g\in \varinjlim _{s>1}\mathcal {O}(B_s\times \mathbb {A})$
such that
$g\in \varinjlim _{s>1}\mathcal {O}(B_s\times \mathbb {A})$
such that
![]() $\omega =dg$
. Thus, the dashed map is surjective, hence the right vertical map is an isomorphism. Comparing the image of the top row in the bottom row with the last exact sequence, using that the image of
$\omega =dg$
. Thus, the dashed map is surjective, hence the right vertical map is an isomorphism. Comparing the image of the top row in the bottom row with the last exact sequence, using that the image of
![]() $\operatorname {Pic}_v(B_s\times \mathbb {A})$
contains
$\operatorname {Pic}_v(B_s\times \mathbb {A})$
contains
![]() $H^0(B_s\times \mathbb {A},\Omega ^1)^{d=0}$
, this shows that, inside
$H^0(B_s\times \mathbb {A},\Omega ^1)^{d=0}$
, this shows that, inside
![]() $H^0(B_s\times \mathbb {A},\Omega ^1)$
, we have
$H^0(B_s\times \mathbb {A},\Omega ^1)$
, we have
6.5 The Picard group of
 $\mathbb {A}^n$
$\mathbb {A}^n$
Proof of Theorem 6.1.
Since
![]() $\operatorname {Pic}_{\mathrm {an}}(\mathbb {A}^n)=1$
, we have by Theorem 1.2 an injective map
$\operatorname {Pic}_{\mathrm {an}}(\mathbb {A}^n)=1$
, we have by Theorem 1.2 an injective map
It is clear from Corollary 4.4 and exactness of the de Rham complex of
![]() $\mathbb {A}^n$
that
$\mathbb {A}^n$
that
To prove the other containment, we first consider the case of
![]() $n=2$
: In this case, the restriction from
$n=2$
: In this case, the restriction from
![]() $\mathbb {A}\times \mathbb {A}$
to
$\mathbb {A}\times \mathbb {A}$
to
![]() $B_s\times \mathbb {A}$
for any
$B_s\times \mathbb {A}$
for any
![]() $s>1$
defines a commutative diagram
$s>1$
defines a commutative diagram

By Proposition 6.17, the image of the bottom map lands in the closed differentials. As the map on the right is injective, this also holds for the top map. This proves the case of
![]() $n=2$
.
$n=2$
.
The general case follows from the one of
![]() $n=2$
: Let
$n=2$
: Let
![]() $f\in H^0(\mathbb {A}^n,\widetilde {\Omega }^1)$
be in the image of
$f\in H^0(\mathbb {A}^n,\widetilde {\Omega }^1)$
be in the image of
![]() $\operatorname {HTlog}$
, and suppose that
$\operatorname {HTlog}$
, and suppose that
![]() $df\neq 0$
. We can write this as
$df\neq 0$
. We can write this as
Then
![]() $df\neq 0$
if and only if there is some
$df\neq 0$
if and only if there is some
![]() $0\neq g_{ij}\in \mathcal {O}(\mathbb {A}^n)$
, and after reordering we can assume
$0\neq g_{ij}\in \mathcal {O}(\mathbb {A}^n)$
, and after reordering we can assume
![]() $0\neq g_{12}:\mathbb {A}^n(K)\to K$
is nontrivial. We may thus find
$0\neq g_{12}:\mathbb {A}^n(K)\to K$
is nontrivial. We may thus find
![]() $z\in \mathbb {A}^{n-2}$
such that, under
$z\in \mathbb {A}^{n-2}$
such that, under
f pulls back to
![]() $\varphi ^{\ast }f$
which still satisfies
$\varphi ^{\ast }f$
which still satisfies
![]() $d(\varphi ^{\ast }f)=\varphi ^{\ast }df\neq 0$
. But the commutative diagram
$d(\varphi ^{\ast }f)=\varphi ^{\ast }df\neq 0$
. But the commutative diagram

shows that
![]() $\varphi ^{\ast }f$
is in the image of
$\varphi ^{\ast }f$
is in the image of
![]() $\operatorname {Pic}_v(\mathbb {A}^2)$
, which implies
$\operatorname {Pic}_v(\mathbb {A}^2)$
, which implies
![]() $d(\varphi ^{\ast }f)=0$
, a contradiction.
$d(\varphi ^{\ast }f)=0$
, a contradiction.
The case of
![]() $\operatorname {Pic}_v(\mathbb {G}_m^k\times \mathbb {A}^n)$
is analogous: Here we first note that
$\operatorname {Pic}_v(\mathbb {G}_m^k\times \mathbb {A}^n)$
is analogous: Here we first note that
![]() $H^0(\mathbb {G}_m^k\times \mathbb {A}^n,\widetilde {\Omega }^1)^{d=0}$
is generated as a group by
$H^0(\mathbb {G}_m^k\times \mathbb {A}^n,\widetilde {\Omega }^1)^{d=0}$
is generated as a group by
![]() $d(\mathcal {O}(\mathbb {G}_m^k\times \mathbb {A}^n))$
plus the differentials
$d(\mathcal {O}(\mathbb {G}_m^k\times \mathbb {A}^n))$
plus the differentials
![]() $a\cdot dY_i/Y_i$
for
$a\cdot dY_i/Y_i$
for
![]() $a\in K$
and for each of the
$a\in K$
and for each of the
![]() $\mathbb {G}_m$
-factors. The latter are in the image of
$\mathbb {G}_m$
-factors. The latter are in the image of
![]() $\operatorname {Pic}_v(\mathbb {G}_m^k\times \mathbb {A}^n)$
as we see via pullback along the projection
$\operatorname {Pic}_v(\mathbb {G}_m^k\times \mathbb {A}^n)$
as we see via pullback along the projection
![]() $\mathbb {G}_m^k\times \mathbb {A}^n\to \mathbb {G}_m$
since
$\mathbb {G}_m^k\times \mathbb {A}^n\to \mathbb {G}_m$
since
![]() $\operatorname {Pic}_v(\mathbb {G}_m)=H^0(\mathbb {G}_m,\widetilde {\Omega }^1)$
by Theorem 1.2.2b. The rest of the proof goes through analogously by considering any embedding
$\operatorname {Pic}_v(\mathbb {G}_m)=H^0(\mathbb {G}_m,\widetilde {\Omega }^1)$
by Theorem 1.2.2b. The rest of the proof goes through analogously by considering any embedding
![]() $B_s\hookrightarrow \mathbb {G}_m$
.
$B_s\hookrightarrow \mathbb {G}_m$
.
Acknowledgements
We thank Johannes Anschütz, David Hansen, Arthur-César Le Bras, Lucas Mann, Peter Scholze and Annette Werner for very useful conversations. We also thank the anonymous referees for their helpful comments.
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC-2047/1—90685813. The author was supported by the DFG via the Leibniz-Preis of Peter Scholze.
Conflicts of Interest
None.