Hostname: page-component-cb9f654ff-5kfdg Total loading time: 0 Render date: 2025-08-26T04:13:04.421Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLICATIVE SUB-HODGE STRUCTURES OF CONJUGATE VARIETIES

Part of: (Co)homology theory Cycles and subschemes Real and complex geometry

Published online by Cambridge University Press:  18 February 2014

STEFAN SCHREIEDER
STEFAN SCHREIEDER*
Affiliation:
Max-Planck-Institut für Mathematik, Vivatsgasse 7, 53111 Bonn, Germany; schreied@math.uni-bonn.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any subfield 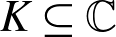$K\subseteq \mathbb{C}$ , not contained in an imaginary quadratic extension of 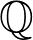$\mathbb{Q}$ , we construct conjugate varieties whose algebras of 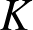$K$ -rational ( 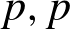$p,p$ )-classes are not isomorphic. This compares to the Hodge conjecture which predicts isomorphisms when 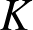$K$ is contained in an imaginary quadratic extension of 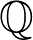$\mathbb{Q}$ ; additionally, it shows that the complex Hodge structure on the complex cohomology algebra is not invariant under the Aut( 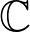$\mathbb{C}$ )-action on varieties. In our proofs, we find simply connected conjugate varieties whose multilinear intersection forms on 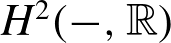$H^{2}(-,\mathbb{R})$ are not (weakly) isomorphic. Using these, we detect nonhomeomorphic conjugate varieties for any fundamental group and in any birational equivalence class of dimension 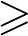$\geq $ 10.

MSC classification

Secondary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture 14F25: Classical real and complex (co)homology 51M15: Geometric constructions 14F35: Homotopy theory; fundamental groups

Information

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e1
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author 2014

References

Abelson, H. ‘Topologically distinct conjugate varieties with finite fundamental group’, Topology 13, (1974), 161–176.Google Scholar
Bauer, I., Catanese, F. and Grunewald, F. Faithful actions of the absolute Galois group on connected components of moduli spaces, Preprint (2013), arXiv:1303.2248.Google Scholar
Charles, F. ‘Conjugate varieties with distinct real cohomology algebras’, J. Reine Angew. Math. 630, (2009), 125–139.Google Scholar
Charles, F. and Schnell, , C. 2014 ‘Notes on absolute Hodge classes’, In Hodge Theory Princeton University Press, Princeton, NJ.Google Scholar
Deligne, P. 1982 In Hodge Cycles on Abelian Varieties (notes by J. S. Milne) Lecture Notes in Mathematics, 900, pp. 9–100. Springer-Verlag.CrossRefGoogle Scholar
Easton, R. W. and Vakil, R. ‘Absolute Galois acts faithfully on the components of the moduli space of surfaces: a Belyi-type theorem in higher dimension’, Int. Math. Res. Not. IMRN 20, (2007), Art. ID rnm080, 10pp.Google Scholar
Freitag, E. 1983 In Siegelsche Modulfunktionen Grundlehren der mathematischen Wissenschaften, vol. 254, Springer-Verlag, Berlin.Google Scholar
von Geemen, B. Some equations for the universal Kummer variety, Preprint (2013), arXiv:1307.2463.Google Scholar
Kollár, J. 1995 Shafarevich Maps and Automorphic Forms. Princeton University Press, Princeton, NJ.CrossRefGoogle Scholar
Rajan, C. S. ‘An example of non-homeomorphic conjugate varieties’, Math. Res. Lett. 18, (2011), 937–943.Google Scholar
Reed, D. ‘The topology of conjugate varieties’, Math. Ann. 305, (1996), 287–309.CrossRefGoogle Scholar
Ren, Q., Sam, S. V., Schrader, G. and Sturmfels, B. ‘The universal Kummer threefold’, Experiment. Math. 22, (2013), 327–362.Google Scholar
Serre, J.-P. ‘Exemples de variétés projectives conjuguées non homéomorphes’, C. R. Acad. Sci. Paris 258, (1964), 4194–4196.Google Scholar
Serre, J.-P. ‘Géométrie algébrique et géométrie analytique’, Ann. Inst. Fourier (Grenoble) 6, (1955–1956), 42.Google Scholar
Shimada, I. ‘Non-homeomorphic conjugate complex varieties’, In Singularities—Niigata–Toyama 2007 Adv. Stud. Pure Math., 56 (Math. Soc. Japan, Tokyo, 2009), pp. 285–301.Google Scholar
Tashiro, Y., Yamazaki, S., Ito, M. and Higuchi, T. ‘On Riemanns period matrix of $y^{2}=x^{2n+1}-1$ ’, RIMS Kokyuroku 963, (1996), 124–141 (in English).Google Scholar
Voisin, C. 2002 Hodge Theory and Complex Algebraic Geometry, I. Cambridge University Press, Cambridge.Google Scholar
Voisin, C. ‘On the homotopy types of Kahler compact and complex projective manifolds’, Invent. Math. 157 (2) (2004), 329–343.CrossRefGoogle Scholar
Voisin, C. ‘Some aspects of the Hodge conjecture’, Jpn. J. Math. 2 (2) (2007), 261–296.Google Scholar