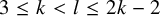1 Introduction
The starting point of this article is the following manifold with boundary
(i.e., the g-fold connected sum of
![]() ${\mathrm {S}^{k}} \times {\mathrm {S}^{l}}$
with an open disk removed). Given this, a natural object to consider is the classifying space
${\mathrm {S}^{k}} \times {\mathrm {S}^{l}}$
with an open disk removed). Given this, a natural object to consider is the classifying space
of the topological monoid of homotopy automorphisms of
![]() $M^{k, l}_{g, 1}$
that fix the boundary pointwise. It classifies fibrations with fiber
$M^{k, l}_{g, 1}$
that fix the boundary pointwise. It classifies fibrations with fiber
![]() $M^{k, l}_{g, 1}$
under the trivial fibration with fiber its boundary (see, for example, [Reference Hepworth and LahtinenHL15, Appendix B]). In particular, the cohomology of
$M^{k, l}_{g, 1}$
under the trivial fibration with fiber its boundary (see, for example, [Reference Hepworth and LahtinenHL15, Appendix B]). In particular, the cohomology of
![]() ${\mathrm {B}} {{\mathrm {aut}}_{\partial }}(M^{k, l}_{g, 1})$
consists of the characteristic classes for such fibrations.
${\mathrm {B}} {{\mathrm {aut}}_{\partial }}(M^{k, l}_{g, 1})$
consists of the characteristic classes for such fibrations.
This cohomology appears to be hard to understand completely. However, at least rationally, it is possible to say something about the behavior of the stabilization maps
obtained by gluing on, along one of its boundary components, a copy of
![]() ${\mathrm {S}^{k}} \times {\mathrm {S}^{l}}$
with two disjoint open disks removed. Namely, in the case
${\mathrm {S}^{k}} \times {\mathrm {S}^{l}}$
with two disjoint open disks removed. Namely, in the case
![]() $2 \le k = l$
, Berglund–Madsen [Reference Berglund and MadsenBM20] have shown this map to be an isomorphism in a certain stable range of degrees,Footnote
1
and this was extended by Grey [Reference GreyGre19] to the cases
$2 \le k = l$
, Berglund–Madsen [Reference Berglund and MadsenBM20] have shown this map to be an isomorphism in a certain stable range of degrees,Footnote
1
and this was extended by Grey [Reference GreyGre19] to the cases
![]() $3 \le k \le l \le 2k - 2$
.
$3 \le k \le l \le 2k - 2$
.
Moreover, [Reference Berglund and MadsenBM20] contains, in the case
![]() $3 \le k = l$
, a combinatorial description (in terms of graph complex homology) of the stable cohomology (i.e., the limit of the maps (1.1) as g goes to infinity). In this paper, we provide a similar description when
$3 \le k = l$
, a combinatorial description (in terms of graph complex homology) of the stable cohomology (i.e., the limit of the maps (1.1) as g goes to infinity). In this paper, we provide a similar description when
![]() $k \neq l$
. The following is our main result.
$k \neq l$
. The following is our main result.
Theorem 1.1 (see Corollary 5.9).
Let
![]() $3 \le k < l \le 2k - 2$
and
$3 \le k < l \le 2k - 2$
and
![]() $2 \le g$
be integers. Then there is, in cohomological degrees
$2 \le g$
be integers. Then there is, in cohomological degrees
![]() $\le g - 2$
, an isomorphism of graded algebras
$\le g - 2$
, an isomorphism of graded algebras
compatible with the stabilization maps on the left-hand side. Here we set ![]() , denote by
, denote by
![]() ${\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
the m-twisted graph complex associated to the cyclic Lie operad (with its canonical coalgebra structure), and write
${\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
the m-twisted graph complex associated to the cyclic Lie operad (with its canonical coalgebra structure), and write
![]() ${(-)^\vee }$
for linear dualization.
${(-)^\vee }$
for linear dualization.
In particular, after stabilizing, we obtain an isomorphism
of graded algebras.
Remark. We also prove a version of Theorem 1.1 for cohomology with certain local coefficients; see Theorem 5.7. In this generality, the description we give is in terms of a directed graph complex (see below). It should be possible to relate this to an undirected graph complex, just as in the case of trivial coefficients above, but we do not carry this out in this paper.
Remark. The proof of Theorem 1.1 does not rely on the stability result of Grey [Reference GreyGre19] (though we do reuse some of its ingredients). In particular, we obtain a new proof of his result (for the manifolds
![]() $M^{k, l}_{g, 1}$
), while also roughly doubling the stable range. This is made possible by a result of Li–Sun [Reference Li and SunLS19], which yields a slope
$M^{k, l}_{g, 1}$
), while also roughly doubling the stable range. This is made possible by a result of Li–Sun [Reference Li and SunLS19], which yields a slope
![]() $1$
vanishing of the rational cohomology of
$1$
vanishing of the rational cohomology of
![]() ${\mathrm {GL}}_{n}({\mathbb {Z}})$
with certain coefficients. That a result of this form would lead to an improvement of the stable range had been suggested by Krannich [Reference KrannichKra20, p. 1070].
${\mathrm {GL}}_{n}({\mathbb {Z}})$
with certain coefficients. That a result of this form would lead to an improvement of the stable range had been suggested by Krannich [Reference KrannichKra20, p. 1070].
Surprisingly, the graph complex appearing in Theorem 1.1 only depends on the dimension
![]() $k + l$
and not on k and l themselves. Moreover, when
$k + l$
and not on k and l themselves. Moreover, when
![]() $k + l$
is even, it is the same graph complex that appears in [Reference Berglund and MadsenBM20] – that is, in the case
$k + l$
is even, it is the same graph complex that appears in [Reference Berglund and MadsenBM20] – that is, in the case
![]() $k = l$
(when
$k = l$
(when
![]() $k + l$
is odd, it is defined similarly to the even case but appears to have quite different homology; see further below). For both of these observations, there seems to be no a priori reason to expect them to be true. The second one is particularly interesting when considering our proof, where first a different graph complex appears, of which we then show that it actually has the same homology as
$k + l$
is odd, it is defined similarly to the even case but appears to have quite different homology; see further below). For both of these observations, there seems to be no a priori reason to expect them to be true. The second one is particularly interesting when considering our proof, where first a different graph complex appears, of which we then show that it actually has the same homology as
![]() ${\mathfrak {UG}}^{k + l - 2} {\operatorname {(\mathscr {L}ie)}}$
.
${\mathfrak {UG}}^{k + l - 2} {\operatorname {(\mathscr {L}ie)}}$
.
We will now describe the terms appearing on the right-hand sides of the isomorphisms of Theorem 1.1 in more detail. First, note that
by a classical result of Borel [Reference BorelBor74]. The graph complex
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
, for
${\mathfrak {UG}}^{m} {(\mathscr C)}$
, for
![]() $\mathscr C$
a cyclic operad, is also a well-known object. Versions of it were first described by Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93, Reference Kontsevich and JosephKon94], but they have, since then, appeared in many different places; see, for example, [Reference Getzler and KapranovGK98, Reference Conant and VogtmannCV03, Reference Lazarev and VoronovLV08, Reference Berglund and MadsenBM20].
$\mathscr C$
a cyclic operad, is also a well-known object. Versions of it were first described by Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93, Reference Kontsevich and JosephKon94], but they have, since then, appeared in many different places; see, for example, [Reference Getzler and KapranovGK98, Reference Conant and VogtmannCV03, Reference Lazarev and VoronovLV08, Reference Berglund and MadsenBM20].
We now sketch the definition of this graph complex. It is generated by graphs (potentially with loops and parallel edges) equipped with an orientation of each edge and a labeling of each vertex with an element of
![]() $\mathscr C$
of cyclic arity the valence of the vertex (which we assume to be at least three). We consider a vertex to have homological degree
$\mathscr C$
of cyclic arity the valence of the vertex (which we assume to be at least three). We consider a vertex to have homological degree
![]() $1 - m$
and an edge to have homological degree m. The resulting graded vector space is quotiented by the actions of the automorphism groups of the graphs, taking into account the homological degrees of the vertices and edges and yielding an extra sign
$1 - m$
and an edge to have homological degree m. The resulting graded vector space is quotiented by the actions of the automorphism groups of the graphs, taking into account the homological degrees of the vertices and edges and yielding an extra sign
![]() $(-1)^{m+1}$
whenever the orientation of an edge is flipped. The differential is defined to be the sum over all possible contractions of non-loop edges. When an edge is contracted, the label of the new vertex is obtained via the cyclic operad composition of the labels of the two contracted vertices, as in the following picture.
$(-1)^{m+1}$
whenever the orientation of an edge is flipped. The differential is defined to be the sum over all possible contractions of non-loop edges. When an edge is contracted, the label of the new vertex is obtained via the cyclic operad composition of the labels of the two contracted vertices, as in the following picture.

The graph complex has the structure of a cocommutative differential graded coalgebra with comultiplication given by the sum over all possible ways to partition the connected components of a graph into two sets.
Note that, up to regrading, the graph complex and, in particular, its homology only depend on the parity of m. Even though this homology could theoretically be computed directly from its definition, this has only be feasible in low degrees so far. Its structure in higher degrees remains largely mysterious. By a result of Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93] (for m even; see also Conant–Vogtmann [Reference Conant and VogtmannCV03]) and Lazarev–Voronov [Reference Lazarev and VoronovLV08] (for m odd), Lie graph complex homology is closely related to the rational homology (with twisted coefficients if m is odd) of the group
![]() $\mathrm {Out}(F_g)$
of outer automorphisms of the free group on g generators. See Remark 4.30 for a summary of what is known about this. In particular, computations of Brun–Willwacher [Reference Brun and WillwacherBW23] imply that
$\mathrm {Out}(F_g)$
of outer automorphisms of the free group on g generators. See Remark 4.30 for a summary of what is known about this. In particular, computations of Brun–Willwacher [Reference Brun and WillwacherBW23] imply that
![]() ${\mathrm {H}}_{p} ({\mathfrak {UG}}^{m} \operatorname {(\mathscr {L}ie)})$
is trivial for
${\mathrm {H}}_{p} ({\mathfrak {UG}}^{m} \operatorname {(\mathscr {L}ie)})$
is trivial for
![]() $0 < p \le 3m + 2$
when
$0 < p \le 3m + 2$
when
![]() $m \ge 3$
is odd (see Remark 4.30). Using this, we obtain the following consequence of our main theorem.
$m \ge 3$
is odd (see Remark 4.30). Using this, we obtain the following consequence of our main theorem.
Corollary 1.2. Let
![]() $3 \le k < l \le 2k - 2$
and
$3 \le k < l \le 2k - 2$
and
![]() $2 \le g$
be integers such that
$2 \le g$
be integers such that
![]() $k + l$
is odd. Then there is, in cohomological degrees
$k + l$
is odd. Then there is, in cohomological degrees
![]() $\le {\min } \left ( g - 2, 3(k + l) - 4 \right )$
, an isomorphism of graded algebras
$\le {\min } \left ( g - 2, 3(k + l) - 4 \right )$
, an isomorphism of graded algebras
compatible with the stabilization maps on the left-hand side.
Sketch of the proof of Theorem 1.1
From now on, we fix some
![]() $3 \le k < l \le 2k - 2$
and drop them from the notation. The starting point of our proof are methods recently developed by Berglund–Zeman [Reference Berglund and ZemanBZ22] which in particular yield an isomorphism
$3 \le k < l \le 2k - 2$
and drop them from the notation. The starting point of our proof are methods recently developed by Berglund–Zeman [Reference Berglund and ZemanBZ22] which in particular yield an isomorphism
for any
![]() $\Gamma ^{\mathbb {Z}}_g$
-representation P (the details of applying their methods to relative self-equivalences are worked out in the upcoming paper [Reference Berglund and StollBS] joint with Berglund). Here, the differential graded Lie algebra
$\Gamma ^{\mathbb {Z}}_g$
-representation P (the details of applying their methods to relative self-equivalences are worked out in the upcoming paper [Reference Berglund and StollBS] joint with Berglund). Here, the differential graded Lie algebra
![]() $\mathfrak g_g$
is the Quillen model of the 1-connected cover of
$\mathfrak g_g$
is the Quillen model of the 1-connected cover of
![]() ${\mathrm {B}} {{\mathrm {aut}}_{\partial }}(M_{g, 1})$
. We write
${\mathrm {B}} {{\mathrm {aut}}_{\partial }}(M_{g, 1})$
. We write
![]() ${\mathrm {H}}_{\mathrm {CE}}^{*} (\mathfrak g_g)$
for its Chevalley–Eilenberg cohomology, and we set
${\mathrm {H}}_{\mathrm {CE}}^{*} (\mathfrak g_g)$
for its Chevalley–Eilenberg cohomology, and we set
where R is a commutative ring and
![]() ${\langle {-},{-}\rangle _\cap }$
is the intersection pairing. The Lie algebra
${\langle {-},{-}\rangle _\cap }$
is the intersection pairing. The Lie algebra
![]() $\mathfrak g_g$
has an explicit description which was shown by Berglund–Madsen [Reference Berglund and MadsenBM20] to be isomorphic to
$\mathfrak g_g$
has an explicit description which was shown by Berglund–Madsen [Reference Berglund and MadsenBM20] to be isomorphic to
equipped with the trivial differential. Here,
![]() $\operatorname {\mathscr {L}ie}$
is (the symmetric sequence underlying) the cyclic Lie operad,
$\operatorname {\mathscr {L}ie}$
is (the symmetric sequence underlying) the cyclic Lie operad,
![]() $\mathrm {s}$
denotes a degree shift,
$\mathrm {s}$
denotes a degree shift,
![]() ${\mathscr A} [{-}]$
is the Schur functor associated to
${\mathscr A} [{-}]$
is the Schur functor associated to
![]() $\mathscr A$
, and
$\mathscr A$
, and
![]() ${(-)}^+$
denotes positive truncation.
${(-)}^+$
denotes positive truncation.
The next step is to simplify the right-hand side of (1.2). To this end, we prove, using the previously mentioned work of Li–Sun [Reference Li and SunLS19], that the canonical map
is an isomorphism in a stable range when P is an algebraic representation of
![]() $\Gamma ^{\mathbb {Q}}_g$
. (See also work of Krannich [Reference KrannichKra20], where an analogous argument is made to obtain a similar stable range in the case
$\Gamma ^{\mathbb {Q}}_g$
. (See also work of Krannich [Reference KrannichKra20], where an analogous argument is made to obtain a similar stable range in the case
![]() $k = l$
.)
$k = l$
.)
This shows that it is enough to identify the (stable) cohomology of the invariants
![]() $\left ( {\operatorname {C}_{\mathrm {CE}}^{*}}(\mathfrak g_g) \mathop{\mathop{\otimes}} P \right )^{\Gamma ^{\mathbb {Q}}_g}$
. For sake of exposition, we will now focus on the case
$\left ( {\operatorname {C}_{\mathrm {CE}}^{*}}(\mathfrak g_g) \mathop{\mathop{\otimes}} P \right )^{\Gamma ^{\mathbb {Q}}_g}$
. For sake of exposition, we will now focus on the case
![]() $P = {\mathbb {Q}}$
. In the paper, we do carry out the first part of the argument for a certain class of nontrivial representations as well, though. Similar situations, arising from
$P = {\mathbb {Q}}$
. In the paper, we do carry out the first part of the argument for a certain class of nontrivial representations as well, though. Similar situations, arising from
![]() ${\mathrm {Sp}}_{2g}$
or
${\mathrm {Sp}}_{2g}$
or
![]() $O_{g,g}$
instead of
$O_{g,g}$
instead of
![]() ${\mathrm {GL}}_{g}$
, have been considered by Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93, Reference Kontsevich and JosephKon94] (see also Conant–Vogtmann [Reference Conant and VogtmannCV03]) in the symplectic case and by Berglund–Madsen [Reference Berglund and MadsenBM20] in both cases. In our situation, we use coinvariant theory methods similar to those of [Reference Berglund and MadsenBM20] to obtain a description of the stable cohomology in terms of a directed version of the Lie graph complex, which we denote by
${\mathrm {GL}}_{g}$
, have been considered by Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93, Reference Kontsevich and JosephKon94] (see also Conant–Vogtmann [Reference Conant and VogtmannCV03]) in the symplectic case and by Berglund–Madsen [Reference Berglund and MadsenBM20] in both cases. In our situation, we use coinvariant theory methods similar to those of [Reference Berglund and MadsenBM20] to obtain a description of the stable cohomology in terms of a directed version of the Lie graph complex, which we denote by
![]() ${\mathfrak {DG}}^{m}{{\operatorname {(\mathscr {L}ie)}}}$
. It is defined in the same way as
${\mathfrak {DG}}^{m}{{\operatorname {(\mathscr {L}ie)}}}$
. It is defined in the same way as
![]() ${\mathfrak {UG}}^{m}{\operatorname {(\mathscr {L}ie)}}$
, except that every edge is equipped with a direction, which (unlike an orientation) must be respected by automorphisms of the graph.
${\mathfrak {UG}}^{m}{\operatorname {(\mathscr {L}ie)}}$
, except that every edge is equipped with a direction, which (unlike an orientation) must be respected by automorphisms of the graph.
Theorem 1.3 (see Corollary 3.33).
There is an isomorphism
of differential graded coalgebras, compatible with the stabilization maps on the left-hand side. Here,
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\operatorname {\mathscr {L}ie})}$
is the subcomplex of
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\operatorname {\mathscr {L}ie})}$
is the subcomplex of
![]() ${\mathfrak {DG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
spanned by truncated directed graphs, which are those that do not have vertices of valence zero or one and whose vertices of valence two have only incoming edges.
${\mathfrak {DG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
spanned by truncated directed graphs, which are those that do not have vertices of valence zero or one and whose vertices of valence two have only incoming edges.
Remark. At the heart of this theorem actually lies an unstable identification of a certain subcomplex of
![]() ${{\operatorname {C}^{\mathrm {CE}}_{*}} (\mathfrak g_g)} _{\Gamma _g}$
. Moreover, we prove a more general statement, which also applies to a certain class of nontrivial representations P, as well as to all cyclic operads and not just
${{\operatorname {C}^{\mathrm {CE}}_{*}} (\mathfrak g_g)} _{\Gamma _g}$
. Moreover, we prove a more general statement, which also applies to a certain class of nontrivial representations P, as well as to all cyclic operads and not just
![]() $\operatorname {\mathscr {L}ie}$
.
$\operatorname {\mathscr {L}ie}$
.
Although less ubiquitous than undirected graph complexes, directed versions have appeared in the literature before; see, for example, [Reference WillwacherWil14, Reference ŽivkovićŽiv20, Reference Dolgushev and RogersDR19]. Surprisingly, it turns out that the homology of the truncated directed graph complex
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\operatorname {\mathscr {L}ie})}$
is actually isomorphic to the one of
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\operatorname {\mathscr {L}ie})}$
is actually isomorphic to the one of
![]() ${\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
. We will now explain the idea of this argument. Restricting the differential of
${\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
. We will now explain the idea of this argument. Restricting the differential of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\operatorname {\mathscr {L}ie})}$
to the two edges incident to a vertex of valence two (which must be labeled by the identity operation) yields the following picture.
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\operatorname {\mathscr {L}ie})}$
to the two edges incident to a vertex of valence two (which must be labeled by the identity operation) yields the following picture.

Thus, intuitively, taking homology should kill the difference between the two orientations of an edge. This can be formalized using a spectral sequence argument to prove the following theorem. Together with the preceding results, this implies Theorem 1.1.
Theorem 1.4 (see Theorem 4.28).
Let
![]() $\mathscr C$
be a cyclic operad such that
$\mathscr C$
be a cyclic operad such that
![]() ${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )} \cong {{\mathbb {Q}} \langle {\mathrm {id}} \rangle }$
. Then there is, for any
${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )} \cong {{\mathbb {Q}} \langle {\mathrm {id}} \rangle }$
. Then there is, for any
![]() $m \in {\mathbb {N}_0}$
, an isomorphism
$m \in {\mathbb {N}_0}$
, an isomorphism
of graded coalgebras.
Remark. We only carry out this argument in the situation arising from trivial coefficients
![]() $P = {\mathbb {Q}}$
. There should exist a more general statement of this form, though.
$P = {\mathbb {Q}}$
. There should exist a more general statement of this form, though.
Remark. For the nontruncated directed graph complex, an argument similar to this has been sketched by Willwacher [Reference WillwacherWil14, Appendix K].
Related work and further research
Building on their work for homotopy automorphisms, Berglund–Madsen [Reference Berglund and MadsenBM20] also computed, for
![]() $k \ge 3$
, the stable cohomology of the classifying spaces
$k \ge 3$
, the stable cohomology of the classifying spaces
![]() ${\mathrm {B}} \widetilde {\mathrm {Diff}}_\partial \left ( M^{k,k}_{g,1} \right )$
of block diffeomorphisms. Combining their methods with the methods of our paper (as well as an upgrade of the methods of [Reference Berglund and ZemanBZ22] to automorphisms of bundles, which is planned to be contained in the upcoming paper [Reference Berglund and StollBS] joint with Berglund or a follow-up) should yield a computation of the stable cohomology of
${\mathrm {B}} \widetilde {\mathrm {Diff}}_\partial \left ( M^{k,k}_{g,1} \right )$
of block diffeomorphisms. Combining their methods with the methods of our paper (as well as an upgrade of the methods of [Reference Berglund and ZemanBZ22] to automorphisms of bundles, which is planned to be contained in the upcoming paper [Reference Berglund and StollBS] joint with Berglund or a follow-up) should yield a computation of the stable cohomology of
![]() ${\mathrm {B}} \widetilde {\mathrm {Diff}}_\partial \left ( M^{k,l}_{g,1} \right )$
for
${\mathrm {B}} \widetilde {\mathrm {Diff}}_\partial \left ( M^{k,l}_{g,1} \right )$
for
![]() $3 \le k < l \le 2k - 2$
. This is currently work in progress. It should significantly simplify and extend a result of Ebert–Reinhold [Reference Ebert and ReinholdER22], who compute, in a hands-on way, the stable cohomology of
$3 \le k < l \le 2k - 2$
. This is currently work in progress. It should significantly simplify and extend a result of Ebert–Reinhold [Reference Ebert and ReinholdER22], who compute, in a hands-on way, the stable cohomology of
![]() ${\mathrm {B}} \widetilde {\mathrm {Diff}}_\partial \left ( M^{k,k+1}_{g,1} \right )$
up to degree roughly k. From this, they deduce, using classical methods as well as a recent result of Krannich [Reference KrannichKra22], the stable cohomology of
${\mathrm {B}} \widetilde {\mathrm {Diff}}_\partial \left ( M^{k,k+1}_{g,1} \right )$
up to degree roughly k. From this, they deduce, using classical methods as well as a recent result of Krannich [Reference KrannichKra22], the stable cohomology of
![]() ${\mathrm {B}} \mathrm {Diff}_\partial \left ( M^{k,k+1}_{g,1} \right )$
in the same range. A complete calculation of the stable cohomology of block diffeomorphisms would, in the same way, allow to extend this result to degree roughly
${\mathrm {B}} \mathrm {Diff}_\partial \left ( M^{k,k+1}_{g,1} \right )$
in the same range. A complete calculation of the stable cohomology of block diffeomorphisms would, in the same way, allow to extend this result to degree roughly
![]() $2k$
. Moreover, one might hope to extend this calculation even further, for example by using methods recently developed by Krannich–Randal-Williams [Reference Krannich and Randal-WilliamsKR21]. This is the goal of current work in progress joint with Krannich.
$2k$
. Moreover, one might hope to extend this calculation even further, for example by using methods recently developed by Krannich–Randal-Williams [Reference Krannich and Randal-WilliamsKR21]. This is the goal of current work in progress joint with Krannich.
One question one might hope to attack with this approach is to determine the images of the cohomology classes coming from the graph complex under the morphism
induced by the forgetful map. When
![]() $k = l$
, the stable cohomology of the right-hand side has been computed completely in celebrated work of Galatius–Randal-Williams [Reference Galatius and Randal-WilliamsGR14], but even in that case, it is mostly unknown what the graph cohomology classes map to. Results in this direction have the potential to yield very interesting information about both the cohomology of the diffeomorphism groups as well as the homology of the graph complex and thus the homology of
$k = l$
, the stable cohomology of the right-hand side has been computed completely in celebrated work of Galatius–Randal-Williams [Reference Galatius and Randal-WilliamsGR14], but even in that case, it is mostly unknown what the graph cohomology classes map to. Results in this direction have the potential to yield very interesting information about both the cohomology of the diffeomorphism groups as well as the homology of the graph complex and thus the homology of
![]() $\mathrm {Out}(F_g)$
.
$\mathrm {Out}(F_g)$
.
Structure of this paper
In Section 2, we fix some conventions, recall various definitions and prove basic lemmas needed throughout the rest of the paper. In Section 3, we use coinvariant theory to prove Theorem 1.3. In Section 4, we prove Theorem 1.4 using a spectral sequence argument. Finally, Section 5 contains the topological part, in which we combine everything to obtain Theorem 1.1.
2 Preliminaries
In this section, we collect a number of basic conventions, notations, definitions and lemmas which we will use throughout the rest of this paper.
2.1 Graded vector spaces
Convention 2.1. The base field is
![]() ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
Notation 2.2. We denote by
![]() ${{\mathbf {Vect}}}$
the category of vector spaces and linear maps.
${{\mathbf {Vect}}}$
the category of vector spaces and linear maps.
Convention 2.3. All gradings are by
![]() ${\mathbb {Z}}$
.
${\mathbb {Z}}$
.
Notation 2.4. We denote by
![]() ${{{\mathbf {GrVect}}}}$
the category of graded vector spaces and grading preserving linear maps. Sometimes we will implicitly consider an ungraded vector space (such as
${{{\mathbf {GrVect}}}}$
the category of graded vector spaces and grading preserving linear maps. Sometimes we will implicitly consider an ungraded vector space (such as
![]() ${\mathbb {Q}}$
) as a graded vector space concentrated in degree
${\mathbb {Q}}$
) as a graded vector space concentrated in degree
![]() $0$
.
$0$
.
Notation 2.5. For
![]() $k \in {\mathbb {Z}}$
, we denote by
$k \in {\mathbb {Z}}$
, we denote by
![]() $\mathrm {s}^{k}(-)$
a k-fold degree shift. For V a graded vector space, the graded vector space
$\mathrm {s}^{k}(-)$
a k-fold degree shift. For V a graded vector space, the graded vector space
![]() $\mathrm {s}^{k} V$
is given by
$\mathrm {s}^{k} V$
is given by ![]() . When
. When
![]() $k = 1$
, we just write
$k = 1$
, we just write ![]() .
.
Notation 2.6. Let
![]() $m \in {\mathbb {Z}}$
. A graded symplectic form of degree
$m \in {\mathbb {Z}}$
. A graded symplectic form of degree
![]() $-m$
on a graded vector spaces V is a nondegenerate bilinear form of degree
$-m$
on a graded vector spaces V is a nondegenerate bilinear form of degree
![]() $-m$
$-m$
such that
![]() $\langle v, w \rangle = (-1)^{ | v | | w | + 1} \langle w, v \rangle $
(i.e. it is graded anti-symmetric).
$\langle v, w \rangle = (-1)^{ | v | | w | + 1} \langle w, v \rangle $
(i.e. it is graded anti-symmetric).
We denote by
![]() ${{\mathbf {Sp}}}^{m}$
the category of finite-dimensional graded vector spaces equipped with a graded symplectic form of degree
${{\mathbf {Sp}}}^{m}$
the category of finite-dimensional graded vector spaces equipped with a graded symplectic form of degree
![]() $-m$
with morphisms those linear maps of degree
$-m$
with morphisms those linear maps of degree
![]() $0$
that preserve the bilinear form.
$0$
that preserve the bilinear form.
Remark 2.7. Note that a morphism of
![]() ${{\mathbf {Sp}}}^{m}$
is automatically injective.
${{\mathbf {Sp}}}^{m}$
is automatically injective.
2.2 Double complexes
Convention 2.8. A double complex is a bigraded vector space
![]() $C_{*,*}$
equipped with a differential
$C_{*,*}$
equipped with a differential
![]() $d^1$
of bidegree
$d^1$
of bidegree
![]() $(-1, 0)$
and a differential
$(-1, 0)$
and a differential
![]() $d^2$
of bidegree
$d^2$
of bidegree
![]() $(0, -1)$
such that
$(0, -1)$
such that
![]() $d^1 \circ d^2 = - d^2 \circ d^1$
.
$d^1 \circ d^2 = - d^2 \circ d^1$
.
Notation 2.9. Let
![]() $(C_{*,*}, d^1, d^2)$
be a double complex. We denote by
$(C_{*,*}, d^1, d^2)$
be a double complex. We denote by
![]() $\operatorname {\mathrm {Tot}} C$
its total complex – that is, the chain complex with underlying graded vector space
$\operatorname {\mathrm {Tot}} C$
its total complex – that is, the chain complex with underlying graded vector space
and differential
![]() $d = d^1 + d^2$
.
$d = d^1 + d^2$
.
Lemma 2.10. Let
![]() $(C_{*,*}, d^1, d^2)$
be a double complex concentrated in nonnegative degrees such that
$(C_{*,*}, d^1, d^2)$
be a double complex concentrated in nonnegative degrees such that
![]() ${\mathrm {H}}_{*} (C_{p,*}, d^2)$
is concentrated in degree
${\mathrm {H}}_{*} (C_{p,*}, d^2)$
is concentrated in degree
![]() $0$
for all p. Denote by
$0$
for all p. Denote by
the map of chain complexes given by the canonical projections
![]() $C_{p, 0} \to {\mathrm {H}}_{0} (C_{p,*}, d^2)$
and the trivial map on
$C_{p, 0} \to {\mathrm {H}}_{0} (C_{p,*}, d^2)$
and the trivial map on
![]() $C_{p, q}$
for
$C_{p, q}$
for
![]() $q> 0$
. Then f is a quasi-isomorphism.
$q> 0$
. Then f is a quasi-isomorphism.
Proof. The map f canonically lifts to a map
![]() $g \colon C_{*,*} \to \left ( {\mathrm {H}}_{0} (C_{\bullet ,*}, d^2), d_1 \right )$
of double complexes, where the target is equipped with the double complex structure concentrated in bidegrees
$g \colon C_{*,*} \to \left ( {\mathrm {H}}_{0} (C_{\bullet ,*}, d^2), d_1 \right )$
of double complexes, where the target is equipped with the double complex structure concentrated in bidegrees
![]() $(p, 0)$
. The map g induces an isomorphism between the
$(p, 0)$
. The map g induces an isomorphism between the
![]() $E^1$
-pages of the spectral sequences associated to these double complexes whose zeroth differential is given by
$E^1$
-pages of the spectral sequences associated to these double complexes whose zeroth differential is given by
![]() $d^2$
(see, for example, Weibel [Reference WeibelWei95, §5.6]). By the Comparison Theorem for spectral sequences, this implies that f is a quasi-isomorphism (see, for example, [Reference WeibelWei95, Theorem 5.2.12]).
$d^2$
(see, for example, Weibel [Reference WeibelWei95, §5.6]). By the Comparison Theorem for spectral sequences, this implies that f is a quasi-isomorphism (see, for example, [Reference WeibelWei95, Theorem 5.2.12]).
2.3 Group actions
Definition 2.11. Let
![]() $\mathcal G$
be a groupoid and
$\mathcal G$
be a groupoid and
![]() $\mathcal C$
a category. A left
$\mathcal C$
a category. A left
![]() $\mathcal G$
-module in
$\mathcal G$
-module in
![]() $\mathcal C$
is a functor
$\mathcal C$
is a functor
![]() $M \colon \mathcal G \to \mathcal C$
, and a right
$M \colon \mathcal G \to \mathcal C$
, and a right
![]() $\mathcal G$
-module is a functor
$\mathcal G$
-module is a functor
![]() $M \colon {{\mathcal G}^{\mathrm {op}}} \to \mathcal C$
.
$M \colon {{\mathcal G}^{\mathrm {op}}} \to \mathcal C$
.
Remark 2.12. Identifying a group G with its associated one-object groupoid, a left G-module in
![]() $\mathcal C$
is an object of
$\mathcal C$
is an object of
![]() $\mathcal C$
together with a left G-action, and a right G-module in
$\mathcal C$
together with a left G-action, and a right G-module in
![]() $\mathcal C$
is an object of
$\mathcal C$
is an object of
![]() $\mathcal C$
together with a right G-action.
$\mathcal C$
together with a right G-action.
Convention 2.13. Unless otherwise stated, ‘module in
![]() $\mathcal C$
’ will mean ‘left module in
$\mathcal C$
’ will mean ‘left module in
![]() $\mathcal C$
’. In particular, group actions will be from the left. If we omit the category
$\mathcal C$
’. In particular, group actions will be from the left. If we omit the category
![]() $\mathcal C$
, we mean a (left or right) module in the category
$\mathcal C$
, we mean a (left or right) module in the category
![]() ${{{\mathbf {GrVect}}}}$
.
${{{\mathbf {GrVect}}}}$
.
Definition 2.14. For
![]() $\mathcal G$
a groupoid,
$\mathcal G$
a groupoid,
![]() $\mathcal C$
a category and M a (left)
$\mathcal C$
a category and M a (left)
![]() $\mathcal G$
-module in
$\mathcal G$
-module in
![]() $\mathcal C$
, we will denote by
$\mathcal C$
, we will denote by
![]() $M^{\mathrm {op}}$
the right
$M^{\mathrm {op}}$
the right
![]() $\mathcal G$
-module in
$\mathcal G$
-module in
![]() $\mathcal C$
given by the composition
$\mathcal C$
given by the composition
where the first map is the isomorphism given by the identity on objects and by taking the inverses of morphisms.
Remark 2.15. If
![]() $\mathcal G = G$
is a group, this means that
$\mathcal G = G$
is a group, this means that
![]() $M^{\mathrm {op}}$
is the right G-module with the opposite action (i.e.,
$M^{\mathrm {op}}$
is the right G-module with the opposite action (i.e., ![]() ).
).
2.4 Kan extensions
The following lemmas will be useful later.
Lemma 2.16. Let G be a group and S a G-set (i.e., a functor
![]() $S \colon G \to {{{\mathbf {Set}}}}$
). Then a functor X from the Grothendieck construction
$S \colon G \to {{{\mathbf {Set}}}}$
). Then a functor X from the Grothendieck construction
![]() ${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S$
to some category
${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S$
to some category
![]() $\mathcal C$
can be equivalently described as a family
$\mathcal C$
can be equivalently described as a family
![]() $(X_s)_{s \in S}$
of objects of
$(X_s)_{s \in S}$
of objects of
![]() $\mathcal C$
equipped with morphisms
$\mathcal C$
equipped with morphisms
![]() $g_s \colon X_s \to X_{g \mathbin {.} s}$
for every
$g_s \colon X_s \to X_{g \mathbin {.} s}$
for every
![]() $g \in G$
and
$g \in G$
and
![]() $s \in S$
such that they are functorial in the sense that
$s \in S$
such that they are functorial in the sense that
![]() $h_{g \mathbin {.} s} \circ g_s = (h g)_s$
.
$h_{g \mathbin {.} s} \circ g_s = (h g)_s$
.
Moreover, let
![]() $H \trianglelefteq G$
be a normal subgroup. If
$H \trianglelefteq G$
be a normal subgroup. If
![]() $\mathcal C$
is cocomplete, then there is an isomorphism
$\mathcal C$
is cocomplete, then there is an isomorphism
 $$\begin{align*}{\left( \coprod_{s \in S} X_s \right)_{H}} \cong \mathop{\operatorname{Lan}_{{\mathop{\mathchoice{\textstyle}{}{}{} \int_{G}}} S \to {{G}/{H}}}} X \end{align*}$$
$$\begin{align*}{\left( \coprod_{s \in S} X_s \right)_{H}} \cong \mathop{\operatorname{Lan}_{{\mathop{\mathchoice{\textstyle}{}{}{} \int_{G}}} S \to {{G}/{H}}}} X \end{align*}$$
of
![]() $({{G}/{H}})$
-modules in
$({{G}/{H}})$
-modules in
![]() $\mathcal C$
. On the left-hand side
$\mathcal C$
. On the left-hand side
![]() $g \in G$
, acts on
$g \in G$
, acts on
![]() $\coprod _{s \in S} X_s$
by mapping
$\coprod _{s \in S} X_s$
by mapping
![]() $X_s$
to
$X_s$
to
![]() $X_{g \mathbin {.} s}$
via
$X_{g \mathbin {.} s}$
via
![]() $g_s$
; the action of
$g_s$
; the action of
![]() ${{G}/{H}}$
is the induced action on the coinvariants. On the right-hand side, we have the left Kan extension of X along the composite
${{G}/{H}}$
is the induced action on the coinvariants. On the right-hand side, we have the left Kan extension of X along the composite
![]() ${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S \to G \to {{G}/{H}}$
of the canonical projection and the quotient map.
${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S \to G \to {{G}/{H}}$
of the canonical projection and the quotient map.
Proof. The first claim follows directly from the definition of the Grothendieck construction. For the second claim, note that the G-module
![]() $\coprod _{s \in S} X_s$
is isomorphic to the left Kan extension of X along the canonical projection
$\coprod _{s \in S} X_s$
is isomorphic to the left Kan extension of X along the canonical projection
![]() ${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S \to G$
. Taking H-coinvariants of this corresponds to left Kan extending further along the quotient map
${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S \to G$
. Taking H-coinvariants of this corresponds to left Kan extending further along the quotient map
![]() $G \to {{G}/{H}}$
. Since Kan extensions compose, the result is isomorphic to the left Kan extension of X along the composite
$G \to {{G}/{H}}$
. Since Kan extensions compose, the result is isomorphic to the left Kan extension of X along the composite
![]() ${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S \to {{G}/{H}}$
.
${\mathop {\mathchoice {\textstyle }{}{}{} \int _{G}}} S \to {{G}/{H}}$
.
We will now provide an explicit identification of the left Kan extension in the lemma above. This takes the form of the following (more general) lemmas.
Lemma 2.17. Let
![]() $\mathcal G$
be a groupoid, H a group and
$\mathcal G$
be a groupoid, H a group and
![]() $F \colon \mathcal G \to H$
a functor. Denote by
$F \colon \mathcal G \to H$
a functor. Denote by
![]() $\mathcal G^F \subseteq \mathcal G$
the wide subcategory of those morphisms that F maps to the neutral element
$\mathcal G^F \subseteq \mathcal G$
the wide subcategory of those morphisms that F maps to the neutral element
![]() $e_H \in H$
. Also denote by
$e_H \in H$
. Also denote by
![]() $*$
the unique object of H considered as a groupoid, and by
$*$
the unique object of H considered as a groupoid, and by
![]() $F \mathbin {\downarrow } *$
the corresponding comma category. Then there is a fully faithful functor
$F \mathbin {\downarrow } *$
the corresponding comma category. Then there is a fully faithful functor
given by sending an object
![]() $G \in \mathcal G^F$
to
$G \in \mathcal G^F$
to
![]() $(G, e_H \colon F(G) = * \to *)$
and a morphism
$(G, e_H \colon F(G) = * \to *)$
and a morphism
![]() $g \colon G \to G'$
to itself.
$g \colon G \to G'$
to itself.
Moreover, assume that, for all
![]() $G \in \mathcal G$
and
$G \in \mathcal G$
and
![]() $h \in H$
, there exists a morphism
$h \in H$
, there exists a morphism
![]() $g_{G,h} \colon G \to K_{G,h}$
in
$g_{G,h} \colon G \to K_{G,h}$
in
![]() $\mathcal G$
such that
$\mathcal G$
such that
![]() $F(g_{G,h}) = h$
. Then
$F(g_{G,h}) = h$
. Then
![]() $\Phi _F$
is an equivalence of categories with an inverse (up to natural isomorphism) given by the functor
$\Phi _F$
is an equivalence of categories with an inverse (up to natural isomorphism) given by the functor
given on objects by
![]() $(G, h) \mapsto K_{G,h}$
and on morphisms by
$(G, h) \mapsto K_{G,h}$
and on morphisms by
![]() $(g \colon (G, h) \to (G', h')) \mapsto g_{G',h'} g {g_{G,h}^{-1}}$
. (Note that
$(g \colon (G, h) \to (G', h')) \mapsto g_{G',h'} g {g_{G,h}^{-1}}$
. (Note that
![]() $\Psi _F$
depends on the choice of
$\Psi _F$
depends on the choice of
![]() $g_{G,h}$
for all
$g_{G,h}$
for all
![]() $G \in \mathcal G$
and
$G \in \mathcal G$
and
![]() $h \in H$
.) The natural isomorphism
$h \in H$
.) The natural isomorphism
![]() ${\mathrm {id}}_{F \mathbin {\downarrow } *} \to \Phi _F \circ \Psi _F$
is, at an object
${\mathrm {id}}_{F \mathbin {\downarrow } *} \to \Phi _F \circ \Psi _F$
is, at an object
![]() $(G, h)$
, given by the map
$(G, h)$
, given by the map
![]() $g_{G,h} \colon G \to K_{G,h}$
.
$g_{G,h} \colon G \to K_{G,h}$
.
Proof. This follows easily from the definitions.
Lemma 2.18. In the situation of the second part of Lemma 2.17, let
![]() $\mathcal C$
be a cocomplete category and
$\mathcal C$
be a cocomplete category and
![]() $X \colon \mathcal G \to \mathcal C$
a functor. Furthermore, for an element
$X \colon \mathcal G \to \mathcal C$
a functor. Furthermore, for an element
![]() $h \in H$
, let
$h \in H$
, let
![]() $A_h$
denote the functor
$A_h$
denote the functor
![]() $\mathcal G^F \to \mathcal G^F$
that is given by
$\mathcal G^F \to \mathcal G^F$
that is given by
![]() $G \mapsto K_{G,h}$
on objects and that sends a morphism
$G \mapsto K_{G,h}$
on objects and that sends a morphism
![]() $g \colon G \to G'$
to
$g \colon G \to G'$
to
![]() $g_{G',h} g {g_{G,h}^{-1}}$
. Then there is an isomorphism
$g_{G',h} g {g_{G,h}^{-1}}$
. Then there is an isomorphism
of H-modules in
![]() $\mathcal C$
. Here an element
$\mathcal C$
. Here an element
![]() $h \in H$
acts on the right-hand side via the functor
$h \in H$
acts on the right-hand side via the functor
![]() $A_h$
and the natural transformation
$A_h$
and the natural transformation
![]() ${\mathrm {inc}}_{\mathcal G^F} \to {{\mathrm {inc}}_{\mathcal G^F}} \circ A_h$
given, at an object
${\mathrm {inc}}_{\mathcal G^F} \to {{\mathrm {inc}}_{\mathcal G^F}} \circ A_h$
given, at an object
![]() $G \in \mathcal G^F$
, by
$G \in \mathcal G^F$
, by
![]() $g_{G,h} \colon G \to K_{G,h}$
.
$g_{G,h} \colon G \to K_{G,h}$
.
Proof. The left Kan extension in the statement is, at the unique object
![]() $*$
of H, isomorphic to
$*$
of H, isomorphic to
![]() ${\mathrm {colim}}_{F \mathbin {\downarrow } *}\ (X \circ {\mathrm {pr}})$
, where
${\mathrm {colim}}_{F \mathbin {\downarrow } *}\ (X \circ {\mathrm {pr}})$
, where
![]() ${\mathrm {pr}} \colon F \mathbin {\downarrow } * \to \mathcal G$
denotes the projection. The action of an element
${\mathrm {pr}} \colon F \mathbin {\downarrow } * \to \mathcal G$
denotes the projection. The action of an element
![]() $h \in H$
on this object is induced by the functor
$h \in H$
on this object is induced by the functor
![]() $F \mathbin {\downarrow } * \to F \mathbin {\downarrow } *$
given by
$F \mathbin {\downarrow } * \to F \mathbin {\downarrow } *$
given by
![]() $(G, h') \mapsto (G, h h')$
(note that this functor commutes with the projection). That this is isomorphic, as an H-module, to the description given in the statement follows from Lemma 2.17.
$(G, h') \mapsto (G, h h')$
(note that this functor commutes with the projection). That this is isomorphic, as an H-module, to the description given in the statement follows from Lemma 2.17.
2.5 Symmetric sequences
Definition 2.19. We denote by
![]() ${{{\mathbf {LinSet}}}}$
the category with objects finite sets equipped with a linear order and morphisms the maps of sets (not necessarily respecting the order), by
${{{\mathbf {LinSet}}}}$
the category with objects finite sets equipped with a linear order and morphisms the maps of sets (not necessarily respecting the order), by ![]() its maximal subgroupoid, and by
its maximal subgroupoid, and by
![]() ${{{\mathbf {P}}}}$
the skeleton of
${{{\mathbf {P}}}}$
the skeleton of
![]() ${{{\mathbf {\Sigma }}}}$
spanned by the objects
${{{\mathbf {\Sigma }}}}$
spanned by the objects ![]() for
for
![]() $n \in {\mathbb {N}_0}$
.
$n \in {\mathbb {N}_0}$
.
Remark 2.20. There exist canonical equivalences of categories
![]() ${{{\mathbf {LinSet}}}} \to {{{\mathbf {FinSet}}}}$
,
${{{\mathbf {LinSet}}}} \to {{{\mathbf {FinSet}}}}$
,
![]() ${{{\mathbf {\Sigma }}}} \to {\operatorname {Core}({{\mathbf {FinSet}}})}$
, and
${{{\mathbf {\Sigma }}}} \to {\operatorname {Core}({{\mathbf {FinSet}}})}$
, and
![]() ${{{\mathbf {P}}}} \to {\operatorname {Core}({{\mathbf {FinSet}}})}$
, though neither of them admit a canonical inverse equivalence. The inclusion
${{{\mathbf {P}}}} \to {\operatorname {Core}({{\mathbf {FinSet}}})}$
, though neither of them admit a canonical inverse equivalence. The inclusion
![]() ${{{\mathbf {P}}}} \to {{{\mathbf {\Sigma }}}}$
, however, is an equivalence that does admit a canonical inverse equivalence – namely, by identifying an object
${{{\mathbf {P}}}} \to {{{\mathbf {\Sigma }}}}$
, however, is an equivalence that does admit a canonical inverse equivalence – namely, by identifying an object
![]() $S \in {{{\mathbf {\Sigma }}}}$
with an object in
$S \in {{{\mathbf {\Sigma }}}}$
with an object in
![]() ${{{\mathbf {P}}}}$
via the unique map that respects the linear order.
${{{\mathbf {P}}}}$
via the unique map that respects the linear order.
Definition 2.21. Let
![]() $\mathcal V$
be a symmetric monoidal category and
$\mathcal V$
be a symmetric monoidal category and
![]() $V \in \mathcal V$
. Then there is a functor
$V \in \mathcal V$
. Then there is a functor
![]() $V^{{{\otimes}} -} \colon {{{\mathbf {P}}}} \to \mathcal V$
given on objects by
$V^{{{\otimes}} -} \colon {{{\mathbf {P}}}} \to \mathcal V$
given on objects by
![]() ${\underline {n}} \mapsto V^{{{\otimes}} n}$
and defined on morphisms via the symmetrizer isomorphism. Pulling this back via the canonical equivalence
${\underline {n}} \mapsto V^{{{\otimes}} n}$
and defined on morphisms via the symmetrizer isomorphism. Pulling this back via the canonical equivalence
![]() ${{{\mathbf {\Sigma }}}} \to {{{\mathbf {P}}}}$
, we obtain a functor
${{{\mathbf {\Sigma }}}} \to {{{\mathbf {P}}}}$
, we obtain a functor
![]() ${{{\mathbf {\Sigma }}}} \to \mathcal V$
which we also denote by
${{{\mathbf {\Sigma }}}} \to \mathcal V$
which we also denote by
![]() $V^{{{\otimes}} -}$
.
$V^{{{\otimes}} -}$
.
Similarly, for
![]() $S \in {{{\mathbf {\Sigma }}}}$
and
$S \in {{{\mathbf {\Sigma }}}}$
and
![]() $(V_s)_{s \in S}$
a family of objects of
$(V_s)_{s \in S}$
a family of objects of
![]() $\mathcal V$
, we write
$\mathcal V$
, we write
![]() $\bigotimes _{s \in S} V_s$
for
$\bigotimes _{s \in S} V_s$
for
![]() $V_{s(1)} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} V_{s(|S|)}$
, where
$V_{s(1)} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} V_{s(|S|)}$
, where
![]() $s \colon {\underline {|S|}} \to S$
is the unique order-preserving bijection. We will also use the notation
$s \colon {\underline {|S|}} \to S$
is the unique order-preserving bijection. We will also use the notation
![]() $\bigotimes _{s \in S} v_s$
to denote elementary tensors of this tensor product.
$\bigotimes _{s \in S} v_s$
to denote elementary tensors of this tensor product.
Definition 2.22. For
![]() $\mathscr M$
a
$\mathscr M$
a
![]() ${{{\mathbf {\Sigma }}}}$
-module and
${{{\mathbf {\Sigma }}}}$
-module and
![]() $a \colon S \to T$
a morphism of
$a \colon S \to T$
a morphism of
![]() ${{{\mathbf {LinSet}}}}$
, we write
${{{\mathbf {LinSet}}}}$
, we write
where
![]() ${a^{-1}}(t) \subseteq S$
has the linear order induced from the one of S. This construction is functorial in
${a^{-1}}(t) \subseteq S$
has the linear order induced from the one of S. This construction is functorial in
![]() $a \in {{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
, with the comma category being taken over
$a \in {{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
, with the comma category being taken over
![]() ${{{\mathbf {LinSet}}}}$
.
${{{\mathbf {LinSet}}}}$
.
Definition 2.23. Let
![]() $\mathscr P$
and
$\mathscr P$
and
![]() $\mathscr Q$
be two
$\mathscr Q$
be two
![]() ${{{\mathbf {\Sigma }}}}$
-modules. Then we can form their composition product – that is, the
${{{\mathbf {\Sigma }}}}$
-modules. Then we can form their composition product – that is, the
![]() ${{{\mathbf {\Sigma }}}}$
-module
${{{\mathbf {\Sigma }}}}$
-module
![]() $\mathscr P \circ \mathscr Q$
given on objects by
$\mathscr P \circ \mathscr Q$
given on objects by
where the slice category
![]() $S \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
is taken over
$S \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
is taken over
![]() ${{{\mathbf {LinSet}}}}$
. A morphism
${{{\mathbf {LinSet}}}}$
. A morphism
![]() $f \colon S \to S'$
of
$f \colon S \to S'$
of
![]() ${{{\mathbf {\Sigma }}}}$
acts via the map
${{{\mathbf {\Sigma }}}}$
acts via the map
induced by the functor
![]() ${f^{-1}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}} \colon S \mathbin {\downarrow } {{{\mathbf {\Sigma }}}} \to S' \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
as well as the natural transformation
${f^{-1}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}} \colon S \mathbin {\downarrow } {{{\mathbf {\Sigma }}}} \to S' \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
as well as the natural transformation
![]() $\mathscr P(T) \mathop{\otimes} \mathscr Q(a) \to \mathscr P(T) \mathop{\otimes} \mathscr Q(a \circ {f^{-1}})$
given by the identity of
$\mathscr P(T) \mathop{\otimes} \mathscr Q(a) \to \mathscr P(T) \mathop{\otimes} \mathscr Q(a \circ {f^{-1}})$
given by the identity of
![]() $\mathscr P(T)$
and the map
$\mathscr P(T)$
and the map
![]() $\mathscr Q(a) \to \mathscr Q(a \circ {f^{-1}})$
induced by the morphism
$\mathscr Q(a) \to \mathscr Q(a \circ {f^{-1}})$
induced by the morphism
![]() $(f, {\mathrm {id}}_{T}) \colon a \to a \circ {f^{-1}}$
of
$(f, {\mathrm {id}}_{T}) \colon a \to a \circ {f^{-1}}$
of
![]() ${{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
.
${{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
.
2.6 Schur functors
Notation 2.24. Let
![]() $\mathscr M$
a
$\mathscr M$
a
![]() ${{{\mathbf {\Sigma }}}}$
-module. We define a functor
${{{\mathbf {\Sigma }}}}$
-module. We define a functor
![]() ${\mathscr M}[{-}] \colon {{{\mathbf {GrVect}}}} \to {{{\mathbf {GrVect}}}}$
by
${\mathscr M}[{-}] \colon {{{\mathbf {GrVect}}}} \to {{{\mathbf {GrVect}}}}$
by
 $$\begin{align*}V \longmapsto \bigoplus_{k \in {\mathbb{N}_0}} \left( {\mathscr M({\underline{k}})^{\mathrm{op}}} \mathop{\otimes}{}_{\!\!\Sigma{}_{{\underline{k}}}} V^{\otimes{\underline{k}}} \right) \end{align*}$$
$$\begin{align*}V \longmapsto \bigoplus_{k \in {\mathbb{N}_0}} \left( {\mathscr M({\underline{k}})^{\mathrm{op}}} \mathop{\otimes}{}_{\!\!\Sigma{}_{{\underline{k}}}} V^{\otimes{\underline{k}}} \right) \end{align*}$$
and call it the Schur functor associated to
![]() $\mathscr M$
.
$\mathscr M$
.
Remark 2.25. There is a canonical, and natural in V, isomorphism
where
![]() ${{{\mathbf {P}}}}$
acts diagonally on the tensor product. We can also replace
${{{\mathbf {P}}}}$
acts diagonally on the tensor product. We can also replace
![]() ${{{\mathbf {P}}}}$
by
${{{\mathbf {P}}}}$
by
![]() ${{{\mathbf {\Sigma }}}}$
since they are canonically equivalent.
${{{\mathbf {\Sigma }}}}$
since they are canonically equivalent.
Lemma 2.26. Let
![]() $\mathscr P$
and
$\mathscr P$
and
![]() $\mathscr Q$
be
$\mathscr Q$
be
![]() ${{{\mathbf {\Sigma }}}}$
-modules. Then there is a natural isomorphism
${{{\mathbf {\Sigma }}}}$
-modules. Then there is a natural isomorphism
with an explicit description as given in the proof.
Proof. We define the isomorphism by sending the element of
represented by
![]() $S \in {{{\mathbf {\Sigma }}}}$
and
$S \in {{{\mathbf {\Sigma }}}}$
and
![]() $(a \colon S \to T) \in S \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
as well as the elements
$(a \colon S \to T) \in S \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
as well as the elements
to
![]() $\varepsilon \in \{\pm 1\}$
times the element of
$\varepsilon \in \{\pm 1\}$
times the element of
represented by
![]() $T \in {{{\mathbf {\Sigma }}}}$
and
$T \in {{{\mathbf {\Sigma }}}}$
and ![]() as well as the elements
as well as the elements
where
![]() $\varepsilon $
is the sign incurred by permuting the two expressions
$\varepsilon $
is the sign incurred by permuting the two expressions
into each other.
2.7 Differential graded Lie algebras
Definition 2.27. Let L be a differential graded Lie algebra. Its positive truncation is the differential graded Lie subalgebra
![]() ${L}^+ \subseteq L$
given by
${L}^+ \subseteq L$
given by

where
![]() $\delta $
is the differential of L.
$\delta $
is the differential of L.
Definition 2.28. Let L be a differential graded Lie algebra. We denote by
![]() ${\operatorname {C}^{\mathrm {CE}}_{*}} (L)$
its Chevalley–Eilenberg complex (i.e., the underlying graded vector space of the free graded commutative algebra
${\operatorname {C}^{\mathrm {CE}}_{*}} (L)$
its Chevalley–Eilenberg complex (i.e., the underlying graded vector space of the free graded commutative algebra
![]() ${\mathrm {\Lambda }}(\mathrm {s} L)$
), equipped with the differential
${\mathrm {\Lambda }}(\mathrm {s} L)$
), equipped with the differential
![]() $d = d_0 + d_1$
, where
$d = d_0 + d_1$
, where

where
![]() $\delta $
is the differential of L.
$\delta $
is the differential of L.
The Chevalley–Eilenberg complex comes equipped with the structure of a cocommutative differential graded coalgebra. Its counit
![]() $\varepsilon \colon {\operatorname {C}^{\mathrm {CE}}_{*}} (L) \to {\mathbb {Q}}$
is given by
$\varepsilon \colon {\operatorname {C}^{\mathrm {CE}}_{*}} (L) \to {\mathbb {Q}}$
is given by
![]() $1$
on the empty wedge and
$1$
on the empty wedge and
![]() $0$
on all higher wedges. The comultiplication
$0$
on all higher wedges. The comultiplication
![]() $\Delta \colon {\operatorname {C}^{\mathrm {CE}}_{*}} (L) \to {\operatorname {C}^{\mathrm {CE}}_{*}} (L) \mathop{\mathop{\otimes}} {\operatorname {C}^{\mathrm {CE}}_{*}} (L)$
is given by
$\Delta \colon {\operatorname {C}^{\mathrm {CE}}_{*}} (L) \to {\operatorname {C}^{\mathrm {CE}}_{*}} (L) \mathop{\mathop{\otimes}} {\operatorname {C}^{\mathrm {CE}}_{*}} (L)$
is given by

where the sum runs over all subsets A of the set
![]() ${\underline {k}} = \{1, \dots , k\}$
. Here,
${\underline {k}} = \{1, \dots , k\}$
. Here,
![]() $\varepsilon (A) \in \{\pm 1\}$
is the sign incurred by permuting
$\varepsilon (A) \in \{\pm 1\}$
is the sign incurred by permuting
![]() $\mathrm {s} x_1 \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \mathrm {s} x_k$
into
$\mathrm {s} x_1 \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \mathrm {s} x_k$
into
![]() ${\textstyle \bigotimes }_{a \in A} \mathrm {s} x_a \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{b \in {\underline {k}} \setminus A} \mathrm {s} x_b$
.
${\textstyle \bigotimes }_{a \in A} \mathrm {s} x_a \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{b \in {\underline {k}} \setminus A} \mathrm {s} x_b$
.
Moreover, we write
![]() ${\mathrm {H}}_{\mathrm {CE}}^{*} (L)$
for the Chevalley–Eilenberg cohomology of L – that is, the cohomology of the linear dual of
${\mathrm {H}}_{\mathrm {CE}}^{*} (L)$
for the Chevalley–Eilenberg cohomology of L – that is, the cohomology of the linear dual of
![]() ${\operatorname {C}^{\mathrm {CE}}_{*}} (L)$
, equipped with its graded commutative algebra structure.
${\operatorname {C}^{\mathrm {CE}}_{*}} (L)$
, equipped with its graded commutative algebra structure.
Lemma 2.29. Let
![]() ${\mathrm {\Lambda }} \mathrm {s}$
denote the
${\mathrm {\Lambda }} \mathrm {s}$
denote the
![]() ${{{\mathbf {\Sigma }}}}$
-module given by
${{{\mathbf {\Sigma }}}}$
-module given by
![]() ${\mathrm {\Lambda }} \mathrm {s}(S) = (\mathrm {s} {\mathbb {Q}})^{{{\otimes}} S}$
. Then there is a canonical isomorphism of graded vector spaces, natural in
${\mathrm {\Lambda }} \mathrm {s}(S) = (\mathrm {s} {\mathbb {Q}})^{{{\otimes}} S}$
. Then there is a canonical isomorphism of graded vector spaces, natural in
![]() $V \in {{{\mathbf {GrVect}}}}$
,
$V \in {{{\mathbf {GrVect}}}}$
,

where ![]() .
.
Proof. The map lifts to an isomorphism
![]() $(\mathrm {s} {\mathbb {Q}})^{{{\otimes}} k} \mathop{\mathop{\otimes}} V^{{{\otimes}} k} \to (\mathrm {s} V)^{{{\otimes}} k}$
that is compatible with the
$(\mathrm {s} {\mathbb {Q}})^{{{\otimes}} k} \mathop{\mathop{\otimes}} V^{{{\otimes}} k} \to (\mathrm {s} V)^{{{\otimes}} k}$
that is compatible with the
![]() ${\Sigma _{k}}$
-actions. Passing to quotients again, we obtain the desired statement.
${\Sigma _{k}}$
-actions. Passing to quotients again, we obtain the desired statement.
2.8 The convolution Lie algebra
Recall that a cyclic operad is an operad
![]() $\mathscr C$
such that the right action of
$\mathscr C$
such that the right action of
![]() ${\Sigma _{n}}$
on
${\Sigma _{n}}$
on
![]() $\mathscr C(n)$
extends to a right action of
$\mathscr C(n)$
extends to a right action of
![]() ${\Sigma _{n+1}}$
in a way compatible with the composition operations (see Getzler–Kapranov [Reference Getzler and KapranovGK95, §2]). Unless explicitly stated otherwise, we will always work in the category of graded vector spaces.
${\Sigma _{n+1}}$
in a way compatible with the composition operations (see Getzler–Kapranov [Reference Getzler and KapranovGK95, §2]). Unless explicitly stated otherwise, we will always work in the category of graded vector spaces.
Notation 2.30. For a cyclic operad
![]() $\mathscr C$
, we write
$\mathscr C$
, we write
![]() ${\mathscr C \left (\mkern -4mu\left (n\right )\mkern -4mu\right )}$
for
${\mathscr C \left (\mkern -4mu\left (n\right )\mkern -4mu\right )}$
for
![]() $\mathscr C(n-1)$
equipped with its right
$\mathscr C(n-1)$
equipped with its right
![]() ${\Sigma _{n}}$
-action. We consider a cyclic operad as a
${\Sigma _{n}}$
-action. We consider a cyclic operad as a
![]() ${{{\mathbf {P}}}}$
-module via (the opposite of) this extended right action. (Note that this is different from the
${{{\mathbf {P}}}}$
-module via (the opposite of) this extended right action. (Note that this is different from the
![]() ${{{\mathbf {P}}}}$
-module associated to the underlying operad.) In particular, the Schur functor associated to
${{{\mathbf {P}}}}$
-module associated to the underlying operad.) In particular, the Schur functor associated to
![]() $\mathscr C$
is
$\mathscr C$
is
![]() ${\mathscr C}[{V}] = \bigoplus _{n \ge 1} {\mathscr C \left (\mkern -4mu\left (n\right )\mkern -4mu\right )} \mathop{\mathop{\otimes}}{\hspace{-2pt}}_{{\Sigma _{n}}} V^{{{\otimes}} n}$
.
${\mathscr C}[{V}] = \bigoplus _{n \ge 1} {\mathscr C \left (\mkern -4mu\left (n\right )\mkern -4mu\right )} \mathop{\mathop{\otimes}}{\hspace{-2pt}}_{{\Sigma _{n}}} V^{{{\otimes}} n}$
.
Definition 2.31. For a cyclic operad
![]() $\mathscr C$
, natural numbers
$\mathscr C$
, natural numbers
![]() $k, l \in {\mathbb {N}_{\ge 1}}$
, operations
$k, l \in {\mathbb {N}_{\ge 1}}$
, operations
![]() $p \in {\mathscr C \left (\mkern -4mu\left ({k} \right )\mkern -4mu\right )}$
and
$p \in {\mathscr C \left (\mkern -4mu\left ({k} \right )\mkern -4mu\right )}$
and
![]() $q \in {\mathscr C \left (\mkern -4mu\left ({l} \right )\mkern -4mu\right )}$
, and
$q \in {\mathscr C \left (\mkern -4mu\left ({l} \right )\mkern -4mu\right )}$
, and
![]() $1 \le i \le k$
and
$1 \le i \le k$
and
![]() $1 \le j \le l$
, we set
$1 \le j \le l$
, we set
where ![]() is the cyclic permutation and
is the cyclic permutation and
![]() ${\circ }_i$
denotes the i-th partial composition of the underlying operad of
${\circ }_i$
denotes the i-th partial composition of the underlying operad of
![]() $\mathscr C$
. In the case that
$\mathscr C$
. In the case that
![]() $i = k$
, we set
$i = k$
, we set ![]() .
.
Remark 2.32. Via the canonical equivalence
![]() ${{{\mathbf {\Sigma }}}} \to {{{\mathbf {P}}}}$
, the operations
${{{\mathbf {\Sigma }}}} \to {{{\mathbf {P}}}}$
, the operations
![]() ${}_i{\circ }_j$
of Definition 2.31 generalize to operations
${}_i{\circ }_j$
of Definition 2.31 generalize to operations
where
![]() $S, T \in {{{\mathbf {\Sigma }}}}$
, and
$S, T \in {{{\mathbf {\Sigma }}}}$
, and
![]() $s \in S$
and
$s \in S$
and
![]() $t \in T$
. Here,
$t \in T$
. Here,
equipped with the linear order such that
with the linear order on each block inherited from S respectively T.
Definition 2.33. Let
![]() $V \in {{\mathbf {Sp}}}^{m}$
,
$V \in {{\mathbf {Sp}}}^{m}$
,
![]() $k, l \in {\mathbb {N}_0}$
,
$k, l \in {\mathbb {N}_0}$
,
![]() $1 \le i \le k$
and
$1 \le i \le k$
and
![]() $1 \le j \le l$
. We denote by
$1 \le j \le l$
. We denote by
the map given by

where, for
![]() $a \le b$
, we set
$a \le b$
, we set ![]() and analogously for
and analogously for
![]() $w_{a,b}$
.
$w_{a,b}$
.
Lemma 2.34. Let
![]() $\mathscr C$
be a cyclic operad in graded vector spaces that is concentrated in even degrees and let
$\mathscr C$
be a cyclic operad in graded vector spaces that is concentrated in even degrees and let
![]() $V \in {{\mathbf {Sp}}}^{m}$
. Then
$V \in {{\mathbf {Sp}}}^{m}$
. Then
![]() $ {(\mathrm {s}^{-m} \mathscr C)}[{V}]$
becomes a graded Lie algebra by setting
$ {(\mathrm {s}^{-m} \mathscr C)}[{V}]$
becomes a graded Lie algebra by setting

for
![]() $\xi \in {\mathscr C \left (\mkern -4mu\left ({k} \right )\mkern -4mu\right )}$
,
$\xi \in {\mathscr C \left (\mkern -4mu\left ({k} \right )\mkern -4mu\right )}$
,
![]() $v \in V^{{{\otimes}} k}$
,
$v \in V^{{{\otimes}} k}$
,
![]() $\zeta \in {\mathscr C \left (\mkern -4mu\left ({l} \right )\mkern -4mu\right )}$
, and
$\zeta \in {\mathscr C \left (\mkern -4mu\left ({l} \right )\mkern -4mu\right )}$
, and
![]() $w \in V^{{{\otimes}} l}$
. This is functorial – that is, the restricted functor
$w \in V^{{{\otimes}} l}$
. This is functorial – that is, the restricted functor
![]() ${{ {(\mathrm {s}^{-m} \mathscr C)}[{-}]}|}_{{{\mathbf {Sp}}}^{m}} \colon {{\mathbf {Sp}}}^{m} \to {{{\mathbf {GrVect}}}}$
lifts to a functor to graded Lie algebras, which we also denote by
${{ {(\mathrm {s}^{-m} \mathscr C)}[{-}]}|}_{{{\mathbf {Sp}}}^{m}} \colon {{\mathbf {Sp}}}^{m} \to {{{\mathbf {GrVect}}}}$
lifts to a functor to graded Lie algebras, which we also denote by
![]() ${(\mathrm {s}^{-m} \mathscr C)}[{-}]$
.
${(\mathrm {s}^{-m} \mathscr C)}[{-}]$
.
Proof. Checking antisymmetry and the Jacobi identity are straightforward, though tedious, computations. The only trick one has to use is that
![]() $v\ {}_i{\circ }_j\ w$
being nonzero implies that
$v\ {}_i{\circ }_j\ w$
being nonzero implies that
![]() $ | {v_i} | + | {w_j} | = m$
. We omit the details. The claim about the functoriality is clear from the definitions.
$ | {v_i} | + | {w_j} | = m$
. We omit the details. The claim about the functoriality is clear from the definitions.
In the case
![]() $\mathscr C = \operatorname {\mathscr {L}ie}$
, a different proof of this fact can be found in [Reference Berglund and MadsenBM20, equation (6.7)].
$\mathscr C = \operatorname {\mathscr {L}ie}$
, a different proof of this fact can be found in [Reference Berglund and MadsenBM20, equation (6.7)].
Remark 2.35. The condition that
![]() $\mathscr C$
is concentrated in even degrees is purely for convenience, as it simplifies the signs occurring.
$\mathscr C$
is concentrated in even degrees is purely for convenience, as it simplifies the signs occurring.
3 The directed graph complex
In this section, our goal is to prove a version of Theorem 1.3 with coefficients. That is, we want to identify (in a stable range)
where
![]() $\Gamma _g^{\mathbb {Q}}$
is the group of automorphisms of the graded vector space
$\Gamma _g^{\mathbb {Q}}$
is the group of automorphisms of the graded vector space
![]() ${\widetilde {\operatorname {H}}_{*}}(M_{g,1}; {\mathbb {Q}})$
that respect the intersection pairing, Q is some
${\widetilde {\operatorname {H}}_{*}}(M_{g,1}; {\mathbb {Q}})$
that respect the intersection pairing, Q is some
![]() $\Gamma ^{\mathbb {Q}}_g$
-module, and the graded Lie algebra structure on the Schur functor is obtained from Lemma 2.34.
$\Gamma ^{\mathbb {Q}}_g$
-module, and the graded Lie algebra structure on the Schur functor is obtained from Lemma 2.34.
To this end, we begin, in the first two subsections, with studying
![]() ${( {\mathscr P} [{H}] \mathop{\mathop{\otimes}} Q)}_{{\mathrm {Aut}}(H)}$
, where
${( {\mathscr P} [{H}] \mathop{\mathop{\otimes}} Q)}_{{\mathrm {Aut}}(H)}$
, where
![]() $\mathscr P$
is a
$\mathscr P$
is a
![]() ${{{\mathbf {\Sigma }}}}$
-module, H is an object of
${{{\mathbf {\Sigma }}}}$
-module, H is an object of
![]() ${{\mathbf {Sp}}}^{m}$
that is concentrated in two degrees
${{\mathbf {Sp}}}^{m}$
that is concentrated in two degrees
![]() $\neq \frac {m}{2}$
, and Q is an
$\neq \frac {m}{2}$
, and Q is an
![]() ${\mathrm {Aut}}(H)$
-representation. From the results we obtain for this situation, we will, via Lemmas 2.26 and 2.29, be able to deduce a description as desired. The arguments we will use are similar to those of [Reference Berglund and MadsenBM20, §9] for the case where H is concentrated in degree
${\mathrm {Aut}}(H)$
-representation. From the results we obtain for this situation, we will, via Lemmas 2.26 and 2.29, be able to deduce a description as desired. The arguments we will use are similar to those of [Reference Berglund and MadsenBM20, §9] for the case where H is concentrated in degree
![]() $\frac m 2$
. We will restrict ourselves to the case that
$\frac m 2$
. We will restrict ourselves to the case that
![]() $Q = V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J}$
for some finite linearly ordered sets I and J, where V and W are the two nontrivial homogeneous pieces of H. Identifying the result in this case with its induced
$Q = V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J}$
for some finite linearly ordered sets I and J, where V and W are the two nontrivial homogeneous pieces of H. Identifying the result in this case with its induced
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-action allows one to deduce the result for more general representations via Schur–Weyl duality (see e.g. [Reference Fulton and HarrisFH04, §6.1] or [Reference EtingofEti+11, §5.19]).
$({\Sigma _{I}} \times {\Sigma _{J}})$
-action allows one to deduce the result for more general representations via Schur–Weyl duality (see e.g. [Reference Fulton and HarrisFH04, §6.1] or [Reference EtingofEti+11, §5.19]).
Throughout this section, we fix two integers n and m such that
![]() $m \neq 2n$
. (They correspond to
$m \neq 2n$
. (They correspond to
![]() $k - 1$
and
$k - 1$
and
![]() $k + l - 2$
above.)
$k + l - 2$
above.)
3.1 Coinvariants of monomial functors
In this subsection, we let
![]() $H = V \oplus W$
be a finite-dimensional graded vector space such that V is concentrated in degree n and W is concentrated in degree
$H = V \oplus W$
be a finite-dimensional graded vector space such that V is concentrated in degree n and W is concentrated in degree
![]() $m - n \neq n$
. Moreover, we assume that H is equipped with a graded symplectic form
$m - n \neq n$
. Moreover, we assume that H is equipped with a graded symplectic form
![]() $\langle -, -\rangle $
of degree
$\langle -, -\rangle $
of degree
![]() $-m$
(see Notation 2.6). We write
$-m$
(see Notation 2.6). We write ![]() for the group of degree
for the group of degree
![]() $0$
symplectic automorphisms of H.
$0$
symplectic automorphisms of H.
Let S, I and J be finite linearly ordered sets and P a
![]() ${\Sigma _{S}}$
-module. Our goal for this subsection is to identify the coinvariants
${\Sigma _{S}}$
-module. Our goal for this subsection is to identify the coinvariants
as a
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-module only in terms of P, without reference to H. We begin with some basic observations about the structures of H and
$({\Sigma _{I}} \times {\Sigma _{J}})$
-module only in terms of P, without reference to H. We begin with some basic observations about the structures of H and
![]() $\Gamma $
.
$\Gamma $
.
Lemma 3.1. The map
![]() $W \to \mathrm {s}^{m} {V^\vee }$
given by
$W \to \mathrm {s}^{m} {V^\vee }$
given by
![]() $w \mapsto \mathrm {s}^{m} \langle w, - \rangle $
is a degree
$w \mapsto \mathrm {s}^{m} \langle w, - \rangle $
is a degree
![]() $0$
isomorphism. After identifying W with
$0$
isomorphism. After identifying W with
![]() $\mathrm {s}^{m} {V^\vee }$
via this isomorphism, the inner product on
$\mathrm {s}^{m} {V^\vee }$
via this isomorphism, the inner product on
![]() $H = V \oplus \mathrm {s}^{m} {V^\vee }$
is given by
$H = V \oplus \mathrm {s}^{m} {V^\vee }$
is given by
![]() $\langle {(v, \mathrm {s}^{m} \phi )}, {(v', \mathrm {s}^{m} \phi ')\rangle } = \phi (v') - (-1)^{n(m-n)} \phi '(v)$
.
$\langle {(v, \mathrm {s}^{m} \phi )}, {(v', \mathrm {s}^{m} \phi ')\rangle } = \phi (v') - (-1)^{n(m-n)} \phi '(v)$
.
Proof. The composition

is a degree
![]() $-m$
isomorphism of the form
$-m$
isomorphism of the form
 $$\begin{align*}\begin{pmatrix} 0 & f \\ f' & 0 \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} 0 & f \\ f' & 0 \end{pmatrix} \end{align*}$$
since
![]() $\langle v, {v'}\rangle = 0 = \langle w, {w'}\rangle $
for all
$\langle v, {v'}\rangle = 0 = \langle w, {w'}\rangle $
for all
![]() $v, v' \in V$
and
$v, v' \in V$
and
![]() $w, w' \in W$
by our assumption that
$w, w' \in W$
by our assumption that
![]() $m \neq 2n$
(which also implies
$m \neq 2n$
(which also implies
![]() $m \neq 2(m - n)$
). In particular, f and
$m \neq 2(m - n)$
). In particular, f and
![]() $f'$
are degree
$f'$
are degree
![]() $-m$
isomorphisms. Noting that
$-m$
isomorphisms. Noting that
![]() $f(w) = \langle w, - \rangle $
, this implies the first claim. The second follows from
$f(w) = \langle w, - \rangle $
, this implies the first claim. The second follows from
![]() $f(w)(v) = \langle w, v\rangle = - (-1)^{n(m-n)} \langle v, w \rangle $
.
$f(w)(v) = \langle w, v\rangle = - (-1)^{n(m-n)} \langle v, w \rangle $
.
Using the preceding lemma we will, in the following, implicitly identify H with
![]() $V \oplus \mathrm {s}^{m} {V^\vee }$
. We now give a description of
$V \oplus \mathrm {s}^{m} {V^\vee }$
. We now give a description of
![]() $\Gamma $
in these terms.
$\Gamma $
in these terms.
Lemma 3.2. The map
![]() ${\mathrm {GL}}(V) \to {\mathrm {Aut}}(V \oplus \mathrm {s}^{m} {V^\vee }, \langle -, -\rangle ) = \Gamma $
given by
${\mathrm {GL}}(V) \to {\mathrm {Aut}}(V \oplus \mathrm {s}^{m} {V^\vee }, \langle -, -\rangle ) = \Gamma $
given by
![]() $f \mapsto f \oplus {({f^{-1}})^\vee }$
is an isomorphism of groups. (Here, we implicitly identify automorphisms of
$f \mapsto f \oplus {({f^{-1}})^\vee }$
is an isomorphism of groups. (Here, we implicitly identify automorphisms of
![]() $\mathrm {s}^{m} {V^\vee }$
with automorphisms of
$\mathrm {s}^{m} {V^\vee }$
with automorphisms of
![]() ${V^\vee }$
.)
${V^\vee }$
.)
Proof. Let
![]() $f \in {\mathrm {GL}}(V)$
. Then the computation
$f \in {\mathrm {GL}}(V)$
. Then the computation
 $$ \begin{align*} &\; \langle {{\left( f(v), {({f^{-1}})^\vee}(\mathrm{s}^{m} \phi) \right)}}, {{\left( f(v'), {({f^{-1}})^\vee}(\mathrm{s}^{m} \phi') \right)\rangle}} \\ =&\; (\phi \circ {f^{-1}})(f(v')) - (-1)^{n(m-n)} (\phi' \circ {f^{-1}})(f(v)) \\ =&\; \phi(v') - (-1)^{n(m-n)} \phi'(v) \\ =&\; \langle {(v, \mathrm{s}^{m} \phi),} {(v', \mathrm{s}^{m} \phi')\rangle} \end{align*} $$
$$ \begin{align*} &\; \langle {{\left( f(v), {({f^{-1}})^\vee}(\mathrm{s}^{m} \phi) \right)}}, {{\left( f(v'), {({f^{-1}})^\vee}(\mathrm{s}^{m} \phi') \right)\rangle}} \\ =&\; (\phi \circ {f^{-1}})(f(v')) - (-1)^{n(m-n)} (\phi' \circ {f^{-1}})(f(v)) \\ =&\; \phi(v') - (-1)^{n(m-n)} \phi'(v) \\ =&\; \langle {(v, \mathrm{s}^{m} \phi),} {(v', \mathrm{s}^{m} \phi')\rangle} \end{align*} $$
shows that the map in the statement is actually well defined. It is clearly injective. We will now show that it is also surjective. For this purpose, let
![]() $f \oplus g \in \Gamma $
, where
$f \oplus g \in \Gamma $
, where
![]() $f \in {\mathrm {GL}}(V)$
and
$f \in {\mathrm {GL}}(V)$
and
![]() $g \in {\mathrm {GL}}(\mathrm {s}^{m} {V^\vee })$
. By using that
$g \in {\mathrm {GL}}(\mathrm {s}^{m} {V^\vee })$
. By using that
![]() ${f^{-1}} \oplus {g^{-1}} \in \Gamma $
as well, we obtain
${f^{-1}} \oplus {g^{-1}} \in \Gamma $
as well, we obtain
and hence
![]() $g = {({f^{-1}})^\vee }$
. This shows surjectivity.
$g = {({f^{-1}})^\vee }$
. This shows surjectivity.
By basic linear algebra, there is a canonical isomorphism of graded vector spaces
![]() $V \mathop{\mathop{\otimes}} \mathrm {s}^{m} {V^\vee } \cong \mathrm {s}^{m} {\mathrm {End}}{(V)}$
(here,
$V \mathop{\mathop{\otimes}} \mathrm {s}^{m} {V^\vee } \cong \mathrm {s}^{m} {\mathrm {End}}{(V)}$
(here,
![]() ${\mathrm {End}}(V)$
is concentrated in degree
${\mathrm {End}}(V)$
is concentrated in degree
![]() $0$
since V is concentrated in a single degree). We will now use this to identify
$0$
since V is concentrated in a single degree). We will now use this to identify
![]() ${(H^{{{\otimes}} S} \mathop{\mathop{\otimes}} V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J})}_\Gamma $
in terms of
${(H^{{{\otimes}} S} \mathop{\mathop{\otimes}} V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J})}_\Gamma $
in terms of
![]() ${\mathrm {End}}{(V)}$
. To make this precise, we need to introduce some notation.
${\mathrm {End}}{(V)}$
. To make this precise, we need to introduce some notation.
Definition 3.3. Let S be a finite linearly ordered set, A and B two disjoint subsets of S such that ![]() (i.e., an ordered partition of S into two subsets), and
(i.e., an ordered partition of S into two subsets), and
![]() $V_1$
and
$V_1$
and
![]() $V_2$
two graded vector spaces. Then we denote by
$V_2$
two graded vector spaces. Then we denote by
![]() $(V_1, V_2)^{{{\otimes}} (A, B)}$
the tensor product
$(V_1, V_2)^{{{\otimes}} (A, B)}$
the tensor product
![]() $\bigotimes _{s \in S} V_s$
, where
$\bigotimes _{s \in S} V_s$
, where ![]() if
if
![]() $s \in A$
and
$s \in A$
and ![]() if
if
![]() $s \in B$
.
$s \in B$
.
A morphism
![]() $f \colon S \to S'$
of
$f \colon S \to S'$
of
![]() ${{{\mathbf {\Sigma }}}}$
induces a map
${{{\mathbf {\Sigma }}}}$
induces a map
by permuting the factors. When
![]() $V_1$
is concentrated in degree n and
$V_1$
is concentrated in degree n and
![]() $V_2$
in degree
$V_2$
in degree
![]() $m-n$
, we denote by
$m-n$
, we denote by
![]() $\operatorname {sgn}_{A,B}(f) \in \{\pm 1\}$
the sign incurred by this permutation – that is, it is chosen such that
$\operatorname {sgn}_{A,B}(f) \in \{\pm 1\}$
the sign incurred by this permutation – that is, it is chosen such that
holds.
Definition 3.4. Let S be a finite linearly ordered set. We denote by
![]() $\operatorname {OM}(S)$
the set of ordered matchings of S (i.e., (ordered) pairs
$\operatorname {OM}(S)$
the set of ordered matchings of S (i.e., (ordered) pairs
![]() $(A, B)$
such that A and B are disjoint subsets of S with
$(A, B)$
such that A and B are disjoint subsets of S with
![]() $|A| = |B|$
and
$|A| = |B|$
and ![]() ). (In particular,
). (In particular,
![]() $\operatorname {OM}(S)$
is empty if
$\operatorname {OM}(S)$
is empty if
![]() $|S|$
is odd.) This assembles into a functor
$|S|$
is odd.) This assembles into a functor
![]() $\operatorname {OM} \colon {{{\mathbf {\Sigma }}}} \to {{{\mathbf {Set}}}}$
by letting a morphism
$\operatorname {OM} \colon {{{\mathbf {\Sigma }}}} \to {{{\mathbf {Set}}}}$
by letting a morphism
![]() $f \colon S \to S'$
act via
$f \colon S \to S'$
act via
![]() $(A, B) \mapsto (f(A), f(B))$
.
$(A, B) \mapsto (f(A), f(B))$
.
Also note that the linear order of S restricts to a linear order on A and a linear order on B. In particular, there is a unique order-preserving bijection
![]() $A \to B$
. We will denote this bijection by
$A \to B$
. We will denote this bijection by
![]() $\mu _{A,B}$
.
$\mu _{A,B}$
.
Definition 3.5. Let S, I and J be finite linearly ordered sets. We denote by
![]() $\operatorname {OM}(S, I, J) \subseteq \operatorname {OM}(S \amalg I \amalg J)$
the subset of those ordered matchings
$\operatorname {OM}(S, I, J) \subseteq \operatorname {OM}(S \amalg I \amalg J)$
the subset of those ordered matchings
![]() $(A, B)$
such that
$(A, B)$
such that
![]() $I \subseteq A$
and
$I \subseteq A$
and
![]() $J \subseteq B$
. This assembles into a functor
$J \subseteq B$
. This assembles into a functor
![]() $\operatorname {OM} \colon {{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}} \to {{{\mathbf {Set}}}}$
by letting a morphism
$\operatorname {OM} \colon {{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}} \to {{{\mathbf {Set}}}}$
by letting a morphism
![]() $(f, g, h)$
act via
$(f, g, h)$
act via
![]() $f \amalg g \amalg h$
.
$f \amalg g \amalg h$
.
Remark 3.6. Note that there is a canonical bijection
![]() $\operatorname {OM}(S, I, J) \cong \operatorname {OM}(S)$
, which is natural in
$\operatorname {OM}(S, I, J) \cong \operatorname {OM}(S)$
, which is natural in
![]() ${{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}}$
.
${{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}} \times {{{\mathbf {\Sigma }}}}$
.
Lemma 3.7. Let S, I and J be finite linearly ordered sets. Then there is an isomorphism of
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules

where
![]() $g \in {\mathrm {GL}}(V) \cong \Gamma $
acts on
$g \in {\mathrm {GL}}(V) \cong \Gamma $
acts on
![]() $f \in {\mathrm {End}}(V)$
via the conjugation
$f \in {\mathrm {End}}(V)$
via the conjugation
![]() $g \mathbin {.} f = g f {g^{-1}}$
, and diagonally on the tensor products. The
$g \mathbin {.} f = g f {g^{-1}}$
, and diagonally on the tensor products. The
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-module structure on the left-hand side is given as follows: a morphism
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-module structure on the left-hand side is given as follows: a morphism
![]() $(f, g, h)$
of
$(f, g, h)$
of
![]() ${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
maps the factor corresponding to
${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
maps the factor corresponding to
![]() $(A, B) \in \operatorname {OM}(S, I, J)$
into the factor corresponding to
$(A, B) \in \operatorname {OM}(S, I, J)$
into the factor corresponding to
![]() $(c(A), c(B))$
via the map given by
$(c(A), c(B))$
via the map given by
where ![]() ,
, ![]() , and
, and ![]() , and the
, and the
![]() $\operatorname {E}_{i, j}$
are single-entry matrices with respect to some fixed basis of V (the resulting map is independent of this choice).
$\operatorname {E}_{i, j}$
are single-entry matrices with respect to some fixed basis of V (the resulting map is independent of this choice).
Moreover,
![]() $\Theta _1$
can be chosen such that, for any basis e of V, it fulfills, on the factor corresponding to
$\Theta _1$
can be chosen such that, for any basis e of V, it fulfills, on the factor corresponding to
![]() $(A, B) \in \operatorname {OM}(S, I, J)$
,
$(A, B) \in \operatorname {OM}(S, I, J)$
,

where the
![]() $E_{i,j}$
are with respect to e.
$E_{i,j}$
are with respect to e.
Proof. There is a canonical isomorphism
where
![]() $(A,B)$
runs over all (ordered) partitions of
$(A,B)$
runs over all (ordered) partitions of
![]() $S \amalg I \amalg J$
into two subsets such that
$S \amalg I \amalg J$
into two subsets such that
![]() $I \subseteq A$
and
$I \subseteq A$
and
![]() $J \subseteq B$
. This is an isomorphism of
$J \subseteq B$
. This is an isomorphism of
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}} \times \Gamma )$
-modules where a morphism
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}} \times \Gamma )$
-modules where a morphism
![]() $(f, g, h)$
of
$(f, g, h)$
of
![]() ${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
acts on both sides by permuting the factors (on the right-hand side this maps the
${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
acts on both sides by permuting the factors (on the right-hand side this maps the
![]() $(A, B)$
summand into the
$(A, B)$
summand into the
![]() $(c(A), c(B))$
summand, where
$(c(A), c(B))$
summand, where ![]() ) and an element
) and an element
![]() $g \in {\mathrm {GL}}(V) \cong \Gamma $
acts diagonally (acting on
$g \in {\mathrm {GL}}(V) \cong \Gamma $
acts diagonally (acting on
![]() ${V^\vee }$
by
${V^\vee }$
by
![]() ${({g^{-1}})^\vee }$
).
${({g^{-1}})^\vee }$
).
Now note that the
![]() $\Gamma $
-coinvariants of
$\Gamma $
-coinvariants of
![]() $(V, \mathrm {s}^{m} {V^\vee })^{{{\otimes}} (A, B)}$
are trivial when
$(V, \mathrm {s}^{m} {V^\vee })^{{{\otimes}} (A, B)}$
are trivial when
![]() $|A| \neq |B|$
since
$|A| \neq |B|$
since
![]() $2 \in {\mathrm {GL}}(V)$
acts via multiplication by
$2 \in {\mathrm {GL}}(V)$
acts via multiplication by
. Hence, the inclusion
becomes an isomorphism after taking
![]() $\Gamma $
-coinvariants.
$\Gamma $
-coinvariants.
Now let T be a finite linearly ordered set. Then there is, for any
![]() $(A, B) \in \operatorname {OM}(T)$
, a canonical isomorphism of
$(A, B) \in \operatorname {OM}(T)$
, a canonical isomorphism of
![]() $\Gamma $
-modules
$\Gamma $
-modules
given by the following permutation: we consider the tensor product on the right-hand side to be indexed over the set
![]() $A \times \{0, 1\}$
equipped with the lexicographical order and permute according to the bijection
$A \times \{0, 1\}$
equipped with the lexicographical order and permute according to the bijection
![]() $\psi _{A, B} \colon T \to A \times \{0, 1\}$
that sends
$\psi _{A, B} \colon T \to A \times \{0, 1\}$
that sends
![]() $a \in A$
to
$a \in A$
to
![]() $(a, 1)$
and
$(a, 1)$
and
![]() $b \in B$
to
$b \in B$
to
![]() $({(\mu _{A, B})^{-1}}(b), 0)$
.
$({(\mu _{A, B})^{-1}}(b), 0)$
.
The isomorphisms
![]() $\operatorname {sgn}_{A, B}(\psi _{A, B}) \cdot \Psi _{A, B}$
assemble into an isomorphism of
$\operatorname {sgn}_{A, B}(\psi _{A, B}) \cdot \Psi _{A, B}$
assemble into an isomorphism of
![]() $({\Sigma _{T}} \times \Gamma )$
-modules
$({\Sigma _{T}} \times \Gamma )$
-modules
where an element
![]() $c \in {\Sigma _{T}}$
acts on the right-hand side by sending the factor corresponding to
$c \in {\Sigma _{T}}$
acts on the right-hand side by sending the factor corresponding to
![]() $(A, B)$
into the factor corresponding to
$(A, B)$
into the factor corresponding to
![]() $(c(A), c(B))$
via
$(c(A), c(B))$
via
where
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are as in the statement of the lemma. Said differently, we have
$\tau $
are as in the statement of the lemma. Said differently, we have
which maybe makes it clearer why
![]() $\Psi $
is compatible with the
$\Psi $
is compatible with the
![]() ${\Sigma _{T}}$
-action.
${\Sigma _{T}}$
-action.
Now consider the case that
![]() $T = S \amalg I \amalg J$
. Then it is clear that the isomorphism
$T = S \amalg I \amalg J$
. Then it is clear that the isomorphism
![]() $\Psi $
restricts to an isomorphism
$\Psi $
restricts to an isomorphism
of
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}} \times \Gamma )$
-modules.
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}} \times \Gamma )$
-modules.
Lastly, note that there is a
![]() $\Gamma $
-module isomorphism
$\Gamma $
-module isomorphism
 $$ \begin{align*} \Phi \colon \mathrm{s}^{m} {V^\vee} \mathop{\otimes} V &\longrightarrow \mathrm{s}^{m} {\mathrm{End}}(V) \\ \mathrm{s}^{m} \phi \mathop{\otimes} v &\longmapsto \mathrm{s}^{m} (v' \mapsto \phi(v') v), \end{align*} $$
$$ \begin{align*} \Phi \colon \mathrm{s}^{m} {V^\vee} \mathop{\otimes} V &\longrightarrow \mathrm{s}^{m} {\mathrm{End}}(V) \\ \mathrm{s}^{m} \phi \mathop{\otimes} v &\longmapsto \mathrm{s}^{m} (v' \mapsto \phi(v') v), \end{align*} $$
where
![]() $\Gamma \cong {\mathrm {GL}}(V)$
acts on
$\Gamma \cong {\mathrm {GL}}(V)$
acts on
![]() ${\mathrm {End}}(V)$
by conjugation. Together with the canonical isomorphism
${\mathrm {End}}(V)$
by conjugation. Together with the canonical isomorphism
![]() $(\mathrm {s}^{m} {\mathrm {End}}(V))^{{{\otimes}} A} \cong \mathrm {s}^{m |A|} ({\mathrm {End}}(V))^{{{\otimes}} A}$
these isomorphisms combine into an isomorphism
$(\mathrm {s}^{m} {\mathrm {End}}(V))^{{{\otimes}} A} \cong \mathrm {s}^{m |A|} ({\mathrm {End}}(V))^{{{\otimes}} A}$
these isomorphisms combine into an isomorphism

as desired. For the claims made about the induced
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-module structure on the left-hand side and the explicit description of
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-module structure on the left-hand side and the explicit description of
![]() $\Theta _1$
, note that, when
$\Theta _1$
, note that, when ![]() is a basis of V, then
is a basis of V, then
![]() $\Phi (\mathrm {s}^{m} {e_j^\vee } \mathop{\mathop{\otimes}} e_i) = \mathrm {s}^{m} \operatorname {E}_{i, j}$
, where
$\Phi (\mathrm {s}^{m} {e_j^\vee } \mathop{\mathop{\otimes}} e_i) = \mathrm {s}^{m} \operatorname {E}_{i, j}$
, where
![]() $\operatorname {E}_{i, j}$
is with respect to e.
$\operatorname {E}_{i, j}$
is with respect to e.
We have now reduced finding a description of
![]() ${\left (H^{{{\otimes}} S} \mathop{\mathop{\otimes}} V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J}\right )}_\Gamma $
independent of H to finding a description of
${\left (H^{{{\otimes}} S} \mathop{\mathop{\otimes}} V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J}\right )}_\Gamma $
independent of H to finding a description of
![]() ${\left ({{\mathrm {End}}(V)}^{{{\otimes}} A}\right )}_\Gamma $
that is independent of V. Such a description is provided by the classical coinvariant theory for the general linear group.
${\left ({{\mathrm {End}}(V)}^{{{\otimes}} A}\right )}_\Gamma $
that is independent of V. Such a description is provided by the classical coinvariant theory for the general linear group.
Proposition 3.8 (Fundamental theorem of coinvariant theory).
Let
![]() $k \in {\mathbb {N}_0}$
such that
$k \in {\mathbb {N}_0}$
such that
![]() $k \le \dim V$
. Then there is an isomorphism of vector spaces
$k \le \dim V$
. Then there is an isomorphism of vector spaces
such that
![]() $[\operatorname {E}_{\omega (1), {\sigma (1)}} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \operatorname {E}_{\omega (k), {\sigma (k)}}] \mapsto {\omega ^{-1}} \sigma $
for all
$[\operatorname {E}_{\omega (1), {\sigma (1)}} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \operatorname {E}_{\omega (k), {\sigma (k)}}] \mapsto {\omega ^{-1}} \sigma $
for all
![]() $\omega , \sigma \in {\Sigma _{k}}$
and any basis of V.
$\omega , \sigma \in {\Sigma _{k}}$
and any basis of V.
Proof. This can, for example, be found in [Reference LodayLod98, 9.2.5, 9.2.8, and 9.2.10].Footnote 2
Applying this to our situation, we obtain the following corollary.
Corollary 3.9. Let S, I and J be finite linearly ordered sets such that
![]() $|S| + |I| + |J| \le 2 (\dim V)$
. Then there is an isomorphism of
$|S| + |I| + |J| \le 2 (\dim V)$
. Then there is an isomorphism of
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules

where
![]() ${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
acts on the left-hand side as in Lemma 3.7 and on the right-hand side as follows: an element
${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
acts on the left-hand side as in Lemma 3.7 and on the right-hand side as follows: an element
![]() $(f, g, h)$
maps the factor corresponding to
$(f, g, h)$
maps the factor corresponding to
![]() $(A, B) \in \operatorname {OM}(S, I, J)$
into the factor corresponding to
$(A, B) \in \operatorname {OM}(S, I, J)$
into the factor corresponding to
![]() $(c(A), c(B))$
via the map
$(c(A), c(B))$
via the map
 $$ \begin{align*} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} &\longrightarrow \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{c(A)}}]} \\ \mathrm{s}^{m |A|} \omega &\longmapsto \mathrm{s}^{m |A|} (\operatorname{sgn}_{A, B}(c) \cdot \sigma \omega {\tau^{-1}}), \end{align*} $$
$$ \begin{align*} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} &\longrightarrow \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{c(A)}}]} \\ \mathrm{s}^{m |A|} \omega &\longmapsto \mathrm{s}^{m |A|} (\operatorname{sgn}_{A, B}(c) \cdot \sigma \omega {\tau^{-1}}), \end{align*} $$
where ![]() , and
, and
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are as in Lemma 3.7.
$\tau $
are as in Lemma 3.7.
Moreover,
![]() $\Theta _2$
can be chosen such that, for any basis of V and
$\Theta _2$
can be chosen such that, for any basis of V and
![]() $\omega \in {\Sigma _{A}}$
, it fulfills, on the factor corresponding to
$\omega \in {\Sigma _{A}}$
, it fulfills, on the factor corresponding to
![]() $(A, B) \in \operatorname {OM}(S, I, J)$
, that
$(A, B) \in \operatorname {OM}(S, I, J)$
, that
where we identify A with ![]() via the unique order-preserving bijection.
via the unique order-preserving bijection.
Proof. On each summand,
![]() $\Theta _2$
is given by a shift of the isomorphism in Proposition 3.8. Now let
$\Theta _2$
is given by a shift of the isomorphism in Proposition 3.8. Now let
![]() $(A, B) \in \operatorname {OM}(S, I, J)$
and
$(A, B) \in \operatorname {OM}(S, I, J)$
and
![]() $\omega \in {\Sigma _{A}}$
, and fix a basis of V. We will also use the notation from Lemma 3.7. First note that by Proposition 3.8, the elements
$\omega \in {\Sigma _{A}}$
, and fix a basis of V. We will also use the notation from Lemma 3.7. First note that by Proposition 3.8, the elements
![]() $[{\operatorname {E}_{1, {\omega (1)}} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \operatorname {E}_{a, {\omega (a)}}}]$
of
$[{\operatorname {E}_{1, {\omega (1)}} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \operatorname {E}_{a, {\omega (a)}}}]$
of
![]() ${\left ({\mathrm {End}}(V)^{{{\otimes}} A}\right )}_\Gamma $
, with
${\left ({\mathrm {End}}(V)^{{{\otimes}} A}\right )}_\Gamma $
, with
![]() $\omega $
running over
$\omega $
running over
![]() ${\Sigma _{A}}$
, form a basis. Hence, it is enough to check the compatibility of
${\Sigma _{A}}$
, form a basis. Hence, it is enough to check the compatibility of
![]() $\Theta _2$
with the
$\Theta _2$
with the
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-action on those elements. To this end, we note that
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-action on those elements. To this end, we note that
![]() $\Theta _2 \left ( \mathrm {s}^{m |A|} [{\operatorname {E}_{1, {\omega (1)}} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \operatorname {E}_{a, {\omega (a)}}}] \right ) = \mathrm {s}^{m |A|} \omega $
and
$\Theta _2 \left ( \mathrm {s}^{m |A|} [{\operatorname {E}_{1, {\omega (1)}} \mathop{\mathop{\otimes}} \dots \mathop{\mathop{\otimes}} \operatorname {E}_{a, {\omega (a)}}}] \right ) = \mathrm {s}^{m |A|} \omega $
and
 $$ \begin{align*} &\; \Theta_2 \left( {\operatorname{sgn}_{A, B}(c)} \cdot \mathrm{s}^{m |A|} [{\operatorname{E}_{{\sigma^{-1}}(1), {\omega({\tau^{-1}}(1))}} \mathop{\otimes} \dots \mathop{\otimes} \operatorname{E}_{{\sigma^{-1}}(a), {\omega({\tau^{-1}}(a))}}}] \right) \\ &\quad = \mathrm{s}^{m |A|} (\operatorname{sgn}_{A, B}(c) \cdot \sigma \omega {\tau^{-1}}), \end{align*} $$
$$ \begin{align*} &\; \Theta_2 \left( {\operatorname{sgn}_{A, B}(c)} \cdot \mathrm{s}^{m |A|} [{\operatorname{E}_{{\sigma^{-1}}(1), {\omega({\tau^{-1}}(1))}} \mathop{\otimes} \dots \mathop{\otimes} \operatorname{E}_{{\sigma^{-1}}(a), {\omega({\tau^{-1}}(a))}}}] \right) \\ &\quad = \mathrm{s}^{m |A|} (\operatorname{sgn}_{A, B}(c) \cdot \sigma \omega {\tau^{-1}}), \end{align*} $$
which is what we wanted to show.
Remark 3.10. Setting
![]() $T = S \amalg I \amalg J$
, we note that
$T = S \amalg I \amalg J$
, we note that
![]() $\Theta _2$
restricts to an isomorphism of
$\Theta _2$
restricts to an isomorphism of
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules on the summands indexed by
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules on the summands indexed by
![]() $\operatorname {OM}(S, I, J) \subseteq \operatorname {OM}(T)$
.
$\operatorname {OM}(S, I, J) \subseteq \operatorname {OM}(T)$
.
We have now almost achieved what we set out do to in this subsection, as we have obtained, when
![]() $|S| + |I| + |J| \le 2 (\dim V)$
, an isomorphism
$|S| + |I| + |J| \le 2 (\dim V)$
, an isomorphism
 $$ \begin{align} {\left(H^{\otimes S} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J}\right)}_\Gamma \cong \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} \end{align} $$
$$ \begin{align} {\left(H^{\otimes S} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J}\right)}_\Gamma \cong \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} \end{align} $$
with the right-hand side independent of H as desired. To generalize this to expressions of the form
![]() ${((P^{\mathrm {op}} \mathop{\mathop{\otimes}}{\hspace{-2pt}}_{\Sigma _{S}}\, H^{{{\otimes}} S}) \mathop{\mathop{\otimes}} V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J})}_\Gamma $
, we will use the abstract lemmas of Section 2.4. To state the result in its simplest form, we need to introduce a bit of notation.
${((P^{\mathrm {op}} \mathop{\mathop{\otimes}}{\hspace{-2pt}}_{\Sigma _{S}}\, H^{{{\otimes}} S}) \mathop{\mathop{\otimes}} V^{{{\otimes}} I} \mathop{\mathop{\otimes}} W^{{{\otimes}} J})}_\Gamma $
, we will use the abstract lemmas of Section 2.4. To state the result in its simplest form, we need to introduce a bit of notation.
Definition 3.11. Let I and J be finite linearly ordered sets. We denote by
![]() ${{\mathbf {Match}}}_{I,J}$
the following groupoid:
${{\mathbf {Match}}}_{I,J}$
the following groupoid:
-
• Objects are tuples
 $(S, A, B, \mu )$
with S a finite linearly ordered set,
$(S, A, B, \mu )$
with S a finite linearly ordered set,
 $(A, B) \in \operatorname {OM}(S, I, J)$
an ordered matching, and
$(A, B) \in \operatorname {OM}(S, I, J)$
an ordered matching, and
 $\mu \colon A \to B$
a bijection.
$\mu \colon A \to B$
a bijection. -
• A morphism
 $(S, A, B, \mu ) \to (S', A', B', \mu ')$
is a tuple
$(S, A, B, \mu ) \to (S', A', B', \mu ')$
is a tuple
 $(f, g, h)$
of bijections
$(f, g, h)$
of bijections
 $f \colon S \to S'$
,
$f \colon S \to S'$
,
 $g \in {\Sigma _{I}}$
, and
$g \in {\Sigma _{I}}$
, and
 $h \in {\Sigma _{J}}$
, such that the map
$h \in {\Sigma _{J}}$
, such that the map  fulfills
fulfills
 $c(A) = A'$
,
$c(A) = A'$
,
 $c(B) = B'$
, and
$c(B) = B'$
, and
 ${{c}|}_B \circ \mu = \mu ' \circ {{c}|}_A$
.
${{c}|}_B \circ \mu = \mu ' \circ {{c}|}_A$
.
Moreover, for
![]() $S \in {{{\mathbf {\Sigma }}}}$
, we denote by
$S \in {{{\mathbf {\Sigma }}}}$
, we denote by
![]() ${{\mathbf {Match}}}^{S}_{I,J} \subseteq {{\mathbf {Match}}}_{I,J}$
the full subgroupoid spanned by objects of the form
${{\mathbf {Match}}}^{S}_{I,J} \subseteq {{\mathbf {Match}}}_{I,J}$
the full subgroupoid spanned by objects of the form
![]() $(S', A', B', \mu ')$
with
$(S', A', B', \mu ')$
with
![]() $S' = S$
. Also note that there is a canonical functor
$S' = S$
. Also note that there is a canonical functor
![]() ${\mathrm {pr}}_{I,J} \colon {{\mathbf {Match}}}_{I,J} \to {\Sigma _{I}} \times {\Sigma _{J}}$
given on morphisms by sending
${\mathrm {pr}}_{I,J} \colon {{\mathbf {Match}}}_{I,J} \to {\Sigma _{I}} \times {\Sigma _{J}}$
given on morphisms by sending
![]() $(f, g, h)$
to
$(f, g, h)$
to
![]() $(g, h)$
. We denote by
$(g, h)$
. We denote by
![]() ${{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \subseteq {{\mathbf {Match}}}_{I,J}$
the wide subgroupoid of those morphisms that are sent to
${{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \subseteq {{\mathbf {Match}}}_{I,J}$
the wide subgroupoid of those morphisms that are sent to
![]() $({\mathrm {id}}_{I}, {\mathrm {id}}_{J})$
by
$({\mathrm {id}}_{I}, {\mathrm {id}}_{J})$
by
![]() ${\mathrm {pr}}_{I,J}$
, and analogously for
${\mathrm {pr}}_{I,J}$
, and analogously for
![]() ${{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \subseteq {{\mathbf {Match}}}^{S}_{I,J}$
.
${{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \subseteq {{\mathbf {Match}}}^{S}_{I,J}$
.
Definition 3.12. We write
![]() $\operatorname {sgn}_{n, m}$
for the
$\operatorname {sgn}_{n, m}$
for the
![]() ${{\mathbf {Match}}}_{I,J}$
-module given by
${{\mathbf {Match}}}_{I,J}$
-module given by
(see Definition 3.3). Said differently, it is
![]() $\mathrm {s}^{m |A|} {\mathbb {Q}}$
on which a morphism
$\mathrm {s}^{m |A|} {\mathbb {Q}}$
on which a morphism
![]() $(f, g, h)$
acts by
$(f, g, h)$
acts by
![]() $\operatorname {sgn}_{A, B}(c)$
, where
$\operatorname {sgn}_{A, B}(c)$
, where ![]() .
.
With only a little bit more work, the lemmas of Section 2.4 now specialize to the following. (See [Reference Berglund and MadsenBM20, Corollary 9.8] for a similar statement in the case where H is concentrated in a single degree and
![]() $I = J = \varnothing $
.)
$I = J = \varnothing $
.)
Proposition 3.13. Let S, I and J be finite linearly ordered sets such that
![]() $|S| + |I| + |J| \le 2 (\dim V) = \dim H$
, and let P be a
$|S| + |I| + |J| \le 2 (\dim V) = \dim H$
, and let P be a
![]() ${\Sigma _{S}}$
-module. Then there is an isomorphism of
${\Sigma _{S}}$
-module. Then there is an isomorphism of
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules

where a morphism
![]() $(f, {\mathrm {id}}_{I}, {\mathrm {id}}_{J})$
of
$(f, {\mathrm {id}}_{I}, {\mathrm {id}}_{J})$
of
![]() ${{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on P by
${{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on P by
![]() $f \in {\Sigma _{S}}$
, and
$f \in {\Sigma _{S}}$
, and
![]() $\Gamma $
acts trivially on P and diagonally on the tensor product. The action of an element
$\Gamma $
acts trivially on P and diagonally on the tensor product. The action of an element
![]() $(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on the left-hand side is given by sending an element represented by
$(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on the left-hand side is given by sending an element represented by
![]() $(A, B, \mu ) \in {{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(A, B, \mu ) \in {{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
![]() $x \in P \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to the element represented by
$x \in P \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to the element represented by
![]() $(A, B, {{c}|}_B \circ \mu \circ {({{c}|}_A)^{-1}})$
and
$(A, B, {{c}|}_B \circ \mu \circ {({{c}|}_A)^{-1}})$
and
![]() $\operatorname {sgn}_{A, B}(c) x$
, where
$\operatorname {sgn}_{A, B}(c) x$
, where ![]() .
.
Moreover, the isomorphism above can be chosen such that, for any basis e of V, it maps the element of the colimit represented by
![]() $(A, B, \mu ) \in {{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(A, B, \mu ) \in {{\mathbf {Match}}}^{S}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
![]() $p \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \in P \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to
$p \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \in P \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to
![]() $[{p \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{t \in S \amalg I \amalg J} h_t}]$
where
$[{p \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{t \in S \amalg I \amalg J} h_t}]$
where

(here
![]() $a \colon {\underline {|A|}} \to A$
is the unique order-preserving bijection).
$a \colon {\underline {|A|}} \to A$
is the unique order-preserving bijection).
Proof. We start by rewriting the expression yielded by Corollary 3.9 and Remark 3.10. We have isomorphisms of
![]() $({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules
 $$ \begin{align*} \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} &\cong \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}} \langle {\mathop{Bij}}{(A,B)} \rangle} \\ &\cong \bigoplus_{(A, B, \mu) \in \operatorname{OM}_\mu(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}} \langle \mu \rangle}, \end{align*} $$
$$ \begin{align*} \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} &\cong \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}} \langle {\mathop{Bij}}{(A,B)} \rangle} \\ &\cong \bigoplus_{(A, B, \mu) \in \operatorname{OM}_\mu(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}} \langle \mu \rangle}, \end{align*} $$
where, for the first isomorphism, we identify
![]() ${\Sigma _{A}}$
with the set of (not necessarily order preserving) bijections
${\Sigma _{A}}$
with the set of (not necessarily order preserving) bijections
![]() ${\mathop {Bij}}{(A,B)}$
via the map
${\mathop {Bij}}{(A,B)}$
via the map
![]() $\omega \mapsto \mu _{A,B} \circ {\omega ^{-1}}$
. For the second isomorphism, we set
$\omega \mapsto \mu _{A,B} \circ {\omega ^{-1}}$
. For the second isomorphism, we set ![]() . An element
. An element
![]() $(f, g, h) \in {\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
acts on
$(f, g, h) \in {\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
acts on
![]() $\operatorname {OM}_\mu (S, I, J)$
via
$\operatorname {OM}_\mu (S, I, J)$
via
where ![]() , and on
, and on
![]() ${{\mathbb {Q}} \langle \mu \rangle }$
by sending
${{\mathbb {Q}} \langle \mu \rangle }$
by sending
![]() $\mu $
to
$\mu $
to
![]() $\operatorname {sgn}_{A,B}(c) \cdot (c \mathbin {.} \mu )$
.
$\operatorname {sgn}_{A,B}(c) \cdot (c \mathbin {.} \mu )$
.
Now we have isomorphisms of
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
 $$ \begin{align*} {\left( (P^{\mathrm{op}} \mathop{\otimes}{}_{\!\!\Sigma_{S}} H^{\otimes S}) \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J} \right)}_\Gamma &= {\left( {(P \mathop{\otimes} H^{\otimes S})}_{{\Sigma_{S}}} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J} \right)}_\Gamma \\ &\cong {\left( {(P \mathop{\otimes} H^{\otimes S} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J})}_\Gamma \right)}_{{\Sigma_{S}}} \\ &\cong {\left( P \mathop{\otimes} {(H^{\otimes S} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J})}_\Gamma \right)}_{{\Sigma_{S}}} \end{align*} $$
$$ \begin{align*} {\left( (P^{\mathrm{op}} \mathop{\otimes}{}_{\!\!\Sigma_{S}} H^{\otimes S}) \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J} \right)}_\Gamma &= {\left( {(P \mathop{\otimes} H^{\otimes S})}_{{\Sigma_{S}}} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J} \right)}_\Gamma \\ &\cong {\left( {(P \mathop{\otimes} H^{\otimes S} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J})}_\Gamma \right)}_{{\Sigma_{S}}} \\ &\cong {\left( P \mathop{\otimes} {(H^{\otimes S} \mathop{\otimes} V^{\otimes I} \mathop{\otimes} W^{\otimes J})}_\Gamma \right)}_{{\Sigma_{S}}} \end{align*} $$
since the actions of
![]() ${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
and
${\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
and
![]() $\Gamma $
commute and since
$\Gamma $
commute and since
![]() $\Gamma $
acts trivially on P. By Lemma 3.7, Corollary 3.9 and Remark 3.10, as well as the preceding discussion, the rightmost expression above is isomorphic to
$\Gamma $
acts trivially on P. By Lemma 3.7, Corollary 3.9 and Remark 3.10, as well as the preceding discussion, the rightmost expression above is isomorphic to
 $$ \begin{align} {\Big( P \mathop{\otimes} \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} \Big)_{{\Sigma_{S}}}} \cong {\Big( \bigoplus_{(A, B, \mu) \in \operatorname{OM}_\mu(S, I, J)} \left( P \mathop{\otimes} \mathrm{s}^{m |A|} {{\mathbb{Q}} \langle \mu \rangle} \right) \Big)_{{\Sigma_{S}}}} \end{align} $$
$$ \begin{align} {\Big( P \mathop{\otimes} \bigoplus_{(A, B) \in \operatorname{OM}(S, I, J)} \mathrm{s}^{m |A|} {{\mathbb{Q}}[{\Sigma_{A}}]} \Big)_{{\Sigma_{S}}}} \cong {\Big( \bigoplus_{(A, B, \mu) \in \operatorname{OM}_\mu(S, I, J)} \left( P \mathop{\otimes} \mathrm{s}^{m |A|} {{\mathbb{Q}} \langle \mu \rangle} \right) \Big)_{{\Sigma_{S}}}} \end{align} $$
as
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules. To describe the action on the sum on the right-hand side, let
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules. To describe the action on the sum on the right-hand side, let
![]() $(f, g, h) \in {\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
and set
$(f, g, h) \in {\Sigma _{S}} \times {\Sigma _{I}} \times {\Sigma _{J}}$
and set ![]() . Then it sends the summand corresponding to
. Then it sends the summand corresponding to
![]() $(A, B, \mu )$
to the summand corresponding to
$(A, B, \mu )$
to the summand corresponding to
![]() $(c(A), c(B), c \mathbin {.} \mu )$
by acting on P via f and on
$(c(A), c(B), c \mathbin {.} \mu )$
by acting on P via f and on
![]() ${{\mathbb {Q}} \langle \mu \rangle }$
as described above. The quotient is taken with respect to the action of
${{\mathbb {Q}} \langle \mu \rangle }$
as described above. The quotient is taken with respect to the action of
![]() ${\Sigma _{S}} \cong {\Sigma _{S}} \times \{{\mathrm {id}}_{I\}} \times \{{\mathrm {id}}_{J\}}$
.
${\Sigma _{S}} \cong {\Sigma _{S}} \times \{{\mathrm {id}}_{I\}} \times \{{\mathrm {id}}_{J\}}$
.
Now we can apply Lemma 2.16. Noting that there is a canonical isomorphism
of categories over
![]() ${\Sigma _{I}} \times {\Sigma _{J}}$
, we obtain an isomorphism of the right-hand side of (3.2) with
${\Sigma _{I}} \times {\Sigma _{J}}$
, we obtain an isomorphism of the right-hand side of (3.2) with
as
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules, where a morphism
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules, where a morphism
![]() $(f, g, h)$
of
$(f, g, h)$
of
![]() ${{\mathbf {Match}}}^{S}_{I,J}$
acts on P by
${{\mathbf {Match}}}^{S}_{I,J}$
acts on P by
![]() $f \in {\Sigma _{S}}$
. To this we can, in turn, apply Lemma 2.18 to obtain the desired description in terms of a colimit: given an object
$f \in {\Sigma _{S}}$
. To this we can, in turn, apply Lemma 2.18 to obtain the desired description in terms of a colimit: given an object
![]() $(A, B, \mu ) \in {{\mathbf {Match}}}^{S}_{I,J}$
and an element
$(A, B, \mu ) \in {{\mathbf {Match}}}^{S}_{I,J}$
and an element
![]() $(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
, we pick the lift
$(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
, we pick the lift
![]() $({\mathrm {id}}_{S}, g, h) \colon (A, B, \mu ) \to (A, B, c \mathbin {.} \mu )$
, where
$({\mathrm {id}}_{S}, g, h) \colon (A, B, \mu ) \to (A, B, c \mathbin {.} \mu )$
, where ![]() .
.
The explicit description of the isomorphism is obtained by chasing through the explicit descriptions of its constituent parts.
3.2 Coinvariants of Schur functors
In this subsection, we want to compute
as a
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-module, where
$({\Sigma _{I}} \times {\Sigma _{J}})$
-module, where
![]() $\mathscr P$
is some
$\mathscr P$
is some
![]() ${{{\mathbf {\Sigma }}}}$
-module, and H, V, W and
${{{\mathbf {\Sigma }}}}$
-module, and H, V, W and
![]() $\Gamma $
are as in the preceding subsection. Noting that
$\Gamma $
are as in the preceding subsection. Noting that
![]() $ {\mathscr P} [{H}]$
is a sum of monomial functors in H, Proposition 3.13 yields an identification as desired in a range depending on the dimension of H. To obtain a description of the whole thing, we thus need to let the dimension of H go to infinity.
$ {\mathscr P} [{H}]$
is a sum of monomial functors in H, Proposition 3.13 yields an identification as desired in a range depending on the dimension of H. To obtain a description of the whole thing, we thus need to let the dimension of H go to infinity.
More precisely, we fix the following notation for the rest of this section:
is a sequence of maps of
![]() ${{\mathbf {Sp}}}^{m}$
(see Notation 2.6) such that
${{\mathbf {Sp}}}^{m}$
(see Notation 2.6) such that
![]() $H_i$
is concentrated in dimensions n and
$H_i$
is concentrated in dimensions n and
![]() $m-n$
and such that the sequence
$m-n$
and such that the sequence
![]() $\dim {H_i}$
diverges. Moreover, we write
$\dim {H_i}$
diverges. Moreover, we write ![]() and denote by
and denote by
![]() $V_i$
and
$V_i$
and
![]() $W_i$
the degree n and
$W_i$
the degree n and
![]() $m - n$
parts of
$m - n$
parts of
![]() $H_i$
, respectively.
$H_i$
, respectively.
Note that there are maps
![]() $\Gamma _i \to \Gamma _{i+1}$
given by extending an automorphism of
$\Gamma _i \to \Gamma _{i+1}$
given by extending an automorphism of
![]() $H_i$
by the identity on the symplectic complement of
$H_i$
by the identity on the symplectic complement of
![]() $H_i$
in
$H_i$
in
![]() $H_{i+1}$
. Moreover, the maps
$H_{i+1}$
. Moreover, the maps
![]() $H_i \to H_{i+1}$
become
$H_i \to H_{i+1}$
become
![]() $\Gamma _i$
-equivariant when
$\Gamma _i$
-equivariant when
![]() $H_{i+1}$
is equipped with the restricted action. In particular, for any functor F from
$H_{i+1}$
is equipped with the restricted action. In particular, for any functor F from
![]() ${{\mathbf {Sp}}}^{m}$
to some cocomplete category
${{\mathbf {Sp}}}^{m}$
to some cocomplete category
![]() $\mathcal C$
, we obtain a sequence
$\mathcal C$
, we obtain a sequence
![]() ${F(H_1)}_{\Gamma _1} \to {F(H_2)}_{\Gamma _2} \to \dots $
and thus can make sense of the expression
${F(H_1)}_{\Gamma _1} \to {F(H_2)}_{\Gamma _2} \to \dots $
and thus can make sense of the expression
![]() ${\mathrm {colim}}_{i \in {\mathbb {N}}}\ {F(H_i)}_{\Gamma _i}$
.
${\mathrm {colim}}_{i \in {\mathbb {N}}}\ {F(H_i)}_{\Gamma _i}$
.
Definition 3.14. A compatible basis of the
![]() $V_i$
is a sequence
$V_i$
is a sequence
![]() $e_1, e_2, \dots $
of elements of
$e_1, e_2, \dots $
of elements of
![]() ${\mathrm {colim}}_{i}\ V_i$
such that, for each
${\mathrm {colim}}_{i}\ V_i$
such that, for each
![]() $i \ge 1$
, each of the elements
$i \ge 1$
, each of the elements
![]() $e_1, \dots , e_{\dim {V_i}}$
is represented by an (automatically unique) element of
$e_1, \dots , e_{\dim {V_i}}$
is represented by an (automatically unique) element of
![]() $V_i$
, and the set of these representatives forms a basis of
$V_i$
, and the set of these representatives forms a basis of
![]() $V_i$
.
$V_i$
.
Proposition 3.15. Let I and J be finite linearly ordered sets and
![]() $\mathscr P$
a
$\mathscr P$
a
![]() ${{{\mathbf {\Sigma }}}}$
-module. Then there is an isomorphism of
${{{\mathbf {\Sigma }}}}$
-module. Then there is an isomorphism of
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
where a morphism
![]() $(f, {\mathrm {id}}_{I}, {\mathrm {id}}_{J})$
of
$(f, {\mathrm {id}}_{I}, {\mathrm {id}}_{J})$
of
![]() ${{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on P by
${{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on P by
![]() $f \in {\Sigma _{S}}$
. The action of an element
$f \in {\Sigma _{S}}$
. The action of an element
![]() $(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on the left-hand side is given by sending an element represented by
$(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on the left-hand side is given by sending an element represented by
![]() $(S, A, B, \mu ) \in {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(S, A, B, \mu ) \in {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
![]() $x \in \mathscr P(S) \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to the element represented by
$x \in \mathscr P(S) \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to the element represented by
![]() $(S, A, B, {{c}|}_B \circ \mu \circ {({{c}|}_A)^{-1}})$
and
$(S, A, B, {{c}|}_B \circ \mu \circ {({{c}|}_A)^{-1}})$
and
![]() $\operatorname {sgn}_{A, B}(c) x$
, where
$\operatorname {sgn}_{A, B}(c) x$
, where ![]() .
.
Moreover, this isomorphism can be chosen such that, for any compatible basis
![]() $(e_j)_{j \in {{\mathbb {N}_{\ge 1}}}}$
of the
$(e_j)_{j \in {{\mathbb {N}_{\ge 1}}}}$
of the
![]() $V_i$
, it maps an element represented by
$V_i$
, it maps an element represented by
![]() $(S, A, B, \mu ) \in {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(S, A, B, \mu ) \in {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
![]() $p \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \in \mathscr P(S) \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to the element
$p \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \in \mathscr P(S) \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
to the element
![]() $ [{p \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{t \in S \amalg I \amalg J} h_t}]$
of
$ [{p \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{t \in S \amalg I \amalg J} h_t}]$
of
where
![]() $h_t$
is as in Proposition 3.13 (and we use the definition of
$h_t$
is as in Proposition 3.13 (and we use the definition of
![]() $ {\mathscr P} [{H_i}]$
of Remark 2.25).
$ {\mathscr P} [{H_i}]$
of Remark 2.25).
Proof. We have
 $$\begin{align*}{\left( {\mathscr P} [{H_i}] \mathop{\otimes} V_i^{\otimes I} \mathop{\otimes} W_i^{\otimes J} \right)}_{\Gamma_i} \cong \bigoplus_{k \in {\mathbb{N}_0}} {\left( ( {\mathscr P({\underline{k}})^{\mathrm{op}}} \mathop{\otimes}{}_{\!\!\Sigma_{{\underline{k}}}} {H_i}^{\otimes {\underline{k}}}) \mathop{\otimes} V_i^{\otimes I} \mathop{\otimes} W_i^{\otimes J} \right)}_{\Gamma_i}\end{align*}$$
$$\begin{align*}{\left( {\mathscr P} [{H_i}] \mathop{\otimes} V_i^{\otimes I} \mathop{\otimes} W_i^{\otimes J} \right)}_{\Gamma_i} \cong \bigoplus_{k \in {\mathbb{N}_0}} {\left( ( {\mathscr P({\underline{k}})^{\mathrm{op}}} \mathop{\otimes}{}_{\!\!\Sigma_{{\underline{k}}}} {H_i}^{\otimes {\underline{k}}}) \mathop{\otimes} V_i^{\otimes I} \mathop{\otimes} W_i^{\otimes J} \right)}_{\Gamma_i}\end{align*}$$
by definition of
![]() ${\mathscr P}[{-}]$
. When
${\mathscr P}[{-}]$
. When
![]() $k \le \dim {H_i} - |I| - |J|$
, there is an isomorphism
$k \le \dim {H_i} - |I| - |J|$
, there is an isomorphism

provided by Proposition 3.13. It is compatible with the maps
![]() $H_i \to H_{i+1}$
(i.e., it is a natural isomorphism of sequential diagrams, where the left-hand side is considered as a constant functor). To see this, we chose a basis of
$H_i \to H_{i+1}$
(i.e., it is a natural isomorphism of sequential diagrams, where the left-hand side is considered as a constant functor). To see this, we chose a basis of
![]() $V_i$
(the degree n part of
$V_i$
(the degree n part of
![]() $H_i$
), extend it to a basis of
$H_i$
), extend it to a basis of
![]() $V_{i+1}$
, and use the explicit description of the isomorphism (3.3). Hence we have, for each
$V_{i+1}$
, and use the explicit description of the isomorphism (3.3). Hence we have, for each
![]() $k \in {\mathbb {N}_0}$
, an isomorphism
$k \in {\mathbb {N}_0}$
, an isomorphism

which, by setting ![]() , assemble into an isomorphism
, assemble into an isomorphism

since colimits commute with direct sums. Since the inclusion
![]() ${{{\mathbf {Match}}}^{{{\mathbf {P}}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}} \to {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
is an equivalence of categories, it induces a canonical isomorphism
${{{\mathbf {Match}}}^{{{\mathbf {P}}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}} \to {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
is an equivalence of categories, it induces a canonical isomorphism
which finishes the construction.
We will now prove the claimed explicit description of the composed isomorphism. To this end, consider the element represented by
![]() $(S, A, B, \mu ) \in {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(S, A, B, \mu ) \in {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
![]() $p \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \in \mathscr P(S) \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
. It is equal, for any choice of bijection
$p \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \in \mathscr P(S) \mathop{\mathop{\otimes}} \operatorname {sgn}_{n, m}$
. It is equal, for any choice of bijection
![]() $f \colon S \to {\underline {|S|}}$
, to the element represented by
$f \colon S \to {\underline {|S|}}$
, to the element represented by
![]() $\left ( {\underline {|S|}}, c(A), c(B), {{c}|}_B \circ \mu \circ {({{c}|}_A)^{-1}} \right )$
and
$\left ( {\underline {|S|}}, c(A), c(B), {{c}|}_B \circ \mu \circ {({{c}|}_A)^{-1}} \right )$
and
![]() $\operatorname {sgn}_{A, B}(c) \cdot \left ( f_*(p) \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \right )$
, where
$\operatorname {sgn}_{A, B}(c) \cdot \left ( f_*(p) \mathop{\mathop{\otimes}} \mathrm {s}^{m |A|} 1 \right )$
, where ![]() . On such an element, the isomorphism is, by construction, given by the isomorphism of Proposition 3.13. The representative one obtains using the explicit description of that isomorphism represents the same element as the representative we provided in the statement of this proposition (by translating it back to S via
. On such an element, the isomorphism is, by construction, given by the isomorphism of Proposition 3.13. The representative one obtains using the explicit description of that isomorphism represents the same element as the representative we provided in the statement of this proposition (by translating it back to S via
![]() ${f^{-1}}$
). In the same way, one proves that the action of
${f^{-1}}$
). In the same way, one proves that the action of
![]() ${\Sigma _{I}} \times {\Sigma _{J}}$
is as claimed.
${\Sigma _{I}} \times {\Sigma _{J}}$
is as claimed.
3.3 Coinvariants of double Schur functors
In this subsection, our goal is to compute
as a
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-module, where
$({\Sigma _{I}} \times {\Sigma _{J}})$
-module, where
![]() $\mathscr P$
and
$\mathscr P$
and
![]() $\mathscr Q$
are
$\mathscr Q$
are
![]() ${{{\mathbf {\Sigma }}}}$
-modules, and
${{{\mathbf {\Sigma }}}}$
-modules, and
![]() $H_i$
,
$H_i$
,
![]() $V_i$
,
$V_i$
,
![]() $W_i$
and
$W_i$
and
![]() $\Gamma _i$
are as in the preceding subsection. By Lemma 2.26, we have an isomorphism
$\Gamma _i$
are as in the preceding subsection. By Lemma 2.26, we have an isomorphism
![]() $ {\mathscr P} { [{\mathscr Q} [{H_i}]]} \cong {(\mathscr P \circ \mathscr Q)}[{H_i}]$
. Hence, we can use Proposition 3.15 to obtain a description as desired. We now introduce some notation to state the result in a nice way.
$ {\mathscr P} { [{\mathscr Q} [{H_i}]]} \cong {(\mathscr P \circ \mathscr Q)}[{H_i}]$
. Hence, we can use Proposition 3.15 to obtain a description as desired. We now introduce some notation to state the result in a nice way.
Definition 3.16. Let I and J be finite linearly ordered sets. We denote by
![]() ${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
the following groupoid:
${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
the following groupoid:
-
• Objects are directed
 $(I,J)$
-graphs – that is, tuples
$(I,J)$
-graphs – that is, tuples
 $(F, N, S, T, \mu , a)$
with F and N finite linearly ordered sets,
$(F, N, S, T, \mu , a)$
with F and N finite linearly ordered sets,
 $(S, T) \in \operatorname {OM}(F, I, J)$
an ordered matching,
$(S, T) \in \operatorname {OM}(F, I, J)$
an ordered matching,
 $\mu \colon S \to T$
a bijection, and
$\mu \colon S \to T$
a bijection, and
 $a \colon F \to N$
a map of sets.
$a \colon F \to N$
a map of sets. -
• A morphism from
 $(F, N, S, T, \mu , a)$
to
$(F, N, S, T, \mu , a)$
to
 $(F', N', S', T', \mu ', a')$
is a tuple of bijections
$(F', N', S', T', \mu ', a')$
is a tuple of bijections
 $(f \colon F \to F'$
,
$(f \colon F \to F'$
,
 $k \colon N \to N')$
such that
$k \colon N \to N')$
such that
 $c(S) = S'$
,
$c(S) = S'$
,
 $c(T) = T'$
,
$c(T) = T'$
,
 ${{c}|}_T \circ \mu = \mu ' \circ {{c}|}_S$
, and
${{c}|}_T \circ \mu = \mu ' \circ {{c}|}_S$
, and
 $k \circ a = a' \circ f$
, where we set
$k \circ a = a' \circ f$
, where we set  .
.
When
![]() $I = J = \varnothing $
, we just write
$I = J = \varnothing $
, we just write
![]() ${{\mathbf {DirGraph}}}$
and call its objects directed graphs.
${{\mathbf {DirGraph}}}$
and call its objects directed graphs.
Remark 3.17. We think of a directed
![]() $(I,J)$
-graph as a directed graph with I inputs and J outputs. Under this viewpoint, we have the following: N is the set of vertices (or nodes), F is the set of internal flags (or half-edges), a describes to which vertex a flag is attached, S is the set of those flags which are sources (i.e., outgoing) which includes the inputs, similarly T is the set of those flags which are targets (i.e., incoming) which includes the outputs, and
$(I,J)$
-graph as a directed graph with I inputs and J outputs. Under this viewpoint, we have the following: N is the set of vertices (or nodes), F is the set of internal flags (or half-edges), a describes to which vertex a flag is attached, S is the set of those flags which are sources (i.e., outgoing) which includes the inputs, similarly T is the set of those flags which are targets (i.e., incoming) which includes the outputs, and
![]() $\mu $
describes the (directed) edges (i.e.,
$\mu $
describes the (directed) edges (i.e.,
![]() $s \in S$
and
$s \in S$
and
![]() $\mu (s) \in T$
are connected and form an edge).
$\mu (s) \in T$
are connected and form an edge).
Lemma 3.18. There is an isomorphism from
![]() $\operatorname {sgn}_{n, m}$
to the
$\operatorname {sgn}_{n, m}$
to the
![]() ${{\mathbf {Match}}}_{I,J}$
-module given by
${{\mathbf {Match}}}_{I,J}$
-module given by
where a morphism
![]() $(f, g, h) \colon (S, A, B, \mu ) \to (S', A', B', \mu ')$
of
$(f, g, h) \colon (S, A, B, \mu ) \to (S', A', B', \mu ')$
of
![]() ${{\mathbf {Match}}}_{I,J}$
acts by permuting the factors according to
${{\mathbf {Match}}}_{I,J}$
acts by permuting the factors according to
![]() ${{c}|}_A \colon A \to A'$
, where
${{c}|}_A \colon A \to A'$
, where ![]() . This isomorphism maps
. This isomorphism maps
![]() $\mathrm {s}^{m |A|} 1 \in \operatorname {sgn}_{n, m}$
to
$\mathrm {s}^{m |A|} 1 \in \operatorname {sgn}_{n, m}$
to
![]() $\varepsilon \cdot \mathrm {s}^{m |A|} 1 \in (\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} A}$
, where
$\varepsilon \cdot \mathrm {s}^{m |A|} 1 \in (\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} A}$
, where
![]() $\varepsilon $
is the sign incurred by permuting
$\varepsilon $
is the sign incurred by permuting
where ![]() if
if
![]() $t \in A$
and
$t \in A$
and ![]() if
if
![]() $t \in B$
.
$t \in B$
.
Proof. Let
![]() $p, q \colon {{\mathbf {Match}}}_{I,J} \to {{\mathbf {Match}}}_{\varnothing ,\varnothing }$
be the canonical functors given, on objects, by
$p, q \colon {{\mathbf {Match}}}_{I,J} \to {{\mathbf {Match}}}_{\varnothing ,\varnothing }$
be the canonical functors given, on objects, by
 $$ \begin{align*} p (S, A, B, \mu) &= (S \amalg I \amalg J, A, B, \mu) \\ q (S, A, B, \mu) &= (T, A, B, \mu), \end{align*} $$
$$ \begin{align*} p (S, A, B, \mu) &= (S \amalg I \amalg J, A, B, \mu) \\ q (S, A, B, \mu) &= (T, A, B, \mu), \end{align*} $$
where T is equal to
![]() $S \amalg I \amalg J$
as a set but is equipped with the linear order uniquely determined by the following two properties:
$S \amalg I \amalg J$
as a set but is equipped with the linear order uniquely determined by the following two properties:
-
• The element
 $a \in A$
is the predecessor of
$a \in A$
is the predecessor of
 $\mu (a) \in B$
.
$\mu (a) \in B$
. -
• Its restriction to A agrees with the linear order on A obtained by restricting the one of
 $S \amalg I \amalg J$
.
$S \amalg I \amalg J$
.
The identity of the underlying sets determines a natural isomorphism
![]() $p \to q$
. The map in the statement is obtained by applying
$p \to q$
. The map in the statement is obtained by applying
![]() $\operatorname {sgn}_{n, m}$
to this natural transformation.
$\operatorname {sgn}_{n, m}$
to this natural transformation.
The following proposition contains the desired description of the
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-module
$({\Sigma _{I}} \times {\Sigma _{J}})$
-module
![]() ${\mathrm {colim}}_{i \in {\mathbb {N}}}\ {( {\mathscr P} {[{\mathscr Q} [{H_i}]]} \mathop{\mathop{\otimes}} V_i^{{{\otimes}} I} \mathop{\mathop{\otimes}} W_i^{{{\otimes}} J} )}_{\Gamma _i}$
. (See [Reference Berglund and MadsenBM20, Theorem 9.12] for a similar statement in the case where H is concentrated in a single degree and
${\mathrm {colim}}_{i \in {\mathbb {N}}}\ {( {\mathscr P} {[{\mathscr Q} [{H_i}]]} \mathop{\mathop{\otimes}} V_i^{{{\otimes}} I} \mathop{\mathop{\otimes}} W_i^{{{\otimes}} J} )}_{\Gamma _i}$
. (See [Reference Berglund and MadsenBM20, Theorem 9.12] for a similar statement in the case where H is concentrated in a single degree and
![]() $I = J = \varnothing $
.)
$I = J = \varnothing $
.)
Proposition 3.19. Let I and J be finite linearly ordered sets and let
![]() $\mathscr P$
and
$\mathscr P$
and
![]() $\mathscr Q$
be
$\mathscr Q$
be
![]() ${{{\mathbf {\Sigma }}}}$
-modules. Then there is an isomorphism of
${{{\mathbf {\Sigma }}}}$
-modules. Then there is an isomorphism of
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
where a morphism
![]() $(f, k)$
of
$(f, k)$
of
![]() ${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on
${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on
![]() $\mathscr P(N)$
by k, on
$\mathscr P(N)$
by k, on
![]() $\mathscr Q(a)$
by
$\mathscr Q(a)$
by
![]() $(f, k)$
considered as a morphism of
$(f, k)$
considered as a morphism of
![]() ${{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
, and on
${{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
, and on
![]() $(\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} S}$
by permuting the factors according to
$(\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} S}$
by permuting the factors according to
![]() ${{c}|{}_{S}}$
where
${{c}|{}_{S}}$
where ![]() . The action of an element
. The action of an element
![]() $(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on the left-hand side is given by sending an element represented by
$(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on the left-hand side is given by sending an element represented by
![]() $(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
![]() $x \in \mathscr P(N) \mathop{\mathop{\otimes}} \mathscr Q(a) \mathop{\mathop{\otimes}} (\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} S}$
to the element represented by
$x \in \mathscr P(N) \mathop{\mathop{\otimes}} \mathscr Q(a) \mathop{\mathop{\otimes}} (\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} S}$
to the element represented by
![]() $(F, N, S, T, {{c}|}_T \circ \mu \circ {({{c}|}_S)^{-1}}, a)$
and
$(F, N, S, T, {{c}|}_T \circ \mu \circ {({{c}|}_S)^{-1}}, a)$
and
![]() $\operatorname {sgn}(g)^m x$
, where
$\operatorname {sgn}(g)^m x$
, where ![]() .
.
Moreover, this isomorphism can be chosen such that, for any compatible basis
![]() $(e_j)_{j \in {{\mathbb {N}_{\ge 1}}}}$
of the
$(e_j)_{j \in {{\mathbb {N}_{\ge 1}}}}$
of the
![]() $V_i$
, it maps an element represented by
$V_i$
, it maps an element represented by
![]() $(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
to the element
where

and
![]() $s \colon {\underline {|S|}} \to S$
is the unique order-preserving bijection. The sign
$s \colon {\underline {|S|}} \to S$
is the unique order-preserving bijection. The sign
![]() $\varepsilon $
is the sign incurred by permuting
$\varepsilon $
is the sign incurred by permuting
according to the Koszul sign rule.
Proof. We have isomorphisms

by Proposition 3.15 and Lemmas 3.18 and 2.26. Moreover, by definition,
so that the leftmost colimit above is isomorphic to
and hence, it is enough to show that the Grothendieck construction of the covariant functor
![]() $U \colon {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \to {{{\mathbf {Cat}}}}$
given by
$U \colon {{\mathbf {Match}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \to {{{\mathbf {Cat}}}}$
given by
![]() $(F, S, T, \mu ) \mapsto F \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
(where a map acts by precomposition with its inverse) is canonically isomorphic to
$(F, S, T, \mu ) \mapsto F \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
(where a map acts by precomposition with its inverse) is canonically isomorphic to
![]() ${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
. For this, we define a functor
${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
. For this, we define a functor
![]() ${\mathop {\mathchoice {\textstyle }{}{}{} \int }} U \to {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
, given, on objects respectively morphisms, by
${\mathop {\mathchoice {\textstyle }{}{}{} \int }} U \to {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
, given, on objects respectively morphisms, by
 $$ \begin{align*} \left( (F, S, T, \mu), a \colon F \to N \right) &\longmapsto \left( F, N, S, T, \mu, a \right) \\ \left( (f \colon F \to F', {\mathrm{id}}_{I}, {\mathrm{id}}_{J}), k \colon a \circ {f^{-1}} \to a' \right) &\longmapsto \left( f, {\mathrm{pr}}(k) \right), \end{align*} $$
$$ \begin{align*} \left( (F, S, T, \mu), a \colon F \to N \right) &\longmapsto \left( F, N, S, T, \mu, a \right) \\ \left( (f \colon F \to F', {\mathrm{id}}_{I}, {\mathrm{id}}_{J}), k \colon a \circ {f^{-1}} \to a' \right) &\longmapsto \left( f, {\mathrm{pr}}(k) \right), \end{align*} $$
where
![]() ${\mathrm {pr}} \colon F \mathbin {\downarrow } {{{\mathbf {\Sigma }}}} \to {{{\mathbf {\Sigma }}}}$
is the projection. This is clearly an isomorphism.
${\mathrm {pr}} \colon F \mathbin {\downarrow } {{{\mathbf {\Sigma }}}} \to {{{\mathbf {\Sigma }}}}$
is the projection. This is clearly an isomorphism.
The explicit description of the
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-action and the explicit description of the isomorphism follow from the explicit descriptions in Proposition 3.15 and Lemmas 3.18 and 2.26.
$({\Sigma _{I}} \times {\Sigma _{J}})$
-action and the explicit description of the isomorphism follow from the explicit descriptions in Proposition 3.15 and Lemmas 3.18 and 2.26.
3.4 Coinvariants of CE chains of convolution Lie algebras
In this subsection, our goal is to compute the
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-module
$({\Sigma _{I}} \times {\Sigma _{J}})$
-module
where
![]() $\mathscr C$
is a cyclic operad, and
$\mathscr C$
is a cyclic operad, and
![]() $H_i$
,
$H_i$
,
![]() $V_i$
,
$V_i$
,
![]() $W_i$
and
$W_i$
and
![]() $\Gamma _i$
are as in the preceding subsections. (For ease of dealing with signs, we will only consider the case where
$\Gamma _i$
are as in the preceding subsections. (For ease of dealing with signs, we will only consider the case where
![]() $\mathscr C$
is concentrated in even degrees.) The cocommutative coalgebra structure on the Chevalley–Eilenberg chains induces a cocommutative coalgebra structure on (3.4) when
$\mathscr C$
is concentrated in even degrees.) The cocommutative coalgebra structure on the Chevalley–Eilenberg chains induces a cocommutative coalgebra structure on (3.4) when
![]() $I = J = \varnothing $
, and the structure of a comodule over this coalgebra for general I and J. We will also identify this coalgebra (resp. comodule) structure explicitly.
$I = J = \varnothing $
, and the structure of a comodule over this coalgebra for general I and J. We will also identify this coalgebra (resp. comodule) structure explicitly.
By Lemma 2.29, there is an isomorphism
of graded vector spaces. Hence, we can apply Proposition 3.19 to obtain a description of the underlying graded vector space of (3.4). The rest of this subsection is concerned with also identifying its differential in these terms. We begin with some useful auxiliary definitions.
Definition 3.20. Let I and J be finite linearly ordered sets and
![]() $(F, N, S, T, \mu , a)$
a directed
$(F, N, S, T, \mu , a)$
a directed
![]() $(I,J)$
-graph. For a vertex
$(I,J)$
-graph. For a vertex
![]() $v \in N$
, we set
$v \in N$
, we set
-
•
 its degree.
its degree. -
•
 its out-degree.
its out-degree. -
•
 its in-degree.
its in-degree. -
•
 its weight.
its weight.
Definition 3.21. Let I and J be finite linearly ordered sets,
![]() $G = (F, N, S, T, \mu , a)$
a directed
$G = (F, N, S, T, \mu , a)$
a directed
![]() $(I,J)$
-graph, and
$(I,J)$
-graph, and
![]() $s \in F \cap S$
an internal outgoing flag. Moreover, we set
$s \in F \cap S$
an internal outgoing flag. Moreover, we set ![]() and
and ![]() and assume that
and assume that
![]() $v \neq v'$
. In this situation, we denote by
$v \neq v'$
. In this situation, we denote by
![]() $\operatorname {ctr}_{s}(G)$
the directed
$\operatorname {ctr}_{s}(G)$
the directed
![]() $(I,J)$
-graph
$(I,J)$
-graph
![]() $(F', N', S', T', \mu ', a')$
with
$(F', N', S', T', \mu ', a')$
with
-
•
 and
and  ,
, -
•
 and
and  ,
, -
•
 and
and  , where
, where
 ${\mathrm {pr}} \colon N \to N'$
is the quotient map.
${\mathrm {pr}} \colon N \to N'$
is the quotient map.
Here,
![]() $N'$
has the linear order such that
$N'$
has the linear order such that
![]() ${\mathrm {pr}}(v) = {\mathrm {pr}}(v')$
is the smallest element and such that
${\mathrm {pr}}(v) = {\mathrm {pr}}(v')$
is the smallest element and such that
![]() ${\mathrm {pr}}$
is order-preserving on all other elements. The set
${\mathrm {pr}}$
is order-preserving on all other elements. The set
![]() $F'$
is equipped with the linear order determined as follows: the elements of
$F'$
is equipped with the linear order determined as follows: the elements of
![]() ${a^{-1}}({\{v, v'\}})$
are smaller than all other elements; these other elements have the order restricted from F; on
${a^{-1}}({\{v, v'\}})$
are smaller than all other elements; these other elements have the order restricted from F; on
![]() ${a^{-1}}({\{v, v'\}})$
, the order is given by
${a^{-1}}({\{v, v'\}})$
, the order is given by
where on each block the order is the one restricted from F. (This convention is chosen such that it interacts nicely with the composition operations of a cyclic operad of Remark 2.32.)
Definition 3.22. Let I and J be finite linearly ordered sets and
![]() $G = (F, N, S, T, \mu , a)$
a directed
$G = (F, N, S, T, \mu , a)$
a directed
![]() $(I,J)$
-graph. A neighbor-closed vertex set of G is a subset
$(I,J)$
-graph. A neighbor-closed vertex set of G is a subset
![]() $N' \subseteq N$
such that
$N' \subseteq N$
such that
![]() $\mu (S \cap {a^{-1}}(N')) = T \cap {a^{-1}}(N')$
. A closed connected component of G is a neighbor-closed vertex set that is inclusion minimal among nonempty neighbor-closed vertex sets.
$\mu (S \cap {a^{-1}}(N')) = T \cap {a^{-1}}(N')$
. A closed connected component of G is a neighbor-closed vertex set that is inclusion minimal among nonempty neighbor-closed vertex sets.
A neighbor-closed vertex set
![]() $N'$
of G determines a directed
$N'$
of G determines a directed
![]() $(\varnothing ,\varnothing )$
-graph and a directed
$(\varnothing ,\varnothing )$
-graph and a directed
![]() $(I,J)$
-graph
$(I,J)$
-graph

where ![]() ,
, ![]() , and
, and ![]() .
.
Remark 3.23. Any neighbor-closed vertex set of G is a disjoint union of a unique set of closed connected components of G. Moreover, when
![]() $I = J = \varnothing $
and
$I = J = \varnothing $
and
![]() $N' \subseteq N$
is a neighbor-closed vertex set of a directed graph
$N' \subseteq N$
is a neighbor-closed vertex set of a directed graph
![]() $G = (F, N, S, T, \mu , a)$
, then
$G = (F, N, S, T, \mu , a)$
, then
![]() $N \setminus N'$
is one as well, and we have
$N \setminus N'$
is one as well, and we have
![]() ${\mathrm {ind}}_{G}(N \setminus N') = {\mathrm {coind}}_{G}(N')$
.
${\mathrm {ind}}_{G}(N \setminus N') = {\mathrm {coind}}_{G}(N')$
.
Definition 3.24. Let I and J be linearly ordered sets. For a
![]() ${{{\mathbf {\Sigma }}}}$
-module
${{{\mathbf {\Sigma }}}}$
-module
![]() $\mathscr C$
, we define the
$\mathscr C$
, we define the
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-module of
$({\Sigma _{I}} \times {\Sigma _{J}})$
-module of
![]() $\mathscr C$
-decorated directed
$\mathscr C$
-decorated directed
![]() $(I,J)$
-graphs to be
$(I,J)$
-graphs to be
(when
![]() $I = J = \varnothing $
, then we omit them from the notation). Here,
$I = J = \varnothing $
, then we omit them from the notation). Here,
![]() ${\operatorname {Dec}^{m}_{\mathscr C; I, J}}$
is the functor
${\operatorname {Dec}^{m}_{\mathscr C; I, J}}$
is the functor
![]() ${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \to {{{\mathbf {GrVect}}}}$
given, on a directed
${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}} \to {{{\mathbf {GrVect}}}}$
given, on a directed
![]() $(I,J)$
-graph
$(I,J)$
-graph ![]() , by
, by
where a morphism
![]() $(f, k)$
of
$(f, k)$
of
![]() ${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on
${{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
acts on
![]() $({\mathrm {s}}^{-m} \mathscr C)(a)$
by
$({\mathrm {s}}^{-m} \mathscr C)(a)$
by
![]() $(f, k)$
considered as a morphism of
$(f, k)$
considered as a morphism of
![]() ${{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
, on
${{{\mathbf {\Sigma }}}} \mathbin {\downarrow } {{{\mathbf {\Sigma }}}}$
, on
![]() $({\mathrm {s}} {\mathbb {Q}})^{{{\otimes}} N}$
by permuting the factors according to k, and on
$({\mathrm {s}} {\mathbb {Q}})^{{{\otimes}} N}$
by permuting the factors according to k, and on
![]() $(\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} S}$
by permuting the factors according to
$(\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} S}$
by permuting the factors according to
![]() ${{(f \amalg {{\mathrm {id}}_{I}} \amalg {{\mathrm {id}}_{J}})}|}_S$
. The action of an element
${{(f \amalg {{\mathrm {id}}_{I}} \amalg {{\mathrm {id}}_{J}})}|}_S$
. The action of an element
![]() $(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on
$(g, h) \in {\Sigma _{I}} \times {\Sigma _{J}}$
on
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
is given by sending an element represented by
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
is given by sending an element represented by
![]() $(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
$(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
and
![]() $x \in {\operatorname {Dec}^{m}_{\mathscr C; I, J}}$
to the element represented by
$x \in {\operatorname {Dec}^{m}_{\mathscr C; I, J}}$
to the element represented by
![]() $(F, N, S, T, {{c}|}_T \circ \mu \circ {({{c}|}_S)^{-1}}, a)$
and
$(F, N, S, T, {{c}|}_T \circ \mu \circ {({{c}|}_S)^{-1}}, a)$
and
![]() $\operatorname {sgn}(g)^m x$
, where
$\operatorname {sgn}(g)^m x$
, where ![]() .
.
Given a family
![]() $\left ( \xi _v \in \mathscr C({a^{-1}}(v)) \right )_{v \in N}$
of elements of
$\left ( \xi _v \in \mathscr C({a^{-1}}(v)) \right )_{v \in N}$
of elements of
![]() $\mathscr C$
, we call
$\mathscr C$
, we call
the element represented by (G and) the decorations
![]() $\xi _v$
.
$\xi _v$
.
If
![]() $\mathscr C$
is concentrated in even degrees and equipped with the structure of a cyclic operad, then
$\mathscr C$
is concentrated in even degrees and equipped with the structure of a cyclic operad, then
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
becomes a chain complex, which we will call the directed
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
becomes a chain complex, which we will call the directed
![]() $(I,J)$
-graph complex associated to
$(I,J)$
-graph complex associated to
![]() $\mathscr C$
. We now describe its differential d. For every directed
$\mathscr C$
. We now describe its differential d. For every directed
![]() $(I,J)$
-graph
$(I,J)$
-graph ![]() , every
, every
![]() $y \in {\operatorname {Dec}^{m}_{\mathscr C; I, J}} (G)$
, and every internal outgoing flag
$y \in {\operatorname {Dec}^{m}_{\mathscr C; I, J}} (G)$
, and every internal outgoing flag
![]() $s \in S \cap F$
(or, equivalently, every internal edge
$s \in S \cap F$
(or, equivalently, every internal edge ![]() ), we define an element
), we define an element
![]() $d^G_s(y) \in {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
by specifying the following properties:
$d^G_s(y) \in {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
by specifying the following properties:
-
• For every isomorphism
 $\chi \colon G \to G'$
of directed
$\chi \colon G \to G'$
of directed
 $(I,J)$
-graphs holds that
$(I,J)$
-graphs holds that
 $d^G_s(y) = d^{G'}_{\chi (s)}(\chi \mathbin {.} y)$
.
$d^G_s(y) = d^{G'}_{\chi (s)}(\chi \mathbin {.} y)$
. -
• If
 $a(s) = a(\mu (s))$
(i.e., if e is a loop), then
$a(s) = a(\mu (s))$
(i.e., if e is a loop), then
 $d^G_s(y) = 0$
.
$d^G_s(y) = 0$
. -
• Assume that
 and
and  are, in this order, the first two elements of N. Moreover, assume that a is order-preserving and that s is the last element of
are, in this order, the first two elements of N. Moreover, assume that a is order-preserving and that s is the last element of
 ${a^{-1}}(v)$
and that
${a^{-1}}(v)$
and that
 $\mu (s)$
is the first element of
$\mu (s)$
is the first element of
 ${a^{-1}}(v')$
. Then
${a^{-1}}(v')$
. Then
 $d^G_s$
applied to the element represented by some decorations
$d^G_s$
applied to the element represented by some decorations
 $\xi _v$
is
$\xi _v$
is
 $(-1)^{m ({ | {v} | ^{\mathrm {out}}} - 1)}$
times the element represented by the directed
$(-1)^{m ({ | {v} | ^{\mathrm {out}}} - 1)}$
times the element represented by the directed
 $(I,J)$
-graph
$(I,J)$
-graph
 $\operatorname {ctr}_{s}(G)$
decorated by
$\operatorname {ctr}_{s}(G)$
decorated by
 $\xi _v\ {{{}_s}{\circ }_{\mu (s)}}\ \xi _{v'}$
at the collapsed vertex
$\xi _v\ {{{}_s}{\circ }_{\mu (s)}}\ \xi _{v'}$
at the collapsed vertex
 ${\mathrm {pr}}(v) = {\mathrm {pr}}(v')$
and by
${\mathrm {pr}}(v) = {\mathrm {pr}}(v')$
and by
 $\xi _w$
at all other vertices w.
$\xi _w$
at all other vertices w.
For
![]() $x \in {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
the element represented by G and y, we set
$x \in {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
the element represented by G and y, we set ![]() .
.
When
![]() $I = J = \varnothing $
, we equip
$I = J = \varnothing $
, we equip
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}$
with the structure of a cocommutative differential graded coalgebra. The counit
${\mathfrak {DG}}^{m}{(\mathscr C)}$
with the structure of a cocommutative differential graded coalgebra. The counit
![]() $\varepsilon \colon {\mathfrak {DG}}^{m}{(\mathscr C)} \to {\mathbb {Q}}$
sends the element represented by the empty graph
$\varepsilon \colon {\mathfrak {DG}}^{m}{(\mathscr C)} \to {\mathbb {Q}}$
sends the element represented by the empty graph
![]() $\varnothing $
and
$\varnothing $
and
![]() $1 \in {\mathbb {Q}} = {\operatorname {Dec}^{m}_{\mathscr C}} (\varnothing )$
to
$1 \in {\mathbb {Q}} = {\operatorname {Dec}^{m}_{\mathscr C}} (\varnothing )$
to
![]() $1$
and an element represented by any other graph to
$1$
and an element represented by any other graph to
![]() $0$
. The comultiplication
$0$
. The comultiplication
![]() $\Delta \colon {\mathfrak {DG}}^{m}{(\mathscr C)} \to {\mathfrak {DG}}^{m}{(\mathscr C)} \mathop{\mathop{\otimes}} {\mathfrak {DG}}^{m}{(\mathscr C)}$
is given as follows: for an element
$\Delta \colon {\mathfrak {DG}}^{m}{(\mathscr C)} \to {\mathfrak {DG}}^{m}{(\mathscr C)} \mathop{\mathop{\otimes}} {\mathfrak {DG}}^{m}{(\mathscr C)}$
is given as follows: for an element
![]() $x \in {\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by G and
$x \in {\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by G and
![]() $(\xi _v)_{v \in N}$
, we set
$(\xi _v)_{v \in N}$
, we set
where the sum runs over all neighbor-closed vertex subsets
![]() $N'$
of G and
$N'$
of G and
![]() $x_A$
is the element of
$x_A$
is the element of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by
${\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by
![]() ${\mathrm {ind}}_{G}(A)$
and
${\mathrm {ind}}_{G}(A)$
and
![]() $(\xi _v)_{v \in A}$
. The sign
$(\xi _v)_{v \in A}$
. The sign
![]() $\varepsilon (N') \in \{\pm 1\}$
is the sign incurred by permuting
$\varepsilon (N') \in \{\pm 1\}$
is the sign incurred by permuting

where ![]() .
.
For general I and J, we equip
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
with the structure of a differential graded left comodule over
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
with the structure of a differential graded left comodule over
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}$
. Its structure map
${\mathfrak {DG}}^{m}{(\mathscr C)}$
. Its structure map
![]() $\rho \colon {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J} \to {\mathfrak {DG}}^{m}{(\mathscr C)} \mathop{\mathop{\otimes}} {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
is given as follows: for an element
$\rho \colon {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J} \to {\mathfrak {DG}}^{m}{(\mathscr C)} \mathop{\mathop{\otimes}} {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
is given as follows: for an element
![]() $x \in {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
represented by G and
$x \in {\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
represented by G and
![]() $(\xi _v)_{v \in N}$
, we set
$(\xi _v)_{v \in N}$
, we set
where the sum runs over all neighbor-closed vertex subsets
![]() $N'$
of G,
$N'$
of G,
![]() $x_{N'}$
is the element of
$x_{N'}$
is the element of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by
${\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by
![]() ${\mathrm {ind}}_{G}(N')$
and
${\mathrm {ind}}_{G}(N')$
and
![]() $(\xi _v)_{v \in N'}$
, and
$(\xi _v)_{v \in N'}$
, and
![]() $x^{\prime }_{N'}$
is the element of
$x^{\prime }_{N'}$
is the element of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
represented by
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
represented by
![]() ${\mathrm {coind}}_{G}(N')$
and
${\mathrm {coind}}_{G}(N')$
and
![]() $(\xi _v)_{v \in N \setminus N'}$
. The sign
$(\xi _v)_{v \in N \setminus N'}$
. The sign
![]() $\varepsilon (N') \in \{\pm 1\}$
is the same as above.
$\varepsilon (N') \in \{\pm 1\}$
is the same as above.
Remark 3.25. It will follow from Theorem 3.29 that the differential d of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
is well defined and actually a differential, that, in the case
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
is well defined and actually a differential, that, in the case
![]() $I = J = \varnothing $
, the maps
$I = J = \varnothing $
, the maps
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\Delta $
actually equip it with the structure of a cocommutative differential graded coalgebra, and, for general I and J, that
$\Delta $
actually equip it with the structure of a cocommutative differential graded coalgebra, and, for general I and J, that
![]() $\rho $
actually equips it with the structure of a differential graded comodule.
$\rho $
actually equips it with the structure of a differential graded comodule.
Note that, for defining the counit and comultiplication (respectively, the comodule structure map), it is not necessary for
![]() $\mathscr C$
to be a cyclic operad. However, our proof below that they yield the structure of a cocommutative graded coalgebra (respectively comodule) only applies in that case; it is certainly also true without this assumption though. The condition that
$\mathscr C$
to be a cyclic operad. However, our proof below that they yield the structure of a cocommutative graded coalgebra (respectively comodule) only applies in that case; it is certainly also true without this assumption though. The condition that
![]() $\mathscr C$
is concentrated in even degrees is purely for convenience; it avoids having to deal with even more signs.
$\mathscr C$
is concentrated in even degrees is purely for convenience; it avoids having to deal with even more signs.
Remark 3.26. We think of elements of
![]() ${\mathfrak {DG}}^{m} {(\mathscr C)}_{I,J}$
as being represented by a directed
${\mathfrak {DG}}^{m} {(\mathscr C)}_{I,J}$
as being represented by a directed
![]() $(I,J)$
-graph
$(I,J)$
-graph
![]() $(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
together with a decoration
$(F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
together with a decoration
![]() $\xi _v \in \mathscr C({a^{-1}}(v))$
for every vertex
$\xi _v \in \mathscr C({a^{-1}}(v))$
for every vertex
![]() $v \in N$
. To understand the action of an
$v \in N$
. To understand the action of an
![]() $(I,J)$
-graph isomorphism, we should additionally think of such an element as being equipped with an orientation on the set of vertices if m is even or an orientation on the set of edges if m is odd; when an
$(I,J)$
-graph isomorphism, we should additionally think of such an element as being equipped with an orientation on the set of vertices if m is even or an orientation on the set of edges if m is odd; when an
![]() $(I,J)$
-graph isomorphism flips the orientation of the respective set, it induces an extra sign.
$(I,J)$
-graph isomorphism flips the orientation of the respective set, it induces an extra sign.
Remark 3.27. The sign
![]() $(-1)^{m ({ | {v} | ^{\mathrm {out}}} - 1)}$
in the definition of the differential above corresponds to moving the to-be-contracted outgoing flag s to the beginning of S.
$(-1)^{m ({ | {v} | ^{\mathrm {out}}} - 1)}$
in the definition of the differential above corresponds to moving the to-be-contracted outgoing flag s to the beginning of S.
Remark 3.28. In the case of the cyclic commutative operad
![]() $\mathscr C = \operatorname {\mathscr {C}om}$
, the directed graph complex
$\mathscr C = \operatorname {\mathscr {C}om}$
, the directed graph complex
![]() ${\mathfrak {DG}}^{m} {(\mathscr C)}$
(or versions of it) has appeared in the work of, for example, Willwacher [Reference WillwacherWil14, Appendix K], Živković [Reference ŽivkovićŽiv20] and Dolgushev–Rogers [Reference Dolgushev and RogersDR19].
${\mathfrak {DG}}^{m} {(\mathscr C)}$
(or versions of it) has appeared in the work of, for example, Willwacher [Reference WillwacherWil14, Appendix K], Živković [Reference ŽivkovićŽiv20] and Dolgushev–Rogers [Reference Dolgushev and RogersDR19].
We are now ready to state and prove the main results of this subsection. (See [Reference Berglund and MadsenBM20, Theorem 9.14] for a similar statement in the case where H is concentrated in a single degree.)
Theorem 3.29. Let I and J be finite linearly ordered sets and let
![]() $\mathscr C$
be a cyclic operad concentrated in even degrees. Then there is an isomorphism of differential graded
$\mathscr C$
be a cyclic operad concentrated in even degrees. Then there is an isomorphism of differential graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
where
![]() $ {({\mathrm {s}}^{-m} \mathscr C)}[{H_i}]$
is equipped with the graded Lie algebra structure of Lemma 2.34. When
$ {({\mathrm {s}}^{-m} \mathscr C)}[{H_i}]$
is equipped with the graded Lie algebra structure of Lemma 2.34. When
![]() $I = J = \varnothing $
, this is an isomorphism of differential graded coalgebras, and, for general I and J, it is compatible with the comodule structures over these algebras.
$I = J = \varnothing $
, this is an isomorphism of differential graded coalgebras, and, for general I and J, it is compatible with the comodule structures over these algebras.
Remark 3.30. Tracing the dimension restriction of Proposition 3.13 through our arguments, the preceding theorem can be strengthened to an unstable isomorphism in a certain stable range that is compatible with the stabilization maps. More precisely, we obtain an isomorphism from the differential graded subcoalgebra (resp. subcomodule) of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
spanned by the decorated graphs with at most
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
spanned by the decorated graphs with at most
![]() $\dim H_i - |I| - |J|$
internal flags to the differential graded subcoalgebra (resp. subcomodule) of
$\dim H_i - |I| - |J|$
internal flags to the differential graded subcoalgebra (resp. subcomodule) of
![]() ${{\operatorname {C}^{\mathrm {CE}}_{*}} \left ({({\mathrm {s}}^{-m} \mathscr C)}[{H_i}] \mathop{\mathop{\otimes}} V_i^{{{\otimes}} I} \mathop{\mathop{\otimes}} W_i^{{{\otimes}} J} \right ) }_{\Gamma _i}$
spanned by the elementary tensors involving at most
${{\operatorname {C}^{\mathrm {CE}}_{*}} \left ({({\mathrm {s}}^{-m} \mathscr C)}[{H_i}] \mathop{\mathop{\otimes}} V_i^{{{\otimes}} I} \mathop{\mathop{\otimes}} W_i^{{{\otimes}} J} \right ) }_{\Gamma _i}$
spanned by the elementary tensors involving at most
![]() $\dim H_i$
elements of
$\dim H_i$
elements of
![]() $H_i$
(including
$H_i$
(including
![]() $V_i$
and
$V_i$
and
![]() $W_i$
).
$W_i$
).
Proof of Theorem 3.29.
Lemma 2.29 and Proposition 3.19 provide us with an isomorphism
![]() $\Phi ^{\prime }_{I,J}$
on the underlying
$\Phi ^{\prime }_{I,J}$
on the underlying
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules (in graded vector spaces). Let
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules (in graded vector spaces). Let
![]() $G = (F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
be a directed
$G = (F, N, S, T, \mu , a) \in {{\mathbf {DirGraph}}}_{{\mathrm {id}}_{I},{\mathrm {id}}_{J}}$
be a directed
![]() $(I,J)$
-graph and
$(I,J)$
-graph and
an element. Denoting by
![]() $[x]$
the element represented by G and x, we set
$[x]$
the element represented by G and x, we set

(the sign
![]() $\gamma (G)$
serves to cancel out a sign encountered below). We have
$\gamma (G)$
serves to cancel out a sign encountered below). We have
![]() $\Phi _{I,J}([x]) = [{\Phi ^G_{I,J}(x)}]$
, where we set
$\Phi _{I,J}([x]) = [{\Phi ^G_{I,J}(x)}]$
, where we set ![]() with y given by
with y given by

(where
![]() $s \colon {\underline {|S|}} \to S$
is the unique order-preserving bijection) and the sign
$s \colon {\underline {|S|}} \to S$
is the unique order-preserving bijection) and the sign
![]() $\varepsilon (x) \in \{\pm 1\}$
is the sign incurred by permuting
$\varepsilon (x) \in \{\pm 1\}$
is the sign incurred by permuting
 $$\begin{align*}({\mathrm{s}} 1)^{\otimes N} \mathop{\otimes} \bigotimes_{v \in N} {\mathrm{s}}^{-m} \xi_v \mathop{\otimes} \bigotimes_{s \in S} (h_s \mathop{\otimes} h_{\mu(s)}) \quad \mathrm{into} \quad \bigotimes_{v \in N} {\mathrm{s}} \bigg( {\mathrm{s}}^{-m} \xi_v \mathop{\otimes} \bigotimes_{f \in {a^{-1}}(v)} h_f \bigg) \mathop{\otimes} \bigotimes_{f \in I \amalg J} h_f \end{align*}$$
$$\begin{align*}({\mathrm{s}} 1)^{\otimes N} \mathop{\otimes} \bigotimes_{v \in N} {\mathrm{s}}^{-m} \xi_v \mathop{\otimes} \bigotimes_{s \in S} (h_s \mathop{\otimes} h_{\mu(s)}) \quad \mathrm{into} \quad \bigotimes_{v \in N} {\mathrm{s}} \bigg( {\mathrm{s}}^{-m} \xi_v \mathop{\otimes} \bigotimes_{f \in {a^{-1}}(v)} h_f \bigg) \mathop{\otimes} \bigotimes_{f \in I \amalg J} h_f \end{align*}$$
according to the Koszul sign rule.
We will now identify the result of pulling the Chevalley–Eilenberg differential
![]() $d = d_0 + d_1$
(cf. Definition 2.28) back to
$d = d_0 + d_1$
(cf. Definition 2.28) back to
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
along the isomorphism
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
along the isomorphism
![]() $\Phi _{I,J}$
. To this end, we first evaluate it on
$\Phi _{I,J}$
. To this end, we first evaluate it on
![]() $\tilde y$
. We have
$\tilde y$
. We have
![]() $d_0 = 0$
(since the differential of
$d_0 = 0$
(since the differential of
![]() $ {({\mathrm {s}}^{-m} \mathscr C)}[{H_i}]$
is trivial) and
$ {({\mathrm {s}}^{-m} \mathscr C)}[{H_i}]$
is trivial) and

where ![]() . In the following, we will, for ease of notation, identify each
. In the following, we will, for ease of notation, identify each
![]() ${a^{-1}}(v)$
with
${a^{-1}}(v)$
with
![]() $\{1, \dots , | v | \}$
via the unique order-preserving bijection and set
$\{1, \dots , | v | \}$
via the unique order-preserving bijection and set ![]() , where
, where
![]() $f(v,i)$
is the i-th element of
$f(v,i)$
is the i-th element of
![]() ${a^{-1}}(v)$
. We recall
${a^{-1}}(v)$
. We recall

and note that, by definition of
![]() $h_f$
, the expression
$h_f$
, the expression
![]() $\langle {h_{v';j}}, {h_{v;i}}\rangle $
is zero unless
$\langle {h_{v';j}}, {h_{v;i}}\rangle $
is zero unless
![]() $\{i, j\} = \{s, \mu (s)\}$
for some
$\{i, j\} = \{s, \mu (s)\}$
for some
![]() $s \in S \cap F$
. Hence, the same is true for the summand in (3.7) corresponding to
$s \in S \cap F$
. Hence, the same is true for the summand in (3.7) corresponding to
![]() $(i, j)$
. We thus obtain the following description:
$(i, j)$
. We thus obtain the following description:

where
![]() $\delta _s \in \{\pm 1\}$
is some sign. We note that
$\delta _s \in \{\pm 1\}$
is some sign. We note that ![]() is equal to some sign
is equal to some sign
![]() $\delta ^{\prime }_s \in \{\pm 1\}$
times the image under
$\delta ^{\prime }_s \in \{\pm 1\}$
times the image under
![]() $\Phi _{I,J}$
of the element
$\Phi _{I,J}$
of the element
![]() $[z]$
represented by the directed
$[z]$
represented by the directed
![]() $(I,J)$
-graph
$(I,J)$
-graph
![]() $\operatorname {ctr}_{s}(G)$
decorated by
$\operatorname {ctr}_{s}(G)$
decorated by
![]() $\xi _{a(s)}\ {}_s{\circ }_{\mu (s)}\ \xi _{a(\mu (s))}$
at the collapsed vertex
$\xi _{a(s)}\ {}_s{\circ }_{\mu (s)}\ \xi _{a(\mu (s))}$
at the collapsed vertex
![]() ${\mathrm {pr}}(a(s)) = {\mathrm {pr}}(a(\mu (s)))$
and by
${\mathrm {pr}}(a(s)) = {\mathrm {pr}}(a(\mu (s)))$
and by
![]() $\xi _v$
at all other vertices v. (Note that the family of basis elements
$\xi _v$
at all other vertices v. (Note that the family of basis elements
![]() $h_\bullet $
obtained for
$h_\bullet $
obtained for
![]() $\operatorname {ctr}_{s}(G)$
does not agree with the family obtained for the noncontracted flags of G. However, they are equivalent under the
$\operatorname {ctr}_{s}(G)$
does not agree with the family obtained for the noncontracted flags of G. However, they are equivalent under the
![]() $\Gamma _i$
-action.)
$\Gamma _i$
-action.)
We will now determine the sign
![]() $\delta ^{\prime }_s$
in a special case. To this end, let
$\delta ^{\prime }_s$
in a special case. To this end, let
![]() $s \in S \cap F$
and
$s \in S \cap F$
and ![]() such that
such that
![]() $a(s) \neq a(t)$
. Assume that
$a(s) \neq a(t)$
. Assume that ![]() and
and ![]() are, in this order, the first two elements of N. Moreover, assume that
are, in this order, the first two elements of N. Moreover, assume that
![]() $a \colon F \to N$
is order-preserving and that s is the last element of
$a \colon F \to N$
is order-preserving and that s is the last element of
![]() ${a^{-1}}(v)$
and that t is the first element of
${a^{-1}}(v)$
and that t is the first element of
![]() ${a^{-1}}(v')$
. (Note that any directed
${a^{-1}}(v')$
. (Note that any directed
![]() $(I,J)$
-graph is isomorphic to one of this form.) We have
$(I,J)$
-graph is isomorphic to one of this form.) We have

by definition. We first note that
![]() $ \langle {h_{v';t}}, {h_{v;s}}\rangle = 1$
, that
$ \langle {h_{v';t}}, {h_{v;s}}\rangle = 1$
, that
![]() $\gamma (G) \gamma (\operatorname {ctr}_{s}(G)) = (-1)^{m |N| + n}$
, and that
$\gamma (G) \gamma (\operatorname {ctr}_{s}(G)) = (-1)^{m |N| + n}$
, and that
 $$ \begin{align*} c &= | {{\mathrm{s}} y_v} | + \left( | {h_{v;s}} | - m \right) \left( | {h_{v'}} | - m \right) + | {h_{v';t}} | | {h_{v';t+1,\deg{v'}}} | + 1 \\ &= \left( 1 - m + \operatorname{w}(v) \right) + (n - m) \left( {\operatorname{w}(v')} - m \right) + (m - n) \left( {\operatorname{w}(v')} - (m - n) \right) + 1, \end{align*} $$
$$ \begin{align*} c &= | {{\mathrm{s}} y_v} | + \left( | {h_{v;s}} | - m \right) \left( | {h_{v'}} | - m \right) + | {h_{v';t}} | | {h_{v';t+1,\deg{v'}}} | + 1 \\ &= \left( 1 - m + \operatorname{w}(v) \right) + (n - m) \left( {\operatorname{w}(v')} - m \right) + (m - n) \left( {\operatorname{w}(v')} - (m - n) \right) + 1, \end{align*} $$
which reduces the question to determining
![]() $\varepsilon (x) \varepsilon (z)$
. To this end, we factor the permutation defining
$\varepsilon (x) \varepsilon (z)$
. To this end, we factor the permutation defining
![]() $\varepsilon $
into three parts: firstly permuting the
$\varepsilon $
into three parts: firstly permuting the
![]() $h_f$
among each other, secondly interleaving the
$h_f$
among each other, secondly interleaving the
![]() ${\mathrm {s}}^{-m} \xi _v$
and
${\mathrm {s}}^{-m} \xi _v$
and
![]() $h_v$
and thirdly interleaving the
$h_v$
and thirdly interleaving the
![]() ${\mathrm {s}} 1$
and
${\mathrm {s}} 1$
and
![]() $y_v$
. The deviation between
$y_v$
. The deviation between
![]() $\varepsilon (x)$
and
$\varepsilon (x)$
and
![]() $\varepsilon (z)$
for the first part is given by
$\varepsilon (z)$
for the first part is given by
![]() $-1$
to the power of
$-1$
to the power of
for the second part, it is
![]() $-1$
to the power of
$-1$
to the power of
and for the the third part, it is
![]() $-1$
to the power of
$-1$
to the power of
so that, putting everything together, we obtain
![]() $\delta ^{\prime }_s = (-1)^{m ({ | {v} | ^{\mathrm {out}}} - 1)}$
.
$\delta ^{\prime }_s = (-1)^{m ({ | {v} | ^{\mathrm {out}}} - 1)}$
.
Lastly, we show that, for any isomorphism of directed
![]() $(I,J)$
-graphs
$(I,J)$
-graphs
![]() $\chi \colon G \to G'$
, we have
$\chi \colon G \to G'$
, we have
which will finish the identification of the differential. The statement is clear up to sign, so it is enough to show that those agree as well. We write
![]() $\chi \mathbin {.} x = \alpha x'$
, where
$\chi \mathbin {.} x = \alpha x'$
, where
![]() $\alpha \in \{\pm 1\}$
and
$\alpha \in \{\pm 1\}$
and
![]() $x'$
is the element represented by
$x'$
is the element represented by
![]() $G'$
and the labels
$G'$
and the labels
![]() $(\chi \mathbin {.} \xi _{{\chi ^{-1}}(w)})_{w \in N'}$
. Lastly, we define
$(\chi \mathbin {.} \xi _{{\chi ^{-1}}(w)})_{w \in N'}$
. Lastly, we define
![]() $y'$
analogously to (3.6), so that
$y'$
analogously to (3.6), so that
![]() $\Phi ^{G'}_{I,J}(x') = \gamma (G') \varepsilon (x') y'$
.
$\Phi ^{G'}_{I,J}(x') = \gamma (G') \varepsilon (x') y'$
.
By definition, we have
![]() $[{\gamma (G) \varepsilon (x) y}] = \Phi _{I,J}([x]) = \Phi _{I,J}({[\chi \mathbin {.} x]}) = [{\alpha \gamma (G') \varepsilon (x') y'}]$
. Noting that
$[{\gamma (G) \varepsilon (x) y}] = \Phi _{I,J}([x]) = \Phi _{I,J}({[\chi \mathbin {.} x]}) = [{\alpha \gamma (G') \varepsilon (x') y'}]$
. Noting that
![]() $\gamma (G) = \gamma (G')$
, it follows from the definitions that
$\gamma (G) = \gamma (G')$
, it follows from the definitions that
![]() $\alpha \gamma (G) \varepsilon (x) \gamma (G') \varepsilon (x') = \alpha \varepsilon (x) \varepsilon (x')$
is the sign induced by permuting
$\alpha \gamma (G) \varepsilon (x) \gamma (G') \varepsilon (x') = \alpha \varepsilon (x) \varepsilon (x')$
is the sign induced by permuting
 $$\begin{align*}\bigotimes_{v \in N} {\mathrm{s}} \bigg( {\mathrm{s}}^{-m} \xi_v \mathop{\otimes} \bigotimes_{f \in {a^{-1}}(v)} h_f \bigg) \quad \mathrm{into} \quad \bigotimes_{w \in N'} {\mathrm{s}} \bigg( {\mathrm{s}}^{-m} \xi_{{\chi^{-1}}(w)} \mathop{\otimes} \bigotimes_{g \in {a^{\prime-1}}(w)} h_{{\chi^{-1}}(g)} \bigg) \end{align*}$$
$$\begin{align*}\bigotimes_{v \in N} {\mathrm{s}} \bigg( {\mathrm{s}}^{-m} \xi_v \mathop{\otimes} \bigotimes_{f \in {a^{-1}}(v)} h_f \bigg) \quad \mathrm{into} \quad \bigotimes_{w \in N'} {\mathrm{s}} \bigg( {\mathrm{s}}^{-m} \xi_{{\chi^{-1}}(w)} \mathop{\otimes} \bigotimes_{g \in {a^{\prime-1}}(w)} h_{{\chi^{-1}}(g)} \bigg) \end{align*}$$
(here, we use that the families
![]() $(h_f)_{f \in F}$
and
$(h_f)_{f \in F}$
and
![]() $(h^{\prime }_{\chi (f)})_{f \in F}$
are equivalent under the action of
$(h^{\prime }_{\chi (f)})_{f \in F}$
are equivalent under the action of
![]() $\Gamma _i$
for large enough i; hence, we can assume that they are equal, which we will do from now on). This sign is the product of the sign
$\Gamma _i$
for large enough i; hence, we can assume that they are equal, which we will do from now on). This sign is the product of the sign
![]() $\alpha '$
incurred by permuting
$\alpha '$
incurred by permuting
![]() $\bigotimes _{v \in N} {\mathrm {s}} y_v$
into
$\bigotimes _{v \in N} {\mathrm {s}} y_v$
into
![]() $\bigotimes _{w \in N'} {\mathrm {s}} y_{{\chi ^{-1}}(w)}$
and the signs
$\bigotimes _{w \in N'} {\mathrm {s}} y_{{\chi ^{-1}}(w)}$
and the signs
![]() $\alpha _v$
incurred by permuting
$\alpha _v$
incurred by permuting
![]() $\bigotimes _{f \in {a^{-1}}(v)} h_f$
into
$\bigotimes _{f \in {a^{-1}}(v)} h_f$
into
![]() $\bigotimes _{g \in {a^{\prime -1}}(\chi (v))} h_{{\chi ^{-1}}(g)}$
.
$\bigotimes _{g \in {a^{\prime -1}}(\chi (v))} h_{{\chi ^{-1}}(g)}$
.
It remains to evaluate the sign difference between
![]() $d^G_s(y)$
and
$d^G_s(y)$
and
![]() $d^{G'}_{\chi (s)}(y')$
. For this, write
$d^{G'}_{\chi (s)}(y')$
. For this, write ![]() , and
, and ![]() such that
such that
![]() $v < v'$
. Also let
$v < v'$
. Also let ![]() such that
such that
![]() $w < w'$
. Then the relevant summands of
$w < w'$
. Then the relevant summands of
![]() $d_1(\tilde y)$
and
$d_1(\tilde y)$
and
![]() $d_1(\tilde y')$
are the ones indexed by
$d_1(\tilde y')$
are the ones indexed by
![]() $(v, v')$
and
$(v, v')$
and
![]() $(w, w')$
. Note that
$(w, w')$
. Note that
![]() $-1$
to the power of
$-1$
to the power of
![]() $b_{v,v'} + b^{\prime }_{w,w'}$
, the sign difference between
$b_{v,v'} + b^{\prime }_{w,w'}$
, the sign difference between
![]() $\textstyle \bigwedge _{\tilde v \in V \setminus \{v, v'\}} {\mathrm {s}} y_{\tilde v}$
and
$\textstyle \bigwedge _{\tilde v \in V \setminus \{v, v'\}} {\mathrm {s}} y_{\tilde v}$
and
![]() $\textstyle \bigwedge _{\tilde w \in V' \setminus \{w, w'\}} {\mathrm {s}} y^{\prime }_{\tilde w}$
, and
$\textstyle \bigwedge _{\tilde w \in V' \setminus \{w, w'\}} {\mathrm {s}} y^{\prime }_{\tilde w}$
, and
![]() $\alpha '$
and
$\alpha '$
and
![]() $\alpha _{\tilde v}$
for
$\alpha _{\tilde v}$
for
![]() $\tilde v \in V \setminus \{v, v'\}$
cancel each other out, except for, if
$\tilde v \in V \setminus \{v, v'\}$
cancel each other out, except for, if
![]() $\chi $
swaps the order of v and
$\chi $
swaps the order of v and
![]() $v'$
, a sign of
$v'$
, a sign of
![]() $-1$
to the power of
$-1$
to the power of
![]() $1 + | {y^{\prime }_w} | | {y^{\prime }_{w'}} | $
. Now note that, in the case that
$1 + | {y^{\prime }_w} | | {y^{\prime }_{w'}} | $
. Now note that, in the case that
![]() $\chi $
swaps the order of v and
$\chi $
swaps the order of v and
![]() $v'$
, we have
$v'$
, we have
![]() ${[y^{\prime }_{w'}, y^{\prime }_w]} = (-1)^{1 + | {y^{\prime }_w} | | {y^{\prime }_{w'}} | } {[y^{\prime }_w, y^{\prime }_{w'}]}$
in the summand of
${[y^{\prime }_{w'}, y^{\prime }_w]} = (-1)^{1 + | {y^{\prime }_w} | | {y^{\prime }_{w'}} | } {[y^{\prime }_w, y^{\prime }_{w'}]}$
in the summand of
![]() $d_1(\tilde y')$
. Hence, the only sign that has not yet canceled is
$d_1(\tilde y')$
. Hence, the only sign that has not yet canceled is
![]() $\alpha _v \alpha _{v'}$
.
$\alpha _v \alpha _{v'}$
.
Thus, it remains to show that the summand of
![]() ${[y_v, y_{v'}]}$
corresponding to
${[y_v, y_{v'}]}$
corresponding to
![]() $(s, t)$
equals the summand of
$(s, t)$
equals the summand of
![]() ${[y^{\prime }_{\chi (v)}, y^{\prime }_{\chi (v')}]}$
corresponding to
${[y^{\prime }_{\chi (v)}, y^{\prime }_{\chi (v')}]}$
corresponding to
![]() $(\chi (s), \chi (t))$
, up to a sign of
$(\chi (s), \chi (t))$
, up to a sign of
![]() $\alpha _v \alpha _{v'}$
. (For ease of notation, we assume from now on that
$\alpha _v \alpha _{v'}$
. (For ease of notation, we assume from now on that
![]() $a(s) = v$
, and we set
$a(s) = v$
, and we set ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , possibly changing notation from before.) These two summands agree in
, possibly changing notation from before.) These two summands agree in
![]() $ {({\mathrm {s}}^{-m} \mathscr C)}[{H_i}]$
up to sign. The difference in signs is given by
$ {({\mathrm {s}}^{-m} \mathscr C)}[{H_i}]$
up to sign. The difference in signs is given by
![]() $-1$
to the power of
$-1$
to the power of
![]() $a_{v,v'}^{s,t} + a_{w,w'}^{s',t'}$
times the sign incurred by permuting
$a_{v,v'}^{s,t} + a_{w,w'}^{s',t'}$
times the sign incurred by permuting
into
![]() $h^{\prime }_w\ {}_{s'}{\tilde {\circ }}_{t'}\ h^{\prime }_{w'}$
. Now we note that
$h^{\prime }_w\ {}_{s'}{\tilde {\circ }}_{t'}\ h^{\prime }_{w'}$
. Now we note that
![]() $-1$
to the power of
$-1$
to the power of
![]() $a_{v,v'}^{s,t} + 1 + m + m ( | {h_{v;s}} | + | {h_{v'}} | )$
is precisely the sign incurred by permuting
$a_{v,v'}^{s,t} + 1 + m + m ( | {h_{v;s}} | + | {h_{v'}} | )$
is precisely the sign incurred by permuting
![]() $h_v \mathop{\mathop{\otimes}} h_{v'}$
into
$h_v \mathop{\mathop{\otimes}} h_{v'}$
into
![]() $(h_v\ {}_s{\tilde {\circ }}_t\ h_{v'}) \mathop{\mathop{\otimes}} h_{v';t} \mathop{\mathop{\otimes}} h_{v;s}$
and analogously for
$(h_v\ {}_s{\tilde {\circ }}_t\ h_{v'}) \mathop{\mathop{\otimes}} h_{v';t} \mathop{\mathop{\otimes}} h_{v;s}$
and analogously for
![]() $a_{w,w'}^{s',t'}$
. Noting that
$a_{w,w'}^{s',t'}$
. Noting that
![]() $ | {h_{v;s}} | = | {h^{\prime }_{w;s'}} | $
and
$ | {h_{v;s}} | = | {h^{\prime }_{w;s'}} | $
and
![]() $ | {h_{v'}} | = | {h^{\prime }_{w'}} | $
, this implies the claim since
$ | {h_{v'}} | = | {h^{\prime }_{w'}} | $
, this implies the claim since
![]() $\alpha _v \alpha _{v'}$
is the sign incurred by permuting
$\alpha _v \alpha _{v'}$
is the sign incurred by permuting
![]() $h_v \mathop{\mathop{\otimes}} h_{v'}$
into
$h_v \mathop{\mathop{\otimes}} h_{v'}$
into
![]() $h^{\prime }_w \mathop{\mathop{\otimes}} h^{\prime }_{w'}$
.
$h^{\prime }_w \mathop{\mathop{\otimes}} h^{\prime }_{w'}$
.
Now we prove that
![]() $\Phi _{\varnothing ,\varnothing }$
is a map of graded coalgebras and that
$\Phi _{\varnothing ,\varnothing }$
is a map of graded coalgebras and that
![]() $\Phi _{I,J}$
is compatible with the comodule structures over these coalgebras. It is clear that
$\Phi _{I,J}$
is compatible with the comodule structures over these coalgebras. It is clear that
![]() $\Phi _{\varnothing ,\varnothing }$
is compatible with the counits. We will now identify the comodule structure map
$\Phi _{\varnothing ,\varnothing }$
is compatible with the counits. We will now identify the comodule structure map
![]() $\rho $
of
$\rho $
of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
obtained by pulling back the one of the Chevalley–Eilenberg chains. When
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
obtained by pulling back the one of the Chevalley–Eilenberg chains. When
![]() $I = J = \varnothing $
, this also deals with the comultiplication
$I = J = \varnothing $
, this also deals with the comultiplication
![]() $\Delta $
of the coalgebra structure since, in this case, we have
$\Delta $
of the coalgebra structure since, in this case, we have
![]() $\Delta = \rho $
on both sides (see Remark 3.23). We continue to use the notation of (3.5) and (3.6). We have
$\Delta = \rho $
on both sides (see Remark 3.23). We continue to use the notation of (3.5) and (3.6). We have
where the sum runs over all subsets
![]() $N'$
of N and
$N'$
of N and
![]() $\delta (N') \in \{\pm 1\}$
is the sign incurred by permuting
$\delta (N') \in \{\pm 1\}$
is the sign incurred by permuting
![]() ${\textstyle \bigotimes }_{v \in N} {\mathrm {s}} y_v$
into
${\textstyle \bigotimes }_{v \in N} {\mathrm {s}} y_v$
into
![]() ${\textstyle \bigotimes }_{v \in N'} {\mathrm {s}} y_v \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{w \in N \setminus N'} {\mathrm {s}} y_w$
. Note that (the equivalence class of)
${\textstyle \bigotimes }_{v \in N'} {\mathrm {s}} y_v \mathop{\mathop{\otimes}} {\textstyle \bigotimes }_{w \in N \setminus N'} {\mathrm {s}} y_w$
. Note that (the equivalence class of)
![]() $\textstyle \bigwedge _{v \in N'} {\mathrm {s}} y_v$
is trivial except when
$\textstyle \bigwedge _{v \in N'} {\mathrm {s}} y_v$
is trivial except when
![]() $\mu (S \cap {a^{-1}}(N')) = T \cap {a^{-1}}(N')$
. Hence, we can also consider the sum in (3.8) to run only over all neighbor-closed vertex sets
$\mu (S \cap {a^{-1}}(N')) = T \cap {a^{-1}}(N')$
. Hence, we can also consider the sum in (3.8) to run only over all neighbor-closed vertex sets
![]() $N'$
of G. For such an
$N'$
of G. For such an
![]() $N'$
, we set
$N'$
, we set

where ![]() . We denote the element of
. We denote the element of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by
${\mathfrak {DG}}^{m}{(\mathscr C)}$
represented by
![]() ${\mathrm {ind}}_{G}(N')$
and
${\mathrm {ind}}_{G}(N')$
and
![]() $x_{N'}$
by
$x_{N'}$
by
![]() $[{x_{N'}}]$
, and the element of
$[{x_{N'}}]$
, and the element of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
represented by
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
represented by
![]() ${\mathrm {coind}}_{G}(N')$
and
${\mathrm {coind}}_{G}(N')$
and
![]() $x^{\prime }_{N'}$
by
$x^{\prime }_{N'}$
by
![]() $[{x^{\prime }_{N'}}]$
. We have
$[{x^{\prime }_{N'}}]$
. We have
 $$ \begin{align*} \Phi_{\varnothing,\varnothing}([{x_{N'}}]) &= \gamma \left( {{\mathrm{ind}}_{G}(N')} \right) \varepsilon(x_{N'}) \cdot \textstyle\bigwedge_{v \in {N'}} {\mathrm{s}} y_v \\ \Phi_{I,J}([{x^{\prime}_{N'}}]) &= \gamma \left( {{\mathrm{coind}}_{G}(N')} \right) \varepsilon(x^{\prime}_{N'}) \cdot \left( { \textstyle\bigwedge_{v \in {N \setminus N'}} {\mathrm{s}} y_v } \mathop{\otimes} {\textstyle\bigotimes}_{f \in I \amalg J} h_f \right) \end{align*} $$
$$ \begin{align*} \Phi_{\varnothing,\varnothing}([{x_{N'}}]) &= \gamma \left( {{\mathrm{ind}}_{G}(N')} \right) \varepsilon(x_{N'}) \cdot \textstyle\bigwedge_{v \in {N'}} {\mathrm{s}} y_v \\ \Phi_{I,J}([{x^{\prime}_{N'}}]) &= \gamma \left( {{\mathrm{coind}}_{G}(N')} \right) \varepsilon(x^{\prime}_{N'}) \cdot \left( { \textstyle\bigwedge_{v \in {N \setminus N'}} {\mathrm{s}} y_v } \mathop{\otimes} {\textstyle\bigotimes}_{f \in I \amalg J} h_f \right) \end{align*} $$
so that it only remains to see that
is equal to the sign in the definition of the comodule structure of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
. Noting that
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
. Noting that
this is clear from the definitions.
3.5 Coinvariants of the truncation
In this subsection, our goal is to obtain a description of the differential graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-module
$({\Sigma _{I}} \times {\Sigma _{J}})$
-module
in terms of a graph complex (including the coalgebra/comodule structures, as before). Here,
![]() $\mathscr C$
is a cyclic operad,
$\mathscr C$
is a cyclic operad,
![]() $H_i$
,
$H_i$
,
![]() $V_i$
,
$V_i$
,
![]() $W_i$
and
$W_i$
and
![]() $\Gamma _i$
are as in the preceding subsections, and
$\Gamma _i$
are as in the preceding subsections, and
![]() ${(-)}^+$
denotes positive truncation (see Definition 2.27). We begin with the following useful definition.
${(-)}^+$
denotes positive truncation (see Definition 2.27). We begin with the following useful definition.
Definition 3.31. Let I and J be finite linearly ordered sets. A directed
![]() $(I,J)$
-graph G is truncated if it has no vertices of valence zero or one, and each vertex of valence two has only incoming edges. We denote by
$(I,J)$
-graph G is truncated if it has no vertices of valence zero or one, and each vertex of valence two has only incoming edges. We denote by
the full subgroupoid spanned by the truncated directed
![]() $(I,J)$
-graphs.
$(I,J)$
-graphs.
We also denote by
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J} \subseteq {\mathfrak {DG}}^{m} {(\mathscr C)}_{I,J}$
the differential graded
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J} \subseteq {\mathfrak {DG}}^{m} {(\mathscr C)}_{I,J}$
the differential graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-submodule spanned by the elements represented by truncated decorated
$({\Sigma _{I}} \times {\Sigma _{J}})$
-submodule spanned by the elements represented by truncated decorated
![]() $(I,J)$
-graphs. When
$(I,J)$
-graphs. When
![]() $I = J = \varnothing $
, we omit them from the notation.
$I = J = \varnothing $
, we omit them from the notation.
Remark 3.32. When
![]() $I = J = \varnothing $
, we have that
$I = J = \varnothing $
, we have that
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)} \subseteq {\mathfrak {DG}}^{m} {(\mathscr C)}$
is a subcoalgebra. For general I and J, the
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)} \subseteq {\mathfrak {DG}}^{m} {(\mathscr C)}$
is a subcoalgebra. For general I and J, the
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}$
-comodule structure of
${\mathfrak {DG}}^{m}{(\mathscr C)}$
-comodule structure of
![]() ${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
restricts to a
${\mathfrak {DG}}^{m}{(\mathscr C)}_{I,J}$
restricts to a
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
-comodule structure on
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
-comodule structure on
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J}$
.
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J}$
.
Corollary 3.33. Let I and J be finite linearly ordered sets and let
![]() $\mathscr C$
be a cyclic operad concentrated in nonnegative even degrees such that
$\mathscr C$
be a cyclic operad concentrated in nonnegative even degrees such that
![]() ${\mathscr C \left (\mkern -4mu\left (0 \right )\mkern -4mu\right )}$
,
${\mathscr C \left (\mkern -4mu\left (0 \right )\mkern -4mu\right )}$
,
![]() ${\mathscr C \left (\mkern -4mu\left (1 \right )\mkern -4mu\right )}$
and
${\mathscr C \left (\mkern -4mu\left (1 \right )\mkern -4mu\right )}$
and
![]() ${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )}$
are concentrated in degree
${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )}$
are concentrated in degree
![]() $0$
. Assume that
$0$
. Assume that
![]() $2n < m < 3n$
and set
$2n < m < 3n$
and set

Then, for all
![]() $i \in {\mathbb {N}_{\ge 1}}$
, there is, in homological degrees
$i \in {\mathbb {N}_{\ge 1}}$
, there is, in homological degrees
![]() $\le \alpha \dim H_i$
, an isomorphism of differential graded
$\le \alpha \dim H_i$
, an isomorphism of differential graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
that is compatible with the stabilization maps on the right-hand side. When
![]() $I = J = \varnothing $
, it is an isomorphism of differential graded coalgebras. For general I and J, it is compatible with the comodule structures over these coalgebras.
$I = J = \varnothing $
, it is an isomorphism of differential graded coalgebras. For general I and J, it is compatible with the comodule structures over these coalgebras.
In particular, after stabilizing, we obtain an isomorphism
of differential graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules. When
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules. When
![]() $I = J = \varnothing $
, it is an isomorphism of differential graded coalgebras. For general I and J, it is compatible with the comodule structures over these coalgebras.
$I = J = \varnothing $
, it is an isomorphism of differential graded coalgebras. For general I and J, it is compatible with the comodule structures over these coalgebras.
Proof. The condition
![]() $2n < m < 3n$
implies that
$2n < m < 3n$
implies that
where
![]() $W_i$
is the degree
$W_i$
is the degree
![]() $m - n$
part of
$m - n$
part of
![]() $H_i$
. Then the explicit description of the isomorphism of Theorem 3.29, together with Remark 3.30, implies that there is an isomorphism from the differential graded
$H_i$
. Then the explicit description of the isomorphism of Theorem 3.29, together with Remark 3.30, implies that there is an isomorphism from the differential graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-submodule
$({\Sigma _{I}} \times {\Sigma _{J}})$
-submodule
![]() $D^{\prime }_*$
of
$D^{\prime }_*$
of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J}$
spanned by the decorated graphs with at most
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J}$
spanned by the decorated graphs with at most
![]() $\dim H_i - |I| - |J|$
internal flags to the differential graded
$\dim H_i - |I| - |J|$
internal flags to the differential graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-submodule
$({\Sigma _{I}} \times {\Sigma _{J}})$
-submodule
![]() $C^{\prime }_*$
of the right-hand side of (3.9) spanned by the elementary tensors involving at most
$C^{\prime }_*$
of the right-hand side of (3.9) spanned by the elementary tensors involving at most
![]() $\dim H_i$
elements of
$\dim H_i$
elements of
![]() $H_i$
(including
$H_i$
(including
![]() $V_i$
and
$V_i$
and
![]() $W_i$
).
$W_i$
).
We will now prove that
![]() $C^{\prime }_p$
is equal to degree p of the right-hand side of (3.9) when
$C^{\prime }_p$
is equal to degree p of the right-hand side of (3.9) when
![]() $p \le \alpha \dim H_i$
. To this end, we take elements
$p \le \alpha \dim H_i$
. To this end, we take elements

and note that
![]() $ | x | = \sum _{v \in N} \left ( 1 - m + | {\xi _v} | + \operatorname {w}(v) \right )$
, where
$ | x | = \sum _{v \in N} \left ( 1 - m + | {\xi _v} | + \operatorname {w}(v) \right )$
, where ![]() . Due to the truncation, we have that
. Due to the truncation, we have that
 $$\begin{align*}\operatorname{w}(v) \begin{cases} = 2 (m - n), & \mathit{if}\ \ k_v = 2 \\ \ge k_v n, & \mathit{if}\ \ k_v \ge 3 \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{w}(v) \begin{cases} = 2 (m - n), & \mathit{if}\ \ k_v = 2 \\ \ge k_v n, & \mathit{if}\ \ k_v \ge 3 \end{cases} \end{align*}$$
and that
![]() $k_v \ge 2$
. Setting
$k_v \ge 2$
. Setting ![]() and similarly for
and similarly for
![]() $N_{\ge 3}$
, we thus obtain
$N_{\ge 3}$
, we thus obtain
since
![]() $ | {\xi _v} | \ge 0$
by assumption. We note
$ | {\xi _v} | \ge 0$
by assumption. We note
![]() $1 - m + 2(m - n) \ge 2$
and, when
$1 - m + 2(m - n) \ge 2$
and, when
![]() $k_v \ge 3$
, that
$k_v \ge 3$
, that
since
![]() $\frac {3n}{1 - m + 3n} \ge 1$
as
$\frac {3n}{1 - m + 3n} \ge 1$
as
![]() $-3n < 1 - m < 0$
. Setting
$-3n < 1 - m < 0$
. Setting
we thus obtain
and hence that
![]() $\beta | x | + |I| + |J|$
is larger or equal to the number of elements of
$\beta | x | + |I| + |J|$
is larger or equal to the number of elements of
![]() $H_i$
involved in y. Furthermore,
$H_i$
involved in y. Furthermore,
since
![]() $ | v | = n |I|$
and
$ | v | = n |I|$
and
![]() $ | w | = (m - n) |J|$
. Hence,
$ | w | = (m - n) |J|$
. Hence,
![]() $\beta | y | = {\alpha ^{-1}} | y | \le \dim H_i$
implies
$\beta | y | = {\alpha ^{-1}} | y | \le \dim H_i$
implies
![]() $[y] \in C^{\prime }_*$
.
$[y] \in C^{\prime }_*$
.
Using the same argument, we can show that
![]() $D^{\prime }_p = {\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_p$
for
$D^{\prime }_p = {\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_p$
for
![]() $p \le \alpha \dim H_i$
. (A combinatorial argument using graphs would produce a better bound here; however, we will not need this.)
$p \le \alpha \dim H_i$
. (A combinatorial argument using graphs would produce a better bound here; however, we will not need this.)
4 The undirected graph complex
Throughout this section, we let
![]() $m \in {\mathbb {N}_0}$
be a natural number and
$m \in {\mathbb {N}_0}$
be a natural number and
![]() $\mathscr C$
a cyclic operad concentrated in nonnegative even degrees such that
$\mathscr C$
a cyclic operad concentrated in nonnegative even degrees such that
![]() ${\mathscr C \left (\mkern -4mu\left (2\right )\mkern -4mu\right )} = {\mathbb {Q} {\langle {\mathrm {id}} \rangle }}$
with the trivial
${\mathscr C \left (\mkern -4mu\left (2\right )\mkern -4mu\right )} = {\mathbb {Q} {\langle {\mathrm {id}} \rangle }}$
with the trivial
![]() ${\Sigma _{2}}$
-action. (As in the previous section, the condition that
${\Sigma _{2}}$
-action. (As in the previous section, the condition that
![]() $\mathscr C$
is concentrated in even degrees is purely for the convenience of avoiding more signs.)
$\mathscr C$
is concentrated in even degrees is purely for the convenience of avoiding more signs.)
Our goal is to obtain a simpler description of the homology of the truncated directed graph complex
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
of Definition 3.31. In fact, we will obtain a description in terms of undirected graphs. The rough idea is as follows. Restricting the differential of
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
of Definition 3.31. In fact, we will obtain a description in terms of undirected graphs. The rough idea is as follows. Restricting the differential of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
to the two edges incident to a vertex of valence two (which must be labeled by the identity operation by our assumption on
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
to the two edges incident to a vertex of valence two (which must be labeled by the identity operation by our assumption on
![]() $\mathscr C$
) yields the following picture.
$\mathscr C$
) yields the following picture.

Thus, intuitively, taking homology should kill the difference between the two orientations of an edge. We formalize this using a spectral sequence argument: filtering
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{\operatorname {(\mathscr {L}ie)}}$
by the number of vertices of valence two yields a spectral sequence, for which we prove that its first page is concentrated in a single row. We moreover show that this row is isomorphic as a chain complex to a (well-known) undirected version of the graph complex, which we denote by
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{\operatorname {(\mathscr {L}ie)}}$
by the number of vertices of valence two yields a spectral sequence, for which we prove that its first page is concentrated in a single row. We moreover show that this row is isomorphic as a chain complex to a (well-known) undirected version of the graph complex, which we denote by
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
. The spectral sequence then implies that there is an isomorphism
${\mathfrak {UG}}^{m} {(\mathscr C)}$
. The spectral sequence then implies that there is an isomorphism
![]() ${\mathrm {H}}_{*} ({\mathfrak {DG}_{\mathrm {trunc}}^{m}}{\operatorname {(\mathscr {L}ie)}}) \cong {\mathrm {H}}_{*} ({\mathfrak {UG}}^{m} {(\mathscr C)})$
. (This argument is similar to a proof sketched by Willwacher [Reference WillwacherWil14, Appendix K].)
${\mathrm {H}}_{*} ({\mathfrak {DG}_{\mathrm {trunc}}^{m}}{\operatorname {(\mathscr {L}ie)}}) \cong {\mathrm {H}}_{*} ({\mathfrak {UG}}^{m} {(\mathscr C)})$
. (This argument is similar to a proof sketched by Willwacher [Reference WillwacherWil14, Appendix K].)
Remark 4.1. There should also be a version of everything we do in this section in the more general situation of the truncated directed
![]() $(I,J)$
-graph complex
$(I,J)$
-graph complex
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J}$
. We will not elaborate on this here though. It might appear in future work.
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{I,J}$
. We will not elaborate on this here though. It might appear in future work.
We begin by noting that the degree k part of the graded vector space
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
splits as a direct sum
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
splits as a direct sum
where
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,l}$
is the subspace generated by elements represented by truncated decorated graphs with exactly l vertices of valence two. Note that a truncated decorated graph with N vertices and E edges represents an element of homological degree
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,l}$
is the subspace generated by elements represented by truncated decorated graphs with exactly l vertices of valence two. Note that a truncated decorated graph with N vertices and E edges represents an element of homological degree
![]() $k \ge N (1 - m) + E m$
(since
$k \ge N (1 - m) + E m$
(since
![]() $\mathscr C$
is concentrated in nonnegative degrees). Since all of its vertices are at least bivalent we have
$\mathscr C$
is concentrated in nonnegative degrees). Since all of its vertices are at least bivalent we have
![]() $E \ge N$
and hence
$E \ge N$
and hence
![]() $k \ge N$
(since
$k \ge N$
(since
![]() $m \ge 0$
). Thus, in the above decomposition, a summand is trivial if
$m \ge 0$
). Thus, in the above decomposition, a summand is trivial if
![]() $l> k$
, and hence, the sum is finite.
$l> k$
, and hence, the sum is finite.
The differential restricts to a map
so that regrading via ![]() yields a double complex
yields a double complex
![]() $C_{*,*}$
with a differential
$C_{*,*}$
with a differential
![]() $d^1$
of bidegree
$d^1$
of bidegree
![]() $(-1,0)$
and a differential
$(-1,0)$
and a differential
![]() $d^2$
of bidegree
$d^2$
of bidegree
![]() $(0, -1)$
– that
$(0, -1)$
– that
![]() $d^1 \circ d^2 = - d^2 \circ d^1$
follows immediately from
$d^1 \circ d^2 = - d^2 \circ d^1$
follows immediately from
![]() $d \circ d = 0$
. The total complex of
$d \circ d = 0$
. The total complex of
![]() $C_{*,*}$
is canonically isomorphic to
$C_{*,*}$
is canonically isomorphic to
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
. Moreover,
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
. Moreover,
![]() $C_{p,q}$
can only be nontrivial if
$C_{p,q}$
can only be nontrivial if
![]() $0 \le q \le p + q$
. Hence, we obtain a convergent spectral sequence of the following form:
$0 \le q \le p + q$
. Hence, we obtain a convergent spectral sequence of the following form:
(see, for example, [Reference WeibelWei95, §5.6]).
We will use this spectral sequence to identify the homology of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
. However, we will need a few preliminaries before we can do so, beginning with an undirected version of Definition 3.16.
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
. However, we will need a few preliminaries before we can do so, beginning with an undirected version of Definition 3.16.
Definition 4.2. We denote by
![]() ${{\mathbf {Graph}}}$
the following groupoid:
${{\mathbf {Graph}}}$
the following groupoid:
-
• Objects are tuples
 $(F, N, \mu , a)$
with F and N finite linearly ordered sets,
$(F, N, \mu , a)$
with F and N finite linearly ordered sets,
 $a \colon F \to N$
a map of sets, and
$a \colon F \to N$
a map of sets, and
 $\mu $
a matching of F (i.e.,
$\mu $
a matching of F (i.e.,
 $\mu $
is a fixed-point-free bijection
$\mu $
is a fixed-point-free bijection
 $F \to F$
of order two).
$F \to F$
of order two). -
• A morphism
 $(F, N, \mu , a) \to (F', N', \mu ', a')$
is a pair of bijections
$(F, N, \mu , a) \to (F', N', \mu ', a')$
is a pair of bijections
 $(f \colon F \to F', g \colon N \to N')$
such that
$(f \colon F \to F', g \colon N \to N')$
such that
 $f \circ \mu = \mu ' \circ f$
and
$f \circ \mu = \mu ' \circ f$
and
 $g \circ a = a' \circ f$
.
$g \circ a = a' \circ f$
.
Moreover, we write
![]() ${{\mathbf {Graph}}}_{\ge 3}$
for the full subgroupoid of
${{\mathbf {Graph}}}_{\ge 3}$
for the full subgroupoid of
![]() ${{\mathbf {Graph}}}$
spanned by those objects
${{\mathbf {Graph}}}$
spanned by those objects
![]() $(F, N, \mu , a)$
such that
$(F, N, \mu , a)$
such that
![]() $|{{a^{-1}}(v)}| \ge 3$
for all
$|{{a^{-1}}(v)}| \ge 3$
for all
![]() $v \in N$
.
$v \in N$
.
Remark 4.3. Analogously to Remark 3.17, we can think of
![]() ${{\mathbf {Graph}}}$
as the groupoid of undirected graphs and of
${{\mathbf {Graph}}}$
as the groupoid of undirected graphs and of
![]() ${{\mathbf {Graph}}}_{\ge 3}$
as the groupoid of undirected graphs such that each vertex has at least valence
${{\mathbf {Graph}}}_{\ge 3}$
as the groupoid of undirected graphs such that each vertex has at least valence
![]() $3$
.
$3$
.
Given
![]() $G = (F, N, \mu , a) \in {{\mathbf {Graph}}}$
, the set F specifies the set of flags, N is the set of vertices (or nodes), the map a specifies to which vertex a flag is incident, and the matching
$G = (F, N, \mu , a) \in {{\mathbf {Graph}}}$
, the set F specifies the set of flags, N is the set of vertices (or nodes), the map a specifies to which vertex a flag is incident, and the matching
![]() $\mu $
specifies how the flags are connected to form edges. In particular, an edge of G is an orbit of
$\mu $
specifies how the flags are connected to form edges. In particular, an edge of G is an orbit of
![]() $\mu $
(i.e., a subset
$\mu $
(i.e., a subset
![]() $\{f, f'\} \subseteq F$
such that
$\{f, f'\} \subseteq F$
such that
![]() $\mu (f) = f'$
and
$\mu (f) = f'$
and
![]() $\mu (f') = f$
).
$\mu (f') = f$
).
Definition 4.4. For
![]() $G = (F, N, \mu , a) \in {{\mathbf {Graph}}}$
, we write
$G = (F, N, \mu , a) \in {{\mathbf {Graph}}}$
, we write
![]() $\operatorname {Edge}(G)$
for the set of edges of G. We equip it with the linear order pulled back along the injection
$\operatorname {Edge}(G)$
for the set of edges of G. We equip it with the linear order pulled back along the injection
![]() $\operatorname {Edge}(G) \to F$
given by
$\operatorname {Edge}(G) \to F$
given by
![]() $\{f, f'\} \mapsto \min (f, f')$
. This construction yields a functor
$\{f, f'\} \mapsto \min (f, f')$
. This construction yields a functor
![]() $\operatorname {Edge} \colon {{\mathbf {Graph}}} \to {{{\mathbf {\Sigma }}}}$
.
$\operatorname {Edge} \colon {{\mathbf {Graph}}} \to {{{\mathbf {\Sigma }}}}$
.
Definition 4.5. Let
![]() $D = (F, N, S, T, \mu , a)$
be a directed graph. Its underlying undirected graph is the undirected graph
$D = (F, N, S, T, \mu , a)$
be a directed graph. Its underlying undirected graph is the undirected graph
![]() $(F, N, \mu ', a)$
, where
$(F, N, \mu ', a)$
, where
![]() $\mu ' \colon F \to F$
is the matching given by
$\mu ' \colon F \to F$
is the matching given by
![]() $\mu '(s) = \mu (s)$
for
$\mu '(s) = \mu (s)$
for
![]() $s \in S \subseteq F$
and
$s \in S \subseteq F$
and
![]() $\mu '(t) = {\mu ^{-1}}(t)$
for
$\mu '(t) = {\mu ^{-1}}(t)$
for
![]() $t \in T \subseteq F$
.
$t \in T \subseteq F$
.
Definition 4.6. For a truncated directed graph D, we define its underlying graph
![]() $\operatorname {U} (D) \in {{\mathbf {Graph}}}_{\ge 3}$
to be the underlying undirected graph of D, except that all vertices of valence two together with their two incident edges are replaced by a single edge.
$\operatorname {U} (D) \in {{\mathbf {Graph}}}_{\ge 3}$
to be the underlying undirected graph of D, except that all vertices of valence two together with their two incident edges are replaced by a single edge.
Remark 4.7. To be entirely precise, we would need to specify a linear order on the set of vertices and the set of flags of
![]() $\operatorname {U} (D)$
. This choice will not matter, however, and so we can make it arbitrarily.
$\operatorname {U} (D)$
. This choice will not matter, however, and so we can make it arbitrarily.
We will now study (the homology of) the chain complexes ![]() occurring in the spectral sequence (4.1). To this end, let D be a truncated directed graph. Note that applying
occurring in the spectral sequence (4.1). To this end, let D be a truncated directed graph. Note that applying
![]() $d^2$
to an element represented by D yields a sum of elements each of which is represented by a directed graph
$d^2$
to an element represented by D yields a sum of elements each of which is represented by a directed graph
![]() $D'$
such that
$D'$
such that
![]() $\operatorname {U}(D') \cong \operatorname {U}(D)$
. Hence, there is a splitting of chain complexes
$\operatorname {U}(D') \cong \operatorname {U}(D)$
. Hence, there is a splitting of chain complexes
where
![]() $[G]$
runs over all isomorphism classes of
$[G]$
runs over all isomorphism classes of
![]() ${{\mathbf {Graph}}}_{\ge 3}$
and
${{\mathbf {Graph}}}_{\ge 3}$
and
![]() $C^G_{p,*}$
is the subcomplex of
$C^G_{p,*}$
is the subcomplex of
![]() $C^2_{p,*}$
generated by the elements represented by directed graphs D with
$C^2_{p,*}$
generated by the elements represented by directed graphs D with
![]() $\operatorname {U}(D) \cong G$
. Thus, we can restrict our attention to the chain complexes
$\operatorname {U}(D) \cong G$
. Thus, we can restrict our attention to the chain complexes
![]() $C^G_{p,*}$
.
$C^G_{p,*}$
.
To understand (the homology of)
![]() $C^G_{p,*}$
, we will construct a functor
$C^G_{p,*}$
, we will construct a functor
![]() $\widetilde C_{\bullet ,*}$
from
$\widetilde C_{\bullet ,*}$
from
![]() ${{\mathbf {Graph}}}_{\ge 3}$
to chain complexes in graded vector spaces (here, the first grading
${{\mathbf {Graph}}}_{\ge 3}$
to chain complexes in graded vector spaces (here, the first grading
![]() $\bullet $
is the one of the graded vector space, and the second grading
$\bullet $
is the one of the graded vector space, and the second grading
![]() $*$
is the one of the chain complex) such that
$*$
is the one of the chain complex) such that

for all G. Since
![]() ${\mathrm {Aut}}(G)$
is finite and, in characteristic
${\mathrm {Aut}}(G)$
is finite and, in characteristic
![]() $0$
, quotienting by a finite group commutes with taking homology, we will then be able to deduce the homology of
$0$
, quotienting by a finite group commutes with taking homology, we will then be able to deduce the homology of
![]() $C^G_{\bullet ,*}$
from the homology of
$C^G_{\bullet ,*}$
from the homology of
![]() $\widetilde C_{\bullet ,*}(G)$
together with its
$\widetilde C_{\bullet ,*}(G)$
together with its
![]() ${\mathrm {Aut}}(G)$
-action.
${\mathrm {Aut}}(G)$
-action.
More precisely, we will take a ‘coordinate-free’ approach to the isomorphism (4.2) and actually construct an isomorphism

of chain complexes in graded vector spaces. This will be the more convenient approach as it does not require us to chose representatives of isomorphism classes of
![]() ${{\mathbf {Graph}}}_{\ge 3}$
. We need a few preliminaries before we can construct
${{\mathbf {Graph}}}_{\ge 3}$
. We need a few preliminaries before we can construct
![]() $\widetilde C_{\bullet ,*}$
.
$\widetilde C_{\bullet ,*}$
.
Definition 4.8. Let S be a set. We write
![]() $\operatorname {dir}(S)$
for the set of functions
$\operatorname {dir}(S)$
for the set of functions
![]() $S \to \{-, 0, +\}$
. For an element
$S \to \{-, 0, +\}$
. For an element
![]() $o \in \operatorname {dir}(S)$
, we set its degree to be
$o \in \operatorname {dir}(S)$
, we set its degree to be ![]() .
.
Moreover, for
![]() ${?} \in \{+, -\}$
,
${?} \in \{+, -\}$
,
![]() $o \in \operatorname {dir}(S)$
, and
$o \in \operatorname {dir}(S)$
, and
![]() $s \in S$
such that
$s \in S$
such that
![]() $o(s) = 0$
, we write
$o(s) = 0$
, we write
![]() $o_s^{?} \in \operatorname {dir}(S)$
for the function with
$o_s^{?} \in \operatorname {dir}(S)$
for the function with
![]() $o_s^{?}(s) = {?}$
and
$o_s^{?}(s) = {?}$
and
![]() $o_s^{?}(s') = o(s')$
for all
$o_s^{?}(s') = o(s')$
for all
![]() $s' \in S \setminus \{s\}$
.
$s' \in S \setminus \{s\}$
.
Definition 4.9. When G is an undirected graph, we write ![]() . This forms a (covariant) functor
. This forms a (covariant) functor
![]() $\operatorname {dir}$
from
$\operatorname {dir}$
from
![]() ${{\mathbf {Graph}}}$
to the category of sets by letting an isomorphism
${{\mathbf {Graph}}}$
to the category of sets by letting an isomorphism
![]() $\chi \colon G \to G'$
act on
$\chi \colon G \to G'$
act on
![]() $o \in \operatorname {dir}(G)$
such that
$o \in \operatorname {dir}(G)$
such that

for each edge
![]() $e = \{f_1 < f_2\}$
of
$e = \{f_1 < f_2\}$
of
![]() $G'$
. (Here, we set
$G'$
. (Here, we set
![]() $-- = +$
,
$-- = +$
,
![]() $-0 = 0$
, and
$-0 = 0$
, and
![]() $-+ = -$
, as expected.)
$-+ = -$
, as expected.)
Remark 4.10. We think of the elements of
![]() $\operatorname {dir}(G)$
as all possible ways to, for each edge of G, either chose an orientation or leave it undirected.
$\operatorname {dir}(G)$
as all possible ways to, for each edge of G, either chose an orientation or leave it undirected.
Definition 4.11. Let
![]() $e = \{f < f'\}$
be an edge of an undirected graph G. We set the vector space
$e = \{f < f'\}$
be an edge of an undirected graph G. We set the vector space
![]() $\operatorname {Or}(e)$
of orientations of e to be
$\operatorname {Or}(e)$
of orientations of e to be
![]() ${\mathbb {Q}}$
(in degree
${\mathbb {Q}}$
(in degree
![]() $0$
). An isomorphism
$0$
). An isomorphism
![]() $\chi \colon G \to G'$
of undirected graphs induces a map
$\chi \colon G \to G'$
of undirected graphs induces a map
![]() $\operatorname {Or}(e) \to \operatorname {Or}(\chi (e))$
by setting it to be
$\operatorname {Or}(e) \to \operatorname {Or}(\chi (e))$
by setting it to be
![]() ${\mathrm {id}}_{\mathbb {Q}}$
if
${\mathrm {id}}_{\mathbb {Q}}$
if
![]() $\chi (f) < \chi (f')$
and
$\chi (f) < \chi (f')$
and
![]() $- {{\mathrm {id}}_{\mathbb {Q}}}$
otherwise.
$- {{\mathrm {id}}_{\mathbb {Q}}}$
otherwise.
Definition 4.12. Let ![]() and
and
![]() $o \in \operatorname {dir}(G)$
. We write
$o \in \operatorname {dir}(G)$
. We write
![]() $\operatorname {D}(G, o)$
for the truncated directed graph obtained from G by, for each edge
$\operatorname {D}(G, o)$
for the truncated directed graph obtained from G by, for each edge
![]() $e = \{f < f'\}$
, doing the following:
$e = \{f < f'\}$
, doing the following:
-
• if
 $o(e) = +$
, we orient it from f to
$o(e) = +$
, we orient it from f to
 $f'$
(i.e.
$f'$
(i.e.
 $f \in S$
and
$f \in S$
and
 $f' \in T$
).
$f' \in T$
). -
• if
 $o(e) = -$
, we orient it from
$o(e) = -$
, we orient it from
 $f'$
to f (i.e.
$f'$
to f (i.e.
 $f' \in S$
and
$f' \in S$
and
 $f \in T$
).
$f \in T$
). -
• if
 $o(e) = 0$
, we replace e by a new vertex
$o(e) = 0$
, we replace e by a new vertex
 $v_e$
with two incoming edges
$v_e$
with two incoming edges
 $(s_e^+, t_e^+)$
and
$(s_e^+, t_e^+)$
and
 $(s_e^-, t_e^-)$
such that the flag
$(s_e^-, t_e^-)$
such that the flag
 $s_e^+$
is incident to
$s_e^+$
is incident to
 $a(f')$
, the flag
$a(f')$
, the flag
 $s_e^-$
is incident to
$s_e^-$
is incident to
 $a(f)$
, and the flags
$a(f)$
, and the flags
 $t_e^+$
and
$t_e^+$
and
 $t_e^-$
are incident to
$t_e^-$
are incident to
 $v_e$
.
$v_e$
.
The linear orders on the set of vertices and the set of flags of
![]() $\operatorname {D}(G, o)$
are inherited from G such that, for
$\operatorname {D}(G, o)$
are inherited from G such that, for
![]() $e = \{f < f'\}$
with
$e = \{f < f'\}$
with
![]() $o(e) = 0$
, the new vertex
$o(e) = 0$
, the new vertex
![]() $v_e$
is inserted as the successor of
$v_e$
is inserted as the successor of
![]() $a(f)$
(if there are multiple such vertices, they are inserted according to the order of the edges e), the two new flags
$a(f)$
(if there are multiple such vertices, they are inserted according to the order of the edges e), the two new flags
![]() $s_e^+$
and
$s_e^+$
and
![]() $t_e^+$
are successively inserted in this order instead of
$t_e^+$
are successively inserted in this order instead of
![]() $f'$
, and similarly for
$f'$
, and similarly for
![]() $s_e^-$
,
$s_e^-$
,
![]() $t_e^-$
, and f.
$t_e^-$
, and f.
This construction yields an equivalence of categories
![]() $\operatorname {D}$
from the Grothendieck construction
$\operatorname {D}$
from the Grothendieck construction
![]() ${\mathop {\mathchoice {\textstyle }{}{}{} \int _{{{{\mathbf {Graph}}}_{\ge 3}}}}} \operatorname {dir}$
to
${\mathop {\mathchoice {\textstyle }{}{}{} \int _{{{{\mathbf {Graph}}}_{\ge 3}}}}} \operatorname {dir}$
to
![]() ${{{\mathbf {DirGraph}}}^{{{\mathbf {trunc}}}}}$
.
${{{\mathbf {DirGraph}}}^{{{\mathbf {trunc}}}}}$
.
Remark 4.13. Note that
![]() $\operatorname {U}(\operatorname {D}(G, o))$
is canonically isomorphic to G for all o.
$\operatorname {U}(\operatorname {D}(G, o))$
is canonically isomorphic to G for all o.
Definition 4.14. We say that a collection of decorations
![]() $\xi _v$
of the vertices v of G represents the element of
$\xi _v$
of the vertices v of G represents the element of
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
that is represented by the
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
that is represented by the
![]() $\xi _v$
and
$\xi _v$
and
![]() ${\mathrm {id}} \in {\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )}$
at all of the added vertices of valence two.
${\mathrm {id}} \in {\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )}$
at all of the added vertices of valence two.
We are now ready to construct the functor
![]() $\widetilde C_{\bullet ,*}$
of (4.2). As a functor to bigraded vector spaces, we set
$\widetilde C_{\bullet ,*}$
of (4.2). As a functor to bigraded vector spaces, we set
bigraded by
![]() $(k - | o | , | o | )$
, where k is the homological degree. An isomorphism
$(k - | o | , | o | )$
, where k is the homological degree. An isomorphism
![]() $\chi \colon G \to G'$
acts on this in the canonical way (i.e., it maps
$\chi \colon G \to G'$
acts on this in the canonical way (i.e., it maps
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
to
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
to
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, \chi \mathbin {.} o))$
via the map induced by
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, \chi \mathbin {.} o))$
via the map induced by
![]() $\operatorname {D}(\chi , o)$
). This is precisely the following left Kan extension
$\operatorname {D}(\chi , o)$
). This is precisely the following left Kan extension

of
![]() ${\operatorname {Dec}^{m}_{\mathscr C}} \circ \operatorname {D}$
along the projection
${\operatorname {Dec}^{m}_{\mathscr C}} \circ \operatorname {D}$
along the projection
![]() ${\mathrm {pr}}$
.
${\mathrm {pr}}$
.
Since
![]() $\operatorname {D}$
is an equivalence of categories and since, by definition of
$\operatorname {D}$
is an equivalence of categories and since, by definition of
![]() $C^2$
, there is an isomorphism of bigraded vector spaces
$C^2$
, there is an isomorphism of bigraded vector spaces
![]() ${\mathrm {colim}}_{{{\mathbf {DirGraph}}}^{{{\mathbf {trunc}}}}}\ {\operatorname {Dec}^{m}_{\mathscr C}} \cong C^2$
, we obtain an isomorphism
${\mathrm {colim}}_{{{\mathbf {DirGraph}}}^{{{\mathbf {trunc}}}}}\ {\operatorname {Dec}^{m}_{\mathscr C}} \cong C^2$
, we obtain an isomorphism
![]() ${\mathrm {colim}}_{{{\mathbf {Graph}}}_{\ge 3}}\ \widetilde C \cong C^2$
of bigraded vector spaces. (This uses that the colimit of a left Kan extension is isomorphic to the colimit of the original functor.)
${\mathrm {colim}}_{{{\mathbf {Graph}}}_{\ge 3}}\ \widetilde C \cong C^2$
of bigraded vector spaces. (This uses that the colimit of a left Kan extension is isomorphic to the colimit of the original functor.)
To construct the differential of
![]() $\widetilde C(G)$
, we will use the technical lemma following the next definition.
$\widetilde C(G)$
, we will use the technical lemma following the next definition.
Definition 4.15. Our standing assumption that
![]() ${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )} = {\mathbb {Q} {\langle {\mathrm {id}} \rangle }}$
implies that the vector spaces
${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )} = {\mathbb {Q} {\langle {\mathrm {id}} \rangle }}$
implies that the vector spaces
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
are independent of o up to isomorphism (when
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
are independent of o up to isomorphism (when
![]() $o(e) = 0$
, the extra vertex
$o(e) = 0$
, the extra vertex
![]() $v_e$
is labeled by an element of
$v_e$
is labeled by an element of
![]() ${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )} \cong {\mathbb {Q}}$
). We denote by
${\mathscr C \left (\mkern -4mu\left (2 \right )\mkern -4mu\right )} \cong {\mathbb {Q}}$
). We denote by
the canonical such isomorphism (by a slight abuse, we do not include o in the notation). It is induced by the canonical bijection
![]() $\sigma $
between the set of initial flags of
$\sigma $
between the set of initial flags of
![]() $\operatorname {D}(G, o_e^+)$
and the set of initial flags of
$\operatorname {D}(G, o_e^+)$
and the set of initial flags of
![]() $\operatorname {D}(G, o_e^-)$
(i.e., it is given by
$\operatorname {D}(G, o_e^-)$
(i.e., it is given by
![]() ${\mathrm {id}} \mathop{\mathop{\otimes}}\, (\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} \sigma }$
).
${\mathrm {id}} \mathop{\mathop{\otimes}}\, (\mathrm {s}^{m} {\mathbb {Q}})^{{{\otimes}} \sigma }$
).
Lemma 4.16. There exist, for all
![]() $G \in {{\mathbf {Graph}}}_{\ge 3}$
,
$G \in {{\mathbf {Graph}}}_{\ge 3}$
,
![]() $e \in \operatorname {Edge}(G)$
, and
$e \in \operatorname {Edge}(G)$
, and
![]() $o \in \operatorname {dir}(G)$
such that
$o \in \operatorname {dir}(G)$
such that
![]() $o(e) = 0$
, two isomorphisms
$o(e) = 0$
, two isomorphisms
 $$ \begin{align*} d_{G,e}^+ &\colon {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o)) \longrightarrow {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o_e^+)) \\ d_{G,e}^- &\colon {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o)) \longrightarrow {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o_e^-)) \end{align*} $$
$$ \begin{align*} d_{G,e}^+ &\colon {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o)) \longrightarrow {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o_e^+)) \\ d_{G,e}^- &\colon {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o)) \longrightarrow {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o_e^-)) \end{align*} $$
such that the following properties hold for all elements
![]() ${?} \in \{\pm \}$
and
${?} \in \{\pm \}$
and
![]() $x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
:
$x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
:
-
1. Let
 $\chi \colon G \to G'$
be an isomorphism of
$\chi \colon G \to G'$
be an isomorphism of
 ${{\mathbf {Graph}}}_{\ge 3}$
and set
${{\mathbf {Graph}}}_{\ge 3}$
and set  . Then
. Then
 $\chi \mathbin {.} d_{G,e}^{?}(x) = d_{G',\chi (e)}^{{?}'}(\chi \mathbin {.} x)$
.
$\chi \mathbin {.} d_{G,e}^{?}(x) = d_{G',\chi (e)}^{{?}'}(\chi \mathbin {.} x)$
. -
2. Let
 $e' \neq e$
be another edge of G such that
$e' \neq e$
be another edge of G such that
 $o(e') = 0$
, and let
$o(e') = 0$
, and let
 ${?}' \in \{\pm \}$
. Then
${?}' \in \{\pm \}$
. Then
 $d_{G,e'}^{{?}'} (d_{G,e}^{?} (x))= - d_{G,e}^{?} (d_{G,e'}^{{?}'} (x))$
.
$d_{G,e'}^{{?}'} (d_{G,e}^{?} (x))= - d_{G,e}^{?} (d_{G,e'}^{{?}'} (x))$
. -
3. We have
 $r (d_{G,e}^{?} (x)) = d^{\operatorname {D}(G,o)}_{s_e^{?}} (r (x))$
, where r denotes the canonical map from
$r (d_{G,e}^{?} (x)) = d^{\operatorname {D}(G,o)}_{s_e^{?}} (r (x))$
, where r denotes the canonical map from
 ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
respectively
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
respectively
 ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o_e^{?}))$
to
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o_e^{?}))$
to
 $C^2$
.
$C^2$
. -
4. We have that
 $d_{G,e}^- \circ {(d_{G,e}^+)^{-1}} \colon {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o_e^+)) \to {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o_e^-))$
is equal to
$d_{G,e}^- \circ {(d_{G,e}^+)^{-1}} \colon {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o_e^+)) \to {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o_e^-))$
is equal to
 $(-1)^m c_{G,e}$
.
$(-1)^m c_{G,e}$
.
Assuming this lemma, we can define a differential on
![]() $\widetilde C(G)$
of bidegree
$\widetilde C(G)$
of bidegree
![]() $(0, -1)$
by
$(0, -1)$
by

(here
![]() $d_{G,e}^{?}$
is understood to be zero on
$d_{G,e}^{?}$
is understood to be zero on
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
when
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
when
![]() $o(e) \neq 0$
). By the second property above, we have
$o(e) \neq 0$
). By the second property above, we have
![]() $d \circ d = 0$
and hence that
$d \circ d = 0$
and hence that ![]() is a chain complex. Moreover, the first property implies functoriality of
is a chain complex. Moreover, the first property implies functoriality of
![]() $\widetilde C_{\bullet ,*}$
, and the third property implies that the isomorphism
$\widetilde C_{\bullet ,*}$
, and the third property implies that the isomorphism
![]() ${\mathrm {colim}}_{{{\mathbf {Graph}}}_{\ge 3}}\ \widetilde C \cong C^2$
is compatible with the differentials.
${\mathrm {colim}}_{{{\mathbf {Graph}}}_{\ge 3}}\ \widetilde C \cong C^2$
is compatible with the differentials.
Proof of Lemma 4.16.
It will be convenient to construct the isomorphisms
![]() $d_{G,e}^+$
and
$d_{G,e}^+$
and
![]() $d_{G,e}^-$
simultaneously for all elements
$d_{G,e}^-$
simultaneously for all elements
![]() $(G, e)$
of some fixed isomorphism class of the category of undirected graphs with a specified edge. To this end, we fix some pair
$(G, e)$
of some fixed isomorphism class of the category of undirected graphs with a specified edge. To this end, we fix some pair
![]() $(G_0 = (F_0, N_0, \mu _0, a_0), e_0)$
in this isomorphism class such that the one or two vertices incident to
$(G_0 = (F_0, N_0, \mu _0, a_0), e_0)$
in this isomorphism class such that the one or two vertices incident to
![]() $e_0$
are the first elements of
$e_0$
are the first elements of
![]() $N_0$
, such that
$N_0$
, such that
![]() $a_0$
is order preserving and such that the two flags making up
$a_0$
is order preserving and such that the two flags making up
![]() $e_0$
come first in the linear orders of their respective vertices (if they are incident to the same vertex, we ask these two flags to be the first two elements).
$e_0$
come first in the linear orders of their respective vertices (if they are incident to the same vertex, we ask these two flags to be the first two elements).
Now let
![]() $o \in \operatorname {dir}(G_0)$
such that
$o \in \operatorname {dir}(G_0)$
such that
![]() $o(e_0) = 0$
and let
$o(e_0) = 0$
and let
![]() $x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G_0, o))$
be the element represented by some decorations
$x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G_0, o))$
be the element represented by some decorations
![]() $(\xi _v)_{v \in N_0}$
. Then we set
$(\xi _v)_{v \in N_0}$
. Then we set
![]() $d_{G_0,e_0}^{?}(x)$
to be
$d_{G_0,e_0}^{?}(x)$
to be
![]() $(-1)^{|N| m + n + b_{?}}$
times the element of
$(-1)^{|N| m + n + b_{?}}$
times the element of
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G_0, o_{e_0}^{?}))$
represented by the
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G_0, o_{e_0}^{?}))$
represented by the
![]() $\xi _v$
. Here,
$\xi _v$
. Here,

where
![]() $v_{1,o}$
is the first element of
$v_{1,o}$
is the first element of
![]() $N_0$
considered as a vertex of
$N_0$
considered as a vertex of
![]() $\operatorname {D}(G_0, o)$
.
$\operatorname {D}(G_0, o)$
.
We extend this to all pairs
![]() $(G, e)$
by choosing some isomorphism
$(G, e)$
by choosing some isomorphism
![]() $\chi \colon G \to G_0$
such that
$\chi \colon G \to G_0$
such that
![]() $\chi (e) = e_0$
, and setting for
$\chi (e) = e_0$
, and setting for
![]() $o \in \operatorname {dir}(G)$
,
$o \in \operatorname {dir}(G)$
,
![]() $x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
, and
$x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
, and
![]() ${?} \in \{\pm \}$
,
${?} \in \{\pm \}$
,
where ![]() . To see that this is well defined, we need to show that equation (4.5) holds when
. To see that this is well defined, we need to show that equation (4.5) holds when
![]() $(G, e) = (G_0, e_0)$
and
$(G, e) = (G_0, e_0)$
and
![]() $\chi $
is any automorphism of
$\chi $
is any automorphism of
![]() $G_0$
such that
$G_0$
such that
![]() $\chi (e_0) = e_0$
. This follows directly from comparing the signs induced by
$\chi (e_0) = e_0$
. This follows directly from comparing the signs induced by
![]() $\operatorname {D}(\chi , o)$
and
$\operatorname {D}(\chi , o)$
and
![]() $\operatorname {D}(\chi , o_{e_0}^{?})$
(distinguishing the cases of
$\operatorname {D}(\chi , o_{e_0}^{?})$
(distinguishing the cases of
![]() $e_0$
being a loop or not and
$e_0$
being a loop or not and
![]() $\chi $
flipping the two flags making up
$\chi $
flipping the two flags making up
![]() $e_0$
or not). The first property in the statement of the lemma is thus true by definition.
$e_0$
or not). The first property in the statement of the lemma is thus true by definition.
To prove the third property, it is enough, by equation (4.5) and the fact that
![]() $r(\chi \mathbin {.} x) = r(x)$
, to do so for the pair
$r(\chi \mathbin {.} x) = r(x)$
, to do so for the pair
![]() $(G_0, e_0)$
. In this case, the equality of the signs involved can be deduced easily from Definitions 4.12 and 3.24.
$(G_0, e_0)$
. In this case, the equality of the signs involved can be deduced easily from Definitions 4.12 and 3.24.
The second property follows from similar arguments: by equation (4.5), it is enough to check this for one member of each of the isomorphism classes of the category of undirected graphs with two distinct specified edges. Distinguishing various cases, corresponding to the different ways the vertices incident to the two edges can coincide or not, we choose representatives of the isomorphism classes that behave nicely with our construction above. In these cases, it is then straightforward (but tedious) to check the equality directly from the definition.
To show the fourth property, we first note that, for all isomorphisms
![]() $\chi \colon G \to G'$
, the following diagram of isomorphisms commutes:
$\chi \colon G \to G'$
, the following diagram of isomorphisms commutes:

where ![]() . Hence, it is enough to prove this property in the cases of the pairs
. Hence, it is enough to prove this property in the cases of the pairs
![]() $(G_0, e_0)$
. There, it is true by definition since
$(G_0, e_0)$
. There, it is true by definition since
![]() $(-1)^{b_+ + b_- + m}$
is (regardless of whether
$(-1)^{b_+ + b_- + m}$
is (regardless of whether
![]() $e_0$
is a loop or not) precisely the m-th power of the sign of the canonical bijection between the set of initial flags of
$e_0$
is a loop or not) precisely the m-th power of the sign of the canonical bijection between the set of initial flags of
![]() $\operatorname {D}(G_0, o_{e_0}^+)$
and the set of initial flags of
$\operatorname {D}(G_0, o_{e_0}^+)$
and the set of initial flags of
![]() $\operatorname {D}(G_0, o_{e_0}^-)$
.
$\operatorname {D}(G_0, o_{e_0}^-)$
.
We now claim that, for any G, the homology of
![]() $\widetilde C_{\bullet ,*}(G)$
is concentrated in bidegrees
$\widetilde C_{\bullet ,*}(G)$
is concentrated in bidegrees
![]() $(p, 0)$
(which implies that the spectral sequence (4.1) collapses on the second page). This follows immediately from the following more general lemma.
$(p, 0)$
(which implies that the spectral sequence (4.1) collapses on the second page). This follows immediately from the following more general lemma.
Lemma 4.17. Let S be a finite set and
![]() $(V_o)_{o \in \operatorname {dir}(S)}$
a family of vector spaces. Furthermore, let there be, for each
$(V_o)_{o \in \operatorname {dir}(S)}$
a family of vector spaces. Furthermore, let there be, for each
![]() $s \in S$
and
$s \in S$
and
![]() $o \in \operatorname {dir}(S)$
such that
$o \in \operatorname {dir}(S)$
such that
![]() $o(s) = 0$
, two isomorphisms
$o(s) = 0$
, two isomorphisms
![]() $d_s^+ \colon V_o \to V_{o_s^+}$
and
$d_s^+ \colon V_o \to V_{o_s^+}$
and
![]() $d_s^- \colon V_o \to V_{o_s^-}$
. Assume that, for all
$d_s^- \colon V_o \to V_{o_s^-}$
. Assume that, for all
![]() ${?}, {?}' \in \{\pm \}$
and
${?}, {?}' \in \{\pm \}$
and
![]() $s \neq s' \in S$
such that
$s \neq s' \in S$
such that
![]() $o(s) = 0 = o(s')$
, we have an equality
$o(s) = 0 = o(s')$
, we have an equality
![]() $d_s^? \circ d_{s'}^{{?}'} = - d_{s'}^{{?}'} \circ d_s^{?}$
of maps
$d_s^? \circ d_{s'}^{{?}'} = - d_{s'}^{{?}'} \circ d_s^{?}$
of maps
![]() $V_o \to V_{o_{s\,s'}^{{?}\,{?}'}} = V_{o_{s'\,s}^{{?}'\,{?}}}$
.
$V_o \to V_{o_{s\,s'}^{{?}\,{?}'}} = V_{o_{s'\,s}^{{?}'\,{?}}}$
.
Let ![]() be graded by the degree of o and equip it with the differential given by
be graded by the degree of o and equip it with the differential given by ![]() (here, we set
(here, we set
![]() $d_s^?(V_o) = 0$
for all o with
$d_s^?(V_o) = 0$
for all o with
![]() $o(s) \neq 0$
). Then
$o(s) \neq 0$
). Then
![]() $C_*$
is a chain complex with homology concentrated in degree
$C_*$
is a chain complex with homology concentrated in degree
![]() $0$
.
$0$
.
Proof. First note that the anticommutativity of the partial differentials implies that
![]() $d \circ d = 0$
, so we only need to show the claim about the homology. Now choose some
$d \circ d = 0$
, so we only need to show the claim about the homology. Now choose some
![]() $s \in S$
. Then C can be bigraded via
$s \in S$
. Then C can be bigraded via

and ![]() for
for
![]() $q \not \in \{0, 1\}$
. The two differentials
$q \not \in \{0, 1\}$
. The two differentials ![]() and
and ![]() give this the structure of a first-quadrant double complex with total complex isomorphic to C. Hence, there is a convergent spectral sequence
give this the structure of a first-quadrant double complex with total complex isomorphic to C. Hence, there is a convergent spectral sequence
with the differential on the first page induced by
![]() $d^1$
(see e.g. [Reference WeibelWei95, §5.6]).
$d^1$
(see e.g. [Reference WeibelWei95, §5.6]).
Note that
![]() $C_{p,*}$
splits as
$C_{p,*}$
splits as
![]() $\bigoplus _o C_{p,*}^o$
where o runs over those elements of
$\bigoplus _o C_{p,*}^o$
where o runs over those elements of
![]() $\operatorname {dir}(S)$
of degree
$\operatorname {dir}(S)$
of degree
![]() $p+1$
such that
$p+1$
such that
![]() $o(s) = 0$
, and
$o(s) = 0$
, and
![]() $C_{p,*}^o$
is the subcomplex
$C_{p,*}^o$
is the subcomplex
of
![]() $C_{p,*}$
. Since
$C_{p,*}$
. Since
![]() $d_s^+$
and
$d_s^+$
and
![]() $d_s^-$
are both isomorphisms, the homology of
$d_s^-$
are both isomorphisms, the homology of
![]() $C_{p,*}^o$
is concentrated in degree 0. Moreover, the inclusion
$C_{p,*}^o$
is concentrated in degree 0. Moreover, the inclusion
![]() $V_{o_s^+} \to C_{p,*}^o$
induces an isomorphism on homology (where the former is considered as a chain complex concentrated in degree 0). Hence, setting
$V_{o_s^+} \to C_{p,*}^o$
induces an isomorphism on homology (where the former is considered as a chain complex concentrated in degree 0). Hence, setting

grading it by the degree of o and equipping it with
![]() $d^1$
as a differential, we obtain an isomorphism of chain complexes
$d^1$
as a differential, we obtain an isomorphism of chain complexes
![]() $C^+_\bullet \to \left ( {\mathrm {H}}_{0}(C_{\bullet ,*}, d^2), d^1 \right )$
. Since the
$C^+_\bullet \to \left ( {\mathrm {H}}_{0}(C_{\bullet ,*}, d^2), d^1 \right )$
. Since the
![]() $E_1$
-page of the spectral sequence (4.6) is concentrated in the row
$E_1$
-page of the spectral sequence (4.6) is concentrated in the row
![]() $q = 0$
, there thus is an isomorphism
$q = 0$
, there thus is an isomorphism
![]() ${\mathrm {H}}_{*}(C) \cong {\mathrm {H}}_{*}(C^+)$
. Hence, it is enough to show that the homology of
${\mathrm {H}}_{*}(C) \cong {\mathrm {H}}_{*}(C^+)$
. Hence, it is enough to show that the homology of
![]() $C^+$
is concentrated in degree
$C^+$
is concentrated in degree
![]() $0$
.
$0$
.
To see this, we note that
![]() $C^+$
is a chain complex as described in the statement of this lemma, but with base set
$C^+$
is a chain complex as described in the statement of this lemma, but with base set
![]() $S \setminus \{s\}$
instead of S. Thus, we can, by induction, reduce to the case where S is empty. In that case, the statement is trivially true, as any such chain complex is concentrated in degree
$S \setminus \{s\}$
instead of S. Thus, we can, by induction, reduce to the case where S is empty. In that case, the statement is trivially true, as any such chain complex is concentrated in degree
![]() $0$
.
$0$
.
Let us recap what we did so far. We constructed the spectral sequence (4.1)
and, in (4.3) and (4.4), a functor
![]() $\widetilde C_{\bullet ,*}$
from
$\widetilde C_{\bullet ,*}$
from
![]() ${{\mathbf {Graph}}}_{\ge 3}$
to chain complexes in graded vector spaces such that there is an isomorphism
${{\mathbf {Graph}}}_{\ge 3}$
to chain complexes in graded vector spaces such that there is an isomorphism
![]() ${\mathrm {colim}}{}\ \widetilde C_{\bullet ,*} \cong C^2_{\bullet ,*}$
. Then we proved, in Lemma 4.17, that the pointwise homology
${\mathrm {colim}}{}\ \widetilde C_{\bullet ,*} \cong C^2_{\bullet ,*}$
. Then we proved, in Lemma 4.17, that the pointwise homology
![]() ${\mathrm {H}}_{*} \circ \widetilde C_{\bullet ,*}$
is concentrated in bidegrees
${\mathrm {H}}_{*} \circ \widetilde C_{\bullet ,*}$
is concentrated in bidegrees
![]() $(p, 0)$
.
$(p, 0)$
.
Now note that
![]() ${{\mathbf {Graph}}}_{\ge 3}$
is a disjoint union of groupoids equivalent to finite groups, and hence that taking rational homology commutes with
${{\mathbf {Graph}}}_{\ge 3}$
is a disjoint union of groupoids equivalent to finite groups, and hence that taking rational homology commutes with
![]() ${{\mathbf {Graph}}}_{\ge 3}$
-colimits (since rational homology commutes with direct sums and quotients by finite groups). Hence, there are isomorphisms
${{\mathbf {Graph}}}_{\ge 3}$
-colimits (since rational homology commutes with direct sums and quotients by finite groups). Hence, there are isomorphisms

of bigraded vector spaces. In particular, the homology of
![]() $C^2_{\bullet ,*}$
is also concentrated in bidegrees
$C^2_{\bullet ,*}$
is also concentrated in bidegrees
![]() $(p, 0)$
. The spectral sequence then implies that the differential
$(p, 0)$
. The spectral sequence then implies that the differential
![]() $d^1$
of the double complex
$d^1$
of the double complex
![]() $C_{*,*}$
induces a differential on
$C_{*,*}$
induces a differential on
![]() ${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
such that there is an isomorphism
${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
such that there is an isomorphism
of graded vector spaces (Lemma 2.10 provides an explicit description of this isomorphism, which we will use later). Pulling back the differential
![]() $d^1$
along the isomorphism (4.7) hence yields a differential on the graded vector space
$d^1$
along the isomorphism (4.7) hence yields a differential on the graded vector space
![]() ${\mathrm {colim}}{}\ ({\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*})$
such that the homology is isomorphic to the homology of
${\mathrm {colim}}{}\ ({\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*})$
such that the homology is isomorphic to the homology of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
. This colimit, equipped with the pulled-back differential, is the undirected graph complex we are looking for. To prove this, we will first give an explicit description of the functor
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
. This colimit, equipped with the pulled-back differential, is the undirected graph complex we are looking for. To prove this, we will first give an explicit description of the functor
![]() ${\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*}$
and then also identify the differential in these terms.
${\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*}$
and then also identify the differential in these terms.
Definition 4.18. For an undirected graph ![]() , we set
, we set

and call it the (graded) vector space of
![]() $\mathscr C$
-decorations on G. This yields a functor
$\mathscr C$
-decorations on G. This yields a functor
![]() ${\operatorname {UDec}^{m}_{\mathscr C}} \colon {{\mathbf {Graph}}}_{\ge 3} \to {{{\mathbf {GrVect}}}}$
. Moreover, we set
${\operatorname {UDec}^{m}_{\mathscr C}} \colon {{\mathbf {Graph}}}_{\ge 3} \to {{{\mathbf {GrVect}}}}$
. Moreover, we set
and call it the (graded) vector space of
![]() $\mathscr C$
-decorated undirected graphs.
$\mathscr C$
-decorated undirected graphs.
Given a family
![]() $\left ( \xi _v \in \mathscr C({a^{-1}}(v)) \right )_{v \in N}$
of elements of
$\left ( \xi _v \in \mathscr C({a^{-1}}(v)) \right )_{v \in N}$
of elements of
![]() $\mathscr C$
, we will call
$\mathscr C$
, we will call
the element represented by (G and) the decorations
![]() $\xi _v$
. By a slight abuse of terminology, we will use the same name for its image in
$\xi _v$
. By a slight abuse of terminology, we will use the same name for its image in
![]() ${\mathfrak {UG}}^{m}{(\mathscr C)}$
.
${\mathfrak {UG}}^{m}{(\mathscr C)}$
.
Lemma 4.19. The following composition
is a natural isomorphism
![]() ${\operatorname {UDec}^{m}_{\mathscr C}} \to {\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*}$
of functors
${\operatorname {UDec}^{m}_{\mathscr C}} \to {\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*}$
of functors
![]() ${{\mathbf {Graph}}}_{\ge 3} \to {{{\mathbf {GrVect}}}}$
. Here, the left-hand map is given by sending the element represented by G and some decorations
${{\mathbf {Graph}}}_{\ge 3} \to {{{\mathbf {GrVect}}}}$
. Here, the left-hand map is given by sending the element represented by G and some decorations
![]() $\xi _v$
to the element represented by
$\xi _v$
to the element represented by
![]() $\operatorname {D}(G, {\mathrm {const}}_{+})$
and the same decorations
$\operatorname {D}(G, {\mathrm {const}}_{+})$
and the same decorations
![]() $\xi _v$
. The right-hand map is the composite of the canonical inclusion of the middle term into
$\xi _v$
. The right-hand map is the composite of the canonical inclusion of the middle term into
![]() $\widetilde C_{\bullet ,0}(G)$
followed by the projection onto the zeroth homology.
$\widetilde C_{\bullet ,0}(G)$
followed by the projection onto the zeroth homology.
Proof. That the left-hand map is an isomorphism is clear. Hence, it is enough to show that the right-hand map is one as well, and that their composition is natural. We begin with the former.
By definition, we have
 $$\begin{align*}{\mathrm{H}}_{0}(\widetilde C_*(G)) = {{\left( \bigoplus_{\substack{o \in \operatorname{dir}(G) \\ | o | = 0}} {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o)) \right)}/{ }}{\sim}, \end{align*}$$
$$\begin{align*}{\mathrm{H}}_{0}(\widetilde C_*(G)) = {{\left( \bigoplus_{\substack{o \in \operatorname{dir}(G) \\ | o | = 0}} {\operatorname{Dec}^{m}_{\mathscr C}}(\operatorname{D}(G, o)) \right)}/{ }}{\sim}, \end{align*}$$
where
![]() $\sim $
is generated by the relations
$\sim $
is generated by the relations
![]() $d_{G,e}^+(x) \sim - d_{G,e}^-(x)$
for each edge e of G, element
$d_{G,e}^+(x) \sim - d_{G,e}^-(x)$
for each edge e of G, element
![]() $o \in \operatorname {dir}(S)$
such that
$o \in \operatorname {dir}(S)$
such that
![]() ${o^{-1}}(0) = \{e\}$
, and
${o^{-1}}(0) = \{e\}$
, and
![]() $x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
. The relation
$x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
. The relation
![]() $\sim $
can be equivalently described as being generated by
$\sim $
can be equivalently described as being generated by
![]() $x \sim - d_{G,e}^- \left ( {(d_{G,e}^+)^{-1}}(x) \right )$
for each edge e, element
$x \sim - d_{G,e}^- \left ( {(d_{G,e}^+)^{-1}}(x) \right )$
for each edge e, element
![]() $o \in \operatorname {dir}(S)$
with
$o \in \operatorname {dir}(S)$
with
![]() $ | o | = 0$
and
$ | o | = 0$
and
![]() $o(e) = +$
, and
$o(e) = +$
, and
![]() $x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
.
$x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o))$
.
By the last property of Lemma 4.16, we have an equality of isomorphisms
![]() $- d_{G,e}^- \circ {(d_{G,e}^+)^{-1}} = (-1)^{m+1} c_{G,e}$
. We also have, by definition, that
$- d_{G,e}^- \circ {(d_{G,e}^+)^{-1}} = (-1)^{m+1} c_{G,e}$
. We also have, by definition, that
![]() $c_{G,e} \circ c_{G,e'} = c_{G,e'} \circ c_{G,e}$
. This implies that each of the canonical maps
$c_{G,e} \circ c_{G,e'} = c_{G,e'} \circ c_{G,e}$
. This implies that each of the canonical maps
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o)) \to {\mathrm {H}}_{0}(\widetilde C_*(G))$
is an isomorphism.
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, o)) \to {\mathrm {H}}_{0}(\widetilde C_*(G))$
is an isomorphism.
We will now identify the functorial structure of
![]() ${\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*}$
in these terms, which will imply the desired naturality. Let
${\mathrm {H}}_{0} \circ \widetilde C_{\bullet ,*}$
in these terms, which will imply the desired naturality. Let
![]() $\chi \colon G \to G'$
be an isomorphism and let
$\chi \colon G \to G'$
be an isomorphism and let
![]() $x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, {\mathrm {const}}_{+}))$
be represented by some decorations
$x \in {\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G, {\mathrm {const}}_{+}))$
be represented by some decorations
![]() $(\xi _v)_{v \in N}$
, where N is the set of vertices of G. Then
$(\xi _v)_{v \in N}$
, where N is the set of vertices of G. Then
![]() $\chi \mathbin {.} x$
is
$\chi \mathbin {.} x$
is
![]() $\varepsilon \in \{\pm 1\}$
times the element y of
$\varepsilon \in \{\pm 1\}$
times the element y of
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G', \chi \mathbin {.} {\mathrm {const}}_{+}))$
represented by the decorations
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G', \chi \mathbin {.} {\mathrm {const}}_{+}))$
represented by the decorations
![]() $(\chi \mathbin {.} \xi _{{\chi ^{-1}}(v)})_{v \in N'}$
, where
$(\chi \mathbin {.} \xi _{{\chi ^{-1}}(v)})_{v \in N'}$
, where
![]() $N'$
is the set of vertices of
$N'$
is the set of vertices of
![]() $G'$
. This element y is equivalent under
$G'$
. This element y is equivalent under
![]() $\sim $
to
$\sim $
to
where ![]() . We hence obtain that
. We hence obtain that
![]() $\chi \mathbin {.} x$
is equivalent under
$\chi \mathbin {.} x$
is equivalent under
![]() $\sim $
to
$\sim $
to
![]() $\varepsilon (-1)^{k(m+1)} \operatorname {sgn}(\sigma )^m$
times the element of
$\varepsilon (-1)^{k(m+1)} \operatorname {sgn}(\sigma )^m$
times the element of
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G', {\mathrm {const}}_{+}))$
represented by the decorations
${\operatorname {Dec}^{m}_{\mathscr C}}(\operatorname {D}(G', {\mathrm {const}}_{+}))$
represented by the decorations
![]() $(\chi \mathbin {.} \xi _{{\chi ^{-1}}(v)})_{v \in N'}$
, where
$(\chi \mathbin {.} \xi _{{\chi ^{-1}}(v)})_{v \in N'}$
, where
![]() $\sigma $
is the canonical bijection between the set of initial flags of
$\sigma $
is the canonical bijection between the set of initial flags of
![]() $\operatorname {D}(G', \chi \mathbin {.} {\mathrm {const}}_{+})$
and the set of initial flags of
$\operatorname {D}(G', \chi \mathbin {.} {\mathrm {const}}_{+})$
and the set of initial flags of
![]() $\operatorname {D}(G', {\mathrm {const}}_{+})$
. Finally, we note that, under the canonical identification of
$\operatorname {D}(G', {\mathrm {const}}_{+})$
. Finally, we note that, under the canonical identification of
![]() $\operatorname {Edge}(G)$
with the initial flags S of
$\operatorname {Edge}(G)$
with the initial flags S of
![]() $\operatorname {D}(G, {\mathrm {const}}_{+})$
and the analogous identification for
$\operatorname {D}(G, {\mathrm {const}}_{+})$
and the analogous identification for
![]() $G'$
(both of which are order preserving), the composition
$G'$
(both of which are order preserving), the composition
![]() $\sigma \circ {{\operatorname {D}(\chi , {\mathrm {const}}_{+})}|{}_{S}}$
corresponds precisely to the map
$\sigma \circ {{\operatorname {D}(\chi , {\mathrm {const}}_{+})}|{}_{S}}$
corresponds precisely to the map
![]() $\operatorname {Edge}(G) \to \operatorname {Edge}(G')$
induced by
$\operatorname {Edge}(G) \to \operatorname {Edge}(G')$
induced by
![]() $\chi $
. This finishes the proof.
$\chi $
. This finishes the proof.
Combining Lemma 4.19 with the isomorphism (4.7), we obtain an isomorphism
of graded vector spaces. As explained after (4.8), we will now identify the result of pulling back the differential
![]() $d^1$
of
$d^1$
of
![]() ${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
to
${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
to
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
along the isomorphism (4.9). Moreover, note that, via the isomorphisms (4.8) and (4.9), the graded coalgebra structure of
${\mathfrak {UG}}^{m} {(\mathscr C)}$
along the isomorphism (4.9). Moreover, note that, via the isomorphisms (4.8) and (4.9), the graded coalgebra structure of
![]() ${\mathrm {H}}_{\bullet } \left ( {\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)} \right )$
determines a graded coalgebra structure on
${\mathrm {H}}_{\bullet } \left ( {\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)} \right )$
determines a graded coalgebra structure on
![]() ${\mathrm {H}}_{\bullet } \left ( {\mathfrak {UG}}^{m}{(\mathscr C)} \right )$
. We will also describe this graded coalgebra structure explicitly.
${\mathrm {H}}_{\bullet } \left ( {\mathfrak {UG}}^{m}{(\mathscr C)} \right )$
. We will also describe this graded coalgebra structure explicitly.
Definition 4.20. Let
![]() $G = (F, N, \mu , a) \in {{\mathbf {Graph}}}_{\ge 3}$
be an undirected graph. A neighbor-closed vertex set of G is a subset
$G = (F, N, \mu , a) \in {{\mathbf {Graph}}}_{\ge 3}$
be an undirected graph. A neighbor-closed vertex set of G is a subset
![]() $N' \subseteq N$
such that
$N' \subseteq N$
such that
![]() $\mu ({a^{-1}}(N')) = {a^{-1}}(N')$
. A connected component of G is a neighbor-closed vertex set that is inclusion minimal among nonempty neighbor-closed vertex sets.
$\mu ({a^{-1}}(N')) = {a^{-1}}(N')$
. A connected component of G is a neighbor-closed vertex set that is inclusion minimal among nonempty neighbor-closed vertex sets.
A neighbor-closed vertex set
![]() $N'$
of G determines an undirected graph
$N'$
of G determines an undirected graph
where ![]() .
.
Remark 4.21. When
![]() $N' \subseteq N$
is a neighbor-closed vertex set of an undirected graph
$N' \subseteq N$
is a neighbor-closed vertex set of an undirected graph
![]() $G = (F, N, \mu , a)$
, then
$G = (F, N, \mu , a)$
, then
![]() $N \setminus N'$
is one as well. Moreover, any neighbor-closed vertex set of G is a disjoint union of a unique set of connected components of G.
$N \setminus N'$
is one as well. Moreover, any neighbor-closed vertex set of G is a disjoint union of a unique set of connected components of G.
Definition 4.22. We equip the graded vector space
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
of
${\mathfrak {UG}}^{m} {(\mathscr C)}$
of
![]() $\mathscr C$
-decorated undirected graphs with the structure of a cocommutative differential graded coalgebra in the following way. The differential is given by
$\mathscr C$
-decorated undirected graphs with the structure of a cocommutative differential graded coalgebra in the following way. The differential is given by

where
![]() $G = (F, N, \mu , a) \in {{\mathbf {Graph}}}_{\ge 3}$
is an undirected graph and
$G = (F, N, \mu , a) \in {{\mathbf {Graph}}}_{\ge 3}$
is an undirected graph and
![]() $x \in {\operatorname {UDec}^{m}_{\mathscr C}}(G)$
. Here, the
$x \in {\operatorname {UDec}^{m}_{\mathscr C}}(G)$
. Here, the
![]() $d^G_e(x)$
are elements of
$d^G_e(x)$
are elements of
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
uniquely determined by the following properties:
${\mathfrak {UG}}^{m} {(\mathscr C)}$
uniquely determined by the following properties:
-
• For every isomorphism
 $\chi \colon G \to G'$
of undirected graphs holds
$\chi \colon G \to G'$
of undirected graphs holds
 $d^G_e(x) = d^{G'}_{\chi (e)}(\chi \mathbin {.} x)$
.
$d^G_e(x) = d^{G'}_{\chi (e)}(\chi \mathbin {.} x)$
. -
• If e is a loop, then
 $d^G_e(x) = 0$
.
$d^G_e(x) = 0$
. -
• If e is not a loop, let
 $f < f'$
be the two flags making up e and assume that
$f < f'$
be the two flags making up e and assume that  and
and  are, in this order, the first two elements of N. Moreover, assume that a is order-preserving and that f is the first element of F (in particular, e is the first element of
are, in this order, the first two elements of N. Moreover, assume that a is order-preserving and that f is the first element of F (in particular, e is the first element of
 $\operatorname {Edge}(G)$
). Then
$\operatorname {Edge}(G)$
). Then
 $d^G_e$
applied to the element represented by G and some decorations
$d^G_e$
applied to the element represented by G and some decorations
 $(\xi _w)_{w \in N}$
is the element represented by the graph (obtained from G by contracting e) decorated by
$(\xi _w)_{w \in N}$
is the element represented by the graph (obtained from G by contracting e) decorated by
 $\omega \mathbin {.} (\xi _v\ {}_f{\circ }_{f'}\ \xi _{v'})$
at the collapsed vertex
$\omega \mathbin {.} (\xi _v\ {}_f{\circ }_{f'}\ \xi _{v'})$
at the collapsed vertex  and by
and by
 $\xi _w$
at all other vertices w. Here,
$\xi _w$
at all other vertices w. Here,
 $\omega $
is the canonical bijection between the linearly ordered set
$\omega $
is the canonical bijection between the linearly ordered set
 ${a^{-1}}(v)\ {}_f{\circ }_{\mu (f)}\ {a^{-1}}(v')$
of Remark 2.32 and
${a^{-1}}(v)\ {}_f{\circ }_{\mu (f)}\ {a^{-1}}(v')$
of Remark 2.32 and
 ${a^{\prime -1}}(\bar v) \subseteq F \setminus e$
.
${a^{\prime -1}}(\bar v) \subseteq F \setminus e$
.
The counit
![]() $\varepsilon \colon {\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathbb {Q}}$
sends the element represented by the empty graph to
$\varepsilon \colon {\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathbb {Q}}$
sends the element represented by the empty graph to
![]() $1$
and an element represented by any other graph to
$1$
and an element represented by any other graph to
![]() $0$
. The comultiplication
$0$
. The comultiplication
![]() $\Delta \colon {\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathfrak {UG}}^{m} {(\mathscr C)} \mathop{\mathop{\otimes}} {\mathfrak {UG}}^{m} {(\mathscr C)}$
is given as follows: for an element
$\Delta \colon {\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathfrak {UG}}^{m} {(\mathscr C)} \mathop{\mathop{\otimes}} {\mathfrak {UG}}^{m} {(\mathscr C)}$
is given as follows: for an element
![]() $x \in {\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
$x \in {\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
![]() $G = (F, N, \mu , a)$
and decorations
$G = (F, N, \mu , a)$
and decorations
![]() $(\xi _v)_{v \in N}$
, we set
$(\xi _v)_{v \in N}$
, we set
where the sum runs over all neighbor-closed vertex subsets
![]() $N'$
of G and
$N'$
of G and
![]() $x_A$
is the element of
$x_A$
is the element of
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
![]() ${\mathrm {ind}}_{G}(A)$
and
${\mathrm {ind}}_{G}(A)$
and
![]() $(\xi _v)_{v \in A}$
. The sign
$(\xi _v)_{v \in A}$
. The sign
![]() $\delta (N') \in \{\pm 1\}$
is the sign incurred by permuting
$\delta (N') \in \{\pm 1\}$
is the sign incurred by permuting
into
where ![]() and
and ![]() .
.
Remark 4.23. Note that it is easy to see that
![]() $\Delta $
is well defined (i.e., that
$\Delta $
is well defined (i.e., that
![]() $\Delta (\chi \mathbin {.} x) = \Delta (x)$
for any isomorphism
$\Delta (\chi \mathbin {.} x) = \Delta (x)$
for any isomorphism
![]() $\chi \colon G \to G'$
). In the proof of Theorem 4.28, we will show that the elements
$\chi \colon G \to G'$
). In the proof of Theorem 4.28, we will show that the elements
![]() $d^G_e(x)$
actually exist, which in particular implies that d is a well-defined map. Moreover, we will construct a surjection from a cocommutative differential graded coalgebra onto
$d^G_e(x)$
actually exist, which in particular implies that d is a well-defined map. Moreover, we will construct a surjection from a cocommutative differential graded coalgebra onto
![]() ${\mathfrak {UG}}^{m}{(\mathscr C)}$
that is compatible with the differentials, the counits and the comultiplications. This implies that the maps above indeed equip
${\mathfrak {UG}}^{m}{(\mathscr C)}$
that is compatible with the differentials, the counits and the comultiplications. This implies that the maps above indeed equip
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
with the structure of a cocommutative differential graded coalgebra.
${\mathfrak {UG}}^{m} {(\mathscr C)}$
with the structure of a cocommutative differential graded coalgebra.
Remark 4.24. The (undirected) graph complex
![]() ${\mathfrak {UG}}^{m}{(\mathscr C)}$
, equipped with the differential graded coalgebra structure of Definition 4.22, is a well-known object. Variants of it were first described by Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93, Reference Kontsevich and JosephKon94] and have, since then, appeared in the works of many different authors. Using the language of modular operads due to Getzler–Kapranov [Reference Getzler and KapranovGK98], one alternative description is
${\mathfrak {UG}}^{m}{(\mathscr C)}$
, equipped with the differential graded coalgebra structure of Definition 4.22, is a well-known object. Variants of it were first described by Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93, Reference Kontsevich and JosephKon94] and have, since then, appeared in the works of many different authors. Using the language of modular operads due to Getzler–Kapranov [Reference Getzler and KapranovGK98], one alternative description is
where
![]() $\mathsf F$
denotes the ‘Feynman transform’,
$\mathsf F$
denotes the ‘Feynman transform’,
![]() $\mathfrak T$
and
$\mathfrak T$
and
![]() $\mathrm {Det}$
are certain ‘hyperoperads’, and
$\mathrm {Det}$
are certain ‘hyperoperads’, and
![]() $\Sigma $
denotes a degree shift. Other descriptions have been given for example by Lazarev–Voronov [Reference Lazarev and VoronovLV08, §3.1] (though with a different grading convention) and, in the case
$\Sigma $
denotes a degree shift. Other descriptions have been given for example by Lazarev–Voronov [Reference Lazarev and VoronovLV08, §3.1] (though with a different grading convention) and, in the case
![]() $m = 0$
, by Conant–Vogtmann [Reference Conant and VogtmannCV03, §2.3].
$m = 0$
, by Conant–Vogtmann [Reference Conant and VogtmannCV03, §2.3].
The homology of
![]() ${\mathfrak {UG}}^{m}{(\mathscr C)}$
is in general very complicated and in most cases of interest, only partial information is known. See, however, the following remarks for a couple of basic observations. Also see Remark 4.30 for an overview of what is known about this homology in the case of the cyclic Lie operad
${\mathfrak {UG}}^{m}{(\mathscr C)}$
is in general very complicated and in most cases of interest, only partial information is known. See, however, the following remarks for a couple of basic observations. Also see Remark 4.30 for an overview of what is known about this homology in the case of the cyclic Lie operad
![]() $\mathscr C = \operatorname {\mathscr {L}ie}$
.
$\mathscr C = \operatorname {\mathscr {L}ie}$
.
Remark 4.25. Note that, up to a regrading, the differential graded coalgebra
![]() ${\mathfrak {UG}}^{m}{(\mathscr C)}$
, and hence its homology, only depend on the parity of m.
${\mathfrak {UG}}^{m}{(\mathscr C)}$
, and hence its homology, only depend on the parity of m.
Remark 4.26. It follows from the description of the coalgebra structure of
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
that the cohomology
${\mathfrak {UG}}^{m} {(\mathscr C)}$
that the cohomology
![]() ${\mathrm {H}}^{*} \left ( {{\mathfrak {UG}}^{m} {(\mathscr C)}^\vee } \right )$
of its linear dual is a free graded commutative algebra generated by the cohomology of the dual of the subcomplex
${\mathrm {H}}^{*} \left ( {{\mathfrak {UG}}^{m} {(\mathscr C)}^\vee } \right )$
of its linear dual is a free graded commutative algebra generated by the cohomology of the dual of the subcomplex
![]() ${\mathfrak {UG}}_{\mathrm {conn}}^{m} {(\mathscr C)} \subseteq {\mathfrak {UG}}^{m} {(\mathscr C)}$
spanned by the connected graphs. This subcomplex splits as a direct sum
${\mathfrak {UG}}_{\mathrm {conn}}^{m} {(\mathscr C)} \subseteq {\mathfrak {UG}}^{m} {(\mathscr C)}$
spanned by the connected graphs. This subcomplex splits as a direct sum
 $$\begin{align*}{\mathfrak{UG}}_{\mathrm{conn}}^{m} {(\mathscr C)} \cong \bigoplus_{g \in {\mathbb{N}_0}} {\mathfrak{UG}}_{\mathrm{conn}; g}^{m} {(\mathscr C)}, \end{align*}$$
$$\begin{align*}{\mathfrak{UG}}_{\mathrm{conn}}^{m} {(\mathscr C)} \cong \bigoplus_{g \in {\mathbb{N}_0}} {\mathfrak{UG}}_{\mathrm{conn}; g}^{m} {(\mathscr C)}, \end{align*}$$
where
![]() ${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {(\mathscr C)}$
denotes the subcomplex spanned by connected graphs of genus g (here, the genus of a graph is
${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {(\mathscr C)}$
denotes the subcomplex spanned by connected graphs of genus g (here, the genus of a graph is
![]() $1$
plus the number of edges minus the number of vertices). Hence, understanding the homology of
$1$
plus the number of edges minus the number of vertices). Hence, understanding the homology of
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
(or the cohomology of its dual) is equivalent to understanding the homology of
${\mathfrak {UG}}^{m} {(\mathscr C)}$
(or the cohomology of its dual) is equivalent to understanding the homology of
![]() ${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {(\mathscr C)}$
for all g (or the cohomologies of their duals).
${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {(\mathscr C)}$
for all g (or the cohomologies of their duals).
Remark 4.27. Let
![]() $G \in {{\mathbf {Graph}}}_{\ge 3}$
be a connected graph with N vertices, E edges and genus
$G \in {{\mathbf {Graph}}}_{\ge 3}$
be a connected graph with N vertices, E edges and genus
![]() $g = 1 - N + E$
. Since every vertex is at least trivalent, we have
$g = 1 - N + E$
. Since every vertex is at least trivalent, we have
![]() $E \ge \frac {3}{2} N$
, which implies
$E \ge \frac {3}{2} N$
, which implies
![]() $E \le 3 (g - 1)$
. Since G is nonempty, we have
$E \le 3 (g - 1)$
. Since G is nonempty, we have
![]() $N \ge 1$
, which implies
$N \ge 1$
, which implies
![]() $g \le E$
. (In particular, there are no such graphs with
$g \le E$
. (In particular, there are no such graphs with
![]() $g \le 1$
.) Now assume that
$g \le 1$
.) Now assume that
![]() $\mathscr C$
is concentrated in degree
$\mathscr C$
is concentrated in degree
![]() $0$
. Then an element of
$0$
. Then an element of
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by G has homological degree
${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by G has homological degree
![]() $p = (1 - m) N + m E = E + (m - 1) (g - 1)$
. This implies that, in this case, the subcomplex
$p = (1 - m) N + m E = E + (m - 1) (g - 1)$
. This implies that, in this case, the subcomplex
![]() ${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {(\mathscr C)}$
of Remark 4.26 is concentrated in those homological degrees p such that
${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {(\mathscr C)}$
of Remark 4.26 is concentrated in those homological degrees p such that
![]() $m (g - 1) + 1 \le p \le (m + 2) (g - 1)$
.
$m (g - 1) + 1 \le p \le (m + 2) (g - 1)$
.
Theorem 4.28. Let
![]() $m \in {\mathbb {N}_0}$
be a natural number and
$m \in {\mathbb {N}_0}$
be a natural number and
![]() $\mathscr C$
a cyclic operad concentrated in nonnegative even degrees such that
$\mathscr C$
a cyclic operad concentrated in nonnegative even degrees such that
![]() ${\mathscr C \left (\mkern -4mu\left (2\right )\mkern -4mu\right )} = {\mathbb {Q} {\langle {\mathrm {id}} \rangle }}$
with the trivial
${\mathscr C \left (\mkern -4mu\left (2\right )\mkern -4mu\right )} = {\mathbb {Q} {\langle {\mathrm {id}} \rangle }}$
with the trivial
![]() ${\Sigma _{2}}$
-action. Then there is an isomorphism of graded coalgebras
${\Sigma _{2}}$
-action. Then there is an isomorphism of graded coalgebras
where
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
is equipped with the differential graded coalgebra structure of Definition 4.22.
${\mathfrak {UG}}^{m} {(\mathscr C)}$
is equipped with the differential graded coalgebra structure of Definition 4.22.
Proof. We first show that there is an isomorphism
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
of chain complexes, where the domain is equipped with the differential of Definition 4.22 and the target with the differential induced by
${\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
of chain complexes, where the domain is equipped with the differential of Definition 4.22 and the target with the differential induced by
![]() $d^1$
. Together with (4.8), this yields the desired isomorphism on the level of the underlying graded vector spaces.
$d^1$
. Together with (4.8), this yields the desired isomorphism on the level of the underlying graded vector spaces.
The isomorphism
![]() $\Phi \colon {\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
of (4.9) maps the element
$\Phi \colon {\mathfrak {UG}}^{m} {(\mathscr C)} \to {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
of (4.9) maps the element
![]() $[x] \in {\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
$[x] \in {\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
![]() $G = (F, N, \mu , a)$
and decorations
$G = (F, N, \mu , a)$
and decorations
![]() $(\xi _v)_{v \in N}$
to the element
$(\xi _v)_{v \in N}$
to the element
![]() $[y]$
of
$[y]$
of
![]() ${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
represented by the directed graph
${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
represented by the directed graph ![]() and the decorations
and the decorations
![]() $\xi _v$
. By Definition 3.24, we have
$\xi _v$
. By Definition 3.24, we have
![]() $d^1([y]) = \sum _{s \in S} d^{D_+(G)}_s(y)$
, where S is the set of initial flags of
$d^1([y]) = \sum _{s \in S} d^{D_+(G)}_s(y)$
, where S is the set of initial flags of
![]() $D_+(G)$
. There is a canonical bijection
$D_+(G)$
. There is a canonical bijection
![]() $\sigma ^G \colon \operatorname {Edge}(G) \to S$
(which is order preserving). We now define, for
$\sigma ^G \colon \operatorname {Edge}(G) \to S$
(which is order preserving). We now define, for
![]() $e \in \operatorname {Edge}(G)$
,
$e \in \operatorname {Edge}(G)$
,
where
![]() $\widetilde \Phi ^G \colon {\operatorname {UDec}^{m}_{\mathscr C}}(G) \to {\operatorname {Dec}^{m}_{\mathscr C}}(D_+(G))$
is the isomorphism from Lemma 4.19. We will now prove that these elements
$\widetilde \Phi ^G \colon {\operatorname {UDec}^{m}_{\mathscr C}}(G) \to {\operatorname {Dec}^{m}_{\mathscr C}}(D_+(G))$
is the isomorphism from Lemma 4.19. We will now prove that these elements
![]() $d^G_e(x)$
fulfill the properties of Definition 4.22. This implies that the map
$d^G_e(x)$
fulfill the properties of Definition 4.22. This implies that the map
![]() $\Phi $
is an isomorphism of chain complexes as desired.
$\Phi $
is an isomorphism of chain complexes as desired.
First note that, if e is a loop, then
![]() $d^{D_+(G)}_{\sigma ^G(e)}(\widetilde \Phi (x)) = 0$
and hence
$d^{D_+(G)}_{\sigma ^G(e)}(\widetilde \Phi (x)) = 0$
and hence
![]() $d^G_e(x) = 0$
. Hence, the second property of Definition 4.22 is fulfilled.
$d^G_e(x) = 0$
. Hence, the second property of Definition 4.22 is fulfilled.
Now we show that
![]() $d^G_e(x) = d^{G'}_{\chi (e)}(\chi \mathbin {.} x)$
for any isomorphism
$d^G_e(x) = d^{G'}_{\chi (e)}(\chi \mathbin {.} x)$
for any isomorphism
![]() $\chi \colon G \to G'$
and edge
$\chi \colon G \to G'$
and edge
![]() $e = \{f_1 < f_2\} \in \operatorname {Edge}(G)$
. This is clear when e is a loop. Hence, it is enough to consider the case where G fulfills that a is order preserving, that
$e = \{f_1 < f_2\} \in \operatorname {Edge}(G)$
. This is clear when e is a loop. Hence, it is enough to consider the case where G fulfills that a is order preserving, that ![]() and
and ![]() are (in this order) the first two elements of N, and that
are (in this order) the first two elements of N, and that
![]() $f_1$
is the last element of
$f_1$
is the last element of
![]() ${a^{-1}}(v_1)$
and
${a^{-1}}(v_1)$
and
![]() $f_2$
the first of
$f_2$
the first of
![]() ${a^{-1}}(v_2)$
. (This is enough since any isomorphism of undirected graphs with a distinguished non-loop edge factors through a graph of this form.) We need to show that
${a^{-1}}(v_2)$
. (This is enough since any isomorphism of undirected graphs with a distinguished non-loop edge factors through a graph of this form.) We need to show that
as elements of
![]() ${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
. We first note that the left-hand side is equal to
${\mathrm {H}}_{0} (C^2_{\bullet ,*})$
. We first note that the left-hand side is equal to
![]() $(-1)^{m ({ | {v_1} | ^{\mathrm {out}}} - 1)}$
times the equivalence class of the element y represented by
$(-1)^{m ({ | {v_1} | ^{\mathrm {out}}} - 1)}$
times the equivalence class of the element y represented by
![]() $\operatorname {ctr}_{\sigma ^G(e)}(D_+(G))$
and the decorations
$\operatorname {ctr}_{\sigma ^G(e)}(D_+(G))$
and the decorations
![]() $\xi _{v_1}\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2}$
at the collapsed vertex
$\xi _{v_1}\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2}$
at the collapsed vertex
![]() ${\mathrm {pr}}(v_1) = {\mathrm {pr}}(v_2)$
and by
${\mathrm {pr}}(v_1) = {\mathrm {pr}}(v_2)$
and by
![]() $\xi _w$
at all other vertices w. Now, we set
$\xi _w$
at all other vertices w. Now, we set ![]() and write
and write
![]() $\psi \colon D' \to \operatorname {D}(G', {\mathrm {const}}_{+}) = D_+(G')$
for the isomorphism induced by
$\psi \colon D' \to \operatorname {D}(G', {\mathrm {const}}_{+}) = D_+(G')$
for the isomorphism induced by
![]() $\chi $
. We further denote by
$\chi $
. We further denote by
![]() $S'$
the linearly ordered set of initial flags of
$S'$
the linearly ordered set of initial flags of
![]() $D'$
and set
$D'$
and set ![]() . Then the right-hand side of (4.10) is equal to
. Then the right-hand side of (4.10) is equal to
![]() $[{ d^{D'}_{s'} ({\psi ^{-1}} \mathbin {.} \widetilde \Phi ^{G'}(\chi \mathbin {.} x))}]$
. It follows from the definitions that
$[{ d^{D'}_{s'} ({\psi ^{-1}} \mathbin {.} \widetilde \Phi ^{G'}(\chi \mathbin {.} x))}]$
. It follows from the definitions that
![]() ${\psi ^{-1}} \mathbin {.} \widetilde \Phi ^{G'}(\chi \mathbin {.} x)$
is
${\psi ^{-1}} \mathbin {.} \widetilde \Phi ^{G'}(\chi \mathbin {.} x)$
is
![]() $\operatorname {sgn}(\omega )^m (-1)^{k (1 + m)}$
times the element
$\operatorname {sgn}(\omega )^m (-1)^{k (1 + m)}$
times the element
![]() $x'$
of
$x'$
of
![]() ${\operatorname {Dec}^{m}_{\mathscr C}}(D')$
represented by the decorations
${\operatorname {Dec}^{m}_{\mathscr C}}(D')$
represented by the decorations
![]() $(\xi _w)_{w \in N}$
, where k is the number of edges whose orientation is flipped by
$(\xi _w)_{w \in N}$
, where k is the number of edges whose orientation is flipped by
![]() $\chi $
, and
$\chi $
, and
![]() $\omega \colon S \to S'$
is the canonical bijection.
$\omega \colon S \to S'$
is the canonical bijection.
There are now two cases: either
![]() $\chi $
preserves the orientation of e (i.e., we have
$\chi $
preserves the orientation of e (i.e., we have
![]() $\chi (f_1) < \chi (f_2)$
) or it reverses it. In both cases, we have that
$\chi (f_1) < \chi (f_2)$
) or it reverses it. In both cases, we have that
![]() $d^{D'}_{s'} (x')$
is some sign
$d^{D'}_{s'} (x')$
is some sign
![]() $\varepsilon \in \{\pm 1\}$
times the element
$\varepsilon \in \{\pm 1\}$
times the element
![]() $y'$
represented by
$y'$
represented by
![]() $\operatorname {ctr}_{s'}(D')$
and the decorations
$\operatorname {ctr}_{s'}(D')$
and the decorations
![]() $\xi _{v_1}\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2}$
(in the first case) or
$\xi _{v_1}\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2}$
(in the first case) or
![]() $\xi _{v_2}\ {}_{f_2}{\circ }_{f_1}\ \xi _{v_1}$
(in the second case) at the collapsed vertex
$\xi _{v_2}\ {}_{f_2}{\circ }_{f_1}\ \xi _{v_1}$
(in the second case) at the collapsed vertex
![]() ${\mathrm {pr}}(v_1) = {\mathrm {pr}}(v_2)$
and
${\mathrm {pr}}(v_1) = {\mathrm {pr}}(v_2)$
and
![]() $\xi _w$
at all other vertices w. In the first case, we have
$\xi _w$
at all other vertices w. In the first case, we have
![]() $\varepsilon = (-1)^{m ({ | {v_1'} | ^{\mathrm {out}}} - 1)}$
, where
$\varepsilon = (-1)^{m ({ | {v_1'} | ^{\mathrm {out}}} - 1)}$
, where ![]() considered as a vertex of
considered as a vertex of
![]() $D'$
. In the second case, we have
$D'$
. In the second case, we have
![]() $\varepsilon = (-1)^{1 + m + m { | {v_1'} | ^{\mathrm {out}}}}$
(to see this, one transforms
$\varepsilon = (-1)^{1 + m + m { | {v_1'} | ^{\mathrm {out}}}}$
(to see this, one transforms
![]() $D'$
into the form necessary to read off
$D'$
into the form necessary to read off
![]() $d^{D'}_{s'}$
and then identifies the result of the contraction with
$d^{D'}_{s'}$
and then identifies the result of the contraction with
![]() $\operatorname {ctr}_{s'}(D')$
). It follows from the proof of Lemma 4.19 that
$\operatorname {ctr}_{s'}(D')$
). It follows from the proof of Lemma 4.19 that
![]() $ [{y'}] = \delta [{y}] \in {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
, where
$ [{y'}] = \delta [{y}] \in {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
, where
![]() $\delta = \operatorname {sgn}(\hat \omega )^m (-1)^{k(1 + m)}$
in the first case, and
$\delta = \operatorname {sgn}(\hat \omega )^m (-1)^{k(1 + m)}$
in the first case, and
![]() $\delta = \operatorname {sgn} (\hat \omega )^m (-1)^{(k - 1)(1 + m)}$
in the second. Here,
$\delta = \operatorname {sgn} (\hat \omega )^m (-1)^{(k - 1)(1 + m)}$
in the second. Here,
![]() $\hat \omega $
is the canonical bijection
$\hat \omega $
is the canonical bijection
![]() $S \setminus \{s\} \to S' \setminus \{s'\}$
, and k is the number of edges flipped by
$S \setminus \{s\} \to S' \setminus \{s'\}$
, and k is the number of edges flipped by
![]() $\chi $
, as above. Lastly, we note that commutativity of
$\chi $
, as above. Lastly, we note that commutativity of

implies that the product
![]() $\operatorname {sgn}(\omega ) \operatorname {sgn}(\hat \omega )$
equals
$\operatorname {sgn}(\omega ) \operatorname {sgn}(\hat \omega )$
equals
![]() $(-1)^{{ | {v_1} | ^{\mathrm {out}}} - 1 + { | {v_1'} | ^{\mathrm {out}}} - 1}$
in the first case, and
$(-1)^{{ | {v_1} | ^{\mathrm {out}}} - 1 + { | {v_1'} | ^{\mathrm {out}}} - 1}$
in the first case, and
![]() $(-1)^{{ | {v_1} | ^{\mathrm {out}}} - 1 + { | {v_1'} | ^{\mathrm {out}}}}$
in the second. This finishes the proof of (4.10).
$(-1)^{{ | {v_1} | ^{\mathrm {out}}} - 1 + { | {v_1'} | ^{\mathrm {out}}}}$
in the second. This finishes the proof of (4.10).
We now prove that the elements
![]() $d^G_e(x)$
fulfill the third property of Definition 4.22. We assume that
$d^G_e(x)$
fulfill the third property of Definition 4.22. We assume that
![]() $e = \{f_1 < f_2\}$
is not a loop, that
$e = \{f_1 < f_2\}$
is not a loop, that ![]() and
and ![]() are (in this order) the first two elements of N, that a is order-preserving, and that
are (in this order) the first two elements of N, that a is order-preserving, and that
![]() $f_1$
is the first element of F. We also assume that
$f_1$
is the first element of F. We also assume that
![]() $f_2$
is the first element of
$f_2$
is the first element of
![]() ${a^{-1}}(v_2)$
(we can arrange this without introducing a sign). Now, we let
${a^{-1}}(v_2)$
(we can arrange this without introducing a sign). Now, we let
![]() $D'$
be equal to
$D'$
be equal to
![]() $D_+(G)$
except that the linear order of F has been changed such that
$D_+(G)$
except that the linear order of F has been changed such that
![]() $f_1$
is the last element of
$f_1$
is the last element of
![]() ${a^{-1}}(v_1)$
instead of the first. Moreover, we denote by
${a^{-1}}(v_1)$
instead of the first. Moreover, we denote by
![]() $\chi \colon D_+(G) \to D'$
the canonical isomorphism. We have
$\chi \colon D_+(G) \to D'$
the canonical isomorphism. We have
![]() $d^{D_+(G)}_{f_1}(\widetilde \Phi (x)) = d^{D'}_{f_1}(\chi \mathbin {.} \widetilde \Phi (x))$
and that
$d^{D_+(G)}_{f_1}(\widetilde \Phi (x)) = d^{D'}_{f_1}(\chi \mathbin {.} \widetilde \Phi (x))$
and that
![]() $\chi \mathbin {.} \widetilde \Phi (x)$
is
$\chi \mathbin {.} \widetilde \Phi (x)$
is
![]() $(-1)^{m ({ | {v_1} | ^{\mathrm {out}}} - 1)}$
times the element represented by
$(-1)^{m ({ | {v_1} | ^{\mathrm {out}}} - 1)}$
times the element represented by
![]() $D'$
and the decorations
$D'$
and the decorations
![]() $(\xi _w)_{w \in N}$
. By definition, we thus have that
$(\xi _w)_{w \in N}$
. By definition, we thus have that
![]() $d^{D'}_{f_1}(\chi \mathbin {.} \widetilde \Phi (x))$
is the element represented by
$d^{D'}_{f_1}(\chi \mathbin {.} \widetilde \Phi (x))$
is the element represented by
![]() $\operatorname {ctr}_{f_1}(D')$
and the decorations
$\operatorname {ctr}_{f_1}(D')$
and the decorations
![]() $({{\sigma }|}_{{a^{-1}}(v_1)} \mathbin {.} \xi _{v_1})\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2}$
at the collapsed vertex and
$({{\sigma }|}_{{a^{-1}}(v_1)} \mathbin {.} \xi _{v_1})\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2}$
at the collapsed vertex and
![]() $\xi _w$
at all other vertices w. Here,
$\xi _w$
at all other vertices w. Here,
![]() $\sigma $
is the canonical bijection from F to the linearly ordered set
$\sigma $
is the canonical bijection from F to the linearly ordered set
![]() $F'$
of flags of
$F'$
of flags of
![]() $D'$
. Lastly, we note that
$D'$
. Lastly, we note that
![]() $\operatorname {ctr}_{f_1}(D') = \operatorname {D}(\operatorname {ctr}_{e}(G), {\mathrm {const}}_{+})$
and that
$\operatorname {ctr}_{f_1}(D') = \operatorname {D}(\operatorname {ctr}_{e}(G), {\mathrm {const}}_{+})$
and that
![]() $({{\sigma }|}_{{a^{-1}}(v_1)} \mathbin {.} \xi _{v_1})\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2} = \omega \mathbin {.} (\xi _{v_1}\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2})$
, where
$({{\sigma }|}_{{a^{-1}}(v_1)} \mathbin {.} \xi _{v_1})\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2} = \omega \mathbin {.} (\xi _{v_1}\ {}_{f_1}{\circ }_{f_2}\ \xi _{v_2})$
, where
![]() $\omega $
is as in Definition 4.22. Thus, the third property is fulfilled as well.
$\omega $
is as in Definition 4.22. Thus, the third property is fulfilled as well.
It remains to prove that the isomorphism is compatible with the graded coalgebra structures. By Lemma 2.10, the isomorphism (4.8) is induced by the surjection of chain complexes
that is given by the canonical projections
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,0} \to {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
and the trivial maps on
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,0} \to {\mathrm {H}}_{0} (C^2_{\bullet ,*})$
and the trivial maps on
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,l}$
for
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,l}$
for
![]() $l> 0$
. Hence, it is enough to show that the surjection
$l> 0$
. Hence, it is enough to show that the surjection
is a map of graded coalgebras.
It is clear that
![]() $\Theta $
is compatible with the counits. Now note that the comultiplication
$\Theta $
is compatible with the counits. Now note that the comultiplication
![]() $\Delta $
of
$\Delta $
of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
is compatible with its bigrading. In particular,
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
is compatible with its bigrading. In particular,
![]() $(\Psi \mathop{\mathop{\otimes}} \Psi )(\Delta (x))$
is trivial for an element
$(\Psi \mathop{\mathop{\otimes}} \Psi )(\Delta (x))$
is trivial for an element
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,l}$
with
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{k,l}$
with
![]() $l> 0$
. Hence, it is enough to check that
$l> 0$
. Hence, it is enough to check that
![]() $\Theta $
is compatible with the comultiplication of
$\Theta $
is compatible with the comultiplication of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{*,0}$
. Let
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{*,0}$
. Let
![]() $D = (F, N, S, T, \mu , a)$
be a truncated directed graph without vertices of valence two and let
$D = (F, N, S, T, \mu , a)$
be a truncated directed graph without vertices of valence two and let
![]() $x \in {\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{*,0}$
be the element represented by D and some decorations
$x \in {\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}_{*,0}$
be the element represented by D and some decorations
![]() $(\xi _v)_{v \in N}$
. Let
$(\xi _v)_{v \in N}$
. Let
![]() $o_D \in \operatorname {dir}(\operatorname {U}(D))$
be defined by setting
$o_D \in \operatorname {dir}(\operatorname {U}(D))$
be defined by setting
![]() $o_D(\{f_1 < f_2\})$
to be
$o_D(\{f_1 < f_2\})$
to be
![]() $+$
if
$+$
if
![]() $f_1 \in S$
and
$f_1 \in S$
and
![]() $-$
otherwise. Then
$-$
otherwise. Then
![]() $\operatorname {D}(\operatorname {U}(D), o_D)$
is equal to D. By the proof of Lemma 4.19, this implies that
$\operatorname {D}(\operatorname {U}(D), o_D)$
is equal to D. By the proof of Lemma 4.19, this implies that
![]() $\Theta (x)$
is
$\Theta (x)$
is ![]() times the element of
times the element of
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
![]() $\operatorname {U}(D)$
and the decorations
$\operatorname {U}(D)$
and the decorations
![]() $\xi _v$
. Here,
$\xi _v$
. Here, ![]() and
and
![]() $\sigma _D \colon S \to \operatorname {Edge}(\operatorname {U}(D))$
is the canonical bijection.
$\sigma _D \colon S \to \operatorname {Edge}(\operatorname {U}(D))$
is the canonical bijection.
Recall that
where the sum runs over all neighbor-closed vertex subsets
![]() $N'$
of D and
$N'$
of D and
![]() $x_A$
is the element of
$x_A$
is the element of
![]() ${\mathfrak {DG}}^{m} {(\mathscr C)}$
represented by
${\mathfrak {DG}}^{m} {(\mathscr C)}$
represented by
![]() ${\mathrm {ind}}_{D}(A)$
and
${\mathrm {ind}}_{D}(A)$
and
![]() $(\xi _v)_{v \in A}$
. The sign
$(\xi _v)_{v \in A}$
. The sign
![]() $\varepsilon (N')$
is specified in Definition 3.24. Applying
$\varepsilon (N')$
is specified in Definition 3.24. Applying
![]() $\Theta \mathop{\mathop{\otimes}} \Theta $
to the right-hand side, we obtain
$\Theta \mathop{\mathop{\otimes}} \Theta $
to the right-hand side, we obtain
where
![]() $y_A$
is
$y_A$
is
![]() $\alpha ({\mathrm {ind}}_{D}(A))$
times the element of
$\alpha ({\mathrm {ind}}_{D}(A))$
times the element of
![]() ${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
${\mathfrak {UG}}^{m} {(\mathscr C)}$
represented by
![]() $\operatorname {U}({\mathrm {ind}}_{D}(A)) = {\mathrm {ind}}_{{\mathrm U}(D)}(A)$
and
$\operatorname {U}({\mathrm {ind}}_{D}(A)) = {\mathrm {ind}}_{{\mathrm U}(D)}(A)$
and
![]() $(\xi _v)_{v \in A}$
. Note that a subset
$(\xi _v)_{v \in A}$
. Note that a subset
![]() $N' \subseteq N$
is a neighbor-closed vertex subset of D if and only if it is a neighbor-closed vertex subset of
$N' \subseteq N$
is a neighbor-closed vertex subset of D if and only if it is a neighbor-closed vertex subset of
![]() $\operatorname {U}(D)$
. Lastly, we observe that
$\operatorname {U}(D)$
. Lastly, we observe that
where
![]() $\delta (N')$
is the sign of Definition 4.22. This finishes the proof.
$\delta (N')$
is the sign of Definition 4.22. This finishes the proof.
Remark 4.29. A proof of Theorem 4.28 for
![]() ${\mathfrak {DG}}^{m} {(\mathscr C)}$
instead of
${\mathfrak {DG}}^{m} {(\mathscr C)}$
instead of
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
has been sketched by Willwacher [Reference WillwacherWil14, Appendix K] (in the case of the commutative cyclic operad
${\mathfrak {DG}_{\mathrm {trunc}}^{m}}{(\mathscr C)}$
has been sketched by Willwacher [Reference WillwacherWil14, Appendix K] (in the case of the commutative cyclic operad
![]() $\mathscr C = \operatorname {\mathscr {C}om}$
). Other related statements have been proven in detail by Živković [Reference ŽivkovićŽiv20] and Dolgushev–Rogers [Reference Dolgushev and RogersDR19].
$\mathscr C = \operatorname {\mathscr {C}om}$
). Other related statements have been proven in detail by Živković [Reference ŽivkovićŽiv20] and Dolgushev–Rogers [Reference Dolgushev and RogersDR19].
Remark 4.30. We quickly survey what is known about the homology of the undirected graph complex
![]() ${\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
associated to the cyclic Lie operad. By work of Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93] (see also Conant–Vogtmann [Reference Conant and VogtmannCV03, Theorem 2 and §3.1]) and Lazarev–Voronov [Reference Lazarev and VoronovLV08, Corollary 3.13], there are, for
${\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}}$
associated to the cyclic Lie operad. By work of Kontsevich [Reference Kontsevich, Corwin, Gelfand and LepowskyKon93] (see also Conant–Vogtmann [Reference Conant and VogtmannCV03, Theorem 2 and §3.1]) and Lazarev–Voronov [Reference Lazarev and VoronovLV08, Corollary 3.13], there are, for
![]() $g \ge 2$
, isomorphisms
$g \ge 2$
, isomorphisms
where
![]() ${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {\operatorname {(\mathscr {L}ie)}}$
is as in Remark 4.26. (Note that it follows from Remark 4.27 that
${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {\operatorname {(\mathscr {L}ie)}}$
is as in Remark 4.26. (Note that it follows from Remark 4.27 that
![]() ${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {\operatorname {(\mathscr {L}ie)}}$
is trivial for
${\mathfrak {UG}}_{\mathrm {conn}; g}^{m} {\operatorname {(\mathscr {L}ie)}}$
is trivial for
![]() $g \le 1$
.) Here,
$g \le 1$
.) Here,
![]() $\mathrm {Out}(\mathrm {F}_{g})$
is the group of outer automorphisms of the free group on g generators, and
$\mathrm {Out}(\mathrm {F}_{g})$
is the group of outer automorphisms of the free group on g generators, and
![]() $\widetilde {\mathbb {Q}}$
is the one-dimensional
$\widetilde {\mathbb {Q}}$
is the one-dimensional
![]() $\mathrm {Out}(\mathrm {F}_{g})$
representation given by
$\mathrm {Out}(\mathrm {F}_{g})$
representation given by
(which is sometimes called the ‘determinant representation’).
The homology
![]() ${\mathrm {H}}_{*} (\mathrm {Out}(\mathrm {F}_{g}); {\mathbb {Q}})$
, occurring when m is even, has been studied intensively. A recent state of the art is summarized in [Reference ConantCHKV16, §1], including certain stability results and computer calculations for small g. The only nontrivial homology (outside of degree
${\mathrm {H}}_{*} (\mathrm {Out}(\mathrm {F}_{g}); {\mathbb {Q}})$
, occurring when m is even, has been studied intensively. A recent state of the art is summarized in [Reference ConantCHKV16, §1], including certain stability results and computer calculations for small g. The only nontrivial homology (outside of degree
![]() $0$
) with
$0$
) with
![]() $g \le 4$
is
$g \le 4$
is
![]() ${\mathrm {H}}_{4} ( \mathrm {Out}(\mathrm {F}_{4}); {\mathbb {Q}} ) \cong {\mathbb {Q}}$
. More recently, Borinsky–Vogtmann [Reference Borinsky and VogtmannBV23] obtained a formula and asymptotics for the Euler characteristic of
${\mathrm {H}}_{4} ( \mathrm {Out}(\mathrm {F}_{4}); {\mathbb {Q}} ) \cong {\mathbb {Q}}$
. More recently, Borinsky–Vogtmann [Reference Borinsky and VogtmannBV23] obtained a formula and asymptotics for the Euler characteristic of
![]() ${\mathrm {H}}_{*} (\mathrm {Out}(\mathrm {F}_{g}); {\mathbb {Q}})$
.
${\mathrm {H}}_{*} (\mathrm {Out}(\mathrm {F}_{g}); {\mathbb {Q}})$
.
The homology
![]() ${\mathrm {H}}_{*} (\mathrm {Out}(\mathrm {F}_{g}); \widetilde {\mathbb {Q}})$
, occurring when m is odd, is less well studied. The only structural results known to the author are Euler characteristic computations and asymptotics, again from [Reference Borinsky and VogtmannBV23], as well as that
${\mathrm {H}}_{*} (\mathrm {Out}(\mathrm {F}_{g}); \widetilde {\mathbb {Q}})$
, occurring when m is odd, is less well studied. The only structural results known to the author are Euler characteristic computations and asymptotics, again from [Reference Borinsky and VogtmannBV23], as well as that
the latter of which follows from the fact that
![]() $\mathrm {Out}(\mathrm {F}_{2}) \cong {\mathrm {GL}}_{2}({\mathbb {Z}})$
and the Eichler–Shimura isomorphism; see Conant–Hatcher–Kassabov–Vogtmann [Reference ConantCHKV16, §3.5]. Apart from this, there are computer calculations for small g by Brun–Willwacher [Reference Brun and WillwacherBW23, Figure 9]. Their work shows that the only nontrivial homology with
$\mathrm {Out}(\mathrm {F}_{2}) \cong {\mathrm {GL}}_{2}({\mathbb {Z}})$
and the Eichler–Shimura isomorphism; see Conant–Hatcher–Kassabov–Vogtmann [Reference ConantCHKV16, §3.5]. Apart from this, there are computer calculations for small g by Brun–Willwacher [Reference Brun and WillwacherBW23, Figure 9]. Their work shows that the only nontrivial homology with
![]() $g \le 4$
is
$g \le 4$
is
![]() ${\mathrm {H}}_{3} (\mathrm {Out}(\mathrm {F}_{4}); \widetilde {\mathbb {Q}}) \cong {\mathbb {Q}}$
. Using Remark 4.27, this implies that
${\mathrm {H}}_{3} (\mathrm {Out}(\mathrm {F}_{4}); \widetilde {\mathbb {Q}}) \cong {\mathbb {Q}}$
. Using Remark 4.27, this implies that
![]() ${\mathrm {H}}_{p} ({\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}})$
is trivial for
${\mathrm {H}}_{p} ({\mathfrak {UG}}^{m} {\operatorname {(\mathscr {L}ie)}})$
is trivial for
![]() $0 < p \le \min (3m + 2, 4m)$
when m is odd.
$0 < p \le \min (3m + 2, 4m)$
when m is odd.
5 Connected sums of products of spheres
Throughout this section, we let
![]() $3 \le k < l \le 2k - 2$
be two integers. We set
$3 \le k < l \le 2k - 2$
be two integers. We set
that is, a g-fold connected sum of
![]() ${\mathrm {S}^{k}} \times {\mathrm {S}^{l}}$
with r disjoint
${\mathrm {S}^{k}} \times {\mathrm {S}^{l}}$
with r disjoint
![]() $(k + l)$
-dimensional open disks removed (we will often omit k and l from the notation and simply write
$(k + l)$
-dimensional open disks removed (we will often omit k and l from the notation and simply write
![]() $M_{g,r}$
). We are interested in the stable cohomology of
$M_{g,r}$
). We are interested in the stable cohomology of
that is, of the classifying space of the group-like topological monoid of homotopy equivalences from
![]() $M_{g,1}$
to itself that fix the boundary pointwise. To make sense of this, we need to specify stabilization maps
$M_{g,1}$
to itself that fix the boundary pointwise. To make sense of this, we need to specify stabilization maps
![]() ${\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M_{g,1}) \to {\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M_{g+1,1})$
. To this end, we note that there is a canonical inclusion
${\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M_{g,1}) \to {\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M_{g+1,1})$
. To this end, we note that there is a canonical inclusion
(where
![]() ${\#}$
denotes connected sum), which induces a map of topological monoids
${\#}$
denotes connected sum), which induces a map of topological monoids
by extending an element of
![]() ${{\mathrm {aut}}_{\partial }}(M_{g,1})$
by the identity.
${{\mathrm {aut}}_{\partial }}(M_{g,1})$
by the identity.
We will now introduce some related objects, which we will need for stating and proving our main result. We start by fixing some basepoints of
![]() ${\mathrm {S}^{k}}$
and
${\mathrm {S}^{k}}$
and
![]() ${\mathrm {S}^{l}}$
. Then, for
${\mathrm {S}^{l}}$
. Then, for
![]() $1 \le i \le g$
, we denote by
$1 \le i \le g$
, we denote by
![]() $\alpha ^g_i \in {\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})$
the homology class represented by the canonical inclusion of
$\alpha ^g_i \in {\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})$
the homology class represented by the canonical inclusion of
![]() ${\mathrm {S}^{k}}$
into the i-th summand, and by
${\mathrm {S}^{k}}$
into the i-th summand, and by
![]() $(\alpha ^g_i)^\# \in {\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Z}})$
the class represented by the canonical inclusion of
$(\alpha ^g_i)^\# \in {\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Z}})$
the class represented by the canonical inclusion of
![]() ${\mathrm {S}^{l}}$
into the i-th summand (we assume that these inclusions do not intersect the disks used to form the connected sum). These classes form bases of
${\mathrm {S}^{l}}$
into the i-th summand (we assume that these inclusions do not intersect the disks used to form the connected sum). These classes form bases of
![]() ${\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}}) \cong {\mathbb {Z}}^g$
and
${\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}}) \cong {\mathbb {Z}}^g$
and
![]() ${\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Z}}) \cong {\mathbb {Z}}^g$
, respectively. We choose the orientations such that the intersection pairing fulfills
${\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Z}}) \cong {\mathbb {Z}}^g$
, respectively. We choose the orientations such that the intersection pairing fulfills
![]() ${\langle {\alpha ^g_i},{(\alpha ^g_i)^\#}\rangle _{\cap }} = 1$
. Also note that
${\langle {\alpha ^g_i},{(\alpha ^g_i)^\#}\rangle _{\cap }} = 1$
. Also note that
![]() ${\langle {\alpha ^g_i},{(\alpha ^g_j)^\#}\rangle _{\cap }} = 0$
when
${\langle {\alpha ^g_i},{(\alpha ^g_j)^\#}\rangle _{\cap }} = 0$
when
![]() $i \neq j$
. For
$i \neq j$
. For
![]() $1 \le i \le g$
, we moreover have
$1 \le i \le g$
, we moreover have
![]() $(\iota _g)_*(\alpha ^g_i) = \alpha ^{g+1}_i$
and
$(\iota _g)_*(\alpha ^g_i) = \alpha ^{g+1}_i$
and
![]() $(\iota _g)_* \left ( (\alpha ^g_i)^\# \right ) = (\alpha ^{g+1}_i)^\#$
.
$(\iota _g)_* \left ( (\alpha ^g_i)^\# \right ) = (\alpha ^{g+1}_i)^\#$
.
Using this, we can define a stabilization map of groups
by letting
![]() $\psi _g(f)$
be the unique automorphism such that
$\psi _g(f)$
be the unique automorphism such that
![]() $\psi _g(f) \circ (\iota _g)_* = (\iota _g)_* \circ f$
and such that
$\psi _g(f) \circ (\iota _g)_* = (\iota _g)_* \circ f$
and such that
![]() $\psi _g(f)$
is the identity on
$\psi _g(f)$
is the identity on
![]() $\alpha ^{g+1}_{g+1}$
and
$\alpha ^{g+1}_{g+1}$
and
![]() $(\alpha ^{g+1}_{g+1})^\#$
. (Here,
$(\alpha ^{g+1}_{g+1})^\#$
. (Here,
![]() ${\mathrm {Aut}}$
denotes automorphisms of graded abelian groups.) We now set
${\mathrm {Aut}}$
denotes automorphisms of graded abelian groups.) We now set
that is, it is the group of those automorphisms of the reduced integral homology of
![]() $M_{g,1}$
that can be realized by a homotopy automorphism that fixes the boundary pointwise. Together, the maps
$M_{g,1}$
that can be realized by a homotopy automorphism that fixes the boundary pointwise. Together, the maps
![]() $\phi _g$
and
$\phi _g$
and
![]() $\psi _g$
induce a stabilization map of groups
$\psi _g$
induce a stabilization map of groups
![]() $\gamma _g \colon \Gamma _g \to \Gamma _{g+1}$
. The group
$\gamma _g \colon \Gamma _g \to \Gamma _{g+1}$
. The group
![]() $\Gamma _g$
has been identified explicitly by Grey [Reference GreyGre19].
$\Gamma _g$
has been identified explicitly by Grey [Reference GreyGre19].
Proposition 5.1 (Grey).
We have
where
![]() ${\langle {-},{-}\rangle _{\cap }}$
is the intersection pairing. Moreover, the canonical map
${\langle {-},{-}\rangle _{\cap }}$
is the intersection pairing. Moreover, the canonical map
has finite kernel.
Proof. This is [Reference GreyGre19, Proposition 5.1]. (The extra structure
![]() $Jq$
mentioned there is necessarily trivial. When
$Jq$
mentioned there is necessarily trivial. When
![]() $k+l$
is odd, it is trivial by definition. When
$k+l$
is odd, it is trivial by definition. When
![]() $k+l$
is even, it is trivial since
$k+l$
is even, it is trivial since
![]() as
as
![]() $k \neq l$
.)
$k \neq l$
.)
This implies, by the same arguments as in the proofs of Lemmas 3.1 and 3.2, that
acts on
![]() ${\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})$
via the standard action and on
${\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})$
via the standard action and on
![]() ${\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Z}}) \cong {{\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})^\vee }$
via its dual. The bases
${\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Z}}) \cong {{\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})^\vee }$
via its dual. The bases
![]() $\alpha ^g_i$
of
$\alpha ^g_i$
of
![]() ${\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})$
constructed above yield isomorphisms
${\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Z}})$
constructed above yield isomorphisms
![]() $\Gamma _g \cong {\mathrm {GL}}_{g}({\mathbb {Z}})$
compatible with the
$\Gamma _g \cong {\mathrm {GL}}_{g}({\mathbb {Z}})$
compatible with the
![]() $\gamma _g$
and the standard inclusions
$\gamma _g$
and the standard inclusions
![]() ${\mathrm {GL}}_{g}({\mathbb {Z}}) \to {\mathrm {GL}}_{g+1}({\mathbb {Z}})$
. Similarly, we obtain isomorphisms
${\mathrm {GL}}_{g}({\mathbb {Z}}) \to {\mathrm {GL}}_{g+1}({\mathbb {Z}})$
. Similarly, we obtain isomorphisms
compatible with the stabilization maps.
Lastly, we set
that is, it is the positive truncation of the graded Lie algebra of derivations that annihilate the element ![]() , where
, where
![]() $\beta _1, \dots , \beta _g$
is some basis of
$\beta _1, \dots , \beta _g$
is some basis of
![]() $\mathrm {s}^{-1} {\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Q}})$
and
$\mathrm {s}^{-1} {\mathrm {H}}_{k}(M_{g,1}; {\mathbb {Q}})$
and
![]() $\beta _1^\#, \dots , \beta _g^\#$
is the basis of
$\beta _1^\#, \dots , \beta _g^\#$
is the basis of
![]() $\mathrm {s}^{-1} {\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Q}})$
dual to it with respect to the intersection pairing; see [Reference Berglund and MadsenBM20, §3.4 f.] for more details. We note that the canonical action of
$\mathrm {s}^{-1} {\mathrm {H}}_{l}(M_{g,1}; {\mathbb {Q}})$
dual to it with respect to the intersection pairing; see [Reference Berglund and MadsenBM20, §3.4 f.] for more details. We note that the canonical action of
![]() $\Gamma ^{\mathbb {Q}}_g$
on
$\Gamma ^{\mathbb {Q}}_g$
on
![]() $\mathrm {s}^{-1} {\widetilde {\operatorname {H}}_{*}}(M_{g,1}; {\mathbb {Q}})$
preserves the element
$\mathrm {s}^{-1} {\widetilde {\operatorname {H}}_{*}}(M_{g,1}; {\mathbb {Q}})$
preserves the element
![]() $\omega $
. Hence, we obtain an action of
$\omega $
. Hence, we obtain an action of
![]() $\Gamma ^{\mathbb {Q}}_g$
on
$\Gamma ^{\mathbb {Q}}_g$
on
![]() $\mathfrak g_g$
by conjugation. Restricting along the canonical inclusion
$\mathfrak g_g$
by conjugation. Restricting along the canonical inclusion
![]() $\Gamma _g \to \Gamma ^{\mathbb {Q}}_g$
, we also obtain an action of
$\Gamma _g \to \Gamma ^{\mathbb {Q}}_g$
, we also obtain an action of
![]() $\Gamma _g$
on
$\Gamma _g$
on
![]() $\mathfrak g_g$
.
$\mathfrak g_g$
.
We now construct a stabilization map
![]() $\delta _g \colon \mathfrak g_g \to \mathfrak g_{g+1}$
. For
$\delta _g \colon \mathfrak g_g \to \mathfrak g_{g+1}$
. For
![]() $\theta \in \mathfrak g_g$
, the derivation
$\theta \in \mathfrak g_g$
, the derivation
![]() $\delta _g(\theta )$
is uniquely determined by requiring it to restrict to
$\delta _g(\theta )$
is uniquely determined by requiring it to restrict to
![]() $\theta $
along the map induced by
$\theta $
along the map induced by
![]() $\iota _g$
and asking that
$\iota _g$
and asking that
![]() $\delta _g(\theta ) \left ( \mathrm {s}^{-1} \alpha ^{g+1}_{g+1} \right ) = 0$
and
$\delta _g(\theta ) \left ( \mathrm {s}^{-1} \alpha ^{g+1}_{g+1} \right ) = 0$
and
![]() $\delta _g(\theta ) \left ( \mathrm {s}^{-1} (\alpha ^{g+1}_{g+1})^\# \right ) = 0$
. Here,
$\delta _g(\theta ) \left ( \mathrm {s}^{-1} (\alpha ^{g+1}_{g+1})^\# \right ) = 0$
. Here,
![]() $\alpha ^{g+1}_i$
is the basis of
$\alpha ^{g+1}_i$
is the basis of
![]() ${\mathrm {H}}_{k}(M_{g+1,1}; {\mathbb {Z}}) \subseteq {\mathrm {H}}_{k}(M_{g+1,1}; {\mathbb {Q}})$
from above. It is clear from the definition that
${\mathrm {H}}_{k}(M_{g+1,1}; {\mathbb {Z}}) \subseteq {\mathrm {H}}_{k}(M_{g+1,1}; {\mathbb {Q}})$
from above. It is clear from the definition that
![]() $\delta _g(\theta )(\omega ) = 0$
, so that
$\delta _g(\theta )(\omega ) = 0$
, so that
![]() $\delta _g$
indeed defines a map
$\delta _g$
indeed defines a map
![]() $\mathfrak g_g \to \mathfrak g_{g+1}$
of graded Lie algebras. Moreover, this becomes a map of
$\mathfrak g_g \to \mathfrak g_{g+1}$
of graded Lie algebras. Moreover, this becomes a map of
![]() $\Gamma ^{\mathbb {Q}}_g$
-modules when the target is equipped with the
$\Gamma ^{\mathbb {Q}}_g$
-modules when the target is equipped with the
![]() $\Gamma ^{\mathbb {Q}}_g$
-action obtained by restricting along
$\Gamma ^{\mathbb {Q}}_g$
-action obtained by restricting along
![]() $\gamma _g$
.
$\gamma _g$
.
Remark 5.2. The graded Lie algebra
![]() $\mathfrak g_g$
is a Lie model for the homotopy fiber of the map
$\mathfrak g_g$
is a Lie model for the homotopy fiber of the map
![]() ${\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M_{g,1}) \longrightarrow {\mathrm {B}} \Gamma _g$
, and one can think of the action of
${\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M_{g,1}) \longrightarrow {\mathrm {B}} \Gamma _g$
, and one can think of the action of
![]() $\Gamma _g$
on
$\Gamma _g$
on
![]() $\mathfrak g_g$
as modeling the action of
$\mathfrak g_g$
as modeling the action of
![]() $\Gamma _g \cong {\pi }_{1}({\mathrm {B}} \Gamma _g)$
on this fiber; see [Reference Berglund and MadsenBM20, Proposition 5.6] and [Reference Berglund and StollBS] for precise statements (for non-relative self-equivalences this is [Reference Berglund and ZemanBZ22, Theorem 3.40]).
$\Gamma _g \cong {\pi }_{1}({\mathrm {B}} \Gamma _g)$
on this fiber; see [Reference Berglund and MadsenBM20, Proposition 5.6] and [Reference Berglund and StollBS] for precise statements (for non-relative self-equivalences this is [Reference Berglund and ZemanBZ22, Theorem 3.40]).
Berglund–Zeman [Reference Berglund and ZemanBZ22] recently developed methods for identifying the cohomology of a classifying space of self-equivalences
![]() ${\mathrm {B}}{\mathrm {aut}}(X)$
in terms of certain group cohomology. The details of applying this to the relative situation will appear in the upcoming paper [Reference Berglund and StollBS] joint with Berglund. In particular, the following statement is proved there; one can think of it as a strengthening of collapse of the Serre spectral sequence associated to the fiber sequence of Remark 5.2.
${\mathrm {B}}{\mathrm {aut}}(X)$
in terms of certain group cohomology. The details of applying this to the relative situation will appear in the upcoming paper [Reference Berglund and StollBS] joint with Berglund. In particular, the following statement is proved there; one can think of it as a strengthening of collapse of the Serre spectral sequence associated to the fiber sequence of Remark 5.2.
Proposition 5.3 (Berglund–Zeman, Berglund–Stoll).
There are, for any
![]() $g \in {\mathbb {N}_0}$
and
$g \in {\mathbb {N}_0}$
and
![]() $\Gamma _g$
-module P, isomorphisms of graded vector spaces
$\Gamma _g$
-module P, isomorphisms of graded vector spaces
that are compatible with the stabilization maps induced by
![]() $\phi _{g-1}$
,
$\phi _{g-1}$
,
![]() $\gamma _{g-1}$
, and
$\gamma _{g-1}$
, and
![]() $\delta _{g-1}$
, in the sense that the diagram
$\delta _{g-1}$
, in the sense that the diagram

commutes when
![]() $g \ge 1$
. The map
$g \ge 1$
. The map
![]() $\Theta _g(P)$
is an isomorphism of graded algebras when
$\Theta _g(P)$
is an isomorphism of graded algebras when
![]() $P = {\mathbb {Q}}$
is trivial, and an isomorphism of modules over these algebras for general P.
$P = {\mathbb {Q}}$
is trivial, and an isomorphism of modules over these algebras for general P.
Proof. For
![]() $P = {\mathbb {Q}}$
and without the compatibility with the stabilization maps, this is stated (without a detailed proof) as [Reference Berglund and ZemanBZ22, Theorem 4.40]. A full proof will appear in the upcoming paper [Reference Berglund and StollBS] joint with Berglund.
$P = {\mathbb {Q}}$
and without the compatibility with the stabilization maps, this is stated (without a detailed proof) as [Reference Berglund and ZemanBZ22, Theorem 4.40]. A full proof will appear in the upcoming paper [Reference Berglund and StollBS] joint with Berglund.
The rest of this section is devoted to providing, for certain
![]() $\Gamma _g$
-modules P, an explicit description of
$\Gamma _g$
-modules P, an explicit description of
![]() ${\mathrm {H}}^{*}(\Gamma _g; {\mathrm {H}}_{\mathrm {CE}}^{*}(\mathfrak g_g) \mathop{\mathop{\otimes}} P)$
in a stable range of degrees.
${\mathrm {H}}^{*}(\Gamma _g; {\mathrm {H}}_{\mathrm {CE}}^{*}(\mathfrak g_g) \mathop{\mathop{\otimes}} P)$
in a stable range of degrees.
5.1 Reduction to invariants
In this subsection, our goal is to prove that there is an isomorphism of bigraded algebras
in a stable range of degrees. This will mainly rely on a result of Li–Sun [Reference Li and SunLS19]. We need some preliminaries.
Definition 5.4. A Schur bifunctor is a functor
![]() $F \colon {{\mathbf {Vect}}} \times {{\mathbf {Vect}}} \to {{\mathbf {Vect}}}$
of the form
$F \colon {{\mathbf {Vect}}} \times {{\mathbf {Vect}}} \to {{\mathbf {Vect}}}$
of the form
where the
![]() $\mathscr M(n_1, n_2)$
are some right
$\mathscr M(n_1, n_2)$
are some right
![]() $({\Sigma _{n_1}} \times {\Sigma _{n_2}})$
-modules in
$({\Sigma _{n_1}} \times {\Sigma _{n_2}})$
-modules in
![]() ${{\mathbf {Vect}}}$
. We say F has degree
${{\mathbf {Vect}}}$
. We say F has degree
![]() $\le d$
if
$\le d$
if
![]() $\mathscr M(n_1, n_2) \cong 0$
for all pairs
$\mathscr M(n_1, n_2) \cong 0$
for all pairs
![]() $(n_1, n_2)$
such that
$(n_1, n_2)$
such that
![]() $n_1 + n_2> d$
. We say F is of finite type if each
$n_1 + n_2> d$
. We say F is of finite type if each
![]() $\mathscr M(n_1, n_2)$
is finite dimensional.
$\mathscr M(n_1, n_2)$
is finite dimensional.
Lemma 5.5. Let F be a finite type Schur bifunctor of degree
![]() $\le d$
. Then the canonical inclusion
$\le d$
. Then the canonical inclusion
is an isomorphism for all finite-dimensional vector spaces V such that
![]() $\dim V> d$
. Here,
$\dim V> d$
. Here,
![]() $f \in {\mathrm {GL}}(V)$
acts on
$f \in {\mathrm {GL}}(V)$
acts on
![]() ${V^\vee }$
by
${V^\vee }$
by
![]() ${({f^{-1}})^\vee }$
and diagonally on
${({f^{-1}})^\vee }$
and diagonally on
![]() $F(V, {V^\vee })$
.
$F(V, {V^\vee })$
.
Proof. Using, for G a group and W a G-module, the natural (in both W and G) isomorphism
![]() ${({W}_G)^\vee } \cong ({W^\vee })^G$
, we can pass to the dual situation (i.e., take coinvariants instead of invariants). (To see that
${({W}_G)^\vee } \cong ({W^\vee })^G$
, we can pass to the dual situation (i.e., take coinvariants instead of invariants). (To see that
![]() ${F(V, {V^\vee })^\vee }$
is again a Schur bifunctor, we use that
${F(V, {V^\vee })^\vee }$
is again a Schur bifunctor, we use that ![]() is finite and that we are working in characteristic zero, so that
is finite and that we are working in characteristic zero, so that
![]() ${(M {\mathop{\otimes}_{\Sigma}} N)^\vee } \cong {M^\vee } {\mathop{\otimes}_{\Sigma}} {N^\vee }$
.)
${(M {\mathop{\otimes}_{\Sigma}} N)^\vee } \cong {M^\vee } {\mathop{\otimes}_{\Sigma}} {N^\vee }$
.)
Both the
![]() ${\mathrm {GL}}(V)$
-action and the
${\mathrm {GL}}(V)$
-action and the
![]() ${\mathrm {SL}}(V)$
-action are compatible with the direct sum composition of
${\mathrm {SL}}(V)$
-action are compatible with the direct sum composition of
![]() $F(V, {V^\vee })$
, so that it is enough to prove for a single summand
$F(V, {V^\vee })$
, so that it is enough to prove for a single summand
with
![]() $n_1 + n_2 < \dim V$
that
$n_1 + n_2 < \dim V$
that
![]() ${W}_{{\mathrm {SL}}(V)} \to {W}_{{\mathrm {GL}}(V)}$
is an isomorphism. Denote by
${W}_{{\mathrm {SL}}(V)} \to {W}_{{\mathrm {GL}}(V)}$
is an isomorphism. Denote by
![]() $e_1, \dots , e_g$
some basis of V. Then the equivalence relation defining
$e_1, \dots , e_g$
some basis of V. Then the equivalence relation defining
![]() ${W}_{{\mathrm {GL}}(V)}$
is generated by
${W}_{{\mathrm {GL}}(V)}$
is generated by
 $$ \begin{align} m \mathop{\otimes} \bigotimes_{j = 1}^{n_1} e_{i_j} \mathop{\otimes} \bigotimes_{j' = 1}^{n_2} e^\#_{i^{\prime}_{j'}} \sim m \mathop{\otimes} \bigotimes_{j = 1}^{n_1} f(e_{i_j}) \mathop{\otimes} \bigotimes_{j' = 1}^{n_2} {({f^{-1}})^\vee} (e^\#_{i^{\prime}_{j'}}) \end{align} $$
$$ \begin{align} m \mathop{\otimes} \bigotimes_{j = 1}^{n_1} e_{i_j} \mathop{\otimes} \bigotimes_{j' = 1}^{n_2} e^\#_{i^{\prime}_{j'}} \sim m \mathop{\otimes} \bigotimes_{j = 1}^{n_1} f(e_{i_j}) \mathop{\otimes} \bigotimes_{j' = 1}^{n_2} {({f^{-1}})^\vee} (e^\#_{i^{\prime}_{j'}}) \end{align} $$
for all
![]() $f \in {\mathrm {GL}}(V)$
,
$f \in {\mathrm {GL}}(V)$
,
![]() $m \in \mathscr M(n_1, n_2)$
and
$m \in \mathscr M(n_1, n_2)$
and
![]() $1 \le i_j, i^{\prime }_{j'} \le g$
. Choose some
$1 \le i_j, i^{\prime }_{j'} \le g$
. Choose some
![]() $1 \le i \le g$
such that
$1 \le i \le g$
such that
![]() $i \neq i_j, i^{\prime }_{j'}$
for all j and
$i \neq i_j, i^{\prime }_{j'}$
for all j and
![]() $j'$
(this is possible by our assumption that
$j'$
(this is possible by our assumption that
![]() $\dim V> n_1 + n_2$
). Now let
$\dim V> n_1 + n_2$
). Now let ![]() , where h is defined by
, where h is defined by
![]() $h(e_i) = {(\det f)^{-1}} e_i$
and
$h(e_i) = {(\det f)^{-1}} e_i$
and
![]() $h(e_j) = e_j$
for all
$h(e_j) = e_j$
for all
![]() $j \neq i$
. Then
$j \neq i$
. Then
![]() $f' \in {\mathrm {SL}}(V)$
and it yields the same relation (5.1) as f did. Hence,
$f' \in {\mathrm {SL}}(V)$
and it yields the same relation (5.1) as f did. Hence,
![]() ${W}_{{\mathrm {SL}}(V)} \to {W}_{{\mathrm {GL}}(V)}$
is injective. Since it is clearly surjective, it is thus an isomorphism.
${W}_{{\mathrm {SL}}(V)} \to {W}_{{\mathrm {GL}}(V)}$
is injective. Since it is clearly surjective, it is thus an isomorphism.
Now we are ready to prove the main result of this subsection. See [Reference Berglund and MadsenBM20, Theorem 8.4] for the analogous statement in the case
![]() $k = l$
; the stable range occurring in their result has been improved by Krannich [Reference KrannichKra20] using an argument similar to the one we will employ.
$k = l$
; the stable range occurring in their result has been improved by Krannich [Reference KrannichKra20] using an argument similar to the one we will employ.
Proposition 5.6. Let Q be a finite type Schur bifunctor of degree
![]() $\le r$
and set
$\le r$
and set ![]() as a
as a
![]() $\Gamma ^{\mathbb {Q}}_g$
-module. Then the canonical map of bigraded vector spaces
$\Gamma ^{\mathbb {Q}}_g$
-module. Then the canonical map of bigraded vector spaces
 $$ \begin{align*} {\mathrm{H}}^{p}(\Gamma_g; {\mathbb{Q}}) \mathop{\otimes} {\mathrm{H}}^{q} \Big( \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} P \right)^{\Gamma^{\mathbb{Q}}_g} \Big) \cong {\mathrm{H}}^{p} \Big( \Gamma_g; {\mathrm{H}}^{q} \Big( \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} P \right)^{\Gamma^{\mathbb{Q}}_g} \Big) \Big) \longrightarrow \\ {\mathrm{H}}^{p} \Big( \Gamma_g; {\mathrm{H}}^{q} \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} P \right) \Big) \cong {\mathrm{H}}^{p} \left( \Gamma_g; {\mathrm{H}}_{\mathrm{CE}}^{q}(\mathfrak g_g) \mathop{\otimes} P \right) \end{align*} $$
$$ \begin{align*} {\mathrm{H}}^{p}(\Gamma_g; {\mathbb{Q}}) \mathop{\otimes} {\mathrm{H}}^{q} \Big( \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} P \right)^{\Gamma^{\mathbb{Q}}_g} \Big) \cong {\mathrm{H}}^{p} \Big( \Gamma_g; {\mathrm{H}}^{q} \Big( \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} P \right)^{\Gamma^{\mathbb{Q}}_g} \Big) \Big) \longrightarrow \\ {\mathrm{H}}^{p} \Big( \Gamma_g; {\mathrm{H}}^{q} \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} P \right) \Big) \cong {\mathrm{H}}^{p} \left( \Gamma_g; {\mathrm{H}}_{\mathrm{CE}}^{q}(\mathfrak g_g) \mathop{\otimes} P \right) \end{align*} $$
is an isomorphism for
![]() $g> {\max } \left ( p + 1, \frac {1}{2} (q + 1) + r \right )$
.
$g> {\max } \left ( p + 1, \frac {1}{2} (q + 1) + r \right )$
.
Proof. A result of Li–Sun [Reference Li and SunLS19, Example 1.10] implies that the canonical map
is an isomorphism for
![]() $g \ge p + 2$
. This uses that [Reference GreyGre19, (Proof of) Proposition 7.1] implies that
$g \ge p + 2$
. This uses that [Reference GreyGre19, (Proof of) Proposition 7.1] implies that
![]() ${\operatorname {C}_{\mathrm {CE}}^{q}}(\mathfrak g_g)$
, and hence also
${\operatorname {C}_{\mathrm {CE}}^{q}}(\mathfrak g_g)$
, and hence also
![]() ${\mathrm {H}}^{q} \left ( {\operatorname {C}_{\mathrm {CE}}^{*}}(\mathfrak g_g) \mathop{\mathop{\otimes}} P \right )$
, is a finite dimensional rational representation of the reductive group
${\mathrm {H}}^{q} \left ( {\operatorname {C}_{\mathrm {CE}}^{*}}(\mathfrak g_g) \mathop{\mathop{\otimes}} P \right )$
, is a finite dimensional rational representation of the reductive group
![]() ${\mathrm {GL}}_{g}$
and thus completely reducible (see, for example, [Reference MilneMil17, Theorem 22.42]).
${\mathrm {GL}}_{g}$
and thus completely reducible (see, for example, [Reference MilneMil17, Theorem 22.42]).
Now, by [Reference GreyGre19, Lemma 3.4], the group
![]() $\Gamma _g$
is rationally perfect (cf. [Reference Berglund and MadsenBM20, Definiton B.3]). Hence, taking
$\Gamma _g$
is rationally perfect (cf. [Reference Berglund and MadsenBM20, Definiton B.3]). Hence, taking
![]() $\Gamma _g$
-invariants is exact when restricted to the category of finite dimensional representations. In particular, the canonical map
$\Gamma _g$
-invariants is exact when restricted to the category of finite dimensional representations. In particular, the canonical map
is an isomorphism.
Lastly we use that, by a result of Borel [Reference BorelBor66, Theorem 1], the arithmetic subgroup
![]() ${\mathrm {SL}}_{g}({\mathbb {Z}})$
is Zariski dense in
${\mathrm {SL}}_{g}({\mathbb {Z}})$
is Zariski dense in
![]() ${\mathrm {SL}}_{g}({\mathbb {Q}})$
(note that the condition of the theorem is fulfilled since
${\mathrm {SL}}_{g}({\mathbb {Q}})$
(note that the condition of the theorem is fulfilled since
![]() ${\mathrm {SL}}_{g}$
is almost simple for
${\mathrm {SL}}_{g}$
is almost simple for
![]() $g \ge 2$
). Hence, we have
$g \ge 2$
). Hence, we have
![]() $V^{{\mathrm {SL}}_{g}({\mathbb {Z}})} = V^{{\mathrm {SL}}_{g}({\mathbb {Q}})}$
for any rational representation V of
$V^{{\mathrm {SL}}_{g}({\mathbb {Z}})} = V^{{\mathrm {SL}}_{g}({\mathbb {Q}})}$
for any rational representation V of
![]() ${\mathrm {SL}}_{g}$
over
${\mathrm {SL}}_{g}$
over
![]() ${\mathbb {Q}}$
. In particular, for F a finite type Schur bifunctor of degree
${\mathbb {Q}}$
. In particular, for F a finite type Schur bifunctor of degree
![]() $\le d$
and
$\le d$
and ![]() , we thus have, when
, we thus have, when
![]() $g> d$
, that
$g> d$
, that
where the third equality uses Lemma 5.5. Now we note that, by [Reference GreyGre19, (Proof of) Proposition 7.1], there exists a finite type Schur bifunctor
![]() $F_q$
of degree
$F_q$
of degree
![]() $\le \frac q 2$
such that there is an isomorphism
$\le \frac q 2$
such that there is an isomorphism
of
![]() $\Gamma ^{\mathbb {Q}}_g$
-modules (where the action on the right-hand side is diagonally). Hence,
$\Gamma ^{\mathbb {Q}}_g$
-modules (where the action on the right-hand side is diagonally). Hence,
![]() ${\operatorname {C}_{\mathrm {CE}}^{q}}(\mathfrak g_g) \mathop{\mathop{\otimes}} P$
is, in the same way, the value of a Schur bifunctor of degree
${\operatorname {C}_{\mathrm {CE}}^{q}}(\mathfrak g_g) \mathop{\mathop{\otimes}} P$
is, in the same way, the value of a Schur bifunctor of degree
![]() $\le \frac q 2 + r$
. This finishes the proof. For the condition on g given in the statement, note that an isomorphism of chain complexes in a range induces an isomorphism of homology in a range smaller by
$\le \frac q 2 + r$
. This finishes the proof. For the condition on g given in the statement, note that an isomorphism of chain complexes in a range induces an isomorphism of homology in a range smaller by
![]() $1$
.
$1$
.
5.2 The main theorem
We are now ready to deduce our main theorem from everything we have done so far.
Theorem 5.7. Let
![]() $3 \le k < l \le 2k - 2$
and
$3 \le k < l \le 2k - 2$
and
![]() $2 \le g$
be integers and let I and J be finite linearly ordered sets. Furthermore, set
$2 \le g$
be integers and let I and J be finite linearly ordered sets. Furthermore, set ![]() as a
as a
![]() ${{\pi }_{0}} \left ( {{\mathrm {aut}}_{\partial }} (M^{k,l}_{g,1}) \right )$
-module. Then there is, in cohomological degrees,
${{\pi }_{0}} \left ( {{\mathrm {aut}}_{\partial }} (M^{k,l}_{g,1}) \right )$
-module. Then there is, in cohomological degrees,
 $$\begin{align*}\le \begin{cases} g - 2, & \mathit{when}\ \ |I| + |J| \le \frac 1 2 g \\ 2 (g - |I| - |J| - 1), & \mathit{otherwise} \end{cases} \end{align*}$$
$$\begin{align*}\le \begin{cases} g - 2, & \mathit{when}\ \ |I| + |J| \le \frac 1 2 g \\ 2 (g - |I| - |J| - 1), & \mathit{otherwise} \end{cases} \end{align*}$$
an isomorphism of graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
 $$ \begin{align*} &{\mathrm{H}}^{*} \left( {\mathrm{B}} {{\mathrm{aut}}_{\partial}} (M^{k,l}_{g,1}); H_{g;l}^{\otimes I} \mathop{\otimes} H_{g;k}^{\otimes J} \right) \cong \\ &\qquad {\mathrm{s}}^{(k-1) |I| + (l-1) |J|} {\mathrm{H}}^{*} \left( {\mathrm{GL}}({\mathbb{Z}}); {\mathbb{Q}} \right) \mathop{\otimes} {\mathrm{H}}^{*} \left( {({\mathfrak{DG}_{\mathrm{trunc}}^{k + l - 2}}{\operatorname{(\mathscr{L}ie)}}_{I,J})^\vee} \right) \mathop{\otimes} \operatorname{sgn}_I^{\otimes k-1} \mathop{\otimes} \operatorname{sgn}_J^{\otimes l-1} \end{align*} $$
$$ \begin{align*} &{\mathrm{H}}^{*} \left( {\mathrm{B}} {{\mathrm{aut}}_{\partial}} (M^{k,l}_{g,1}); H_{g;l}^{\otimes I} \mathop{\otimes} H_{g;k}^{\otimes J} \right) \cong \\ &\qquad {\mathrm{s}}^{(k-1) |I| + (l-1) |J|} {\mathrm{H}}^{*} \left( {\mathrm{GL}}({\mathbb{Z}}); {\mathbb{Q}} \right) \mathop{\otimes} {\mathrm{H}}^{*} \left( {({\mathfrak{DG}_{\mathrm{trunc}}^{k + l - 2}}{\operatorname{(\mathscr{L}ie)}}_{I,J})^\vee} \right) \mathop{\otimes} \operatorname{sgn}_I^{\otimes k-1} \mathop{\otimes} \operatorname{sgn}_J^{\otimes l-1} \end{align*} $$
compatible with the stabilization maps on the left-hand side (here, the shift refers to the cohomological grading). It is an isomorphism of algebras when
![]() $I = J = \varnothing $
, and an isomorphism of modules over these algebras for general I and J. Here,
$I = J = \varnothing $
, and an isomorphism of modules over these algebras for general I and J. Here, ![]() and
and
![]() $\operatorname {sgn}_S$
is the sign representation of
$\operatorname {sgn}_S$
is the sign representation of
![]() ${\Sigma _{S}}$
. Also, recall that
${\Sigma _{S}}$
. Also, recall that
![]() ${\mathfrak {DG}_{\mathrm {trunc}}^{k + l - 2}}{\operatorname {(\mathscr {L}ie)}}_{I,J}$
is the truncated directed
${\mathfrak {DG}_{\mathrm {trunc}}^{k + l - 2}}{\operatorname {(\mathscr {L}ie)}}_{I,J}$
is the truncated directed
![]() $(I,J)$
-graph complex (see Definition 3.31) associated to the cyclic Lie operad.
$(I,J)$
-graph complex (see Definition 3.31) associated to the cyclic Lie operad.
In particular, after stabilizing, we obtain an isomorphism

of graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules. It is an isomorphism of algebras when
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules. It is an isomorphism of algebras when
![]() $I = J = \varnothing $
, and an isomorphism of modules over these algebras for general I and J.
$I = J = \varnothing $
, and an isomorphism of modules over these algebras for general I and J.
Proof. Combining Propositions 5.3 and 5.6, we obtain, in the stable range
an isomorphism of graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
 $$\begin{align*}{\mathrm{H}}^{s} \left( {\mathrm{B}} {{\mathrm{aut}}_{\partial}} (M^{k,l}_{g,1}); H_{g;l}^{\otimes I} \mathop{\otimes} H_{g;k}^{\otimes J} \right) \cong \bigoplus_{p + q = s} {\mathrm{H}}^{p}(\Gamma_g; {\mathbb{Q}}) \mathop{\otimes} {\mathrm{H}}^{q} \Big( \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} H_{g;l}^{\otimes I} \mathop{\otimes} H_{g;k}^{\otimes J} \right)^{\Gamma^{\mathbb{Q}}_g} \Big), \end{align*}$$
$$\begin{align*}{\mathrm{H}}^{s} \left( {\mathrm{B}} {{\mathrm{aut}}_{\partial}} (M^{k,l}_{g,1}); H_{g;l}^{\otimes I} \mathop{\otimes} H_{g;k}^{\otimes J} \right) \cong \bigoplus_{p + q = s} {\mathrm{H}}^{p}(\Gamma_g; {\mathbb{Q}}) \mathop{\otimes} {\mathrm{H}}^{q} \Big( \left( {\operatorname{C}_{\mathrm{CE}}^{*}}(\mathfrak g_g) \mathop{\otimes} H_{g;l}^{\otimes I} \mathop{\otimes} H_{g;k}^{\otimes J} \right)^{\Gamma^{\mathbb{Q}}_g} \Big), \end{align*}$$
which is compatible with the stabilization maps and the algebra/module structures. It follows from work of Borel [Reference BorelBor74] (see also [Reference Kupers, Miller and PatztKMP22, Theorem A]Footnote
3
) that the canonical map
![]() ${\mathrm {H}}^{p}({\mathrm {GL}}({\mathbb {Z}}); {\mathbb {Q}}) \to {\mathrm {H}}^{p}({\mathrm {GL}}_{g}({\mathbb {Z}}); {\mathbb {Q}})$
is an isomorphism for
${\mathrm {H}}^{p}({\mathrm {GL}}({\mathbb {Z}}); {\mathbb {Q}}) \to {\mathrm {H}}^{p}({\mathrm {GL}}_{g}({\mathbb {Z}}); {\mathbb {Q}})$
is an isomorphism for
![]() $g \ge p + 2$
; in particular, we can replace
$g \ge p + 2$
; in particular, we can replace
![]() ${\mathrm {H}}^{p}(\Gamma _g; {\mathbb {Q}}) \cong {\mathrm {H}}^{p}({\mathrm {GL}}_{g}({\mathbb {Z}}); {\mathbb {Q}})$
with
${\mathrm {H}}^{p}(\Gamma _g; {\mathbb {Q}}) \cong {\mathrm {H}}^{p}({\mathrm {GL}}_{g}({\mathbb {Z}}); {\mathbb {Q}})$
with
![]() ${\mathrm {H}}^{p}({\mathrm {GL}}({\mathbb {Z}}); {\mathbb {Q}})$
in the formula above.
${\mathrm {H}}^{p}({\mathrm {GL}}({\mathbb {Z}}); {\mathbb {Q}})$
in the formula above.
Now, by [Reference Berglund and MadsenBM20, Proposition 6.6], there is an isomorphism of Lie algebras
that is compatible with the
![]() $\Gamma ^{\mathbb {Q}}_g$
-actions and the stabilization maps. Here, the right-hand side is equipped with the graded Lie algebra structure of Lemma 2.34, where
$\Gamma ^{\mathbb {Q}}_g$
-actions and the stabilization maps. Here, the right-hand side is equipped with the graded Lie algebra structure of Lemma 2.34, where
![]() $\mathrm {s}^{-1} {\widetilde {\operatorname {H}}_{*}}(M_{g,1}; {\mathbb {Q}})$
is equipped with the anti-symmetric pairing given by
$\mathrm {s}^{-1} {\widetilde {\operatorname {H}}_{*}}(M_{g,1}; {\mathbb {Q}})$
is equipped with the anti-symmetric pairing given by
![]() $\langle {\mathrm {s}^{-1} a}, {\mathrm {s}^{-1} b}\rangle = (-1)^{ | a | + 1} {\langle {a},{b}\rangle _{\cap }}$
. Then Corollary 3.33 implies that, in degrees
$\langle {\mathrm {s}^{-1} a}, {\mathrm {s}^{-1} b}\rangle = (-1)^{ | a | + 1} {\langle {a},{b}\rangle _{\cap }}$
. Then Corollary 3.33 implies that, in degrees
![]() $q \le \frac {4}{3} g - 1$
if
$q \le \frac {4}{3} g - 1$
if
![]() $l = 2k - 2$
or
$l = 2k - 2$
or
![]() $q \le 2g - 1$
if
$q \le 2g - 1$
if
![]() $l \neq 2k - 2$
, there is an isomorphism of graded
$l \neq 2k - 2$
, there is an isomorphism of graded
![]() $({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
$({\Sigma _{I}} \times {\Sigma _{J}})$
-modules
compatible with the stabilization maps on the left-hand side as well as the coalgebra/comodule structures. (Note that an isomorphism of chain complexes up to degree p induces an isomorphism on homology up to degree
![]() $p - 1$
.) Dualizing this yields the desired statement since there is an isomorphism
$p - 1$
.) Dualizing this yields the desired statement since there is an isomorphism
of
![]() $(\Gamma ^{\mathbb {Q}}_g \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules and
$(\Gamma ^{\mathbb {Q}}_g \times {\Sigma _{I}} \times {\Sigma _{J}})$
-modules and
![]() $H_{g;k}$
and
$H_{g;k}$
and
![]() $H_{g;l}$
are dual to each other.
$H_{g;l}$
are dual to each other.
Remark 5.8. Via Schur–Weyl duality (see, for example, [Reference Fulton and HarrisFH04, §6.1] or [Reference EtingofEti+11, §5.19]), Theorem 5.7 can be used to deduce descriptions of
![]() ${\mathrm {H}}^{*} \left ( {\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M^{k,l}_{g,1}); P \right )$
for more general
${\mathrm {H}}^{*} \left ( {\mathrm {B}} {{\mathrm {aut}}_{\partial }} (M^{k,l}_{g,1}); P \right )$
for more general
![]() $\Gamma ^{\mathbb {Q}}_g$
-modules P.
$\Gamma ^{\mathbb {Q}}_g$
-modules P.
Corollary 5.9. Let
![]() $3 \le k < l \le 2k - 2$
and
$3 \le k < l \le 2k - 2$
and
![]() $2 \le g$
be integers. Then there is, in cohomological degrees
$2 \le g$
be integers. Then there is, in cohomological degrees
![]() $\le g - 2$
, an isomorphism of graded algebras
$\le g - 2$
, an isomorphism of graded algebras
compatible with the stabilization maps on the left-hand side. (Recall that
![]() ${\mathfrak {UG}}^{k + l - 2} \operatorname {(\mathscr {L}ie)}$
denotes the undirected graph complex associated to the cyclic Lie operad; see Definition 4.22.)
${\mathfrak {UG}}^{k + l - 2} \operatorname {(\mathscr {L}ie)}$
denotes the undirected graph complex associated to the cyclic Lie operad; see Definition 4.22.)
In particular, after stabilizing, we obtain an isomorphism
of graded algebras.
Remark 5.10. It should be possible to obtain a version of this corollary for cohomology with nontrivial coefficients by generalizing the arguments of Section 4 (see Remark 4.1).
Remark 5.11. Note that
by a classical result of Borel [Reference BorelBor74, p. 11.4]. The homology of
![]() ${\mathfrak {UG}}^{k + l - 2} \operatorname {(\mathscr {L}ie)}$
is more mysterious. See Remark 4.30 for a summary of what is known.
${\mathfrak {UG}}^{k + l - 2} \operatorname {(\mathscr {L}ie)}$
is more mysterious. See Remark 4.30 for a summary of what is known.
Acknowledgements
First and foremost, I would like to thank my PhD advisor, Alexander Berglund, for suggesting the topic of this article to me and for guiding me through the process of writing it. Moreover, I am grateful to him and Tomáš Zeman for providing me with a preliminary version of their paper [Reference Berglund and ZemanBZ22], as well as to Thomas Willwacher for a preliminary version of the computational results of [Reference Brun and WillwacherBW23]. I would also like to thank Fabian Hebestreit and Manuel Krannich for useful discussions, and the latter for making me aware of the article [Reference Li and SunLS19]. Last but not least, I would like to thank Alexander Berglund, Manuel Krannich and the anonymous referee for many useful comments on earlier versions of this paper.
Competing interest
The authors have no competing interests to declare.