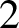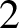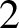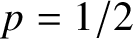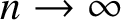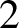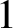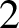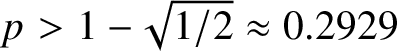1 Introduction
Denote the n-dimensional cube by ![]() $Q^n = [0,1]^n$ and the set of vertices of the n-dimensional cube by
$Q^n = [0,1]^n$ and the set of vertices of the n-dimensional cube by ![]() $Q^n_0$. In other words,
$Q^n_0$. In other words, ![]() $Q^n_0 = \{0,1\}^n$, which is the set of all n-tuples with binary entries. More generally, let
$Q^n_0 = \{0,1\}^n$, which is the set of all n-tuples with binary entries. More generally, let ![]() $Q^n_k$ denote the k-dimensional skeleton of
$Q^n_k$ denote the k-dimensional skeleton of ![]() $Q^n$. For example,
$Q^n$. For example, ![]() $Q^n_1$ is the graph with vertex set
$Q^n_1$ is the graph with vertex set ![]() $Q^n_0$ and an edge (i.e., a
$Q^n_0$ and an edge (i.e., a ![]() $1$-dimensional face) between two vertices if and only if they differ by exactly one coordinate. Define the random
$1$-dimensional face) between two vertices if and only if they differ by exactly one coordinate. Define the random ![]() $2$-dimensional cubical complex
$2$-dimensional cubical complex ![]() $Q_2(n,p)$ as having
$Q_2(n,p)$ as having ![]() $1$-skeleton equal to
$1$-skeleton equal to ![]() $Q^n_1$, and where each
$Q^n_1$, and where each ![]() $2$-dimensional face of
$2$-dimensional face of ![]() $Q^n$ is included with probability p, independently.
$Q^n$ is included with probability p, independently.
The random complex ![]() $Q_2(n,p)$ is a cubical analogue of the random simplicial complex
$Q_2(n,p)$ is a cubical analogue of the random simplicial complex ![]() $Y_2(n,p)$ introduced by Linial and Meshulam in [Reference Linial and Meshulam22], whose theory is well developed. The random complex
$Y_2(n,p)$ introduced by Linial and Meshulam in [Reference Linial and Meshulam22], whose theory is well developed. The random complex ![]() $Y_2(n,p)$ is defined by taking the complete
$Y_2(n,p)$ is defined by taking the complete ![]() $1$-skeleton of the n-dimensional simplex
$1$-skeleton of the n-dimensional simplex ![]() $\Delta ^n$ and including each
$\Delta ^n$ and including each ![]() $2$-face independently and with probability p. In this way,
$2$-face independently and with probability p. In this way, ![]() $Q_2(n,p)$ is constructed in exactly the same way as
$Q_2(n,p)$ is constructed in exactly the same way as ![]() $Y_2(n,p)$, except that the underlying polytope
$Y_2(n,p)$, except that the underlying polytope ![]() $\Delta ^n$ is replaced by
$\Delta ^n$ is replaced by ![]() $Q^n$.
$Q^n$.
The random complex ![]() $Q_2(n,p)$ is also the
$Q_2(n,p)$ is also the ![]() $2$-dimensional analogue of the random cubical graph; see [Reference Kostochka, Sapozhenko and Weber21] for a 1992 survey. To make the connection precise and review some of the history, let
$2$-dimensional analogue of the random cubical graph; see [Reference Kostochka, Sapozhenko and Weber21] for a 1992 survey. To make the connection precise and review some of the history, let ![]() $Q(n,p)$ denote the random subgraph of the n-cube defined by including all vertices of
$Q(n,p)$ denote the random subgraph of the n-cube defined by including all vertices of ![]() $Q^n$, and including each edge in
$Q^n$, and including each edge in ![]() $Q_1^n$ independently with probability p.
$Q_1^n$ independently with probability p.
Burtin [Reference Burtin6] and later Erdoős and Spencer [Reference Erdős and Spencer14] studied the threshold for connectivity in the random cubical graph:
Theorem 1.1 Burtin [Reference Burtin6], Erdoős and Spencer [Reference Erdős and Spencer14]
For ![]() $Q \sim Q(n,p)$ and for any fixed
$Q \sim Q(n,p)$ and for any fixed ![]() $p \in [0,1]$,
$p \in [0,1]$,
 $$ \begin{align} \lim_{n \to \infty} \mathbb{P}[Q \text{ is connected}] = \begin{cases} 0 &\text{if } p<1/2,\\ e^{-1} & \text{if } p=1/2,\\ 1 &\text{if } p>1/2.\\ \end{cases} \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \mathbb{P}[Q \text{ is connected}] = \begin{cases} 0 &\text{if } p<1/2,\\ e^{-1} & \text{if } p=1/2,\\ 1 &\text{if } p>1/2.\\ \end{cases} \end{align} $$ Let ![]() $f_n(p)=\mathbb {P}[Q \sim Q(n,p) \text { is connected}]$. It is easy to see that if
$f_n(p)=\mathbb {P}[Q \sim Q(n,p) \text { is connected}]$. It is easy to see that if ![]() $p < 1/2$, then
$p < 1/2$, then ![]() $\lim _{n \to \infty }f_n(p) =0$. Burtin showed that this is sharp; if
$\lim _{n \to \infty }f_n(p) =0$. Burtin showed that this is sharp; if ![]() $p> 1/2$, then
$p> 1/2$, then ![]() $\lim _{n \to \infty }f_n(p) =1$.
$\lim _{n \to \infty }f_n(p) =1$.
Erdoős and Spencer refined this argument to show what happens at ![]() $p=1/2$ exactly. They also showed that near
$p=1/2$ exactly. They also showed that near ![]() $p=1/2$, the only connected components of
$p=1/2$, the only connected components of ![]() $Q(n,p)$ are isolated vertices and a giant component. Then it is straightforward to show that the number of isolated vertices has a limiting Poisson distribution with mean
$Q(n,p)$ are isolated vertices and a giant component. Then it is straightforward to show that the number of isolated vertices has a limiting Poisson distribution with mean ![]() $1$, and as a consequence
$1$, and as a consequence
for every integer ![]() $k \ge 0$, where
$k \ge 0$, where ![]() ${\beta }_0$ denotes the number of connected components.
${\beta }_0$ denotes the number of connected components.
This picture strongly parallels what is seen in Erdoős–Rényi graphs ![]() $G \sim G(n,p)$. Let
$G \sim G(n,p)$. Let ![]() $p = (\log n + c)/n$ with
$p = (\log n + c)/n$ with ![]() $c \in \mathbb {R}$ fixed. Then
$c \in \mathbb {R}$ fixed. Then
 $$ \begin{align*} \lim_{n \to \infty} \mathbb{P}[ G \text{ is connected} ] = e^{-e^{-c}} \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \mathbb{P}[ G \text{ is connected} ] = e^{-e^{-c}} \end{align*} $$(see [Reference Erdős and Rényi13] or [Reference Bollobás5]). Letting ![]() $c \to \pm \infty $, the probability tends to
$c \to \pm \infty $, the probability tends to ![]() $0$ or
$0$ or ![]() $1$.
$1$.
The proofs share a strong similarity, in that the method is to enumerate potential cut sets and show that they are rare by making a first moment estimate of the number of cut sets.
It is therefore perhaps reasonable to speculate that the topological phenomenology of the higher-dimensional process ![]() $Q_2(n,p)$ mirrors that of
$Q_2(n,p)$ mirrors that of ![]() $Y_2(n,p)$ after appropriately adjusting how p is chosen as a function of n. We shall show, however, that there are major differences between
$Y_2(n,p)$ after appropriately adjusting how p is chosen as a function of n. We shall show, however, that there are major differences between ![]() $Q_2(n,p)$ and
$Q_2(n,p)$ and ![]() $Y_2(n,p)$.
$Y_2(n,p)$.
Before discussing our results and illustrating these differences, we introduce some standard terminology. Our focus is on typical behaviour of random objects for large values of n. So we will say that a sequence of statements ![]() $\mathcal {P}_n$ holds with high probability (abbreviated ‘w.h.p.’) if
$\mathcal {P}_n$ holds with high probability (abbreviated ‘w.h.p.’) if
 $$ \begin{align*} \lim_{n \to \infty} \mathbb{P}[\mathcal{P}_n]=1. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \mathbb{P}[\mathcal{P}_n]=1. \end{align*} $$ We will make use of the Landau notations ![]() $O, o, \omega , \Omega , \Theta $ in the asymptotic sense, so that
$O, o, \omega , \Omega , \Theta $ in the asymptotic sense, so that ![]() $f = O(g)$ means
$f = O(g)$ means ![]() $f/g$ is eventually bounded above as
$f/g$ is eventually bounded above as ![]() $n \to \infty $ and
$n \to \infty $ and ![]() $f = o(g)$ means
$f = o(g)$ means ![]() $f/g \to 0$ as
$f/g \to 0$ as ![]() $n \to \infty $. Also,
$n \to \infty $. Also, ![]() $f = \omega (g)$ means
$f = \omega (g)$ means ![]() $g = o(f)$ and
$g = o(f)$ and ![]() $f = \Omega (g)$ means
$f = \Omega (g)$ means ![]() $g = O(f)$. Finally, we will use
$g = O(f)$. Finally, we will use ![]() $f = \Theta (g)$ to mean
$f = \Theta (g)$ to mean ![]() $f = O(g)$ and
$f = O(g)$ and ![]() $f = \Omega (g)$. We occasionally display parameters like
$f = \Omega (g)$. We occasionally display parameters like ![]() $O_{a,b,c}(\cdot )$, emphasising that the implied constants depend on
$O_{a,b,c}(\cdot )$, emphasising that the implied constants depend on ![]() $a,b,c$.
$a,b,c$.
We will also make use of the notion of thresholds. A function ![]() $f = f(n)$ is said to be a threshold for a property P of a sequence of random objects
$f = f(n)$ is said to be a threshold for a property P of a sequence of random objects ![]() $G=G_{n,p}$ if
$G=G_{n,p}$ if ![]() $p=\omega (f)$ implies
$p=\omega (f)$ implies ![]() $G \in P$ w.h.p. and
$G \in P$ w.h.p. and ![]() $p=o(f)$ implies
$p=o(f)$ implies ![]() $G \not \in P$ w.h.p. Such a threshold is defined only up to n-independent scalar multiples. If there is a function
$G \not \in P$ w.h.p. Such a threshold is defined only up to n-independent scalar multiples. If there is a function ![]() $g = o(f)$ such that
$g = o(f)$ such that ![]() $p \geq f + g$ implies
$p \geq f + g$ implies ![]() $G \in P$ w.h.p. and
$G \in P$ w.h.p. and ![]() $p \leq f - g$ implies
$p \leq f - g$ implies ![]() $G \not \in P$ w.h.p., the threshold is said to be sharp.
$G \not \in P$ w.h.p., the threshold is said to be sharp.
In this paper we study the fundamental group ![]() $\pi _1(Q)$ for
$\pi _1(Q)$ for ![]() $Q \sim Q_2(n,p)$. The fundamental group can be given a purely combinatorial representation for a space such as
$Q \sim Q_2(n,p)$. The fundamental group can be given a purely combinatorial representation for a space such as ![]() $Q_2(n,p)$, which we discuss in Section 2.1. Our first result establishes the threshold for
$Q_2(n,p)$, which we discuss in Section 2.1. Our first result establishes the threshold for ![]() $\pi _1(Q)=0$ – that is, for
$\pi _1(Q)=0$ – that is, for ![]() $Q\sim Q_2(n,p)$ to be simply connected. Here we formulate the theorem for p fixed independently of n.
$Q\sim Q_2(n,p)$ to be simply connected. Here we formulate the theorem for p fixed independently of n.
The ![]() $2$-dimensional analogues of isolated vertices are maximal
$2$-dimensional analogues of isolated vertices are maximal ![]() $1$-faces. It is not hard to see that the threshold for maximal
$1$-faces. It is not hard to see that the threshold for maximal ![]() $1$-faces is
$1$-faces is ![]() $p=1/2$, and that for any fixed
$p=1/2$, and that for any fixed ![]() $p \leq 1/2$, there are maximal
$p \leq 1/2$, there are maximal ![]() $1$-dimensional faces w.h.p. If there are any maximal
$1$-dimensional faces w.h.p. If there are any maximal ![]() $1$-faces, then any loop passing through such an edge is not contractible, so
$1$-faces, then any loop passing through such an edge is not contractible, so ![]() $\pi _1(Q) \neq 0$. Most of our work is to prove the following:
$\pi _1(Q) \neq 0$. Most of our work is to prove the following:
Theorem 1.2. If ![]() $Q \sim Q_2(n,p)$ and
$Q \sim Q_2(n,p)$ and ![]() $p>1/2$, then w.h.p.,
$p>1/2$, then w.h.p., ![]() $\pi _1 (Q)= 0$.
$\pi _1 (Q)= 0$.
This theorem marks a substantial difference between the behaviours of the random cubical complex ![]() $Q \sim Q_2(n,p)$ and the random simplicial complex
$Q \sim Q_2(n,p)$ and the random simplicial complex ![]() $Y \sim Y_2(n,p)$. The threshold for
$Y \sim Y_2(n,p)$. The threshold for ![]() $\pi _1(Y) = 0$ is roughly
$\pi _1(Y) = 0$ is roughly ![]() $p = n^{-1/2}$ [Reference Babson, Billera and Chan4]. The threshold is sharpened by Luria and Peled in [Reference Luria and Peled25]. There is a sharp threshold for
$p = n^{-1/2}$ [Reference Babson, Billera and Chan4]. The threshold is sharpened by Luria and Peled in [Reference Luria and Peled25]. There is a sharp threshold for ![]() $H_1(Y) = 0$ vanishing at
$H_1(Y) = 0$ vanishing at ![]() $p=2\log n / n$. This is due to Linial and Meshulam [Reference Linial and Meshulam22], for the statement with
$p=2\log n / n$. This is due to Linial and Meshulam [Reference Linial and Meshulam22], for the statement with ![]() $\mathbb {Z} / 2\mathbb {Z}$ coefficients. This was extended by Meshulam and Wallach [Reference Meshulam and Wallach26] to all finite coefficient rings, and finally to
$\mathbb {Z} / 2\mathbb {Z}$ coefficients. This was extended by Meshulam and Wallach [Reference Meshulam and Wallach26] to all finite coefficient rings, and finally to ![]() $\mathbb {Z}$ coefficients by Łuczak and Peled [Reference Łuczak and Peled24]; see also [Reference Newman and Paquette28] for the extension of the
$\mathbb {Z}$ coefficients by Łuczak and Peled [Reference Łuczak and Peled24]; see also [Reference Newman and Paquette28] for the extension of the ![]() $\mathbb {Z}$-coefficients result to higher dimensions. In summary, there is a big gap between the thresholds for
$\mathbb {Z}$-coefficients result to higher dimensions. In summary, there is a big gap between the thresholds for ![]() $\pi _1(Y)=0$ and
$\pi _1(Y)=0$ and ![]() $H_1(Y)=0$, but Theorem 1.2 implies that the thresholds for
$H_1(Y)=0$, but Theorem 1.2 implies that the thresholds for ![]() $\pi _1(Q)=0$ and
$\pi _1(Q)=0$ and ![]() $H_1(Q)=0$ (with any coefficients) coincide.
$H_1(Q)=0$ (with any coefficients) coincide.
For ![]() $p> 1-(1/2)^{1/2}$, we characterise the structure of the fundamental group
$p> 1-(1/2)^{1/2}$, we characterise the structure of the fundamental group ![]() $\pi _1(Q)$ for
$\pi _1(Q)$ for ![]() $Q \sim Q_2(n,p))$. For the following statement, recall that in a simplicial complex, a maximal
$Q \sim Q_2(n,p))$. For the following statement, recall that in a simplicial complex, a maximal ![]() $1$-face is a
$1$-face is a ![]() $1$-face which is not contained in any
$1$-face which is not contained in any ![]() $2$-face.
$2$-face.
Theorem 1.3. For  $p> 1-\left (\tfrac 12\right )^{1/2}$, with high probability, for
$p> 1-\left (\tfrac 12\right )^{1/2}$, with high probability, for ![]() $Q \sim Q_2(n,p)$,
$Q \sim Q_2(n,p)$,
where ![]() $F_N$ denotes a free group on N generators and N denotes the number of maximal
$F_N$ denotes a free group on N generators and N denotes the number of maximal ![]() $1$-dimensional faces in Q.
$1$-dimensional faces in Q.
Hence, just below the ![]() $p = 1/2$ threshold, only maximal
$p = 1/2$ threshold, only maximal ![]() $1$-faces contribute to the fundamental group. Again, this is in contrast with the corresponding story for
$1$-faces contribute to the fundamental group. Again, this is in contrast with the corresponding story for ![]() $\pi _1(Y)$. The fundamental group of the random
$\pi _1(Y)$. The fundamental group of the random ![]() $2$-dimensional simplicial complex
$2$-dimensional simplicial complex ![]() $\pi _1(Y)$ is known to have property (T) with high probability once
$\pi _1(Y)$ is known to have property (T) with high probability once ![]() $p \ge (2 + \epsilon ) \log n / n$ [Reference Hoffman, Kahle and Paquette19], and this precludes it being a nontrivial free group or even having any nontrivial free quotients.
$p \ge (2 + \epsilon ) \log n / n$ [Reference Hoffman, Kahle and Paquette19], and this precludes it being a nontrivial free group or even having any nontrivial free quotients.
Theorem 1.3 has the following corollary, a limiting Poisson distribution for the Betti number ![]() $\beta _1$:
$\beta _1$:
Corollary 1.4. If ![]() $c \in \mathbb {R}$ is fixed and
$c \in \mathbb {R}$ is fixed and
 $$ \begin{align*} p = \frac{1}{2}\left( 1 + \frac{\log n + c}{n} \right), \end{align*} $$
$$ \begin{align*} p = \frac{1}{2}\left( 1 + \frac{\log n + c}{n} \right), \end{align*} $$then
 $$ \begin{align*} \mathbb{P}[ \beta_1(Q_2(n,1/2)) = k] \to \frac{e^{ck}e^{-e^{-c}}}{k!}. \end{align*} $$
$$ \begin{align*} \mathbb{P}[ \beta_1(Q_2(n,1/2)) = k] \to \frac{e^{ck}e^{-e^{-c}}}{k!}. \end{align*} $$ Here ![]() $\beta _1$ represents the dimension of homology
$\beta _1$ represents the dimension of homology ![]() $H_1(Q, \mathbb {R})$. It is also the number of generators of the free group
$H_1(Q, \mathbb {R})$. It is also the number of generators of the free group ![]() $\pi _1(Q)$. This all follows from Theorem 1.3, together with showing that the number of maximal
$\pi _1(Q)$. This all follows from Theorem 1.3, together with showing that the number of maximal ![]() $1$-faces is Poisson distributed with mean
$1$-faces is Poisson distributed with mean ![]() $e^{-c}$.
$e^{-c}$.
It is also possible to formulate a process version of this statement. Here one couples all ![]() $Q_2(n,p)$ together for all
$Q_2(n,p)$ together for all ![]() $p \in [0,1]$ in a monotone fashion, so the
$p \in [0,1]$ in a monotone fashion, so the ![]() $2$-faces of
$2$-faces of ![]() $Q_2(n,p_1)$ are a subset of
$Q_2(n,p_1)$ are a subset of ![]() $Q_2(n,p_2)$ whenever
$Q_2(n,p_2)$ whenever ![]() $p_1 \leq p_2$. Let
$p_1 \leq p_2$. Let ![]() $\left (Q_p : p \in [0,1]\right )$ have this distribution, and let
$\left (Q_p : p \in [0,1]\right )$ have this distribution, and let ![]() $N_p$ be the number of maximal
$N_p$ be the number of maximal ![]() $1$-faces in
$1$-faces in ![]() $Q_p$. Then we can formulate the stopping times
$Q_p$. Then we can formulate the stopping times ![]() $T_{sc}$ and
$T_{sc}$ and ![]() $T_{2d}$ as
$T_{2d}$ as
 $$ \begin{align*} T_{sc} = \inf\left\{ p : \pi_1\left(Q_p\right) = 0 \right\}, \qquad T_{2d} = \inf\left\{ p : N_p = 0 \right\}. \end{align*} $$
$$ \begin{align*} T_{sc} = \inf\left\{ p : \pi_1\left(Q_p\right) = 0 \right\}, \qquad T_{2d} = \inf\left\{ p : N_p = 0 \right\}. \end{align*} $$We have the following:
Corollary 1.5. ![]() $T_{sc} = T_{2d}$ w.h.p.
$T_{sc} = T_{2d}$ w.h.p.
Theorem 1.3 characterises the structure of ![]() $\pi _1(Q)$ for
$\pi _1(Q)$ for ![]() $Q \sim Q_2(n,p)$ and
$Q \sim Q_2(n,p)$ and
 $$ \begin{align*} 1- \left( \frac{1}{2} \right)^{1/2} < p < \frac{1}{2}. \end{align*} $$
$$ \begin{align*} 1- \left( \frac{1}{2} \right)^{1/2} < p < \frac{1}{2}. \end{align*} $$For smaller p, we are not able to completely describe the structure of the fundamental group, but we give a partial characterisation in terms of its free factorisation.
For a finitely presented group H, we say that H is indecomposable if whenever H is written as a free product of two groups ![]() $H \cong H_1 * H_2$, either
$H \cong H_1 * H_2$, either ![]() $H_1$ or
$H_1$ or ![]() $H_2$ is a trivial group. It is well known that a finitely presented group G be may be written as a free product
$H_2$ is a trivial group. It is well known that a finitely presented group G be may be written as a free product
where every ![]() $G_i$ is indecomposable. Moreover, this free-product factorisation is unique, up to isomorphism types of the factors and reordering.
$G_i$ is indecomposable. Moreover, this free-product factorisation is unique, up to isomorphism types of the factors and reordering.
Definition 1.6. For a cubical subcomplex T of ![]() $Q^n$, let
$Q^n$, let ![]() $e(T)$ denote the number of edges in T. Let
$e(T)$ denote the number of edges in T. Let ![]() $\mathscr {T}_p$ be the set of pure
$\mathscr {T}_p$ be the set of pure ![]() $2$-dimensional strongly connected cubical complexes T that are subcomplexes of (the
$2$-dimensional strongly connected cubical complexes T that are subcomplexes of (the ![]() $2$-dimensional skeleton of)
$2$-dimensional skeleton of) ![]() $Q^n$ for some n and such that
$Q^n$ for some n and such that ![]() $1-(1/2)^{1/e(T)}> p$.
$1-(1/2)^{1/e(T)}> p$.
While we do not characterise all the free factors, we are able to characterise some of them. Essentially, we show that everything that can happen will happen, somewhere, with high probability.
Theorem 1.7. For ![]() $p \in (0,1)$ fixed and
$p \in (0,1)$ fixed and ![]() $Q \sim Q_2(n,p)$, let the free-product factorisation of
$Q \sim Q_2(n,p)$, let the free-product factorisation of ![]() $G = \pi _1(Q)$ be given by
$G = \pi _1(Q)$ be given by
With high probability, for every ![]() $T \in \mathscr {T}_p$ with nontrivial fundamental group,
$T \in \mathscr {T}_p$ with nontrivial fundamental group, ![]() $\pi _1(T)$ appears as a free factor – that is, we have
$\pi _1(T)$ appears as a free factor – that is, we have ![]() $\pi _1(T) \cong G_j $ for some
$\pi _1(T) \cong G_j $ for some ![]() $1 \le j \le \ell $.
$1 \le j \le \ell $.
Indeed, every finitely presented group G can appear as a free factor (see Section 5 for details). One can also ask the extremal topological combinatorial question: For given homotopy classes of ![]() $2$-dimensional complexes T, what is the smallest
$2$-dimensional complexes T, what is the smallest ![]() $e(T)$ attainable? Furthermore, one can ask what is the threshold for specific groups to appear as a free factor in G. In Section5, we give some examples of specific complexes which we believe to be minimal – the torus, the projective plane and the Klein bottle.
$e(T)$ attainable? Furthermore, one can ask what is the threshold for specific groups to appear as a free factor in G. In Section5, we give some examples of specific complexes which we believe to be minimal – the torus, the projective plane and the Klein bottle.
Using the case of the projective plane, when  $0 < p < 1 - \left (\tfrac 12\right )^{1/40} \approx 0.017179$ and
$0 < p < 1 - \left (\tfrac 12\right )^{1/40} \approx 0.017179$ and ![]() $Q \sim Q_2(n,p)$, we show that
$Q \sim Q_2(n,p)$, we show that ![]() $\pi _1(Q)$ has a
$\pi _1(Q)$ has a ![]() $\mathbb {Z}/2\mathbb {Z}$ free factor with high probability (see Corollary 5.4). This shows in particular that
$\mathbb {Z}/2\mathbb {Z}$ free factor with high probability (see Corollary 5.4). This shows in particular that ![]() $H_1(Q;\mathbb {Z})$ has torsion elements for small enough fixed
$H_1(Q;\mathbb {Z})$ has torsion elements for small enough fixed ![]() $p>0$. The question of whether torsion ever appears in
$p>0$. The question of whether torsion ever appears in ![]() $H_1(Y; \mathbb {Z})$ is an open one, although it appears that there is almost always a short burst of enormous torsion [Reference Kahle, Lutz, Newman and Parsons20].
$H_1(Y; \mathbb {Z})$ is an open one, although it appears that there is almost always a short burst of enormous torsion [Reference Kahle, Lutz, Newman and Parsons20].
Conjecture 1.8. For  $p> 1 - \left (\tfrac 12\right )^{1/40}$ and
$p> 1 - \left (\tfrac 12\right )^{1/40}$ and ![]() $Q \sim Q_2(n,p)$,
$Q \sim Q_2(n,p)$, ![]() $\pi _1(Q)$ is torsion free with high probability.
$\pi _1(Q)$ is torsion free with high probability.
We further believe it is possible that for p above this threshold, ![]() $\pi _1(Q)$ is free with high probability. For the case of
$\pi _1(Q)$ is free with high probability. For the case of ![]() $\pi _1(Y)$ with
$\pi _1(Y)$ with ![]() $Y\sim Y_2(n,p)$, the sharp threshold is found by Newman in [Reference Newman27], improving on previous work of [Reference Cohen, Costa, Farber and Kappeler7].
$Y\sim Y_2(n,p)$, the sharp threshold is found by Newman in [Reference Newman27], improving on previous work of [Reference Cohen, Costa, Farber and Kappeler7].
1.1 Discussion
We have not addressed many results about the fundamental group of ![]() $\pi _1(Y)$ for
$\pi _1(Y)$ for ![]() $Y\sim Y_2(n,p)$, which may have interesting analogues in
$Y\sim Y_2(n,p)$, which may have interesting analogues in ![]() $Q_2(n,p)$ that could further elucidate what appear to be deep differences between simplicial and random cubical complexes. As the body of literature on
$Q_2(n,p)$ that could further elucidate what appear to be deep differences between simplicial and random cubical complexes. As the body of literature on ![]() $Y_2(n,p)$, is substantial, we discuss possible directions of interest for questions about
$Y_2(n,p)$, is substantial, we discuss possible directions of interest for questions about ![]() $Q_2(n,p)$.
$Q_2(n,p)$.
Many interesting topological phases of ![]() $\pi _1(Q)$ are likely to exist when
$\pi _1(Q)$ are likely to exist when ![]() $p \to 0$ at an appropriate rate as
$p \to 0$ at an appropriate rate as ![]() $n \to \infty $. For
$n \to \infty $. For ![]() $Y_2(n,p)$, a particularly rich regime of p is when the mean degree of an edge
$Y_2(n,p)$, a particularly rich regime of p is when the mean degree of an edge ![]() $np$ tends to a constant. We would expect this regime to be similarly rich for
$np$ tends to a constant. We would expect this regime to be similarly rich for ![]() $Q_2(n,p)$ and to name a few transitions that should appear in this regime: the collapsibility threshold [Reference Aronshtam, Linial, Ł uczak and Meshulam2], the threshold for a giant shadow [Reference Linial and Peled23] and the threshold for
$Q_2(n,p)$ and to name a few transitions that should appear in this regime: the collapsibility threshold [Reference Aronshtam, Linial, Ł uczak and Meshulam2], the threshold for a giant shadow [Reference Linial and Peled23] and the threshold for ![]() $\pi _1(Q)$ to have an irreducible factor in its free-product factorisation with growing rank.
$\pi _1(Q)$ to have an irreducible factor in its free-product factorisation with growing rank.
A natural direction is to consider higher-dimensional complexes ![]() $Q_d(n,p)$ built in an analogous way to
$Q_d(n,p)$ built in an analogous way to ![]() $Y_d(n,p)$. For
$Y_d(n,p)$. For ![]() $Q_d(n,p)$, it may be possible to analyse the higher homotopy groups in a similar fashion to what is done here.
$Q_d(n,p)$, it may be possible to analyse the higher homotopy groups in a similar fashion to what is done here.
In a different direction, we mention that all of the results we present are about the ![]() $n\to \infty $ limit, but also have some content for some large n. These could provide useful results for understanding
$n\to \infty $ limit, but also have some content for some large n. These could provide useful results for understanding ![]() $2$-dimensional percolation on a sufficiently high-dimensional lattice
$2$-dimensional percolation on a sufficiently high-dimensional lattice ![]() $\mathbb {Z}^n$. There are some recent related results for such higher-dimensional cubical percolation [Reference Dowling and Lundberg12, Reference Hiraoka and Tsunoda18, Reference Hiraoka and Shirai17].
$\mathbb {Z}^n$. There are some recent related results for such higher-dimensional cubical percolation [Reference Dowling and Lundberg12, Reference Hiraoka and Tsunoda18, Reference Hiraoka and Shirai17].
1.1.1 Multiparameter generalisations
In the literature on random cubical graphs, there is a ![]() $2$-parameter model
$2$-parameter model ![]() $Q(n; p_0, p_1)$ (see [Reference Kostochka, Sapozhenko and Weber21] for a survey of some results). First we take a random induced subgraph of the n-cube, where every vertex has probability
$Q(n; p_0, p_1)$ (see [Reference Kostochka, Sapozhenko and Weber21] for a survey of some results). First we take a random induced subgraph of the n-cube, where every vertex has probability ![]() $p_0$ independently. Then we include each of the remaining edges with probability
$p_0$ independently. Then we include each of the remaining edges with probability ![]() $p_1$ independently. Bond percolation on the hypercube is the random cubical graph where
$p_1$ independently. Bond percolation on the hypercube is the random cubical graph where ![]() $p_0=1$ and
$p_0=1$ and ![]() $p_1$ varies, and site percolation is where
$p_1$ varies, and site percolation is where ![]() $p_1 = 1$ and
$p_1 = 1$ and ![]() $p_0$ varies.
$p_0$ varies.
It seems natural to form a higher-dimensional generalisation of this model ![]() $Q_2(n; p_0, p_1, p_2)$. Indeed, Costa and Farber [Reference Costa and Farber8, Reference Costa and Farber9, Reference Costa and Farber10] have made a detailed study of the analogous model
$Q_2(n; p_0, p_1, p_2)$. Indeed, Costa and Farber [Reference Costa and Farber8, Reference Costa and Farber9, Reference Costa and Farber10] have made a detailed study of the analogous model ![]() $Y_2(n; p_0, p_1, p_2)$, including many interesting results on the fundamental group. (See also [Reference Farber and Nowik15], wherein new questions about the fundamental group are discussed for this multiparameter model.) Our discussion has been about the special case where
$Y_2(n; p_0, p_1, p_2)$, including many interesting results on the fundamental group. (See also [Reference Farber and Nowik15], wherein new questions about the fundamental group are discussed for this multiparameter model.) Our discussion has been about the special case where ![]() $p_0=p_1=1$ and
$p_0=p_1=1$ and ![]() $p_2$ varies.
$p_2$ varies.
For ![]() $Q_2(n; p_0, p_1, p_2)$, it is natural to ask if there is a critical surface for homology
$Q_2(n; p_0, p_1, p_2)$, it is natural to ask if there is a critical surface for homology ![]() $H_1$ vanishing in the unit cube. The case of setting
$H_1$ vanishing in the unit cube. The case of setting ![]() $p_1 = p_2 =1$ and letting
$p_1 = p_2 =1$ and letting ![]() $p_0$ vary looks particularly interesting, analogous to the site-percolation model. Higher homology is no longer monotone, as in, for example, a random clique complex or a Vietoris–Rips complex. Are there separate thresholds for
$p_0$ vary looks particularly interesting, analogous to the site-percolation model. Higher homology is no longer monotone, as in, for example, a random clique complex or a Vietoris–Rips complex. Are there separate thresholds for ![]() $H_0$ vanishing,
$H_0$ vanishing, ![]() $H_1$ appearing,
$H_1$ appearing, ![]() $H_1$ vanishing and
$H_1$ vanishing and ![]() $H_2$ appearing?
$H_2$ appearing?
1.2 Overview and organisation
We begin with Section 2, where we define some key notions for working with ![]() $Q_2(n,p)$, and make some elementary estimates about it. In Section 2.1 we give a combinatorial definition of
$Q_2(n,p)$, and make some elementary estimates about it. In Section 2.1 we give a combinatorial definition of ![]() $\pi _1$. In Section 2.2 we introduce notation to work with subcomplexes of
$\pi _1$. In Section 2.2 we introduce notation to work with subcomplexes of ![]() $Q^n$ and we introduce the notions of the random cubical complex
$Q^n$ and we introduce the notions of the random cubical complex ![]() $Q_2(n,p)$ and the random graph
$Q_2(n,p)$ and the random graph ![]() $Q\left (n,p^4\right )$. In Section 2.3 we summarise some estimates from [Reference Erdős and Spencer14] that we need about the random graph
$Q\left (n,p^4\right )$. In Section 2.3 we summarise some estimates from [Reference Erdős and Spencer14] that we need about the random graph ![]() $Q(n,p)$. In Section 2.4 we make estimates for the existence of maximal
$Q(n,p)$. In Section 2.4 we make estimates for the existence of maximal ![]() $1$-faces and use these to deduce Theorem 1.2 from Theorem 1.3.
$1$-faces and use these to deduce Theorem 1.2 from Theorem 1.3.
In Section 3 we introduce an algorithm for identifying contractible ![]() $4$-cycles in
$4$-cycles in ![]() $\pi _1$. This algorithm reduces the analysis of
$\pi _1$. This algorithm reduces the analysis of ![]() $\pi _1$ to determining the topology of small subcomplexes. We also finish the proof of Theorem 1.2 and give a proof of Theorem 1.3.
$\pi _1$ to determining the topology of small subcomplexes. We also finish the proof of Theorem 1.2 and give a proof of Theorem 1.3.
In Section 4 we show a general structure theorem that describes the free-product factorisation of ![]() $\pi _1(Q_2(n,p))$, and we then prove Theorem 1.7. In Section 5 we construct specific complexes which show that certain interesting free factors appear.
$\pi _1(Q_2(n,p))$, and we then prove Theorem 1.7. In Section 5 we construct specific complexes which show that certain interesting free factors appear.
2 Preliminaries
2.1 The edge-path group
For subcomplexes Q of ![]() $Q^n$, the fundamental group
$Q^n$, the fundamental group ![]() $\pi _1(Q)$ has a nice combinatorial definition as the edge-path group, which we now define.
$\pi _1(Q)$ has a nice combinatorial definition as the edge-path group, which we now define.
Say that two edges (![]() $1$-faces) of
$1$-faces) of ![]() $Q^n$ are adjacent if they intersect at a vertex. An edge path in
$Q^n$ are adjacent if they intersect at a vertex. An edge path in ![]() $Q^n$ is defined to be a sequence of edges in which every consecutive pair are adjacent.
$Q^n$ is defined to be a sequence of edges in which every consecutive pair are adjacent.
In ![]() $Q^n$, any
$Q^n$, any ![]() $2$-face has a
$2$-face has a ![]() $4$-cycle as its boundary. Conversely, every
$4$-cycle as its boundary. Conversely, every ![]() $4$-cycle in
$4$-cycle in ![]() $Q^n$ is the boundary of a
$Q^n$ is the boundary of a ![]() $2$-face. Hence, any two adjacent edges are contained in a unique
$2$-face. Hence, any two adjacent edges are contained in a unique ![]() $2$-face and therefore in a unique
$2$-face and therefore in a unique ![]() $4$-cycle in
$4$-cycle in ![]() $Q^n$.
$Q^n$.
Two edge paths in Q are said to be edge-equivalent if one can be obtained from the other by successively doing one of the following moves:
1) Replacing two consecutive adjacent edges by the two opposite edges of the
 $4$-cycle x that contains them, if the
$4$-cycle x that contains them, if the  $2$-face that bounds x is in Q
$2$-face that bounds x is in Q2) Replacing one edge contained in a
 $4$-cycle x with the other three consecutive edges in x, if the
$4$-cycle x with the other three consecutive edges in x, if the  $2$-face that bounds x is in Q
$2$-face that bounds x is in Q3) Replacing three consecutive edges in a
 $4$-cycle x with the complementary edge in x, if the
$4$-cycle x with the complementary edge in x, if the  $2$-face that bounds x is in Q
$2$-face that bounds x is in Q4) Removing an edge that appears twice consecutively or adding an edge that appears twice consecutively
Define ![]() $\overline {0}$ to be the vector with only zero entries in
$\overline {0}$ to be the vector with only zero entries in ![]() $Q^n_0$. An edge loop at
$Q^n_0$. An edge loop at ![]() $\overline {0}$ is an edge path starting and ending at
$\overline {0}$ is an edge path starting and ending at ![]() $\overline {0}$. The edge-path group
$\overline {0}$. The edge-path group ![]() $\pi _1(Q)$ of a complex
$\pi _1(Q)$ of a complex ![]() $Q \subset Q^n$ (for any
$Q \subset Q^n$ (for any ![]() $n\geq 1$) is defined as the set of edge-equivalence classes of edge loops at
$n\geq 1$) is defined as the set of edge-equivalence classes of edge loops at ![]() $\overline {0}$ (with product and inverse defined by concatenation and reversal of edge loops).
$\overline {0}$ (with product and inverse defined by concatenation and reversal of edge loops).
For random cubical complexes ![]() $Q \sim Q_2(n,p)$, we explore first the extremal cases. If
$Q \sim Q_2(n,p)$, we explore first the extremal cases. If ![]() $p=0$, then any
$p=0$, then any ![]() $Q \sim Q_2(n,p)$ is equal to
$Q \sim Q_2(n,p)$ is equal to ![]() $Q^n_1$ – that is, with a probability of
$Q^n_1$ – that is, with a probability of ![]() $1$, the complex Q has not a single
$1$, the complex Q has not a single ![]() $2$-face included. Observing that in any graph G the number of independent generators in
$2$-face included. Observing that in any graph G the number of independent generators in ![]() $\pi _1(G)$ is equal to
$\pi _1(G)$ is equal to ![]() $E(G)-V(G)+1$, in the case of an element
$E(G)-V(G)+1$, in the case of an element ![]() $Q \sim Q_2(n,p)$ we get
$Q \sim Q_2(n,p)$ we get
which implies that the number of independent generators in ![]() $\pi _1(Q)$ will be at most
$\pi _1(Q)$ will be at most ![]() $2^{n-1}(n-2)+1$. Thus, when
$2^{n-1}(n-2)+1$. Thus, when ![]() $p=0$ we have that
$p=0$ we have that ![]() $\pi _1(Q)$ is a free group with
$\pi _1(Q)$ is a free group with ![]() $2^{n-1}(n-2)+1$ independent generators, and this is the maximum number of independent generators that the edge-path group of a random
$2^{n-1}(n-2)+1$ independent generators, and this is the maximum number of independent generators that the edge-path group of a random ![]() $2$-cubical complex can attain. This number of independent generators is less than the total number of
$2$-cubical complex can attain. This number of independent generators is less than the total number of ![]() $4$-cycles in
$4$-cycles in ![]() $Q^n$, which is
$Q^n$, which is ![]() $2^{n-3}n(n-1)$. If
$2^{n-3}n(n-1)$. If ![]() $p=1$, then any
$p=1$, then any ![]() $Q \sim Q_2(n,p)$ will have all the
$Q \sim Q_2(n,p)$ will have all the ![]() $2$-faces included, which implies that
$2$-faces included, which implies that ![]() $\pi _1(Q)=0$ with a probability of
$\pi _1(Q)=0$ with a probability of ![]() $1$.
$1$.
2.2 Star notation and the parallel relation
In ![]() $Q^n$, the four vertices belonging to a
$Q^n$, the four vertices belonging to a ![]() $4$-cycle have
$4$-cycle have ![]() $n-2$ equal entries and two coordinate entries that are not equal in all of them. Denote these nonequal coordinate entries as i and j; then we can uniquely represent a
$n-2$ equal entries and two coordinate entries that are not equal in all of them. Denote these nonequal coordinate entries as i and j; then we can uniquely represent a ![]() $4$-cycle using an n-tuple with
$4$-cycle using an n-tuple with ![]() $n-2$ fixed binary values and two
$n-2$ fixed binary values and two ![]() $*$s. One
$*$s. One ![]() $*$ will be located on coordinate i and the other will be located on coordinate j. As an example, the
$*$ will be located on coordinate i and the other will be located on coordinate j. As an example, the ![]() $4$-cycles of
$4$-cycles of ![]() $Q^3$ are
$Q^3$ are ![]() $\{(0,*,*), (*,1,*), (*,*,1), (*,0,*), (1,*,*), (*,*,0)\}$, with, for instance,
$\{(0,*,*), (*,1,*), (*,*,1), (*,0,*), (1,*,*), (*,*,0)\}$, with, for instance, ![]() $(*,*,0)=\{(1,1,0), (1,0,0), (0,1,0), (0,0,0)\}$.
$(*,*,0)=\{(1,1,0), (1,0,0), (0,1,0), (0,0,0)\}$.
For dice, physical realisations of the cube ![]() $Q^3$, we have a physical intuitive notion of parallel faces; there are three pairs of parallel faces, and if the die is fair, each pair should add up to
$Q^3$, we have a physical intuitive notion of parallel faces; there are three pairs of parallel faces, and if the die is fair, each pair should add up to ![]() $7$. Using the
$7$. Using the ![]() $*$ notation of
$*$ notation of ![]() $4$-cycles just introduced, we extend this notion of parallel faces to
$4$-cycles just introduced, we extend this notion of parallel faces to ![]() $Q^n$:
$Q^n$:
Definition 2.1. Two ![]() $4$-cycles in
$4$-cycles in ![]() $Q^n$ are parallel if they have the two
$Q^n$ are parallel if they have the two ![]() $*$s in the same entries, and if their Hamming distance is
$*$s in the same entries, and if their Hamming distance is ![]() $1$.
$1$.
Thus, in ![]() $Q^3$ (the cube), there are three pairs of parallel
$Q^3$ (the cube), there are three pairs of parallel ![]() $4$-cycles:
$4$-cycles: ![]() $(0,*,*)$ and
$(0,*,*)$ and ![]() $(1,*,*)$, the
$(1,*,*)$, the ![]() $4$-cycles
$4$-cycles ![]() $(0,*,*)$ and
$(0,*,*)$ and ![]() $(1,*,*)$, and the
$(1,*,*)$, and the ![]() $4$-cycles
$4$-cycles ![]() $(0,*,*)$ and
$(0,*,*)$ and ![]() $(1,*,*)$. With this parallel notion, we are able to define a binary relation in the set of
$(1,*,*)$. With this parallel notion, we are able to define a binary relation in the set of ![]() $4$-cycles of a random
$4$-cycles of a random ![]() $2$-cubical complex.
$2$-cubical complex.
We represent a ![]() $3$-dimensional cube in
$3$-dimensional cube in ![]() $Q^n$ with a vector with n entries, three of which have a fixed
$Q^n$ with a vector with n entries, three of which have a fixed ![]() $*$ and the rest of which are binary numbers. If we have two parallel faces x and y that have
$*$ and the rest of which are binary numbers. If we have two parallel faces x and y that have ![]() $*$ in the i and j coordinates and differ (only) in the binary value of the k coordinate, then the cube that contains them is represented by a vector with the three fixed
$*$ in the i and j coordinates and differ (only) in the binary value of the k coordinate, then the cube that contains them is represented by a vector with the three fixed ![]() $*$s in entries
$*$s in entries ![]() $i, j, k$ and with the rest of the
$i, j, k$ and with the rest of the ![]() $n-3$ entries equal to the entries of x (which are also equal to the entries of y).
$n-3$ entries equal to the entries of x (which are also equal to the entries of y).
Observe that the other four ![]() $4$-cycles of the cube will have all the entries that are not i, j, or k equal to the entries of x, two
$4$-cycles of the cube will have all the entries that are not i, j, or k equal to the entries of x, two ![]() $*$s in positions either
$*$s in positions either ![]() $\{i,k\}$ or
$\{i,k\}$ or ![]() $\{j,k\}$ and a binary number in the remaining coordinate. Also, given two parallel
$\{j,k\}$ and a binary number in the remaining coordinate. Also, given two parallel ![]() $2$-faces in
$2$-faces in ![]() $Q^n$, there is a unique
$Q^n$, there is a unique ![]() $3$-dimensional cube in
$3$-dimensional cube in ![]() $Q^n$ that contains them.
$Q^n$ that contains them.
Definition 2.2. Given a subcomplex Q of ![]() $Q^n$, two parallel
$Q^n$, two parallel ![]() $4$-cycles
$4$-cycles ![]() $x, y \in Q$ are related if the (unique)
$x, y \in Q$ are related if the (unique) ![]() $3$-dimensional cube that contains them has a
$3$-dimensional cube that contains them has a ![]() $2$-face attached to each one of the other four
$2$-face attached to each one of the other four ![]() $4$-cycles in the cube. We represent this by
$4$-cycles in the cube. We represent this by ![]() $x \parallel y$.
$x \parallel y$.
Lemma 2.3. If two ![]() $4$-cycles x and y are related (
$4$-cycles x and y are related (![]() $x \parallel y$), then they are edge-equivalent.
$x \parallel y$), then they are edge-equivalent.
Definition 2.4 Graph of parallel related  $4$-cycles
$4$-cycles
Given a subcomplex Q of ![]() $Q^n$, we define its graph of parallel cycles, which we represent by
$Q^n$, we define its graph of parallel cycles, which we represent by ![]() $G[Q]$, as the graph with set of vertices
$G[Q]$, as the graph with set of vertices ![]() $V^n$ whose elements are all the the
$V^n$ whose elements are all the the ![]() $4$-cycles in
$4$-cycles in ![]() $Q^n$ (there are
$Q^n$ (there are ![]() $2^{n-3}n(n-1)\, 4$-cycles), and an edge between two of them if they are related by
$2^{n-3}n(n-1)\, 4$-cycles), and an edge between two of them if they are related by ![]() $\parallel $.
$\parallel $.
Observe that ![]() $\parallel $ is reflexive but not transitive. This implies, for instance, that
$\parallel $ is reflexive but not transitive. This implies, for instance, that  $G\left [Q^n_2\right ]$ (remember that
$G\left [Q^n_2\right ]$ (remember that ![]() $Q^n_2$ is the
$Q^n_2$ is the ![]() $2$-skeleton of
$2$-skeleton of ![]() $Q^n$) is not the complete graph. We can completely characterise
$Q^n$) is not the complete graph. We can completely characterise  $G\left [Q^n_2\right ]$.
$G\left [Q^n_2\right ]$.
Lemma 2.5. The graph  $G\left [Q^n_2\right ]$ has
$G\left [Q^n_2\right ]$ has ![]() $\binom {n}{2}$ components, and each one of these components is isomorphic to a
$\binom {n}{2}$ components, and each one of these components is isomorphic to a  $Q^{n-2}_1$ graph.
$Q^{n-2}_1$ graph.
Proof. Fix an ![]() $n>0$. By definition of the relation
$n>0$. By definition of the relation ![]() $\parallel $, a necessary condition for two
$\parallel $, a necessary condition for two ![]() $4$-cycles to be related is to have their two
$4$-cycles to be related is to have their two ![]() $*$s in the same position. There are
$*$s in the same position. There are ![]() $\binom {n}{2}$ ways of choosing the positions of two
$\binom {n}{2}$ ways of choosing the positions of two ![]() $*$s in a vector of size n, which implies that there are at most
$*$s in a vector of size n, which implies that there are at most ![]() $\binom {n}{2}$ components in
$\binom {n}{2}$ components in  $G\left [Q^n_2\right ]$. This gives us a partition of the set of vertices, which we represent by
$G\left [Q^n_2\right ]$. This gives us a partition of the set of vertices, which we represent by
 $$ \begin{align*} V^n=\bigcup _{i=1}^{\binom{n}{2}} V_i^n. \\[-17pt] \end{align*} $$
$$ \begin{align*} V^n=\bigcup _{i=1}^{\binom{n}{2}} V_i^n. \\[-17pt] \end{align*} $$ Set ![]() $1\leq i\leq {\binom {n}{2}}$; in what follows we prove that the induced subgraph of
$1\leq i\leq {\binom {n}{2}}$; in what follows we prove that the induced subgraph of ![]() $V^n_i$ in
$V^n_i$ in  $G\left [Q^n_2\right ]$ is isomorphic to
$G\left [Q^n_2\right ]$ is isomorphic to  $Q^{n-2}_1$. Any element in
$Q^{n-2}_1$. Any element in ![]() $V^n_i$ has the two
$V^n_i$ has the two ![]() $*$s in the same position, and the rest of the
$*$s in the same position, and the rest of the ![]() $n-2$ entries have all possible binary entries. This implies that
$n-2$ entries have all possible binary entries. This implies that  $\left \lvert V^n_{i}\right \rvert = \left \lvert Q_0^{n-2}\right \rvert $. Let
$\left \lvert V^n_{i}\right \rvert = \left \lvert Q_0^{n-2}\right \rvert $. Let  $\phi : V^n_{i} \to Q_0^{n-2}$ be the natural bijection between these two sets of vertices. It is clear from Definition 2.3 that two
$\phi : V^n_{i} \to Q_0^{n-2}$ be the natural bijection between these two sets of vertices. It is clear from Definition 2.3 that two ![]() $4$-cycles x and y in
$4$-cycles x and y in ![]() $V^n_{i}$ are connected in
$V^n_{i}$ are connected in  $G\!\left [Q^n_2\right ]$ if and only if the Hamming distance of
$G\!\left [Q^n_2\right ]$ if and only if the Hamming distance of ![]() $\phi (x)$ and
$\phi (x)$ and ![]() $\phi (y)$ is
$\phi (y)$ is ![]() $1$. This implies that
$1$. This implies that  $G\left [V_i^{n}\right ] \equiv Q^{n-2}_1$.
$G\left [V_i^{n}\right ] \equiv Q^{n-2}_1$.
In this paper we restrict ourselves to complexes ![]() $Q \sim Q_2(n,p)$, and thus the graphs
$Q \sim Q_2(n,p)$, and thus the graphs ![]() $G[Q]$ that we analyse are always subgraphs of
$G[Q]$ that we analyse are always subgraphs of  $G\left [Q^n_2\right ]$. We say that a vertex in
$G\left [Q^n_2\right ]$. We say that a vertex in ![]() $V^n$ is coloured if the
$V^n$ is coloured if the ![]() $4$-cycle that it represents has its
$4$-cycle that it represents has its ![]() $2$-face present in Q, and we say that it is not coloured otherwise. We use the previous established partition of
$2$-face present in Q, and we say that it is not coloured otherwise. We use the previous established partition of ![]() $V^n$ in
$V^n$ in ![]() $\binom {n}{2}$ sets to denote accordingly the induced subgraphs
$\binom {n}{2}$ sets to denote accordingly the induced subgraphs  $G_1, \dotsc , G_{\binom {n}{2}}$ of the graph
$G_1, \dotsc , G_{\binom {n}{2}}$ of the graph  $G\left [Q^n_2\right ]$. For a
$G\left [Q^n_2\right ]$. For a ![]() $Q \sim Q_2(n,p)$, this partition defines
$Q \sim Q_2(n,p)$, this partition defines ![]() $\binom {n}{2}$ random subgraphs, which we represent by
$\binom {n}{2}$ random subgraphs, which we represent by  $G_1[Q], \dotsc , G_{\binom {n}{2}}[Q]$. Then the edges that are included in
$G_1[Q], \dotsc , G_{\binom {n}{2}}[Q]$. Then the edges that are included in ![]() $G_i[Q]$, for
$G_i[Q]$, for ![]() $1 \leq i\leq {\binom {n}{2}}$, depend on the
$1 \leq i\leq {\binom {n}{2}}$, depend on the ![]() $2$-faces included in Q. The next lemma characterises the probability distribution of each
$2$-faces included in Q. The next lemma characterises the probability distribution of each ![]() $G_i[Q]$:
$G_i[Q]$:
Lemma 2.6. Set ![]() $p \in (0,1)$ and let
$p \in (0,1)$ and let ![]() $Q \sim Q_2(n,p)$. Then for
$Q \sim Q_2(n,p)$. Then for ![]() $1 \leq i\leq {\binom {n}{2}}$, each random graph
$1 \leq i\leq {\binom {n}{2}}$, each random graph ![]() $G_i[Q]$ is a random graph on
$G_i[Q]$ is a random graph on  $Q^{n-2}_1$, with each edge included independently with probability
$Q^{n-2}_1$, with each edge included independently with probability ![]() $p^4$ and each vertex coloured independently with probability p. Moreover, the vertex colourings are independent of the edge set. Using the notation established in the Introduction, the uncoloured graph
$p^4$ and each vertex coloured independently with probability p. Moreover, the vertex colourings are independent of the edge set. Using the notation established in the Introduction, the uncoloured graph ![]() $G_i[Q]$ has the same distribution as
$G_i[Q]$ has the same distribution as ![]() $Q\left (n-2,p^4\right )$ for all
$Q\left (n-2,p^4\right )$ for all ![]() $1 \leq i\leq {\binom {n}{2}}$.
$1 \leq i\leq {\binom {n}{2}}$.
Proof. Set ![]() $Q \sim Q_2(n,p)$. From Lemma 2.5, we know that each
$Q \sim Q_2(n,p)$. From Lemma 2.5, we know that each ![]() $G_i[Q]$ is a random graph on
$G_i[Q]$ is a random graph on  $Q^{n-2}_1$. Let x and y be two vertices in
$Q^{n-2}_1$. Let x and y be two vertices in ![]() $G_i[Q]$ that are connected in
$G_i[Q]$ that are connected in ![]() $G[Q^n_2]$, and represent this edge by
$G[Q^n_2]$, and represent this edge by ![]() $\overline {xy}$. This implies in particular that x and y are
$\overline {xy}$. This implies in particular that x and y are ![]() $4$-cycles that have, with the previously defined star notation, the
$4$-cycles that have, with the previously defined star notation, the ![]() $*$ in the same entries and Hamming distance equal to
$*$ in the same entries and Hamming distance equal to ![]() $1$. Let
$1$. Let ![]() $c_{\overline {xy}} \in Q^n$ be the unique
$c_{\overline {xy}} \in Q^n$ be the unique ![]() $3$-dimensional cube that contains x and y.
$3$-dimensional cube that contains x and y.
The probability of ![]() $\overline {xy}$ being an edge in
$\overline {xy}$ being an edge in ![]() $G_i[Q]$ is equal to the probability of the other
$G_i[Q]$ is equal to the probability of the other ![]() $4$-cycles in
$4$-cycles in ![]() $c_{\overline {xy}}$ being covered by
$c_{\overline {xy}}$ being covered by ![]() $2$-faces in Q. This event happens with probability
$2$-faces in Q. This event happens with probability ![]() $p^4$ because in
$p^4$ because in ![]() $Q_2(n,p)$ each
$Q_2(n,p)$ each ![]() $2$-face is added independently with probability p.
$2$-face is added independently with probability p.
Moreover, observe that any of these ![]() $4$-cycles in
$4$-cycles in ![]() $c_{\overline {xy}}$ are not vertices in
$c_{\overline {xy}}$ are not vertices in ![]() $G_i[Q]$, because they do not have the two
$G_i[Q]$, because they do not have the two ![]() $*$s in the same location as x (or y). This implies the independence between the colouring of the vertices and the inclusion of the edges in
$*$s in the same location as x (or y). This implies the independence between the colouring of the vertices and the inclusion of the edges in ![]() $G_i[Q]$.
$G_i[Q]$.
Let ![]() $\mathcal {C}$ be the set of all
$\mathcal {C}$ be the set of all ![]() $3$-dimensional cubes
$3$-dimensional cubes ![]() $c_{\overline {xy}}$ with x and y varying among all unordered pairs of vertices in
$c_{\overline {xy}}$ with x and y varying among all unordered pairs of vertices in ![]() $G_i[Q]$ that are connected in
$G_i[Q]$ that are connected in  $G\left [Q^n_2\right ]$. Then, by the uniqueness of the cube
$G\left [Q^n_2\right ]$. Then, by the uniqueness of the cube ![]() $c_{\overline {xy}} \in Q^n$, we have that
$c_{\overline {xy}} \in Q^n$, we have that ![]() $\lvert \mathcal {C} \rvert $ is equal to the number of edges in
$\lvert \mathcal {C} \rvert $ is equal to the number of edges in ![]() $G_i[Q]$. Finally, edges in
$G_i[Q]$. Finally, edges in ![]() $G_i[Q]$ are added independently with probability
$G_i[Q]$ are added independently with probability ![]() $p^4$ because each
$p^4$ because each ![]() $4$-face in a cube in
$4$-face in a cube in ![]() $\mathcal {C}$ appears in only one
$\mathcal {C}$ appears in only one ![]() $3$-dimensional cube in
$3$-dimensional cube in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Remark. Even if the edges within each subgraph ![]() $G_i[Q]$ of the graph
$G_i[Q]$ of the graph ![]() $G[Q]$ are included independently with probability
$G[Q]$ are included independently with probability ![]() $p^4$, this independence does not extend to events related to edges selected from two or more of the subgraphs
$p^4$, this independence does not extend to events related to edges selected from two or more of the subgraphs ![]() $G_i[Q]$. An illustrative example of this dependence can be easily seen in the
$G_i[Q]$. An illustrative example of this dependence can be easily seen in the ![]() $3$-dimensional cube where there is only one cube containing all the
$3$-dimensional cube where there is only one cube containing all the ![]() $4$-cycles.
$4$-cycles.
2.3 The sizes of the components of  $Q(n,p)$
$Q(n,p)$
For a given ![]() $p \in (0,1)$, we want to understand the sizes of the components of
$p \in (0,1)$, we want to understand the sizes of the components of ![]() $Q(n,p)$. We will require an argument from [Reference Erdős and Spencer14] that rules out components of small sizes. Because we slightly adapt those lemmas, we include proofs.
$Q(n,p)$. We will require an argument from [Reference Erdős and Spencer14] that rules out components of small sizes. Because we slightly adapt those lemmas, we include proofs.
Denote by ![]() $\mathscr {Q}_s$ the set of all subsets of vertices in
$\mathscr {Q}_s$ the set of all subsets of vertices in ![]() $Q^n$ which are connected and have cardinality s. Given a subset S of vertices in
$Q^n$ which are connected and have cardinality s. Given a subset S of vertices in ![]() $Q^n$ that are connected, define
$Q^n$ that are connected, define
Let
 $$ \begin{align} g(s)= \sum_{S\in \mathscr{Q}_s}(1-p)^{b(S)}. \end{align} $$
$$ \begin{align} g(s)= \sum_{S\in \mathscr{Q}_s}(1-p)^{b(S)}. \end{align} $$Then from a union bound, ![]() $g(s)$ is an upper bound for the probability of the existence of a connected component on s vertices appearing in
$g(s)$ is an upper bound for the probability of the existence of a connected component on s vertices appearing in ![]() $Q(n,p)$.
$Q(n,p)$.
Lemma 2.7. We have
 $$ \begin{align} g(s)\leq 2^n(ns)^s(1-p)^{s\left(n-\left\lfloor\log_2(s)\right\rfloor\right)}. \end{align} $$
$$ \begin{align} g(s)\leq 2^n(ns)^s(1-p)^{s\left(n-\left\lfloor\log_2(s)\right\rfloor\right)}. \end{align} $$Proof. Set ![]() $s \geq 1$; then for any
$s \geq 1$; then for any ![]() $S \in \mathscr {Q}_s$ we have (from [Reference Hart16])
$S \in \mathscr {Q}_s$ we have (from [Reference Hart16])
Also, using the fact that the degree of each vertex of ![]() $Q^n$ is at most n,
$Q^n$ is at most n,
Hence,
 $$ \begin{align} g(s)\leq \sum_{S\in \mathscr{Q}_s}(1-p)^{ s\left(n-\left\lfloor \log_2(s)\right\rfloor \right)} \leq 2^n(ns)^s (1-p)^{ s\left(n-\left\lfloor \log_2(s)\right\rfloor\right)}. \\[-36pt]\nonumber \end{align} $$
$$ \begin{align} g(s)\leq \sum_{S\in \mathscr{Q}_s}(1-p)^{ s\left(n-\left\lfloor \log_2(s)\right\rfloor \right)} \leq 2^n(ns)^s (1-p)^{ s\left(n-\left\lfloor \log_2(s)\right\rfloor\right)}. \\[-36pt]\nonumber \end{align} $$Lemma 2.8. For any ![]() $p \in (0,1)$, there is a number
$p \in (0,1)$, there is a number ![]() $T_p \in \mathbb {N}$ and there exist
$T_p \in \mathbb {N}$ and there exist ![]() $\delta $,
$\delta $, ![]() $\epsilon>0$ such that
$\epsilon>0$ such that
 $$ \begin{align} \sum_{s} g(s)<2^{-\delta n} \end{align} $$
$$ \begin{align} \sum_{s} g(s)<2^{-\delta n} \end{align} $$with the sum over all s such that ![]() $T_p\leq s\leq 2^{\epsilon n}$.
$T_p\leq s\leq 2^{\epsilon n}$.
Proof. Let ![]() $T_p$ be defined by
$T_p$ be defined by
 $$ \begin{align*} T_p = \inf_{T \in \mathbb{N}} \left\{ 2\cdot (1-p)^T \right\} < 1. \end{align*} $$
$$ \begin{align*} T_p = \inf_{T \in \mathbb{N}} \left\{ 2\cdot (1-p)^T \right\} < 1. \end{align*} $$ Then for ![]() $s \leq 2^{\epsilon n}$, by Lemma 2.7,
$s \leq 2^{\epsilon n}$, by Lemma 2.7,
 $$ \begin{align*} g(s) \leq 2^n(ns)^s(1-p)^{s\left(n-\left\lfloor\log_2(s)\right\rfloor\right)} \leq 2^n(1-p)^{-2\epsilon n} (n 2^{\epsilon n}(1-p)^{n})^s \end{align*} $$
$$ \begin{align*} g(s) \leq 2^n(ns)^s(1-p)^{s\left(n-\left\lfloor\log_2(s)\right\rfloor\right)} \leq 2^n(1-p)^{-2\epsilon n} (n 2^{\epsilon n}(1-p)^{n})^s \end{align*} $$for all n sufficiently large. Then
 $$ \begin{align*} \sum_{s=T_p}^{\lfloor 2^{\epsilon n}\rfloor} g(s) &\leq 2^n(1-p)^{-2\epsilon n} \sum_{s=T_p}^\infty (n 2^{\epsilon n}(1-p)^{n})^s \\ &\leq 2^n(1-p)^{-2\epsilon n} (n 2^{\epsilon n}(1-p)^{n})^{T_p}(1+o(1)), \end{align*} $$
$$ \begin{align*} \sum_{s=T_p}^{\lfloor 2^{\epsilon n}\rfloor} g(s) &\leq 2^n(1-p)^{-2\epsilon n} \sum_{s=T_p}^\infty (n 2^{\epsilon n}(1-p)^{n})^s \\ &\leq 2^n(1-p)^{-2\epsilon n} (n 2^{\epsilon n}(1-p)^{n})^{T_p}(1+o(1)), \end{align*} $$provided ![]() $\epsilon $ is chosen so that
$\epsilon $ is chosen so that ![]() $2^\epsilon (1-p) <1$ and n is taken large. Taking
$2^\epsilon (1-p) <1$ and n is taken large. Taking ![]() $\epsilon $ sufficiently small,
$\epsilon $ sufficiently small,
Hence, in terms of ![]() $\alpha $,
$\alpha $,
 $$ \begin{align*} \sum_{s=T_p}^{\left\lfloor 2^{\epsilon d}\right\rfloor} g(s) \leq \alpha^n n^{T_p} (1+o(1)) \leq 2^{-\delta n} \end{align*} $$
$$ \begin{align*} \sum_{s=T_p}^{\left\lfloor 2^{\epsilon d}\right\rfloor} g(s) \leq \alpha^n n^{T_p} (1+o(1)) \leq 2^{-\delta n} \end{align*} $$for some ![]() $\delta> 0$ sufficiently small and all n sufficiently large.
$\delta> 0$ sufficiently small and all n sufficiently large.
2.4 The threshold for maximal  $1$-faces
$1$-faces
Any element ![]() $Q \sim Q_2(n,p)$ has
$Q \sim Q_2(n,p)$ has ![]() $2^{n-1}n$ edges, which we represent by
$2^{n-1}n$ edges, which we represent by
with each one of these edges being in ![]() $n-1$ different
$n-1$ different ![]() $4$-cycles. We represent by
$4$-cycles. We represent by ![]() $I_{i}$ the indicator function of the event that the edge
$I_{i}$ the indicator function of the event that the edge ![]() $e_i$ is maximal – that is, that none of the
$e_i$ is maximal – that is, that none of the ![]() $(n-1)\, 4$-cycles that contain
$(n-1)\, 4$-cycles that contain ![]() $e_i$ has an attached
$e_i$ has an attached ![]() $2$-face. Then
$2$-face. Then
Let ![]() $\mathcal {I}(Q)$ be the random variable that counts the number of maximal edges in Q:
$\mathcal {I}(Q)$ be the random variable that counts the number of maximal edges in Q:
 $$ \begin{align*} \mathcal{I}=\sum_{i=1}^{2^{n-1}n}I_i. \end{align*} $$
$$ \begin{align*} \mathcal{I}=\sum_{i=1}^{2^{n-1}n}I_i. \end{align*} $$Then
Observe that if ![]() $p=1/2$, then
$p=1/2$, then ![]() $\mathbb {E}[\mathcal {I}]=n$.
$\mathbb {E}[\mathcal {I}]=n$.
We now prove that Theorem 1.2 follows from Theorem 1.3:
Proof of Theorem 1.2. We first establish that for  $p> \tfrac 12$,
$p> \tfrac 12$, ![]() $\mathcal {I} = 0$ w.h.p., and for
$\mathcal {I} = 0$ w.h.p., and for  $p \leq \tfrac 12$,
$p \leq \tfrac 12$, ![]() $\mathcal {I} \geq 2$ w.h.p. For the first claim, the expectation (10) tends to
$\mathcal {I} \geq 2$ w.h.p. For the first claim, the expectation (10) tends to ![]() $0$. For the second, again from equation (10), if
$0$. For the second, again from equation (10), if ![]() $(1-p) \geq 1/2$ for a random
$(1-p) \geq 1/2$ for a random ![]() $2$-cubical complex,
$2$-cubical complex, ![]() $Q \sim Q_2(n,p)$, then
$Q \sim Q_2(n,p)$, then
Thus ![]() $\mathbb {E}[\mathcal {I}] \to \infty $ as
$\mathbb {E}[\mathcal {I}] \to \infty $ as ![]() $n \to \infty $. Now, we use a second moment argument (see [Reference Alon and Spencer1, Corollary 4.3.5]) to prove that
$n \to \infty $. Now, we use a second moment argument (see [Reference Alon and Spencer1, Corollary 4.3.5]) to prove that ![]() $\mathbb {P}[\mathcal {I} \geq 2]\to 1$ as
$\mathbb {P}[\mathcal {I} \geq 2]\to 1$ as ![]() $n\to \infty $.
$n\to \infty $.
Fix an edge ![]() $e_i$. Any other edge
$e_i$. Any other edge ![]() $e_j$ such that
$e_j$ such that ![]() $I_j$ is not independent from
$I_j$ is not independent from ![]() $I_i$ – we represent this nonindependent relation between edges
$I_i$ – we represent this nonindependent relation between edges ![]() $e_i$ and
$e_i$ and ![]() $e_j$ by
$e_j$ by ![]() $j \sim i$ – will be an edge of one and only one of the
$j \sim i$ – will be an edge of one and only one of the ![]() $(n-1)\, 4$-cycles that contain
$(n-1)\, 4$-cycles that contain ![]() $e_i$. There are
$e_i$. There are ![]() $3(n-1)$ such edges and
$3(n-1)$ such edges and  $\mathbb {P}\left [I_j \mid I_i\right ] = (1-p)^{n-2}$. If we define
$\mathbb {P}\left [I_j \mid I_i\right ] = (1-p)^{n-2}$. If we define  $\Delta ^*_i=\sum _{j\sim i} \mathbb {P}\left [I_j \mid I_i\right ]$, then
$\Delta ^*_i=\sum _{j\sim i} \mathbb {P}\left [I_j \mid I_i\right ]$, then
 $$ \begin{align*} \Delta^*_i=\sum_{j \sim i} \mathbb{P}\left[I_j\mid I_i\right]=3(n-1)(1-p)^{n-2}. \end{align*} $$
$$ \begin{align*} \Delta^*_i=\sum_{j \sim i} \mathbb{P}\left[I_j\mid I_i\right]=3(n-1)(1-p)^{n-2}. \end{align*} $$Thus ![]() $\Delta ^*_i=o(\mathbb {E}[I_n])$, which implies that
$\Delta ^*_i=o(\mathbb {E}[I_n])$, which implies that ![]() $\mathbb {P}[\mathcal {I}>n/2] \to 1$ as
$\mathbb {P}[\mathcal {I}>n/2] \to 1$ as ![]() $n \to \infty $.
$n \to \infty $.
Hence from Theorem 1.3, we have that for  $p> \tfrac 12$,
$p> \tfrac 12$, ![]() $\pi _1(Q_2(n,p))=0$ with high probability, and for any
$\pi _1(Q_2(n,p))=0$ with high probability, and for any  $p<\tfrac 12$,
$p<\tfrac 12$, ![]() $\pi _1(Q_2(n,p)) = G * \mathbb {Z} * \mathbb {Z}$ for some group G with high probability. The event that
$\pi _1(Q_2(n,p)) = G * \mathbb {Z} * \mathbb {Z}$ for some group G with high probability. The event that ![]() $Q_2(n,p)$ has such a free factorisation is a decreasing event, in that for any complex Q that satisfies
$Q_2(n,p)$ has such a free factorisation is a decreasing event, in that for any complex Q that satisfies ![]() $\pi _1(Q) = G * \mathbb {Z} * \mathbb {Z}$ for some group G, removing any
$\pi _1(Q) = G * \mathbb {Z} * \mathbb {Z}$ for some group G, removing any ![]() $2$-face (i.e., removing relations from
$2$-face (i.e., removing relations from ![]() $\pi _1(Q)$) yields a complex
$\pi _1(Q)$) yields a complex ![]() $Q'$ so that
$Q'$ so that ![]() $\pi _1(Q') = G' * \mathbb {Z} * \mathbb {Z}$ for some other group
$\pi _1(Q') = G' * \mathbb {Z} * \mathbb {Z}$ for some other group ![]() $G'$. It follows that for any
$G'$. It follows that for any  $p \leq \tfrac 12$,
$p \leq \tfrac 12$,
 $$ \begin{align*} \mathbb{P}[\exists~G: \pi_1(Q_2(n,p)) = G * \mathbb{Z} * \mathbb{Z}] \geq \mathbb{P}\left[\exists~G: \pi_1\left(Q_2\left(n,\tfrac12\right)\right) = G * \mathbb{Z} * \mathbb{Z}\right] \to 1 \end{align*} $$
$$ \begin{align*} \mathbb{P}[\exists~G: \pi_1(Q_2(n,p)) = G * \mathbb{Z} * \mathbb{Z}] \geq \mathbb{P}\left[\exists~G: \pi_1\left(Q_2\left(n,\tfrac12\right)\right) = G * \mathbb{Z} * \mathbb{Z}\right] \to 1 \end{align*} $$as ![]() $n \to \infty $, which completes the proof.
$n \to \infty $, which completes the proof.
3 Parallel homotopy algorithm
In this section, we introduce a simple iterative algorithm for finding contractible ![]() $4$-cycles. For
$4$-cycles. For ![]() $Q_2(n,p)$ with
$Q_2(n,p)$ with ![]() $p> 0$, this algorithm rapidly and dramatically simplifies the fundamental group to its nontrivial parts.
$p> 0$, this algorithm rapidly and dramatically simplifies the fundamental group to its nontrivial parts.
We begin by introducing the algorithm. We have defined ![]() $V^n$ as the set of all
$V^n$ as the set of all ![]() $4$-cycles in
$4$-cycles in ![]() $Q^n_1$. For any subset
$Q^n_1$. For any subset ![]() $V \subset V^n$, we define the graph of parallel related
$V \subset V^n$, we define the graph of parallel related ![]() $4$-cycles denoted by
$4$-cycles denoted by ![]() $G(V)$ in a similar fashion to Definition 2.4: the vertex set of
$G(V)$ in a similar fashion to Definition 2.4: the vertex set of ![]() $G(V)$ is given by the
$G(V)$ is given by the ![]() $V^n$, and two
$V^n$, and two ![]() $4$-cycles x and y are connected if they have
$4$-cycles x and y are connected if they have ![]() $*$s in the same positions and are contained in a
$*$s in the same positions and are contained in a ![]() $3$-cube c and all other
$3$-cube c and all other ![]() $4$-cycles in c are in V. That is, two
$4$-cycles in c are in V. That is, two ![]() $4$-cycles x and y are connected in
$4$-cycles x and y are connected in ![]() $G(V)$ if they are connected in
$G(V)$ if they are connected in ![]() $G[Q]$, with Q being the cubical complex
$G[Q]$, with Q being the cubical complex ![]() $Q \subset Q^n_{2}$ such that the
$Q \subset Q^n_{2}$ such that the ![]() $2$-faces included in Q are exactly those corresponding to the
$2$-faces included in Q are exactly those corresponding to the ![]() $4$-cycles that are in V.
$4$-cycles that are in V.
Given a ![]() $Q \sim Q_2(n,p)$, we denote by
$Q \sim Q_2(n,p)$, we denote by ![]() $V^n_1$ the subset of
$V^n_1$ the subset of ![]() $V^n$ which contains the boundaries of
$V^n$ which contains the boundaries of ![]() $2$-faces in Q. We then iteratively run the following procedure, with
$2$-faces in Q. We then iteratively run the following procedure, with ![]() $t \in \mathbb {N}$:
$t \in \mathbb {N}$:
Stage t: Build the graph of parallel related ![]() $4$-cycles
$4$-cycles ![]() $G\left (V^n_t\right )$. Define the set of
$G\left (V^n_t\right )$. Define the set of ![]() $4$-cycles
$4$-cycles ![]() $V^n_{t+1}$ as the set of
$V^n_{t+1}$ as the set of ![]() $4$-cycles that are in a component in
$4$-cycles that are in a component in ![]() $G\left (V^n_t\right )$ that contains a
$G\left (V^n_t\right )$ that contains a ![]() $4$-cycle in
$4$-cycle in ![]() $V^n_t$.
$V^n_t$.
The algorithm stops at the first t for which ![]() $V^n_{t+1}=V^n_t$. This will happen, in particular, if there exists a t such that
$V^n_{t+1}=V^n_t$. This will happen, in particular, if there exists a t such that ![]() $V^n_t=V^n$, in which case all
$V^n_t=V^n$, in which case all ![]() $4$-cycles of
$4$-cycles of ![]() $Q^n$ are in a component of
$Q^n$ are in a component of ![]() $G\left (V^n_t\right )$ that contains a
$G\left (V^n_t\right )$ that contains a ![]() $4$-cycle in
$4$-cycle in ![]() $V^n_t$. Thus, Theorem 1.2 follows from the following result:
$V^n_t$. Thus, Theorem 1.2 follows from the following result:
Theorem 3.1. For ![]() $p>1/2$,
$p>1/2$,
 $$ \begin{align*} \lim_{n \to \infty}\mathbb{P}\left[V^n_3=V^n\right]=1. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty}\mathbb{P}\left[V^n_3=V^n\right]=1. \end{align*} $$3.1 Stage 1: Explosive growth
For any set of ![]() $4$-cycles
$4$-cycles ![]() $V \subset V^n$, say that a set of vertices S in
$V \subset V^n$, say that a set of vertices S in ![]() $G(V)$ is a quasicomponent if S is connected in
$G(V)$ is a quasicomponent if S is connected in ![]() $G(V^n)$ and S is disconnected from its complement in
$G(V^n)$ and S is disconnected from its complement in ![]() $G(V)$.
$G(V)$.
Theorem 3.2. Set ![]() $Q \sim Q_2(n,p)$. For any
$Q \sim Q_2(n,p)$. For any ![]() $p \in (0,1)$, there exists an integer
$p \in (0,1)$, there exists an integer ![]() $T_p$ so that w.h.p. there is no quasicomponent of
$T_p$ so that w.h.p. there is no quasicomponent of  $G\left (V_1^n\right )$ bigger than
$G\left (V_1^n\right )$ bigger than ![]() $T_p$ that is disjoint from
$T_p$ that is disjoint from ![]() $V_1^n$.
$V_1^n$.
Proof. The proof will follow from two key steps. Let ![]() $A_s$ be the event that a quasicomponent of size s in
$A_s$ be the event that a quasicomponent of size s in  $G\left (V^n_1\right )$ exists.
$G\left (V^n_1\right )$ exists.
(Step i) For any
 $p \in (0,1)$, there exist an integer
$p \in (0,1)$, there exist an integer  $T_p$ and
$T_p$ and  $\epsilon ,\delta>0$ such that for all n sufficiently large, (11)
$\epsilon ,\delta>0$ such that for all n sufficiently large, (11) $$ \begin{align} \mathbb{P}\left[ \cup_{s=T_p}^{2^{\epsilon n}}A_s \right]<2^{-\delta n}. \end{align} $$
$$ \begin{align} \mathbb{P}\left[ \cup_{s=T_p}^{2^{\epsilon n}}A_s \right]<2^{-\delta n}. \end{align} $$(Step ii) For any
 $\epsilon> 0$, the probability that there exists a component of
$\epsilon> 0$, the probability that there exists a component of  $G\left (V_1^n\right )$ bigger than
$G\left (V_1^n\right )$ bigger than  $2^{\epsilon n}$ with no vertex in
$2^{\epsilon n}$ with no vertex in  $V^n_1$ tends to zero with n.
$V^n_1$ tends to zero with n.
We show first how to complete the proof from this point. We now suppose that there is no quasicomponent of  $G\left (V_1^n\right )$ of size between
$G\left (V_1^n\right )$ of size between ![]() $T_p$ and
$T_p$ and ![]() $2^{\epsilon n}$ for some integer
$2^{\epsilon n}$ for some integer ![]() $T_p$ and some
$T_p$ and some ![]() $\epsilon>0$, and we further suppose that there is no component of
$\epsilon>0$, and we further suppose that there is no component of  $G\left (V_1^n\right )$ of size
$G\left (V_1^n\right )$ of size ![]() $2^{\left (\epsilon /2\right )n}$ with no vertex in
$2^{\left (\epsilon /2\right )n}$ with no vertex in ![]() $V_1^n$.
$V_1^n$.
Let X be a minimal quasicomponent of  $G\left (V_1^n\right )$ which is bigger than
$G\left (V_1^n\right )$ which is bigger than ![]() $T_p$ and which is disjoint from
$T_p$ and which is disjoint from ![]() $V_1^n$, if it exists. Then the size of X must be at least
$V_1^n$, if it exists. Then the size of X must be at least ![]() $2^{\epsilon n}$. As it is so large (in particular larger than
$2^{\epsilon n}$. As it is so large (in particular larger than ![]() $2^{\left (\epsilon /2\right )n}$), it cannot be that X is connected. So we must be able to remove a connected component (say by building a spanning tree in
$2^{\left (\epsilon /2\right )n}$), it cannot be that X is connected. So we must be able to remove a connected component (say by building a spanning tree in ![]() $G(V)$ of X by connecting spanning trees of its components and removing a component which contains a leaf) to form a smaller quasicomponent
$G(V)$ of X by connecting spanning trees of its components and removing a component which contains a leaf) to form a smaller quasicomponent ![]() $X'$. The component we remove must be smaller than
$X'$. The component we remove must be smaller than ![]() $2^{\left (\epsilon /2\right )n}$, and so for all n sufficiently large, we conclude that
$2^{\left (\epsilon /2\right )n}$, and so for all n sufficiently large, we conclude that ![]() $X'$ is a strictly smaller quasicomponent of
$X'$ is a strictly smaller quasicomponent of  $G\left (V_1^n\right )$ which is bigger than
$G\left (V_1^n\right )$ which is bigger than ![]() $T_p$ and which is disjoint from
$T_p$ and which is disjoint from ![]() $V_1^n$ – a contradiction.
$V_1^n$ – a contradiction.
We turn to proving Step (i). For any s, we have ![]() $\mathbb {P}[A_s]\leq g(s)$ (recalling g from equation (4)), as
$\mathbb {P}[A_s]\leq g(s)$ (recalling g from equation (4)), as ![]() $g(s)$ is the expected number of quasicomponents of size s in
$g(s)$ is the expected number of quasicomponents of size s in ![]() $Q_2(n,p)$, and hence from a union bound,
$Q_2(n,p)$, and hence from a union bound,
 $$ \begin{align*} \mathbb{P}\left[ \cup_{s=T_p}^{2^{\epsilon n}}A_s \right] \leq \sum_{s} g(s), \end{align*} $$
$$ \begin{align*} \mathbb{P}\left[ \cup_{s=T_p}^{2^{\epsilon n}}A_s \right] \leq \sum_{s} g(s), \end{align*} $$with the sum over all ![]() $T_p \leq s \leq 2^{\epsilon n}$. The existence of
$T_p \leq s \leq 2^{\epsilon n}$. The existence of ![]() $\epsilon ,\delta ,T_p$ such that formula (11) holds is then a direct consequence of Lemma 2.8.
$\epsilon ,\delta ,T_p$ such that formula (11) holds is then a direct consequence of Lemma 2.8.
We turn to showing Step (ii). Let W be the event that there exists a component in  $G\left (V_1^n\right )$ of size greater than or equal than
$G\left (V_1^n\right )$ of size greater than or equal than ![]() $2^{\epsilon n}$ that does not intersect
$2^{\epsilon n}$ that does not intersect ![]() $V_1^n$. We show in what follows that
$V_1^n$. We show in what follows that ![]() $\mathbb {P}[W]\to 0$ as
$\mathbb {P}[W]\to 0$ as ![]() $n \to \infty $. First, we observe that
$n \to \infty $. First, we observe that  $G\left (V_1^n\right )=G[Q]$ and that the vertices in
$G\left (V_1^n\right )=G[Q]$ and that the vertices in ![]() $V_1^n$ are precisely the coloured vertices in
$V_1^n$ are precisely the coloured vertices in ![]() $G[Q]$, which by Lemma 2.6 are coloured independently with probability equal to p. For
$G[Q]$, which by Lemma 2.6 are coloured independently with probability equal to p. For ![]() $1 \leq i \leq {\binom {n}{2}}$, define
$1 \leq i \leq {\binom {n}{2}}$, define ![]() $W_i$ as the event that there exists in
$W_i$ as the event that there exists in ![]() $G_i[Q]$ a component of size greater than or equal to
$G_i[Q]$ a component of size greater than or equal to ![]() $2^{\epsilon n}$ that has all its vertices uncoloured. Thus, by Lemma 2.6,
$2^{\epsilon n}$ that has all its vertices uncoloured. Thus, by Lemma 2.6,
 $$ \begin{align} W = \bigcup_{i=1}^{\binom{n}{2}} W_i. \end{align} $$
$$ \begin{align} W = \bigcup_{i=1}^{\binom{n}{2}} W_i. \end{align} $$Set ![]() $1 \leq i \leq {\binom {n}{2}}$. Conditioned on knowing
$1 \leq i \leq {\binom {n}{2}}$. Conditioned on knowing ![]() $G_i[Q]$ – in particular on knowing that there are exactly l components with uncoloured vertices and with sizes
$G_i[Q]$ – in particular on knowing that there are exactly l components with uncoloured vertices and with sizes ![]() $s_1, s_2, \dotsc , s_l$ greater than
$s_1, s_2, \dotsc , s_l$ greater than ![]() $2^{\epsilon n}$ in
$2^{\epsilon n}$ in ![]() $G_i[Q]$ – we get
$G_i[Q]$ – we get
 $$ \begin{align} \mathbb{P}[W_i \mid G_i] \leq \sum_{k=1}^{l}(1-p)^{s_j}. \end{align} $$
$$ \begin{align} \mathbb{P}[W_i \mid G_i] \leq \sum_{k=1}^{l}(1-p)^{s_j}. \end{align} $$Observing that ![]() $s_1 + s_2 + \dotsb + s_l \leq 2^{n-2}$, it has to be the case that
$s_1 + s_2 + \dotsb + s_l \leq 2^{n-2}$, it has to be the case that ![]() $l\leq 2^{n-2}$, and because
$l\leq 2^{n-2}$, and because ![]() $(1-p)< 1$, we have
$(1-p)< 1$, we have ![]() $(1-p)^{s_{k}} \leq (1-p)^{2^{\epsilon n}}$ for all
$(1-p)^{s_{k}} \leq (1-p)^{2^{\epsilon n}}$ for all ![]() $1\leq k \leq l$. Thus from formula (13) we get
$1\leq k \leq l$. Thus from formula (13) we get
 $$ \begin{align} \mathbb{P}[W_i \mid G_i] \leq \sum_{k=1}^{l}(1-p)^{2^{\epsilon n}} \leq 2^{n-2}(1-p)^{2^{\epsilon n}}. \end{align} $$
$$ \begin{align} \mathbb{P}[W_i \mid G_i] \leq \sum_{k=1}^{l}(1-p)^{2^{\epsilon n}} \leq 2^{n-2}(1-p)^{2^{\epsilon n}}. \end{align} $$This implies that ![]() $ \mathbb {E}[\mathbb {P}[W_i \mid G_i]] \leq 2^{n-2}(1-p)^{2^{\epsilon n}}$, and thus
$ \mathbb {E}[\mathbb {P}[W_i \mid G_i]] \leq 2^{n-2}(1-p)^{2^{\epsilon n}}$, and thus
for all ![]() $1 \leq i \leq {\binom {n}{2}}$. Finally, by a union bound argument on equation (12) and inequality (15), we have that
$1 \leq i \leq {\binom {n}{2}}$. Finally, by a union bound argument on equation (12) and inequality (15), we have that
 $$ \begin{align} \mathbb{P}[W] \leq {\binom{n}{2}} 2^{n-2}(1-p)^{2^{\epsilon n}}, \end{align} $$
$$ \begin{align} \mathbb{P}[W] \leq {\binom{n}{2}} 2^{n-2}(1-p)^{2^{\epsilon n}}, \end{align} $$with
 $$ \begin{align} \lim_{n \to \infty} {\binom{n}{2}} 2^{n-2}(1-p)^{2^{\epsilon n}}= 0. \\[-36pt]\nonumber\end{align} $$
$$ \begin{align} \lim_{n \to \infty} {\binom{n}{2}} 2^{n-2}(1-p)^{2^{\epsilon n}}= 0. \\[-36pt]\nonumber\end{align} $$3.2 Stage 2: Only local defects remain
Let ![]() $\mathcal {F}$ be the event that there is no quasicomponent of
$\mathcal {F}$ be the event that there is no quasicomponent of  $G\left (V_1^n\right )$ bigger than
$G\left (V_1^n\right )$ bigger than ![]() $T_p$ that is disjoint from
$T_p$ that is disjoint from ![]() $V_1^n$. This event was shown to hold w.h.p. by Theorem 3.2.
$V_1^n$. This event was shown to hold w.h.p. by Theorem 3.2.
Lemma 3.3. In the event ![]() $\mathcal {F}$, any
$\mathcal {F}$, any ![]() $4$-cycle v with at least
$4$-cycle v with at least ![]() $T_p$ neighbors in
$T_p$ neighbors in  $G\left (V_2^n\right )$ is in
$G\left (V_2^n\right )$ is in ![]() $V_3^n$. Likewise, any
$V_3^n$. Likewise, any ![]() $4$-cycle v with at least
$4$-cycle v with at least ![]() $T_p$ neighbors in
$T_p$ neighbors in  $G\left (V_1^n\right )$ is in
$G\left (V_1^n\right )$ is in ![]() $V_2^n$.
$V_2^n$.
Proof. Suppose ![]() $\mathcal {F}$ holds, and let v be any
$\mathcal {F}$ holds, and let v be any ![]() $4$-cycle. Suppose that v has at least
$4$-cycle. Suppose that v has at least ![]() $T_p$ neighbors in
$T_p$ neighbors in  $G\left (V_1^n\right )$. Then the connected component of v in
$G\left (V_1^n\right )$. Then the connected component of v in ![]() $G(V_1^n)$ has at least
$G(V_1^n)$ has at least ![]() $T_p$ neighbors, and therefore this connected component intersects
$T_p$ neighbors, and therefore this connected component intersects ![]() $V_1^n$. It follows by the definition of
$V_1^n$. It follows by the definition of ![]() $V_2^n$ that
$V_2^n$ that ![]() $v \in V_2^n$.
$v \in V_2^n$.
Suppose now that v has at least ![]() $T_p$ neighbors in
$T_p$ neighbors in  $G\left (V_2^n\right )$. We would like to show that at least one of these neighbors is also in
$G\left (V_2^n\right )$. We would like to show that at least one of these neighbors is also in ![]() $V_2^n$, for then in the next step of the parallel transport algorithm, we would have
$V_2^n$, for then in the next step of the parallel transport algorithm, we would have ![]() $v \in V_3^n$. We may also suppose that v is not in a component of
$v \in V_3^n$. We may also suppose that v is not in a component of  $G\left (V_1^n\right )$ that intersects
$G\left (V_1^n\right )$ that intersects ![]() $V_1^n$, for if it is, then
$V_1^n$, for if it is, then ![]() $v \in V_2^n$ and we are done.
$v \in V_2^n$ and we are done.
Suppose by way of a contradiction that none of the neighbors of v is in ![]() $V_2^n$, which implies that each is in a component of
$V_2^n$, which implies that each is in a component of  $G\left (V_1^n\right )$ disjoint from
$G\left (V_1^n\right )$ disjoint from ![]() $V_1^n$. Hence the union of these components and the component of
$V_1^n$. Hence the union of these components and the component of  $G\left (V_1^n\right )$ containing v is a quasicomponent of
$G\left (V_1^n\right )$ containing v is a quasicomponent of  $G\left (V_1^n\right )$ that is disjoint from
$G\left (V_1^n\right )$ that is disjoint from ![]() $V_1^n$. Moreover, it is a quasicomponent which is larger than
$V_1^n$. Moreover, it is a quasicomponent which is larger than ![]() $T_p$, which is disjoint from
$T_p$, which is disjoint from ![]() $V_1^n$. This does not exist in
$V_1^n$. This does not exist in ![]() $\mathcal {F}$, and therefore v has a neighbor in
$\mathcal {F}$, and therefore v has a neighbor in ![]() $V_2^n$. Hence
$V_2^n$. Hence ![]() $v \in V_3^n$.
$v \in V_3^n$.
We will show that as a consequence of Lemma 3.3, in Stage 2 all those ![]() $4$-cycles whose every constituent edge has a high enough degree will be collapsed. For any p, define
$4$-cycles whose every constituent edge has a high enough degree will be collapsed. For any p, define
 $$ \begin{align} M_p =\inf_{M> 0} \mathbb{P} \left( \text{Binomial}\left( \lfloor M/4 \rfloor, p^3\right) < T_p\right) < \left(\tfrac{1}{2}\right)^{1/4}. \end{align} $$
$$ \begin{align} M_p =\inf_{M> 0} \mathbb{P} \left( \text{Binomial}\left( \lfloor M/4 \rfloor, p^3\right) < T_p\right) < \left(\tfrac{1}{2}\right)^{1/4}. \end{align} $$For any ![]() $1$-face f in
$1$-face f in ![]() $Q^n$, define
$Q^n$, define ![]() $\deg (f)$ as the number of
$\deg (f)$ as the number of ![]() $2$-faces in Q containing f. Call a
$2$-faces in Q containing f. Call a ![]() $1$-face of
$1$-face of ![]() $Q \sim Q_2(n,p)$ light if its degree is less than or equal to
$Q \sim Q_2(n,p)$ light if its degree is less than or equal to ![]() $M_p$; otherwise, call it heavy. We show that
$M_p$; otherwise, call it heavy. We show that ![]() $4$-cycles made from heavy edges are contracted in the second stage of the algorithm:
$4$-cycles made from heavy edges are contracted in the second stage of the algorithm:
Lemma 3.4. For any ![]() $p \in (0,1)$, with probability tending to
$p \in (0,1)$, with probability tending to ![]() $1$ as
$1$ as ![]() $n\to \infty $, every
$n\to \infty $, every ![]() $4$-cycle whose every
$4$-cycle whose every ![]() $1$-face is heavy is contained in
$1$-face is heavy is contained in ![]() $V_3^n$.
$V_3^n$.
We will introduce some additional notation for working with faces of Q. For two disjoint sets ![]() $U, W \subset [n]$, let
$U, W \subset [n]$, let ![]() $\left (U^*, W^1\right )$ denote the
$\left (U^*, W^1\right )$ denote the ![]() $\lvert U\rvert $-dimensional face of Q with
$\lvert U\rvert $-dimensional face of Q with ![]() $*$s in the positions given by U and
$*$s in the positions given by U and ![]() $1$s exactly in the positions given by W.
$1$s exactly in the positions given by W.
Using symmetry, it will be enough to analyse the ![]() $4$-cycle
$4$-cycle ![]() $\left (\{1,2\}^*, \emptyset ^1\right )$. With
$\left (\{1,2\}^*, \emptyset ^1\right )$. With ![]() $M_p$ from equation (18), define
$M_p$ from equation (18), define ![]() $\mathcal {E}$ as the event that all the
$\mathcal {E}$ as the event that all the ![]() $1$-faces in the
$1$-faces in the ![]() $4$-cycle
$4$-cycle ![]() $\left (\{1,2\}^*, \emptyset ^1\right )$ are heavy – that is,
$\left (\{1,2\}^*, \emptyset ^1\right )$ are heavy – that is,
 $$ \begin{align*} \mathcal{E} = & \left\{ \deg\left( \left(\{1\}^*, \emptyset^1\right)\right)> M_p, \deg\left( \left(\{1\}^*, \{2\}^1\right)\right) > M_p, \right. \\ & \ \ \left. \deg\left( \left(\{2\}^*, \emptyset^1\right)\right) > M_p, \deg\left( \left(\{2\}^*, \{1\}^1\right)\right) > M_p \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{E} = & \left\{ \deg\left( \left(\{1\}^*, \emptyset^1\right)\right)> M_p, \deg\left( \left(\{1\}^*, \{2\}^1\right)\right) > M_p, \right. \\ & \ \ \left. \deg\left( \left(\{2\}^*, \emptyset^1\right)\right) > M_p, \deg\left( \left(\{2\}^*, \{1\}^1\right)\right) > M_p \right\}. \end{align*} $$To prove Lemma 3.4, it suffices to show the following:
Lemma 3.5. For any ![]() $p \in (0,1)$, there is an
$p \in (0,1)$, there is an ![]() $\epsilon> 0$ such that
$\epsilon> 0$ such that
 $$ \begin{align*} \mathbb{P}\left[\mathcal{E} \cap \mathcal{F} \cap \left\{ \text{the degree of}\ \left( \{1,2\}^*,\emptyset^1\right)\ \text{in}\ G\left(V_2^n\right)\ \text{is less than}\ T_p\right\}\right] \leq n^{O(1)}2^{-(1+\epsilon)n}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left[\mathcal{E} \cap \mathcal{F} \cap \left\{ \text{the degree of}\ \left( \{1,2\}^*,\emptyset^1\right)\ \text{in}\ G\left(V_2^n\right)\ \text{is less than}\ T_p\right\}\right] \leq n^{O(1)}2^{-(1+\epsilon)n}. \end{align*} $$Proof. The possible neighbors of ![]() $\left ( \{1,2\}^*,\emptyset ^1\right )$ in
$\left ( \{1,2\}^*,\emptyset ^1\right )$ in ![]() $G(V^n)$ all have the form
$G(V^n)$ all have the form ![]() $\left ( \{1,2\}^*,\{j\}^1\right )$ for some
$\left ( \{1,2\}^*,\{j\}^1\right )$ for some ![]() $3 \leq j \leq n$. To have an edge between these
$3 \leq j \leq n$. To have an edge between these ![]() $4$-cycles in
$4$-cycles in  $G\left (V^n_2\right )$, we must have
$G\left (V^n_2\right )$, we must have
 $$ \begin{align*} &\left( \{1,j\}^*, \emptyset^1\right) \in V^n_2, \qquad \left( \{1,j\}^*, \{2\}^1\right) \in V^n_2, \\ &\left( \{2,j\}^*, \emptyset^1\right) \in V^n_2, \qquad \left( \{2,j\}^*, \{1\}^1\right) \in V^n_2. \end{align*} $$
$$ \begin{align*} &\left( \{1,j\}^*, \emptyset^1\right) \in V^n_2, \qquad \left( \{1,j\}^*, \{2\}^1\right) \in V^n_2, \\ &\left( \{2,j\}^*, \emptyset^1\right) \in V^n_2, \qquad \left( \{2,j\}^*, \{1\}^1\right) \in V^n_2. \end{align*} $$In the event ![]() $\mathcal {F}$, we must only lower-bound the degree of these
$\mathcal {F}$, we must only lower-bound the degree of these ![]() $4$-cycles in
$4$-cycles in  $G\left (V^n_1\right )$ to ensure that they are in
$G\left (V^n_1\right )$ to ensure that they are in ![]() $V^n_2$. Hence, define
$V^n_2$. Hence, define
 $$ \begin{align} \begin{aligned} Y_{1j} & = \mathbf{1}\left\{ \deg\left( \left(\{1,j\}^*, \emptyset^1\right) \right) \geq T_p \right\}, \qquad Y_{2j} = \mathbf{1}\left\{\deg\left( \left(\{1,j\}^*, \{2\}^1\right) \right) \geq T_p \right\}, \\ Y_{3j} & = \mathbf{1}\left\{\deg\left( \left(\{2,j\}^*, \emptyset^1\right) \right) \geq T_p\right\}, \qquad Y_{4j} = \mathbf{1}\left\{\deg\left( \left(\{2,j\}^*, \{1\}^1\right) \right) \geq T_p\right\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} Y_{1j} & = \mathbf{1}\left\{ \deg\left( \left(\{1,j\}^*, \emptyset^1\right) \right) \geq T_p \right\}, \qquad Y_{2j} = \mathbf{1}\left\{\deg\left( \left(\{1,j\}^*, \{2\}^1\right) \right) \geq T_p \right\}, \\ Y_{3j} & = \mathbf{1}\left\{\deg\left( \left(\{2,j\}^*, \emptyset^1\right) \right) \geq T_p\right\}, \qquad Y_{4j} = \mathbf{1}\left\{\deg\left( \left(\{2,j\}^*, \{1\}^1\right) \right) \geq T_p\right\}. \end{aligned} \end{align} $$Here, ‘![]() $\deg $’ refers to the degree of the
$\deg $’ refers to the degree of the ![]() $4$-cycle in
$4$-cycle in  $G\left (V^n_1\right )$. We would like to show that there are at least
$G\left (V^n_1\right )$. We would like to show that there are at least ![]() $T_p$ choices j for which all
$T_p$ choices j for which all ![]() $Y_{\ell j}$,
$Y_{\ell j}$, ![]() $\ell \in \{1,2,3,4\}$, are
$\ell \in \{1,2,3,4\}$, are ![]() $1$.
$1$.
In the event ![]() $\mathcal {E}$, there are four disjoint sets
$\mathcal {E}$, there are four disjoint sets ![]() $R_\ell \subset \{3,4, \dotsc , d\}$ for
$R_\ell \subset \{3,4, \dotsc , d\}$ for ![]() $\ell \in \{1,2,3,4\}$ of size
$\ell \in \{1,2,3,4\}$ of size  $\left \lfloor M_p/4 \right \rfloor $ such that
$\left \lfloor M_p/4 \right \rfloor $ such that
 $$ \begin{align*} &\left( \{1,k\}^*, \emptyset^1\right) \in V^n_1 \text{ for } j \in R_1, \qquad \left( \{1,k\}^*, \{2\}^1\right) \in V^n_1 \text{ for } j \in R_2, \\ &\left( \{2,k\}^*, \emptyset^1\right) \in V^n_1 \text{ for } j \in R_3, \qquad \left( \{2,k\}^*, \{1\}^1\right) \in V^n_1 \text{ for } j \in R_4. \end{align*} $$
$$ \begin{align*} &\left( \{1,k\}^*, \emptyset^1\right) \in V^n_1 \text{ for } j \in R_1, \qquad \left( \{1,k\}^*, \{2\}^1\right) \in V^n_1 \text{ for } j \in R_2, \\ &\left( \{2,k\}^*, \emptyset^1\right) \in V^n_1 \text{ for } j \in R_3, \qquad \left( \{2,k\}^*, \{1\}^1\right) \in V^n_1 \text{ for } j \in R_4. \end{align*} $$ Observe that the possible neighbors of ![]() $\left (\{1,j\}^*, \emptyset ^1\right )$,
$\left (\{1,j\}^*, \emptyset ^1\right )$, ![]() $j \in \{3,4, \dotsc , n\}$, are given by
$j \in \{3,4, \dotsc , n\}$, are given by ![]() $\left (\{1,j\}^*, \{k\}^1\right )$ for
$\left (\{1,j\}^*, \{k\}^1\right )$ for ![]() $k \not \in \{1,j\}$. For simplicity, we will also discard the case
$k \not \in \{1,j\}$. For simplicity, we will also discard the case ![]() $k=2$. To have this edge in
$k=2$. To have this edge in  $G\left (V^n_1\right )$, we would need
$G\left (V^n_1\right )$, we would need
 $$ \begin{align*} &\left( \{1,k\}^*, \emptyset^1\right) \in V^n_1, \qquad \left( \{1,k\}^*, \{j\}^1\right) \in V^n_1, \\ &\left( \{j,k\}^*, \emptyset^1\right) \in V^n_1, \qquad \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1. \end{align*} $$
$$ \begin{align*} &\left( \{1,k\}^*, \emptyset^1\right) \in V^n_1, \qquad \left( \{1,k\}^*, \{j\}^1\right) \in V^n_1, \\ &\left( \{j,k\}^*, \emptyset^1\right) \in V^n_1, \qquad \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1. \end{align*} $$In particular, for ![]() $k \in R_1$ the first of these requirements is guaranteed. Hence we can define
$k \in R_1$ the first of these requirements is guaranteed. Hence we can define
 $$ \begin{align*} Z_{1jk} = \mathbf{1}\left\{ \left( \{1,k\}^*, \{j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \emptyset^1\right) \in V^n_1, \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1 \right\}, \end{align*} $$
$$ \begin{align*} Z_{1jk} = \mathbf{1}\left\{ \left( \{1,k\}^*, \{j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \emptyset^1\right) \in V^n_1, \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1 \right\}, \end{align*} $$and define
 $$ \begin{align*} Z_{1j} = \sum_{k \in R_1} Z_{1jk}. \end{align*} $$
$$ \begin{align*} Z_{1j} = \sum_{k \in R_1} Z_{1jk}. \end{align*} $$Then ![]() $Z_{1j}$ is a lower bound for
$Z_{1j}$ is a lower bound for ![]() $\deg \left ( \left (\{1,j\}^*, \emptyset ^1\right ) \right )$, and so if
$\deg \left ( \left (\{1,j\}^*, \emptyset ^1\right ) \right )$, and so if ![]() $Z_{1j}$ is at least
$Z_{1j}$ is at least ![]() $T_p$, then
$T_p$, then ![]() $Y_{1j}=1$.
$Y_{1j}=1$.
We do a similar construction for ![]() $\ell \in \{2,3,4\}$, making appropriate modifications. We list them for clarity:
$\ell \in \{2,3,4\}$, making appropriate modifications. We list them for clarity:
 $$ \begin{align*} Z_{2jk} & = \mathbf{1}\left\{ \left( \{1,k\}^*, \{2,j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{2\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{1,2\}^1\right) \in V^n_1 \right\}, \\ Z_{3jk} & = \mathbf{1}\left\{ \left( \{2,k\}^*, \{j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \emptyset^1\right) \in V^n_1, \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1 \right\}, \\ Z_{4jk} & = \mathbf{1}\left\{ \left( \{2,k\}^*, \{1,j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{1,2\}^1\right) \in V^n_1 \right\}. \end{align*} $$
$$ \begin{align*} Z_{2jk} & = \mathbf{1}\left\{ \left( \{1,k\}^*, \{2,j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{2\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{1,2\}^1\right) \in V^n_1 \right\}, \\ Z_{3jk} & = \mathbf{1}\left\{ \left( \{2,k\}^*, \{j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \emptyset^1\right) \in V^n_1, \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1 \right\}, \\ Z_{4jk} & = \mathbf{1}\left\{ \left( \{2,k\}^*, \{1,j\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{1\}^1\right) \in V^n_1, \left( \{j,k\}^*, \{1,2\}^1\right) \in V^n_1 \right\}. \end{align*} $$In terms of these, we set ![]() $Z_{\ell j} = \sum _{k \in R_\ell } Z_{\ell jk}$.
$Z_{\ell j} = \sum _{k \in R_\ell } Z_{\ell jk}$.
Let  $J = \{3,4, \dotsc , d\} \setminus \left (\cup _1^4 R_\ell \right )$. Then the family
$J = \{3,4, \dotsc , d\} \setminus \left (\cup _1^4 R_\ell \right )$. Then the family
 $$ \begin{align*} \left\{ Z_{\ell jk} : \ell \in \{1,2,3,4\}, \ j \in J, \ k \in R_\ell \right\} \end{align*} $$
$$ \begin{align*} \left\{ Z_{\ell jk} : \ell \in \{1,2,3,4\}, \ j \in J, \ k \in R_\ell \right\} \end{align*} $$is independent random variables. Moreover, for any ![]() $\ell \in \{1,2,3,4\}$ and
$\ell \in \{1,2,3,4\}$ and ![]() $j \in J$, from equation (18) we have
$j \in J$, from equation (18) we have
 $$ \begin{align*} \mathbb{P}\left(Z_{\ell j} < T_p\right) < \mathbb{P} \left( \text{Binomial}\left( \left\lfloor M_p/4 \right\rfloor, p^3\right) < T_p\right) \leq \left(\tfrac{1}{2}\right)^{1/4}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(Z_{\ell j} < T_p\right) < \mathbb{P} \left( \text{Binomial}\left( \left\lfloor M_p/4 \right\rfloor, p^3\right) < T_p\right) \leq \left(\tfrac{1}{2}\right)^{1/4}. \end{align*} $$It follows that with
 $$ \begin{align*} Z = \sum_{j \in J} \prod_{\ell = 1}^4 \mathbf{1}\left\{ Z_{\ell j} \geq T_p\right\} \end{align*} $$
$$ \begin{align*} Z = \sum_{j \in J} \prod_{\ell = 1}^4 \mathbf{1}\left\{ Z_{\ell j} \geq T_p\right\} \end{align*} $$and with  $q = \mathbb {P}\left (Z_{\ell j} \geq T_p\right )^4> \tfrac 12$, we have
$q = \mathbb {P}\left (Z_{\ell j} \geq T_p\right )^4> \tfrac 12$, we have
 $$ \begin{align*} \mathbb{P}\left(Z < T_p\right) \leq \mathbb{P}\left( \text{Binomial}\left( n - 3 - M_p, q\right) < T_p\right) =n^{O(1)}(1-q)^{n}, \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(Z < T_p\right) \leq \mathbb{P}\left( \text{Binomial}\left( n - 3 - M_p, q\right) < T_p\right) =n^{O(1)}(1-q)^{n}, \end{align*} $$which completes the proof.
3.3 Stage 3: The final squeeze
In this section, we draw conclusions on what remains noncontracted in the complex in the third stage.
3.3.1 The simply connected regime,  $p> \tfrac 12$
$p> \tfrac 12$
We begin by showing that for ![]() $p> 1/2$, there are simply no light
$p> 1/2$, there are simply no light ![]() $1$-faces. Hence in fact for
$1$-faces. Hence in fact for  $p> \tfrac 12$,
$p> \tfrac 12$, ![]() $V_3^n=V_n$ with high probability (proving Theorem 3.1).
$V_3^n=V_n$ with high probability (proving Theorem 3.1).
Lemma 3.6. For any ![]() $p> 1/2$, there is an
$p> 1/2$, there is an ![]() $M_p> 0$ such that with probability tending to
$M_p> 0$ such that with probability tending to ![]() $1$ with n, for every
$1$ with n, for every ![]() $1$-face f of
$1$-face f of ![]() $Q \sim Q_2(n,p)$,
$Q \sim Q_2(n,p)$, ![]() $\deg (f)>M_p$.
$\deg (f)>M_p$.
Proof. The degree of a ![]() $1$-face is distributed as
$1$-face is distributed as ![]() $\text {Binomial}(n-2,p)$. For
$\text {Binomial}(n-2,p)$. For  $p> \tfrac 12$, the probability that this is less than any fixed constant M is
$p> \tfrac 12$, the probability that this is less than any fixed constant M is ![]() $n^{O(1)}(1-p)^{n}$. Hence by a union bound, the lemma follows.
$n^{O(1)}(1-p)^{n}$. Hence by a union bound, the lemma follows.
3.3.2 Completely shielded  $1$-faces
$1$-faces
Call a ![]() $1$-face
$1$-face ![]() $f \in Q \sim Q_2(n,p)$ completely shielded if every
$f \in Q \sim Q_2(n,p)$ completely shielded if every ![]() $3$-face
$3$-face ![]() $c \in Q^n$ that contains f contains only heavy
$c \in Q^n$ that contains f contains only heavy ![]() $1$-faces of Q, besides possibly f. Completely shielded
$1$-faces of Q, besides possibly f. Completely shielded ![]() $1$-faces modify the fundamental group of Q in a simple way, contributing a free factor of
$1$-faces modify the fundamental group of Q in a simple way, contributing a free factor of ![]() $\mathbb {Z}$ if f is maximal.
$\mathbb {Z}$ if f is maximal.
To see this we begin with the following definition:
Definition 3.7. Let f be any ![]() $1$-face of
$1$-face of ![]() $Q^n$. Define the n-bubble around f to be the subcubical complex of
$Q^n$. Define the n-bubble around f to be the subcubical complex of ![]() $Q^n$ given by the union of the complete
$Q^n$ given by the union of the complete ![]() $1$-skeletons of all
$1$-skeletons of all ![]() $3$-faces containing f and every
$3$-faces containing f and every ![]() $2$-face on this skeleton which does not contain f.
$2$-face on this skeleton which does not contain f.
An n-bubble has fundamental group ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Lemma 3.8. For any ![]() $n \geq 3$ and any n-bubble X around f,
$n \geq 3$ and any n-bubble X around f,
Furthermore, the complex ![]() $X \setminus \{f\}$ and the complex
$X \setminus \{f\}$ and the complex ![]() $X \cup \{e\}$, where e is any
$X \cup \{e\}$, where e is any ![]() $2$-face containing f, are simply connected.
$2$-face containing f, are simply connected.
Proof. Without loss of generality, suppose that f is the face ![]() $\left (\{1\}^*,\emptyset ^1\right )$. The
$\left (\{1\}^*,\emptyset ^1\right )$. The ![]() $3$-faces containing f all have the form
$3$-faces containing f all have the form ![]() $\left (\{1,i,j\}^*, \emptyset ^1\right )$, and so the
$\left (\{1,i,j\}^*, \emptyset ^1\right )$, and so the ![]() $1$-skeleton of X is
$1$-skeleton of X is
 $$ \begin{align*} \left\{ \left(\{ i \}^*, A^1\right) : A \subset \{1,2,\dotsc,n\}, \ i \not\in A, \ \lvert A \cup \{i\}\rvert \leq 3 \right\}. \end{align*} $$
$$ \begin{align*} \left\{ \left(\{ i \}^*, A^1\right) : A \subset \{1,2,\dotsc,n\}, \ i \not\in A, \ \lvert A \cup \{i\}\rvert \leq 3 \right\}. \end{align*} $$We claim that all the ![]() $4$-cycles containing f are homotopic. As all other
$4$-cycles containing f are homotopic. As all other ![]() $4$-cycles are contractible from the definition of X, the statements in the lemma follow.
$4$-cycles are contractible from the definition of X, the statements in the lemma follow.
The ![]() $4$-cycles that contain f are boundaries of the
$4$-cycles that contain f are boundaries of the ![]() $2$-faces of
$2$-faces of ![]() $Q^n$ of the form
$Q^n$ of the form
 $$ \begin{align*} \left\{ \left(\{ 1,i \}^*, \emptyset^1\right) : 2 \leq i \leq n \right\}. \end{align*} $$
$$ \begin{align*} \left\{ \left(\{ 1,i \}^*, \emptyset^1\right) : 2 \leq i \leq n \right\}. \end{align*} $$For any ![]() $2 \leq i < j \leq n$, the
$2 \leq i < j \leq n$, the ![]() $3$-face
$3$-face ![]() $c=(\{1,i,j\}^*, \emptyset )$ intersected with X contains four
$c=(\{1,i,j\}^*, \emptyset )$ intersected with X contains four ![]() $2$-faces. Moreover, the
$2$-faces. Moreover, the ![]() $2$-faces
$2$-faces ![]() $(\{1,i\}^*, \emptyset )$ and
$(\{1,i\}^*, \emptyset )$ and ![]() $(\{1,j\}^*, \emptyset )$ are adjacent in this cube. Hence, these cycles can be deformed through c to one another. As this holds for any such i and j, the proof follows.
$(\{1,j\}^*, \emptyset )$ are adjacent in this cube. Hence, these cycles can be deformed through c to one another. As this holds for any such i and j, the proof follows.
Lemma 3.9. For any ![]() $p \in (0,1)$, let
$p \in (0,1)$, let ![]() $\hat Q$ be the cubical complex that results from deleting from
$\hat Q$ be the cubical complex that results from deleting from ![]() $Q \sim Q_2(n,p)$ every completely shielded
$Q \sim Q_2(n,p)$ every completely shielded ![]() $1$-face f and any
$1$-face f and any ![]() $2$-face of Q containing f. Then with high probability,
$2$-face of Q containing f. Then with high probability,
 $$ \begin{align*} \pi_1(Q) \cong \pi_1\left(\hat Q\right) * \underbrace{( \mathbb{Z} * \mathbb{Z} * \dotsb * \mathbb{Z} )}_{N}, \end{align*} $$
$$ \begin{align*} \pi_1(Q) \cong \pi_1\left(\hat Q\right) * \underbrace{( \mathbb{Z} * \mathbb{Z} * \dotsb * \mathbb{Z} )}_{N}, \end{align*} $$where N denotes the number of completely shielded ![]() $1$-faces in Q that are isolated.
$1$-faces in Q that are isolated.
Proof. From Lemma 3.4, all ![]() $4$-cycles whose every
$4$-cycles whose every ![]() $1$-face is heavy are contractible. In particular, we do not modify the fundamental group of Q if we include all those
$1$-face is heavy are contractible. In particular, we do not modify the fundamental group of Q if we include all those ![]() $2$-faces into Q whose boundary is in
$2$-faces into Q whose boundary is in ![]() $V_3^n$. Let
$V_3^n$. Let ![]() $\hat Q$ be this cubical complex.
$\hat Q$ be this cubical complex.
We now remove completely shielded ![]() $1$-faces from
$1$-faces from ![]() $\hat Q$ one at a time, tracking the changes to the fundamental group. We will show what happens after removing the first. It will be clear that by using induction, a similar analysis would give the claim in the lemma.
$\hat Q$ one at a time, tracking the changes to the fundamental group. We will show what happens after removing the first. It will be clear that by using induction, a similar analysis would give the claim in the lemma.
Let f be a completely shielded ![]() $1$-face of
$1$-face of ![]() $\hat Q$. Let
$\hat Q$. Let ![]() $Q_1$ be the complex that results after removing f from
$Q_1$ be the complex that results after removing f from ![]() $\hat Q$ and any
$\hat Q$ and any ![]() $2$-face containing f, and let
$2$-face containing f, and let ![]() $Q_2$ be the union of all the complete
$Q_2$ be the union of all the complete ![]() $2$-skeletons of all
$2$-skeletons of all ![]() $3$-faces that contain f. Then
$3$-faces that contain f. Then ![]() $Q_2$ contains an n-bubble, and it is exactly an n-bubble if f is isolated.
$Q_2$ contains an n-bubble, and it is exactly an n-bubble if f is isolated.
As ![]() $Q_2 \cup Q_1 = \hat Q$ and
$Q_2 \cup Q_1 = \hat Q$ and ![]() $Q_1 \cap Q_2$ is open and path-connected (compare Lemma 3.8, as this complex is an n-bubble with its central
$Q_1 \cap Q_2$ is open and path-connected (compare Lemma 3.8, as this complex is an n-bubble with its central ![]() $1$-face deleted). Moreover, every
$1$-face deleted). Moreover, every ![]() $4$-cycle in
$4$-cycle in ![]() $Q_1 \cap Q_2$ is contractible, and so
$Q_1 \cap Q_2$ is contractible, and so ![]() $\pi _1(Q_1 \cap Q_2)$ is trivial. From the Siefert–van Kampen theorem, we therefore have
$\pi _1(Q_1 \cap Q_2)$ is trivial. From the Siefert–van Kampen theorem, we therefore have
 $$ \begin{align*} \pi_1\left(\hat Q\right) \cong \pi_1(Q_1) * \pi_1(Q_2). \end{align*} $$
$$ \begin{align*} \pi_1\left(\hat Q\right) \cong \pi_1(Q_1) * \pi_1(Q_2). \end{align*} $$If f is maximal, then from Lemma 3.8 the fundamental group ![]() $\pi _1(Q_2)$ is isomorphic
$\pi _1(Q_2)$ is isomorphic ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
3.3.3 The velvety bubble phase
For  $p> 1-\left (\tfrac 12\right )^{1/2} \approx 0.292893$, we further show that the fundamental group completely reduces to its maximal
$p> 1-\left (\tfrac 12\right )^{1/2} \approx 0.292893$, we further show that the fundamental group completely reduces to its maximal ![]() $1$-faces. In this phase, while light
$1$-faces. In this phase, while light ![]() $1$-faces may exist in
$1$-faces may exist in ![]() $Q_2(n,p)$ (for
$Q_2(n,p)$ (for  $p \leq \tfrac 12$), they are well separated.
$p \leq \tfrac 12$), they are well separated.
Lemma 3.10. For  $p> 1-\left (\tfrac 12\right )^{1/2}$, with high probability, there are no
$p> 1-\left (\tfrac 12\right )^{1/2}$, with high probability, there are no ![]() $3$-faces
$3$-faces ![]() $c \in Q^n$ that contain more than one light
$c \in Q^n$ that contain more than one light ![]() $1$-face of
$1$-face of ![]() $Q \sim Q_2(n,p)$.
$Q \sim Q_2(n,p)$.
Proof. For a fixed c and a fixed choice of two ![]() $1$-faces
$1$-faces ![]() $f_1,f_2$, the degrees of
$f_1,f_2$, the degrees of ![]() $f_1$ and
$f_1$ and ![]() $f_2$ are both light with probability at most
$f_2$ are both light with probability at most ![]() $n^{O(1)}(1-p)^{2n-1}$. Hence for any p as in the statement of the lemma, there is an
$n^{O(1)}(1-p)^{2n-1}$. Hence for any p as in the statement of the lemma, there is an ![]() $\epsilon> 0$ such that the probability that this occurs is
$\epsilon> 0$ such that the probability that this occurs is ![]() $2^{-(1+\epsilon )n + O\left (\log n\right )}$. As there are
$2^{-(1+\epsilon )n + O\left (\log n\right )}$. As there are ![]() $2^n n^{O(1)}$ many ways to pick a
$2^n n^{O(1)}$ many ways to pick a ![]() $3$-face with two designated edges, the lemma follows from a first moment estimate.
$3$-face with two designated edges, the lemma follows from a first moment estimate.
We now give the proof of Theorem 1.3, which we recall for convenience:
Theorem 3.11. For  $p> 1-\left (\tfrac 12\right )^{1/2}$, with high probability, for
$p> 1-\left (\tfrac 12\right )^{1/2}$, with high probability, for ![]() $Q \sim Q_2(n,p)$,
$Q \sim Q_2(n,p)$,
 $$ \begin{align*} \pi_1(Q) \cong \underbrace{( \mathbb{Z} * \mathbb{Z} * \dotsb * \mathbb{Z} )}_{N}, \end{align*} $$
$$ \begin{align*} \pi_1(Q) \cong \underbrace{( \mathbb{Z} * \mathbb{Z} * \dotsb * \mathbb{Z} )}_{N}, \end{align*} $$where N denotes the number of maximal ![]() $1$-faces in Q.
$1$-faces in Q.
Proof. From Lemma 3.4, with high probability every ![]() $4$-cycle containing only heavy
$4$-cycle containing only heavy ![]() $1$-faces is in
$1$-faces is in ![]() $V_3^n$. From Lemma 3.10, with high probability no
$V_3^n$. From Lemma 3.10, with high probability no ![]() $3$-faces
$3$-faces ![]() $c \in Q^n$ contain more than one light face. Hence taking
$c \in Q^n$ contain more than one light face. Hence taking ![]() $\tilde Q$ as Q together with all
$\tilde Q$ as Q together with all ![]() $2$-faces bounded by some element of
$2$-faces bounded by some element of ![]() $V_3^n$ (so that
$V_3^n$ (so that ![]() $\pi _1\left (\tilde Q\right ) = \pi _1(Q)$), every light
$\pi _1\left (\tilde Q\right ) = \pi _1(Q)$), every light ![]() $1$-face f of
$1$-face f of ![]() $\tilde Q$ is completely shielded in
$\tilde Q$ is completely shielded in ![]() $\tilde Q$. Moreover, every
$\tilde Q$. Moreover, every ![]() $4$-cycle of
$4$-cycle of ![]() $\tilde Q$ either intersects a light
$\tilde Q$ either intersects a light ![]() $1$-face or is the boundary of a
$1$-face or is the boundary of a ![]() $2$-face. Hence in the notation of Lemma 3.9,
$2$-face. Hence in the notation of Lemma 3.9,  $\pi _1\left (\hat Q\right )=0$. It follows that from Lemma 3.9 we have a free group on
$\pi _1\left (\hat Q\right )=0$. It follows that from Lemma 3.9 we have a free group on ![]() $N'$ generators, with
$N'$ generators, with ![]() $N'$ the number of completely shielded maximal
$N'$ the number of completely shielded maximal ![]() $1$-faces. As every light
$1$-faces. As every light ![]() $1$-face is completely shielded w.h.p., it follows that
$1$-face is completely shielded w.h.p., it follows that ![]() $N'=N$ with high probability.
$N'=N$ with high probability.
4 Structure theorem for general p
In this section, we prove Theorem 1.7. For convenience, we recall some definitions from the introduction. Recall Definition 1.6:
Definition 4.1. For a cubical subcomplex T of any cube ![]() $Q^n$, let
$Q^n$, let ![]() $e(T)$ denote the number of edges in T. Let
$e(T)$ denote the number of edges in T. Let ![]() $\mathscr {T}_p$ be the set of pure
$\mathscr {T}_p$ be the set of pure ![]() $2$-dimensional strongly connected cubical complexes T that are subcomplexes of
$2$-dimensional strongly connected cubical complexes T that are subcomplexes of ![]() $Q_2^n$ for some n and such that
$Q_2^n$ for some n and such that  $(1-\left (\frac 12\right )^{1/e(T)}) < p$.
$(1-\left (\frac 12\right )^{1/e(T)}) < p$.
We will prove Theorem 1.7, which we recall:
Theorem 4.2. For any ![]() $p \in (0,1)$ and for
$p \in (0,1)$ and for ![]() $Q \sim Q_2(n,p)$, let the free-product factorisation of
$Q \sim Q_2(n,p)$, let the free-product factorisation of ![]() $\pi _1(Q)$ be given by
$\pi _1(Q)$ be given by
with F a free group. With high probability, any ![]() $T \in \mathscr {T}_p$ appears as a factor
$T \in \mathscr {T}_p$ appears as a factor ![]() $\pi _1\left (X_j\right )$ for some
$\pi _1\left (X_j\right )$ for some ![]() $1 \leq j \leq \ell $.
$1 \leq j \leq \ell $.
Our main technical tool will be the following:
Definition 4.3. For a cubical subcomplex T of a cubical complex ![]() $W\subset Q^n$, denote by
$W\subset Q^n$, denote by ![]() $h(T)$ the minimal cubical subcomplex of W such that
$h(T)$ the minimal cubical subcomplex of W such that
1. the
 $1$-skeleton of
$1$-skeleton of  $h(T)$ is the
$h(T)$ is the  $1$-skeleton of a k-dimensional hypercube,
$1$-skeleton of a k-dimensional hypercube,2. every
 $2$-face of W that is incident to T is contained in
$2$-face of W that is incident to T is contained in  $h(T)$ and
$h(T)$ and3. every
 $2$-face of
$2$-face of  $Q^n_2$ with
$Q^n_2$ with  $1$-skeleton in
$1$-skeleton in  $h(T)$ which is not incident to T is in
$h(T)$ which is not incident to T is in  $h(T)$.
$h(T)$.
Also denote by ![]() $H(T) \subset W$ a complete
$H(T) \subset W$ a complete ![]() $2$-skeleton of a k-dimensional hypercube which is parallel to
$2$-skeleton of a k-dimensional hypercube which is parallel to ![]() $h(T)$, so that any
$h(T)$, so that any ![]() $2$-face that has an edge in
$2$-face that has an edge in ![]() $h(T) \setminus T$ and another edge in
$h(T) \setminus T$ and another edge in ![]() $H(T)$ is contained in W.
$H(T)$ is contained in W.
We emphasise that T need not be connected in any sense and that ![]() $H(T)$ is not unique; we just need to choose one.
$H(T)$ is not unique; we just need to choose one.
Lemma 4.4. For any ![]() $p \in (0,1)$, with
$p \in (0,1)$, with ![]() $Q \sim Q_2(n,p)$, there exists a number
$Q \sim Q_2(n,p)$, there exists a number ![]() $k_p$ such that w.h.p., every
$k_p$ such that w.h.p., every  $\left (\left (M_p +2\right )\times k_p\right )^2$-dimensional cube in
$\left (\left (M_p +2\right )\times k_p\right )^2$-dimensional cube in ![]() $Q^n$ contains fewer than
$Q^n$ contains fewer than ![]() $k_p$ light edges of Q.
$k_p$ light edges of Q.
Proof. We argue by a first moment estimate. For any ![]() $\ell $, the number of
$\ell $, the number of ![]() $\ell $-dimensional cubes in
$\ell $-dimensional cubes in ![]() $Q^n$ is given by
$Q^n$ is given by  $2^{n-\ell }\binom {n}{\ell }$. The probability that any such cube contains k light edges is
$2^{n-\ell }\binom {n}{\ell }$. The probability that any such cube contains k light edges is ![]() $O_{k,\ell ,p}\left ((1-p)^{nk}\right )$. Hence taking
$O_{k,\ell ,p}\left ((1-p)^{nk}\right )$. Hence taking  $\ell = \left (\left (M_p+2\right ) k\right )^2$, if we pick k sufficiently large that
$\ell = \left (\left (M_p+2\right ) k\right )^2$, if we pick k sufficiently large that  $(1-p)^k < \tfrac {1}{2}$, then the expected number of
$(1-p)^k < \tfrac {1}{2}$, then the expected number of ![]() $\ell $-dimensional cubes containing more than k light edges tends to
$\ell $-dimensional cubes containing more than k light edges tends to ![]() $0$ exponentially in n.
$0$ exponentially in n.
Lemma 4.5. Set ![]() $p \in (0,1)$ and let
$p \in (0,1)$ and let ![]() $\ell \in \mathbb {N}$ be fixed; then w.h.p., for
$\ell \in \mathbb {N}$ be fixed; then w.h.p., for ![]() $Q \sim Q_2(n,p)$, every
$Q \sim Q_2(n,p)$, every ![]() $\ell $-dimensional cube X has a parallel cube Y that has no light edges in Q and for which there are no light edges in Q between X and Y.
$\ell $-dimensional cube X has a parallel cube Y that has no light edges in Q and for which there are no light edges in Q between X and Y.
Proof. This is similar to Lemma 4.4. We argue by a first moment estimate. For any ![]() $\ell $, the number of
$\ell $, the number of ![]() $\ell $-dimensional cubes in
$\ell $-dimensional cubes in ![]() $Q^n$ is given by
$Q^n$ is given by  $2^{n-\ell }\binom {n}{\ell }$. For a fixed
$2^{n-\ell }\binom {n}{\ell }$. For a fixed ![]() $\ell $-dimensional cube
$\ell $-dimensional cube ![]() $X \subset Q^n$, the probability that every parallel
$X \subset Q^n$, the probability that every parallel ![]() $\ell $-dimensional cube Y contains either
$\ell $-dimensional cube Y contains either
(i) at least one light edge or
(ii) the endpoint of a light edge between X and Y
is at most
 $$ \begin{align*} \left((\ell+2)2^{\ell-1}\right)^{n-\ell} (1-p)^{n(n-\ell)} = o\left(n^\ell 2^{-n}\right). \end{align*} $$
$$ \begin{align*} \left((\ell+2)2^{\ell-1}\right)^{n-\ell} (1-p)^{n(n-\ell)} = o\left(n^\ell 2^{-n}\right). \end{align*} $$Hence from a first moment estimate, for any fixed ![]() $\ell $ and any
$\ell $ and any ![]() $p \in (0,1)$, w.h.p. every
$p \in (0,1)$, w.h.p. every ![]() $\ell $-dimensional cube X has a parallel cube Y that contains no light edges of Q and shares no endpoint of a light edge between X and Y.
$\ell $-dimensional cube X has a parallel cube Y that contains no light edges of Q and shares no endpoint of a light edge between X and Y.
Theorem 4.6. Set ![]() $p \in (0,1)$ and
$p \in (0,1)$ and ![]() $k_p$ as in Lemma 4.4, and
$k_p$ as in Lemma 4.4, and ![]() $Q \sim Q_2(n,p)$. Let
$Q \sim Q_2(n,p)$. Let ![]() $\overline {Q}$ be Q with all the
$\overline {Q}$ be Q with all the ![]() $2$-faces bounded by
$2$-faces bounded by ![]() $4$-cycles having no light edges. With high probability, there are disjoint cubical complexes
$4$-cycles having no light edges. With high probability, there are disjoint cubical complexes ![]() $\{ \tau _1, \tau _2, \dotsc , \tau _\ell \}$ in Q such that
$\{ \tau _1, \tau _2, \dotsc , \tau _\ell \}$ in Q such that
(i) the union of
 $1$-faces over all
$1$-faces over all  $\left \{\tau _j : 1\leq j \leq \ell \right \}$ is the set of all light
$\left \{\tau _j : 1\leq j \leq \ell \right \}$ is the set of all light  $1$-faces;
$1$-faces;(ii) for each
 $1 \leq j \leq \ell $, both
$1 \leq j \leq \ell $, both  $h\left (\tau _j\right )$ and
$h\left (\tau _j\right )$ and  $H\left (\tau _j\right )$ exist in
$H\left (\tau _j\right )$ exist in  $\overline {Q}$; and
$\overline {Q}$; and(iii) for each
 $1 \leq i \neq j \leq \ell $, the Hamming distance between the
$1 \leq i \neq j \leq \ell $, the Hamming distance between the  $0$-skeletons of
$0$-skeletons of  $h\left (\tau _j\right )$ and
$h\left (\tau _j\right )$ and  $h\left (\tau _i\right )$ is at least
$h\left (\tau _i\right )$ is at least  $2$.
$2$.
We need the next definition for proving Theorem 4.6:
Definition 4.7. Let X and Y be two subcomplexes of ![]() $Q^n$. Define
$Q^n$. Define ![]() $X \square Y$ to be the face of smallest dimension
$X \square Y$ to be the face of smallest dimension ![]() $Q^m$ such that
$Q^m$ such that ![]() $Q^m \subset Q^n$ and
$Q^m \subset Q^n$ and ![]() $X \cup Y \subset Q^m$. Observe that
$X \cup Y \subset Q^m$. Observe that ![]() $m\leq n$. More generally, let
$m\leq n$. More generally, let ![]() $X_1, X_2, \dotsc , X_l$ be any finite collection of subcomplexes of
$X_1, X_2, \dotsc , X_l$ be any finite collection of subcomplexes of ![]() $Q^n$ and
$Q^n$ and ![]() $I=\{1,2, \dotsc , l\}$. We define
$I=\{1,2, \dotsc , l\}$. We define
as the face of smallest dimension ![]() $Q^m$ such that
$Q^m$ such that ![]() $Q^m \subset Q^n$ and such that
$Q^m \subset Q^n$ and such that
In this case, ![]() $m\leq n$ as well.
$m\leq n$ as well.
Proof of Theorem 4.6. We first show that for every light ![]() $1$-face e there is a cubical complex
$1$-face e there is a cubical complex ![]() $\sigma _e$ containing e and having all its
$\sigma _e$ containing e and having all its ![]() $1$-faces light such that
$1$-faces light such that ![]() $h(\sigma _e)$ exists in
$h(\sigma _e)$ exists in ![]() $\overline {Q}$. We will then merge these
$\overline {Q}$. We will then merge these ![]() $h(\sigma _e)$ to form the partition claimed to exist in the theorem.
$h(\sigma _e)$ to form the partition claimed to exist in the theorem.
Let ![]() $e_1 := e$ be any light edge of Q. Let
$e_1 := e$ be any light edge of Q. Let ![]() $T_1$ be the cubical complex which is the down closure of
$T_1$ be the cubical complex which is the down closure of ![]() $e_1$. Let
$e_1$. Let ![]() $X_1$ be the smallest induced complex in
$X_1$ be the smallest induced complex in ![]() $\overline {Q}$ which contains
$\overline {Q}$ which contains ![]() $T_1$, which contains all
$T_1$, which contains all ![]() $2$-faces of
$2$-faces of ![]() $\overline {Q}$ incident to
$\overline {Q}$ incident to ![]() $e_1$ and whose
$e_1$ and whose ![]() $1$-skeleton is a hypercube. If
$1$-skeleton is a hypercube. If ![]() $X_1=h(T_1)$, we are finished. Otherwise, by definition, there must be a
$X_1=h(T_1)$, we are finished. Otherwise, by definition, there must be a ![]() $2$-face f of
$2$-face f of ![]() $Q^n_2$ with
$Q^n_2$ with ![]() $1$-skeleton in
$1$-skeleton in ![]() $X_1$ but not itself in
$X_1$ but not itself in ![]() $X_1$. Then there must be at least one light edge
$X_1$. Then there must be at least one light edge ![]() $e_2 \in X_1 \setminus T_1$.
$e_2 \in X_1 \setminus T_1$.
We then define ![]() $T_2$ as the induced subcomplex of Q on edges
$T_2$ as the induced subcomplex of Q on edges ![]() $e_1,e_2$. Let
$e_1,e_2$. Let ![]() $X_2$ be the smallest induced complex in
$X_2$ be the smallest induced complex in ![]() $\overline {Q}$ which contains
$\overline {Q}$ which contains ![]() $T_2$, which contains all
$T_2$, which contains all ![]() $2$-faces of
$2$-faces of ![]() $\overline {Q}$ incident to
$\overline {Q}$ incident to ![]() $T_2$ and whose
$T_2$ and whose ![]() $1$-skeleton is a hypercube. Once more, if
$1$-skeleton is a hypercube. Once more, if ![]() $X_2 = h(T_2)$, we are done. Otherwise, we proceed inductively by the same argument.
$X_2 = h(T_2)$, we are done. Otherwise, we proceed inductively by the same argument.
This produces a nested sequence of complexes ![]() $\{T_k\}$ each having k edges. It also produces a sequence of complexes
$\{T_k\}$ each having k edges. It also produces a sequence of complexes ![]() $\{ X_k \}$ such that each
$\{ X_k \}$ such that each ![]() $X_k \supset T_k$ and each
$X_k \supset T_k$ and each ![]() $X_k$ contains at least k light edges and such that
$X_k$ contains at least k light edges and such that ![]() $X_k$ has the
$X_k$ has the ![]() $1$-skeleton of a hypercube of dimension at most
$1$-skeleton of a hypercube of dimension at most ![]() $k \times M_p$. By Lemma 4.4, with high probability, this sequence must terminate at some
$k \times M_p$. By Lemma 4.4, with high probability, this sequence must terminate at some ![]() $k^* \leq k_p$. The complex
$k^* \leq k_p$. The complex ![]() $X_{k^*}=h(T_{k^*})$ by definition, and we define
$X_{k^*}=h(T_{k^*})$ by definition, and we define ![]() $\sigma _e = T_{k^*}$.
$\sigma _e = T_{k^*}$.
We define a graph G with vertex set given by the collection of ![]() $\sigma _e$. Two vertices
$\sigma _e$. Two vertices ![]() $\sigma _{e_1}$,
$\sigma _{e_1}$, ![]() $\sigma _{e_2}$ in this graph are connected if the Hamming distance between
$\sigma _{e_2}$ in this graph are connected if the Hamming distance between ![]() $h\left (\sigma _{e_1}\right )$ and
$h\left (\sigma _{e_1}\right )$ and ![]() $h\left (\sigma _{e_2}\right )$ is less than
$h\left (\sigma _{e_2}\right )$ is less than ![]() $2$. Let
$2$. Let ![]() $\{ \tau _1, \tau _2, \dotsc , \tau _\ell \}$ be the unions of the connected components in G. Then for each
$\{ \tau _1, \tau _2, \dotsc , \tau _\ell \}$ be the unions of the connected components in G. Then for each ![]() $1 \leq j \leq \ell $, we construct the hypercube
$1 \leq j \leq \ell $, we construct the hypercube
It is easy to see that ![]() $\Sigma _j=h\left (\tau _j\right )$, which implies that
$\Sigma _j=h\left (\tau _j\right )$, which implies that ![]() $h\left (\tau _j\right )$ exists and is exactly
$h\left (\tau _j\right )$ exists and is exactly ![]() $\Sigma _j$.
$\Sigma _j$.
The dimension of ![]() $\Sigma _j$ is at most
$\Sigma _j$ is at most
 $$ \begin{align} \sum_{\sigma_e} [\dim(h(\sigma_{e}))+2], \end{align} $$
$$ \begin{align} \sum_{\sigma_e} [\dim(h(\sigma_{e}))+2], \end{align} $$where the sum is over all ![]() $\sigma _{e}$ contained in
$\sigma _{e}$ contained in ![]() $\tau _j$. Therefore by Lemma 4.4, each
$\tau _j$. Therefore by Lemma 4.4, each ![]() $\tau _j$ has at most
$\tau _j$ has at most ![]() $k_p$ edges. Hence by Lemma 4.5, each
$k_p$ edges. Hence by Lemma 4.5, each ![]() $H\left (\tau _j\right )$ exists as well.
$H\left (\tau _j\right )$ exists as well.
Lemma 4.8. Let W be a subcomplex of ![]() $Q_2^n$ and T a subcomplex of W. Suppose that
$Q_2^n$ and T a subcomplex of W. Suppose that ![]() $h(T)$ and
$h(T)$ and ![]() $H(T)$ exist in W. Let
$H(T)$ exist in W. Let ![]() $\hat {W}$ be the complex formed by adding to W the complete
$\hat {W}$ be the complex formed by adding to W the complete ![]() $1$-skeleton of
$1$-skeleton of ![]() $h(T) \square H(T)$ and any
$h(T) \square H(T)$ and any ![]() $2$-face of
$2$-face of ![]() $Q_2^n$ with
$Q_2^n$ with ![]() $1$-skeleton in
$1$-skeleton in ![]() $h(T) \square H(T)$. Then
$h(T) \square H(T)$. Then
 $$ \begin{align*} \pi_1(W) \cong \pi_1\left(\hat W\right) * \pi_1(W \cap (h(T) \square H(T))). \end{align*} $$
$$ \begin{align*} \pi_1(W) \cong \pi_1\left(\hat W\right) * \pi_1(W \cap (h(T) \square H(T))). \end{align*} $$ Recall that for a disconnected cubical complex X, we define ![]() $\pi (X)$ as the free product of its connected components.
$\pi (X)$ as the free product of its connected components.
Proof. Let ![]() $\hat {T}$ be all the
$\hat {T}$ be all the ![]() $1$-faces in T and any
$1$-faces in T and any ![]() $2$-face of W incident to T. Let
$2$-face of W incident to T. Let ![]() $\tilde T$ be the down closure of
$\tilde T$ be the down closure of ![]() $\hat T$. Let
$\hat T$. Let ![]() $S=W \cap (h(T) \square H(T))$.
$S=W \cap (h(T) \square H(T))$.
Let ![]() $X = \left (W \setminus \hat {T}\right ) \cap S$. We claim that
$X = \left (W \setminus \hat {T}\right ) \cap S$. We claim that ![]() $\pi _1(X)\cong 1$. The
$\pi _1(X)\cong 1$. The ![]() $1$-faces of X that are in
$1$-faces of X that are in ![]() $h(T)$ are not in T. Therefore, by Definition 4.3, for every edge
$h(T)$ are not in T. Therefore, by Definition 4.3, for every edge ![]() $e \in X \cap h(T)$, the unique
$e \in X \cap h(T)$, the unique ![]() $4$-cycle connecting e to
$4$-cycle connecting e to ![]() $H(T)$ is the boundary of a
$H(T)$ is the boundary of a ![]() $2$-face in X. Thus, every closed curve in X is homotopic to a curve in
$2$-face in X. Thus, every closed curve in X is homotopic to a curve in ![]() $H(T)$. Since
$H(T)$. Since ![]() $\pi _1(H(T))\cong 1$, it follows that
$\pi _1(H(T))\cong 1$, it follows that ![]() $\pi _1(X) \cong 1$. Therefore, the Siefert–van Kampen theorem states that
$\pi _1(X) \cong 1$. Therefore, the Siefert–van Kampen theorem states that
 $$ \begin{align*} \pi_1(W) \cong \pi_1\left(W \setminus \hat{T}\right) * \pi_1(S). \end{align*} $$
$$ \begin{align*} \pi_1(W) \cong \pi_1\left(W \setminus \hat{T}\right) * \pi_1(S). \end{align*} $$ We now show that ![]() $\pi _1\left (W \setminus \hat {T}\right ) \cong \pi _1\left (\hat W\right )$. Define a complex
$\pi _1\left (W \setminus \hat {T}\right ) \cong \pi _1\left (\hat W\right )$. Define a complex ![]() $S^*$ as the down closure of all
$S^*$ as the down closure of all ![]() $2$-faces in
$2$-faces in ![]() $Q_2^n$ incident to T with
$Q_2^n$ incident to T with ![]() $1$-skeleton in
$1$-skeleton in ![]() $h(T) \square H(T)$, union with
$h(T) \square H(T)$, union with ![]() $H(T)$. Any
$H(T)$. Any ![]() $1$-face e of
$1$-face e of ![]() $S^* \cap \left (W \setminus \hat T\right )$ that is in
$S^* \cap \left (W \setminus \hat T\right )$ that is in ![]() $h(T)$ must be in
$h(T)$ must be in ![]() $h(T) \setminus T$. In particular, there is a
$h(T) \setminus T$. In particular, there is a ![]() $2$-face f containing e which has a
$2$-face f containing e which has a ![]() $1$-face in
$1$-face in ![]() $H(T)$. Hence, any closed curve in
$H(T)$. Hence, any closed curve in ![]() $S^* \cap \left (W \setminus \hat T\right )$ is homotopic to one in
$S^* \cap \left (W \setminus \hat T\right )$ is homotopic to one in ![]() $H(T)$, which is simply connected. Therefore by the Siefert–van Kampen theorem,
$H(T)$, which is simply connected. Therefore by the Siefert–van Kampen theorem,
 $$ \begin{align*} \pi_1\left(\hat W\right) = \pi_1\left(S^* \cup \left(W \setminus \hat{T}\right)\right) \cong \pi_1\left(W \setminus \hat{T}\right) * \pi_1(S^*). \end{align*} $$
$$ \begin{align*} \pi_1\left(\hat W\right) = \pi_1\left(S^* \cup \left(W \setminus \hat{T}\right)\right) \cong \pi_1\left(W \setminus \hat{T}\right) * \pi_1(S^*). \end{align*} $$ It remains to evaluate the fundamental group of ![]() $S^*$. Any edge in
$S^*$. Any edge in ![]() $S^* \cap h(T)$ has a
$S^* \cap h(T)$ has a ![]() $4$-cycle that has an edge in
$4$-cycle that has an edge in ![]() $H(T)$. By construction, we know that this
$H(T)$. By construction, we know that this ![]() $4$-cycle has a
$4$-cycle has a ![]() $2$-face added. Therefore, any closed curve in
$2$-face added. Therefore, any closed curve in ![]() $S^*$ is homotopic to a closed curve in
$S^*$ is homotopic to a closed curve in ![]() $H(T)$. Thus
$H(T)$. Thus ![]() $S^*$ is simply connected, because
$S^*$ is simply connected, because ![]() $H(T)$ is by definition.
$H(T)$ is by definition.
Lemma 4.9. Let W be a subcomplex of ![]() $Q_2^n$ and T a subcomplex of W. Suppose that
$Q_2^n$ and T a subcomplex of W. Suppose that ![]() $h(T)$ and
$h(T)$ and ![]() $H(T)$ exist in W. Let
$H(T)$ exist in W. Let ![]() $P_1, \dotsc ,P_m$ be all the pure
$P_1, \dotsc ,P_m$ be all the pure ![]() $2$-dimensional strongly connected components completely contained in T, such that any
$2$-dimensional strongly connected components completely contained in T, such that any ![]() $2$-face adjacent to the
$2$-face adjacent to the ![]() $1$-skeleton of any
$1$-skeleton of any ![]() $P_i$ is also contained in
$P_i$ is also contained in ![]() $P_i$. Suppose that
$P_i$. Suppose that ![]() $T = \cup _{i=1}^m P_i$. Then there is a free group F such that
$T = \cup _{i=1}^m P_i$. Then there is a free group F such that
Proof. Let ![]() $S=W \cap (h(T) \square H(T))$. Suppose we fill
$S=W \cap (h(T) \square H(T))$. Suppose we fill ![]() $H(T)$ by taking the flag cubical complex of
$H(T)$ by taking the flag cubical complex of ![]() $H(T)$. The fundamental group of S is unchanged, and we can contract
$H(T)$. The fundamental group of S is unchanged, and we can contract ![]() $H(T)$ to a point x. We denote this complex by
$H(T)$ to a point x. We denote this complex by ![]() $\hat S$. If e is an edge in T, then e forms an unfilled triangle with x in
$\hat S$. If e is an edge in T, then e forms an unfilled triangle with x in ![]() $\hat S$. Let
$\hat S$. Let ![]() $T_x \subset \hat S$ be the union of T, x and all the edges between T and x. Any edge
$T_x \subset \hat S$ be the union of T, x and all the edges between T and x. Any edge ![]() $f \in h(T)$ which is not contained in T is the base of a filled triangle with x in
$f \in h(T)$ which is not contained in T is the base of a filled triangle with x in ![]() $\hat S$, and so any closed curve in
$\hat S$, and so any closed curve in ![]() $\hat S$ is homotopic to a closed curve in
$\hat S$ is homotopic to a closed curve in ![]() $T_x$. Hence
$T_x$. Hence
 $$ \begin{align*} \pi_1(S) = \pi_1\left( \hat S\right) = \pi_1(T_x) = \pi_1(P_1) * \pi_1(P_2)* \dotsb * \pi_1(P_m) * F, \end{align*} $$
$$ \begin{align*} \pi_1(S) = \pi_1\left( \hat S\right) = \pi_1(T_x) = \pi_1(P_1) * \pi_1(P_2)* \dotsb * \pi_1(P_m) * F, \end{align*} $$where F is a free group.
Theorem 4.10. Fix ![]() $p\in (0,1)$. For
$p\in (0,1)$. For ![]() $Q \sim Q_2(n,p)$, w.h.p., if
$Q \sim Q_2(n,p)$, w.h.p., if ![]() $\tau _1, \tau _2, \dotsc ,\tau _\ell $ are as constructed in Theorem 4.6, then with
$\tau _1, \tau _2, \dotsc ,\tau _\ell $ are as constructed in Theorem 4.6, then with ![]() $S_j = C \cap \left (h\left (\tau _j\right ) \square H\left (\tau _j\right )\right )$ for all
$S_j = C \cap \left (h\left (\tau _j\right ) \square H\left (\tau _j\right )\right )$ for all ![]() $1 \leq j \leq \ell $,
$1 \leq j \leq \ell $,
Proof. Let ![]() $\overline {Q}$ be Q with all the
$\overline {Q}$ be Q with all the ![]() $2$-faces bounded by
$2$-faces bounded by ![]() $4$-cycles having no light edges. By Lemma 3.4, all
$4$-cycles having no light edges. By Lemma 3.4, all ![]() $4$-cycles with no light edges are in
$4$-cycles with no light edges are in ![]() $V_3^n$ w.h.p., and so
$V_3^n$ w.h.p., and so  $\pi _1\left (\overline {Q}\right ) = \pi _1(Q)$. We apply Lemma 4.8 inductively to each of the complexes
$\pi _1\left (\overline {Q}\right ) = \pi _1(Q)$. We apply Lemma 4.8 inductively to each of the complexes ![]() $\tau _j$. As a result, we have
$\tau _j$. As a result, we have
 $$ \begin{align*} \pi_1\left(\overline{Q}\right) = \pi_1(J) * \pi_1(S_1) * \pi_1(S_2) * \dotsb * \pi_1(S_\ell), \end{align*} $$
$$ \begin{align*} \pi_1\left(\overline{Q}\right) = \pi_1(J) * \pi_1(S_1) * \pi_1(S_2) * \dotsb * \pi_1(S_\ell), \end{align*} $$where J is the complex ![]() $\overline {Q}$ together with all
$\overline {Q}$ together with all ![]() $2$-faces in
$2$-faces in ![]() $Q_2^n$ having
$Q_2^n$ having ![]() $1$-skeleton contained in some
$1$-skeleton contained in some ![]() $h\left (\tau _j\right ) \square H\left (\tau _j\right )$ for some
$h\left (\tau _j\right ) \square H\left (\tau _j\right )$ for some ![]() $1 \leq j \leq \ell $.
$1 \leq j \leq \ell $.
It just remains to prove that ![]() $\pi _1(J) \cong 1$. The
$\pi _1(J) \cong 1$. The ![]() $1$-skeleton of J is
$1$-skeleton of J is ![]() $Q^n_1$, and so it suffices to show that every
$Q^n_1$, and so it suffices to show that every ![]() $4$-cycle in J is contractible. The only
$4$-cycle in J is contractible. The only ![]() $4$-cycles x in J that do not bound a
$4$-cycles x in J that do not bound a ![]() $2$-face are those that contain a
$2$-face are those that contain a ![]() $1$-face e of some
$1$-face e of some ![]() $\tau _j$ for
$\tau _j$ for ![]() $1\leq j \leq \ell $ but which are not contained in
$1\leq j \leq \ell $ but which are not contained in ![]() $h\left (\tau _j\right )\square H\left (\tau _j\right )$. However, as e is in
$h\left (\tau _j\right )\square H\left (\tau _j\right )$. However, as e is in ![]() $h\left (\tau _j\right )$, it has a parallel
$h\left (\tau _j\right )$, it has a parallel ![]() $1$-face f in
$1$-face f in ![]() $H\left (\tau _j\right )$. The unique cube
$H\left (\tau _j\right )$. The unique cube ![]() $c = x \square e$ that contains x and e has all
$c = x \square e$ that contains x and e has all ![]() $2$-faces except for the face bounded by x, which implies that x is contractible.
$2$-faces except for the face bounded by x, which implies that x is contractible.
Proof of Theorem 1.7. Let ![]() $T \in \mathscr {T}_p$ be fixed. By assumption, there is a k-dimensional cube X such that T is a subcomplex of X, and we may choose k minimal. We do not take the full
$T \in \mathscr {T}_p$ be fixed. By assumption, there is a k-dimensional cube X such that T is a subcomplex of X, and we may choose k minimal. We do not take the full ![]() $2$-skeleton for X, but instead we choose exactly those
$2$-skeleton for X, but instead we choose exactly those ![]() $2$-faces which either are in T or share no edge with T. Note that this makes
$2$-faces which either are in T or share no edge with T. Note that this makes ![]() $X = h(T)$. Let
$X = h(T)$. Let ![]() $\phi $ be a cubical embedding of the
$\phi $ be a cubical embedding of the ![]() $2$-skeleton of X into
$2$-skeleton of X into ![]() $Q^n_2$. Define the event
$Q^n_2$. Define the event ![]() $\mathcal {E}_\phi $, for
$\mathcal {E}_\phi $, for ![]() $Q \sim Q_2(n,p)$:
$Q \sim Q_2(n,p)$:
1. The
 $2$-faces of Q that are contained in the
$2$-faces of Q that are contained in the  $1$-skeleton of
$1$-skeleton of  $\phi (X)$ are exactly the
$\phi (X)$ are exactly the  $2$-faces of
$2$-faces of  $\phi (X)$.
$\phi (X)$.2. No other
 $2$-face in Q contains a
$2$-face in Q contains a  $1$-face of
$1$-face of  $\phi (T)$.
$\phi (T)$.3. There are no light
 $1$-faces in
$1$-faces in  $\phi (X\setminus T)$ and no light
$\phi (X\setminus T)$ and no light  $1$-faces within Hamming distance
$1$-faces within Hamming distance  $2k_p +2$ of
$2k_p +2$ of  $\phi (T)$, except possibly those in
$\phi (T)$, except possibly those in  $\phi (T)$. Here,
$\phi (T)$. Here,  $k_p$ is defined as in Lemma 4.4.
$k_p$ is defined as in Lemma 4.4.
We now estimate the probability of ![]() $\mathcal {E}_\phi $ under the law of
$\mathcal {E}_\phi $ under the law of ![]() $Q_2(n,p)$. Note that this probability does not depend on
$Q_2(n,p)$. Note that this probability does not depend on ![]() $\phi $, and so these estimates will be uniform in
$\phi $, and so these estimates will be uniform in ![]() $\phi $. First, observe that each edge of
$\phi $. First, observe that each edge of ![]() $\phi (T)$ has degree bounded independently of n on this event, so there are
$\phi (T)$ has degree bounded independently of n on this event, so there are ![]() $(e(T)*d)-O(1)\, 2$-faces which must be absent for
$(e(T)*d)-O(1)\, 2$-faces which must be absent for ![]() $\mathcal {E}_\phi $ to hold. There are
$\mathcal {E}_\phi $ to hold. There are ![]() $O(1)\, 2$-faces that must be present for
$O(1)\, 2$-faces that must be present for ![]() $\mathcal {E}_\phi $ to hold, also. There are also
$\mathcal {E}_\phi $ to hold, also. There are also ![]() $O\left (d^{2k_p+2}\right ) 1$-faces which are contained in the Hamming distance
$O\left (d^{2k_p+2}\right ) 1$-faces which are contained in the Hamming distance ![]() $\left (2k_p+2\right )$-neighbourhood of
$\left (2k_p+2\right )$-neighbourhood of ![]() $\phi (X)$, which we require to be not light. As the probability that a
$\phi (X)$, which we require to be not light. As the probability that a ![]() $1$-face is light is
$1$-face is light is ![]() $O( (1-p)^{n})$, we conclude that
$O( (1-p)^{n})$, we conclude that
 $$ \begin{align*} \mathbb{P}\left(\mathcal{E}_\phi\right) = \Theta\left( (1-p)^{e(T)d} \right) = \Omega\left( 2^{-(1-\epsilon)d}\right), \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(\mathcal{E}_\phi\right) = \Theta\left( (1-p)^{e(T)d} \right) = \Omega\left( 2^{-(1-\epsilon)d}\right), \end{align*} $$for some ![]() $\epsilon> 0$, where the second equality follows from Definition 1.6. So the expected number of occurrences of
$\epsilon> 0$, where the second equality follows from Definition 1.6. So the expected number of occurrences of ![]() $\mathcal {E}_\phi $ goes to infinity exponentially fast as
$\mathcal {E}_\phi $ goes to infinity exponentially fast as ![]() $n\to \infty $.
$n\to \infty $.
We can now show that some ![]() $\mathcal {E}_\phi $ now occurs with high probability by using a second moment computation (see [Reference Alon and Spencer1, Corollary 4.3.5]). Observe that if the Hamming distance of
$\mathcal {E}_\phi $ now occurs with high probability by using a second moment computation (see [Reference Alon and Spencer1, Corollary 4.3.5]). Observe that if the Hamming distance of ![]() $\phi (X)$ to
$\phi (X)$ to ![]() $\psi (X)$ is greater than
$\psi (X)$ is greater than ![]() $4$, then the events
$4$, then the events ![]() $\mathcal {E}_{\phi }$ and
$\mathcal {E}_{\phi }$ and ![]() $\mathcal {E}_{\psi }$ are independent. Let
$\mathcal {E}_{\psi }$ are independent. Let ![]() $\psi \sim \phi $ if
$\psi \sim \phi $ if ![]() $\mathcal {E}_{\phi }$ and
$\mathcal {E}_{\phi }$ and ![]() $\mathcal {E}_{\psi }$ are not independent. Then
$\mathcal {E}_{\psi }$ are not independent. Then
 $$ \begin{align*} \Delta_\phi^* = \sum_{\psi \sim \phi} \mathbb{P}\left[ \mathcal{E}_{\psi} \mid \mathcal{E}_{\phi} \right] \leq \sum_{\psi \sim \phi} 1 = O\left( d^{O(1)}\right), \end{align*} $$
$$ \begin{align*} \Delta_\phi^* = \sum_{\psi \sim \phi} \mathbb{P}\left[ \mathcal{E}_{\psi} \mid \mathcal{E}_{\phi} \right] \leq \sum_{\psi \sim \phi} 1 = O\left( d^{O(1)}\right), \end{align*} $$which is much smaller than the expected number of ![]() $\mathcal {E}_{\phi }$ that occur (which grows exponentially in n).
$\mathcal {E}_{\phi }$ that occur (which grows exponentially in n).
Hence, with the factorisation given by Theorem 4.10,
where ![]() $S_j = Q \cap \left (h\left (\tau _j\right ) \square H\left (\tau _j\right )\right )$ and where
$S_j = Q \cap \left (h\left (\tau _j\right ) \square H\left (\tau _j\right )\right )$ and where ![]() $\tau _j$ are the complexes from Theorem 4.6. For any embedding
$\tau _j$ are the complexes from Theorem 4.6. For any embedding ![]() $\phi $, if
$\phi $, if ![]() $\mathcal {E}_\phi $ occurs, then
$\mathcal {E}_\phi $ occurs, then ![]() $\phi (X) \in Q$ is such that
$\phi (X) \in Q$ is such that ![]() $\phi (X)=h(\phi (T))$. Moreover,
$\phi (X)=h(\phi (T))$. Moreover, ![]() $\phi (T) = \tau _j$ for some j with
$\phi (T) = \tau _j$ for some j with ![]() $1 \leq j \leq \ell $, as the Hamming distance of
$1 \leq j \leq \ell $, as the Hamming distance of ![]() $\phi (T)$ to any other light
$\phi (T)$ to any other light ![]() $1$-face is at least
$1$-face is at least ![]() $2k_p + 2$. By Lemma 4.9,
$2k_p + 2$. By Lemma 4.9, ![]() $\pi _1\left (S_j\right ) \cong F * \pi _1(T)$ for some free group F.
$\pi _1\left (S_j\right ) \cong F * \pi _1(T)$ for some free group F.
5 Below the threshold for maximal edges
In this section, we discuss in slightly more detail the idea that everything that can happen will happen.
First we show that in terms of finitely presented groups, everything can happen. The following is well known (see, e.g., [Reference Davis11, Appendix A] or [Reference Babson, Billera and Chan3, Section 2]):
Theorem 5.1. Let S be a finite simplicial complex with k vertices. Then S is homeomorphic to a cubical complex. Indeed, S is homeomorphic to a subcomplex of the k-dimensional cube.
Theorem 5.1 has the following immediate corollary:
Corollary 5.2. Let G be any finitely presented group. Then there exists a number ![]() $P_G>0$ such that whenever
$P_G>0$ such that whenever ![]() $0 < p < P_G$ and
$0 < p < P_G$ and ![]() $Q \sim Q_2(n,p)$, we have that G exists as a free factor in
$Q \sim Q_2(n,p)$, we have that G exists as a free factor in ![]() $\pi _1( Q)$ with high probability.
$\pi _1( Q)$ with high probability.
We give concrete bounds on ![]() $P_G$ for a few groups G in the following. The constructions used in Theorems 5.4 and 5.5 and Figure 1 are from joint work of Dejan Govc and the third author of this paper.
$P_G$ for a few groups G in the following. The constructions used in Theorems 5.4 and 5.5 and Figure 1 are from joint work of Dejan Govc and the third author of this paper.

Figure 1 Diagram of ![]() $T_2^\square $ with the vertices labeled.
$T_2^\square $ with the vertices labeled.
Theorem 5.3. Let ![]() $T^2$ be the
$T^2$ be the ![]() $2$-dimensional torus. For
$2$-dimensional torus. For  $0 < p < \left (1-(1/2)^{1/2^5}\right )\approx 0.021428$,
$0 < p < \left (1-(1/2)^{1/2^5}\right )\approx 0.021428$, ![]() $\pi _1(T_2) \cong \mathbb {Z} \times \mathbb {Z}$ is a free factor of
$\pi _1(T_2) \cong \mathbb {Z} \times \mathbb {Z}$ is a free factor of ![]() $\pi _1(Q)$ for
$\pi _1(Q)$ for ![]() $Q \sim Q_2(n,p)$ with high probability.
$Q \sim Q_2(n,p)$ with high probability.
Proof. We will create a cubical complex which is a subcomplex of ![]() $Q_2^4$ and is homeomorphic to
$Q_2^4$ and is homeomorphic to ![]() $T^2$. Let
$T^2$. Let ![]() $T_1^\square $ be the minimal cubical subcomplex of
$T_1^\square $ be the minimal cubical subcomplex of ![]() $Q_2^4$ with
$Q_2^4$ with ![]() $2$-faces given by
$2$-faces given by
 $$ \begin{align*} \{&(*,0,0,*), (0, *, 0, *), (*, 1, 0, *), (1, *, 0, *),\\&(*, 0, *, 1), (0, *, *, 1), (*, 1, *, 1), (1, *, *, 1),\\& (*, 0, 1, *), (0, *, 1, *), (*, 1, 1, *), (1, *, 1, *),\\& (*, 0, *, 0), (0, *, *, 0), (*, 1, *, 0), (1, *, *, 0)\}. \end{align*} $$
$$ \begin{align*} \{&(*,0,0,*), (0, *, 0, *), (*, 1, 0, *), (1, *, 0, *),\\&(*, 0, *, 1), (0, *, *, 1), (*, 1, *, 1), (1, *, *, 1),\\& (*, 0, 1, *), (0, *, 1, *), (*, 1, 1, *), (1, *, 1, *),\\& (*, 0, *, 0), (0, *, *, 0), (*, 1, *, 0), (1, *, *, 0)\}. \end{align*} $$Observe that ![]() $T_1^\square $ has
$T_1^\square $ has  $e\left (T_1^\square \right ) =32$. Hence, from Theorem 1.7, for
$e\left (T_1^\square \right ) =32$. Hence, from Theorem 1.7, for ![]() $0<p \neq 0$, if
$0<p \neq 0$, if  $ p < \left (1-(1/2)^{1/32}\right )$, the fundamental group of
$ p < \left (1-(1/2)^{1/32}\right )$, the fundamental group of ![]() $Q \sim Q_2(n,p)$ has a copy of
$Q \sim Q_2(n,p)$ has a copy of ![]() $\mathbb {Z} \times \mathbb {Z}$ in its free-product factorisation with high probability.
$\mathbb {Z} \times \mathbb {Z}$ in its free-product factorisation with high probability.
Theorem 5.4. Let ![]() $T_2$ be the projective plane. For
$T_2$ be the projective plane. For ![]() $p \neq 0$, if
$p \neq 0$, if  $ p < \left (1-(1/2)^{1/40}\right )\approx 0.017179$,
$ p < \left (1-(1/2)^{1/40}\right )\approx 0.017179$, ![]() $\pi _1(T_2) \cong \mathbb {Z} / 2\mathbb {Z}$ is a free factor of
$\pi _1(T_2) \cong \mathbb {Z} / 2\mathbb {Z}$ is a free factor of ![]() $\pi _1(Q)$ for
$\pi _1(Q)$ for ![]() $Q \sim Q_2(n,p)$ with high probability.
$Q \sim Q_2(n,p)$ with high probability.
Proof. Let ![]() $T_2^\square $ be the minimal cubical subcomplex of
$T_2^\square $ be the minimal cubical subcomplex of ![]() $Q_2^5$ with
$Q_2^5$ with ![]() $2$-faces given by
$2$-faces given by
 $$ \begin{align*} \{&(0,0, 0, *, *), (0, 0, 1, *, *), (0, 0, *, 1, *), (0, 0, *, *, 1),\\ &(0, 1, *, *, 0), (0, *, 0, 0, *), (0, *, 1, *, 0), (0, *, *, 0, 0),\\ &(0, *, *, 1, 0), (1, 0, *, 0, *), (1, *, 0, 0, *), (1, *, 0, *, 0),\\ & (*, 0, 0, *, 0), (*, 0, 1, 0, *), (*, 0, *, 0, 0), (*, 0, *, 0, 1),\\ & (*, 1, 0, 0, *), (*, *, 0, 0, 1), (*, 1, 0, *, 0), (*, *, 0, 1, 0)\}, \end{align*} $$
$$ \begin{align*} \{&(0,0, 0, *, *), (0, 0, 1, *, *), (0, 0, *, 1, *), (0, 0, *, *, 1),\\ &(0, 1, *, *, 0), (0, *, 0, 0, *), (0, *, 1, *, 0), (0, *, *, 0, 0),\\ &(0, *, *, 1, 0), (1, 0, *, 0, *), (1, *, 0, 0, *), (1, *, 0, *, 0),\\ & (*, 0, 0, *, 0), (*, 0, 1, 0, *), (*, 0, *, 0, 0), (*, 0, *, 0, 1),\\ & (*, 1, 0, 0, *), (*, *, 0, 0, 1), (*, 1, 0, *, 0), (*, *, 0, 1, 0)\}, \end{align*} $$so that  $e\left (T_2^\square \right ) =40$. Hence for
$e\left (T_2^\square \right ) =40$. Hence for ![]() $p \neq 0$, if
$p \neq 0$, if  $ p < \left (1-(1/2)^{1/40}\right )\approx 0.017179$, the fundamental group of
$ p < \left (1-(1/2)^{1/40}\right )\approx 0.017179$, the fundamental group of ![]() $Q \sim Q_2(n,p)$ has a torsion group in its free-product factorisation with high probability.
$Q \sim Q_2(n,p)$ has a torsion group in its free-product factorisation with high probability.
Theorem 5.5. Let  $G = \left \langle x, y \mid x y x^{-1} y \right \rangle $ be the fundamental group of the Klein bottle. If
$G = \left \langle x, y \mid x y x^{-1} y \right \rangle $ be the fundamental group of the Klein bottle. If  $0 < p < \left (1-(1/2)^{1/56}\right )\approx 0.01230134$ and
$0 < p < \left (1-(1/2)^{1/56}\right )\approx 0.01230134$ and ![]() $Q \sim Q_2(n,p)$, then with high probability,
$Q \sim Q_2(n,p)$, then with high probability, ![]() $\pi _1(Q)$ has G as a free factor.
$\pi _1(Q)$ has G as a free factor.
Proof. Let ![]() $T_3^\square $ be the minimal cubical subcomplex of
$T_3^\square $ be the minimal cubical subcomplex of ![]() $Q_2^5$ with
$Q_2^5$ with ![]() $2$-faces given by
$2$-faces given by
 $$ \begin{align*} \{&(*,*,1,0,0), (*,*,0,0,0), (0,*,*,0,0), (1,*,*,0,0),\\&(0,1,*,*,0),(1,1,*,*,0),(*,1,0,*,0),(*,1,1,*,0),\\ &(0,*,*,1,0),(1,*,*,1,0),(*,*,1,1,0),(*,0,*,1,0),\\ &(0,*,0,1,*),(1,*,0,1,*),(*,0,0,1,*),(*,1,0,1,*), \\ &(*,1,*,1,1),(0,*,*,1,1),(1,*,*,1,1),(*,*,1,1,1),\\ &(0,0,*,*,1),(1,0,*,*,1),(*,0,0,*,1),(*,0,1,*,1),\\ &(0,0,*,0,*),(1,0,*,0,*),(*,0,0,0,*),(*,0,1,0,*)\}. \end{align*} $$
$$ \begin{align*} \{&(*,*,1,0,0), (*,*,0,0,0), (0,*,*,0,0), (1,*,*,0,0),\\&(0,1,*,*,0),(1,1,*,*,0),(*,1,0,*,0),(*,1,1,*,0),\\ &(0,*,*,1,0),(1,*,*,1,0),(*,*,1,1,0),(*,0,*,1,0),\\ &(0,*,0,1,*),(1,*,0,1,*),(*,0,0,1,*),(*,1,0,1,*), \\ &(*,1,*,1,1),(0,*,*,1,1),(1,*,*,1,1),(*,*,1,1,1),\\ &(0,0,*,*,1),(1,0,*,*,1),(*,0,0,*,1),(*,0,1,*,1),\\ &(0,0,*,0,*),(1,0,*,0,*),(*,0,0,0,*),(*,0,1,0,*)\}. \end{align*} $$Then  $e\left (T_3^\square \right ) = 56$.
$e\left (T_3^\square \right ) = 56$.
Acknowledegments
We would like to thank Yuval Peled for interesting conversations that helped launch this work. We thank Dejan Govc for the constructions used in Theorems 5.4 and 5.5, and for Figure 1.
Funding statement
The first author was supported by NSF DMS #1547357, DMS #2005630 and CCF #1740761. He is also grateful to the Simons Foundation for a Simons Fellowship, and to the Deutsche Forschungsgemeinschaft (DFG) for a Mercator Fellowship. The second author is supported by an NSERC Discovery grant. The third author was supported in part by NSF-DMS #1352386 and NSF-DMS #1812028. She has also received funding from the European Union’s Horizon 2020 research and innovation program under Marie Skłodowska-Curie grant agreement No. 754462.
Conflicts of interest
None.