Article contents
WAVE FRONT HOLONOMICITY OF 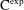 $\text{C}^{\text{exp}}$-CLASS DISTRIBUTIONS ON NON-ARCHIMEDEAN LOCAL FIELDS
$\text{C}^{\text{exp}}$-CLASS DISTRIBUTIONS ON NON-ARCHIMEDEAN LOCAL FIELDS
Published online by Cambridge University Press: 30 June 2020
Abstract
Many phenomena in geometry and analysis can be explained via the theory of 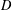 $D$-modules, but this theory explains close to nothing in the non-archimedean case, by the absence of integration by parts. Hence there is a need to look for alternatives. A central example of a notion based on the theory of
$D$-modules, but this theory explains close to nothing in the non-archimedean case, by the absence of integration by parts. Hence there is a need to look for alternatives. A central example of a notion based on the theory of 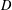 $D$-modules is the notion of holonomic distributions. We study two recent alternatives of this notion in the context of distributions on non-archimedean local fields, namely
$D$-modules is the notion of holonomic distributions. We study two recent alternatives of this notion in the context of distributions on non-archimedean local fields, namely 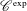 $\mathscr{C}^{\text{exp}}$-class distributions from Cluckers et al. [‘Distributions and wave front sets in the uniform nonarchimedean setting’, Trans. Lond. Math. Soc.5(1) (2018), 97–131] and WF-holonomicity from Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)]. We answer a question from Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)] by showing that each distribution of the
$\mathscr{C}^{\text{exp}}$-class distributions from Cluckers et al. [‘Distributions and wave front sets in the uniform nonarchimedean setting’, Trans. Lond. Math. Soc.5(1) (2018), 97–131] and WF-holonomicity from Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)]. We answer a question from Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)] by showing that each distribution of the 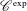 $\mathscr{C}^{\text{exp}}$-class is WF-holonomic and thus provides a framework of WF-holonomic distributions, which is stable under taking Fourier transforms. This is interesting because the
$\mathscr{C}^{\text{exp}}$-class is WF-holonomic and thus provides a framework of WF-holonomic distributions, which is stable under taking Fourier transforms. This is interesting because the 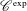 $\mathscr{C}^{\text{exp}}$-class contains many natural distributions, in particular, the distributions studied by Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)]. We show also another stability result of this class, namely, one can regularize distributions without leaving the
$\mathscr{C}^{\text{exp}}$-class contains many natural distributions, in particular, the distributions studied by Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)]. We show also another stability result of this class, namely, one can regularize distributions without leaving the 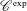 $\mathscr{C}^{\text{exp}}$-class. We strengthen a link from Cluckers et al. [‘Distributions and wave front sets in the uniform nonarchimedean setting’, Trans. Lond. Math. Soc.5(1) (2018), 97–131] between zero loci and smooth loci for functions and distributions of the
$\mathscr{C}^{\text{exp}}$-class. We strengthen a link from Cluckers et al. [‘Distributions and wave front sets in the uniform nonarchimedean setting’, Trans. Lond. Math. Soc.5(1) (2018), 97–131] between zero loci and smooth loci for functions and distributions of the 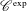 $\mathscr{C}^{\text{exp}}$-class. A key ingredient is a new resolution result for subanalytic functions (by alterations), based on embedded resolution for analytic functions and model theory.
$\mathscr{C}^{\text{exp}}$-class. A key ingredient is a new resolution result for subanalytic functions (by alterations), based on embedded resolution for analytic functions and model theory.
MSC classification
Information
- Type
- Algebra
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 1
- Cited by

