1. Introduction
The classical model of quantitative genetics assumes that genotypes differ in mean but the environmental variance (conditional variance of phenotype, given genotype) is homogeneous across genotypes (this model is referred to as HOM hereinafter). The assumption of homogeneity may not be valid and models with non-genetically structured departures from variance homogeneity were introduced in the 1990s (Foulley et al., Reference Foulley, San Cristobal, Gianola and Im1992; Gianola et al., Reference Gianola, Foulley, Fernando, Henderson and Weigel1992; San Cristobal et al., Reference San Cristobal, Foulley and Manfredi1993). In particular, Foulley & Quaas (Reference Foulley and Quaas1995) proposed models of heterogeneity for both residual and other components of variance.
A significant extension of the classical genetic model, with implications in breeding and evolutionary studies, posits that both mean and variability differ between genotypes (San Cristobal-Gaudy et al., Reference San Cristobal-Gaudy, Elsen, Bodin and Chevalet1998). (The extended model is labelled HET hereinafter). In animal and plant breeding, the focus is to change the mean of a trait by selection; the HET model opens the possibility to reduce variation by selection leading to more homogeneous products (e.g. Hill & Zhang, Reference Hill and Zhang2004; Mulder et al., Reference Mulder, Bijma and Hill2007, Reference Mulder, Bijma and Hill2008). In evolutionary biology, most of the models developed to study the maintenance of phenotypic variation assume that environmental variance is constant and explain the levels of variation by invoking a balance between the gain of genetic variance by mutation and its loss by different forms of selection and drift. Zhang & Hill (Reference Zhang and Hill2005) discuss models where environmental variance is partly under genetic control and study conditions for its maintenance under stabilizing selection.
Early evidence for a genetic component affecting environmental variation stems from comparisons of levels of variation between inbred lines and the F1 cross between them, with inbreds showing in general larger variance (Falconer & Mackay, Reference Falconer and Mackay1996). More recently, experimental evidence from isogenic chromosome substitution lines in Drosophila was presented by Mackay & Lyman (Reference Mackay and Lyman2005). Using genetic marker information, support for genetic variance heterogeneity has been reported also by Ordas et al., (Reference Ordas, Malvar and Hill2008) in maize and by Ansel et al. (Reference Ansel, Bottin, Rodriguez-Beltran, Damon, Nagarajan, Fehrmann, François and Yvert2008) in yeast. Ansel et al. (Reference Ansel, Bottin, Rodriguez-Beltran, Damon, Nagarajan, Fehrmann, François and Yvert2008) work with isogenic yeast cells and provide convincing evidence for heterogeneity of gene expression between genotypes, and identify three quantitative trait loci (QTLs) involved in its control.
With the exception of the limited experimental evidence specifically designed to test for genetic control of residual variability, support for the presence of genes acting on environmental variation can be sought fitting the HET model to data and studying the quality of its fit using modern computation tools. Evidence of this kind has been reported using litter size in pigs (Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003), adult weight in snails (Ros et al., Reference Ros, Sorensen, Waagepetersen, Dupont-Nivet, SanCristobal, Bonnet and Mallard2004), uterine capacity in rabbits (Ibáñez et al., Reference Ibáñez, Sorensen, Waagepetersen and Blasco2008), body weight in poultry (Rowe et al., Reference Rowe, White, Avendano and Hill2006; Wolc et al., Reference Wolc, White, Avendano and Hill2009), slaughter weight in pigs (Ibáñez et al., Reference Ibáñez, Varona, Sorensen and Noguera2007) and litter size and weight at birth in mice (Gutierrez et al., Reference Gutierrez, Nieto, Piqueras, Ibáñez and Salgado2006).
In all the cases where the quality of fit of the HET and HOM models was compared, various statistical criteria favoured the HET model. An important issue is to clarify whether these results are an artefact of the scale of measurement. Under the HET model, the skewness of the marginal distribution of the data is directly proportional to the correlation between additive genetic values affecting mean and variance (Ros et al., Reference Ros, Sorensen, Waagepetersen, Dupont-Nivet, SanCristobal, Bonnet and Mallard2004). However skewness can arise in other ways and if it does it can cause the HET model to fit better than the HOM model, leading to the spurious conclusion that genetic heterogeneity is present, when it is absent. Alternatively, genetic heterogeneity of variance may be present, in which case skewness from other causes may affect inferences about the correlation between genetic effects on mean and variance.
These problems can be partly addressed finding the appropriate scale on which to analyse the data using the Box–Cox transformation parameter (Box & Cox, Reference Box and Cox1964). A large body of literature dealing with transformations has developed following the classical paper of Box & Cox (Reference Box and Cox1964). Early work using transformations in animal breeding are Ibe & Hill (Reference Ibe and Hill1988) and Gianola et al. (Reference Gianola, Im, Fernando, Foulley, Gianola and Hammond1990). Compelling reasons for using the transformed model have typically been the need to achieve additivity of parameters at the level of the mean, constancy and homogeneity of the error variance and normality of the distribution of observations, although a transformation may not achieve all these goals simultaneously. Here, a transformation is sought that induces normality and linearity at the level of the conditional distribution of data. This is an important modelling assumption that must be fulfilled to avoid distorted inferences.
The main objective of this work is to investigate whether an analysis performed under the ‘appropriate’ scale still supports the HET model, or whether simpler models are to be preferred. The Box–Cox transformation parameter is regarded as an unknown to be inferred from the data, jointly, with the remaining parameters of the model. The model is fitted to data on litter size in pigs and rabbits. In order to obtain insight into the quality of inferences about the transformation parameter when it is fitted simultaneously with the remaining parameters, including the coefficient of correlation, a simulation study involving sets of data that differ in the number of repeated records per individual is also conducted.
Implementation of the model is via McMC (Markov chain Monte Carlo) and two steps are involved. The first step aims at finding the modal value of the marginal posterior distribution of the transformation parameter. In the second step, the model is fitted conditional on this modal value. Several McMC strategies were investigated and the reported results are based on a fixed scan hybrid algorithm that resulted in the best mixing behaviour.
The article is organized as follows: section 2 introduces the Box–Cox model with genetically structured variance heterogeneity and discusses the prior specifications and McMC implementation. Section 3 describes briefly the simulated, the rabbit and the pig litter size data. Section 4 contains the outcome of applying the methodology to the simulated data and to the rabbit and pig litter size data. A discussion is provided in section 5.
2. Methods
(i) Box–Cox model with genetically structured variance heterogeneity
The proposed model, labelled BCHET hereinafter, combines the HET model with a Box–Cox transformation parameter. Let y=(y i)i=1n be the vector of records, which are assumed to be strictly positive. The model states that conditionally on the vectors of location and dispersion parameters, for some unknown transformation parameter λ, the distribution of the transformed vector of phenotypic data y(λ)=(y i(λ))i=1n satisfies the normal theory assumptions, that is,

Here R, the conditional variance of the sampling model, is the diagonal matrix with ![]() on its diagonal, and is interpreted as the environmental variance. The transformation is defined as follows (Box & Cox, Reference Box and Cox1964):
on its diagonal, and is interpreted as the environmental variance. The transformation is defined as follows (Box & Cox, Reference Box and Cox1964):

Note that here the transformation parameter λ is introduced to guarantee normality of the conditional distribution and linearity of the conditional expectation, but not to achieve constant variance. Indeed, R in (1) is heterogeneous due to the presence of ![]() , a* and p*; the last two terms being specific to each individual.
, a* and p*; the last two terms being specific to each individual.
Matrices X, ![]() , Z and W are known incidence matrices, the scalar μ is the mean, the vector b contains the regression coefficients, the scalar exp (μ*) is the mean environmental variance, while the vector exp (b*) contains the environment-specific scaling effects. The vectors of genetic effects a=(ai
)i=1n 1 and
, Z and W are known incidence matrices, the scalar μ is the mean, the vector b contains the regression coefficients, the scalar exp (μ*) is the mean environmental variance, while the vector exp (b*) contains the environment-specific scaling effects. The vectors of genetic effects a=(ai
)i=1n 1 and ![]() are assumed to jointly follow a multivariate normal distribution
are assumed to jointly follow a multivariate normal distribution

where A is the known additive relationship matrix and G is a 2×2 covariance matrix

In equation (3), ρ is the coefficient of genetic correlation between a and a*, and σa2 and ![]() are the additive genetic variances at the level of the mean and environmental variance, respectively. Vectors
are the additive genetic variances at the level of the mean and environmental variance, respectively. Vectors ![]() and
and ![]() represent permanent environmental effects (on mean and on variance) and are assumed to be independently normally distributed with
represent permanent environmental effects (on mean and on variance) and are assumed to be independently normally distributed with

where I is the identity matrix, and σp2 and σp*2 are the permanent environmental variances at the level of the mean and environmental variance, respectively.
The coefficient of skewness of the marginal distribution of the datum yi (λ) (marginalized over a, a*, p, p*) under BCHET is (Ros et al., Reference Ros, Sorensen, Waagepetersen, Dupont-Nivet, SanCristobal, Bonnet and Mallard2004)

indicating that the sign of the coefficient of skewness is governed by ρ.
(ii) Conditional likelihood function
The conditional likelihood is proportional to the probability density function of the data given the parameters, including a, a*, p, p*. Written in terms of the original untransformed observations, from (1), this leads to

where
R and y(λ) have been defined in connection with (1), and the Jacobian of the transformation is

(iii) Prior specifications
The general size and range of the transformed phenotypic data y(λ) may depend strongly on λ, and so would the interpretation of the model parameters. Therefore, the prior distributions must be carefully chosen to avoid meaningless inferences. Here, we follow the approach suggested in Box & Cox (Reference Box and Cox1964) to establish the conditional prior distribution, given λ, whereby the relationship between parameters is consistent under different values of λ. Calculations sketched out in Appendix A show that the prior distribution of the parameters that depend on λ is

(iv) Posterior distribution
Including in (6) the prior distribution of the parameters conditionally independent of λ, ![]() , leads to the joint prior distribution for all model parameters. This takes the form
, leads to the joint prior distribution for all model parameters. This takes the form

The joint posterior distribution is proportional to the product of (4) and the prior (7).
The inferential strategy in this study is based on, firstly, estimating the modal value of λ from its marginal posterior distribution. This is done fitting jointly all the parameters of the BCHET model, including the correlation coefficient ρ. The final inferences are based on a second implementation of the BCHET model, where the value of λ is fixed at its posterior mode.
(v) Model comparison and model checking
Models are compared using the pseudo marginal probability of data. This is a method of comparison (Gelfand, Reference Gelfand, Gilks, Richardson and Spiegelhalter1996) based on the relative global fits of the models. In addition, the skewness of the conditional distribution of the data under both models is investigated using posterior predictive model checking. This provides insight into the ability of the models to address a specific feature of the data that is of primary interest. In this study, one wishes to investigate whether the transformation succeeds in inducing normality at the level of the conditional distribution of the data, which is a basic premise of the model and a necessary condition for correct inferences. Details are in Appendix B.
(vi) McMC algorithm
The BCHET model (1) is implemented using an McMC algorithm, where the components in the model are updated sequentially. The algorithm is based on a combination of Gibbs updates, updates based on random walk proposals and updates based on Langevin–Hastings proposals. In addition, a reparameterization of the additive genetic values (a, a*) to standard normal variates (γ, γ*) was performed to improve the mixing of the algorithm.
In summary, the BCHET model (1) is implemented using the following McMC algorithm.
• Metropolis–Hasting steps:
1. (λ, μ, exp (μ*),b) updated jointly using a random walk proposal for λ and fully conditional proposals for (μ, exp (μ*),b).
2. exp (b*) and (γ, γ*) updated using Langevin–Hastings proposals.
3. (p, p*) updated using a fully conditional proposal for p and a Langevin–Hastings proposal for p*.
4. (σa2, σa*2) updated using random walk proposals (on the log scale).
5. ρ updated using a random walk proposal.
• Gibbs Steps: σp2, σp*2.
Convergence of the algorithm was checked informally using traceplots. We report confidence intervals of Monte Carlo estimates of various posterior means in order to give an idea of the accuracy of the Monte Carlo computations.
3. Data
(i) Simulated data
It is difficult to gain insight about the degree of identifiability of λ in the marginal likelihood when it is fitted jointly with ρ (together with the remaining parameters of the model), because the marginal likelihood cannot be written in closed form. One can conjecture that the number of repeated records per individual plays an important role. Therefore, a small simulation study was conducted to investigate how the quality of inferences about λ from its marginal posterior distribution is affected with increasing number of records per individual. A family structure based on the pedigree of the rabbit litter size data was simulated, with 1, 2, 3, 5 and 10 records per individual. The true value of λ was set equal to 1, and of ρ equal to −0·74, in all cases. These true values are compared with those inferred from the marginal posterior distribution of these parameters.
(ii) Rabbit litter size data
The data originate from a selection experiment for uterine capacity in rabbits spanning 10 generations, carried out at the Universidad Politécnica de Valencia. Uterine capacity will be referred to as litter size hereinafter. Details of the selection experiments and data can be found in Argente et al. (Reference Argente, Santacreu, Climent, Bolet and Blasco1997) and Ibáñez et al. (Reference Ibáñez, Sorensen, Waagepetersen and Blasco2008). The number of individuals in the pedigree was 1281, where 929 of them had litter size records (a maximum of four records per female), and the total number of records was 2996. Reproduction was organized in discrete generations.
(iii) Pig litter size data
The data originate from a large-scale selection experiment for the total number of piglets born per litter (referred to as litter size hereinafter). Details of the selection experiments and data descriptions are provided in Sorensen et al. (Reference Sorensen, Vernersen and Andersen2000). The number of individuals in the pedigree was 6437, where 4078 of them had phenotypic records, and the total number of litter size records was 9778.
4. Results
(i) Simulation study
The results reported for different simulated data sets were obtained from McMC output consisting of between 1 000 000 and 3 000 000 iterations. The total number of stored samples was 10 000 for each simulated data set and these were used to infer the marginal distribution of λ.
Results are shown in Table 1. The 95% posterior intervals of λ always include the true value 1 in all simulated data sets, and inferences are sharper with increasing number of records per individual. The posterior distributions are symmetric (not shown); posterior means and modes agree to two decimal figures.
Table 1. MC estimates of posterior means and 95% posterior interval (95% P.I.) for λ and ρ with increasing number of repeated records per individual

Estimates of the posterior means are clearly subject to sampling variation of the data. This frequentist variation may be characterized by replication of the experiment, but this was judged to be computationally too demanding.
The simulation study showed that the posterior correlation of λ and ρ decreased with increasing number of records per individual (not shown). In the data set mimicking the rabbit structure, this posterior correlation is equal to 0·34. The results indicate that the size of the smallest data set, corresponding to the rabbit experiment, is adequate to arrive at satisfactory inferences about features of the marginal posterior distribution of λ.
(ii) Analyses of litter size in rabbits and pigs
(a) The models
The models for the rabbit and pig data are similar to those in Sorensen & Waagepetersen (Reference Sorensen and Waagepetersen2003) and Ibáñez et al. (Reference Ibáñez, Sorensen, Waagepetersen and Blasco2008). The scalar μ is the mean and the scalar exp (μ*) is the mean environmental variance. In the rabbit data, vector b contains year–season effects with 30 levels and parity order effects with four levels (first, second, third and fourth or higher parities). The vector exp (b*) contains the environment-specific scalings effects associated with year–season and parity. Vectors a and a* contain additive genetic values with 1281 levels, and vectors p and p* contain permanent environmental effects with 929 levels. The parameters of the scaled inverted chi-square distributions associated with σa2, σa*2, σp2, σp*2, are ν=5, ![]() ,
, ![]() ,
, ![]() and
and ![]() . In the pig data, b is a vector containing the effects of four categorical variables: parity (eight levels), season (four levels), herd (50 levels) and type of insemination (artificial or natural). The vector exp (b*) contains the environment-specific scalings effects with two categorical variables: parity (eight levels) and type of insemination (artificial or natural). Vectors a and a* contain additive genetic effects with 6437 levels, and vectors p and p* contain permanent environmental effects with 4078 levels. The parameters of the scaled inverted chi-square distributions associated with σa2, σa*2, σp2, σp*2, are ν=5,
. In the pig data, b is a vector containing the effects of four categorical variables: parity (eight levels), season (four levels), herd (50 levels) and type of insemination (artificial or natural). The vector exp (b*) contains the environment-specific scalings effects with two categorical variables: parity (eight levels) and type of insemination (artificial or natural). Vectors a and a* contain additive genetic effects with 6437 levels, and vectors p and p* contain permanent environmental effects with 4078 levels. The parameters of the scaled inverted chi-square distributions associated with σa2, σa*2, σp2, σp*2, are ν=5, ![]() ,
, ![]() ,
, ![]() and
and ![]() . The hyperparameters of the prior distributions are taken from Sorensen & Waagepetersen (Reference Sorensen and Waagepetersen2003) and Ibáñez et al. (Reference Ibáñez, Sorensen, Waagepetersen and Blasco2008).
. The hyperparameters of the prior distributions are taken from Sorensen & Waagepetersen (Reference Sorensen and Waagepetersen2003) and Ibáñez et al. (Reference Ibáñez, Sorensen, Waagepetersen and Blasco2008).
(b) The mode of λ
Inference about the modal value of λ from its marginal posterior distribution was accomplished running the McMC algorithm with a chain length equal to 1 405 000 in the rabbit data and 750 000 in the pig data. In the rabbit data, the Monte Carlo estimate of the mode of λ was equal to 1·41 and the 95% posterior interval was (1·30, 1·51). In the pig data, the corresponding figures are 1·39 and (1·32, 1·47). In both cases, the posterior distribution was symmetric (the estimated posterior means agreed with the modal values to two decimal figures). In neither case do the 95% posterior intervals of λ contain the value 1. This indicates that in both species the phenotypic data are not conditionally normally distributed under λ=1.
In the rabbit data, the 95% confidence interval of the posterior mean, reflecting Monte Carlo sampling variation, was (1·405, 1·411) and (1·390,1·398) in the pig data, indicating that the degree of accuracy of the Monte Carlo computation was satisfactory.
In order to gain insight into the sensitivity of inferences on prior assumptions, a similar analysis was conducted with scale parameters ![]() ,
, ![]() ,
, ![]() ,
, ![]() set equal to 0·124, 0·024, 0·066 and 0·018 in the rabbit data and to 0·234, 0·014, 0·090 and 0·009 in the pig data. Under these prior assumptions, the posterior mode of λ in the rabbit data is 1·40, and the 95% posterior interval for λ was (1·31, 1·51). In the pig data, the corresponding figures are 1·39 and the 95% posterior interval is (1·32, 1·46) reflecting minor differences with the original values in both cases.
set equal to 0·124, 0·024, 0·066 and 0·018 in the rabbit data and to 0·234, 0·014, 0·090 and 0·009 in the pig data. Under these prior assumptions, the posterior mode of λ in the rabbit data is 1·40, and the 95% posterior interval for λ was (1·31, 1·51). In the pig data, the corresponding figures are 1·39 and the 95% posterior interval is (1·32, 1·46) reflecting minor differences with the original values in both cases.
(c) Variance components
Results for the rabbit data set are shown in the top rows of Table 2. The figures report Monte Carlo estimates of posterior means, 95% posterior intervals and 95% Monte Carlo confidence intervals for chosen parameters of BCHET under λ=1 (M) and BCHET under the modal value of λ=1·41 (Mλ). Estimates of σa2 and σp2 increase by factors of 3 and 7, respectively, when the data are analysed under Mλ, as expected, due to dependence on λ. Despite the lack of prior dependence of σa*2 and σp*2 on λ, the posterior mean of σa*2 decreases by a factor >2 under Mλ, while σp*2 is slightly reduced. The posterior mean of ρ changes from −0·73 under M to 0·28 under Mλ, and the 95% posterior interval of ρ includes zero under Mλ.
Table 2. MC estimates of posterior means (first row for each model), 95% posterior intervals (second row for each model) and of 95% Monte Carlo confidence intervals (third row for each model) of chosen parameters based on models M and Mλ, for the rabbit litter size data (top) and on models M and Mλ for the pig data set (bottom).

Under M, the smallest posterior mean of the environmental variance (95% posterior intervals in brackets), corresponding to year–season 30 and parity 1, was 3·28 (1·55,5·34). The corresponding largest number, for year–season 15 and parity 3 was 8·23 (4·61, 11·92). Under Mλ, the corresponding figures are 11·16 (5·72, 17·56) and 36·92 (26·39, 52·99).
Under M, there is one heritability for each combination of environment-specific scalings effects ![]() at the level of the environmental variance. The average heritability over all combinations of environmental effects is 0·12 with a minimum of 0·09 (0·04, 0·14) (year–season effect 15 and parity 3) and a maximum of 0·18 (0·09, 0·28) (year–season effect 30 and parity 1). Under Mλ, the average heritability is 0·10 with a minimum of 0·07 (0·03, 0·11) (year–season effect 15 and parity 3) and a maximum of 0·19 (0·08, 0·31) (year–season effect 30 and parity 1), reflecting little change due to the transformation. It can be shown that the prior heritability is not affected by the transformation (to the degree of approximation (A1)), a result that agrees with the conclusion from Solomon & Taylor (Reference Solomon and Taylor1999), who worked with a variance homogeneous, one-way classification model.
at the level of the environmental variance. The average heritability over all combinations of environmental effects is 0·12 with a minimum of 0·09 (0·04, 0·14) (year–season effect 15 and parity 3) and a maximum of 0·18 (0·09, 0·28) (year–season effect 30 and parity 1). Under Mλ, the average heritability is 0·10 with a minimum of 0·07 (0·03, 0·11) (year–season effect 15 and parity 3) and a maximum of 0·19 (0·08, 0·31) (year–season effect 30 and parity 1), reflecting little change due to the transformation. It can be shown that the prior heritability is not affected by the transformation (to the degree of approximation (A1)), a result that agrees with the conclusion from Solomon & Taylor (Reference Solomon and Taylor1999), who worked with a variance homogeneous, one-way classification model.
Figure 1 shows the estimated marginal posterior distributions of σa2, σa*2, σp2 and σp*2 based on Mλ. The solid line superimposed on each graph represents the densities of the scaled inverted chi-square prior distributions of σa2, σa*2, σp2 and σp*2. On the top of the figure, the variance parameters σa2, σa*2, σp2 and σp*2 are assigned scaled inverted chi-squared distributions with degrees of freedom ν=5 and scale parameters ![]() ,
, ![]() ,
, ![]() and
and ![]() , resulting in prior modes equal to 0·35, 0·07, 0·19 and 0·05, respectively. The bottom of the figure shows corresponding distributions obtained setting
, resulting in prior modes equal to 0·35, 0·07, 0·19 and 0·05, respectively. The bottom of the figure shows corresponding distributions obtained setting ![]() ,
, ![]() ,
, ![]() and
and ![]() , leading to prior modes equal to 0·09, 0·02, 0·05 and 0·013, respectively, a four-fold reduction. Prior input does not influence inferences about σa2 and σp2 but σa*2 and σp*2 are strongly affected. In fact, the posterior distribution of σa*2 shows little divergence from the prior distribution in both scenarios, suggesting that there is little information in the data about this parameter.
, leading to prior modes equal to 0·09, 0·02, 0·05 and 0·013, respectively, a four-fold reduction. Prior input does not influence inferences about σa2 and σp2 but σa*2 and σp*2 are strongly affected. In fact, the posterior distribution of σa*2 shows little divergence from the prior distribution in both scenarios, suggesting that there is little information in the data about this parameter.

Figure 1. Top: Monte Carlo estimates of σa2 and σa
*2 (left) and σp2 and σp*2 (right) under Mλ for rabbit data. The thick lines represent the prior scaled inverted chi-square densities with degrees of freedom ν=5 and scale parameters ![]() ,
, ![]() ,
, ![]() and
and ![]() under Mλ. Bottom: as above, with ν=5 and
under Mλ. Bottom: as above, with ν=5 and ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
In conclusion, the analysis indicates that the support for a genetically structured variance heterogeneous model in the rabbit data is markedly weaker when the data are analysed under a scale corresponding to the modal value of λ.
Estimated posterior means of dispersion parameters for the pig data set are shown in the bottom rows of Table 2. The figures show a similar pattern as for the rabbit litter size data. The posterior mean of ρ changes sign from negative under M (BCHET with λ=1) to positive under Mλ (BCHET conditional on the mode of λ=1·39). However, in contrast with the rabbit data, the 95% posterior interval of ρ does not include the value ρ=0. Thus, the analysis in the transformed scale results in a strong, positive correlation between additive genetic values affecting mean and variance.
Under M, the smallest posterior mean of the environmental variance, corresponding to natural insemination and parity 1, is 5·87 (5·27, 6·53). The largest posterior mean, corresponding to artificial insemination and parity 2, is 9·33 (8·27, 10·42). Under Mλ, these figures are 33·01 (30·01, 36·02) and 58·06 (47·59, 69·62).
Under M, there is one heritability for each combination of the environment-specific scalings effects ![]() . The average heritability is 0·16 with a minimum of 0·14 (0·11, 0·18) (artificial insemination and parity 2) and a maximum of 0·20 (0·16, 0·25) (natural insemination and parity 1). Under Mλ, the average heritability is 0·14 with a minimum of 0·12 (0·08, 0·15) (artificial insemination and parity 6) and a maximum of 0·18 (0·13, 0·23) (natural insemination and parity 1).
. The average heritability is 0·16 with a minimum of 0·14 (0·11, 0·18) (artificial insemination and parity 2) and a maximum of 0·20 (0·16, 0·25) (natural insemination and parity 1). Under Mλ, the average heritability is 0·14 with a minimum of 0·12 (0·08, 0·15) (artificial insemination and parity 6) and a maximum of 0·18 (0·13, 0·23) (natural insemination and parity 1).
Figure 2 illustrates the sensitivity of inferences to prior assumptions for the pig data. In contrast with the rabbit data, a five-fold reduction in prior modes leads to very small changes in the posterior distributions, except for σp*2.

Figure 2. Top: Monte Carlo estimates of σa2 and σa*2 (left) and σp2 and σp*2 (right) under Mλ for pig data. The thick lines represent the prior scaled inverted χ2 densities with degrees of freedom ν=5 and scale parameters ![]() ,
, ![]() ,
, ![]() and
and ![]() under Mλ. Bottom: as above, with ν=5 and scale parameters
under Mλ. Bottom: as above, with ν=5 and scale parameters ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
To give a further idea of the sensitivity of inferences to λ, the rabbit data were also analysed conditional on the lower (λ=1·30) and the upper λ=1·51 cut-off points of the 95% posterior interval for λ. The posterior distribution of σa*2 was hardly affected, but the posterior distribution of ρ shifted to the right with increasing values of λ. The posterior means and 95% posterior intervals for λ=1·30, 1·41 and 1·51 were −0·10 (−0·55, 0·37), 0·28 (−0·24, 0·79) and 0·56 (0·13, 0·96). Although the distributions are highly overlapping, the support at λ=1·51 does not contain the value of ρ=0. At the modal value λ=1·41, the residual skewness is practically zero, and the assumption of conditional normality is satisfied. Lower and higher values of λ generate slight negative and positive skewness, respectively (results not shown), and this results in the observed pattern of ρ.
The 95% confidence intervals for the MC estimates of posterior means indicate that the lengths of the chains (sample sizes) result in adequate accuracy in both analyses.
(d) Model comparison and posterior model checking
The Monte Carlo estimate of the pseudo marginal probabilities of the rabbit data under M and under Mλ are equal to −3930·7 and −3919·5, respectively. The corresponding figures for the pig data are −23 999·0 for M and −15 269·1 for Mλ. In both cases, the best fits correspond to the analysis on the transformed scale.
Figure 3 shows histograms of posterior realizations of the discrepancy measure (17) under M and under Mλ in the rabbit data and M and Mλ in the pig data, designed to test skewness at the level of the conditional distribution of the data. In both species, the distribution of (17) discloses negative skewness when the data are analysed in the original scale (first and third histograms from left), whereas under the transformed model, the mean residual skewness is zero (second and fourth histograms from left). This indicates that the transformation was successful in inducing normality at the level of the conditional distribution of the data.

Figure 3. Histograms of posterior predictive realization of ![]() , designed to test residual skewness for the rabbit data (first two from left) and pig data (last two from left). The first and third figures correspond to analyses on the original scale; the second and fourth to analyses on the transformed scale.
, designed to test residual skewness for the rabbit data (first two from left) and pig data (last two from left). The first and third figures correspond to analyses on the original scale; the second and fourth to analyses on the transformed scale.
Since estimates of posterior means of σa*2 and σp*2 in the rabbit data were fairly small under Mλ, and sensitive to prior specifications, we investigated further whether heterogeneity could be accounted solely by systematic effects, without inclusion of random effects at the level of the environmental variance. In this model, labelled HMλ, σa*2=0 and σp*2=0. The ![]() for HMλ is −3927·3 indicating a poorer fit than the full model and thus support for σa*2 and σp*2. The corresponding figure for the pig data for HMλ is −15 297·1, indicating also support for the full model.
for HMλ is −3927·3 indicating a poorer fit than the full model and thus support for σa*2 and σp*2. The corresponding figure for the pig data for HMλ is −15 297·1, indicating also support for the full model.
Both data sets were also analysed using the classical infinitesimal model with homogeneous variance, conditional on the modal value of the Box–Cox parameter. The posterior mode of λ (95% posterior interval in brackets) is 1·41 (1·33,1·49), in the rabbit data and 1·26 (1·21,1·31) in the pig data. The ![]() under the classical infinitesimal model is −4009·5 in the rabbit data and −15 337·23 in the pig data. In the rabbit data, the result indicates that the global fit of the infinitesimal model is worse than that obtained fitting the genetically structured variance heterogeneity model Mλ (and also worse than model M). In the pig data, the global fit from the classical infinitesimal model is worse than that obtained fitting the genetically structured variance heterogeneity model Mλ, but better than the M model.
under the classical infinitesimal model is −4009·5 in the rabbit data and −15 337·23 in the pig data. In the rabbit data, the result indicates that the global fit of the infinitesimal model is worse than that obtained fitting the genetically structured variance heterogeneity model Mλ (and also worse than model M). In the pig data, the global fit from the classical infinitesimal model is worse than that obtained fitting the genetically structured variance heterogeneity model Mλ, but better than the M model.
The overall conclusion from the analyses of both data sets is that the transformed model induces conditional normality of the sampling distribution of the data (as opposed to the untransformed model), and that the transformed model is best supported in terms of the overall fit relative to the untransformed model. Under the transformed model there is considerably weaker evidence in the rabbit data for a genetically structured variance heterogeneity model than that provided by the analysis in the original scale. In the pig data set, the transformed model provides evidence for the presence of genetic variation at the level of the environmental variance, but in contrast with the results of the analysis in the original scale, the correlation ρ between additive genetic values affecting mean and variance is strong and positive.
5. Discussion
This work has confirmed that inferences at the level of the residual variance are strongly affected by the scale on which the data are analysed. This is certainly not a surprising result, but it rather reflects the difficulties in learning about the state of nature via a statistical analysis of data using models that build on strong distributional assumptions. One option is to avoid introducing such assumptions and complex modelling, and instead use simple functions of the data specifically designed to uncover the structure associated with a genetic component at the level of variance. Uncertainty concerning the final result could be incorporated using resampling methods, such as permutation tests or the bootstrap. A limitation of this option is the difficulty of finding a measure that is free from artefacts and that signals unambiguously the existence of genetic variance on variance. Another limitation is whether the structure in the data related to the existence of genetic variance on variance is strong enough to be detected by these means. For example, we have attempted to regress sampling variance of repeated measurements within individuals in daughters on mothers and could not find a convincing pattern. A second option, followed in this work, is to use a fully parametric model that addresses specifically the putative presence of a genetic component affecting environmental variance. Support for the model is sought by comparing the quality of its fit with that of other models that neglect the presence of a genetic component on the environmental variance, using various criteria. An unambiguous favourable comparison is interpreted as evidence for the presence of a genetic component on the environmental variance. Spurious results can never be excluded using this approach either. The exercise reflects merely that, among the models considered, there is one that does better than the rest. It does not provide decisive evidence.
The results of the study differ in the rabbit and pig data. The transformed rabbit litter size data yields a Monte Carlo estimate of the posterior mean for the correlation (95% posterior interval in brackets) of 0·28 (−0·24, 0·79), compared to a value equal to −0·73 (−0·89, −0·50) obtained in the untransformed data. Further, the additive genetic variance at the level of the environmental variance based on the transformed data falls by a factor of 2·4, and its posterior distribution is considerably affected by prior assumptions. Thus, under the transformed scale, the support for a genetic component at the level of the environmental variance is markedly weaker. The picture is different for the pig litter size data. The correlation changes from −0·64 (−0·82, −0·45) to 0·70 (0·44,0·98) under the transformed model, the additive genetic variance at the level of the environmental variance falls by a factor of <2, and its posterior distribution is very little affected by prior input. On the basis of these results, the statistical evidence in favour of the genetically heterogeneous variance model is not disputed, but in the transformed model the correlation changes sign and its posterior distribution has positive support.
There has been some controversy concerning how inferences should be drawn using the Box–Cox family of transformations. Bickel & Doksum (Reference Bickel and Doksum1981) show that joint inferences of the transformation and the remaining parameters of a linear model lead to highly correlated estimates and the marginal variances of the latter are much larger compared to the conditional variances for fixed values of the transformation parameter. Hinkley & Runger (Reference Hinkley and Runger1984) and Box & Cox (Reference Box and Cox1982) argue that inferences should be drawn conditional on a fixed value of the transformation parameter, since linear model parameters have meaning only with reference to a particular scale. This is an important point that argues against reporting inferences marginalizing over the distribution λ. The consequences on statements of posterior uncertainty fitting the model conditional on λ do not change the conclusions of our analysis. For example, for the rabbit litter size data, the 95% posterior interval of ρ changes from (−0·24, 0·79) for fixed λ, to (−0·36, 0·80) when the analysis is done marginalizing over λ. In the pig data, these figures are (0·44, 0·98) and (0·36, 0·99). In the context of prediction of future data, as in De Oliveira et al. (Reference De Oliveira, Kedem and Short1997, Reference De Oliveira, Fokianos and Kedem2002) and Lee et al. (Reference Lee, Lin, Lee and Hsu2005), it may be sensible that posterior intervals of future data incorporate uncertainty about λ.
The problem of scale has clearly important implications in an animal breeding context and we consider two scenarios. First, assume that one is interested in selecting at the level of the mean only (via predicted additive genetic values) and that the ‘correct’ model is the transformed BCHET model. Here, the term ‘correct’ model is to be understood as the model under which the assumptions for the data in question hold. Does it make any difference whether predictions and subsequent selection decisions are obtained via the transformed BCHET or the untransformed HET model? For the pig data (the rabbit data show an almost identical pattern), the left-hand side of Figure 4 shows that there is a very close positive association between the posterior means of additive genetic values affecting the mean under both models, implying that approximately the same individuals are selected when ranked on the basis of either model. On the other hand, the right-hand side of Figure 4 discloses no association between additive genetic values affecting the variance under both models. Therefore, the efficiency of selection at the level of the variance will be impaired if selection operates on the basis of the ‘incorrect’ model.

Figure 4. Left: plot of the posterior means of the vector a under M (aλ=1) versus the posterior means of the vector a under Mλ (aλ=1·393). Right: plot of the posterior means of the vector a* under M (aλ=1*) versus the posterior means of the vector a* under Mλ (aλ=1·393*) in pig litter size data.
In the second scenario, assume again that the ‘correct’ model is BCHET and selection under this model (to change the mean, the variance, or both) leads to displacements at the level of additive genetic values affecting mean and variance. One may wish to know how changes in the transformed scale translate into changes in the original scale and report results in that metric. Under the BCHET model, genetic values operating on mean and variance are additive and the correlation between them has a clear interpretation. When transformed back to the original scale, genetic values are no longer additive and the correlation is difficult to define. However, the problem can be investigated by deriving the mean and variance of the conditional distribution of the data in the original scale, given knowledge of the transformed BCHET model. More specifically, consider the simplified version of the transformed BCHET model y(λ)|λ, μ,μ*, a, a*~N (1μ+Za, exp (1μ*+Za*)). A Taylor expansion shows that the mean and variance in the original scale can be approximated by

and
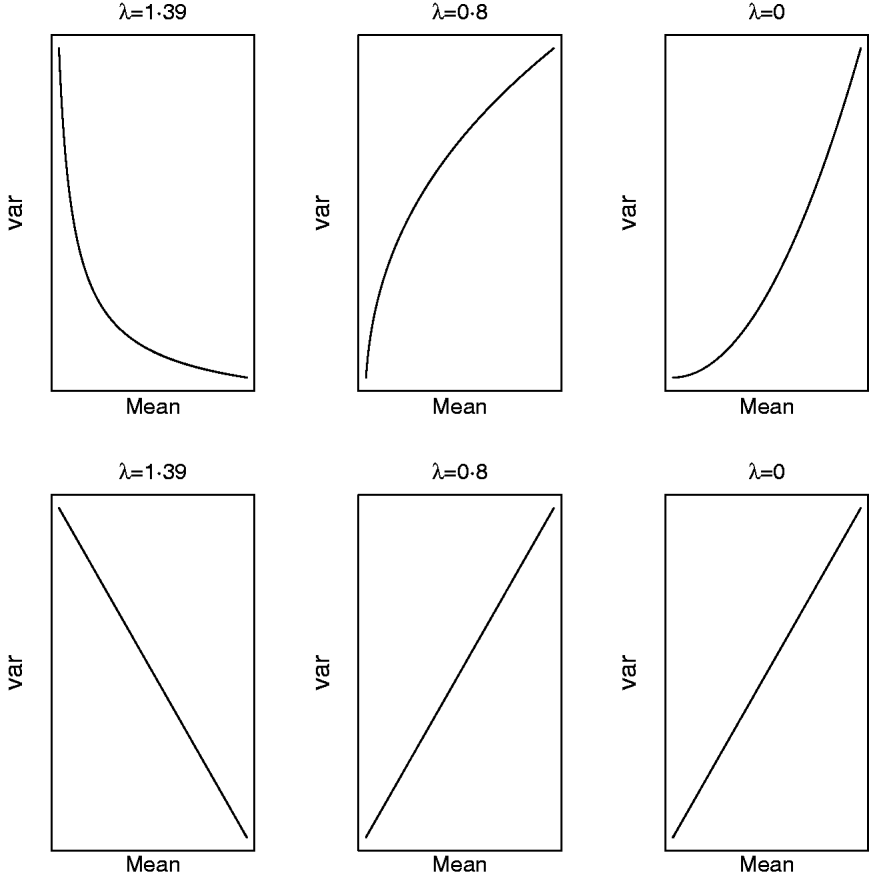
respectively. For a given value of λ (and μ) one can study how the mean and variance in the original scale change due to displacements in (a,a*|ρ) on the transformed scale. Clearly, (a,a*|ρ) is non-linearly related to both (8) and (9) and Figure 5 illustrates some special cases. When λ=1·39, the variance in the original scale falls at a decreasing rate as ai increases and ai * is kept constant (implying ρ=0 in the transformed scale). The same scenario at a value of λ=0·8/0·0 shows that the variance in the original scale grows at a decreasing/increasing rate as ai increases. On the other hand, selection for ai * in the transformed scale, keeping ai constant (implying again ρ=0 in the transformed scale), leads to a negative linear relationship between mean and variance in the original scale when λ=1·39. When λ=0·8 or λ=0·0, this relationship is linear and positive, respectively. When ai and ai * change simultaneously (results not shown), the relationship between mean and variance in the original scale is again highly dependent on λ and ρ. The overall conclusion is that it is not possible to make general statements about how changes taking place on the transformed scale translate into changes in the original metric.
In this work, the Box–Cox transformation was used to achieve normality (and not homogeneity of variance) at the level of the conditional distribution of the sampling model. The work can be extended in an obvious way by applying an unknown transformation to the additive genetic effects to induce normally at this level. For example under the homogeneous variance model, if data are conditionally normally distributed, but additive genetic effects a are not, then the marginal distribution of the data may display skewness. This can lead to spurious ρ when the (incorrect) HET model is fitted to the data. Other situations that can lead to misleading inferences include the presence of unaccounted mixtures, the wrong functional relationship between mean and variance, the wrong model for the sampling distribution of the data, or the presence of an unaccounted correlation between additive genetic and environmental effects. This makes it strikingly clear that an attempt to understand the state of nature via a statistical analysis of data must be regarded only as a first step until more fundamental knowledge becomes available.
Appendix A
The starting point in the derivation of the prior distribution is to assume that it admits the factorization

Let (μλ, exp (μλ*), bλ, exp (bλ*), σa,λ2, σp,λ2, ![]() ,
, ![]() ) be the parameters for a given λ, and hence, for λ=1, the parameters are represented by (μλ=1, exp (μλ=1*), bλ=1, exp (bλ=1*), σa,λ=12, σp,λ=12,
) be the parameters for a given λ, and hence, for λ=1, the parameters are represented by (μλ=1, exp (μλ=1*), bλ=1, exp (bλ=1*), σa,λ=12, σp,λ=12, ![]() ,
, ![]() ). The relationship between these parameters under an arbitrary λ and λ=1 are derived as follows, assuming that the relationship between the transformed datum yi
(λ) and the untransformed datum yi
(λ=1) is approximately (Box & Cox, Reference Box and Cox1964)
). The relationship between these parameters under an arbitrary λ and λ=1 are derived as follows, assuming that the relationship between the transformed datum yi
(λ) and the untransformed datum yi
(λ=1) is approximately (Box & Cox, Reference Box and Cox1964)
where

The model for the untransformed datum can be formulated as

where Xi
′ is an (1×h 1) row vector associated with ith observation from the matrix X with the rank h 1, and ![]() is an (1×h 2) row vector associated with ith observation from the matrix
is an (1×h 2) row vector associated with ith observation from the matrix ![]() with the rank h 2. Substituting (A3) in (A1),
with the rank h 2. Substituting (A3) in (A1),

which shows that to the level of approximation (A2), the relationship between the parameters of the transformed and untransformed models is

These relationships are used together with the transformation theorem to construct a conditional prior distribution for an arbitrary λ based on a specified prior distribution for λ=1.The prior distribution assumptions under λ=1 are as follows. Improper uniform distributions are assigned to μλ=1, exp (μλ=1*), bλ=1, exp (bλ=1*); scaled inverted chi-squared distributions with degrees of freedom ν and scale parameters ![]() ,
, ![]() ,
, ![]() ,
, ![]() are assigned to the variance parameters σa,λ=12,
are assigned to the variance parameters σa,λ=12, ![]() , σp,λ=12,
, σp,λ=12, ![]() ; the parameter ρλ=1 is assigned a uniform prior bounded in (−1,1) and the parameter λ is assigned a uniform prior bounded in (−3,3).
; the parameter ρλ=1 is assigned a uniform prior bounded in (−1,1) and the parameter λ is assigned a uniform prior bounded in (−3,3).
Appendix B
(i) Pseudo marginal probability of the data
The pseudo log-marginal probability of the data is a measure of model comparison (Gelfand, Reference Gelfand, Gilks, Richardson and Spiegelhalter1996) and is defined and computed as follows. Consider data vector y′=(yi , y′−1), where yi is the ith datum, and y−1 is the vector of data with the ith datum deleted. For a particular model, the conditional predictive distribution can be written as
and can be interpreted as the likelihood of each datum given the remainder of the data, where θ is the vector of all model parameters. The actual value of P (yi |y−i) is known as the conditional predictive ordinate (CPO) for the ith observation. A Monte Carlo approximation of the CPO in (B1) for observation i is given by
![{\hat P}\, \lpar y_{i} \vert {\bf y}_{ \minus i} \rpar \equals \mathop {\left[ {{1 \over N}\sum\limits_{j \equals \setnum{1}}^{N} \,{1 \over {P \, \lpar y_{i} \vert \theta ^{\lpar j\rpar } \rpar }}} \right]}\nolimits^{ \minus \setnum{1}} \comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160927085929236-0540:S0016672310000418:S0016672310000418_eqnB2.gif?pub-status=live)
where N is the number of McMC draws and θ(j) is the jth draw from the posterior distribution of θ. In this study, from (4), the sampling distribution of the untransformed datum yi has density
In (B2), P(yi |θ(j)) therefore takes the form
A common summary statistic based on the CPO is ![]() , known as the pseudo log marginal probability of the data. A larger value of
, known as the pseudo log marginal probability of the data. A larger value of ![]() indicates a better relative fit of a model.
indicates a better relative fit of a model.
(ii) Posterior predictive model checking
A technique for checking the fit of a model to observed data y is to draw simulated values yrep from the posterior predictive distributions of replicated data and compare yrep with the observed data (Gelman et al., Reference Gelman, Carlin, Stern and Rubin2004). Any systematic differences between the observed and the simulated data indicate potential failings of the model. More specifically, the idea is to define a so-called discrepancy measure T(y,θ), which depends on the data and perhaps also on θ, an unknown vector of parameters of the model under scrutiny, called null-model below. In this work, the null model is the model for the untransformed data. The measure T is specifically designed to test a particular feature of the data y that may be of scientific relevance. Replicated data are then simulated from the posterior predictive distribution of the null model, given θ(j) for the jth iteration, from which T (yrep,θ(j)) is constructed and compared with T (yrep,θ(j)). Differences between the Ts may be due to sampling or due to the inability of the null model to account for the feature of the observed data disclosed by the discrepancy measure T.
In this study, we are concerned with investigating the residual skewness under the model with λ=λ0. This is accomplished using the discrepancy measure

where

and ![]() . The simulated datum
. The simulated datum ![]() follows N(1μ+Xb+Za+Wp,R), that is
follows N(1μ+Xb+Za+Wp,R), that is

Therefore zrep=(z rep,i)n
i=1 is directly simulated from a standard normal distribution, followed by the computation of T(zrep,θ(j)) and ![]() in each McMC iteration. Depending on whether the null model or the transformed model is under scrutiny, λ0=1 or λ0 is equal to its posterior mode. A graphical display involves plotting histograms of
in each McMC iteration. Depending on whether the null model or the transformed model is under scrutiny, λ0=1 or λ0 is equal to its posterior mode. A graphical display involves plotting histograms of ![]() for both models and for the rabbit and pig litter size data.
for both models and for the rabbit and pig litter size data.