1. Introduction
Genetic variation in resistance to internal parasites has been demonstrated in numerous species, including humans and several livestock species (Kloosterman et al., Reference Kloosterman, Parmentier and Ploeger1992; Quinnell, Reference Quinnell2003; Bishop & Morris, Reference Bishop and Morris2007). However, the genetic architecture underlying such traits is poorly understood. Genetic architecture, that is, the size and distribution of polymorphisms affecting the trait, influences the success of association studies and the ability to predict future phenotypes, such as when predicting genetic risk to disease or when selecting livestock for breeding (Wray et al., Reference Wray, Goddard and Visscher2007; Hayes et al., Reference Hayes, Pryce, Chamberlain, Bowman and Goddard2010). From an evolutionary perspective, knowledge of the genetic architecture in disease traits may help to elucidate the evolutionary influence of disease on hosts (Dawkins & Krebs, Reference Dawkins and Krebs1979). Livestock provide a suitable model for studying diseases (e.g. Lanzas et al., Reference Lanzas, Ayscue, Ivanek and Gröhn2010), particularly when (subclinical) artificial infections are used to maximize the expression of genetic difference between individuals (Bishop & Woolliams, Reference Bishop and Woolliams2010).
Studies of complex diseases, mostly in humans, have generally failed to explain most of the known genetic variation influencing the trait (Manolio et al., Reference Manolio, Collins, Cox, Goldstein, Hindorff, Hunter, McCarthy, Ramos, Cardon, Chakravarti, Cho, Guttmacher, Kong, Kruglyak, Mardis, Rotimi, Slatkin, Valle, Whittemore, Boehnke, Clark, Eichler, Gibson, Haines, MacKay, McCarroll and Visscher2009). These studies typically test each marker independently for an association with the trait. The expectation is that the variance explained by each marker is proportional to the size of effect of the (unobserved) polymorphism on the trait, the degree of association between the marker and the polymorphism (i.e. the linkage disequilibrium (LD)) and the experimental error associated with the measurement. Attempts to increase the power of association studies have focused either on increasing the number of markers, and hence the likely LD between the marker and the polymorphism, or increasing the number of observations for a trait, thus reducing the relative size of the experimental error. Few have attempted to formally estimate the distribution of marker effects with dense single nucleotide polymorphism (SNP) markers (Hayes et al., Reference Hayes, Pryce, Chamberlain, Bowman and Goddard2010) and thus the required power of experiments for disease traits, such as resistance to worms, is still unknown. This study conducts a genome-wide association study and uses available information, including the LD between makers and the expected magnitude of the experimental error, to assess the power of this study to detect polymorphisms.
A key motivation for genome-wide association studies is to predict genetic risk to disease, either in healthy human or livestock populations. Prediction of aggregate genotype or genetic merit from markers (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001) is distinct from association studies because many markers are used for the prediction. The methods of Meuwissen et al. (Reference Meuwissen, Hayes and Goddard2001) shrink the estimated effect of each marker and predict genetic merit using a linear combination of their effects. This process reduces the relative impact of experimental error, compared with single-marker regressions, because the expectation of the error over all markers is zero. Predictions of genetic merit from all markers are being implemented in livestock breeding programmes, typically within a single breed or strain of animals (Gonzalez-Recio et al., Reference Gonzalez-Recio, Gianola, Rosa, Weigel and Kranis2009; Hayes et al., Reference Hayes, Bowman, Chamberlain and Goddard2009; van Raden et al., Reference van Raden, van Tassell, Wiggans, Sonstegaard, Schnabel, Taylor and Schenkel2009; Harris & Johnson, Reference Harris and Johnson2010).
In this study, a large mixed breed population of sheep was artificially infected with gastrointestinal worms to (1) investigate the genetic architecture underlying resistance to worm infections and (2) evaluate the feasibility of using molecular markers to predict genetic merit for this trait. The DNA markers used in this study were from the Illumina OvineSNP50 BeadChip. Results from single marker regressions were used for the genome-wide association study, with significant markers validated in a second (independent) population of sheep. We assessed the power of the association study by estimating the true distribution of the marker effects using a novel technique to directly account for the experimental error associated with the experiment. The technique was verified by calculating the average effect of significant markers in the validation population and the consistency of the marker distributions across the different phenotypes was also examined. The final part of the study used all markers to predict breeding values or additive genetic merit. The reference population was used to estimate the effects of markers and the validation population was used to assess the predictions made using the reference population. The tested hypotheses were that (1) there are many loci of small effect underlying faecal worm egg count (WEC) and (2) WEC breeding values can be predicted from genomic markers.
2. Materials and methods
(i) Reference population
(a) Population structure
Animals in the reference population were from 20 large half-sib families, produced via artificial insemination during 2005 and 2006 in the SheepGenomics project (Supplementary Table S1 available at http://journals.cambridge.org/grh). Sires were from six different breeds, including some cross-bred animals, and there were an average of 193 progeny per sire (range: 87–388). Dams were used in both 2005 and 2006, but maternal pedigree was only collected for 2006 born animals. From the 2006 records, most dams were Merino sheep (76%) and there were some Merino cross Border Leicester (17%), White-Faced Suffolk (3%) and Poll Dorset (2%) ewes. Merino dams were predominantly from Strong and Medium wool strains, although some were from Super-fine-wool strains. The pedigree of the dam was not considered reliable and, as it was also incomplete, it was not formally used in any of the analyses. Principal components derived from progeny genotypes were used to account for maternal pedigree (see below).
(b) Phenotypic records
Records for resistance to worms, both Trichostrongylus colubriformis and Haemonchus contortus, and an independent trait, bare breech area, were collected from the reference population before 9 months of age (Supplementary Fig. S1 available at http://journals.cambridge.org/grh). Not all measurements were collected on all animals. Bare breech area was assessed before weaning, by measuring the dimensions of the bare area under the tail of the animal with digital callipers and calculating the area in cm2. There were two measurements of bare area width, level with the anus and vulva (an approximation in males), and one of dorso–ventral bare area depth. The area was calculated as an approximate ellipse as:
Body weight at the time of measurement was used to account for different sizes of the lambs. It was fitted in subsequent models as a covariate to approximate skin surface area, i.e. skin surface~ weight0·67 (James, Reference James2006). Thus, the bare area trait, after analyses, was akin to bare area per unit of skin area.
Host resistance to T. colubriformis and H. contortus was assessed in lambs using WEC. Each animal was challenged twice and, in each case, residual worm burdens were removed 4–7 days before challenge with a combined treatment of benzimidazole and levamisole. This product was known to be of high efficacy. Animals were first challenged at about 5 months with 20 000 T. colubriformis larvae. The second challenge was at about 8 months with 8000 H. contortus larvae (see Supplementary Fig. S1 available at http://journals.cambridge.org/grh). Two faecal samples were collected for each challenge; 1 week apart at 3 and 4 (H. contortus) or 4 and 5 (T. colubriformis) weeks post-challenge. The nematode eggs in faeces were counted with a detection limit of 20 eggs per gram. The identity of the technician conducting the WEC was recorded. Some animals were not available for challenge with H. contortus, and hence there was a reduction in the number of animals and small change in flock composition between the two challenges. All animals included in the analyses had two measurements of WEC.
(c) Genotypes
DNA was extracted from blood samples and genotyping was conducted by GeneSeek (Lincoln, USA). The genotypes were quality checked and set to missing if the call rate was <90%, if the minor allele frequency was <1% or if the genotypes were not in Hardy−Weinberg equilibrium, i.e. observed genotype frequencies were inconsistent with observed allele frequencies. Alleles were phased into paternal and maternal haplotypes using a simple rules-based approach and exploiting the large number of progeny per sire. Sire genotypes were used during phasing when available (15 sires) or otherwise imputed from progeny genotypes (5 sires). Within each sire family, SNP parental origin was assigned when unambiguous (e.g. for SNP where the sire was heterozygous and the progeny homozygous). The most likely phase for SNP adjacent to unambiguous SNP in the sire was generally far more likely that the alternate phase, because of dense SNP and large half-sib families, and thus was assumed correct and without error. Phase was inferred between adjacent assigned SNP in the progeny when there was no observed recombination between a pair of adjacent assigned SNP, assuming no double-recombination events. For SNP where a recombination was observed between adjacent assigned SNP, the intervening SNP haplotype was assumed unknown. Missing alleles were imputed using fastPHASE (Scheet & Stephens, Reference Scheet and Stephens2006). Positions of SNP markers were obtained from the Sheep Genome browser V1.0 (http://www.livestockgenomics.csiro.au/sheep/). The final dataset comprised genotypes for 48 640 SNP markers on 3860 progeny.
(d) Accounting for population structure
The available pedigree information was inadequate to account for the breed structure in the reference population, particularly on the dam (female) side. Accounting for population structure will reduce false-positive associations due to population stratification (Lander & Schork, Reference Lander and Schork1994). Hence, the population structure was inferred from the marker data using principal components of the genomic relationship matrix (Patterson et al., Reference Patterson, Price and Reich2006). With our dataset, plots of the data suggested that the first four components would account for known structure. However, empirical estimates of the number of false-positive associations were also made. The genomic relationship matrix (G) was constructed by computing (modified from Patterson et al., Reference Patterson, Price and Reich2006):
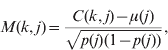
where C(k, j) is the number of copies of the first allele for marker j and individual k (i.e. 0, 1 or 2), μ(j) is the mean number of copies of the first allele per individual at marker j in the population, p(j) is the allele frequency (thus p(j)=μ(j)/2) and m is the total number of markers. The principal component decomposition was conducted with R 2.6.1 (R Development Core Team, 2007). For illustrative purposes, principal components were also determined for the relationship matrices built with only paternal or maternal haplotypes.
(e) Descriptive analysis of the phenotypes
The heritability and repeatability of the traits were estimated from the realized relationship between animals (Hayes & Goddard, Reference Hayes and Goddard2008). The models fitted were:


where WEC is either square-root (T. colubriformis, tWEC) or cube-root (H. contortus, hWEC) transformed, μ is the mean, sirebreed is the breed of sire, yr is the year of measurement, yr/sex is the sex of the animal nested within year, yr/week is the week of measurement nested within year, date is the date of measurement, grp is the technician measuring WEC, PC1–PC4 are the first four principal components of the genomic relationship matrix for the reference population fitted as co-variates, PE is the permanent environmental effect distributed PE~N(0, IσPE2), where I is the identity matrix, wt0·67 is a co-variate of body weight (kg) approximating skin surface area, anim is the animal effect distributed N(0, Gσanim2), where G is the genomic relationship matrix and e is the residual error term. Transformations for WEC were chosen so as to best normalize the residuals.
(ii) Validation population
Australian Sheep Breeding Values (ASBV) for post-weaning strongyle WEC were obtained from Sheep Genetics for 316 genotyped industry sires (Table 1, for details see http://www.sheepgenetics.org.au). The information for these breeding values is derived from a large number of progeny, such that the ASBV are accurate predictors of true breeding values (TBV). Sires were from Border Leicester, Terminal (White-Faced Suffolk and Poll Dorset) and Merino breeds, with Merino sheep further subdivided into wool types (Ultrafine/Superfine, Fine/Medium-Fine, Medium/Strong). ASBV are comparable only within Border Leicester, Terminal or Merino sires. ASBV were not available for bare breech area. Sire genotypes were obtained, quality checked and missing genotypes imputed, as described for the reference population. Principal components from the genomic relationship matrix (G) built with only industry sires were used to correct for population stratification.
Table 1. Number, breed and wool type of sires in the validation dataset. Shown are the mean, range and accuracy of their Australian Sheep Breeding Values (ASBV) for post-weaning faecal worm egg count (WEC)

(iii) LD between markers
The extent of LD in a population is critical for the prediction of genetic merit from markers and for quantitative trait loci (QTL) detection (Goddard & Hayes, Reference Goddard and Hayes2009). LD between SNP marker pairs less than 1×106 bp (1 Mbp) apart was quantified with the r 2 statistic (Hill & Robertson, Reference Hill and Robertson1968), denoted r HR2, using the maternal haplotypes from the reference population. Paternal haplotypes were not included because only 20 sires were used in the reference. LD was first estimated across all progeny, and then for the specific breeds represented in the maternal haplotypes. Maternal breeds were assigned to progeny by matching the clusters from the principal components of the genomic relationship matrix to a breed according to the recorded maternal pedigree (see Supplementary Fig. S2 available at http://journals.cambridge.org/grh). Progeny not tightly clustered were discarded, leaving progeny representing Merino (n=2689), Border Leicester cross Merino (n=820), White-Faced Suffolk (n=122) and Poll Dorset (n=153) maternal breeds. Bias in r HR2 due to sample size was adjusted by r HR2−1/N, where N is the breed sample size (i.e. the number of haplotypes per breed).
(iv) Genome-wide association using SNP marker regressions
(a) SNP regressions
Regressions of traits on SNP marker genotype were fitted for the genome-wide association analysis and to estimate the distribution of SNP marker effects. Regressions were fitted, one at a time, using ASReml (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2006). The models fitted to the reference population were:
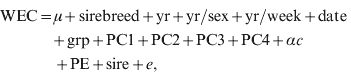

where terms were as previously defined for models 1 and 2, sire is the random sire term distributed N(0, Iσsire2), where I is the identity matrix and σsire2 is the sire variance, α is the allele substitution effect and c is the SNP genotype (i.e. 0, 1, 2 copies of the first allele). Sire was fitted to minimize the effects of population stratification and so the SNP marker effects were estimated within sire families. Thus, for a SNP marker to have a large effect, it must be consistent across sire families.
The regression of SNP markers for the validation population was
where ASBV is the industry breeding value, μ is the mean, sirebreed is the sire breed (Border Leicester, Terminal, Merino), PC1val to PC4val are the first four principal components from the genomic relationship matrix from the validation population, α is the allele substitution effect, c is number of copies of the first allele and e is the residual error.
(b) Identifying significant SNP markers
Marker associations were initially identified in the reference population and then validated in the validation population. However, the significance thresholds (i.e. P-value) chosen for each stage of the analysis is important for the outcomes. If stringent thresholds are set then few validated associations will be recorded. However, if the thresholds are too lax then many false-positive associations are to be expected. In this dataset, very few SNP were significant using P<0·0001 in the reference population (<20 SNP) and hence a threshold of P<0·001 was used. A threshold of P<0·05 was used for the validation population.
(c) The expected number of significant associations
The false discovery rate (FDR) is the ratio of expected significant associations to the actual number of significant associations. It assesses the Type I error rate (Lynch & Walsh, Reference Lynch and Walsh1998), and a low FDR means that there are more significant associations than expected by chance. FDR was calculated for the reference population as FDRref=mP/S (Benjamini & Hochberg, Reference Benjamini and Hochberg1995), where m is the number of markers tested, P is the significance threshold (P-value) and S is the number of markers with significant associations. In the validation population, the calculation was FDRval=S refP val/S val (Benjamini & Hochberg, Reference Benjamini and Hochberg1995), where S ref and S val are the number of markers declared significant in the reference or validation populations and P val is the significance threshold in the validation population.
(v) Estimating the true marker effects using the validation population
(a) The average phenotypic variance explained by a SNP marker (r SNP2)
The average phenotypic variance explained by an SNP was calculated for SNP identified as significant in the reference population. This was done using the F-values obtained in the validation population, as these estimates are not biased by the sampling error associated with the discovery of the SNP. The F-values for the SNP marker regressions obtained from eqns (3) and (4) have the expectation:
where σerror2 is the error variance, N is the denominator degrees of freedom of the F-value and 2p(1−p)α2 is the variance explained by the marker (where α is the allele substitution effect and p the frequency of the allele). Rearranging, the average proportion of phenotypic variance explained (per SNP) by the n SNP markers is then:
where N is the denominator degrees of freedom associated with the F-value and, assuming that the variance explained by the SNP is small, using σerror2 as an approximation for the phenotypic variance. The total variance explained by the n markers (R 2) is nr SNP2.
(b) Permutation of WEC within sire families
The FDR assumes that under the null-hypothesis, the test statistic in the reference population will follow an F-distribution. However, MacLeod et al. (Reference MacLeod, Hayes, Savin, Chamberlain, McPartlan and Goddard2010) show that FDR may be higher than expected under the null-hypothesis if population structure is not properly accounted for. Thus, WECs were randomly shuffled (permuted) within sire families 10 times to estimate the expected number of false-positive associations. The r SNP2 for significant SNP using the permuted data was calculated using eqn (7).
(vi) Estimating the distribution of true marker effects directly from the reference population
The estimated effect of each SNP contains a sampling error and so the distribution of estimated effects is not the same as the distribution of true effects. We estimate the distribution of true effects as follows:
First, consider an SNP in many repetitions of this experiment. The distribution of observed F-values follows a non-central F-distribution with 1, N df, where N is the denominator degrees of freedom. Thus, the distribution is ![]() with non-centrality parameter λ1. Since χN2 is approximately N when N is large, the distribution of the F statistic is approximately
with non-centrality parameter λ1. Since χN2 is approximately N when N is large, the distribution of the F statistic is approximately ![]() with λ1=N[2p(1−p)α2]/σerror2 (from eqn (6)). If X~N(μ,σ2) then (X/σ)2~χ1,λ2 where λ=(μ/σ)2. Therefore, since
with λ1=N[2p(1−p)α2]/σerror2 (from eqn (6)). If X~N(μ,σ2) then (X/σ)2~χ1,λ2 where λ=(μ/σ)2. Therefore, since ![]() then
then ![]() when r SNP2 is [2p(1−p)]α2/σerror2. Assuming that σerror2 approximates the phenotypic variance, then r SNP2 is the proportion of phenotypic variance explained by the SNP and r SNP is the absolute value of the correlation between the phenotype and the SNP genotype, where the genotype is coded 0, 1 or 2 according to the number of copies of one allele. The variance of the distribution for the estimates (
when r SNP2 is [2p(1−p)]α2/σerror2. Assuming that σerror2 approximates the phenotypic variance, then r SNP2 is the proportion of phenotypic variance explained by the SNP and r SNP is the absolute value of the correlation between the phenotype and the SNP genotype, where the genotype is coded 0, 1 or 2 according to the number of copies of one allele. The variance of the distribution for the estimates (![]() SNP) is equal to the sampling variance (1/N).
SNP) is equal to the sampling variance (1/N).
Now consider the F-values observed from this experiment for the j SNP markers. Each ![]() SNP(j)~N(r SNP(j), 1/N), where r SNP(j) varies from one SNP to another. Let us assume that r SNP(j) is a random variable from a mixture of i normal distributions with probability ρi that it comes from N(0, v i), where v i is the average variance explained by SNP from the distribution, i.e. E(r SNP2)=v. Then, the observed correlation,
SNP(j)~N(r SNP(j), 1/N), where r SNP(j) varies from one SNP to another. Let us assume that r SNP(j) is a random variable from a mixture of i normal distributions with probability ρi that it comes from N(0, v i), where v i is the average variance explained by SNP from the distribution, i.e. E(r SNP2)=v. Then, the observed correlation, ![]() SNP(j), would be from a mixture of normal distributions with the probability ρi of coming from N(0, v i+1/N).
SNP(j), would be from a mixture of normal distributions with the probability ρi of coming from N(0, v i+1/N).
An EM algorithm (Dempster et al., Reference Dempster, Laird and Rubin1977; Lynch & Walsh, Reference Lynch and Walsh1998) was used to estimate the proportion of SNP markers from each of the i normal distributions. If the probability density function of drawing ![]() SNP(j) from N(0, v i+1/N) is
SNP(j) from N(0, v i+1/N) is
![\phi \lpar \hat{r}_{{\rm SNP}\lpar j\rpar } \vert i\rpar \equals {1 \over {\sqrt {2\pi \lpar v_{i} \plus 1\sol N\rpar } }}\exp {\kern 1pt} \left[ {{{\hat{r}_{{\rm SNP}\lpar j\rpar }^{\setnum{2}} } \over { \minus 2\lpar v_{i} \plus 1\sol N\rpar }}} \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235904575-0858:S0016672311000097:S0016672311000097_eqn8.gif?pub-status=live)
The probability that ![]() SNP(j) is from the normal distribution i, conditional on the observed value of
SNP(j) is from the normal distribution i, conditional on the observed value of ![]() SNP(j), is then:
SNP(j), is then:
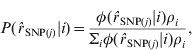
where ρi is the current estimate for the proportion of SNP from the ith normal distribution. Starting values for ρi were initially chosen and updated for each iteration as:
where m is the total number of SNP. Updating continued until the change in ρi was very small, i.e. until ρi–ρ′i<1×10−9. The variances for the normal distributions were 0, 0·0001, 0·0002, 0·0004, 0·0008 and 0·0012. These distributions were chosen to include the full range of observed F-values.
The density function (eqn (8)) is influenced by the sampling error (1/N) associated with each trait. An example of the distribution used to model the F-values from association study for WEC following T. colubriformis infection (tWEC) are shown (Fig. 1). Most notably, this shows that F-values of up to about 12 can be obtained due to experimental error even when there is no true association between the marker and the trait (i.e. v=0).

Fig. 1. The density function (eqn (8)) for modelling the distribution of marker effects for WEC following T. colubriformis challenge [denominator degrees of freedom (N)=3294]. Shown are the distributions, with variance (v i) equal to 0, 0·0001, 0·0002, 0·0004, 0·0008 and 0·0012, over a range of correlations between the marker and trait (|r SNP|). The corresponding F-values are shown.
(vii) The power of detection using LD
The power of an experiment assesses the ability of an experiment to reject the null-hypothesis when it is false (Type II error rate; Lynch & Walsh, Reference Lynch and Walsh1998). Thus, it may be thought of as assessing the repeatability of the results. The power to detect polymorphisms using LD was calculated using the ‘ldDesign’ package in R 2.6.1 (R Development Core Team, 2007; Luo, Reference Luo1998; Ball, Reference Ball2005). The linkage equilibrium coefficient (D) was calculated as [p(1−p)t(1−t)r HR2]1/2, i.e. the numerator from Hill & Robertson (Reference Hill and Robertson1968), where p is the frequency of the first allele at the marker, t is the frequency of the first variant at the QTL or polymorphism and r HR2 is the LD between the allele and the QTL variant. The level of LD between the marker allele and the QTL variant, and the effect size of the QTL have the greatest impact on estimated power, with the frequency of the marker allele and QTL variant of lesser (relative) importance (Luo, Reference Luo1998). Only additive effects were assumed and the frequency of the allele and variant were assumed to be 0·2.
(viii) Predicting genetic merit using genomic markers
Genomic estimated breeding values (GEBV) were calculated for the validation population, using data only from the reference population. GEBV were estimated using two different methods, referred to as GBLUP and BayesA (Meuwissen et al., Reference Meuwissen, Hayes and Goddard2001).
(a) Estimating GEBV using GBLUP
The GBLUP approach assumes that each SNP effect comes from a normal distribution with equal variance. Goddard (Reference Goddard2009) shows that, in practice, this can be achieved by using the genomic relationship matrix (G) to describe the relationship between all animals (reference and validation populations) and taking the animal solutions as GEBV. Hence, it is computationally efficient and similar to calculating BLUP breeding values (e.g. Lynch & Walsh, Reference Lynch and Walsh1998). The model was fitted using ASReml (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2006) as:

where the terms are as described previously. Note that both the sire pedigree and the genomic relationship matrix are fitted. This means that GEBV predictions were made based on within-sire variation in WEC.
(b) Estimating marker effects using BayesA
The BayesA method assumes the SNP effects follow a t-distribution, where there is a higher prior probability of effects that are moderate to large than with the prior used for GBLUP. GEBV are then the linear combination of SNP marker effects, GEBV=Xĝ, where X is the design matrix of validation genotypes and ĝ is the vector of estimated SNP effects. In practice, BayesA uses Gibbs sampling to estimate the effect of an SNP conditional on the effect of all other SNP. Sampling from the posterior is achieved by sampling a variance from an inverted chi-square distribution and then sampling a normal deviate with that variance. To implement BayesA, the hWEC and tWEC traits were corrected for fixed and permanent environmental effects as listed in model 4, excluding the random sire term. A model was fitted to the solutions for each animal as
where y is the vector of pre-corrected phenotypes, X is a design matrix with dimension of n×j allocating phenotypes to marker effects (n is the number of animals, j is the number of markers), g is a vector of marker effects assumed to be normally distributed u i~N(0, σui2), Z is a design matrix allocating phenotypes to breeding values, v is a vector of breeding values associated with the sire with variance v i~N(0, Aσsire2) (where A is the additive genetic relationship matrix calculated from the sire for each animal) and e is the vector of residual deviations distributed e i~N(0,σe2). The prior used for σui2 was inverse chi-squared distribution as in Meuwissen et al. (Reference Meuwissen, Hayes and Goddard2001) . The estimated effects (ĝ) were the posterior mean of 10 Gibbs sampling chains, each with either 30 000 (hWEC) or 50 000 (tWEC) iterations. More iterations were used for tWEC to improve the correlation of marker effects between replicates. The first 10 000 iterations were discarded as burn-in.
(c) Comparing GEBV predictions from GBLUP and BayesA
Correlations (r) were estimated between GEBV and ASBV, and between GEBV and the estimated TBV. Defining the accuracy of ASBV as ASBVacc, then:
The estimated proportion of genetic variance explained by the SNP markers is then r(GEBV,TBV)2.
(d) Using a subset of SNP markers
GEBV predicted from a subset of SNP markers were used to assess the proportion of the genetic variation that could be explained by a reduced number of markers. Markers with the largest effects from the model described in eqn (10) were included in the analysis, progressively, for subsets of 50, 100, 250, 500, 1000, 1500, 2000, 3000, 5000 and 10 000 markers. Effects were re-estimated for each subset of SNP using the BayesA approach (eqn (10)) and five replicate chains for each analysis. In each chain up to 20 000 iterations were used, with up to 5000 discarded as burn-in.
3. RESULTS
(i) Reference population phenotypes
The number of animals measured for worm resistance and bare area varied between 2669 and 3616 (Table 2). For WEC following T. colubriformis challenge (tWEC) there were 18·5, 22·5 and 59% of records from Maternal (Border Leicester, East Friesian, Coopworth), Terminal (White-Faced Suffolk, Poll Dorset) and Merino sires; while for WEC following challenge with H. contortus (hWEC) this composition had changed to 16·0, 18·5 and 65·5%. WEC were generally high and there were less than 3% of animals with zero WEC. The repeatability of measurements taken within a worm challenge was high (0·58–0·71). All traits had low-to-moderate heritability (Table 2). There were 2487 animals measured for both worm resistance traits, and there was a moderate correlation between the estimated breeding values obtained from each analysis (0·32).
Table 2. Summary data for faecal worm egg count following T. colubriformis (tWEC) and H. contortus (hWEC) challenge, and bare breech area in the reference population. Shown are the number of animals; the range and mean of trait values; phenotypic (σphen2), permanent environment (σPE2) and animal relationship (σanim2) variance components; and estimates of heritability (h 2) and repeatability for each trait. Standard errors are shown in parentheses

na=not applicable, only one measurement of bare breech area per animal.
a Data presented on the transformed scale, transformations were hWEC0·333 and tWEC0·5.
(ii) Population structure
Principal components clearly showed the breed structure of the reference population. When the genomic relationship matrix was built with only paternal or maternal haplotypes, there was evidence for clear sire and maternal breed clusters (Supplementary Fig. S2 available at http://journals.cambridge.org/grh). Individual sires are very tightly clustered owing, presumably, to the limited number of haplotypes available from each sire. The maternal analysis shows four clusters that are more loosely defined. Errors in the recorded maternal pedigree are shown as individuals clustering with the incorrect maternal breed (e.g. a blue or green dot in the red cluster of Merino sheep). Principal components derived from the complete genomic relationship matrix show the total breed composition of the progeny (Fig. 2). From these figures, and from exploration of further principal components, it was determined that the first four principal components should be sufficient to account for the known population structure in subsequent analysis. The genomic relationship matrix (Supplementary Fig. S3 available at http://journals.cambridge.org/grh) shows that the Merino sires were only mated to Merino ewes, and that sires from other breeds were mated to a mix of non-Merino and Merino ewes. These plots highlight the necessity of accounting for the maternal pedigree, which was achieved by fitting the principal components as co-variates in all models.

Fig. 2. The first and second (a) or third and fourth (b) principal components from the genomic relationship matrix. Each point represents an animal, and individuals are coloured according to the breed of their sire. Sire breeds are Merino, Poll Dorset (PD), White-Faced Suffolk (WFS), Border Leicester (BL), East Fresian (EF), Coopworth (Coop), the Golden Ram selection line [GR, see Marshall et al. (Reference Marshall, Maddox, Lee, Zhang, Kahn, Graser, Gondro, Walkden-Brown and van der Werf2009) ] and their crosses.
(iii) LD between markers
The LD between markers, assessed from maternal haplotypes, was generally low in the population although some marker pairs show high levels of LD at longer distances (Fig. 3). The average marker spacing between adjacent markers was about 54 kbp and the mean r HR2 at this distance was 0·11, across the whole population. Higher LD was found for Poll Dorset and White-Faced Suffolk breeds compared to Border Leicester cross Merino or Merinos. The mean r HR2 at the average marker spacing was 0·12 for Merinos, 0·14 for Border Leicester cross Merino, 0·15 for White-Faced Suffolk and 0·19 for Poll Dorset.

Fig. 3. Linkage disequilibrium between marker pairs as a function of distance between the markers. Shown are all pairs less than 1×106 bp apart (a), and the average for pairs in increments of 10 000 bp (b). Only maternal haplotypes were used and breeds were allocated using the principal component clusters. The average marker spacing, indicated by the grey line, was approximately 54 000 bp.
(iv) Genome-wide association study
(a) SNP markers associated with tWEC
There were 99 SNP markers identified as significant (P<0·001, uncorrected for multiple testing) in the reference population following T. colubriformis challenge and, of these SNP, 10 were identified as significant in the validation population (P<0·05, Table 3). The FDR was 49·1 and 49·5% for the reference and validation population, respectively. This suggests there would be ca. five real SNP with validated associations (i.e. 10 validated associations×49·5% FDR=4·9 false-positive SNP).
Table 3. The number, name, chromosome (chr.) and chromosome position (base pairs, bp) of the validated markers following T. colubriformis or H. contortus challenge in the reference population. The F-value and either the direction of effect or effect in units of ASBV (for the validation with standard errors, s.e.) are shown for each marker in the reference and validation populations

a σP=34·57, standard deviation of the residual when the model contains all fixed effects from model 5, excluding the marker term.
The direction of effect for the SNP markers in the reference and the effect in the validation populations is shown (Table 3). Although it is tempting to declare SNP with inconsistent effects between the two populations as false positive, the LD phase may change between the reference and validation populations. The estimated effects in Table 3 are also likely to be overestimated because of the significance thresholds applied during the SNP discovery process. An unbiased approach to estimate the effect of significant markers is discussed in detail below.
(b) SNP markers associated with hWEC
Fewer SNP were validated for the H. contortus (hWEC) compared to the T. colubriformis challenge. There were 65 significant associations in the reference (P<0·001) and, of these SNP, five showed significant effects in the validation population (P<0·05, Table 3). The FDR were 74·8 and 65·0% in the reference and validation population, respectively. Thus, there are potentially two true SNP markers associated with hWEC that meet our significance criteria in both populations.
(v) Variation explained in the validation population by markers identified as significant the reference population
The 99 significant SNP markers identified following T. colubriformis challenge explained an estimated 11% of the variance in WEC breeding value in the validation population (Table 4). On average, each SNP explained approximately 0·11% of the variance in WEC. The number of SNP markers and the variance explained by these markers, either the average per SNP or for all markers combined, was significantly greater than SNP identified with permuted data (P⩽0·01). Random SNP from the null-distribution, i.e. those identified with the permutations, explained a small percentage of variance in the validation dataset. This proportion was not significantly different from zero but it may suggest a small bias in the analysis because SNP identified with the permuted data did not follow the assumed F-distribution. If F-values from the SNP identified following permutation followed the assumed F distribution, the variance explained should be close to zero (see eqn (7)). Thus, the calculated FDR in the validation population might in reality be greater than the calculated 49·5%.
Table 4. Number of significant markers (no. of markers, P<0·001) and the average variance explained by a single marker (r SNP2) or all markers (R 2) in the validation population for the actual and the (within-sire) permutations of WEC. Traits are WEC following challenge with either T. colubriformis or H. contortus (tWEC or hWEC). The standard error of the mean (s.e.m.) is shown in parentheses for the permuted data

** Significantly different from the permuted data, i.e. the null-distribution (P⩽0·01, one-sided t-test).
The number of significant SNP markers following the H. contortus challenge was significantly different to significant SNP from permuted data (P⩽0·01, Table 4). However, the variance explained by these SNP was not different to significant SNP identified with permuted data. This suggests that most of the SNP identified in the reference population using hWEC probably had no true association with the trait, which is consistent with the high FDR (74·8%) in the reference population. The variance explained (R 2) in the validation population by permutated data was significant greater than zero, suggesting that the FDR for SNP validated for hWEC may be greater than the assumed 65·0%.
(vi) Estimating the distribution of true marker effects directly from the reference population
The estimated distribution of SNP effects is shown (Table 5) for tWEC, hWEC and the third trait, bare breech area. The EM technique estimates the proportion of SNP from six normal distributions, each with a successively larger variance, where the variance of the distribution is the average true effect for the SNP (v i or the average variance explained per SNP, r SNP2) plus the sampling error (1/N). The solutions for all traits are similar and estimates that 66–73% of SNP were not correlated with the traits. That is, most of the SNP came from the normal distribution with variance 1/N and where the average true marker effect was zero (v=0), and thus the observed effect was due to sampling error alone. There were an estimated 27–34% of SNP with very small correlations with the traits, explaining an average of 0·01% of the phenotypic variance per marker. For tWEC a small proportion (0·00087) of markers explained a larger amount of the phenotypic variance. However, the effect of these SNP was still small and on average they explained only 0·12% of the phenotypic variance per marker.
Table 5. Proportion of markers (ρ), and the average phenotypic variance explained (R 2)Footnote a by each of the i normal distributions used to model SNP marker effects. The variance (v i) and standard deviation (v i1/2) for each distribution represent the mean variance explained (r SNP2) and the mean correlation between a marker and the trait (|r SNP|) for markers from the ith distribution. The traits are T. colubriformis and H. contortus faecal WEC (tWEC and hWEC) and bare breech area.

a The average variation explained by all markers in the distribution, R 2=ρi×48 640×v i, where v i is the average variance explained per marker and ρi is the proportion of markers from the ith normal distribution.
The average variance explained by a SNP from a particular distribution (r SNP2) is equal to the variance of the corresponding normal distribution. Thus the markers from the normal distribution with the largest variance for tWEC (v=0·0012) have an average r SNP2 of 0·12%. However, the SNP with the largest effects from this distribution may explain up to 0·48% of the variance (i.e. 2 standard deviations from the mean, |r SNP|=0·069). Similarly, the average variance explained by SNP coming from the distribution with the largest variance for hWEC and bare breech area was 0·02%, but the largest effects for SNP from this distribution would explain about 0·08% of the phenotypic variance. The results for the parasite resistance traits are in broad agreement with the estimated variance explained by significant SNP in the validation population (Table 4), which showed that SNP meeting our significance threshold explain an average of 0·11 and 0·03% of the variance in ASBVs for tWEC for hWEC, respectively.
The method to estimate the distribution of marker effects does not account for the LD between markers, and hence the variance due to one polymorphism may be picked up by multiple SNP. To illustrate this point, the average phenotypic variance explained by all SNP is calculated (R 2, Table 5). The total phenotypic variance explained by all markers was 160, 131 and 165% for tWEC, hWEC and bare breech area. This overestimates the additive genetic variance by a minimum of 20 times for tWEC and 5·5 times for hWEC and bare breech area, assuming that SNP can explain all the genetic variance from Table 2. The proportion of markers showing small associations with each trait is potentially the most distorted. For instance, markers showing a small association with the trait may be in weak LD with a polymorphism and so the variance they explain is small. However, because many SNP can be in low LD with a single polymorphism, the effect of the polymorphism can be counted several times.
The reconstructed mixture of normal distributions shows that about 20% of SNP markers had weak correlations with the traits (|r SNP|=0·005), and that few SNP had correlations greater than 0·035 (Fig. 4). However, there were slightly more SNP in the normal distribution with the largest variance for tWEC (i.e. the distribution of effects has a slightly fatter tail). There were fewer markers associated with hWEC than with tWEC and for the markers associated with hWEC, only weak correlations were estimated.

Fig. 4. The mixture of normal distributions for the (absolute) correlation of traits and SNP markers. Traits were WEC following T. colubriformis or H. contortus challenge (tWEC or hWEC) and bare breech area. The x-axis shows the mid-point for each category. The tail of the distribution is magnified in the insert.
To assess the modelling of the marker effects, the sampling error was added back to the variance for each normal distribution (i.e. vi+1/N) and the mixture of normal distributions was compared directly with the observed correlations (Supplementary Fig. S4 available at http://journals.cambridge.org/grh). Generally, the mixture described the observed distribution of correlations well. Although there were some discrepancies, there were few discernable trends. Assessing only the tail of the distributions, the mixture model may have overestimated the number of larger correlations for hWEC and bare breech area but appears to accurately describe the tail for tWEC.
(vii) Power of the genome-wide association study
Assuming an average LD between marker and QTL of 0·2, this study had more than 70% power to detect QTL explaining more than 2·5 or 3·2% of the phenotypic variance in tWEC or hWEC (P<0·001, Fig. 5 a). In other words, the study should have detected 70% of polymorphisms explaining more than 2·5 or 3·2% of the phenotypic variance. However, the largest marker effects were estimated to explain only 0·1–0·48% and 0·02–0·08% of the phenotypic variance for tWEC and hWEC, respectively. This study had less than a 4% chance of detecting these SNP. If we assume a higher LD between the markers and the polymorphisms, then the power of detection increases. However, LD between adjacent markers was low and therefore it is unlikely that the (maximum) LD between a marker and a polymorphism was high. Even if we assume the LD between a marker and polymorphism was 0·6, this study had 30% power to detect the largest estimated effect explaining 0·48% of the phenotypic variance. The chance of an independent study (with similar power) to detect this same SNP is only about 9% (i.e. 0·32=0·09).

Fig. 5. Linkage disequilibrium power for detection of QTL with small effects. Shown is the power for the number of current observations (n=3326) with increasing LD (r HR2) between markers and QTL (a), and the power when r HR2=0·4 and the number of records is increased up to 15 000 (b). Note the different scale on the x-axes. The grey vertical line indicates the largest estimated marker effect (i.e. 0·48% of phenotypic variance).
Greater than 70% power to detect QTL explaining 0·1–0·48% of the phenotypic variance requires a higher level of LD between markers and polymorphism, and a greater number of observations. Increased marker density or using a single breed with low effective population size, such as Poll Dorset, would increase the likely LD between markers and polymorphism. Reliable detection of polymorphism explaining about 0·5% of the phenotypic variance (e.g. >70% power), could be achieved when the LD between markers and QTL is 0·4 and with about 10 000 records (Fig. 5 b). Detection of smaller polymorphisms, such as those estimated for hWEC, would require greater marker density and many more phenotypes.
viii Prediction of genetic merit
(a) Correlations between GEBV and ASBV
The prediction of genetic merit uses all markers simultaneously. Relative to the SNP marker regressions, this reduces the impact of experimental error on results and assists in accounting for the LD between markers. Of the two prediction methods BayesA had slightly better accuracy, although the differences between the methods were small (Table 6). The correlation between GEBV and ASBV generally ranged between 0·2 and 0·3, but there was little predictive power in the Fine and Medium to Fine Merino Wool types using any method. The correlation for Border Leicester sires was not reliable due to the small number of records in the validation population (not shown). The proportion of the genetic variance explained by all markers was 35% for Terminal sires using tWEC and 24% for Strong and Medium wool Merinos using hWEC.
Table 6. Correlation between genomic estimated breeding values and Australian Sheep Breeding Values [r(GEBV, ASBV)] or the proportion of genetic variance explained [r(GEBV,TBV)2], for the Terminal or Merino validation sires. Shown are the correlations when GEBV were estimated either with GBLUP or BayesA, following challenge with either T. colubriformis (tWEC) or H. contortus (hWEC)

Markers with the largest effects, when all markers were included in the analysis, were used to predict GEBV from a reduced subset of markers using BayesA (Supplementary Fig. S5 available at http://journals.cambridge.org/grh). GEBV show that 10 000 markers can generally explain 80–90% of the genetic variation explained by all markers. This was consistent for Merino sires and for Terminal sires using tWEC. The accuracy of GEBV reduced with the addition of more markers in some analyses, for example, from 5000 to 10 000 markers for Terminal sires using hWEC, and it is unclear as to why this occurred. However, the correlations were generally not strong and small changes could be magnified during the calculation of the proportion of genetic variance explained [i.e. r(GEBV, TBV)2]. Results suggest that a minimum of 3000 markers could explain 60–70% of the genetic variation explained by all markers. However, the accuracy of GEBV in general was low to moderate and predictions with all markers should be improved before attempting to use reduced subsets of markers.
(ix) Comparing marker regressions to effects estimated with BayesA
SNP regressions and BayesA analyses make subtly different assumptions when estimating the marker effects. The SNP regressions assume that each SNP is independent, although this not strictly true because of the LD between markers. Conversely, BayesA estimates the effect of each SNP after adjusting for the effects of all other SNP. Thus, comparing results from both analyses is of interest because the independence of the SNP regressions can be assessed using results from BayesA.
The 50 SNP with largest effects, as estimated by BayesA, and the F-values from single-marker regressions were generally consistent (Supplementary Fig. S6 available at http://journals.cambridge.org/grh). Many of the markers with large F-values were also estimated by BayesA to have large effects on the traits. This is reasonable because sampling error associated with each marker is confounded between the analyses, and there was low LD observed between SNP markers greater than 100 kbp apart. SNP markers with large estimated effects from BayesA were spread across most chromosomes for both tWEC and hWEC. Notably, there were several SNP markers on Chromosome 1 for tWEC with large F-values that were also estimated by BayesA to have large (independent) effects. Many of the SNP that were validated in the genome-wide association study also had relatively large effects estimated with BayesA.
4. DISCUSSION
The primary aim of this paper was to estimate the size and distribution of SNP marker effects on a parasite resistance trait, namely WEC in sheep. Two approaches were used, which aimed to take account of the sampling error associated with single-marker regressions. The first estimated the proportion of variation explained in the validation population by significant SNP identified from the reference population. The second approach modelled the distribution of marker effects directly using a novel technique that accounted for the sampling error associated with each estimate. The results from the two approaches were in agreement. The largest effects were estimated to explain between 0·12 and 0·48% of the phenotypic variance for WEC following challenge with T. colubriformis, and between 0·02 and 0·08% of the phenotypic variance following H. contortus challenge. The effect sizes are small but analysis of a third trait, bare breech area, suggests that the results are not specific to parasite resistance. The conclusion is that there are many polymorphisms of small effect underlying variation in WEC. This is potentially a common architecture for many complex traits (e.g. Hayes et al., Reference Hayes, Pryce, Chamberlain, Bowman and Goddard2010; Yang et al., Reference Yang, Benyamin, McEvoy, Gordon, Henders, Nyholt, Madden, Heath, Martin, Montgomery, Goddard and Visscher2010).
The distribution of marker effects has implications for the findings of this genome-wide association study, and other QTL detection studies in the literature. First, this experiment had little power to detect SNP linked to causative mutations having the size of the largest effects estimated (i.e. 0·48% of the phenotypic variance). Probably only a few of the most important markers associated with WEC following T. colubriformis challenge were identified but it was impossible to distinguish the true associations from the false-positive results using these analyses. There was less power for identifying markers associated with WEC following the H. contortus challenge because of the smaller estimated marker effects and the slightly reduced number of observations for this trait. This study had good power (>70%) to detect QTL explaining greater than 2·5–3·2% of the phenotypic variance, but we did not convincingly identify any markers with this magnitude of effect. This contrasts to results from past linkage studies that have estimated large (8% of the phenotypic variance; Davies et al., Reference Davies, Stear, Benothman, Abuagob, Kerr, Mitchell and Bishop2006) and modest (0·19–0·36 phenotypic standard deviations, Marshall et al., Reference Marshall, Maddox, Lee, Zhang, Kahn, Graser, Gondro, Walkden-Brown and van der Werf2009) QTL effects for WEC. Differences between our estimates and those of linkage studies can be partly attributed to the overestimation of effects in linkage studies (Xu, Reference Xu2003) and also to the possibility of multiple linked QTL contributing to linkage peaks. Also we do not attempt to quantify the reduction in marker effects due to incomplete LD between markers and QTL (Goddard et al., Reference Goddard, Wray, Verbyla and Visscher2009; Yang et al., Reference Yang, Benyamin, McEvoy, Gordon, Henders, Nyholt, Madden, Heath, Martin, Montgomery, Goddard and Visscher2010). The difference between the sizes of QTL effects when estimated from (within-family) linkage or (across-population) genome-wide association studies remains unresolved.
The distribution of marker effects and subsequent lack of experimental power could explain, in part, the inconsistencies between results for linkage analyses in the literature (Dominik, Reference Dominik2005; Sayers & Sweeney, Reference Sayers and Sweeney2005; Bishop & Morris, Reference Bishop and Morris2007). Assuming that many past experiments were underpowered to detect the largest effects estimated here, the proportion of true markers identified reduces and the results become almost impossible to reproduce in (similarly underpowered) subsequent experiments. A further issue is that most past studies have relied on within-family linkage to detect polymorphisms. Thus, replicating results in a second family where the polymorphism is not segregating is not possible. Polymorphisms may not be segregating in families due to low allele frequencies in the breed, or because the polymorphism is fixed in a particular breed of sheep. Replicating linkage peaks caused by multiple linked QTL is also difficult because of changes to linkage phase between families. Many authors have identified the Major Histocompatibility Complex (MHC) complex and the region containing the interferon gamma gene for resistance to worms (Schwaiger et al., Reference Schwaiger, Gostomski, Stear, Duncan, McKellar, Epplen and Buitkamp1995; Outteridge et al., Reference Outteridge, Andersson, Douch, Green, Gwakisa, Hohenhaus and Mikko1996; Paterson et al., Reference Paterson, Wilson and Pemberton1998; Coltman et al., Reference Coltman, Wilson, Pilkington, Stear and Pemberton2001; Patterson et al., Reference Patterson, McEwan, Dodds, Morris, Crawford and Jopson2001; Davies et al., Reference Davies, Stear, Benothman, Abuagob, Kerr, Mitchell and Bishop2006). However, this study found no validated SNP in these regions.
The results from our genome-wide association study are in agreement with previously published genome-wide association studies for other complex traits. That is, markers that passed our significance threshold in the reference population explained only a small proportion (11·0 and 2·3%) of the genetic variation in an independent population. There are two likely explanations for this result. First, the variance explained by an individual marker is small and, because many markers were tested for associations with the trait, stringent significance thresholds are applied (Goddard et al., Reference Goddard, Wray, Verbyla and Visscher2009). Yang et al. (Reference Yang, Benyamin, McEvoy, Gordon, Henders, Nyholt, Madden, Heath, Martin, Montgomery, Goddard and Visscher2010) recently demonstrated that these thresholds also exclude many markers, each of which only explains only a small proportion of the genetic variation. Thus, even if the power of this experiment was sufficient to detect the largest marker effects, probably most of the genetic variation would still be unexplained. In addition, this study searched for what may be considered old polymorphisms because we constrained the effect of SNP genotype to be consistent across different breeds of sheep. Such polymorphisms are likely to have small effects because any polymorphisms with a large effect on resistance to worms are expected to be removed due to purifying selection (Kimura, Reference Kimura1985). The second cause may be due to incomplete LD between the markers and the causative mutations (Goddard et al., Reference Goddard, Wray, Verbyla and Visscher2009; Yang et al., Reference Yang, Benyamin, McEvoy, Gordon, Henders, Nyholt, Madden, Heath, Martin, Montgomery, Goddard and Visscher2010). This has the effect of reducing the variance explained by a marker, particularly if the minor allele frequency of the polymorphism is lower than the genotyped SNP.
This paper used genomic markers to predict genetic merit for resistance to worm infections. We demonstrated that an approach that uses single (or a limited number of) markers is impractical for predicting genetic merit, primarily because of the small proportion of genetic variance explained by single markers. When all markers were used, we explained a moderate proportion of the genetic variance in the trait. However, improvements are still necessary and previous research in dairy cattle shows clearly how the accuracies of genomic predictions can be increased. The first step is to increase the size of the reference population. Deterministic predictions indicate a steady, almost linear, increase in GEBV accuracy if up to 20 000 extra records were added to this reference dataset (Goddard & Hayes, Reference Goddard and Hayes2009). The rate of increase is conditional on the heritability of the trait and thus artificial challenges for the reference population may still be required to maximize exposure to infection and the potential heritability for WEC (Bishop & Woolliams, Reference Bishop and Woolliams2010), at least under Australian conditions. The next step is to increase the potential LD between markers and polymorphisms by increasing the density of SNP markers. Low LD between markers in breeds such as Merinos suggests that the value of increasing the size of the reference population will be limited unless the density of markers is increased. For example, Calus et al. (Reference Calus, Meuwissen, de Roos and Veerkamp2008) estimate that GEBV can reach accuracies of 60–80% when the level of LD between marker alleles (r HR2) is greater than 0·2. In contrast to the Merino breed, accuracies will increase most rapidly with additional records in breeds with higher LD between markers, such as Poll Dorset, because of their lower effective population size (Hayes et al., Reference Hayes, Visscher, McPartlan and Goddard2003; Goddard & Hayes, Reference Goddard and Hayes2009). Predictions of genetic merit using the current density of markers would be maximized by restricting predictions and concentrating the reference population on a single breed.
Accurate prediction of genetic merit across breeds requires an increased density of markers. If denser markers were available then cross-bred populations, such as those in the current study, could be used more effectively to predict genetic merit. For example, Toosi et al. (Reference Toosi, Fernando and Dekkers2010) show that mixed breed populations can predict GEBV without a large loss in accuracy provided that (i) all constituent breeds are represented in the reference population and (ii) the marker density is sufficiently high for the marker-polymorphism associations to persist across breeds. To achieve an LD between marker alleles of greater than 0·2 (Calus et al., Reference Calus, Meuwissen, de Roos and Veerkamp2008), data from the current study suggest that an average marker spacing of approximately 10 kbp is required (Fig. 3). This is about five times the current density of SNP markers, i.e. about 250 000 SNP in total. de Roos et al. (Reference de Roos, Hayes, Spelman and Goddard2008) found a similar density for effective across-breed Bos taurus GEBV predictions and estimated an average required spacing of about 12 kbp. The sheep breeds in this study have the advantage of being mostly of European origin (Kijas et al., Reference Kijas, Townley, Dalrymple, Heaton, Maddox, McGrath, Wilson, Ingersoll, McCulloch, McWilliam, Tang, McEwan, Cockett, Oddy, Nicholas and Raadsma2009), which reduces their (across-breed) effective population size compared to more distantly related sheep breeds.
In conclusion, we used a mixed breed population of sheep to show that the detectable polymorphisms affecting resistance to worm infections have relatively small effects. We showed that the distribution of effects was consistent between worm species and with another trait not obviously associated with disease. Considering that the additive genetic effects for WEC accounted for between 10 and 24% of the phenotypic variance in this population, this means that there are likely to be hundreds or thousands of underlying mutations influencing these phenotypes. These mutations are probably spread across the genome. We used a novel approach to demonstrate how sampling error may bias the estimated effect size of SNP marker effects and subsequently showed that our experiment was underpowered to detect SNP with small effects we estimated. Any true markers that we identified are likely to be only a subset of the larger number of polymorphisms affecting resistance to worms. When all markers were used to predict genetic merit we were able to capture a larger proportion of the genetic variation compared to single marker regressions. Other livestock industries have already implemented techniques that use all makers to predict genetic merit and the research in these industries provides a good basis for future recommendations in sheep.
The authors thank the sheep breeders and other industry contributors who donated semen for use in the SheepGenomics flock, namely Lynton Arney (Inverbrackie, Strathalbyn SA), Kim Barnet (Miramoona, Walcha NSW), Guy Bowen (Mount Ronan, York WA), Andrew Burgess (Ruby Hills, Walcha NSW), George Carter (Linton, Woolbrook NSW), Neil and Jeff Johnson (Johnos, Keith SA), John Karlsson (Department of Agriculture Western Australia, WA), Jim Litchfield (Hazeldean, Cooma NSW), Robert Mortimer (Centre Plus, Tullamore NSW), Don Pegler (Oaklea, Mt Gambier SA), Ian Purvis (CSIRO Livestock Industries, Armidale NSW) and Julius van der Werf (University of New England, Armidale NSW). We are grateful for the contributions of Amy Bell, John Owens, Nigel Strutt, George Nichols, Alistair Donelson, Jason Siddell, Troy Fisher, Darryl Smith, Alex Ball, James Kijas, Russell McCulloch and Fiona McLoughlin for collecting and processing the samples used in this study. The authors also thank Australian Wool growers and the Australian government through Australian Wool Innovation, the Department of Agriculture and Food at the University of Melbourne and the BBSRC for financial support. SheepGenomics is an initiative of Australian Wool Innovation, Meat and Livestock Australia and 11 Research Organisations throughout Australia and New Zealand.












