1. Introduction
The phenotypic variation (V P) in quantitative traits comprises genetic and non-genetic components, plus possible interactions and covariances between them (Falconer & Mackay, Reference Falconer and Mackay1996; Lynch & Walsh, Reference Lynch and Walsh1998). The proportion of each component differs markedly among traits, although the proportion that is genetic is typically highest for traits related to morphology (e.g. mature size and conformation) and lowest for traits more closely related to fitness (e.g. litter size). For any type of trait, however, the values are typically quite similar among species.
The genotypic variance, V G, is usually partitioned into additive genetic (V A) and non-additive components, and the parameter most often used to compare the magnitudes of genetic and phenotypic variance is the narrow sense heritability (h 2=V A/V P), because it is easiest to estimate from information on relatives and is used in prediction of progeny performance. In practice, however, it can be difficult to distinguish between non-additive genetic and environmental variance without the use of clones or inbred lines, as both are components of within-family variance. An alternative measure of the phenotypic variability is the coefficient of variation (CV=√V P/μ), which facilitates comparisons among traits and species, and the coefficient of evolvability (CVA=√V A/μ) defines its additive genetic component (Houle, Reference Houle1992).
Variation in quantitative traits is ubiquitous, and there has been extensive analysis and discussion as to what maintains genetic variation. This requires some balance between the input from mutation and loss by drift and by most, if not all, selective forces acting directly on the trait itself or through pleiotropic effects. There is not yet, however, an unequivocal conclusion as to how the typical levels of genetic variance are maintained (e.g. Bürger, Reference Bürger2000; Johnson & Barton, Reference Johnson and Barton2005; Zhang & Hill, Reference Zhang and Hill2005a; Hill, Reference Hill2010).
Much less attention has been paid to factors accounting for the magnitude of the V P, V E or the CV. The CV is typically smaller for morphological traits (e.g. adult size) than for traits related to reproductive fitness (e.g. litter size and egg number). These quantities are not functions of the genetic variance, although typically the CV and heritability are negatively correlated. Understanding the forces that determine the magnitude of the non-genetic component of phenotypic variance is a broad question in evolutionary biology.
Thus, we wish to know how selection and other evolutionary forces are likely to influence V E, both the variance observable among repeated records on the same individual (expressed as what is often termed ‘fluctuating asymmetry’ (FA)) and that between individuals. Selective forces may include stabilizing selection, which is likely to reduce variation and environmental heterogeneity in time and space, which might increase variation as individuals have to be plastic to cope successfully with varying resources.
A related topic, but which we will not pursue here, is that of canalization in its specific sense of reduced variation found for a particular phenotype (Waddington, Reference Waddington1942; Rendel et al. Reference Rendel, Sheldon and Finlay1966), which has been subject to theoretical analysis in recent years by Wagner et al. (Reference Wagner, Booth and Bagheri-Chaichian1997), Gavrilets & Hastings (Reference Gavrilets and Hastings1994) and others. Here we concentrate on the more general nature of V E found over any range of genotypic or phenotypic mean.
The level of variation is also of importance in agricultural production because product consistency is desirable in growing, processing and consumption of foods. While it may be possible to avoid genetic variation by the use of inbred lines or their crosses, the non-genetic component cannot be avoided. Hence, there has been research recently in animal breeding on the extent to which variation can be reduced by selection so as to improve homogeneity, with the potential additional benefit of increasing accuracy of selection.
In this review we are concerned with the variation among or within individuals maintained in the same environment. A rather different but related topic is that of ‘robustness’ or sensitivity, which describes the extent to which the mean phenotype changes according to the environment. Differences among genotypes in such robustness give rise to genotype×environment interaction, but we shall not discuss these further in this review and focus on analyses within an identifiable (macro-) environment. Individuals within such an environment will each experience their own micro-environment, but these environmental differences are not identified. Differences among genotypes in V E may therefore reflect, at least in part, their differing sensitivity to micro-environmental factors (e.g. Falconer & Mackay, Reference Falconer and Mackay1996).
The approach used to analyse and understand the magnitude of the environmental variance (or of the CV or CVE) is to consider it as a trait in its own right. For traits that are expressed or recorded only once in an individual's lifetime, there is only one environmental component, E, that can be considered. If there are two or more records, for example, of bristles on opposite sides of a fly or of piglet weight within a litter, this can be partitioned into two components, the general or permanent environment effect, E g and that specific to individual records, E s (Falconer & Mackay, Reference Falconer and Mackay1996). In principle, there can be genetic variation in both components, but it may not be possible to separate them. An indicator of robustness and of fitness, widely used in evolutionary studies, is FA (Van Valen, Reference Van Valen1962), which is a measure of individual asymmetry in bilateral traits that are symmetric at the population level, for example, features of a fly's wing or a human face and is measured as the variance in E s. In this review, we shall concentrate primarily on the variation among individuals; reviews on FA have been published elsewhere (e.g. Leamy & Klingenberg, Reference Leamy and Klingenberg2005).
Since the genotype for the magnitude of environmental variation can be regarded as a quantitative trait, it is assumed to be determined by the actions and interactions of multiple genes. Much of the standard methodology of quantitative genetics can then be invoked. We do, however, have to recognize that the variances are unlikely to be normally (Gaussian) distributed, that there are inevitable problems of scale when considering the correlation or covariance of trait mean and variance and that natural selection acts on the individual phenotype, not on the ‘variation trait’.
Here we review the current state of knowledge of inheritance of environmental variance. We start by discussing quantitative genetic and statistical modelling of V E, methods of analysis and experimental designs for estimating the genetic variance in V E, and estimates which have been obtained of its magnitude. We subsequently consider the dynamics: the influences of artificial and of natural selection on V E and the evolutionary forces that determine the levels of heritability in natural and domesticated populations. We conclude with uncertainties and questions to be answered in the future.
2. Quantitative genetic models
(i) Alternative models
In standard quantitative genetic models, the variation in phenotype given genotype, Var(P|G), or V E, is assumed to be constant. When different genotypes differ in their environmental variance, we can postulate that some genes affect the phenotype and others affect the environmental variance or both, such that Var(P|G) depends on genotype. We can then define genotypic effects on both the mean and the variance. For simplicity and practicality of estimation, these are typically restricted to additive genetic effects. Different mathematical functions have been proposed to model the effect of genes on environmental variance, and here we discuss and compare their mathematical and statistical properties and their utility for predicting response to selection. We start with models assuming a single observation on an individual, and then extend the principles to include repeated observations on an individual.
In the additive model, the genetic component for variance is modelled as an additive effect on the environment variance (Hill & Zhang, Reference Hill and Zhang2004; Mulder et al., Reference Mulder, Bijma and Hill2007):
where μ and σE2 are, respectively, the mean trait value and the mean environmental variance of the population, A m and A v are, respectively, the additive genetic effects for the mean and environmental variance and χ is a standard normal deviate, N(0,1), for the environmental effect. The additive genetic effects for individuals are assumed to follow a bivariate normal distribution, where ![]() ,
, ![]() ,
, ![]() and r A are the additive genetic variances, covariance and correlation of A m and A v, respectively. Covariances among individuals are additionally defined by the additive genetic relationship matrix. Note that
and r A are the additive genetic variances, covariance and correlation of A m and A v, respectively. Covariances among individuals are additionally defined by the additive genetic relationship matrix. Note that ![]() is defined only if σE2+A v>0, and so the model breaks down if
is defined only if σE2+A v>0, and so the model breaks down if ![]() is very high. The model can easily be extended to include systematic environmental sources of heterogeneity of environmental variance such as herd effects. Random non-systematic environmental effects on the environmental variance are observed as sampling effects, but are not explicit in the quantitative genetic model.
is very high. The model can easily be extended to include systematic environmental sources of heterogeneity of environmental variance such as herd effects. Random non-systematic environmental effects on the environmental variance are observed as sampling effects, but are not explicit in the quantitative genetic model.
In the standard deviation model, the genetic component for variance is modelled as an additive effect on the environmental standard deviation (Garcia et al., Reference Garcia, David, Garreau, Ibañez-Escriche, Mallard, Masson, Pommeret, Robert-Granié and Bodin2009):
It is very similar to model (1) and has the same limitation in being defined only when σE+A v,SD>0. The magnitudes of ![]() differ between the models, however.
differ between the models, however.
The exponential model (SanCristobal-Gaudy et al., Reference SanCristobal-Gaudy, Elsen, Bodin and Chevalet1998) is multiplicative on the level of the environmental effect, but additive on the level of the natural logarithm of the variance scale
Modelling variances on the log scale is convenient because the log of a variance estimate tends to a normal distribution when the degrees of freedom are large. Modelling the log of variances has been applied in structural models to account for heterogeneity of variance between experimental units or farms (e.g. Foulley & Quaas, Reference Foulley and Quaas1995; Foulley et al., Reference Foulley, Quaas and Thaon d'Arnoldi1998) and for genetic heterogeneity of environmental variance (SanCristobal-Gaudy et al., Reference SanCristobal-Gaudy, Elsen, Bodin and Chevalet1998; Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003).
In the reaction norm model, the genetic component of variance is additive on the level of the reaction norm (Gavrilets & Hastings, Reference Gavrilets and Hastings1994; Gimelfarb, Reference Gimelfarb1994; Wagner et al., Reference Wagner, Booth and Bagheri-Chaichian1997; Wu & O'Malley, Reference Wu and O'Malley1998):
where γ is the multiplication factor, with mean β and e is the unscaled environmental effect. It is equivalent to the linear reaction norm model (Finlay & Wilkinson, Reference Finlay and Wilkinson1963), but the unscaled environmental effect is used instead of an environmental descriptive parameter.
(ii) Comparison of models
When the models are compared in terms of their expectations and variances (Table 1), the standard deviation and the reaction norm models are equivalent and can be re-parameterized from one to the other. The average environmental variance is a function of ![]() for the standard deviation model, the exponential model and the reaction norm model, but not for the additive model. Additive genetic values, A v, can be converted from the standard deviation, exponential and reaction norm model to the additive model (Table 2) by equating the second central moments of the environmental effects and similarly those for additive genetic variances,
for the standard deviation model, the exponential model and the reaction norm model, but not for the additive model. Additive genetic values, A v, can be converted from the standard deviation, exponential and reaction norm model to the additive model (Table 2) by equating the second central moments of the environmental effects and similarly those for additive genetic variances, ![]() , by equating their fourth central moments.
, by equating their fourth central moments.
Table 1. Expectation of environmental effect and environmental variance with additive models on variance and standard deviation, exponential and reaction norm models on variance (modified from Walsh & Lynch, Reference Walsh and Lynch2010)

a A v is the additive genetic effect for environmental variance, E is the environmental effect, χ is standard normal deviate, e exp and e RN are the unscaled environmental effects for exponential and reaction norm models and β is the average reaction norm=1.
Table 2. Conversion of breeding values (Av) and its genetic variance of (![]() ) from standard deviation, exponential and reaction norm models to the additive model (based on Mulder et al., Reference Mulder, Bijma and Hill2007)
) from standard deviation, exponential and reaction norm models to the additive model (based on Mulder et al., Reference Mulder, Bijma and Hill2007)

The expectation of the environmental variance given A v is linear for the additive model, but shows some non-linearity (concave upwards) for the other models, starting to become substantial when |A v|>2SD; the curvilinearity increases with increasing ![]() . The departure from the additive model is greatest for the exponential model.
. The departure from the additive model is greatest for the exponential model.
(iii) Extension to repeated observations on an individual
As there may be genetic variation in environmental variation both within and between individuals, we extend the additive model for repeated observations using the additive model, but the principles are straightforward to extend to the other models.
Repeated observations lead to covariances between environmental effects. To account for these, the environmental effects can be expressed as a sum of permanent environmental effects, common to all records of the individual (Falconer & Mackay, Reference Falconer and Mackay1996), and specific environmental effects Pij=μ+A m,i+PE m,i+Eij. Analyses of genetic heterogeneity of variance have so far included only one of these effects, but any of the fuller models can be obtained by extending eqns (1–4), assuming that both general and specific environmental effects are under genetic control. For the additive model, from (1):

where definitions are extensions of those given previously and χPE,i and χE,ij are N(0,1). The additive genetic effects A m,i, A v,PE,i and Av ,E,i are assumed to be trivariate normal and the permanent environmental effects PEm,i and PEv,i to be bivariate normal, each with corresponding variances and covariances.
The model is highly parameterized and needs very good designs if all parameters are to be estimated. In principle it postulates that the repeatability of a trait is genetically determined, by genetic variance not only of specific environmental effects, but also of permanent environmentally effects. These genetic effects on the permanent and specific environment effects may be highly correlated, as both depend on the individual's ability to respond to environmental conditions. The estimation of ![]() requires family relationships, whereas
requires family relationships, whereas ![]() can be estimated based on both repeated observations on the individual itself and family relationships. Analysis of the power to estimate all parameters and development of statistical methods need further research.
can be estimated based on both repeated observations on the individual itself and family relationships. Analysis of the power to estimate all parameters and development of statistical methods need further research.
3. Statistical analysis of large populations
Several methods have been proposed for estimating genetic heterogeneity in V E. As the between-individual environmental variance can never be estimated directly unless clones or MZ twins are used, some measure of residual variance or squared residuals is modelled in order to estimate (additive) genetic variance in V E.
The simplest type of analysis in segregating populations uses the within-family variances to estimate directly the genetic variance in V E (e.g. Rowe et al., Reference Rowe, White, Avendano and Hill2006; Ordas et al., Reference Ordas, Malvar and Hill2008), i.e. by restricted maximum likelihood (REML) or least squares. In this analysis, the strong assumption is made that there are no systematic environmental effects that influence the within-family variance, although heterogeneity of environmental or residual variance has been observed in many situations. The method used by Rowe et al. (Reference Rowe, White, Avendano and Hill2006) gave upwardly biased estimates of genetic variance in V E of broiler body weights in the data of Mulder et al. (Reference Mulder, Hill, Vereijken and Veerkamp2009), as the records spanned a long time period. More advanced methods have been developed that are aimed at reducing such bias (e.g. SanCristobal-Gaudy et al., Reference SanCristobal-Gaudy, Elsen, Bodin and Chevalet1998, Reference SanCristobal-Gaudy, Bodin, Elsen and Chevalet2001; Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003; Mulder et al., Reference Mulder, Hill, Vereijken and Veerkamp2009; Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010).
SanCristobal-Gaudy et al. (Reference SanCristobal-Gaudy, Elsen, Bodin and Chevalet1998, Reference SanCristobal-Gaudy, Bodin, Elsen and Chevalet2001) developed an EM–REML algorithm using expectation-maximisation and incorporating a structural model on the residual variance. In a structural model, fixed and random effects for both the mean and the log of the residual variance are fitted simultaneously, allowing for covariance structures between random effects on mean and on residual variance. To obtain solutions they used an iterative system because analytical integrals of some expressions were not available. Other simpler REML applications make use of a two-step approach, fitting a model on the phenotype in the first step and a model in which the (transformed) squared residuals are used as proxies for squared environmental effects in the second step. There are two main problems with using squared residuals, however: the residual is a mixture of true environmental effects and unexplained other effects; and if residuals are truly normally distributed, their squares are χ2 distributed, violating the normality assumptions when the squared residuals are analysed as a trait.
The accuracy of squared residuals (i.e. correlation between squared environmental effects and squared residuals) is a function of the accuracy of the estimated effects (i.e. correlation between true and estimated effects) and is reflected in the so-called hat-matrix of the mixed model equations, for which diagonal elements are called ‘leverages’ (Hoaglin & Welsch, Reference Hoaglin and Welsch1978). The hat-matrix describes the influence each observed value has on each fitted value and the leverage describes the influence each observed value has on the fitted value for that same observation (Hoaglin & Welsch, Reference Hoaglin and Welsch1978). This idea of accounting for leverages is implemented in the double hierarchical generalized linear model (DHGLM) (Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010), where the squared residuals are assumed to be gamma distributed, the residual variance is fitted using a generalized linear model (GLM) with gamma-distributed residuals to resolve the non-normality problem and the algorithm iterates between a model on the phenotype and a model on the residual variance. The DHGLM algorithm can be implemented in ASREML (Gilmour et al., Reference Gilmour, Gogel, Cullis and Thompson2006), but estimation of the genetic correlation between effects for mean and residual variance is not possible with the current algorithm (Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010). Although less appealing in theory than GLM, the non-normality of squared residuals can be resolved by appropriate transformations (Mulder et al., Reference Mulder, Hill, Vereijken and Veerkamp2009).
An alternative way to model genetic heterogeneity of residual variance is to use structural modelling of variances in a Bayesian framework (Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003; Sorensen, Reference Sorensen2009) and Markov chain Monte Carlo (MCMC) sampling to estimate all the parameters, both on phenotype and residual variance. Complex sampling algorithms (e.g. mixtures of Gibbs sampling and Metropolis–Hastings or Langevin–Hastings algorithms) are necessary in order to estimate all parameters because full conditional distributions are not of standard form, and some approximations may be used to increase efficiency and reduce computing time (Waagepetersen et al., Reference Waagepetersen, Ibáñez-Escriche and Sorensen2008). Even so, computing time may prohibit the use of these highly dimensional models on extremely large data sets. Although a potential downside of the Bayesian approach is its dependence on priors and prior distributions, results are not strongly dependent on them (Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003; Ibáñez-Escriche et al., Reference Ibáñez-Escriche, Moreno, Nieto, Piquears, Salgado and Gutierrez2008a).
In the Bayesian approach, all parameters can be estimated in all designs, posterior intervals give information about the precision and model selection criteria such as the deviance information criterion and Bayes factors can be used to compare the fit of different models (Sorensen & Waagepetersen, Reference Sorensen and Waagepetersen2003). In the computationally much less demanding REML framework, methods of comparison are less developed and there is not yet a well-established way to estimate the genetic correlation between the additive genetic effects on mean and V E.
The Bayesian methodology has been used in a number of studies to estimate the genetic variation in V E (Table 3) and a software package is now freely available (Ibáñez-Escriche et al., Reference Ibáñez-Escriche, Garcia and Sorensen2010). Some published studies using both REML and Bayesian methods on the same data have given similar estimates of genetic variance in V E (Rönnegård et al., Reference Rönnegård, Felleki, Fikse, Mulder and Strandberg2010; Wolc et al., Reference Wolc, White, Avendano and Hill2009) and others quite different estimates (Gutierrez et al., Reference Gutierrez, Nieto, Piqueras, Ibáñez and Salgado2006). A more formal comparison on simulated and on real data using cross-validation is recommended for repeated observations on the same individual or with large family groups.
Table 3. Published estimates of heritability (![]() , genetic coefficients of variation (
, genetic coefficients of variation (![]() ) and genetic correlation (
) and genetic correlation (![]() ) between additive genetic effects for mean and environmental variance. (– no estimate published)
) between additive genetic effects for mean and environmental variance. (– no estimate published)

a Methods classified into ANOVA, REML and MCMC. Within the REML methods in particular there are substantial differences in procedures applied (see text).
b Before and after Box–Cox transformation of data.
One of the main dilemmas in estimating genetic variation in V E is that these highly dimensional models may pick up some confounding effects. Perhaps most importantly, skew and kurtosis in the data may lead to biased estimates. Therefore, Box–Cox transformation has been proposed to transform the data and can have a substantial effect on estimates of the genetic variance in V E and the genetic correlation between mean and V E (Yang et al., Reference Yang, Christensen and Sorensen2010). Another solution might be to use residuals with a Student's t-distribution, which are more robust to their non-normality (Rosa et al., Reference Rosa, Padovani and Gianola2003; Cardoso et al., Reference Cardoso, Rosa and Tempelman2005).
There are some important assumptions in many of these analyses. The first is that there is no confounding of environmental variance with non-additive genetic components. These are overtly confounded in simple analyses such as those in which heterogeneity of variance within half-sib families is undertaken. In other more sophisticated methods such as fitting a structural model, there again can be confounding because covariances of relatives include both additive genetic and other genetic variance components. The particular concern is that there are individual genes or quantitative trait loci (QTL) segregating with individually large effect on the trait. Although these may lead to heterogeneity of within-family variance, Rowe et al. (Reference Rowe, White, Avendano and Hill2006) concluded that it could not explain the amount of heterogeneity found in their study. In general, however, all methods rely to some extent on the infinitesimal model and normality assumptions and all methods may be biased if these are violated.
4. Empirical evidence for genetic variation in environmental variance
(i) Direct estimates of VE
Inbred lines (Whitlock & Fowler, Reference Whitlock and Fowler1999; Sorensen et al., Reference Sorensen, Kristensen, Loeschcke, Ibáñez and Sorensen2007) and chromosome substitution lines (Mackay & Lyman, Reference Mackay and Lyman2005) have provided direct evidence of overall genetic variation in V E in Drosophila melanogaster. The differences in V E for bristle number observed by Mackay and Lyman, for example, cannot be accounted for solely by scale transformation. Individual genes associated with differences in V E or CVE have also been identified, e.g. .the Dopa decarboxylase (Ddc) gene in D. melanogaster was shown to cause differences of up to 5% between homozygotes in CVE of abdominal bristle number (Mackay & Lyman, Reference Mackay and Lyman2005). There are widely accepted differences in environmental variability between inbred lines and their hybrid crosses (Lerner, Reference Lerner1954; Falconer & Mackay, Reference Falconer and Mackay1996; Lynch & Walsh, Reference Lynch and Walsh1998). At a more basic level, genetic differences in variability of gene expression differences among cells have been observed (Ansel et al., Reference Ansel, Bottin, Rodriguez-Beltran, Damon, Nagarajan, Fehrmann, Francois and Yueot2008), which may in turn provide insight into the magnitude of differences found at the level of the observable trait.
(ii) Estimates in large segregating populations
In the last ten years many estimates of genetic variance in V E between individuals have been published, predominately of body weight or litter traits. Table 3 updates that of Mulder et al. (Reference Mulder, Bijma and Hill2007)
and shows estimates of heritability (hv 2), genetic coefficient of variation (GCVE; note also that ![]() ) based on the linear model and genetic correlations (
) based on the linear model and genetic correlations (![]() ) between the additive genetic effects for mean and V E. With one exception (Gutierrez et al., Reference Gutierrez, Nieto, Piqueras, Ibáñez and Salgado2006, for body weight in mice), estimates of hv 2 range between 0·0 and 0·05 and those for GCVE between 0·0 and 0·60, albeit with some consistency, and median values are 3 and 30%, respectively. Estimates of
) between the additive genetic effects for mean and V E. With one exception (Gutierrez et al., Reference Gutierrez, Nieto, Piqueras, Ibáñez and Salgado2006, for body weight in mice), estimates of hv 2 range between 0·0 and 0·05 and those for GCVE between 0·0 and 0·60, albeit with some consistency, and median values are 3 and 30%, respectively. Estimates of ![]() take up the whole parameter space between −1·0 and 1·0, but tend to be negative for the body weight traits. Estimates are based on different models (see above) and data structures, however, and the studies using MCMC all have quite large 95%-posterior intervals. In addition, Yang et al. (Reference Yang, Christensen and Sorensen2010)
showed that Box–Cox transformation of litter size data of pigs and rabbits reduced hv 2 by, respectively, 45 and 51% and
take up the whole parameter space between −1·0 and 1·0, but tend to be negative for the body weight traits. Estimates are based on different models (see above) and data structures, however, and the studies using MCMC all have quite large 95%-posterior intervals. In addition, Yang et al. (Reference Yang, Christensen and Sorensen2010)
showed that Box–Cox transformation of litter size data of pigs and rabbits reduced hv 2 by, respectively, 45 and 51% and ![]() changed sign.
changed sign.
Studies are not included in Table 3 if published results were insufficient to compute hv 2 and GCVE. In these the heritability reported for within-litter variability of birth weight generally lies in the range 0·06–0·11 (Damgaard et al., Reference Damgaard, Rydhmer, Løvendahl and Grandinson2003; Wittenburg et al., Reference Wittenburg, Guiard, Teuscher and Reinsch2008; Canario et al., Reference Canario, Lundgren, Haandlykken and Rydhmer2010). In some older studies, ANOVA techniques were used to analyse within-family variances of dairy bulls with large offspring groups, and substantial differences between sires were found (Van Vleck, Reference Van Vleck1968; Clay et al., Reference Clay, Vinson and White1979).
There is substantial literature and discussion on estimates of genetic parameters for FA, which are de facto repeat records with only two observations. The data come particularly from Drosophila and humans (Møller & Thornhill, Reference Møller and Thornhill1997; Gangestad & Thornhill, Reference Gangestad and Thornhill1999; Fuller & Houle, Reference Fuller, Houle and Polak2003; Leamy & Klingenberg, Reference Leamy and Klingenberg2005). The general finding is that heritability estimates are low and averaging about 0·03 (Fuller & Houle, Reference Fuller, Houle and Polak2003), but depend to some extent on the trait and on the statistical methodology used. By aggregating traits on each side of the body, for example physical dimensions in humans, Johnson et al. (Reference Johnson, Gangestad, Segal and Bouchard2008) show that heritabilities over 0·25 can be obtained.
(iii) Results from selection experiments
Other evidence for the existence of genetic variation in V E comes from selection experiments, but changes in genetic and environmental variances are often confounded and results are not clear cut. No significant changes in phenotypic variance of body size of mice were found by Falconer & Robertson (Reference Falconer and Robertson1956) Falconer & Robertson (Reference Falconer and Robertson1956) who selected mice with either the largest deviations or the smallest deviations from their litter-mean. Following canalizing selection in both D. melanogaster (Rendel et al., Reference Rendel, Sheldon and Finlay1966) and Tribolium castaneum (Kaufman et al., Reference Kaufman, Enfield and Comstock1977) substantial decreases in phenotypic variance were obtained, both V G and V E decreasing in the latter. Disruptive selection in D. melanogaster led to increases in V G and V E in one experiment (Scharloo et al. Reference Scharloo, Zweep, Schuitema and Wijnstra1972), but only in V G in another (Sorensen & Hill, Reference Sorensen and Hill1983), and there were substantial changes in phenotypic variance following selection on higher and lower within-family variance in Tribolium (Cardin & Minvielle, Reference Cardin and Minvielle1986). Although phenotypic variance can change greatly in directional selection experiments (Clayton & Robertson, Reference Clayton and Robertson1957; Falconer & Mackay, Reference Falconer and Mackay1996), these changes are further confounded by scale effects.
A few selection experiments have been conducted to reduce phenotypic variance by selecting on estimated breeding value (EBV) for environmental variance. No response to divergent selection in pigs on EBV for V E in pH was observed by Larzul et al. (Reference Larzul, Le Roy, Tribout, Gogue and SanCristobal2006), but EBVs were based on only four progeny and had low accuracy. In experiments with rabbits, divergent selection was practised for eight generations on within-litter variability in birth weight (Garreau et al., Reference Garreau, Bolet, Larzul, Robert-Granie, Saleil, SanCristobal and Bodin2008; Bodin et al., Reference Bodin, Bolet, Garcia, Garreau, Larzul and David2010) and for high or low variability in litter size for three generations in another population (Argente et al., Reference Argente, Garcia, Muelas, Santacreu and Blasco2010). Although a substantial response was obtained in the first generation in both experiments, only after generation 5 was further response achieved in the experiment of Bodin et al. (Reference Bodin, Bolet, Garcia, Garreau, Larzul and David2010) and little further response was obtained by Argente et al. (Reference Argente, Garcia, Muelas, Santacreu and Blasco2010) .
(iv) Conclusion
There are data from genetically homogeneous populations showing genetic variation in V E. From the published results on analyses of large outbred populations and selection experiments, it can be concluded that there is much empirical evidence for the existence of additive genetic variation in V E, although appropriate modelling of genetic heterogeneity of environmental variance remains a challenging area. The results from the selection experiments are not convincing, but changes in variance in the expected direction seem to be observed in the majority. There may, however, be some publication bias.
5. Experimental design for estimating genetic parameters
In laboratory- and population-based studies where new information has to be collected in order to obtain estimates of parameters such as the variance or QTL effects for genetic heterogeneity of V E, designs can be optimized and the minimal experimental size determined. For field data already collected, there is little opportunity to influence design, but the expected sampling errors of estimates and power of detection can determine whether it is worthwhile doing any analysis. It is assumed that the basic observations X are normally distributed, and also, where necessary, that the distributions among groups of log variance estimates are also normally distributed.
(i) Estimating QTL or other fixed effects
For comparing two groups each with n observations, and assuming only V E is unaccounted for, the sampling error of the difference in means is 2V E/n and of (natural) log variance 4/n. Hence, roughly twice as many observations are required to detect a proportional effect on variance of the same size as an effect on mean expressed in SD units. For example, if the sample size is 1000 and there is a real 10% proportionate difference (b) in variance, b/SE(b)~1·6 and the power to detect the difference would be low. More records are needed if degrees of freedom are lost through fixed effects and/or if genetic variance in addition to V E is included in the error variance. Yang (Reference Yang2010) considered detection of QTL in an association study more formally but, as she assumed the variance in one of the groups was known without error, sampling variances were half the above.
The analysis was further developed by Visscher & Posthuma (Reference Visscher and Posthuma2010) for a linear regression of (mean or) variances of genotype (scored 1, 2, 3), with estimation of V P and V E from sets of either unrelated individuals or identical twin pairs. They argue that, as genome-wide association studies rarely find loci accounting for over 1% of variation in mean human height, effects on V E are also likely to be small. As tiny type-I errors are needed in whole genome investigations, very large samples will be needed, e.g. over 10 000 individuals or monozygotic (MZ) twin pairs (over all genotypes) to detect a QTL with an effect of 10% on the variance. They further show that, if the QTL affects only V E, identical twin pairs give a more efficient design than unrelated individuals. Even though power is low, seeking QTL affecting variance is a cheap by-product of studying genome-wide associations for trait mean.
(ii) Estimation of components of variance
To study the inheritance of V E, measures of variance on relatives are needed. The more highly related they are, the smaller is the sampling variance of the estimates, but the greater is the risk of confounding by environmental covariances. If interest is in estimating the genotypic rather than the additive genetic variance, and if they are available, clones or highly inbred/isogenic lines are most efficient. Otherwise family studies are needed, and design considerations are similar to those for estimating the usual genetic variances (i.e. σ2Am).
For simplicity consider a one-way classification with n individuals, each with single records; if repeat records are being analysed, a further nested effect is needed. Results initially derived for an additive model (Hill, Reference Hill2004), are simpler to optimize using the exponential variance model. If ![]() in group i, zi has an approximate normal distribution with variance 2/(n−1)+γ2, where γ2 is the CV2 of the variance within groups. For large n and m (needed for useful estimates) and γ2→0, it can be shown that SE(
in group i, zi has an approximate normal distribution with variance 2/(n−1)+γ2, where γ2 is the CV2 of the variance within groups. For large n and m (needed for useful estimates) and γ2→0, it can be shown that SE(![]() )~[√(8/m)]/n and is increased by a factor 1/R to estimate ‘heritability’ if family members have relationship R. For example, with 100 half-sib families each of size 20, SE(
)~[√(8/m)]/n and is increased by a factor 1/R to estimate ‘heritability’ if family members have relationship R. For example, with 100 half-sib families each of size 20, SE(![]() )~0·014, so a much larger experiment would be needed to get much power to detect
)~0·014, so a much larger experiment would be needed to get much power to detect ![]() >0, if the true value of γ2 is small (see also Mulder, Reference Mulder2007). The SE would be halved by a doubling of family size or by a fourfold increase in the number of families. The optimum family size, 2/γ2 for a specified total number recorded, is large because the genetic variance in V E is generally low, just as for estimating the usual heritability of a very lowly heritable trait (Robertson, Reference Robertson1959; Falconer & Mackay, Reference Falconer and Mackay1996).
>0, if the true value of γ2 is small (see also Mulder, Reference Mulder2007). The SE would be halved by a doubling of family size or by a fourfold increase in the number of families. The optimum family size, 2/γ2 for a specified total number recorded, is large because the genetic variance in V E is generally low, just as for estimating the usual heritability of a very lowly heritable trait (Robertson, Reference Robertson1959; Falconer & Mackay, Reference Falconer and Mackay1996).
(iii) Selection experiments
As selection intensities for disruptive selection can be higher than for stabilizing selection, the former is likely to provide a more powerful test of whether ![]() >0, but analysis is complicated by changes in genetic variance due to gametic disequilibrium. For a trait recorded only once on each individual, selection has to be practised among families and so, to maintain large-enough families to practise accurate selection with adequate effective population size, selection intensity has to be low. Power calculations for short-term experiments to detect between individual variance in V E show that such experiments may be feasible, but need large resources (Mulder, Reference Mulder2007).
>0, but analysis is complicated by changes in genetic variance due to gametic disequilibrium. For a trait recorded only once on each individual, selection has to be practised among families and so, to maintain large-enough families to practise accurate selection with adequate effective population size, selection intensity has to be low. Power calculations for short-term experiments to detect between individual variance in V E show that such experiments may be feasible, but need large resources (Mulder, Reference Mulder2007).
If, however, the trait of interest is variance among repeated observations on each individual, truncation selection can be practised on within-individual variance among n records. Ibáñez-Escriche et al. (Reference Ibáñez-Escriche, Sorensen, Waagepetersen and Blasco2008b) consider the optimization and concluded that such a selection experiment to estimate the genetic variance in V Ew would also have to be large, particularly when n is small (e.g. n=2, for bilateral traits).
In principle, information on the between individual heterogeneity can come from data on traditional mass selection experiments to increase or decrease the mean. In practice, however, analysis and interpretation of data to reveal the genetic variance in heterogeneity is complicated by potential changes in genetic variance caused by selection, which are predictable under infinitesimal model assumptions, but not otherwise (Hill & Zhang, Reference Hill and Zhang2004; Mulder, Reference Mulder2007; Mulder et al., Reference Mulder, Bijma and Hill2008).
6. Effects of selection on environmental variance
Selection changes gene frequencies and hence the population mean and the genetic variance. Selection can also influence the magnitude of non-genetic components of phenotypic variance if these are at least partially under genetic control and genes responsible are segregating in the population. In the evolutionary literature, following Bull (Reference Bull1987), much of the interest has been on studying the extent to which stabilizing selection might reduce the environmental variance and on other factors, such as the ability to cope with changing environments, which might favour increasing variance (e.g. Zhang & Hill, Reference Zhang and Hill2005b). In the breeding literature emphasis has been on how quickly V E could be reduced by artificial selection (SanCristobal-Gaudy et al. Reference SanCristobal-Gaudy, Elsen, Bodin and Chevalet1998; Mulder et al., Reference Mulder, Bijma and Hill2007; Reference Mulder, Bijma and Hill2008; Ibáñez-Escriche et al., Reference Ibáñez-Escriche, Moreno, Nieto, Piquears, Salgado and Gutierrez2008a, Reference Ibáñez-Escriche, Sorensen, Waagepetersen and Blascob) and on the correlated response in V E with directional selection on phenotype (Hill & Zhang, Reference Hill and Zhang2004; Mulder et al., Reference Mulder, Bijma and Hill2007). Here, we deal with theory that has been undertaken both at the level of individual genotypes and using the infinitesimal model. In addition we quantify how response to selection with artificial selection can be increased using family information or repeated observations, but defer fuller discussion of the evolution of V E to the subsequent section.
Rather than review the development of the methodology we utilize a recent generalization (Zhang & Hill, Reference Zhang and Hill2010) based on the Price (Reference Price1970) equation. Relevant formulae are summarized in Box 1 eqs (B1–B6). A genotype is assumed to have an effect a on mean phenotype, i.e. on genotypic value G and corresponding effect b on environmental variance, Var(G|E). From the Price equation, the expected genetic changes in trait mean Δμ and environmental variance ΔV E between generations due to selection are given by the covariance of genotypic value and relative fitness, with the addition of other segregation effects, restricted here to those from mutation (eqn. B1 in Box 1).
Box 1. Some formulae for predicting response to selection in mean, μ and environmental variance, VE
Changes due to a gene with effect a on mean and b on V E as a function of relative fitness ![]() and magnitude of mutation effects
and magnitude of mutation effects
Under stabilizing selection with optimum Θ and strength V S, relative fitness is
Assuming a normal distribution of a and b,
For truncation selection of a proportion p, with i the corresponding selection intensity and x the standardized truncation point, relative fitness is
The predicted changes in μ and V E are, ignoring mutation,
Here cov(P, P 2) is ignored; otherwise more complicated formulae apply (Mulder et al., Reference Mulder, Bijma and Hill2007).
For n-repeat records on each individual with truncation selection on I=log[Σj(Xij−![]() )2/(n−1)], predictions in terms of I are:
)2/(n−1)], predictions in terms of I are:
See Ibáñez-Escriche et al. Reference Ibáñez-Escriche, Sorensen, Waagepetersen and Blasco2008b) for more accurate formulae if ![]() is not small.
is not small.
(i) Stabilizing selection
Stabilizing selection in a natural population towards an optimum Θ is usually modelled as a nor-optimal fitness function (i.e. with shape that of a normal distribution), with ‘variance’ ω2 about the optimum (i.e. ω2 is small when selection is strong) (Bürger, Reference Bürger2000). Selection strength then depends on V S=ω2+V E (eqns. B2 and B3). If the population is at or near the optimum, genotypes causing an increase in V E are at a selective disadvantage. The strength is reduced if the population mean departs from the optimum, but if the mean is far from the optimum, genes increasing phenotypic variance and V E could be at a selective advantage (Slatkin & Lande, Reference Slatkin and Lande1976; Bull, Reference Bull1987). The former would pertain if the environment and optimum remain fairly constant, the latter if it shows trends or fluctuates. The same patterns in selective advantage for optimum traits can be achieved by deriving economic values for mean and variance (Mulder et al., Reference Mulder, Bijma and Hill2008).
Providing the position of the optimum remains constant, the trait mean converges at or close to the optimum, although it can be displaced somewhat by mutation and by a covariance of gene effects on mean and variance. The environmental variance declines to zero as long as there is genetic variance affecting V E, i.e. ![]() >0 and there is no increase in V E from mutation (Bull, Reference Bull1987; Zhang & Hill, Reference Zhang and Hill2005b, Reference Zhang and Hill2010).
>0 and there is no increase in V E from mutation (Bull, Reference Bull1987; Zhang & Hill, Reference Zhang and Hill2005b, Reference Zhang and Hill2010).
Disruptive selection where intermediates are at a disadvantage will have opposite effects to those of stabilizing selection near what is then an unstable optimum, but as the population departs from the optimum the population will increasingly behave as for directional selection.
(ii) Truncation selection
The impact of directional selection on both phenotypic mean and V E is quite different from that of stabilizing selection acting on fitness (Hill & Zhang, Reference Hill and Zhang2004; Zhang & Hill, Reference Zhang and Hill2010). If there is no genetic covariance between the effects of genes on mean and V E, i.e. ![]() =0, response in the mean is given by the breeders’ equation, R=h 2S. If
=0, response in the mean is given by the breeders’ equation, R=h 2S. If ![]() >0, selection also increases V E if selection is intense (<50% selected), and the responses in mean and variance are both influenced if effects are correlated (
>0, selection also increases V E if selection is intense (<50% selected), and the responses in mean and variance are both influenced if effects are correlated (![]() ). Thus, under intense truncation selection whereby extreme individuals are favoured, V E is predicted to increase if it varies genetically (eqns. B4 and B5). Scale effects complicate interpretation.
). Thus, under intense truncation selection whereby extreme individuals are favoured, V E is predicted to increase if it varies genetically (eqns. B4 and B5). Scale effects complicate interpretation.
These arguments can also be shown under multiple locus models, but a full multi-generation analysis requires that changes in the components such as ![]() be computed. This can be done under infinitesimal model assumptions, i.e. to account for reduction in
be computed. This can be done under infinitesimal model assumptions, i.e. to account for reduction in ![]() due to gametic phase disequilibrium (‘Bulmer effect’) (Hill & Zhang, Reference Hill and Zhang2004), but otherwise it depends on knowledge of individual gene effects.
due to gametic phase disequilibrium (‘Bulmer effect’) (Hill & Zhang, Reference Hill and Zhang2004), but otherwise it depends on knowledge of individual gene effects.
If selection is weak and gene effects are additive the responses to multi-locus selection can be predicted adequately from eqn (B5), where terms such as ![]() and
and ![]() now refer to sums over loci. With intense artificial selection on mean or variance complications arise because, if there is heterogeneity of environmental variance, the regression of breeding value (A m) on phenotype (P) is no longer linear (Mulder et al., Reference Mulder, Bijma and Hill2007). As extreme scoring individuals are more likely to come from high variance families, this regression is slightly sigmoid. Hence, P and P 2 can be regarded as two traits in a bivariate selection index and response in mean and variance predicted more accurately. Predictions for response to stabilizing selection in a breeding programme carried out by truncation of extremes can be predicted similarly from the reduction in selection differential.
now refer to sums over loci. With intense artificial selection on mean or variance complications arise because, if there is heterogeneity of environmental variance, the regression of breeding value (A m) on phenotype (P) is no longer linear (Mulder et al., Reference Mulder, Bijma and Hill2007). As extreme scoring individuals are more likely to come from high variance families, this regression is slightly sigmoid. Hence, P and P 2 can be regarded as two traits in a bivariate selection index and response in mean and variance predicted more accurately. Predictions for response to stabilizing selection in a breeding programme carried out by truncation of extremes can be predicted similarly from the reduction in selection differential.
Family information can be utilized in animal and plant breeding to increase the accuracy of selection decisions. As prediction of breeding values for environmental variance (A v) can be regarded as predictions for a trait with a low heritability, records on large numbers of relatives are needed to get high accuracy. Selection index theory can be used to predict the accuracy of ![]() based on family size and relationship (Mulder et al., Reference Mulder, Bijma and Hill2007, Reference Mulder, Bijma and Hill2008), and examples are given in Table 4. Observations on clones, feasible in some plant species, are most effective in realizing high accuracy. Half-sib progeny can provide higher accuracy than sibs, and so progeny testing may be more efficient than sib-testing schemes in reducing V E by selection (Mulder et al., Reference Mulder, Bijma and Hill2008).
based on family size and relationship (Mulder et al., Reference Mulder, Bijma and Hill2007, Reference Mulder, Bijma and Hill2008), and examples are given in Table 4. Observations on clones, feasible in some plant species, are most effective in realizing high accuracy. Half-sib progeny can provide higher accuracy than sibs, and so progeny testing may be more efficient than sib-testing schemes in reducing V E by selection (Mulder et al., Reference Mulder, Bijma and Hill2008).
Table 4. Approximate accuracy rA of predicted breeding value ![]() for VE using family information
for VE using family information
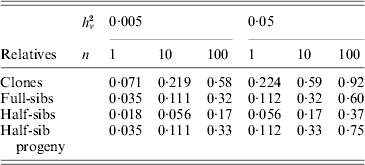
![]() , for n phenotypic records, and additive (unless clones) genetic relationships, ρb between the evaluated animal and the group of relatives and ρw among individuals within the group (based on Mulder et al. Reference Mulder, Bijma and Hill2007).
, for n phenotypic records, and additive (unless clones) genetic relationships, ρb between the evaluated animal and the group of relatives and ρw among individuals within the group (based on Mulder et al. Reference Mulder, Bijma and Hill2007).
Multiple objectives feature if, for example, amount and consistency of product at the farm and/or consumer level are desirable, including, for example, robustness to environmental fluctuation. Selection for reduced variance is therefore of interest for traits with an optimum, and more generally there is a non-linear profit equation (Mulder et al., Reference Mulder, Bijma and Hill2008). To bring the mean closer to the optimum and decrease the variance around it, selection both on mean and variance is needed. SanCristobal-Gaudy et al. (Reference SanCristobal-Gaudy, Elsen, Bodin and Chevalet1998) derived an appropriate quadratic index, although a linearized selection index with updated weights can bring the mean to the optimum more rapidly (Mulder et al., Reference Mulder, Bijma and Hill2008).
Repeated records allow individual animals to have a direct measure of within-individual variation in the trait (V Es). The analysis therefore differs from that above which is based on one record per individual. If selection operates on the variation among the n observations on each individual, a simple prediction is that the response in variance will equal the product of selection differential on variance and its ‘heritability’ as a function of the number of records (eqn. B6, from SanCristobal-Gaudy et al., Reference SanCristobal-Gaudy, Elsen, Bodin and Chevalet1998; Ibáñez-Escriche et al., Reference Ibáñez-Escriche, Sorensen, Waagepetersen and Blasco2008b).
The more general case of a repeated trait such as the distribution of flowering time among florets of a plant, where natural selection may operate within and between plants, is considered by Deveaux & Lande (Reference Deveaux and Lande2010) . The effects of artificial selection for the similar situation, e.g. egg weight of birds where homogeneity among both individual eggs within birds and average egg size between birds may be desirable, have not been worked out.
7. Factors affecting the magnitude of V E
The presence of genetic variance for a trait requires that genes with influence on the trait are segregating in the population. In contrast, the presence of V E does not require segregation and in that sense is more like the population mean. If no mutations occur that influence V E then obviously it will fix at a constant level, but there is plenty of evidence for genetic variation in V E (Table 3) and, by inference, mutations that affect V E. Therefore, we need to consider what determines the levels maintained. We review what forces may be acting and discuss some of the models, but recognize that the analysis is far from being conclusive: indeed, this is hardly surprising as our real understanding is weak of why trait means take the values they do, and is poorer for why genetic variance and V E take the values they do. It should be emphasized that we are considering just the magnitude of V E expressed by quantitative traits in segregating populations and are not concerned with major transitions or with, for example, evolution of canalization to a specific phenotype.
Stabilizing selection in a constant environment where extreme organisms are at a disadvantage provides selective pressure to reduce V E in all traits (Slatkin & Lande, Reference Slatkin and Lande1976; Bull, Reference Bull1987; Box 1), and there is no reason to assume that the nor-optimal model would lead to different general conclusions than others in which extremes are at a disadvantage. Hence, stabilizing selection acts like directional selection downwards on V E among individuals. Similarly, any selection against variation within individuals, e.g. FA, whether it is stabilizing selection on individual records or selection against asymmetry among trait expressions, similarly leads to downward selection pressure. The theoretical problem is basically, therefore, to establish why V E does not decline towards zero and is maintained at values typical for the trait. We distinguish between potential extrinsic opposing forces, such as variability in the optimum phenotype among generations or niches (Bull, Reference Bull1987), and intrinsic forces such as those associated with costs of regulating the phenotype.
(i) Extrinsic factors
Environmental heterogeneity. There is extensive discussion on the impact of environmental heterogeneity in the evolution of plasticity and maintenance of genetic variation, but rather little on its influence on the maintenance of V E, although variation in plasticity to local heterogeneity would appear in analyses as V E. Bull (Reference Bull1987), in a pioneering study, proposes a model whereby stabilizing selection operates within the environment (Box 1), but with Θt, the position of the optimum at generation t, varying among generations. If Θt is constant, the population mean stabilizes at the optimum and there is consistent selection to reduce V E towards 0. If the position of the optimum varies, however, the expected fitness of a genotype k with mean μk and environmental variance V Ek is then also a function of V Ek at generation t. The optimum genotype maximizes the expectation of this quantity over generations. If μk has a constant mean and the optima Θt are uncorrelated over generations, the presence of genetic variation in V Ek leads to an optimum at V E=π2−ω2, where π2 is the variance of μk and must exceed ω2 (Bull, Reference Bull1987). If the fluctuation in the mean is large, the optimum V E is greater than 0, but this is a very stringent requirement. Even at what are generally regarded as typical values of ω2 of at least 20 (but see Kingsolver et al., Reference Kingsolver, Hoekstra, Hoekstra, Berrigan, Vignieri, Hill, Hoang, Gibert and Beerli2001, indicating higher values), this implies that the position of the optimum has a variation across generations in excess of 20 phenotypic standard deviations.
Fluctuations in the width of the selection profile, i.e. in ωk 2, can reduce this stringency a little, however, dependent on the correlation of mean and width of the fitness profile (Zhang & Hill, Reference Zhang and Hill2005b). Nevertheless, simple fluctuations in the position of the optimum or width of the fitness profile do not seem sufficient forces on their own to maintain V E.
In the presence of heterogeneity in the environment, V E may reflect plastic responses to this heterogeneity in addition to intrinsic factors such as developmental noise. Zhang (Reference Zhang2005) shows that plasticity can be adaptive if a correlation can be established between the optimal phenotype and environmental quality if it varies over time or space. The consequent increase in evolved plasticity induces increases in the V E of the trait. While the sum of spatial and temporal variation needs to be larger than the observed V E, which is a stringent requirement, variation in environmental quality can be much less than V E. Some of these issues have been further explored subsequently (Zhang, Reference Zhang2006). The inter-relationship between parameters such as heterogeneity of environment in time and space and rates of migration are complicated, although the magnitude of V G maintained is much less sensitive to them than is V E. Even so, there are circumstances with high levels of environmental variability that can lead to reductions in V E.
Competition within species. Competition between individuals for resources, e.g. seeds as food for birds, would appear to favour high V E in, say, bill size in that it increases differences between them and thereby reduces direct competition. Although under strong assumptions such a model can lead to increases in V G in the presence of stabilizing selection, it has little impact on maintaining V E because competing genotypes diverge and stabilizing selection still acts within each (Zhang & Hill, Reference Zhang and Hill2007).
Interactions among species. A specific example is considered by Deveaux & Lande (Reference Deveaux and Lande2010) who model the variation in flowering time of an insect-pollinated plant species for which there are two levels of variation, between individual flowers within one plant and that between plants. They show that selective forces may act to increase (environmental) variation in flowering time within plants, in particular if there is a limitation in pollinator availability at any one time and a temporal autocorrelation of individual pollinator visitation. Such a model might apply in other organisms in which the phenotype is repeated at different times or in different locations, but not for bilateral traits.
Conclusion. None of the above models lead to an equilibrium in V E at observed levels except for special situations (e.g. flowering time) without very stringent requirements on the parameters, such as the magnitude of variation in the optimum genotype.
(ii) Intrinsic factors
Cost of uniformity. If the same genes are assumed to be expressed on bilaterally repeated traits, then variation in a trait between sides can be regarded as developmental noise. This is, presumably, under some degree of selective control: in Drosophila, for example, the CV within individuals for wing size is much smaller than that of sternopleural bristle number. While stabilizing selection would be expected to reduce the V Es, one can reasonably assume it is stronger for maintaining symmetry of wings than of bristles. It does not address what magnitude is maintained. One simple model is that there is a cost to the organism associated with reducing variability, an ‘engineering cost’ of control of the trait or homeostasis in Lerner's (Reference Lerner1954) terms.
The same cost argument pertains in principle to reducing V E between individuals for a trait such as body size. Zhang & Hill (Reference Zhang and Hill2005b) applied a rather arbitrary cost function of exp(C/V E), which increases as V E decreases, such that fitness with stabilizing selection is proportional to exp(C/V E) exp[−½(X−Θ)2/ω2]. The model predicts a stable equilibrium at V E~√(2Cω2), with quite a small accompanying loss of mean fitness (selection load) compared to an equilibrium at V E=0. The equilibrium in the CV and, for repeated traits, an equilibrium point in within-individual V E can be computed similarly. The model is appealing but direct evidence, such as observations showing the energetic cost of developmental stability, is lacking.
Mutation effects on V E. Mutation influences the genotypic mean and can also affect the variance, typically upwards, by more than can be explained by a simple scale effect. The scute gene in Drosophila is an example, albeit associated with canalizing effects (Rendel et al., Reference Rendel, Sheldon and Finlay1966). If the mutations have symmetrically distributed effects on V E, i.e. are equally likely to increase or decrease it, they merely provide fuel for V E to evolve and are unlikely to affect equilibrium points. If, however, mutants tend to increase V E, i.e. to reduce developmental control, equilibria can be obtained (Zhang & Hill, Reference Zhang and Hill2008). These depend on the mean effect of mutations on V E, on the relation between effects of mutation on the mean and the variance and on the fitness function. As the mutation rate affects both the amount of genetic variance maintained and the amount of environmental variance, it leads to stable values of the heritability, for which we know of no other model.
A basic model with stabilizing selection which yields analytic solutions is to assume that mutant effects a on the mean are normally distributed N(0, ∊a 2), and so a 2 is gamma distributed with shape parameter 1/2, and effects b on V E are independently gamma (½) distributed with variance ∊b 2. Equilibria are obtained for ![]() and
and ![]() and consequently for heritability, at h 2=∊a/(∊a+√∊b) (Zhang & Hill, Reference Zhang and Hill2008). For h 2 in the range 0·1–0·5, ∊b has to lie in the range ∊a 2 to almost 81∊a 2, implying that mutants must have as large or greater effects on V E as on the trait itself. Evidence for the effects of mutations on V E of quantitative traits is limited, but there is some from mutation accumulation experiments that show a net increase in variance (Fry et al., Reference Fry, deRonde and Mackay1995; Baer, Reference Baer2008). Even so, the magnitude of mutational increase in V E needed seems so large that, judging by this simplistic model, a mutation–selection balance is no more than a partial candidate for explaining the levels of V E or heritability.
and consequently for heritability, at h 2=∊a/(∊a+√∊b) (Zhang & Hill, Reference Zhang and Hill2008). For h 2 in the range 0·1–0·5, ∊b has to lie in the range ∊a 2 to almost 81∊a 2, implying that mutants must have as large or greater effects on V E as on the trait itself. Evidence for the effects of mutations on V E of quantitative traits is limited, but there is some from mutation accumulation experiments that show a net increase in variance (Fry et al., Reference Fry, deRonde and Mackay1995; Baer, Reference Baer2008). Even so, the magnitude of mutational increase in V E needed seems so large that, judging by this simplistic model, a mutation–selection balance is no more than a partial candidate for explaining the levels of V E or heritability.
Conclusion. The models that appear to have most promise are those in which a cost is attached to homogeneity, and are plausible in that if a more intense selection is applied to inequality of wing size than to bristles, the latter would show relatively higher within-individual variance, as is indeed the case. These are compatible with stabilizing selection, but other forms of selection have not been investigated in this context. Our understanding of why variances and heritabilities take the levels they do is at best, however, superficial.
8. Concluding remarks
While we have attempted to assess some of the current state of knowledge, we see there are many uncertainties and questions still to be answered. We emphasize a few which we consider as most important:
(i) Estimates of the magnitude of genetic variance in V E in segregating populations are potentially biased upwards by factors such as non-normality of data, confounding with fixed effects, confounding with non-additive sources of genetic variance such as epistasis and simple errors in data. The magnitude of such biases remains to be assessed.
(ii) There is no consistent choice of the statistical model, e.g. between the exponential and the additive model of variance partition. The importance in practice for estimation of parameters and predictions of breeding values for V E has not been fully evaluated, and might lead to choice of a more uniform approach.
(iii) The magnitude of parameter estimates indicates that there are substantial opportunities to change the magnitude of V E by selection, but the possible biases noted in (i) show that, for example, cross-validation in breeding programmes is needed.
(iv) Current models to explain the levels of V E and heritability of traits maintained in nature are both simplistic and inadequate, but it will be difficult to obtain sufficient information on selective forces and parameters to improve our understanding forward.
(v) The level of understanding of the genetic basis of V E is poor, for example, the extent to which it is related to and can be explained by biological phenomena such as epigenetic and other non-Mendelian variation, to plasticity in response to micro-environment and between- and within-individual variation.
We are grateful to Trudy Mackay and Anna Wolc for helpful comments. HAM was partially financed by the RobustMilk project supported by the European Commission under the Seventh Research Framework Programme, Grant Agreement 211708. The content of this paper is the sole responsibility of the publishers, and it does not necessarily represent the views of the Commission or its services. WGH is supported by USS.





