Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cwikel, Michael
and
Sagher, Yoram
1988.
Analytic families of operators on some quasi-Banach spaces.
Proceedings of the American Mathematical Society,
Vol. 102,
Issue. 4,
p.
979.
Kalton, N. J.
Leranoz, C.
and
Wojtaszczyk, P.
1990.
Uniqueness of unconditional bases in quasi-banach spaces with applications to Hardy spaces.
Israel Journal of Mathematics,
Vol. 72,
Issue. 3,
p.
299.
Xu, Quanhua
1991.
Analytic functions with values in lattices and symmetric spaces of measurable operators.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 109,
Issue. 3,
p.
541.
Bukhvalov, A. V.
1991.
Order-bounded operators in vector lattices and in spaces of measurable functions.
Journal of Soviet Mathematics,
Vol. 54,
Issue. 5,
p.
1131.
Kalton, N. J.
and
Montgomery-Smith, S. J.
1993.
Set-functions and factorization.
Archiv der Mathematik,
Vol. 61,
Issue. 2,
p.
183.
Wojtaszczyk, P.
1997.
Uniqueness of unconditional bases in quasi-banach spaces with applications to hardy spaces, II.
Israel Journal of Mathematics,
Vol. 97,
Issue. 1,
p.
253.
Mendez, Osvaldo
and
Mitrea, Marius
2000.
The Banach envelopes of Besov and Triebel-Lizorkin spaces and applications to partial differential equations.
Journal of Fourier Analysis and Applications,
Vol. 6,
Issue. 5,
p.
503.
2003.
Vol. 2,
Issue. ,
p.
1099.
Kamińska, Anna
and
Maligranda, Lech
2004.
On Lorentz spaces Γ p,w.
Israel Journal of Mathematics,
Vol. 140,
Issue. 1,
p.
285.
Albiac, F.
Kalton, N.
and
Leránoz, C.
2004.
Uniqueness of the Unconditional Basis of ℓ1 (ℓp) and ℓp (ℓ1), 0 < p < 1.
Positivity,
Vol. 8,
Issue. 4,
p.
443.
Grafakos, Loukas
and
Mastyło, Mieczysław
2006.
Interpolation of Bilinear Operators Between Quasi-Banach Spaces.
Positivity,
Vol. 10,
Issue. 3,
p.
409.
Curbera, Guillermo P.
García-Cuerva, José
María Martell, José
and
Pérez, Carlos
2006.
Extrapolation with weights, rearrangement-invariant function spaces, modular inequalities and applications to singular integrals.
Advances in Mathematics,
Vol. 203,
Issue. 1,
p.
256.
Lee, Han Ju
2007.
Complex convexity and monotonicity in quasi-Banach lattices.
Israel Journal of Mathematics,
Vol. 159,
Issue. 1,
p.
57.
Bownik, Marcin
2008.
Duality and interpolation of anisotropic Triebel–Lizorkin spaces.
Mathematische Zeitschrift,
Vol. 259,
Issue. 1,
p.
131.
Albiac, F.
and
Leránoz, C.
2008.
Uniqueness of symmetric basis in quasi-Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 348,
Issue. 1,
p.
51.
Kamińska, Anna
and
Raynaud, Yves
2009.
Isomorphic copies in the lattice E and its symmetrization E(∗) with applications to Orlicz–Lorentz spaces.
Journal of Functional Analysis,
Vol. 257,
Issue. 1,
p.
271.
Albiac, F.
and
Kalton, N. J.
2009.
Lipschitz structure of quasi-Banach spaces.
Israel Journal of Mathematics,
Vol. 170,
Issue. 1,
p.
317.
Albiac, Fernando
and
Leránoz, Camino
2010.
Uniqueness of unconditional basis in quasi-Banach spaces which are not sufficiently Euclidean.
Positivity,
Vol. 14,
Issue. 4,
p.
579.
Kühn, Thomas
and
Mastyło, Mieczysław
2010.
Weyl numbers and eigenvalues of abstract summing operators.
Journal of Mathematical Analysis and Applications,
Vol. 369,
Issue. 1,
p.
408.
Albiac, F.
and
Leránoz, C.
2011.
Uniqueness of unconditional bases in nonlocally convex c0-products.
Israel Journal of Mathematics,
Vol. 184,
Issue. 1,
p.
79.

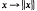 satisfying
satisfying