Hostname: page-component-857557d7f7-s7d9s Total loading time: 0 Render date: 2025-11-20T10:20:47.817Z Has data issue: false hasContentIssue false
  • English
  • Français

Exceptional Integrals of a not completely Integrable Total Differential Equation

Published online by Cambridge University Press:  18 May 2009

H. T. H. Piaggio
H. T. H. Piaggio
Affiliation:
University of Nottingham
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. There are exceptional integrals of the total differential equation

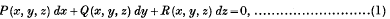
in the case when it is not completely integrable, and so when the invariant

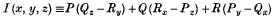
is not identically zero, which do not seem to be mentioned by any standard authorities such as Cartan, Goursat, de la Vallée Poussin, and Schouten and Kulk. These are integrals of (1) which do not reduce I to zero. They arise only when the first partial derivates of P, Q, R are not all continuous. A simple example is z = 0 as an integral of

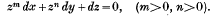
Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 1 , Issue 3 , September 1953 , pp. 137 - 138
Copyright
Copyright © Glasgow Mathematical Journal Trust 1953

References

REFERENCES

(1)Cartan, E., Ann. Éc. Norm. Sup., (3), 16, 279, 280 (1899).Google Scholar
(2)Goursat, E., Leçons sur le problème de Pfqff (Paris, 1922), pp. 187–190.Google Scholar
(3)de la Vallée Poussin, Ch.-J., Cours d'Analyse Infinitésimale, t. II. (7th ed., 1946), pp. 303–4.Google Scholar
(4)Sohouten, J. A., and Kulk, W. V. D., Pfqff's Problem and its Generalizations (Oxford, 1949).Google Scholar