Suppose we are given complex manifolds X and Y together with substacks 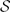$\mathcal{S}$ and 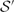$\mathcal{S}'$ of modules over algebras of formal deformation 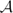$\mathcal{A}$ on X and 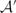$\mathcal{A}'$ on Y, respectively. Also, suppose we are given a functor Φ from the category of open subsets of X to the category of open subsets of Y together with a functor F of prestacks from 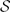$\mathcal{S}$ to $\mathcal{S}'\circ\Phi$ . Then we give conditions for the existence of a canonical functor, extension of F to the category of coherent 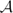$\mathcal{A}$ -modules such that the cohomology associated to the action of the formal parameter 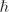$\hbar$ takes values in 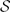$\mathcal{S}$ . We give an explicit construction and prove that when the initial functor F is exact on each open subset, so is its extension. Our construction permits to extend the functors of inverse image, Fourier transform, specialisation and micro-localisation, nearby and vanishing cycles in the framework of 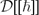$\mathcal{D}[[\hbar]]$ -modules. We also obtain the Cauchy–Kowalewskaia–Kashiwara theorem in the non-characteristic case as well as comparison theorems for regular holonomic 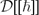$\mathcal{D}[[\hbar]]$ -modules and a coherency criterion for proper direct images of good 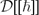$\mathcal{D}[[\hbar]]$ -modules.