Hostname: page-component-5b777bbd6c-ks5gx Total loading time: 0 Render date: 2025-06-18T05:12:38.986Z Has data issue: false hasContentIssue false
  • English
  • Français

The Formanek-Procesi group with base a right-angled Artin group: Lie algebra and residual nilpotence

Part of: Lie algebras and Lie superalgebras Special aspects of infinite or finite groups

Published online by Cambridge University Press:  13 May 2025

V. Metaftsis  and
A.I. Papistas
V. Metaftsis*
Affiliation:
Department of Mathematics, University of the Aegean, Karlovassi, 832 00 Samos, Greece
A.I. Papistas
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, Thessaloniki, 541 24 Thessaloniki, Greece
*
Corresponding author: V. Metaftsis; Email: vmet@aegean.gr
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present work, we investigate the Lie algebra of the Formanek-Procesi group $\textrm {FP}(A_{\Gamma })$ with base group 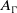$A_{\Gamma }$ a right-angled Artin group. We show that the Lie algebra $\textrm {gr}(\textrm {FP}(A_{\Gamma }))$ has a presentation that is dictated by the group presentation. Moreover, we show that if the base group $G$ is a finitely generated residually finite $p$-group, then $\textrm { FP}(G)$ is residually nilpotent. We also show that $\textrm {FP}(A_{\Gamma })$ is a residually torsion-free nilpotent group.

Keywords

Formanek-Procesi groupLie algebraresidual nilpotenceresidually torsion free nilpotent

MSC classification

Primary: 17B01: Identities, free Lie (super)algebras
Secondary: 17B40: Automorphisms, derivations, other operators 17B70: Graded Lie (super)algebras 20F40: Associated Lie structures 20F28: Automorphism groups of groups
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bahturin, Y. A., Identical relations in Lie Algebras, Nauka, Moscow, 1985 (in Russian). English translation: (VNU Science Press, Utrecht, 1987).Google Scholar
Bourbaki, N., Lie Groups and Lie Algebras Part I, (Hermann, Paris, 1987).(Chapters 1-3)Google Scholar
Charney, R., An introduction to right angled Artin groups, Geom. Dedicata. 125(1) (2007), 141–158.CrossRefGoogle Scholar
Clement, A. E., Majewicz, S. and Zyman, M., The theory of Nilpotent groups, (Birkhäuser, 2017).CrossRefGoogle Scholar
Droms, C., Graph groups, PhD thesis (Syracuse University, 1983).Google Scholar
Duchamp, G. and Krob, D., The free partially commutative Lie algebra: bases and ranks, Adv. Math. 95(1) (1992), 92–126.CrossRefGoogle Scholar
Duchamp, G. and Krob, D., The lower central series of the free partially commutative group, Semigroup Forum 45(1) (1992), 385–394.CrossRefGoogle Scholar
Formanek, E. and Procesi, C., The automorphism group of a free group is not linear, J. Algebra 149(2) (1992), 494–499.CrossRefGoogle Scholar
Gruenberg, K. W., Residual properties of infinite soluble groups, Proc. London Math. Soc. 7 (1957), 29–62.(3)CrossRefGoogle Scholar
Guaschi, J. and Pereiro, C. M., Lower central and derived series of semidirect products and applications to surface braid groups, J. Pure and Applied Algebra 224 (2020), 1–39.CrossRefGoogle Scholar
Hall, M., A basis for free Lie rings and higher commutators in free groups, Proc. Amer. Math. Soc 1(5) (1950), 575–581.CrossRefGoogle Scholar
Hall, P., Some sufficient conditions for a group to be nilpotent, Illinois J. Math. 2(4B) (1958), 787–801.CrossRefGoogle Scholar
Labute, J. P., The determination of the Lie algebra associated to the lower central series of a group, Trans. Amer. Math. Soc. 288(1) (1985), 51–57.CrossRefGoogle Scholar
Lazard, M., Sur les groupes nilpotents et les anneaux de Lie, Ann. Sci. Ecole Norm. Sup. 71(3) (1954), 101–190.CrossRefGoogle Scholar
Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory: presentations of groups in terms of generators and relations. (Dover Publications, 1978).Google Scholar
Papadima, S. and Suciu, A., Algebraic invariants for right-angled Artin groups, Math. Ann. 334(3) (2006), 533–555.CrossRefGoogle Scholar
Sevaslidou, I., The associated Lie algebra of an HNN-extension of a group, J. Gen. Lie Theory Appl., acceptedGoogle Scholar
Suciu, A., Lower central series and split extensions, arXiv:2105.14129.Google Scholar
Wade, R., The lower central series of a right-angled Artin group, Enseign. Math. 61(3–4) (2015), 343–371.CrossRefGoogle Scholar