Article contents
THE GROUP OF AUTOMORPHISMS OF THE FIRST WEYL ALGEBRA IN PRIME CHARACTERISTIC AND THE RESTRICTION MAP
Published online by Cambridge University Press: 01 May 2009
Abstract
Let K be a perfect field of characteristic p > 0; A1 := K〈x, ∂|∂x−x∂=1〉 be the first Weyl algebra; and Z:=K[X:=xp, Y:=∂p] be its centre. It is proved that (i) the restriction map res : AutK(A1)→ AutK(Z), σ ↦ σ|Z is a monomorphism with im(res) = Γ := {τ ∈ AutK(Z)|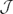 (τ)=1}, where
(τ)=1}, where 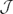 (τ) is the Jacobian of τ, (Note that AutK(Z)=K* ⋉ Γ, and if K is not perfect then im(res) ≠ Γ.); (ii) the bijection res : AutK(A1) → Γ is a monomorphism of infinite dimensional algebraic groups which is not an isomorphism (even if K is algebraically closed); (iii) an explicit formula for res−1 is found via differential operators
(τ) is the Jacobian of τ, (Note that AutK(Z)=K* ⋉ Γ, and if K is not perfect then im(res) ≠ Γ.); (ii) the bijection res : AutK(A1) → Γ is a monomorphism of infinite dimensional algebraic groups which is not an isomorphism (even if K is algebraically closed); (iii) an explicit formula for res−1 is found via differential operators 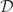 (Z) on Z and negative powers of the Fronenius map F. Proofs are based on the following (non-obvious) equality proved in the paper:
(Z) on Z and negative powers of the Fronenius map F. Proofs are based on the following (non-obvious) equality proved in the paper: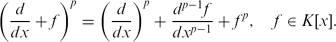
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2008
References
REFERENCES
- 9
- Cited by

