No CrossRef data available.
Article contents
A Helfrich functional for compact surfaces in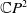 
$\mathbb{C}P^{2}$
Published online by Cambridge University Press: 04 October 2023
Abstract
Let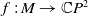 
$f\;:\; M\rightarrow \mathbb{C}P^{2}$ be an isometric immersion of a compact surface in the complex projective plane 
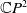$\mathbb{C}P^{2}$. In this paper, we consider the Helfrich-type functional 
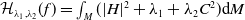$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)=\int _{M}(|H|^{2}+\lambda _{1}+\lambda _{2} C^{2})\textrm{d} M$, where 
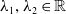$\lambda _{1}, \lambda _{2}\in \mathbb{R}$ with 
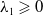$\lambda _{1}\geqslant 0$, 
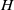$H$ and 
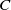$C$ are respectively the mean curvature vector and the Kähler function of 
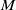$M$ in 
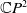$\mathbb{C}P^{2}$. The critical surfaces of 
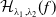$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$ are called Helfrich surfaces. We compute the first variation of 
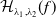$\mathcal{H}_{\lambda _{1},\lambda _{2}}(f)$ and classify the homogeneous Helfrich tori in 
$\mathbb{C}P^{2}$. Moreover, we study the Helfrich energy of the homogeneous tori and show the lower bound of the Helfrich energy for such tori.
MSC classification
Primary:
53A05: Surfaces in Euclidean space
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Bernard, Y., Wheeler, G. and Wheeler, V. M., Rigidity and stability of spheres in the Helfrich model, Interfaces Free Bound 19(4) (2017), 495–523.CrossRefGoogle Scholar
Castro, I. and Urbano, F., Willmore surfaces of
$\mathbb{R}^{4}$
and the Whitney sphere, Ann. Global Anal. Geom. 19 (2001), 153–175.CrossRefGoogle Scholar
$\mathbb{R}^{4}$
and the Whitney sphere, Ann. Global Anal. Geom. 19 (2001), 153–175.CrossRefGoogle ScholarChern, S. S. and Wolfson, J. G., Minimal surfaces by moving frames, Am. J. Math. 105(1) (1983), 59–83.CrossRefGoogle Scholar
Choksi, R. and Veneroni, M., Global minimizers for the doubly-constrained Helfrich energy: the axisymmetric case, Calc. Var. Partial Differ. Equ. 48 (2013), 337–366.Google Scholar
Deckelnick, K., Doemeland, M. and Grunau, H. C., Boundary value problems for a special Helfrich functional for surfaces of revolution: existence and asymptotic behaviour, Calc. Var. Partial Differ. Equ. 60(1) (2021), 1–31.CrossRefGoogle Scholar
Eichmann, S., The Helfrich boundary value problem, Calc. Var. Partial Differ. Equ. 58(1) (2019), Art.–34.CrossRefGoogle Scholar
Helfrich, W., Elastic properties of lipid bilayers: theory and possible experiments, Z. Naturforsch. C. 28(11) (1973), 693–703.CrossRefGoogle ScholarPubMed
Hu, Z. and Li, H., Willmore submanifolds in a Riemannian manifold, in Proceedings of the Workshop Contemporary Geometry and Related Topics (2004), 251–275.CrossRefGoogle Scholar
Hu, Z. and Li, H., Willmore Lagrangian spheres in the complex Euclidean space C
n
, Ann. Glob. Anal. Geom. 25 (2004), 73–98.CrossRefGoogle Scholar
Kenmotsu, K. and Zhou, D., The classification of the surfaces with parallel mean curvature vector in two dimensional complex space form, Am. J. Math. 122(2) (2000), 295–317.CrossRefGoogle Scholar
Ma, H., Mironov, A. E. and Zuo, D., An energy functional for Lagrangian tori in CP
2
, Ann. Glob. Anal. Geom. 53 (2018), 583–595.CrossRefGoogle Scholar
Marques, F. C. and Neves, A., MinCmax theory and the Willmore conjecture, Ann. Math. 2(179) (2014), 683–782.CrossRefGoogle Scholar
McCoy, J. and Wheeler, G., A classification theorem for Helfrich surfaces, Math. Ann. 357(4) (2013), 1485–1508.CrossRefGoogle Scholar
Mondino, A. and Scharrer, C., Existence and regularity of spheres minimising the Canham-Helfrich energy, Arch. Ration. Mech. Anal. 236(3) (2020), 1455–1485.CrossRefGoogle Scholar
Montiel, S. and Urbano, F., A Willmore functional for compact surfaces in the complex projective space, J. Reine Angew. Math. 546 (2002), 139–154.Google Scholar
Tu, Z. C., Compatibility between shape equation and boundary conditions of lipid membranes with free edges, J. Chem. Phys. 132(8) (2010), 084111.CrossRefGoogle ScholarPubMed
Willmore, T. J., Notes on embedded surfaces, Ann. Stiint. Univ. Al. I. Cuza, Iasi, Sect. I a Mat. 11 (1965), 493–496.Google Scholar