Published online by Cambridge University Press: 18 May 2009
Let K be a totally real number field of degree nover ℚ and let c be an integral ideal of a maximal order 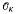 of K. Given a nonnegative integer j and a Hecke character on the group
of K. Given a nonnegative integer j and a Hecke character on the group 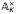 of ideles of K, let
of ideles of K, let 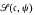 denote the space of Hilbert cusp forms of holomorphic type on ℋn of weight j, level c and character ψ where ℋn is the n-th power of the Poincaré upper half plane ℋ.Let g be an element of
denote the space of Hilbert cusp forms of holomorphic type on ℋn of weight j, level c and character ψ where ℋn is the n-th power of the Poincaré upper half plane ℋ.Let g be an element of 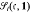 , where 1 is the trivial character. If u ∈ Sk(c, ψ), then the product gu is an element of Sk+l (c, ψ), and therefore we can consider the linear map
, where 1 is the trivial character. If u ∈ Sk(c, ψ), then the product gu is an element of Sk+l (c, ψ), and therefore we can consider the linear map 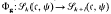 sending u to gu. Let
sending u to gu. Let 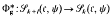 be the adjoint of the linear map Φg with respect to the Petersson inner product.
be the adjoint of the linear map Φg with respect to the Petersson inner product.