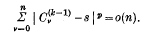Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Harington, C. F.
and
Hyslop, J. M.
1953.
An Analogue for Strong Summability of Abel's Summability Method.
Proceedings of the Edinburgh Mathematical Society,
Vol. 9,
Issue. 1,
p.
28.
Glatfeld, Martin
1957.
On strong Rieszian summability.
Proceedings of the Glasgow Mathematical Association,
Vol. 3,
Issue. 3,
p.
123.
Boyd, A. V.
1958.
Multiplication of Strongly Summable Series.
Proceedings of the Glasgow Mathematical Association,
Vol. 4,
Issue. 1,
p.
29.
Borwein, D.
1960.
On Strong and Absolute Summability.
Proceedings of the Glasgow Mathematical Association,
Vol. 4,
Issue. 3,
p.
122.
Mishra, Babban Prasad
1965.
Some theorems on strong summability.
Mathematische Zeitschrift,
Vol. 90,
Issue. 4,
p.
310.
Mishra, Babban Prasad
1967.
Strong summability of infinite series on a scale of Abel type summability methods.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 1,
p.
119.
Kuttner, B.
and
Thorpe, B.
1969.
On the strong N�rlund summability of a Cauchy product series.
Mathematische Zeitschrift,
Vol. 111,
Issue. 1,
p.
69.
Mishra, Babban Prasad
1970.
Some Tauberian theorems on a scale of Abel type summability methods.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 68,
Issue. 2,
p.
401.
Kuttner, B.
1974.
Some theorems on strong regularity of Nörlund methods.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 76,
Issue. 1,
p.
195.
Indlekofer, Karl-Heinz
and
Warlimont, Richard
1974.
Über die starke Cesàro Summierbarkeit von Potenzreihen auf dem Rande des Konvergenzkreises.
Mathematische Nachrichten,
Vol. 63,
Issue. 1,
p.
393.
Mishra, Babban Prasad
and
Srivastava, Anand Prakash
1979.
Strong and absolute summabilities of functions based on (D, α) summability methods.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 2,
p.
279.
Tanović-Miller, N.
1983.
On strong convergence of trigonometric and Fourier series.
Acta Mathematica Hungarica,
Vol. 42,
Issue. 1-2,
p.
35.
Nurcombe, J. R.
1983.
A note on the strong regularity of Nrlund means.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 94,
Issue. 2,
p.
261.
Szalay, I.
1989.
On the properties of the strong Cesàro summability and strong convergence of series.
Analysis Mathematica,
Vol. 15,
Issue. 3,
p.
195.
Móricz, F.
1989.
OnΛ-strong convergence of numerical sequences and Fourier series.
Acta Mathematica Hungarica,
Vol. 54,
Issue. 3-4,
p.
319.
Borwein, D.
Cass, F. P.
and
Sayre, J. E.
1989.
On strong generalized Hausdorff summability.
Acta Mathematica Hungarica,
Vol. 53,
Issue. 1-2,
p.
95.
Móricz, F.
1990.
On Λ-strong convergence of double numerical sequences and Fourier series.
Acta Mathematica Hungarica,
Vol. 56,
Issue. 1-2,
p.
125.
Szalay, I.
1990.
A high-indices theorem for strong Cesàro summability of double series.
Analysis Mathematica,
Vol. 16,
Issue. 1,
p.
65.
Buntinas, Martin
and
Tanović-Miller, Naza
1991.
Strong Boundedness and Strong Convergence in Sequence Spaces.
Canadian Journal of Mathematics,
Vol. 43,
Issue. 5,
p.
960.
Mittal, Madan Lal
2006.
On strong Nörlund summability of Fourier series.
Journal of Mathematical Analysis and Applications,
Vol. 314,
Issue. 1,
p.
75.
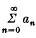 ,the n-th Casáro sum of order k is defined by the relation
,the n-th Casáro sum of order k is defined by the relation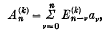
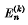 is the binomial coefficient
is the binomial coefficient 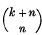 . Let
. Let 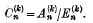 Then Σan is said to be summable (C; K) to the sum s if, as n → ∞,
Then Σan is said to be summable (C; K) to the sum s if, as n → ∞, 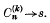 The series is said to be absolutely summable (C; k), or summable |
The series is said to be absolutely summable (C; k), or summable | 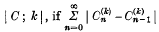 is convergent. The series is said to be strongly summable (C; k) with index p, or summable [Ck, p], to the sum s if
is convergent. The series is said to be strongly summable (C; k) with index p, or summable [Ck, p], to the sum s if