Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Faltings, Gerd
1987.
Hodge-tate structures and modular forms.
Mathematische Annalen,
Vol. 278,
Issue. 1-4,
p.
133.
Bayer, Pilar
and
González, Josep
1997.
On the Hasse–Witt Invariants of Modular Curves.
Experimental Mathematics,
Vol. 6,
Issue. 1,
p.
57.
Dieulefait, Luis
and
Vila, Núria
2000.
Projective Linear Groups as Galois Groups overQvia Modular Representations.
Journal of Symbolic Computation,
Vol. 30,
Issue. 6,
p.
799.
Ochiai, Tadashi
2000.
Control Theorem for Bloch–Kato's Selmer Groups of p-Adic Representations.
Journal of Number Theory,
Vol. 82,
Issue. 1,
p.
69.
Ochiai, Tadashi
2001.
Control Theorem for Greenberg's Selmer Groups of Galois Deformations.
Journal of Number Theory,
Vol. 88,
Issue. 1,
p.
59.
Dieulefait, Luis V.
2001.
Newforms, inner twists, and the inverse Galois problem for projective linear groups.
Journal de théorie des nombres de Bordeaux,
Vol. 13,
Issue. 2,
p.
395.
Dieulefait, Luis V.
2002.
Explicit Determination of the Images of the Galois Representations Attached to Abelian Surfaces with End(A) = Z.
Experimental Mathematics,
Vol. 11,
Issue. 4,
p.
503.
Fischman, Ami
2002.
On the image of Λ-adic Galois representations.
Annales de l'Institut Fourier,
Vol. 52,
Issue. 2,
p.
351.
Dieulefait, Luis V.
2002.
On the images of the Galois representations attached to genus 2 Siegel modular forms.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2002,
Issue. 553,
Iovita, Adrian
and
Spiess, Michael
2003.
Derivatives of p-adic L-functions, Heegner cycles and monodromy modules attached to modular forms.
Inventiones mathematicae,
Vol. 154,
Issue. 2,
p.
333.
Bruinier, Jan H.
and
Ono, Ken
2003.
Coefficients of half-integral weight modular forms.
Journal of Number Theory,
Vol. 99,
Issue. 1,
p.
164.
Dieulefait, Luis V.
and
Rotger, Victor
2004.
The arithmetic of QM-abelian surfaces through their Galois representations.
Journal of Algebra,
Vol. 281,
Issue. 1,
p.
124.
Vila, Núria
2004.
Algebra, Arithmetic and Geometry with Applications.
p.
775.
Ahlgren, Scott
and
Boylan, Matthew
2005.
Coefficients of half-integral weight modular forms modulo ?j.
Mathematische Annalen,
Vol. 331,
Issue. 1,
p.
219.
Kiming, Ian
and
Verrill, Helena A.
2005.
On modular modℓ Galois representations with exceptional images.
Journal of Number Theory,
Vol. 110,
Issue. 2,
p.
236.
Virdol, Cristian
2006.
Zeta functions of twisted modular curves.
Journal of the Australian Mathematical Society,
Vol. 80,
Issue. 1,
p.
89.
Dieulefait, Luis
and
Dimitrov, Mladen
2006.
Explicit determination of images of Galois representations attached to Hilbert modular forms.
Journal of Number Theory,
Vol. 117,
Issue. 2,
p.
397.
Kumar Murty, V.
2007.
A variant of Lehmer's conjecture.
Journal of Number Theory,
Vol. 123,
Issue. 1,
p.
80.
Dieulefait, Luis
and
Taixés i Ventosa, Xavier
2009.
Congruences between modular forms and lowering the level mod ℓ n .
Journal de théorie des nombres de Bordeaux,
Vol. 21,
Issue. 1,
p.
109.
CHIDA, MASATAKA
2009.
INDIVISIBILITY OF ORDERS OF SELMER GROUPS FOR MODULAR FORMS.
International Journal of Number Theory,
Vol. 05,
Issue. 02,
p.
271.

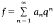 is a newform of weight
is a newform of weight 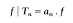
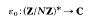
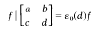
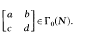 .
.