Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-31T16:26:56.265Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE HOMOGENIZED ENVELOPING ALGEBRA OF THE LIE ALGEBRA Sℓ(2,ℂ) II

Part of: Lie algebras and Lie superalgebras Rings and algebras arising under various constructions

Published online by Cambridge University Press:  10 June 2016

ROBERTO MARTÍNEZ-VILLA
ROBERTO MARTÍNEZ-VILLA*
Affiliation:
Centro de Ciencias Matemáticas, UNAM, Campus Morelia, Apartado Postal 61-3 Xangari, C.P. 58089, Morelia Michoacán, México e-mail: mvilla@matmor.unam.mx
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper, we studied the homogenized enveloping algebra of the Lie algebra sℓ(2,ℂ) and the homogenized Verma modules. The aim of this paper is to study the homogenization 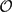$\mathcal{O}$ B of the Bernstein–Gelfand–Gelfand category 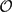$\mathcal{O}$ of sℓ(2,ℂ), and to apply the ideas developed jointly with J. Mondragón in our work on Groebner basis algebras, to give the relations between the categories 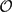$\mathcal{O}$ B and 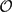$\mathcal{O}$ as well as, between the derived categories 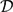$\mathcal{D}$ b ( 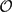$\mathcal{O}$ B ) and 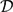$\mathcal{D}$ b ( 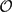$\mathcal{O}$ ).

MSC classification

Primary: 16S30: Universal enveloping algebras of Lie algebras 17B35: Universal enveloping (super)algebras
Secondary: 17B10: Representations, algebraic theory (weights)

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 1 , January 2017 , pp. 189 - 219
Copyright
Copyright © Glasgow Mathematical Journal Trust 2016 

References

REFERENCES

1. Apel, J., Gröbnerbasen in nichtkommutativen Algebren und Anwendung, Dissertation (Universität Leipzig, 1988).Google Scholar
2. Berger, R., The quantum Poincaré-Birkoff-Witt theorem, Commun. Math. Phys. 143 (2) (1992), 215–234.Google Scholar
3. Berger, R., Quantification de l'identité de Jacobi, C. R.Acad. Sci. Paris, Sér. I 312 (10) (1991), 721–724.Google Scholar
4. Bernstein, I., Gelfand, I., Gelfand, S. A certain category of $\mathfrak{g}$ -modules, Funckcional. Anal. i Prilozen. 10 (2) (1976), 1–8.Google Scholar
5. Coutinho, S.C., A primer of algebraic D-modules, London Math. Soc., Students Texts 33 (1995), 1–208.Google Scholar
6. Dade, E. C., Group-graded rings and modules, Math. Z. 174 (3) (1980), 241–262.Google Scholar
7. Erdmann, K. and Wildon, M. J., Introduction to lie algebras, Springer Undergraduate Mathematics Series (2006).Google Scholar
8. Gabriel, P., Des catégories abéliennes, Bull. Soc. Math. France 90 (1962), 323–448.Google Scholar
9. Green, E. L., Multiplicative basis, Gröbner bases, and right Gröbner bases, J. Symb. Comput. 29 (4/5) (2000).Google Scholar
10. Green, E. L., Noncommutative Gröbner bases, and projective resolutions progress in mathematics vol. 173, (Birkhäuser Verlag, 1999), 29–60.Google Scholar
11. Green, E. L. and Huang, R., Q. Projective resolutions of straightening closed algebras generated by Minors, Adv. Math. 110 (2) (1995), 314–333.CrossRefGoogle Scholar
12. Green, E. L., Martínez Villa, R., Koszul and Yoneda algebras, Representation theory of algebras (Cocoyoc, 1994), CMS Conf. Proc., vol. 18 (Amer. Math. Soc., Providence, RI, 1996), 247–297.Google Scholar
13. Green, E. L., Martínez-Villa, R., Koszul and Yoneda algebras. II, Algebras and modules, II (Geiranger, 1996), CMS Conf. Proc., vol. 24 (Amer. Math. Soc., Providence, RI, 1998), 227–244.Google Scholar
14. Krause, G. R. and Lenagan, T. H., Growth of Algebras and Gelfand-Kirillov Dimension, Graduate Studies in Mathematics, vol. 22 (AMS, 1999).Google Scholar
15. Le Bruyn, L. and Smith, S. P., Homogenized sl(2), Proc. Amer. Math. Soc. 118 (3) (1993).Google Scholar
16. Levandovskyy, V., On Gröbner bases for noncommutative G-algebras, Proceedings of the 8th Rhine Workshop on Computer Algebra (Mannheim, Germany, 2002).Google Scholar
17. MacLane, S. and Birkhof, G., Algebra (AMS Chelsea Publishing, 1999).Google Scholar
18. Martínez-Villa, R., On the homogenized enveloping algebra of the Lie algebra sℓ(2, $\mathbb{C}$ ). Glasgow Math. J. 56 (3) (2014), 551–568.Google Scholar
19. Martínez-Villa, R. and Martsinkovsky, A., Stable projective homotopy theory of modules, tails, and Koszul duality, Comm. Algebra 38 (10) (2010), 3941–3973.Google Scholar
20. Martínez-Villa, R. and Mondragón, J., Homogeneous G-algebras I, Int. Journal of Algebra 8 (16) (2014), 753–802.Google Scholar
21. Martínez-Villa, R. and Mondragon, J., Homogeneous G-algebras II, Int. J. Algebra 8 (17) (2014), 803–851.Google Scholar
22. Martínez-Villa, R. and Montaño-Bermúdez, , Node delition and stably equivalent Koszul algebras, Com. Algebra 33 (2005), 2569–2585.Google Scholar
23. Martínez-Villa, R. and Saorín, M., Koszul equivalences and dualities, Pacific J. Math. 214 (2) (2004), 359–378.Google Scholar
24. Martínez-Villa, R. and Zacharia, D., Approximations with modules having linear resolutions, J. Algebra 266 (2) (2003), 671–697.Google Scholar
25. Mazorchuk, V., Lectures on sℓ2( $\mathbb{C}$ )-modules, (Imperial College Press, London, 2010).Google Scholar
26. Miličić, D., Lectures on algebraic theory of D-modules, (University of Utah, 1986). Available at: www.math.utah.edu/~milicic/Eprints/dmodules.pdf.Google Scholar
27. Miyachi, J.-I., Derived categories with applications to representations of Algebras, Chiba Lectures (2002).Google Scholar
28. Popescu, N., Abelian categories with applications to rings and modules, L.M.S. Monographs, vol. 3 Academic Press, London, 1973.Google Scholar
29. Yamagata, K., Frobenius algebras, Handbook of algebra, vol. 1 (North-Holland, Amsterdam, 1996), 841–887.Google Scholar