Article contents
ON THE SYMMETRIC SQUARES OF COMPLEX AND QUATERNIONIC PROJECTIVE SPACE
Published online by Cambridge University Press: 13 February 2018
Abstract
The problem of computing the integral cohomology ring of the symmetric square of a topological space has long been of interest, but limited progress has been made on the general case until recently. We offer a solution for the complex and quaternionic projective spaces 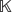 $\mathbb{K}$Pn, by utilising their rich geometrical structure. Our description involves generators and relations, and our methods entail ideas from the literature of quantum chemistry, theoretical physics, and combinatorics. We begin with the case
$\mathbb{K}$Pn, by utilising their rich geometrical structure. Our description involves generators and relations, and our methods entail ideas from the literature of quantum chemistry, theoretical physics, and combinatorics. We begin with the case 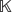 $\mathbb{K}$P∞, and then identify the truncation required for passage to finite n. The calculations rely upon a ladder of long exact cohomology sequences, which compares cofibrations associated to the diagonals of the symmetric square and the corresponding Borel construction. These incorporate the one-point compactifications of classic configuration spaces of unordered pairs of points in
$\mathbb{K}$P∞, and then identify the truncation required for passage to finite n. The calculations rely upon a ladder of long exact cohomology sequences, which compares cofibrations associated to the diagonals of the symmetric square and the corresponding Borel construction. These incorporate the one-point compactifications of classic configuration spaces of unordered pairs of points in 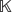 $\mathbb{K}$Pn, which are identified as Thom spaces by combining Löwdin's symmetric orthogonalisation (and its quaternionic analogue) with a dash of Pin geometry. The relations in the ensuing cohomology rings are conveniently expressed using generalised Fibonacci polynomials. Our conclusions are compatible with those of Gugnin mod torsion and Nakaoka mod 2, and with homological results of Milgram.
$\mathbb{K}$Pn, which are identified as Thom spaces by combining Löwdin's symmetric orthogonalisation (and its quaternionic analogue) with a dash of Pin geometry. The relations in the ensuing cohomology rings are conveniently expressed using generalised Fibonacci polynomials. Our conclusions are compatible with those of Gugnin mod torsion and Nakaoka mod 2, and with homological results of Milgram.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2018
References
REFERENCES
This addendum applies to the following article(s):
- 4
- Cited by

