Article contents
The solution of certain simultaneous pairs of dual integral equations†
Published online by Cambridge University Press: 18 May 2009
Extract
In the analysis of mixed boundary value problems by Hankel transforms, one often encounters dual integral equations of the form
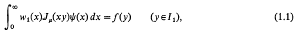
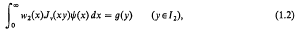
where I1 = (0, 1), I2 = (1, ∞); w1(x), w2(x) are weight functions, ψ(x) is the unknown function, and f(y), g(y) are functions continuously differentiate on I1 and I2 respectively. Many successful attempts have been made to solve (1.1) and (1.2). These are all discussed in a recent book by Sneddon [7]. As pointed out in a recent paper by Erdogan and Bahar [4], in mixed boundary value problems of semi-infinite domains involving more than one unknown function such as those arising in elastostatics, viscoelasticity, and electrostatics, the formulation will lead to a system of simultaneous dual integral equations which is a generalization of (1.1) and (1.2). These equations may be expressed as follows:
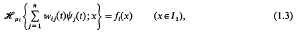
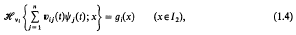
with i = 1, 2, …, n, where we use the notation
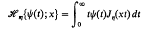
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1968
References
REFERENCES
- 3
- Cited by

