Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-23T09:13:50.660Z Has data issue: false hasContentIssue false
  • English
  • Français

STRATIFYING SYSTEMS FOR EXACT CATEGORIES

Part of: Abelian categories Homological algebra

Published online by Cambridge University Press:  23 July 2018

VALENTE SANTIAGO
VALENTE SANTIAGO*
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad Nacional Autónoma de México, Circuito Exterior, Ciudad Universitaria, C.P. 04510, Mexico, D.F. Mexico, Mexico E-mail: valente@matem.unam.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we develop the theory of stratifying systems in the context of exact categories as a generalisation of the notion of stratifying systems in module categories, which have been studied by different authors. We prove that attached to a stratifying system in an exact category 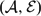$(\mathcal{A},\mathcal{E})$ there is an standardly stratified algebra B such that the category 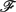$\mathscr{F}$F(Θ), of F-filtered objects in the exact category 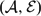$(\mathcal{A},\mathcal{E})$ is equivalent to the category 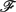$\mathscr{F}$(Δ) of Δ-good modules associated to B. The theory we develop in exact categories, give us a way to produce standardly stratified algebras from module categories by just changing the exact structure on it. In this way, we can construct exact categories whose bounded derived category is equivalent to the bounded derived category of an standardly stratified algebra. Finally, applying the relative homological algebra developed by Auslander–Solberg, we can construct examples of stratifying systems that are not a stratifying system in the classical sense, so our approach really produces new stratifying systems.

MSC classification

Primary: 18E10: Exact categories, abelian categories
Secondary: 18G25: Relative homological algebra, projective classes
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 3 , September 2019 , pp. 501 - 521
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ágoston, I., Dlab, V. and Lukács, E., Stratified algebras, Math. Rep. Acad. Sci. Can. 20 (1) (1998), 22–28.Google Scholar
Ágoston, I., Happel, D., Lukács, E. and Unger, L., Standardly stratified algebras and tilting, J. Algebra 226 (1) (2000), 144–160.CrossRefGoogle Scholar
Auslander, M., Representation dimension of Artin algebras, reprint of the 1971 original, in Selected works of Maurice Auslander. Queen Mary College mathematics notes (American Mathematical Society, Providence, RI, 1999), 505–574.Google Scholar
Auslander, M. and Solberg, Ø., Relative homology and representation theory I, relative homology and homologically finite subcategories, Commun. Algebra 21 (9) (1993), 2995–3031.CrossRefGoogle Scholar
Auslander, M. and Solberg, Ø, Relative homology and representation theory II, relative cotilting theory, Commun. Algebra 21 (9) (1993), 3033–3079.CrossRefGoogle Scholar
Bühler, T., Exact categories, Expo. Math. 28 (2010), 1–69.CrossRefGoogle Scholar
Butler, M. C. R. and Horrocks, G., Classes of extensions and resolutions, Philos. Trans. R. Soc. Lond. Ser. A 254 (1961), 155–222.CrossRefGoogle Scholar
Cadavid, P. and Marcos, E. N., Stratifying systems over the hereditary path algebra with quiver $\mathbb{A}_{p,q}$, São Paolo J. Math. Sci. 10 (2016), 73–90.CrossRefGoogle Scholar
Cline, E., Parshall, B. J. and Scott, L. L., Stratifying endomorphism algebras, Mem. AMS 591 (1996), 1–119.Google Scholar
Dlab, V., Quasi-hereditary algebras revisited, Analele Stiintifice Univ. Ovidius Constanta 4 (1996), 43–54.Google Scholar
Dlab, V. and Ringel, C. M., The module theoretical approach to Quasi-hereditary algebras, in Representations of algebras and related topics, London Mathematical Society lecture note series 168 (Cambridge University Press, New York, 1992), 200–224.CrossRefGoogle Scholar
Dräxler, P., Reiten, I., Smalø, S. and Solberg, Ø, Exact categories and vector espace categories, Trans. Amer. Math. Soc. 351 (1999), 647–682.CrossRefGoogle Scholar
Erdmann, K. and Sáenz, C., On standardly stratified algebras, Commun. Algebra 32 (2003), 3429–3446.CrossRefGoogle Scholar
Gorodentsev, A. L. and Rudakov, A. N., Exceptional vector bundles on projective spaces, Duke Math. J. 54 (1987), 115–130.CrossRefGoogle Scholar
Happel, D., Triangulated categories in the representation theory of finite dimensional algebras, London Mathematical Society lecture note series 119 (Cambridge University Press, New York, 1988).CrossRefGoogle Scholar
Hochschild, G., Relative homological algebra, Trans. Amer. Math. Soc. 82 (1956), 246–269.CrossRefGoogle Scholar
Keller, B., Chain complexes and stable categories, Manuscr. Math. 67 (1990), 379–417.CrossRefGoogle Scholar
Krause, H., Highest weight categories and recollements, Ann. Inst. Fourier 67 (2017), 2679–2701.CrossRefGoogle Scholar
Lenzing, H. and Meltzer, H., Exceptional pairs in hereditary categories, Commun. Algebra 37 (8) (2009), 2547–2556.CrossRefGoogle Scholar
Marcos, E. N., Mendoza, O. and Sáenz, C., Stratifying systems via relative simple modules, J. Algebra 280 (2004), 472–487.CrossRefGoogle Scholar
Marcos, E. N., Mendoza, O. and Sáenz, C., Stratifying systems via relative projective modules, Commun. Algebra 33 (2005), 1559–1573.CrossRefGoogle Scholar
Mazorchuk, V., On finitistic dimension of stratified algebras, Algebra Discrete Math. 3 (3) (2004), 77–88.Google Scholar
Mazorchuk, V., Stratified algebras arising in Lie theory, in Representations of finite dimensional algebras and related topics in Lie theory and geometry, Fields Institute Communications (Dlab, V. and Ringel, C. M., Editors), vol. 40, (American Mathematical Society, Providence, RI, 2004), 245–260.Google Scholar
Mazorchuk, V. and Parker, P., On the relation between finitistic and good filtration dimensions, Commun. Algebra 32 (5) (2004), 1903–1917.CrossRefGoogle Scholar
Mendoza, O. and Santiago, V., Homological systems in triangulated categories, Appl. Categorical Struct. 24 (1) (2016), 1–35.CrossRefGoogle Scholar
Mendoza, O., Sáenz, C. and Xi, C., Homological systems in module categories over pre-ordered sets, Quart. J. Math. 60 (2009), 75–103.CrossRefGoogle Scholar
Neeman, A., The derived category of an exact category, J. Algebra 135 (1990), 388–394.CrossRefGoogle Scholar
Quillen, D., Higher algebraic K-theory I, in Algebraic K-theory I. Proceedings of the Conference Held at Battelle Memorial Institute, Seattle, WA, 1972. Lecture notes in mathematics, vol. 341 (Springer, Berlin, 1973), 85–147.Google Scholar
Ringel, C. M., The category of modules with good filtrations over a quasi-hereditary algebra has almost split sequences, Math. Z. 208 (1991), 209–223.CrossRefGoogle Scholar
Rudakov, A. N., Helices and vector bundles: Seminaire Rudakov, London Mathematical Society Lecture Note Series, volume 148 (Cambridge University Press, New York, 1990).CrossRefGoogle Scholar
Seidel, U., Exceptional sequences for quivers of Dynkin type, Commun. Algebra 29 (3) (2001), 1373–1386.CrossRefGoogle Scholar