Hostname: page-component-cb9f654ff-r5d9c Total loading time: 0 Render date: 2025-08-30T16:24:52.811Z Has data issue: false hasContentIssue false
  • English
  • Français

TOPOLOGY OF 1-PARAMETER DEFORMATIONS OF NON-ISOLATED REAL SINGULARITIES

Part of: Theory of singularities and catastrophe theory

Published online by Cambridge University Press:  30 July 2021

NICOLAS DUTERTRE  and
JUAN ANTONIO MOYA PÉREZ
NICOLAS DUTERTRE
Affiliation:
Univ Angers, CNRS, LAREMA, SFR MATHSTIC, F-49000 Angers, France. e-mail: nicolas.dutertre@univ-angers.fr
JUAN ANTONIO MOYA PÉREZ
Affiliation:
Departament de Matemàtiques, Universitat de València, Campus de Burjassot, 46100 Burjassot SPAIN e-mail: Juan.Moya@uv.es
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 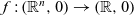$f\,{:}\,(\mathbb R^n,0)\to (\mathbb R,0)$ be an analytic function germ with non-isolated singularities and let 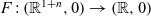$F\,{:}\, (\mathbb{R}^{1+n},0) \to (\mathbb{R},0)$ be a 1-parameter deformation of f. Let 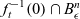$ f_t ^{-1}(0) \cap B_\epsilon^n$, 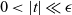$0 < \vert t \vert \ll \epsilon$, be the “generalized” Milnor fiber of the deformation F. Under some conditions on F, we give a topological degree formula for the Euler characteristic of this fiber. This generalizes a result of Fukui.

MSC classification

Primary: 32B05: Analytic algebras and generalizations, preparation theorems
Secondary: 58K05: Critical points of functions and mappings 58K65: Topological invariants

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 484 - 498
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Arnol’d, V.I., Index of a singular point of a vector field, the Petrovski-Oleinik inequality, and mixed Hodge structures, Funct. Anal. Appli. 12 (1978), 1–14.CrossRefGoogle Scholar
Bruce, J.W., Euler characteristics of real varieties, Bull. London Math. Soc. 22 (1990), 547–552.CrossRefGoogle Scholar
Durfee, A., Neighborhoods of algebraic sets, Trans. Amer. Math. Soc. 276(2) (1983), 517–530.CrossRefGoogle Scholar
Dutertre, N., Topology and geometry of real singularities, Adv. Stud. Pure Math. 68 (2016), School on Real and Complex Singularities in São Carlos (2012), pp. 1–40.Google Scholar
Dutertre, N., On the topology of non-isolated real singularities, J. Singular. 22 (2020), 159–179.CrossRefGoogle Scholar
Eisenbud, D. and Levine, H.I., An algebraic formula for the degree of a $C^{\infty}$ map-germ, Ann. Math. 106 (1977), 19–44.CrossRefGoogle Scholar
Fukui, T., An algebraic formula for a topological invariant of bifurcation of 1-parameter family of function-germs, Stratifications, Singularities, and Differential Equations, II (Marseille, 1990; Honolulu, HI, 1990), Travaux en cours 55 (1997), 45–54.Google Scholar
Khimshiashvili, G.M., On the local degree of a smooth map, Soobshch. Akad. Nauk Gruz. SSR 85 (1977), 309–312.Google Scholar
Łojasiewicz, S., Ensembles semi-analytiques, Inst. Hautes Etudes Sci., Bures-sur-Yvette (1965).Google Scholar
Milnor, J., Singular points of complex hypersurfaces, Ann. Math. Stud. 61 (1968).CrossRefGoogle Scholar
Szafraniec, Z., On the Euler characteristic of analytic and algebraic sets, Topology 25(4) (1986), 411–414.CrossRefGoogle Scholar
Szafraniec, Z., Topological invariants of weighted homogeneous polynomials, Glasgow Math. J. 33 (1991), 241–245.CrossRefGoogle Scholar
Wall, C.T.C., Topological invariant of the Milnor number mod 2, Topology 22 (1983), 345–350.CrossRefGoogle Scholar