No CrossRef data available.
Article contents
Unique factorization in Cayley arithmetics and cryptology
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 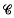 be the classical Cayley algebra defined over the reals with basis
be the classical Cayley algebra defined over the reals with basis 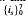 where
where 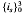 gives a quaternion algebra ℋ4 with i0 = 1, i1i2i3 = −1, i1i4 = i5, i2i4 = i6 and i3i4 = i7. The multiplication table of the imaginary basic units follows:
gives a quaternion algebra ℋ4 with i0 = 1, i1i2i3 = −1, i1i4 = i5, i2i4 = i6 and i3i4 = i7. The multiplication table of the imaginary basic units follows:

Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1991
References
REFERENCES
2.van der Blij, F. and Springer, T. A., The arithmetics of the octaves and of the group G2, Nederl. Akad. Wetensch. Proc. (=Indag. Math.) 62A (1959), 406–418.CrossRefGoogle Scholar
3.Dickson, L. E., On quaternions and their generalization and the history of the eight square theorem, Annals of Math. (2), 20 (1919), 155–171, 297.CrossRefGoogle Scholar
4.Hurwitz, A., Über die Composition der quadratischen Formen von beliebig vielen Variabeln, Nachr. Gesell. Wiss. Göttingen (1898), 309–316.Google Scholar
5.Lamont, P. J. C., Arithmetics in Cayley's algebra, Proc. Glasgow Math. Assoc. 6 (1963), 99–106.CrossRefGoogle Scholar
6.Lamont, P. J. C., Ideals in Cayley's algebra, Nederl. Akad. Wetensch. Proc. (= Indag. Math.) 66A (1963), 394–400.CrossRefGoogle Scholar
7.Lamont, P. J. C., Approximation theorems for the group G2, Nederl. Akad. Wetensch. Proc. (=Indag. Math.) 67A (1964), 187–192.CrossRefGoogle Scholar
8.Lamont, P. J. C., Factorization and arithmetic functions for orders in composition algebras, Glasgow Math. J. 14 (1973), 86–95.CrossRefGoogle Scholar
9.Lamont, P. J. C., The number of Cayley integers of given norm, Proc. Edinburgh Math. Soc. 25 (1982), 101–103.CrossRefGoogle Scholar
10.Lamont, P. J. C., Computer generated natural inner automorphisms of Cayley's algebra, Glasgow Math. J. 23 (1982), 187–189.CrossRefGoogle Scholar
11.Lamont, P. J. C., The nonexistence of a factorization formula for Cayley numbers, Glasgow Math. J. 24 (1983), 131–132.CrossRefGoogle Scholar
12.Rankin, R. A., On representations of a number as a sum of squares and certain related identities, Proc. Camb. Phil. Soc. 41 (1945), 1–11.CrossRefGoogle Scholar
13.Rankin, R. A., A certain class of multiplicative functions, Duke Math. J. 13 (1946), 281–306.CrossRefGoogle Scholar

