Article contents
Degree correlations in scale-free random graph models
Published online by Cambridge University Press: 01 October 2019
Abstract
We study the average nearest-neighbour degree a(k) of vertices with degree k. In many real-world networks with power-law degree distribution, a(k) falls off with k, a property ascribed to the constraint that any two vertices are connected by at most one edge. We show that a(k) indeed decays with k in three simple random graph models with power-law degrees: the erased configuration model, the rank-1 inhomogeneous random graph, and the hyperbolic random graph. We find that in the large-network limit for all three null models, a(k) starts to decay beyond 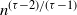 $n^{(\tau-2)/(\tau-1)}$ and then settles on a power law
$n^{(\tau-2)/(\tau-1)}$ and then settles on a power law 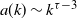 $a(k)\sim k^{\tau-3}$, with
$a(k)\sim k^{\tau-3}$, with  $\tau$ the degree exponent.
$\tau$ the degree exponent.
Keywords
MSC classification
Primary:
05C80: Random graphs
Secondary:
60F05: Central limit and other weak theorems
Information
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2019
References
Albert, R., Jeong, H. and Barabási, A.-L. (1999). Internet: diameter of the world-wide web. Nature 401, 130–131.CrossRefGoogle Scholar
Barrat, A., Barthélemy, M., Pastor-Satorras, R. and Vespignani, A. (2004). The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA 101, 3747–3752.CrossRefGoogle ScholarPubMed
Bhamidi, S., Dhara, S., van der Hofstad, R. and Sen, S. (2017). Universality for critical heavy-tailed network models: metric structure of maximal components. Available at arXiv:1703.07145.Google Scholar
Bhamidi, S., van der Hofstad, R. and Hooghiemstra, G. (2017). Universality for first passage percolation on sparse random graphs. Ann. Probab. 45, 2568–2630.CrossRefGoogle Scholar
Bhamidi, S., Sen, S. and Wang, X. (2017). Continuum limit of critical inhomogeneous random graphs. Probab. Theory Related Fields 169, 565–641.CrossRefGoogle Scholar
Bode, M., Fountoulakis, N. and Müller, T. (2015). On the largest component of a hyperbolic model of complex networks. Electron. J. Combin. 22, P3.24.CrossRefGoogle Scholar
Bode, M., Fountoulakis, N. and Müller, T. (2016). The probability of connectivity in a hyperbolic model of complex networks. Random Structures Algorithms 49, 65–94.CrossRefGoogle Scholar
Boguñá, M. and Pastor-Satorras, R. (2003). Class of correlated random networks with hidden variables. Phys. Rev. E 68, 036112.CrossRefGoogle ScholarPubMed
Boguñá, M., Pastor-Satorras, R. and Vespignani, A. (2003). Absence of epidemic threshold in scale-free networks with degree correlations. Phys. Rev. Lett. 90, 028701.CrossRefGoogle ScholarPubMed
Bollobás, B. (1980). A probabilistic proof of an asymptotic formula for the number of labelled regular graphs. European J. Combin
. 1, 311–316.CrossRefGoogle Scholar
Bringmann, K., Keusch, R. and Lengler, J. (2015). Sampling geometric inhomogeneous random graphs in linear time. In 25th European Symposium on Algorithms (ESA 2017) (Leibniz International Proceedings in Informatics 87), art. 20. Leibniz-Zentrum für Informatik, Schloss Dagstuhl.Google Scholar
Britton, T., Deijfen, M. and Martin-Löf, A. (2006). Generating simple random graphs with prescribed degree distribution. J. Stat. Phys. 124, 1377–1397.CrossRefGoogle Scholar
Candellero, E. and Fountoulakis, N. (2014). Clustering and the hyperbolic geometry of complex networks. In Algorithms and Models for the Web Graph (WAW 2014) (Lecture Notes in Computer Science 8882), pp. 1–12. Springer, Cham.Google Scholar
Catanzaro, M., Boguñá, M. and Pastor-Satorras, R. (2005). Generation of uncorrelated random scale-free networks. Phys. Rev. E 71, 027103.CrossRefGoogle ScholarPubMed
Chung, F. and Lu, L. (2002). The average distances in random graphs with given expected degrees. Proc. Natl Acad. Sci. USA 99, 15879–15882.CrossRefGoogle ScholarPubMed
Colomer-de Simon, P. and Boguñá, M. (2012). Clustering of random scale-free networks. Phys. Rev. E 86, 026120.CrossRefGoogle ScholarPubMed
van den Esker, H., van der Hofstad, R. and Hooghiemstra, G. (2008). Universality for the distance in finite variance random graphs. J. Stat. Phys. 133, 169–202.CrossRefGoogle Scholar
Faloutsos, M., Faloutsos, P. and Faloutsos, C. (1999). On power-law relationships of the internet topology. In ACM SIGCOMM Computer Communication Review, vol. 29, pp. 251–262. ACM.Google Scholar
Friedrich, T. and Krohmer, A. (2015). Cliques in hyperbolic random graphs. In INFOCOM Proceedings 2015, pp. 1544–1552. IEEE.Google Scholar
Gradshteyn, I. and Ryzhik, I. (2015). Table of Integrals, Series, and Products. Elsevier.Google Scholar
Gugelmann, L., Panagiotou, K. and Peter, U. (2012). Random hyperbolic graphs: degree sequence and clustering. In ICALP Proceedings 2012, Part II, pp. 573–585. Springer, Berlin and Heidelberg.Google Scholar
van der Hofstad, R. (2017). Random Graphs and Complex Networks, vol. 1. Cambridge University Press.CrossRefGoogle Scholar
van der Hofstad, R., Hooghiemstra, G. and Van Mieghem, P. (2005). Distances in random graphs with finite variance degrees. Random Structures Algorithms 27, 76–123.CrossRefGoogle Scholar
van der Hofstad, R., van der Hoorn, P., Litvak, N. and Stegehuis, C. (2017). Limit theorems for assortativity and clustering in the configuration model with scale-free degrees. Available at arxiv:1712.08097.Google Scholar
van der Hofstad, R., Janssen, A. J. E. M., van Leeuwaarden, J. S. H. and Stegehuis, C. (2017). Local clustering in scale-free networks with hidden variables. Phys. Rev. E 95, 022307.CrossRefGoogle ScholarPubMed
van der Hofstad, R., van Leeuwaarden, J. S. H. and Stegehuis, C. (2017). Optimal subgraph structures in scale-free configuration models. Available at arXiv:1709.03466.Google Scholar
van der Hoorn, P. and Litvak, N. (2015). Upper bounds for number of removed edges in the erased configuration model. In Algorithms and Models for the Web Graph (WAW 2015) (Lecture Notes in Computer Science 9479), pp. 54–65. Springer, Cham.CrossRefGoogle Scholar
Janson, S. and Luczak, M. J. (2007). A simple solution to the k-core problem. Random Structures Algorithms 30, 50–62.CrossRefGoogle Scholar
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N. and Barabási, A.-L. (2000). The large-scale organization of metabolic networks. Nature 407, 651–654.CrossRefGoogle ScholarPubMed
Krioukov, D., Papadopoulos, F., Kitsak, M., Vahdat, A. and Boguná, M. (2010). Hyperbolic geometry of complex networks. Phys. Rev. E 82, 036106.CrossRefGoogle ScholarPubMed
Leskovec, J. and Krevl, A. (2014). SNAP Datasets: Stanford large network dataset collection. Available at http://snap.stanford.edu/data.Google Scholar
Maslov, S., Sneppen, K. and Zaliznyak, A. (2004). Detection of topological patterns in complex networks: correlation profile of the internet. Phys. A 333, 529–540.CrossRefGoogle Scholar
Mayo, M., Abdelzaher, A. and Ghosh, P. (2015). Long-range degree correlations in complex networks. Comput. Social Networks 2, 4.CrossRefGoogle Scholar
Newman, M. E. J. (2002). Assortative mixing in networks. Phys. Rev. Lett. 89, 208701.CrossRefGoogle ScholarPubMed
Ostilli, M. (2014). Fluctuation analysis in complex networks modeled by hidden-variable models: necessity of a large cutoff in hidden-variable models. Phys. Rev. E 89, 022807.CrossRefGoogle ScholarPubMed
Park, J. and Newman, M. E. J. (2003). Origin of degree correlations in the internet and other networks. Phys. Rev. E 68, 026112.CrossRefGoogle ScholarPubMed
Pastor-Satorras, R., Vázquez, A. and Vespignani, A. (2001). Dynamical and correlation properties of the internet. Phys. Rev. Lett. 87, 258701.CrossRefGoogle ScholarPubMed
Ravasz, E. and Barabási, A.-L. (2003). Hierarchical organization in complex networks. Phys. Rev. E 67, 026112.CrossRefGoogle ScholarPubMed
Serrano, M. Á. and Boguñá, M. (2006). Percolation and epidemic thresholds in clustered networks. Phys. Rev. Lett. 97, 088701.CrossRefGoogle ScholarPubMed
Stegehuis, C., van der Hofstad, R., van Leeuwaarden, J. S. H. and Janssen, A. J. E. M. (2017). Clustering spectrum of scale-free networks. Phys. Rev. E 96, 042309.CrossRefGoogle ScholarPubMed
Vázquez, A. (2003). Growing network with local rules: preferential attachment, clustering hierarchy, and degree correlations. Phys. Rev. E 67, 056104.CrossRefGoogle ScholarPubMed
Vázquez, A., Pastor-Satorras, R. and Vespignani, A. (2002). Large-scale topological and dynamical properties of the internet. Phys. Rev. E 65, 066130.CrossRefGoogle ScholarPubMed
Yao, D., van der Hoorn, P. and Litvak, N. (2018). Average nearest neighbor degrees in scale-free networks. Internet Mathematics 2018. doi:10.24166/im.02.2018.CrossRefGoogle Scholar
- 7
- Cited by

