Hostname: page-component-76d6cb85b7-dqfph Total loading time: 0 Render date: 2026-07-19T01:34:26.680Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit results on conditional distributions of generalized exponential mixtures

Part of: Special processes Distribution theory Operations research and management science Distribution theory - Probability

Published online by Cambridge University Press:  04 September 2020

Claudia Klüppelberg  and
Miriam Isabel Seifert
Claudia Klüppelberg*
Affiliation:
Technical University of Munich
Miriam Isabel Seifert*
Affiliation:
Ruhr University Bochum
*
*Postal address: Boltzmannstraße 3, 85748 Garching, Germany. Email: cklu@tum.de
**Postal address: Universitätsstraße 150, 44801 Bochum, Germany. Email: miriam.seifert@rub.de
Get access Rights & Permissions [Opens in a new window]

Abstract

For independent exponentially distributed random variables 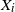$X_i$, 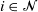$i\in {\mathcal{N}}$, with distinct rates 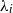${\lambda}_i$ we consider sums 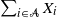$\sum_{i\in\mathcal{A}} X_i$ for 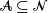$\mathcal{A}\subseteq {\mathcal{N}}$ which follow generalized exponential mixture distributions. We provide novel explicit results on the conditional distribution of the total sum 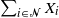$\sum_{i\in {\mathcal{N}}}X_i$ given that a subset sum 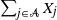$\sum_{j\in \mathcal{A}}X_j$ exceeds a certain threshold value 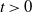$t>0$, and vice versa. Moreover, we investigate the characteristic tail behavior of these conditional distributions for 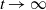$t\to\infty$. Finally, we illustrate how our probabilistic results can be applied in practice by providing examples from both reliability theory and risk management.

Keywords

Conditional distributionconvolutionexponential distributiongeneralized exponential mixture distributionphase-type distributionsreliability theoryrisk managementtail behavior

MSC classification

Primary: 62E10: Characterization and structure theory
Secondary: 60E05: Distributions 60K10: Applications (reliability, demand theory, etc.) 90B25: Reliability, availability, maintenance, inspection

Information

Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 3 , September 2020 , pp. 760 - 774
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Albrecher, H. and Bladt, M. (2019). Inhomogeneous phase-type distributions and heavy tails. J. Appl. Prob. 56, 1044–1064.CrossRefGoogle Scholar
Amari, S. V. and Misra, R. B. (1997). Closed-form expressions for distribution of sum of exponential random variables. IEEE Trans. Reliab. 46, 519–522.CrossRefGoogle Scholar
Anjum, B. and Perros, H. (2011). Adding percentiles of Erlangian distributions. IEEE Commun. Lett. 15, 346–348.CrossRefGoogle Scholar
Asmussen, S. (2000). Matrix-analytic models and their analysis. Scand. J. Statist. 27, 193–226.10.1111/1467-9469.00186CrossRefGoogle Scholar
Asmussen, S., Nerman, O. and Olsson, M. (1996). Fitting phase-type distributions via the EM algorithm. Scand. J. Statist. 23, 419–441.Google Scholar
Barbe, P. and Seifert, M. I. (2016). A conditional limit theorem for a bivariate representation of a univariate random variable and conditional extreme values. Extremes 19, 351–370.CrossRefGoogle Scholar
Bartholomew, D. J. (1969). Sufficient conditions for a mixture of exponentials to be a probability density function. Ann. Math. Statist. 40, 2183–2188.CrossRefGoogle Scholar
Bekker, R. and Koeleman, P. M. (2011). Scheduling admissions and reducing variability in bed demand. Health Care Manage. Sci. 14, 237–249.CrossRefGoogle ScholarPubMed
Bergel, A. I. and Egídio dos Reis, A. D. (2016). Ruin problems in the generalized Erlang(n) risk model. Europ. Actuarial J. 6, 257–275.CrossRefGoogle Scholar
Bladt, M. and Nielsen, B. F. (2017). Matrix-Exponential Distributions in Applied Probability. Springer, New York.CrossRefGoogle Scholar
Dufresne, D. (2007). Fitting combinations of exponentials to probability distributions. Appl. Stoch. Models Business Industry 23, 23–48.10.1002/asmb.635CrossRefGoogle Scholar
Favaro, S. and Walker, S. G. (2010). On the distribution of sums of independent exponential random variables via Wilks’ integral representation. Acta Appl. Math. 109, 1035–1042.10.1007/s10440-008-9357-5CrossRefGoogle Scholar
Harris, C. M., Marchal, W. G. and Botta, R. F. (1992). A note on generalized hyperexponential distributions. Commun. Statist. Stoch. Models 8, 179–191.CrossRefGoogle Scholar
Jasiulewicz, H. and Kordecki, W. (2003). Convolutions of Erlang and of Pascal distributions with applications to reliability. Demonstr. Math. 36, 231–238.Google Scholar
Jewell, N. P. (1982). Mixtures of exponential distributions. Ann. Statist. 10, 479–484.CrossRefGoogle Scholar
Klüppelberg, C. and Seifert, M. I. (2019). Financial risk measures for a network of individual agents holding portfolios of light-tailed objects. Finance Stoch. 23, 795–826.CrossRefGoogle Scholar
Kochar, S. and Xu, M. (2010). On the right spread order of convolutions of heterogeneous exponential random variables. J. Multivar. Anal. 101, 165–176.CrossRefGoogle Scholar
Kordecki, W. (1997). Reliability bounds for multistage structures with independent components. Statist. Prob. Lett. 34, 43–51.CrossRefGoogle Scholar
Li, K.-H. and Li, C. T. (2019). Linear combination of independent exponential random variables. Methodology Comput. Appl. Prob. 21, 253–277.CrossRefGoogle Scholar
McLachlan, G. J. (1995). Mixtures – models and applications. In The Exponential Distribution: Theory, Methods and Applications, eds. N. Balakrishnan and A. P. Basu. Gordon and Breach, Amsterdam, pp. 307–325.Google Scholar
Mathai, A. M. (1982). Storage capacity of a dam with gamma type inputs. Ann. Inst. Statist. Math. 34, 591–597.CrossRefGoogle Scholar
Moschopoulos, P. G. (1985). The distribution of the sum of independent Gamma random variables. Ann. Inst. Statist. Math. 37, 541–544.CrossRefGoogle Scholar
Navarro, J., Balakrishnan, N. and Samaniego, F. J. (2008). Mixture representations of residual lifetimes of used systems. J. Appl. Prob. 45, 1097–1112.CrossRefGoogle Scholar
Seifert, M. I. (2016). Weakening the independence assumption on polar components: Limit theorems for generalized elliptical distributions. J. Appl. Prob. 53, 130–145.CrossRefGoogle Scholar
Steutel, F. W. (1967). Note on the infinite divisibility of exponential mixtures. Ann. Inst. Statist. Math. 38, 1303–1305.CrossRefGoogle Scholar
Willmot, G. E. and Woo, J.-K. (2007). On the class of Erlang mixtures with risk theoretic applications. N. Amer. Actuarial J. 11, 99–115.CrossRefGoogle Scholar
Yin, M.-L., Angus, J. E. and Trivedi, K. S. (2013). Optimal preventive maintenance rate for best availability with hypo-exponential failure distribution. IEEE Trans. Reliab. 62, 351–361.Google Scholar