Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Duffield, N. G.
1994.
Exponential bounds for queues with Markovian arrivals.
Queueing Systems,
Vol. 17,
Issue. 3-4,
p.
413.
Botvich, D. D.
and
Duffield, N. G.
1995.
Large deviations, the shape of the loss curve, and economies of scale in large multiplexers.
Queueing Systems,
Vol. 20,
Issue. 3-4,
p.
293.
Zhi-Li Zhang
Towsley, D.
and
Kurose, J.
1995.
Statistical analysis of the generalized processor sharing scheduling discipline.
IEEE Journal on Selected Areas in Communications,
Vol. 13,
Issue. 6,
p.
1071.
Yan, J.
and
Beshai, M.
1995.
Designing an ATM-based broadband network: an overview.
Vol. 1,
Issue. ,
p.
245.
Jamoussi, B.
Rabie, S.
and
Aboul-Magd, O.
1996.
Performance evaluation of connection admission control techniques in ATM networks.
Vol. 1,
Issue. ,
p.
659.
Artiges, D.
and
Nain, P.
1996.
Upper and lower bounds for the multiplexing of multiclass Markovian on/off sources.
Performance Evaluation,
Vol. 27-28,
Issue. ,
p.
673.
Duffield, N. G.
1996.
Economies of scale in queues with sources having power-law large deviation scalings.
Journal of Applied Probability,
Vol. 33,
Issue. 03,
p.
840.
Palmowski, Zbigniew
and
Rolski, Tomasz
1996.
A note on martingale inequalities for fluid models.
Statistics & Probability Letters,
Vol. 31,
Issue. 1,
p.
13.
Crosby, S.
Leslie, I.
McGurk, B.
Lewis, J.T.
Russell, R.
and
Toomey, F.
1997.
Statistical properties of a near-optimal measurement-based CAC algorithm.
p.
103.
McGurk, Brian
and
Russell, Raymond
1997.
Computer Performance Evaluation Modelling Techniques and Tools.
Vol. 1245,
Issue. ,
p.
206.
Lewis, John T.
Russell, Raymond
Toomey, Fergal
McGurk, Brian
Crosby, Simon
and
Leslie, Ian
1998.
Practical connection admission control for ATM networks based on on-line measurements.
Computer Communications,
Vol. 21,
Issue. 17,
p.
1585.
Srinivasan, R.
and
Talim, H.
2002.
Fuzzy connection admission control for self-managed networks.
Vol. 3,
Issue. ,
p.
1516.
Ciucu, Florin
2007.
Managing Traffic Performance in Converged Networks.
Vol. 4516,
Issue. ,
p.
495.
Shioda, Shigeo
2008.
Loss bounds for a finite-capacity queue based on interval-wise traffic observation.
Queueing Systems,
Vol. 60,
Issue. 1-2,
p.
153.
Ali, Z.
Sheikh, W.
Chong, E.K.P.
and
Ghafoor, A.
2008.
A Scalable Call Admission Control Algorithm.
IEEE/ACM Transactions on Networking,
Vol. 16,
Issue. 2,
p.
424.
Kittipiyakul, Somsak
Javidi, Tara
and
Subramanian, Vijay G.
2008.
Many-sources large deviations for max-weight scheduling.
p.
1495.
Subramanian, Vijay G.
Javidi, Tara
and
Kittipiyakul, Somsak
2011.
Many-Sources Large Deviations for Max-Weight Scheduling.
IEEE Transactions on Information Theory,
Vol. 57,
Issue. 4,
p.
2151.
Poloczek, Felix
and
Ciucu, Florin
2014.
Scheduling analysis with martingales.
Performance Evaluation,
Vol. 79,
Issue. ,
p.
56.
Poloczek, Felix
and
Ciucu, Florin
2014.
A martingale-envelope and applications.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 41,
Issue. 3,
p.
43.
Rizk, Amr
Poloczek, Felix
and
Ciucu, Florin
2015.
Computable Bounds in Fork-Join Queueing Systems.
p.
335.
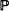 [queue length
[queue length 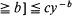 for any
for any 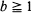 where c < 1 and y > 1 are given explicitly in terms of the parameters of the model. The model can be viewed as an approximation for the burst-level component of the queue in an ATM multiplexer. We obtain heavy traffic bounds for the mean queue length and show that for typical parameters this far exceeds the mean queue length for independent arrivals at the same load. We compare our results on the mean queue length with an analytic expression for the case of unit service rate, and compare our results on the full distribution with computer simulations.
where c < 1 and y > 1 are given explicitly in terms of the parameters of the model. The model can be viewed as an approximation for the burst-level component of the queue in an ATM multiplexer. We obtain heavy traffic bounds for the mean queue length and show that for typical parameters this far exceeds the mean queue length for independent arrivals at the same load. We compare our results on the mean queue length with an analytic expression for the case of unit service rate, and compare our results on the full distribution with computer simulations.
