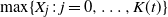Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baeriswyl, Fabien
Chavez-Demoulin, Valérie
and
Wintenberger, Olivier
2025.
Tail asymptotics and precise large deviations for some Poisson cluster processes.
Advances in Applied Probability,
Vol. 57,
Issue. 1,
p.
204.