Published online by Cambridge University Press: 16 November 2022
The existence of moments of first downward passage times of a spectrally negative Lévy process is governed by the general dynamics of the Lévy process, i.e. whether it is drifting to 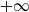 $+\infty$,
$+\infty$, 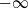 $-\infty$, or oscillating. Whenever the Lévy process drifts to
$-\infty$, or oscillating. Whenever the Lévy process drifts to 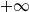 $+\infty$, we prove that the
$+\infty$, we prove that the  $\kappa$th moment of the first passage time (conditioned to be finite) exists if and only if the
$\kappa$th moment of the first passage time (conditioned to be finite) exists if and only if the 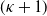 $(\kappa+1)$th moment of the Lévy jump measure exists. This generalizes a result shown earlier by Delbaen for Cramér–Lundberg risk processes. Whenever the Lévy process drifts to
$(\kappa+1)$th moment of the Lévy jump measure exists. This generalizes a result shown earlier by Delbaen for Cramér–Lundberg risk processes. Whenever the Lévy process drifts to 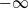 $-\infty$, we prove that all moments of the first passage time exist, while for an oscillating Lévy process we derive conditions for non-existence of the moments, and in particular we show that no integer moments exist.
$-\infty$, we prove that all moments of the first passage time exist, while for an oscillating Lévy process we derive conditions for non-existence of the moments, and in particular we show that no integer moments exist.