Hostname: page-component-cb9f654ff-rkzlw Total loading time: 0 Render date: 2025-08-19T10:58:20.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform asymptotic normality of weighted sums of short-memory linear processes

Part of: Limit theorems Parametric inference

Published online by Cambridge University Press:  04 May 2020

Rimas Norvaiša  and
Alfredas Račkauskas
Rimas Norvaiša*
Affiliation:
Vilnius University
Alfredas Račkauskas*
Affiliation:
Vilnius University
*
*Postal address: Naugarduko 24, LT-03225 Vilnius, Lithuania.
*Postal address: Naugarduko 24, LT-03225 Vilnius, Lithuania.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 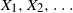$X_1, X_2,\dots$ be a short-memory linear process of random variables. For 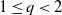$1\leq q<2$, let 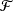${\mathcal{F}}$ be a bounded set of real-valued functions on [0, 1] with finite q-variation. It is proved that 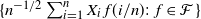$\{n^{-1/2}\sum_{i=1}^nX_i\,f(i/n)\colon f\in{\mathcal{F}}\}$ converges in outer distribution in the Banach space of bounded functions on 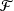${\mathcal{F}}$ as 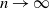$n\to\infty$. Several applications to a regression model and a multiple change point model are given.

Keywords

Uniform limit theoremweak invariance principlep-variationchange pointsregressionshort memory linear process

MSC classification

Primary: 60F17: Functional limit theorems; invariance principles
Secondary: 62F05: Asymptotic properties of tests

Information

Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 1 , March 2020 , pp. 174 - 195
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abadir, K. M., Distaso, W., Giraitis, L. and Koul, H. L. (2014). Asymptotic normality for weighted sums of linear processes. Econometric Theory 30, 252–284.10.1017/S0266466613000182CrossRefGoogle Scholar
Basseville, M. and Nikiforov, N. (1993). The Detection of Abrupt Changes: Theory and Applications (Information and System Sciences series). Prentice-Hall, Upper Saddle River, NJ.Google Scholar
Brodsky, B. E. and Darkhovsky, B. S. (1993). Non Parametric Methods in Change Point Problems. Kluwer Academic Publishers, Dordrecht.CrossRefGoogle Scholar
Butkus, V. and Norvaiša, R. Computation of p-variation. (2018). Lith. Math. J. 58, 360–378.CrossRefGoogle Scholar
Chen, J. and Gupta, A. K. (2000). Parametric Statistical Change Point Analysis. Birkhauser, Boston, MA.CrossRefGoogle Scholar
Csörgo, M. and Horváth, L. (1997). Limit Theorems in Change-Point Analysis. John Wiley, New York.Google Scholar
Dudley, R. M. Sample functions of the Gaussian process. (1953). Ann. Prob. 1, 66–103.10.1214/aop/1176997026CrossRefGoogle Scholar
Dudley, R. M. Fréchet differentiability, p-variation and uniform Donsker classes. (1992). Ann. Prob. 20, 1968–1982.CrossRefGoogle Scholar
Dudley, R. M. (1999). Uniform Central Limit Theorems. Cambridge University Press.CrossRefGoogle Scholar
Dudley, R. M. (2002). Real Analysis and Probability. Cambridge University Press.CrossRefGoogle Scholar
Dudley, R. M. and Norvaiša, R. (1999) Differentiability of Six Operators on Nonsmooth Functions and p-Variation (Lecture Notes in Mathematics 1703). Springer, New York.CrossRefGoogle Scholar
Giné, E. and Nickl, R. (2016). Mathematical Foundations of Infinite-Dimensional Statistical Models. Cambridge University Press.CrossRefGoogle Scholar
Kisliakov, S. V. (1984). A remark on the space of functions of bounded p-variation. Math. Nachr. 119, 137–140.CrossRefGoogle Scholar
Norvaiša, R. and Račkauskas, A. (2008). Convergence in law of partial sum processes in p-variation norm. Lith. Math. J. 48, 212–227.CrossRefGoogle Scholar
Van der Vaart, A. W. and Wellner, J. A. (1996). Weak Convergence and Empirical Processes with Applications to Statistics. Springer, New York.CrossRefGoogle Scholar