Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-04-30T23:38:27.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal and stable approximation to subgraph counts in superpositions of Bernoulli random graphs

Part of: Graph theory Limit theorems Social and behavioral sciences: general topics

Published online by Cambridge University Press:  18 August 2023

Mindaugas Bloznelis ,
Joona Karjalainen  and
Lasse Leskelä
Mindaugas Bloznelis*
Affiliation:
Vilnius University
Joona Karjalainen*
Affiliation:
Aalto University
Lasse Leskelä*
Affiliation:
Aalto University
*
*Postal address: Institute of Computer Science, Vilnius University, Didlaukio 47, LT-08303, Vilnius, Lithuania. Email: mindaugas.bloznelis@mif.vu.lt
*Postal address: Institute of Computer Science, Vilnius University, Didlaukio 47, LT-08303, Vilnius, Lithuania. Email: mindaugas.bloznelis@mif.vu.lt
*Postal address: Institute of Computer Science, Vilnius University, Didlaukio 47, LT-08303, Vilnius, Lithuania. Email: mindaugas.bloznelis@mif.vu.lt
Get access Rights & Permissions [Opens in a new window]

Abstract

Real networks often exhibit clustering, the tendency to form relatively small groups of nodes with high edge densities. This clustering property can cause large numbers of small and dense subgraphs to emerge in otherwise sparse networks. Subgraph counts are an important and commonly used source of information about the network structure and function. We study probability distributions of subgraph counts in a community affiliation graph. This is a random graph generated as an overlay of m partly overlapping independent Bernoulli random graphs (layers) 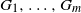$G_1,\dots,G_m$ with variable sizes and densities. The model is parameterised by a joint distribution of layer sizes and densities. When m grows linearly in the number of nodes n, the model generates sparse random graphs with a rich statistical structure, admitting a nonvanishing clustering coefficient and a power-law limiting degree distribution. In this paper we establish the normal and $\alpha$-stable approximations to the numbers of small cliques, cycles, and more general 2-connected subgraphs of a community affiliation graph.

Keywords

Subgraph countoverlapping communitiesErdös–Rényi graphnormal approximationclusteringpower lawcomplex networkaffiliation networkrandom intersection graph

MSC classification

Primary: 60F05: Central limit and other weak theorems 05C80: Random graphs
Secondary: 05C82: Small world graphs, complex networks 91C20: Clustering
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambroise, C. and Matias, C. (2012). New consistent and asymptotically normal parameter estimates for random-graph mixture models. J. R. Statist. Soc. B 74, 3–35.CrossRefGoogle Scholar
Benson, A. R., Gleich, D. and Leskovec, J. (2016). Higher-order organization of complex networks. Science 353, 163–166.CrossRefGoogle ScholarPubMed
Bhattacharya, B. B., Chatterjee, A. and Janson, S. (2021). Fluctuations of subgraph counts in graphon-based random graphs. Preprint, arXiv:2104.07259.Google Scholar
Bloznelis, M. and Jaworski, J. (2018). The asymptotic normality of the global clustering coefficient in sparse random intersection graphs. In Algorithms and Models for the Web Graph – 15th International Workshop, WAW 2018 (Lect. Notes Comp. Sci. 10836), eds A. Bonato. P. Prałat and A. Raigorodskii. Springer, New York, pp. 16–29.CrossRefGoogle Scholar
Bloznelis, M. and Kurauskas, V. (2016). Clustering coefficient of random intersection graphs with infinite degree variance. Internet Math. doi: 10.24166/im.02.2017.CrossRefGoogle Scholar
Bloznelis, M. and Leskelä, L. (2023). Clustering and percolation on superpositions of Bernoulli random graphs. Random Structures Algorithms 63, 283–342.CrossRefGoogle Scholar
Bloznelis, M., Karjalainen, J. and Leskelä, L. (2022). Assortativity and bidegree distributions on Bernoulli random graph superpositions. Prob. Eng. Inf. Sci. 36, 1188–1213.CrossRefGoogle Scholar
Eikmeier, N., Ramani, A. S. and Gleich, D. (2018). The HyperKron graph model for higher-order features. In Proc. 2018 IEEE International Conference on Data Mining. IEEE, Piscataway, NJ, pp. 941–946.CrossRefGoogle Scholar
Gnedenko, B. V. and Kolmogorov, A. N. (1954). Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Cambridge.Google Scholar
Godehardt, E. and Jaworski, J. (2001). Two models of random intersection graphs and their applications. Electron. Notes Discrete Math. 10, 129–132.CrossRefGoogle Scholar
Gröhn, T., Karjalainen, J. and Leskelä, L. (2019). Clique and cycle frequencies in a sparse random graph model with overlapping communities. Preprint, arXiv:1911.12827.Google Scholar
Hladký, J., Pelekis, Ch. and Šileikis, M. (2021). A limit theorem for small cliques in inhomogeneous random graphs. J. Graph Theory 97, 578–599.CrossRefGoogle Scholar
Honey, C. J., Kötter, R., Breakspear, M. and Sporns, O. (2007). Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc. Nat. Acad. Sci. USA 104, 10240–10245.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000). Random Graphs. John Wiley, New York.CrossRefGoogle Scholar
Janson, S., Oleszkiewicz, K. and Ruciński, A. (2004). Upper tails for subgraph counts in random graphs. Israel. J. Math. 142, 61–92.CrossRefGoogle Scholar
Karjalainen, J., van Leeuwaarden, J. S. H. and Leskelä, L. (2018). Parameter estimators of random intersection graphs with thinned communities. In Algorithms and Models for the Web Graph – 15th International Workshop, WAW 2018 (Lect. Notes Comp. Sci. 10836), eds A. Bonato, P. Prałat and A. Raigorodskii. Springer, New York, pp. 44–58.CrossRefGoogle Scholar
Kaur, G. and Röllin, A. (2021). Higher-order fluctuations in dense random graph models. Electron. J. Prob. 26, 1–36.CrossRefGoogle Scholar
Kurauskas, V. (2022). On local weak limit and subgraph counts for sparse random graphs. J. Appl. Prob. 59, 755–776.CrossRefGoogle Scholar
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chlovskii, D. and Alon, U. (2002): Network motifs: Simple building blocks of complex networks. Science 298, 824–827.CrossRefGoogle ScholarPubMed
Ospina-Forero, L., Deane, C. M. and Reinert, G. (2019). Assessment of model fit via network comparison methods based on subgraph counts. J. Complex Networks 7, 226–253.CrossRefGoogle Scholar
Privault, N. and Serafin, G. (2020). Normal approximation for sums of weighted U-statistics: Application to Kolmogorov bounds in random subgraph counting. Bernoulli 26, 587–615.CrossRefGoogle Scholar
Röllin, A. (2022). Kolmogorov bounds for the normal approximation of the number of triangles in the Erdös–Rényi random graph. Prob. Eng. Inf. Sci. 36, 747–773.CrossRefGoogle Scholar
Ruciński, A. (1988). When are small subgraphs of a random graph normally distributed? Prob. Theory Relat. Fields 78, 1–10.CrossRefGoogle Scholar
Shen-Orr, S. S., Milo, R., Mangan, S. and Alon, U. (2002). Network motifs in the transcriptional regulation network of Escherichia coli . Nature Genetics 31, 64–68.CrossRefGoogle ScholarPubMed
Ugander, J., Backstrom, L. and Kleinberg, J. (2013). Subgraph frequencies: Mapping the empirical and extremal geography of large graph collections. In Proc. 22nd Int. Conf. World Wide Web, 1307–1318.CrossRefGoogle Scholar
van der Hofstad, R., Komjáthy, J. and Vadon, V. (2021). Random intersection graphs with communities. Adv. Appl. Prob. 53, 1061–1089.CrossRefGoogle Scholar
van Leeuwaarden, J. S. and Stegehuis, C. (2021). Robust subgraph counting with distribution-free random graph analysis. Phys. Rev. E 104, 044313.CrossRefGoogle ScholarPubMed
Yang, J. and Leskovec, J. (2012). Community affiliation graph model for overlapping network community detection. In Proc. 2012 IEEE 12th Int. Conf. Data Mining. IEEE, Piscataway, NJ, pp. 1170–1175.CrossRefGoogle Scholar
Yang, J. and Leskovec, J. (2014). Structure and overlaps of ground-truth communities in networks. ACM Trans. Intell. Syst. Technol. 5, 1–35.CrossRefGoogle Scholar
Zhang, Z. S. (2022). Berry–Esseen bounds for generalized U-statistics. Electron. J. Prob. 27, 1–36.CrossRefGoogle Scholar