Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-28T22:39:01.951Z Has data issue: false hasContentIssue false
  • English
  • Français

On moments of downward passage times for spectrally negative Lévy processes

Part of: Stochastic processes

Published online by Cambridge University Press:  16 November 2022

Anita Behme Open the ORCID record for Anita Behme [Opens in a new window]  and
Philipp Lukas Strietzel Open the ORCID record for Philipp Lukas Strietzel [Opens in a new window]
Anita Behme*
Affiliation:
Technische Universität Dresden
Philipp Lukas Strietzel*
Affiliation:
Technische Universität Dresden
*
*Postal address: Technische Universität Dresden, Institut für Mathematische Stochastik, Helmholtzstraße 10, 01069 Dresden, Germany
*Postal address: Technische Universität Dresden, Institut für Mathematische Stochastik, Helmholtzstraße 10, 01069 Dresden, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

The existence of moments of first downward passage times of a spectrally negative Lévy process is governed by the general dynamics of the Lévy process, i.e. whether it is drifting to 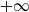$+\infty$ 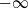, $-\infty$ , or oscillating. Whenever the Lévy process drifts to 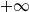$+\infty$ , we prove that the $\kappa$ th moment of the first passage time (conditioned to be finite) exists if and only if the 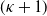$(\kappa+1)$ th moment of the Lévy jump measure exists. This generalizes a result shown earlier by Delbaen for Cramér–Lundberg risk processes. Whenever the Lévy process drifts to 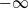$-\infty$ , we prove that all moments of the first passage time exist, while for an oscillating Lévy process we derive conditions for non-existence of the moments, and in particular we show that no integer moments exist.

Keywords

Conjugate subordinatorCramér–Lundberg risk processexit timefluctuation theoryfirst hitting timefractional calculusmomentsruin theoryspectrally negative Lévy processsubordinatortime to ruin

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes 60G40: Stopping times; optimal stopping problems; gambling theory
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 2 , June 2023 , pp. 452 - 464
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aurzada, F., Iksanov, A. and Meiners, M. (2015). Exponential moments of first passage times and related quantities for Lévy processes. Math. Nachr. 288, 1921–1938.CrossRefGoogle Scholar
Avram, F., Grahovac, D. and Vardar-Acar, C. (2020). The W, Z scale functions kit for first passage problems of spectrally negative Lévy processes, and applications to control problems. ESAIM Prob. Statist. 24, 454–525.CrossRefGoogle Scholar
Delbaen, F. (1990). A remark on the moments of ruin time in classical risk theory. Insurance Math. Econom. 9, 121–126.CrossRefGoogle Scholar
Doney, R. A. (1991). Hitting probabilities for spectrally positive Lévy processes. J. London Math. Soc. 44, 566–576.CrossRefGoogle Scholar
Doney, R. A. (2007). Fluctuation Theory for Lévy processes (Lect. Notes Math. 1897). Springer, New York.Google Scholar
Johnson, W. P. (2002). The curious history of Faà di Bruno’s formula. Amer. Math. Monthly 109, 217–234.Google Scholar
Kuznetsov, A., Kyprianou, A. E., Pardo, J. C. and Watson, A. R. (2014). The hitting time of zero for a stable process. Electron. J. Prob. 19, 1–26.CrossRefGoogle Scholar
Kuznetsov, A., Kyprianou, A. E. and Rivero, V. (2013). The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II, eds S. Cohen, A. Kuznetsov, A. E. Kyprianou and V. Rivero (Lect. Notes Math. 2061). Springer, New York, pp. 97–186.Google Scholar
Kyprianou, A. E. (2014). Fluctuations of Lévy processes with Applications, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Kyprianou, A. and Rivero, V. (2008). Special, conjugate and complete scale functions for spectrally negative Lévy processes. Electron. J. Prob. 13, 1672–1701.CrossRefGoogle Scholar
Peskir, G. (2008). The law of the hitting times to points by a stable Lévy process with no negative jumps. Electron. Commun. Prob. 13, 653–659.CrossRefGoogle Scholar
Rogers, L. C. G. and Williams, D. (2000). Diffusions, Markov Processes and Martingales, Vol 1, 2nd edn. Cambridge University Press.Google Scholar
Rudin, W. (1987). Real and Complex Analysis, 3rd edn. McGraw-Hill, New York.Google Scholar
Samko, S. G., Kilbas, A. A. and Marichev, O. I. (1993). Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Newark, NJ.Google Scholar
Sato, K. (2013). Lévy Processes and Infinitely Divisible Distributions, 2nd edn. Cambridge University Press.Google Scholar
Schilling, R. L., Song, R. and Vondracek, Z. (2012). Bernstein Functions: Theory and Applications, 2nd edn. De Gruyter, Berlin.CrossRefGoogle Scholar
Simon, T. (2011). Hitting densities for spectrally positive stable processes. Stochastics 83, 203–214.CrossRefGoogle Scholar
Uchaikin, V. V. (2013). Fractional Derivatives for Physicists and Engineers, Vol. I. Springer, New York.CrossRefGoogle Scholar
Wolfe, S. J. (1975). On moments of probability distribution functions. In Fractional Calculus and its Applications, ed B. Ross (Lect. Notes Math. 457). Springer, New York, pp. 306–316.CrossRefGoogle Scholar