Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T16:50:14.200Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal stopping on trajectories and the ballot problem

Part of: Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Mitsushi Tamaki
Mitsushi Tamaki*
Affiliation:
Aichi University
*
∗ Postal address: Department of Business Administration, Aichi University, Nagoya Campus, 370 Kurozasa Miyoshi, Nishikamo, Aichi 470–0296, Japan. Email address: tamaki@vega.aichi-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

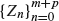An urn contains m minus balls and p plus balls, and we draw balls from this urn one at a time randomly without replacement until we wish to stop. Let Pn and Mn denote the respective numbers of plus balls and minus balls drawn by time n and define Z0 = 0, Zn = Pn - Mn, 1 ≤ n ≤ m + p. The main problem of this paper is to stop with maximum probability on the maximum of the trajectory formed by . This problem is closely related to the celebrated ballot problem, so that we obtain some identities concerning the ballot problem and then derive the optimal stopping rule explicitly. Some related modifications are also studied.

Keywords

Dynamic programmingOLA policyurn samplingBrownian bridgeodds theorem

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 38 , Issue 4 , December 2001 , pp. 946 - 959
Copyright
Copyright © by the Applied Probability Trust 2001 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boyce, W. M. (1970). Stopping rules for selling bonds. Bell J. Econom. Manag. Sci. 1, 27–53.CrossRefGoogle Scholar
Boyce, W. M. (1973). On a simple optimal stopping problem. Discrete Math. 5, 297–312.CrossRefGoogle Scholar
Bruss, F. T. (2000). Sum the odds to one and stop. Ann. Prob. 28, 1384–1391.CrossRefGoogle Scholar
Bruss, F. T., and Paindaveine, D. (2000). Selecting a sequence of last successes in independent trials. J. Appl. Prob. 37, 389–399.CrossRefGoogle Scholar
Chen, W., and Starr, N. (1980). Optimal stopping in an urn. Ann. Prob. 8, 451–464.CrossRefGoogle Scholar
Chow, Y. S., Robbins, H., and Siegmund, D. (1971). Great Expectations. Houghton-Mifflin, Boston.Google Scholar
Delbaen, F., and Haezendonck, J. (1985). Inversed martingale in risk theory. Insurance Math. Econom. 4, 201–206.CrossRefGoogle Scholar
Grimmett, G. R., and Stirzaker, D. R. (1992). Probability and Random Processes. Oxford University Press.Google Scholar
Karlin, S., and Taylor, H. M. (1981). A Second Course in Stochastic Processes. Academic Press, Orlando, FL.Google Scholar
Ross, S. M. (1983). Introduction to Stochastic Dynamic Programming. Academic Press, Orlando, FL.Google Scholar
Sakaguchi, M. (1998). ‘Secretary’ problems and their related areas. J. Econom. Manag. 42, 85–137 (in Japanese).Google Scholar
Shepp, L. A. (1969). Explicit solutions to some problems of optimal stopping. Ann. Math. Statist. 40, 993–1010.CrossRefGoogle Scholar