Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Stadje, Wolfgang
and
Zuckerman, Dror
1990.
Optimal strategies for some repair replacement models.
Advances in Applied Probability,
Vol. 22,
Issue. 3,
p.
641.
Kijima, Masaaki
and
Nakagawa, Toshio
1991.
A cumulative damage shock model with imperfect preventive maintenance.
Naval Research Logistics,
Vol. 38,
Issue. 2,
p.
145.
Stadje, Wolfgang
and
Zuckerman, Dror
1991.
Optimal maintenance strategies for repairable systems with general degree of repair.
Journal of Applied Probability,
Vol. 28,
Issue. 02,
p.
384.
Yeh, Lam
1991.
An optimal repairable replacement model for deteriorating systems.
Journal of Applied Probability,
Vol. 28,
Issue. 04,
p.
843.
LAM, YEH
1992.
Optimal policy for a general repair replacement model: discounted reward case.
Communications in Statistics. Stochastic Models,
Vol. 8,
Issue. 2,
p.
245.
Kijima, Masaaki
and
Nakagawa, Toshio
1992.
Replacement policies of a shock model with imperfect preventive maintenance.
European Journal of Operational Research,
Vol. 57,
Issue. 1,
p.
100.
Stadje, Wolfgang
and
Zuckerman, Dror
1992.
Optimal repair policies with general degree of repair in two maintenance models.
Operations Research Letters,
Vol. 11,
Issue. 2,
p.
77.
Finkelstein, M.S.
1993.
On some models of general repair.
Microelectronics Reliability,
Vol. 33,
Issue. 5,
p.
663.
Rangan, A.
and
Sarada, G.
1993.
Some results on the life distribution properties of systems subject to shocks and general repair.
Microelectronics Reliability,
Vol. 33,
Issue. 1,
p.
1.
Ebrahimi, Nader
1993.
Modeling of repairable systems.
Advances in Applied Probability,
Vol. 25,
Issue. 04,
p.
926.
Finkelstein, M.S.
1993.
A scale model of general repair.
Microelectronics Reliability,
Vol. 33,
Issue. 1,
p.
41.
Presnell, Brett
Hollander, Myles
and
Sethuraman, Jayaram
1994.
Testing the Minimal Repair Assumption in an Imperfect Repair Model.
Journal of the American Statistical Association,
Vol. 89,
Issue. 425,
p.
289.
Zhao, M.
1994.
Availability for repairable components and series systems.
IEEE Transactions on Reliability,
Vol. 43,
Issue. 2,
p.
329.
Douer, Nir
and
Yechiali, Uri
1994.
Optimal repair and replacement in markovian systems.
Communications in Statistics. Stochastic Models,
Vol. 10,
Issue. 1,
p.
253.
Guo, R.
and
Love, C. E.
1994.
Simulating nonhomogeneous poisson processes with proportional intensities.
Naval Research Logistics,
Vol. 41,
Issue. 4,
p.
507.
Love, C. E.
and
Guo, R.
1994.
Simulation strategies to identify the failure parameters of repairable systems under the influence of general repair.
Quality and Reliability Engineering International,
Vol. 10,
Issue. 1,
p.
37.
Shaked, Moshe
George Shanthikumar, J.
and
Benigno Valdez-Torres, Jose
1995.
Discrete hazard rate functions.
Computers & Operations Research,
Vol. 22,
Issue. 4,
p.
391.
Liu, Xiao-Gao
Makis, Viliam
and
Jardine, Andrew K. S.
1995.
A replacement model with overhauls and repairs.
Naval Research Logistics,
Vol. 42,
Issue. 7,
p.
1063.
WANG, HONGZHOU
and
PHAM, HOANG
1996.
Optimal maintenance policies for several imperfect repair models.
International Journal of Systems Science,
Vol. 27,
Issue. 6,
p.
543.
WANG, HONGZHOU
and
PHAM, HOANG
1996.
A quasi renewal process and its applications in imperfect maintenance.
International Journal of Systems Science,
Vol. 27,
Issue. 10,
p.
1055.
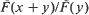 where
where 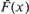 is the survival function of the failure-time of a new system. A general repair is represented as a sequence of random variables An taking a value between 0 and 1, where An denotes the degree of the nth repair. For the extremal values 0 and 1, An = 1 means a minimal repair and An= 0 a perfect repair. Two models are constructed depending on how the repair affects the virtual age process: Vn = Vn – 1+ AnXn as Model 1 and Vn = An (Vn – 1 + Xn ) as Model II. Various monotonicity properties of the process with respect to stochastic orderings of general repairs are obtained. Using a result, an upper bound for E[Sn ] when a general repair is used is derived.
is the survival function of the failure-time of a new system. A general repair is represented as a sequence of random variables An taking a value between 0 and 1, where An denotes the degree of the nth repair. For the extremal values 0 and 1, An = 1 means a minimal repair and An= 0 a perfect repair. Two models are constructed depending on how the repair affects the virtual age process: Vn = Vn – 1+ AnXn as Model 1 and Vn = An (Vn – 1 + Xn ) as Model II. Various monotonicity properties of the process with respect to stochastic orderings of general repairs are obtained. Using a result, an upper bound for E[Sn ] when a general repair is used is derived.
