Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-28T11:41:32.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Time-convergent random matrices from mean-field pinned interacting eigenvalues

Published online by Cambridge University Press:  18 November 2022

Levent Ali Mengütürk Open the ORCID record for Levent Ali Mengütürk [Opens in a new window]
Levent Ali Mengütürk*
Affiliation:
University College London
*
*Postal address: Department of Mathematics, University College London, London WC1E 6BT, United Kingdom. Email address: ucaheng@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a multivariate system over a finite lifespan represented by a Hermitian-valued random matrix process whose eigenvalues (i) interact in a mean-field way and (ii) converge to their weighted ensemble average at their terminal time. We prove that such a system is guaranteed to converge in time to the identity matrix that is scaled by a Gaussian random variable whose variance is inversely proportional to the dimension of the matrix. As the size of the system grows asymptotically, the eigenvalues tend to mutually independent diffusions that converge to zero at their terminal time, a Brownian bridge being the archetypal example. Unlike commonly studied random matrices that have non-colliding eigenvalues, the proposed eigenvalues of the given system here may collide. We provide the dynamics of the eigenvalue gap matrix, which is a random skew-symmetric matrix that converges in time to the 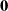$\textbf{0}$ matrix. Our framework can be applied in producing mean-field interacting counterparts of stochastic quantum reduction models for which the convergence points are determined with respect to the average state of the entire composite system.

Keywords

Mean-field interacting systemspinned diffusionsquantum reductionrandom matrix
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 2 , June 2023 , pp. 394 - 417
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, M., Delépine, J. and van Moerbeke, P. (2009). Dyson’s nonintersecting Brownian motions with a few outliers. Commun. Pure Appl. Math. 62, 334–395.CrossRefGoogle Scholar
Adler, M., Ferrari, P. L. and van Moerbeke, P. (2010). Airy processes with wanderers and new universality classes. Ann. Prob. 38, 714–769.CrossRefGoogle Scholar
Adler, M. and van Moerbeke, P. (2005). PDEs for the joint distributions of the Dyson, Airy and Sine Processes. Ann. Prob. 33, 1326–1361.CrossRefGoogle Scholar
Adler, M., van Moerbeke, P. and Wang, D. (2013). Random matrix minor processes related to percolation theory. Random Matrices Theory Appl. 2, article no. 1350008.CrossRefGoogle Scholar
Adler, S. L., Brody, D. C., Brun, T. A. and Hughston, L. P. (2001). Martingale models for quantum state reduction. J. Phys. A 34, article no. 8795.CrossRefGoogle Scholar
Adler, S. L. and Horwitz, L. P. (2000). Structure and properties of Hughston’s stochastic extension of the Schrödinger equation. J. Math. Phys. 41, article no. 2485.CrossRefGoogle Scholar
Akemann, G. (2007). Matrix models and QCD with chemical potential. Internat. J. Mod. Phys. A 22, 1077–1122.CrossRefGoogle Scholar
Bahcall, S. R. (1996). Random matrix model for superconductors in a magnetic field. Phys. Rev. Lett. 77, article no. 5276.CrossRefGoogle Scholar
Barczy, M. and Kern, P. (2011). General $\alpha$ -Wiener bridges. Commun. Stoch. Anal. 5, 585–608.Google Scholar
Barczy, M. and Pap, G. (2010). $\alpha$ -Wiener bridges: singularity of induced measures and sample path properties. Stoch. Anal. Appl. 28, 447–466.CrossRefGoogle Scholar
Beenakker, C. W. J. (1997). Random-matrix theory of quantum transport. Rev. Mod. Phys. 69, article no. 731.CrossRefGoogle Scholar
Bhadola, P. and Deo, N. (2015). Study of RNA structures with a connection to random matrix theory. Chaos Solitons Fractals 81, 542–550.CrossRefGoogle Scholar
Bleher, P. M. and Kuijlaars, A. B. J. (2004). Large n limit of Gaussian random matrices with external source, Part I. Commun. Math. Phys. 252, 43–76.CrossRefGoogle Scholar
Bohigas, O., Giannoni, M. J. and Schmit, C. (1984). Characterization of chaotic quantum spectra and universality of level fluctuation laws. Phys. Rev. Lett. 52, article no. 1.CrossRefGoogle Scholar
Brézin, E. and Hikami, S. (1998). Level spacing of random matrices in an external source. Phys. Rev. E 58, 7176–7185.CrossRefGoogle Scholar
Brézin, E. and Hikami, S. (1998). Universal singularity at the closure of a gap in a random matrix theory. Phys. Rev. E 57, 4140–4149.CrossRefGoogle Scholar
Brody, D. C. and Hughston, L. P. (2005). Finite-time stochastic reduction models. J. Math. Phys. 46, article no. 082101.CrossRefGoogle Scholar
Brody, D. C. and Hughston, L. P. (2006). Quantum noise and stochastic reduction. J. Phys. A 39, article no. 833.CrossRefGoogle Scholar
Bru, M.-F. (1989). Diffusions of perturbed principal component analysis. J. Multivariate Anal. 29, 127–136.CrossRefGoogle Scholar
Bru, M.-F. (1991). Wishart processes. J. Theoret. Prob. 4, 725–751.CrossRefGoogle Scholar
Carmona, R. A., Fouque, J. P. and Sun, L. H. (2015). Mean field games and systemic risk. Commun. Math. Sci. 13, 911–933.CrossRefGoogle Scholar
Corwin, I. and Hammond, A. (2014). Brownian Gibbs property for Airy line ensembles. Invent. Math. 195, 441–508.CrossRefGoogle Scholar
Dyson, F. J. (1962). A Brownian-motion model for the eigenvalues of a random matrix. J. Math. Phys. 3, article no. 1191.CrossRefGoogle Scholar
García del Molino, L. C., Pakdaman, K., Touboul, J. and Wainrib, G. (2013). Synchronization in random balanced networks. Phys. Rev. E 88, article no. 042824.CrossRefGoogle ScholarPubMed
Gisin, N. and Percival, I. C. (1992). The quantum-state diffusion model applied to open systems. J. Phys. A 25, article no. 5677.CrossRefGoogle Scholar
Grabiner, D. J. (1999). Brownian motion in a Weyl chamber, non-colliding particles, and random matrices. Ann. Inst. H. Poincaré Prob. Statist. 35, 177–204.CrossRefGoogle Scholar
Guhr, T., Müller-Groeling, A. and Weidenmüller, H. A. (1998). Random-matrix theories in quantum physics: common concepts. Phys. Reports 299, 189–425.CrossRefGoogle Scholar
Haake, F. (2001). Quantum Signatures of Chaos. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Hildebrandt, F. and Rœlly, S. (2020). Pinned diffusions and Markov bridges. J. Theoret. Prob. 33, 906–917.CrossRefGoogle Scholar
Hughes, C. P., Keating, J. P. and O’Connell, N. (2000). Random matrix theory and the derivative of the Riemann zeta function. Proc. R. Soc. London A 456, 2611–2627.CrossRefGoogle Scholar
Hughston, L. P. (1996). Geometry of stochastic state vector reduction. Proc. R. Soc. London A 452, 953–979.CrossRefGoogle Scholar
Johansson, K. (2005). The arctic circle boundary and the Airy process. Ann. Prob. 33, 1–30.CrossRefGoogle Scholar
Katori, M. (2014). Determinantal martingales and noncolliding diffusion processes. Stoch. Process. Appl. 124, 3724–3768.CrossRefGoogle Scholar
Katori, M. and Tanemura, H. (2004). Symmetry of matrix-valued stochastic processes and noncolliding diffusion particle systems. J. Math. Phys. 45, article no. 3058.CrossRefGoogle Scholar
Keating, J. P. and Snaith, N. C. (2003). Random matrices and L-functions. J. Phys. A 36, article no. 2859.Google Scholar
Laloux, L., Cizeau, P., Bouchaud, J.-P. and Potters, M. (1999). Noise dressing of financial correlation matrices. Phys. Rev. Lett. 83, article no. 1467.CrossRefGoogle Scholar
Laloux, L., Cizeau, P., Potters, M. and Bouchaud, J.-P. (2000). Random matrix theory and financial correlations. Internat. J. Theoret. Appl. Finance 3, 391–397.CrossRefGoogle Scholar
Li, X.-M. (2018). Generalised Brownian bridges: examples. Markov Process. Relat. Fields 24, 151–163.Google Scholar
Liechty, K. and Wang, D. (2016). Nonintersecting Brownian motions on the unit circle. Ann. Prob. 44, 1134–1211.CrossRefGoogle Scholar
Lillo, F. and Mantegna, R. N. (2005). Spectral density of the correlation matrix of factor models: a random matrix theory approach. Phys. Rev. E 72, article no. 016219.CrossRefGoogle ScholarPubMed
Mengütürk, L. A. (2016). Stochastic Schrödinger evolution over piecewise enlarged filtrations. J. Math. Phys. 57, article no. 032106.CrossRefGoogle Scholar
Mengütürk, L. A. (2021). A family of interacting particle systems pinned to their ensemble average. J. Phys. A. 54, article no. 435001.CrossRefGoogle Scholar
Mengütürk, L. A. and Mengütürk, M. C. (2020). Stochastic sequential reduction of commutative Hamiltonians. J. Math. Phys. 61, article no. 102104.CrossRefGoogle Scholar
Mezzadri, F. and Snaith, N. C. (2005). Recent Perspectives in Random Matrix Theory and Number Theory. Cambridge University Press.CrossRefGoogle Scholar
Muir, D. R. and Mrsic-Flogel, T. (2015). Eigenspectrum bounds for semirandom matrices with modular and spatial structure for neural networks. Phys. Rev. E 91, article no. 042808.CrossRefGoogle ScholarPubMed
Orland, H. and Zee, A. (2002). RNA folding and large N matrix theory. Nuclear Phys. B 620, 456–476.CrossRefGoogle Scholar
Prähofer, M. and Spohn, H. (2002). Scale invariance of the PNG droplet and the Airy process. J. Statist. Phys. 108, 1071–1106.CrossRefGoogle Scholar
Rajan, K. and Abbott, L. F. (2006). Eigenvalue spectra of random matrices for neural networks. Phys. Rev. Lett. 97, article no. 188104.CrossRefGoogle ScholarPubMed
Seligman, T. H., Verbaarschot, J. J. M. and Zirnbauer, M. R. (1984). Quantum spectra and transition from regular to chaotic classical motion. Phys. Rev. Lett. 53, article no. 215.CrossRefGoogle Scholar
Tracy, C. A. and Widom, H. (2006). The Pearcey process. Commun. Math. Phys. 263, 381–400.CrossRefGoogle Scholar
Verbaarschot, J. J. M. and Wettig, T. (2000). Random matrix theory and chiral symmetry in QCD. Annual Rev. Nuclear Particle Sci. 50, 343–410.CrossRefGoogle Scholar
Vernizzi, G. and Orland, H. (2015). Random matrix theory and ribonucleic acid (RNA) folding. In The Oxford Handbook of Random Matrix Theory, Oxford University Press, pp. 873–897.Google Scholar
Wigner, E. (1955). Characteristic vectors of bordered matrices with infinite dimensions. Ann. Math. 62, 548–564.CrossRefGoogle Scholar
Yamamoto, N. and Kanazawa, T. (2009). Dense QCD in a finite volume. Phys. Rev. Lett. 103, article no. 032001.CrossRefGoogle Scholar