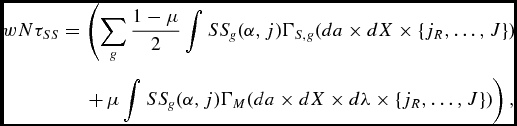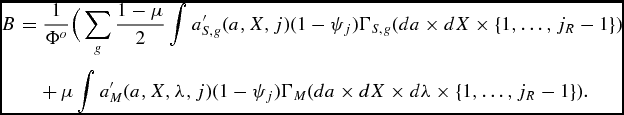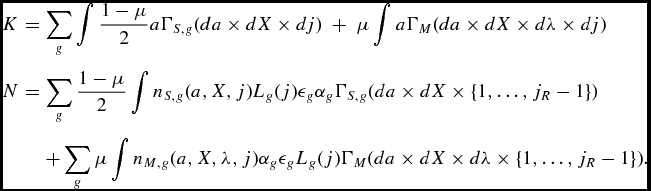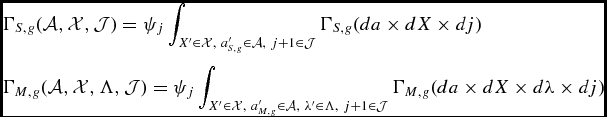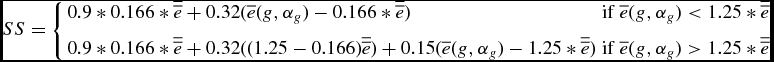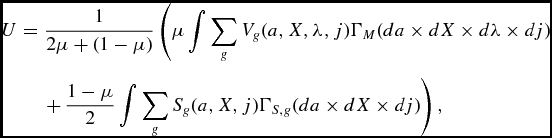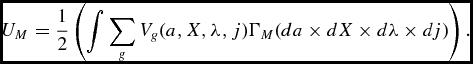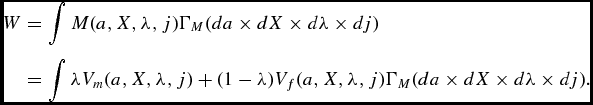1. INTRODUCTION
A recent literature in dynamic quantitative macroeconomics studying the effects of taxes in models of heterogeneous ‘bachelor’ households has found large welfare gains from positive capital taxation. For example, Conesa et al. (Reference Chiappori2009) illustrate that a high tax rate on capital is optimal for young households. Domeij and Heathcote (Reference Domeij and Heathcote2004) illustrate that from abolishing capital taxation only a small fraction of wealthy families benefit; at the same time large welfare losses are incurred by the rest of the population. Given that these conclusions are based on models where the well being of the household coincides with the well being of a single individual (typically the male household head) they represent a good laboratory to study the between household distributional effects, but ignore potentially important analogous effects at the intrahousehold level. It is, for example, conceivable that a policy change which sets capital taxes to zero or to a lower level than the current one, and raises labor taxes to balance the budget, on the one hand exacerbates the between household inequality and on the other makes the distribution of resources more equitable within households. In such cases it is obvious that a more explicit modeling of the intrahousehold decision making process is needed.
In this paper, we advocate that the empirical evidence presented in Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) concerning the joint decisions of couples in the US, supports this hypothesis. In particular, the evidence suggests that the following two assumptions are accurate with regards to the joint decision making process of married couples: First, wealth is a commonly held (pooled) resource within the family and second, (individual) labor income is not.
Based on this observation we investigate how tax policies, by influencing the relative importance of wealth and labor income on the household’s budget, may affect the intrahousehold allocation. In our experiment, we consider a policy change whereby the government eliminates capital taxation and raises labor taxes. Our key finding is that though this reform is likely to reduce intrahousehold inequality, in quantitative terms the effects from the policy change are rather small.
Our conclusion is drawn from a dynamic model where households (couples) live for several periods and make savings and labor supply decisions. They experience shocks to their labor income but are unable to fully hedge against them. Imperfect insurance derives from the fact that households can only trade in a single non-state-contingent bond and face borrowing constraints, but also because risk sharing is imperfect within the household. To model incomplete intrahousehold insurance, we add the following ingredient: We assume that the intrahousehold allocation is the outcome of a limited commitment contract whereby the two spouses maximize joint welfare according to a sharing rule which reflects their bargaining power. When the labor income of one spouse increases, the sharing rule allocates more resources to her, implying that the couple has to give up some risk sharing to satisfy a participation constraint. This feature of our model represents an extension of the collective model of the intrahousehold allocation (see for example Chiappori (Reference Chiappori1988, Reference Conesa, Carlos, Kitao and Krueger1992), Apps and Rees (Reference Apps and Rees1988), and Blundell and Etheridge (Reference Blundell and Etheridge2010)) to a dynamic economy. Similar models have been considered by Ligon et al. (Reference Ligon, Thomas and Worrall2000), Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) and Voena (Reference Voena2015).
As in Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) and Voena (Reference Voena2015), we assume that the bargaining power is determined by the value that the spouses get if they divorce. However, we do not allow divorces to occur in equilibrium. We impose this feature to our model because we wish give to it the possible best chance to yield a substantial welfare improvement from policy. Divorce is practically a breakdown of commitment, it limits the scope and the horizon over which intrahousehold insurance is relevant. Through ruling out divorce we can maximize the scope of risk sharing within the household.
In Section 2 of our paper, we present a simplified version of the theory (a two period model) that enables us to derive analytically the effect of the tax schedule on the intrahousehold allocation. Our results are as follows: First, lower capital taxes are shown to improve commitment and risk sharing. We show that as the household’s financial income increases, and a larger fraction of consumption is financed through wealth, the participation constraints are relaxed. Second, labor taxes have an ambiguous effect on intrahousehold risk sharing: On the one hand, higher labor taxes reduce intrahousehold inequality in income and therefore improve the household’s insurance possibilities, but through a second channel they tighten the participation constraint as they impoverish the household and make it more tempting to rebargain. The latter effect is more important when consumption and hours are complements in utility and at low levels of household savings.
In the quantitative life cycle model the balance of these effects varies across age cohorts. Young individuals typically have little wealth and therefore are more likely to be adversely affected by the rise in labor taxes. In contrast, middle aged and older households accumulate sufficient wealth and they can benefit from the change in both capital and labor taxes. However, at the same time, the fact that older households are wealthy (even before the elimination of capital taxes) means that the limited commitment friction is less severe for them; a policy which abolishes capital taxation and encourages further wealth accumulation does not improve welfare significantly. Overall, we find that there are only minor effects from the reform, on the intrahousehold allocation and on welfare. Rebargaining is less frequent, however the gains from risk sharing, measured in terms of lower consumption variability, are very modest.
1.1. Literature Review
This paper is related to several strands in the literature. First, there is considerable literature on the intrahousehold allocation within the so called collective framework (see for example Chiappori (Reference Chiappori1988, Reference Conesa, Carlos, Kitao and Krueger1992), Blundell and Etheridge (Reference Blundell and Etheridge2010)). Our assumption that family members do not pool labor income and that changes in income lead to an updating of the sharing rule is based on this literature.
Many papers have used the collective framework to investigate the properties of optimal taxation with particular focus on whether tax schedules should be different between men and women (for example Apps and Rees (Reference Apps and Rees1999), Apps and Rees (Reference Apps and Rees2011) and Alesina et al. (Reference Alesina, Ichino and Karabarbounis2011)). Though this analysis is clearly important and bears significant effects on the welfare of families, the models are typically static and therefore not suitable to analyze how the tax schedule affects the intertemporal behavior of couples. Our approach is to abstract from the complexities of the tax code and to summarize the institutions in a simple linear tax system. But since our model is dynamic, we add to the literature by formalizing how changes in taxes can affect welfare and the risk sharing arrangements of families.
As discussed previously, Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) provide the empirical evidence that wealth is a commonly held resource in the household. This evidence derives from the institutional framework governing divorces in the US (see also Voena (Reference Voena2015)). In particular, in 49 statesFootnote 1 of the US the division of assets during divorce is made either according to ‘community property law’, or according to ‘equitable property law’. In the case of ‘community property’ wealth is divided equally between the spouses. In the case of ‘equitable property’, wealth is divided ‘equitably’ which, as Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) go on to show, on average means that roughly 50% of the family’s wealth is given to each spouse. Based on this evidence, we impose the following features in our model: First, we treat wealth as a common state variable, meaning that we do not allow individuals to save in private accounts. Second, we treat as our benchmark the case where in divorce, each spouse gets 50% of all savings accumulated during the marriage. The second assumption is mainly a simplification of the environment, it enables us to derive analytical results (in Section 2) and simplifies our computations in the quantitative version of our model. The first assumption of jointly held savings can also be found in Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007), Guner et al. (Reference Guner, Kaygusuz and Ventura2012a, Reference Guner, Kaygusuz and Ventura2012b), and Cubeddu and Ríos-Rull (Reference Cubeddu and Ríos-Rull1997).
As discussed previously, dynamic life cycle models with intrahousehold bargaining have been recently considered by Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) and Voena (Reference Voena2015) (these theoretical frameworks are based on the infinite horizon model of Ligon et al. (Reference Ligon, Thomas and Worrall2000)). Our model is similar, however, the aspects of the intrahousehold allocation which we study are not the focus of either one of these papers. Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) study the effects of divorce on female labor supply. Voena (Reference Voena2015) studies the effect of changes in divorce laws on the intertemporal behavior of couples. Our results, which show that the impact of taxes is modest, should not be misconstrued to mean that studying the dynamic aspects of intrahousehold bargaining is not important; Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) and Voena (Reference Voena2015) both make a strong case to the contrary, focusing on different aspects of intrahousehold decisions than we do.
Ligon et al. (Reference Ligon, Thomas and Worrall2000) were the first to introduce storage to a dynamic model with limited commitment and with many risk averse (bachelor) households. They are interested in identifying cases in which access to storage may reduce risk sharing and welfare, assuming in their study that individuals can save in private accounts.Footnote 2 The different treatment of wealth in our model changes the predictions of the theory: When assets are commonly held, a higher wealth level can help mitigate the impact of shocks through improving commitment. This is not the case when household members save privately (in fact some examples given by Ligon et al. (Reference Ligon, Thomas and Worrall2000) demonstrate that the opposite is true).
Finally, in recent work Guner et al. (Reference Guner, Kaygusuz and Ventura2012a, Reference Guner, Kaygusuz and Ventura2012b) extend the macro literature on the optimal tax code to dual earner households. They document considerable efficiency gains from a reform which replaces joint filling with separate filling. These gains derive mainly from the response of female participation in the labor market. Our paper also presents a model with gender and marital status heterogeneity, but relative to Guner et al. (Reference Guner, Kaygusuz and Ventura2012a, Reference Guner, Kaygusuz and Ventura2012b) who consider a unitary model with no shocks to the labor income of individuals, our focus is on the effects of policy changes on the intrahousehold allocation and on risk sharing in a non-unitary model and in the presence of idiosyncratic income shocks.
The paper proceeds as follows: Section 2 studies the effects of taxes in the two period version of our theory. Section 3 presents the quantitative model and Section 4 summarizes the choice of parameters and functional forms. Section 5 discusses the results from the reform. A final section concludes.
2. INTRAHOUSEHOLD BARGAINING IN TWO PERIODS
This section presents a simplified version of our theory. It investigates the optimal behavior of a couple which consists of a male and a female spouse, lives for two periods, but faces the limited commitment problem only in period two. We derive analytical results that show the impact of the tax schedule on the intrahousehold decision making process.
We assume that preferences of both the male and the female spouse, are represented by the utility function u(cg t , lt g ) with the properties uc > 0, ul > 0, ucc < 0, ull < 0 ucl ⩽ 0, where cg t denotes consumption and lg t is leisure in period t = 1, 2. The superscript g denotes gender (g ∈ {m, f} (male, female)). Moreover, we assume each household member enjoys a constant utility flow ξ > 0 each period from being married. Following Voena (Reference Voena2015), we label ξ an affection parameter which (in our model) both spouses enjoy from being together. However, it should be understood that ξ may equally represent (in reduced form) a benefit accruing to married households from complementarity in the production of a home good which is not modeled here.Footnote 3 If the marriage breaks up we set ξ equal to zero.
Our analysis in this section is derived in partial equilibrium. That is to say, we state our results keeping prices (wages w and interest rate r) as exogenous and constant. Moreover, we assume that there is a government which levies capital and labor taxes denoted by τ K and τ N respectively. The household is born with a level of wealth a 0, and accumulates wealth in period 1 to finance consumption in t = 2. The household’s members are assumed to be identical initially in terms of productivity (normalized to unity for simplicity), but in period two each individual experiences a shock to their productivity endowment which alters their labor income potential. We let ε g be the productivity for the household member of gender g at t = 2. In each period, individuals have a time endowment, normalized to unity, which they split between leisure and work.
2.1. The Marital Contract
The limited commitment problem emerges from the fact that differences in productivity across the two members affect the relative bargaining power within the household, and thus affect the intrahousehold allocation. To characterize this allocation we assign a weight to the welfare of each individual in the household. We let λ m t = λ t be the share of the male spouse for t = 1, 2 and λ f t = 1 − λ t the analogous share of the female spouse. Note that λ t is a state variable in the household’s program.
The fact that the share is time dependent reflects the lack of commitment in the model. Consider the following example: Assume that we are in the beginning of period 2, and the household has brought forward from the previous period a value of the share
![]() $\lambda _1 =\frac{1}{2}$
. Now assume that each member of the household draws a value of idiosyncratic productivity and that the draws give ε
m
≫ ε
f
. In this case, it may be that the male spouse needs to be made better off and the sharing rule in period 2 needs to be updated so that λ2 > λ1. We will assume, following Ligon et al. (Reference Ligon, Thomas and Worrall2000) and Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007), that this new value λ2 must be such that the male spouse is as well-off as they would be if the marriage broke up. Analogously, if the female spouse has to be made better off then λ2 < λ1. If participation is not violated for either spouse, then λ2 = λ1.
$\lambda _1 =\frac{1}{2}$
. Now assume that each member of the household draws a value of idiosyncratic productivity and that the draws give ε
m
≫ ε
f
. In this case, it may be that the male spouse needs to be made better off and the sharing rule in period 2 needs to be updated so that λ2 > λ1. We will assume, following Ligon et al. (Reference Ligon, Thomas and Worrall2000) and Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007), that this new value λ2 must be such that the male spouse is as well-off as they would be if the marriage broke up. Analogously, if the female spouse has to be made better off then λ2 < λ1. If participation is not violated for either spouse, then λ2 = λ1.
The household contract may be represented as a joint program given these weights. We let M 1(a 0, λ1) be the value function that characterizes this joint maximization problem in period 1 and M 2(a 1, λ2, ε) the analogous function for t = 2. Notice that the latter has ε as an argument which now represents the vector of idiosyncratic productivities in period 2. To characterize the household’s program we solve backwards. Given the wealth endowment and the levels of productivity M 2(a 1, λ2, ε) is a solution to
 \begin{eqnarray}
M_2 ( a_1,\lambda _2, \epsilon ) &=&\max _{c_2^g,l_2^g} \lambda _2 u(c_2^m,l_2^m)+(1-\lambda _2) u(c_2^f,l_2^f) + \xi , \\
&&\text{Subject to:} \;\;\;\; l_2^g+n_2^g \le 1 \;\;\; \text{ for }\;\; g \in \lbrace m, f\rbrace \nonumber \\
\sum _g c_2^g &=& \sum _g n_2^g w (1-\tau _N) \epsilon _g + a_1 (1+r (1-\tau _K)). \nonumber
\end{eqnarray}
\begin{eqnarray}
M_2 ( a_1,\lambda _2, \epsilon ) &=&\max _{c_2^g,l_2^g} \lambda _2 u(c_2^m,l_2^m)+(1-\lambda _2) u(c_2^f,l_2^f) + \xi , \\
&&\text{Subject to:} \;\;\;\; l_2^g+n_2^g \le 1 \;\;\; \text{ for }\;\; g \in \lbrace m, f\rbrace \nonumber \\
\sum _g c_2^g &=& \sum _g n_2^g w (1-\tau _N) \epsilon _g + a_1 (1+r (1-\tau _K)). \nonumber
\end{eqnarray}
Moreover, M 1(a 0, λ1) solves the following Bellman equation:
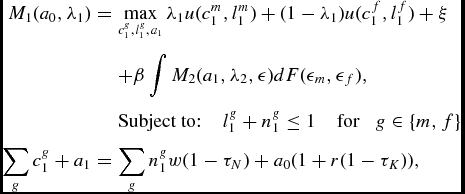 \begin{eqnarray}
M_1 ( a_0,\lambda _1) &=&\max _{c_1^g,l_1^g,a_1} \lambda _1 u(c_1^m,l_1^m)+(1-\lambda _1) u(c_1^f,l_1^f) + \xi\nonumber\\
&& + \beta \int M_2 ( a_1,\lambda _2, \epsilon ) d F(\epsilon _m ,\epsilon _f), \\
&&\text{Subject to:} \;\;\;\; l_1^g+n_1^g \le 1 \;\;\; \text{ for }\;\; g \in \lbrace m, f\rbrace \nonumber \\
\sum _g c_1^g +a_1 &=& \sum _g n_1^g w (1-\tau _N) + a_0 (1+r (1-\tau _K)), \nonumber
\end{eqnarray}
\begin{eqnarray}
M_1 ( a_0,\lambda _1) &=&\max _{c_1^g,l_1^g,a_1} \lambda _1 u(c_1^m,l_1^m)+(1-\lambda _1) u(c_1^f,l_1^f) + \xi\nonumber\\
&& + \beta \int M_2 ( a_1,\lambda _2, \epsilon ) d F(\epsilon _m ,\epsilon _f), \\
&&\text{Subject to:} \;\;\;\; l_1^g+n_1^g \le 1 \;\;\; \text{ for }\;\; g \in \lbrace m, f\rbrace \nonumber \\
\sum _g c_1^g +a_1 &=& \sum _g n_1^g w (1-\tau _N) + a_0 (1+r (1-\tau _K)), \nonumber
\end{eqnarray}
where β is the discount factor of the household, and F(ε m , ε f ) represents the joint cdf of productivity shocks in the family.
2.1.1. Rebargaining
To introduce formally the notion that the contract may be rebargained in period 2 we let Sg (Dg (a 1), ε g ) be the utility of the household member of gender g if the marriage breaks up in that period. Dg (a 1) is a division of family wealth in the event of divorce with the property ∑ g Dg (a 1) ⩽ a 1. The following participation constraints have to be satisfied in t = 2.Footnote 4
where Vg is the level of utility that individual g derives when program (1) is solved.
Now, consider the previous example where
![]() $\lambda _1 = \frac{1}{2}$
and ε
m
> >ε
f
and assume that
$\lambda _1 = \frac{1}{2}$
and ε
m
> >ε
f
and assume that
![]() $V_m(a_1, \frac{1}{2}, \epsilon ) < S_m (D_m(a_1), \epsilon _m)$
, in other words that the male spouse’s participation constraint is violated. Assume further that there is a range of values [λ
L
2, λ2
U
] with
$V_m(a_1, \frac{1}{2}, \epsilon ) < S_m (D_m(a_1), \epsilon _m)$
, in other words that the male spouse’s participation constraint is violated. Assume further that there is a range of values [λ
L
2, λ2
U
] with
![]() $\lambda _2^L>\frac{1}{2}$
so that (i) Vm
(a
1, λ
L
2, ε) = Sm
(Dm
(a
1), ε
m
) and Vf
(a
1, λ
L
2, ε) > Sf
(Df
(a
1), ε
f
) and (ii) Vf
(a
1, λ
U
2, ε) = Sf
(Df
(a
1), ε
f
) and Vm
(a
1, λ
U
2, ε) > Sm
(Dm
(a
1), ε
m
). Moreover, assume that for any λ2 ∈ (λ
L
2, λ
U
2) the participation constraints are slack.Footnote
5
$\lambda _2^L>\frac{1}{2}$
so that (i) Vm
(a
1, λ
L
2, ε) = Sm
(Dm
(a
1), ε
m
) and Vf
(a
1, λ
L
2, ε) > Sf
(Df
(a
1), ε
f
) and (ii) Vf
(a
1, λ
U
2, ε) = Sf
(Df
(a
1), ε
f
) and Vm
(a
1, λ
U
2, ε) > Sm
(Dm
(a
1), ε
m
). Moreover, assume that for any λ2 ∈ (λ
L
2, λ
U
2) the participation constraints are slack.Footnote
5
We need to find a value of λ2 within [λ L 2, λ2 U ] so that the both constraints are satisfied. We choose a value λ2 so that
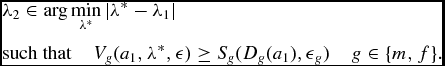 \begin{eqnarray}
&&\lambda _2 \in \text{arg} \min _{\lambda ^*} | \lambda ^* - \lambda _1 | \nonumber\\
&& \text{such that} \;\; \;\; V_g(a_1, \lambda ^*, \epsilon ) \ge S_g (D_g(a_1) ,\epsilon _g) \;\;\; \;g \in \lbrace m,f\rbrace .
\end{eqnarray}
\begin{eqnarray}
&&\lambda _2 \in \text{arg} \min _{\lambda ^*} | \lambda ^* - \lambda _1 | \nonumber\\
&& \text{such that} \;\; \;\; V_g(a_1, \lambda ^*, \epsilon ) \ge S_g (D_g(a_1) ,\epsilon _g) \;\;\; \;g \in \lbrace m,f\rbrace .
\end{eqnarray}
Note that (3) says that when there is a change in λ2 relative to λ1, this change is the minimum required to satisfy with equality the constraint which is violated. In terms of the previous example, we choose to set λ2 = λ L 2.
2.1.2. A representation with recursive contracts
It has been customary in the literature (see for example Cooley et al. (Reference Cooley, Marimon and Quadrini2004) and Kehoe and Perri (Reference Kehoe and Perri2002), among others) to solve dynamic limited commitment models using a Lagrangian formulation, then to apply the results of Marcet and Marimon (Reference Marcet and Marimon1994) to obtain the recursive representation of the program. It is useful to briefly illustrate that the above derivations are consistent with this approach, in particular the Bellman equations in (1) and (2) can be derived from the saddle point problem described in Marcet and Marimon (Reference Marcet and Marimon1994).
The maximization problem can be stated as follows:
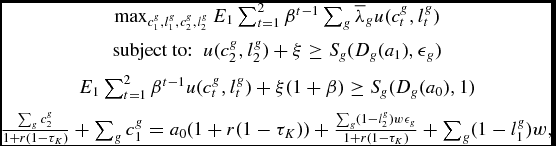 \begin{eqnarray*}
\begin{array}{c}
\max _{c_1^g,l_1^g,c_2^g,l_2^g} E_1 \sum _{t=1}^2 \beta ^{t-1} \sum _g \overline{\lambda }_g u(c_t^g,l_t^g) \\[6pt]
\text{subject to:} \;\; u(c_2^g,l_2^g)+ \xi \ge S_g (D_g(a_1), \epsilon _g) \\[6pt]
E_1 \sum _{t=1}^2 \beta ^{t-1} u(c_t^g,l_t^g) + \xi (1+\beta ) \ge S_g (D_g(a_0), 1) \\[6pt]
\frac{\sum _g c_2^g }{1+r(1-\tau _K)} +\sum _g c_1^g = a_0 (1+r(1-\tau _K)) + \frac{\sum _g (1-l_2^g) w \epsilon _g }{1+r(1-\tau _K)} + \sum _g (1-l_1^g) w,
\end{array}
\end{eqnarray*}
\begin{eqnarray*}
\begin{array}{c}
\max _{c_1^g,l_1^g,c_2^g,l_2^g} E_1 \sum _{t=1}^2 \beta ^{t-1} \sum _g \overline{\lambda }_g u(c_t^g,l_t^g) \\[6pt]
\text{subject to:} \;\; u(c_2^g,l_2^g)+ \xi \ge S_g (D_g(a_1), \epsilon _g) \\[6pt]
E_1 \sum _{t=1}^2 \beta ^{t-1} u(c_t^g,l_t^g) + \xi (1+\beta ) \ge S_g (D_g(a_0), 1) \\[6pt]
\frac{\sum _g c_2^g }{1+r(1-\tau _K)} +\sum _g c_1^g = a_0 (1+r(1-\tau _K)) + \frac{\sum _g (1-l_2^g) w \epsilon _g }{1+r(1-\tau _K)} + \sum _g (1-l_1^g) w,
\end{array}
\end{eqnarray*}
where the last equation is the intertemporal budget constraint of the household and a
1 = a
0(1 + r(1 − τ
K
)) + ∑
g
(1 − lg
1)w − ∑
g
cg
1 also has to be remembered to find the optimum.
![]() $\overline{\lambda }_g$
are constant weights satisfying
$\overline{\lambda }_g$
are constant weights satisfying
![]() $\frac{\overline{\lambda }_m}{\sum _g \overline{\lambda }_g }=\lambda _1$
from the previous definition of the sharing rule.Footnote
6
Moreover, notice that for completeness we have now included in the constraint set the two participation constraints in period 1, i.e. E
1∑2
t = 1β
t − 1
u(cg
t
, lt
g
) + ξ(1 + β) ⩾ Sg
(Dg
(a
0), 1), where Sg
(Dg
(a
0), 1) is the outside option in the first period. It is trivial to show that these constraints will not bind if for instance we set
$\frac{\overline{\lambda }_m}{\sum _g \overline{\lambda }_g }=\lambda _1$
from the previous definition of the sharing rule.Footnote
6
Moreover, notice that for completeness we have now included in the constraint set the two participation constraints in period 1, i.e. E
1∑2
t = 1β
t − 1
u(cg
t
, lt
g
) + ξ(1 + β) ⩾ Sg
(Dg
(a
0), 1), where Sg
(Dg
(a
0), 1) is the outside option in the first period. It is trivial to show that these constraints will not bind if for instance we set
![]() $\overline{\lambda }_m=\overline{\lambda }_f$
(because of ξ > 0).
$\overline{\lambda }_m=\overline{\lambda }_f$
(because of ξ > 0).
Define x t, g = 1 for t = 1 and x t, g = ε g , t = 2. The above program can be represented with the Lagrangian:
 \begin{eqnarray*}
L &=&E_1 \Bigg(\sum _{t=1}^2 \beta ^{t-1} \sum _g \Bigg (\overline{\lambda }_g u(c_t^g,l_t^g) + v_{t,g} \Bigg [\sum _{j=t}^2 \beta ^{j-1} (u(c_j^g,l_j^g)+ \xi )\nonumber\\
&&\qquad -\, S_g (D_g(a_{t-1}), x_{t,g})\Bigg ] \Bigg )\Bigg ) \\
&&+\, \phi \Bigg[ \frac{\sum _g c_2^g }{1+r(1-\tau _K)} +\sum _g c_1^g - a_0 (1+r(1-\tau _K))\nonumber\\
&&\qquad -\, \frac{\sum _g (1-l_2^g) w \epsilon _g }{1+r(1-\tau _K)} - \sum _g (1-l_1^g) w \Bigg],
\end{eqnarray*}
\begin{eqnarray*}
L &=&E_1 \Bigg(\sum _{t=1}^2 \beta ^{t-1} \sum _g \Bigg (\overline{\lambda }_g u(c_t^g,l_t^g) + v_{t,g} \Bigg [\sum _{j=t}^2 \beta ^{j-1} (u(c_j^g,l_j^g)+ \xi )\nonumber\\
&&\qquad -\, S_g (D_g(a_{t-1}), x_{t,g})\Bigg ] \Bigg )\Bigg ) \\
&&+\, \phi \Bigg[ \frac{\sum _g c_2^g }{1+r(1-\tau _K)} +\sum _g c_1^g - a_0 (1+r(1-\tau _K))\nonumber\\
&&\qquad -\, \frac{\sum _g (1-l_2^g) w \epsilon _g }{1+r(1-\tau _K)} - \sum _g (1-l_1^g) w \Bigg],
\end{eqnarray*}
where v t, g is the multiplier on the participation constraint of g at t. Rearranging this expression, we can write:
 \begin{eqnarray*}
L &=&E_1 \Bigg (\sum _{t=1}^2 \beta ^{t-1} \sum _g \Bigg ( ( \overline{\lambda }_g +\overline{v}_{t-1,g} +v_{t,g} ) u(c_t^g,l_t^g) + (\overline{v}_{t-1,g} +v_{t,g} ) \xi\nonumber\\
&&\qquad -\, v_{t,g} S_g (D_g(a_{t-1}), x_{t,g})\Bigg )\Bigg )\\
&& +\,\phi \Bigg[ \frac{\sum _g c_2^g }{1+r(1-\tau _K)} +\sum _g c_1^g - a_0 (1+r(1-\tau _K))\nonumber\\
&& \qquad-\, \frac{\sum _g (1-l_2^g) w \epsilon _g }{1+r(1-\tau _K)} - \sum _g (1-l_1^g) w \Bigg],
\end{eqnarray*}
\begin{eqnarray*}
L &=&E_1 \Bigg (\sum _{t=1}^2 \beta ^{t-1} \sum _g \Bigg ( ( \overline{\lambda }_g +\overline{v}_{t-1,g} +v_{t,g} ) u(c_t^g,l_t^g) + (\overline{v}_{t-1,g} +v_{t,g} ) \xi\nonumber\\
&&\qquad -\, v_{t,g} S_g (D_g(a_{t-1}), x_{t,g})\Bigg )\Bigg )\\
&& +\,\phi \Bigg[ \frac{\sum _g c_2^g }{1+r(1-\tau _K)} +\sum _g c_1^g - a_0 (1+r(1-\tau _K))\nonumber\\
&& \qquad-\, \frac{\sum _g (1-l_2^g) w \epsilon _g }{1+r(1-\tau _K)} - \sum _g (1-l_1^g) w \Bigg],
\end{eqnarray*}
where
![]() $\overline{v}_{t,g}=\overline{v}_{t-1,g} +v_{t,g}$
with
$\overline{v}_{t,g}=\overline{v}_{t-1,g} +v_{t,g}$
with
![]() $\overline{v}_{0,g}=0$
.
$\overline{v}_{0,g}=0$
.
Marcet and Marimon (Reference Marcet and Marimon1994) show that the above program defines a saddle point problem which can be resolved through finding a minimum with respect to v t, g (subject to v t, g ⩾ 0) and a maximum with respect to consumption and hours. This problem can also be represented recursively with the Bellman equation. For the sake of brevity, we omit this derivation.
Note that the first order conditions with respect to cg
t
give:
![]() $\frac{u_c(c_t^m,l_t^m)}{u_c(c_t^f,l_t^f)} = \frac{\overline{\lambda }_f+\overline{v}_{t,f}}{\overline{\lambda }_m+\overline{v}_{t,m}}$
. It is well known that in the presence of limited commitment the ratio of marginal utilities is not constant over time, it varies when the participation constraints bind. Now consider the problem at hand: Obviously we can set
$\frac{u_c(c_t^m,l_t^m)}{u_c(c_t^f,l_t^f)} = \frac{\overline{\lambda }_f+\overline{v}_{t,f}}{\overline{\lambda }_m+\overline{v}_{t,m}}$
. It is well known that in the presence of limited commitment the ratio of marginal utilities is not constant over time, it varies when the participation constraints bind. Now consider the problem at hand: Obviously we can set
![]() $\overline{v}_{0,g}=0$
(as the initial condition) and also
$\overline{v}_{0,g}=0$
(as the initial condition) and also
![]() $\overline{v}_{1,g} =0$
(since the period 1 constraints can be ignored). In period 2, we can have any of the following (i) v
2, m
> 0, v
2, f
= 0 (male constraint binds), (ii) v
2, m
= 0, v
2, f
> 0 (female constraint binds) or (iii) v
2, m
= 0, v
2, f
= 0 (both constraints are slack). This means that the
$\overline{v}_{1,g} =0$
(since the period 1 constraints can be ignored). In period 2, we can have any of the following (i) v
2, m
> 0, v
2, f
= 0 (male constraint binds), (ii) v
2, m
= 0, v
2, f
> 0 (female constraint binds) or (iii) v
2, m
= 0, v
2, f
= 0 (both constraints are slack). This means that the
![]() $\frac{u_c(c_t^m,l_t^m)}{u_c(c_t^f,l_t^f)}$
will either drop to
$\frac{u_c(c_t^m,l_t^m)}{u_c(c_t^f,l_t^f)}$
will either drop to
![]() $\frac{\overline{\lambda }_f}{\overline{\lambda }_m+\overline{v}_{t,m}}$
, increase to
$\frac{\overline{\lambda }_f}{\overline{\lambda }_m+\overline{v}_{t,m}}$
, increase to
![]() $\frac{\overline{\lambda }_f+\overline{v}_{t,f}}{\overline{\lambda }_m}$
or remain constant
$\frac{\overline{\lambda }_f+\overline{v}_{t,f}}{\overline{\lambda }_m}$
or remain constant
![]() $\frac{\overline{\lambda }_f}{\overline{\lambda }_m}$
. Moreover, based on the above it is obvious that the adjustments in the weight in cases (i) and (ii) are the minimum required so that a participation constraint just binds.Footnote
7
In other words, the optimal contract described in the previous subsection is essentially what we get if we apply the method of Marcet and Marimon (Reference Marcet and Marimon1994).Footnote
8
$\frac{\overline{\lambda }_f}{\overline{\lambda }_m}$
. Moreover, based on the above it is obvious that the adjustments in the weight in cases (i) and (ii) are the minimum required so that a participation constraint just binds.Footnote
7
In other words, the optimal contract described in the previous subsection is essentially what we get if we apply the method of Marcet and Marimon (Reference Marcet and Marimon1994).Footnote
8
2.2. The Effect of Taxes on Household Decision Making
We now illustrate how capital and labor taxes affect the properties of the sharing rule in period 2. We derive our results under the following assumptions: First, as is customary in the literature (see for example Conesa et al. (Reference Chiappori2009)), we assume that individual utility is of the following form:
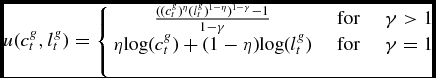 \begin{eqnarray*}
u(c_t^g,l_t^g)=\left\lbrace \begin{array}{ccc}\frac{((c_t^g)^{\eta } (l_t^g)^{1-\eta })^{1-\gamma }-1}{1-\gamma } &\quad \text{for} &\quad \gamma >1 \\
\eta \text{log}(c_t^g ) + ({1-\eta }) \text{log}(l_t^g ) &\quad \text{for}&\quad \gamma =1\\
\end{array} \right.
\end{eqnarray*}
\begin{eqnarray*}
u(c_t^g,l_t^g)=\left\lbrace \begin{array}{ccc}\frac{((c_t^g)^{\eta } (l_t^g)^{1-\eta })^{1-\gamma }-1}{1-\gamma } &\quad \text{for} &\quad \gamma >1 \\
\eta \text{log}(c_t^g ) + ({1-\eta }) \text{log}(l_t^g ) &\quad \text{for}&\quad \gamma =1\\
\end{array} \right.
\end{eqnarray*}
As we will later illustrate the exact specification of preferences (whether or not they are separable in consumption and leisure) has a significant impact on the effects of taxes in our model. We will therefore separately study the cases where γ = 1 and where γ > 1 in order to better highlight their properties. Second, for our baseline results we assume, as Mazzocco et al. (Reference Mazzocco, Ruiz and Yamaguchi2007) do, that divorce leads to an equal division of assets and therefore set
![]() $D_m(a_1) = D_f (a_1) = \frac{a_1}{2}$
. As discussed previously, this assumption follows from the empirical evidence. In the Appendix, we illustrate that our results go through under different specifications for divorce outcomes and divisions of assets.
$D_m(a_1) = D_f (a_1) = \frac{a_1}{2}$
. As discussed previously, this assumption follows from the empirical evidence. In the Appendix, we illustrate that our results go through under different specifications for divorce outcomes and divisions of assets.
2.2.1. Separable preferences
Let us first assume that γ equals one. Assume that we are in period 2 and let Ac
= (1 + r(1 − τ
K
))a
1 be the total financial income of the household brought forward from period one. It is trivial to show that the optimal consumption is cm
2 = λ2η(Ac
+ ∑
g
w(1 − τ
N
)ε
g
) and cf
2 = (1 − λ2)η(Ac
+ ∑
g
w(1 − τ
N
)ε
g
). Similarly, the optimal choice of leisure is given by:
![]() $l ^m_2= \lambda _2 (1-\eta ) \frac{ A_c + \sum _g w (1-\tau _N) \epsilon _g}{\epsilon _m w (1-\tau _N)}$
and
$l ^m_2= \lambda _2 (1-\eta ) \frac{ A_c + \sum _g w (1-\tau _N) \epsilon _g}{\epsilon _m w (1-\tau _N)}$
and
![]() $l ^f_2= (1- \lambda _2) (1-\eta ) \frac{ A_c + \sum _g w (1-\tau _N) \epsilon _g}{\epsilon _f w (1-\tau _N)}$
.
$l ^f_2= (1- \lambda _2) (1-\eta ) \frac{ A_c + \sum _g w (1-\tau _N) \epsilon _g}{\epsilon _f w (1-\tau _N)}$
.
To respect the participation constraint of each household member the allocation rule λ2 must satisfy the following conditions:
 \begin{eqnarray*}
&&\log \lambda _2^g + \eta \log \eta (A_c + w (1-\tau _N) (\epsilon _m+\epsilon _f))\nonumber\\
&&\quad +\, (1-\eta ) \log \eta \frac{(A_c + w (1-\tau _N) (\epsilon _m+\epsilon _f))}{\epsilon _g w (1-\tau _N)} \nonumber\\
&&\quad +\, \xi \ge\eta \log \eta \Bigg(\frac{A_c}{2} + w (1-\tau _N) \epsilon _g\Bigg) + (1-\eta ) \log \eta \frac{( \frac{A_c}{2} + w (1-\tau _N) \epsilon _g)}{\epsilon _g w (1-\tau _N)} ,\nonumber\\
&&\quad g \in \lbrace m,f \rbrace ,
\end{eqnarray*}
\begin{eqnarray*}
&&\log \lambda _2^g + \eta \log \eta (A_c + w (1-\tau _N) (\epsilon _m+\epsilon _f))\nonumber\\
&&\quad +\, (1-\eta ) \log \eta \frac{(A_c + w (1-\tau _N) (\epsilon _m+\epsilon _f))}{\epsilon _g w (1-\tau _N)} \nonumber\\
&&\quad +\, \xi \ge\eta \log \eta \Bigg(\frac{A_c}{2} + w (1-\tau _N) \epsilon _g\Bigg) + (1-\eta ) \log \eta \frac{( \frac{A_c}{2} + w (1-\tau _N) \epsilon _g)}{\epsilon _g w (1-\tau _N)} ,\nonumber\\
&&\quad g \in \lbrace m,f \rbrace ,
\end{eqnarray*}
where the capital tax τ K enters through Ac . Solving these conditions for λ2 we get
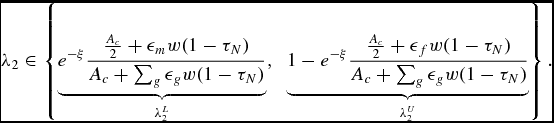 \begin{eqnarray}
\lambda _2 \in \left\lbrace \underbrace{ e^{-\xi } \frac{ \frac{A_c}{2}+\epsilon _m w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)}}_{ \lambda _2^L}, \;\; \underbrace{ 1-e^{-\xi } \frac{ \frac{A_c}{2}+\epsilon _f w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)} }_{ \lambda _2^U} \right\rbrace .
\end{eqnarray}
\begin{eqnarray}
\lambda _2 \in \left\lbrace \underbrace{ e^{-\xi } \frac{ \frac{A_c}{2}+\epsilon _m w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)}}_{ \lambda _2^L}, \;\; \underbrace{ 1-e^{-\xi } \frac{ \frac{A_c}{2}+\epsilon _f w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)} }_{ \lambda _2^U} \right\rbrace .
\end{eqnarray}
Expression (4) defines the upper and the lower bound we have previously seen. Given ε
f
and Ac
, there is a threshold
![]() $\underline{\epsilon }_m(A_c, \epsilon _f )$
such that if
$\underline{\epsilon }_m(A_c, \epsilon _f )$
such that if
![]() $\epsilon _m > \overline{\epsilon }_m(A_c, \epsilon _f)$
the contract updates λ2 to be equal to the lower bound in (4) (since in that case it holds that
$\epsilon _m > \overline{\epsilon }_m(A_c, \epsilon _f)$
the contract updates λ2 to be equal to the lower bound in (4) (since in that case it holds that
![]() $\lambda _2^L> \frac{1}{2}$
). Similarly, there is another threshold
$\lambda _2^L> \frac{1}{2}$
). Similarly, there is another threshold
![]() $\underline{\epsilon }_m (A_c, \epsilon _f)$
such that for an ε
m
below this threshold the new contract gives λ2 equal to
$\underline{\epsilon }_m (A_c, \epsilon _f)$
such that for an ε
m
below this threshold the new contract gives λ2 equal to
![]() $\lambda _2^U < \frac{1}{2}$
. Notice that when ξ = 0, λ
L
2 equals λ
U
2. In this case, the intrahousehold allocation is such that in every state a household member’s share on total resources is essentially what they would get as a single. Being together is therefore no different than being single when ξ = 0.Footnote
9
$\lambda _2^U < \frac{1}{2}$
. Notice that when ξ = 0, λ
L
2 equals λ
U
2. In this case, the intrahousehold allocation is such that in every state a household member’s share on total resources is essentially what they would get as a single. Being together is therefore no different than being single when ξ = 0.Footnote
9
Labor Taxes. Given the intrahousehold allocation, we can derive the effect of changes in the level of labor taxes τ N and capital taxes τ K . First, consider that labor taxes fall, i.e. (1 − τ N ) increases. We can write
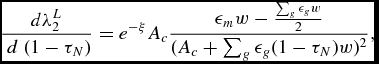 \begin{equation}
\frac{d \lambda _2^L}{\ d \; (1-\tau _N) } = e^{-\xi } A_c \frac{ \epsilon _m w- \frac{\sum _g \epsilon _g w}{2} }{ (A_c +\sum _g \epsilon _g (1-\tau _N) w) ^2},
\end{equation}
\begin{equation}
\frac{d \lambda _2^L}{\ d \; (1-\tau _N) } = e^{-\xi } A_c \frac{ \epsilon _m w- \frac{\sum _g \epsilon _g w}{2} }{ (A_c +\sum _g \epsilon _g (1-\tau _N) w) ^2},
\end{equation}
Consider the case where
![]() $\epsilon _m > \overline{\epsilon }_m (A_c, \epsilon _f)$
. It must be that
$\epsilon _m > \overline{\epsilon }_m (A_c, \epsilon _f)$
. It must be that
![]() $\lambda _2 = \lambda _2^L>\frac{1}{2}$
, i.e. the male spouse’s weight needs to increase. The derivative (5) is positive, meaning that a reduction in the level of labor taxes increases λ
L
2, this makes the change in λ2 relative to λ1 even greater. Therefore, a drop in the tax rate reduces risk sharing within the household; in those states where the male labor income is high, the husband’s consumption share increases even more than if labor taxation is high.
$\lambda _2 = \lambda _2^L>\frac{1}{2}$
, i.e. the male spouse’s weight needs to increase. The derivative (5) is positive, meaning that a reduction in the level of labor taxes increases λ
L
2, this makes the change in λ2 relative to λ1 even greater. Therefore, a drop in the tax rate reduces risk sharing within the household; in those states where the male labor income is high, the husband’s consumption share increases even more than if labor taxation is high.
A similar argument can be made for the case where ε f ≫ ε m , i.e. when the upper bound λ U 2 is relevant. We summarize the result in the following proposition:
Proposition 1. Assume that the household’s financial income is positive ( Ac > 0). A reduction in labor income taxes reduces insurance within the household under log-separable preferences. The household sharing rule and thus the intrahousehold allocation become more responsive to changes in idiosyncratic productivity. Footnote 10
The intuition for this result is as follows: First, note that inequality in labor income is the root of the limited commitment problem in the model. Therefore, a policy reform which lowers the tax rate, exacerbates the intrahousehold income inequality and exacerbates the limited commitment problem. This effect is captured by the fact that the partial derivative
![]() $\frac{d \lambda _2^L}{\ d \; (1-\tau _N) }$
is positive, at least insofar as financial income is positive. Second, to understand why wealth is important notice that the labor taxes, besides making the distribution of the net labor income more equitable in the household, they also impoverish the household by reducing its disposable income. When the household has fewer resources the temptation to renege on the marital contract is stronger, this makes the limited commitment problem more severe. This effect under log-separable utility is relevant only insofar as Ac
< 0. However, for the case where γ > 1 the effect will be present even if the household has savings rather than debt. We will return to this feature of the model in a subsequent paragraph.
$\frac{d \lambda _2^L}{\ d \; (1-\tau _N) }$
is positive, at least insofar as financial income is positive. Second, to understand why wealth is important notice that the labor taxes, besides making the distribution of the net labor income more equitable in the household, they also impoverish the household by reducing its disposable income. When the household has fewer resources the temptation to renege on the marital contract is stronger, this makes the limited commitment problem more severe. This effect under log-separable utility is relevant only insofar as Ac
< 0. However, for the case where γ > 1 the effect will be present even if the household has savings rather than debt. We will return to this feature of the model in a subsequent paragraph.
Capital Taxes. We now derive the impact of wealth and capital taxation on the participation constraints. For brevity, consider the partial derivative of λ L 2 with respect to 1 − τ K :
 \begin{eqnarray}
\frac{d \lambda _2^L}{\ d \;(1- \tau _K)} = e^{-\xi } (1-\tau _N) \frac{ \frac{\sum _g \epsilon _g w}{2} - \epsilon _m w }{ (A_c +\sum _g \epsilon _g (1-\tau _N) w) ^2} a_1 r,
\end{eqnarray}
\begin{eqnarray}
\frac{d \lambda _2^L}{\ d \;(1- \tau _K)} = e^{-\xi } (1-\tau _N) \frac{ \frac{\sum _g \epsilon _g w}{2} - \epsilon _m w }{ (A_c +\sum _g \epsilon _g (1-\tau _N) w) ^2} a_1 r,
\end{eqnarray}
Notice that if ε
m
> ε
f
(male participation constraint may bind and λ
L
2 is relevant), then (6) gives
![]() $\frac{d \lambda _2^L}{\ d \; (1- \tau _K)} <0$
. This implies that a rise in asset income increases intrahousehold household risk sharing.
$\frac{d \lambda _2^L}{\ d \; (1- \tau _K)} <0$
. This implies that a rise in asset income increases intrahousehold household risk sharing.
Proposition 2. Lower capital taxes improve insurance under log-log preferences. The household sharing rule and thus intrahousehold allocation are less responsive to changes in labor income.
Several remarks are in order: First, equations (5) and (6) reveal that the effects of taxes depend on the wealth level of the household. The higher wealth is, the bigger the impact of the tax schedule on the intrahousehold allocation. This implies that richer households are more likely to benefit from a change in policy which eliminates capital taxes. However, for these households the limited commitment friction is less severe, precisely because wealth is high. This property is key to understanding the modest effects from the reform that we uncover in our quantitative exercise in the next sections.
Second, it is important to emphasize that the improvement in intrahousehold insurance identified in Proposition 2 does not stem from the standard role of assets as a buffer against income shocks (e.g. precautionary savings) but is related to the division of resources in the household and the notion that wealth, in contrast to labor income, is a common resource for the household. This channel is new to the literature.
2.2.2. Non-separable preferences
We now derive the impact of changes in taxation assuming γ > 1. We can write the participation constraints as follows:
 \begin{eqnarray*}
&&\left( s_g (\lambda _2, \epsilon )\frac{A_c + w (1-\tau _N) (\epsilon _m+\epsilon _f) }{((w (1-\tau _N) \epsilon _g) )^{1-\eta }} \right)^{1-\gamma } \frac{\chi }{1-\gamma }\nonumber\\
&&\quad +\, \xi \ge \left(\frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _g }{(w (1-\tau _N) \epsilon _g)^{1-\eta }} \right)^{1-\gamma } \frac{\chi }{1-\gamma },
\end{eqnarray*}
\begin{eqnarray*}
&&\left( s_g (\lambda _2, \epsilon )\frac{A_c + w (1-\tau _N) (\epsilon _m+\epsilon _f) }{((w (1-\tau _N) \epsilon _g) )^{1-\eta }} \right)^{1-\gamma } \frac{\chi }{1-\gamma }\nonumber\\
&&\quad +\, \xi \ge \left(\frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _g }{(w (1-\tau _N) \epsilon _g)^{1-\eta }} \right)^{1-\gamma } \frac{\chi }{1-\gamma },
\end{eqnarray*}
where χ = (ηη(1 − η)1 − η)1 − γ and
![]() $s_m(\lambda _2 ,\epsilon ) = (\frac{\lambda _2}{1-\lambda _2} ( \frac{\epsilon _f}{\epsilon _m})^{(1-\eta ) (1-\gamma )} )^{1/\gamma }-1$
, sf
(λ2, ε) = 1 − sm
(λ2, ε). We show in the Appendix that the sign of the effect of a rise in 1 − τ
N
on λ
L
2 is inversely related to the sign of the following expression:
$s_m(\lambda _2 ,\epsilon ) = (\frac{\lambda _2}{1-\lambda _2} ( \frac{\epsilon _f}{\epsilon _m})^{(1-\eta ) (1-\gamma )} )^{1/\gamma }-1$
, sf
(λ2, ε) = 1 − sm
(λ2, ε). We show in the Appendix that the sign of the effect of a rise in 1 − τ
N
on λ
L
2 is inversely related to the sign of the following expression:
 \begin{eqnarray}
&&(1-\gamma )\left[ \tilde{\xi } \left(\frac{A_c (1-\eta )}{1-\tau _N}-\eta \sum _g w \epsilon _g \right) \kappa _1 (A_c ,\epsilon )\right.\nonumber\\
&&\quad\left. +\, \left( A_c w \left( \epsilon _m - \frac{\sum _g \epsilon _g}{2}\right)\right) \kappa _2(A_c , \epsilon ) \right],
\end{eqnarray}
\begin{eqnarray}
&&(1-\gamma )\left[ \tilde{\xi } \left(\frac{A_c (1-\eta )}{1-\tau _N}-\eta \sum _g w \epsilon _g \right) \kappa _1 (A_c ,\epsilon )\right.\nonumber\\
&&\quad\left. +\, \left( A_c w \left( \epsilon _m - \frac{\sum _g \epsilon _g}{2}\right)\right) \kappa _2(A_c , \epsilon ) \right],
\end{eqnarray}
where
![]() $\kappa _1 = \frac{ (w (1-\tau _N) \epsilon _m)^{(1-\eta )(1-\gamma )}}{(A_c + \sum _g w (1-\tau _N) \epsilon _g )^{2-\gamma }} >0$
,
$\kappa _1 = \frac{ (w (1-\tau _N) \epsilon _m)^{(1-\eta )(1-\gamma )}}{(A_c + \sum _g w (1-\tau _N) \epsilon _g )^{2-\gamma }} >0$
,
![]() $\kappa _2 = \frac{(\frac{A_c}{2} +w (1-\tau _w) \epsilon _m )^{-\gamma } }{( A_c + \sum _g w (1-\tau _w) \epsilon _g )^{2-\gamma } } >0$
and
$\kappa _2 = \frac{(\frac{A_c}{2} +w (1-\tau _w) \epsilon _m )^{-\gamma } }{( A_c + \sum _g w (1-\tau _w) \epsilon _g )^{2-\gamma } } >0$
and
![]() $\tilde{\xi } = \frac{ -\xi (1-\gamma )}{ \eta ^{\eta } (1-\eta )^{1-\eta }} >0$
.
$\tilde{\xi } = \frac{ -\xi (1-\gamma )}{ \eta ^{\eta } (1-\eta )^{1-\eta }} >0$
.
In (7), if Ac = 0, only the leading term is different from zero and in fact it is positive. In this case, we can show that an increase in 1 − τ N will increase intrahousehold risk sharing or, to put it differently, it will reduce the response of the sharing rule to variations in income. When Ac > 0, the second term is added and also the first term in (7) eventually switches sign. When the overall partial derivative is negative, the fall in labor taxation exacerbates inequality within the family and reduces risk sharing. This is the result we established under log-separable utility. What non-separability brings to the equation is the leading term in (7) which yields the non-monotonicity that makes the effect of changes in labor income taxation ambiguous.
To understand what this term captures, note that as discussed previously, a rise in the tax rate reduces inequality in terms of labor incomes but it also impoverishes the household. When utility is curved, the reduction in household income translates into an increase in the marginal utility which tightens the participation constraints. In the case of log utility, this effect was balanced by the larger equity in household resources; it dominated only when the household had negative savings. But under γ > 1 the income effect may dominate even when household financial income is positive.
In the Appendix, we show that a similar result applies to the upper bound λ U 2. We also establish that the effect of lower capital taxation is unambiguous; it always improves the household’s insurance possibilities.
Proposition 3. Assume Ac > 0 and γ > 1. Lowering labor income taxes reduces intrahousehold risk sharing when household wealth is low. In contrast, when the household is wealthy, reducing labor taxation has a detrimental effect on intrahousehold insurance. Lower capital taxes always improve the household’s insurance possibilities.
Proof: See Appendix.
In our quantitative analysis in Section 5, following the rest of the macro literature on optimal taxation, we focus on the case of non-separable utility. It is however important to disentangle the channels through which preferences affect our results, and for this purpose we also considered separable preferences. Note that since the change in policy considered in Section 5 is one which eliminates capital taxation and raises labor income taxes, our results under non-separable utility illustrate that for some households, the limited commitment problem may even be more severe after the reform. This could be the case for young households which are typically wealth poor.
3. QUANTITATIVE MODEL
This section presents our quantitative life cycle model. We consider an economy populated by a continuum of individuals, equally many males and females. Gender is indexed by g ∈ {m, f} and age by j ∈ {1, 2, . . ., J}. Individuals survive from age j to j + 1 with probability ψ j . At each date, a new cohort of individuals enters the economy; we assume that the population grows exogenously at rate θ.
The life cycle of individuals comprises of the following three stages: Marriage (matching), work and retirement. Since our model does not endogenize family formation, we simplify the first stage by letting matching take place in a pre-labor-market period of life labeled age zero. A fraction μ of individuals will find partners at this stage and form households as couples, the remaining agents will be bachelors forever.Footnote 11 Marital status does not change over time. After date, zero individuals work for jR − 1 periods – conditional on survival – and then retire at date jR . At age J, they die with probability one.
3.1. Endowments
Agents in the economy differ in terms of their labor productivity along three dimensions: a deterministic (life cycle) component Lg (j), a fixed effect α g and an idiosyncratic labor productivity shock ε g . When entering the labor market each agent draws a value of α g , the value of which remains constant throughout their working life. We assume that there are N possible realizations {α1, g , α2, g , . . .α N, g } for each gender. The assignment of a value α i, g , i = 1, 2, . . ., N is made according to some probabilities pS g (α g ) when the agent is single, and according to probabilities pM (α m , α f ) when the individual is married. Note that pM is the joint distribution of the spouses across all possible values of α m and α f . This formulation allows the endowments to be correlated across spouses.
Idiosyncratic productivity ε g changes stochastically over time according to a first order Markov process. We let π g (ε′ g |ε g ) be the conditional pdf for this process. The analogous object for couples is denoted by π(ε′|ε), where ε is the vector of productivities of spouses. We further assume π(ε′|ε) ≠ Π g = m, f π g (ε′ g |ε g ), i.e. that shocks to productivity are correlated across spouses.
3.2. Markets and Technology
The production technology is Cobb–Douglas
where K denotes the economy’s aggregate capital stock, and N is the aggregate labor input (in efficiency units), and A is the level of labor-augmenting technology. The resource constraint is given by K′ = (1 − δ)K + Y − G − C where, by convention, primes denote the next model period. C is aggregate consumption in the economy, G is government spending and δ is the depreciation rate of the aggregate capital stock.
Factor prices are determined in competitive markets. Wages, measured in efficiency units, are equal to the marginal product of labor, and the return to capital is its marginal product net of depreciation. We denote these objects by w and r respectively.
Financial markets are incomplete. There are no state contingent securities. By trading claims on the aggregate capital stock households can self-insure. In keeping with the literature, we assume that these trades are subject to an ad hoc borrowing constraint. The value for the constraint is set to zero, so that the model rules out borrowing altogether. Moreover, there are no annuity markets and households leave accidental bequests which we denote by B. Bequests are taxed by the government and redistributed (uniformly) across individuals in the economy.Footnote 12
3.3. Government
The government engages in two activities: First, it levies taxes on consumption τ C , on financial income τ K , and on labor income τ N , to finance the (constant) level of expenditures G. We rule out government debt so that the government runs a balanced budget each period.
Second, the government runs a Pay-as-you-go social security system, which is financed through a proportional tax on the earnings of the working population. We denote by τ SS the social security tax, and by SS(g, α g ) the transfer that a retired individual receives from the government. Notice that transfers depend on gender g, and on the fixed effect α g . Our aim with this formulation is to capture the current US social security system in a parsimonious way. SS(g, α g ) depends also on gender because life cycle productivity Lg (j) differs across men and women in the economy.
3.4. Value Functions
3.4.1. Bachelor households
We first consider the program of a bachelor of gender g and age j. We let Sg (a, X, j) be the lifetime utility for this agent when her (his) stock of wealth is a, her permanent productivity is α g , her idiosyncratic time varying productivity is ε g . To save on notation, we summarize the fixed effect and the time varying component of productivity in a vector X. The agent must choose consumption c and hours worked n (if not retired, i.e. j < jR ) to maximize her utility subject to the budget and the borrowing constraints. She solves the following functional equation:
 \begin{eqnarray}
S_g (a, X , j ) &=& \max _{c,l,a^{\prime } \ge 0 , l} u(c,l) + \beta \psi _j \int S_g(a^{\prime },X^{\prime } , j+1 ) d \pi _g (X^{\prime }| X),\\
&&\text{Subject to:} \;\;\;\; l+n \le 1 \nonumber \\
a^{\prime } + (1+\tau _C) c &=& (a+B) (1+r(1-\tau _K))\nonumber\\
&& +\, w \epsilon _g \alpha _{g} L_g(j)(1-\tau _N -\tau _{SS}) n \; \text{ if } j <j_R \nonumber \\
a^{\prime } + (1+\tau _C) c &=& (a+B) (1+r(1-\tau _K)) + SS( g, \alpha _{g}) \; \text{ if } j \ge j_R. \nonumber
\end{eqnarray}
\begin{eqnarray}
S_g (a, X , j ) &=& \max _{c,l,a^{\prime } \ge 0 , l} u(c,l) + \beta \psi _j \int S_g(a^{\prime },X^{\prime } , j+1 ) d \pi _g (X^{\prime }| X),\\
&&\text{Subject to:} \;\;\;\; l+n \le 1 \nonumber \\
a^{\prime } + (1+\tau _C) c &=& (a+B) (1+r(1-\tau _K))\nonumber\\
&& +\, w \epsilon _g \alpha _{g} L_g(j)(1-\tau _N -\tau _{SS}) n \; \text{ if } j <j_R \nonumber \\
a^{\prime } + (1+\tau _C) c &=& (a+B) (1+r(1-\tau _K)) + SS( g, \alpha _{g}) \; \text{ if } j \ge j_R. \nonumber
\end{eqnarray}
3.4.2. Couples
In this paragraph, we describe the program of the couple. Because the optimization problem was previously discussed, here we simply show the Bellman equations in the life cycle model of this section. Let λ and 1 − λ be the shares of the male and the female spouses respectively and M(a, X, λ, j) be the value function of a household of age j, where X summarizes the productive endowments of its members.Footnote 13 As before a is the level of wealth, and ξ is the (constant) benefit that accrues to each spouse in the marriage. The program of the couple can be written as:
 \begin{eqnarray*}
M(a,X,\lambda ,j ) &=& \max _{c^g,l^g,a^{\prime }\ge 0} \lambda u(c^m,l^m) + (1- \lambda ) u(c^f,l^f))\nonumber\\
&& +\, \xi + \beta \psi _j \int M(a^{\prime }, X^{\prime } , \lambda ^{\prime }, j+1 ) d \pi (X^{\prime } | X), \nonumber \\
&&\text{Subject to:} \;\;\;\; l^g+n^g \le 1 \;\;\; \text{ for }\;\; g \in \lbrace m, f\rbrace \nonumber \\
a^{\prime } + (1+\tau _C)(c^m +c^f) &=& (a+2 B) (1+r(1-\tau _K))\nonumber\\
&& +\, w \Big ( \sum _g L_g(j) \alpha _i \epsilon _{i,g} n^g (1-\tau _N -\tau _{SS} )\Big ) \; \text{ if } j <j_R\nonumber \\
a^{\prime } + (1+\tau _C)(c^m +c^f) &=& (a+2 B) (1+r(1-\tau _K)) + \sum _g SS( g, \alpha _{g}) \; \text{ if } j \ge j_R,\nonumber
\end{eqnarray*}
\begin{eqnarray*}
M(a,X,\lambda ,j ) &=& \max _{c^g,l^g,a^{\prime }\ge 0} \lambda u(c^m,l^m) + (1- \lambda ) u(c^f,l^f))\nonumber\\
&& +\, \xi + \beta \psi _j \int M(a^{\prime }, X^{\prime } , \lambda ^{\prime }, j+1 ) d \pi (X^{\prime } | X), \nonumber \\
&&\text{Subject to:} \;\;\;\; l^g+n^g \le 1 \;\;\; \text{ for }\;\; g \in \lbrace m, f\rbrace \nonumber \\
a^{\prime } + (1+\tau _C)(c^m +c^f) &=& (a+2 B) (1+r(1-\tau _K))\nonumber\\
&& +\, w \Big ( \sum _g L_g(j) \alpha _i \epsilon _{i,g} n^g (1-\tau _N -\tau _{SS} )\Big ) \; \text{ if } j <j_R\nonumber \\
a^{\prime } + (1+\tau _C)(c^m +c^f) &=& (a+2 B) (1+r(1-\tau _K)) + \sum _g SS( g, \alpha _{g}) \; \text{ if } j \ge j_R,\nonumber
\end{eqnarray*}
where the updating of the sharing rule for λ (which generalizes the analogous object in Section 2) is
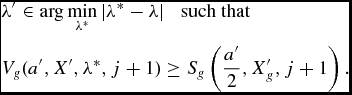 \begin{eqnarray}
&&\lambda ^{\prime } \in \text{arg} \min _{\lambda ^*} | \lambda ^* - \lambda | \;\;\; \text{such that} \\
&&V_g(a^{\prime },X^{\prime } ,\lambda ^*,j+1 ) \ge S_g \left(\frac{a^{\prime }}{2} , X_g^{\prime } , j+1 \right). \nonumber
\end{eqnarray}
\begin{eqnarray}
&&\lambda ^{\prime } \in \text{arg} \min _{\lambda ^*} | \lambda ^* - \lambda | \;\;\; \text{such that} \\
&&V_g(a^{\prime },X^{\prime } ,\lambda ^*,j+1 ) \ge S_g \left(\frac{a^{\prime }}{2} , X_g^{\prime } , j+1 \right). \nonumber
\end{eqnarray}
Xg is a vector formed by elements of X that are relevant to household member g if he or she were to be single. Vg is the lifetime utility that individual g derives when program (3.4.2) is solved.
We assume that value of λ is initiated at the matching stage of the life cycle as a solution to the following Nash bargaining problem:
 \begin{eqnarray}
&&\lambda _1 \in \text{arg} \max _{\lambda } \left[ V_m(a,X ,\lambda ,1 ) - S_m\left( \frac{a}{2},X ,\lambda ,1 \right) + \overline{\xi }_m \right] \; \Big[ V_f(a,X ,\lambda ,1 )\nonumber\\
&&\quad - S_f\left(\frac{a}{2},X ,\lambda ,1 \right) + \overline{\xi }_f \Big].
\end{eqnarray}
\begin{eqnarray}
&&\lambda _1 \in \text{arg} \max _{\lambda } \left[ V_m(a,X ,\lambda ,1 ) - S_m\left( \frac{a}{2},X ,\lambda ,1 \right) + \overline{\xi }_m \right] \; \Big[ V_f(a,X ,\lambda ,1 )\nonumber\\
&&\quad - S_f\left(\frac{a}{2},X ,\lambda ,1 \right) + \overline{\xi }_f \Big].
\end{eqnarray}
Notice that the Nash sharing rule determines the initial allocation under the influence of two gender specific utility gains
![]() $\overline{\xi }_g$
for g ∈ {m, f}. Since we will assume that
$\overline{\xi }_g$
for g ∈ {m, f}. Since we will assume that
![]() $\sum _g \overline{\xi }_g =0$
,
$\sum _g \overline{\xi }_g =0$
,
![]() $\overline{\xi }_m$
and
$\overline{\xi }_m$
and
![]() $\overline{\xi }_f$
do not affect the marital surplus, they simply determine the share of the surplus which each spouse receives.Footnote
14
$\overline{\xi }_f$
do not affect the marital surplus, they simply determine the share of the surplus which each spouse receives.Footnote
14
We will use these terms to determine the magnitude of income transfers from one spouse to the other; the ultimate goal is to make the model match the inequality in hours between married men and women that we observe in the data. If
![]() $\overline{\xi }_m >0$
and
$\overline{\xi }_m >0$
and
![]() $\overline{\xi }_f<0$
then the household contract will give an initial allocation with large transfers from the male to the female spouse, this will lead to substantial inequality in hours within the family. Because the updating rule (10) will make λ persistent over time (we will demonstrate this in a later subsection) inequality in hours will carry over in subsequent periods.
$\overline{\xi }_f<0$
then the household contract will give an initial allocation with large transfers from the male to the female spouse, this will lead to substantial inequality in hours within the family. Because the updating rule (10) will make λ persistent over time (we will demonstrate this in a later subsection) inequality in hours will carry over in subsequent periods.
Note that an alternative way to target the hours inequality would be to simply pick the initial shares (as we did in Section 3 for instance). However, we need to close the model with the Nash rule in (11) for the following reason: When we consider the change in the tax policy, the intrahousehold allocation may be impacted through changes in the initial value of λ. These changes would be absent if we fixed exogenously the initial share, and they may have significant effects on the welfare gains of husbands and wives.
We characterize the competitive equilibrium in Section A.2 in the Appendix.
4. CALIBRATION AND MODEL EVALUATION
4.1. Calibration
4.1.1. Preferences and demographics
The demographic parameters have been set so that the model has a stationary demographic structure that matches the age distribution in the US economy. We assume that individuals are born at age 25 and live at most until age 95. Retirement is at age 65. The survival probabilities are taken from Arias (Reference Arias2010), based on the US National Vital Statistics Reports and correspond to probabilities concerning the entire population (pooling men and women). The model period is set to five years. This means that there are fifteen periods and the retirement age is jR = 10. Although we make this assumption for computational reasons, in what follows we report annual values for the parameters.
We set the fraction of households that are married (μ) equal to 52%, which is the corresponding statistic in the PSID data over all age groups. Population growth is assumed to be θ = 0.012. We calibrate the preference parameters as follows: first, we follow Conesa et al. (Reference Chiappori2009) and Fuster et al. (Reference Fuster, Imrohoroglu and Imrohoroglu2008), and set γ = 4.Footnote 15 We also choose a value of η = 0.41 so that our model gives in the steady state average hours worked of one third. With these numbers the intertemporal elasticity of substitution, (1 − η(1 − γ))− 1, is equal to 0.4484.
For married couples we have to determine the utility gains
![]() $\overline{\xi }_m$
and
$\overline{\xi }_m$
and
![]() $\overline{\xi }_f$
at the Nash bargaining stage, and the flow gain ξ that couples enjoy at each period. As discussed earlier, these parameters govern the following two aspects of the intrahousehold allocation: First,
$\overline{\xi }_f$
at the Nash bargaining stage, and the flow gain ξ that couples enjoy at each period. As discussed earlier, these parameters govern the following two aspects of the intrahousehold allocation: First,
![]() $\overline{\xi }_m$
and
$\overline{\xi }_m$
and
![]() $\overline{\xi }_f$
determine the transfers from one spouse to the other, and along with differences in the age productivity profiles Lj
(g), they determine inequality in hours within the household. We pick numbers for these parameters to match average hours worked for married men and women as in the US data; according to the PSID married males worked 2104 hours in 2006, married females 1420 hours.Footnote
16
We map these numbers into model units.Footnote
17
$\overline{\xi }_f$
determine the transfers from one spouse to the other, and along with differences in the age productivity profiles Lj
(g), they determine inequality in hours within the household. We pick numbers for these parameters to match average hours worked for married men and women as in the US data; according to the PSID married males worked 2104 hours in 2006, married females 1420 hours.Footnote
16
We map these numbers into model units.Footnote
17
![]() $^,$
Footnote
18
$^,$
Footnote
18
Second, ξ determines the ability of the household to commit to a sharing rule λ. The smaller ξ is, the more the household members will be tempted to renege on this rule and the more frequent rebargaining will be. Our strategy to calibrate the value of ξ is the following: We choose a value that is as low as possible so that we maximize the frequency of rebargaining in the model but also so that divorce never occurs in equilibrium. We find that a value ξ = 1.2 is appropriate to accomplish this goal. To show what this means we have calculated the compensating variation, the increment in consumption that the average married individual would require to be as well-off as if we set ξ = 0. We obtained a value equal to 19.8% of average consumption. Therefore, the model predicts a substantial utility gain from being married.Footnote 19
There are two model mechanisms which explain this finding: First, because of the fixed effects which maybe high for one spouse and low for the other, we need a large gain to keep the couple together. Since the α g are permanent characteristics, there is virtually no insurance value accruing to a couple for which α m ≫ α f , this basically says that we cannot sustain any mutual insurance arrangement against this shock.Footnote 20
The second reason is the presence of wealth in the model. We previously saw in the two period model that a couple would remain married even if we set ξ = 0 in t = 2 (in that case the intrahousehold allocation gives to each individual what they would get as a single). This also holds in the multiperiod setup if families cannot save (or if they can save in separate accounts). But with common wealth in the household it does not hold. To understand why suppose that the husband draws a high value of ε m today. If the couple divorces, then high productivity leads to more savings for the husband and persistently higher consumption. If they do not divorce, then wealth needs to be shared and (partly) used to finance a higher consumption level for the wife. Unless we assume ξ > 0, the marital surplus becomes negative and the couple divorces. We will comment further on this feature of the model in a subsequent section.
4.1.2. Technology and endowments
The technology parameters are chosen as follows: We allow At to grow at a rate equal to 1.4% per year.Footnote 21 Moreover, following Fuster et al. (Reference Fuster, Imrohoroglu and Imrohoroglu2008) we set the capital share in value added ζ equal to 0.36 and we choose the depreciation rate of capital δ to match an investment to output ratio of 21% in the steady state. This gives us an annual value for this parameter of 5.26%. The subjective discount factor β is calibrated so that the economy in the steady state produces the capital output ratio of 2.7. This procedure yields a value of 0.998.
Individual wages in the model are the product of three components; the gender specific life cycle profile, the fixed effect, and the temporary idiosyncratic productivity shock, i.e. Lg (j)α g ε g . Following the bulk of the literature we take the life cycle profiles Lg (j) from Hansen (Reference Hansen1993). Moreover, our principle to calibrate the fixed effect component and the distribution of the idiosyncratic shocks ε is to reproduce the life cycle pattern of the cross-sectional variance of the log of family earnings as is documented in Storesletten et al. (Reference Storesletten, Telmer and Yaron2004).
As in Storesletten et al. (Reference Storesletten, Telmer and Yaron2004) we assume that both α
g
and ε
g
are log-normally distributed random variables. The fact that these variables in the model are represented as discrete may be thought as an approximation of the processes using standard techniques (for example Adda and Cooper (Reference Adda and Cooper2003)). For the fixed effect, we have chosen two values (α1, α2), these are common across gender and marital status. We follow Conesa and Krueger (Reference Conesa and Krueger2006) and set α1 = e
− σα
and α2 = e
σα
(where σα governs the variance of the process) and (for bachelor) agents we calibrate
![]() $p^S_{g}(\alpha _1)=p^S_{g}(\alpha _2) =\frac{1}{2}$
. This is an obvious choice since if we apply any standard numerical discretization procedure to approximate a continuous log normal variable with a constant variance we will get probabilities equal to 1/2.
$p^S_{g}(\alpha _1)=p^S_{g}(\alpha _2) =\frac{1}{2}$
. This is an obvious choice since if we apply any standard numerical discretization procedure to approximate a continuous log normal variable with a constant variance we will get probabilities equal to 1/2.
For couples, we calibrate the joint probabilities pM (α m , α f ) so that our economy reproduces the degree of marital sorting in earnings ability that has been documented in the US data; for instance Hyslop (Reference Hyslop2001) estimates a 0.5 correlation of fixed effects within the family in his PSID sample. We will choose the pdf pM (α m , α f ) to match this correlation coefficient. To explain how this is done, note that for married individuals the process α g again takes two values α g ∈ {e − σα , e σα }. This gives us the following combinations for the pair: (α m , α f ) ∈ {(e − σα , e − σα ), (e − σα , e σα ), (e σα , e − σα ), (e σα , e σα )}. pM (α m , α f ) then gives the probability of having any one of these pairs. To match a correlation coefficient of 0.5 we have to set pM ((e − σα , e − σα )) = pM ((e σα , e σα )) = 0.375 (i.e. for spouses who have the same fixed effect). For the remaining nodes we set the probabilities equal to 0.125.
Analogously the stochastic process of the logarithm of ε has the following AR(1) representation:
where u
(2 × 1) is a vector of shocks to productivity and follows
![]() $\mathcal {N} (0_{(2\times 1)}, \Sigma _u)$
and Σ
u
is the variance covariance matrix of the shocks. The diagonal elements of Σ
u
are σ2
u
, the off-diagonal elements (covariances) are
$\mathcal {N} (0_{(2\times 1)}, \Sigma _u)$
and Σ
u
is the variance covariance matrix of the shocks. The diagonal elements of Σ
u
are σ2
u
, the off-diagonal elements (covariances) are
![]() $\sigma _{u_1,u_2}=\tilde{\rho }_{u_1,u_2} \sigma _u^2$
where
$\sigma _{u_1,u_2}=\tilde{\rho }_{u_1,u_2} \sigma _u^2$
where
![]() $\tilde{\rho }_{u_1,u_2}$
is the correlation coefficient of the two shocks. We set
$\tilde{\rho }_{u_1,u_2}$
is the correlation coefficient of the two shocks. We set
![]() $\tilde{\rho }_{u_1,u_2} =0.15$
following the empirical evidence presented in Hyslop (Reference Hyslop2001). Finally, let
$\tilde{\rho }_{u_1,u_2} =0.15$
following the empirical evidence presented in Hyslop (Reference Hyslop2001). Finally, let
![]() $A =\rho _{\epsilon } \mathcal {I}_{2\times 2}$
where
$A =\rho _{\epsilon } \mathcal {I}_{2\times 2}$
where
![]() $\mathcal {I}_{2\times 2}$
is the identity matrix and ρε is the first order autocorrelation coefficient of the ε process.
$\mathcal {I}_{2\times 2}$
is the identity matrix and ρε is the first order autocorrelation coefficient of the ε process.
The above stochic process is also applied to bachelor households, so the parameters ρε and σ u are common to singles and couples.
We now have three numbers to pick: ρε, σα and σ u . We proceed as follows: First, we choose σα to reproduce the cross-sectional variance of the logarithm of household labor income (pooling bachelors and couples) at age 25 reported in Storesletten et al. (Reference Storesletten, Telmer and Yaron2004). This target gives us σα = 0.2. Second, we choose ρε and σ u so that we can get a cross-sectional variance which rises linearly with age and reaches 0.9 at age 65. This procedure gives ρε = 0.89 (a yearly analogue of 0.977) and σ u = 0.05 (yearly analogue of 0.0108). The stochastic process is then discretized using nine nodes. To obtain an approximation which gives a positive correlation between the u shocks, we apply the methodology of Burnside (Reference Burnside, Marimon and Scott1999).
4.1.3. Government
In order to parameterize the steady state tax code we proceed as follows: The level of expenditures G is chosen so that on the balanced growth path the government consumes 21% of output. This spending is financed by the tax levies on consumption, capital and labor income. We follow Fuster et al. (Reference Fuster, Imrohoroglu and Imrohoroglu2008) and fix the consumption tax τ C to 0.05 and the capital income tax τ K to 0.35. The value of τ N is then chosen so that the government runs a balanced budget. In the initial steady state, the model gives us a value of roughly 15% for this parameter. In our numerical experiment, we eliminate capital income taxation and adjust labor income taxes while holding the level of expenditures constant to their steady state value.
Our principle to calibrate the social security benefit system is the following: First, as explained previously, we consider the individual as the unit to which benefits are distributed and not the household. Second, we try to capture in a parsimonious way, with the functional SS(g, α g ), the fact that social security in the US contains a redistributive component. For instance, in 2004 individuals received 90% of the first $7,300 of their total social security entitlement, 32% for earnings between $7,300 and $44,000, and 15% for earnings above $44,000.Footnote 22 We calibrate SS(g, α g ) so that the model economy gives roughly the same redistribution of income in retirement in terms of median lifetime earnings as in the US economy. To give an idea of the numbers, we calculate that men of the highest earning ability (fixed effect) get roughly 1.3 times as much as men of the lowest ability, whereas their lifetime earnings are twice as high. Furthermore, women with the lowest ability receive in benefits roughly 67% of what poor men receive, and women of high ability get slightly (3%) more than poor men. We fix the social security tax rate at 12.5% and solve for the average level of benefits. In the computational experiment, we keep the tax rate constant across environments and vary the level of benefits. We summarize the calibrated parameters in Table 1.
Table 1. Calibrated parameters

For growth rates (
![]() $\hat{A}$
, θ, δ) the reported values are annual, but we solve on 5-yearly frequency.
$\hat{A}$
, θ, δ) the reported values are annual, but we solve on 5-yearly frequency.
4.2. Model Evaluation
In Table 2, we summarize relevant cross-sectional observations in the model and in the data. Because our focus is on the behavior of couples we report our model’s performance in matching a set of cross-sectional moments that refer to married households. All data moments are computed from the PSID.
Table 2. Cross-sectional moments: Model and data
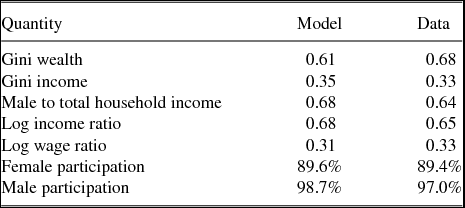
The table summarizes in various moments the performance of the model vs. the US data. The data are extracted from the PSID and refer to wealth, income wages and participation in the labor market for married individuals.
In the first row, we look at between married household wealth inequality. According to the results in the table the model produces a wealth Gini coefficient of 0.61 whereas in the 2007 PSID data the analogous quantity is in the order of 0.68.Footnote 23 Note however, that given the structure of the PSID, we cannot disentangle which part of a household’s net worth is accumulated in the marriage, and which part was brought into the marriage by the spouses. On the other hand, in the model, all wealth is common marital property. In this respect the data Gini may overestimate the between married household inequality in wealth.
In the second row of the table, we report the Gini index for between household income inequality. This statistic reflects the sum of male and female labor income and therefore refers to the income distribution of US couples. The model matches the data counterpart very accurately, generating a Gini coefficient of 0.35 vs. 0.33 in the data. Rows 3 to 5 summarize inequality in income and wages within the household. The third row reports the average fraction of male to total household labor income, the fourth row the mean difference between the log male income and the log of female income, and the fifth column reports the analogous difference for wages. In all of the statistics the model matches the US data very well. In particular, on average, married men earn 64% of total family income in the US; the model produces a value of 68%. The average of the difference of the logs of income (wages) is 0.68 (0.68) in the model, and it is 0.64 (0.65) in the data.
As discussed earlier, we have targeted average hours worked for married men and married women as in the US data. In the last two rows of the table we investigate how well the model performs in matching male and female participation in the labor market. Note that in spite of the fact that there is no explicit extensive margin in the model, individuals may nonetheless choose zero hours, in which case the optimal allocation is at a corner solution. In the data columns we report the fraction of working age households which, in a five year interval in the PSID, have positive hours. This fraction is 89.4% in the data for married women and it is 97% for married men. The model generates numbers for these statistics of 89.6% and 98.7% respectively. Therefore, on average it can match very accurately non-participation.Footnote 24
5. QUANTITATIVE RESULTS
This section contains our main quantitative results. We evaluate how a reform which sets capital taxation permanently to zero and raises labor taxes affects the economy in terms of aggregates, welfare and the intrahousehold allocation. In order to fully investigate the impact of this change in the tax schedule, we consider both the long run and the short run effects, meaning both the behavior of the economy in the final steady state as well as in the first period of the transition.
5.1. The Behavior of the Sharing Rule
Before we investigate the impact of the change in policy, it is instructive to highlight a few model properties, in particular to show how couples bargain over the intrahousehold allocation over the life cycle. The findings presented in this section are new to the literature:Footnote 25 Though many papers have studied dynamic limited commitment models, typically they assume infinitely lived individuals. Here we show how household bargaining takes place in a life cycle model with wealth accumulation when we also assume that wealth is commonly held in the household.
The top left panel of Figure 1 illustrates the behavior of the male share λ over the life cycle (in the initial steady state) for one household in our simulations. This couple starts at the mean productivity in the first period, and at age 40 the female spouse’s productivity drops by about one third, triggering a rise in the male spouse’s share. The share λ increases from a half to roughly 0.66. From age 40 and until the end of the household’s life, the share remains constant. Prior to age 40 the share of the household is roughly constant in spite of the fact that individuals experience changes to their idiosyncratic productivity. This pattern suggests that it is shocks which occur towards the middle of the life cycle that are more likely to make participation constraints bind.

Figure 1. Evolution of the male share.
Note: The figure gives an example of the behavior of the male share over the life cycle. The top left shows the share in the initial steady state. The top right shows the change in the share that is due to shocks to the household’s labor income. The bottom panel compares the initial steady state (solid line), final (dashed line) and first period of the transition (crossed line).
In the top right panel of Figure 1, we investigate the influence of shocks vs. the life cycle productivity component, on the evolution of the weight. This graph represents the difference of the actual weight from a path where no shock occurs throughout. There are two noteworthy features: First, as the graph shows, the bulk of the adjustment at age 40 is due to changes in idiosyncratic productivity rather than (changes in) life cycle prices. Second, according to the results shown in the figure, predictable gender differences in the life cycle paths Lg (j) are factored in the sharing rule at age 25 (there is only a modest increase in the male share of roughly 2 percentage points at age 35).Footnote 26
To explain the pattern, we see in the figure the following remarks are important: First, from the analysis of Kocherlakota (Reference Kocherlakota1996) and Ligon et al. (Reference Ligon, Thomas and Worrall2002) we know that discount factors exert a crucial influence on the ability of the couple to sustain an allocation without renegotiations. When individuals discount future consumption more heavily, they are less likely to share risks efficiently. In infinite horizon models, the discount rates are constant over time but in the life cycle model they change with the age of the household (older families discount future utility flows more heavily because of the lower survival probabilities). It is therefore evident that older individuals should be less able to sustain commitment.
Second, the age of the household is crucial, because the longer individuals are exposed to idiosyncratic uncertainty, the more they value the insurance contract that the marriage offers. Close to retirement there are no further shocks to the labor income (moreover we have assumed that social security is not contingent on the realizations of ε g ) and therefore the value from risk sharing is effectively zero. But when the household is young, risk sharing is important. This tells us that we should expect fewer (or smaller) renegotiations of the marital contract at age 30.
These factors can explain why the sharing rule for very young households reacts too little to changes in income. We can therefore explain why we see the first considerable change in λ at age 40 in the figure. However, we cannot explain why we see no further changes at age 50 and beyond. This model property is driven by the impact of household wealth. By the time the household is at age 50 it has accumulated enough assets to be able to ward off changes in productivity without any change in λ. The mechanism we identified in Section 3, that common wealth in the couple can improve commitment therefore has an important impact on the behavior of the sharing rule.
In Table 3 (first column), we show the frequency of rebargaining (the fraction of periods we observe a change in λ in a panel of households that is representative of the population) across different age groups. This measure captures changes in the weight no matter how small. According to the results in the table, on average 23.37% of households rebargain. Most renegotiations occur at ages 25–45 (38.04%). Between ages 50 and 65, we find changes in λ take place in 6.60% of the sample. Finally, the frequency of rebargaining for retired households is 1.9%.Footnote 27 These results are in line with the patterns we highlighted in Figure 1.
Table 3. Participation constraints
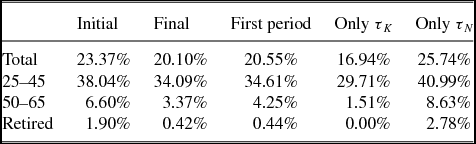
The table shows the frequency with which participation constraints bind, before and after the reform. The statistics are computed from panel of families that is representative of the population.
5.2. Long run and Short run Effects on Aggregates
In Figure 2 we plot the response of aggregate capital (top left), aggregate output (top right), benefits (bottom left) and returns (bottom right). Period zero stands for the old steady state, before the reform. In period one, there is an unanticipated permanent shift in the tax schedule. The figure shows the path of the variables from the initial period until the new steady state is reached, after 30 model periods.

Figure 2. Responses of Capital, Output, Benefits and Returns to the Reform.
Note: The figure plots the response of aggregate capital (top left), aggregate output (top right), retirement benefits (bottom left) and rate of returns (bottom right), where the solid line shows the gross return and the dashed line the return net of capital taxation.
Notice that aggregate capital is predetermined and therefore does not change when the reform takes place. However, when capital taxation is abolished individuals are more willing to save due to the rise in the after tax return on savings. We represent the net return with the dashed line in the bottom right panel. It increases by roughly 41% on impact and even in the long run is considerably higher than in the initial steady state. The solid line in the plot, indicates that the build-up of capital lowers the gross return to savings by 11% in the final steady state.
Notice that when the reform takes place there is a considerable drop in aggregate output deriving from the response of hours to the change in the tax schedule. In Table 4 (rows 2 and 3), we report the behavior of hours and labor taxes. Aggregate hours fall by roughly 8.5% initially and labor taxes increase by 201% in period 1, and by 193% in the final steady state. The reason for this pattern is that higher capital eventually increases wages and individual labor income which, after the reform, is the tax base. Therefore, in the long run a lower labor tax is needed to balance the government’s budget than in the first period of the transition. Moreover, due to the joint behavior of capital and hours, output falls by 5.25% initially and then rises until the new steady state. After thirty periods aggregate output is 1.6% lower than it was before the reform.
Table 4. Responses of aggregate variables to the reform
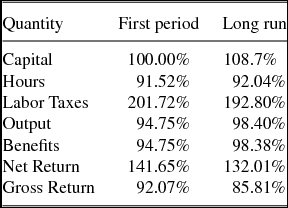
The table expresses aggregate variables in the first period of the transition and the final steady state as a percentage of the variables in the original steady state.
In Table 5, we disaggregate the responses of wealth and hours into household types. The largest increase in wealth accumulation is experienced by couples (9.48% relative to the initial steady state). Single households experience a more modest increase in assets. For single male households the increase is in the order of 6.12% and for single females it is 7.1%. Rows 4 to 7 of Table 5 report hours for married and single individuals. Married males reduce their work time by roughly 7.3% and married females by 8.25%.Footnote 28
Table 5. Responses of variables to the reform

The table expresses aggregate variables in the first period of the transition and the final steady state, as a percentage of the variables in the original steady state.
![]() $\overline{a}$
denotes average assets.
$\overline{a}$
denotes average assets.
![]() $\overline{n}$
is average hours. The superscripts indicate individual and household type. Cf and Cm are married females and males and Sf and Sm are single females and males respectively.
$\overline{n}$
is average hours. The superscripts indicate individual and household type. Cf and Cm are married females and males and Sf and Sm are single females and males respectively.
5.3. The Intrahousehold Allocation
5.3.1. Sharing rule
Consider again Figure 1 where we showed the behavior of the sharing rule for a typical couple and over time. The bottom panel of the figure represents with the dashed line the path of λ, in the final steady state and with the crossed line the analogous path in the first period of the transition. The solid line represents the initial steady state (same as in the top left panel).
Notice first that after the reform, the couple at age 25, draws a starting value of the weight that is different from the value in the initial steady state. The reform, therefore, has a differential impact on the male and the female spouses and redistributes bargaining power within the household. We will return to this model feature in a subsequent paragraph.
Second, note that in the new steady state with zero capital taxation, the household can better commit to this initial allocation and changes in the share are smaller. This effect is consistent our previous findings. Indeed the rise in λ at age 40 is roughly 8 percentage points in the final steady state, where as it is roughly 12 percentage points before the reform.Footnote 29
Are these changes large enough to impart a big effect on individual consumption and on the intrahousehold allocation? The answer is probably not. To see this note that under non-separable preferences the share of the female spouse on total household consumption is given by
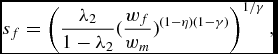 \begin{eqnarray}
s_f = \left(\frac{\lambda _2}{1-\lambda _2}( \frac{w_f}{w_m})^{(1-\eta ) (1-\gamma )} \right)^{1/\gamma },
\end{eqnarray}
\begin{eqnarray}
s_f = \left(\frac{\lambda _2}{1-\lambda _2}( \frac{w_f}{w_m})^{(1-\eta ) (1-\gamma )} \right)^{1/\gamma },
\end{eqnarray}
and wg = wLg (j)α g ε g .
According to (12), the female consumption share changes either due to changes in the ratio
![]() $\frac{w_f}{w_m}$
(which correspond to the efficient allocation) or due to changes in the sharing rule λ (which are ex ante inefficient). In the case where the female wage drops by a third in the original steady state, her share of consumption drops by 8.7 percentage points. Removing the volatility of the share λ (i.e. imposing λ = 0.5 throughout) reduces the drop to 4.6 percentage points. Under the new tax schedule (in the final steady state) the reduction is in the order of 7.9 percentage points.
$\frac{w_f}{w_m}$
(which correspond to the efficient allocation) or due to changes in the sharing rule λ (which are ex ante inefficient). In the case where the female wage drops by a third in the original steady state, her share of consumption drops by 8.7 percentage points. Removing the volatility of the share λ (i.e. imposing λ = 0.5 throughout) reduces the drop to 4.6 percentage points. Under the new tax schedule (in the final steady state) the reduction is in the order of 7.9 percentage points.
We see that in the final steady state there is a benefit measured in reduced consumption variability, but overall it seems quite modest, at least relative to a full commitment allocation which keeps λ equal to 0.5. Notice however that since the effects are permanent it is possible that even a small (per period) change represents a considerable benefit for the individual. We will resolve this issue in a later paragraph.
5.3.2. Household rebargaining
In order to further investigate the impact of the reform on intrahousehold commitment let us return to the statistics reported in Table 3. As the results in Column 2 show, the change in policy causes a drop in the frequency of rebargaining by about 3.2 percentage points in the new steady state. Between ages 25 and 45 contracts are renegotiated nearly 10% less frequently, for households aged 50 to 65 roughly 39% less frequently, and for retired households roughly 78%. The largest drops (in percentage terms) are therefore experienced by older households. Our model produces similar results for the first period of the transition (e.g. Column 3 of the table).
These effects are clearly modest and it would be surprising if they contributed considerably towards increasing intrahousehold risk sharing for the following reasons: First, because as discussed previously, young households which bargain more frequently experience only a moderate drop in rebargaining (in fact there is a rise in rebargaining at age 25 as households start their working lives with zero wealth). Second, because older households rebargain too little anyway since they own sufficient wealth in the initial steady state and therefore do not benefit from the more substantial loosening of the limited commitment friction.
5.3.3. Partial equilibrium effects
The last two columns of Table 3 present statistics drawn from a partial equilibrium analysis. In the column labeled ‘Only τ K ’ we consider setting the capital tax equal to zero, and keeping all other quantities (taxes, wages, interest rates, etc.) to the original steady state values. The column labeled ‘Only τ N ’ refers to a model where the labor tax increases to the final steady state value and all other aggregates are kept constant.
Two remarks are important: First, as we noted in Section 2.2, increasing labor taxation may, or may not, lead to less frequently binding participation constraints when γ > 1. On the one hand, as after-tax income inequality within the household is reduced, rebargaining will probably occur less often; on the other, when total household labor income is lower, the temptation to renege on the contract increases. The results shown in Column 5 demonstrate that overall the second channel dominates. Therefore, it is only the reduction in τ K in the model which improves commitment. Second, these results confirm that accounting for general equilibrium effects is important to not overstate the gains from the reform on the intrahousehold allocation. In Section 2.2 we had stated our analysis in partial equilibrium, but we had explained that movements in interest rates and wages may mitigate the effects of changes in the tax schedule. The results shown in the last columns of the table are in line with this intuition.
5.3.4. Consumption volatility effects of improved commitment
When shocks to individual labor income occur, individual consumption is affected more if the household sharing rule changes. In the case where λ is constant over time, intrahousehold risk sharing is maximized. This corresponds to a full commitment allocation. When λ is updated frequently in response to shocks, intrahousehold insurance is weakened. We measure the effects of the policy change on the volatility of individual consumption in Figure 3. We have computed the conditional standard deviation of the log of consumption for each individual from a panel of 3,60,000 individuals and averaged by age group. Subsequently, we have computed the percentage changes in the volatility in various models relative to the original steady state. The figure reports these changes.Footnote 30
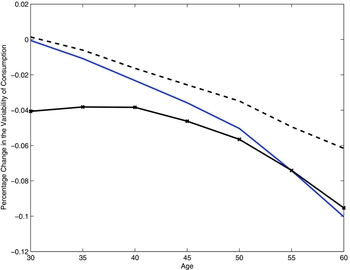
Figure 3. Individual Consumption Uncertainty.
Note: The figure plots changes in the variance of individual consumption relative to the original steady state. The solid line is the change in the final steady state. In order to measure the contribution of improved commitment, in the dashed line we represent the change in consumption volatility when we remove the influence of wealth but allow the household to be able to commit to the allocation as in the new steady state. For the sake of comparison, the crossed line in the figure represents a constant λ (full commitment) allocation.
The solid line represents the change in the final steady state. Notice that individual consumption uncertainty drops over the working life. By age 40, there is a 2% drop in the standard deviation and by age 50 a 4% drop. There are two possible explanations for this: First, more commitment, under the new policy, improves risk sharing (owing to the fact that families rebargain less frequently as we previously established). Second, higher wealth permits to the household to smooth the impact of shocks to consumption (e.g. through precautionary savings).
In order to measure the contribution of improved commitment in the dashed line we represent the change in consumption volatility when we remove the influence of wealth but allow the household to be able to commit to the initial allocation as in the new steady state. We accomplish this by keeping wealth constant as in the initial steady state and simulating household behavior under the final steady state paths for λ.
The graph indicates that across all age cohorts (with the exception of age 30), more commitment accounts for roughly 50% of the overall drop in consumption variability, the remaining 50% being accounted for by wealth.Footnote 31 Notice however that these changes are again not a significant improvement; they do not lead to a large drop in consumption uncertainty for young individuals, that typically face higher consumption variability. Therefore, the new policy confers only a small improvement in terms of reducing variability when variability is high and rather it reduces uncertainty when households have already build-up wealth so that the overall consumption uncertainty is smaller.
To further highlight these findings, in the crossed line in the figure we represent a constant λ (full commitment) allocation with household wealth as in the initial steady state. Under full commitment, there is a much larger reduction in consumption uncertainty at young ages. We conclude that at least for young households, the policy reform does not bring the allocation sufficiently close to the full commitment benchmark.
5.3.5. Conditional volatility of the sharing rule
In this paragraph we illustrate the effects of the change in taxes separately by household age and wealth. In Figure 4, we show the standard deviation of the share λ across different age groups and for different wealth levels. The solid line shows this standard deviation when households are at the borrowing constraint (age varies along the horizontal axis but initial wealth is kept constant for each age group). The dashed line represents the analogous object when initial wealth is set equal to the average wealth of families with the lowest fixed effect. The crossed line corresponds to the average wealth in the economy as the initial condition. The left panel in the figure represents the initial steady state and the right panel the final steady state. The figure shows clearly the influence of age and wealth on commitment that we previously identified.Footnote 32
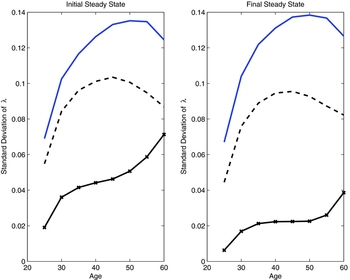
Figure 4. Volatility of the Sharing Rule.
Note: The figure plots the standard deviation of λ for various age groups, controlling for wealth. For each age, we have computed the share for all possible realizations of the state vector in the next period. In the solid line, we represent the standard deviation of the sharing rule when the household is at the borrowing constraint. In the dashed line wealth is at the average of the low fixed effect families in the model. In the crossed line wealth is set equal to the average wealth in the economy.
Let us now look at how these curves shift in the final steady state. Notice that the only curve which shifts downwards (thus showing a reduction in the variance of λ) is the crossed curve. Basically, households with very little initial wealth do not gain at all from the reform in terms of commitment. Wealthier households gain more, at the same time these households suffer much less from the limited commitment friction. This is another way of summarizing the modest impact from policy found in the previous paragraphs.
5.4. Welfare Evaluation
In Table 6, we look at the welfare effects of the change in the tax code. We define our welfare measure as the percentage increment in consumption that keeps expected welfare constant across the two economies (with and without the reform). We report the average value of this quantity for all individuals in our economy, assigning equal weight to each individual in the welfare function, and separately for males and females single and married.Footnote 33
Table 6. Welfare effects from the reform
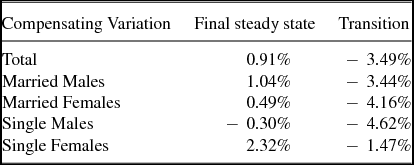
The table shows the percentage increment in consumption that keeps expected welfare constant as in the original steady state.
As the first column shows married households and single female households are on average better off in the final steady state without capital taxation. Single females enjoy the largest welfare gains (2.32% in terms of consumption). Married men seem to benefit more than married women from the reform (1.04% vs. 0.49%). In contrast, single male households are on average worse off in the final steady state. In the first period of the transition (Column 2), individuals lose on average from the change in policy, and the largest loses are incurred by single males who are willing to give up 4.62% of consumption to stay in the old regime.
To understand the different welfare responses across household types several remarks are important. First, note that single male and single female households differ mainly in terms of their respective life cycle productivity paths. As discussed previously, in the US data the productivity path of men rises steeply with age (see the results of Hansen (Reference Hansen1993)). Consequently, in the model men want to borrow against their permanent income to smooth consumption but cannot do so due to the presence of the borrowing constraint. When capital taxes are replaced by labor taxes, young single men experience a fall in income which makes their consumption path even steeper over the life cycle.Footnote 34 Female productivity on the other hand is not steeply rising. Therefore, young single women in the model are not made as worse off when the policy changes.
Second, consider the case of couples. As most of the married household’s income comes from the husband, couples are more like single men than single women. That is to say, the couple cannot to a great effect smooth the life cycle income profile by allocating more hours to the wife at the early stages of the working life. Therefore in terms of the welfare outcomes the gender differences in life cycle labor income are not important.
However, couples are different from singles in one other respect. They are at least partially able to insure against fluctuations in labor income through joint adjustments in labor supply and through transfers from one spouse to the other. These transfers are substantial in the model, even in the presence of the limited commitment friction, and weaken the incentive of couples to self-insure against income shocks via precautionary savings.Footnote 35 In this case, we can make the argument that high capital taxes should be more distortionary for couples than for single households since, as is well known, a strong demand for precautionary savings is associated with a less distortionary impact of capital taxation (see Domeij and Heathcote (Reference Domeij and Heathcote2004)).Footnote 36 We illustrated in a previous subsection that after the reform, there is a stronger increase in capital accumulation in dual earner households. The wealth of married households increased by 9.5% in the final steady state whereas the average increase in single households was in the order of 6.6%. Therefore, through this channel couples benefit more from the reform.Footnote 37
Now let us return to the impact of the new policy on intrahousehold risk sharing. Suppose that policy had a large impact on this margin (through enhancing commitment). Then we would anticipate to find considerably larger welfare gains for couples than for single households. The results documented here show that there is only a modest impact which does not add much to the welfare calculation. Couples experience gains and loses from the reform which are well within the range of gains experienced by single households.
5.4.1. Division of welfare gains and loses within the household
Married men do better than married women according to the welfare measure in Table 6. This may seem surprising in light of the fact single women do better than single men. However, the outside options of married individuals exhibit a different welfare response to the reform because the wealth profiles between singles and couples are different.
To explain why married women do worse than married men note that as we have previously shown, after the reform couples are better able to commit to the initial allocation. This is a crucial observation because in our calibration we gave to women a large initial share (low λ) to match average hours as in the data. Consequently, in the model married men seek to rebargain after a few periods when male (relative to female) life cycle productivity grows. The expectation of this future rebargaining makes men willing to tolerate a lower starting value of λ in the initial steady state. When the tax code changes, however, and commitment to the initial allocation improves, married men anticipate a smaller renegotiation of the contract in the future. In effect, they want an increase in λ at the matching stage to compensate. Consistent with this view our model generates an increase in the average male share at the initial allocation by roughly one percentage point.
5.4.2. Welfare gains from commitment
Our theory predicts that lowering capital taxation affects intrahousehold risk sharing and lowers individual consumption uncertainty. In this paragraph, we investigate whether the improvement in insurance possibilities documented previously generates substantial welfare gains to households. In order to isolate the effect of ‘more commitment’ from changes in the wealth paths, we keep wealth constant as in the old steady state. We consider the following cases: 1. the household is able to commit as in the final steady state (the paths of λ are those of the final steady state), 2. the household can commit as in the old steady state (the paths of λ are those of the old steady state) and 3. the household can fully commit (λ is constant over time). To calculate the welfare benefit from commitment we compute the average value of the compensating variation between 2. and 1. In order to quantify how far this welfare gain is from the full commitment allocation we compare 2. and 3.
Our results are as follows: First we find that the welfare gain from improved commitment in the final steady state is tiny, roughly 0.062% of consumption. Second, we obtain a welfare gain from full commitment that is substantial, roughly 0.82% of consumption. These results reinforce our previous findings.
5.5. Robustness and Discussion
5.5.1. Log-separable utility
We briefly discuss the effects of the reform when utility is separable in consumption and leisure. In this version of our model, we keep all of the parameters as in the benchmark.Footnote 38 We find that in the old steady state, families rebargain 10.47% on average. This fraction is 12.58% for ages 25–45, 11.30% between ages 50 and 65 and 0.26% in retirement. In the new steady state, overall rebargaining drops to 9.83%. For the age groups we obtain 13.06%, 8.48% and 0.05% respectively. These results are in line with our previous analysis of non-separable utility. This suggests that the exact specification of preferences is not important for our quantitative findings.
5.5.2. The (Potential) effects of the tax code on the decision to divorce
Our theoretical results were derived from a model in which couples do not divorce in equilibrium. This assumption, which is rather common in the literature (see for example Alesina et al. (Reference Alesina, Ichino and Karabarbounis2011), Guner et al. (Reference Guner, Kaygusuz and Ventura2012a) and Guner et al. (Reference Guner, Kaygusuz and Ventura2012b)), is made to isolate our focus on the effects of the tax code on the limited commitment friction within the marriage. However, we wish in this paragraph to briefly describe the potential effects of taxes on the decision to divorce if we were to give this option to the family.
We begin with two period model of Section 2. In that model a couple would not divorce as long as ξ > 0, since, as discussed previously, it is always possible in the second period to give to the spouses what they would get if they were singles (i.e.
![]() $\frac{A_c}{2} + \epsilon _g w (1-\tau _N)$
). Divorces may occur in that model if ξ in period 2 can be negative.Footnote
39
We describe here how changes in the value of ξ over time, which can motivate endogenous divorces, affect our results.
$\frac{A_c}{2} + \epsilon _g w (1-\tau _N)$
). Divorces may occur in that model if ξ in period 2 can be negative.Footnote
39
We describe here how changes in the value of ξ over time, which can motivate endogenous divorces, affect our results.
To simplify assume that preferences are log-separable. If the couple draws a random value ξ2 in period 2 we can derive the updating rule for the share λ as
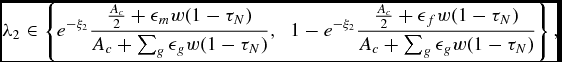 \begin{eqnarray}
\lambda _2 \in \left\lbrace e^{-\xi _2} \frac{ \frac{A_c}{2}+\epsilon _m w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)}, \;\; 1-e^{-\xi _2} \frac{ \frac{A_c}{2}+\epsilon _f w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)} \right\rbrace ,
\end{eqnarray}
\begin{eqnarray}
\lambda _2 \in \left\lbrace e^{-\xi _2} \frac{ \frac{A_c}{2}+\epsilon _m w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)}, \;\; 1-e^{-\xi _2} \frac{ \frac{A_c}{2}+\epsilon _f w (1-\tau _N)}{A_c + \sum _g \epsilon _g w (1-\tau _N)} \right\rbrace ,
\end{eqnarray}
for ξ2 ⩾ 0. Note that if the couple were to divorce (with ξ2 < 0) the above expression becomes irrelevant; then the tax schedule has no effect on the intrahousehold allocation. Moreover, since the decision to divorce solely hinges on the value of ξ2, changes in taxes have no impact on this margin. The tax schedule cannot make the marital surplus positive and sustain the marriage.
This however does not mean that shocks which produce endogenous divorces do not have a potentially important interaction with tax rates. To see this consider the case of a low (but positive) value of ξ2. Then if ε m ≫ ε f , the impact of limited commitment becomes more severe. In this case having higher wealth is useful to insulate the share λ2 from shocks to the value ξ2.
The following observation is important: Notice that from (15) it is easy to show that wealth and taxes have a bigger effect the closer ξ2 is to zero. Conversely, if ξ2 is large, the limited commitment problem is not severe, and changes in policy will not affect risk sharing substantially. In the quantitative model we have set ξ to a very low value. Therefore, our results exacerbate the effect of the limited commitment friction and the effects of policy.Footnote 40
Finally, it is worth noting that under the multiperiod model we should not anticipate that taxes are neutral with respect to the decision to divorce. To investigate how the change in the tax schedule impacts the divorce decision in the quantitative model we have conducted the following experiment: We solved the model with a lower value of ξ (relative to our benchmark calibration) and looked at the marital surplus from the value functions. The numerical solution of the model suggested that when we abolish the capital tax the regions in the state space over which divorce is optimal, widens.Footnote 41 Therefore, it seems that if we were to endogenize divorce in the model, we would obtain a rise in divorce rates in equilibrium. Though we acknowledge that such effects are not trivial, a higher divorce rate goes against the notion that lowering capital taxation generates insurance gains for married households. It therefore does not contradict our conclusions.
6. CONCLUSION
In this paper, we study the welfare effects of a reform that eliminates capital taxation in a model with gender and marital status heterogeneity, uncertain labor income and incomplete financial markets. Decision making within the couple is represented as a contract under limited commitment. When the labor income of one spouse increases the household must allocate a higher weight to her well being. The household gives up some risk sharing to satisfy a participation constraint.
We investigate how the tax code affects the intrahousehold allocation and especially the risk sharing possibilities of the couple. We show that lower capital taxes lead to wealth accumulation and more insurance within the family. Our theory motivates this through the empirical observation that wealth is a commonly held resource within US households. On the other hand, we show that higher labor taxes, have an ambiguous effect; they make the distribution of disposable income less dispersed and therefore alleviate the limited commitment problem, but they also reduce the overall household resources and may make more tempting to renege on past commitments.
In our quantitative life cycle model, we find that when the policy changes the new intrahousehold allocation features less rebargaining, and therefore more insurance, but the overall effect is small. The reason for this is that young households which typically do not hold a lot of assets, do not experience any gain in commitment, and old households which theoretically could gain more from the policy change, have accumulated sufficient wealth and are not impacted by the limited commitment friction.
Though we have found a small effect, considering a shift in a linear tax schedule, we believe that there is scope to further investigate the impact of taxes on the intrahousehold allocation. For example, in the case of nonlinear taxation the effects from policy on the outside options of individuals and on the distribution of resources within the family could be substantial. The two period model we presented can be a useful apparatus to think of such policies: For instance, if the government gives a subsidy to poor households and taxes the labor income of wealthy families, our results demonstrated that this scheme will improve intrahousehold risk sharing. The quantitative model proposed in this paper can be used to study the dynamic aspects of such policies.
SUPPLEMENTARY MATERIAL
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/dem.2015.7.
A. APPENDIX
A.1. Derivations in the Two Period Model
In this section, we derive explicitly the formulas from the two period model of Section 2 that were omitted from the text. We assume that household members value the consumption-leisure bundle according to a utility function of the form
![]() $\frac{(c_g^{\eta } l_g ^{1-\eta })^{1-\gamma }}{1-\gamma }$
. The optimal consumption and leisure choices in period 2 satisfy:
$\frac{(c_g^{\eta } l_g ^{1-\eta })^{1-\gamma }}{1-\gamma }$
. The optimal consumption and leisure choices in period 2 satisfy:
Assuming an interior solution, we can substitute the intraperiod consumption-leisure optimality condition into the consumption first-order condition and obtain:
 \begin{equation*}
\lambda _2 \frac{ c_m^{-\gamma }}{ (w(1-\tau _N) \epsilon _m)^{(1-\eta )(1-\gamma )}}=(1-\lambda _2) \frac{ c_f^{-\gamma }}{ (w(1-\tau _N) \epsilon _f)^{(1-\eta )(1-\gamma )}},
\end{equation*}
\begin{equation*}
\lambda _2 \frac{ c_m^{-\gamma }}{ (w(1-\tau _N) \epsilon _m)^{(1-\eta )(1-\gamma )}}=(1-\lambda _2) \frac{ c_f^{-\gamma }}{ (w(1-\tau _N) \epsilon _f)^{(1-\eta )(1-\gamma )}},
\end{equation*}
which gives that female consumption is
![]() $f(\lambda _2 ,\epsilon ) = (\frac{\lambda _2}{1-\lambda _2}( \frac{\epsilon _f}{\epsilon _m})^{(1-\eta ) (1-\gamma )} )^{-1/\gamma }$
times male consumption in the model. Solving for the optimal choices, we can write male and female utility as
$f(\lambda _2 ,\epsilon ) = (\frac{\lambda _2}{1-\lambda _2}( \frac{\epsilon _f}{\epsilon _m})^{(1-\eta ) (1-\gamma )} )^{-1/\gamma }$
times male consumption in the model. Solving for the optimal choices, we can write male and female utility as
 \begin{eqnarray*}
\left( \frac{A_c + \sum _g w (1-\tau _N) \epsilon _g }{(1+ f(\lambda _2, \epsilon ) ) {(w (1-\tau _N) \epsilon _m)} )^{1-\eta } } \right)^{1-\gamma } \frac{\chi }{1-\gamma }
+ \xi &\ge& \left( \frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _m }{(w (1-\tau _N) \epsilon _m )^{1-\eta }} \right) ^{1-\gamma }\nonumber\\
&&\times\, \frac{\chi }{1-\gamma }\nonumber\\
\left( \frac{f(\lambda _2, \epsilon )}{(1+ f(\lambda _2, \epsilon ))} \frac{A_c + \sum _g w (1-\tau _N) \epsilon _g }{ (w (1-\tau _N) \epsilon _f) ^{1-\eta }} \right)^{1-\gamma } \frac{\chi }{1-\gamma }+ \xi &\ge& \left(\frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _f }{ (w (1-\tau _N) \epsilon _f )^{1-\eta } }\right)^{1-\gamma }\nonumber\\
&&\times\, \frac{\chi }{1-\gamma }
\end{eqnarray*}
\begin{eqnarray*}
\left( \frac{A_c + \sum _g w (1-\tau _N) \epsilon _g }{(1+ f(\lambda _2, \epsilon ) ) {(w (1-\tau _N) \epsilon _m)} )^{1-\eta } } \right)^{1-\gamma } \frac{\chi }{1-\gamma }
+ \xi &\ge& \left( \frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _m }{(w (1-\tau _N) \epsilon _m )^{1-\eta }} \right) ^{1-\gamma }\nonumber\\
&&\times\, \frac{\chi }{1-\gamma }\nonumber\\
\left( \frac{f(\lambda _2, \epsilon )}{(1+ f(\lambda _2, \epsilon ))} \frac{A_c + \sum _g w (1-\tau _N) \epsilon _g }{ (w (1-\tau _N) \epsilon _f) ^{1-\eta }} \right)^{1-\gamma } \frac{\chi }{1-\gamma }+ \xi &\ge& \left(\frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _f }{ (w (1-\tau _N) \epsilon _f )^{1-\eta } }\right)^{1-\gamma }\nonumber\\
&&\times\, \frac{\chi }{1-\gamma }
\end{eqnarray*}
where χ = (ηη(1 − η)1 − η)1 − γ. Rearranging, we can express the sharing rule with the following nonlinear equations:
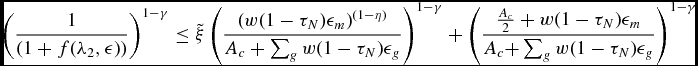 \begin{eqnarray}
\left(\frac{1}{(1+ f(\lambda _2, \epsilon ) ) } \right)^{1-\gamma } \le \tilde{\xi } \left(\frac{ (w (1-\tau _N) \epsilon _m )^{(1-\eta ) }}{A_c + \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma } + \left(\frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _m }{A_c {+} \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma }\!\!\!\!\!\!\!\! \nonumber\\
\end{eqnarray}
\begin{eqnarray}
\left(\frac{1}{(1+ f(\lambda _2, \epsilon ) ) } \right)^{1-\gamma } \le \tilde{\xi } \left(\frac{ (w (1-\tau _N) \epsilon _m )^{(1-\eta ) }}{A_c + \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma } + \left(\frac{\frac{ A_c}{2} +w (1-\tau _N) \epsilon _m }{A_c {+} \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma }\!\!\!\!\!\!\!\! \nonumber\\
\end{eqnarray}
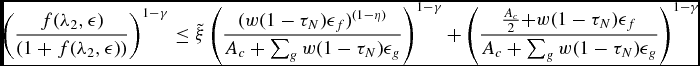 \begin{eqnarray}
\left( \frac{f(\lambda _2, \epsilon )}{(1+ f(\lambda _2, \epsilon ))} \right)^{1-\gamma } \le \tilde{\xi } \left(\frac{ (w (1-\tau _N) \epsilon _f )^{(1-\eta ) }}{A_c + \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma } {+} \left(\frac{\frac{ A_c}{2} {+}w (1-\tau _N) \epsilon _f }{A_c + \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma }\!\!\!\!\!\!\! \nonumber\\
\end{eqnarray}
\begin{eqnarray}
\left( \frac{f(\lambda _2, \epsilon )}{(1+ f(\lambda _2, \epsilon ))} \right)^{1-\gamma } \le \tilde{\xi } \left(\frac{ (w (1-\tau _N) \epsilon _f )^{(1-\eta ) }}{A_c + \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma } {+} \left(\frac{\frac{ A_c}{2} {+}w (1-\tau _N) \epsilon _f }{A_c + \sum _g w (1-\tau _N) \epsilon _g} \right)^{1-\gamma }\!\!\!\!\!\!\! \nonumber\\
\end{eqnarray}
where
![]() $\tilde{\xi } = - \frac{ \xi (1-\gamma )}{( \eta ^{\eta } (1-\eta )^{1-\eta })^{1-\gamma }} >0$
. In the text, we have used the notation
$\tilde{\xi } = - \frac{ \xi (1-\gamma )}{( \eta ^{\eta } (1-\eta )^{1-\eta })^{1-\gamma }} >0$
. In the text, we have used the notation
![]() $s_m(\lambda _2, \epsilon ) \equiv ( \frac{1}{(1+ f(\lambda _2, \epsilon ))} )$
.
$s_m(\lambda _2, \epsilon ) \equiv ( \frac{1}{(1+ f(\lambda _2, \epsilon ))} )$
.
The effect of changes in labor taxes. Equations (16) and (17) define the upper and the lower bound that the weight λ2 needs to respect in order for the participation constraints to be satisfied. The partial derivatives of the right-hand side of equation (16) with respect to (1 − τ N ) are
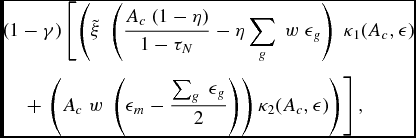 \begin{eqnarray}
&&(1-\gamma )\left[ \left (\tilde{\xi } \; \left( \frac{A_c \; (1-\eta )}{1-\tau _N} - \eta \sum _g \; w\; \epsilon _g \right) \; \kappa _1 (A_c , \epsilon )\right.\right.\nonumber\\
&&\quad\left.\left. +\, \left( A_c\; w \; \left( \epsilon _m - \frac{\sum _g \; \epsilon _g}{2}\right)\right) \kappa _2(A_c , \epsilon ) \right)\right],\nonumber\\
\end{eqnarray}
\begin{eqnarray}
&&(1-\gamma )\left[ \left (\tilde{\xi } \; \left( \frac{A_c \; (1-\eta )}{1-\tau _N} - \eta \sum _g \; w\; \epsilon _g \right) \; \kappa _1 (A_c , \epsilon )\right.\right.\nonumber\\
&&\quad\left.\left. +\, \left( A_c\; w \; \left( \epsilon _m - \frac{\sum _g \; \epsilon _g}{2}\right)\right) \kappa _2(A_c , \epsilon ) \right)\right],\nonumber\\
\end{eqnarray}
where
![]() $\kappa _1 = \frac{ (w (1-\tau _N) \epsilon _g)^{(1-\eta )(1-\gamma )}}{ (A_c + \sum _g w (1-\tau _N) \epsilon _m )^{2-\gamma }} >0$
,
$\kappa _1 = \frac{ (w (1-\tau _N) \epsilon _g)^{(1-\eta )(1-\gamma )}}{ (A_c + \sum _g w (1-\tau _N) \epsilon _m )^{2-\gamma }} >0$
,
![]() $\kappa _2 = \frac{(\frac{A_c}{2} +w (1-\tau _w) \epsilon _m )^{-\gamma } }{( A_c + \sum _g w (1-\tau _w) \epsilon _g )^{2-\gamma } } >0$
. The derivative of equation (17) is similar and for the sake of brevity omitted. As discussed in text, (18) illustrates that the effect of changes in labor taxation on the household sharing rule depends on the level of wealth of the household Ac
. If Ac
= 0, it reduces to
$\kappa _2 = \frac{(\frac{A_c}{2} +w (1-\tau _w) \epsilon _m )^{-\gamma } }{( A_c + \sum _g w (1-\tau _w) \epsilon _g )^{2-\gamma } } >0$
. The derivative of equation (17) is similar and for the sake of brevity omitted. As discussed in text, (18) illustrates that the effect of changes in labor taxation on the household sharing rule depends on the level of wealth of the household Ac
. If Ac
= 0, it reduces to
 \begin{eqnarray}
- (1-\gamma ) \left[\tilde{\xi } \eta \sum _g \; w\; \epsilon _g \right] \; \kappa _1 (A_c , \epsilon ) >0,
\end{eqnarray}
\begin{eqnarray}
- (1-\gamma ) \left[\tilde{\xi } \eta \sum _g \; w\; \epsilon _g \right] \; \kappa _1 (A_c , \epsilon ) >0,
\end{eqnarray}
As the LHS of (16) is decreasing in λ2, a positive partial derivative means that λ2 has to increase by less to satisfy the participation constraint of the male spouse. Therefore, in the case where ε m ≫ε f (the lower bound applies), the disturbance to the household sharing rule is smaller. The converse may obtain if Ac > 0. As in the case of log-separable utility, an overall negative derivative (18) yields that lowering labor taxes makes it more difficult for household members to commit to an allocation.
The effect of changes in capital taxes. We derive the partial derivative of equation (16) with respect to financial income as
 \begin{eqnarray}
&&(\gamma -1)\left[ \tilde{\xi } \; (\frac{ (w (1-\tau _N) \epsilon _m )^{(1-\eta ) }}{A_c + \sum _g w (1-\tau _N) \epsilon _g )^{2-\gamma }}\right.\nonumber\\
&&\quad\left. +\, (\frac{(\frac{ A_c}{2} +w (1-\tau _N) \epsilon _m )^{-\gamma } }{(A_c + \sum _g w (1-\tau _N) \epsilon _g)^{2-\gamma })} \left( \epsilon _m-\frac{\sum _g \epsilon _g}{2}\right)\right].
\end{eqnarray}
\begin{eqnarray}
&&(\gamma -1)\left[ \tilde{\xi } \; (\frac{ (w (1-\tau _N) \epsilon _m )^{(1-\eta ) }}{A_c + \sum _g w (1-\tau _N) \epsilon _g )^{2-\gamma }}\right.\nonumber\\
&&\quad\left. +\, (\frac{(\frac{ A_c}{2} +w (1-\tau _N) \epsilon _m )^{-\gamma } }{(A_c + \sum _g w (1-\tau _N) \epsilon _g)^{2-\gamma })} \left( \epsilon _m-\frac{\sum _g \epsilon _g}{2}\right)\right].
\end{eqnarray}
The leading term in (20) is always positive, meaning that an increase of financial income relaxes the constraint. The second term is positive only when ε m > ε f . Since equation (16) defines the lower bound on λ2, it binds only when male productivity exceeds female productivity. Therefore, higher financial wealth and lower capital taxation enhance the household’s commitment. This proves Proposition 3 in the main text.
A.2. Competitive Equilibrium
In this section, we briefly define the time invariant competitive equilibrium. Given a level of expenditure G in the steady state, the tax schedule {τ K , τ W , τ C , τ SS }, social security policy and unintended bequests, the competitive equilibrium is a set of value functions {Sg , M, Vg }, household decision rules for consumption, savings and leisure, and measures of households over the state vector of assets, productivity, age, gender, marital status and the sharing rule λ such that:
-
1. Given prices, Sm , Sf and M solve the functional equations and optimal policies derive. In particular, optimal policies are functions c S, g (a, X, j), a′ S, g (a, X, j), n S, g (a, X, j) for consumption, assets and hours for singles and analogously c M, g (a, X, λ, j), a′ M (a, X, λ, j), n M, g (a, X, λ, j) for couples.
-
2. Prices w and r satisfy:
where N is the aggregate labor input in units of effective labor. \begin{equation*}
w= (1-\alpha ) K^{\alpha } N^{-\alpha } \;\;\;\;\;\; r = \alpha K^{\alpha -1} N^{1-\alpha } - \delta ,
\end{equation*}
\begin{equation*}
w= (1-\alpha ) K^{\alpha } N^{-\alpha } \;\;\;\;\;\; r = \alpha K^{\alpha -1} N^{1-\alpha } - \delta ,
\end{equation*}
-
3. The social security policy satisfies:
where Γ S, g is the measure of bachelors over relevant states and Γ M is the analogous object for married couples. \begin{eqnarray*}
{w N\tau _{SS} }&=& \left(\sum _g \frac{1-\mu }{2} \int SS_g(\alpha ,j) \Gamma _{S,g} ( da \times dX \times \lbrace j_R, \ldots ,J\rbrace )\right.\nonumber\\
&&\left.+\, \mu \int SS_g(\alpha ,j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace j_R, \ldots , J\rbrace ) \right),
\end{eqnarray*}
\begin{eqnarray*}
{w N\tau _{SS} }&=& \left(\sum _g \frac{1-\mu }{2} \int SS_g(\alpha ,j) \Gamma _{S,g} ( da \times dX \times \lbrace j_R, \ldots ,J\rbrace )\right.\nonumber\\
&&\left.+\, \mu \int SS_g(\alpha ,j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace j_R, \ldots , J\rbrace ) \right),
\end{eqnarray*}
-
4. Accidental bequests satisfy:
 \begin{eqnarray*}
B&=& \frac{1 }{\Phi ^o} \Big( \sum _g \frac{1-\mu }{2} \int a^{\prime }_{S,g}(a, X , j) (1-\psi _j) \Gamma _{S,g} ( da \times dX \times \lbrace 1 , \ldots , j_R-1\rbrace ) \nonumber\\
&&+\, \mu \int a^{\prime }_{M} (a, X , \lambda , j) (1-\psi _j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace 1 , \ldots , j_R-1\rbrace ).
\end{eqnarray*}
\begin{eqnarray*}
B&=& \frac{1 }{\Phi ^o} \Big( \sum _g \frac{1-\mu }{2} \int a^{\prime }_{S,g}(a, X , j) (1-\psi _j) \Gamma _{S,g} ( da \times dX \times \lbrace 1 , \ldots , j_R-1\rbrace ) \nonumber\\
&&+\, \mu \int a^{\prime }_{M} (a, X , \lambda , j) (1-\psi _j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace 1 , \ldots , j_R-1\rbrace ).
\end{eqnarray*}
-
5. The government budget constraint is balanced:
 \begin{eqnarray*}
G&=& w \tau _N \left( \sum _g \frac{1-\mu }{2}\int n_{S,g}(a, X , j) L_g(j) \epsilon _g \alpha _g \Gamma _{S,g} ( da \times dX \times \lbrace 1 , \ldots , j_R-1\rbrace )\right. \nonumber\\
&&\left.+\, \sum _g \mu \int n_{M,g} (a, X , \lambda , j) \alpha _g \epsilon _g L_g(j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace 1 , \ldots , j_R-1\rbrace ) \right) \nonumber\\
&&+\, \tau _C \left( \sum _g \frac{1-\mu }{2} \int c_{S,g}(a, X , j) \Gamma _{S,g} ( da \times dX \times dj )\right. \nonumber\\
&&\left. +\, \sum _g \mu \int c_{M,g} (a, X , \lambda , j) \Gamma _{M} ( da \times dX \times d \lambda \times dj)\right) \nonumber\\
&&+\, \tau _K \Big( \sum _g \frac{1-\mu }{2}\int ( r a +B) \Gamma _{S,g} ( da \times dX \times dj\nonumber\\
&& +\, \mu \int ( r a +2 B) \Gamma _{M} ( da \times dX \times d \lambda \times dj ).
\end{eqnarray*}
\begin{eqnarray*}
G&=& w \tau _N \left( \sum _g \frac{1-\mu }{2}\int n_{S,g}(a, X , j) L_g(j) \epsilon _g \alpha _g \Gamma _{S,g} ( da \times dX \times \lbrace 1 , \ldots , j_R-1\rbrace )\right. \nonumber\\
&&\left.+\, \sum _g \mu \int n_{M,g} (a, X , \lambda , j) \alpha _g \epsilon _g L_g(j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace 1 , \ldots , j_R-1\rbrace ) \right) \nonumber\\
&&+\, \tau _C \left( \sum _g \frac{1-\mu }{2} \int c_{S,g}(a, X , j) \Gamma _{S,g} ( da \times dX \times dj )\right. \nonumber\\
&&\left. +\, \sum _g \mu \int c_{M,g} (a, X , \lambda , j) \Gamma _{M} ( da \times dX \times d \lambda \times dj)\right) \nonumber\\
&&+\, \tau _K \Big( \sum _g \frac{1-\mu }{2}\int ( r a +B) \Gamma _{S,g} ( da \times dX \times dj\nonumber\\
&& +\, \mu \int ( r a +2 B) \Gamma _{M} ( da \times dX \times d \lambda \times dj ).
\end{eqnarray*}
-
6. Market Clearing:
 \begin{eqnarray*}
K &=& \sum _g \int \frac{1-\mu }{2} a \Gamma _{S,g} ( da \times dX \times dj )\; + \; \mu \int a \Gamma _{M} ( da \times dX \times d \lambda \times dj )\nonumber\\
N &=& \sum _g \frac{1-\mu }{2}\int n_{S,g}(a, X , j) L_g(j) \epsilon _g \alpha _g \Gamma _{S,g} ( da \times dX \times \lbrace 1 , \ldots , j_R-1\rbrace ) \nonumber\\
&&+ \sum _g \mu \int n_{M,g} (a, X , \lambda , j) \alpha _g \epsilon _g L_g(j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace 1 , \ldots , j_R-1\rbrace ).
\end{eqnarray*}
\begin{eqnarray*}
K &=& \sum _g \int \frac{1-\mu }{2} a \Gamma _{S,g} ( da \times dX \times dj )\; + \; \mu \int a \Gamma _{M} ( da \times dX \times d \lambda \times dj )\nonumber\\
N &=& \sum _g \frac{1-\mu }{2}\int n_{S,g}(a, X , j) L_g(j) \epsilon _g \alpha _g \Gamma _{S,g} ( da \times dX \times \lbrace 1 , \ldots , j_R-1\rbrace ) \nonumber\\
&&+ \sum _g \mu \int n_{M,g} (a, X , \lambda , j) \alpha _g \epsilon _g L_g(j) \Gamma _{M} ( da \times dX \times d \lambda \times \lbrace 1 , \ldots , j_R-1\rbrace ).
\end{eqnarray*}
-
7. The measures Γ S, g and Γ M are consistent. In particular, for all subsets
 $\mathcal {A} , \mathcal {X} , \Lambda , \mathcal {J}$
of the state space such that
$\mathcal {A} , \mathcal {X} , \Lambda , \mathcal {J}$
of the state space such that
 $1 \notin \mathcal {J}$
$1 \notin \mathcal {J}$
 \begin{eqnarray*}
&&\Gamma _{S,g}( \mathcal {A} , \mathcal {X} , \mathcal {J}) = \psi _j \int _{X^{\prime } \in \mathcal {X} , \; a^{\prime }_{S,g} \in \mathcal {A}, \; j+1 \in \mathcal {J} } \Gamma _{S,g} ( da \times dX \times d j )\nonumber\\
&&\Gamma _{M,g}( \mathcal {A} , \mathcal {X} , \Lambda , \mathcal {J}) = \psi _j \int _{X^{\prime } \in \mathcal {X} , \; a^{\prime }_{M,g} \in \mathcal {A}, \; \lambda ^{\prime } \in \Lambda , \; j+1 \in \mathcal {J} } \Gamma _{M,g} ( da \times dX \times d \lambda \times d j )
\end{eqnarray*}
\begin{eqnarray*}
&&\Gamma _{S,g}( \mathcal {A} , \mathcal {X} , \mathcal {J}) = \psi _j \int _{X^{\prime } \in \mathcal {X} , \; a^{\prime }_{S,g} \in \mathcal {A}, \; j+1 \in \mathcal {J} } \Gamma _{S,g} ( da \times dX \times d j )\nonumber\\
&&\Gamma _{M,g}( \mathcal {A} , \mathcal {X} , \Lambda , \mathcal {J}) = \psi _j \int _{X^{\prime } \in \mathcal {X} , \; a^{\prime }_{M,g} \in \mathcal {A}, \; \lambda ^{\prime } \in \Lambda , \; j+1 \in \mathcal {J} } \Gamma _{M,g} ( da \times dX \times d \lambda \times d j )
\end{eqnarray*}