1 Introduction
Dependently typed languages such as Coq, Agda, Idris, and F* allow programmers to write full-functional specifications for a program (or program component), implement the program, and prove that the program meets its specification. These languages have been widely used to build formally verified high-assurance software including the CompCert C compiler (Leroy, Reference Leroy2009), the CertiKOS operating system kernel (Gu et al., Reference Gu, Koenig, Ramananandro, Shao, Wu, Weng, Zhang and Guo2015; Gu et al., Reference Gu, Shao, Chen, Wu, Kim, SjÖberg and Costanzo2016), and cryptographic primitives (Appel, Reference Appel2015) and protocols (Barthe et al., Reference Barthe, Grégoire and Zanella-Béguelin2009).
Unfortunately, even these machine-verified programs can misbehave when executed due to errors introduced during compilation and linking. For example, suppose we have a program component S written and proven correct in a source language like Coq. To execute S, we first compile S from Coq to a component T in OCaml. If the compiler from Coq to OCaml introduces an error, we say that a miscompilation error occurs. Now T contains an error despite S being verified. Because S and T are not whole programs, T will be linked with some external (i.e., not verified in Coq) code C to form the whole program P. If C violates the original specification of S, then we say a linking error occurs and P may contain safety, security, or correctness errors.
A verified compiler prevents miscompilation errors, since it is proven to preserve the run-time behavior of a program, but it cannot prevent linking errors. Note that linking errors can occur even if S is compiled with a verified compiler, since the external code we link with, C, is outside of the control of either the source language or the verified compiler. Ongoing work on CertiCoq (Anand et al., Reference Anand, Appel, Morrisett, Paraskevopoulou, Pollack, Bélanger, Sozeau and Weaver2017) seeks to develop a verified compiler for Coq, but it cannot rule out linking with unsafe target code. One can develop simple examples in Coq that, once compiled to OCaml and linked with an unverified OCaml component, jump to an arbitrary location in memory—despite the Coq component being proven memory safe. We provide an example of this in the supplementary materials.
To rule out both miscompilation and linking errors, we could combine compiler verification with type-preserving compilation. A type-preserving compiler preserves types, representing specifications, into a target typed intermediate language (IL). The IL uses type checking at link time to enforce specifications when linking with external code, essentially implementing proof-carrying code (Necula, Reference Necula1997). After linking in the IL, we have a whole program, so we can erase types and use verified compilation to machine code. To support safe linking with untyped code, we could use gradual typing to enforce safety at the boundary between the typed IL and untyped components (Ahmed, Reference Ahmed2015; Lennon-Bertrand et al., Reference Lennon-Bertrand, Maillard, Tabareau and Tanter2022). Applied to Coq, this technique would provide significant confidence that the executable program P is as correct as the verified program S.
We consider this particular application of type preservation important for compiler verification and for protecting the trusted computing base when working in a dependently typed language, but type preservation has other long studied applications. Type-preserving compilers can provide a lightweight verification procedure using type-directed proof search (Chlipala, Reference Chlipala2007), can be better equipped to handle optimizations and changes than a certified compiler (Tarditi et al., Reference Tarditi, Morrisett, Cheng, Stone, Harper and Lee1996; Chen et al., Reference Chen, Hawblitzel, Perry, Emmi, Condit, Coetzee and Pratikaki2008), and can support debugging internal compiler passes (Peyton Jones, Reference Peyton Jones1996).
Unfortunately, dependent-type preservation is difficult because compilation that preserves the semantics of the program may disrupt the syntax-directed typing of the program. This is particularly problematic with dependent types since expressions from a program end up in specifications expressed in the types. As the compiler transforms the syntax of the program, the expressions in types can become “out of sync” with the expressions in the compiled program.
To preserve dependent typing, the type system of the IL needs access to the semantic equivalences relied upon by compilation. Past work has used strong axioms, including parametricity and impredicativity, to recover these equivalences (Bowman et al., Reference Bowman, Cong, Rioux and Ahmed2018). However, this approach does not support all dependent type system features, particularly predicative universe hierarchies (which are anti-impredicative) or ad hoc polymorphism and type quotation (which is anti-parametric) (Boulier et al., Reference Boulier, Pédrot and Tabareau2017). Dependently typed languages, such as Coq, restrict impredicative quantification as it is inconsistent with other features and axioms, such as excluded middle and large elimination. Restricting impredicativity restricts type-level abstraction, so such languages often add a predicative universe hierarchy—abstractions over types live in a higher universe than the parameter, and so on. Higher universes enable recovering the ability to abstract over types and the types of types, etc., which is useful for generic programming and abstract mathematics. This means reliance on parametricity and impredicativity restrict which source programs can be compiled and thus cannot be applied in practice. To scale to a realistic dependently typed language such as Coq, we must encode these semantic equivalences in the type system without restricting core features.
To preserve dependent types, the compiler IL must encode the semantic equivalences relied upon by compilation. In this work, we do this using extensionality, which allows the type system to consider two types (or two terms embedded in a type) definitionally equivalent if the program contains an expression representing a proof that the two types (or terms) are equal. Using this feature, the translation can insert hints for the type system about which terms it can assume to be equivalent and provide proofs of those facts elsewhere to discharge these assumptions. This approach scales to higher universes and other features that prior work could not handle and does so without relying on parametricity or impredicativity in the target IL. Relying on extensionality has one key downside: decidable type checking becomes more complex. We discuss how to mitigate this downside in Section 7.
We present a dependent-type-preserving translation to A-normal form (ANF), a compiler intermediate representation that makes control flow explicit and facilitates optimizations (Sabry & Felleisen, Reference Sabry and Felleisen1992; Flanagan et al., Reference Flanagan, Sabry, Duba and Felleisen1993). The source of this translation is ECC, the Extended Calculus of Constructions with dependent elimination of booleans and natural numbers. ECC represents a significant subset of Coq. The translation supports all core features of dependency, including higher universes, without relying on parametricity or impredicativity, in contrast to prior work (Bowman et al., Reference Bowman, Cong, Rioux and Ahmed2018; Cong & Asai Reference Cong and Asai2018a). This ensures that the translation works for existing dependently typed languages and that we can reuse existing work on ANF translations, such as join-point optimization. This work provides substantial evidence that dependent-type preservation can, in theory, scale to the practical dependently typed languages currently used for high-assurance software.
Our translation targets our typed IL ![]() $\mathrm{CC}_{e}^{A}$, the ANF-restricted extensional Calculus of Constructions.
$\mathrm{CC}_{e}^{A}$, the ANF-restricted extensional Calculus of Constructions. ![]() $\mathrm{CC}_{e}^{A}$ features a machine-like semantics for evaluating ANF terms, and we prove correctness of separate compilation with respect to this machine semantics. To support the type-preserving translation of dependent elimination for booleans,
$\mathrm{CC}_{e}^{A}$ features a machine-like semantics for evaluating ANF terms, and we prove correctness of separate compilation with respect to this machine semantics. To support the type-preserving translation of dependent elimination for booleans, ![]() $\mathrm{CC}_{e}^{A}$ uses two extensions to ECC: it records propositional equalities in typing derivations and applies equality reflection to access these equalities. These extensions make type checking undecidable. We discuss how to recover decidability in Section 7.
$\mathrm{CC}_{e}^{A}$ uses two extensions to ECC: it records propositional equalities in typing derivations and applies equality reflection to access these equalities. These extensions make type checking undecidable. We discuss how to recover decidability in Section 7.
Our ANF translation is useful as a compiler pass, but it also provides insights into dependent-type preservation and ANF translations. The target IL is designed to express and check semantic equivalences that the translation relies on for correctness. This lesson likely extends to other translations in a type-preserving compiler for dependent types.
We also develop a new proof architecture for reasoning about the ANF translation. This proof architecture is useful when ANF is achieved through a translation rather than a reduction system. Our translation is indexed by a continuation, a program with a hole, to build up the translated term. Thus, the type of the translated term can only be determined when the hole is filled with a well-typed term. Mirroring the translation, we use the type of the continuation to build up a proof of type-preservation.
This paper includes key definitions and proof cases; extended figures and proofs are available in Appendix 1.
2 Main ideas
ANF 101. A-normal form (ANF)Footnote 1 is a syntactic form that makes control flow explicit in the syntax of a program (Sabry & Felleisen, Reference Sabry and Felleisen1992; Flanagan et al., Reference Flanagan, Sabry, Duba and Felleisen1993). ANF encodes computation (e.g., reducing an expression to a value) as a sequence of primitive intermediate computations composed through intermediate variables, similar to how all computation works in an assembly language.
For example, to reduce ![]() , which projects the second element of a pair, we need to describe the evaluation order and control flow of each language primitive. We evaluate
, which projects the second element of a pair, we need to describe the evaluation order and control flow of each language primitive. We evaluate ![]() to a value, and then, we project out the second component. ANF makes control flow explicit in the syntax by decomposing
to a value, and then, we project out the second component. ANF makes control flow explicit in the syntax by decomposing ![]() into the series of primitive computations that the machine must execute, sequenced by
into the series of primitive computations that the machine must execute, sequenced by ![]() . Roughly, we can think of the ANF translation
. Roughly, we can think of the ANF translation ![]() as
as ![]() . However,
. However, ![]() could also be a deeply nested expression in the source language. In general, the ANF translation reassociates all the intermediate computations from
could also be a deeply nested expression in the source language. In general, the ANF translation reassociates all the intermediate computations from ![]() so there are no nested
so there are no nested ![]() expressions, and we end up with
expressions, and we end up with ![]() .
.
Once in ANF, it is simple to formalize a machine semantics to implement evaluation. Each ![]() -bound computation
-bound computation ![]() is some primitive machine step, performing the computation
is some primitive machine step, performing the computation ![]() and binding the value to
and binding the value to ![]() . In this way, control flow has been compiled into data flow. The machine proceeds by always reducing the left-most machine step, which will be a primitive operation with values for operands. For a lazy semantics, we can instead delay each machine step and begin forcing the inner-most body (right-most expression).
. In this way, control flow has been compiled into data flow. The machine proceeds by always reducing the left-most machine step, which will be a primitive operation with values for operands. For a lazy semantics, we can instead delay each machine step and begin forcing the inner-most body (right-most expression).
Why Translation Disrupts Typing and How to Fix it. The problem with dependent-type preservation has little to do with ANF itself and everything to do with dependent types. Transformations which ought to be fine are not because the type theory is so beholden to details of syntax. This is essentially the problem of commutative cuts in type theory (Herbelin, Reference Herbelin2009; Boutillier, Reference Boutillier2012). Transformations that change the structure (syntax) of a program can disrupt dependencies. By dependency, we mean an expression ![]() whose type and evaluation depends on a sub-expression
whose type and evaluation depends on a sub-expression ![]() . We call a sub-expression such as
. We call a sub-expression such as ![]() depended upon. These dependencies occur in dependent elimination forms, such as application, projection, and if expressions. Transforming a dependent elimination can disrupt dependencies.
depended upon. These dependencies occur in dependent elimination forms, such as application, projection, and if expressions. Transforming a dependent elimination can disrupt dependencies.
For example, the dependent type of a second projection of a dependent pair ![]() is typed as follows:
is typed as follows:
Notice that the depended upon sub-expression ![]() is copied into the type, indicated by the solid line arrow. Dependent pairs can be used to define refinement types, such as encoding a type that guarantees an index is in bounds:
is copied into the type, indicated by the solid line arrow. Dependent pairs can be used to define refinement types, such as encoding a type that guarantees an index is in bounds: ![]() . Then, the second projection
. Then, the second projection ![]() represents an explicit proof about first projection. Unfortunately, transforming the expression
represents an explicit proof about first projection. Unfortunately, transforming the expression ![]() can easily change its type.
can easily change its type.
For example, suppose we have the nested expression ![]() , and we want to
, and we want to ![]() -bind all intermediate computations (which, incidentally, ANF does).
-bind all intermediate computations (which, incidentally, ANF does).
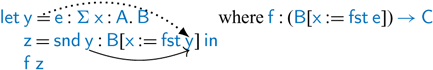
This is not well typed, even with the following dependent-![]() rule (treated as syntactic sugar for dependent application):
rule (treated as syntactic sugar for dependent application):
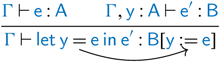
The problem now is the dependent elimination ![]() is
is ![]() -bound and then used, changing the type to
-bound and then used, changing the type to ![]() . This means the equality
. This means the equality ![]() is missing,Footnote 2
but is needed to type check this term (indicated by the dotted line arrow). This fails since
is missing,Footnote 2
but is needed to type check this term (indicated by the dotted line arrow). This fails since ![]() expects
expects ![]() , but is applied to
, but is applied to ![]() . The typing rule essentially forgets that, by the time
. The typing rule essentially forgets that, by the time ![]() happens, the machine will have performed the step of computation
happens, the machine will have performed the step of computation ![]() , forcing
, forcing ![]() to take on the value of
to take on the value of ![]() , so it ought to be safe to assume that
, so it ought to be safe to assume that ![]() in the types. When type checking in linearized machine languages, we need to record these machine steps throughout the typing derivation.
in the types. When type checking in linearized machine languages, we need to record these machine steps throughout the typing derivation.
The above explanation applies to all dependent eliminations of negative types, such as dependently typed functions and compound data structures (modeled as ![]() $\Pi$ and
$\Pi$ and ![]() $\Sigma$ types).
$\Sigma$ types).
An analogous problem occurs with dependent elimination of positive types, which include data types eliminated through branching such as booleans with ![]() expressions. In the dependent typing rule for
expressions. In the dependent typing rule for ![]() , the types of the branches learn whether the predicate of the
, the types of the branches learn whether the predicate of the ![]() is either
is either ![]() . This allows the type system to statically reflect information from dynamic control flow.
. This allows the type system to statically reflect information from dynamic control flow.
Now consider an ![]() expression and a function
expression and a function ![]() . The expression
. The expression ![]() is well typed, but if we want to push the application into the branches to make
is well typed, but if we want to push the application into the branches to make ![]() behave a little more like goto (like the ANF translation does), this result is not well typed.
behave a little more like goto (like the ANF translation does), this result is not well typed.
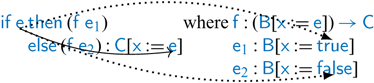
This transformation fails when type checking the applications of ![]() to the branches
to the branches ![]() and
and ![]() . The function
. The function ![]() is expecting an argument of type
is expecting an argument of type ![]() but is applied to arguments of type
but is applied to arguments of type ![]() and
and ![]() . The type system cannot prove that
. The type system cannot prove that ![]() is equal to both
is equal to both ![]() and
and ![]() . In essence, this transformation relies on the fact that, by the time the expression
. In essence, this transformation relies on the fact that, by the time the expression ![]() executes, the machine has evaluated
executes, the machine has evaluated ![]() to
to ![]() (and, analogously,
(and, analogously, ![]() to
to ![]() in the other branch), but the type system has no way to express this.
in the other branch), but the type system has no way to express this.
We design a ![]() type system in which we can express these intuitions and recover type preservation of these kinds of transformations. We use two extensions to ECC: one for negative types (
type system in which we can express these intuitions and recover type preservation of these kinds of transformations. We use two extensions to ECC: one for negative types (![]() $\Pi$ and
$\Pi$ and ![]() $\Sigma$ in ECC) and one for positive types (booleans and natural numbers in ECC).
$\Sigma$ in ECC) and one for positive types (booleans and natural numbers in ECC).
For negative types, it suffices to use definitions (Severi & Poll Reference Severi and Poll1994), a standard extension to type theory that changes the typing rule for ![]() to thread equalities into sub-derivations and resolve dependencies. The relevant typing rule is:
to thread equalities into sub-derivations and resolve dependencies. The relevant typing rule is:
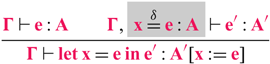
The highlighted part, ![]() , is the only difference from the standard dependent typing rule. This definition is introduced when type checking the body of the
, is the only difference from the standard dependent typing rule. This definition is introduced when type checking the body of the ![]() and can be used to solve type equivalence in sub-derivations, instead of only in the substitution
and can be used to solve type equivalence in sub-derivations, instead of only in the substitution ![]() in the “output” of the typing rule. While this is an extension to the type theory, it is a standard extension that is admissible in any Pure Type System (PTS) (Severi & Poll Reference Severi and Poll1994) and is a feature already found in dependently typed languages such as Coq. With this addition, the transformation of
in the “output” of the typing rule. While this is an extension to the type theory, it is a standard extension that is admissible in any Pure Type System (PTS) (Severi & Poll Reference Severi and Poll1994) and is a feature already found in dependently typed languages such as Coq. With this addition, the transformation of ![]() type checks in the target language by recording the definition
type checks in the target language by recording the definition ![]() while type checking the body of a
while type checking the body of a ![]() expression.
expression.
For positive types, we record a propositional equality between the term being eliminated and its value. For booleans, we need the following typing rule for ![]() .Footnote 3
.Footnote 3
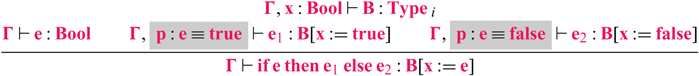
The two highlighted portions of the rule are modifications over the standard typing rule. This rule introduces a propositional equality ![]() between the term
between the term ![]() that appears in the calling context’s type to the value known in the branches. This represents an assumption that
that appears in the calling context’s type to the value known in the branches. This represents an assumption that ![]() and
and ![]() are equal in the type system and allows pushing the context surrounding the
are equal in the type system and allows pushing the context surrounding the ![]() expression into the branches.
expression into the branches.
Like definitions, propositional equalities thread “machine steps” into the typing derivations of ![]() and
and ![]() . In contrast, these equalities are accessed through an additional type equivalence rule
. In contrast, these equalities are accessed through an additional type equivalence rule ![]() , which states that an equivalence holds between two terms if some proof of equality exists between them.
, which states that an equivalence holds between two terms if some proof of equality exists between them.
Our earlier example ![]() expression now type checks using the modified typing rule for
expression now type checks using the modified typing rule for ![]() and
and ![]() . We thread the equivalence
. We thread the equivalence ![]() (respectively
(respectively ![]() ) which allows
) which allows ![]() to be applied to
to be applied to ![]() (respectively
(respectively ![]() ) at the correct type.
) at the correct type.
Equality reflection is not a perfect solution, as adding this type equivalence rule can introduce undecidable type checking. While equality reflection allows definitions like ![]() to be subsumed by a propositional equality
to be subsumed by a propositional equality ![]() , we use definitions when sufficient (such as for negative types) to avoid undecidable type checking. We discuss how to recover decidability of
, we use definitions when sufficient (such as for negative types) to avoid undecidable type checking. We discuss how to recover decidability of ![]() $\mathrm{CC}_{e}^{A}$ in Section 7; however, this would distract us from the ANF translation in the present work.
$\mathrm{CC}_{e}^{A}$ in Section 7; however, this would distract us from the ANF translation in the present work.
Formalizing Type-Preserving ANF Translation. Despite these simple extensions to ![]() $\mathrm{CC}_{e}^{A}$, formalizing the ANF type-preservation argument is still tricky. In the source, looking at an expression such as
$\mathrm{CC}_{e}^{A}$, formalizing the ANF type-preservation argument is still tricky. In the source, looking at an expression such as ![]() , we do not know whether the expression is embedded in a larger context. To formalize the ANF translation, it helps to have a compositional syntax for translating and reasoning about the types of an expression and the unknown context.
, we do not know whether the expression is embedded in a larger context. To formalize the ANF translation, it helps to have a compositional syntax for translating and reasoning about the types of an expression and the unknown context.
To make the translation compositional, we index the ANF translation by a target language (non-first-class) continuation ![]() representing the rest of the computation in which a translated expression will be used.Footnote 4 A continuation
representing the rest of the computation in which a translated expression will be used.Footnote 4 A continuation ![]() is a program with a hole (single linear variable)
is a program with a hole (single linear variable) ![]() $[\cdot]$ and can be composed with a computation
$[\cdot]$ and can be composed with a computation ![]() , written
, written ![]() , to form a program
, to form a program ![]() . Keeping continuations non-first-class ensures that continuations must be used linearly and avoids control effects, which cause inconsistency with dependent types (Barthe & Uustalu, Reference Barthe and Uustalu2002; Herbelin, 2005). In ANF, there are only two continuations: either
. Keeping continuations non-first-class ensures that continuations must be used linearly and avoids control effects, which cause inconsistency with dependent types (Barthe & Uustalu, Reference Barthe and Uustalu2002; Herbelin, 2005). In ANF, there are only two continuations: either ![]() $[\cdot]$ or
$[\cdot]$ or ![]() . Using continuations, we define ANF translation for
. Using continuations, we define ANF translation for ![]() $\Sigma$ types and second projections as follows. We use
$\Sigma$ types and second projections as follows. We use ![]() as shorthand for translating
as shorthand for translating ![]() with an empty continuation,
with an empty continuation, ![]() .
.
This allows us to focus on composing the primitive operations instead of reassociating ![]() bindings.
bindings.
For compositional reasoning, we develop a type system for continuations. The key typing rule is the following.

The type ![]() of continuations describes that the continuation must be composed with the term
of continuations describes that the continuation must be composed with the term ![]() of type
of type ![]() , and the result will be of type
, and the result will be of type ![]() . Note that this type allows us to introduce the definition
. Note that this type allows us to introduce the definition ![]() via the type, before we know how the continuation is used.Footnote 5 We discuss this rule further in Section 4, and how continuation typing is not an extension to the target type theory.
via the type, before we know how the continuation is used.Footnote 5 We discuss this rule further in Section 4, and how continuation typing is not an extension to the target type theory.
The key lemma to prove type preservation is the following.
Lemma 2.1 ![]()
The intuition behind this lemma shows that type preservation follows if every time we construct a continuation ![]() , we show that
, we show that ![]() is well typed. The translation starts with an empty continuation
is well typed. The translation starts with an empty continuation ![]() , which is trivially well typed. We systematically build up the translation of
, which is trivially well typed. We systematically build up the translation of ![]() in
in ![]() by recurring on sub-expressions of
by recurring on sub-expressions of ![]() and building up a new continuation
and building up a new continuation ![]() . If each time we can show that this
. If each time we can show that this ![]() is well typed, then by induction, the whole translation is type preserving. This lemma is indexed by an additional environment
is well typed, then by induction, the whole translation is type preserving. This lemma is indexed by an additional environment ![]() and answer type
and answer type ![]() . Intuitively, this is because it is the continuation
. Intuitively, this is because it is the continuation ![]() , not the expression
, not the expression ![]() , that dictates the final answer type
, that dictates the final answer type ![]() of the translation, and the environment will provide some additional equalities and definitions in
of the translation, and the environment will provide some additional equalities and definitions in ![]() under which we can type check the transformed
under which we can type check the transformed ![]() .
.
3 Source: ECC with definitions
Our source language, ECC, is Luo’s Extended Calculus of Constructions (ECC) (Luo, Reference Luo1990) extended with dependent elimination of booleans, natural numbers with the recursive eliminator, and definitions (Severi & Poll, Reference Severi and Poll1994). This language is a subset of CIC and is based on the presentation given in the Coq reference manualFootnote 6; Timany & Sozeau, (Reference Timany and Sozeau2017) give a recent account of the metatheory for the CIC, including all the features of ECC. We typeset ECC in a ![]() . We present the syntax of ECC in Figure 15. ECC extends the Calculus of Constructions (CC) (Coquand & Huet, Reference Coquand and Huet1988) with
. We present the syntax of ECC in Figure 15. ECC extends the Calculus of Constructions (CC) (Coquand & Huet, Reference Coquand and Huet1988) with ![]() $\Sigma$ types (strong dependent pairs) and an infinite predicative hierarchy of universes. There is no explicit phase distinction; that is, there is no syntactic distinction between terms, which represent run-time expressions, and types, which classify terms. However, we usually use the meta-variable
$\Sigma$ types (strong dependent pairs) and an infinite predicative hierarchy of universes. There is no explicit phase distinction; that is, there is no syntactic distinction between terms, which represent run-time expressions, and types, which classify terms. However, we usually use the meta-variable ![]() to evoke a term and the meta-variables
to evoke a term and the meta-variables ![]() and
and ![]() to evoke a type. The language includes one impredicative universe,
to evoke a type. The language includes one impredicative universe, ![]() , and an infinite hierarchy of predicative universes
, and an infinite hierarchy of predicative universes ![]() . The syntax of expressions
. The syntax of expressions ![]() includes names
includes names ![]() , universes
, universes ![]() , dependent function types
, dependent function types ![]() , functions
, functions ![]() , application
, application ![]() , dependent pair types
, dependent pair types ![]() , dependent pairs
, dependent pairs ![]() , first
, first ![]() and second
and second ![]() projections of dependent pairs, dependent let
projections of dependent pairs, dependent let ![]() , the boolean type
, the boolean type ![]() , the boolean values
, the boolean values ![]() , dependent if
, dependent if ![]() , the natural number type
, the natural number type ![]() , the natural number values
, the natural number values ![]() and
and ![]() , and the recursive eliminator for natural numbers
, and the recursive eliminator for natural numbers ![]() . For brevity, we omit the type annotation on dependent pairs, as in
. For brevity, we omit the type annotation on dependent pairs, as in ![]() . Note that
. Note that ![]() bound definitions do not include type annotations; this is not standard, but type checking is still decidable (Severi & Poll, Reference Severi and Poll1994), and it simplifies our ANF translation. As is standard, we assume uniqueness of names and consider syntax up to
bound definitions do not include type annotations; this is not standard, but type checking is still decidable (Severi & Poll, Reference Severi and Poll1994), and it simplifies our ANF translation. As is standard, we assume uniqueness of names and consider syntax up to ![]() $\alpha$-equivalence.
$\alpha$-equivalence.
The following table summarizes the judgments for ECC and the new notation introduced, in particular the notation for definitions in contexts and substitution of variables for expressions.

In Figure 2, we give the reductions ![]() for ECC, which are entirely standard. We extend reduction to conversion by defining
for ECC, which are entirely standard. We extend reduction to conversion by defining ![]() to be the reflexive, transitive, compatible closure of reduction
to be the reflexive, transitive, compatible closure of reduction ![]() $\triangleright$. The conversion relation is used to compute equivalence between types, but we can also view it as the operational semantics for the language. We define
$\triangleright$. The conversion relation is used to compute equivalence between types, but we can also view it as the operational semantics for the language. We define ![]() as the evaluation function for whole programs using conversion, which we use in our compiler correctness proof.
as the evaluation function for whole programs using conversion, which we use in our compiler correctness proof.

Fig. 1: ECC syntax.

Fig. 2: ECC dynamic semantics (excerpt).
In Figure 3, we define definitional equivalence (or just equivalence) ![]() as conversion up to
as conversion up to ![]() $\eta$-equivalence. We use the notation
$\eta$-equivalence. We use the notation ![]() for equivalence, eliding the environment when it is obvious or unnecessary. We also define cumulativity (subtyping)
for equivalence, eliding the environment when it is obvious or unnecessary. We also define cumulativity (subtyping) ![]() , to allow types in lower universes to inhabit higher universes.
, to allow types in lower universes to inhabit higher universes.

Fig. 3: ECC equivalence and subtyping (excerpt).
We define the type system for ECC in Figure 4, which is mutually defined with well-formedness of environments. The typing rules are entirely standard for a dependent type system. Note that types themselves, such as ![]() have types (called universes), and universes also have types which are higher universes. In [AX-PROP], the type of
have types (called universes), and universes also have types which are higher universes. In [AX-PROP], the type of ![]() is
is ![]() , and in [Ax-Type], the type of each universe
, and in [Ax-Type], the type of each universe ![]() is the next higher universe
is the next higher universe ![]() . Note that we have impredicative function types in
. Note that we have impredicative function types in ![]() , given by [Prod-Prop]. For this work, we ignore the
, given by [Prod-Prop]. For this work, we ignore the ![]() versus
versus ![]() distinction used in some type theories, such as Coq’s, although adding it causes no difficulty. Note that the rules for second projection, [Snd], let, [Let], if, [If], and the eliminator for natural numbers [ElimNat] substitute sub-expressions into the type system. These are the key typing rules that introduce difficulty in type-preserving compilation for dependent types.
distinction used in some type theories, such as Coq’s, although adding it causes no difficulty. Note that the rules for second projection, [Snd], let, [Let], if, [If], and the eliminator for natural numbers [ElimNat] substitute sub-expressions into the type system. These are the key typing rules that introduce difficulty in type-preserving compilation for dependent types.

Fig. 4: ECC typing (excerpt).
4 Target: ECC with ANF support
Our target language, ![]() $\mathrm{CC}_{e}^{A}$, is a variant of ECC with a modified typing rule for dependent
$\mathrm{CC}_{e}^{A}$, is a variant of ECC with a modified typing rule for dependent ![]() that introduces propositional equalities between terms and equality reflection for accessing assumed equalities. The type system of
that introduces propositional equalities between terms and equality reflection for accessing assumed equalities. The type system of ![]() $\mathrm{CC}_{e}^{A}$ is not particularly novel as its type theory is adapted from the extensional Calculus of Constructions (Oury, Reference Oury2005). While
$\mathrm{CC}_{e}^{A}$ is not particularly novel as its type theory is adapted from the extensional Calculus of Constructions (Oury, Reference Oury2005). While ![]() $\mathrm{CC}_{e}^{A}$ supports ANF syntax, the full language is not ANF-restricted; it has the same syntax as ECC. We do not restrict the full language because maintaining ANF while type checking adds needless complexity, especially when checking for equality since conversion often breaks ANF. Instead, we show that our compiler generates only ANF restricted terms in
$\mathrm{CC}_{e}^{A}$ supports ANF syntax, the full language is not ANF-restricted; it has the same syntax as ECC. We do not restrict the full language because maintaining ANF while type checking adds needless complexity, especially when checking for equality since conversion often breaks ANF. Instead, we show that our compiler generates only ANF restricted terms in ![]() $\mathrm{CC}_{e}^{A}$ and define a separate ANF-preserving machine-like semantics for evaluating programs in ANF. We typeset
$\mathrm{CC}_{e}^{A}$ and define a separate ANF-preserving machine-like semantics for evaluating programs in ANF. We typeset ![]() $\mathrm{CC}_{e}^{A}$ in a
$\mathrm{CC}_{e}^{A}$ in a ![]() ; in later sections, we reserve this font exclusively for the ANF restricted
; in later sections, we reserve this font exclusively for the ANF restricted ![]() $\mathrm{CC}_{e}^{A}$. This ability to break ANF locally to support reasoning is similar to the language
$\mathrm{CC}_{e}^{A}$. This ability to break ANF locally to support reasoning is similar to the language ![]() $F_J$ of Maurer et al. (Reference Maurer, Downen, Ariola and Peyton Jones2017), which does not enforce ANF syntactically, but supports ANF transformation and optimization with join points.
$F_J$ of Maurer et al. (Reference Maurer, Downen, Ariola and Peyton Jones2017), which does not enforce ANF syntactically, but supports ANF transformation and optimization with join points.
We can imagine the compilation process as either (1) generating ANF syntax in ![]() $\mathrm{CC}_{e}^{A}$ from ECC or (2) as first embedding ECC in
$\mathrm{CC}_{e}^{A}$ from ECC or (2) as first embedding ECC in ![]() $\mathrm{CC}_{e}^{A}$ and then rewriting
$\mathrm{CC}_{e}^{A}$ and then rewriting ![]() $\mathrm{CC}_{e}^{A}$ terms into ANF. In Section 5, we present the compiler as process (1), a compiler from ECC to ANF
$\mathrm{CC}_{e}^{A}$ terms into ANF. In Section 5, we present the compiler as process (1), a compiler from ECC to ANF ![]() $\mathrm{CC}_{e}^{A}$. In this section, we develop most of the supporting metatheory necessary for ANF as intra-language equivalences and process (2) may be a more helpful intuition.
$\mathrm{CC}_{e}^{A}$. In this section, we develop most of the supporting metatheory necessary for ANF as intra-language equivalences and process (2) may be a more helpful intuition.
We give the ANF syntax for ![]() $\mathrm{CC}_{e}^{A}$ in Figure 5(a). We impose a syntactic distinction between values
$\mathrm{CC}_{e}^{A}$ in Figure 5(a). We impose a syntactic distinction between values ![]() which do not reduce, computations
which do not reduce, computations ![]() which eliminate values and can be composed using continuations
which eliminate values and can be composed using continuations ![]() , and configurations
, and configurations ![]() which represent the machine configurations executed by the ANF machine semantics. We add the identity type
which represent the machine configurations executed by the ANF machine semantics. We add the identity type ![]() and
and ![]() to enable preserving dependent typing for
to enable preserving dependent typing for ![]() expressions and the join-point optimization, further described in Section 6. We do not require an elimination form for identity types; they are instead used via the restricted form of equality reflection in the equivalence judgment. A continuation
expressions and the join-point optimization, further described in Section 6. We do not require an elimination form for identity types; they are instead used via the restricted form of equality reflection in the equivalence judgment. A continuation ![]() is a program with a hole and is composed
is a program with a hole and is composed ![]() with a computation
with a computation ![]() to form a configuration
to form a configuration ![]() . For example,
. For example, ![]() . Since continuations are not first-class objects, we cannot express control effects. Note that despite the syntactic distinctions, we still do not enforce a phase distinction—configurations (programs) can appear in types. Finally in Figure 5(b), we give the full non-ANF syntax, denoted by meta-variables
. Since continuations are not first-class objects, we cannot express control effects. Note that despite the syntactic distinctions, we still do not enforce a phase distinction—configurations (programs) can appear in types. Finally in Figure 5(b), we give the full non-ANF syntax, denoted by meta-variables ![]() . As done with ECC, we usually use the meta-variable
. As done with ECC, we usually use the meta-variable ![]() to evoke a term and the meta-variables
to evoke a term and the meta-variables ![]() to evoke a type.
to evoke a type.

Fig. 5: ![]() $\mathrm{CC}_{e}^{A}$ syntax.
$\mathrm{CC}_{e}^{A}$ syntax.
To summarize, the meaning of the judgments of ![]() $\mathrm{CC}_{e}^{A}$ is the same as ECC. However,
$\mathrm{CC}_{e}^{A}$ is the same as ECC. However, ![]() $\mathrm{CC}_{e}^{A}$ has additional syntax for the identity type.
$\mathrm{CC}_{e}^{A}$ has additional syntax for the identity type.

We give the new typing rules in Figure 6. The rules for the identity type are standard. The key change in ![]() $\mathrm{CC}_{e}^{A}$ is in the typing rule for
$\mathrm{CC}_{e}^{A}$ is in the typing rule for ![]() . The typing rule for
. The typing rule for ![]() introduces a propositional equality into the typing environment for each branch. These record a machine step: the machine will have reduced
introduces a propositional equality into the typing environment for each branch. These record a machine step: the machine will have reduced ![]() to
to ![]() before jumping to the first branch and reduced
before jumping to the first branch and reduced ![]() to
to ![]() before jumping to the second branch. This is necessary to support the type-preserving ANF transformation of
before jumping to the second branch. This is necessary to support the type-preserving ANF transformation of ![]() .
.

Fig. 6: ![]() $\mathrm{CC}_{e}^{A}$ typing (excerpt).
$\mathrm{CC}_{e}^{A}$ typing (excerpt).
We require a new definition of equivalence to support extensionality, as shown in Figure 7. The rule ![]() is used to determine two terms are equivalent if there is a proof of their equality. In particular, we use this rule to access equalities in the context such as those introduced in the typing rule for
is used to determine two terms are equivalent if there is a proof of their equality. In particular, we use this rule to access equalities in the context such as those introduced in the typing rule for ![]() . We add congruence rules for all syntactic forms including the identity type. The rules
. We add congruence rules for all syntactic forms including the identity type. The rules ![]() Footnote 7 and
Footnote 7 and ![]() state that equivalence is preserved under substitution and the standard reduction defined for ECC. We also include
state that equivalence is preserved under substitution and the standard reduction defined for ECC. We also include ![]() $\eta$-equivalence as defined for ECC and
$\eta$-equivalence as defined for ECC and ![]() $\eta$-equivalences for booleans.
$\eta$-equivalences for booleans.

Fig. 7: ![]() $\mathrm{CC}_{e}^{A}$ equivalence (excerpt).
$\mathrm{CC}_{e}^{A}$ equivalence (excerpt).

Fig. 8: Composition of configurations.
To ensure reduction preserves ANF, we define composition of a continuation ![]() and a configuration
and a configuration ![]() , Figure 24, typically called renormalization in the literature (Sabry & Wadler Reference Sabry and Wadler1997; Kennedy Reference Kennedy2007). In ANF, all continuations are left associated, so the standard definition of substitution does not preserve ANF, unlike in alternatives such as CPS or monadic form. Note that
, Figure 24, typically called renormalization in the literature (Sabry & Wadler Reference Sabry and Wadler1997; Kennedy Reference Kennedy2007). In ANF, all continuations are left associated, so the standard definition of substitution does not preserve ANF, unlike in alternatives such as CPS or monadic form. Note that ![]() $\beta$-reduction takes an ANF configuration
$\beta$-reduction takes an ANF configuration ![]() but would naßvely produce
but would naßvely produce ![]() . Substituting the term
. Substituting the term ![]() , a configuration, into the continuation
, a configuration, into the continuation ![]() could result in the non-ANF term
could result in the non-ANF term ![]() . When composing a continuation with a configuration,
. When composing a continuation with a configuration, ![]() , we unnest all continuations so they remain left associated. Note that these definitions rely on our uniqueness-of-names assumption.
, we unnest all continuations so they remain left associated. Note that these definitions rely on our uniqueness-of-names assumption.
Digression on composition in ANF. In the literature, the composition operation ![]() is usually introduced as renormalization, as if the only intuition for why it exists is “well, it happens that ANF is not preserved under
is usually introduced as renormalization, as if the only intuition for why it exists is “well, it happens that ANF is not preserved under ![]() $\beta$-reduction.” It is not mere coincidence; the intuition for this operation is composition, and having a syntax for composing terms is not only useful for stating
$\beta$-reduction.” It is not mere coincidence; the intuition for this operation is composition, and having a syntax for composing terms is not only useful for stating ![]() $\beta$-reduction, but useful for all reasoning about ANF. This should not come as a surprise—compositional reasoning is useful. The only surprise is that the composition operation is not the usual one used in programming language semantics, that is, substitution. In ANF, as in monadic normal form, substitution can be used to compose any expression with a value, since names are values and values can always be replaced by values. But substitution cannot just replace a name, which is a value, with a computation or configuration. That would not be well typed. So how do we compose computations with configurations? We can use
$\beta$-reduction, but useful for all reasoning about ANF. This should not come as a surprise—compositional reasoning is useful. The only surprise is that the composition operation is not the usual one used in programming language semantics, that is, substitution. In ANF, as in monadic normal form, substitution can be used to compose any expression with a value, since names are values and values can always be replaced by values. But substitution cannot just replace a name, which is a value, with a computation or configuration. That would not be well typed. So how do we compose computations with configurations? We can use ![]() , as in
, as in ![]() , which we can imagine as an explicit substitution. In monadic form, there is no distinction between computations and configurations, so the same term works to compose configurations. But in ANF, we have no object-level term to compose configurations or continuations. We cannot substitute a configuration
, which we can imagine as an explicit substitution. In monadic form, there is no distinction between computations and configurations, so the same term works to compose configurations. But in ANF, we have no object-level term to compose configurations or continuations. We cannot substitute a configuration ![]() into a continuation
into a continuation ![]() , since this would result in the non-ANF (but valid monadic) expression
, since this would result in the non-ANF (but valid monadic) expression ![]() . Instead, ANF requires a new operation to compose configurations:
. Instead, ANF requires a new operation to compose configurations: ![]() . This operation is more generally known as hereditary substitution (Watkins et al., Reference Watkins, Cervesato, Pfenning and Walker2003), a form of substitution that maintains canonical forms. So we can think of it as a form of substitution, or, simply, as composition.
. This operation is more generally known as hereditary substitution (Watkins et al., Reference Watkins, Cervesato, Pfenning and Walker2003), a form of substitution that maintains canonical forms. So we can think of it as a form of substitution, or, simply, as composition.
In Figure 9, we present the call-by-value (CBV) evaluation semantics for ANF ![]() $\mathrm{CC}_{e}^{A}$ terms. The semantics is only for the run-time evaluation of configurations; during type checking, we continue to use the conversion relation defined in Section 3. The semantics is essentially standard, but recall that
$\mathrm{CC}_{e}^{A}$ terms. The semantics is only for the run-time evaluation of configurations; during type checking, we continue to use the conversion relation defined in Section 3. The semantics is essentially standard, but recall that ![]() $\beta$-reduction produces a configuration
$\beta$-reduction produces a configuration ![]() which must be composed with the existing continuation
which must be composed with the existing continuation ![]() . To maintain ANF, the natural number eliminator for the
. To maintain ANF, the natural number eliminator for the ![]() case must first let-bind the intermediate application and recursive call before plugging the final application into the existing continuation
case must first let-bind the intermediate application and recursive call before plugging the final application into the existing continuation ![]() .
.

Fig. 9: ![]() $\mathrm{CC}_{e}^{A}$ evaluation.
$\mathrm{CC}_{e}^{A}$ evaluation.
4.1 Dependent continuation typing
The ANF translation manipulates continuations ![]() as independent entities. To reason about them, and thus to reason about the translation, we introduce continuation typing, defined in Figure 10. The type
as independent entities. To reason about them, and thus to reason about the translation, we introduce continuation typing, defined in Figure 10. The type ![]() of a continuation expresses that this continuation expects to be composed with a term equal to the configuration
of a continuation expresses that this continuation expects to be composed with a term equal to the configuration ![]() of type
of type ![]() and returns a result of type
and returns a result of type ![]() when completed. Normally,
when completed. Normally, ![]() is equivalent to some computation
is equivalent to some computation ![]() , but it must be generalized to a configuration
, but it must be generalized to a configuration ![]() to support typing
to support typing ![]() expressions. This type formally expresses the idea that
expressions. This type formally expresses the idea that ![]() is depended upon in the rest of the computation. The [K-Bind] rule ensures we have access to the specific
is depended upon in the rest of the computation. The [K-Bind] rule ensures we have access to the specific ![]() needed to type body of the
needed to type body of the ![]() continuation and is similar to the rule [T-Cont] used in the type-preserving CPS translation by Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018). The rule [K-Empty] has an arbitrary term
continuation and is similar to the rule [T-Cont] used in the type-preserving CPS translation by Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018). The rule [K-Empty] has an arbitrary term ![]() , since an empty continuation
, since an empty continuation ![]() $[\cdot]$ has no “rest of the program” that could depend on anything.
$[\cdot]$ has no “rest of the program” that could depend on anything.

Fig. 10: ![]() $\mathrm{CC}_{e}^{A}$ continuation typing.
$\mathrm{CC}_{e}^{A}$ continuation typing.
Intuitively, what we want from continuation typing is a compositionality property—that we can reason about the types of configurations ![]() (generally, for configurations
(generally, for configurations ![]() ) by composing the typing derivations for
) by composing the typing derivations for ![]() and
and ![]() . To get this property, a continuation type must express not merely the type of its hole
. To get this property, a continuation type must express not merely the type of its hole ![]() , but which term
, but which term ![]() will be bound in the hole. We see this formally from the typing rule [Let] (the same for
will be bound in the hole. We see this formally from the typing rule [Let] (the same for ![]() $\mathrm{CC}_{e}^{A}$ as for ECC in Section 3), since showing that
$\mathrm{CC}_{e}^{A}$ as for ECC in Section 3), since showing that ![]() is well typed requires showing that
is well typed requires showing that ![]() , that is, requires knowing the definition
, that is, requires knowing the definition ![]() . If we omit the expression
. If we omit the expression ![]() from the type of a continuation, we know there are some configurations
from the type of a continuation, we know there are some configurations ![]() that we cannot type check compositionally. Intuitively, if all we knew about
that we cannot type check compositionally. Intuitively, if all we knew about ![]() was its type, we would be in exactly the situation of trying to type check a continuation that has abstracted some dependent type that depends on the specific
was its type, we would be in exactly the situation of trying to type check a continuation that has abstracted some dependent type that depends on the specific ![]() into one that depends on an arbitrary
into one that depends on an arbitrary ![]() . We prove that our continuation typing is compositional in this way, Lemma 4.1 (Continuation Cut).
. We prove that our continuation typing is compositional in this way, Lemma 4.1 (Continuation Cut).
Note that the result of a continuation type cannot depend on the term that will be plugged in for the hole, that is, for a continuation ![]() does not depend on
does not depend on ![]() . To see this, first note that the initial continuation must be empty and thus cannot have a result type that depends on its hole. The ANF translation will take this initial empty continuation and compose it with intermediate continuations
. To see this, first note that the initial continuation must be empty and thus cannot have a result type that depends on its hole. The ANF translation will take this initial empty continuation and compose it with intermediate continuations ![]() . Since composing any continuation
. Since composing any continuation ![]()
![]() with any continuation
with any continuation ![]() results in a new continuation with the final result type
results in a new continuation with the final result type ![]() , then the composition of any two continuations cannot depend on the type of the hole.
, then the composition of any two continuations cannot depend on the type of the hole.
To prove that continuation typing is not an extension to the type system—that is, is admissible—we prove Lemmas 4.1 and 4.3, that plugging a well-typed computation or configuration into a well-typed continuation results in a well-typed term of the expected type.
We first show Lemma 4.1 (Continuation Cut), which is simple. This lemma tells us that our continuation typing allows for compositional reasoning about configurations ![]() whose result types do not depend on
whose result types do not depend on ![]() .
.
Lemma 4.1 (Continuation Cut) ![]()
Proof. By cases on ![]() .
.
Case:
 , trivial.
, trivial.-
Case:

We must show that ![]() , which follows directly from [Let] since, by the continuation typing derivation, we have that
, which follows directly from [Let] since, by the continuation typing derivation, we have that ![]() .
.
Continuation typing seems to require that we compose a continuation ![]() syntactically with
syntactically with ![]() , but we will need to compose with some
, but we will need to compose with some ![]() . It is preferable to prove this as a lemma instead of building it into continuation typing to get a nicer induction property for continuation typing. The proof is essentially that substitution respects equivalence.
. It is preferable to prove this as a lemma instead of building it into continuation typing to get a nicer induction property for continuation typing. The proof is essentially that substitution respects equivalence.
Lemma 4.2 (Continuation Cut Modulo Equivalence) If ![]()
![]() , and
, and ![]() , then
, then ![]() .
.
Proof. By cases on the structure of ![]() .
.
Case:
 Trivial.
Trivial.-
Case:

It suffices to show that: If ![]() then
then ![]() .
.
Note that anywhere in the derivation ![]() that
that ![]() is used, it must be used essentially as:
is used, it must be used essentially as: ![]() . We can replace any such use by
. We can replace any such use by ![]()
![]() to construct a derivation for
to construct a derivation for ![]() .
.
Some presentations of context typing (Gordon, Reference Gordon1995)Footnote 8, in non-dependent settings, use a rule like the following.
This suggests we could define continuation typing as follows.
That is, instead of adding separate rules [K-Empty] and [K-Bind], we define a well-typed continuation to be one whose composition with the expected term in the hole is well typed. Then, Lemma 4.1 (Continuation Cut) is definitional rather than admissible. This rule is somewhat surprising; it appears very much like the definition of [Cut], except the computation ![]() being composed with the continuation comes from its type, and the continuation remains un-composed in what we would consider the output of the rule.
being composed with the continuation comes from its type, and the continuation remains un-composed in what we would consider the output of the rule.
The presentations are equivalent, but it is less clear how [K-Type] is related to the definitions we wish to focus on. It is exactly the premises of [K-Bind] that we need to recover type-preservation for ANF, so we choose the presentation with [K-Bind]. However, the rule [K-Type] is more general in the sense that the continuation typing does not need any changes as the definition of continuations change.
The final lemma about continuation typing is also the key to why ANF is type preserving for ![]() . The heterogeneous composition operations perform the ANF translation on
. The heterogeneous composition operations perform the ANF translation on ![]() expressions by composing the branches with the current continuation, reassociating all intermediate computations. The following lemma states that if a configuration
expressions by composing the branches with the current continuation, reassociating all intermediate computations. The following lemma states that if a configuration ![]() is well typed and equivalent to another (well-typed) configuration
is well typed and equivalent to another (well-typed) configuration ![]() under an extended environment
under an extended environment ![]() , and the continuation
, and the continuation ![]() is well typed with respect to
is well typed with respect to ![]() , then the composition
, then the composition ![]() is well typed. We include the additional environment
is well typed. We include the additional environment ![]() , as this environment contains information about new variables introduced through the composition with
, as this environment contains information about new variables introduced through the composition with ![]() , such as definitions and propositional equalities. We choose to include an explicit extra environment
, such as definitions and propositional equalities. We choose to include an explicit extra environment ![]() to avoid needing to prove tedious properties about individual environments. Thus, the proof is simple, except for the
to avoid needing to prove tedious properties about individual environments. Thus, the proof is simple, except for the ![]() case, which essentially must prove that ANF is type preserving for
case, which essentially must prove that ANF is type preserving for ![]() .
.
Lemma 4.3 (Heterogeneous Continuation Cut) If ![]()
![]() such that
such that ![]() and
and ![]() , then
, then ![]() .
.
Proof. By induction on ![]() .
.
Case:
 , by Lemma 4.2.
, by Lemma 4.2.-
Case:

Our goal follows by the induction hypothesis applied to the sub-expression
 if we can show (1)
if we can show (1)  and (2)
and (2)  under a context
under a context  . (1) follows by the following equations and transitivity of
. (1) follows by the following equations and transitivity of  $\equiv:$:
For (2), note that
$\equiv:$:
For (2), note that
 from our premises.
from our premises.

-
Case:

These follow by the induction hypotheses applied to the sub-expressions
 and
and  if we can show (1)
if we can show (1)  and (2)
and (2)  under a context
under a context  (analogously for
(analogously for  . For (1), note that
. For (1), note that  by [
by [ $\equiv$-Reflect] and the typing rule [Var].
For (2), note that
$\equiv$-Reflect] and the typing rule [Var].
For (2), note that
 from our premises and weakening. By [
from our premises and weakening. By [ $\equiv$-Subst], we know
$\equiv$-Subst], we know  , which follows by [
, which follows by [ $\equiv$-Reflect] and the typing rule [Var].
$\equiv$-Reflect] and the typing rule [Var].
4.2 Metatheory
To demonstrate that the new typing rule for ![]() is consistent, we develop a syntactic model of
is consistent, we develop a syntactic model of ![]() $\mathrm{CC}_{e}^{A}$ in extensional CIC (eCIC). We also prove subject reduction for
$\mathrm{CC}_{e}^{A}$ in extensional CIC (eCIC). We also prove subject reduction for ![]() $\mathrm{CC}_{e}^{A}$. Subject reduction is valuable property for a typed IL to model various optimizations through the equational theory of the language, such as modeling inlining as
$\mathrm{CC}_{e}^{A}$. Subject reduction is valuable property for a typed IL to model various optimizations through the equational theory of the language, such as modeling inlining as ![]() $\beta$-reduction. If subject reduction holds, then all these optimizations are type preserving.
$\beta$-reduction. If subject reduction holds, then all these optimizations are type preserving.
4.2.1 Consistency
Our syntactic model essentially implements the new ![]() rule using the convoy pattern (Chlipala, Reference Chlipala2013), but leaves the rest of the propositional equalities and equality reflection essentially unchanged. Each
rule using the convoy pattern (Chlipala, Reference Chlipala2013), but leaves the rest of the propositional equalities and equality reflection essentially unchanged. Each ![]() expression
expression ![]() is modeled as an
is modeled as an ![]() expression that returns a function expecting a proof that the predicate
expression that returns a function expecting a proof that the predicate ![]() is equal to
is equal to ![]() in the first branch and
in the first branch and ![]() in the second branch. The function, after receiving that proof, executes the code in the branch. The model
in the second branch. The function, after receiving that proof, executes the code in the branch. The model ![]() expression is then immediately applied to refl, the canonical proof of the identity type. We could eliminate equality reflection using the translation of Oury (Reference Oury2005), but this is not necessary for consistency.
expression is then immediately applied to refl, the canonical proof of the identity type. We could eliminate equality reflection using the translation of Oury (Reference Oury2005), but this is not necessary for consistency.
The essence of the model is given in Figure 11. There is only one interesting rule, corresponding to our altered dependent if rule. The model relies on auxiliary definitions in CIC, including subst, if-eta1 and if-eta2, whose types are given as inference rules in Figure 11. Note that the model for ![]() $\mathrm{CC}_{e}^{A}$’s
$\mathrm{CC}_{e}^{A}$’s ![]() is not valid ANF, so it does not suffice to merely use the convoy pattern if we want to take advantage of ANF for compilation.
is not valid ANF, so it does not suffice to merely use the convoy pattern if we want to take advantage of ANF for compilation.

Fig. 11: ![]() $\mathrm{CC}_{e}^{A}$ model in eCIC (excerpt).
$\mathrm{CC}_{e}^{A}$ model in eCIC (excerpt).
We show this is a syntactic model using the usual recipe, which is explained well by Boulier et al. (Reference Boulier, Pédrot and Tabareau2017): we show the translation from ![]() $\mathrm{CC}_{e}^{A}$ to eCIC preserves equivalence, typing, and the definition of
$\mathrm{CC}_{e}^{A}$ to eCIC preserves equivalence, typing, and the definition of ![]() $\perp$ (the empty type). This means that if
$\perp$ (the empty type). This means that if ![]() $\mathrm{CC}_{e}^{A}$ were inconsistent, then we could translate the proof of
$\mathrm{CC}_{e}^{A}$ were inconsistent, then we could translate the proof of ![]() $\perp$ into a proof of
$\perp$ into a proof of ![]() in eCIC, but no such proof exists in eCIC, so
in eCIC, but no such proof exists in eCIC, so ![]() $\mathrm{CC}_{e}^{A}$ is consistent.
$\mathrm{CC}_{e}^{A}$ is consistent.
We use the usual definition of ![]() as
as ![]() , and the same in eCIC. It is trivial that the definition is preserved.
, and the same in eCIC. It is trivial that the definition is preserved.
Lemma 4.4 (Model Preserves Empty Type) ![]()
The essence of showing both that equivalence is preserved and that typing is preserved is in showing that the auxiliary definitions in Figure 11 exist and are well typed. We give these definitions in Coq in the supplementary materials, and the equivalences hold and are well typed without any additional axioms.
Lemma 4.5 (Model Preserves Equivalence) ![]()
Lemma 4.6 (Model Preserves Typing) ![]()
Consistency tells us that there does not exist a closed term of the empty type ![]() . This allows us to interpret types as specifications and well-typed terms as proofs.
. This allows us to interpret types as specifications and well-typed terms as proofs.
Theorem 4.7 (Consistency) There is no ![]() such that
such that ![]()
4.2.2 Syntactic metatheory
![]() $\mathrm{CC}_{e}^{A}$ satisfies all the usual syntactic metatheory properties, but the main property of interest for developing our typed IL is subject reduction. We present the proof of subject reduction, which follows the structure presented by Luo (Reference Luo1990).
$\mathrm{CC}_{e}^{A}$ satisfies all the usual syntactic metatheory properties, but the main property of interest for developing our typed IL is subject reduction. We present the proof of subject reduction, which follows the structure presented by Luo (Reference Luo1990).
Theorem 4.8 (Subject Reduction) ![]()
Proof. By induction on ![]() ■
■
The proof of subject reduction relies on some additional lemmas. In particular, the proof relies on subject reduction for single step reduction (in the [Red-Trans] case), and a lemma called Luo calls context replacement (in the [Red-Cong-Lam] and [Red-Cong-Let] cases).
Lemma 4.9 (Single Step Subject Reduction) ![]() .
.
Proof. By cases on ![]() . Most cases are straightforward, except for
. Most cases are straightforward, except for ![]() $\rhd_{\beta}$ and
$\rhd_{\beta}$ and ![]() $\rhd_{\zeta}$, which rely on Lemmas 4.12 and 4.13, respectively.
$\rhd_{\zeta}$, which rely on Lemmas 4.12 and 4.13, respectively.
Lemma 4.10 (Context Replacement) If ![]() and
and ![]() , then
, then ![]() .
.
Proof. By (mutual) induction on ![]() .
.
Because our typing contexts also contain definitions, we must also be able to replace a definition expression with an equivalent expression. This is required specifically for the [Red-Cong-Let] case in the proof of subject reduction.
Lemma 4.11 (Context Definition Replacement) If ![]() and
and ![]() , then
, then ![]() .
.
Proof. By (mutual) induction on ![]() .
.
Finally, the proof of single step subject reduction relies on a lemma Luo calls Cut, named after the cut rule in sequent calculus. We must also prove an additional similar lemma due to definitions in our context, specifically for the ![]() $\rhd_{\delta}$ case.
$\rhd_{\delta}$ case.
Lemma 4.12 (Cut) If ![]() and
and ![]() then
then ![]()
![]() .
.
Proof. By (mutual) induction on ![]() .
.
Lemma 4.13 (Cut With Definitions) ![]()
![]() .
.
Proof. By (mutual) induction on ![]() .
.
The proofs of both versions of context replacement and Cut are done by mutual induction, because typing in ![]() $\mathrm{CC}_{e}^{A}$ is mutually defined with well-formedness of contexts. Typing also relies on subtyping in the [Conv] case, subtyping relies on equivalence, and equivalence now relies on typing due to the equality reflection rule [
$\mathrm{CC}_{e}^{A}$ is mutually defined with well-formedness of contexts. Typing also relies on subtyping in the [Conv] case, subtyping relies on equivalence, and equivalence now relies on typing due to the equality reflection rule [![]() $\equiv$-Reflect]. The mutual reliance of all these judgments requires that these lemmas be proven by mutual induction. The lemma statements above are not the full statement of the lemma, which we omit for brevity, but the corollaries are of interest. For example, the full lemma definition for Lemma 4.10 is as follows:
$\equiv$-Reflect]. The mutual reliance of all these judgments requires that these lemmas be proven by mutual induction. The lemma statements above are not the full statement of the lemma, which we omit for brevity, but the corollaries are of interest. For example, the full lemma definition for Lemma 4.10 is as follows:
Lemma 4.14 (Context Replacement (full definition))

The full definitions for Lemmas 4.11, 4.12, and 4.13 are included in Appendix 1.
4.3 Correctness of ANF evaluation
In ![]() $\mathrm{CC}_{e}^{A}$, we have an ANF evaluation semantics for run time and a separate definitional equivalence and reduction system for type checking. We prove that these two coincide: running in our ANF evaluation semantics produces a value definitionally equivalent to the original term.
$\mathrm{CC}_{e}^{A}$, we have an ANF evaluation semantics for run time and a separate definitional equivalence and reduction system for type checking. We prove that these two coincide: running in our ANF evaluation semantics produces a value definitionally equivalent to the original term.
When computing definitional equivalence, we end up with terms that are not in ANF and can no longer be used in the ANF evaluation semantics. This is not a problem—we could always ANF translate the resulting term if needed—but can be confusing when reading equations. When this happens, we wrap terms in a distinctive boundary such as ![]() and
and ![]() . The boundary indicates the term is not normal, that is, not in A-normal form. The boundary is only meant to communicate with the reader; formally,
. The boundary indicates the term is not normal, that is, not in A-normal form. The boundary is only meant to communicate with the reader; formally, ![]() .
.
The heart of the correctness proof is actually naturality, a property found in the literature on continuations and CPS that essentially expresses freedom from control effects (e.g., (Thielecke Reference Thielecke2003) explain this well). Lemma 4.15 is the formal statement of naturality in ANF: composing a term ![]() with its continuation
with its continuation ![]() in ANF is equivalent to running
in ANF is equivalent to running ![]() to a value and plugging the result into the hole of the continuation
to a value and plugging the result into the hole of the continuation ![]() . Formally, this states that composing continuations in ANF is sound with respect to standard substitution. The proof follows by straightforward equational reasoning.
. Formally, this states that composing continuations in ANF is sound with respect to standard substitution. The proof follows by straightforward equational reasoning.
Lemma 4.15 (Naturality) ![]()
Proof By induction on the structure of ![]() .
.
Next we show that our ANF evaluation semantics are sound with respect to definitional equivalence. To do that, we first show that the small-step semantics are sound. Then, we show soundness of the evaluation function.
Lemma 4.16 (Small-step soundness) If ![]() .
.
Proof By cases on ![]() . Most cases follow easily from the ECC reduction relation and congruence, except for
. Most cases follow easily from the ECC reduction relation and congruence, except for ![]() $\mapsto_{\beta}$ which requires Lemma 4.15. We give representative cases.
$\mapsto_{\beta}$ which requires Lemma 4.15. We give representative cases.
Theorem 4.17 (Evaluation soundness) ![]() ■
■
Proof. By induction on the length n of the reduction sequence given by ![]() . Note that, unlike conversion, the ANF evaluation semantics have no congruence rules.
. Note that, unlike conversion, the ANF evaluation semantics have no congruence rules.
5 ANF translation
The ANF translation is presented in Figure 12. The translation is standard, defined inductively over syntax and indexed by a current continuation. The continuation is used when translating a value and is composed together “inside-out” the same way continuation composition is defined in Section 4. When translating a value such as ![]() , we plug the value into the current continuation and recursively translate the sub-expressions of the value if applicable. For non-values such as application, we make sequencing explicit by recursively translating each sub-expression with a continuation that binds the result and performs the rest of the computation.
, we plug the value into the current continuation and recursively translate the sub-expressions of the value if applicable. For non-values such as application, we make sequencing explicit by recursively translating each sub-expression with a continuation that binds the result and performs the rest of the computation.

Fig. 12: Naïve ANF translation.
We prove that the translation always produces syntax in ANF (Theorem 5.1). The proof is straightforward.
Theorem 5.1 (ANF) For all ![]() and
and ![]() ,
, ![]() for some
for some ![]() .
.
Our goal is to prove type preservation: if ![]() is well typed in the source, then
is well typed in the source, then ![]() is well typed at a translated type in the target. But to prove type preservation, we must also preserve the rest of the judgmental and syntactic structure that the dependent type system relies on. The type judgment is defined mutually inductively only with well-formedness of environments; all other judgments relied on are defined inductively. We proceed top-down, starting from our main theorem, in order to motivate where each lemma comes into play. The full proof of type preservation is omitted for brevity but is included in Appendix 1.
is well typed at a translated type in the target. But to prove type preservation, we must also preserve the rest of the judgmental and syntactic structure that the dependent type system relies on. The type judgment is defined mutually inductively only with well-formedness of environments; all other judgments relied on are defined inductively. We proceed top-down, starting from our main theorem, in order to motivate where each lemma comes into play. The full proof of type preservation is omitted for brevity but is included in Appendix 1.
Type-preservation is stated below. We do not prove it directly. Since the ANF translation is indexed by a continuation ![]() , we need a stronger induction hypothesis to reason about the type of the continuation
, we need a stronger induction hypothesis to reason about the type of the continuation ![]() .
.
Theorem 5.2 (Type Preservation) If ![]()
Proof. By Lemma 5.3, it suffices to show that ![]() , which follows by [K-Empty].
, which follows by [K-Empty].
To see why we need a stronger induction hypothesis, consider the ![]() case of ANF translation:
case of ANF translation: ![]() . The induction hypothesis for Theorem 5.2 proves that
. The induction hypothesis for Theorem 5.2 proves that ![]() , but this cannot be used to show that the translation of
, but this cannot be used to show that the translation of ![]() with the new continuation
with the new continuation ![]() is well typed. We need the induction hypothesis to also include typing information for the new continuation that expects the translated sub-expression
is well typed. We need the induction hypothesis to also include typing information for the new continuation that expects the translated sub-expression ![]() . Note the new continuation also composes the original continuation
. Note the new continuation also composes the original continuation ![]() with a target computation
with a target computation ![]() . Intuitively, the composition
. Intuitively, the composition ![]() is well typed because it appears in a context where
is well typed because it appears in a context where ![]() is equivalent to the translation of the source expression
is equivalent to the translation of the source expression ![]() .
.
We abstract this pattern into Lemma 5.3, which takes both a well-typed source term and a well-typed continuation as input, just like the translation. The ANF translation takes an accumulator (the continuation ![]() ) and builds up the translation in an accumulator as a procedure from values to ANF terms. The lemma builds up a proof of correctness as an accumulator as well. The accumulator is a proposition that if the computation it receives is well typed, then composing the continuation with the computation is well typed. Formally, we phrase this as: if we start with a well-typed term
) and builds up the translation in an accumulator as a procedure from values to ANF terms. The lemma builds up a proof of correctness as an accumulator as well. The accumulator is a proposition that if the computation it receives is well typed, then composing the continuation with the computation is well typed. Formally, we phrase this as: if we start with a well-typed term ![]() , and a well-typed continuation
, and a well-typed continuation ![]() , then translating
, then translating ![]() with
with ![]() results in a well-typed term. The continuation
results in a well-typed term. The continuation ![]() expects a term that is the translation of the source expression directly, under an extended environment
expects a term that is the translation of the source expression directly, under an extended environment ![]() . Intuitively, this extended environment
. Intuitively, this extended environment ![]() contains information about new variables introduced through the ANF translation, such as definitions and propositional equivalences. This lemma and its proof are main contributions of this work.
contains information about new variables introduced through the ANF translation, such as definitions and propositional equivalences. This lemma and its proof are main contributions of this work.
Lemma 5.3. ![]()
Proof. The proof is by induction on the mutually defined judgments ![]() and
and ![]() . Cases [Ax-Prop], [Snd], [ElimNat], and [If] are given, as they are representative.
. Cases [Ax-Prop], [Snd], [ElimNat], and [If] are given, as they are representative.
Note that for all sub-expressions, ![]() of type
of type ![]() holds by instantiating the induction hypothesis with the empty continuation
holds by instantiating the induction hypothesis with the empty continuation ![]() . The general structure of each case is similar; we proceed by induction on a sub-expression and prove the new continuation
. The general structure of each case is similar; we proceed by induction on a sub-expression and prove the new continuation ![]() is well typed by applications of [K-Bind]. Proving the body of
is well typed by applications of [K-Bind]. Proving the body of ![]() is well typed requires using Lemma 4.3. This requires proving that
is well typed requires using Lemma 4.3. This requires proving that ![]() is composed with a configuration
is composed with a configuration ![]() equivalent to
equivalent to ![]() , and showing their types are equivalent. To show
, and showing their types are equivalent. To show ![]() is equivalent to
is equivalent to ![]() $[\!\![\texttt{e}]\!\!]$, we use the Lemmas 5.4 and 4.15 to allow for composing configurations and continuations. Additionally, since several typing rules substitute sub-expressions into the type system, we use Lemma 5.5 in these cases to show the types of
$[\!\![\texttt{e}]\!\!]$, we use the Lemmas 5.4 and 4.15 to allow for composing configurations and continuations. Additionally, since several typing rules substitute sub-expressions into the type system, we use Lemma 5.5 in these cases to show the types of ![]() and
and ![]() are equivalent. Each non-value proof case focuses on showing these two equivalences.
are equivalent. Each non-value proof case focuses on showing these two equivalences.
Case: [Ax-Prop]
We must show that
 . This follows from Lemma 4.2.
. This follows from Lemma 4.2.
-
Case: [Snd] Following our general structure, we must show (1)
 in an environment where
in an environment where  and (2)
and (2)  . For goal (1), we focus on
. For goal (1), we focus on  :
:

For goal (2), since
 by Lemma 5.5, we focus on showing
by Lemma 5.5, we focus on showing  . Focusing on
. Focusing on  , we have:
, we have:

Case: [ElimNat] Following our general structure, we must show (1)

 in an environment where
in an environment where 
-
For goal (1), we focus on
 :
:

For goal (2), since
 by Lemma 5.5, and
by Lemma 5.5, and  by the definition
by the definition  , we conclude using [
, we conclude using [ $\equiv$-Subst].
$\equiv$-Subst].-
Case: [If] Following our general structure, we must show (1)
 in an environment where
in an environment where  and (2)
and (2)  (and analogously for
(and analogously for  where
where  ). Focusing on
). Focusing on  in goal (1), we have:
in goal (1), we have:

For goal (2),
 by Lemma 5.5. Since
by Lemma 5.5. Since  we conclude with [
we conclude with [ $\equiv$-Subst]
$\equiv$-Subst]
Key steps in the proof require reasoning about equivalence of terms. To prove equivalence of terms, we need to know their syntax so a structural equivalence rule applies, which is not true of terms of the form ![]() . To reason about this term, we need to show an equivalence between the compiler and ANF-composition, so we can reason instead about
. To reason about this term, we need to show an equivalence between the compiler and ANF-composition, so we can reason instead about ![]() , a definition we can unroll and we know is correct with respect to evaluation via Lemma 4.15 (Naturality). We prove this equivalence, Lemma 5.4 next. This essentially tells us that our compiler is compositional, that is, respects separate compilation and composition in the target language. We can either first translate a program
, a definition we can unroll and we know is correct with respect to evaluation via Lemma 4.15 (Naturality). We prove this equivalence, Lemma 5.4 next. This essentially tells us that our compiler is compositional, that is, respects separate compilation and composition in the target language. We can either first translate a program ![]() under continuation
under continuation ![]() and then compose it with a continuation
and then compose it with a continuation ![]() , or we can first compose the continuations
, or we can first compose the continuations ![]() and
and ![]() and then translate
and then translate ![]() under the composed continuation.
under the composed continuation.
Lemma 5.4 (Compositionality) ![]()
Proof. By induction on the structure of ![]() . All value cases are trivial. The cases for non-values are all similar, following by definition of composition for continuations or configurations.
. All value cases are trivial. The cases for non-values are all similar, following by definition of composition for continuations or configurations.
Corollary 5.4.1. ![]() .
.
Similarly, at times we need to reason about the translation of terms or types that have a variable substituted, such as ![]() . We often use induction on a judgment
. We often use induction on a judgment ![]() , which gives us the structure of the expression
, which gives us the structure of the expression ![]() but not much of the structure of the type
but not much of the structure of the type ![]() . The type
. The type ![]() may have a term substituted, as
may have a term substituted, as ![]() , but we have no information about the structure of
, but we have no information about the structure of ![]() itself. Since we cannot reason about
itself. Since we cannot reason about ![]() directly, we cannot obtain the final term after substitution, and thus, we do not know the syntax of the compilation of this arbitrary term. We show another kind of compositionality with respect to this substitution, Lemma 5.5, which shows that substitution is equivalent to composing via continuations. Since standard substitution does not preserve ANF, this lemma does not equate terms in ANF, but
directly, we cannot obtain the final term after substitution, and thus, we do not know the syntax of the compilation of this arbitrary term. We show another kind of compositionality with respect to this substitution, Lemma 5.5, which shows that substitution is equivalent to composing via continuations. Since standard substitution does not preserve ANF, this lemma does not equate terms in ANF, but ![]() $\mathrm{CC}_{e}^{A}$ terms that are not normal. We again mark this shift with the boundary term
$\mathrm{CC}_{e}^{A}$ terms that are not normal. We again mark this shift with the boundary term ![]() $\mathcal{NN}()$.
$\mathcal{NN}()$.
Lemma 5.5 (Substitution). ![]()
Our type system relies on a subtyping judgment, so we must show subtyping is preserved. The proof is uninteresting, except insofar as it is simple, while it seems to be impossible in prior work for CPS translation (Bowman et al., Reference Bowman, Cong, Rioux and Ahmed2018).
Lemma 5.6 If ![]() .
.
Subtyping relies on type equivalence (but not vice versa), so we must also show the equivalence judgment is preserved. This lemma is also useful as a kind of compiler correctness property, ensuring that our notion of program equivalence (since types and terms are the same) is preserved through compilation.
Lemma 5.7 If ![]()
Since equivalence is defined in terms of reduction and conversion, we must also show reduction and conversion are preserved up to equivalence in the target language. This is convenient, since reduction and conversion also define the dynamic semantics of programs. These proofs correspond to a forward simulation proof up to target language equivalence and also imply compiler correctness. The proofs are straightforward; intuitively, ANF is just adding a bunch of ![]() $\zeta$-reductions.
$\zeta$-reductions.
Lemma 5.8. If ![]()
Lemma 5.9. If ![]()
Proof. By induction on the structure of ![]() .
.
As a result of proving that ANF preserves the judgmental and syntactic structure that a dependent type system relies on, we can also easily prove correctness of separate compilation (with respect to the ANF evaluation semantics). To do this, we must define linking and a specification of when outputs are related across languages, independent of the compiler.
We define an independent specification relating observation across languages, which allows us to understand the correctness theorem without reading the compiler. We define the relation ![]() to compare ground values in Figure 13.
to compare ground values in Figure 13.

Fig. 13: Separate compilation definitions.
We define linking as substitution with well-typed closed terms and define a closing substitution ![]() with respect to the environment
with respect to the environment ![]() (also in Figure 13). Linking is defined by closing a term
(also in Figure 13). Linking is defined by closing a term ![]() such that
such that ![]() with a substitution
with a substitution ![]() , written
, written ![]() . Any
. Any ![]() is valid for
is valid for ![]() if it maps each
if it maps each ![]() to a closed term
to a closed term ![]() of type
of type ![]() . For definitions in
. For definitions in ![]() , we require that if
, we require that if ![]() , then
, then ![]() , that is, the substitution must map
, that is, the substitution must map ![]() to a closed version of its definition
to a closed version of its definition ![]() . We lift the ANF translation to substitutions.
. We lift the ANF translation to substitutions.
Correctness of separate compilation says that we can either link then run a program in the source language semantics, that is, using the conversion semantics, or separately compile the term and its closing substitution then run in the ANF evaluation semantics. Either way, we get equivalent terms. The proof is straightforward from the compositionality properties and forward simulations we proved for type preservation.
Theorem 5.10 (Correctness of Separate Compilation) If ![]() , (and
, (and ![]() a base type) and
a base type) and ![]() then
then ![]() .
.
Proof. The following diagram commutes, because ![]() $\equiv$ corresponds to
$\equiv$ corresponds to ![]() $\approx$ on base types (
$\approx$ on base types (![]() or
or ![]() ), the translation commutes with substitution, and preserves equivalence.
), the translation commutes with substitution, and preserves equivalence.

6 Join-point optimization
Recall from Figure 8 that the composition of a continuation ![]() with an
with an ![]() configuration,
configuration, ![]() , duplicates
, duplicates ![]() in the branches:
in the branches: ![]() . Similarly, the ANF translation in Figure 12 performs the same duplication when translating
. Similarly, the ANF translation in Figure 12 performs the same duplication when translating ![]() expressions. This can cause exponential code duplication, which is no problem in theory but is a problem in practice.
expressions. This can cause exponential code duplication, which is no problem in theory but is a problem in practice.
![]() $\mathrm{CC}_{e}^{A}$ supports implementing the join-point optimization, which avoids this code duplication. We modify the ANF translation from Section 5 to use the definition in Figure 14 and prove it is still correct and type preserving. Note that the new translation requires access to the type
$\mathrm{CC}_{e}^{A}$ supports implementing the join-point optimization, which avoids this code duplication. We modify the ANF translation from Section 5 to use the definition in Figure 14 and prove it is still correct and type preserving. Note that the new translation requires access to the type ![]() from the derivation. We can do this either by defining the translation by induction over typing derivations or (preferably) modifying the syntax of
from the derivation. We can do this either by defining the translation by induction over typing derivations or (preferably) modifying the syntax of ![]() to include
to include ![]() as a type annotation, similar to dependent pairs in ECC or dependent case analysis in Coq.
as a type annotation, similar to dependent pairs in ECC or dependent case analysis in Coq.

Fig. 14: Join-point optimized ANF translation.
Lemma 6.1. ![]()
Proof. By induction.
Case: [If] We proceed by induction on the branch sub-expressions and ensure their corresponding continuation is well typed. This means the application of the join point
 must be on well-typed arguments of (1)
must be on well-typed arguments of (1)  and (2)
and (2)  (analogously for
(analogously for  in the
in the  branch). (1) follows from the equivalence
branch). (1) follows from the equivalence 
 , which has been shown before in Lemma 5.3. (2) follows if we show
, which has been shown before in Lemma 5.3. (2) follows if we show  in an environment where
in an environment where  . By [
. By [ $\equiv$-Cong-Equiv], we must show
$\equiv$-Cong-Equiv], we must show  , which by definition is
, which by definition is  , previously shown in Lemma 5.3.
, previously shown in Lemma 5.3.
7 Future and related work
We first discuss possible extensions to the source language. We sketch adding recursion and inductive data types to our source language ECC and conjecture that our proof technique can scale to these features. However, extending the source with extensional equality seems more difficult. We then discuss ways to efficiently type check ![]() $\mathrm{CC}_{e}^{A}$ terms constructed from the ANF translation. We conclude by discussing related work as alternatives to the ANF translation, in particular the CPS translation, Call-by-Push-Value, and monadic form. These alternatives either fail to scale to higher universes, or fail to compile to a language as “low-level” as
$\mathrm{CC}_{e}^{A}$ terms constructed from the ANF translation. We conclude by discussing related work as alternatives to the ANF translation, in particular the CPS translation, Call-by-Push-Value, and monadic form. These alternatives either fail to scale to higher universes, or fail to compile to a language as “low-level” as ![]() $\mathrm{CC}_{e}^{A}$ in ANF.
$\mathrm{CC}_{e}^{A}$ in ANF.
7.1 Costs of type-preserving compilation
Compared to other approaches to solving linking errors, such as PCC (Necula, Reference Necula1997) which requires finding and encoding witnesses of safety proofs, type-preserving compilation is a lightweight and effective technique (Morrisett et al., Reference Morrisett, Walker, Crary and Glew1999; Xi & Harper Reference Xi and Harper2001; Shao et al., Reference Shao, Trifonov, Saha and Papaspyrou2005).
Unfortunately, one major disadvantage is the compilation time. TIL (Tarditi et al., Reference Tarditi, Morrisett, Cheng, Stone, Harper and Lee1996), a type-preserving compiler for Standard ML, was found to be eight times slower than the non-type-preserving compiler SML/NJ. Chen et al., (Reference Chen, Hawblitzel, Perry, Emmi, Condit, Coetzee and Pratikaki2008) found that their type-preserving compiler for Microsoft’s Common Intermediate Language (CIL) was 82.8% slower than their base compiler, mostly due to type inference and writing type information to object files. We consider long compilation times a relatively small price to pay for the safety guarantees provided for the compiled program, particularly given the cost of unsafety (Stecklein et al., Reference Stecklein, Dabney, Dick, Haskins, Lovell and Moroney2004; Briski et al., Reference Briski, Chitale, Hamilton, Pratt, Starr, Veroulis and Villard2008).
It is also unclear that this cost is necessary. Shao et al., (Reference Shao, League and Monnier1998) show that careful attention to representation of typed intermediate language nearly eliminated compile time overhead introduced in the FLINT compiler compared to the SML/NJ compiler. The focus in that work is with respect to large types, which is particularly relevant for dependent-type preservation.
However, annotations overhead with dependent types can be far larger. For example, annotation size (including both types and proofs) was 6x time larger than the code size in CompCert (Leroy, Reference Leroy2009), and one extension to CompCert doubled that (Stewart et al., Reference Stewart, Beringer, Cuellar and Appel2015). If this sort of difference between annotation size and code size is typical, it could be a huge problem. It is not clear that is typical; Stewart et al., (Reference Stewart, Beringer, Cuellar and Appel2015) note that the doubling was in part due to duplication of definitions which should be unnecessary.
Removing inference from the type system could significantly improve compile time (Chen et al., Reference Chen, Hawblitzel, Perry, Emmi, Condit, Coetzee and Pratikaki2008), but could increase code size and require more annotations. This time/space tradeoff has been studied in the context of LF (Necula & Rahul, Reference Necula and Rahul2001; Sarkar et al., Reference Sarkar, Pientka and Crary2005). Adapting these techniques to dependently typed languages in the style of Coq would likely be necessary for practical implementation of dependent-type preservation, but the issues are very similar to that of LF.
7.2 Recursive functions and match
Our source language ECC still lacks some key features of a general purpose dependently typed language. In particular, our language does not have a ![]() construct for defining recursive functions and a
construct for defining recursive functions and a ![]() construct for eliminating general inductive datatypes. These features require a termination condition to ensure termination of programs; thus, building a type-preserving compiler for a language with these features would require the compiler preserve the termination condition as well. We could preserve a syntactic termination condition, as used by Coq; however, this requires a significantly more complex target guard condition. Bowman & Ahmed (Reference Bowman and Ahmed2018) provide an example of preserving the guard condition through the closure conversion pass, where the guard condition must essentially become a data-flow analysis in order to track the flow of recursive calls through closures. This would greatly increase the complexity of the target type system and possibly affect type checking performance. This suggests that using a syntactic condition is undesirable for a dependently typed intermediate language. An alternative could be compiling this syntactic guard condition to sized types, but adding sized types to Coq is still a work in progress (Chan & Bowman, Reference Chan and Bowman2020).
construct for eliminating general inductive datatypes. These features require a termination condition to ensure termination of programs; thus, building a type-preserving compiler for a language with these features would require the compiler preserve the termination condition as well. We could preserve a syntactic termination condition, as used by Coq; however, this requires a significantly more complex target guard condition. Bowman & Ahmed (Reference Bowman and Ahmed2018) provide an example of preserving the guard condition through the closure conversion pass, where the guard condition must essentially become a data-flow analysis in order to track the flow of recursive calls through closures. This would greatly increase the complexity of the target type system and possibly affect type checking performance. This suggests that using a syntactic condition is undesirable for a dependently typed intermediate language. An alternative could be compiling this syntactic guard condition to sized types, but adding sized types to Coq is still a work in progress (Chan & Bowman, Reference Chan and Bowman2020).
However, assuming we have preserved the guard condition through the ANF translation with the aforementioned possible complexities, we conjecture that the technique presented in this paper scales to these language features. In particular, proving that the ANF translation of ![]() is type preserving would be very similar to the technique used for dependent
is type preserving would be very similar to the technique used for dependent ![]() . Suppose we have added a syntactic form
. Suppose we have added a syntactic form ![]() and typing rule:
and typing rule:
The target language would have a similar syntactic ![]() construct as a configuration
construct as a configuration ![]() . Any proofs of lemmas over configurations
. Any proofs of lemmas over configurations ![]() should be updated to include the
should be updated to include the ![]() construct. The ANF translation would first translate the scrutinee
construct. The ANF translation would first translate the scrutinee ![]() and then push
and then push ![]() into each branch of the
into each branch of the ![]() . In order to prove this translation type preserving, we would change the target typing rule for
. In order to prove this translation type preserving, we would change the target typing rule for ![]() to include a propositional equality when checking each branch. That is, the premises
to include a propositional equality when checking each branch. That is, the premises ![]() in the source
in the source ![]() rule above would change to
rule above would change to ![]() . The target typing rule threads the equality
. The target typing rule threads the equality ![]() when checking each branch, to record that the scrutinee
when checking each branch, to record that the scrutinee ![]() has reduced to a particular case of the match
has reduced to a particular case of the match ![]() .
.
Threading an equality into the branches proves type preservation in the same way as with ![]() statements with the equality
statements with the equality ![]() . The continuation
. The continuation ![]() originally expects something of type
originally expects something of type ![]() but then is pushed into the branches and translated with something of type
but then is pushed into the branches and translated with something of type ![]() . The equality
. The equality ![]() in the context introduced by the target typing rule helps resolve the discrepancy between the substitution
in the context introduced by the target typing rule helps resolve the discrepancy between the substitution ![]() and
and ![]() .
.
Assuming the termination condition can be preserved through the ANF translation, proving that ANF is type-preserving for ![]() would be similar to proving type preservation for functions. Given the typing rule for
would be similar to proving type preservation for functions. Given the typing rule for ![]() and the ANF translation:
and the ANF translation:

We could show that the ANF translation is type preserving by Lemma 4.2 and show that the target fix expression ![]() is well typed. This is easy to show using the target [Fix] typing rule, assuming the guard condition is preserved, and by induction on
is well typed. This is easy to show using the target [Fix] typing rule, assuming the guard condition is preserved, and by induction on ![]() .
.
7.3 Preserving extensional equality
A natural question is whether we can preserve extensional equality through ANF translation. Since the target language already supports this, it seems trivial to preserve, no?
Our study so far suggests that adding new features with the same pattern of dependency and judgmental structural does not take much effort. Adding new positive or negative types is not significantly more complicated if the translation already supports positive and negative types. Adding recursion does not seem difficult since the dependency is not new, although it adds a new judgment that must be preserved.
By contrast, extensional equality is a radical change to the judgmental structure of the source language. Currently, in our source language, the typing and equivalence judgments are separately defined—typing depends on equivalence, but not vice versa. Adding extensional equality typically makes these two judgment mutually dependent. This completely changes the structure of the type preservation proof—as we discussed in Section 5, we stage our proof by first showing reduction is preserved, then equivalence, etc, and finally that typing is preserved. This structure follows the structure of the source typing derivations. Because adding extensional equality changes the structure of source typing derivations, this entire proof could no longer be staged and would need to be mutually inductive.
Past authors have not had much success in solving these large mutual inductive proofs and instead avoid them. Barthe et al., (Reference Barthe, Hatcliff and SØrensen1999) discuss this problem as choose to use a Curry-style type system to avoid the problem. Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018) discuss it also, but choose to use untyped equivalence and untyped reduction to avoid it. We follow the latter approach, but that is not tenable if we extend the source language with extensional equability.
We have considered alternative variants of extensional equality. For example, consider the following idea for a simplification of the Rule [![]() $\equiv$-Reflect] which avoids mutual dependency.
$\equiv$-Reflect] which avoids mutual dependency.
In this version of extensional equality, we avoid dependence on the typing judgment by restricting extensionality to apply only when we have a proof that we can use in the current context. Unfortunately, this breaks subject reduction, and if equivalence is untyped, it can lead to unsoundness. Since the only purpose was to break the dependence between equivalence and typing, and subject reduction is important for a compiler IL, we end up with the standard reflection rule.
That said, these issues about typed equivalence are only about complicating the proof technique, not the translation. Extensional equivalence does not introduce any new dependencies that ANF can disrupt, so it seems likely that ANF would still be type preserving, but it will almost certainly be difficult to prove.
7.4 Recovering decidability
Our target language ![]() $\mathrm{CC}_{e}^{A}$ is extensional type theory, which is well known to have undecidable type checking. An IL with undecidable type checking affects our type-check-then-link approach, even though linking may not necessarily occur at
$\mathrm{CC}_{e}^{A}$ is extensional type theory, which is well known to have undecidable type checking. An IL with undecidable type checking affects our type-check-then-link approach, even though linking may not necessarily occur at ![]() $\mathrm{CC}_{e}^{A}$. This is because the decidability of type checking of earlier ILs may affect the type checking of later ILs in the compiler, where linking is to be done. If some information is lost resulting in undecidability, then that information is unlikely to be regained later.
$\mathrm{CC}_{e}^{A}$. This is because the decidability of type checking of earlier ILs may affect the type checking of later ILs in the compiler, where linking is to be done. If some information is lost resulting in undecidability, then that information is unlikely to be regained later.
There are then two main approaches to avoid undecidable type checking. One is to find ways to recover decidability for the subset of ![]() $\mathrm{CC}_{e}^{A}$ constructed by the compiler. The other is to remove equivalence reflection from
$\mathrm{CC}_{e}^{A}$ constructed by the compiler. The other is to remove equivalence reflection from ![]() $\mathrm{CC}_{e}^{A}$ and attempt to recover the proof of type preservation, which is much more difficult and not ideal for compilation.
$\mathrm{CC}_{e}^{A}$ and attempt to recover the proof of type preservation, which is much more difficult and not ideal for compilation.
Recovering Decidability for ![]() $\mathrm{CC}_{e}^{A}$. Intuitively, the target terms in
$\mathrm{CC}_{e}^{A}$. Intuitively, the target terms in ![]() $\mathrm{CC}_{e}^{A}$ constructed by the compiler should be decidable. This is because the terms are constructed from terms in a decidable source language. In principle, the translation could make use of this fact and insert whatever annotations are necessary into the target term to ensure it can be decidably checked in an extensional type theory. Determining small, suitable annotations for compilation is the main subject of future work.
$\mathrm{CC}_{e}^{A}$ constructed by the compiler should be decidable. This is because the terms are constructed from terms in a decidable source language. In principle, the translation could make use of this fact and insert whatever annotations are necessary into the target term to ensure it can be decidably checked in an extensional type theory. Determining small, suitable annotations for compilation is the main subject of future work.
One approach for annotating the compiled term is a technique from proof-carrying code (PCC). In a variant of PCC by Necula & Rahul (Reference Necula and Rahul2001), the inference rules are represented as a higher-order logic program, and the proof checker is a non-deterministic logic interpreter. The proofs are made deterministic by recording non-deterministic choices as a bit-string. Our compiler could be modified to produce a similar bit-string encoding the non-deterministic choices. The type checker could then be modified to interpret the encoding to ensure type checking is decidable.
If all else fails, we can recover decidability to translating typing derivations rather than syntax. Donning our propositions-as-types hat once again, we can obtain the desired typing derivation by using the proof of type preservation. The proof can be viewed as a function from source typing derivations to target typing derivations. The target typing derivation can then be translated to CIC with additional axioms and be decidably checked (Oury, Reference Oury2005). However, this would require shipping the type preservation proof with the compiler, which might be undesirable.
Using a Target Language Without Equivalence Reflection. We could use the convoy pattern (Chlipala, Reference Chlipala2013) to compile if expressions, as we did to show consistency of ![]() $\mathrm{CC}_{e}^{A}$ in Section 4.2.1. However, there are two issues with this approach: (1) the convoy pattern is not in ANF and (2) the resulting code generated just to show types are preserved (i.e., code not related to execution) is extremely large.
$\mathrm{CC}_{e}^{A}$ in Section 4.2.1. However, there are two issues with this approach: (1) the convoy pattern is not in ANF and (2) the resulting code generated just to show types are preserved (i.e., code not related to execution) is extremely large.
One could attempt to reduce the code size generated by the convoy pattern by using type safe coercions. Consider the addition of the following coercion, ![]() :
:
Naive additions of such coercions, however, result in a non-type-preserving translation. For example, the coercions could be inserted into the translation for ![]() as follows:
as follows:

The type preservation proof fails in the branches of the ![]() , despite the coercion. This is because our judgmental equivalence cannot determine that the expression expected by the continuation,
, despite the coercion. This is because our judgmental equivalence cannot determine that the expression expected by the continuation, ![]() , is equivalent to the expression
, is equivalent to the expression ![]() . Equality reflection was key in proving this equivalence in our proof of type preservation.
. Equality reflection was key in proving this equivalence in our proof of type preservation.
7.5 CPS translation
ANF is favored as a compiler intermediate representation, although not universally. Cong et al., (Reference Cong, Osvald, Essertel and Rompf2019) include a thorough summary of the arguments for and against both CPS and ANF as intermediate representations.
Most recent work on CPS translation of dependently typed languages focuses on expressing control effects (Miquey, Reference Miquey2017; Pédrot, Reference Pédrot2017; Cong & Asai, Reference Cong and Asai2018a, 2018b), which we discuss further in Section 7.7. When expressing control effects with dependent types, it is necessary for consistency to prevent certain dependencies from being expressed (Barthe & Uustalu, Reference Barthe and Uustalu2002; Herbelin, 2005), so these translations do not try to recover dependencies in the way we discuss in Section 2.
Two CPS translations exist that do try to recover dependencies in the absence of effects, but fail to scale to a predicative universe hierarchy. Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018) present a type-preserving CPS translation for the Calculus of Constructions. They add a special form and typing rule for the application of a computation to a continuation which essentially records a machine step and is essentially similar to the ![]() typing rule. They also add a non-standard equality rule that essentially corresponds to Lemma 4.15 (Naturality). Cong & Asai (Reference Cong and Asai2018a) extend the translation of Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018) to dependent pattern matching using essentially the same typing rule for
typing rule. They also add a non-standard equality rule that essentially corresponds to Lemma 4.15 (Naturality). Cong & Asai (Reference Cong and Asai2018a) extend the translation of Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018) to dependent pattern matching using essentially the same typing rule for ![]() as we do in
as we do in ![]() $\mathrm{CC}_{e}^{A}$.
$\mathrm{CC}_{e}^{A}$.
Unfortunately, this rule relies on interpreting all functions as parametric and in a single computationally relevant impredicative universe. Both of these restrictions are a problem; Boulier et al., (Reference Boulier, Pédrot and Tabareau2017) give an example of a type theory that is anti-parametric because it enables ad hoc polymorphism and type quotation. It is simpler to demonstrate the problems that occur when relying on impredicativity.
Impredicativity is inconsistent with large elimination, that is, eliminating a type to a term (Huet, Reference Huet1986; Chan, Reference Chan2021)Footnote 9 This means the CPS translation cannot be used for a consistent type theory with large elimination, while our ANF translation can. For a concrete example of what kind of expressiveness is regained, consider the following definition of the type of arbitrary arity functions.

This definition lets us build well-typed multi-arity functions over natural numbers. For example, the type of the n-ary summation function is ![]() . But, this requires large elimination and would be inconsistent in an impredicative universe and thus cannot be supported by the CPS translation of Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018). The desire for this sort of definitions makes a predicative universe hierarchy almost, but not quite, universal in dependently typed languages. Cedille is a notable exception, instead trying to take full advantage of impredicativity (Stump & Jenkins, Reference Stump and Jenkins2018).
. But, this requires large elimination and would be inconsistent in an impredicative universe and thus cannot be supported by the CPS translation of Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018). The desire for this sort of definitions makes a predicative universe hierarchy almost, but not quite, universal in dependently typed languages. Cedille is a notable exception, instead trying to take full advantage of impredicativity (Stump & Jenkins, Reference Stump and Jenkins2018).
7.6 Call-by-push-value and monadic form
Call-by-push-value (CBPV) is similar to our ANF target language and to CPS target languages. In essence, CBPV is a ![]() $\lambda$ calculus in monadic form suitable for reasoning about call-by-value (CBV) or call-by-name (CBN), due to explicit sequencing of computations (Levy, Reference Levy2012). It has values, computations, and continuations, as we do, and has compositional typing rules (which inspired much of our own presentation). The structure of CBPV is of useful for modeling effects; all computations should be considered to carry an arbitrary effect, while values do not.
$\lambda$ calculus in monadic form suitable for reasoning about call-by-value (CBV) or call-by-name (CBN), due to explicit sequencing of computations (Levy, Reference Levy2012). It has values, computations, and continuations, as we do, and has compositional typing rules (which inspired much of our own presentation). The structure of CBPV is of useful for modeling effects; all computations should be considered to carry an arbitrary effect, while values do not.
Work on designing a dependent call-by-push-value (dCBPV) runs into some of the same design issues that we see in ANF (Ahman, Reference Ahman2017; Vákár, Reference Vákár2017; Pédrot & Tabareau, Reference Pédrot and Tabareau2019), but critically avoids the central difficulties introduced in Section 2. The reason is essentially that monadic form is more compositional than ANF, so dependency is not disrupted in the same way.
Recall from Section 4 that our definition of composition was entirely motivated by the need to compose configurations and continuations. In monadic form generally, there is no distinction between computation and configurations, and let is free to compose configurations. This means that configurations can return intermediate computations, instead of composing the entire rest of the continuation inside the body of a let. The monadic translation of ![]() , which is problematic in ANF, is given below and is easily type preserving.
, which is problematic in ANF, is given below and is easily type preserving.
Note that since let can bind the “configuration” ![]() , the typing rule [Let] and the compositionality lemma suffice to show type preservation, without any reasoning about definitions. In fact, we do not even need definitions for monadic form; we only need a dependent result type for let. A similar argument applies to the monadic translation of dependent if: since we can still nest if on the right-hand side of a let, the difficulties we encounter in the ANF translation are avoided.
, the typing rule [Let] and the compositionality lemma suffice to show type preservation, without any reasoning about definitions. In fact, we do not even need definitions for monadic form; we only need a dependent result type for let. A similar argument applies to the monadic translation of dependent if: since we can still nest if on the right-hand side of a let, the difficulties we encounter in the ANF translation are avoided.
The dependent typing rule for let without definitions is essentially the rule given by Vákár (Reference Vákár2017), called the dependent Kleisli extension, to support the CBV monadic translation of type theory into dCBPV, and the CBN translation with strong dependent pairs. Vákár (Reference Vákár2017) observes that without the dependent Kleisli extension, CBV translation is ill-defined (not type preserving), and CBN only works for dependent elimination of positive types. This is the same as the observation made independently by Bowman et al., (Reference Bowman, Cong, Rioux and Ahmed2018) that type-preserving CBV CPS fails for ![]() $\Pi$ types, in addition to the well-known result that the CBN translation failed for
$\Pi$ types, in addition to the well-known result that the CBN translation failed for ![]() $\Sigma$ types (Barthe & Uustalu Reference Barthe and Uustalu2002).
$\Sigma$ types (Barthe & Uustalu Reference Barthe and Uustalu2002).
Recently, Pédrot & Tabareau (Reference Pédrot and Tabareau2019) introduce another variant of dependent call-by-push-value dubbed ![]() $\delta$CBPV and discuss the thunkability extension in order to develop a monadic translation to embed from CC
$\delta$CBPV and discuss the thunkability extension in order to develop a monadic translation to embed from CC![]() $_\omega$ into
$_\omega$ into ![]() $\delta$CBPV. Thunkability expresses that a computation behaves like a pure computation, and so it can be depended upon. This justifies the addition of an equation to their type theory that is similar to our Lemma 4.15, but should hold even when the language is extended with effects. The authors note that the thunkability extensions seems to require that the target of the thunkable translation be an extensional type theory.
$\delta$CBPV. Thunkability expresses that a computation behaves like a pure computation, and so it can be depended upon. This justifies the addition of an equation to their type theory that is similar to our Lemma 4.15, but should hold even when the language is extended with effects. The authors note that the thunkability extensions seems to require that the target of the thunkable translation be an extensional type theory.
Monadic form has been studied for compilation (Benton et al., Reference Benton, Kennedy and Russell1998; Benton & Kennedy, Reference Benton and Kennedy1999). In these instances, the compiler simplifies from monadic form to ANF as a series of intra-language rewrites. Once in ANF, that is, a form that is normal with respect to the commuting conversions within monadic form, code generation is greatly simplified since all nesting has been eliminated. This more practical implementation technique, not strictly adhering to ANF until necessary, is also used in GHC (Maurer et al., Reference Maurer, Downen, Ariola and Peyton Jones2017) and Chez Scheme.Footnote 10
These commutative conversions are called commutative cuts in the dependent type theory literature (Herbelin Reference Herbelin2009; Boutillier Reference Boutillier2012). Formally, the problem of commutative cuts can be phrased as: Is the following transformation type preserving?
ANF necessarily performs this transformation, as we have shown.
These same commuting conversion do not preserve typing in a standard dependently typed language, but do in our target language ![]() $\mathrm{CC}_{e}^{A}$. While we study this through the ANF translation directly, the more practical application of this work is likely in the design of the target language, which is designed to support ANF, rather than in the ANF translation itself. In this view, the ANF translation can be seen as a proof technique that all intermediate rewrites from monadic form to ANF are support in the target language.
$\mathrm{CC}_{e}^{A}$. While we study this through the ANF translation directly, the more practical application of this work is likely in the design of the target language, which is designed to support ANF, rather than in the ANF translation itself. In this view, the ANF translation can be seen as a proof technique that all intermediate rewrites from monadic form to ANF are support in the target language.
7.7 CPS for control effects in dependent types
Most work on CPS for dependent types is primarily concerned with integrating control effects and dependent types, not with type-preserving compilation. Therefore, these CPS translations necessarily make different design choices than we describe in Section 2. For example, we want to avoid any restriction on the source language. However, one must necessarily restrict certain dependencies to integrate control effects and dependent types, at least for the effectful parts of the language. For our translation, naturality is important, but it is non-goal for effectful terms, or is a goal only up to a boundary. We briefly describe some of these translations.
To justify soundness of a dependent sequent calculus, Miquey (Reference Miquey2017) present a CPS translation based on double negation. Sequent calculi make co-values (essentially, continuation) explicit in the language and thus express control effects. Miquey (Reference Miquey2017) develop their CPS translation and avoid relying on parametricity and impredicativity. They rely on modified source type system to track equalities when checking co-values that depend on expression, which is essentially similar to the definitions in our continuation typing. They use delimited continuations to enforce naturality at certain boundaries, to constrain the scope of effects. They also rely on the negative-elimination-free (NEF) restriction (Herbelin, Reference Herbelin2012), which disallows proofs that contain certain kinds of computations, such as arbitrary dependent projection from ![]() $\Sigma$ types. If we want to compile existing languages, such as Coq, which have significant code bases, we cannot admit restrictions like the NEF restriction.
$\Sigma$ types. If we want to compile existing languages, such as Coq, which have significant code bases, we cannot admit restrictions like the NEF restriction.
7.8 Non-dependently typed ANF translation
There has not been much work on type preservation for simply typed (or, more specifically, non-dependently typed) ANF translation. Most of the type preservation literature focuses on CPS translation (Shao, Reference Shao1997; Morrisett et al., Reference Morrisett, Walker, Crary and Glew1999; Thielecke, Reference Thielecke2003; Kennedy, Reference Kennedy2007; Ahmed & Blume, Reference Ahmed and Blume2011; Perconti & Ahmed, Reference Perconti and Ahmed2014; Patterson et al., Reference Patterson, Perconti, Dimoulas and Ahmed2017).
This is probably because ANF translation without dependent types is, essentially, not interesting. CPS translation transforms every expression, making explicit a representation of computation and continuation. This requires a (typed) encoding that captures all the properties of interest and changes the types of every term change. This makes type preservation non-trivial and raises interesting questions about exactly type computations and continuations should be assigned. This can be particularly interesting when considering a compiled component interacting with a hostile context (Ahmed & Blume, Reference Ahmed and Blume2011).
By contrast, ANF essentially just reorders existing terms and binds them to names without introducing any new objects into the syntax. No types change at all, so long as types do not depend on the syntax of terms.
A cursory study of non-dependently typed ANF appears in the technical appendix by Ahmed & Blume, (Reference Ahmed and Blume2011), companion to Ahmed & Blume, (Reference Ahmed and Blume2011), which briefly studies ANF translation of System F. They show that, in System F, ANF is type preserving and fully abstract, since System F in ANF is actually just a subset of System F. The proof is not given in detail, however.
Another tangential study of type-preserving ANF appears in the work of Saffrich & Thiemann (Reference Saffrich and Thiemann2020), which use ANF as part of a proof to show that imperative session types are subsumed by a functional session types API. The correctness and type-preservation of ANF translation is similarly considered trivial in the text since ANF does not affect typing, although they provide a detailed proof of type preservation in the appendix.
8 Conclusion
We develop a type-preserving ANF translation for ECC—a significant subset of Coq including dependent functions, dependent pairs, dependent elimination of booleans, natural numbers, and the infinite hierarchy of universes—and prove correctness of separate compilation with respect to a machine semantics for the target language. The translation, these proofs, and our proof technique for ANF are main contributions. This translation provides strong evidence that type-preserving compilation can support all of dependent type theory. It gives insights into type preservation for dependent types in general and into related work on type-preserving control flow transformations.
Acknowledgments
We gratefully acknowledge Youyou Cong, Max S. New, Hugo Herbelin, Matthias Felleisen, Greg Morrisett, Simon Peyton Jones, Paul Downen, Andrew Kennedy, Brian LaChance, Danel Ahman, Carlo Angiuli, and the many anonymous reviewers for their time in discussing ANF, CPS and related problems during the course of this work. Thank you all. We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), funding reference number RGPIN-2019-04207. Cette recherche a été financée par le Conseil de recherches en sciences naturelles et en génie du Canada (CRSNG), numéro de référence RGPIN-2019-04207
Conflicts of interest
None.
1. Appendix: Full proof of type preservation and extended figures
1.

-
2.
 .
.
Proof. The proof is by induction on the mutually defined judgments ![]() and
and ![]() . Cases [Ax-Prop], [Lam], [App], [Snd], [ElimNat], and [If] are given, as they are representative.
. Cases [Ax-Prop], [Lam], [App], [Snd], [ElimNat], and [If] are given, as they are representative.
Note that for all sub-expressions ![]() of type
of type ![]() holds by instantiating the induction hypothesis with the empty continuation
holds by instantiating the induction hypothesis with the empty continuation ![]() . The general structure of each case is similar; we proceed by induction on a sub-expression and prove the new continuation
. The general structure of each case is similar; we proceed by induction on a sub-expression and prove the new continuation ![]() is well typed by applications of [K-Bind]. Proving the body of
is well typed by applications of [K-Bind]. Proving the body of ![]() is well typed requires using Lemma 4.3. This requires proving that
is well typed requires using Lemma 4.3. This requires proving that ![]() is composed with a configuration
is composed with a configuration ![]() equivalent to
equivalent to ![]() , and showing their types are equivalent. To show
, and showing their types are equivalent. To show ![]() is equivalent to
is equivalent to ![]() , we use the Lemma 5.4 and Lemma 4.15 to allow for composing configuations and continuations. Additionally, since several typing rules subsitute sub-expressions into the type system, we use Lemma 5.5 in these cases to show the types of
, we use the Lemma 5.4 and Lemma 4.15 to allow for composing configuations and continuations. Additionally, since several typing rules subsitute sub-expressions into the type system, we use Lemma 5.5 in these cases to show the types of ![]() and
and ![]() are equivalent. Each non-value proof case focuses on showing these two equivalences.
are equivalent. Each non-value proof case focuses on showing these two equivalences.
Case: [Ax-Prop] We must show that
 . This follows from Lemma 4.2.
. This follows from Lemma 4.2.-
Case: [Lam] Must show
 . This follows from Lemma 4.2 if we can show
. This follows from Lemma 4.2 if we can show  . This follows from [Lam] if we can show
. This follows from [Lam] if we can show  . This follows by induction on the judgment
. This follows by induction on the judgment  with the empty continuation
with the empty continuation  .
. -
Case: [App] Must show that
 .
. -
Let
 . Our conclusion follows by induction on
. Our conclusion follows by induction on  if we show
if we show  . By [K-Bind], we must show
. By [K-Bind], we must show  and
and 
 . The first goal follows from induction on
. The first goal follows from induction on  with the empty continuation
with the empty continuation  . The second goal also follows by induction on
. The second goal also follows by induction on  , but we must show
, but we must show 
 :. By [K-Bind] again, we must show
:. By [K-Bind] again, we must show  (which again follows by induction with the empty continuation) and
(which again follows by induction with the empty continuation) and 
 . This follows from Lemma 4.3 if we can show (1)
. This follows from Lemma 4.3 if we can show (1) 
 (2)
(2) 
 and (3)
and (3) 
 . By
. By  $\vartriangleright_{\delta}$ and [
$\vartriangleright_{\delta}$ and [ $\equiv$-Step], goal (1) changes to
$\equiv$-Step], goal (1) changes to 
 . We have previously shown that
. We have previously shown that 
 and
and  . Using these facts with [App], we derive
. Using these facts with [App], we derive  . We have that
. We have that  by Lemma 5.5 and derive our conclusion by [Conv]. By
by Lemma 5.5 and derive our conclusion by [Conv]. By  $\vartriangleright_{\delta}$ and [
$\vartriangleright_{\delta}$ and [ $\equiv$-Step], goal (3) changes to
$\equiv$-Step], goal (3) changes to 
 . We find that the left-hand side of the equivalence can be converted as well:
Then goal (2) follows from combining the fact that
. We find that the left-hand side of the equivalence can be converted as well:
Then goal (2) follows from combining the fact that
 and
and  :
:  .
.
-
Case: [Snd]
-
Must show
 . This follows by the induction hypothesis for the sub-derivation
. This follows by the induction hypothesis for the sub-derivation  if we can show
if we can show  By [K-Bind], it suffices to show (1)
By [K-Bind], it suffices to show (1)  and (2)
and (2) 
 . Goal (1) follows by the induction hypothesis for
. Goal (1) follows by the induction hypothesis for  with the well-typed empty continuation
with the well-typed empty continuation  . Goal (2) follows by Lemma 4.3 if we can show (3)
. Goal (2) follows by Lemma 4.3 if we can show (3) 
 , (4)
, (4)  , and (5)
, and (5)  .
. -
By
 $\rhd_{\delta}$, we are trying to show
$\rhd_{\delta}$, we are trying to show  . We have previously shown that
. We have previously shown that  . Using this fact with [Snd], we derive that
. Using this fact with [Snd], we derive that  . We can derive our goal by [Conv] if we can show that
. We can derive our goal by [Conv] if we can show that  is equivalent to
is equivalent to  . By Lemma 5.5, we have that
. By Lemma 5.5, we have that  is equivalent to
is equivalent to  . Focusing on
. Focusing on  , we have:
Finally,
, we have:
Finally,
 is equivalent to
is equivalent to  by [
by [ $\equiv$-Subst].
$\equiv$-Subst].
-
By
 $\rhd_{\delta}$ and [
$\rhd_{\delta}$ and [ $\equiv$-Step], we are trying to show
$\equiv$-Step], we are trying to show 
 . Focusing on
. Focusing on  , we have:
Combining goals (3) and (4), we can show goal (5).
, we have:
Combining goals (3) and (4), we can show goal (5).
-
Case: [If]
-
Must show
 Let
Let  . Our conclusion follows by induction on
. Our conclusion follows by induction on  if we show
if we show  . By [K-Bind], we must show (1)
. By [K-Bind], we must show (1)  and (2)
and (2)  . Goal (1) follows from induction on
. Goal (1) follows from induction on  with the empty continuation
with the empty continuation 
 . By [If] in goal (2), we focus on showing the new sub-goal
. By [If] in goal (2), we focus on showing the new sub-goal 
 as it is the most interesting. This follows by Lemma 4.3 if we can show (3)
as it is the most interesting. This follows by Lemma 4.3 if we can show (3) 
 , (4)
, (4)  and (5)
and (5)  . Goal (3) follows from induction with the empty continuation and [Conv] if we can show that
. Goal (3) follows from induction with the empty continuation and [Conv] if we can show that  . By Lemma 5.5, we are trying to show
. By Lemma 5.5, we are trying to show  . By [
. By [ $\equiv$-Reflect] and [Var], as well as equivalence by
$\equiv$-Reflect] and [Var], as well as equivalence by  $\rhd_{\delta}$, we can derive that under the extended environment
$\rhd_{\delta}$, we can derive that under the extended environment  , and we conclude with [
, and we conclude with [ $\equiv$-Subst]. Focusing the right-hand side of goal (4), we have:
Combining goals (3) and (4), we can show goal (5).
$\equiv$-Subst]. Focusing the right-hand side of goal (4), we have:
Combining goals (3) and (4), we can show goal (5).
-
Case: [ElimNat]
-
Must show
 . This can be proven using the techniques in the [App] case: induction on subexpressions and showing that each continuation is well typed. The body of the final
. This can be proven using the techniques in the [App] case: induction on subexpressions and showing that each continuation is well typed. The body of the final  expression must be shown to be of type
expression must be shown to be of type  , which can be proven by Lemma 4.2 if we show
, which can be proven by Lemma 4.2 if we show  This can be done by focusing on the left-hand side of the equivalence:
This can be done by focusing on the left-hand side of the equivalence:

Lemma 1.2 (Context Replacement (full definition))
1.
 .
.-
2.

-
3.

-
4.

-
5.

-
6.

Lemma 1.3 (Context Definition Replacement (full definition))
1.

-
2.

-
3.

-
4.

-
5.

-
6.

Lemma 1.4 (Cut (full definition))
1.

-
2.

-
3.

-
4.

-
5.

-
6.

Lemma 1.5 (Cut With Definitions (full definition))
1.

-
2.

-
3.

-
4.

-
5.

-
6.


Fig. A15: ECC syntax.

Fig. A16: ECC dynamic semantics (excerpt).

Fig. A17: ECC congruence conversion rules.

Fig. A18: ECC equivalence and subtyping

Fig. A19: ECC typing

Fig. A20: ECC well-formed environments.

Fig. A21: ![]() $\mathrm{CC}_{e}^{A}$ syntax.
$\mathrm{CC}_{e}^{A}$ syntax.

Fig. A22: ![]() $\mathrm{CC}_{e}^{A}$ equivalence
$\mathrm{CC}_{e}^{A}$ equivalence

Fig. A23: ![]() $\mathrm{CC}_{e}^{A}$ evaluation.
$\mathrm{CC}_{e}^{A}$ evaluation.

Fig. A24: Composition of configurations.

Fig. A25: ![]() $\mathrm{CC}_{e}^{A}$ continuation typing.
$\mathrm{CC}_{e}^{A}$ continuation typing.

Fig. A26: ![]() $\mathrm{CC}_{e}^{A}$ typing
$\mathrm{CC}_{e}^{A}$ typing













 This can be done by focusing on the left-hand side of the equivalence:
This can be done by focusing on the left-hand side of the equivalence:







































Discussions
No Discussions have been published for this article.