Hostname: page-component-6bb9c88b65-dwch4 Total loading time: 0 Render date: 2025-07-24T23:15:59.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Boxes go bananas: Encoding higher-order abstract syntax with parametric polymorphism*

Part of: JFP Research Articles

Published online by Cambridge University Press:  01 January 2008

GEOFFREY WASHBURN  and
STEPHANIE WEIRICH
GEOFFREY WASHBURN
Affiliation:
Department of Computer and Information Science, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA (email: geoffw@cis.upenn.edu, sweirich@cis.upenn.edu)
STEPHANIE WEIRICH
Affiliation:
Department of Computer and Information Science, University of Pennsylvania, Philadelphia, Pennsylvania 19104, USA (email: geoffw@cis.upenn.edu, sweirich@cis.upenn.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Higher-order abstract syntax is a simple technique for implementing languages with functional programming. Object variables and binders are implemented by variables and binders in the host language. By using this technique, one can avoid implementing common and tricky routines dealing with variables, such as capture-avoiding substitution. However, despite the advantages this technique provides, it is not commonly used because it is difficult to write sound elimination forms (such as folds or catamorphisms) for higher-order abstract syntax. To fold over such a data type, one must either simultaneously define an inverse operation (which may not exist) or show that all functions embedded in the data type are parametric. In this paper, we show how first-class polymorphism can be used to guarantee the parametricity of functions embedded in higher-order abstract syntax. With this restriction, we implement a library of iteration operators over data structures containing functionals. From this implementation, we derive “fusion laws” that functional programmers may use to reason about the iteration operator. Finally, we show how this use of parametric polymorphism corresponds to the Schürmann, Despeyroux and Pfenning method of enforcing parametricity through modal types. We do so by using this library to give a sound and complete encoding of their calculus into System 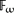. This encoding can serve as a starting point for reasoning about higher-order structures in polymorphic languages.

Information

Type
Articles
Information
Journal of Functional Programming , Volume 18 , Issue 1 , January 2008 , pp. 87 - 140
Copyright
Copyright © Cambridge University Press 2007

References

Acar, U., Blelloch, G. & Harper, R. (2002) Selective memoization. In 30th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. New Orleans, LA: ACM Press, pp. 14–25.Google Scholar
Ambler, S., Crole, R. L. & Momigliano, A. (2002) Combining higher order abstract syntax with tactical theorem proving and (co)induction. In 15th International Conference on Theorem Proving in Higher Order Logics. Lecture Notes in Computer Science, vol. 2410. Hampton, VA: Springer.Google Scholar
Bekić, H. (1984) Definable operation in general algebras, and the theory of automata and flowcharts. Programming Languages and Their Definition. Springer-Verlag. LNCS vol. 177.Google Scholar
Böhm, C. & Berarducci, A. (1985) Automatic synthesis of typed Λ-programs on term algebras. Theor. Comput. Sci. 39, 135–154.CrossRefGoogle Scholar
Church, A. (1940) A formulation of the simple theory of types. J. Symbolic Logic, 5, 56–68.CrossRefGoogle Scholar
Clarke, D., Hinze, R., Jeuring, J., Löh, A. & de Wit, J. (2001) The Generic Haskell User's Guide. Tech. rept. UU-CS-2001-26. Utrecht University.Google Scholar
Danvy, O. & Filinski, A. (1992) Representing control: A study of the CPS transformation. Math. Struct. Comput. Sci. 2 (4), 361–391.CrossRefGoogle Scholar
Davies, R. & Pfenning, F. (2001) A modal analysis of staged computation. J. ACM, 48 (3), 555–604.Google Scholar
Despeyroux, J. (2000) A higher-order specification of the π–calculus. In IFIP International Theoretical Computer Science. Sendai, Japan: Springer.Google Scholar
Despeyroux, J. & Leleu, P. (2001) Recursion over objects of functional type. Math. Struct. Comput. Sci. 11, 555–572.Google Scholar
Despeyroux, J., Felty, A. P. & Hirschowitz, A. (1995) Higher-order abstract syntax in Coq. In Second International Conference on Typed Lambda Calculi and Applications. London, UK: Springer-Verlag.Google Scholar
Fegaras, L. & Sheard, T. (1996) Revisiting catamorphisms over data types with embedded functions (or, programs from outer space). In 23rd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. St. Petersburg Beach, FL: ACM Press.Google Scholar
Gabbay, M. J. & Cheney, J. (2004) A sequent calculus for nominal logic. In 19th IEEE Symposium on Logic in Computer Science.Google Scholar
Girard, J.-Y. (1971) Une extension de l'interprétation de Gödel à l'analyse, et son application à l'élimination de coupures dans l'analyse et la théorie des types. In Fenstad, J. E. (ed), Second Scandinavian Logic Symposium. North-Holland Publishing Co.Google Scholar
Hinze, R. (2002) Polytypic values possess polykinded types. Sci. Computer Programming, 43 (2–3), 129–159. MPC Special Issue.Google Scholar
Honsell, F. & Miculan, M. (1995, June) A natural deduction approach to dynamic logic. In TYPES 1995, Berardi, C. (ed). Published in LNCS 1158, 1996.CrossRefGoogle Scholar
Honsell, F., Miculan, M. & Scagnetto, I. (2001) An axiomatic approach to metareasoning on nominal algebras in HOAS. Lecture Notes Comput. Sci. 2076.CrossRefGoogle Scholar
Johann, P. (2002) A generalization of short-cut fution and its correctness proof. Higher-order Symbolic Comput. 15, 273–300.CrossRefGoogle Scholar
Jones, M. P. (1995) A system of constructor classes: overloading and implicit higher-order polymorphism. J. Funct. Program. 5 (1), 1–35.CrossRefGoogle Scholar
Jones, M. P. (2000) Type classes with functional dependencies. Ninth European Symposium on Programming. LNCS, no. 1782. Berlin, Germany: Springer-Verlag.Google Scholar
Kripke, S. A. (1959) A completeness theorem in modal logic. J. Symb. Logic. 24, 1–15.CrossRefGoogle Scholar
Leszczyłowski, J. (1971) A theory on resolving equations in the space of languages. Bull. Polish Acad. Sci. 19 (Oct.), 967–970.Google Scholar
Meijer, E. & Hutton, G. (1995) Bananas in space: Extending fold and unfold to exponential types. In Conference on Functional Programming Languages and Computer Architecture. La Jolla, CA: ACM Press.Google Scholar
Meijer, E., Fokkinga, M. M. & Paterson, R. (1991) Functional programming with bananas, lenses, envelopes and barbed wire. In Conference on Functional Programming Languages and Computer Architecture. Cambridge, MA: Springer-Verlag.Google Scholar
Miller, D. (1990, May) An extension to ML to handle bound variables in data structures: Preliminary report. Proceedings of the Logical Frameworks BRA Workshop.Google Scholar
Miller, D. & Tiu, A. (2005) A proof theory for generic judgments. ACM Trans. Computat. Logic. 6 (4), 749–783.Google Scholar
Nanevski, A. (2002) Meta-programming with names and necessity. In Seventh ACM SIGPLAN International Conference on Functional Programming. ACM Press, pp. 206–217.CrossRefGoogle Scholar
Peyton Jones, S. (ed). (2003) Haskell 98 Language and Libraries: The Revised Report. Cambridge University Press.Google Scholar
Peyton Jones, S., Vytiniotis, D., Weirich, S. & Shields, M. (2005) Practical type inference for arbitrary-rank types. J. Funct. Program. 17 (1), 1–82.CrossRefGoogle Scholar
Pfenning, F. & Davies, R. (2001) A judgmental reconstruction of modal logic. Math. Struct. Comput. Sci. 11 (4), 511–540.CrossRefGoogle Scholar
Pfenning, F. & Elliott, C. (1988). Higher-order abstract syntax. In ACM SIGPLAN Conference on Programming Language Design and Implementation. Atlanta, GA: ACM Press.Google Scholar
Pfenning, F. & Schürmann, C. (1999) System description: Twelf—a meta-logical framework for deductive systems. In 16th International Conference on Automated Deduction, Ganzinger, H. (ed). Trento, Italy: Springer-Verlag.Google Scholar
Pitts, A. M. & Gabbay, M. J. (2000) A metalanguage for programming with bound names modulo renaming. In Mathematics of Program Construction. Port de Lima, Portugal: Springer-Verlag.Google Scholar
Poswolsky, A. & Carsten Schrmann, C. (2007, Jan.). Delphin: A Functional Programming Language with Higher-Other Encodings and Dependent Types. Tech. Rept. YALEU/DCS/TR-1375. Yale University.Google Scholar
Reynolds, J. C. (1983) Types, abstraction and parametric polymorphism. Information Processing /83. North-Holland. Proceedings of the IFIP 9th World Computer Congress.Google Scholar
Schürmann, C., Despeyroux, J. & Pfenning, F. (2001) Primitive recursion for higher-order abstract syntax. Theor. Comput. Sci. 266 (1–2), 1–58.CrossRefGoogle Scholar
Schürmann, C., Poswolsky, A. & Sarnat, J. (2004, Nov.) The ∇-Calculus: Functional Programming With Higher-Order Encodings. Tech. Rept. YALEU/DCS/TR-1272. Yale University.CrossRefGoogle Scholar
Sumii, E. & Kobayashi, N. (2001) A hybrid approach to online and offline partial evaluation. Higher-order Symbol. Comput. 14 (2/3), 101–142.CrossRefGoogle Scholar
Trifonov, V., Saha, B. & Shao, Z. (2000) Fully reflexive intensional type analysis. Fifth ACM SIGPLAN International Conference on Functional Programming. Montreal, Quebec, Canada: ACM Press. Extended version is YALEU/DCS/TR-1194.Google Scholar
Wadler, P. (1989) Theorems for free! In Conference on Functional Programming Languages and Computer Architecture. London, UK: ACM Press.Google Scholar
Washburn, G. (2001) Modal Typing for Specifying Run-time Code Generation. Available at http://www.cis.upenn.edu/geoffw/research/. accessed 31 July 2007.Google Scholar
Washburn, G. & Weirich, S. (2003) Boxes go bananas: Encoding higher-order abstract syntax with parametric polymorphism. In Eighth ACM SIGPLAN International Conference on Functional Programming. Uppsala, Sweden: ACM Press, for ACM SIGPLAN.Google Scholar
Weirich, S. (2006) Type-safe run-time polytypic programming. J. Funct. Program. 16 (10), 681–710.CrossRefGoogle Scholar
Xi, H., Chen, C. & Chen, G. (2003) Guarded recursive data type constructors. In 30th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. New Orleans, LA: ACM Press.Google Scholar
Submit a response

Discussions

No Discussions have been published for this article.