The connection between polymorphic and dynamic typing was originally considered by Curry et al. (1972, Combinatory Logic, vol. ii) in the form of “polymorphic type assignment” for untyped λ-terms. Types are assigned after the fact to what is, in modern terminology, a dynamic language. Interest in type assignment was revitalized by the proposals of Bracha et al. (1998, OOPSLA) and Bank et al. (1997, POPL) to enrich Java with polymorphism (generics), which in turn sparked the development of other languages, such as Scala, with similar combinations of features. In such a setting, where the target language already has a monomorphic type system, it is desirable to compile polymorphism to dynamic typing in such a way that as much static typing as possible is preserved, relying on dynamics only insofar as genericity is actually required. The basic approach is to compile polymorphism using embeddings from each type into a universal “top” type, 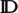${\mathbb{D}}$, and partial projections that go in the other direction. This scheme is intuitively reasonable, and, indeed, has been used in practice many times. Proving its correctness, however, is non-trivial. This paper studies the compilation of System F to an extension of Moggi's computational meta-language with a dynamic type and shows how the compilation may be proved correct using a logical relation.