Article contents
Extensional equality preservation and verified generic programming
Published online by Cambridge University Press: 21 October 2021
Abstract
In verified generic programming, one cannot exploit the structure of concrete data types but has to rely on well chosen sets of specifications or abstract data types (ADTs). Functors and monads are at the core of many applications of functional programming. This raises the question of what useful ADTs for verified functors and monads could look like. The functorial map of many important monads preserves extensional equality. For instance, if 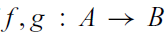 $$f,g \, : \, A \, \to \, B$$ are extensionally equal, that is,
$$f,g \, : \, A \, \to \, B$$ are extensionally equal, that is, 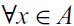 $$\forall x \in A$$,
$$\forall x \in A$$, 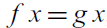 $$f \, x = g \, x$$, then
$$f \, x = g \, x$$, then 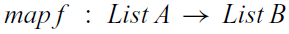 $$map \, f \, : \, List \, A \to List \, B$$ and
$$map \, f \, : \, List \, A \to List \, B$$ and 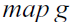 $$map \, g$$ are also extensionally equal. This suggests that preservation of extensional equality could be a useful principle in verified generic programming. We explore this possibility with a minimalist approach: we deal with (the lack of) extensional equality in Martin-Löf’s intensional type theories without extending the theories or using full-fledged setoids. Perhaps surprisingly, this minimal approach turns out to be extremely useful. It allows one to derive simple generic proofs of monadic laws but also verified, generic results in dynamical systems and control theory. In turn, these results avoid tedious code duplication and ad-hoc proofs. Thus, our work is a contribution toward pragmatic, verified generic programming.
$$map \, g$$ are also extensionally equal. This suggests that preservation of extensional equality could be a useful principle in verified generic programming. We explore this possibility with a minimalist approach: we deal with (the lack of) extensional equality in Martin-Löf’s intensional type theories without extending the theories or using full-fledged setoids. Perhaps surprisingly, this minimal approach turns out to be extremely useful. It allows one to derive simple generic proofs of monadic laws but also verified, generic results in dynamical systems and control theory. In turn, these results avoid tedious code duplication and ad-hoc proofs. Thus, our work is a contribution toward pragmatic, verified generic programming.
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by



Discussions
No Discussions have been published for this article.