1 Introduction
Designing a function that uses an accumulator always requires some thought, witness the explanations we need to conjure up to explain to our students what accumulators are, what they are good for, how to use them, and in which circumstances to use them. Too hasty an explanation leads to the proverbial dangerous thing: for example, no, using an accumulator is not solely for writing tail-recursive programs, since flattening a tree without using list concatenation is carried out with an accumulator and the resulting flattening function is not tail recursive. And likewise, one needs to become aware of the reverse order induced by accumulation in tail-recursive programs.
Against this backdrop, fold functions are an unexpectedly sustainable resource for teaching how to program recursive functions reliably. If a recursive function can be expressed using a fold function and if inlining the call to this fold function and simplifying yields this recursive function back, then this function was expressed in a structurally recursive manner: it can be reasoned about using structural induction (Burstall, Reference Burstall1969). This litmus test is a time saver for all parties that builds on the idea that our programs are not mere write-once, forget-forever artifacts: they are objects in our computational discourse we reason about.
Flat data structures such as Peano numbers and lists invite a processing that is iterative. This iterative processing is carried out by tail-recursive functions that use an accumulator. There too, fold functions are a sustainable resource for teaching how to program tail-recursive functions that use an accumulator: if a tail-recursive function with an accumulator can be expressed using a fold function and if inlining the call to this fold function and simplifying yields this tail-recursive function back, then this function was expressed in a structurally recursive manner: it can also be reasoned about using structural induction.
Historically (see App. 1), fold functions that abstract the ordinary pattern of recursion for lists are named “fold right” (or “reduce”) and fold functions that abstract the pattern of accumulator-based tail recursion for lists are named “fold left” (or “accumulate”).
The goal of this article is to describe the calculational diagram depicted in Fig. 1, where structurally recursive functions are abstracted into instances of fold functions (“fold introduction”) and instances of fold functions are concretized into recursive functions (“fold elimination”). This diagram hinges on the facts that for flat data structures, structurally recursive functions in “direct style” (Stoy, Reference Stoy1977) can be expressed as an instance of a fold-right function and that structurally tail-recursive functions with an accumulator can be expressed not only as an instance of a fold-left function but also as an instance of a fold-right function (see Sec. 1.7.1).

Fig. 1. Folding left and right matters, diagrammatically
The starting point, at the top of the diagram, is the definition of a structurally recursive function in direct style over Peano numbers or over lists – let us refer to this definition as a “d-definition.” This function can be expressed as an instance of a fold-right function, giving rise to a “d-right definition.” When this fold-right function and the corresponding fold-left function are equivalent, one can be replaced by the other in this d-right definition, giving rise to a “a-left definition.” Inlining the call to fold-left in this a-left definition and simplifying then yields the “a-definition” of a first-order tail-recursive function that uses an accumulator and is equivalent to the original function. This accumulator-based function is still structurally recursive, and therefore it can be expressed as an instance of the fold-right function, giving rise to an “a-right definition.” Under the same assumption that this fold-right function and the corresponding fold-left function are equivalent, one can be replaced by the other in this a-right definition, giving rise to an “h-left definition.” Inlining the call to fold-left in this h-left definition and simplifying then yields the “h-definition” of a second-order tail-recursive function that uses an first-order accumulator (i.e., a function) and is equivalent to the original function. Applying Ohori and Sasano’s lightweight fusion by fixed-point promotion (see Sec. 1.7.5) to this h-definition yields the “c-definition” of a function which is in delimited continuation-passing style and is equivalent to the original function. Each step is reversible.
For Peano numbers, the fold-left function and the fold-right function are unconditionally equivalent. For lists, the fold-left function and the fold-right function are conditionally equivalent, and this condition is stated in Bird and Wadler’s second duality theorem (Reference Bird and Wadler1988).
The entirety of this work is formalized in the Coq Proof Assistant (Bertot and Castàan, Reference Bertot and Castéran2004), including the second duality theorem (see App. 2.2). In the two accompanying .v files, the names in d-definitions are suffixed with _d, the names in d-right definitions are suffixed with _d_right, the names in a-left definitions are suffixed with _a_left, etc.
The significance of this work is both qualitative and quantitative. Qualitative: each of the inter-derived programming artifacts – recursive definitions in direct style, tail-recursive definitions using an accumulator, and tail-recursive definitions in delimited continuation-passing style – are definitions we would be happy to see our students write by hand. And quantitative: any two of these definitions can be calculated from the third. As such, they need not be invented: they can be systematically discovered.
The rest of this introduction is structured as follows. We first present the domain of discourse (primitive iteration and primitive recursion over Peano numbers and lists, Sec. 1.1). We then describe the elements of discourse on the right (fold-right functions, Sec. 1.2) and on the left (fold-left functions, Sec. 1.3). We then review the properties of the discourse (i.e., under which conditions are each pair of fold-left and fold-right functions equivalent Sec. 1.4) and their converse (Sec. 1.5). We then explain why there are two accompanying .v files instead of one (one uses an axiom for extensionality (the equality of functions) and Coq’s implicit axiomatization of Leibniz equality and the other uses an explicit axiomatization for type-indexed equality, Sec. 1.6). We then survey the tools of the discourse (abstracting a recursive function definition into an instance of a fold function and concretizing an instance of a fold function into a recursive function definition, and Ohori and Sasano’s lightweight fusion by fixed-point promotion (Reference Ohori and Sasano2007), Sec. 1.7). We then depict the discourse into a refined version of Fig. 1 (Sec. 1.8 and Fig. 2) before outlining the structure of the said discourse (Sec. 1.9).
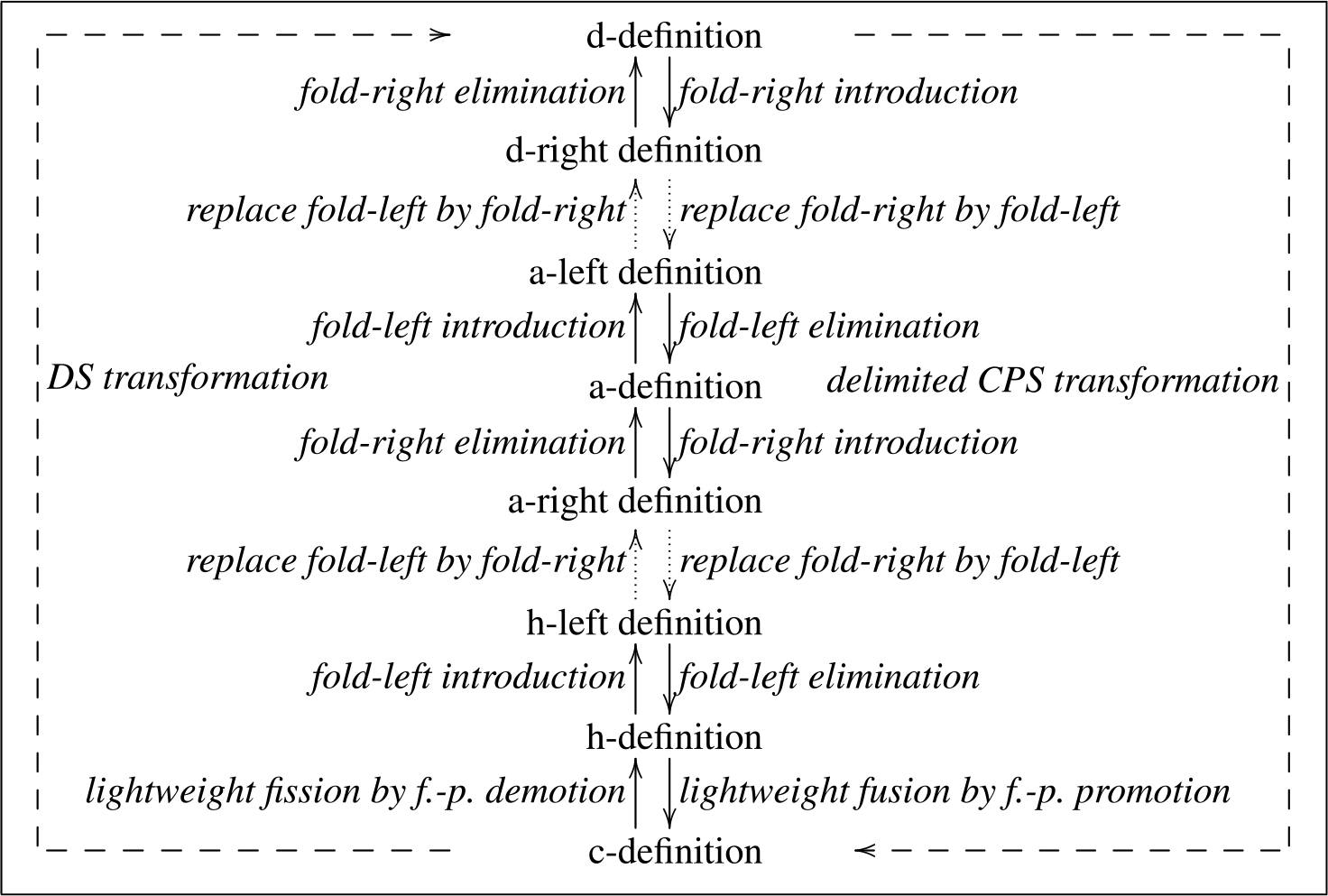
Fig. 2. Materialization of Fig. 1
1.1 The domain of discourse
We consider Peano numbers and lists (since Peano numbers are isomorphic to lists of unit values, the results about Peano numbers are corollaries of the corresponding results about lists of unit values). Gallina, the resident pure and total functional programming language in the Coq Proof Assistant, provides built-in implementations for these two data types: one is named Nat.nat (or nat for short) and its two constructors are O : nat and S : nat -> nat; and the other is polymorphic and named List.list (or list for short) and its two polymorphic constructors are nil and cons (noted with the infix notation ::).
1.1.1 Primitive iteration over Peano numbers
The concept of primitive iteration originates in recursion theory, as reviewed in Sec. 7. It is akin to Church encoding of Peano numbers (Reference Church1941), with zero as
![]() $\lambda z.\lambda s.z$
and the successor function as
$\lambda z.\lambda s.z$
and the successor function as
![]() $\lambda n.\lambda z.\lambda s.s\,(n\,z\,s)$
, and is defined as follows:
$\lambda n.\lambda z.\lambda s.s\,(n\,z\,s)$
, and is defined as follows:

1.1.2 Primitive recursion over Peano numbers
The concept of primitive recursion dates back to Dedekind and Skolem (Hermes, Reference Hermes1965; Kleene, Reference Kleene1952; Odifreddi, Reference Odifreddi1989), as reviewed in Sec. 7. In contrast to primitive iteration, the induction-step parameter is also applied to each successive predecessor of the given Peano number:

1.1.3 Primitive iteration over lists
Primitive iteration over lists is an analogue of primitive iteration over Peano numbers where the induction-step parameter is applied to each successive element in the given list:

That list_of_units_from_nat (defined in Sec. 1.1.1) and nat_from_list_of_units are inverses of each other is proved by induction, which establishes the isomorphism between nat and list unit mentioned in the opening sentence of Sec. 1.1.
1.1.4 Primitive recursion over lists
Primitive recursion over lists is an analogue of primitive recursion over Peano numbers where the induction-step parameter is applied to each successive element in the given list as well as to the following suffix:

1.1.5 Summary and synthesis
Overall, primitive iteration does not give access to the value to which the induction hypothesis applies, and primitive recursion does. So concretely, primitive iteration over Peano numbers formalizes a for-loop where the index is not used and primitive recursion over Peano numbers formalizes a for-loop where the index is used.
Primitive recursion over Peano numbers makes it immediate to program a predecessor function for positive numbers that works in constant time using call by name:
Primitive iteration over Peano numbers requires Kleene’s insight while at the dentist in 1932 (Kleene, Reference Kleene1981) or a higher-order version of it and yields a predecessor function for positive numbers that works in linear time:

And likewise for computing the tail of a nonempty list.
1.2 The elements of discourse, on the right
Fold-right functions are the computational counterpart of primitive iteration and primitive recursion. Let us proceed in the same order as in Sec. 1.1: fold functions for Peano numbers, “parafold” functions for Peano numbers (discovered by Cooper), fold functions for lists (discovered by Strachey and named by Turner, see App. 1), and parafold functions for lists (also discovered by Cooper). (Using the prefix “para” for primitive recursion was suggested by a reviewer (Danvy, Reference Danvy2019) in reference to Meertens’s work on paramorphisms (Reference Meertens1992).)
1.2.1 Primitive iteration over Peano numbers
The function nat_fold_right is an implementation of primitive iteration over Peano numbers that abstracts structurally recursive functions in direct style:

Applying nat_fold_right to z (the base-case parameter), s (the induction-step parameter), and, e.g., 3 gives rise to s (s (s z)), where s is applied 3 times, as per the last argument of the fold function, i.e., 3.
So for example, the addition function can be abstracted into an instance of nat_fold_right and this instance of nat_fold_right can be concretized into this definition of the addition function:

Likewise (see Sec. 1.1.5), we can compute the predecessor of a positive Peano number recursively with nat_fold_right, using Kleene’s insight.
1.2.2 Primitive recursion over Peano numbers
The function nat_parafold_right is an implementation of primitive recursion over Peano numbers that abstracts structurally recursive functions in direct style:

Applying nat_parafold_right to z (the base-case parameter), s (the induction-step parameter), and 3 gives rise to s 2 (s 1 (s 0 z)), where s is applied 3 times, as per the last argument of the parafold function, i.e., 3.
So for example, the factorial function can be abstracted into an instance of nat_parafold_right and this instance of nat_parafold_right can be concretized into this definition of the factorial function:

Likewise (see Sec. 1.1.5), we can compute the predecessor of a positive Peano number recursively with nat_parafold_right.
In the Coq Proof Assistant, nat_parafold_right is essentially nat_rect (see the accompanying .v files).
In Cooper’s work on the equivalence of computations (Reference Cooper1966), nat_parafold_right is Fr (Eqn. (1), p. 46).
1.2.3 Primitive iteration over lists
The function list_fold_right is an implementation of primitive iteration over lists that abstracts structurally recursive functions that are in direct style:

Applying list_fold_right to n (the base-case parameter), c (the induction-step parameter), and v1 :: v2 :: nil gives rise to c v1 (c v2 n), where c is applied twice, as per the length of the given list.
So for example, the list-copy function can be abstracted into an instance of list_fold_right and this instance of list_fold_right can be concretized into this definition of the list-copy function by inlining the definition of list_fold_right and simplifying:

The definition of list_copy_right is originally due to Strachey (Reference Strachey1961).
1.2.4 Primitive recursion over lists
The function list_parafold_right is an implementation of primitive recursion over lists that abstracts structurally recursive functions in direct style:

In the Coq Proof Assistant, list_parafold_right is essentially list_rect (see the accompanying .v files).
In Cooper’s work on the equivalence of computations (Reference Cooper1966), list_parafold_right is sketched on p. 47. Cooper also points out that list_parafold_right can be used to reverse a list, which might be the first occurrence of what is now classically referred to as a quadratic-time “naive reverse function” (Hughes, Reference Hughes1986):
1.3 The elements of discourse, on the left
Many recursive functions can be expressed tail recursively with an accumulator, and on the ground that these tail-recursive versions can be implemented more efficiently, a lot of attention has been given to them, starting with lists. Let us proceed in the same order as in Sec. 1.2: fold functions for Peano numbers, parafold functions for Peano numbers (discovered by Cooper), fold functions for lists (discovered by Strachey and named by Turner, see App. 1), and parafold functions for lists (also discovered by Cooper).
1.3.1 Primitive iteration over Peano numbers, tail recursively
The function nat_fold_left is an implementation of primitive iteration over Peano numbers that abstracts structurally tail-recursive functions that use an accumulator:

This implementation is akin to Church encoding of Peano numbers Church (Reference Church1941) where the successor function is
![]() $\lambda n.\lambda z.\lambda s.n\,(s\,z)\,s$
.
$\lambda n.\lambda z.\lambda s.n\,(s\,z)\,s$
.
Applying nat_fold_left to z, s, and, e.g., 3 gives rise to s 0 (s 1 (s 2 z)), where s is applied 3 times, as per the last argument of the fold function, i.e., 3.
So for example, a tail-recursive version of the addition function can be abstracted into an instance of nat_fold_left and this instance of nat_fold_left can be concretized into this tail-recursive version of the addition function:

Likewise (see Sec. 1.1.5), we can compute the predecessor of a positive Peano number tail recursively with nat_fold_left, using Kleene’s insight.
This fold-left function reconciles theory (classically, “primitive iteration” characterizes a class of computations) and practice (nowadays, “iteration” characterizes the execution of a for-loop and is achieved by applying a tail-recursive function).
1.3.2 Primitive recursion over Peano numbers, tail recursively
The function nat_parafold_left is an implementation of primitive recursion over Peano numbers that abstracts structurally tail-recursive functions that use an accumulator:

Applying nat_parafold_left to z, s, and 3 gives rise to s 0 (s 1 (s 2 z)), where the induction-step parameter, s, is applied 3 times, as per the last argument of the parafold function, i.e., 3.
So for example, a tail-recursive version of the factorial function can be abstracted into an instance of nat_parafold_left and this instance of nat_parafold_left can be concretized into this tail-recursive version of the factorial function:

And so we are now in position to theorize about primitive tail recursion.
In Cooper’s work on the equivalence of computations (Reference Cooper1966), nat_parafold_left is Fu (Eqn. (2), p. 46). To quote: “Notice that equations (2) are essentially the scheme for definition by primitive recursion.”
1.3.3 Primitive iteration over lists, tail recursively
The function list_fold_left is an implementation of primitive iteration over lists that abstracts structurally tail-recursive functions that use an accumulator:

Applying list_fold_left to n, c, and v1 :: v2 :: nil gives rise to c v2 (c v1 n), where the induction-step parameter, c, is applied twice, as per the length of the given list.
So for example, the list-reverse function can be abstracted into an instance of list_fold_left and this instance of list_fold_left can be concretized into this definition of the list-reverse function:

The definition of list_reverse_left is originally due to Strachey (Reference Strachey1961) and the definition list_reverse is now classically referred to as a linear-time “fast reverse function” (Hughes, Reference Hughes1986). In his design, list_fold_left had the same type as list_fold_right. Since the mid-1980s, however, functional programmers favor a version of list_fold_left where the arguments of the induction-step parameter are swapped, as reviewed in App. 1:

1.3.4 Primitive recursion over lists, tail recursively
The function list_parafold_left is an implementation of primitive recursion over lists that abstracts structurally tail-recursive functions that use an accumulator:

Consistently with Strachey’s design, list_parafold_left and list_parafold_right have the same type.
In Cooper’s work on the equivalence of computations (Reference Cooper1966), list_parafold_left is sketched on p. 47, and used to implement an iterative function for reversing a list.
1.4 The properties in the discourse
Under which conditions are each left and right fold and parafold functions equivalent?
1.4.1 Primitive iteration over Peano numbers (nat-fold-left & nat-fold-right)
As it happens, the two fold functions are unconditionally equivalent (Danvy, Reference Danvy2019):
And indeed (see Sec. 2) constructing
recursively or tail recursively by accumulating s over z n times gives the same result. So the two successor functions for Church numerals –
![]() $\lambda n.\lambda z.\lambda s.s\,(n\,z\,s)$
and
$\lambda n.\lambda z.\lambda s.s\,(n\,z\,s)$
and
![]() $\lambda n.\lambda z.\lambda s.n\,(s\,z)\,s$
– are indeed equivalent, which suggests that in Coq Proof Assistant, Nat.iter should not be implemented with nat_rect, i.e., nat_parafold_right, but with nat_fold_left, for efficiency.
$\lambda n.\lambda z.\lambda s.n\,(s\,z)\,s$
– are indeed equivalent, which suggests that in Coq Proof Assistant, Nat.iter should not be implemented with nat_rect, i.e., nat_parafold_right, but with nat_fold_left, for efficiency.
1.4.2 Primitive recursion over Peano numbers (nat-parafold-left & nat-parafold-right)
As it happens, the two parafold functions are only equivalent when their induction-step parameter is left-permutative:
(If an induction-step parameter is associative and commutative, it is also left-permutative, but the converse does not hold, e.g., for typing reasons.)

And indeed (see Sec. 3), one can equivalently compute a factorial number recursively (by successively computing the preceding factorial numbers, starting from 1) and tail recursively (by successively performing the converse multiplications, i.e., for a given n and for its successive predecessors i, by successively computing the preceding falling factorial numbers
![]() $n!/i!$
). That said, iota and atoi are not equivalent since cons is not left-permutative:
$n!/i!$
). That said, iota and atoi are not equivalent since cons is not left-permutative:

(The names “iota” and “atoi” (which is “iota” spelled backward) come from APL (Iverson, Reference Iverson1962), and “ih” stands for “induction hypothesis,” a handy acronym since in a structurally recursive function, a recursive call implements the induction hypothesis.)
In Cooper’s work on the equivalence of computations (Reference Cooper1966), Eqn. (4), p 46, both prefigure left-permutativity and anticipate the two premises in Bird and Wadler’s second duality theorem (see App. 2.2).
1.4.3 Primitive iteration over lists (list-fold-left & list-fold-right)
As it happens, these two fold functions are only equivalent when their induction-step parameter is left-permutative:

And indeed (see Sec. 4), one can equivalently compute the length of a list recursively (by successively computing the lengths of all the suffixes of the given list, starting from the shortest one) and tail recursively (by successively computing the lengths of all its prefixes, starting from the shortest one). That said, list_copy and list_reverse are not equivalent since cons is not left-permutative, witness Strachey’s two definitions in Sec. 1.2.3 and 1.3.3.
Modulo the order of arguments in the induction-step parameter for list_fold_left (see App. 1), the proposition above is Bird and Wadler’s second duality theorem (Reference Bird and Wadler1988), which is revisited in App. 2.2.
As foreshadowed in the opening sentence of Sec. 1.1, the accompanying .v files prove folding_left_and_right_over_Peano_numbers (Sec. 1.4.1) as a corollary of the proposition above using the isomorphism between Peano numbers and lists of unit values.
1.4.4 Primitive recursion over lists (list-parafold-left & list-parafold-right)
As it happens, these two parafold functions are only equivalent when their induction-step parameter is left-permutative. The following proposition generalizes Bird and Wadler’s second duality theorem in the expected way:

Cooper (Reference Cooper1966) also mentions this conditional equivalence.
1.5 The converse properties in the discourse
These sufficient conditions for folds and parafolds to be equivalent, are they necessary too?
1.5.1 Primitive iteration over lists (list-fold-left & list-fold-right)
Left-permutativity is not only sufficient for equivalently folding left and right over lists, it is also necessary if the equivalence holds for any given base-case parameter:

1.5.2 Primitive recursion over Peano numbers (nat-parafold-left & nat-parafold-right)
Left-permutativity is not necessary for equivalently parafolding left and right over Peano numbers. For example, the following function is not left-permutative but parafolding left and right with it yields the same result:

For example, parafolding left and right with any given z, baz, and 3 gives rise to
The right-hand side simplifies to nil in one step. In the left-hand side, the inner call to baz simplifies to nil, and then, the two other calls also simplify to nil. But baz is not left-permutative: for example, evaluating baz 1 (baz 2 (3 :: nil)) yields 1 :: 2 :: 3 :: nil but evaluating baz 2 (baz 1 (3 :: nil)) yields 2 :: 1 :: 3 :: nil.
1.5.3 Primitive recursion over lists (list-parafold-left & list-parafold-right)
Left-permutativity is not necessary either for equivalently parafolding left and right over lists. For example, the following function is not left-permutative but parafolding left and right with it yields the same result:

1.6 On the power and limitation of Leibniz equality in the Coq Proof Assistant
So far, all the propositions about folding left and right have been stated using the resident equality in the Coq Proof Assistant, i.e., Leibniz equality. But this equality does not cater to functions. Consider two expressions where x may occur free and that are Leibniz equal:
It does not seem unreasonable to wish for fun x => e1 and fun x => e2 to be Leibniz equal, which justifies adding the following axiom:
The present article and one of the two accompanying .v files assume this axiom, and so all equalities are Leibniz equalities here.
Instead of using an extensionality axiom for functional equality, the other .v file contains an axiomatization of equality as an inductive family of type-indexed functions. So building on Coq’s resident equality at type unit, bool, and nat, type-indexed polymorphic equality functions are defined for the option type, for pairs, for triples, and for functions. For example, equality for pairs and equality for functions are defined as follows:

Each definition comes together with a proof that this equality is an equivalence relation (reflexive, symmetric, and transitive) whenever its component equalities are equivalence relations too. For example, the equality for pairs is an equivalence relation whenever the equality for their two components is an equivalence relation too:

For functions, we also require the equality for their domain to be sound:

We are then in position to define our own equalities. For example:

So left-permutativity is quantified both with a type and with an equality at that type:

For example, here are two typical statements of left-permutativity – here for the factorial function (see Sec. 3):

The theorems about folding left and right also require the induction-step parameter to be compatible with the given equalities:

So all in all, this second .v file uses an explicit axiomatization for type-indexed equality and the first .v file uses an extensionality axiom for functional equality and Coq’s implicit axiomatization of Leibniz equality. For presentational simplicity, the present article uses the code from the first .v file:

But this simplicity is not mindless, witness the second .v file.
1.7 The tools for the discourse
Our primary tool here is calculational, starting with abstracting a recursive (resp. tail-recursive) function into an instance of a fold-right (resp. fold-left) function and concretizing an instance of a fold-right (resp. fold-left) function into a recursive (resp. tail-recursive) function. But then one can also abstract a tail-recursive function into an instance of a fold-right function (Sec. 1.7.1), which suggests that a fold-left function can also be expressed as an instance of the corresponding fold-right function (Sec. 1.7.2). Symmetrically, one can abstract a recursive function into an instance of a fold-left function, (Sec. 1.7.3), which suggests that a fold-right function can also be expressed as an instance of the corresponding fold-left function (Sec. 1.7.4). We also present lightweight fusion by fixed-point promotion (Sec. 1.7.5).
What I cannot create, I do not understand.
– Richard Feynman
1.7.1 Abstracting a tail-recursive function into an instance of a fold-right function
Let us revisit nat_fac_acc from Sec. 1.3.2:

With a pinch less syntactic sugar, we can make it more apparent that visit takes one argument (and returns a function):

Since a and i do not depend on each other, we can commute the function abstraction and the conditional expression:

We can also use lightweight fission by fixed-point demotion to make it more apparent that applying visit to n yields a function that is applied to 1:

This massaged definition is a fit for nat_parafold_right (applications associate to the left):
So a tail-recursive function that uses an accumulator can be expressed as an instance of a fold-right function.
1.7.2 Corollary: expressing each fold-left function as an instance of the corresponding fold-right function
Since nat_parafold_left and list_fold_left also involve tail-recursive functions that use an accumulator, they can be massaged mutatis mutandis to become a fit for nat_parafold_right and list_fold_right:

1.7.3 Abstracting a recursive function into an instance of a fold-left function
To express a recursive function into an instance of a fold-left function, we need something more radical than the syntactic massaging ministered in Sec. 1.7.1. Socrates to the rescue:
Question: What is accumulated, e.g., in the recursive definition of the factorial function in direct style?

Answer:The context of the recursive calls to visit, but this context is implicit due to the very nature of direct style.
Question:If we were to make this context explicit, what would be a suitable representation for it?
Answer:As a function of course. This function would be the identity function for the initial call, and then it would grow by being composed with fun a => S i’ * a on the right, exactly like a delimited continuation (Danvy and Filinski, Reference Danvy and Filinski1990):

Inlining the call to compose, simplifying, swapping the argument of visit, and using lightweight fission yields a definition that is fit for nat_parafold_left:

1.7.4 Corollary: expressing each fold-right function as an instance of the corresponding fold-left function
Generalizing, since nat_parafold_right and list_fold_right can also be expressed using a delimited continuation, they can also be expressed as instances of nat_parafold_left and list_fold_left:

Fascinatingly, in the mutual simulations of nat_parafold_left and nat_parafold_right and of list_fold_left and list_fold_right, the arguments of the fold functions are the same. However, as proved in the accompanying. v files, fun v k w => k (c v w) is left-permutative if and only if c is itself left-permutative:

So there is no dragon here.
1.7.5 Lightweight fusion by fixed-point promotion
We make use of Ohori and Sasano’s lightweight fusion by fixed-point promotion (Reference Ohori and Sasano2007) and of its left inverse (logically named “lightweight fission by fixed-point demotion”) where the context of the initial call to a tail-recursive function is relocated to the return point(s) in the body of this function. Here is a simple example:

In both definitions, the recursive call to visit is a tail call. In the candidate for lightweight fusion, visit eventually returns its accumulator, which is then passed to g, the result of which is then passed to f. The same happens in the candidate for lightweight fission, except that the initial call to visit is a tail call. The equivalence of these two functions is proved in the accompanying .v files.
To program is to understand.
– Kristen Nygaard
To prove our programs is to understand our understanding.
– Tyrion Lannister
To program our proofs is to understand them.
– Kristen Nygaard (persisting)
Er… OK.
– Tyrion Lannister
1.8 The discourse
The discourse is depicted in Fig. 2. Structurally recursive functions in direct style (“d-definitions”) can be abstracted as instances of a fold-right function (“d-right definitions”). When this fold-right function is equivalent to the corresponding fold-left function, these instances of a fold-right function are also instances of this corresponding fold-left function (“a-left definitions”). These instances can be concretized as structurally tail-recursive functions that use an accumulator (“a-definitions”). Structurally tail-recursive functions that use an accumulator can be abstracted as instances of a fold-right function (“a-right definitions”). When this fold-right function is equivalent to the corresponding fold-left function, these instances of a fold-right function are also instances of this corresponding fold-left function (“h-left definitions”). These instances can be concretized as structurally tail-recursive functions with a higher-order accumulator (“h-definitions”). Lightweight fusing these structurally tail-recursive functions with a higher-order accumulator yields structurally tail-recursive functions in delimited continuation-passing style (“c-definitions”).
Each of these steps is reversible. Lightweight fissioning a c-definition yields an h-definition. An h-definition can be abstracted as an instance of a fold-left function, yielding a h-left definition. When this fold-left function is equivalent to the corresponding fold-right function, this instance of a fold-left function is also an instance of the corresponding fold-right function, yielding an a-right definition. This instance can be concretized as an a-definition. An a-definition can be abstracted as an instance of a fold-left function, yielding an a-left definition. When this fold-left function is equivalent to the corresponding fold-right function, this instance of a fold-left function is also an instance of the corresponding fold-right function, yielding a d-right definition. This instance can be concretized as a d-definition.
1.9 Structure of the discourse
Sec. 2 illustrates the inter-derivation for primitive iteration over Peano numbers, using the power function as a running example and starting from its definition in direct style. Sec. 3 illustrates the inter-derivation for primitive recursion over Peano numbers, using the factorial function as a running example and starting with its definition in delimited continuation-passing style. Sec. 4 illustrates the inter-derivation for primitive iteration over lists, using the length function as a running example and starting with its tail-recursive definition that uses an accumulator. Sec. 5 outlines the inter-derivation for primitive recursion over lists. Sec. 6 describes applications as well as a generalization of Fig. 2. Sec. 7 reviews related work. Sec. 8 concludes. App. 1 provides a brief history of folding left and right over lists, from their origin (Strachey) to how they got their name (Turner) and how the order of arguments for the induction-step parameter of list_fold_left was swapped (Bird). App. 2 revisits Bird and Wadler’s duality theorems.
2 Folding left and right over Peano numbers
The goal of this section is to illustrate the inter-derivation depicted in Fig. 1 and 2 with primitive iteration over natural numbers, either recursively (nat_fold_right) or tail-recursively with an accumulator (nat_fold_left).
To illustrate the inter-derivation, let us start with the traditional definition of the linear power function in direct style:

Since this definition is structurally recursive on the exponent, it can be expressed with nat_fold_right:
The induction-step parameter is fun ih => x * ih. Since nat_fold_right and nat_fold_left are equivalent, we can replace the call to one by a call to the other in the definition of power_d_right:
The equivalence of power_d_right and of power_a_left is a corollary of folding left and right over Peano numbers. Inlining the call to nat_fold_left in the definition of power_a_left, renaming ih to a, and simplifying then yields the traditional tail-recursive definition of the power function that uses an accumulator:

Since this definition is structurally recursive on the exponent, it can be expressed with nat_fold_right:

The induction-step parameter is fun ih a => ih (x * a). Again, we can replace nat_fold_right by nat_fold_left in the definition of power_a_right:

The equivalence of power_a_right and of power_h_left is a corollary of folding left and right over Peano numbers. Inlining the call to nat_fold_left in the definition of power_h_left, renaming ih to k, and simplifying then yields a tail-recursive definition with a higher-order accumulator:

Performing lightweight fusion yields the traditional definition of the power function in delimited continuation-passing style (delimited because the continuation is initialized and so its co-domain is not a polymorphic domain of answers):

The inter-derivation from direct style to accumulator-passing style and then to delimited continuation-passing style is illustrated further in the accompanying .v files with a parity predicate and with the linear Fibonacci function that, given a natural number, returns a pair of consecutive Fibonacci numbers (Burstall and Darlington, Reference Burstall and Darlington1977; Danvy, Reference Danvy2019).
3 Parafolding left and right over Peano numbers
The goal of this section is to illustrate the inter-derivation depicted in Fig. 1 and 2 with primitive recursion over natural numbers, either recursively (nat_parafold_right) or tail recursively with an accumulator (nat_parafold_left).
To illustrate the inter-derivation, let us start with the traditional definition of the factorial function in delimited continuation-passing style:

This definition is a candidate for lightweight fission by fixed-point demotion, the left inverse of lightweight fusion by fixed-point promotion:

After lightweight fission, this definition fits the pattern of nat_parafold_left:

The induction-step parameter is fun n’ k a => k (S n’ * a). It is left-permutative:
Therefore we can replace nat_parafold_left by nat_parafold_right in the definition of fac_h_left:

The equivalence of fac_h_left and of fac_c_right is a corollary of parafolding left and right over Peano numbers. Inlining the call to nat_parafold_right in the definition of fac_a_right and simplifying then yields the traditional tail-recursive definition of the factorial function that uses an accumulator:

This definition fits the pattern of nat_parafold_left:

The induction-step parameter is fun n’ a => S n’ * a. It is left-permutative:
Therefore, we can replace nat_parafold_left by nat_parafold_right in the definition of fac_h_left:

The equivalence of fac_a_left and fac_d_right is a corollary of parafolding left and right over Peano numbers. Inlining the call to nat_parafold_right in the definition of fac_d_right and simplifying then yields the traditional recursive definition of the factorial function in direct style:

The inter-derivation from delimited continuation-passing style to accumulator-passing style and then to direct style is illustrated further in the accompanying .v files with a sum function that, given a function f and a natural number n, adds up the results of applying f to the first n natural numbers, i.e., computes
![]() $\Sigma_{i=0}^{n-1}f(i)$
.
$\Sigma_{i=0}^{n-1}f(i)$
.
4 Folding left and right over lists
The goal of this section is to illustrate the inter-derivation depicted in Fig. 1 and 2 with primitive iteration over lists, either recursively (list_fold_right) or tail recursively with an accumulator (list_fold_left).
To illustrate the inter-derivation, let us start with the traditional tail-recursive definition of the length function that uses an accumulator:

This definition fits the pattern of list_fold_left:
The induction-step parameter is fun v a => S a. It is left-permutative:
Therefore, we can replace list_fold_left by list_fold_right in the definition of length_d_left:
The equivalence of length_a_left and of length_d_right is a corollary of folding left and right over lists. Inlining the call to list_fold_right in the definition of length_d_right and simplifying then yields the traditional recursive definition of the length function in direct style:

Conversely, since the definition of length_a is structurally recursive on the given list, it can be expressed with list_fold_right:
The induction-step parameter is fun v ih a => ih (S a). It is left-permutative:
Therefore, we can replace list_fold_right by list_fold_left in the definition of length_h_right:
The equivalence of length_a_right and of length_h_left is a corollary of folding left and right over lists. Inlining the call to list_fold_left in the definition of length_h_left, renaming ih to k, and simplifying then yields the following definition:

This definition is a candidate for lightweight fusion by fixed-point promotion. The result is the traditional definition of the length function in delimited continuation-passing style:

The accompanying .v files also feature a function that, given a list of natural numbers, returns an optional pair containing the smallest and the largest numbers in the given list. This function is defined by induction on the tail of the given list if this list is not empty.
5 Parafolding left and right over lists
The inter-derivation depicted in Fig. 1 and 2 also works for primitive recursion over lists, either recursively (list_parafold_right) or tail recursively with an accumulator (list_parafold_left).
6 Applications and generalization
6.1 A tail-recursive version of du Feu’s powerset function
The author’s first stab at folding left and right (Reference Danvy2019) started with a listless powerset function that maps the representation of a set as the list of its elements (in any order and without repetition) to the representation of its powerset, i.e., the list of all of its subsets. This powerset function is listless (Wadler, Reference Wadler1984) in that all the lists it constructs are part of the result. It is also structurally recursive and so it can be expressed using list_fold_right, yielding a definition with two nested occurrences of list_fold_right that Michael Gordon attributes to Dave du Feu (Reference Gordon1979). Assuming that the order of elements in the resulting subsets and the order of these subsets do not matter, the two induction-step parameters in du Feu’s definition are as good as left-permutative, and the two nested occurrences of list_fold_right can be safely replaced by two nested occurrences of list_fold_left. Inlining these two calls to list_fold_left, simplifying, and performing lightweight fusion by fixed-point promotion yields a tail-recursive version of the powerset function that one might be hard pressed to write by hand in the first place, especially because like du Feu’s definition, it is still listless.
6.2 A tail-recursive version of Barron and Strachey’s Cartesian-product function
A similar story can be told about Barron and Strachey’s definition of the Cartesian product of sets represented as lists of their elements without repetition (Reference Barron and Strachey1966). Barron and Strachey’s definition is famously written with nested occurrences of list_fold_right. Assuming that the order of elements in the resulting sublists and the order of these sublists do not matter, the induction-step parameters in Barron and Strachey’s definition are as good as left-permutative, and the nested occurrences of list_fold_right can be safely replaced by nested occurrences of list_fold_left. Again, inlining these calls to list_fold_left, simplifying, and performing lightweight fusion by fixed-point promotion yields a listless tail-recursive version of the Cartesian-product function that one might be hard pressed to write by hand in the first place:

In both cases, if the length of the first list is
![]() $i_1$
and if the length of the second list is
$i_1$
and if the length of the second list is
![]() $i_2$
, visit1 is called
$i_2$
, visit1 is called
![]() $i_1 + 1$
times and visit2 is called
$i_1 + 1$
times and visit2 is called
![]() $i_2 + 1$
times, once for the empty list and once for each of their elements, yielding a list of length
$i_2 + 1$
times, once for the empty list and once for each of their elements, yielding a list of length
![]() $i_1 \times i_2$
in
$i_1 \times i_2$
in
![]() $(i_1 + 1) \times (i_2 + 1)$
calls to the visit functions. In the latter case, all calls are tail calls and the Cartesian product is accumulated at tail-call time. In the former case, if the result of the recursive call to visit1 is not named, all calls occur in the same order as in the latter case, and the Cartesian product is constructed at return time. (Naming the result of the recursive call to visit1 with a strict let expression mitigates the number of nested recursive calls to be
$(i_1 + 1) \times (i_2 + 1)$
calls to the visit functions. In the latter case, all calls are tail calls and the Cartesian product is accumulated at tail-call time. In the former case, if the result of the recursive call to visit1 is not named, all calls occur in the same order as in the latter case, and the Cartesian product is constructed at return time. (Naming the result of the recursive call to visit1 with a strict let expression mitigates the number of nested recursive calls to be
![]() $(i_1 + 1) + (i_2 + 1)$
at the most and yields the same result.)
$(i_1 + 1) + (i_2 + 1)$
at the most and yields the same result.)
Bird and Wadler’s third duality theorem (see App. 2.1) says that folding a list one way yields the same result as folding the reverse of this list the other way. The following proposition is a corollary of this theorem:
Applying these functions to any two lists yields lists that are reverses of each other:
6.3 Abstracting a recursive function into an instance of a fold-left function, revisited
Based on Fig. 2, we can take the long road on the right of the diagram and start with the continuation-passing counterpart of the direct-style definition at hand. Going up two steps in the diagram gives us a version of the function that used a fold-left function, as we did in Sec. 1.7.3 and at the beginning of Sec. 3. And there we are.
6.4 Primitive iteration and recursion over Peano numbers, revisited
Since nat_fold_left and nat_fold_right are equivalent, they trivially simulate each other. Since applying them to z, s, and, e.g., 4 gives rise to s (s (s (s z))) whereas applying nat_parafold_right to z, s, and 4 gives rise to s 3 (s 2 (s 1 (s 0 z))), one can uncurry s, which gives s (3, s (2, s (1, s (0, z)))), which suggests how to simulate nat_parafold_right using either nat_fold function:

(As reviewed in Sec. 1.1.5, using a pair is known since 1932 (Kleene, Reference Kleene1981) to implement the predecessor function using nat_fold_right. Justifying this pair as an instance of uncurrying might be new.)
In contrast, applying nat_parafold_left to z, s, and 4 gives rise to s 0 (s 1 (s 2 (s 3 z))), which suggests accumulating a counter instead:

Finally, one can get the best of both, i.e., s 3 0 (s 2 1 (s 1 2 (s 0 3 z))) by using both a pair and an accumulator:

6.5 Fig. 2, revisited and generalized
By now two questions should be burning bright in the mind of the reader:
• Are there “d-left definitions”?
The answer is no. The only way to introduce fold-left in a d-definition is to use the version of fold-left that uses fold-right. But as it happens, the result is the corresponding h-definition. And so the diagram in Fig. 2 does not expand at the top.
• Are there “h-right definitions”?
Yes, very much. And so the diagram expands at the bottom because of the lemma that says that fun v k w => k (c v w) is left-permutative whenever c is itself left-permutative (see Sec. 1.7.4).
This expansion is depicted in Fig. 3, with a change of notation: “d” is now “h
![]() $_0$
” to signify that the function has no accumulator, “a” is now “h
$_0$
” to signify that the function has no accumulator, “a” is now “h
![]() $_1$
” to signify that the function is first order (it is passed a zeroth-order accumulator), “h” is now “h
$_1$
” to signify that the function is first order (it is passed a zeroth-order accumulator), “h” is now “h
![]() $_2$
” to signify that the function is second order (it is passed a first-order accumulator). The next function is named “h
$_2$
” to signify that the function is second order (it is passed a first-order accumulator). The next function is named “h
![]() $_3$
” to signify that it is third order (it is passed a second-order accumulator), and so on.
$_3$
” to signify that it is third order (it is passed a second-order accumulator), and so on.

Fig. 3. Fig. 2, revisited and expanded
We can introduce fold-left in any h
 $_i$
-definition using the version of fold-right that uses fold-left. As it happens,
$_i$
-definition using the version of fold-right that uses fold-left. As it happens,– if i is 0, the result is a h
 $_2$
-definition, confirming that the diagram cannot be expanded at the top, and
$_2$
-definition, confirming that the diagram cannot be expanded at the top, and– if i is positive, the result is a h
 $_{i+1}$
-definition. In general, if i is positive, introducing fold-left in any h
$_{i+1}$
-definition. In general, if i is positive, introducing fold-left in any h
 $_i$
-definition using the version of fold-right that uses fold-left has the same effect as (1) introducing fold-right, (2) replacing fold-left by fold-right, and (3) eliminating fold-left.
$_i$
-definition using the version of fold-right that uses fold-left has the same effect as (1) introducing fold-right, (2) replacing fold-left by fold-right, and (3) eliminating fold-left.
We can introduce fold-right in any h
 $_i$
-definition using the version of fold-left that uses fold-right if i is positive. As it happens, the result is the same h
$_i$
-definition using the version of fold-left that uses fold-right if i is positive. As it happens, the result is the same h
 $_i$
-definition.
$_i$
-definition.We can introduce fold-right in a h
 $_2$
-definition – the second-order definition of a structurally tail-recursive function with a first-order accumulator. The result is a h
$_2$
-definition – the second-order definition of a structurally tail-recursive function with a first-order accumulator. The result is a h
 $_2$
-right definition. The new induction-step parameter is left-permutative if the previous induction-step parameter was also left-permutative. Replacing fold-right by fold-left in the h
$_2$
-right definition. The new induction-step parameter is left-permutative if the previous induction-step parameter was also left-permutative. Replacing fold-right by fold-left in the h
 $_2$
-right definition yields a h
$_2$
-right definition yields a h
 $_3$
-left definition. Eliminating fold-left in the h
$_3$
-left definition. Eliminating fold-left in the h
 $_3$
-left definition yields a h
$_3$
-left definition yields a h
 $_3$
-definition that iterates not just on W as in h
$_3$
-definition that iterates not just on W as in h
 $_1$
-definitions and not just on W -> W as in h
$_1$
-definitions and not just on W -> W as in h
 $_2$
-definitions, but on (W -> W) -> W -> W.
$_2$
-definitions, but on (W -> W) -> W -> W.We can introduce fold-right in a h
 $_3$
-definition – the third-order definition of a structurally tail-recursive function with a second-order accumulator. The result is a h
$_3$
-definition – the third-order definition of a structurally tail-recursive function with a second-order accumulator. The result is a h
 $_3$
-right definition. The new induction-step parameter is left-permutative if the previous induction-step parameter was also left-permutative. Replacing fold-right by fold-left in the h
$_3$
-right definition. The new induction-step parameter is left-permutative if the previous induction-step parameter was also left-permutative. Replacing fold-right by fold-left in the h
 $_3$
-right definition yields a h
$_3$
-right definition yields a h
 $_4$
-left definition. Eliminating fold-left in the h
$_4$
-left definition. Eliminating fold-left in the h
 $_4$
-left definition yields a h
$_4$
-left definition yields a h
 $_4$
-definition that iterates not just on W as in h
$_4$
-definition that iterates not just on W as in h
 $_1$
-definitions, not just on W -> W as in h
$_1$
-definitions, not just on W -> W as in h
 $_2$
-definitions, not just on (W -> W) -> W -> W as in h
$_2$
-definitions, not just on (W -> W) -> W -> W as in h
 $_3$
-definitions, but on ((W -> W) -> W -> W) -> (W -> W) -> W -> W.
$_3$
-definitions, but on ((W -> W) -> W -> W) -> (W -> W) -> W -> W.And so on.
Let us illustrate this nesting of endofunctions with the factorial function. Fig. 4 displays the first members of the family of successive factorial functions. In these successive definitions, nat_parafold_left and nat_parafold_right can be equivalently used, thanks to the left-permutativity of the successive induction-step parameters (see Fig. 5).

Fig. 4. Successive factorial functions

Fig. 5. Left-permutativity of the successive induction-step parameters in Fig. 4
Lest the reader is curious, here are the three next h-definitions of the factorial function:


7 Related work
The present article intersects with many research avenues.
Primitive recursion and primitive iteration originate in recursion theory, from Dedekind, Skolem, Gödel, Hilbert and Bernays, Péter, and Tait and onwards (Dowek, Reference Dowek2006; Hermes, Reference Hermes1965; Kleene, Reference Kleene1952; Odifreddi, Reference Odifreddi1989; Thompson, Reference Thompson1991), at a time when “recursive” meant “computable” whereas nowadays “recursive” means “self-referential,” “structurally recursive” means “compositional,” “iterative” means “repeated,” and “tail recursive” means “iterative using a particular pattern of recursion.” Fold-right functions are an abstraction of primitive recursive functions for flat structures such as Peano numbers and lists. The relevance here is that fold-left functions do not seem to appear in recursion theory. They do, however, very much appear in tail-recursion practice. (The last two sentences play on the classical meaning of “recursion” and on the modern meaning of “tail recursion.”) And intuitively, it makes more sense for primitive iteration over Peano numbers (in the classical sense of “iteration”) to be carried out iteratively (in the modern sense of “iteration”).
Fold functions have a rich history in functional programming (Hutton, Reference Hutton1999) and their connection with universal algebras and categorical constructs has been pointed out (Meijer et al., Reference Meijer, Fokkinga and Paterson1991), a topic of continued study ever since (Hutton et al., Reference Hutton, Jaskelioff and Gill2010). The relevance here is that folding left and right over Peano numbers has already been put in this picture (Oliveira, Reference Oliveira2020).
As elucidated in App. 1, the original order of arguments in the induction-step parameter for list_fold_left was swapped to accommodate Bird’s theory of lists. Swapping it back reveals a unity for primitive recursion over Peano numbers and for primitive iteration and primitive recursion over lists in that folding left and folding right are equivalent when their induction-step parameter is left-permutative.
As it happens, left-permutativity is a sufficient condition for “inverting the order of evaluation” from Cooper (Reference Cooper1966) and onwards (Bauer and Wössner, Reference Bauer and Wössner1982; Boiten, Reference Boiten1992). The relevance here is that for flat structures such as Peano numbers and lists, replacing the fold-right function by the corresponding fold-left function – and this should not come as a surprise in the light of Cooper’s seminal paper (Reference Cooper1966) – achieves this “re-bracketing” generically, as per the upper half of Fig. 1.
The motivation for inverting the order of evaluation was to obtain tail-recursive programs, for efficiency. However, and Giesl took this point to heart (Reference Giesl1999), tail-recursive programs are more complicated to reason about than their recursive counterpart, due to their accumulators. He set out to map accumulator-passing programs back to direct style so that they can be reasoned about by structural induction, which is simpler. The relevance here is that for flat structures such as Peano numbers and lists, replacing the fold-left function by the corresponding fold-right function achieves this de-inversion generically.
Also, Giesl’s work aims for the converse of Ohori and Sasano’s lightweight fusion by fixed-point promotion (Reference Ohori and Sasano2007) by relocating the context of the final version of the accumulator around the initial call to the corresponding tail-recursive function. Giesl’s work is non-trivial because inlining the call to a fold-left function often yields a tail-recursive program that one might be hard pressed to write by hand in the first place, witness, e.g., the powerset function in Sec. 6.1 and the Cartesian-product function in Sec. 6.2.
8 Conclusion and perspectives
For flat structures such as Peano numbers and lists, this article shows how to inter-derive recursive functions in direct style (d-definitions), tail-recursive functions with an accumulator (a-definitions), and tail-recursive functions with a higher-order accumulator (h-definitions) in a minimalistic way by expressing either of these functions as an instance of a fold function and then proceed as in Fig. 1. Inter-deriving a d-definition and an a-definition is done by twisting the way data are constructed, and inter-deriving an a-definition and a h-definition is done by twisting the way control is constructed. Lightweight fusing a h-definition gives a definition in delimited continuation-passing style. Pursuing the inter-derivation on a h-definition gives rise to a nesting of endofunctions that does not correspond to the CPS hierarchy as arises from iterating the CPS transformation (Danvy and Filinski, Reference Danvy and Filinski1990), so there is not that.
Besides its Platonistic take (in Computer Science, do we invent or do we discover?), this inter-derivation also made it possible to illustrate the usefulness of lightweight fusion by fixed-point promotion (Ohori and Sasano) and of its converse (Giesl), to shed light on the swapped version of list_fold_left that is favored by functional programmers since the mid-1980’s, and to point out the relevance of Bird and Wadler’s second duality theorem in the general area of program development (Cooper).
Je ne sais pas le reste.
– Évariste Galois
Acknowledgements
The author is grateful to the anonymous reviewers and to Julia Lawall for insightful comments, to Kira Kutscher for a last-minute round of proofreading, to Chantal Keller for a key point of vocabulary, and to Philip Wadler for instantly making a pertinent point when sent a preprint of this article. Thanks are also due to Richard Bird and to David Turner for their historical input and to Ralf Hinze for his editorship.
Conflicts of interest
None.
Supplementary material
For supplementary material for this article, please visit https://doi.org/10.1017/S0956796822000156.
1 A brief history of folding left and right over lists
In the early 1960s (Reference Strachey1961), Christopher Strachey studied the first documented instances of list_fold_right (naming it R0) and list_fold_left (naming it R1). He pointed out how instantiating R0 with nil and cons gave rise to the list-copy function (see Sec. 1.2.3) and how instantiating R1 with nil and cons gave rise to the list-reverse function (see Sec. 1.3.3). A few years later (Reference Barron and Strachey1966), Barron and Strachey wrote what is probably the world’s first functional pearl, an application of list_fold_right to express the Cartesian product of sets represented as lists (see Sec. 6.2). Gordon investigated the expressive power of list_fold_right (Reference Gordon1979) and Burstall, MacQueen, and Sannella pointed out its similarity with the reduction operator from APL (Iverson, Reference Iverson1962), in their presentation of Hope (Reference Burstall, MacQueen and Sannella1980).
Under various names (e.g., “reduce” and “accumulate”), these functions then became a staple of functional programming, witness the introductory textbooks that flourished near the turn of the 1990s – e.g., Henson (Reference Henson1987), Bird and Wadler (Reference Bird and Wadler1988), Field and Harrison (Reference Field and Harrison1988), Reade (Reference Reade1989), Bailey (Reference Bailey1990), Clack, Myers, & Poon (Reference Clack, Myers and Poon1995), and Thompson (Reference Thompson1995). Each of these textbooks featured folding left and right over lists.
The first parameters of the fold functions stand for the base case (nil) and the induction step (cons), in either order, despite the tradition to follow the same order as the one in the definition of the inductive data type at hand. Footnote 1 In the late 1980s, however, and for undocumented reasons, something strange happened: to fold left, the order of arguments for the induction-step parameter was swapped, making the type of list_fold_left read
instead of
One can surmise that the swap aimed to stress the eponymous laterality of the two fold functions – namely folding left vs. folding right, which is particularly visible using an infix notation. To wit, applying list_fold_right to a,
![]() $(\oplus)$
, and
$(\oplus)$
, and
![]() $1\,{::}\,2\,{::}\,3\,{::}\,{nil}$
gives rise to
$1\,{::}\,2\,{::}\,3\,{::}\,{nil}$
gives rise to
where
![]() $\oplus$
is visibly associated to the right, whereas applying the swapped version of list_fold_left to a,
$\oplus$
is visibly associated to the right, whereas applying the swapped version of list_fold_left to a,
![]() $(\oplus)$
, and
$(\oplus)$
, and
![]() $1\,{::}\,2\,{::}\,3\,{::}\,{nil}$
gives rise to
$1\,{::}\,2\,{::}\,3\,{::}\,{nil}$
gives rise to
where
![]() $\oplus$
is visibly associated to the left.
$\oplus$
is visibly associated to the left.
The author perused all the textbooks and users’ manuals he had access to but could not spot the tipping point, neither in Bird’s writings – though the title of Section 3 in his Introduction to the Theory of Lists (Reference Bird1986) comes close: “Left and right reduction” – nor in Turner’s epistemological arc from SASL (Reference Turner1976) to KRC (Reference Turner1982) and then Miranda (Reference Turner1985, Reference Turner1986). Indeed, according to the SASL language manual (Reference Turner1976) and the KRC prelude, written by Turner and dated April 2016: Footnote 2
• foldl :- folds up a list using a given binary operator opl and start value w in a left-associative way, so that
• foldr :- folds up a list using a given binary operator opr and start value w in a right-associative way, so that
where opl, w, v1, v2, and opr were renamed (and both opl and opr come before w).
In his homage to Dijkstra (Reference Danvy and Filinski1990), Turner points out that the version of foldl where the arguments of the given binary operator are swapped is due to Bird. And in an e-mail exchange with the author (15 to 21 Dec 2021), he wrote that in 1988, he changed the definition of foldl for Release 2 of Miranda, so that Bird and Wadler’s book (Reference Bird and Wadler1988) could be used as a textbook with Miranda, its Appendix C notwithstanding. The subsequent textbooks about Miranda (Clack et al., Reference Clack, Myers and Poon1995; Thompson, Reference Thompson1995) echoed this change, and that is how the order of arguments for the induction-step parameter of foldl got swapped, a fait accompli.
So all in all, the names “foldl” (read “fold left” in reference to associating to the left) and “foldr” (read “fold right” in reference to associating to the right) appeared in SASL and are due to Turner, the order of arguments for the induction-step parameter of foldl got swapped for compatibility with Bird and Wadler’s book, and the swapping is due to Bird.
In Bird and Wadler’s second duality theorem (App. 2.2), one of the two conditions for
to hold is
Without the eye crossing induced by swapping the arguments of opl, the operators opl and opr are the same and so this condition reads
which is left-permutativity. As for the other condition, it is
and is no longer needed since opl and opr are the same.
The situation is mirrored for “tsils” (i.e., right-to-left lists): tsil_fold_left and tsil_fold_right are equivalent if and only if their induction-step parameter is right-permutative. In that light, swapping the argument of the binary operator for list_fold_left is akin to first mapping the given list into a tsil and then applying tsil_fold_left (not swapping any arguments!):

At any rate, the current state of things is confusing for programmers, making foldl come across as, well, gauche. For example, in Standard ML and in Common Lisp, the type of foldl is the same as the type of foldr, but not so in, e.g., Haskell, OCaml, and Scheme, where the user needs to swap the arguments of the inductive parameter of foldl in their programs to undo the swapping in the implementation of foldl. For example, in Scheme:

On the one hand, this swap makes for left-leaning and right-leaning trees of applications that are visually compelling, and it has been put to beautiful use in, e.g., Gibbons’s work (Reference Gibbons2006). But on the other hand,
for programming, Strachey’s original order makes it a lot easier to grow an awareness of the reverse order induced by accumulation – for example, applying the original version of fold-left to a,
 $\mathit{op}$
, and
$\mathit{op}$
, and
 $1\,{::}\,2\,{::}\,3\,{::}\,{nil}$
gives rise to
$1\,{::}\,2\,{::}\,3\,{::}\,{nil}$
gives rise to
 $\mathit{op} \: 3 \: (\mathit{op} \: 2 \: (\mathit{op} \: 1 \: a))$
where 1, 2, and 3 were visibly accumulated in reverse order on top of a, iteratively,
$\mathit{op} \: 3 \: (\mathit{op} \: 2 \: (\mathit{op} \: 1 \: a))$
where 1, 2, and 3 were visibly accumulated in reverse order on top of a, iteratively,for proving, left-permutativity makes it a lot simpler to formalize Bird and Wadler’s duality theorems, as articulated in App. 2 (a routine induction vs. a Eureka lemma), and
for programming and proving, one can reason about one’s computation using structural induction (i.e., with fold-right) for simplicity, and one can then implement it using tail recursion (i.e., with fold-left) for efficiency, with no other refactoring than changing “right” into “left,” as illustrated throughout the present article.
The following note was added by the author after Richard Bird passed away in April 2022.
Was it shyness? Modesty? Discretion? Over the years, Richard Bird was asked by the author about the origins of the swapping in list_fold_left. But he never volunteered the information that it originates in his introduction to the theory of lists (Reference Bird1986), magisterially directing the author to David Turner instead. Be that as it may, the author got to revisit many classics with a more mature eye, starting with Bird’s theory of lists.
Richard Bird was such a keen giant (Reference Bird2010).
2 Bird and Wadler’s duality theorems, revisited
For completeness, let us review Bird and Wadler’s three duality theorems (Reference Bird and Wadler1988), starting with the swapped definition of list_fold_left:

In the spirit of swapping, we start with the third theorem, since our Eureka lemma for the the second uses it, and we finish with the first, since it is a corollary of the second.
2.1 The third duality theorem, revisited
The third duality theorem says that folding left over a list is equivalent to folding right over the reverse of this list and that folding left over the reverse of a list is equivalent to folding right over this list, a property that Burge and Landin were familiar with (Burge, Reference Burge1975). So this theorem is stated in two ways:

Either version is proved by routine induction, and the other is proved as a corollary, using the extensionality axiom for functions (see Sec. 1.6) to account for the swapping.
2.2 The second duality theorem, revisited
The second duality theorem is about folding left and right over lists:

Without the swap, this theorem is proved by routine induction. With the swap, a Eureka lemma is required, e.g., the following one about folding left and right over the concatenation of two lists:

This lemma is proved by induction on v2s, using the third duality theorem as well as the following characterizations of applying a fold function to the concatenation of two lists:

The Eureka in this lemma is that when reasoning about
rather than trying to relate w in the left-hand side and the context of the call to list_fold_right in the right-hand side, as done in Sec. 1.7.3 to abstract a recursive function into an instance of a fold-left function, we are better off reasoning about the calls to list_fold_left_swapped and to list_fold_right that constructed w and this context, reflectively.
2.3 The first duality theorem, revisited
Bird and Wadler characterized the first duality theorem as a corollary of the second where V and W are the same type and opl and opr are the same operator, which is associative. The following statement is slightly tighter than the original, in that W, the base-case parameter, and the induction-step parameter, rather than forming a monoid, only need to form a semi group with a commuting element, since there is no need for the base-case parameter to be neutral. The proof is tighter too:

An impressive point about the first duality theorem is that op is not required to be commutative – only to have a commuting element, a.








Discussions
No Discussions have been published for this article.