Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-17T08:42:41.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Implementing a normalizer using sized heterogeneous types

Part of: JFP Research Articles

Published online by Cambridge University Press:  01 July 2009

ANDREAS ABEL
ANDREAS ABEL*
Affiliation:
Institut für Informatik, Ludwig-Maximilians-Universität München, Oettingenstraße 67, D-80538 München, Germany (e-mail: andreas.abel@ifi.lmu.de)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the simply typed λ-calculus, a hereditary substitution replaces a free variable in a normal form r by another normal form s of type a, removing freshly created redexes on the fly. It can be defined by lexicographic induction on a and r, thus giving rise to a structurally recursive normalizer for the simply typed λ-calculus. We implement hereditary substitutions in a functional programming language with sized heterogeneous inductive types 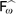, arriving at an interpreter whose termination can be tracked by the type system of its host programming language.

Type
Articles
Information
Journal of Functional Programming , Volume 19 , Issue 3-4 , July 2009 , pp. 287 - 310
Copyright
Copyright © Cambridge University Press 2009

References

Abel, A. (2004) Termination checking with types, Theor. Inform. Appl., 38 (4): 277–319.CrossRefGoogle Scholar
Abel, A. (2006a) Implementing a normalizer using sized heterogeneous types. In Proceedings of the Workshop on Mathematically Structured Functional Programming, MSFP 2006 (Kuressaare, July 2006), McBride, C. & Uustalu, T. (eds), Electronic Workshops in Computing. BCS.Google Scholar
Abel, A. (2006b) A Polymorphic Lambda-Calculus with Sized Higher-Order Types, PhD thesis. Ludwig-Maximilians-Universität München.Google Scholar
Abel, A. (2006c) Semi-continuous sized types and termination. In Proceedings of the 20th International Workshop on Computer Science Logic, CSL 2006 (Szeged, September 2006), Ésik, Z. (ed), Lecture Notes in Computer Science, vol. 4207. Springer, pp. 72–88.Google Scholar
Abel, A. (2008) Normalization for the simply-typed lambda-calculus in Twelf. In Proceedings of the 4th International Workshop on Logical Frameworks and Meta-Languages, LFM 2004 (Cork, July 2004), Schürmann, C. (ed), Electronic Notes in Theoretical Computer Science, vol. 199. Elsevier, pp. 3–16.Google Scholar
Adams, R. (2006) Formalized metatheory with terms represented by an indexed family of types. In Revised Selected Papers from 1st International Workshop on Types for Proofs and Programs, TYPES 2004 (Jouy-en-Josas, December 2004), Filliâtre, J.-C., Paulin-Mohring, C. & Werner, B. (eds), Lecture Notes in Computer Science, vol. 3839. Springer, pp. 1–16.Google Scholar
Altenkirch, T. (1993) A formalization of the strong normalization proof for System F in LEGO. In Proceedings of the 1st International Conference on Typed Lambda Calculi and Applications, TLCA '93 (Utrecht, March 1993), Bezem, M. & Groote, J. F. (eds), Lecture Notes in Computer Science, vol. 664. Springer, pp. 13–28.CrossRefGoogle Scholar
Altenkirch, T. & Reus, B. (1999) Monadic presentations of lambda terms using generalized inductive types. In Proceedings of the 13th International Workshop on Computer Science Logic, CSL '99 (Madrid, September 1999), Flum, J. & Rodríguez-Artalejo, M. (eds), Lecture Notes in Computer Science, vol. 1683. Springer, pp. 453–468.Google Scholar
Amadio, R. & Coupet-Grimal, S. (1998) Analysis of a guard condition in type theory (extended abstract). In Proceedings of the 1st International Conference on Foundations of Software Science and Computation Structures, FoSSaCS '98 (Lisbon, March/April 1998), Nivat, M. (ed), Lecture Notes in Computer Science, vol. 1378. Springer, pp. 48–62.CrossRefGoogle Scholar
Barthe, G., Frade, M. J., Giménez, E., Pinto, L. & Uustalu, T. (2004) Type-based termination of recursive definitions, Math. Struct Comp. Sci., 14 (1): 97–141.CrossRefGoogle Scholar
Barthe, G., Grégoire, B. & Pastawski, F. (2005) Practical inference for type-based termination in a polymorphic setting. In Proceedings of the 7th International Conference on Typed Lambda Calculi and Applications, TLCA 2005 (Nara, April 2005), Urzyczyn, P. (ed), Lecture Notes in Computer Science, vol. 3461. Springer, pp. 71–85.Google Scholar
Barthe, G., Grégoire, B. & Pastawski, F. (2006) : Type-based termination of recursive definitions in the calculus of inductive constructions. In Proceedings of the 13th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning, LPAR 2006 (Phnom Penh, November 2006), Hermann, M. & Voronkov, A. (eds), Lecture Notes in Artificial Intelligence, vol. 4246. Springer, pp. 257–271.Google Scholar
Bellegarde, F. & Hook, J. (1994) Substitution: A formal methods case study using monads and transformations, Sci. Comput. Program., 23 (2–3): 287–311.CrossRefGoogle Scholar
Berghofer, S. (2006) Extracting a normalization algorithm in Isabelle/HOL. In Revised Selected Papers from 1st International Workshop on Types for Proofs and Programs, TYPES 2004 (Jouy-en-Josas, December 2004), Filliâtre, J.-C., Paulin-Mohring, C. & Werner, B. (eds), Lecture Notes in Computer Science, vol. 3839. Springer, pp. 50–65.Google Scholar
Bird, R. S. & Paterson, R. (1999) De Bruijn notation as a nested datatype, J. Funct. Program., 9 (1): 77–91.CrossRefGoogle Scholar
Blanqui, F. (2004) A type-based termination criterion for dependently-typed higher-order rewrite systems. In Proceedings of the 15th International Conference on Rewriting Techniques and Applications, RTA 2004 (Aachen, June 2004), van Oostrom, V. (ed), Lecture Notes in Computer Science, vol. 3091. Springer, pp. 24–39.Google Scholar
Blanqui, F. (2005) Decidability of type-checking in the Calculus of Algebraic Constructions with size annotations. In Proceedings of the 19th International Workshop on Computer Science Logic, CSL 2005 (Oxford, August 2005), Ong, C.-H. L. (ed), Lecture Notes in Computer Science, vol. 3634. Springer, pp. 135–150.Google Scholar
David, R. & Nour, K. (2005) Arithmetical proofs of strong normalization results for the symmetric lambda-mu-calculus. In Proceedings of the 7th International Conference on Typed Lambda Calculi and Applications, TLCA 2005 (Nara, April 2005), Urzyczyn, P. (ed), Lecture Notes in Computer Science, vol. 3461. Springer, pp. 162–178.Google Scholar
Gentzen, G. (1935) Untersuchungen über das logische Schließen, Math. Z., 39, 176–210: 405–431. English translation (1969) in The Collected Papers of Gerhard Gentzen, Szabo, M. E. (ed), North-Holland, pp. 68–131.Google Scholar
Giménez, E. (1998) Structural recursive definitions in type theory. In Proceedings of the 25th International Colloquium on Automata, Languages and Programming, ICALP '98 (Aalborg, July 1998), Larsen, K. G., Skyum, S. & Winskel, G. (eds), Lecture Notes in Computer Science, vol. 1443. Springer, pp. 397–408.Google Scholar
Harper, R. & Licata, D. (2007) Mechanizing metatheory in a logical framework, J. Funct. Program., 17 (4–5): 613–673.CrossRefGoogle Scholar
Hughes, J., Pareto, L. & Sabry, A. (1996) Proving the correctness of reactive systems using sized types. In Conference Record of 23rd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL '96 (St. Petersburg Beach, FL, January 1996). ACM Press, pp. 410–423.Google Scholar
INRIA. (2009) The Coq proof assistant, version 8.2 [online]. Available at: http://www.lix.polytechnique.fr/coq (Accessed 4 May 2009).Google Scholar
Joachimski, F. & Matthes, R. (2003) Short proofs of normalization, Arch. Math. Logic, 42 (1): 59–87.CrossRefGoogle Scholar
Mac Lane, S. (1971) Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5. Springer.CrossRefGoogle Scholar
Manes, E. G. (1976) Algebraic Theories, Graduate Texts in Mathematics, vol. 26. Springer.CrossRefGoogle Scholar
McBride, C. (2006) Type-Preserving Renaming and Substitution. Manuscript.Google Scholar
Mendler, N. P. (1987) Recursive types and type constraints in second-order lambda calculus. In Proceedings of the 2nd Annual IEEE Symposium on Logic in Computer Science, LICS '87 (Ithaca, NY, June 1987). IEEE CS Press, pp. 30–36.Google Scholar
Mendler, N. P. (1991) Inductive types and type constraints in the second-order lambda calculus, Ann. Pure Appl. Logic, 51 (1–2): 159–172.CrossRefGoogle Scholar
Pareto, L. (2000) Types for Crash Prevention, PhD thesis. Chalmers University of Technology.Google Scholar
Prawitz, D. (1965) Natural Deduction: A Proof-Theoretic Study, Stockholm Studies in Philosophy, vol. 3. Almqvist & Wiksell.Google Scholar
Tait, W. W. (1967) Intensional interpretations of functionals of finite type I, J. Symb. Logic, 32 (2): 198–212.CrossRefGoogle Scholar
Watkins, K., Cervesato, I., Pfenning, F. & Walker, D. (2004) A concurrent logical framework: the propositional fragment. In Revised Selected Papers from 3rd International Workshop on Types for Proofs and Programs, TYPES 2003 (Torino, April/May 2003), Berardi, S., Coppo, M. & Damiani, F. (eds), Lecture Notes in Computer Science, vol. 3085. Springer, pp. 355–377.CrossRefGoogle Scholar
Submit a response

Discussions

No Discussions have been published for this article.