1 Introduction
Given a string of parentheses, the task is to find a longest consecutive segment that is balanced. For example, for input "))(()())())()(" the output should be "(()())()". We also consider a reduced version of the problem in which we return only the length of the segment. While there is no direct application of this problem, Footnote 1 the authors find it interesting because it involves two techniques. Firstly, derivation for such optimal segment problems (those whose goal is to compute a segment of a list that is optimal up to certain criteria) usually follows a certain pattern (e.g. Bird Reference Bird and Broy1987; Zantema Reference Zantema1992; Gibbons Reference Gibbons1997). We would like to see how well that works for this case. Secondly, at one point, we will need to construct the right inverse of a function. It will turn out that we will discover an instance of shift-reduce parsing.
Specification Balanced parentheses can be captured by a number of grammars, for example,
![]() ${\textsf{S}\rightarrow \epsilon\mid (\textsf{S})\mid \textsf{SS}}$, or
${\textsf{S}\rightarrow \epsilon\mid (\textsf{S})\mid \textsf{SS}}$, or
![]() ${\textsf{S}\rightarrow \textsf{T}^{*}}$ and
${\textsf{S}\rightarrow \textsf{T}^{*}}$ and
![]() ${\textsf{T}\rightarrow (\textsf{S})}$. After trying some of them, the authors decided on
${\textsf{T}\rightarrow (\textsf{S})}$. After trying some of them, the authors decided on
![]() $\textsf{S}\rightarrow \epsilon\mid (\textsf{S})\;\textsf{S},$
$\textsf{S}\rightarrow \epsilon\mid (\textsf{S})\;\textsf{S},$
because it is unambiguous and the most concise. Other grammars have worked too, albeit leading to lengthier algorithms. The parse tree of the chosen grammar can be represented in Haskell as below, with a function pr specifying how a tree is printed:
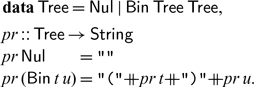
For example, letting
![]() ${{t}_{1}{=}\textsf{Bin}\;\textsf{Nul}\;\textsf{Nul}}$ and
${{t}_{1}{=}\textsf{Bin}\;\textsf{Nul}\;\textsf{Nul}}$ and
![]() ${{t}_{2}{=}\textsf{Bin}\;\textsf{Nul}\;(\textsf{Bin}\;\textsf{Nul}\;\textsf{Nul})}$, we have
${{t}_{2}{=}\textsf{Bin}\;\textsf{Nul}\;(\textsf{Bin}\;\textsf{Nul}\;\textsf{Nul})}$, we have![]() and
and![]() (parentheses are coloured to aid the reader).
(parentheses are coloured to aid the reader).
Function pr is injective but not surjective: it does not yield unbalanced strings. Therefore its right inverse, that is, the function
![]() ${{pr}^{{-1}}}$ such that
${{pr}^{{-1}}}$ such that
![]() ${{pr}\;({{pr}}^{{-1}}\;{xs}){=}{xs}}$, is partial; its domain is the set of balanced parenthesis strings. We implement it by a function that is made total by using the
${{pr}\;({{pr}}^{{-1}}\;{xs}){=}{xs}}$, is partial; its domain is the set of balanced parenthesis strings. We implement it by a function that is made total by using the
![]() ${\textsf{Maybe}}$ monad. This function
${\textsf{Maybe}}$ monad. This function
![]() ${{parse}{::}\textsf{String}\rightarrow \textsf{Maybe}\;\textsf{Tree}}$ builds a parse tree—
${{parse}{::}\textsf{String}\rightarrow \textsf{Maybe}\;\textsf{Tree}}$ builds a parse tree—
![]() ${{parse}\;{xs}}$ should return
${{parse}\;{xs}}$ should return
![]() ${\textsf{Just}\;{t}}$ such that
${\textsf{Just}\;{t}}$ such that
![]() ${{pr}\;{t}{=}{xs}}$ if
${{pr}\;{t}{=}{xs}}$ if
![]() ${{xs}}$ is balanced and return
${{xs}}$ is balanced and return
![]() ${\textsf{Nothing}}$ otherwise. While this defines
${\textsf{Nothing}}$ otherwise. While this defines
![]() ${{parse}}$ already, a direct definition of
${{parse}}$ already, a direct definition of
![]() ${{parse}}$ will be presented in Section 4.
${{parse}}$ will be presented in Section 4.
The problem can then be specified as below, where
![]() ${{lbs}}$ stands for “longest balanced segment (of parentheses)”:
${{lbs}}$ stands for “longest balanced segment (of parentheses)”:

The function
![]() ${{segments}{::}[ {a}]\rightarrow [ [ {a}]]}$ returns all segments of a list, with inits,tails::[ a]
${{segments}{::}[ {a}]\rightarrow [ [ {a}]]}$ returns all segments of a list, with inits,tails::[ a]
![]() $\rightarrow$ [[a]], respectively, computing all prefixes and suffixes of their input lists. The result of map parse is passed to filtJust ::[
$\rightarrow$ [[a]], respectively, computing all prefixes and suffixes of their input lists. The result of map parse is passed to filtJust ::[
![]() $\textsf{Maybe}$ a]
$\textsf{Maybe}$ a]
![]() $\rightarrow$ [ a], which collects only those elements wrapped by
$\rightarrow$ [ a], which collects only those elements wrapped by
![]() $\textsf{Just}$. For example, filtJust [
$\textsf{Just}$. For example, filtJust [
![]() $\textsf{Just}$ 1,
$\textsf{Just}$ 1,
![]() $\textsf{Nothing}$,
$\textsf{Nothing}$,
![]() $\textsf{Just}$ 2]=[ 1,2].
Footnote 2 For this problem filtJust always returns a non-empty list, because the empty string, which is a member of segments xs for any xs, can always be parsed to
$\textsf{Just}$ 2]=[ 1,2].
Footnote 2 For this problem filtJust always returns a non-empty list, because the empty string, which is a member of segments xs for any xs, can always be parsed to
![]() $\textsf{Just}$
$\textsf{Just}$
![]() $\textsf{Nul}$. Given f::a
$\textsf{Nul}$. Given f::a
![]() $\rightarrow$ b where b is a type that is ordered, maxBy f::[ a]
$\rightarrow$ b where b is a type that is ordered, maxBy f::[ a]
![]() $\rightarrow$ a picks a maximum element from the input. Finally, size t computes the length of pr t.
$\rightarrow$ a picks a maximum element from the input. Finally, size t computes the length of pr t.
The length-only problem can be specified by lbsl=size
![]() $\cdot$
lbs.
$\cdot$
lbs.
2 The prefix–suffix decomposition
It is known that many optimal segment problems can be solved by following a fixed pattern (Bird Reference Bird and Broy1987; Zantema Reference Zantema1992; Gibbons Reference Gibbons1997), which we refer to as prefix–suffix decomposition. In the first step, finding an optimal segment is factored into finding, for each suffix, an optimal prefix. For our problem, the calculation goes

For each suffix returned by tails, the program above computes its longest prefix of balanced parentheses by maxBy size
![]() $\cdot$
filtJust
$\cdot$
filtJust
![]() $\cdot$
map parse
$\cdot$
map parse
![]() $\cdot$
inits. We abbreviate the latter to lbp (for “longest balanced prefix”).
$\cdot$
inits. We abbreviate the latter to lbp (for “longest balanced prefix”).
Generating every suffix and computing lbp for each of them is rather costly. The next step is to try to apply the following scan lemma, which says that if a function f can be expressed as right fold, there is a more efficient algorithm to compute map f
![]() $\cdot$
tails:
$\cdot$
tails:
Lemma 2.1 map (foldr (
![]() $\oplus$) e)
$\oplus$) e)
![]() $\cdot$tails=scanr (
$\cdot$tails=scanr (
![]() $\oplus$) e, where
$\oplus$) e, where
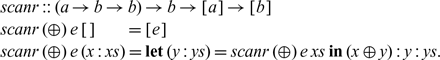
If lbp can be written in the form foldr (⊕) e, we do not need to compute lbp of each suffix from scratch; each optimal prefix can be computed, in scanr, from the previous optimal prefix by (⊕). If (
![]() $\oplus$) is a constant-time operation, we get a linear-time algorithm.
$\oplus$) is a constant-time operation, we get a linear-time algorithm.
The next challenge is therefore to express lbp as a right fold. Since inits can be expressed as a right fold—![]() , a reasonable attempt is to fuse maxBy size
, a reasonable attempt is to fuse maxBy size
![]() $\cdot$
filtJust
$\cdot$
filtJust
![]() $\cdot$
map parse with inits, to form a single foldr. Recall the foldr-fusion theorem:
$\cdot$
map parse with inits, to form a single foldr. Recall the foldr-fusion theorem:
Theorem 2.2 ![]() .
.
The antecedent h (f x y)=g x (h y) will be referred to as the fusion condition. To fuse map parse and inits using Theorem 2.2, we calculate from the LHS of the fusion condition (with h=map parse and f=(
![]() $\lambda$ x xss
$\lambda$ x xss
![]() $\rightarrow$ [ ]:map (x:) xss)):
$\rightarrow$ [ ]:map (x:) xss)):

We can construct g if (and only if) there is a function g’ such that g’ x (map parse xss)=map (parse
![]() $\cdot$(x:)) xss. Is that possible?
$\cdot$(x:)) xss. Is that possible?
It is not hard to see that the answer is no. Consider xss=[ ")", ")()"] and x= ’(’. Since both strings in xss are not balanced, map parse xss gives us [
![]() $\textsf{Nothing}$,
$\textsf{Nothing}$,
![]() $\textsf{Nothing}$]. However, map (x:) xss=[ "()", "()()"], a list of balanced strings. Therefore, g’ has to produce something from nothing—an impossible task. We have to generalise our problem such that g’ receives inputs that are more informative.
$\textsf{Nothing}$]. However, map (x:) xss=[ "()", "()()"], a list of balanced strings. Therefore, g’ has to produce something from nothing—an impossible task. We have to generalise our problem such that g’ receives inputs that are more informative.
3 Partially balanced strings
A string of parentheses is said to be left-partially balanced if it may possibly be balanced by adding zero or more parentheses to the left. For example,![]() is left-partially balanced because
is left-partially balanced because![]() is balanced—again we use colouring to help the reader parsing the string. Note that
is balanced—again we use colouring to help the reader parsing the string. Note that![]() is also balanced. For a counter example, the string
is also balanced. For a counter example, the string![]() is not left-partially balanced—due to the unmatched
is not left-partially balanced—due to the unmatched![]() in the middle of ys, there is no zs such that zs++ys can be balanced.
in the middle of ys, there is no zs such that zs++ys can be balanced.
While parsing a fully balanced string cannot be expressed as a right fold, it is possible to parse left-partially balanced strings using a right fold. In this section, we consider what data structure such a string should be parsed to. We discuss how to how to parse it in the next section.
A left-partially balanced string can always be uniquely factored into a sequence of fully balanced substrings, separated by one or more right parentheses. For example, xs can be factored into two balanced substrings,![]() and
and![]() , separated by
, separated by![]() . One of the possible ways to represent such a string is by a list of trees—a
. One of the possible ways to represent such a string is by a list of trees—a
![]() $\textsf{Forest}$, where the trees are supposed to be separated by a ‘)’. That is, such a forest can be printed by:
$\textsf{Forest}$, where the trees are supposed to be separated by a ‘)’. That is, such a forest can be printed by:

For example,![]() can be represented by a forest containing three trees:
can be represented by a forest containing three trees:
![]()
where![]() prints to
prints to![]() prints to
prints to![]() , and there is a
, and there is a
![]() $\textsf{Nul}$ between them due to the consecutive right parentheses
$\textsf{Nul}$ between them due to the consecutive right parentheses![]() in xs (
in xs (
![]() $\textsf{Nul}$ itself prints to " "). One can verify that prF ts=xs indeed. Note that we let the type
$\textsf{Nul}$ itself prints to " "). One can verify that prF ts=xs indeed. Note that we let the type
![]() $\textsf{Forest}$ be non-empty lists of trees.
Footnote 3 The empty string can be represented by [
$\textsf{Forest}$ be non-empty lists of trees.
Footnote 3 The empty string can be represented by [
![]() $\textsf{Nul}$], since prF [
$\textsf{Nul}$], since prF [
![]() $\textsf{Nul}$]=pr
$\textsf{Nul}$]=pr
![]() $\textsf{Nul}$="".
$\textsf{Nul}$="".
The aim now is to construct the right inverse of prF, such that a left-partially balanced string can be parsed using a right fold.
4 Parsing partially balanced strings
Given a function f::b
![]() $\rightarrow$ t, the converse-of-a-function theorem (Bird & de Moor Reference Bird and de Moor1997; de Moor & Gibbons Reference de Moor, Gibbons and Rus2000) constructs the relational converse—a generalised notion of inverse—of f. The converse is given as a relational fold whose input type is t, which can be any inductively defined datatype with a polynomial base functor. We specialise the general theorem to our needs: we use it to construct only functions, not relations, and only for the case where t is a list type.
$\rightarrow$ t, the converse-of-a-function theorem (Bird & de Moor Reference Bird and de Moor1997; de Moor & Gibbons Reference de Moor, Gibbons and Rus2000) constructs the relational converse—a generalised notion of inverse—of f. The converse is given as a relational fold whose input type is t, which can be any inductively defined datatype with a polynomial base functor. We specialise the general theorem to our needs: we use it to construct only functions, not relations, and only for the case where t is a list type.
Theorem 4.1 Given f::b
![]() $\rightarrow$ [ a], if we have base::b and step::a
$\rightarrow$ [ a], if we have base::b and step::a
![]() $\rightarrow$ b
$\rightarrow$ b
![]() $\rightarrow$ b satisfying:
$\rightarrow$ b satisfying:
![]() then
then
![]() $f^{-1}=foldr step base$ is a partial right inverse of f. That is, we have
$f^{-1}=foldr step base$ is a partial right inverse of f. That is, we have
![]() $f(f^{-1}xs)=xs$ for all xs in the range of f.
$f(f^{-1}xs)=xs$ for all xs in the range of f.
While the general version of the theorem is not trivial to prove, the version above, specialised to functions and lists, can be verified by an easy induction on the input list.
Recall that we wish to construct the right inverse of prF using Theorem 4.1. It will be easier if we first construct a new definition of prF, one that is inductive, does not use (++) and does not rely on pr. For a base case, prF [
![]() $\textsf{Nul}$]="". It is also immediate that prF (
$\textsf{Nul}$]="". It is also immediate that prF (
![]() $\textsf{Nul}$:ts)= ’)’:prF ts. When the list contains more than one tree and the first tree is not
$\textsf{Nul}$:ts)= ’)’:prF ts. When the list contains more than one tree and the first tree is not
![]() $\textsf{Nul}$, we calculate
$\textsf{Nul}$, we calculate

We have thus derived the following new definition of prF:
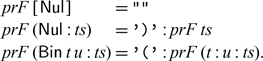
We are now ready to invert prF by Theorem 4.1, which amounts to finding base and step such that prF base= and prF (step x ts)=x:prF ts for x= ’(’ or ’)’.
With the inductive definition of prF in mind, we pick base=[
![]() $\textsf{Nul}$], and the following step meets the requirement:
$\textsf{Nul}$], and the following step meets the requirement:
![]()
We have thus constructed
![]() ${{{prF}}^{{-1}}{=}{foldr}\;{step}\;[{Nul}]}$. If we expand the definitions, we have
${{{prF}}^{{-1}}{=}{foldr}\;{step}\;[{Nul}]}$. If we expand the definitions, we have
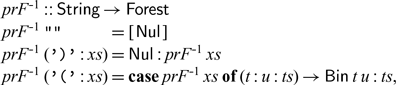
which is pleasingly symmetrical to the inductive definition of prF.
For an operational explanation, a right parenthesis ’)’ indicates starting a new tree, thus we start freshly with a
![]() $\textsf{Nul}$; a left parenthesis ’(’ ought to be the leftmost symbol of some "(t)u", thus we wrap the two most recent siblings into one tree. When there are no such two siblings (i.e.
$\textsf{Nul}$; a left parenthesis ’(’ ought to be the leftmost symbol of some "(t)u", thus we wrap the two most recent siblings into one tree. When there are no such two siblings (i.e.
![]() $prF^{-1}$ xs in the case expression evaluates to a singleton list), the input ’(’:xs is not a left-partially balanced string— ’(’ appears too early, and the result is undefined.
$prF^{-1}$ xs in the case expression evaluates to a singleton list), the input ’(’:xs is not a left-partially balanced string— ’(’ appears too early, and the result is undefined.
Readers may have noticed the similarity to shift-reduce parsing, in which, after reading a symbol we either “shift” the symbol by pushing it onto a stack, or “reduce” the symbol against a top segment of the stack. Here, the forest is the stack. The input is processed right-to-left, as opposed to left-to-right, which is more common when talking about parsing. We shall discuss this issue further in Section 7.
We could proceed to work with
![]() $prF^{-1}$ for the rest of this pearl but, for clarity, we prefer to make the partiality explicit. Let parseF be the monadified version of
$prF^{-1}$ for the rest of this pearl but, for clarity, we prefer to make the partiality explicit. Let parseF be the monadified version of
![]() $prF^{-1}$, given by:
$prF^{-1}$, given by:

where stepM is monadified step—for the case [ t] missing in step we return
![]() $\textsf{Nothing}$.
$\textsf{Nothing}$.
To relate parseF to parse, notice that prF [ t]=pr t. We therefore have

where
![]() $\nLeftarrow$::(b
$\nLeftarrow$::(b
![]() $\rightarrow$
$\rightarrow$
![]() $\textsf{M}$ c)
$\textsf{M}$ c)
![]() $\rightarrow$ (a
$\rightarrow$ (a
![]() $\rightarrow$
$\rightarrow$
![]() $\textsf{M}$ b)
$\textsf{M}$ b)
![]() $\rightarrow$ (a
$\rightarrow$ (a
![]() $\rightarrow$
$\rightarrow$
![]() $\textsf{M}$ c) is (reversed) Kleisli composition. That is, parse calls parseF and declares success only when the input can be parsed into a single tree.
$\textsf{M}$ c) is (reversed) Kleisli composition. That is, parse calls parseF and declares success only when the input can be parsed into a single tree.
5 Longest balanced prefix in a fold
Recall our objective at the close of Section 2: to compute lbp=maxBy size
![]() $\cdot$
filtJust
$\cdot$
filtJust
![]() $\cdot$
map parse
$\cdot$
map parse
![]() $\cdot$
inits in a right fold in order to obtain a faster algorithm using the scan lemma. Now that we have
$\cdot$
inits in a right fold in order to obtain a faster algorithm using the scan lemma. Now that we have![]() where parseF is a right fold, and we perform some initial calculation whose purpose is to factor the post-processing unwrapM out of the main computation:
where parseF is a right fold, and we perform some initial calculation whose purpose is to factor the post-processing unwrapM out of the main computation:

In the penultimate step![]() is moved leftwards past filtJust and becomes unwrap::
is moved leftwards past filtJust and becomes unwrap::
![]() $\textsf{Forest}$
$\textsf{Forest}$
![]() $\rightarrow$
$\rightarrow$
![]() $\textsf{Tree}$, defined by:
$\textsf{Tree}$, defined by:
![]()
Recall that inits=foldr (
![]() $\lambda$ x xss
$\lambda$ x xss
![]() $\rightarrow$ [ ]:map (x:) xss) [ [ ]]. The aim now is to fuse map parseF, filtJust and maxBy (size
$\rightarrow$ [ ]:map (x:) xss) [ [ ]]. The aim now is to fuse map parseF, filtJust and maxBy (size
![]() $\cdot$
unwrap) with inits.
$\cdot$
unwrap) with inits.
By Theorem 2.2, to fuse map parseF with inits, we need to construct g that meets the fusion condition:
![]()
Now that we know that parseF is a fold, the calculation goes

Therefore, we have

Next, we fuse filtJust with map parseF
![]() $\cdot$
inits by Theorem 2.2. After some calculations, we get
$\cdot$
inits by Theorem 2.2. After some calculations, we get

After the fusion, we need not keep the
![]() $\textsf{Nothing}$ entries in the fold; the computation returns a collection of forests. If the next character is ’)’, we append
$\textsf{Nothing}$ entries in the fold; the computation returns a collection of forests. If the next character is ’)’, we append
![]() $\textsf{Nul}$ to every forest. If the next entry is ’(’, we choose those forests having at least two trees and combine them—the list comprehension keeps only the forests that match the pattern (t:u:ts) and throws away those do not. Note that [
$\textsf{Nul}$ to every forest. If the next entry is ’(’, we choose those forests having at least two trees and combine them—the list comprehension keeps only the forests that match the pattern (t:u:ts) and throws away those do not. Note that [
![]() $\textsf{Nul}$], to which the empty string is parsed, is always added to the collection of forests.
$\textsf{Nul}$], to which the empty string is parsed, is always added to the collection of forests.
To think about how to deal with unwrap
![]() $\cdot$
maxBy (size
$\cdot$
maxBy (size
![]() $\cdot$
unwrap), we consider an example. Figure 1 shows the results of map parseF and filtJust for prefixes of "())()(", where
$\cdot$
unwrap), we consider an example. Figure 1 shows the results of map parseF and filtJust for prefixes of "())()(", where
![]() $\textsf{Just}$,
$\textsf{Just}$,
![]() $\textsf{Nul}$ and
$\textsf{Nul}$ and
![]() $\textsf{Bin}$ are, respectively, abbreviated to
$\textsf{Bin}$ are, respectively, abbreviated to
![]() $\textsf{J}$,
$\textsf{J}$,
![]() $\textsf{N}$ and
$\textsf{N}$ and
![]() $\textsf{B}$. The function maxBy (size
$\textsf{B}$. The function maxBy (size
![]() $\cdot$
unwrap) chooses between [
$\cdot$
unwrap) chooses between [
![]() $\textsf{N}$] and [
$\textsf{N}$] and [
![]() $\textsf{B}$
$\textsf{B}$
![]() $\textsf{N}$
$\textsf{N}$
![]() $\textsf{N}$], the two parses resulting in single trees, and returns [
$\textsf{N}$], the two parses resulting in single trees, and returns [
![]() $\textsf{B}$
$\textsf{B}$
![]() $\textsf{N}$
$\textsf{N}$
![]() $\textsf{N}$]. However, notice that
$\textsf{N}$]. However, notice that
![]() $\textsf{B}$
$\textsf{B}$
![]() $\textsf{N}$
$\textsf{N}$
![]() $\textsf{N}$ is also the head of [
$\textsf{N}$ is also the head of [
![]() $\textsf{B}$
$\textsf{B}$
![]() $\textsf{N}$
$\textsf{N}$
![]() $\textsf{N}$,
$\textsf{N}$,
![]() $\textsf{B}$
$\textsf{B}$
![]() $\textsf{N}$
$\textsf{N}$
![]() $\textsf{N}$], the last forest returned by filtJust. In general, the largest singleton parse tree will also present in the head of the last forest returned by filtJust
$\textsf{N}$], the last forest returned by filtJust. In general, the largest singleton parse tree will also present in the head of the last forest returned by filtJust
![]() $\cdot$
map parseF
$\cdot$
map parseF
![]() $\cdot$
inits. One can intuitively see why: if we print them both, the former is a prefix of the latter. Therefore, unwrap
$\cdot$
inits. One can intuitively see why: if we print them both, the former is a prefix of the latter. Therefore, unwrap
![]() $\cdot$
maxBy (size
$\cdot$
maxBy (size
![]() $\cdot$
unwrap) can be replaced by head
$\cdot$
unwrap) can be replaced by head
![]() $\cdot$
last.
$\cdot$
last.
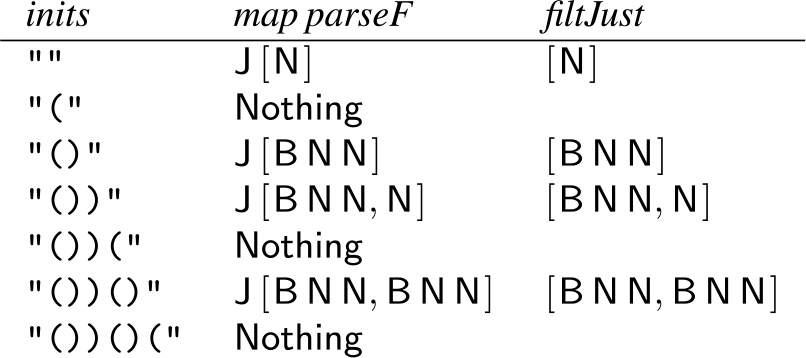
Figure 1. Results of parseF and filtJust for prefixes of "())()(".
To fuse last with filtJust
![]() $\cdot$
map parseF
$\cdot$
map parseF
![]() $\cdot$
inits by Theorem 2.2, we need to construct a function step that satisfies the fusion condition:
$\cdot$
inits by Theorem 2.2, we need to construct a function step that satisfies the fusion condition:
![]()
where tss is a non-empty list of forests. The case when x= ’)’ is easy—choosing step ’)’ ts=
![]() $\textsf{Nul}$:ts will do the job. For the case when x= ’(’ we need to analyse the result of last tss and use the property that forests in tss are ordered in ascending lengths.
$\textsf{Nul}$:ts will do the job. For the case when x= ’(’ we need to analyse the result of last tss and use the property that forests in tss are ordered in ascending lengths.
-
(a) If last tss=[ t], a forest having only one tree, there are no forest in tss that contains two or more trees. Therefore, extend ’(’ tss returns an empty list, and last ([
 $\textsf{Nul}$]:extend ’(’ tss)=[
$\textsf{Nul}$]:extend ’(’ tss)=[
 $\textsf{Nul}$].
$\textsf{Nul}$]. -
(b) Otherwise, extend ’(’ tss would not be empty, and last ([
 $\textsf{Nul}$]:extend x tss)=last (extend x tss). We may then combine the first two trees, as extend would do.
$\textsf{Nul}$]:extend x tss)=last (extend x tss). We may then combine the first two trees, as extend would do.
In summary, we have

which is now a total function on strings of parentheses.
The function derived above turns out to be
![]() $prF^{-1}$ with one additional case (step ’(’ [ t]=[
$prF^{-1}$ with one additional case (step ’(’ [ t]=[
![]() $\textsf{Nul}$]). What we have done in this section can be seen as justifying this extra case (which is a result of case (1) in the fusion of last), which is not as trivial as one might think.
$\textsf{Nul}$]). What we have done in this section can be seen as justifying this extra case (which is a result of case (1) in the fusion of last), which is not as trivial as one might think.
6 Wrapping up
We can finally resume the main derivation in Section 2:

We have therefore derived:
![]()
where step is as defined in the end of Section 5. To avoid recomputing the sizes in maxBy size, we can annotate each tree by its size: letting
![]() $\textsf{Forest}$=[ (
$\textsf{Forest}$=[ (
![]() $\textsf{Tree}$,
$\textsf{Tree}$,
![]() $\textsf{Int}$)], resulting in an algorithm that runs in linear time:
$\textsf{Int}$)], resulting in an algorithm that runs in linear time:

Finally, the size-only version can be obtained by fusing size into lbs. It turns out that we do not need to keep the actual trees, but only their sizes—
![]() $\textsf{Forest}$=[
$\textsf{Forest}$=[
![]() $\textsf{Int}$]:
$\textsf{Int}$]:

We ran some simple experiments to measure the efficiency of the algorithm. The test machine was a laptop computer with a Apple M1 chip (8 core, 3.2GHz) and 16GB RAM. We ran lbs on randomly generated inputs containing 1, 2, 4, 6, 8 and 10 million parentheses and measured the user times. The results, shown in Figure 2, confirmed the linear-time behaviour.

Figure 2. Measured running time for some input sizes.
7 Conclusions and discussions
So we have derived a linear-time algorithm for solving the problem. We find it an interesting journey because it relates two techniques: prefix–suffix decomposition for solving segment problems and the converse-of-a-function theorem for program inversion.
In Section 3, we generalised from trees to forests. Generalisations are common when applying the converse-of-a-function theorem. It was observed that the trees in a forest are those along the left spine of the final tree; therefore, such a generalisation is referred to as switching to a “spine representation” (Mu & Bird Reference Mu and Bird2003).
What we derived in Sections 4 and 5 is a compacted form of shift-reduce parsing, where the input is processed right to left. The forest serves as the stack, but we do not need to push the parser state to the stack, as is done in shift-reduce parsing. If we were to process the input in the more conventional left-to-right order, the corresponding grammar would be
![]() $\textsf{S}\rightarrow \epsilon\mid\textsf{S}\;(\textsf{S})$. It is an SLR(1) grammar whose parse table contains five states. Our program is much simpler. A possible reason is that consecutive shifting and reducing are condensed into one step. It is likely that parsing SLR(1) languages can be done in a fold. The relationship between LR parsing and the converse-of-a-function theorem awaits further investigation.
$\textsf{S}\rightarrow \epsilon\mid\textsf{S}\;(\textsf{S})$. It is an SLR(1) grammar whose parse table contains five states. Our program is much simpler. A possible reason is that consecutive shifting and reducing are condensed into one step. It is likely that parsing SLR(1) languages can be done in a fold. The relationship between LR parsing and the converse-of-a-function theorem awaits further investigation.
There are certainly other ways to solve the problem. For example, one may interpret a ’(’ as a
![]() $-1$, and a ’)’ as a
$-1$, and a ’)’ as a
![]() $+1$. A left-partially balanced string would be a list whose right-to-left running sum is never negative. One may then apply the method in Zantema (Reference Zantema1992) to find the longest such prefix for each suffix. The result will be an algorithm that maintains the sum in a loop—an approach that might be more commonly adopted by imperative programmers. The problem can also be seen as an instance of maximum-marking problems—choosing elements in a data structure that meet a given criteria while maximising a cost function—to which methods of Sasano et al. (Reference Sasano, Hu and Takeichi2001) can be applied.
$+1$. A left-partially balanced string would be a list whose right-to-left running sum is never negative. One may then apply the method in Zantema (Reference Zantema1992) to find the longest such prefix for each suffix. The result will be an algorithm that maintains the sum in a loop—an approach that might be more commonly adopted by imperative programmers. The problem can also be seen as an instance of maximum-marking problems—choosing elements in a data structure that meet a given criteria while maximising a cost function—to which methods of Sasano et al. (Reference Sasano, Hu and Takeichi2001) can be applied.
Acknowledgements
The problem was suggested by Yi-Chia Chen. The authors would like to thank our colleagues in the PLFM group in IIS, Academia Sinica, in particular Hsiang-Shang ‘Josh’ Ko, Liang-Ting Chen and Ting-Yan Lai, for valuable discussions. Also thanks to Chung-Chieh Shan and Kim-Ee Yeoh for their advice on earlier drafts of this paper. We are grateful to the reviewers of previous versions of this article who gave detailed and constructive criticisms that helped a lot in improving this work.
Conflicts of interest
None.





Discussions
No Discussions have been published for this article.