Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-04T10:26:51.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Well-founded recursion with copatterns and sized types

Part of: JFP Research Articles

Published online by Cambridge University Press:  03 March 2016

ANDREAS ABEL  and
BRIGITTE PIENTKA
ANDREAS ABEL
Affiliation:
Department of Computer Science and Engineering, Gothenburg University, Sweden (e-mail: andreas.abel@gu.se)
BRIGITTE PIENTKA
Affiliation:
School of Computer Science, McGill University, Montreal, Canada (e-mail: bpientka@cs.mcgill.ca)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study strong normalization of a core language based on System 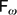${\mathsf{F}_\omega}$ which supports programming with finite and infinite structures. Finite data such as finite lists and trees is defined via constructors and manipulated via pattern matching, while infinite data such as streams and infinite trees is defined by observations and synthesized via copattern matching. Taking a type-based approach to strong normalization, we track size information about finite and infinite data in the type. We exploit the duality of pattern and copatterns to give a unifying semantic framework which allows us to elegantly and uniformly support both well-founded induction and coinduction by rewriting. The strong normalization proof is structured around Girard's reducibility candidates. As such, our system allows for non-determinism and does not rely on coverage. Since System 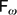${\mathsf{F}_\omega}$ is general enough that it can be the target of compilation for the Calculus of Constructions, this work is a significant step towards representing observation-based infinite data in proof assistants such as Coq and Agda.

Type
Articles
Information
Journal of Functional Programming , Volume 26 , 2016 , e2
Copyright
Copyright © Cambridge University Press 2016 

References

Abel, A. (2006) A Polymorphic Lambda-Calculus with Sized Higher-Order Types. Ph.D. thesis, Ludwig-Maximilians-Universität München.Google Scholar
Abel, A. (2008a) Polarized subtyping for sized types. Math. Struct. Comput. Sci. 18 (5), 797–822.Google Scholar
Abel, A. (2008b) Semi-continuous sized types and termination. Logical Meth. Comput. Sci. 4 (2:3), 1–33.Google Scholar
Abel, A. (2010) MiniAgda: Integrating sized and dependent types. In (Bove et al., 2010).Google Scholar
Abel, A. (2012) Type-based termination, inflationary fixed-points, and mixed inductive-coinductive types. In Proceedings of the 8th Wksh. on Fixed Points in Comp. Sci. (FICS 2012), Miller, D. & Ésik, Z. (eds), Electr. Proc. in Theor. Comp. Sci., vol. 77 pp. 1–11.Google Scholar
Abel, A., Pientka, B., Thibodeau, D. & Setzer, A. (2013) Copatterns: Programming infinite structures by observations. In Proceedings of the 40th ACM Symp. on Principles of Programming Languages, POPL 2013, Giacobazzi, R. & Cousot, R. (eds), ACM Press, pp. 27–38.Google Scholar
AgdaTeam. (2015) The Agda Wiki.Google Scholar
Altenkirch, T. & Danielsson, N. A. (2012) Termination checking in the presence of nested inductive and coinductive types. In Wksh. on Partiality And Recursion in Interactive Theorem Provers, PAR 2010, Bove, A., Komendantskaya, E. & Niqui, M. (eds), EPiC Series in Comput. Sci., vol. 5. EasyChair, pp. 101–106.Google Scholar
Amadio, R. M. & Coupet-Grimal, S. (1998) Analysis of a guard condition in type theory (extended abstract) In Proceedings of the 1st International Conference on Foundations of Software Science and Computation Structure, FoSSaCS'98, Nivat, M. (ed), Lect. Notes in Comput. Sci., vol. 1378. Springer, pp. 48–62.Google Scholar
Barthe, G., Frade, M. J., Giménez, E., Pinto, L. & Uustalu, T. (2004) Type-based termination of recursive definitions. Math. Struct. Comput. Sci. 14 (1), 97–141.Google Scholar
Barthe, G., Grégoire, B. & Pastawski, F. (2005) Practical inference for type-based termination in a polymorphic setting. In Proceedings of the 7th International Conference on Typed Lambda Calculi and Applications, TLCA 2005, Urzyczyn, P. (ed), Lect. Notes in Comput. Sci., vol. 3461. Springer, pp. 71–85.Google Scholar
Barthe, G., Grégoire, B. & Riba, C. (2008) Type-based termination with sized products. In Computer Science Logic, 22nd Int. Wksh., CSL 2008, 17th Annual Conf. of the EACSL, Kaminski, M. & Martini, S. (eds), Lect. Notes in Comput. Sci., vol. 5213. Springer, pp. 493–507.Google Scholar
Blanqui, F. (2004) A type-based termination criterion for dependently-typed higher-order rewrite systems. In Rewriting Techniques and Applications, RTA 2004, Aachen, Germany, van Oostrom, V. (ed), Lect. Notes in Comput. Sci., vol. 3091. Springer, pp. 24–39.Google Scholar
Blanqui, F. & Riba, C. (2006) Combining typing and size constraints for checking the termination of higher-order conditional rewrite systems. In Proceedings of the 13th Int. Conf. on Logic for Programming, Artificial Intelligence, and Reasoning, LPAR 2006, Hermann, M. & Voronkov, A. (eds), Lect. Notes in Comput. Sci., vol. 4246. Springer, pp. 105–119.Google Scholar
Bove, A., Komendantskaya, E. & Niqui, M. (eds). (2010) Wksh. on Partiality and Recursion in Interactive Theorem Provers, PAR 2010. Electr. Proc. in Theor. Comp. Sci., vol. 43.Google Scholar
Coquand, T. (1994) Infinite objects in type theory. In Types for Proofs and Programs, Int. Wksh., TYPES'93, Barendregt, H. & Nipkow, T. (eds), Lect. Notes in Comput. Sci., vol. 806. Springer, pp. 62–78.Google Scholar
Danielsson, N. A. (2010) Beating the productivity checker using embedded languages. In (Bove et al., 2010).CrossRefGoogle Scholar
Dybjer, P. (2000) A general formulation of simultaneous inductive-recursive definitions in type theory. J. Symb. Logic 65 (2), 525–549.Google Scholar
Ghani, N., Hancock, P. & Pattinson, D. (2009) Representations of stream processors using nested fixed points. Logical Meth. Comput. Sci. 5 (3:9) Google Scholar
Giménez, E. (1996) Un calcul de constructions infinies et son application a la vérification de systèmes communicants. Ph.D. thesis, Ecole Normale Supérieure de Lyon.Google Scholar
Girard, J.-Y., Lafont, Y. & Taylor, P. (1989) Proofs and Types. Cambridge Tracts in Theoret. Comput. Sci., vol. 7. Cambridge University Press.Google Scholar
Hughes, J., Pareto, L. & Sabry, A. (1996) Proving the correctness of reactive systems using sized types. In Proceedings of the 23rd ACM Symposium on Principles of Programming Languages, POPL'96, pp. 410–423.CrossRefGoogle Scholar
INRIA. (2012) The Coq Proof Assistant Reference Manual. Version 8.4 edn. INRIA.Google Scholar
Jones, G. & Gibbons, J. (1993) Linear-Time Breadth-fFrst Tree Algorithms: An Exercise in the Arithmetic of Folds and Zips. Technical Report, University of Auckland.Google Scholar
Mendler, N. P. (1987) Recursive types and type constraints in second-order lambda calculus. In Proceedings of the 2nd IEEE Symp. on Logic in Computer Science (LICS'87). IEEE Computer Soc. Press, pp. 30–36.Google Scholar
Oury, N. (2008) Coinductive Types and Type Preservation. Message on the Coq-club mailing list on 6 June 2008.Google Scholar
Pareto, L. (2000) Types for Crash Prevention. PhD Thesis, Chalmers University of Technology.Google Scholar
Reihl, F. (2013) Solving Size Constraints using Graph Representation. Bachelor's Thesis, Institut für Informatik, Ludwig-Maximilians-Universität München.Google Scholar
Sacchini, J. L. (2011) On Type-Based Termination and Pattern Matching in the Calculus of Inductive Constructions. PhD Thesis, INRIA Sophia-Antipolis and École des Mines de Paris.Google Scholar
Sacchini, J. L. (2013) Type-based productivity of stream definitions in the calculus of constructions. In Proceedings of the 28th IEEE Symposium on Logic in Computer Science (LICS'13). IEEE Computer Soc. Press, pp. 233–242.Google Scholar
Sijtsma, B. A. (1989) On the productivity of recursive list definitions. ACM Trans. Program. Lang. Syst. 11 (4), 633–649.Google Scholar
Sprenger, C. & Dam, M. (2003) On the structure of inductive reasoning: Circular and tree-shaped proofs in the μ-calculus. In Proceedings of the 6th International Conference on Foundations of Software Science and Computational Structures, FoSSaCS 2003, Gordon, A. D. (ed), Lect. Notes in Comput. Sci., vol. 2620. Springer, pp. 425–440.Google Scholar
Steffen, M. (1998) Polarized Higher-Order Subtyping. PhD Thesis, Technische Fakultät, Universität Erlangen.Google Scholar
Taylor, P. (1996) Intuitionistic sets and ordinals. J. Symb. Logic 61 (3), 705–744.Google Scholar
Vouillon, J. & Melliès, P.-A. (2004) Semantic types: A fresh look at the ideal model for types. In Proceedings of the 31st ACM Symp. on Principles of Programming Languages, POPL 2004. ACM Press, pp. 52–63.Google Scholar
Watkins, K., Cervesato, I., Pfenning, F. & Walker, D. (2003) A Concurrent Logical Framework I: Judgements and Properties. Technical Report. School of Computer Science, Carnegie Mellon University, Pittsburgh.Google Scholar
Xi, H. (2002) Dependent types for program termination verification. J. Higher-Order and Symb. Comput. 15 (1), 91–131.Google Scholar
Submit a response

Discussions

No Discussions have been published for this article.